Triage and monitoring of COVID-19 patients in intensive care using unsupervised machine learning

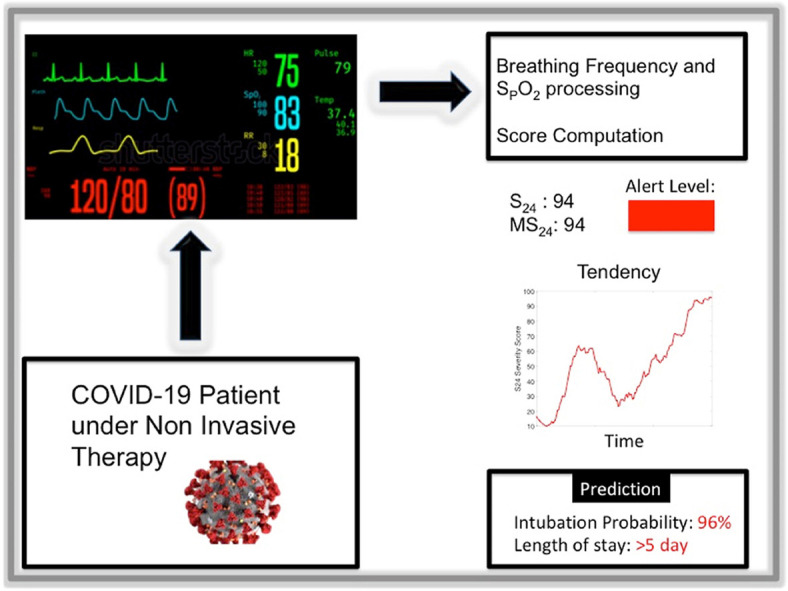
Abstract

Background

We designed an algorithm to assess COVID-19 patients severity and dynamic intubation needs and predict their length of stay using the breathing frequency (BF) and oxygen saturation (SpO₂) signals.

Methods

We recorded the BF and SpO₂ signals for confirmed COVID-19 patients admitted to the ICU of a teaching hospital during both the first and subsequent outbreaks of the pandemic in France. An unsupervised machine-learning algorithm (the Gaussian mixture model) was applied to the patients' data for clustering. The algorithm's robustness was ensured by comparing its results against actual intubation rates. We predicted intubation rates using the algorithm every hour, thus conducting a severity evaluation. We designed a S₂₄ severity score that represented the patient's severity over the previous 24 h; the validity of MS₂₄, the maximum S₂₄ score, was checked against rates of intubation risk and prolonged ICU stay.

Results

Our sample included 279 patients. . The unsupervised clustering had an accuracy rate of 87.8% for intubation recognition (AUC = 0.94, True Positive Rate 86.5%, true Negative Rate 90.9%). The S₂₄ score of intubated patients was significantly higher than that of non-intubated patients at 48 h before intubation. The MS₂₄ score allowed for the distinguishing between three severity levels with an increased risk of intubation: green (3.4%), orange (37%), and red (77%). A MS₂₄ score over 40 was highly predictive of an ICU stay greater than 5 days at an accuracy rate of 81.0% (AUC = 0.87).

Conclusions

Our algorithm uses simple signals and seems to efficiently visualize the patients' respiratory situations, meaning that it has the potential to assist staffs' in decision-making. Additionally, real-time computation is easy to implement.

Graphical abstract

1. Background

The rapid spread of coronavirus disease (COVID-19) challenged intensive care units (ICU) worldwide, and increases in cases may overwhelm ICU capacity [1,2]. This situation calls for the early screening and monitoring of these patients to distinguish those that are likely to worsen and should therefore be directed to intermediate care facilities or regular hospital wards. Therefore, in this study, we present a method that allows for the real-time analysis of respiratory signals using an AI algorithm for dynamic severity assessment. COVID-19 patients might experience profound, repeated hypoxia without requiring intubation. Indeed, prior to the pandemic, severely hypoxic patients were mostly treated via mechanical ventilation after intubation. Many COVID-19 patients are treated with high-flow oxygen therapy using a non-invasive method. Additionally, high flow oxygen therapy has proven to be efficient for COVID-19 pneumonia [[3], [4], [5]]. However, some patients may be over-treated with these methods, leading to delayed intubation, hence the interest in early potential failure detection.

Besides intubation prediction, the SAPS2 score seems unsuitable for severity assessment of COVID-19 patients. Indeed, this score is not suitable for these patients. Upon ICU admission, these patients generally present only one mild failure that then changes or worsens during the first days of their stay. The respiratory score is 0 for almost all patients at 24 h post-admission because more than 93% are not intubated. Therefore, all COVID-19 patients have the same SAPS2 respiratory score regardless of their future evolution. This means that standard scoring methods fail to accurately predict COVID-19 evolution [6]. Recent efforts have been made to design an effective scoring method [7,8], but these more efficient methods require lab results and may therefore be more challenging to implement. In this study, we therefore present an entirely automated scoring system that uses only two physiological respiratory signals (breathing frequency (BF) and oxygen saturation (S_PO₂)) to assess patients' infection severity, predicting the potential for both intubation and prolonged stay in the ICU (>5 days).

In sum, the early detection of patients that will require an extended stay in the ICU may help regulate patient flow and resource management for hospitals.

2. Methods

This retrospective, observational study included confirmed COVID-19 patients that were admitted to our ICU during both the first and subsequent outbreaks of the pandemic in France (March to May 2020 and September 2020–September 2021). We excluded patients that had been intubated prior to admission, patients with missing data, and patients with a non-intubation decision. The local ethics committee (CCP1 SUD Mediterranée) approved the use of physiological data for study within the framework of our physios project. Participants or their families were informed of the research's purpose and their right to decline to participate.

2.1. General conception

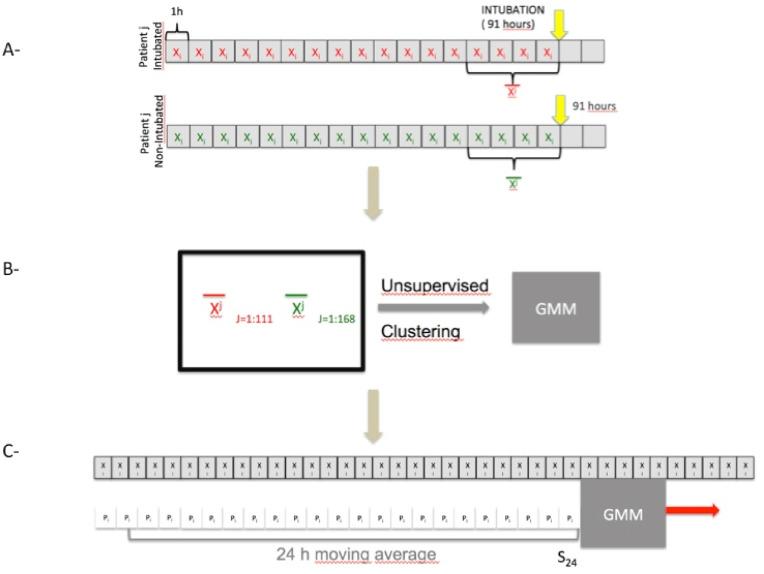
This study used standard monitoring data (BF and S_PO₂) to judge the severity of infection in patients with COVID-19. More specifically, we investigated whether a clustering algorithm could accurately recognize patients at risk for intubation without supervision. We, therefore, used a clustering algorithm fed with data from BF and SPO2 from intubated and non-intubated patients. Each intubated patient gave a mean state vector averaged over the 4 h before intubation. Non-intubated patients provided a state vector averaged 4 h prior to the theoretical average time of intubation (91 h after ICU admission. We then hourly applied this algorithm to gauge the severity of the patients at various other times. The principle is shown in Fig. 1

Fig. 1.

General Principles: A-The SpO₂ and BF signals are used to calculate a state vector representing the patient's respiratory status every hour. This state vector is averaged over the last 4 h before intubation. We set a fictitious date of intubation for patients who were not intubated, which is 91 h after admission (91 h the average date of intubation for patients). The state vector is also averaged over the last 4 h prior to this fictitious intubation date. B- All state vectors of the 279 patients are provided to an unsupervised clustering algorithm (GMM). We compared the performance of this algorithm to the actual classification. C- The algorithm calculates the probability of intubation in 4 h every hour. However, this prediction is often distorted by brief periods of instability. This probability is therefore averaged over 24 h.

2.2. Data collection

Physiological data was extracted from the bedside monitors every 5 s, and a python script transformed the HL7 format into an exploitable monitor parameters CSV file containing all patients' parameters.

2.3. Data processing

Our two parameters (BF and S_PO₂₎ were recorded for all patients, and may also be easily deployed outside of the ICU for regular wards monitoring of COVID-19 patients. Artefacts as disconnection or movements were removed using a median filter. We computed 10 basic parameters derived from BF and S_PO₂; they are listed in Table 1 .

Table 1.

Parameters computed from BF and S_PO₂.

Parameter ai	Description
BFM	Mean value of BF
BFmax	Maximum value of BF
BF40	Percentage of time over 40 breaths/minute
BF20	Percentage of time under 20 breaths/minute
varBF	Variance of BF
SPO2M	Mean value of SPO2
SpO2min	Minimum value of SPO2
ITS	Integral of 100-SPO2
varSpO2	Variance of SPO2
SPO2-90	Percentage of time under 90% of SPO2

A 10-parameters vector x = [ a_i], that is, the hourly mean of the ten parameters listed in Table 1, represents the patients' respiratory condition.

2.4. Intubation recognition

We used a Gaussian mixture model-clustering algorithm for intubation pattern recognition, using either part of or the whole x vector.

We assumed that a patient's situation will worsen in the 4 h leading up to actual intubation. Indeed, we assumed that intubation was performed for unstable patients for which non-invasive therapy was no longer sufficient. For intubated patients, we calculated the mean state vector x = [a_i] of the 4 h immediately before intubation (Fig. 1). Intubation was timed using a capnogram curve. Capnography is the measurement of exhaled CO₂ and is required for ventilation monitoring. Our ICU protocol specifies a mandatory capnogram for all patients prior to any intubation. Therefore, intubation timing is detected by a non-zero capnogram. For non-intubated patients, we computed the mean state vector of the 4 h prior to median intubation time (91 h) (Fig. 1). Each patient provided a state vector representing the supposed worst condition for intubated patients. Two-class unsupervised clustering was then applied to the data (Fig. 1).

Prior to clustering, we reduced the dimensionality. Feature selection was performed pragmatically using logistic regression analysis. Only those results with p < 0.1 were kept for further analysis. Features were then reduced to the minimum according to parsimony principles while clustering was performed using various combinations of the remaining features; only the model that performed best was kept. The state vector x = [a_i], which was made up of the kept features, described the patient's situation each hour.

The vector x served as an input for the Gaussian mixture model. We used the algorithm embedded in Matlab (The Mathworks, Inc., Natick, MA, USA) with a full covariance matrix and specified two clusters. The clustering was then compared to the actual classification. The probability density function of the multivariate Gaussian for cluster k = 0 or 1, as computed by Expectation-Maximization, is given by:

$$g_k\left(X\right)=\frac{1}{\sqrt{{\left(2\pi \right)}^n\left|{\text{Σ}}_k\right|}}{e}^{-\frac{1}{2}{\left(X-{\mu }_k\right)}^T{\text{Σ}}_k^{-1}\left(X-{\mu }_k\right)}$$ (1)

where k is the cluster number (0 or 1), X is the input vector (column), n is the input vector length, μ_k is the centers of the Gaussian for cluster k, Σ_k is the covariance matrix for cluster k, Σ_k is the determinant of Σ_k, and Σ_k ⁻¹ is the inverse of Σ_k.

Therefore the probability of belonging to cluster k for vector x_i is:

$$p_k^i=\frac{g_k\left(x_i\right){\phi }_k}{{\sum }_{l=0}^{l=1}{g}_l\left(x_i\right){\phi }_l}$$ (2)

where Φ_k is the prior probability of cluster k.

2.5. Score construction

2.5.1. S₂₄

The algorithm, by reflecting the state of a given patient at a given moment, expresses the instantaneous probability that a given patient will be intubated within 4 h. The positive prediction of intubation is therefore associated with high levels of respiratory severity. However, this state may also be due to the patient moving (from a chair to a bed or vice versa), speaking, or getting of the high flow nasal canula, among other things. Therefore, we computed the average intubation probability over 24 h to reflect the patient's state on a more wider time window (Fig. 1). Indeed, a patient with a positive prediction of intubation during 24 h is more severe than one that has 1 h or two episodes of high intubation probability over 24 h.

A given patient's situation was characterized by its state vector x = [a_i] as computed during the last hour. The algorithm was then applied to x, resulting in a p(x), the posterior probability as predicted by the Gaussian mixture model (Equation (2)). The S₂₄ score is computed according to Equation (3), and this probability is updated hourly.

$$S_{24}\left(t\right)=100.\left(\frac{1}{24}\sum _{i=1}^{i=24}p\left(t-i\right)\right)$$ (3)

Patients were classified into three categories depending on their maximum MS₂₄.

$$M{S}_{24}\left(T\right)=\underset{24<t<T}{\max }{S}_{24}$$ (3)

We excluded the first 24 h because most patients were unstable at admission and had a high score that decreased with support therapy initiation. We also excluded the 4 h immediately prior to intubation because that time was used for algorithm learning. Therefore, a patient was categorized as green if their score remained in the green category. They were categorized as orange or red if their S₂₄ maximum was in the orange or red category, respectively. A given patient's score may increase, but never decreases. All computations were performed using Matlab® (The Mathworks, Inc., Natick, MA, USA).

2.6. Length of stay

We studied the link between a patient's MS₂₄ and their length of stay in the ICU to use our data for triage. We chose to study whether this score was predictive of a prolonged stay in intensive care. In particular, if it could predict a long length of stay, i.e. more than five days. W chose this value because it corresponds to our cohort's median length of stay in the ICU of non-intubated patients. The five days reflects a standard ICU stay for COVID-19.

3. Results

3.1. Population

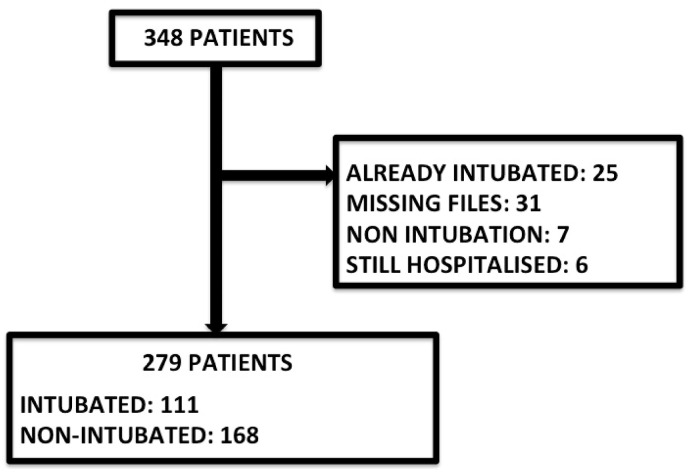
We included 279 patients (63 [56–70] years of age, 93 females, and 76 deaths). 23 patients came from the first outbreak and 256 came from the others (see flow chart diagrams, Fig. 2 ). Their baseline characteristics are listed in Table 2 :

Fig. 2.

Study flow chart, including patients from ongoing pandemic, March 2020 to September 2021.

Table 2.

Patients' characteristics.

Number	279
Age	63 [56–70]
Sex ratio F/M	93/186 (33%/67%)
Intubation	111 (40%)
ECMO	41 (14.7%)
Length of Stay	8 [4–20]
Death	76 (27.2%)

3.2. Feature selection

The logistic regression p-values for all parameters are listed in Table 3 .

Table 3.

P-values for the logistic regressions for all parameters in Table 1.

Parameter ai	P
BFM	0.05
BFmax	0.6
BF40	0.3
BF20	0.3
varBF	0.2
SpO2M	6.10–3
SpO2min	3.10–7
ITS	0.05
varSpO2	0.02
SpO2-90	8.10–4

We kept the following parameters for the first evaluation: BFM, SpO₂M, SpO₂min, ITS, varSpO₂, and SpO₂-90. As the significances of SpO₂M, SpO₂min, and SpO₂-90 were particularly high, these parameters were kept for all classifications as we tried all combinations including three others predictors: BFM, ITS, varSpO₂. That gave eight combinations corresponding to eight different models numbered from 1 to 8. Models and their predictors are listed in Table 4 .

Table 4.

Tested models with their predictors (GMM: Gaussian Mixture Model).

MODEL	ALGORITHM	PREDICTORS
1	GMM	SpO2M SpO2min SpO2-90
2	GMM	SpO2M SpO2min SpO2-90 BFM ITS varSpO2
3	GMM	SpO2M SpO2min SpO2-90 BFM ITS
4	GMM	SpO2M SpO2min SpO2-90 BFM
5	GMM	SpO2M SpO2min SpO2-90 ITS
6	GMM	SpO2M SpO2min SpO2-90 ITS varSpO2
7	GMM	SpO2M SpO2min SpO2-90 varSpO2
8	GMM	SpO2M SpO2min SpO2-90 BFM varSpO2

3.3. Classification accuracy

The clustering performances of each model are shown in Table 5 :

Table 5.

Models' performances.TPR: True Positive Rate, True Negative Rate, RI: Rand Index.

MODEL	TPR(%)	TNR(%)	ACCURACY (%)
1	83.8	88.1	86.4
2	60.4	92.9	79.9
3	84.7	49.4	63.4
4	86.5	90.9	87.8
5	84.7	49.4	63.4
6	17.1	96.4	64.9
7	63.1	92.1	81
8	70.3	92.9	83.9

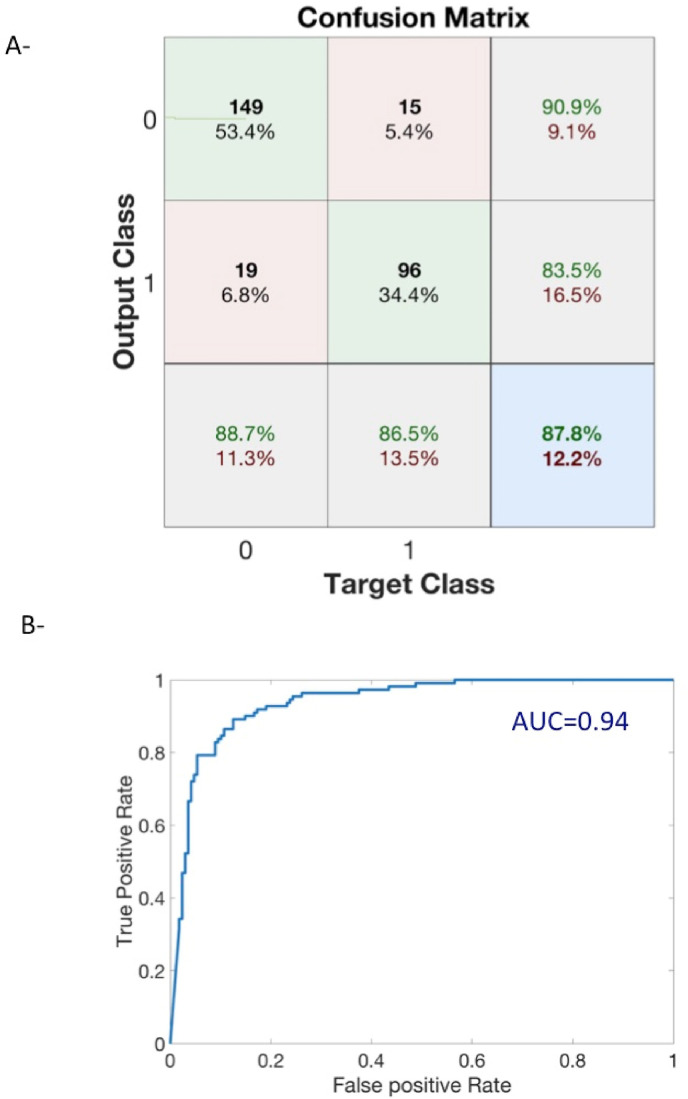
Model 4 had the best performance (Fig. 3 ), and was therefore retained for the rest of the study. Patients' situations are represented each hour by the four-parameter [BFM, SpO₂M, SpO₂min, and SpO2-90] state vector.

Fig. 3.

Unsupervised clustering performances of Model 4 as listed in Table 2. A – The confusion matrix shows an accuracy of 87.8%. Class 0 is non-intubated and class 1 intubated. Numbers are actual number of patients in each predicted class according to the ground true class. Green percentages (resp. red) are true rate (positive or negative) or positive predictive values (resp.: false and negative predictive values). B - ROC curve had an AUC = 0.94.

The model's parameters can be found in Table 6, Table 7, Table 8 :

Table 6.

μ_k represents the centers of the Gaussian mixture model for cluster k = 0 (non-intubated) and k = 1 (intubated patients).

Parameters	BFM	SpO2M	SpO2min	SpO2-90
μ0	24.0	94.6	90.8	0.06
μ1	30.0	90.4	83.1	0.43

Table 7.

Covariance matrix for non-intubated patients.

Σ0	BFM	SpO2M	SpO2min	SpO2-90
BFM	20.3	−2.9	−4.3	0.10
SpO2M	−2.9	3.4	4.3	−0.08
SpO2min	−4.3	4.3	7.9	−0.14
SpO2-90	0.10	−0.08	−0.14	0.004

Table 8.

Covariance matrix for intubated patients.

Σ1	BFM	SpO2M	SpO2min	SpO2-90
BFM	46.4	−1.9	−6.6	0.11
SpO2M	−1.9	7.5	8.5	−0.60
SpO2min	−6.6	8.5	27.2	−0.38
SpO2-90	0.11	−0.60	−0.38	0.06

The two covariance matrices were:

3.4. S₂₄ score

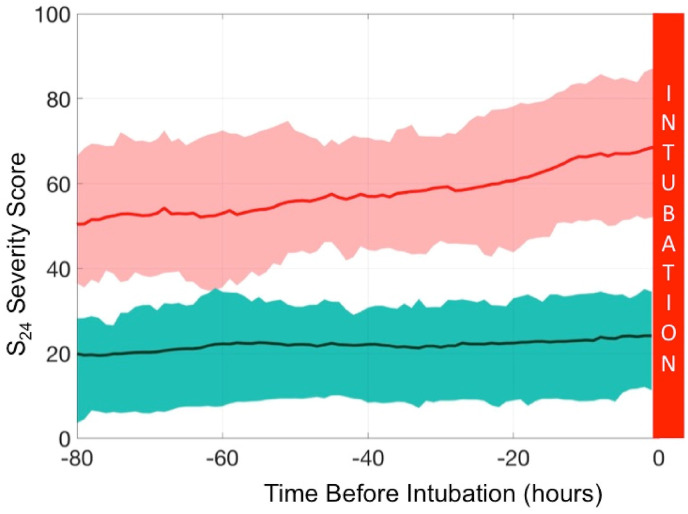
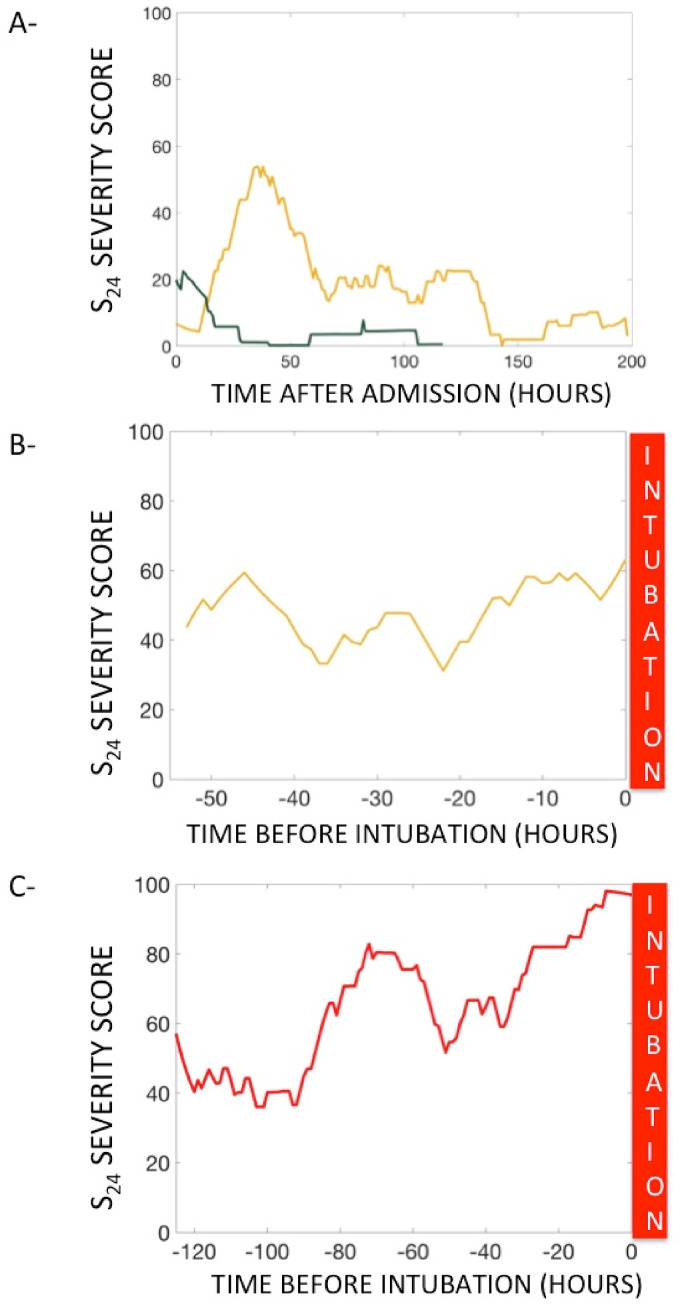
Patients that were intubated had a higher S₂₄ score at least 80 h prior to intubation, and remained high until intubation, with a continuous increase that accelerated in the last 24 h (Fig. 4 ).

Fig. 4.

The cohort dynamic changes of the S₂₄ score during the 80 h prior to intubation. Patients from the intubated group are in red. The plain thick line is the mean and the fine lines correspond to the 25%–75% confidence interval. The green area represents the non-intubated group; the dashed thick line is the mean and the fine lines correspond to the 25–75% confidence interval. The S₂₄ score discriminates both groups at least 80 h before intubation. We noted a net increase in S₂₄ score at 24 h prior to intubation.

3.5. MS₂₄ score

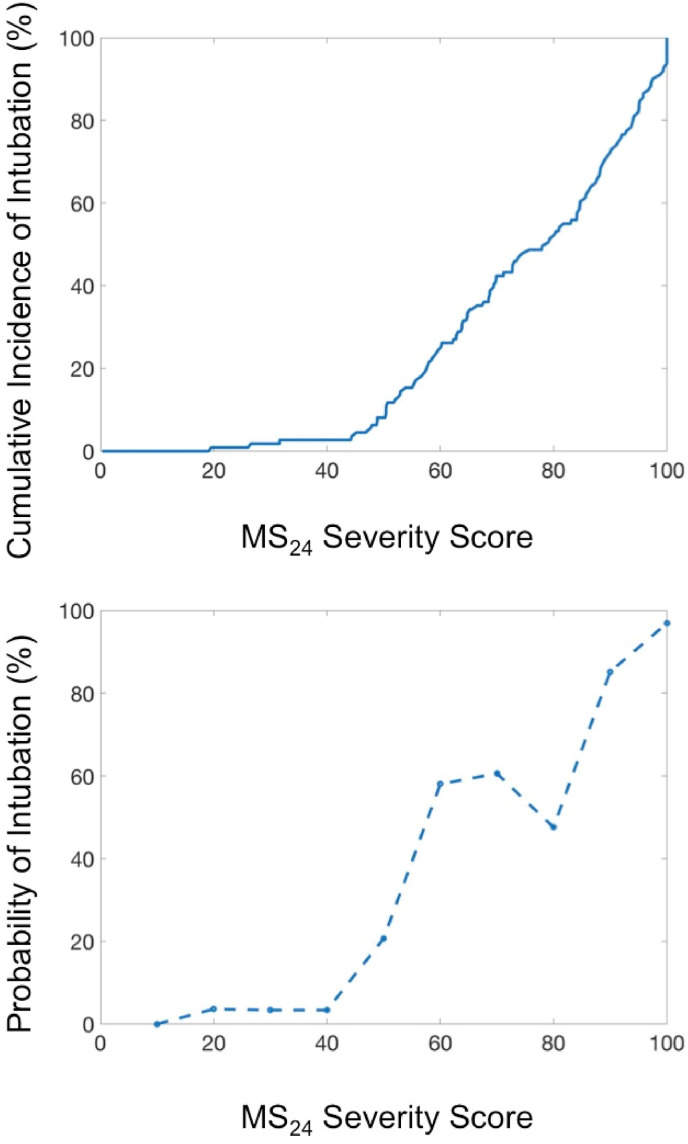
The MS₂₄ score is the maximum S₂₄ score after disregarding the first 24 h of the patient's stay. MS₂₄ was found to be highly correlated with the occurrence of intubation (Fig. 5 -A). Simply put, the rate of intubation increases with the MS₂₄ score, and we established a probability law that also increases with MS₂₄ score (Fig. 5-B). The MS₂₄ allows for distinguishing between three severity situations (green, orange, and red). The cut-offs for these categories were arbitrarily established by dividing in three the scale of 100 (Table 9 ).

Fig. 5.

A - Evolution of the cumulative incidence of intubation with the severity score expressed as the rate of intubation. B - Evolution of the probability of intubation according to MS₂₄ score. The probability increased continuously until it reached almost 1 for MS₂₄ = 100.

Table 9.

Number of intubations according to MS₂₄ score.

The MS24 score also helped distinguish between different patient behaviors:

Green: (MS₂₄ < 33) corresponds to patients that responded well to the therapeutics, meaning that their hourly score could increase but generally quickly returned to zero, indicating a low risk of intubation (3.4%). Fig. 6 -A shows typical S₂₄ evolution in such patients; they experience a mild increase in S₂₄ score that quickly regressed. Two of the intubated patients in the green zone were admitted during the first COVID-19 outbreak.

Fig. 6.

A - Score evolution of a stable patient (green). The S₂₄ score had the potential to increase, but quickly returned to zero, staying under 33 overall. The orange line shows an unstable patient with large score increases; this patient's condition improved without tracheal intubation. B – Score evolution of an unstable patient with a prolonged stay in the warning orange zone. This patient had to be intubated. C – Score evolution of an unstable patient with a terminal increase to a final S₂₄ score of 96 (MS₂₄ = 88).

Orange: (MS₂₄ ≤ 66) corresponds to patients that were unstable and experienced large increases in hourly score value that returned somewhat quickly to 0 with an increased risk of intubation (37%) (Fig. 6-A and B). It is difficult to say whether the patients intubated in this category were intubated prematurely or, conversely, were prevented from worsening through intubation. It is worth noting, however, that the patient in 6-A stabilized and improved dramatically while the patient in 6-B remained in the orange zone.

Red: (MS₂₄ > 66) corresponds to highly unstable patients with prolonged higher hourly scores and an increased risk of intubation (77%). Fig. 6-C shows the typical evolution of a red category patient. The increase in S₂₄ score was continuous and the patient's condition continued to worsen in the 40 h prior to intubation.

3.6. MS₂₄ score and length of ICU stay

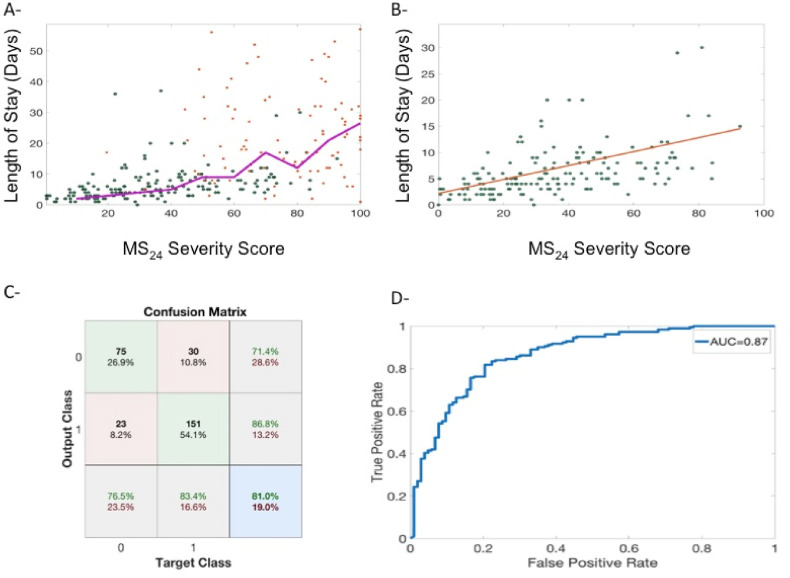
MS₂₄ was correlated to the length of ICU stay for all patients (Fig. 7 - A); for non-intubated patients, this correlation was linear (Fig. 7 – B). We found that a MS₂₄ score over 40 was predictive of an ICU stay of greater than five days with an accuracy rate of 81.0% (PPV = 86.8%, sensibility = 83.4%, AUC = 0.87) (Fig. 7-C and D).

Fig. 7.

A - Changes in length of stay alongside MS₂₄ score (lengths of stay greater than 50 days were not plotted). Green dots represent non-intubated patients while red dots represent intubated patients. The purple line represents the moving average of length of stay with MS₂₄. B - Changes in length of stay with MS₂₄ score for non-intubated patients (red line is the linear regression) C -Confusion matrix of a prediction of a length of stay of >5 days using a MS₂₄ score greater than 40 that corresponds to the optimum of the ROC curve plotted in D.

3.7. Computational complexity

The EM algorithm has an O(nkd) complexity per iteration [9]. It can be updated on a regular basis, but this does not lead to an explosion of the computation time considering the number of patients entering the intensive care unit for COVID-19.

Regarding the algorithm for calculating the severity scores, it is a linear process with a complexity O(n) which is economical in time and could lead to an embedded technology easily.

4. Discussion

We used BF and SpO₂ to assess COVID-19 patients' level of respiratory severity by means of the IA unsupervised algorithm. The algorithm output was used to design two scores, namely S₂₄ and MS₂₄. S₂₄ was computed continuously and reflected the patient's state in real time while MS₂₄ reflected the patient's absolute level of respiratory severity and helped categorize the patient. The results allowed for patient monitoring and other related decision-making by dividing the patients into three categories, namely green, orange, and red. First, green patients have a lower risk of intubation. They could therefore be directed to intermediate care while others remain under careful monitoring because of higher intubation risk. Secondly, COVID-19 patients are highly hypoxic and experience profound desaturation episodes that may lead to premature intubation in a constrained pandemic situation [10]; this is becoming even more pronounced as the benefits of intubation are debated [10,11]. During an episode of desaturation, a low MS₂₄ may help postpone intubation. Finally, intubation should immediately be considered for a red patient with a continuously increasing score. Indeed, prompt detection of non-invasive treatment failure is of great importance. It avoids unnecessary delays in intubation [12]. Recent studies have shown that patients' self-inflected injuries during spontaneous breathing could potentially lead to aggravated lung damage, which could, in turn, be responsible for increased mortality rates [13]. However, this theory is up for debate [13,14].

The three categories distinguish the way that various patients react to non-invasive therapy. Green patients respond well; their instantaneous score (i.e., algorithm classification) sometimes rises to 1 during moments of effort or active treatment, but it quickly returns to zero. In the orange category, the algorithm prediction may stay high for a longer time, reflecting a high level of instability, leading to intubation. Finally, the red category characterizes highly unstable patients that usually cannot be successfully stabilized via non-invasive therapy.

These scores have multiple uses. They could assist in resource management during periods of constraint; green patients may be cared for at intermediate facilities or even on regular hospital floors with adequate non-invasive oxygen therapy and simple SpO₂ and BF monitoring [17]. The same algorithm could then be used to continuously monitor regular floor patients [15,16]. The early detection of a potential prolonged stay in the ICU also helps with resource management, as a high number of bed-blocking patients could trigger the opening of new premises [18] or the evacuation of patients to remote regions [19]. This score could also be used to determine the patients with the most severe cases at ICU admission in order to immediately initiate treatment for those patients. Finally, the scores could be used to compare patients' severity as SpO₂ and BF are repeatedly recorded.

This pilot study has limitations. First, we focalized the algorithm on COVID-19 patients, and did not consider all patients at risk of intubation. A universal intubation prediction algorithm could have been developed and then calibrated for COVID-19 patients. However, it seemed to us that the policy surrounding the intubation of COVID-19 patients is different, especially since our center involves very heterogeneous patients.

Secondly, this monocentric study reflects our institution's intubation policy for COVID-19 patients. However, the unsupervised characteristic of the learning revealed that all patients are intrinsically different. The Gaussian mixture model is easy to modify and adapt for other centers; for modification, a center could add its own data and then modify the coefficient of the probability computation. We can also continuously update the algorithm by training it on all previous patients; training sets are provided in electronic supplementary file.

Finally, we intentionally chose not to include clinical data in the classification to have the most straightforward algorithm possible, especially since the patients are relatively homogeneous and not different from the published national cohort [20].

5. Conclusion

The score we designed uses simple signals and seems to be efficient in terms of visualizing a given patient's respiratory situation and could help in decision-making. Real-time computation is easy to implement, allowing for the prediction of both tracheal intubation and prolonged ICU stay for COVID-19 patients. The algorithm could also be used on regular floors when patients are monitored with continuous portable devices. The use of the algorithm for non-COVID-19 patients with potentially worsening respiratory situations, however, requires its own dedicated study.

Declaration of competing interest

None Declared.

Appendix A. Supplementary data

The following is the supplementary data related to this article: