Abstract
Coronavirus disease 2019 (COVID-19) is a contagious disease caused by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). It may cause serious ailments in infected individuals and complications may lead to death. X-rays and Computed Tomography (CT) scans can be used for the diagnosis of the disease. In this context, various methods have been proposed for the detection of COVID-19 from radiological images. In this work, we propose an end-to-end framework consisting of deep feature extraction followed by feature selection (FS) for the detection of COVID-19 from CT scan images. For feature extraction, we utilize three deep learning based Convolutional Neural Networks (CNNs). For FS, we use a meta-heuristic optimization algorithm, Harmony Search (HS), combined with a local search method, Adaptive -Hill Climbing (AHC) for better performance. We evaluate the proposed approach on the SARS-COV-2 CT-Scan Dataset consisting of 2482 CT scan images and an updated version of the previous dataset containing 2926 CT scan images. For comparison, we use a few state-of-the-art optimization algorithms. The best accuracy scores obtained by the present approach are 97.30% and 98.87% respectively on the said datasets, which are better than many of the algorithms used for comparison. The performances are also at par with some recent works which use the same datasets. The codes for the FS algorithms are available at: https://github.com/khalid0007/Metaheuristic-Algorithms.
Keywords: COVID-19 detection, Convolutional Neural Network, Harmony Search, Adaptive β-Hill Climbing
1. Introduction
COVID-19 is a contagious respiratory infection caused by SARS-CoV-2. It was first detected in 2019 in Wuhan, China and was subsequently declared a global pandemic by the World Health Organization (WHO) in March 2020. It has resulted in a large-scale global and social disruption. Common symptoms include fever, dry cough, fatigue, breathing difficulties, loss of smell and taste, and headache. Complications may result in pneumonia and acute respiratory distress syndrome. The standard method for detection is by real-time reverse transcription polymerase chain reaction (rRT-PCR). However, the time taken for the results is high when taking into account the low sensitivity (Fang et al., 2020). Therefore, conventional radiological imaging such as X-rays and CT scans have also been widely used as an initial screening measure. This is especially important considering the fact that it will take some time before a significant portion of the population is vaccinated.
In the past few years, deep learning (DL) has become a popular tool for automatically learning feature representations from the input data. This is mainly due to the increase in computing capability in the past years. Convolutional Neural Networks (CNNs) have been applied to many image processing domains like classification, segmentation, etc. Several works have been proposed in the domain of medical image analysis using CNNs where the methods achieve competitive results. This demonstrates the robustness as well as the widespread adoption of CNNs.
Whenever we have something in abundance, choosing the best one or the required one becomes very difficult due to the time required for searching from a huge search space. Similarly for a feature set used for classification purposes, we may not need all the features as there may be a lot of redundant features. For this case, choosing the best combination of features from the original feature set can be a very expensive operation because of the huge number of possible combinations of features. Feature selection (FS) is about choosing the most relevant features out of the existing features without compromising the performance of the learning model. In recent days, meta-heuristic algorithms have gained a lot of attention from the research community in this particular field and proved their potential for producing competent results.
In this work, we propose a two-stage framework for the detection of COVID-19 in CT scan images. The first stage involves feature extraction from the input image using a CNN model. Transfer learning is employed during the training stage to obtain improved and robust performance due to the small quantity of training data. In the second stage, FS technique is applied on the features extracted in the first stage. This involves the use of Harmony Search (HS), a global search algorithm, combined with Adaptive -Hill Climbing (AHC), a local search algorithm. The proposed approach manages to greatly reduce the number of features and also leads to a better classification performance as indicated by the obtained results.
Recently, there are many works which use DL based features (CNNs in many cases) for the detection of COVID-19 in radiological images like CT scans and X-rays. The main issue with the raw features in CNNs is that there may be some irrelevant or redundant features. Some features may be highly correlated while others or may be unimportant for the final prediction task. The elimination of the correlated and redundant features can help in reducing the size of the features and also the inference time. In some cases, this can also result in an improvement in the classification performance. Hence, FS is considered as an important method for improving the performance of such learning systems, even those using DL. Keeping this fact in mind, in the present work, the effect of FS is analyzed for COVID-19 detection from CT scan images. Importantly, it is observed that a modest improvement is achieved over the base feature extractor CNNs when FS module is incorporated in the overall system.
In line with the above, works have been proposed where different optimization algorithms have been used to obtain an improvement in performance. Some of them are highlighted in Section 2. In the present work, we have mainly explored an optimization algorithm i.e., HS, whereas the other works have focused on some different algorithms. This choice is motivated by the No Free Lunch theorem (Wolpert & Macready, 1997) which states that no single algorithm exists which can guarantee the best performance on all sets of optimization problems. Therefore, it is worthwhile to explore different algorithms and their variants to find the best performing method for the problem under consideration. Apart from the above, another motivating factor is to explore the effect of local search when used with HS. In many cases it has been found that optimization algorithms converge to a local optima and also converge prematurely. In such scenarios, a local search method like AHC can direct the search away from a local optima towards the global optima. This will manifest as better detection accuracy, which is observed to hold in the present case.
The SARS-COV-2 CT-Scan Dataset (Soares, Angelov, Biaso, Froes, & Abe, 2020) and its updated version are used for training and testing the proposed approach. The first dataset contains 2482 CT scans in total among which 1252 scans are from COVID-19 positive patients while the remaining 1230 scans are from COVID-19 negative patients. The second dataset contains 2926 CT scans of which are from 2168 COVID-19 positive patients and the remaining 758 are from COVID-19 negative patients. The proposed FS method consistently leads to a reduction of more than 50% in the number of features. This reduces the redundancy among the extracted features and also improves the overall performance. The best accuracies of 97.30% and 98.87% are obtained on the above two datasets using features extracted by the DenseNet201 and the Xception models respectively at a training to testing split of 85% to 15%.
In summary, the contributions of this work are as follows:
-
1.
An end-to-end framework of feature extraction and FS is developed to detect COVID-19 from CT scan images.
-
2.
Three state-of-the-art pre-trained CNN models (DenseNet, ResNet and Xception) are utilized as feature extractors to obtain feature vectors from the input images.
-
3.
FS is performed by using a combination of an optimization algorithm (HS) with a local search algorithm (Adaptive -Hill Climbing). Many meta-heuristic algorithms suffer from premature convergence to local optima, and in our case, to overcome this problem, a local search method, is used with HS.
-
4.
Experimental outcomes indicate that such a FS stage obtains better results than when using only models or when using a single optimization algorithm in the FS stage.
The remainder of the paper has been organized as follows: Section 2 provides a quick survey of prior works on the associated topics. Section 3 discusses the proposed approach. Section 4 contains the results and some relevant discussion followed by the concluding remarks in Section 5.
2. Related work
The last decades have seen a marked increase in computing power with the advent of graphics processing units (GPUs). This, along with the availability of large datasets, has paved the way for the practical applications of DL techniques. DL techniques are now extensively being researched in the domain of computer vision along with others. They have been applied to many areas in medical image processing.
For instance, medical image classification is a process where an input image (2D or 3D) is classified into one of the several target classes. The classes commonly represent disease types. Kermany et al. (2018) have used a transfer learning based approach with an InceptionV3 network to classify age-related macular degeneration and diabetic macular edema in optical coherence tomography images. The authors show that the network achieves performance comparable to that of human experts. They have also shown the generalizability of their approach by training the model to detect viral and bacterial pneumonia in chest X-rays.
Several works (Maier, Syben, Lasser, & Riess, 2019) have also been proposed in related medical realms like image segmentation, image registration, computer aided diagnosis, simulation, reconstruction, etc. Considering the above works, it is only natural for DL based research works to be proposed in the domain of medical image processing to aid in detecting COVID-19.
The availability of a large amount of training data is important for the performance and generalizability of DL models. Conventional augmentation methods like rotation, flipping, etc. have been widely used to increase the variety of the training data. However, such methods are limited in their effectiveness because they produce slightly altered samples from existing data. The work by Waheed et al. (2020) aims to tackle this problem by generating synthetic images via a Auxiliary Classifier Generative Adversarial Network (ACGAN) based model termed as CovidGAN. They show that including the synthetic images in a VGG16 classifier improves the performance of the model. The accuracy, F1 score, sensitivity and specificity improve to 95%, 0.95, 90% and 97% respectively from 85%, 0.85, 69% and 95% respectively.
Several works also employ transfer learning to improve the performance of DL models as opposed to training from scratch. For example, Jaiswal, Gianchandani, Singh, Kumar, and Kaur (2020), in their work, use DL models to classify CT scan images as COVID-19 infected or normal. The models are originally trained on the ImageNet dataset. After that, they have been trained on the SARS-CoV-2 CT scan dataset. The authors have noted that the DenseNet201 based model performs the best as compared to the VGG16, ResNet152V2 and InceptionResNetV2 models. The reported training, validation and testing accuracies are 99.82%, 97.40% and 96.25% respectively.
Rajaraman et al. (2020) use iterative pruning and ensembling after training the DL models to obtain improved classification performance. They have proposed a pipeline to detect pneumonia-related and COVID-19 related irregularities in chest X-rays. A notable stage in the pipeline is the modality-specific training. The models are pretrained on a pneumonia-associated chest X-ray dataset before being trained on the data containing COVID-19 X-rays. The intuition is that, since COVID-19 data is scarce, the pretraining helps the models to learn domain-specific features. This is very similar to transfer learning, though the modality-specific training is applied to the models already pretrained on ImageNet. The authors report their accuracy and AUC as 99.01% and 0.9972 respectively. The work by Dey, Bhattacharya, Malakar, Mirjalili, and Sarkar (2021) is a similar recent work where an ensembling technique is used which utilizes a Choquet Fuzzy Integral-based approach.
From the above works, it is observed that DL based CNNs are very popular for the purpose of feature extraction from images (X-rays, CT scans, etc.). It is also noted that transfer learning is an useful technique to deal with the lack of data, especially in emerging domains. However, there are some limitations in CNNs: the hyperparameters need to be carefully chosen, there may be redundancy in the extracted features, etc. Several works have been proposed to mitigate these limitations. In particular, it is noted that searching-based and optimization-based algorithms have been used in many works to augment the performance of DL models.
It is also important to note that in addition to CNNs, there are also works reporting competitive results using other relevant approaches. For example, the works by Yu, Lu, Guo, Wang, and Zhang (2020) and Yu, Wang, and Zhang (2021) are a few examples where graph-based CNNs have been used. The work by Garain, Basu, Giampaolo, Velasquez, and Sarkar (2021) is another recent work for COVID-19 detection based on Spiking Neural Networks as opposed to DL based networks.
As mentioned earlier, in recent times, optimization algorithms have attracted a lot of attention from researchers. In particular, meta-heuristic algorithms have seen a lot of improvement over the years. Meta-heuristic is a genre of randomized algorithm where the algorithm learns to find the optimal solution through the iteration process. Meta-heuristic algorithms can be divided into multiple categories: single solution based and population based (Gendreau & Potvin, 2005), nature inspired and non-nature inspired (Fister Jr, Yang, Fister, Brest, & Fister, 2013), metaphor based and non-metaphor based (Abdel-Basset, Abdel-Fatah, & Sangaiah, 2018), etc. From the ‘inspiration’ point of view, these algorithms can roughly be divided into four categories (Nematollahi, Rahiminejad, & Vahidi, 2019): Evolutionary, Swarm inspired, Physics based, and, Human related.
FS is a binary optimization problem. In FS, the most relevant useful features are chosen from the existing feature set. In the final selected features, each feature of the existing feature set has only two possibilities. It may either be included in the selected feature set or excluded from the final feature set. So, there are a total of ( being the size of original feature set) possible combinations of selected feature sets, and to find the best combination is indeed a challenging task. Here, the meta-heuristic algorithm comes handy. The stochastic nature of meta-heuristic algorithms helps find any optimum solution with a reasonable time complexity. The algorithms mentioned in the previous paragraph are all extensively used for FS. Ghamisi and Benediktsson, 2015, Huang et al., 2007 and Leardi (2000) are a few GA based approaches for FS. Chakraborty, 2008, Lee et al., 2008 and Wang, Yang, Teng, Xia, and Jensen (2007) are a few PSO based approaches for FS. One other FS related work is Ke, Feng, and Ren (2008). One of the recently published works using meta-heuristic algorithms on COVID-19 data is by Wu, Liao, Karatas, Chen, and Zheng (2020). A few recent works utilizing local search based algorithms are: Al-Betar et al., 2020, Chatterjee et al., 2020 and Ghosh, Ahmed, Singh, Geem, and Sarkar (2020). In Al-Betar et al. (2020) the authors have used a -Hill Climbing based method with a S shaped transfer function. Ghosh et al. (2020) used -Hill Climbing to improve performance of the Binary Selfish Optimization Algorithm. On the other hand, a few recent works on HS algorithms based FS are: Abualigah et al., 2020, Ahmed et al., 2020, Saha et al., 2020 and Sheikh et al. (2020). In these papers, the authors have used novel combinations of HS with other meta-heuristic or local search methods. In Sheikh et al. (2020) authors have used a novel hybrid method composed of HS algorithm and Artificial Electric Field Algorithm (AEFA). In Ahmed et al. (2020), the authors have used a hybrid method of HS algorithm and a Ring Theory based evolutionary algorithm for FS.
Goel, Murugan, Mirjalili, and Chakrabartty (2020) have proposed an Optimized CNN (OptCoNet) for the diagnosis of COVID-19 from chest X-rays. The proposed model consists of typical feature extraction components (convolution, pooling, etc.) and classification components (fully-connected layers, dense layers, etc.). After that, the authors have used the Grey Wolf Optimization algorithm for optimizing the hyperparameters of the CNN. The authors demonstrate that such an approach performs better in comparison to state-of-the-art CNNs. Their dataset consisted of chest X-rays of normal, pneumonia affected and COVID-19 affected patients collected from publicly available repositories. There were 2700 images in total with 900 being COVID-19 images. A training to testing split of 70% to 30% used. The authors reported the accuracy, sensitivity, specificity, precision, and F1 score values as 97.78%, 97.75%, 96.25%, 92.88% and 95.25% respectively.
Ezzat et al. (2020) have an approach where they select the optimal hyperparameters for a pretrained DenseNet121 based model using the Gravitational Search Algorithm (GSA). They have prepared a binary COVID-19 dataset by combining the Cohen COVID19 chest X-ray dataset and the Kaggle chest X-ray dataset. The final dataset contains two categories: positive and negative. The positive category includes 99 X-rays of patients affected by COVID-19. The negative category includes 207 X-rays among which 104 are from healthy cases, 80 are pneumonia affected cases and the remaining 23 are from cases affected by other diseases like SARS, ARDS, etc. The data was divided into three partitions for training, validation and testing with the ratios being 70%, 15% and 15% respectively. The authors report the accuracy and F1 score of their method as 98.38% and 98% respectively.
Elaziz et al. (2020) have proposed a two-stage framework consisting of feature extraction followed by FS to classify X-rays into 2 classes: COVID-19 positive and COVID-19 negative. The features were extracted from the image using Fractional Multichannel Exponent Moments (FrMEMs). A parallel implementation was used to speed up the task of finding moments. Thereafter, the Manta Ray Foraging Optimization (MRFO) algorithm based on Differential Evolution (DE) was used to find the most significant features from the features obtained from the feature extractor. The authors have used two datasets for the purpose of evaluation. The first dataset that they use is a combination of two datasets: the Cohen dataset and a pneumonia dataset from Kaggle. It consists of 216 COVID-19 positive images and 1675 COVID-19 negative images. The second dataset was collected by a team of researchers in collaboration with doctors. It has 219 COVID-19 positive images and 1341 COVID-19 negative images. The authors report accuracies of 96.09% and 98.09% on the first and second datasets respectively.
Sahlol et al. (2020) have used an approach consisting of two stages: feature extraction followed by FS. For the purpose of feature extraction, they utilized the robust CNN architecture known as Inception. To filter out the irrelevant features, they used a swarm-based FS method: a combination of fractional-order calculus with the Marine Predators Algorithm (FO-MPA). They used the same two datasets for evaluation as the previously mentioned work by Elaziz et al. (2020). The authors reported the accuracy and F-score values as 98.7% and 98.2% for the first dataset, and as 99.6%, 99.0% for the second dataset.
Altan and Karasu (2020) have also used an optimization algorithm based approach. Initially they converted each chest X-ray image to grayscale and applied a 2D curvelet transform to obtain a feature matrix. The coefficients in the feature matrix were then optimized with the help of the Chaotic Salp Swarm Algorithm (CSSA). Finally, a DL model, EfficientNet-B0, was used for the purpose of detecting COVID-19 using the optimized features. The authors obtained accuracy, specificity, precision, recall and F-Measure values of 99.69%, 99.81%, 99.62%, 99.44% and 99.53% respectively.
Soui et al. (2021) have developed a model to predict cases of COVID-19 based on clinical symptoms and features. The authors have used two datsets: (i) the Wolfram Data Research Repository (2020); and (ii) the dataset provided in the work by Zoabi, Deri-Rozov, and Shomron (2021). Both the datasets contain clinical and demographic features like age, gender, presence of symptoms (cough, fever, etc.), and so on. For FS, the authors have used the non-dominated sorting genetic algorithm (NSGA-II) to select the best features. The objective function that they have used considered a trade-off between two opposite objectives: minimizing the number of features, and maximizing the weights of the selected features. Finally, an AdaBoost classifier is used to obtain the predictions. The authors have obtained accuracy and AUC values of 85% and 87.16% on the first dataset, and of 95.56% and 96.87% on the second dataset. The authors have also shown that their approach of using NSGA-II provides a statistically significant improvement when compared with some other approaches.
Turkoglu (2021) has developed a model for detecting COVID-19 in chest X-rays termed as COVIDetectioNet. The work utilizes a pretrained AlexNet based model for extracting features. Unlike some works which use the outputs from the final fully connected layers as features, here the outputs from the intermediate convolution layers are used as well. The final feature vector is obtained via the concatenation of the individual vectors obtained from all the intermediate outputs. For FS, the Relief algorithm is used, and for classification, an SVM model is trained. The dataset used is a combination of three individual publicly available datasets and the final dataset consists of 6092 total X-rays of which 219 are from COVID-19 affected patients, 1583 are normal and the rest are from pneumonia-affected individuals. The authors have obtained an accuracy of 99.18%.
Sen et al. (2021) have proposed an approach for COVID-19 prediction in chest CT images. The main idea is of performing the FS in two stages. Initially, a CNN model has been trained to obtain the features. Thereafter, FS is carried out. In the first stage, two filter methods called Mutual Information (MI) and ReliefF have been used for FS, and the highest ranked features from the two algorithms are taken as the selections. These features are then passed into the Dragonfly algorithm (DA) for the selection of the most relevant features. Finally, the classification is performed using an SVM model. The authors have used two open access datasets to validate their model: the SARS-COV-2 CT-Scan dataset and the COVID CT database. The authors have obtained accuracy and F1 scores of 95.77% and 0.9579 on the first dataset, and of 85.33% and 0.8281 on the second dataset.
Too and Mirjalili (2021) have proposed a novel wrapper based method called Hyper Learning Binary Dragonfly Algorithm (HLBDA) for FS. The authors have first established the better performance of HLBDA with respect to some recent algorithms. Thereafter, the authors have used the data provided in Iwendi et al. (2020) for FS and subsequent COVID-19 prediction. The authors have reported an accuracy value of 92.21% using only three selected features.
2.1. Limitations of present COVID-19 papers
In this subsection we highlight some limitations which are observed in recent methods tackling COVID-19 detection from radiological images. The common issues are tabulated in Table 1.
Table 1.
Some common issues that are present in recent works on Covid-19 detection.
| Issue | Description |
|---|---|
| Dataset quality | This is perhaps the most important issue for COVID-19 detection methods (Ezzat et al., 2020, Sen et al., 2021, Soui et al., 2021). Current datasets are of comparatively smaller sizes when compared to other benchmark medical datasets. Obtaining more data is difficult due to the privacy of patient data. As a result, the quality of the predictions may reduced on data outside the training set. DL based approaches are more affected by this issue as these kind of models easily overfit on small datasets. In addition to the quantity of data, there are various factors which reduce the quality of the dataset. For example, radiological abnormalities may be different in different regions. However, most datasets have X-rays or CT scans restricted to a single geography. |
| Feature extraction | Recent methods extract features from the input images by one of the following techniques: classical techniques i.e., using feature engineering, DL-based techniques or a hybrid of the previous two. Classical techniques generally produce inferior results when compared to DL-based or hybrid techniques. At the same time, DL-based techniques are mostly black-box models and it is difficult to interpret their results easily. Hence, it is a practical trade-off between classification performance and the explainability of the model, both of which are important for medical image classification. |
| Parameter tuning | Parameter tuning is an important stage in both meta-heuristic and DL-based approaches (Goel et al., 2020, Turkoglu, 2021) in which the optimal values for the input parameters of a model are decided. The advent of various exhaustive and randomized tuning techniques has automated the entire process. However, the tuning stage is still an important and time-consuming part of various methods which contributes significantly to the performance. It is often difficult to find parameters which perform well on both training and testing data. |
| Heavyweight DL-based methods | In general, DL based methods produce better results as compared to conventional methods. There are a few disadvantages associated with them as mentioned above. However, many DL based approaches using the latest architectures like graph neural networks (Bhowal, Sen, Yoon, et al., 2021, Biswas et al., 2021, Kundu, Singh, Ferrara, et al., 2021, Kundu, Singh, Mirjalili, and Sarkar, 2021, Yu et al., 2021) or spiking neural networks (Garain et al., 2021) require a lot of computational resources. This is also valid for methods using techniques such as ensembling and pruning (Rajaraman et al., 2020). These methods are able to obtain very high performance scores but their resource-hungry nature makes them uneconomical to use practically in many scenarios. |
| Computing environment | This issue is especially common in methods where one step involves the use of DL and another step involves the use of meta-heuristic algorithms. Some times, DL algorithms are implemented in Python while meta-heuristic algorithms are implemented in any other language. This is because Python provides many features and libraries suited for implementing DL algorithms which other languages may be lacking. This can sometimes produce a marked change in the results due to data-interchange issues like incompatible formats, different representation of vectors, etc. Sahlol et al. (2020) are one of the first to mention this issue. |
| Limitations of FS Methods | In various COVID-19 papers FS is also used like in Bandyopadhyay, Basu, Cuevas, and Sarkar (2021), Bhowal, Sen, and Sarkar (2021) and Chattopadhyay, Kundu, Singh, Mirjalili, and Sarkar (2021). But there are a few disadvantages associated with each meta-heuristic method and choosing the best meta-heuristic very critical Tuning the parameters of each algorithms is also a challenging task. For example, Genetic Algorithm (GA) has a slower convergence rate and is less flexible. For Particle Swarm Optimization (PSO), it can be difficult to define the initial parameter values. It also has a problem of premature convergence. In addition, Grey Wolf Optimizer (GWO) may fail sometime to find optimal solution. |
3. Proposed approach
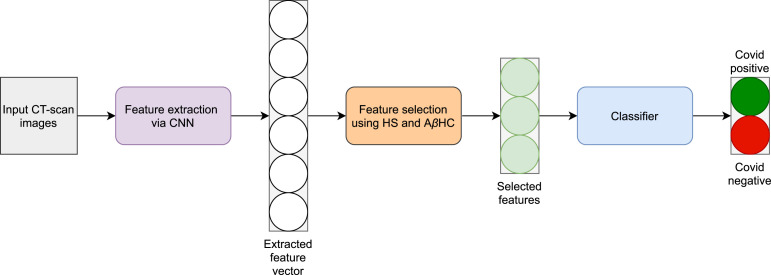
In this section we discuss our proposed approach. Fig. 1 gives a high-level overview of the classification pipeline. First, the input CT-scan images are used to train a CNN model which serves as the feature extractor. The features are essentially the output from the layer just before the layer containing the prediction probabilities. The features are then used for FS using the HS and AHC algorithms to obtain the most relevant features. Thereafter, the features are used to train a classifier to obtain the final predictions i.e., whether the input CT-scan image is COVID-19 positive or negative.
Fig. 1.
A pictorial overview of the proposed work used for COVID-19 detection. HS and AHC denote the Harmony Search and Adaptive -Hill Climbing algorithms respectively.
In the following subsections, we discuss each major stage of the above pipeline in detail.
3.1. Feature extraction
For the purpose of feature extraction, we use a CNN based model (LeCun et al., 1995). A CNN generally consists of convolutional layers and pooling layers along with non-linear activation functions. The output from the last convolutional layer is usually followed by a flattening or global pooling layer to produce a 1D tensor. This is followed by one or more dense layers. The last dense layer produces a 1D tensor with dimension equal to the number of output classes and usually has a softmax activation associated with it. It encodes a probability distribution denoting the likelihood of the image belonging to any of the classes. Modern architectures also use techniques such as batch normalization (Ioffe & Szegedy, 2015) and dropout (Srivastava, Hinton, Krizhevsky, Sutskever, & Salakhutdinov, 2014) to improve network performance.
Neural networks in general require a large quantity of input data to produce good results and for generalizability of the trained model. This is because of the problem of overfitting in small datasets, especially in heavyweight networks. To mitigate this effect, many researchers use transfer learning. It involves the use of knowledge gained in some source domain and applying it to the target domain of interest. As it is difficult to get a large amount of data (especially in new domains), CNNs are rarely trained from scratch with random initialization. It is common to initialize the weights of the base model with weights obtained after training on another larger dataset, e.g. ImageNet.1 Here, the base model refers to the CNN up to the flattening or global pooling layer. The base model is then followed by custom dense layer(s) with the last layer having the number of outputs as required in the target task. In general, the base is used as a feature extractor with fixed weights while the dense layers are trained as usual. Fine tuning is an additional step where the entire network (including the base) is again trained with a low learning rate.
In this work, we use two main modes of training. The first mode (referred to as mode 1) uses transfer learning and fine tuning as described above with a single dense layer following the global pooling layer. In this mode, the dense layer following the global pooling layer is trained for 40 epochs at a learning rate of 0.001 keeping the weights of the base model frozen. Thereafter, the entire network is fine tuned for another 10 epochs at a low learning rate of 0.0001.
In the second mode (referred to as mode 2), the dense layers are not trained to convergence first. Instead, the entire network is trained for 40 epochs with a higher learning rate of 0.001 as compared to the fine tuning step in the first mode. In both the modes, the ImageNet dataset is used for the initialization of the weights of the base model and the Adam (Kingma & Ba, 2014) optimization algorithm is used for training. Mode 1 represents the conventional fine tuning approach with a low learning rate. However, some recent works (Horry et al., 2020, Loey et al., 2020) have benefitted from higher learning rates. Hence we also use mode 2 for the purpose of comparison.
We consider the following state-of-the-art CNNs for the purpose of classifying the input images: ResNet152 (He, Zhang, Ren, & Sun, 2016), DenseNet201 (Huang, Liu, Van Der Maaten, & Weinberger, 2017) and Xception (Chollet, 2017).
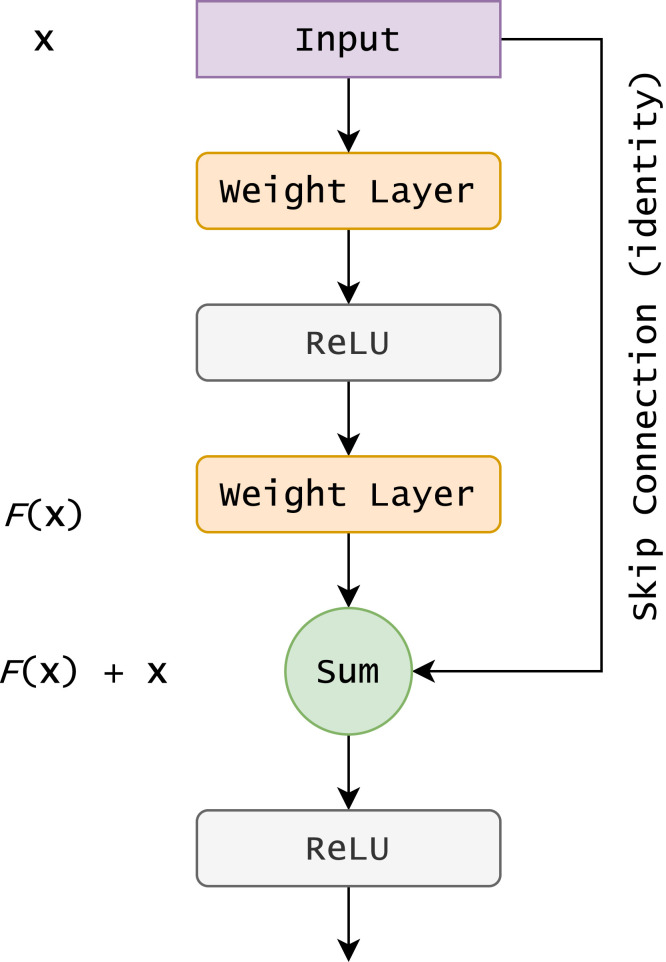
The ResNet architecture was first proposed to tackle the common challenges faced while training very deep neural networks. It adds skip connections between layers which diminish the vanishing gradients problem in deep networks and improve the overall performance. The skip connections are highlighted in Fig. 2 as the “identity” path.
Fig. 2.
A pictorial representation of the skip connections in the ResNet architecture (He et al., 2016).
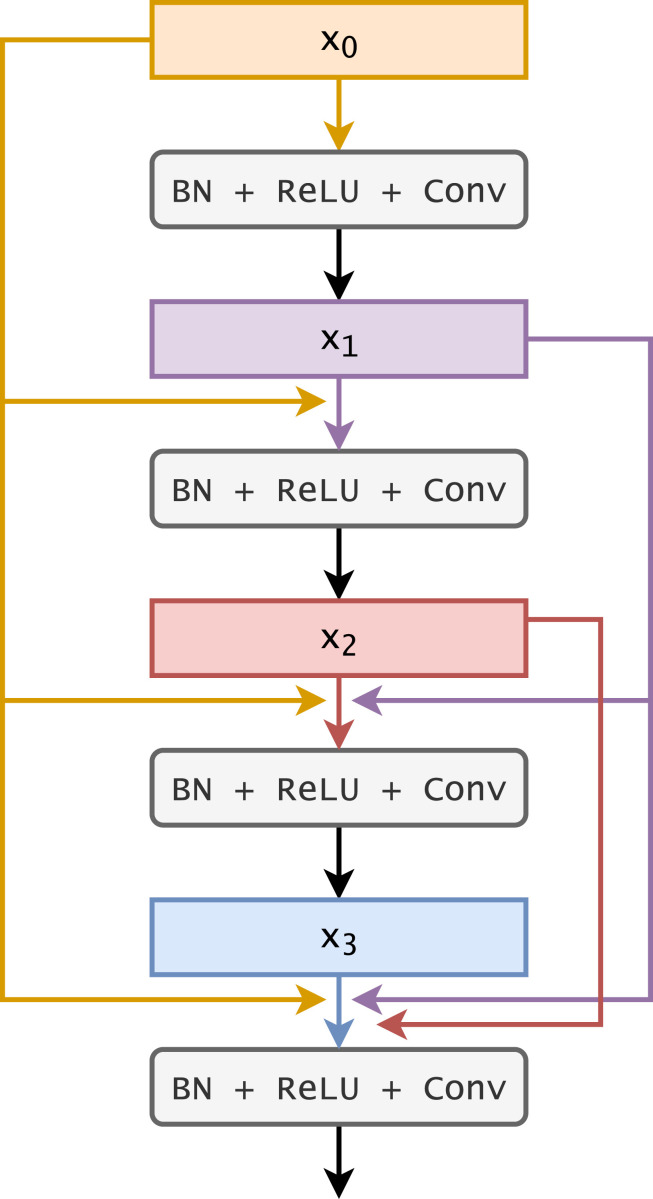
The DenseNet architecture is similar to the ResNet architecture. Instead of skip connections, it consists of layers which are directly connected to each other. Fig. 3 provides a pictorial representation of the basic architecture. It can be seen (in the figure) that the output of a particular layer is connected to all the subsequent layers. These direct connections lead to parameter efficiency since the learning of redundant features are avoided due to the direct connections. Another advantage is that this leads to improved flow of information and gradients through the network.
Fig. 3.
A pictorial representation of the dense connections in the DenseNet architecture (Huang et al., 2017).
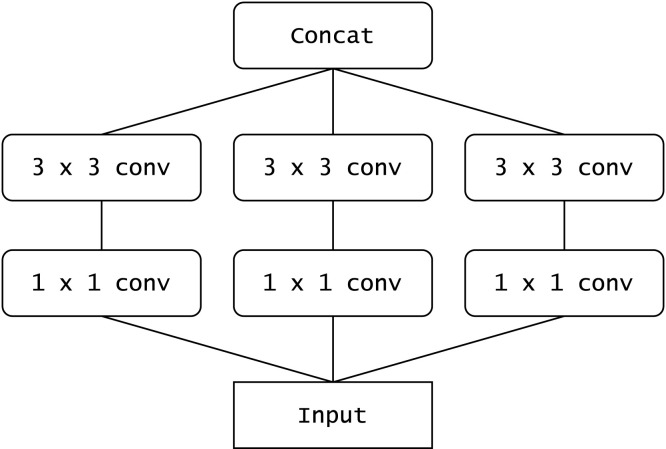
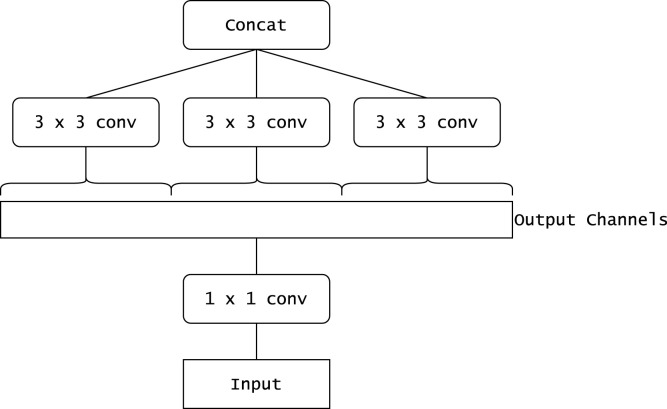
Xception presents an interpretation of inception blocks (used in the Inception architectures (Szegedy et al., 2015)) as depthwise separable convolutions. Fig. 4 shows a simplified schematic of an inception block. Fig. 5 shows an equivalent reformulation of the inception block. When each spatial convolution in Fig. 5 is applied per output channel, the situation is almost the same as when using depthwise separable convolutions. As compared to the InceptionV3 architecture, it obtains better results on the ImageNet dataset despite having approximately the same number of parameters. This indicates that the Xception architecture makes more efficient use of the parameters.
Fig. 4.
A schematic diagram representing a simplified inception block (Chollet, 2017).
Fig. 5.
A schematic diagram representing a strictly equivalent reformulation of the simplified inception block (Chollet, 2017).
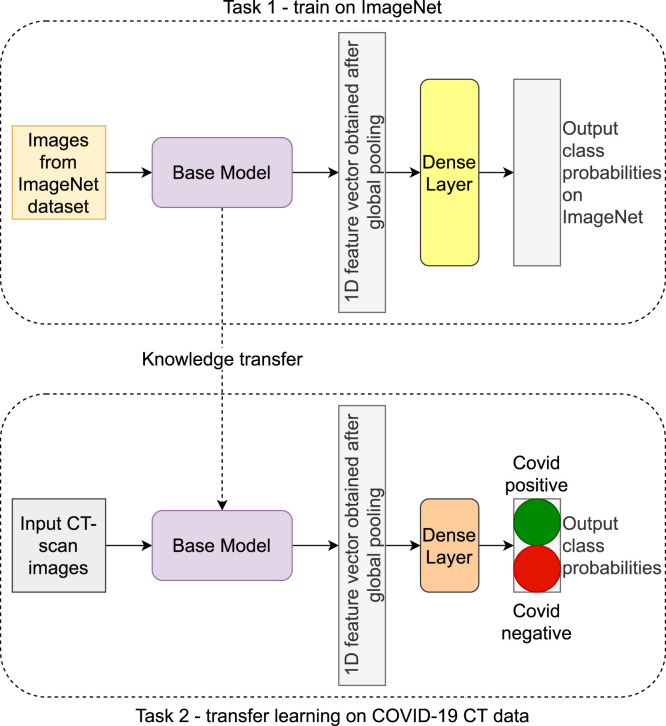
The models considered above are all pre-trained on the ImageNet dataset. It is also noted that all the models have a global (average) pooling layer instead of a flattening layer. This is followed by a dense layer having two classes each corresponding to COVID-19 positive and COVID-19 negative respectively. The basic workflow and architecture of the models is shown in Fig. 6.
Fig. 6.
A schematic diagram of the feature extraction approach.
Task 1 refers to the pretraining performed on the ImageNet dataset. Task 2 refers to the training process on the CT scan dataset used in this work. The base model architecture remains the same in both the tasks. The only modification is a custom dense layer used in the final task (Task 2) due to the mismatch in the number of output classes. The output of the global pooling layer is the required feature vector in our case, which is a 1D tensor. We obtain 1D tensors of dimensions 1920, 2048 and 2048 corresponding to the DenseNet, ResNet and Xception models respectively. These feature vectors are used in the next stage of FS as explained in the next subsection. Before that the implementation details and the various parameters are summarized in the next subsection.
3.1.1. Implementation details
The Tensorflow Keras framework is used to implement the feature extractor CNNs. The three models used in the present work are implemented in the above framework using the tf.keras.applications module. The exact names of the classes are: ResNet152V2, DenseNet201 and Xception. When instantiating the classes, the include_top argument is set to False to indicate that custom layers will be used at the end. The following layers are added at the end of the base model: 2D global average pooling, batch normalization, dropout (probability = 0.2) and a fully-connected layer with 2 output units having a softmax activation.
The input images are loaded and partitioned using the data loader modules available in the above framework. The images have been partitioned into 2 parts: the training set and the test set. Models are trained on the training set and evaluated on the test set. Furthermore, 20% of the training set are used as the validation set. The exact details are mentioned in Section 4 since some aspects depend on the dataset being used.
As mentioned previously, there are two modes used for training the CNNs. The exact details and parameters involved are summarized below:
-
1.
Mode 1: This is the classic transfer learning approach. At first, a base model is initialized with the ImageNet weights. Then, the base model’s parameters are freezed and the custom layers are trained for 40 epochs with an initial learning rate of 0.001. After that the weights of the base model are unfreezed, and the model is trained for another 10 epochs at a reduced initial learning rate of 0.0001.
-
2.
Mode 2: Here, instead of freezing the weights, the entire model is trained for 40 epochs with an initial learning rate of 0.001.
In both the modes, during training, the Adam optimizer is used for training, categorical cross-entropy is used as the loss function and the ReduceLROnPlateau callback is used to reduce the learning rate by a factor of 10 if the loss does not improve for 10 epochs.
3.2. Feature selection
In this section, the basic framework of the FS process is discussed. Before that, we highlight the reasons for the selection of the algorithms used in the present work. The reasons why HS algorithm is used along with AHC are the following:
-
•
HS is fast compared to other traditional meta-heuristic algorithms.
-
•
Unlike GA, HS improvises a new solution based on the whole population rather than best two solutions, which may often lead to premature convergence.
-
•
According to the No Free Lunch theorem (Wolpert & Macready, 1997), for no two algorithms can it can be proved that one is superior than the other. Rather, only for a particular problem can one meta-heuristic algorithm be proved to be better based on experimental results.
-
•
Almost all meta-heuristics suffer from the probability of premature convergence in local optima. To overcome this issue often a local search method comes handy.
-
•
For general HC and HC, the value of has to be chosen beforehand, if the value of is too large, the local search cannot guarantee proper exploitation of the good element of the current solution. Rather, in AHC the parameter is deterministically updated during the search.
3.2.1. Harmony search
HS is an algorithm proposed by Geem, Kim, and Loganathan (2001). The core concept of HS is influenced from the artificial phenomenon of musical harmony. Musical harmony is composition various musical tones, which is considered pleasing from an aesthetic point of view. In musical harmony the relation between frequency of some tunes may induce better aesthetic quality of the harmony. Musical performance is the process to find the best aesthetically pleasing harmony, and this can be achieved through practice. Similarly an optimization problem also seeks the solution with best performance measured by the objective function. HS Algorithm introduces Harmony Memory (HM) which is just collection of harmonies. The HS algorithm follows few simple steps:
-
•
Step 1: Initialize HM on randomized form.
-
•
Step 2: Improvise new harmony from the HM on random basis.
-
•
Step 3: If improvised outperforms worst performing harmony replace it.
-
•
Step 4: If stopping criterion is not met, continue from Step 2.
The key features of HS algorithms are:
-
•
Unlike other nature-inspired meta heuristic algorithms, HS does not require too much mathematical parameter setting.
-
•
In the improvisation step, new harmony is generated purely based on randomized stochastic method.
-
•
In GA new cross-over generation is generated based on the two best performing individuals in population, but in HS, a new harmony is generated based on all the existing harmonies in harmony memory. This may help HS algorithm to increase its stochastic nature.
Due to the above reasons HS algorithm can find the global best solution in lesser time than other meta-heuristic algorithms. However, it also lacks some qualities. Because the proposed algorithm in Geem et al. (2001) improvises new harmony solely based on the random initialized HM, it lacks exploration qualities unlike other contemporary algorithms. That is why in Mahdavi, Fesanghary, and Damangir (2007), an improved HS algorithm is proposed, by introducing few mathematical parameters, which in turn increases the fine-tuning of the algorithm. The authors of Mahdavi et al. (2007) introduced two major additions to standard HS algorithm. One is, Harmony Memory Consideration Rate (HMCR) and other one is Pitch Adjustment Rate (PAR). Let, us define the HM:
| (1) |
Where is th harmony and is number of harmonies in HM. Again the th harmony can be refactored in the following way:
| (2) |
Where is the th decision variable of th harmony and the K is the dimension of solution vector.
Let, a new improvised harmony is denoted by where, for each . Here, and are the upper-bound and lower-bound of th decision variable respectively. The HMCR is defined as the rate of choosing values from solution history of HM. On the other hand, (1 - HMCR) denotes the rate of choosing any random value from the possible range of values of any decision variable. The HMCR undertakes values in range [0, 1]. For example, if HMCR undertakes the value of 0.75, that means 75% times the decision values of an improvised harmony will be taken from the HM, and 25% times decision values will be random value from the range of that specific decision variable.
| (3) |
Now, for will undergo pitch adjustment. As, PAR also takes values in range [0, 1] so pitch adjustment process is as followed.
| (4) |
Where Rand() is the uniform random number generator which gives values in the range of [0,1].
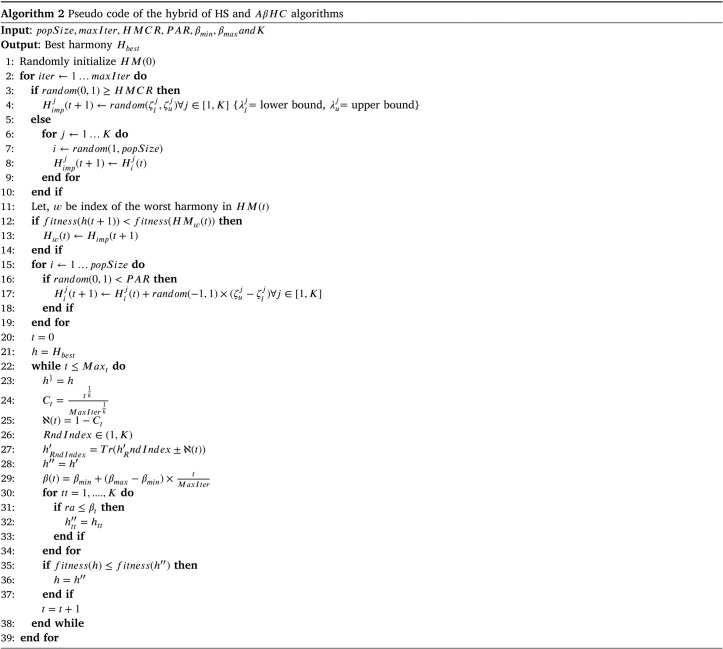
Algorithm 1 is a comprehensive pseudo code for HS algorithm considering HMCR and PAR. In case of FS, and . Here corresponding to selection of that feature in the reduced feature set represented by th harmony and correspond to discarding of feature from the reduced feature set.
3.2.2. Adaptive -Hill Climbing
Hill Climbing (HC) is a simple local search algorithm. But, it has some flaws like it may not able to find the global solution. To overcome this flaw in Al-Betar (2016), an improved HC algorithm called HC was proposed. In HC the local search has two operators, - operator (Neighborhood operator) and - operator. The - operator randomly chooses a neighboring solution of an existing solution. Suppose, is an existing solution, we can find an local solution , with respect to the existing solution in the following way:
| (5) |
Here denotes highest possible distance between existing solution and neighboring solution. U(0, 1) generates random number in range of [0, 1]
The -operator is inspired by the uniform mutation operator of GA. The -operator manipulates the local solution in following way:
| (6) |
where is a value in the range of . is a number in range of and rand() generates random value in range of . The performance of HC largely depends on parameter settings, which means coming up with best possible values and . And this require lot of experimentation. To avoid this step Adaptive HC is proposed in Al-Betar, Aljarah, Awadallah, Faris, and Mirjalili (2019), which takes away to the additional step of experimentation to find the best possible value of and . In AHC algorithm and are represented as function iteration value. Suppose is the value of at th iteration.
| (7) |
Where MaxIter is the maximum iteration and k is a constant value. is the value of in th iteration.
| (8) |
Where and are lower-bound and upper-bound of respectively. If have better performance than , then is replaced with in the population.
3.2.3. Fitness function
The fitness function used to judge the quality of a particular solution is defined below:
Here H is the harmony for which the score is being calculated, is a constant in range [0, 1]. represents the number of selected features in the harmony. is a function which computes classification accuracy for the selected features represented by Harmony H.
In our proposed method we have used and KNN classifier with 5 neighbors as a classifier for .
3.2.4. Implementation details
The implementation of the FS2 part is done in MatLab. For the other meta-heuristic based algorithms used, we have used Py_FS3 4 open source library in python.
4. Results and discussion
In this section, we first highlight the two datasets that are used for evaluating the proposed approach. Thereafter, the results and some relevant discussions are presented.
4.1. Datasets used
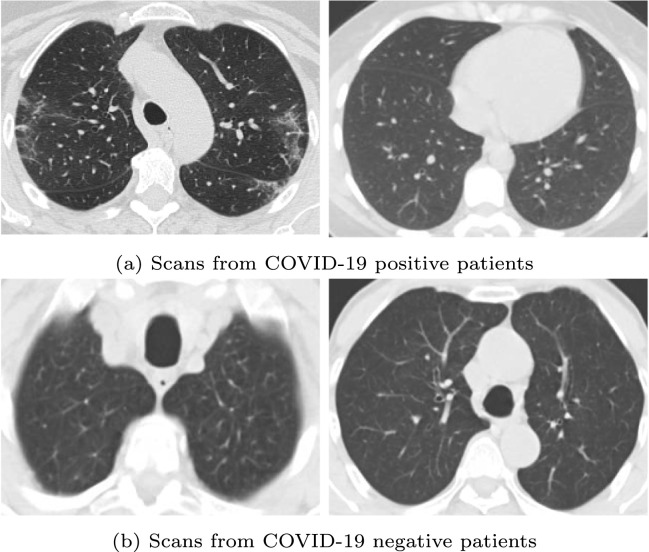
The SARS-COV-2 CT-Scan Dataset5 (Soares et al., 2020) is the first used for training and testing the proposed approach. It is referred to as dataset 1 in the subsequent text. It contains 2482 CT scans in total among which 1252 scans are COVID-19 positive while the remaining 1230 scans are COVID-19 negative. For this dataset, the ratio of the training set to the test set is 85% to 15%. Fig. 7 shows some sample images from the dataset.
Fig. 7.
Some sample CT images from the SARS-COV-2 CT-Scan Dataset.
The authors of the first dataset also released a second updated dataset6 on Kaggle. This is referred to as dataset 2 in the subsequent sections. From this dataset, 758 CT scans from healthy patients (15 CT scans per patient on an average) and 2168 CT scans from COVID-19 affected patients (27 CT scans per patient on an average) are used for training and testing the models. In this dataset, the scans from different patients are clearly separated into different folders. As a result, to construct the training and test splits, we split at the same ratio of 85% to 15% randomly at the folder level instead of the file level. This helps to prevent scans from the same patient from occurring in both the training and test sets, though the splits may not be entirely as per the required ratio. The final training set contains 643 normal scans and 1840 COVID-19 affected scans, and the final test set contains 115 normal scans and 328 COVID-19 affected scans.
4.2. Preprocessing
The images are resized to fixed dimensions of 224 × 224. Online data augmentation is employed while training the CNN based feature extractors to improve the diversity of the training data. Offline data augmentation generally increases the size of the dataset by a large amount which greatly affects the time taken to train the models and run the FS algorithms. As a result, online augmentation is considered as a good approach because it can achieve the same effect of data diversity without requiring new image files on the system. This also reduces the training time.
For augmentation, the ImageDataGenerator 7 module in Tensorflow Keras is used. The applied augmentation techniques include: random rotation up to 45 degrees, random height and width shifts up to a factor of 0.2 of the height or width of the entire image, random zoom up to a factor of 0.2 and random horizontal flip. All the images are normalized from the range of into the range of .
The exact arguments corresponding to the above are as follows:
-
1.
Random rotation: rotation_range=45
-
2.
Random height and width shifts: height_shift_range=0.2, width_shift_range=0.2
-
3.
Random zoom: zoom_range=0.2
-
4.
Procedure for filling points outside image boundaries: fill_mode=‘nearest’
-
5.
Random horizontal flip: horizontal_flip=True
-
6.
Rescale factor: rescale=1/255
4.3. Performance metrics
In this subsection, a brief discussion is presented on the various metrics used for quantifying the performance of the algorithms used for comparison.
The most common basic metric used is accuracy. It represents the fraction of the CT-scans in the test set that are correctly identified as normal or COVID-19 affected. In real-world scenarios, this is the primary metric for any computer-aided prediction method. A higher accuracy is essential for any method to be used as an initial screening measure. In the following subsections, the accuracy is presented, as well as the increase in accuracy obtained over the basic feature extractor CNNs. Ideally, the FS algorithm should provide a decent increase over the base extractor, and also have a good enough accuracy to be used in real-world scenarios.
Apart from accuracy, the next important metric is the number of selected features. A lesser number of selected features means that the inference time will reduce considerably. At the same time, this reduction in the number of features should also preserve the accuracy since we have a lesser number of features during prediction. It is expected that the FS algorithm will provide a good accuracy score while selecting the least number of features. This can be thought of as a trade-off between the quality of predictions (accuracy) and the inference time (number of selected features).
4.4. Parameter settings
In addition to HS, we also use some notable meta-heuristic algorithms like GA (Whitley, 1994), PSO (Kennedy & Eberhart, 1995), GWO (Mirjalili, Mirjalili, & Lewis, 2014), Whale Optimization Algorithm (WOA) (Mirjalili & Lewis, 2016) and Binary Bat Algorithm (BBA) (Mirjalili, Mirjalili, & Yang, 2014) for the purpose of comparison. Table 2 highlights the parameters associated with the above algorithms. The values are set experimentally.
Table 2.
Parameter values used for all the meta-heuristic algorithms.
| Algorithm | Parameters |
|---|---|
| GA | Mutation rate = 0.3, Crossover rate = 0.4 |
| PSO | weight = [1 0] |
| GWO | a = [2 0] |
| WOA | a = [2 0] |
| BBA | L = 1, PER = 0.15, = 0.95, = 0.5 |
| HS | HMCR = 0.9 |
Here L is loudness and PER is pulse emission rate of a bat.
4.5. Execution time
The execution times for the CNN based feature extractors on the two datasets are reported in Table 3. The common trend is that the DenseNet201 model takes the least time per iteration while the ResNet152 model takes the most time. The Xception model takes slightly more time per iteration (around 2 s to 4 s more) than the DenseNet201 model.
Table 3.
The average time taken per iteration for each of the CNN feature extractors applied on two datasets. Times reported correspond to a 14 GB NVIDIA GPU.
| Model | Time taken |
|
|---|---|---|
| Dataset 1 | Dataset 2 | |
| DenseNet201 | 38.7 s | 44.7 s |
| ResNet152 | 50.9 s | 58.9 s |
| Xception | 40.6 s | 48.7 s |
The average execution time for FS per iteration of meta-heuristic algorithm is approximately 23.13 s for the featureset with 2048 features and 19.66 s for the featureset with 1920 features.
4.6. Results on dataset 1
Table 4 shows accuracies and F1-scores of the DL models on the testing partition of the dataset. Apart from the Xception model, it is noted that the performance is quite similar in both the modes of training. The performances of the DenseNet and ResNet models are slightly lower in mode 2. The Xception model, however, performs much better in mode 2 where the learning rate is higher.
Table 4.
Accuracies and F1-scores of the DL models on the test partition of dataset 1.
| Mode | Model | Accuracy (%) | F1 score (%) |
|---|---|---|---|
| Mode 1 | DenseNet201 | 93.93 | 93.93 |
| ResNet152 | 93.12 | 93.12 | |
| Xception | 91.90 | 91.90 | |
| Mode 2 | DenseNet201 | 93.52 | 93.53 |
| ResNet152 | 92.18 | 92.17 | |
| Xception | 94.34 | 94.34 | |
The proposed FS method has performed the best with all of the 6 deep features in comparison to the other state-of-the-art methods like GA, PSO, WOA, GWO and BBA.
Table 5 shows the improvement in accuracy on the basic DL models obtained after FS in training mode 1. It is noted that there is a marked improvement in the accuracy after FS is carried out. Additionally, apart from the DenseNet model, all the models benefit from the inclusion of a local search in the FS process. The Xception model obtains the highest accuracy of 97.16% and also the greatest increase in accuracy. For the DenseNet model, however, there is no improved performance with the inclusion of the local search with the HS algorithm. This indicates that, in this particular case, the initial search converged to the optimal local configurations.
Table 5.
The results of feature selection (FS) in mode 1 on dataset 1.
| Model | FS algorithm | Accuracy (%) | % increase |
|---|---|---|---|
| DenseNet201 | GA | 95.54 | 1.61 |
| PSO | 94.33 | 0.40 | |
| GWO | 95.54 | 1.61 | |
| WOA | 93.11 | −0.82 | |
| BBA |
94.73 |
0.80 |
|
| HS | 95.54 | 1.61 | |
| HS + AHC | 95.54 | 1.61 | |
| ResNet152 | GA | 94.33 | 1.21 |
| PSO | 94.73 | 1.61 | |
| GWO | 94.73 | 1.61 | |
| WOA | 95.14 | 2.02 | |
| BBA |
93.52 |
0.40 |
|
| HS | 94.33 | 1.21 | |
| HS + AHC | 95.14 | 2.02 | |
| Xception | GA | 96.76 | 4.86 |
| PSO | 95.95 | 4.05 | |
| GWO | 96.35 | 4.45 | |
| WOA | 94.73 | 2.83 | |
| BBA |
95.95 |
4.05 |
|
| HS | 96.35 | 4.45 | |
| HS + AHC | 97.16 | 5.26 | |
Table 6 highlights the reductions in the number of features after performing FS in training mode 1. It is observed that the percentage reduction in the number of features is more than 50% in all the cases. The entry with the greatest accuracy in Table 5 is Xception using HS and a local search. It has a reduction percentage of 55.42% which is the lowest among the other entries.
Table 6.
The reduction in the number of features after FS (FS) in mode 1 on dataset 1.
| Model | FS algorithm | No. of features |
% reduction | |
|---|---|---|---|---|
| initially | finally | |||
| DenseNet201 | HS | 1920 | 800 | 58.33 |
| HS + AHC | 1920 | 786 | 59.06 | |
| ResNet152 | HS | 2048 | 793 | 61.28 |
| HS + AHC | 2048 | 888 | 56.64 | |
| Xception | HS | 2048 | 781 | 61.86 |
| HS + AHC | 2048 | 913 | 55.42 | |
Table 7 shows the accuracy improvements on the basic DL models obtained after FS in training mode 2. Unlike mode 1, here we note that the accuracy increases for all the models. The DenseNet model achieves the best accuracy of 97.30%.
Table 7.
The results of feature selection (FS) in mode 2 on dataset 1.
| Model | FS algorithm | Accuracy (%) | % increase |
|---|---|---|---|
| DenseNet201 | GA | 95.68 | 2.16 |
| PSO | 96.49 | 2.97 | |
| GWO | 96.49 | 2.97 | |
| WOA | 96.49 | 2.97 | |
| BBA |
95.95 |
2.43 |
|
| HS | 96.77 | 3.25 | |
| HS + AHC | 97.30 | 3.78 | |
| ResNet152 | GA | 92.18 | 0.00 |
| PSO | 92.72 | 0.54 | |
| GWO | 92.45 | 0.27 | |
| WOA | 92.18 | 0.00 | |
| BBA |
92.45 |
0.27 |
|
| HS | 92.45 | 0.27 | |
| HS + AHC | 94.34 | 2.16 | |
| Xception | GA | 95.95 | 1.61 |
| PSO | 96.76 | 2.42 | |
| GWO | 95.68 | 1.34 | |
| WOA | 95.68 | 1.34 | |
| BBA |
95.95 |
1.61 |
|
| HS | 95.42 | 1.08 | |
| HS + AHC | 96.22 | 1.88 | |
Table 8 highlights the reductions in the number of features after performing FS in training mode 2. Like mode 1, the reduction percentages are greater than 50% in all the cases.
Table 8.
The reduction in the number of features after feature selection (FS) in mode 2 on dataset 1.
| Model | FS algorithm | No. of features |
% reduction | |
|---|---|---|---|---|
| initially | finally | |||
| DenseNet201 | HS | 1920 | 870 | 54.68 |
| HS + AHC | 1920 | 807 | 57.96 | |
| ResNet152 | HS | 2048 | 833 | 59.32 |
| HS + AHC | 2048 | 838 | 59.08 | |
| Xception | HS | 2048 | 848 | 58.59 |
| HS + AHC | 2048 | 876 | 57.22 | |
Table 9 compares the performance of the proposed approach with some state-of-the-art methods. It is noted the present method is comparable in terms of accuracy with the methods considered.
Table 9.
Comparison of the proposed approach with some state-of-the-art approaches on dataset 1.
| Method | Accuracy (%) |
|---|---|
| DenseNet201 + transfer learning | 96.25 |
| (Jaiswal et al., 2020) | |
| Explainable DL (xDNN) | 97.38 |
| (Soares et al., 2020) | |
| COVID-Net + contrastive training | 90.83 |
| (Wang, Liu, & Dou, 2020) | |
| CNN + bi-stage FS | 95.77 |
| (Sen et al., 2021) | |
| CNN | 94.98 |
| (Jin et al., 2020) | |
| Norm-VGG16 | 96.39 |
| (Ibrahim, Youssef, & Fathalla, 2021) | |
| COV-CAF | 97.59 |
| (Ibrahim et al., 2021) | |
| Proposed | 97.30 |
From the above observations, it can be seen that the proposed method is able to reduce more than 50% of the original number of features. Parallelly, this also leads to an improved classification performance. It can therefore be said that the feature vectors obtained from the CNN models contain some inherent redundancies. Removing the insignificant features not only leads to a saving in terms of memory and time, but also produces an increase in overall performance in terms of the detection accuracy. This is especially important in the medical field where rapid but highly accurate results are of paramount importance.
We can observe from Table 7 that the proposed method outperforms almost all the FS methods considered here for comparison in DenseNet201 and ResNet152 feature sets. Only for the Xception feature set PSO outperforms proposed method with a slight margin. However, this can be considered as an outlier because the present method outperforms PSO in all other cases. The reason behind the proposed method’s good performance can be attributed to the good exploitation capabilities for the HS method. Other meta-heuristic methods take into consideration a few best agents from the population. HS takes into consideration all of the agents to generate the new offspring, which can give HS an edge over he other methods. Coupled with AHC, HS can simply perform very well over various feature sets. As the proposed FS method outperforms state-of-the-art and popular meta-heuristic methods, it can be useful for helping the medical professionals in screening COVID-19 from radiological inputs.
4.7. Results on dataset 2
Table 10 shows the accuracies and F1-scores obtained by the DL models on the testing partition of the dataset. The accuracies obtained by the models are close to each other, but like the previous dataset, there are clear leaders in each mode. The ResNet152 model achieves the best accuracy and F1-score in mode 1 whereas in mode 2, the Xception model achieves the best accuracy and F1 score. It is an interesting observation that in both the datasets, Xception performs the worst in mode 1 and the best in mode 2 when considering the initial results.
Table 10.
Accuracies and F1-scores of the DL models on the test partition of dataset 2.
| Mode | Model | Accuracy (%) | F1 score (%) |
|---|---|---|---|
| Mode 1 | DenseNet201 | 92.74 | 91.27 |
| ResNet152 | 93.88 | 91.95 | |
| Xception | 90.93 | 89.10 | |
| Mode 2 | DenseNet201 | 90.70 | 89.47 |
| ResNet152 | 89.80 | 87.25 | |
| Xception | 93.42 | 91.59 | |
Table 11 shows the results after applying the FS algorithms. Here, the best accuracy overall is obtained by the present FS approach when using the feature from the Xception model trained in mode 1 (conventional transfer learning).
Table 11.
The results of FS on dataset 2. The Model + Mode column indicates in brief the feature extraction model and the testing mode. D, R and X denote the DenseNet201, ResNet152 and Xception models respectively. M1 and M2 denote mode 1 and mode 2 respectively.
| Model + Mode | FS algorithm | Accuracy (%) | % increase |
|---|---|---|---|
| D + M1 | HS | 94.84 | 2.1 |
| HS + AEFA | 95.23 | 2.49 | |
| HS + AHC | 95.23 | 2.49 | |
| R + M1 | HS | 95.23 | 1.35 |
| HS + AEFA | 96.44 | 2.56 | |
| HS + AHC | 96.82 | 2.94 | |
| X + M1 | HS | 96.14 | 5.21 |
| HS + AEFA | 98.59 | 7.66 | |
| HS + AHC | 98.87 | 7.94 | |
| D + M2 | HS | 92.06 | 1.36 |
| HS + AEFA | 92.51 | 1.81 | |
| HS + AHC | 92.51 | 1.81 | |
| R + M2 | HS | 92.07 | 2.27 |
| HS + AEFA | 92.74 | 2.94 | |
| HS + AHC | 92.74 | 2.94 | |
| X + M2 | HS | 95.71 | 2.29 |
| HS + AEFA | 96.14 | 2.72 | |
| HS + AHC | 97.62 | 4.2 | |
4.8. Statistical test
Here, we report the results of a statistical test that is conducted to show that the results obtained by the present method are statistically significant. Specifically, the Wilcoxon rank-sum test (Carrasco, García, Rueda, Das, & Herrera, 2020) is used for this purpose. The above test examines the null hypothesis that two sets of measurements are drawn from the same distribution essentially indicating that the performance of the two models being considered are similar to each other. The alternative hypothesis is that values in one sample are more likely to be larger than the values in the other sample. A -value of less than 0.05 indicates that the null hypothesis is rejected at the 5% significance level.
Table 12, Table 13 highlight the p-values obtained from the Wilcoxon test on dataset 1. It is observed that the p-values are less than 0.05 for all of the algorithms considered for comparison on dataset 1. Thus the alternative hypothesis holds here: the present method achieves higher accuracy than the other methods.
Table 12.
The p-values obtained from the Wilcoxon rank-sum test on the dataset 1 in mode 1 when comparing the present method in the best setting (Xception features) with the other algorithms.
| FS algorithm | -value |
|---|---|
| GA | 0.0001 |
| PSO | 0.0001 |
| GWO | 0.0001 |
| WOA | 0.0001 |
| BBA | 0.0001 |
| HS | 0.0001 |
Table 13.
The p-values obtained from the Wilcoxon rank-sum test on the dataset 1 in mode 2 when comparing the present method in the best setting (DenseNet201 features) with the other algorithms.
| FS algorithm | -value |
|---|---|
| GA | 0.0001 |
| PSO | 0.0001 |
| GWO | 0.0001 |
| WOA | 0.0001 |
| BBA | 0.0001 |
| HS | 0.0001 |
4.9. Findings
Here we summarize the important observations from the above experiments:
-
•
Using FS on features extracted via CNNs provides a noticeable improvement in the detection accuracies. This is true for almost all the FS methods considered here.
-
•
The present approach using HS + AHC for FS is able to consistently outperform several standard algorithms like GWO, PSO, BBA, etc.
-
•
Integration of a local search (AHC) is able to provide a considerable boost to model accuracy over the basic HS algorithm without local search.
-
•
The final performance after FS cannot be predicted using the initial accuracies obtained from the CNNs. In our case, the Xception model in training mode 1 is such an example. It obtains the least accuracy by itself, but shows the best performance when FS is used.
5. Conclusion
In this work, we propose an end-to-end framework for detecting COVID-19 from CT scan images. The proposed approach consists of two stages: feature extraction followed by FS. The feature extraction stage utilizes CNN models to obtain a feature vector from the input images. We use three state-of-the-art CNN architectures: DenseNet, ResNet and Xception as feature extractors in this stage. Thereafter, a FS stage is applied to filter out insignificant features from the obtained feature vectors. A combination of an optimization algorithm, called HS, with a local optimization algorithm, called AHC, is employed in this stage.
The experimental results indicate that a FS stage using an optimization algorithm is able to improve on the performance of the feature extractor CNNs. Furthermore, it is also observed that the inclusion of the local search improves the classification accuracy in most of the cases. The best accuracy scores obtained by the present approach (HS and local search via AHC) are 97.30% and 98.87% respectively on the two datasets.
One limitation of the proposed approach is that it may not be able to detect CT scans as COVID-19 positive in the very early stages of infection. This is mainly due to the fact that there may not be any significant artifacts in these kind of scans. Thus, the CNNs used here may not be able to find suitable features. In future work, we aim to tackle this limitation by improving the feature extraction stage. Optimization algorithms can be introduced in the feature extraction stage as well to improve performance. Meta-heuristic approaches may be used to tune the parameters of the CNNs. In addition to this, techniques such as ensembling, pruning, attention, etc. can explored in order to make the feature extractors more robust.
CRediT authorship contribution statement
Arpan Basu: Methodology, Software, Validation, Investigation, Writing - original draft. Khalid Hassan Sheikh: Methodology, Software, Validation, Investigation, Writing - original draft. Erik Cuevas: Writing - review & editing, Supervision. Ram Sarkar: Conceptualization, Writing - review & editing, Supervision.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgment
Arpan Basu, Khalid Hassan Sheikh and Ram Sarkar are thankful to the Centre for Microprocessor Applications for Training, Education and Research (CMATER) research laboratory of the Computer Science and Engineering Department, Jadavpur University, Kolkata, India for providing infrastructural support.
Footnotes
14 million+ images, http://www.image-net.org/.
References
- Abdel-Basset M., Abdel-Fatah L., Sangaiah A.K. Computational intelligence for multimedia big data on the cloud with engineering applications. Elsevier; 2018. Metaheuristic algorithms: A comprehensive review; pp. 185–231. [DOI] [Google Scholar]
- Abualigah L.M., Al-diabat M., Shinwan M.A., Dhou K., Alsalibi B., Hanandeh E.S., et al. Wiley; 2020. Hybrid harmony search algorithm to solve the feature selection for data mining applications; pp. 19–37. [DOI] [Google Scholar]
- Ahmed S., Ghosh K.K., Singh P.K., Geem Z.W., Sarkar R. Hybrid of harmony search algorithm and ring theory-based evolutionary algorithm for feature selection. IEEE Access. 2020;8:102629–102645. doi: 10.1109/access.2020.2999093. [DOI] [Google Scholar]
- Al-Betar M.A. -Hill climbing: an exploratory local search. Neural Computing and Applications. 2016;28(S1):153–168. doi: 10.1007/s00521-016-2328-2. [DOI] [Google Scholar]
- Al-Betar M.A., Aljarah I., Awadallah M.A., Faris H., Mirjalili S. Adaptive -hill climbing for optimization. Soft Computing. 2019;23(24):13489–13512. doi: 10.1007/s00500-019-03887-7. [DOI] [Google Scholar]
- Al-Betar M.A., Hammouri A.I., Awadallah M.A., Doush I.A. Binary $$\beta$$-hill climbing optimizer with S-shape transfer function for feature selection. Journal of Ambient Intelligence and Humanized Computing. 2020;12(7):7637–7665. doi: 10.1007/s12652-020-02484-z. [DOI] [Google Scholar]
- Altan A., Karasu S. Recognition of COVID-19 disease from X-ray images by hybrid model consisting of 2D curvelet transform, chaotic salp swarm algorithm and deep learning technique. Chaos, Solitons & Fractals. 2020;140 doi: 10.1016/j.chaos.2020.110071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bandyopadhyay R., Basu A., Cuevas E., Sarkar R. Harris hawks optimisation with simulated annealing as a deep feature selection method for screening of COVID-19 CT-scans. Applied Soft Computing. 2021;111:107698. doi: 10.1016/j.asoc.2021.107698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhowal P., Sen S., Sarkar R. 2021. A two-tier feature selection method using coalition game and nystrom sampling for screening COVID-19 from chest X-Ray images. Springer Science and Business Media LLC. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhowal P., Sen S., Yoon J.H., Geem Z.W., Sarkar R. 2021. Choquet integral and coalition game-based ensemble of deep learning models for COVID-19 screening from chest X-ray images; p. 1. Institute of Electrical and Electronics Engineers (IEEE) [DOI] [PubMed] [Google Scholar]
- Biswas S., Chatterjee S., Majee A., Sen S., Schwenker F., Sarkar R. Prediction of COVID-19 from chest CT images using an ensemble of deep learning models. Applied Sciences. 2021;11(15) doi: 10.3390/app11157004. [DOI] [Google Scholar]
- Carrasco J., García S., Rueda M., Das S., Herrera F. Recent trends in the use of statistical tests for comparing swarm and evolutionary computing algorithms: Practical guidelines and a critical review. Swarm and Evolutionary Computation. 2020;54 [Google Scholar]
- Chakraborty B. 2008 3rd international conference on intelligent system and knowledge engineering. Vol. 1. 2008. Feature subset selection by particle swarm optimization with fuzzy fitness function; pp. 1038–1042. [DOI] [Google Scholar]
- Chatterjee B., Bhattacharyya T., Ghosh K.K., Singh P.K., Geem Z.W., Sarkar R. Late acceptance hill climbing based social ski driver algorithm for feature selection. IEEE Access. 2020;8:75393–75408. doi: 10.1109/access.2020.2988157. [DOI] [Google Scholar]
- Chattopadhyay S., Kundu R., Singh P.K., Mirjalili S., Sarkar R. 2021. Pneumonia detection from lung X-ray images using local search aided sine cosine algorithm based deep feature selection method. Wiley. [DOI] [Google Scholar]
- Chollet F. 2017 IEEE conference on computer vision and pattern recognition. 2017. Xception: Deep learning with depthwise separable convolutions; pp. 1800–1807. [DOI] [Google Scholar]
- Dey S., Bhattacharya R., Malakar S., Mirjalili S., Sarkar R. Choquet fuzzy integral-based classifier ensemble technique for COVID-19 detection. Computers in Biology and Medicine. 2021 doi: 10.1016/j.compbiomed.2021.104585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elaziz M.A., Hosny K.M., Salah A., Darwish M.M., Lu S., Sahlol A.T. New machine learning method for image-based diagnosis of COVID-19. PLoS One. 2020;15(6) doi: 10.1371/journal.pone.0235187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ezzat D., Hassanien A.E., Ella H.A. An optimized deep learning architecture for the diagnosis of COVID-19 disease based on gravitational search optimization. Applied Soft Computing. 2020 doi: 10.1016/j.asoc.2020.106742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fang Y., Zhang H., Xie J., Lin M., Ying L., Pang P., et al. Sensitivity of chest CT for COVID-19: comparison to RT-PCR. Radiology. 2020 doi: 10.1148/radiol.2020200432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fister Jr I., Yang X.-S., Fister I., Brest J., Fister D. 2013. A brief review of nature-inspired algorithms for optimization. arXiv:1307.4186. [Google Scholar]
- Garain A., Basu A., Giampaolo F., Velasquez J.D., Sarkar R. Detection of COVID-19 from CT scan images: A spiking neural network-based approach. Neural Computing and Applications. 2021:1–14. doi: 10.1007/s00521-021-05910-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geem Z.W., Kim J.H., Loganathan G. A new heuristic optimization algorithm: Harmony search. SIMULATION. 2001;76(2):60–68. doi: 10.1177/003754970107600201. [DOI] [Google Scholar]
- Gendreau M., Potvin J.-Y. Metaheuristics in combinatorial optimization. Annals of Operations Research. 2005;140(1):189–213. doi: 10.1007/s10479-005-3971-7. [DOI] [Google Scholar]
- Ghamisi P., Benediktsson J.A. Feature selection based on hybridization of genetic algorithm and particle swarm optimization. IEEE Geoscience and Remote Sensing Letters. 2015;12(2):309–313. doi: 10.1109/LGRS.2014.2337320. [DOI] [Google Scholar]
- Ghosh K.K., Ahmed S., Singh P.K., Geem Z.W., Sarkar R. Improved binary sailfish optimizer based on adaptive -hill climbing for feature selection. IEEE Access. 2020;8:83548–83560. doi: 10.1109/access.2020.2991543. [DOI] [Google Scholar]
- Goel T., Murugan R., Mirjalili S., Chakrabartty D.K. OptCoNet: an optimized convolutional neural network for an automatic diagnosis of COVID-19. Applied Intelligence: The International Journal of Artificial Intelligence, Neural Networks, and Complex Problem-Solving Technologies. 2020:1–16. doi: 10.1007/s10489-020-01904-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He K., Zhang X., Ren S., Sun J. 2016 IEEE conference on computer vision and pattern recognition. 2016. Deep residual learning for image recognition; pp. 770–778. [DOI] [Google Scholar]
- Horry M.J., Chakraborty S., Paul M., Ulhaq A., Pradhan B., Saha M., et al. COVID-19 detection through transfer learning using multimodal imaging data. IEEE Access. 2020;8:149808–149824. doi: 10.1109/ACCESS.2020.3016780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang J., Cai Y., Xu X. A hybrid genetic algorithm for feature selection wrapper based on mutual information. Pattern Recognition Letters. 2007;28(13):1825–1844. doi: 10.1016/j.patrec.2007.05.011. [DOI] [Google Scholar]
- Huang G., Liu Z., Van Der Maaten L., Weinberger K.Q. 2017 IEEE conference on computer vision and pattern recognition. 2017. Densely connected convolutional networks; pp. 2261–2269. [DOI] [Google Scholar]
- Ibrahim M.R., Youssef S.M., Fathalla K.M. 2021. Abnormality detection and intelligent severity assessment of human chest computed tomography scans using deep learning: a case study on SARS-COV-2 assessment. Springer Science and Business Media LLC. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ioffe S., Szegedy C. 2015. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv preprint arXiv:1502.03167. [Google Scholar]
- Iwendi C., Bashir A.K., Peshkar A., Sujatha R., Chatterjee J.M., Pasupuleti S., et al. Covid-19 patient health prediction using boosted random forest algorithm. Frontiers in Public Health. 2020;8:357. doi: 10.3389/fpubh.2020.00357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaiswal A., Gianchandani N., Singh D., Kumar V., Kaur M. Classification of the COVID-19 infected patients using DenseNet201 based deep transfer learning. Journal of Biomolecular Structure and Dynamics. 2020:1–8. doi: 10.1080/07391102.2020.1788642. PMID: 32619398. [DOI] [PubMed] [Google Scholar]
- Jin Y.-H., Cai L., Cheng Z.-S., Cheng H., Deng T., et al. A rapid advice guideline for the diagnosis and treatment of 2019 novel coronavirus (2019-nCoV) infected pneumonia (standard version) Military Medical Research. 2020;7(1):4. doi: 10.1186/s40779-020-0233-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ke L., Feng Z., Ren Z. An efficient ant colony optimization approach to attribute reduction in rough set theory. Pattern Recognition Letters. 2008;29(9):1351–1357. doi: 10.1016/j.patrec.2008.02.006. URL: http://www.sciencedirect.com/science/article/pii/S0167865508000652. [DOI] [Google Scholar]
- Kennedy J., Eberhart R. Proceedings of ICNN’95-international conference on neural networks. Vol. 4. IEEE; 1995. Particle swarm optimization; pp. 1942–1948. [Google Scholar]
- Kermany D.S., Goldbaum M., Cai W., Valentim C.C., Liang H., Baxter S.L., et al. Identifying medical diagnoses and treatable diseases by image-based deep learning. Cell. 2018;172(5):1122–1131. doi: 10.1016/j.cell.2018.02.010. [DOI] [PubMed] [Google Scholar]
- Kingma D.P., Ba J. 2014. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980. [Google Scholar]
- Kundu R., Singh P.K., Ferrara M., Ahmadian A., Sarkar R. ET-NET: an ensemble of transfer learning models for prediction of COVID-19 infection through chest CT-scan images. Multimedia Tools and Applications. 2021:1–20. doi: 10.1007/s11042-021-11319-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kundu R., Singh P.K., Mirjalili S., Sarkar R. COVID-19 detection from lung CT-scans using a fuzzy integral-based CNN ensemble. Computers in Biology and Medicine. 2021;138:104895. doi: 10.1016/j.compbiomed.2021.104895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leardi R. Application of genetic algorithm-PLS for feature selection in spectral data sets. Journal of Chemometrics. 2000;14(5–6):643–655. doi: 10.1002/1099-128x(200009/12)14:5/6¡643::aid-cem621¿3.0.co;2-e. [DOI] [Google Scholar]
- LeCun Y., Bengio Y., et al. The handbook of brain theory and neural networks, vol. 3361. 1995. Convolutional networks for images, speech, and time series; p. 1995. [Google Scholar]
- Lee S., Soak S., Oh S., Pedrycz W., Jeon M. Modified binary particle swarm optimization. Progress in Natural Science. 2008;18(9):1161–1166. doi: 10.1016/j.pnsc.2008.03.018. [DOI] [Google Scholar]
- Loey M., Manogaran G., Khalifa N.E.M. A deep transfer learning model with classical data augmentation and cgan to detect covid-19 from chest ct radiography digital images. Neural Computing and Applications. 2020:1–13. doi: 10.1007/s00521-020-05437-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahdavi M., Fesanghary M., Damangir E. An improved harmony search algorithm for solving optimization problems. Applied Mathematics and Computation. 2007;188(2):1567–1579. doi: 10.1016/j.amc.2006.11.033. [DOI] [Google Scholar]
- Maier A., Syben C., Lasser T., Riess C. A gentle introduction to deep learning in medical image processing. Zeitschrift für Medizinische Physik. 2019;29(2):86–101. doi: 10.1016/j.zemedi.2018.12.003. [DOI] [PubMed] [Google Scholar]
- Mirjalili S., Lewis A. The whale optimization algorithm. Advances in Engineering Software. 2016;95:51–67. [Google Scholar]
- Mirjalili S., Mirjalili S.M., Lewis A. Grey wolf optimizer. Advances in Engineering Software. 2014;69:46–61. [Google Scholar]
- Mirjalili S., Mirjalili S.M., Yang X.-S. Binary bat algorithm. Neural Computing and Applications. 2014;25(3–4):663–681. [Google Scholar]
- Nematollahi A.F., Rahiminejad A., Vahidi B. A novel meta-heuristic optimization method based on golden ratio in nature. Soft Computing. 2019;24(2):1117–1151. doi: 10.1007/s00500-019-03949-w. [DOI] [Google Scholar]
- Rajaraman S., Siegelman J., Alderson P.O., Folio L.S., Folio L.R., Antani S.K. Iteratively pruned deep learning ensembles for COVID-19 detection in chest X-Rays. IEEE Access. 2020;8:115041–115050. doi: 10.1109/ACCESS.2020.3003810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saha S., Ghosh M., Ghosh S., Sen S., Singh P.K., Geem Z.W., et al. Feature selection for facial emotion recognition using cosine similarity-based harmony search algorithm. Applied Sciences. 2020;10(8):2816. doi: 10.3390/app10082816. [DOI] [Google Scholar]
- Sahlol A.T., Yousri D., Ewees A.A., Al-Qaness M.A., Damasevicius R., Abd Elaziz M. COVID-19 image classification using deep features and fractional-order marine predators algorithm. Scientific Reports. 2020;10(1):1–15. doi: 10.1038/s41598-020-71294-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sen S., Saha S., Chatterjee S., Mirjalili S., Sarkar R. A bi-stage feature selection approach for COVID-19 prediction using chest CT images. Applied Intelligence: The International Journal of Artificial Intelligence, Neural Networks, and Complex Problem-Solving Technologies. 2021:1–16. doi: 10.1007/s10489-021-02292-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheikh K.H., Ahmed S., Mukhopadhyay K., Singh P.K., Yoon J.H., Geem Z.W., et al. EHHM: Electrical harmony based hybrid meta-heuristic for feature selection. IEEE Access. 2020;8:158125–158141. doi: 10.1109/access.2020.3019809. [DOI] [Google Scholar]
- Soares E., Angelov P., Biaso S., Froes M.H., Abe D.K. 2020. Sars-CoV-2 CT-scan dataset: A large dataset of real patients CT scans for SARS-CoV-2 identification. MedRxiv, Cold Spring Harbor Laboratory Press. [Google Scholar]
- Soui M., Mansouri N., Alhamad R., Kessentini M., Ghedira K. NSGA-II as feature selection technique and AdaBoost classifier for COVID-19 prediction using patient’s symptoms. Nonlinear Dynamics. 2021:1–23. doi: 10.1007/s11071-021-06504-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Srivastava N., Hinton G., Krizhevsky A., Sutskever I., Salakhutdinov R. Dropout: a simple way to prevent neural networks from overfitting. Journal of Machine Learning Research. 2014;15(1):1929–1958. [Google Scholar]
- Szegedy C., Liu W., Jia Y., Sermanet P., Reed S., Anguelov D., et al. 2015 IEEE conference on computer vision and pattern recognition. 2015. Going deeper with convolutions; pp. 1–9. [DOI] [Google Scholar]
- Too J., Mirjalili S. A hyper learning binary dragonfly algorithm for feature selection: A COVID-19 case study. Knowledge-Based Systems. 2021;212 [Google Scholar]
- Turkoglu M. CoviDetectioNet: COVID-19 diagnosis system based on X-ray images using features selected from pre-learned deep features ensemble. Applied Intelligence: The International Journal of Artificial Intelligence, Neural Networks, and Complex Problem-Solving Technologies. 2021;51(3):1213–1226. doi: 10.1007/s10489-020-01888-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waheed A., Goyal M., Gupta D., Khanna A., Al-Turjman F., Pinheiro P.R. Covidgan: Data augmentation using auxiliary classifier gan for improved covid-19 detection. IEEE Access. 2020;8:91916–91923. doi: 10.1109/ACCESS.2020.2994762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Z., Liu Q., Dou Q. Contrastive cross-site learning with redesigned net for COVID-19 CT classification. IEEE Journal of Biomedical and Health Informatics. 2020;24(10):2806–2813. doi: 10.1109/JBHI.2020.3023246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X., Yang J., Teng X., Xia W., Jensen R. Feature selection based on rough sets and particle swarm optimization. Pattern Recognition Letters. 2007;28(4):459–471. doi: 10.1016/j.patrec.2006.09.003. [DOI] [Google Scholar]
- Whitley D. A genetic algorithm tutorial. Statistics and Computing. 1994;4(2):65–85. [Google Scholar]
- Wolpert D., Macready W. No free lunch theorems for optimization. IEEE Transactions on Evolutionary Computation. 1997;1(1):67–82. doi: 10.1109/4235.585893. [DOI] [Google Scholar]
- Wu C.-X., Liao M.-H., Karatas M., Chen S.-Y., Zheng Y.-J. Real-time neural network scheduling of emergency medical mask production during COVID-19. Applied Soft Computing. 2020;97 doi: 10.1016/j.asoc.2020.106790. URL: http://www.sciencedirect.com/science/article/pii/S1568494620307286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu X., Lu S., Guo L., Wang S.-H., Zhang Y.-D. Resgnet-c: A graph convolutional neural network for detection of COVID-19. Neurocomputing. 2020 doi: 10.1016/j.neucom.2020.07.144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu X., Wang S.-H., Zhang Y.-D. CGNet: A graph-knowledge embedded convolutional neural network for detection of pneumonia. Information Processing & Management. 2021;58(1) doi: 10.1016/j.ipm.2020.102411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zoabi Y., Deri-Rozov S., Shomron N. Machine learning-based prediction of COVID-19 diagnosis based on symptoms. Npj Digital Medicine. 2021;4(1):1–5. doi: 10.1038/s41746-020-00372-6. [DOI] [PMC free article] [PubMed] [Google Scholar]