Classification of amyotrophic lateral sclerosis by brain volume, connectivity, and network dynamics

Abstract

Emerging studies corroborate the importance of neuroimaging biomarkers and machine learning to improve diagnostic classification of amyotrophic lateral sclerosis (ALS). While most studies focus on structural data, recent studies assessing functional connectivity between brain regions by linear methods highlight the role of brain function. These studies have yet to be combined with brain structure and nonlinear functional features. We investigate the role of linear and nonlinear functional brain features, and the benefit of combining brain structure and function for ALS classification. ALS patients (N = 97) and healthy controls (N = 59) underwent structural and functional resting state magnetic resonance imaging. Based on key hubs of resting state networks, we defined three feature sets comprising brain volume, resting state functional connectivity (rsFC), as well as (nonlinear) resting state dynamics assessed via recurrent neural networks. Unimodal and multimodal random forest classifiers were built to classify ALS. Out‐of‐sample prediction errors were assessed via five‐fold cross‐validation. Unimodal classifiers achieved a classification accuracy of 56.35–61.66%. Multimodal classifiers outperformed unimodal classifiers achieving accuracies of 62.85–66.82%. Evaluating the ranking of individual features' importance scores across all classifiers revealed that rsFC features were most dominant in classification. While univariate analyses revealed reduced rsFC in ALS patients, functional features more generally indicated deficits in information integration across resting state brain networks in ALS. The present work undermines that combining brain structure and function provides an additional benefit to diagnostic classification, as indicated by multimodal classifiers, while emphasizing the importance of capturing both linear and nonlinear functional brain properties to identify discriminative biomarkers of ALS.

The current study aims at identifying neuroimaging biomarkers for diagnostic classification of amyotrophic lateral sclerosis (ALS). We investigate the potential of combining brain structure and function for the classification of ALS and examine a novel feature set capturing nonlinear functional features from network dynamics based on recurrent neural networks. We demonstrate that combining different modalities improves classification, and that both linear and nonlinear functional brain features indeed deliver discriminative biomarkers of the disease.

1. INTRODUCTION

Amyotrophic lateral sclerosis (ALS) is a fatal neurodegenerative disease that is predominantly characterized by the progressive loss of motor neuron function (see also Kiernan, Vucic, & Cheah, 2011). Nowadays, ALS is considered a progressive multisystemic neurological disease, affecting multiple domains of the central nervous system beyond classical motor areas (Menke et al., 2014; Pradat & El Mendili, 2014). On average, patients die three years after symptom onset despite continuous efforts to develop curative therapies (see also Hardimann, 2010; Kiernan et al., 2011). The only globally approved therapy, Riluzole, was discovered over two decades ago (Miller, Mitchell, Lyon, & Moore, 2012; Petrov, Mansfield, Moussy, & Hermine, 2017). Both research in ALS and therapeutic management are challenged by the substantial heterogeneity in the patients' disease courses, resulting in different progressivity and survival time (Simon et al., 2014; Westeneng et al., 2018). Therefore, biomarkers that reliably reflect disease‐specific characteristics are urgently needed, aiding early diagnosis and yielding outcome parameters for clinical trials to improve therapies (Goyal et al., 2020; Pradat & El Mendili, 2014).

The potential of neuroimaging as a noninvasive biomarker method has been accepted in the wider ALS research community (Chio et al., 2014; Pradat & El Mendili, 2014). Former studies have focused mainly on classifying ALS patients versus healthy controls based on gray and white matter brain volume assessed for instance via structural magnetic resonance imaging (MRI) and/or diffusion tensor imaging (DTI) (Ferraro et al., 2017; Sarica et al., 2017; Schuster, Hardiman, & Bede, 2016). Combining these modalities, these studies report classification accuracies between 62.5% and 80.0% (mean = 77.12%; Ferraro et al., 2017; Sarica et al., 2017; Schuster et al., 2016). More recently, there have been efforts to also apply features relating to brain connectivity derived from resting state functional MRI (rsfMRI) for classification, reporting accuracies of 65.0% and 71.50% (Fratello et al., 2017; Welsh, Jelsone‐Swain, & Foerster, 2013). Although classification performance seems slightly lower here, there are generally large variations in reported accuracy which more likely reflect the large range of validation procedures, classifiers, and potential biases in prediction error assessment, such as increased misclassification of a minority class in case of unbalanced sample sizes for instance (Cearns, Hahn, & Baune, 2019; He & Garcia, 2009; Koppe, Meyer‐Lindenberg, & Durstewitz, 2020; López, Fernández, & Herrera, 2014; Sun, Wong, & Kamel, 2009), than meaningful differences in the discriminability of the actual feature modality (see also Section 4 on these points). Rather, these studies may be taken as evidence that combining different neuroimaging modalities, in this case relating to brain volume and structural connectivity, improves classification accuracy, by providing complementary discriminative information (see also Ferraro et al., 2017; Schuster et al., 2016; van der Burgh et al., 2017). However, to date, no studies have actually combined brain volume and functional connectivity features, although this combination has proven particularly effective for other neurodegenerative disorders (see for example Ballarini et al., 2020; Castellazzi et al., 2020; Nemmi et al., 2019; see also Durstewitz, Koppe, & Meyer‐Lindenberg, 2019). One major focus of the present study is to, therefore, investigate whether the multimodal fusion of resting state functional connectivity and brain volume results in improved classification accuracies of patients suffering from ALS as compared with healthy controls (HCs).

A second major focus is to evaluate and integrate a third functional feature set, namely features related to nonlinear network dynamics. While functional connectivity typically captures only linear and static (i.e., time‐independent) dependencies between brain regions or networks (Chen, Azeez, Chen, & Biswal, 2020; Rosazza, Minati, Ghielmetti, Mandelli, & Bruzzone, 2012), it neglects that the brain is a highly interconnected nonlinear dynamical system (DS) which can generate very complex and flexible patterns of activity, neuronal dependencies, and associated phenomena (Izhikevich, 2007; Lin, Wang, Yao, & Tan, 2020; Michaels, Schaffelhofer, Agudelo‐Toro, & Scherberger, 2020; Sani, Abbaspourazad, Wong, Pesaran, & Shanechi, 2021). It is precisely these dynamical phenomena which have been argued to implement cognition (e.g., Durstewitz, Seamans, & Sejnowski, 2000; Hopfield, 1982; Rabinovich, Huerta, Varona, & Afraimovich, 2008; Tsuda, 2015; Wang, 2001; Wang, 2008), and, in turn, underlie cognitive dysfunction (Armbruster, Ueltzhöffer, Basten, & Fiebach, 2012; Dakka et al., 2017; Durstewitz & Seamans, 2008; see also Durstewitz, Huys, & Koppe, 2020 for a recent review).

One method to effectively extract the underlying generative network dynamics from multivariate time series are recurrent neural networks (RNNs; Durstewitz, 2017; Koppe, Toutounji, Kirsch, Lis, & Durstewitz, 2019; Pandarinath et al., 2018; Zhao & Park, 2018). They have already been successfully employed to extract dynamics from fMRI recordings (e.g., Koppe et al., 2019), as well as to infer discriminative biomarkers based on longitudinal structural MRI and resting state fMRI in neurodegenerative and psychiatric disorders (e.g., Cui & Liu, 2019; Yan et al., 2019; see also Bhagwat, Pipitone, Voineskos, & Chakravarty, 2019; Lian, Liu, Zhang, & Shen, 2020). Some of these models have the additional advantage of delivering dynamically interpretable features (Durstewitz et al., 2020), in contrast to many other neurological classification approaches based on deep neural networks (see Durstewitz et al., 2019 for a recent review). Our study is, to our knowledge, the first to explore the potential of such RNNs for the classification of patients with ALS.

In sum, the aims of the present study are twofold: for one, we evaluate whether the multimodal fusion of brain volume and function (including functional resting state connectivity and nonlinear network dynamics) benefits the classification of ALS, and second, we investigate the potential of features derived from nonlinear network dynamics as discriminative biomarkers of ALS. To increase interpretability of these multivariate and multimodal analyses, we additionally explore the relevance of features identified as important within the classifiers by univariate statistical analyses.

2. METHODS

2.1. Sample and clinical data

A total of 137 patients with ALS and 67 HCs were consecutively recruited from the Department of Neurology at Jena University Hospital. The patients with ALS met the revised El‐Escorial‐criteria of definite, probable, or laboratory‐supported probable ALS (Brooks, Miller, Swash, & Munsat, 2000) as examined by a trained neurologist. Fourteen subjects were discarded due to irregularities in the rsfMRI scans. From the remaining sample, age matched patients with ALS (N = 97) and HCs (N = 59) were selected. To account for the imbalanced sample size and prevent the classifiers of extracting information primarily of the majority class (also known as “imbalance problem”; He & Garcia, 2009; López et al., 2014; Sun et al., 2009), we applied a stratified cross‐validation scheme. In this scheme, an equal number of individuals per group is assigned to the training set to avoid misclassifications due to imbalance and associated biases in prediction error assessment (He & Garcia, 2009; López et al., 2014; Sun et al., 2009; please see Section 2.4 for details).

To validate the trained classifier, we exploratorily tested the trained classifiers on an independent data set of 10 ALS mimics. These ALS mimics expressed symptoms that led to the impression of an ALS disease, but were diagnosed to suffer from another disorder. Details and results will be presented in Appendix S1.

Disease severity was consecutively assessed during regular follow‐ups with the revised ALS Functional Rating Scale (ALSFRS‐R; Cedarbaum et al., 1999). To further relate neuroimaging features to the individual disease state and trajectory at the time of MRI acquisition, the D50 disease progression model was applied (Poesen et al., 2017; Prell, Gaur, Steinbach, Witte, & Grosskreutz, 2020; Steinbach, Batyrbekova, et al., 2020; Steinbach, Guar, et al., 2020a). The D50 model uses consecutive scorings of patients via the ALSFRS‐R to fit an individualized sigmoidal state transition from full health to functional loss. According to recent improvements of the D50 model, a variable elevated functional reserve level up to 5 months prior to symptom onset was applied as offset for the calculation of the curve. We thus accounted for the common uncertainties in the exact time of symptom onset as remembered and reported by the patients. Main resulting parameters of the D50 model are: the D50 value depicting overall disease aggressiveness (defined as the estimated time since symptom onset taken in months for a patient to lose 50% of his/her functionality), and local measures of the disease at the time of MRI, namely the calculated functional state (cFS), the calculated functional loss (cFL), and the relative D50 (rD50). The latter depicts the individual disease covered, independent of aggressiveness as an open‐ended reference point with 0 defining symptom onset and 0.5 depicting the time‐point of halved functionality (Steinbach, Gaur, et al., 2020b; Steinbach, Batyrbekova, et al., 2020). More traditional disease metrics were also assessed, that is, the symptom duration (months from symptom onset until MRI scan) and the progression rate [calculated as (48‐ALSFRS‐R)/symptom duration].

Demographic and clinical data is summarized in Table 1. After matching, individuals with ALS did not differ from HCs in gender (odds ratio = 0.64; p = .186) or age (T ₁₅₄ = 1.54; p = .114).

TABLE 1.

Sample characteristics

	ALS		HC		STATS
	N = 97		N = 59
	Mean/N	SD/%	Mean/N	SD/%	Test‐statistic	dof	p
Age at MRI (years)	57.92	11.1 c	55.06	10.6 c	1.59 a	154	.114
Gender
Male	60	61.9 d	30	50.8 d	0.64 b		.186
Female	37	38.1 d	29	49.2 d
Handedness
Right	89	91.8 d	54	91.5 d
Left	8	8.2 d	5	8.5 d
Onset‐type
Bulbar	28	28.9 d
Limb	69	71.1 d
Riluzole intake at MRI
Yes	80	82.5 d
No	17	17.5 d
Relevant riluzole intake during the disease course (>50%)
Yes	78	80.4 d
No	19	19.6 d
Age at symptom onset (years)	56.4	11.0 c
Symptom duration (months)	18.59	17.98 c
ALSFRS‐R total score (points)	39.15	6.09 c
Progression rate (points lost per month)	0.65	0.53 c
D50 (months)	41.29	39.84 c
rD50	0.25	0.1 c
Phase
I	50	51.5 d
II	47	48.5 d
cFL (points lost per month)	0.91	0.9 c
cFS (points)	38.99	5.8 c

Abbreviations: ALS, amyotrophic lateral sclerosis; ALSFRS‐R, ALS Functional Rating Scale Revised; cFL, calculated functional loss; cFS, calculated functional state at the time point of scanning; dof, degrees of freedom; D50, overall disease aggressiveness; HC, healthy controls; MRI, magnetic resonance imaging; rD50, relative disease aggressiveness; SD, standard deviation; p, p‐value.

^a T‐value.

^b Odds ratio.

^c Standard deviation.

^d %.

All procedures conducted for this study were approved by the local ethics committee (Nr 3633‐11/12) and all experimental procedures were in accordance with the ethical standards defined in the 1964 Declaration of Helsinki and its later amendments.

2.2. Preprocessing imaging data

2.2.1. Scanning parameter

MRI images were collected using a 1.5 T whole‐body MRI scanner (Siemens Sonata) with a manufacturer's four‐channel phased array head coil. T1‐weighted anatomical images, serving as structural MRI data, were collected with 1 mm isotropic resolution (FLASH 3D, TR/TE = 15 ms/5 ms, FA 30°, FOV = 240 × 256 mm, slice thickness 1 mm, pixel size 1 mm × 1 mm). Blood‐oxygenation level dependent signal (BOLD) functional images were obtained with the standard gradient‐echo echo planar imaging (EPI) pulse sequence: FOV = 256 × 256 mm, slice thickness 3 mm, pixel size 4 mm × 4 mm (64 × 64 matrix, 40 slices), TR/TE = 3,060 ms/40 ms, flip angle = 90°, 137 volumes).

Subjects were instructed to let their mind wander during the 6.98 minutes resting state scan (TR = 3.06 s, 137 scans).

2.2.2. Structural MRI

Preprocessing of the structural data (T1 images) was conducted with the Statistical Parametric Mapping software (SPM12; Wellcome Trust Center of Neuroimaging, London, UK: http://www.fil.ion.ucl.ac.uk/spm) by applying the voxel‐based morphometry (VBM) toolbox 8 (Matsuda et al., 2012): all 3D T1‐weighted MR images were first segmented into gray matter volume (GMV), white matter volume (WMV), and cerebrospinal fluid (CSF) components, and registered using affine transformations followed by a nonlinear registration to a standard SPM template (IXI‐550 MNI template; Ashburner & Friston, 2005). The gray matter anatomical images were then normalized to MNI space by using the implemented Diffeomorphic Anatomic Registration Through Exponentiated Lie (DARTEL) algebra algorithm (IXI550 template; McConnell Brain Imaging Center, DARTEL normalization; Yassa & Stark, 2009). The voxel values were multiplied with the Jacobian determinant during normalization. Finally, the images were further smoothed using an 8‐mm full‐width‐half‐maximum (FWHM) Gaussian kernel.

Total GMV, WMV, and CSF were estimated by integrating all voxel values within the segmented GMV, WMV, and CSF, respectively, and normalized by the total intracranial volume (TIV), where TIV = GMV + WMV + CSF (Menke, Agosta, Grosskreutz, Filippi, & Turner, 2017; Welton et al., 2019).

2.2.3. Resting state functional MRI

The rsfMRI data were corrected for differences in time acquisition via realignment to the first image, and then re‐sliced to the mean image for each subject. Six realignment parameters for changes in motion across the different planes were derived. The realigned and resliced images (mean image) were co‐registered to the anatomical image of each subject. Functional images were then spatially normalized to the MNI standard template (deformation field saved during segmentation, see Section 2.2.2) and smoothed with a 6 mm FWHM Gaussian kernel.

2.2.4. ROIs and covariates

Regions of interest (ROIs) were selected based on the most common findings of alterations in resting state functional connectivity (rsFC) in ALS (for a systematic overview, please see Table S1). We decided to base our selection on expert knowledge, as the limited sample size of our data set restricts performing data‐driven feature selection steps to identify relevant ROIs and at the same time leave a sufficiently large sample to assess an independent and robust out‐of‐sample prediction error (see Cearns et al., 2019; Koppe et al., 2020). Broadly, two approaches have been applied to study rsFC in ALS in the literature, a seed‐based approach, which assesses the coherence between a single brain region (or “seed”) with multiple other brain regions, and a large‐scale brain network approach, where neuronal activity is separated into distinct spatial patterns of coherent activity, for example, via independent component analysis or related methods (e.g., Allen et al., 2011; Menon, 2011). Reduced rsFC has been observed between brain regions associated with motor processing, such as the primary motor cortex, the precentral gyrus, the postcentral gyrus, the supplementary motor area (SMA), and the cerebellum, together forming the sensorimotor network (seed‐based: Jelsone‐Swain et al., 2010; Lee, Lee, Lee, Park, & Ryu, 2019; Loewe et al., 2017; Meoded et al., 2015; Qiu et al., 2019; Schmidt et al., 2014; Zhou et al., 2014; large‐scale brain networks: Menke, Proudfoot, Talbot, & Turner, 2018; Mohammadi et al., 2009; Trojsi et al., 2015; see also: Douaud, Filippini, Knight, Talbot, & Turner, 2011; Fekete, Zach, Mujica‐Parodi, & Turner, 2013; Menke et al., 2017; Schulthess et al., 2016). Altered functional connectivity has been further detected between brain regions related to self‐referential and autobiographical memory processing, namely, the posterior cingulate cortex, the precuneus, and the ventromedial prefrontal cortex, collectively known to form the default mode network (Menon, 2011), with some studies reporting increased rsFC (Agosta et al., 2013; Meoded et al., 2015; Schulthess et al., 2016) while others report decreased rsFC within the latter network (Li, Zhou, Huang, Gong, & Xu, 2017; Mohammadi et al., 2009; Trojsi et al., 2015). Furthermore, increased rsFC has been observed between brain regions related to attention and goal‐directed processing (Cole et al., 2012; Marek et al., 2018), such as lateral prefrontal (e.g., middle, superior frontal gyrus), and parietal brain regions (e.g., inferior, superior parietal gyrus), together forming the fronto‐parietal network (Douaud et al., 2011; Menke et al., 2018; Schulthess et al., 2016; Serra et al., 2019; but see also Trojsi et al., 2015).

To accommodate for findings in both approaches (i.e., seed‐based and large‐scale brain network approaches), ROI masks were taken from the functional ROI atlas introduced by Shirer, Ryali, Rykhlevskaia, Menon, and Greicius (2012) (https://findlab.stanford.edu/functional_ROIs.html). The atlas provides masks for the most common large‐scale brain networks (i.e., network masks), as well as masks covering the individual brain regions included within those networks (see also Dadi et al., 2019). The dimensions of the ROI masks were resliced to match the dimensions of the MRI and fMRI images.

In agreement with the reported findings to date, we focused on the sensorimotor network, the fronto‐parietal network, as well as the default mode network. Individual brain regions from these large‐scale network masks provided by Shirer et al. (2012) were selected based on the reported group differences found in the literature (see Table S1). Specifically, the following brain regions were selected: the precentral/postcentral gyrus, the SMA, the thalamus (thal), and the cerebellum (cereb) from the sensorimotor network (SMN); the medial prefrontal cortex (mPFC), and the posterior cingulate cortex (PCC) from the default mode network (DMN); as well as the superior frontal gyrus (SFG), the superior, and the inferior parietal cortex (SPC, IPC) from the fronto‐parietal network (FPN).

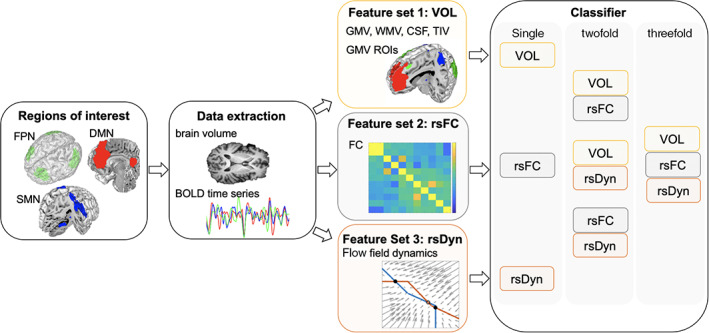
2.3. Feature extraction

Three distinct feature sets relating to brain volume (termed “VOL”), resting state functional connectivity (termed “rsFC”), and nonlinear resting state network dynamics (termed “rsDyn”) were selected to investigate their separate and combined contribution to prediction.

2.3.1. Feature set 1: brain volume (VOL)

From the preprocessed data, we selected global measures, namely the normalized and non‐normalized GM, WM and CSF volumes, and the TIV (amounting to N = 7 global VOL features), as well as the normalized regional GMV per subject within the individual pre‐selected ROIs (amounting to N = 12 regional VOL features; see also Section 2.2.4).

2.3.2. Feature set 2: resting state functional connectivity

BOLD time series from the preprocessed fMRI images were extracted within the selected ROIs (Section 2.2), band‐pass filtered (0.012–0.1 Hz), and averaged. RsFC was assessed by setting up N − 1 multiple linear regression models for each of the N ROIs (i.e., without regression each feature on itself), considering one ROI as a regressor of interest each time. Motion artifacts (six realignment parameters, cf. Section 2.2), as well as physiological artifacts (i.e., the average CSF and white matter signals accounting for cardiac activity and respiration) were included as regressors of no interest (Chenji et al., 2016; Li et al., 2017, 2018; Meoded et al., 2015; Zhang et al., 2017). The inferred ROI regression coefficients [N × (N − 1) = 132] were used as rsFC features for further analyses.

2.3.3. Feature set 3: resting state dynamics

To assess resting state network dynamics, we inferred RNN based latent variable models from the extracted time series (cf. Section 2.2). RNNs are particularly well suited for this task as they are universal dynamical system approximators, meaning they are capable of representing almost any type of dynamics (Funahashi & Nakamura, 1993; Kimura & Nakano, 1998). The proposed model in particular has moreover previously been shown to successfully retrieve dynamics from fMRI recordings (Koppe et al., 2019) and render dynamically interpretable features (Durstewitz et al., 2020).

The models consist of a latent state equation which specifies the evolution of the system's state, and thus the generative system dynamics (Equation (1)), and an observation equation which links this state to the actual extracted time series, or observations (Equation (2)). In more detail, the temporal evolution of the latent state z _t $\in {ℝ}^M$ is given by

$${\mathbf{z}}_t={\mathbf{Az}}_{t-1}+\mathbf{W}\phi \left({\mathbf{z}}_{t-1}\right)+\mathbf{h}+{\mathbf{\epsilon }}_t,{\mathbf{\epsilon }}_t\sim N\left(\mathbf{0},\mathbf{\sum }\right),$$ (1)

where, A is a (M × M) diagonal matrix of auto‐regression weights, W is an (M × M) off‐diagonal matrix of connection weights, φ(x):=max(x,0) is an elementwise piecewise linear activation function, h is a vector of constant bias terms, and ε _t represents Gaussian process noise with diagonal covariance ∑. The observations are then generated from these states by

$${\mathbf{x}}_t=\mathbf{B}\left(\mathit{hrf}*{\mathbf{z}}_{\tau :t}\right)+{\mathbf{Jr}}_t+{\mathbf{\eta }}_t,{\mathbf{\eta }}_t\sim N\left(\mathbf{0},\mathbf{Г}\right),$$ (2)

with, B representing a (N × M) matrix of regression coefficients multiplied with the time‐lagged latent states convolved with the hemodynamic response function (hrf), r _t is a P‐dimensional vector of noise artifacts comprising motion artifacts (i.e., six realignment parameters, cf. manuscript Section 2.2), as well as physiological artifacts (i.e., the average CSF and white matter signals accounting for cardiac activity and respiration; Chenji et al., 2016; Li et al., 2017, 2018; Meoded et al., 2015; Zhang et al., 2017; cf. Section 2.2) and J is their (N × P) regression coefficient matrix. Lastly, η _t , is a vector of Gaussian observation noise with diagonal noise covariance Г. Note that Equation (2) takes on the form of the conventional linear regression model as implemented in SPM with the latent states acting as predictors of interest.

For each subject, the extracted time series were handed over to the inference algorithm and RNN models with latent state dimension M = 6, …, 12 regularized toward manifold attractor configurations with regularization factor λ = 1000 were inferred (please see Schmidt, Koppe, Monfared, Beutelspacher, & Durstewitz, 2021 for details on inference and regularization approach). From these, we selected models with M = 8 latent states for further analysis, as these generated the lowest mean squared error between true and predicted observations, where the prediction was obtained by running Equation (2) on the inferred states (running the full generative model [Equations (1) and (2)], also resulted in lowest errors for M = 7 and M = 8; see also Figure 3d for an example of BOLD response prediction based on the full generative model).

FIGURE 3.

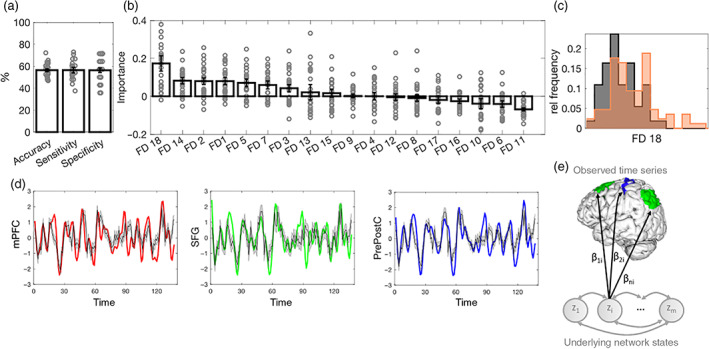
Classification of ALS versus HC based on resting state network dynamics (rsDyn). (a) Mean and standard error of the mean (SEM) of classification performance of the rsDyn classifier. (b) Mean and SEM of the feature importance of rsDyn features in classifying ALS diagnosis. (c) Significant group differences in the univariate analyses in feature FD18 at a Bonferroni corrected threshold (please see Table S4 for more details on rsDyn features). (d) Examples for true BOLD time series of the mPFC (red), the SFG (green), and the pre‐ and postcentral cortex (blue), and (generated) model predictions (gray with 90% confidence interval) of one individual. (e) Schematic illustration of FD18: according to the model (Equations (1) and (2)), the observed time series are regressed onto each underlying network state z _i via regression coefficients ${\beta }_{1,i},{\beta }_{2,i},\dots ,{\beta }_{n,i}\in {\mathbf{B}}_{:,i}$ (see Equation (2)). A low variance across columns of B thus indicates that each state z _i is evenly represented across all observed time series. ALS, amyotrophic lateral sclerosis; FD, feature dynamics (see Section 2.3 for details); HC, healthy controls; mPFC, medial prefrontal cortex; rel, relative; SFG, superior frontal gyrus

As each model consists of a large set of parameters Θ = {A, W, h, ∑, B, J, Г}, rather than handing over the entire parameters as rsDyn feature set to the classification algorithms, we defined summary statistics capturing first and second moments of the parameter distributions, as well as other features directly related to network dynamics and state space geometry. The state space represents the space spanned by all dynamical variables, in this case the latent states z, and thus define the dynamical system. The geometric objects in this space, such as fixed point attractors, k‐cycles and chaotic attractors, determine how the system changes over time, that is, its dynamics (please see Durstewitz et al., 2020 for detailed examples and a simple introduction to dynamical systems). The features we extracted relate to these dynamics, although we emphasize that the chosen set is not exhaustive, and rather represents a first attempt at collecting dynamics features which are easily accessible and at the same time remain interpretable.

We enumerate these features with the labels “FD1”–“FD18” for simplicity and list these features below for completeness. We also provide a loose interpretation for readers without DS background and refer the reader to the supplement for more extensive information on the formal interpretation of these features (see section 1.1 of Appendix S1), and to MATLAB code for replication purposes (https://github.com/JanineT‐oss/ALS_PLRNN_classification). We (analytically) assessed the total number of fixed points (“FD1”) as well as the number of unstable fixed points (“FD2”; together indicative of the presence of fixed point attractors and roughly relating to “state space complexity”), the average over the maximum absolute imaginary eigenvalues of the transition matrix around all fixed points (“FD3”; indicative of spiral points and oscillatory behavior), the average absolute deviation of the maximum absolute eigenvalues around these points from 1 (“FD4”; indicative of how close the system is to a bifurcation, cf. Durstewitz, 2017), the variance of the parameters in the transition matrices (where high variance favors a less stable and more chaotic dynamics, cf. Bertschinger & Natschläger, 2004) separated for both regularized and nonregularized parameters (“FD5–FD7”), the average magnitude of the bias terms h separated for regularized and non‐regularized parameters (“FD8” and “FD9”; relating to mean activity of the system), the (numerically assessed) number of stable cycles (“FD10”; capturing stable oscillations of the system), the net sum of weights W averaged across states (“FD11–FD12”; indicating average rate of change across states) separately for regularized and nonregularized parameters, the net sum of absolute weights averaged across states and evaluated along the system's trajectory (“FD13”; relating to functional interactions), the average Euclidean distance between the inferred states over time (“FD14”; also relating to the velocity of the dynamics), and the average variance of the states over time (“FD15”; loosely relating to the magnitude of oscillations). As another measure to characterize the variability and complexity of the dynamics, we quantified how often the system switched between different orthants in state space (“FD16”). Lastly, we assessed the average and variance over columns of regression coefficient matrix B (“FD17–FD18”; where the variance for instance indicates whether state information is distributed evenly or unevenly across observations). In total, this amounted to N = 18 features defined on the inferred DS and its parameters (please see section 1.1 of Appendix S1 and MATLAB code for details, and Durstewitz et al. (2020), for further information on DS theory).

2.3.4. Age correction

Lastly, a well‐documented confounding factor in neuroimaging features sets and classification studies is age, showing a strong relationship to both brain volume (Batouli, Trollor, Wen, & Sachdev, 2014; Royle et al., 2013; Wierenga et al., 2018; see also Fjell & Walhovd, 2010), and function (Betzel et al., 2014; Cunningham, Tomasi, & Volkow, 2017; Zhang et al., 2016; see also Mak et al., 2017). In fact, performing a simple classification analysis by age on our own sample revealed a classification accuracy of 60.85%, despite age‐matching our groups prior to the analysis (please see section 1.2 of Appendix S1 and Figure S1). To therefore explicitly rule out that our classifiers learned age‐related features, we additionally removed effects of age from all features by linear regression (Fratello et al., 2017). The residuals from these analyses were used as features for the classifiers.

2.4. Classification

2.4.1. Classifier

Random forest (RF) classifiers (Breiman, 2001) were used to classify individuals with ALS and HCs. The RF classifier is an ensemble tree‐based learning algorithm (Breiman, 2001) which achieves classification by averaging over the outputs, that is, the “votes”, of multiple single trees (Breiman, 1996a, 1996b, 2001). Each tree represents a separate independent classifier trained on a random sub‐sample (a procedure referred to as bagging), and a random subset of features. Ensemble tree‐based learning algorithms have become very popular in various scientific fields, including medicine and epidemiology, as they can represent nonlinear relationships, large numbers of features, and are not tied to a specific data distribution (Strobl, Malley, & Tutz, 2009). At each leaf node of a tree, a subset of features is randomly (re‐)drawn and the best separating feature is selected to further split the tree. In this way, the tree continues to grow until a predefined number of observations in a leaf node is reached. The number of trees, the number of features per tree, the number of observations in the last leaf node, and the number of observations drawn to build each tree are tunable parameters of the algorithm. At the same time RF classifiers are quite robust, in the sense that they are rather insensitive to parameter changes or number of input features (Probst, Wright, & Boulesteix, 2019; Strobl et al., 2009). This spares the need for additional feature selection and parameter fine‐tuning steps that would come with an increased risk of overfitting and poor generalization, as for instance needed in neural networks and, to a lesser degree, support vector machines (SVMs). Such additional steps need to be validated on an independent data set (please see Durstewitz et al., 2019; Koppe et al., 2020 for reviews), which in our case is challenging in light of the limited sample size available (cf. Koppe et al., 2020; Probst et al., 2019). We therefore fixed the RF parameters to the common default values during training (number of trees = 5,000; number of features available at each split = √n; minimum leaf size = 1; sample size drawn for each tree = 2/3; e.g., Probst et al., 2019).

Feature importance

Beside an average classification vote, the RF algorithm also enables to ascribe each single feature x a so‐called importance score which assesses the relative contribution of each feature in predicting the output y. The importance score of x is assessed by averaging the predictions on the left‐out sample (out‐of‐bag sample) over all trees containing x, and subtracting from it the predictions obtained after randomly permuting x (Breiman, 2001). It is important to note that the importance of a feature can only be interpreted in the context of the features included in the classifier as it depends on and interacts with the choices the algorithm makes on all of the features.

Classification certainty

To obtain an estimate of the level of certainty by which an RF classifier assigned each subject to the ALS group, we assessed the relative frequency of ALS votes across all trees. High values (close to 1) indicate a high level of certainty for belonging to the ALS group as many trees voted for ALS consistently in this case.

2.4.2. Cross‐validation

The estimation of the out‐of‐sample prediction error (PE) was performed via stratified five‐fold cross‐validation (CV; Probst et al., 2019; Varma & Simon, 2006; see also Ferraro et al., 2017; Sarica et al., 2017; Schuster et al., 2016), to avoid biases in the PE assessment due to imbalanced training set sizes (He & Garcia, 2009; López et al., 2014; Sun et al., 2009). The folds consisted of N = 22 individuals with equal sample size per group, each fold serving once as test set for PE assessment. The remaining 42 subjects which were not assigned to any fold to warrant equal sample sizes were added to the test set such that each test set consisted of 22 + 42 = 64 subjects. To avoid potential sampling related effects and obtain a more robust PE estimate, we repeated this procedure five times, each time randomly redrawing the five folds. As out‐of‐sample PE estimates, we assessed the balanced accuracy, the sensitivity, and the specificity averaged across all test sets.

Individuals with more than 10 missing values were excluded when training the classifiers (amounting to N = 6 exclusions when training on rsFC and rsDyn features).

2.5. Statistical analyses

Demographic characteristics were compared by applying independent sample t‐tests (age), and ${\chi }^2$‐test (gender). Multivariate classification was performed via the RF classifiers. Since the multivariate RF classifiers may identify important features, but do not allow to interpret the exact direction of their relationship, we followed up on these analyses with post hoc independent t‐tests. While these tests neglect higher order interaction effects, they may at least indicate whether volumetric features were larger or smaller, or functional connectivity was higher or lower between ALS and HCs. Effect sizes were calculated according to Cohen's d for unequal sample sizes (Cohen, 1988; Lenhard & Lenhard, 2016). Moreover, Pearson correlation coefficients were inferred to investigate the linear relationship between these features, as well as the classification certainty, and ALS characteristics (i.e., cFS, cFL, D50, age at symptom onset, symptom duration, and progression rate). Statistical significance was initially set to p < .05 and the threshold was Bonferroni adjusted for multiple comparisons. All analyses were conducted in MATLAB (version 2019b).

3. RESULTS

We assessed the ability of classifying ALS patients and HCs based on brain volume (VOL), resting state functional connectivity (rsFC), and resting state dynamics (rsDyn), as well as based on combinations of these feature sets, respectively (i.e., multimodal classifiers; see also Figure 1). Please note that we have refrained from performing a feature selection step on the feature sets, as a selection needs to be done on a separate sample. Using the same sample would result in an underestimation of the PE. Given the limited sample size of the present investigation, an efficient splitting would not have been feasible.

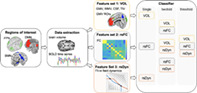
FIGURE 1.

General procedure. Time series and volumes from hub brain regions of interest (ROI) of three major resting state networks were extracted: the fronto‐parietal network (FPN), the default mode network (DMN), and the sensorimotor network (SMN) during resting state functional MRI (fMRI). Global brain volume (GMV, WMV, CSF, and TIV), as well as regional GMV of ROIs were estimated for each individual (feature set 1: VOL). For the extracted time series, features relating to functional connectivity (feature set 2: rsFC) and nonlinear resting state dynamics (feature set 3: rsDyn) were assessed. Network dynamics were inferred subject‐wise via recurrent neural networks (RNNs). Features were then assessed based on the inferred RNNs illustrated here in terms of a flow field containing stable (open circles) and unstable (filled circles) fixed points, and nullclines (blue and red lines). Feature sets were used to build random forest classifiers classifying group membership (ALS vs. HC) based on the unimodal feature sets, as well as based on two and three (i.e., multimodal) feature sets. BOLD, blood‐oxygen level dependent signal; CSF, cerebrospinal fluid; GMV, gray matter volume; TIV, total intracranial volume; WMV, white matter volume

3.1. Feature set 1: VOL

The RF classifier trained on VOL features achieved a mean balanced accuracy of 59.66%, a mean specificity of 66.93%, and a mean sensitivity of 52.38% (see Table 2, Figure 2a). Averaged feature importance scores indicated that, in descending order, the normalized global WMV, the GMV of the right thalamus, the normalized global CSF volume, the WMV, as well as the GMV of the bilateral mPFC ranged among the five most important features in classifying groups (see Figure 2b).

TABLE 2.

Classification performance of all random forest classifiers

Feature set	Accuracy		Sensitivity		Specificity
	Mean	SEM	Mean	SEM	Mean	SEM
VOL	59.66	1.19	52.38	1.44	66.93	2.40
rsFC	61.66	1.50	54.74	1.66	68.57	1.43
rsDyn	56.35	1.37	56.42	2.48	56.29	2.09
VOL + rsFC	66.82	0.01	62.50	0.02	71.14	0.04
VOL + rsDyn	62.85	0.01	63.42	0.01	62.29	0.03
rsFC + rsDyn	64.36	0.01	61	0.01	67.71	0.02
VOL + rsFC + rsDyn	65.01	0.005	58.58	0.02	71.43	0.01

Abbreviations: rsFC, resting state functional connectivity; rsDyn, resting state dynamics; SEM, standard error of the mean; VOL, brain volume. The bold values represent the highest accuracy/sensitivity/specificity.

FIGURE 2.

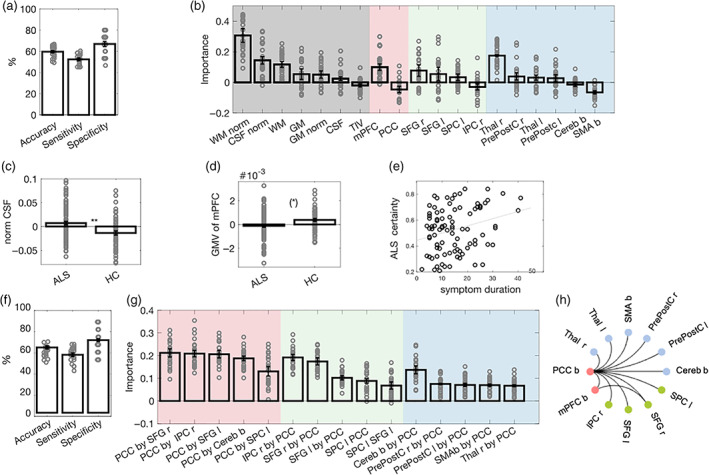
Classification of ALS versus HCs based on brain volume (VOL) and resting state functional connectivity (rsFC). (a) Mean and standard error of the mean (SEM) across samples for performance measures of the VOL classifier. Dots represent the performance on individual test sets. (b) Mean and SEM of feature importance scores of VOL features. The background is color‐coded to highlight brain regions related to global brain volume in gray, the DMN in red, the FPN in green, and the SMN in blue. (c) Mean and SEM of the normalized CSF volume of each group. (d) Mean and SEM of the normalized mPFC GMV of each group. Group comparisons are reported at a Bonferroni‐adjusted threshold in c and d, and dots represent individual volumina (please see Table S2 for more details). (e).Relationship between the certainty of ALS classification and symptom duration in individuals with ALS, thresholded at an exploratory level of p < .01. (f) Mean and SEM of classification performance of the rsFC classifier. (g) Mean and SEM of feature importance scores of rsFC features. The background is color‐coded to highlight features related to the DMN in red, the FPN in green, and the SMN in blue. Please note that for illustrational purposes, we displayed the five most important rsFC features for each network. (h) Significant group differences in rsFC features at a Bonferroni‐adjusted threshold in the univariate analyses. Black lines indicate decreased connectivity for ALS as compared with HC (please see Table S3 for more details). ** p < .01; (*) p < .1 (Bonferroni‐adjusted); ALS, amyotrophic lateral sclerosis; b, bilateral; Cereb, cerebellum; CSF, cerebrospinal fluid; DMN, default mode network; FPN, fronto‐parietal network; GM, gray matter; HC, healthy controls; IPC, inferior parietal cortex; l, left; mPFC, medial prefrontal cortex; norm, normalized; PrePostC, precentral/ postcentral cortex; PCC, posterior cingulate cortex; r, right; SMN, sensorimotor network; SFG, superior frontal gyrus; SMA, supplementary motor area; SPC, superior parietal gyrus; Thal, thalamus; TIV, transcranial volume; WM, white matter

Subsequent t‐tests confirmed that some of these features differed significantly between groups. Compared with HC, individuals with ALS showed an increased CSF volume (T ₁₅₁ = 3.69, p _corr = .002, d _cohen = 0.61), and marginally reduced GMV of the bilateral mPFC (T ₁₅₃ = 2.72, p _corr = .087, d _cohen = 0.44). No differences between groups were observed in the GMV of the right thalamus, or the WMV (normalized or non‐normalized; p _corr‐values > .1; see also Figure 2c,d; Table S2).

3.2. Feature set 2: rsFC

The RF classifier trained on rsFC features achieved a mean balanced accuracy of 61.66%, a mean specificity of 68.57%, and a mean sensitivity of 54.74% (see Table 2, Figure 2f). Averaged feature importance scores indicated that, in descending order, the rsFC between the PCC and the right SFG, the PCC and the right IPC, the PCC and the left SFG, the right IPC and the PCC, as well as the PCC and the bilateral cerebellum ranged among the most important features in classifying groups (Figure 2g).

Subsequent post hoc t‐tests confirmed that these features significantly differed between groups. As compared with HC, individuals with ALS showed a reduced rsFC between the PCC and the left and right SFG (left: T ₁₄₇ = 5.76, p _corr < .001, d _cohen = 0.96; right: T ₁₄₆ = 5.69, p _corr < .001, d _cohen = 0.97), the PCC and the right IPC (T ₁₄₇ = 5.24, p _corr < .001, d _cohen = 0.88), as well as the PCC and the cerebellum (T ₁₄₈ = 5.37, p _corr < .001, d _cohen = 0.9; Figure 2h).

3.3. Feature set 3: rsDyn

The RF classifier trained on rsDyn features achieved a mean balanced accuracy of 56.35%, a mean specificity of 56.29%, and a mean sensitivity of 56.42% (Table 2, Figure 3a). Averaged feature importance scores indicated that, in descending order, the average variance of the regression coefficients (FD18; cf. Section 2.3, Figure 3c,e), the Euclidean distance between inferred states over time (FD14), the total number of unstable fixed points (FD2), the total number of fixed points (FD1), as well as variance of the parameters in the transition matrices (FD5) ranged among the five most important features in classifying groups (see Figure 3b).

Subsequent post hoc Bonferroni corrected t‐tests confirmed that one of these features differed significantly between groups. As compared with HC, individuals with ALS showed an increased average variance in the regression coefficients (T ₁₃₈ = 3.61, p _corr = .008, d _cohen = 0.63; see Figure 3c).

3.4. Feature set combinations

Combining individual feature sets (i.e., combination of two or three feature sets) outperformed unimodal classifiers (see Table 2 and Figure 4a–c). Specifically, the classifier combining VOL and rsFC features achieved the highest classification accuracy (66.82%), followed by the classifier combining all three feature sets (65.01%).

FIGURE 4.

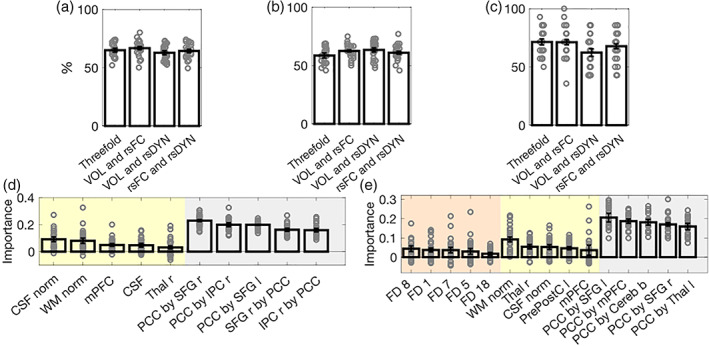
Random forest multimodal classifiers. Mean and standard error of the mean (SEM) of the classification accuracy (a), sensitivity (b), and specificity (c) of multimodal classifiers (two, as well as three feature set combinations), respectively. The mean and SEM of the feature importance scores of the two classifier achieving the highest (i.e., bimodal: VOL and rsFC) and second highest (i.e., combination of three feature sets) performance are displayed in d and e, respectively. Yellow indicates VOL features, gray indicates rsFC features, and orange indicates rsDyn features (see Figure S2 for information on the feature importance scores of the remaining multimodal classifiers). b, bilateral; Cereb, cerebellum; CSF, cerebrospinal fluid; FD, feature dynamics; l, left; IPC, inferior parietal cortex; mPFC, medial prefrontal cortex; norm, normalized; PCC, posterior cingulate cortex; PrePostC, precentral/ postcentral cortex; r, right; rsDyn, resting state dynamics; rsFC, resting state functional connectivity; SFG, superior frontal gyrus; Thal, thalamus; VOL, brain volume; WM, white matter

3.4.1. VOL and rsFC

We built a classifier by combining all VOL and rsFC features to classify group membership (ALS vs. HC). The RF classifier achieved a mean balanced accuracy of 66.82%, a mean specificity of 71.14%, and a mean sensitivity of 62.50% (Figure 4a–c). Averaged feature importance scores indicated that overall rsFC features were most important for classification. In descending order, these features included the rsFC between the PCC and the right SFG, the PCC and the right IPC, the PCC and left SFG, the right SFG and the PCC, as well as the right IPC and the PCC (see also Figure 4d).

Subsequent post hoc t‐tests confirmed that these features significantly differed between groups. As compared with HC, individuals with ALS showed a reduced rsFC between the PCC and the left and right SFG (left: T ₁₄₇ = 5.76, p _corr < .001, d _cohen = 0.96; right: T ₁₄₆ = 5.69, p _corr < .001, d _cohen = 0.97), as well as the PCC and the right IPC (T ₁₄₇ = 5.24, p _corr < .001, d _cohen = 0.88).

3.4.2. VOL and rsDyn

The classifier combining VOL and rsDyn features achieved a mean balanced accuracy of 62.85%, a mean specificity of 62.29%, and a mean sensitivity of 63.42% (Figure 4a–c). Averaged feature importance indicated that, in descending order, the normalized global WMV, the average variance of the regression coefficients (FD18), the GMV of the right thalamus, the bilateral mPFC, as well as the normalized global CSF ranged among the most important features in classifying groups (see also Figure S2a).

Subsequent t‐tests confirmed that some of these features differed significantly between groups. Compared with HC, individuals with ALS showed an increased CSF volume (T ₁₅₁ = 3.69, p _corr = .002, d _cohen = .61), and an increased average variance in the regression coefficients (T ₁₃₈ = 3.61, p _corr = .008, d _cohen = 0.63), as well as a marginally reduced GMV of the bilateral mPFC (T ₁₅₃ = 2.72, p _corr = .087, d _cohen = 0.44). No differences between groups were observed in the GMV of the right thalamus, or the normalized WMV (p _corr's > .1).

3.4.3. rsFC and rsDyn

The classifier combining all rsFC and rsDyn features achieved a mean balanced accuracy of 64.36%, a mean specificity of 67.71%, and a mean sensitivity of 61% (Figure 4a–c). Averaged feature importance indicated that overall features from the rsFC classifier were most important in classifying ALS diagnosis. These included the rsFC between the PCC and the left SFG, the PCC and the right SFG, the PCC and the cerebellum, the PCC and the right IPC, as well as the PCC and the left thalamus (see also Figure S2b).

Subsequent post hoc t‐tests confirmed that these features significantly differed between groups. As compared with HC, individuals with ALS showed a reduced rsFC between the PCC and the left and right SFG (left: T ₁₄₇ = 5.76, p _corr < .001, d _cohen = 0.96; right: T ₁₄₆ = 5.69, p _corr < .001, d _cohen = 0.97), the PCC and the cerebellum (T ₁₄₈ = 5.37, p _corr < .001, d _cohen = 0.9), as well as the PCC and the right IPC (T ₁₄₇ = 5.24, p _corr < 0.001, d _cohen = 0.88).

3.4.4. VOL, rsFC, and rsDyn

The classifier combining all three feature sets achieved a mean balanced accuracy of 65.01%, a mean specificity of 71.43%, and a mean sensitivity of 58.58% (see Table 2, Figure 4a–c).

Averaged feature importance scores indicated that overall, rsFC features were most important in classifying ALS, and yielded the five features of highest importance. These features included, in descending order, the rsFC between the PCC and the left SFG, the PCC and the bilateral mPFC, the PCC and the bilateral cerebellum, the PCC and the right SFG, as well as the PCC and the left thalamus (see also Figure 4e).

Subsequent post hoc t‐tests confirmed that some of these most important features significantly differed between groups. As compared with HC, individuals with ALS showed a reduced rsFC between the PCC and the left and right SFG (left: T ₁₄₇ = 5.76, p _corr < .001, d _cohen = 0.96; right: T ₁₄₆ = 5.69, p _corr < .001, d _cohen = 0.97), the PCC and the mPFC (T ₁₄₆ = 4.58, p _corr = .001, d _cohen = 0.77), as well as the PCC and the cerebellum (T ₁₄₈ = 5.37, p _corr < .001, d _cohen = 0.9; see Table S3).

3.5. Relationship between features, clinical characteristics, and ALS classification

No significant correlations between the most important features per classifier and ALS clinical characteristics were observed, either after adjusting for multiple testing (VOL global: p _corr < .007, VOL regional: p _corr < .004, rsFC: p _corr < .0004, rsDyn: p _corr < .003), or using a more lenient exploratory threshold of p < .01. No significant correlations between the certainty of ALS classification per classifier and ALS clinical characteristics were observed after adjusting for multiple testing (p _corr < .007). Adopting a more lenient exploratory threshold of p < .01 revealed a positive relationship between the certainty of the VOL classifier and symptom duration (r = .277, see Figure 2e).

4. DISCUSSION

The present study expands on efforts to find discriminative and generalizable neuroimaging biomarkers of ALS which may improve diagnostic classification and aid in future therapeutic trials. We examined the ability of unimodal feature sets relating to brain structure and brain function, namely brain volume, resting state functional connectivity, and nonlinear resting state dynamics, as well as combinations of these sets, to predict ALS and HC. For classifiers based on unimodal feature sets, we obtained classification accuracies of 59.66%, 61.66%, and 56.35% for brain volume, resting state functional connectivity, and resting state dynamics, respectively. Importantly, the combination of feature sets increased classification accuracy to 62.85%–66.88%, indicating that brain structure and brain function indeed carry complementary disease related information. Opposed to the more common view that structural brain information is more discriminative than functional brain information in this disorder, resting state connectivity features turned out as most relevant in both the unimodal, as well as the combined classifiers, highlighting the importance of functional brain features when discriminating between ALS and HC.

4.1. Unimodal classifier: Brain volume

Our classifier trained on brain volume achieved a classification accuracy of 59.66% (sensitivity = 52.38% and specificity = 66.93%). The certainty of the classifier was further positively related to symptom duration, indicating that the volume classifier was more sensitive in detecting ALS patients at later disease stages at which biomarkers may be expected to manifest more strongly. The present sample is characterized by a relatively low level of disease accumulation, that is, early‐stage ALS (see Table 1), which may partly explain the low sensitivity of the volume classifier.

To the best of our knowledge, no study has yet reported results of a classifier trained exclusively on brain volume, although evidence toward the importance of volumetric features stems from studies combining brain volume and structural brain connectivity (Ferraro et al., 2017; Schuster et al., 2016). These studies reveal slightly higher classification accuracies, namely 73% and 78.37%, partly attributable to the combination of these modalities (see also van der Burgh et al., 2017).

Feature importance scores of the unimodal classifier indicated that the global brain volume measures WMV, CSF volume, as well as the GMV of the right thalamus and the mPFC were most important for classification. These features were found consistently across all trained classifiers, independent of focusing on unimodal, or multimodal feature sets.

Further contrasting groups with respect to the most important features, revealed that as compared with HC, ALS individuals exhibited an increased CSF volume, as well as a reduced GMV of the bilateral mPFC, though the latter was only marginally significant. These findings are in line with previous investigations (Cerami et al., 2014; Grosskreutz et al., 2006; Raaphorst et al., 2014; Steinbach, Gaur, et al., 2020a; Tavazzi et al., 2015; Zhang et al., 2017; see also Shen et al., 2018). The low level of disease accumulation might partly explain the rather limited differences in brain volume. Differences become more evident during later disease stages, which may further explain a higher rate of misclassification of ALS individuals in the present investigation (see also Menke et al., 2018; Shen et al., 2018; Steinbach, Batyrbekova, et al., 2020; van der Burgh et al., 2020). The present investigation points toward the importance of global features, especially CSF volume, during earlier stages of the disease, as these ranked relatively stable across the trained classifier among the most important brain volume features.

4.2. Unimodal classifier: Resting state functional connectivity

The classifier trained on resting state functional connectivity between regions related to large‐scale brain networks (i.e., DMN, SMN, and FPN) achieved an accuracy of 61.66% (sensitivity = 54.74% and specificity = 68.57%). While this is in line with a previous investigation focusing on discriminating between groups based on functional connectivity within the DMN (classification accuracy of 65%; Fratello et al., 2017), another investigation focusing on several resting state brain networks achieved a higher classification accuracy of 71.50% (Welsh et al., 2013). The lower performance found by us and Fratello et al. (2017) may partly be driven by a stricter control for age in the effect of the input features, which in both cases was ensured by matching the samples for age and additionally regressing out residual age‐related effects. While Welsh et al. (2013) also matched their groups for age, this matching alone was, at least in our case, not sufficient to rule out age‐related effects (see also Figure S1). As age significantly impacts both functional connectivity (Betzel et al., 2014; Cunningham et al., 2017; Zhang et al., 2016; see also Mak et al., 2017) and brain volume (Batouli et al., 2014; Royle et al., 2013; Wierenga et al., 2018), we therefore argue that a strict age correction is elementary to identify discriminative features of the disease.

Feature importance scores additionally revealed that resting state functional connectivity between the DMN and (a) the FPN, as well as (b) the SMN were particularly relevant for classifying ALS, which is in line with a previous publication (Welsh et al., 2013).

Our results indicated a reduction in resting state functional connectivity within the DMN, as well as between the DMN and both the SMN and the FPN, in ALS as compared with HC. Specifically, the observed reduction was primarily related to the functional connectivity between the PCC and all other brain regions, supporting findings of previous investigations (for an overview of functional connectivity reductions in DMN see Chiò et al., 2014; Trojsi, Sorrentino, Sorrentino, & Tedeschi, 2018; Turner et al., 2012; for specific reductions of PCC functional connectivity see Bueno et al., 2018; Bueno et al., 2019; Matías‐Guiu et al., 2016; Mohammadi et al., 2009). The PCC and the DMN in general underly self‐referential and episodic memory processing (for an overview see Menon, 2011). Reduced functional connectivity within this network might be related to episodic memory deficits reported in ALS (Machts et al., 2014). In sum, reduced resting state functional connectivity within the DMN and between the DMN and both the FPN and SMN seem to be critical, pointing towards the importance of resting brain synchronization for classifying ALS.

4.3. Unimodal classifier: Resting state network dynamics

Network dynamics—which we understand here strictly in terms of properties of the generative dynamical system underlying the observed brain activation—is seen in computational neuroscience as the basis for cognition and computational function (e.g., Durstewitz et al., 2000; Durstewitz et al., 2019; Koppe et al., 2019; Rabinovich et al., 2008; Wang, 2001; Albantakis & Deco, 2009; Durstewitz et al., 2000; Wang, 2001; Wang, 2002, 2008a; Wills, Lever, Cacucci, Burgess, & O'Keefe, 2005). Aberrant dynamics may in turn cause many neurological or psychiatric deficits or dysfunctions (e.g., Armbruster et al., 2012; Floresco, Block, & Maric, 2008; Forster & Lavie, 2016; Koppe et al., 2020; Rolls, Loh, & Deco, 2008). Efficiently capturing dynamics may thereby prove effective in discriminating between the diseased and healthy brain.

To assess dynamics, here we investigated a novel approach that has never been applied in this context before: We inferred piecewise linear RNNs from the resting state BOLD time‐series of each individual (cf. Section 2.3). We then defined (interpretable) summary statistics on these RNNs which summarize to a certain degree the properties of the inferred systems and assigned them as features to train an RF classifier. The resting state dynamics classifier yielded an accuracy of 56.35% (sensitivity = 56.24% and specificity = 56.29%) when classifying ALS.

Feature importance scores of individual features revealed that the average variance of the regression coefficients, the Euclidean distance of the inferred states over time, the total number of fixed points and unstable fixed points, as well as variance of the parameters in the transition matrices ranged among the most important features when classifying groups. Collectively, these features indicate alterations in the dynamics relating to instability as well as information disintegration in the ALS group. Although overall the resting dynamics classifier performed slightly below the other unimodal classifiers, this is the first study to demonstrate altered network dynamics in ALS patients using a novel and recent approach, bearing high potential for future applications.

Subsequent univariate analyses revealed that the (column‐wise) variance in regression coefficients strongly discriminated between groups, with ALS individuals characterized by a higher variation as compared with HCs. This feature measures the variation by which each of the dynamical variables, or latent states of the DS model, contributes to generating the observed ROI time series (see also Figure 3e). A low variance indicates that each dynamical variable contributes to a similar degree to all observed time series, and thus information contained in the generative DS is evenly distributed in each ROI. In contrast, a high variance indicates that some dynamical variables may dominate the information present in a certain ROI over another. In other words, low values of this feature are indicative of evenly distributed and integrated information processing across all examined brain regions, while high values may indicate an integration loss (i.e., disintegration, see Figure 3e). This could provide first evidence pointing toward a deficit in information integration as a distinct biomarker of ALS. Note that this feature does not directly indicate alterations in the underlying generative dynamics. Rather, it suggests that information transfer may be aggravated, in line with the findings that altered (and in our case reduced) brain functional connectivity is an important biomarker of ALS. Although groups did not differ statistically between the remaining resting state dynamics features identified as important, the classification was further mainly driven by alterations in fixed points, the latent state velocity, as well as a feature for which higher values are associated with more chaotic as compared with stable dynamics. Collectively, these features may indicate alterations in the dynamics relating to increased instability (see also Appendix S1).

4.4. Multimodal classification

When we combined the different neuroimaging feature sets, our multimodal classifiers, consisting either of two or three feature sets, achieved accuracies ranging between 62.85% and 66.82%, thereby outperforming all unimodal classifiers. The highest classification accuracy was achieved by combining brain volume and functional connectivity features, followed by the combination of all three feature sets. Our findings are in line with recent classification studies reporting higher accuracies when combining, rather than focusing on unimodal feature sets such as combining brain volume and structural connectivity (DMN: 65.0%, fractional anisotropy [FA]: 58.2%, DMN + FA: 66.70%–67.50%; Fratello et al., 2017).

Feature importance scores of the multimodal classifiers provided further evidence for the relevance of brain function, indicating that functional connectivity features were most important in classifying ALS (both observed for the combination of two, as well as three feature sets). Once more, subsequent univariate analyses revealed reduced resting state functional connectivity in ALS as compared with HC between the DMN and the FPN, as well as between the DMN and the SMN (for previous overviews see Chiò et al., 2014; Trojsi et al., 2018; Turner et al., 2012). Although previous investigations mainly focused on structural brain features (for an overview see Grollemund et al., 2019), our evidence therefore undermines the role of functional brain features as discriminative biomarkers of ALS.

4.5. Methodological differences to other studies and explaining classification accuracy differences to other studies

Several explanations may account for differences in classification accuracies obtained by us in contrast to other studies. First, the present sample is characterized by a relatively low level of accumulated disease at the time of MRI scanning: patients had a mean relative D50 (rD50) of 0.25 and could all be allocated either to disease phases I or II (see also Table 1). This probably affects both volumetric and functional features, as additional disease accumulation along with the disease course will lead to larger differences in these features and therefore higher discriminative power on a case–control level (Menke et al., 2018; Shen et al., 2018; Steinbach, Batyrbekova, et al., 2020; van der Burgh et al., 2020).

Second, we controlled for the effect of age on classification performance by both age matching groups, and subsequently removing linear effects of age from all features. This may partly explain the slightly lower classification performance than observed in some studies, as a few of these studies did not match for age at all (Ferraro et al., 2017; Schuster et al., 2016), or did not regress out residual age‐related effects (Sarica et al., 2017; Welsh et al., 2013). This notion is supported by a study following a comparable procedure in removing age effects and also providing slightly lower classification accuracies (Fratello et al., 2017).

Differences in classification performance could furthermore be related to the applied PE assessment scheme. While we applied a stratified five‐fold cross‐validation where accuracy was averaged across the five folds (see also Sarica et al., 2017), others selected the best model across their ten‐fold cross‐validation (Schuster et al., 2016), or used a different validation scheme such as leave‐one‐out cross validation (Pagani et al., 2016; Welsh et al., 2013). Both of the latter strategies can bias the PE estimate for instance by causing overfitting (e.g., Koppe et al., 2020; Vabalas, Gowen, Poliakoff, & Casson, 2019; Varma & Simon, 2006). Moreover, while we trained the classifier on all pre‐defined features, others applied feature selection steps prior to training, where feature selection was performed on data used for testing/PE assessment (e.g., in a non‐nested feature selection fashion; Pagani et al., 2016; Sarica et al., 2017; Schuster et al., 2016), also potentially causing a biased PE estimate (Cearns et al., 2019; Koppe et al., 2020; Vabalas et al., 2019). Lastly, differences in accuracy could also be due to differences in sample sizes between studies which may affect classification performance indirectly by affecting the possible complexity or the standard error of the learned classifier (see also Durstewitz et al., 2019; Dwyer, Falkai, & Koutsouleris, 2018; Koppe et al., 2020).

5. LIMITATIONS

Several limitations of the present investigation should be mentioned. The (f)MRI recordings in the present study were collected using a 1.5 Tesla whole‐body MRI scanner while other classification studies were based on a 3 Tesla scanner (Bede et al., 2018; Ferraro et al., 2017; Fratello et al., 2017; Sarica et al., 2017; Schuster et al., 2016; Welton et al., 2019). The lower magnetic field strength applied here may be inferior in detecting subtler changes related to the disease due to a smaller signal‐to‐noise ratio. This might partly account for the somewhat more modest sensitivity level of the volume classifier, in contrast to the unimodal classifier related to brain function, as the present sample is characterized by a rather low disease accumulation (see Table 1) and differences in structural brain features become more evident the more the disease progresses (Menke et al., 2018; Shen et al., 2018; Steinbach, Batyrbekova, et al., 2020; van der Burgh et al., 2020). Nevertheless, even though the data was collected on a less sensitive (f)MRI scanner, we did find predictive features. This was further supported by an exploratory application of the classifiers on an independent data set comprising ten ALS mimics (see section 2.2 Appendix S1). If the trained classifiers had rather learned features unrelated to the specific disease, one could have expected them to misclassify ALS mimics more often as ALS, which would be reflected in low specificities. Instead, however, we observed a comparable pattern of specificities across all trained classifiers as found when distinguishing ALS from healthy individuals (see Table 2, section 2.2 Appendix S1, and Table S5), supporting that the classifiers did learn discriminatory ALS‐specific information (Ferraro et al., 2017; see also Feneberg et al., 2018; Poesen et al., 2017; Van Weehaeghe et al., 2020).

Critically, the findings must be interpreted in the context that the (f)MRIs used for this study were acquired on a clinical scanner used in clinical routine procedures from 2009 onwards, which may have implications for using (f)MRI in ALS as a surrogate parameter applicable in more common clinical situations (also outside of university settings), where often only 1.5 Tesla scanners are available. Also, using samples with low disease accumulation is crucial for early disease detection. Lastly, the study is based on a relatively small sample size which was further limited to allow to match the groups according to current age and gender and therefore control for potential age effects (see also Fratello et al., 2017; Pagani et al., 2016; Sarica et al., 2017; Welsh et al., 2013). Due to the limited sample size, we further decided on pre‐defining features and regions of interest based on previous findings (cf. Section 2.2) or, in the case of network dynamics, on prior experience and intuition. While on the one hand, this is a safer procedure to avoid overfitting and poor generalization, on the other hand, it precluded the detection of other potential brain area candidates, or dynamics features. On the other hand, our feature selection procedure resulted in a higher number of functional connectivity features than volumetric and dynamics features, the latter of which were comparable. Although RF classifiers are particularly robust against different numbers of input features (Probst et al., 2019; Strobl et al., 2009), we cannot entirely exclude the possibility that the importance of the functional connectivity features was therefore slightly inflated. However, as the classifier based on all three feature sets did not outperform all others, and that the bimodal classifiers all performed in a similar range, renders this explanation rather unlikely. In any case, this would once more emphasize the importance of our new tested feature set of network dynamics and brain volume for classification.

We also want to note that features identified as important here may only be interpreted as such in the context of the entire investigated feature set. Since the importance score reflects the average decrease in prediction accuracy caused by a random permutation of a given feature in each tree (for more details see, e.g., Strobl et al., 2009), it may be partly related to the interaction with the remaining features (as expected for a multivariate classifier). Lastly, we did not include structural connectivity features (as, e.g., measured via DTI), which have been proven to discriminate well between groups. Integrating this feature set into our multimodal classifier could further improve the detection of ALS based on neuroimaging biomarkers.

6. CONCLUSION AND OUTLOOK

In the present study, we show that combining functional and structural neuroimaging features distinctly contributes to the discrimination of ALS and HC. Specifically, the combination of brain volume and resting state functional connectivity achieved the highest classification performance. Out of all features sets, resting state functional connectivity produced the most discriminative biomarkers overall, being identified as most important within the multimodal classifiers and achieving the highest unimodal classification results. Both this feature set, as well as our RNN features, further indicated that ALS may be characterized by disturbances in information integration across large‐scale brain networks. Our study is the first to evaluate the potential of resting state network dynamics as discriminatory biomarkers for ALS. Larger multicenter data sets are needed to disentangle the effects of network dynamics and its interaction with other features to develop on objective neuroimaging markers of ALS.

CONFLICT OF INTEREST

The authors declare no conflicts of interest.

Supporting information

Appendix S1 Supporting Information

Thome, J. , Steinbach, R. , Grosskreutz, J. , Durstewitz, D. , & Koppe, G. (2022). Classification of amyotrophic lateral sclerosis by brain volume, connectivity, and network dynamics. Human Brain Mapping, 43(2), 681–699. 10.1002/hbm.25679

DATA AVAILABILITY STATEMENT

The extracted data features and all code used to support the findings can be found here https://github.com/JanineT-oss/ALS_PLRNN_classification. Classifier will be send upon request. Data is available via the NiSALS repository.