Abstract
Purpose:
To resolve the motion-induced phase variations in multi-shot multi-direction diffusion-weighted imaging (DWI) by applying regularization to magnitude images.
Theory and Methods:
A nonlinear model was developed to estimate phase and magnitude images separately. A locally low-rank regularization (LLR) term was applied to the magnitude images from all diffusion-encoding directions to exploit the spatial and angular correlation. In vivo experiments with different resolutions and b-values were performed to validate the proposed method.
Results:
The proposed method significantly reduces the noise level compared to the conventional reconstruction method and achieves submillimeter (0.8mm and 0.9mm isotropic resolutions) DWI with a b-value of 1,000 s/mm2 and 1-mm isotropic DWI with a b-value of 2,000 s/mm2 without modification of the sequence.
Conclusions:
A joint reconstruction method with spatial-angular LLR regularization on magnitude images substantially improves multi-direction DWI reconstruction, simultaneously removes motion-induced phase artifacts, and denoises images.
Keywords: angular correlation, diffusion-weighted imaging, locally low rank, multi-shot imaging, phase variation
1 |. INTRODUCTION
Diffusion-weighted MRI (DWI) noninvasively measures Brownian motion of water molecules along the direction of diffusion-encoding gradients. It has been widely used for clinical and neuroscientific applications.1–4 Typically, DW images are acquired using single-shot echo-planar imaging (EPI) to provide robustness against motion artifacts. However, in single-shot EPI, the spatial resolution and signal-to-noise ratio (SNR) are limited due to the long readout window, and distortion artifacts can be severe.5
To enable high-resolution DWI with reduced artifacts, numerous techniques such as simultaneous multi-slice imaging,6,7 multi-shot imaging,8 reduced field-of-view (FOV) imaging,9 image denoising,10 and some advanced image reconstruction methods11–13 have been proposed. Nonetheless, diffusion encoding leads to a motion-induced phase that varies between repetitions and may limit the application of many techniques to DWI. To address this challenge, many navigatorless reconstruction methods have been proposed for multi-shot DWI. In MUSE,14 SENSE is first applied to each individual shot to estimate the motion-induced phase, which is then included into the forward model for a SENSE-like reconstruction. POCS-MUSE15 and POCS-ICE11 further improve this method by updating the phase estimation during each iteration. To bypass the phase estimation step, low-rank matrices in k-space and image space are constructed in MUSSELS16 and shot-LLR,17 respectively, and matrix completion is performed to reconstruct multi-shot images.
Acquisition of DW images along multiple directions is needed for deriving microstructural metrics from diffusion models such as the diffusion tensor imaging (DTI),3 neurite orientation dispersion and density imaging (NODDI),18 and others. Some post-processing methods have been proposed to denoise each individual magnitude image based on various assumptions.10,19 The angular correlation of diffusion signal along multiple encoding directions has also been incorporated into DWI reconstruction methods to enable higher reduction factors, increase SNR, and reduce scan time. Gao et al. used globally low-rank regularization,20 and Shi et al applied a joint sparsity constraint to multi-shot spiral imaging.21 Ma et al applied a combination of these two constraints to cardiac DTI.22 Wu et al assumed the diffusion signal along different encoding directions was a Gaussian process and incorporated this prior into parallel imaging.23 To reduce the influence of phase variations between different diffusion-encoding directions, these joint reconstruction methods first estimate the low-resolution phase and then eliminate this phase when performing image reconstruction with those constraints. Since the phase is fixed during later iterations, one possible limitation of these methods is that the residual phase variation due to inaccurate initial phase estimation can decrease the angular correlation.
In this work, we propose a nonlinear model for multi-shot DWI reconstruction. Our method differs from existing methods as it separately reconstructs both magnitude and phase images rather than complex images. This property enables the direct application of constraints on the magnitude images without influence from phase variations. We apply locally low-rank regularization (LLR) to multi-direction DW images to utilize the angular correlation between different encoding directions without explicit modeling. A pipeline, including how to initialize and update the magnitude and phase images, is developed to jointly reconstruct multi-shot multi-direction DW images. When compared with results from the MUSE reconstruction, a significantly reduced noise level can be visualized. In vivo experiments demonstrate that using a nonlinear model coupled with this SPatial-Angular LLR regularization (SPA-LLR), high-quality submillimeter resolution DWI can be achieved.
2 |. THEORY
2.1 |. Locally low-rank regularization
LLR has been used successfully for calibrationless parallel imaging,24 dynamic imaging,25 T2 estimation,26 and correction of phase variations.17 It shows better denoising performance compared with globally low-rank regularization.24 In this work, we apply LLR regularization to multi-direction DWI. In many applications, DW images along 30 or even more diffusion-encoding directions are typically acquired to fit diffusion models and obtain sufficient SNR. Redundancy exists between DW signals along different diffusion-encoding directions. To utilize this redundancy, we construct so-called spatial-angular matrices with the magnitude images from all directions (Figure 1) and apply a rank penalty on the sum of ranks of these matrices. To construct a spatial-angular matrix, one small spatial block is first chosen. The magnitude images along each diffusion-encoding direction in this block are then reshaped into a vector. Finally, vectors from all directions are concatenated together. The entire FOV is covered by many local blocks.
FIGURE 1.
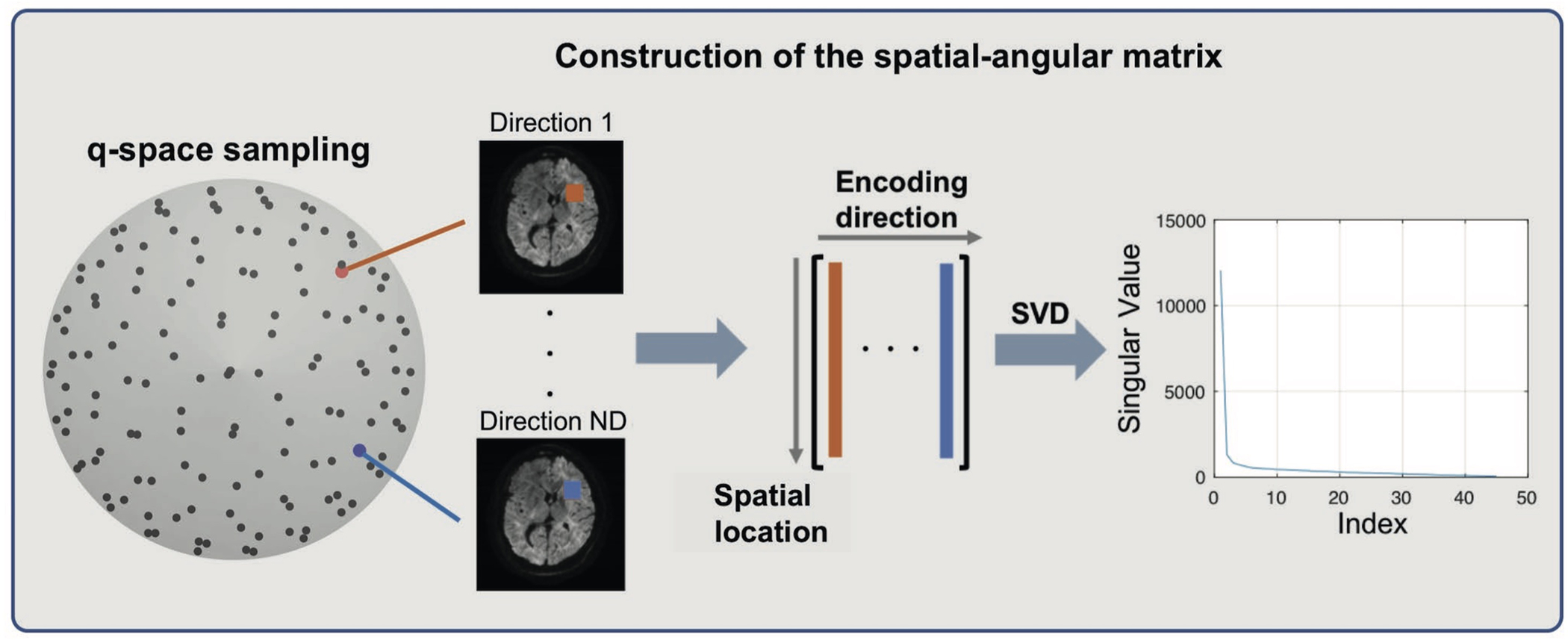
Construction of the spatial-angular matrix from magnitude images of different directions. Each column of the matrix represents one block of pixels from one diffusion-encoding direction, and different columns together form a matrix. After singular value decomposition (SVD), most of the eigenvalues of this matrix are close to 0, which suggests that the rank of this matrix is low, and this can be used as a regularization term in reconstruction
2.2 |. Nonlinear model
The signal in DWI can be written in the following matrix form,
| (1) |
where y denotes the acquired k-space signal, E, F, and S represent sampling operator, Fourier transform and sensitivity encoding operator, respectively, x denotes the complex DW image to be estimated, and n denotes noise.
To utilize the angular correlation between magnitude images along different encoding directions, motion-induced phase variations need to be considered. The complex image can be written in terms of magnitude and phase explicitly, so the k-space signal for direction d, shot s, can be represented as:
| (2) |
where md represents the magnitude image along the diffusion-encoding direction d, an represents the phase image along the diffusion-encoding direction d for shot s, which may arise from B0 inhomogeneity, bulk motion, eddy currents, or other sources.
The general model we propose for joint reconstruction of multi-direction DWI is as follows:
| (3) |
where ND denotes the number of directions, NS denotes the number of shots, , and .
The first term encourages consistency with the forward model based on Equation 2, and the second term gm(m) is a regularization term to utilize the correlation between images from different diffusion-encoding directions. In this work, we use LLR as introduced in the previous section. The reconstruction can be formulated as the following problem,
| (4) |
where Rl is an operator that extracts and reshapes one local spatial block at pixel index l as a vector for each direction and concatenates vectors from all directions into a matrix as shown in Figure 1, and Ω is the set of all nonoverlapping blocks that uniformly tile the image domain. The nuclear norm (‖ ‖*), which is the convex envelope of the rank constraint and which is equivalent to the sum of the matrix’s eigenvalues, is used to reduce the computational complexity.27
2.3 |. Algorithm
The proposed model is bilinear in terms of magnitude and phase, and we use alternating minimization with respect to the magnitude and phase separately to solve the above problem. The phase of each shot and each direction can be updated individually. In terms of phase θd,s, the subproblem is
| (5) |
Let
| (6) |
and
| (7) |
The gradient with respect to θd,s can be derived as follows,
| (8) |
where Real(x) takes the real part of x. We use this to apply a gradient descent step and the update rule for θd,s in the kth iteration is
| (9) |
where α is the step size.
Unlike phase images, magnitude images from all directions have to be updated simultaneously because of the use of the LLR regularization term. We use the proximal gradient method to update the magnitude images. The subproblem in terms of magnitude m is as follows,
| (10) |
Similarly, the gradient of the first term with respect to md is,
| (11) |
Defining , the update rule for m in the kth iteration is
| (12) |
| (13) |
where is the proximal operator of λ1gm. In this case, gm(m) is the LLR regularization term, which is the summation of nuclear norms of all spatial-angular matrices. Based on the definition of the proximal operator, Equation 13 could be written as follows,
| (14) |
By using nonoverlapped blocks, this problem can be separated into many subproblems, and an analytical solution exists. Each matrix can be updated separately by applying soft-thresholding to its eigenvalues. In each iteration, random shifts along frequency encoding and phase encoding directions are added when constructing those blocks to achieve shift invariance.28
In summary, the phase and magnitude images are updated based on Equation 9 and Equation 13 separately in each iteration, until convergence or a maximum number of iterations is reached. The full pipeline is shown in Figure 2, and the pseudo-algorithm is shown in Supporting Information Table S1.
FIGURE 2.
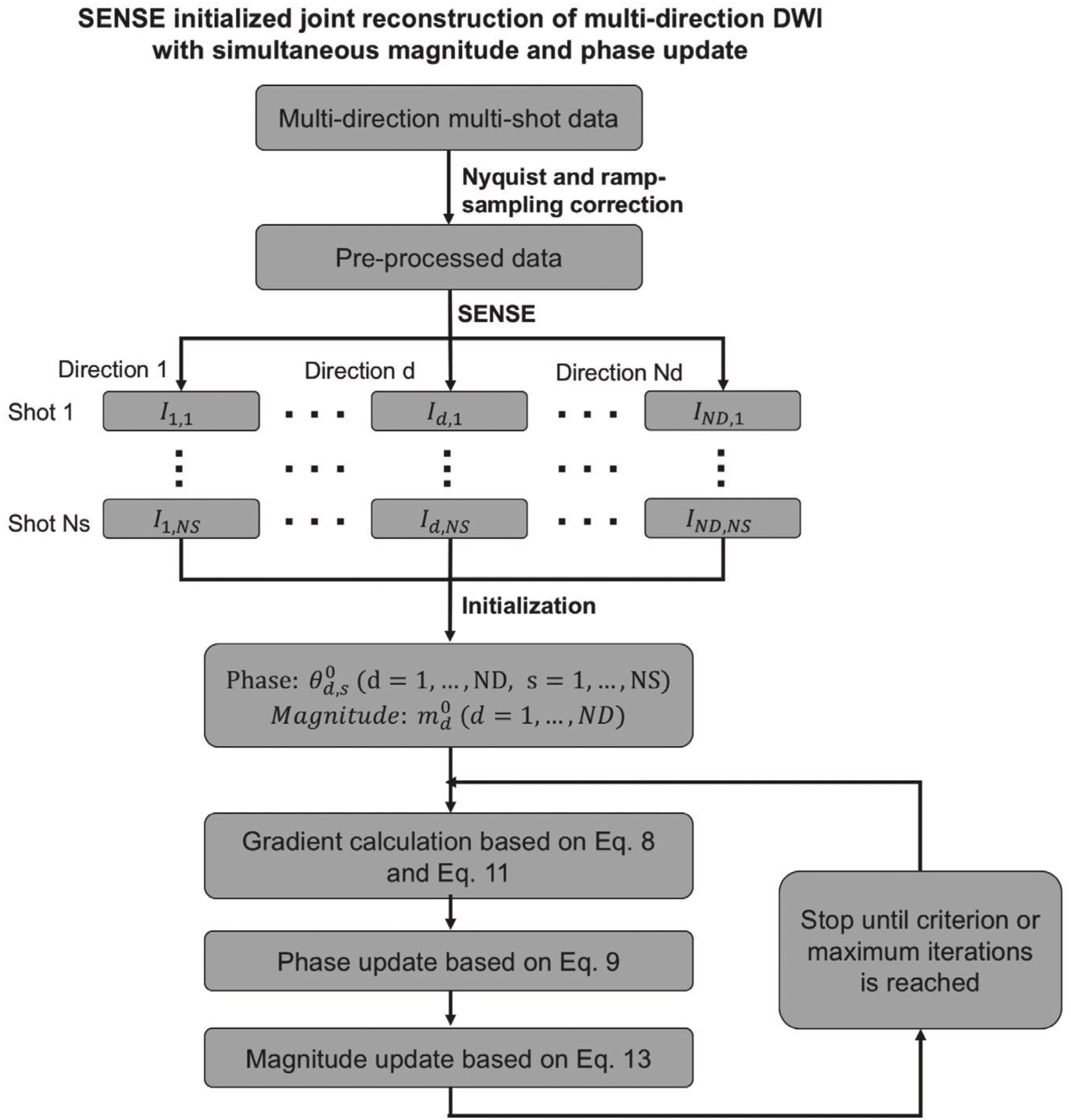
The reconstruction pipeline of the proposed method. SENSE reconstruction results for each individual shot and direction are used as initialization of the nonlinear model. In each iteration, phase and magnitude images are updated separately based on Equation 9 and Equation 13
3 |. METHODS
3.1 |. Data acquisition
With approval from the institutional review board and written informed consent, data were acquired from seven healthy volunteers on a 3 T GE Signa Premier scanner using a 48-channel head receive-only coil. Six experiments were performed for different purposes. For all scans, a 2D single-refocused Stejskal-Tanner diffusion-weighted spin-echo EPI sequence was used to acquire about 10 axial slices covering the corpus callosum, with left-right readout direction, ± 250 kHz bandwidth, four shots (except for Experiments 0 and 4), a b-value of 1,000 s/mm2 (except for Experiments 0 and 5), and one interleaved nondiffusion-weighted image (b = 0) for every 14 DW images for image co-registration. The scan parameters of all experiments are summarized in Table 1.
TABLE 1.
Summary of acquisition parameters of different experiments
| Parameters | Ex0 (to validate the method) | Ex1 (parameter selection) | Ex2 (four-shot vs single-shot with R = 3) | Ex3 (different resolutions) | Ex4 (more directions) | Ex5 (high b-value) | |
|---|---|---|---|---|---|---|---|
| TR/TE (ms) | 3266/70 | 3375/50 | 2278/51 | 2478/64 | 2627/53, 2759/54, 2993/57 | 2853/53 | 2908/59 |
| Effective echo spacing (μs) | 334 | 264 | 245 | 324 | 264, 281, 310 | 264 | 245 |
| Scan time (min) | 6:45 | 08:09 | 22:58 | 24:58 | 13:21, 14:01, 15:13 | 28:46 | 14:47 |
| In-plane resolution (mm) | 2 | 0.9 | 1 | 0.9, 0.8, 0.7 | 0.9 | 1 | |
| Slice thickness (mm) | 2 | 0.9 | 1 | 0.9, 0.8, 0.7 | 0.9 | 1 | |
| FOV (cm) | 20 | 20 | 18.4 | 20 | 20 | 20 | |
| Number of slices | 12 | 14 | 10 | 11 | 12 | 10 | |
| Partial Fourier factor | 1 | 0.61 | 0.67 | 0.75 | 0.64, 0.63, 0.61 | 0.64 | 0.66 |
| Number of directions | 60 | 30 | 150 | 75 | 150 | 75 | |
| Nex | 1 | 1 | 1 | 4 | 1 | 1 | 1 |
| b-value | 2000 | 1000 | 1000 | 1000 | 1000 | 2000 | |
| Number of subjects | 1 | 1 | 1 | 1 | 2 | 2 | |
Experiment 0 acquired high SNR data to validate the feasibility of the proposed method and investigate the influence of the regularization parameter λ on the reconstruction results. Experiment 1 was performed to select reconstruction parameters. Data were acquired along only 30 directions to enable fast reconstruction. Experiment 2 included two consecutive scans to compare the performance of single-shot and multi-shot scans with the same resolution and number of diffusion-encoding directions. Four repetitions were acquired in the single-shot scan to match the acquisition time of the four-shot scan. Experiment 3 was designed to test the performance of the proposed method on data with different resolutions (0.9, 0.8, and 0.7 mm isotropic). The data were acquired along 75 diffusion-encoding directions such that the total scan time was within 1 hour. Experiment 4 only included a four-shot scan with 0.9-mm isotropic resolution and 150 directions to further improve the angular resolution compared with Experiment 3. Experiment 5 was designed to validate the proposed method on data acquired with a higher b-value.
3.2 |. Image reconstruction and processing
All multi-shot data were reconstructed by the online GE MUSE reconstruction and the proposed method. The reconstruction pipeline of the proposed method is depicted in Figure 2. The acquired raw k-space data were first processed for Nyquist ghost correction and ramp-sampling correction using the product algorithm provided by GE’s Orchestra software. The multi-shot nondiffusion-weighted k-space data were simply combined together since there were no phase variations in the absence of diffusion-encoding gradients. Sensitivity maps were calculated from the nondiffusion-weighted images using ESPIRiT.29 SENSE reconstruction30 was performed on DW data of each individual shot and direction using BART.31 Low-resolution phase images after Hanning windowing15 and averaged magnitude images of the SENSE results were used as the initialization of the proposed algorithm. The reconstruction settings were selected based on the reconstruction results of Experiment 1 and were summarized in Table 2. The same settings were used for all experiments. A small range of the regularization parameter was suggested based on Experiment 1. The step size α was chosen as 0.9 as in Ref. 32, and 100 iterations (chosen empirically) achieved good convergence. The block size of the LLR term was chosen as eight following previous LLR methods.17 The absolute value of reconstructed magnitude images was used for the diffusion model fitting. For the product MUSE reconstruction, sensitivity maps were calculated from an extra calibration scan, and homodyne was used after MUSE reconstruction for partial Fourier reconstruction.
TABLE 2.
Summary of selected reconstruction parameters as described in “methods” for the proposed reconstruction
| Parameters | Values |
|---|---|
| Number of iterations | 100 |
| Initialization of phase | Hanning window (width = matrix size) |
| Step size for phase and magnitude update | 0.9 |
| Regularization parameter for LLR | 0.12∼0.18 |
| Block size | 8 |
| Phase update (Yes/No) | Yes |
DWI data were corrected for eddy current distortions and bulk motion, and co-registered using the “eddy” function from the FMRIB Software Library (FSL, http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/).33 The diffusion tensor model was then fitted using FSL’s “dtifit” function to derive the fractional anisotropy (FA) and the primary eigenvector (V1). The “ball-and-stick” model (3 sticks) was fitted using FSL’s “bedpostx” function on the b = 0 and 2,000 s∕mm2 data to derive the primary, secondary, and tertiary fiber orientations (dyads1, dyads2, and dyads3, respectively) and their associated volume fractions (f1, f2, and f3, respectively).
4 |. RESULTS
4.1 |. Choice of reconstruction parameters
Figure 3 shows the reconstruction results with different regularization parameters (λ1 in Equation 4 and Equation 12). When λ1 is 0, ie, no angular correlation is used and each direction is reconstructed individually, the result (Figure 3A) is very noisy. As λ1 increases, the noise level decreases (Figure 3B,C). When λ1 is too large, some structures are lost and blocky artifacts show up (Figure 3D). Notice that the noise level of the data can also influence the choice of this regularization parameter. Consequently, we provide a range of λ1 in Table 2. We use λ = 0.12 for 1.2 mm isotropic data and λ = 0.15 for 0.9 mm isotropic data. Supporting Information Figure S1 shows how this parameter would influence the estimated number of crossing fibers, which highly depends on the angular anisotropy.
FIGURE 3.
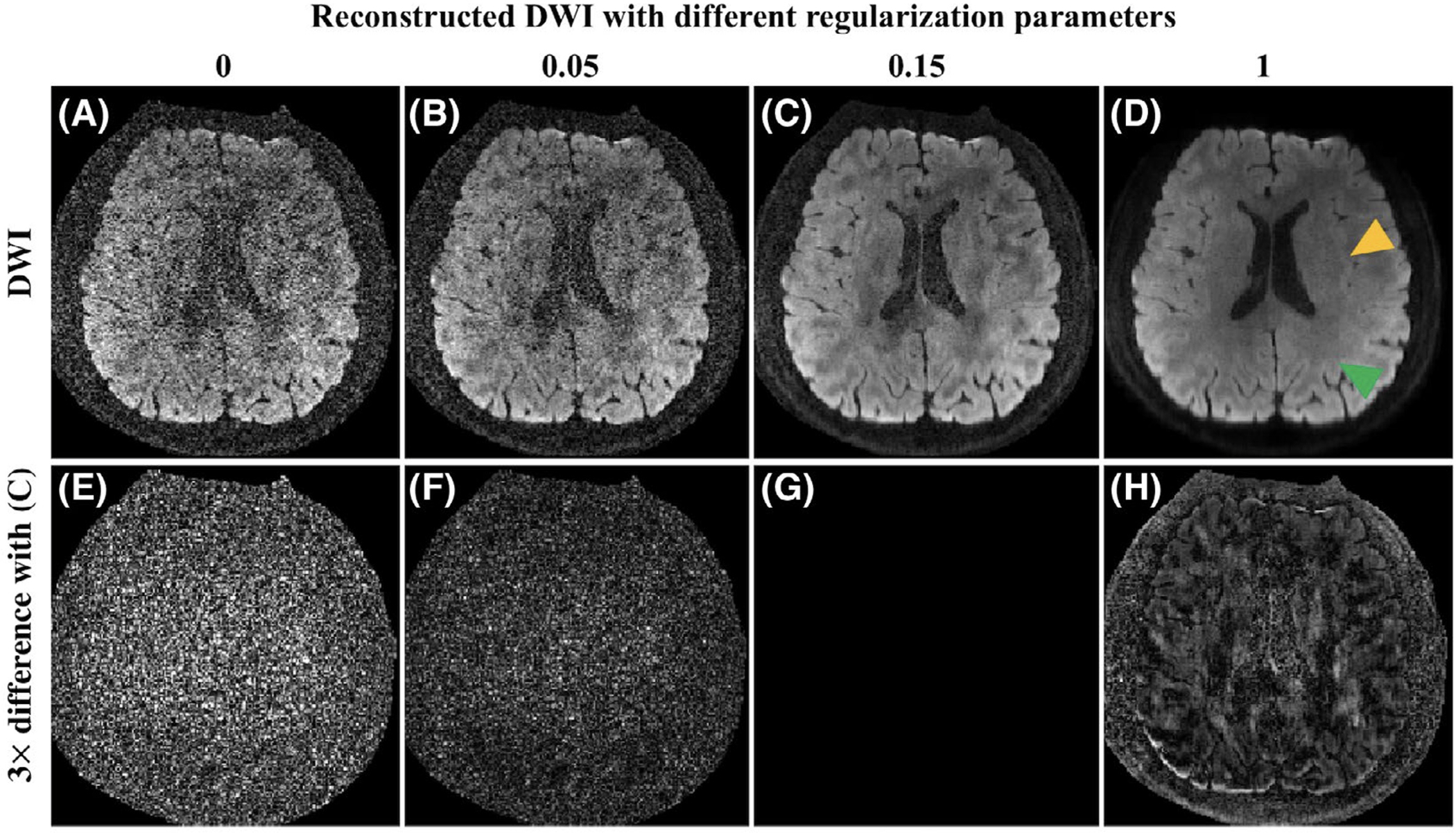
Reconstructed DW images with different regularization parameters (λ1 in Equation 4) (A-D) and their 3× differences (E-H) with (C). When the regularization parameter is not large enough, the noise level is still high (A and B). When this regularization parameter is too large, the image looks blocky and some structures are lost as indicated by the green and yellow triangles in (D), respectively
The advantage of phase update and SENSE initialization is shown in Figure 4. Without any initialization, the reconstruction fails, and artifacts exist due to the difficulty of nonlinear optimization (Figure 4A). Initialization with the SENSE reconstruction removes these artifacts (Figure 4B). In addition, performing phase update can help to recover high-frequency phase information (Figure 4I) and to further decrease noise levels in the magnitude image (Figure 4C).
FIGURE 4.
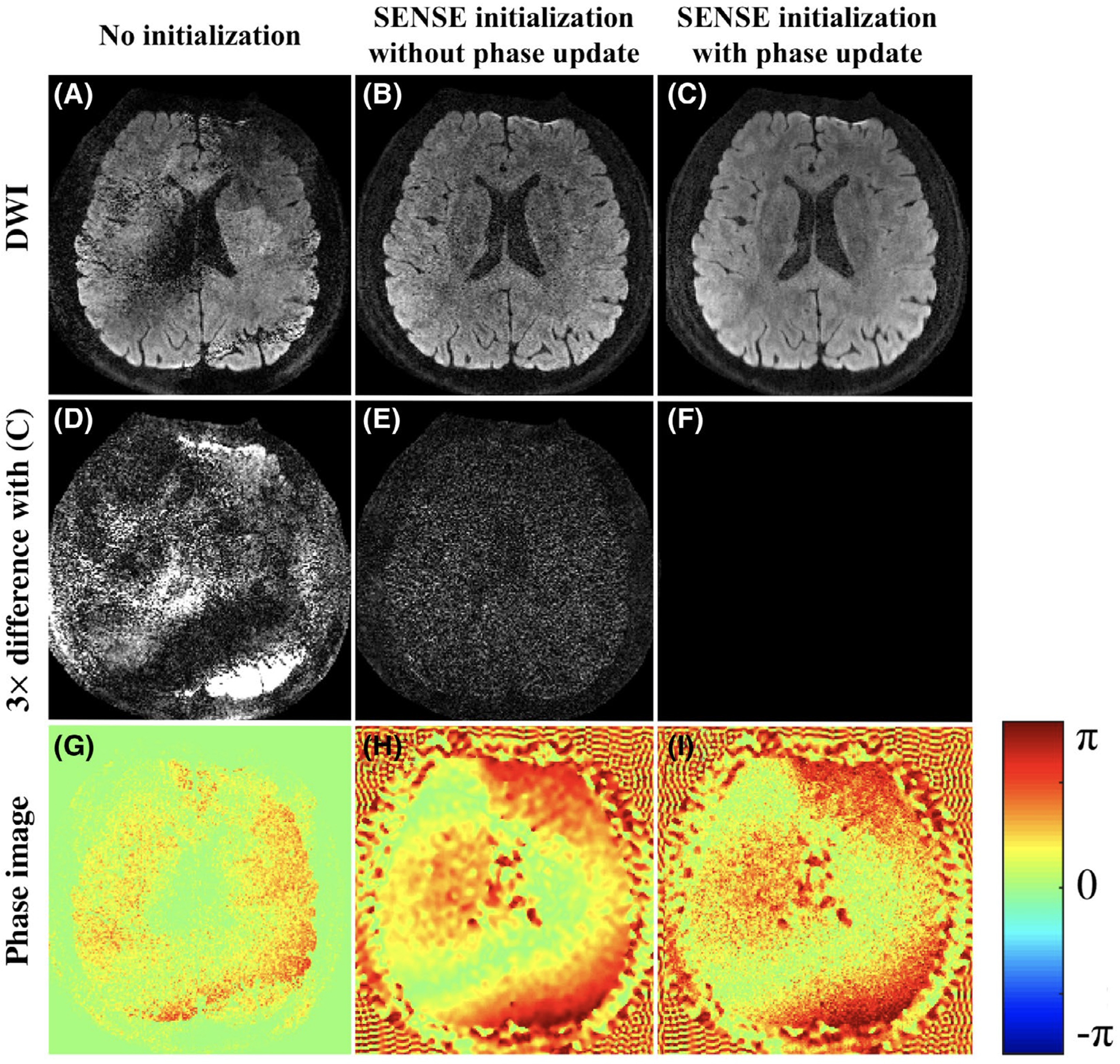
Reconstructed DW images with different reconstruction settings (A-C), their 3× difference (D-F) compared to (C), and phase images of the first shot (G-I). Artifacts exist without using any initialization (A). Using SENSE as initialization avoids the artifacts (B), and updating the phase during reconstruction further refines the results (C)
4.2 |. Comparison of single-shot and multi-shot imaging
Figure 5 shows comparisons of single-shot imaging and multi-shot imaging with matched scan time. Multi-shot images were reconstructed by the product MUSE and the proposed reconstruction method, respectively. A 4-shot acquisition with MUSE reconstruction (Figure 5, row B) shows decreased noise level compared to single-shot imaging with multiple repetitions (Figure 5, row A). Some structure is lost due to the high noise level in single-shot imaging as indicated by the red box (Figure 5, row A, column I). The noise levels in both DW images and direction-encoded color FA maps are significantly reduced by our proposed method (Figure 5, row C) compared with MUSE (Figure 5, row B), which demonstrates the ability of our proposed method to utilize the correlation between different diffusion-encoding directions. The distortion level due to off-resonance in multi-shot images is reduced by a factor of 1.3 compared with that of single-shot images with a parallel imaging factor of 3, which is consistent with the effective echo spacing as shown in Table 2. However, the distortion levels are visually similar since the brain regions covered by the displayed axial slices contain minimal susceptibility variations.
FIGURE 5.
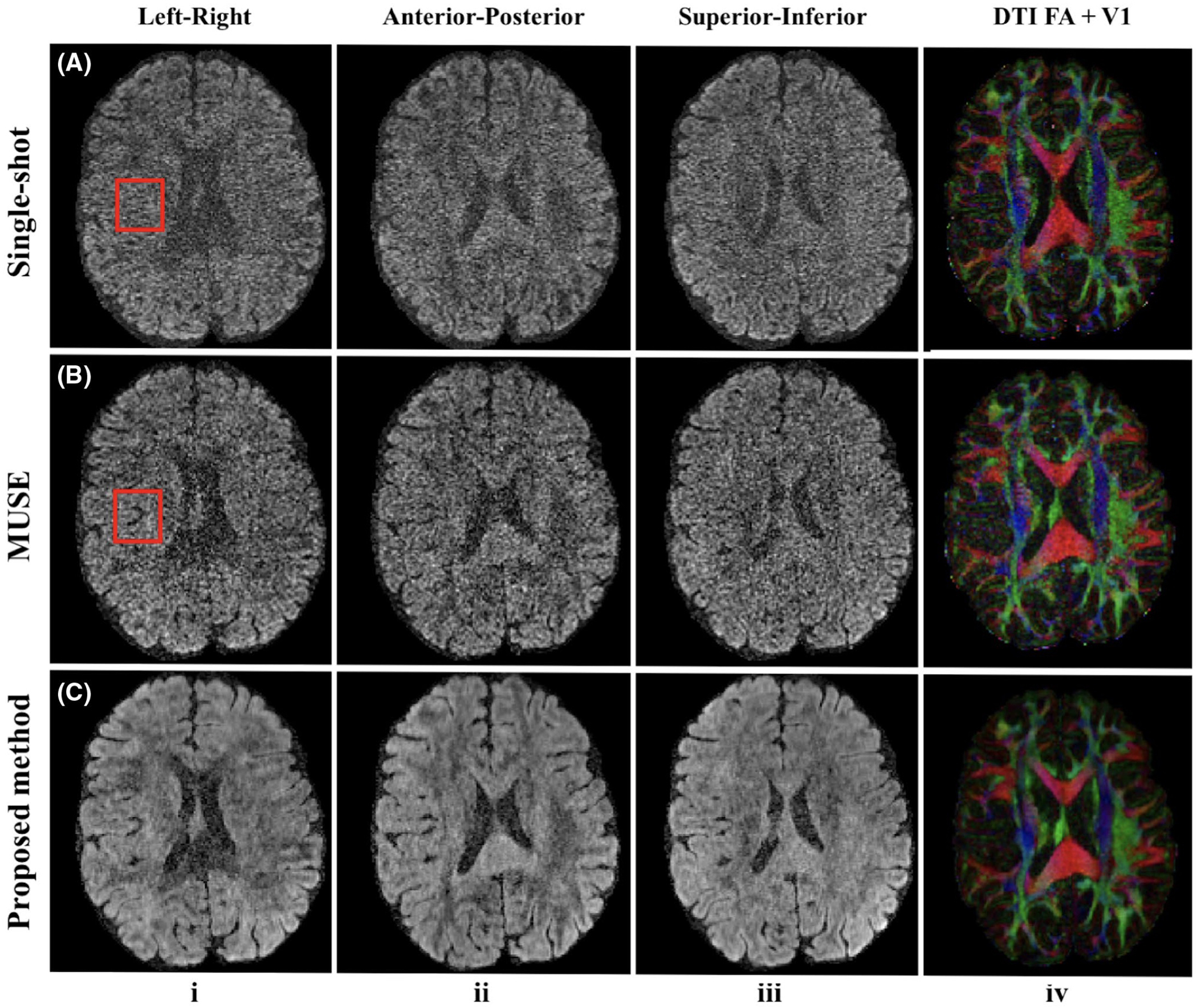
Reconstructed DW images along left-right, anterior-posterior, superior-inferior diffusion-encoding directions out of 150 directions (columns i-iii) and corresponding color-encoded V1 maps weighted by FA (column iv). Row (A) shows single-shot results (R = 3, nex = 4), and the red box indicates the structure loss due to the high noise level. Rows (B) and (C) show four-shot results reconstructed by MUSE and the proposed method from Experiment 2 (1 mm isotropic resolution, 1,000 s∕mm2 b-value). Four-shot acquisition with the proposed reconstruction shows the least noisy results
4.3 |. Different resolutions
The improvement of our proposed method compared with MUSE is more significant at a higher resolution. Figure 6 shows a representative axial slice reconstructed by these two methods under different resolutions. The DW images reconstructed by MUSE (Figure 6A,C,E) are very noisy, resulting in noisy FA maps and erroneous V1 vectors (Figure 6B,D,F). The proposed method shows markedly reduced noise levels, and the reconstructed DW images and V1 maps are visually better (Figure 6G–L).
FIGURE 6.
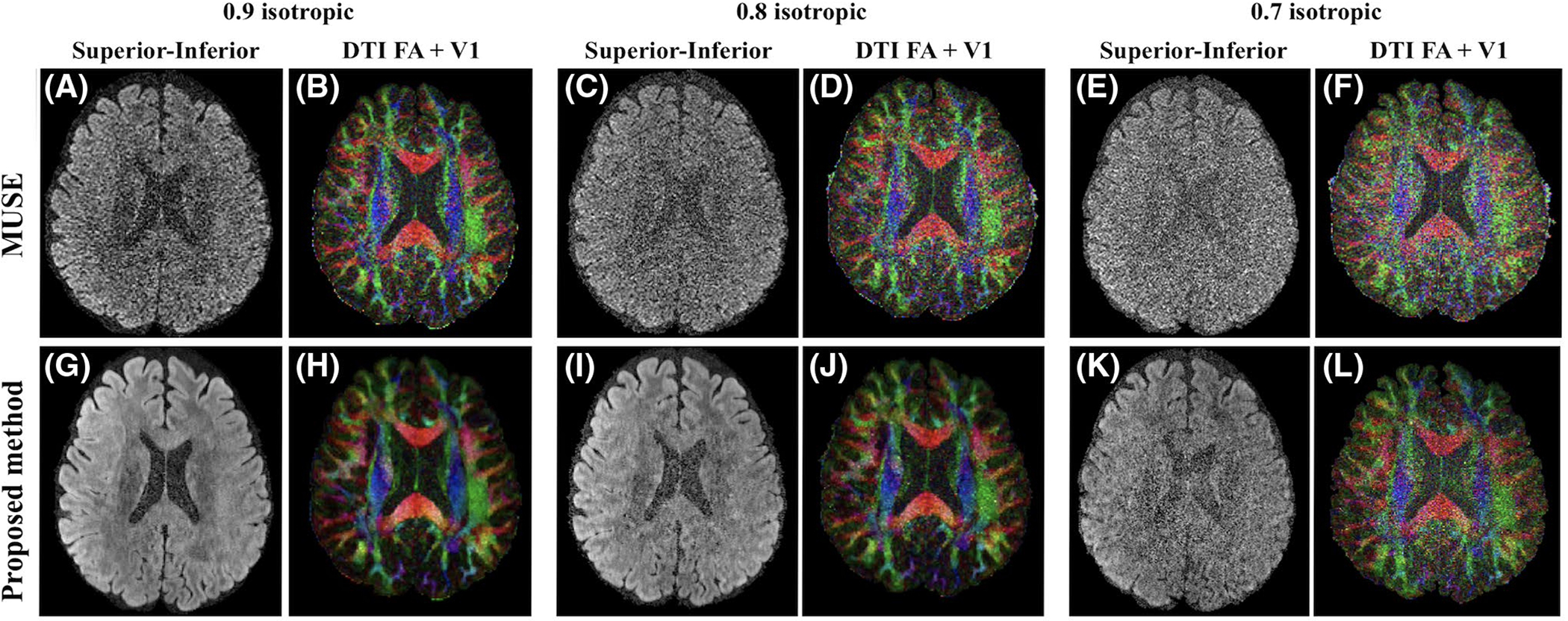
Reconstructed DW images along the superior‐inferior diffusion‐encoding directions from an acquisition of 75 directions and corresponding color‐encoded V1 maps weighted by FA by MUSE (A‐F) and the proposed method (G‐L) from Experiment 3 (0.9, 0.8, and 0.7 mm isotropic resolution, 1,000 s∕mm2 b‐value). The windows of V1 maps are tuned separately for better visual quality (0‐1 for MUSE, and 0‐0.8 for the proposed method). The proposed method shows significantly reduced noise levels
Figure 7 displays direction-encoded color FA maps with 0.9-mm isotropic resolution and 150 diffusion-encoding directions reconstructed by the proposed method from two subjects. The primary eigenvector V1 in the cortex can be clearly visualized, which is dominantly radial to the cortical surface. In addition, we selected and reconstructed 15, 30, 45, 60, and 75 out of 150 directions using our proposed method and MUSE. The estimated FA maps based on the reconstruction results are shown in Supporting Information Figure S2. For different numbers of selected directions, our proposed method shows significantly decreased noise levels compared with MUSE by inspection. With an increased number of diffusion-encoding directions, the noise level in FA maps decreases for both our proposed method and MUSE. Starting from 60 directions, no noticeable difference could be visualized in our proposed method when comparing with the FA map from 150 directions.
FIGURE 7.
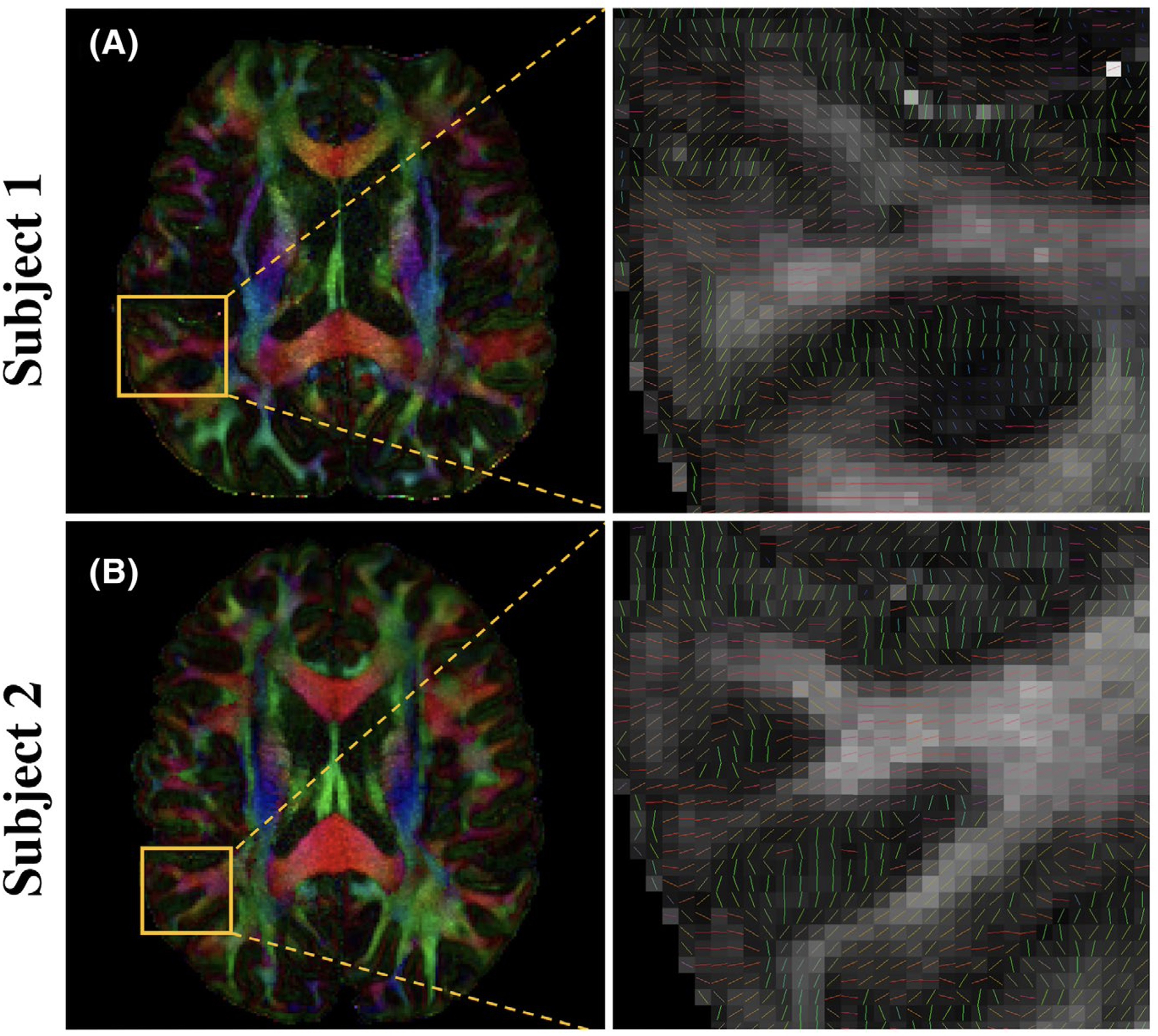
Color‐encoded V1 maps weighted by FA with 0.9 mm isotropic resolution and 150 diffusion‐encoding directions reconstructed by the proposed method on two subjects. The window level is tuned separately for better visual quality (0‐0.8 for subject 1, and 0‐1 for subject 2). The zoomed‐in view in the second column shows the primary eigenvector V1 in the cortex
4.4 |. High b-value images
The proposed method shows similar improvements for high b-value images as shown in Figure 8 with 1 mm isotropic resolution and b-value 2,000 s∕mm2. The proposed method (Figure 8, row B, column v) estimates more voxels with a second fiber compared with MUSE (Figure 8, row A, column v).
FIGURE 8.
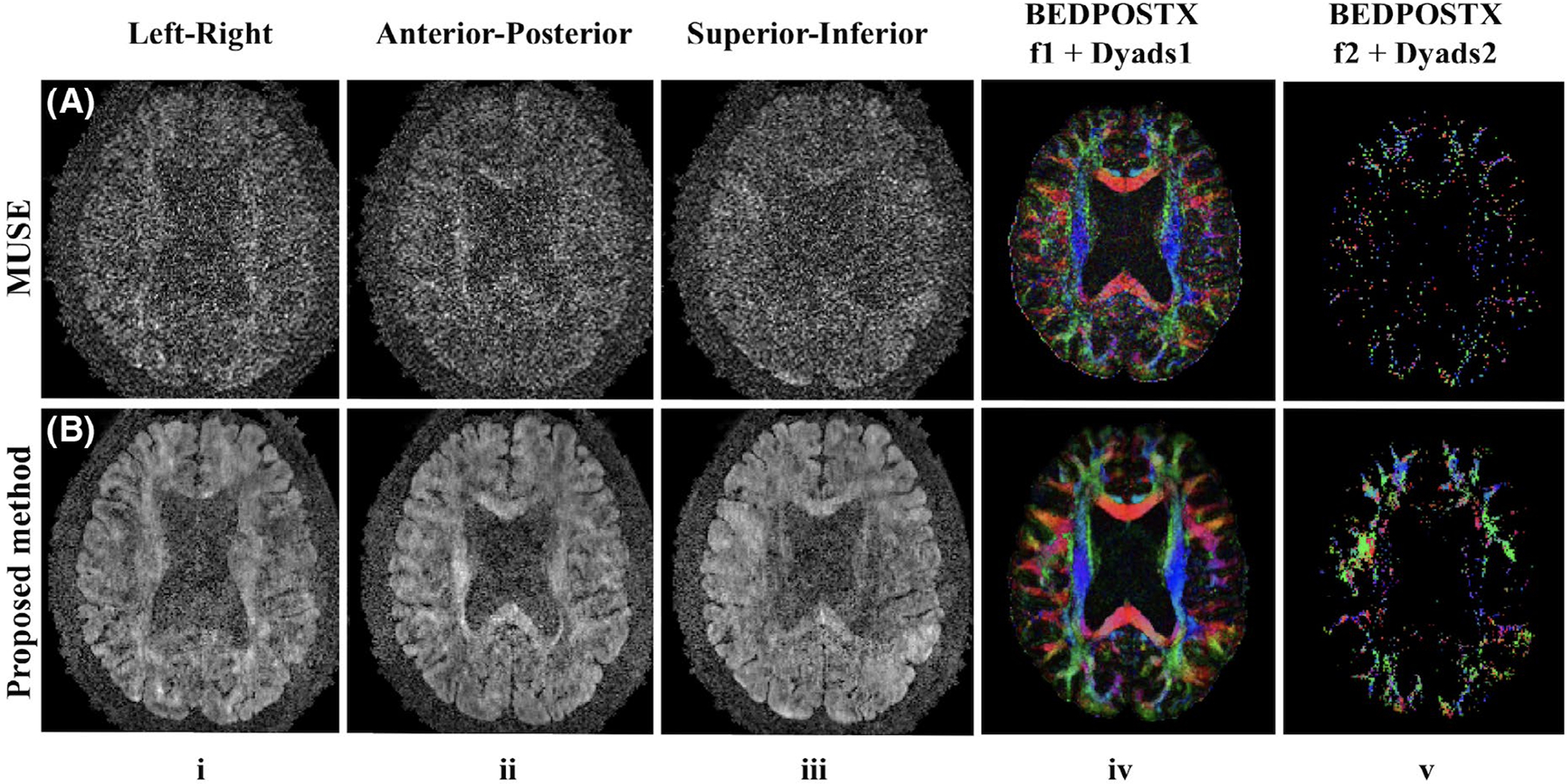
Three out of 75 directions from four‐shot high b‐value DW images (columns i‐iii), corresponding f1‐encoded Dyads1 maps (column iv) and f2‐encoded Dyads2 maps (column v) reconstructed by MUSE (row A) and the proposed method (row B) from Experiment 5 (1 mm isotropic resolution, 2,000 s∕mm2 b‐value). A threshold of 0.05 was used for both results
5 |. DISCUSSION
A nonlinear model with simultaneous phase and magnitude updates solves the phase variation problem in DWI reconstruction. The separate estimation of phase and magnitude images allows constraints to be directly applied to the magnitude images. We use LLR on the magnitude images from all diffusion-encoding directions to utilize their angular correlation. The nonlinear model and spatial-angular LLR regularization together remove phase variations between both shots and directions and substantially reduce noise levels in DW images. The proposed method is demonstrated in submillimeter resolution DWI experiments.
The proposed nonlinear model also allows other regularization terms such as a Gaussian prior or total variation to be incorporated. The separation of magnitude and phase estimation and the low-resolution phase initialization inherently provide partial Fourier reconstruction. In addition, the results may be further improved by adding constraints on the phase images.32 However, this increases the complexity of the algorithm, which needs to account for phase wraps. The current reconstruction of one slice with size 224-by-224, 48 channels and 150 directions takes approximately 3 hours on a Linux workstation with a 2.3 GHz CPU and a 256-GB RAM.
In the proposed method, the regularization parameter for LLR must be determined as in other optimization problems. Other reconstruction settings such as whether or not to perform phase update, block size, and others are consistent for different datasets and are determined based on Experiment 1. We notice that when the regularization parameter is large, the reconstructed DW images can still look clean without blocky artifacts, while the FA maps become blurry with reduced values. This is because a very large regularization term may eliminate the real variations of the diffusion signals along different directions. Supporting Information Figure S1 shows that there is a tradeoff between the denoising level and angular smoothing. The joint reconstruction with a suitable regularization parameter (about 0.1 in this case) enables more crossing fibers to be detected, while further increasing the regularization parameter oversmooths the images such that fewer crossing fibers can be detected. Increasing the number of diffusion-encoding directions or decreasing spatial resolution helps to avoid this problem because a smaller regularization parameter can be used in these cases. The choice of the optimal regularization parameter is an art and it depends on spatial resolution, b-value, block size, and the number of diffusion-encoding directions. We performed a grid search in Experiment 1 to empirically select a small range for this parameter. We fine-tuned this parameter by a small amount within this range when applied to data acquired with different parameters, and this strategy worked well. Auto-selection of the regularization parameters using more advanced methods34 may ultimately benefit this method.
We note that a proper initialization, especially for the phase images, is necessary since the proposed model is nonconvex. Using SENSE reconstruction as initialization works well in our study, but other initialization methods and optimization methods remain to be explored. Further refining the phase estimation in each iteration also helps with the estimation of magnitude images, because the initial phase estimation from the SENSE reconstruction is not sufficiently accurate. The block size of LLR is set as 8, and it does not make much difference to change it to 6 or 10.
We have shown that multi-shot imaging can achieve better image quality compared with single-shot imaging within the same scan time. This improvement may be because of (1) the reduction of TE (64 ms for single-shot and 51 ms for four-shot as in Table 1) and (2) the fact that multi-shot reconstruction utilizes the shot-to-shot correlation to obtain the DW images of each direction, while using only magnitude averaging to combine different repetitions of single-shot images can increase noise levels.35,36 More experiments need to be performed to further validate this point. Because the online GE MUSE reconstruction works robustly with no ghosting artifacts and is readily available, we use it as a reference for comparison. Significantly reduced noise levels could be visualized when comparing our proposed method with the product MUSE reconstruction. Notably, our reconstruction method and the product MUSE reconstruction utilize different sensitivity maps (computed based on the b = 0 image and from an external reference scan, respectively) and homodyne is used after product MUSE for partial Fourier reconstruction. Those differences might introduce some confounding factors especially for quantitative comparisons.
One disadvantage of multi-shot imaging is the increased scan time. Some advanced acquisition strategies like simultaneous multi-slice imaging6 or reduced-FOV excitation9 could be combined with multi-shot imaging to help accelerate the acquisition. Our method can also be applied to other sampling patterns37,38 with a minor modification of the data consistency term in Equation 4. Currently, our model only takes phase variations into account, and the inter-volume rigid motion (displacement) is corrected in the post-processing step. The image translation due to the rigid motion and the mismatched image distortion due to eddy currents between different diffusion-encoding directions may decrease the angular correlation. For scan times as long as 30 minutes and b-values as high as 2,000 s/m2, the proposed method still shows remarkable improvements. A linear or nonlinear transform could also be included in the data consistency term to correct this mismatch between directions.
6 |. CONCLUSION
We propose a nonlinear model for multi-shot DWI reconstruction with simultaneous phase and magnitude updates, which enables regularization on magnitude images. We construct spatial-angular matrices from magnitude images of all diffusion-encoding directions and apply low-rank regularization to these matrices to utilize the angular correlation. Our experiments demonstrate that the proposed joint reconstruction method (SPA-LLR) substantially improves the quality of high-resolution and high b-value DWI.
Supplementary Material
FIGURE S1 The total number of pixels with the second (in blue) and the third (in red) fibers using “bedpostx” results from Experiment 0 (2 mm isotropic resolution, 2,000 s/mm2 b-value) with different regularization parameters for reconstruction. A threshold of 0.05 was used for counting
FIGURE S2 Estimated FA maps from reconstruction results of 15, 30, 45, 60, and 75 directions selected from 150 directions by MUSE (A-F) and the proposed method (G-L) from Experiment 4 (0.9 mm isotropic resolution, 1,000 s/mm2 b-value)
TABLE S1 Pseudo-algorithm to solve the proposed model
ACKNOWLEDGMENTS
We thank Dr Frank Ong for sharing reconstruction code, and Dr Wenchuan Wu for helpful discussions.
Funding information
GE Healthcare, Grant/Award Number: R01-EB009055 and P41-EB015891
Footnotes
SUPPORTING INFORMATION
Additional supporting information may be found online in the Supporting Information section at the end of the article.
REFERENCES
- 1.Rubesova E, Grell AS, De Maertelaer V, Metens T, Chao SL, Lemort M. Quantitative diffusion imaging in breast cancer: a clinical prospective study. J Magn Reson Imaging. 2006;24:319–324. [DOI] [PubMed] [Google Scholar]
- 2.Kim Y, Thepurpose O. Report brain abscess and necrotic or cystic brain tumor: discrimination with signalIntensityon diffusion weighted MR Imaging. Am J Roentgenol. 1998;171:1487–1490. [DOI] [PubMed] [Google Scholar]
- 3.Basser PJ, Pajevic S, Pierpaoli C, Duda J, Aldroubi A. In vivo fiber tractography using DT-MRI data. Magn Reson Med. 2000;44:625–632. [DOI] [PubMed] [Google Scholar]
- 4.Tian Q, Wintermark M, Jeffrey Elias W, et al. Diffusion MRI tractography for improved transcranial MRI-guided focused ultrasound thalamotomy targeting for essential tremor. NeuroImage. 2018;19:572–580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wu W, Miller KL. Image formation in diffusion MRI: a review of recent technical developments. J Magn Reson Imaging. 2017;46:646–662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Setsompop K, Cohen-Adad J, Gagoski BA, et al. Improving diffusion MRI using simultaneous multi-slice echo planar imaging. NeuroImage. 2012;63:569–580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Liao C, Stockmann J, Tian Q, et al. High-fidelity, high-isotropic-resolution diffusion imaging through gSlider acquisition with and T1 corrections and integrated ΔB0/Rx shim array. Magn Reson Med. 2019. 10.1002/mrm.27899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Robson MD, Anderson AW, Gore JC. Diffusion-weighted multiple shot echo planar imaging of humans without navigation. Magn Reson Med. 1997;38:82–88. [DOI] [PubMed] [Google Scholar]
- 9.Taviani V, Alley MT, Banerjee S, et al. High-resolution diffusion-weighted imaging of the breast with multiband 2D radiofrequency pulses and a generalized parallel imaging reconstruction. Magn Reson Med. 2017;77:209–220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Veraart J, Novikov DS, Christiaens D, Ades-aron B, Sijbers J, Fieremans E. Denoising of diffusion MRI using random matrix theory. NeuroImage. 2016;142:394–406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Guo H, Ma X, Zhang Z, Zhang B, Yuan C, Huang F. POCS-enhanced inherent correction of motion-induced phase errors (POCS-ICE) for high-resolution multishot diffusion MRI. Magn Reson Med. 2016;75:169–180. [DOI] [PubMed] [Google Scholar]
- 12.Bilgic B, Chatnuntawech I, Manhard MK, et al. Highly accelerated multishot echo planar imaging through synergistic machine learning and joint reconstruction. Magn Reson Med. 2019;82:1343–1358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Liao C, Manhard MK, Bilgic B, et al. Phase-matched virtual coil reconstruction for highly accelerated diffusion echo-planar imaging. NeuroImage. 2019;194:291–302. [DOI] [PubMed] [Google Scholar]
- 14.kuei Chen N, Guidon A, Chang HC, Truong TK, Song Aw, Chen NK. A robust multi-shot scan strategy for high-resolution diffusion weighted MRI enabled by multiplexed sensitivity-encoding (MUSE). NeuroImage. 2013;72:41–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chu ML, Chang HC, Chung HW, Truong TK, Bashir MR, Chen NK. POCS-based reconstruction of multiplexed sensitivity encoded MRI (POCSMUSE): a general algorithm for reducing motion-related artifacts. Magn Reson Med. 2015;74:1336–1348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Mani M, Jacob M, Kelley D, Magnotta V. Multi-shot sensitivity-encoded diffusion data recovery using structured low-rank matrix completion (MUSSELS). Magn Reson Med. 2017;78:494–507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hu Y, Levine EG, Tian Q, et al. Motion-robust reconstruction of multishot diffusion-weighted images without phase estimation through locally low-rank regularization. Magn Reson Med. 2019;81:1181–1190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhang H, Schneider T, Wheeler-Kingshott CA, Alexander DC. NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain. NeuroImage. 2012;61:1000–1016. [DOI] [PubMed] [Google Scholar]
- 19.Manjón JV, Coupé P, Buades A. MRI noise estimation and denoising using non-local PCA. Med Image Anal. 2015;22:35–47. [DOI] [PubMed] [Google Scholar]
- 20.Gao H, Li L, Zhang K, Zhou W, Hu X. PCLR: phase-constrained low-rank model for compressive diffusion-weighted MRI. Magn Reson Med. 2014;72:1330–1341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Shi X, Ma X, Wu W, Huang F, Yuan C, Guo H. Parallel imaging and compressed sensing combined framework for accelerating high-resolution diffusion tensor imaging using inter-image correlation. Magn Reson Med. 2015;73:1775–1785. [DOI] [PubMed] [Google Scholar]
- 22.Ma S, Nguyen CT, Christodoulou AG, et al. Accelerated cardiac diffusion tensor imaging using joint low-rank and sparsity constraints. IEEE Trans Biomed Eng. 2018;65:2219–2230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wu W, Koopmans PJ, Andersson J, Miller KL. Diffusion acceleration with Gaussian process estimated reconstruction (DAGER). Magn Reson Med. 2019;82:107–125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Trzasko J, Manduca A. Local versus global low-rank promotion in dynamic MRI series reconstruction. In Proceedings of the 19th Annual Meeting of ISMRM, Montreal, QC, Canada, 2011. p. 4371. [Google Scholar]
- 25.Haldar JP, Liang ZP. Spatiotemporal imaging with partially separable functions: a matrix recovery approach. In Proceedings of the 7th IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Rotterdam, Netherlands, 2010. pp. 716–719. [Google Scholar]
- 26.Zhang T, Pauly JM, Levesque IR. Accelerating parameter map-ping with a locally low rank constraint. Magn Reson Med. 2015;73:655–661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Candès EJ, Recht B. Exact matrix completion via convex optimization. Foundations Computat Math. 2009;9:717–772. [Google Scholar]
- 28.Saucedo A, Lefkimmiatis S, Rangwala N, Sung K. Improved computational efficiency of locally low rank MRI reconstruction using iterative random patch adjustments. IEEE Trans Med Imaging. 2017;36:1209–1220. [DOI] [PubMed] [Google Scholar]
- 29.Uecker M, Lai P, Murphy MJ, et al. ESPIRiT—An eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn Reson Med. 2014;71:990–1001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med. 1999;42:952–962. [PubMed] [Google Scholar]
- 31.Uecker M, Tamir J, Ong F, Holme C, Lustig M. Bart: Version 0.4.01; 2017. 10.5281/zenodo.817472. [DOI]
- 32.Ong F, Cheng JY, Lustig M. General phase regularized reconstruction using phase cycling. Magn Reson Med. 2018;80:112–125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Jenkinson M, Beckmann CF, Behrens TEJ, Woolrich MW, Smith SM. Fsl. NeuroImage. 2012;62:782–790. [DOI] [PubMed] [Google Scholar]
- 34.Ramani S, Liu Z, Rosen J, Nielsen JF, Fessler JA. Regularization parameter selection for nonlinear iterative image restoration and MRI reconstruction using GCV and SURE-based methods. IEEE Trans Image Process. 2012;21:3659–3672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Larsson EG, Erdogmus D, Yan R, Principe JC, Fitzsimmons JR. SNR-optimality of sum-of-squares reconstruction for phased-array magnetic resonance imaging. J Magn Reson. 2003;163:121–123. [DOI] [PubMed] [Google Scholar]
- 36.Eichner C, Cauley SF, Cohen-Adad J, et al. Real diffusion-weighted MRI enabling true signal averaging and increased diffusion contrast. NeuroImage. 2015;122:373–384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Liu C, Moseley ME, Bammer R. Simultaneous phase correction and SENSE reconstruction for navigated multi-shot DWI with non-cartesian k-space sampling. Magn Reson Med. 2005;54:1412–1422. [DOI] [PubMed] [Google Scholar]
- 38.Chen F, Taviani V, Tamir JI, et al. Self-calibrating wave-encoded variable-density single-shot fast spin echo imaging. J Magn Reson Imaging. 2018;47:954–966. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
FIGURE S1 The total number of pixels with the second (in blue) and the third (in red) fibers using “bedpostx” results from Experiment 0 (2 mm isotropic resolution, 2,000 s/mm2 b-value) with different regularization parameters for reconstruction. A threshold of 0.05 was used for counting
FIGURE S2 Estimated FA maps from reconstruction results of 15, 30, 45, 60, and 75 directions selected from 150 directions by MUSE (A-F) and the proposed method (G-L) from Experiment 4 (0.9 mm isotropic resolution, 1,000 s/mm2 b-value)
TABLE S1 Pseudo-algorithm to solve the proposed model


