Mapping vestibular and visual contributions to angular head velocity tuning in the cortex

Eivind Hennestad; Aree Witoelar; Anna R Chambers; Koen Vervaeke

doi:10.1016/j.celrep.2021.110134

. 2021 Dec 21;37(12):110134. doi: 10.1016/j.celrep.2021.110134

Mapping vestibular and visual contributions to angular head velocity tuning in the cortex

Eivind Hennestad ^1,², Aree Witoelar ^1,², Anna R Chambers ¹, Koen Vervaeke ^1,^3,^∗

PMCID: PMC8721284 PMID: 34936869

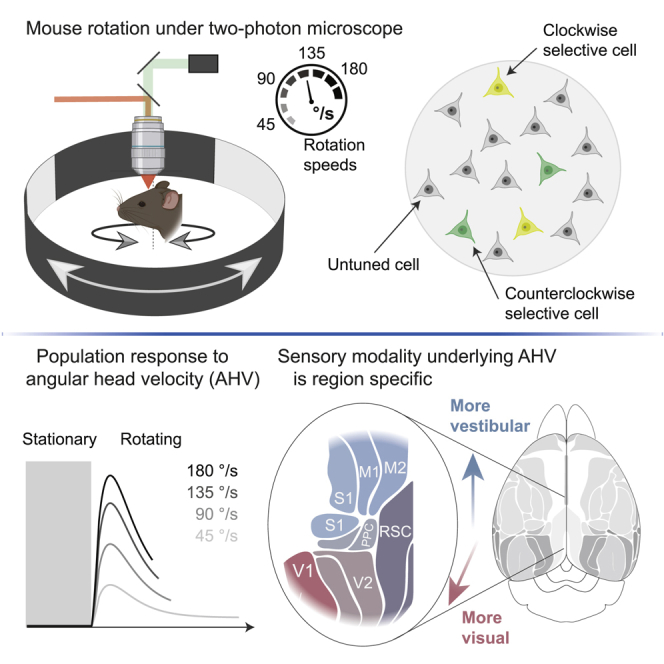
Summary

Neurons that signal the angular velocity of head movements (AHV cells) are important for processing visual and spatial information. However, it has been challenging to isolate the sensory modality that drives them and to map their cortical distribution. To address this, we develop a method that enables rotating awake, head-fixed mice under a two-photon microscope in a visual environment. Starting in layer 2/3 of the retrosplenial cortex, a key area for vision and navigation, we find that 10% of neurons report angular head velocity (AHV). Their tuning properties depend on vestibular input with a smaller contribution of vision at lower speeds. Mapping the spatial extent, we find AHV cells in all cortical areas that we explored, including motor, somatosensory, visual, and posterior parietal cortex. Notably, the vestibular and visual contributions to AHV are area dependent. Thus, many cortical circuits have access to AHV, enabling a diverse integration with sensorimotor and cognitive information.

Keywords: retrosplenial cortex, angular head velocity, vestibular and visual processing, spatial navigation, two-photon microscopy, calcium imaging, head direction cells, secondary motor cortex, primary visual cortex, posterior parietal cortex

Graphical abstract

Highlights

•
Neuronal tuning to angular head velocity (AHV) is widespread in L2/3 of mouse cortex
•
In most areas, AHV can be decoded with an accuracy close to psychophysical limits
•
AHV tuning is driven by vestibular and visual input in an area-dependent manner

Head motion signals are critical for spatial navigation and visual perception. Hennestad et al. develop a technique for rotating mice under a two-photon microscope and find neurons tuned to head rotation speed in many cortical areas. This tuning depends on vestibular and visual input in an area-dependent manner.

Introduction

Neural circuits have access to head motion information through a population of neurons whose firing rate is correlated with angular head velocity (AHV) (Bassett and Taube, 2001; Büttner and Buettner, 1978; Sharp et al., 2001; Turner-Evans et al., 2017). Beside their well-known importance for eye movements, these cells also enable operations essential for perception and cognition (Angelaki and Cullen, 2008; Cullen, 2019). For example, all moving organisms require self-motion information to determine whether a changing visual stimulus is due to their own movements or due to a moving object (Angelaki and Cullen, 2008; Sasaki et al., 2017; Vélez-Fort et al., 2018). In addition, by integrating angular speed signals across short time windows, the brain can estimate displacement to update the animal’s internal representation of orientation that is mediated by so-called “head direction cells” (Skaggs et al., 1995; Taube et al., 1990). Such diverse operations likely require the integration of AHV and sensory and motor information at multiple levels along the hierarchy of brain organization. However, although AHV tuning is well characterized in the brain stem and cerebellum, comparatively little is known about AHV tuning in the cortex.

Unlike tuning properties in the visual and auditory system, AHV tuning can depend on multiple sensory and motor modalities. Although AHV tuning was thought to rely primarily on head motion signals from the vestibular organs, it can also rely on neck motor commands (efference copies) (Guitchounts et al., 2020; Medrea and Cullen, 2013; Wolpert and Miall, 1996; Roy and Cullen, 2001), proprioceptive feedback signals from the neck (Gdowski and McCrea, 2000; Medrea and Cullen, 2013; Mergner et al., 1997) and eye muscles (Sikes et al., 1988), and visual flow (Waespe and Henn, 1977). Adding to this complexity, AHV signals can be entangled with linear speed, body posture, and place signals (Cho and Sharp, 2001; McNaughton et al., 1983; Mimica et al., 2018; Sharp, 1996; Wilber et al., 2014). Nevertheless, influential theories about neuronal coding require us to determine the exact modality. For example, models (Cullen and Taube, 2017; Hulse and Jayaraman, 2020; Skaggs et al., 1995) and data (Stackman et al., 2002; Valerio and Taube, 2016) predict that AHV tuning driven by the vestibular organs plays a critical role in generating head direction tuning. However, because motor commands and the ensuing vestibular and other sensory feedback signals occur quasi-simultaneously, their individual contribution to AHV tuning is difficult to disentangle. Therefore, to characterize AHV tuning in the cortex, we used head-fixed mice that are passively rotated, enhancing experimental control by isolating the contributions of the vestibular organs and visual input.

Recent work in the primary visual cortex of the rodent shows that vestibular input plays a central role in AHV tuning and is thought to be conveyed by direct projections from the retrosplenial cortex (RSC) (Bouvier et al., 2020; Vélez-Fort et al., 2018). The RSC is well positioned to convey head motion information because it plays a key role in vision-based navigation (Vann et al., 2009). About 22% of RSC neurons are selective for left or right turns during a navigation task (Alexander and Nitz, 2015), and 5%–10% of neurons report head direction (Alexander and Nitz, 2015; Chen et al., 1994; Cho and Sharp, 2001; Jacob et al., 2017). There are also reports of RSC neurons tuned to AHV in freely moving rodents (Cho and Sharp, 2001), but whether they are driven by vestibular input or by other sensory or motor input is not known. In macaque RSC, angular velocity tuning depends on vestibular input, but because the homologous cortical areas of mammalian species have been defined differently, it is not straightforward to compare these data to the rodent cortex (Liu et al., 2021). In rodents, it is also not clear whether AHV tuning is limited to specific cortical areas. Stimulation of the vestibular nerve evokes widespread activation of cortical circuits (Lopez and Blanke, 2011; Rancz et al., 2015), but this method does not reveal whether the activated neurons are tuned to angular direction and speed. Therefore, how AHV is represented in the rodent RSC and whether AHV tuning in the cortex is area specific remain to be determined.

The lack of knowledge about vestibular representations in the cortex stems, in part, from the fundamental obstacle that the animal’s head needs to move. This obstacle has limited the use of powerful methods such as two-photon microscopy to study neural circuits. To overcome this technical limitation, we developed a setup to perform large-scale neuronal recordings from mice rotated around the z axis (yaw) under a two-photon microscope. Using this method, we found that 10% of neurons in layer 2/3 of RSC are tuned to the velocity of angular head movements. We show that these tuning properties persist when rotating the animals in darkness and are generally consistent with the hypothesis that AHV tuning is vestibular dependent. Strikingly, we discovered that AHV tuning is not limited to RSC. By mapping large parts of the cortex, we found a similar fraction of neurons tuned to AHV in all cortical areas explored, including visual, somatosensory, and motor and posterior parietal cortex. Finally, the contribution of vestibular and visual input to AHV tuning was distinct between areas. This finding shows that AHV tuning is more widespread in the cortex than previously thought and that the underlying sensory modality is area dependent.

Results

Rotation-selective neurons in the RSC

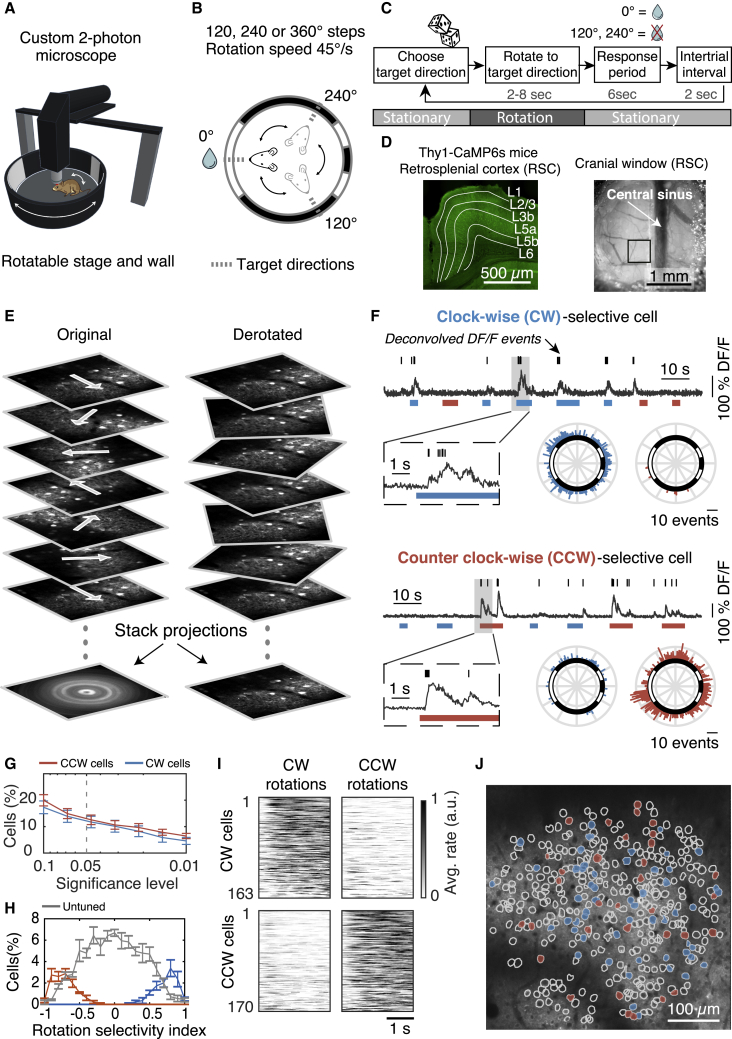
How do neurons in the RSC respond to angular head motion? To control the velocity of head movements, we positioned awake but head-restrained mice in the center of a motorized platform that enables rotation in the horizontal plane around the yaw axis (Figure 1A). A cylindrical wall with visual cues surrounded the platform (Figures 1A and 1B; see details in STAR Methods). This wall could be rotated independently from the platform to determine whether motion-sensitive neurons depend on vestibular input or visual flow. We also performed pupil tracking to determine whether neurons are tuned to eye movements (Video S1). The mice were rotated clockwise (CW) or counter clockwise (CCW) between three randomly chosen target directions (Figures 1B and 1C). The speed profile of the motion was trapezoidal, with fast accelerations and decelerations (200°/s²) such that most of the rotation occurred at a constant speed (45°/s). The mice received water rewards when facing one of the three target positions to keep them aroused and engaged (Figures 1B and 1C).

Rotation-selective neurons in the retrosplenial cortex (RSC)

(A) Cartoon of a head-fixed mouse in an arena with visual cues. The mouse and visual cues can be rotated together or independently while performing two-photon microscopy.

(B) Top-view schematic: The mouse is randomly rotated between three target directions (dashed lines) but only gets a water reward in one direction. The circle represents the arena wall with white cues on a black background.

(C) Block diagram of the sequence of events for a single trial.

(D) (Left) Confocal fluorescence image of RSC coronal brain slice with cortical layers indicated (Thy1-GCaMP6s/ GP4.3 mice). (Right) Top view of cranial window implanted on dorsal (agranular) RSC and centered over the central sinus. Black box shows the typical size and location of an imaging field of view (FOV).

(E) Two-photon image sequence of layer 2/3 neurons during rotation experiment (left) and when de-rotated during postprocessing (right).

(F) Example fluorescence traces (fractional change of fluorescence [DF/F]) of a clockwise (CW) and counter-clockwise (CCW) selective cell. Ticks indicate deconvolved DF/F events. Blue and red bars are CW and CCW rotation trials, respectively. Polar histograms show the DF/F events as a function of direction (the arena wall with visual cues is superimposed).

(G) Logarithmic plot of the fraction of rotation-selective cells at different significance levels (average ± SEM, 1,368 cells, 4 mice, 4 FOVs).

(H) Distribution of rotation-selectivity index for all rotation-selective (p ≤ 0.05) and non-selective cells (average ± SEM).

(I) Average activity of all rotation-selective cells separated in CW and CCW rotations.

(J) Example FOV showing the spatial distribution of CW- (blue) and CCW-selective cells (red), for p ≤ 0.05.

Video S1. Rotating mouse and rotating walls, related to Figure 1

Head-restrained mouse rotated under the two-photon microscope. Example trials, rotating either the mouse or the arena wall with visual cues. Inset shows pupil tracking.

Download video file^{(9.9MB, mp4)}

To perform large-scale recordings from neurons with high spatial resolution and without bias toward active neurons or specific cell types, which is a disadvantage of extracellular recordings, we rotated mice expressing the Ca²⁺ indicator GCaMP6s under a two-photon microscope (Figures 1D and 1E). We solved several technical challenges to record fluorescence transients free of image artifacts (Figure 1E; see details in STAR Methods; Videos S2, S3, and S4). The rotation platform is ultra-stable and vibration free such that neurons moved less than 1 μm in the focal plane during 360° rotations (see details in STAR Methods). In addition, it was key to align the optical path of the custom-built two-photon microscope with high precision (see details in STAR Methods). Having solved these challenges, we found that this method now enables us to record the activity of neuronal somata, spines, and axons of specific cell types during head rotations.

Video S2. Rotating FOV and de-rotated FOV, related to Figure 1

Example of two-photon image sequence obtained while rotating the mouse (left), and after post-processing when images are de-rotated and corrected for brain movement (right).

Download video file^{(31.1MB, mp4)}

Video S3. Example of luminance artifacts during rotation under a two-photon microscope, related to Figure 1

Even minor misalignments of the excitation laser beam will result in major luminance changes within the image during rotation.

Download video file^{(9.6MB, mp4)}

Video S4. Illustration of how minor excitation beam misalignment results in major luminance changes, related to Figure 1

(Left) Schematic of two-photon microscope objective and mouse brain with cranial window above dorsal (agranular) RSC. The two-photon excitation beam scans across neurons in layer 2/3. Here, for simplicity, we assume only a simple line-scan (green). We also represent inhomogeneities in the brain tissue, predominantly blood vessels, by the gray dot. (Right, top) Simulated % of collected light during the line scan. (Right, bottom) Simulated difference in collected light (% DF/F) when the center ray of the excitation beam is of the perpendicular by 1 to 5°. When the center ray of the excitation beam is perfectly perpendicular to the cranial window, there is no luminance artifact. However, if the center ray is only 1 to 5° of the perpendicular, then luminance changes increase up to 30% DF/F.

Download video file^{(2.2MB, mp4)}

We first measured the activity of excitatory neurons in layer 2/3 of agranular RSC (1,368 cells, 4 thy1-GCaMP6s mice; Dana et al., 2014). During rotations, we found neurons that preferred either the CW or CCW direction (Figures 1F and 1G; CW = 12%, CCW = 12%, for p ≤ 0.05). To quantify the rotation direction preference, we calculated a rotation-selectivity index (Figure 1H; see details in STAR Methods), for which a value of −1 or +1 indicates that a cell responds only during CCW or CW rotation trials, respectively. We found that only a small percentage of cells were exclusively active in one direction. Instead, most cells were predominantly active in one direction but also, to a lesser degree, in the other direction (Figures 1H and 1I). Because we always recorded in the left hemisphere, we also considered whether direction selectivity is lateralized. However, the percentages of CW and CCW cells in the same hemisphere were similar (Figures 1G–1I). Finally, because recent data from macaques indicated that rotation-selective neurons in posterior parietal cortex are organized in clusters (Avila et al., 2019), we tested how CW- or CCW-selective cells are spatially organized. Instead of spatial clustering, we found that CW and CCW cells in the mouse RSC are rather organized in a “salt and pepper” fashion (Figure 1J; Figure S1). Altogether, these data show that RSC contains a substantial fraction of rotation-selective neurons that are spatially intermingled.

Many rotation-selective neurons are biased by head direction

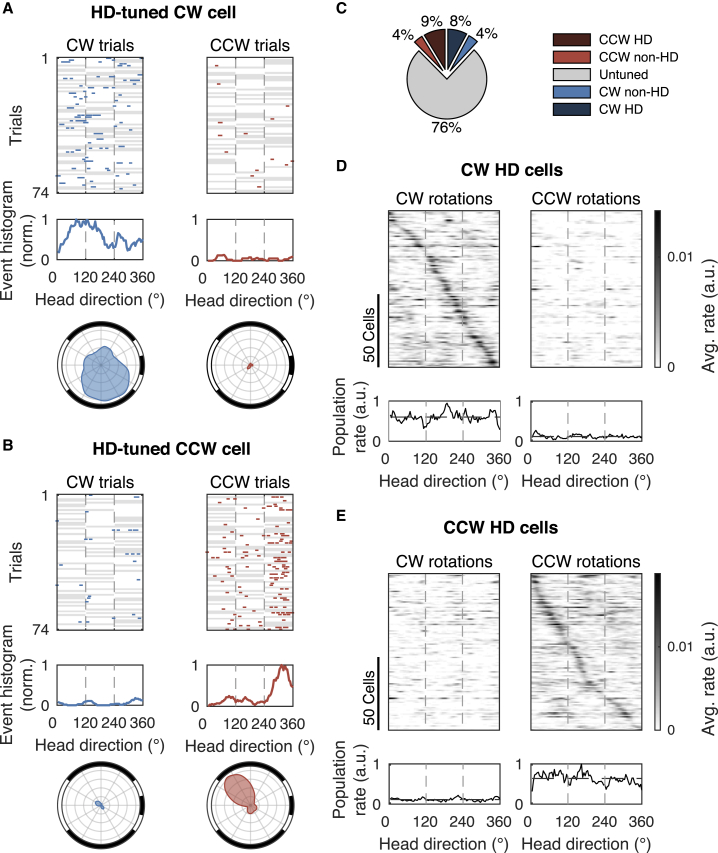
We observed two types of rotation-selective neurons, as follows: neurons that responded during CW or CCW rotations regardless of the direction that the mouse was facing (see examples in Figure 1F) and neurons that were rotation selective but highly biased by head direction (Figures 2A and 2B). The latter response type is reminiscent of the head direction cells that are known to be present in RSC (Chen et al., 1994). Of all rotation-selective neurons, the majority (68%) was significantly biased by head direction (Figure 2C; see details in STAR Methods). When we selected only those cells biased by head direction and ranked them according to their preferred direction, we observed that this neuronal population represented all 360° directions evenly (Figures 2D and 2E). Therefore, it is unlikely that head direction tuning was influenced by a specific visual cue or by the rewarded direction. We also verified that the rotation protocol allowed the mouse to spend an equal amount of time facing each direction, thus avoiding a bias toward a specific direction by oversampling (see details in STAR Methods). In summary, these data show that a significant fraction of rotation-selective cells in RSC conjunctively encode information about head direction.

A large fraction of rotation-selective neurons encode AHV

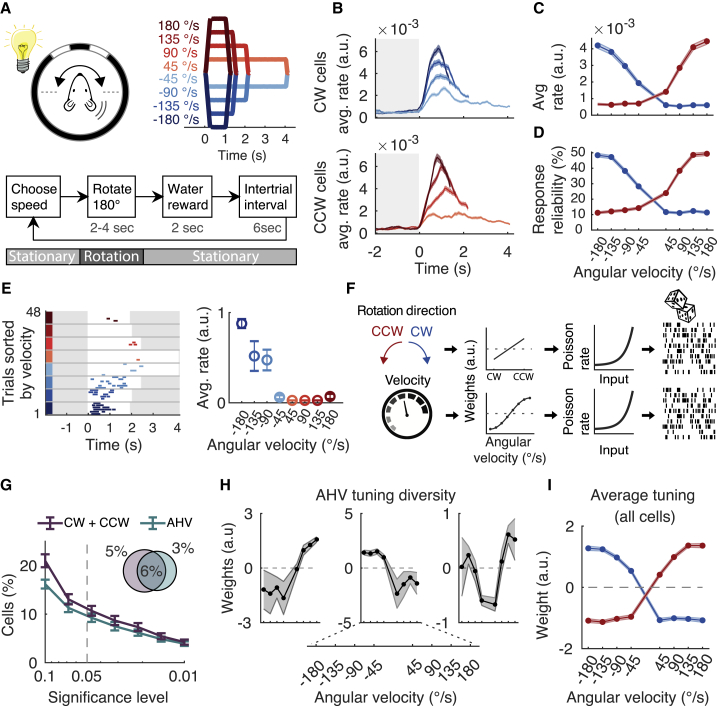
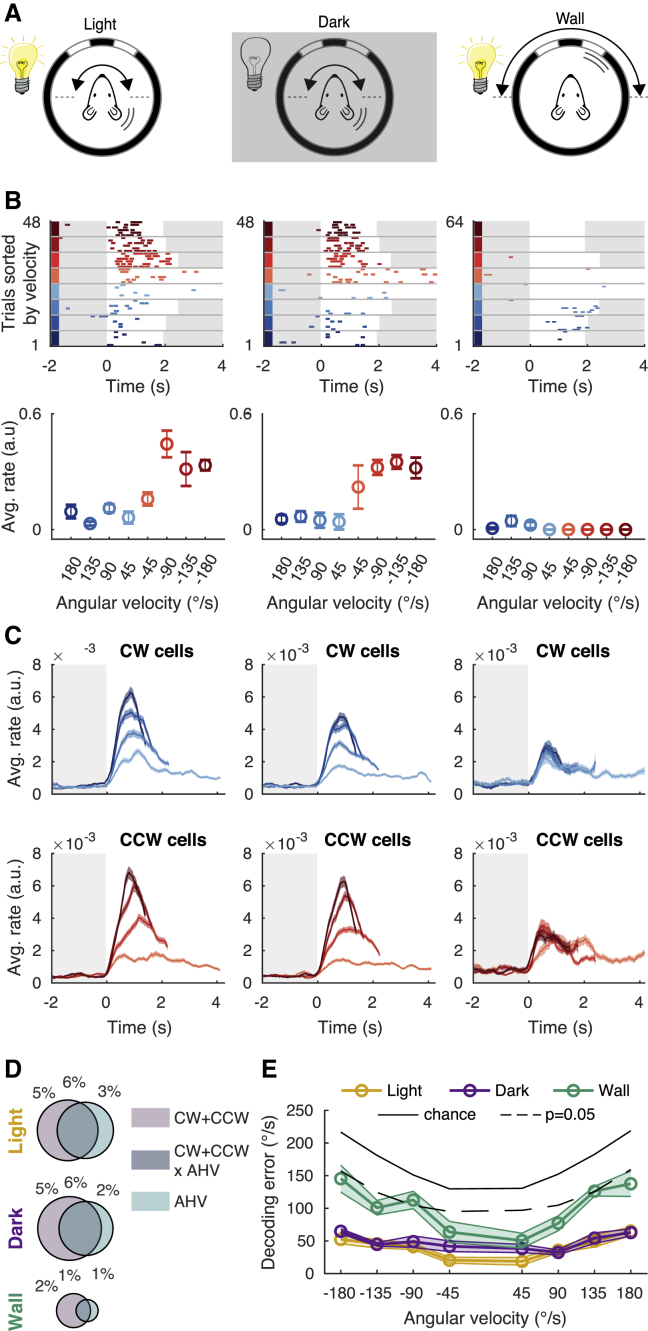
Next, we determined whether CW- and CCW-selective neurons encode not only the direction but also the angular head velocity (AHV). The difference being that CW/CCW cells prefer a specific rotation direction, whereas AHV cells prefer specific rotation velocities (see details in STAR Methods). To reduce the influence of conjunctive head direction tuning, we limited the range of directions that the mouse could face by rotating the stage back and forth between two target positions located 180° apart (Figure 3A; 4,928 cells, 10 mice). To determine the distribution of behaviorally relevant AHV, we analyzed published data of freely moving mice (Laurens et al., 2019) and found that about 90% of all head rotations are slower than 180°/s (see details in STAR Methods; n = 25 mice; see also Mallory et al., 2021). Therefore, we rotated the mice at velocities between −180 and +180°/s in steps of 45°/s (Figure 3A).

For every rotation velocity, we calculated the average response of all CW- and CCW-selective neurons (Figure 3B). This calculation revealed that the response amplitude increased monotonically as a function of AHV (Figure 3C). However, the increase saturated for the highest velocities (Figure 3C). We observed a similar relationship between AHV and the response reliability (Figure 3D). In line with the average response of all CW and CCW cells, we found examples of individual neurons that had similar monotonic relationships between response amplitude and AHV (Figure 3E).

To determine how individual cells are tuned to AHV without imposing assumptions about the shape of the neural tuning curves, we used an unbiased statistical approach (Hardcastle et al., 2017; Figure 3F). This method fits nested linear non-linear Poisson (LNP) models to the activity of each cell (see details in STAR Methods). We tested the dependence of neural activity on both rotation direction (CW or CCW) and AHV (Figure 3F). From the total population, 10.7% of neurons were rotation selective (Figure 3G; 527 out of 4,928 cells). Among these rotation-selective cells, 57% significantly encoded AHV (303 out of 527 cells). With this model, we found that AHV tuning curves were heterogenous. Some cells had a simple monotonic relationship with angular velocity, and other cells had a more complex relationship (Figure 3H). As a sanity check of the model results, the average tuning curve of all AHV cells reproduced the simple monotonic relationship of the population response (Figure 3I compared to Figure 3C). Altogether, these data show that a significant number of rotation-selective cells encode AHV and that although the average response of all cells has a simple monotonic relationship with AHV, the tuning curves of individual cells are heterogenous.

AHV can be decoded from neural activity in the RSC

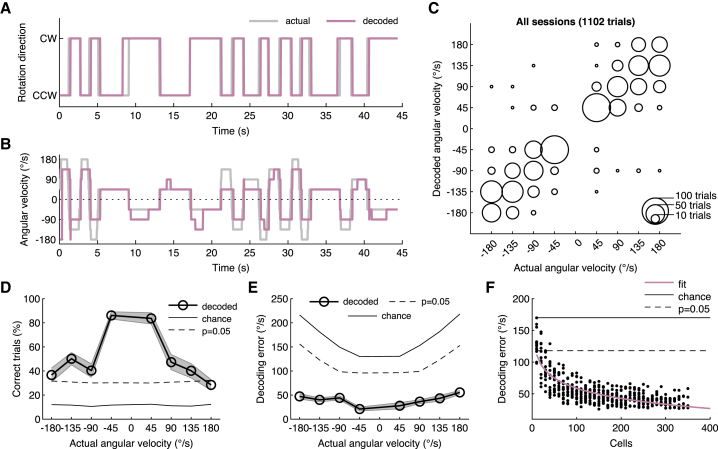
We used the LNP model to quantify how well neurons in the RSC report the motion stimulus. Although neurons of a single recording session could reliably discriminate CW from CCW rotations (Figure 4A;, average 308 cells/session, 10 mice), the estimate of angular velocity was less reliable (Figure 4B; Video S5). We further illustrate this result by comparing the actual AHV with the decoded AHV by using a confusion matrix (Figure 4C). However, the reliability of reporting the correct velocity was speed dependent. Low velocity trials were more often correctly reported than the high velocity trials (Figure 4D). For 45°/s rotations, neurons reported the correct velocity in almost 90% of trials, whereas for higher speeds (90-180°/s), this reduced to about 30%–50%. Still, they were better estimates than predicted by chance (Figure 4D). The velocity-dependent decoding of AHV was also apparent when we calculated the velocity error (Figure 4E). For low angular speeds, the velocity error was about 25°/s, whereas for higher speeds it increased to about 50°/s. Another way to measure how well a neuronal circuit reports a behavioral variable is to quantify how the decoding error scales with the population size (Figure 4F). Because we typically record 300–350 neurons simultaneously, we subsampled each population and quantified the decoding error for different population sizes. These data show that around 350 cells reported angular velocities between −180°/s and +180°/s with an average error of around 30°/s (Figure 4F). This finding is close to the psychophysical limit of 24°/s that mice can discriminate in a similar task in darkness (Vélez-Fort et al., 2018). Altogether, these data indicate that a substantial amount of information about angular head movements is embedded in the RSC network and that as few as 350 RSC neurons can provide an estimate of the actual AHV with an error of 30°/s.

Video S5. Example of AHV decoding using RSC neurons, related to Figure 5

Example trial sequence showing a mouse being rotated in the CW or CCW direction. (Top) Responses of all neurons in the FOV (DF/F events). (Middle) Histogram of population response (DF/F events). (Bottom) Traces show the actual rotation direction and speed, and that predicted by the LNP model. For decoding, all neurons in a FOV were used regardless of whether they were rotation-selective or not.

Download video file^{(1.6MB, mp4)}

AHV tuning in the RSC depends on sensory transduction in the vestibular organs

To determine the sensory origin of neuronal responses during rotation, we first considered whether neurons are driven by head motion or by visual flow. To distinguish between these two possibilities, we rotated mice either in complete darkness, or we kept the mice stationary and simulated visual flow by rotating the enclosure with visual cues (Figure 5A; rotation in light, 4,928 cells; rotation in darkness, 4,963 cells; visual flow, 3,192 cells). Cells that were tuned to AHV in light typically remained tuned to AHV in darkness, but they lost their tuning when only rotating the visual cues (Figure 5B). Similarly, when we calculated the average responses of all rotation-selective neurons (281 CW cells, 246 CCW cells, n = 10 mice), we observed clear AHV tuning during rotations in both light and darkness, but not during presentation of visual flow (Figure 5C). Overall, the percentage of rotation-selective and velocity-tuned cells was similar in light and darkness but was significantly less when presenting only visual flow (Figure 5D). These data are further supported by the LNP model. We decoded angular velocity under all three conditions. During rotations in light or darkness, neurons reported angular velocity almost equally well (Figure 5E). Decoding angular velocity in the dark degraded only for the lowest velocities (±45°/s). In contrast, when we rotated only the visual cues, the decoded velocity error increased substantially, and only the lowest velocities could be decoded better than expected by chance (Figure 5E). Altogether, these data suggest that angular velocity tuning is mediated mostly by head motion and that visual flow contributes only to low (45°/s) rotation speeds.

Are neuronal responses during rotation driven by mechanical activation of the semi-circular canals in the vestibular organs? To test this question, we compared neuronal responses in the RSC with the responses of the vestibular nerves that convey the output of the canals to the brainstem (Figure S2A). We first simulated how mechanical activation of the canals is translated into nerve impulses in the vestibular nerve under a variety of rotation conditions (Laurens and Angelaki, 2017), and then we performed experiments to test whether neuronal responses in the RSC resemble them. First, we rotated mice in the dark at the same speed but with different accelerations (Figure S2B). Although the canals inherently sense acceleration, they transform it into a neuronal speed signal due to their biomechanical properties (Fernandez and Goldberg, 1971). Therefore, the vestibular nerve conveys speed information, at least for short lasting rotations (Figure S2C). Then, we selected only those neurons that were CW or CCW selective and calculated their mean response (Figure S2D; 594 neurons, 4 mice). For different accelerations, the neuronal responses in the RSC resembled the simulated responses of the vestibular nerve (Figure S2C), suggesting that neuronal activity in the RSC is driven by a speed signal from the vestibular organs. Next, we took advantage of the well-known observation that when the head is rotated at constant speed, the inertia signal in the canals attenuates, causing a reduction of vestibular nerve impulses (Goldberg and Fernandez, 1971; Figures S2E and S2F). In mice, this occurs with a time constant of ∼2.2–3.7 s (Lasker et al., 2008; Figure S2F). To test whether RSC responses have the same temporal profile, we rotated mice at a constant speed for different durations (Figure S2G). The average response of all CW- or CCW-selective neurons indeed resembled the simulated vestibular nerve activity and decayed with a time constant of 3.1 s. Finally, when animals are rotated at a constant speed so that the inertial signal in the canals adapts, a sudden stop will be reported by the contralateral canals as a rotation in the opposite direction. When we analyzed the average response of CW-selective neurons at the end of CCW rotations, we found indeed that a sudden stop activated these cells (Figure S2H). Altogether, these observations are fully compatible with the hypothesis that the vestibular organs drive neuronal responses in the RSC during rotations in the dark.

Finally, inspired by previous work in rabbits (Sikes et al., 1988), we tested whether RSC neurons encode eye movements. Such neuronal signals may represent proprioceptive feedback, possibly mediated by stretch receptors in the eye muscles (Blumer et al., 2016). Because AHV cells remained in the dark, we analyzed eye movements in darkness by using infrared illumination (Figure S3). First, we investigated eye movements during rotations. These eye movements show the typical nystagmus, a saw-tooth pattern of compensatory eye movements that occur because of the vestibulo-ocular reflex (Figure S3A). As the rotation speed increased, we found, as expected, that the beat frequency of the nystagmus also increased (Figures S3A and S3B). To disentangle whether neuronal activity encodes head rotation or pupil movement, we aligned neuronal responses to the onset of the nystagmus during rotation (Figures S3C–S3E; see details in STAR Methods) or to spontaneous eye movements during stationary periods (Figures S3F–S3H). We found that 4.9% of all cells (19% of AHV cells) were significantly modulated by eye movements during the nystagmus and only 2.5% of all cells (0.01% of AHV cells) were significantly modulated by spontaneous eye movements. However, because the nystagmus-related eye movements are tightly correlated with AHV (Figure S3A) and because of the poor temporal resolution of two photon Ca²⁺ imaging, we cannot exclude that nystagmus-modulated cells are AHV cells. Therefore, 19% is an upper estimate of how many AHV cells could be driven by eye movements, but because of the small fraction of cells modulated by spontaneous eye movements, this number is likely substantially lower.

In summary, these data are consistent with the hypothesis that AHV signals depend primarily on sensory transduction in the vestibular organs, with visual flow playing a substantial role only during low velocities. However, we cannot exclude that a fraction of AHV cells isinstead related to eye movements.

AHV is widespread in cortical circuits

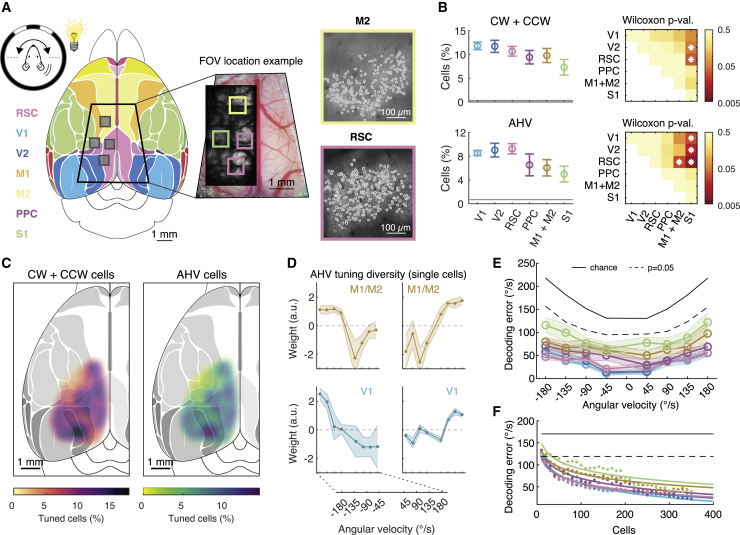
Are AHV cells restricted to the RSC or are they widespread in the cortex? To address this question, we explored large areas of the cortex with cellular resolution. Because the rotation experiments prevented us from tilting either the microscope or the mouse, we limited our exploration to the most dorsal and medial parts of the cortex (Figure 6A; 16,642 cells, 15 mice). We implanted large cranial windows (∼5 × 5 mm) that gave access to all imageable cortical areas (Kim et al., 2016). They included parts of the primary and secondary visual cortex (V1 and V2), the posterior parts of the primary and secondary motor cortex (M1 and M2), the posterior parietal cortex (PPC), and the medial aspect of somatosensory cortex (S1; mostly hindlimb and trunk). To align two-photon cellular-resolution images with a standardized atlas of the cortex (Kirkcaldie, 2012), we performed intrinsic optical imaging of the tail somatosensory cortex (Figure S4). This procedure had several key advantages. Because the tail area is a small cortical area (∼300 μm) closely located to the intersections of S1, M1, M2, PPC, and RSC, identifying its location enables us to register these areas with high precision (Lenschow et al., 2016; Sigl-Glöckner et al., 2019; Figures S4A–S4D).

We rotated mice at different velocities under light conditions (as in Figure 3A) and found CW/CCW-selective neurons and AHV neurons in all areas that we explored (Figures 6B and 6C and examples in Figure S5A). Compared to the RSC, the percentage of cells in V1 and V2 was very similar (Figure 6B), but the numbers in PPC, M1/M2, and S1 were lower (Figure 6B). To quantify how well neurons in these different areas report AHV, we used the LNP model (Figures 6D–6F). Neurons in all areas decoded AHV better than expected by chance (Figure 6E). However, although neurons in RSC, V1, V2, and PPC reported AHV equally well, neurons in M1/M2 and notably S1 performed worse (Figure 6E). The overall number of recorded neurons per session was slightly different between cortical areas, and this can affect the decoding performance. To account for this difference, we down sampled the number of neurons in individual recording sessions and quantified the decoding error as a function of population size (Figure 6F; Figure S6). These data show that, except for M1/M2 and S1, a population size of 300–350 neurons in each area can report AHV with a performance close to psychophysical limits for mice (Vélez-Fort et al., 2018). Thus, altogether, AHV tuning is widespread in cortical circuits, but with some differences in how well AHV can be decoded from the neural population.

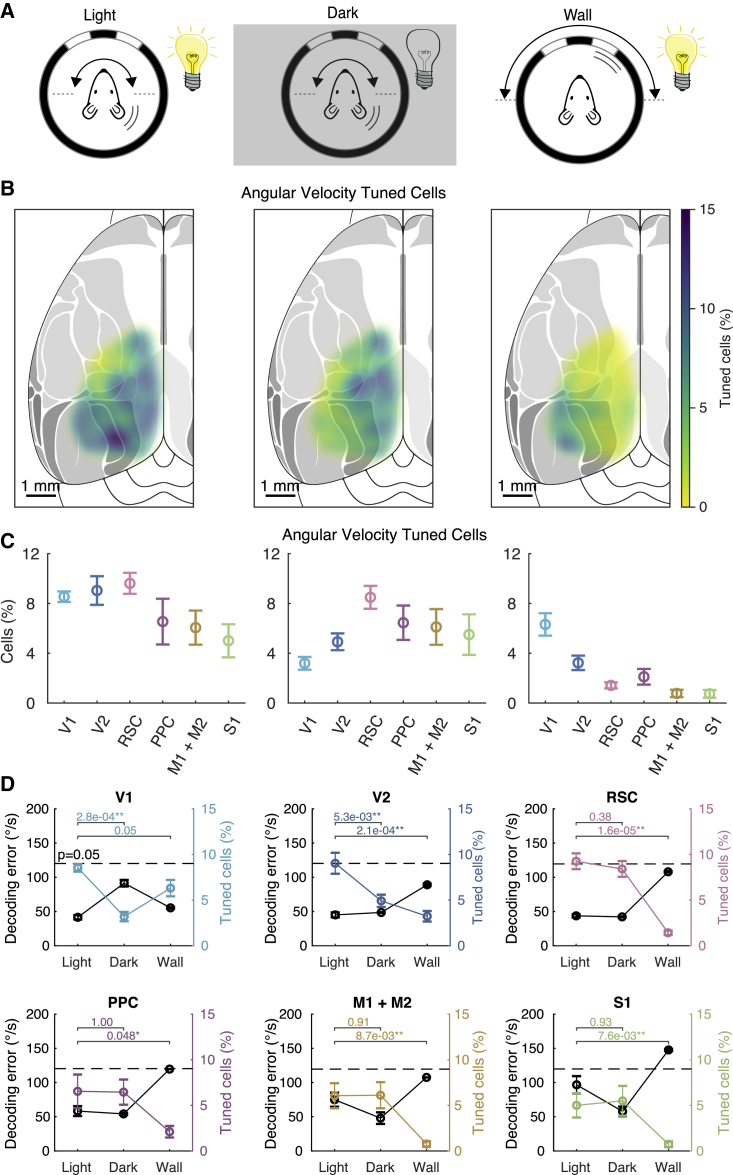
The sensory origin of AHV tuning is dependent on cortical area

To test whether AHV tuning in different cortical areas depends on head motion or visual flow, we compared neuronal responses when rotating mice in light or darkness or when rotating only the visual cues (Figure 7A). Maps of angular velocity-tuned cells under these three conditions showed notable differences between brain areas (Figure 7B). Compared to rotations in light, rotations in the dark reduced the percentage of tuned cells in V1 and V2 but did not substantially affect other brain areas (Figures 7C and 7D; Figure S5B). Conversely, when rotating only the visual cues, the percentage of tuned cells in V1 remained similar, strongly reduced in V2, and was near zero in all other brain areas. This result is consistent with the known speed dependence of some direction-selective neurons in mouse V1 (Niell and Stryker, 2008). Interestingly, the posterior RSC has stronger connections with the visual areas than the anterior RSC (Vann et al., 2009). Although the percentage of AHV cells was not significantly different, there was a trend showing that AHV tuning in the posterior RSC was more dependent on visual input than the anterior RSC (Figure S7A). Altogether, these data show that except for V1 and V2 where angular velocity tuning is strongly dependent on visual flow, tuning in all other areas (PPC, RSC, M1/M2, and S1) depends mostly on head motion.

Whether AHV tuning depend on head motion or visual flow is area dependent

(A) Experimental configuration. (Left) Mouse is rotated 180° back and forth in CW and CCW directions and at different rotation speeds. (Middle) Same experiment repeated in the dark. (Right) Mouse is stationary, but now the wall of the arena with visual cues is rotated to simulate the visual flow experienced when the mouse is rotating.

(B) Percentage of angular velocity-tuned neurons mapped onto the mouse dorsal cortex, tested under each of the three conditions.

(C) Percentage angular velocity-tuned cells across different cortical areas (average ± SEM) tested under each of the three conditions.

(D) The decoding error (black, average ± SEM) and percentage of angular velocity-tuned cells (color coded) under the three different conditions. The horizontal bars above show the Mann-Whitney unpaired test p values. The dashed line shows the p = 0.05 level for the decoding error. The numbers of cells and mice recorded under light conditions are given in the legend of Figure 6. Under dark conditions, results were as follows: V1, 2,385 cells from 8 mice; V2, 4,564 cells from 10 mice; RSC, 4,963 cells from 10 mice; PPC, 1,044 cells from 4 mice; M1+M2, 2,489 cells from 7 mice; and S1: 3,398 cells from 9 mice. During wall rotations, results were as follows: V1, 1,864 cells from 6 mice; V2, 3,560 cells from 8 mice; RSC, 3,192 cells from 7 mice; PPC, 816 cells from 3 mice; M1+M2, 1,095 cells from 4 mice; and S1: 1,562 cells from 6 mice.

Finally, we used the LNP model to test whether decoding angular velocity under these three different conditions varied between brain regions (Figure 7D; Figure S7B). Except for V1, rotations in the dark did not increase the decoding error in any other brain area. In contrast, rotating only the visual cues increased the decoding error in all cortical areas, except area V1. In summary, angular velocity tuning in V1, and to a lesser degree V2, depends mostly on visual flow, whereas in all other cortical areas that we explored (PPC, RSC, M1/M2, and S1), tuning depends mostly on head motion.

Discussion

Cortical AHV neurons that track the activity of the vestibular organs were first reported in head-fixed monkeys and cats decades ago (Büttner and Buettner, 1978; Vanni-Mercier and Magnin, 1982). Later, AHV neurons were also found in the rodent cortex, specifically in the pre- and postsubiculum (Preston-Ferrer et al., 2016; Sharp, 1996), entorhinal cortex (Mallory et al., 2021), posterior parietal cortex (Wilber et al., 2014), medial precentral cortex (Mehlman et al., 2019), and RSC (Cho and Sharp, 2001). However, the underlying modalities that drive tuning have remained unknown. These modalities were recently investigated by studying head-motion-sensitive neurons in area V1 (Bouvier et al., 2020). By rotating mice in the dark, they showed that deep cortical layers 5 and 6 contain cells that were either excited or suppressed, whereas superficial layers 2/3 contained cells that were generally suppressed. Consistent with this result, we found that very few neurons in layer 2/3 of V1 encode AHV in the dark. However, we did not observe neuronal suppressions. Given the low basal firing rates of neurons in superficial layers, and hence the large number of repetitions necessary to observe a suppressive effect, it is possible that suppressions remained undetected. Vélez-Fort et al. (2018)) also found AHV-modulated synaptic input to neurons in L6 of V1. Based on retrograde tracing, they proposed that the RSC may be the origin of this input. However, although they found that V1-projecting RSC neurons responded during head rotations, they did not report direction-selective or AHV-tuned RSC neurons. However, a recent preprint by the same group reported up to 60% AHV-tuned neurons in granular and agranular RSCs, which were mostly sampled in L5 and L6 (Keshavarzi et al., 2021). Similar to our results, many AHV cells were conjunctively coding head direction and were predominantly driven by the vestibular organs. Notably, they found that most AHV neurons maintained their tuning properties when animals were both freely moving or passively rotated (measured in darkness). Despite the similarities, the biggest disparity is our lower percentage of AHV cells. This difference could depend on the recorded layer (L2/3 versus L5/6) and the recording method (Ca²⁺ imaging versus extracellular recording). Differences could also be explained by the more stringent LNP model that we used to classify AHV cells, which requires that AHV tuning is stable during the whole session. Altogether, our work extends current knowledge by showing that cortical AHV cells are far more widespread than previously reported. This conclusion suggests that AHV-modulated input to V1 can indeed originate from the RSC but also from other anatomically connected areas such as V2, PPC, and M2.

By comparing rotations in light and darkness, we show that vestibular input contributes most of the information to decode AHV from neurons in RSC (Figure 5E). However, it depends on the range of angular velocities. Indeed, visual flow selectively improves decoding of lower velocities (Figure 5E) that explains, in part, the higher number of correct decoded trials at ±45°/s (Figure 4D). This finding indicates that vestibular and visual information play complementary roles to support a wider range of angular velocity tuning, which is consistent with classic work studying compensatory eye movements as a readout of AHV in subcortical circuits (Stahl, 2004). These studies show that, during the vestibulo-ocular reflex, the vestibular organs are better at reporting fast head rotations, whereas during the optokinetic reflex, subcortical circuits are better at reporting slow visual motion (<40°/s). Therefore, AHV tuning driven by different modalities may not be redundant but plays complementary roles by expanding the bandwidth of angular velocity coding.

We found that AHV cells in many cortical areas depend on vestibular input. But how can vestibular signals be so widely distributed? Recent work suggested that vestibular-dependent AHV cells in V1 are driven by neurons in the RSC, which in turn receive AHV input from the anterodorsal thalamic nucleus (ADN) (Vélez-Fort et al., 2018). It is generally assumed that ADN encodes angular head motion because it receives input from the lateral mammillary nucleus, which contains many AHV cells (Cullen and Taube, 2017; Stackman and Taube, 1998). However, although ADN has been extensively studied, AHV cells in ADN have not been reported. Therefore, it is unclear how AHV could be transmitted by this route. An alternative pathway is the more direct system of vestibulo-thalamocortical or the cerebello-thalamocortical projections (Lopez and Blanke, 2011). This broad projection pattern may explain why AHV cells are so widely distributed in the cortex. However, these vestibular pathways remain poorly understood and need to be functionally characterized to determine which convey AHV. This characterization could be achieved in a projection-specific manner by imaging thalamocortical axons in the cortex by using two-photon microscopy as described here.

Animals may use cortical AHV signals to determine whether a changing visual stimulus is due to their own movement or due to a moving object. The brain likely implements this determination by building internal models that, based on experience, compare intended motor commands (efference copies) with the sensory consequences of actual movements (von Holst and Mittelstaedt, 1950; Wolpert and Miall, 1996). Such efference copies could then anticipate and cancel self-generated sensory input that would otherwise be unnecessarily salient. Consistent with this hypothesis, a classic example is the response of vestibular neurons in the brainstem that, compared to passive rotation, are attenuated during voluntary head movements (Brooks et al., 2015; Medrea and Cullen, 2013; Roy and Cullen, 2001). This information raises questions about the role of AHV signals recorded during passive rotation. However, internal models also predict that, during movements, the ever-ongoing comparison between expected and actual sensory stimuli often results in a mismatch. A necessary corollary is that AHV signals during passive rotation are essentially mismatch signals because the lack of intended movements cannot cancel the incoming vestibular input. Therefore, vestibular mismatch signals may play two fundamental roles, as follows: (1) to update self-motion estimates and to correct motor commands and (2) to provide a teaching signal to calibrate internal models for motor control and so facilitate motor learning (Laurens and Angelaki, 2017; Wolpert and Miall, 1996). Both of these functions likely require that cortical circuits have access to AHV information.

The widespread existence of AHV cells in the cortex also has implications for how animals orient while navigating through an environment. Attractor network-dependent head direction models require AHV neurons (Hulse and Jayaraman, 2020; Knierim and Zhang, 2012; Taube, 2007). These neurons dynamically update head direction cell activity in accordance with the animal’s movement in space. In mammals, the mainstream hypothesis positions the attractor network in circuits spanning the mesencephalon and hypothalamus, in part because that is where AHV cells are commonly found (Cullen and Taube, 2017; Taube, 2007). However, several studies report cortical neurons that are selective for left or right turns, but whether these cells also encode velocity is not known (Alexander and Nitz, 2015; McNaughton et al., 1994; Whitlock et al., 2012). In addition to AHV cells, attractor networks also need cells that conjunctively code AHV and head direction (Hulse and Jayaraman, 2020; McNaughton et al., 1991; Taube, 2007). Such cells were previously discovered in subcortical structures such as the lateral mammillary nucleus (Stackman and Taube, 1998) and dorsal tegmental nucleus (Bassett and Taube, 2001; Sharp et al., 2001). There is, however, also evidence for such cells in the cortex (Angelaki et al., 2020; Cho and Sharp, 2001; Liu et al., 2021; Sharp, 1996; Wilber et al., 2014). Here, we show that AHV cells are far more common in cortical circuits than previously thought. We also report a considerable fraction of cells in RSC that conjunctively encode rotation selectivity and head direction. Altogether, these data indicate that the basic components of the attractor network architecture are not limited to subcortical structures but are also present in the cortex. Therefore, our findings add to the debate about which circuits are involved in generating head direction tuning.

In conclusion, our results show that cortical AHV cells are widespread and rely on vestibular or visual input in an area-dependent manner. How the distributed nature of AHV cells contributes to calibrating internal models for motor control and movement perception and generating head direction signals are important questions that remain to be addressed. The ability to perform two-photon imaging in head-fixed animals subjected to rotations and in freely moving animals (Vélez-Fort et al., 2018; Voigts and Harnett, 2020; Zong et al., 2017) will provide exciting new opportunities to explore these important questions at both the population and subcellular level in a cell-type-dependent manner.

Limitations of the study

Despite its many advantages, two-photon Ca²⁺ imaging is only an indirect measure of spiking activity, and inferring the underlying spike trains remains challenging. This method reports the relative change in spike rate, but the absolute spike rates are typically unknown. In addition, the large field of views needed to record hundreds of cells simultaneously come at the cost of a smaller signal-to-noise ratio of individual neurons. For this reason, even the latest genetically encoded Ca²⁺ indicators do not resolve single spikes, and therefore, our data may underestimate the number of responsive neurons and the percentage of tuned cells. Finally, the slow onset and decay kinetics of the intracellular Ca²⁺ concentration and indicators also prevent us from inferring precise spike times. Therefore, this method does not provide information about neuronal adaptation and the multi-synaptic delay between activation of the sensory organs and the cortical responses.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Experimental models: Organisms/strains

Mouse: Thy1-GCaMP6 GP4.3	The Jackson Laboratory	JAX:024275

Software and algorithms

MATLAB	Mathworks	https://www.mathworks.com/
LabView 2013	National Instruments	https://www.ni.com/en-gb.html
SciScan	Scientifica	https://www.scientifica.uk.com/products/scientifica-sciscan
CaImAn	Pnevmatikakis et al., 2016	https://github.com/flatironinstitute/CaImAn
NoRMCorre	Pnevmatikakis and Giovannucci, 2017	https://github.com/flatironinstitute/NoRMCorre
Model vestibular information processing	Laurens and Angelaki, 2017	https://github.com/JeanLaurens/Laurens_Angelaki_Kalman_2017
Linear Non-linear Poisson	This paper	https://doi.org/10.5281/zenodo.5680380
Pupil movement analysis	This paper	https://doi.org/10.5281/zenodo.5680380

Other

Custom two-photon microscope	This paper	https://doi.org/10.5281/zenodo.5680380
Custom built rotating experimental setup	This paper	https://doi.org/10.5281/zenodo.5680380

Open in a new tab

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Koen Vervaeke (koenv@medisin.uio.no)

Materials availability

This study did not generate new unique reagents.

Experimental model and subject details

Data include recordings from 18 Thy1-GCaMP6s mice (Dana et al., 2014) (16 male, 2 female, Jackson Laboratory, GP4.3 mouse line #024275). Mice were 2-5 months old at the time of surgery and were always housed with littermates in groups of 2-5. Mice were kept on a reversed 12-hour light/ 12-hour dark cycle, and experiments were carried out during their dark phase. To keep mice engaged during experiments, they received water drop rewards throughout a session and therefore, they were kept on a water restriction regime as described in Guo et al. (2014). All procedures were approved by the Norwegian Food Safety Authority (projects #FOTS 6590, 7480, 19129). Experiments were performed in accordance with the Norwegian Animal Welfare Act.

Method details

Rotation arena

The rotation platform (Figure S8) consisted of a circular aluminum breadboard (Ø300mm, Thorlabs, MBR300/M) fixed on a high-load rotary stage (Steinmeyer Mechatronik, DT240-TM). The stage was driven by a direct-drive motor. This has the important benefit that the motor does not have a mechanical transmission of force and hence is vibration-free, which is critical during imaging. We placed the mice in a head post and clamp system (Guo et al., 2014) on a two-axis micro-adjustable linear translation stage (Thorlabs, XYR1), which was mounted on the rotation platform in a position where the head of the mouse was close to the center of the platform and the axis of rotation. The linear stage was necessary to micro-adjust the position of the mouse so that the field of view (FOV) for imaging was perfectly centered on the axis of rotation.

To test whether the sample stays in the focal plane during rotations, we tested the stability and the precision of the rotation platform using a microscope slide with pollen grains (∼30 μm diameter). We rotated the slide from 0 to 360° in 45° steps. In each orientation, we took a z stack of images, extracted the fluorescence profile along the z axis for each pollen grain, and fitted these with a Gaussian function to determine the center position of the pollen along the z axis. Finally, by determining the variance of the center position along the z axis for different angular positions, we concluded that the center of each pollen moved less than 1 μm along the z axis during 360° rotations. A sub-μm quantification was prohibited by the limited precision of the z axis stepper motors of the microscope, which was 1 μm.

Commutator

Electrical signals of devices mounted on the rotation platform were carried through a commutator (MUSB2122-S10, MOFLON Technologies) to allow continuous rotations without cable twisting. The commutator had 10 analog and 2 USB channels and was placed in a hollow cavity within the rotary stage. This configuration provided unlimited rotational freedom in both directions.

Pupil tracking camera

An infrared-sensitive camera (Basler dart 1600-60um) was mounted on the rotation platform. To avoid that the camera occupied the mouse’s field of vision, we positioned it behind the mouse, and the pupil was recorded through a so-called hot mirror (#43-956, Edmund Optics), which was positioned in front of the mouse. This mirror is transparent in the visible range but reflects infrared light. The frame rate was 30 fps, and data were acquired using custom-written LabVIEW code (National Instruments). During post-processing, we measured the pupil position and diameter using scripts in MATLAB. The pupil was back-illuminated by the infrared light from the two-photon laser during imaging experiments, which created a high contrast image of the pupil.

Mouse body camera

To track the overall movements of the mouse, we used an infrared camera (25 fps) placed behind the mouse. Body movement was quantified in MATLAB by calculating the absolute sum of the frame-by-frame difference in pixel values within a region of interest centered on the mouse’s back.

Lick port

To keep the mouse engaged during experiments, the mouse received water rewards through a lick spout. Water delivery was controlled by a solenoid valve. The lick spout was part of a custom-built electrical circuit that detected when the tongue contacted the lick spout (Guo et al., 2014).

Arena wall and roof

The arena was enclosed by a 10 cm high cylindrical wall (30 cm diameter) with visual cues. The wall was custom-built and consisted of a 2 mm thick plastic plate fixed onto a circular “Lazy-Susan” ball bearing (Ø 30 cm). The visual cues where 2 white plastic cards of 7 cm width, and 1 white plastic card of 20 cm width. The height of the visual cues was restricted to avoid triggering an optokinetic reflex when moving the walls while the mouse is stationary. The walls were driven by a stepper motor (SMD-7611, National Instruments), and a rotary encoder (National Instruments) was used to read the wall position.

An illuminated roof covered the arena to prevent the mouse from observing cues outside the arena. The roof was made from two snug-fitting pieces of frosted plexiglass with an array of white LEDs mounted on top. This provided an evenly dim illumination of the arena without creating fixed visual cues. The roof was resting on the walls and therefore rotated together with the wall.

Light-shield

Because the arena was illuminated, we designed a light shield to protect the light-sensitive photomultipliers (PMTs) of the microscope. The light-shield consisted of a 3D-printed cone-shaped cup that clamped on the titanium head bar with neodymium magnets and fitted snugly over the microscope objective.

Two-photon microscope

We used a custom-built two-photon microscope, designed with two key objectives: 1) to provide enough space around the objective to accommodate the large rotation arena and 2) provide easy access for aligning the laser beam through the optics of the excitation path. The latter was critical for reducing fluorescence artifacts in the recording that arose from rotating the sample. The microscope was built in collaboration with Independent Neuroscience Services (INSS). The microscope consists of Thorlabs components, and a parts list, Autodesk Inventor files, and Zemax files of the optical design are available.

Rotating a sample while imaging can create two types of recording artifacts. The most intuitive, and the easiest to fix, is an asymmetry in the sample illumination. Due to vignetting, the illumination of the sample is usually not uniform. Suppose the point of maximum brightness is offset from the image center. In that case, parts of the sample will become brighter and dimmer during rotation, giving rise to an artifact in the fluorescence signal. Another, less intuitive artifact, arises if one considers the angle of the laser beam when parked in its center position. If this angle is not perfectly parallel with the axis of rotation, then, even deviations of 1° will give rise to a severe luminance artifact. While by itself not critical, it is the combination of this angle offset and inhomogeneous brain tissue that leads to this type of artifact. An example of this artifact is shown in Video S3, and an intuitive explanation is shown in Video S4. While it is generally assumed that the laser beam is perfectly centered through all the optics of the excitation path, in practice this is rarely the case, at least not with the precision required to scan a rotating sample. Finally, it is important to note that the laser beam’s precise alignment through the excitation path optics requires easy access, which can be difficult with commercial microscopes. Hence, our motivation to design a custom microscope.

Control and acquisition software

The rotary stage and all associated components were controlled by a custom-written LabVIEW program (LabVIEW 2013, NI). Except for the rotary stage, which had its own controller, control signals for these components were sent through a DAQ (X-Series, PCIe 6351, NI). The two-photon frame-clock, lick-port signals and wall positions were all acquired using the DAQ. The two-photon frame clock signal was used to synchronize the two-photon recording with the recorded signals from the DAQ. The angular position of the rotation stage was recorded independently through the software for two-photon acquisition.

Surgery

Surgery was carried out under isoflurane anesthesia (3% induction, 1% maintenance), while body temperature was maintained at 37°C with a heating pad (Harvard Apparatus). Subcutaneous injection of 0.1 mL Marcaine (bupivacaine 0.25% mass/volume in sterile water) was delivered at scalp incision sites. Post-operative injections of analgesia (Temgesic, 0.1 mg/kg) were administered subcutaneously.

Several weeks before imaging, mice underwent surgery to receive a head bar and a cranial window implant. The cranial window was either a 2.5 mm diameter round glass (7 mice) or a 5x5 mm trapezoidal glass (11 mice, see Figures 6 and 7). The center of the round window was −2.2 mm AP, and the front edge of the trapezoid window was +1.0 AP. Both windows consisted of two pieces of custom-cut #1.5 coverslip glass (each ∼170 μm thick) glued together with optical adhesive (Norland Optical Adhesive, ThorLabs NOA61). The aim was to create a plug-like implant such that the inner piece of glass fits in the craniotomy, flush with the surface of the brain, while the outer piece rests on the skull. Therefore, the outer piece of the window extended by 0.5 mm compared to the inner window. Heated agar (1%; Sigma #A6877) was applied to seal any open spaces between the skull and edges of the window, and the window was fixed to the skull with cyanoacrylate glue. A detailed protocol of the surgery can be found in Holtmaat et al. (2009).

Water restriction

Starting minimum 1 week after surgery, mice were placed on water restriction (described in Guo et al., 2014). Mice were given 1-1.5 mL water once per day while body weight was monitored and maintained at 10%–15% of the initial body weight. During experiments, mice would receive water drops of 5 μl to keep them engaged.

Animal training and habituation

During the first week of water restriction, mice were picked up and handled daily to make them comfortable with the person performing the experiments. Before experiments started, mice were placed in the arena and allowed to explore it for about 5 minutes. Next, they were head-fixed for about 30 minutes to screen the window implant. Experimental sessions would then start the next day.

Two-photon Imaging

All imaging data were acquired at 31 fps (512x512 pixels) using a custom-built two-photon microscope and acquisition software called SciScan (open-source, written in LabVIEW). The excitation wavelength was 950 nm using a MaiTai DeepSee ePH DS laser (Spectra-Physics). The average power measured under the objective (N16XLWD-PF, Nikon) was typically 50-100 mW. Photons were detected using GaAsP photomultiplier tubes (PMT2101/M, Thorlabs). The primary dichroic mirror was a 700 nm LP (Chroma), and the photon detection path consisted of a 680 nm SP filter (Chroma), a 565 nm LP dichroic mirror (Chroma), and a 510/80 nm BP filter (Chroma). The FOV size varied between 500-700 μm.

All data were recorded 100-170 μm below the cortical surface, corresponding to L2/3 of agranular RSC. The coordinates of the field of view center when using round windows (Figures 1, 2, 3, 4 and 5) was −1.6 to −4.1 mm Anterior-Posterior, and 0.35 to 0.87 Medio-Lateral. At the start of a recording, we adjusted the mouse position to align the FOV center with the axis of rotation. This required three steps: 1) Before placing the mouse, we scanned a rotating slide with 30 μm pollen grains to align the axis of the objective with the center of rotation of the FOV. 2) Because positioning the mouse caused small (< 100 μm) displacements, a final small adjustment of the objective position is needed. This was done automatically by recording an average projection image stack at 0° and 180°, respectively, and then aligning the de-rotated images to estimate the offset from the center of rotation. 3) When the objective was in place, we manually adjusted the position of the mouse (using the translation platform) to find a FOV and avoiding areas with large blood vessels.

Allocentric rotation protocol

Data presented in Figures 1 and 2 were recorded during 360° rotations. Mice were rotated in randomly selected steps of 120-, 240- or 360° within a range of ± 720°. The angular rotation speed was 45°/s, and the acceleration was 200°/s². This ensured that most of the rotation was taking place at a constant speed. Mice were stationary for 4-8 s between rotations while facing 1 of 3 possible directions (0, 120 and 240°). The mouse received a 5 μL water reward if its tongue touched the lick spout while stationary in the 0° direction. Mice typically performed 120-150 trials before they lost interest in water and the experiment was terminated.

Angular velocity protocol

Data presented in Figures 3, 4, 5, 6, and 7 were recorded while rotating the mice back and forth in 180° steps (alternating CW and CCW rotations) at four different speeds. The speed for each rotation was selected randomly from 45°/s to 180°/s in step of 45°/s. We chose this range of speeds based on data from freely moving mice (Figure S9).

Angular head acceleration varied between 300-800°/s² depending on which angular velocity was selected. During higher speeds, the acceleration was increased to ensure that a longer rotation period took place at a constant speed. Rotations were interleaved with 8-10 s breaks during which mice received a 5 μL water drop.

To separate the contributions of vestibular and visual inputs to AHV tuning, each recording session consisted of three consecutive blocks of 50-64 trials. First, the mouse was rotated in light, then the mouse was rotated in darkness and finally the wall was rotated while the mouse was stationary. For the wall rotation block, the wall was rotated using the same motion profile that was used with the rotary stage.

During the early explorations, we observed that the number of rotation-selective cells consistently decreased during the first three days of recording but then remained stable (Figure S10). This may be related to the mice’s overall arousal levels as they become more familiar with the apparatus. To prevent this from influencing the percentage of cells measured in different brain regions (which required recording across several days in the same mouse), we did not include sessions recorded in the first three days for this analysis.

Intrinsic imaging

To verify the accuracy of the FOV registration, we performed intrinsic imaging of the tail somatosensory cortex in a subset of mice (6 mice, see Figure S4). Mice were injected with the sedative (chlorprothixene, 1 mg/kg intramuscular) and maintained on a low concentration of isoflurane (∼0.5%). The mice rested on a heating pad, and their eyes were covered with Vaseline. Images were acquired through the cranial window using a CCD camera (Hamamatsu, ImagEM X2) mounted on a Leica MZ12.5 stereo microscope. Intrinsic signals were obtained using 630 nm red LED light, while images of the blood vessels were obtained using 510 nm green LED light. We stimulated the tail with a cotton swap and recorded the intrinsic signal over 5 repetitions. Each repetition consisted of a 10 s baseline recording, a 15 s stimulation period and a 20 s pause. The final intrinsic signal image was the difference between the average projection of all stimulation images and the average projection of all baseline images. Using this method, the tail somatosensory cortex obtained by intrinsic imaging was within 100-200 μm of the expected tail region based on stereotactic coordinates.

Quantification and statistical analysis

Image registration

To correct image distortion due to rotation of the sample, and brain movements in awake mice, the images were registered using a combination of custom written and published code (Pnevmatikakis et al., 2016) following three steps. 1) Image de-stretching: The resonance scan mirror follows a sinusoidal speed profile which distorts the images along the x axis. This was corrected using a lookup table generated from scanning a microgrid. 2) Image de-rotation: during post-processing, images were first de-rotated using the angular positions recorded from the rotary stage. Additional jitter in the angular position was corrected for using FFT-based image registration (NoRMCorre) (Pnevmatikakis and Giovannucci, 2017). Finally, to correct rotational stretch of images due to the rotation speed, a custom MATLAB script was used for a line-by-line correction. 3) Motion correction: De-rotated images were motion-corrected using a combination of custom-written scripts and NoRMCorre (Pnevmatikakis and Giovannucci, 2017).

Image segmentation

Registered images were segmented using custom-written MATLAB scripts. Regions of interest (ROI) for neuronal somas were either drawn manually or detected automatically. All ROIs were inspected visually. When ROIs were overlapping, the overlapping parts were excluded. A doughnut-shaped ROI of surrounding neuropil was automatically created for each ROI, by dilating the ROI so that the doughnut area was four times larger than the soma ROI area. If this doughnut overlapped with another soma ROI, then that soma ROI was excluded from the doughnut.

Signal and event extraction

Signals were extracted using custom MATLAB scripts. ROI fluorescence changes were defined as a fractional change $f (t) = (F (t) - F_{0}) / F_{0}$ , with F₀ being the baseline defined as the 20th percentile of the signal. This was calculated for both the soma and neuropil ROI. Then the neuropil DF/F was subtracted from the soma DF/F, and finally, a correction factor was added to ensure that the soma DF/F remained positive. The DF/F of each cell was then deconvolved using the CaImAn package (Giovannucci et al., 2019) to obtain event rates that approximate the cell’s activity level. Note that the outcome of the deconvolution procedure is given in arbitrary units (a.u.).

Quantification of rotation selectivity

Rotation selective cells

We quantified rotation-selectivity by comparing deconvolved DF/F event rates between CW and CCW trials. Rotation-selectivity was then determined using the Linear - Non-Linear Poisson model (see section “Statistical Model”). Cells with significance values p ≤ 0.05 were marked as rotation-selective (RS) cells.

Rotation selectivity Index

We defined this as:

R - i n d e x = \frac{r_{C W} - r_{C C W}}{r_{C W} + r_{C C W}}

where R-index is [-1, +1], and r is the average event rate during CCW (or CW) trials. Cells with R-index < 0 are considered CCW-preferring cells and cells with R-index > 0 are CW-preferring cells. Extreme values −1 (or +1) denote cells that fire exclusively during CCW or CW trials, respectively.

Spatial clustering

To determine whether rotation-selective cells are spatially clustered, we plotted the difference of R-indices as a function of physical distance: $Δ R_{ij} = | R_{i} - R_{j} |$ . We first tested this measure using simulated FOVs containing a typical number of cells using a Gaussian mixture model (Figure S1A; MATLAB gmdistribution, two clusters with center of mass $μ$ and $σ,$ $μ_{1} = [0,0], σ_{1} = 1, μ_{2} = [1,1], σ_{2} = 0.5$ ). In the first simulated FOV, each cell is assigned a R-index $\in$ [-1, +1] randomly (to mimic a “salt-and-pepper” case). In the other simulated FOV, cells of the same cluster were assigned a similar R-index (to mimic the clustered case). We then averaged $Δ R_{ij}$ for each spatial distance bin (Figure S1B). For a “salt-and-pepper” organization, this measure is not dependent on the distance between cells. For a “spatially clustered” organization, this measure increases with distance. In the experimental data (example FOV in Figure S1C), we binned the spatial distance $d_{i j}$ from 20 to 400 μm into 20 bins and averaged $Δ R_{i j}$ for each bin.

Classification of head direction tuning

Head direction tuning curves

For each cell, these were calculated by binning deconvolved DF/F events in angular bins of 30°. To correct for potential sampling bias, we divided the number of events by the occupancy vector, that is, the total amount of time spent in each bin (Figure S11). Lastly, the tuning curves were smoothed with a Gaussian kernel with a standard deviation of 6°.

Classification of HD

To classify cells, we computed the mutual information denoted as I between HD and average event rates as in Skaggs et al., 1993. We chose this measure because we often observed multiple peaks in the HD tuning curve. This is a more general measure than the standard mean vector length HD-score, which assumes single-peaked HD tuning curves. The mutual information of a cell is defined as:

I = \sum_{i} p (i) r (i) \log_{2} \frac{r (i)}{r}

where I is the mutual information rate of the cell in bits per second, i indexes the head direction bin, p(i) is the normalized occupancy vector of the head direction, r(i) is the mean firing rate when the mouse is facing head direction i, and r is the overall mean firing rate of the cell.

We compared the mutual information to a null hypothesis determined by shuffling the data. To preserve the time dynamics of the signal, we shifted each trial by a random amount of time. We performed this operation 1,000 times to obtain a distribution of mutual information values. We defined a cell as HD-tuned if the mutual information of the original data is higher than 95% of the mutual information in the shuffled data.

Response reliability

We measured the response reliability as the percent of trials where a cell was active. For each cell, we counted the number of trials where the sum of the deconvolved signal was different from zero over a truncated part of the trial (truncated to match the length of trials with the fastest speeds, i.e., the shortest duration trials) and divided by the total number of trials.

Statistical model

We used the Linear Non-Linear Poisson (LNP) model (Hardcastle et al., 2017) to determine whether cells encode the rotation direction and/or AHV of head movements. The difference being that CW/CCW cells prefer a specific rotation direction, while AHV cells prefer specific rotation velocities. We chose the LNP model because it has no prior assumptions about the tuning curve shape. In brief, these models predict the observed events by fitting a parameter to each behavioral variable. First, the probability of observing the number of events k for each time bin t is described by a Poisson process P(k(t)|λ(t)). The estimated event rate $\hat{r} (t) = λ (t) / d t$ , with time bin size $d t = 32.2 m s$ and dimensionless quantity $λ (t)$ , is calculated as an exponential function of the weighted sum of input variables.

λ (t) = \exp (b_{0} + \sum_{i} X_{i}^{T} (t) * w_{i})

Here, b₀ is a time-invariant constant, i indexes the behavioral variable, X_i is the state matrix and w_i is a vector of learned weight parameters. We designed the state matrix X_i where each column is an animal state vector x_i at one instant time bin t, defined as 1 at its current state and 0 in other states. We binned the rotation direction into two classes, and AHV into eight classes by 45°/s increments from −180°/s to +180°/s and excluding stationary states (0°/s).

Optimization of parameters

We measured performance by the log-likelihood (LLH) measure, defined as the log product of probabilities over all time bins $LLH = l o g \prod_{t} P (k (t) | λ (t))$ . The log-likelihood becomes simplified for a Poisson process:

L L H = \sum_{t} (k (t) \log λ (t) - λ (t)) + C

where C is a constant independent of the parameters b₀ and w. To learn the parameters w for each cell, we maximize the log-likelihood with an additional constraint that the parameters should be smooth. That is, we find:

w = a r g m a x_{w} (L L H - \frac{1}{2} \sum_{i, j} β {(w_{i, j} - w_{i, j + 1})}^{2})

where parameter β_i is a smoothing hyperparameter and j cycles through adjacent components of w. Based on testing from cross-validation, we applied a uniform β = 0.01 to all cells for AHV. We optimized the parameter search using MATLAB’s fminunc function.

Classification of tuned cells

To classify whether a cell is tuned to a specific behavioral variable, we ran two models on each cell: one without the variable, and one with the variable. If the model’s performance improved significantly with the inclusion of that variable, then the cell is classified as being tuned to the behavior. To quantify this method, we performed an 8-fold cross-validation on both models. For each fold, we used 7/8 of all trials as the training set and 1/8 of all trials as the test set. The test set LLHs of the model with the variable is compared to that of the model without the variable using paired Wilcoxon tests. Cells with a consistent increase of LLH (single tailed, p = 0.05) are marked as tuned to the variable.

To estimate the percentage of classified cells expected by chance (Figure 6B), we uncoupled AHV and neural activity by randomly permuting the order of trials and following the same cell classification procedure. Averaging from a sample of 54 sessions across all brain regions and all protocols, we found that chance levels were 0.34% for CW and CCW cells, and 0.68% for AHV cells.

In angular velocity protocols, slow-rotating trials take longer than fast-rotating trials to span the entire 180° rotation. This produces a bias that slow-rotating trials have a larger data sample size. To remove this bias, we truncated the data to the duration of the shortest trial.

Decoding

We used the Bayesian decoding method to reconstruct the animal’s state from its neural data. Given parameters w, we decode individual trials by summing the log-likelihood of observing events $k_{n} (t)$ over all cells n for each possible animal state. The decoded trial is the state ${\hat{X}}_{t r i a l}$ which maximizes the log-likelihood:

{\hat{X}}_{t r i a l} = a r g m a x_{X} \sum_{n} \sum_{t \in t r i a l} (k_{n} (t) \log λ_{n} (t) - λ_{n} (t))

where n indexes the cell and t sums all the time bins within the trial.

The decoding performance is visualized through a confusion matrix C. For the confusion matrix, each element C_ij is the number of times that a trial i is decoded as trial j. The confusion matrix shows systematic errors when reconstructing the state. The confusion matrix is shown in Figure 4C.

Furthermore, we quantified the AHV decoding error for each trial type i as the root-mean-square error:

ε_{i} = \frac{1}{n_{i}} {(\sum_{t r i a l \in i} {(X_{t r i a l} - {\hat{X}}_{t r i a l})}^{2})}^{1 / 2}

where ε_i is the decoding error, n_i is the number of trials, $X_{t r i a l}$ is the actual state and ${\hat{X}}_{t r i a l}$ is the decoded state. We compared this decoding error to a null hypothesis by shuffling the trial label 1,000 times. Note that the form of the decoding error is not circularly symmetric, thus the decoding error at chance level is higher at the edges (higher AHV). The overall measure of decoding error is calculated as average over all trial types.

To ensure that the experiments contain enough trials to find a reasonable decoding error, we calculated the decoding error from a random sample of sessions (Figure S12). Based on these data, we concluded that 40-50 rotation trials were sufficient as the decoding error did not significantly improve.

Comparing cortical areas and rotation conditions

We grouped the percentages of AHV cells for each brain region (V1, V2, RSC, PPC, M1+M2 and S1) and compared groups using Wilcoxon-Mann-Whitney tests (Figure 6B). Our aim is to provide the reader with a lookup table for statistical difference between pairs of brain areas. We present the uncorrected p values in Figure S13. Because recordings from different brain areas have varying numbers of cells, to compare the decoded errors between pairs of brain areas, we downsampled the analyses to 100 cells and performed the same Wilcoxon-Mann-Whitney tests (Figure S6). We performed the same test to compare percentages of AHV cells under different rotation conditions (Figure 7, rotations in light/dark and rotations of the arena wall).

Model of vestibular nerve activity

To simulate how mechanical activation of vestibular organs is translated into neural impulses in the vestibular nerve (Figures S2C and S2F), we used a model of head motion and vestibular sensors as described in Laurens and Angelaki (2017). In brief, the model uses a Kalman filter based on a forward model of a dynamical system, defined by a set of state variables that are driven by their own dynamics, motor commands, and internal or external perturbations. For a complete set of equations, we refer to Laurens and Angelaki (2017).

Two internal state variables are relevant here: the head angular velocity $Ω (t)$ and the hidden vestibular canal dynamics $C (t)$ . The semicircular canal signals are described by $V (t) = Ω (t) - C (t) .$ For passive rotation, the internal state $Ω (t)$ is fully described by experiment velocity profiles shown in Figures S2B and S2E. The canal dynamics are described as $C (t) = k_{1} C (t - Δ t) + k_{2} Ω (t)$ with $k 1 = τ_{c} / (1 + Δ t)$ and $k_{2} = Δ_{t} / (1 + τ_{c})$ . We used $δt$ = 32.2 ms and found the best matching fit using $τ_{c} = 2.2$ s. For other constants, we used the default values of the model with no sensory noise. V(t) is plotted on Figures S2C and S2F. The code is available at:

https://github.com/JeanLaurens/Laurens_Angelaki_Kalman_2017.

Pupil movement analysis

We tested whether RSC neurons are modulated by eye movements such as the nystagmus during rotations or spontaneous eye movements when the mouse is stationary. To determine such eye movements, we took the pupil position and derived the pupil velocity (Figure S3A). We then labeled pupil movement events as time points where the pupil moves at an absolute velocity over the 95^th percentile.

Next, we constructed the peristimulus time histogram (PSTH) of a window ± 5 s aligned to pupil movement events. We performed this for rotating (Figures S3C–S3E) and stationary conditions (Figures S3F–S3H). To avoid confounding neural activity due to slow decaying calcium transients of preceding events, we restricted the analysis to events that were not preceded by another event in a 1 s window. We then averaged the neural activity of a cell and compared this to 1000 instantiations of its average neural activity randomized by circular time-shuffling for individual events. We classified cells as pupil movement cells if their response amplitude was larger than the 95^th percentile within a ± 500 ms window around events (Figures S3D and S3G). The overlap between pupil movement cells and AHV cells are shown with a Venn diagram (Figures S3E and S3H). We measured the significance of this overlap by comparing it to randomly shuffled labels of pupil movement cells and AHV cells.

Registration of FOVs across brain regions

The FOV positions were registered onto a map of the dorsal brain surface in two steps. 1) A picture of the blood vessels in the cranial window was anchored to the map based on stereotaxic coordinates determined during surgery. 2) Next, two-photon images tiling the brain surface were also positioned on the map by matching the vessel pattern (see example in Figure 6A, middle panel). Finally, we used intrinsic imaging to verify the accuracy of this approach.

Acknowledgments

This work was funded by the European Research Council (ERC starting grant 639272) to K.V., the Research Council of Norway (231495, 276047, and 274306), and an EEA grant to K.V. (RO-NO-2019-0504). We thank Kristin Larsen Sand, Rune Lanton, and Michele Gianatti for technical assistance. We thank Bruno Pichler (Independent NeuroScience Services; INSS) for developing the custom two-photon microscope and providing technical assistance. Some schematics were created with Biorender.com. Finally, we thank Tsai-Wen Chen, Lyle Graham, Hua Hu, Sepiedeh Keshavarzi, Jean Laurens, Nuo Li, Raul Muresan, and Ning-long Xu for providing critical comments that significantly improved a draft of the manuscript.

Author contributions

E.H., A.W., A.R.C., and K.V. designed research. E.H. performed all experiments and model-free data analysis. A.W. performed all model-based data analysis. A.R.C. performed pilot experiments and data analysis. K.V. performed surgeries. E.H., A.W., and K.V. wrote the paper.

Declaration of interests

The authors declare no competing interests.

Published: December 21, 2021

Footnotes

Supplemental information can be found online at https://doi.org/10.1016/j.celrep.2021.110134.

Supplemental information

Document S1. Figures S1–S13

mmc1.pdf^{(8.2MB, pdf)}

Document S2. Article plus supplemental information

mmc7.pdf^{(20.2MB, pdf)}

Data and code availability

•
All data reported in this paper will be shared by the lead contact upon request.
•
Technical drawings of the setup and microscope (Autodesk Inventor files) are available on GitHub (DOI available in the Key resources table).
•
All original code has been deposited on GitHub and is publicly available as of the date of publication (DOI available in the Key resources table).
•
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.

References

Alexander A.S., Nitz D.A. Retrosplenial cortex maps the conjunction of internal and external spaces. Nat. Neurosci. 2015;18:1143–1151. doi: 10.1038/nn.4058. [DOI] [PubMed] [Google Scholar]
Angelaki D.E., Cullen K.E. Vestibular system: the many facets of a multimodal sense. Annu. Rev. Neurosci. 2008;31:125–150. doi: 10.1146/annurev.neuro.31.060407.125555. [DOI] [PubMed] [Google Scholar]
Angelaki D.E., Ng J., Abrego A.M., Cham H.X., Asprodini E.K., Dickman J.D., Laurens J. A gravity-based three-dimensional compass in the mouse brain. Nat. Commun. 2020;11:1855. doi: 10.1038/s41467-020-15566-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
Avila E., Lakshminarasimhan K.J., DeAngelis G.C., Angelaki D.E. Visual and Vestibular Selectivity for Self-Motion in Macaque Posterior Parietal Area 7a. Cereb. Cortex. 2019;29:3932–3947. doi: 10.1093/cercor/bhy272. [DOI] [PMC free article] [PubMed] [Google Scholar]
Bassett J.P., Taube J.S. Neural correlates for angular head velocity in the rat dorsal tegmental nucleus. J. Neurosci. 2001;21:5740–5751. doi: 10.1523/JNEUROSCI.21-15-05740.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
Blumer R., Maurer-Gesek B., Gesslbauer B., Blumer M., Pechriggl E., Davis-López de Carrizosa M.A., Horn A.K., May P.J., Streicher J., de la Cruz R.R., Pastor Á.M. Palisade Endings Are a Constant Feature in the Extraocular Muscles of Frontal-Eyed, But Not Lateral-Eyed, Animals. Invest. Ophthalmol. Vis. Sci. 2016;57:320–331. doi: 10.1167/iovs.15-18716. [DOI] [PMC free article] [PubMed] [Google Scholar]
Bouvier G., Senzai Y., Scanziani M. Head Movements Control the Activity of Primary Visual Cortex in a Luminance-Dependent Manner. Neuron. 2020;108:500–511.e5. doi: 10.1016/j.neuron.2020.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
Brooks J.X., Carriot J., Cullen K.E. Learning to expect the unexpected: rapid updating in primate cerebellum during voluntary self-motion. Nat. Neurosci. 2015;18:1310–1317. doi: 10.1038/nn.4077. [DOI] [PMC free article] [PubMed] [Google Scholar]
Büttner U., Buettner U.W. Parietal cortex (2v) neuronal activity in the alert monkey during natural vestibular and optokinetic stimulation. Brain Res. 1978;153:392–397. doi: 10.1016/0006-8993(78)90421-3. [DOI] [PubMed] [Google Scholar]
Chen L.L., Lin L.H., Green E.J., Barnes C.A., McNaughton B.L. Head-direction cells in the rat posterior cortex. I. Anatomical distribution and behavioral modulation. Exp. Brain Res. 1994;101:8–23. doi: 10.1007/BF00243212. [DOI] [PubMed] [Google Scholar]
Cho J., Sharp P.E. Head direction, place, and movement correlates for cells in the rat retrosplenial cortex. Behav. Neurosci. 2001;115:3–25. doi: 10.1037/0735-7044.115.1.3. [DOI] [PubMed] [Google Scholar]
Cullen K.E. Vestibular processing during natural self-motion: implications for perception and action. Nat. Rev. Neurosci. 2019;20:346–363. doi: 10.1038/s41583-019-0153-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
Cullen K.E., Taube J.S. Our sense of direction: progress, controversies and challenges. Nat. Neurosci. 2017;20:1465–1473. doi: 10.1038/nn.4658. [DOI] [PMC free article] [PubMed] [Google Scholar]
Dana H., Chen T.-W., Hu A., Shields B.C., Guo C., Looger L.L., Kim D.S., Svoboda K. Thy1-GCaMP6 transgenic mice for neuronal population imaging in vivo. PLoS One. 2014;9:e108697. doi: 10.1371/journal.pone.0108697. [DOI] [PMC free article] [PubMed] [Google Scholar]
Fernandez C., Goldberg J.M. Physiology of peripheral neurons innervating semicircular canals of the squirrel monkey. II. Response to sinusoidal stimulation and dynamics of peripheral vestibular system. J. Neurophysiol. 1971;34:661–675. doi: 10.1152/jn.1971.34.4.661. [DOI] [PubMed] [Google Scholar]
Gdowski G.T., McCrea R.A. Neck proprioceptive inputs to primate vestibular nucleus neurons. Exp. Brain Res. 2000;135:511–526. doi: 10.1007/s002210000542. [DOI] [PubMed] [Google Scholar]
Giovannucci A., Friedrich J., Gunn P., Kalfon J., Brown B.L., Koay S.A., Taxidis J., Najafi F., Gauthier J.L., Zhou P., et al. CaImAn an open source tool for scalable calcium imaging data analysis. eLife. 2019;8:e38173. doi: 10.7554/eLife.38173. [DOI] [PMC free article] [PubMed] [Google Scholar]
Goldberg J.M., Fernandez C. Physiology of peripheral neurons innervating semicircular canals of the squirrel monkey. I. Resting discharge and response to constant angular accelerations. J. Neurophysiol. 1971;34:635–660. doi: 10.1152/jn.1971.34.4.635. [DOI] [PubMed] [Google Scholar]
Guitchounts G., Masís J., Wolff S.B.E., Cox D. Encoding of 3D Head Orienting Movements in the Primary Visual Cortex. Neuron. 2020;108:512–525.e4. doi: 10.1016/j.neuron.2020.07.014. [DOI] [PubMed] [Google Scholar]
Guo Z.V., Hires S.A., Li N., O’Connor D.H., Komiyama T., Ophir E., Huber D., Bonardi C., Morandell K., Gutnisky D., et al. Procedures for behavioral experiments in head-fixed mice. PLoS One. 2014;9:e88678. doi: 10.1371/journal.pone.0088678. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hardcastle K., Maheswaranathan N., Ganguli S., Giocomo L.M. A Multiplexed, Heterogeneous, and Adaptive Code for Navigation in Medial Entorhinal Cortex. Neuron. 2017;94:375–387.e7. doi: 10.1016/j.neuron.2017.03.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
Holtmaat A., Bonhoeffer T., Chow D.K., Chuckowree J., De Paola V., Hofer S.B., Hübener M., Keck T., Knott G., Lee W.-C.A., et al. Long-term, high-resolution imaging in the mouse neocortex through a chronic cranial window. Nat. Protoc. 2009;4:1128–1144. doi: 10.1038/nprot.2009.89. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hulse B.K., Jayaraman V. Mechanisms Underlying the Neural Computation of Head Direction. Annu. Rev. Neurosci. 2020;43:31–54. doi: 10.1146/annurev-neuro-072116-031516. [DOI] [PubMed] [Google Scholar]
Jacob P.-Y., Casali G., Spieser L., Page H., Overington D., Jeffery K. An independent, landmark-dominated head-direction signal in dysgranular retrosplenial cortex. Nat. Neurosci. 2017;20:173–175. doi: 10.1038/nn.4465. [DOI] [PMC free article] [PubMed] [Google Scholar]
Keshavarzi S., Bracey E.F., Faville R.A., Campagner D., Tyson A.L., Lenzi S.C., Branco T., Margrie T.W. The retrosplenial cortex combines internal and external cues to encode head velocity during navigation. bioRxiv. 2021 doi: 10.1101/2021.01.22.427789. [DOI] [Google Scholar]
Kim T.H., Zhang Y., Lecoq J., Jung J.C., Li J., Zeng H., Niell C.M., Schnitzer M.J. Long-Term Optical Access to an Estimated One Million Neurons in the Live Mouse Cortex. Cell Rep. 2016;17:3385–3394. doi: 10.1016/j.celrep.2016.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
Kirkcaldie M.T.K. The Mouse Nervous System. Academic Press; 2012. Chapter 4—The Neocortex; pp. 52–111. [Google Scholar]
Knierim J.J., Zhang K. Attractor dynamics of spatially correlated neural activity in the limbic system. Annu. Rev. Neurosci. 2012;35:267–285. doi: 10.1146/annurev-neuro-062111-150351. [DOI] [PMC free article] [PubMed] [Google Scholar]
Lasker D.M., Han G.C., Park H.J., Minor L.B. Rotational responses of vestibular-nerve afferents innervating the semicircular canals in the C57BL/6 mouse. J. Assoc. Res. Otolaryngol. 2008;9:334–348. doi: 10.1007/s10162-008-0120-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
Laurens J., Angelaki D.E. A unified internal model theory to resolve the paradox of active versus passive self-motion sensation. eLife. 2017;6:129. doi: 10.7554/eLife.28074. [DOI] [PMC free article] [PubMed] [Google Scholar]
Laurens J., Abrego A., Cham H., Popeney B., Yu Y., Rotem N., Aarse J., Asprodini E.K., Dickman J.D., Angelaki D.E. Multiplexed code of navigation variables in anterior limbic areas. bioRxiv. 2019 doi: 10.1101/684464. [DOI] [Google Scholar]
Lenschow C., Copley S., Gardiner J.M., Talbot Z.N., Vitenzon A., Brecht M. Sexually Monomorphic Maps and Dimorphic Responses in Rat Genital Cortex. Curr. Biol. 2016;26:106–113. doi: 10.1016/j.cub.2015.11.041. [DOI] [PubMed] [Google Scholar]
Liu B., Tian Q., Gu Y. Robust vestibular self-motion signals in macaque posterior cingulate region. eLife. 2021;10:e64569. doi: 10.7554/eLife.64569. [DOI] [PMC free article] [PubMed] [Google Scholar]
Lopez C., Blanke O. The thalamocortical vestibular system in animals and humans. Brain Res. Brain Res. Rev. 2011;67:119–146. doi: 10.1016/j.brainresrev.2010.12.002. [DOI] [PubMed] [Google Scholar]
Mallory C.S., Hardcastle K., Campbell M.G., Attinger A., Low I.I.C., Raymond J.L., Giocomo L.M. Mouse entorhinal cortex encodes a diverse repertoire of self-motion signals. Nat. Commun. 2021;12:671. doi: 10.1038/s41467-021-20936-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
McNaughton B.L., Barnes C.A., O’Keefe J. The contributions of position, direction, and velocity to single unit activity in the hippocampus of freely-moving rats. Exp. Brain Res. 1983;52:41–49. doi: 10.1007/BF00237147. [DOI] [PubMed] [Google Scholar]
McNaughton B.L., Chen L.L., Markus E.J. “Dead reckoning,” landmark learning, and the sense of direction: a neurophysiological and computational hypothesis. J. Cogn. Neurosci. 1991;3:190–202. doi: 10.1162/jocn.1991.3.2.190. [DOI] [PubMed] [Google Scholar]
McNaughton B.L., Mizumori S.J.Y., Barnes C.A., Leonard B.J., Marquis M., Green E.J. Cortical Representation of Motion during Unrestrained Spatial Navigation in the Rat. Cereb. Cortex. 1994;4:27–39. doi: 10.1093/cercor/4.1.27. [DOI] [PubMed] [Google Scholar]
Medrea I., Cullen K.E. Multisensory integration in early vestibular processing in mice: the encoding of passive vs. active motion. J. Neurophysiol. 2013;110:2704–2717. doi: 10.1152/jn.01037.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
Mehlman M.L., Winter S.S., Valerio S., Taube J.S. Functional and anatomical relationships between the medial precentral cortex, dorsal striatum, and head direction cell circuitry. I. Recording studies. J. Neurophysiol. 2019;121:350–370. doi: 10.1152/jn.00143.2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
Mergner T., Huber W., Becker W. Vestibular-neck interaction and transformation of sensory coordinates. J. Vestib. Res. 1997;7:347–367. [PubMed] [Google Scholar]
Mimica B., Dunn B.A., Tombaz T., Bojja V., Whitlock J.R. Efficient cortical coding of 3D posture in freely behaving rats. Science. 2018;362:584–589. doi: 10.1126/science.aau2013. [DOI] [PubMed] [Google Scholar]
Niell C.M., Stryker M.P. Highly selective receptive fields in mouse visual cortex. J. Neurosci. 2008;28:7520–7536. doi: 10.1523/JNEUROSCI.0623-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
Pnevmatikakis E.A., Giovannucci A. NoRMCorre: An online algorithm for piecewise rigid motion correction of calcium imaging data. J. Neurosci. Methods. 2017;291:83–94. doi: 10.1016/j.jneumeth.2017.07.031. [DOI] [PubMed] [Google Scholar]
Pnevmatikakis E.A., Soudry D., Gao Y., Machado T.A., Merel J., Pfau D., Reardon T., Mu Y., Lacefield C., Yang W., et al. Simultaneous Denoising, Deconvolution, and Demixing of Calcium Imaging Data. Neuron. 2016;89:285–299. doi: 10.1016/j.neuron.2015.11.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
Preston-Ferrer P., Coletta S., Frey M., Burgalossi A. Anatomical organization of presubicular head-direction circuits. eLife. 2016;5:e14592. doi: 10.7554/eLife.14592. [DOI] [PMC free article] [PubMed] [Google Scholar]
Rancz E.A., Moya J., Drawitsch F., Brichta A.M., Canals S., Margrie T.W. Widespread vestibular activation of the rodent cortex. J. Neurosci. 2015;35:5926–5934. doi: 10.1523/JNEUROSCI.1869-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
Roy J.E., Cullen K.E. Selective processing of vestibular reafference during self-generated head motion. J. Neurosci. 2001;21:2131–2142. doi: 10.1523/JNEUROSCI.21-06-02131.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
Sasaki R., Angelaki D.E., DeAngelis G.C. Dissociation of Self-Motion and Object Motion by Linear Population Decoding That Approximates Marginalization. J. Neurosci. 2017;37:11204–11219. doi: 10.1523/JNEUROSCI.1177-17.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
Sharp P.E. Multiple spatial/behavioral correlates for cells in the rat postsubiculum: multiple regression analysis and comparison to other hippocampal areas. Cereb. Cortex. 1996;6:238–259. doi: 10.1093/cercor/6.2.238. [DOI] [PubMed] [Google Scholar]
Sharp P.E., Tinkelman A., Cho J. Angular velocity and head direction signals recorded from the dorsal tegmental nucleus of gudden in the rat: implications for path integration in the head direction cell circuit. Behav. Neurosci. 2001;115:571–588. [PubMed] [Google Scholar]
Sigl-Glöckner J., Maier E., Takahashi N., Sachdev R., Larkum M., Brecht M. Effects of Sexual Experience and Puberty on Mouse Genital Cortex revealed by Chronic Imaging. Curr. Biol. 2019;29:3588–3599.e4. doi: 10.1016/j.cub.2019.08.062. [DOI] [PubMed] [Google Scholar]
Sikes R.W., Vogt B.A., Swadlow H.A. Neuronal responses in rabbit cingulate cortex linked to quick-phase eye movements during nystagmus. J. Neurophysiol. 1988;59:922–936. doi: 10.1152/jn.1988.59.3.922. [DOI] [PubMed] [Google Scholar]
Skaggs W.E., Knierim J.J., Kudrimoti H.S., McNaughton B.L. A model of the neural basis of the rat’s sense of direction. Adv. Neural Inf. Process. Syst. 1995;7:173–180. [PubMed] [Google Scholar]
Stackman R.W., Taube J.S. Firing properties of rat lateral mammillary single units: head direction, head pitch, and angular head velocity. J. Neurosci. 1998;18:9020–9037. doi: 10.1523/JNEUROSCI.18-21-09020.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
Skaggs W., McNaughton B., Gothard K. Advances in neural information processing systems. Morgan-Kaufmann; 1993. An Information-theoretic approach to deciphering the hippocampal code; pp. 1030–1037. [Google Scholar]
Stackman R.W., Clark A.S., Taube J.S. Hippocampal spatial representations require vestibular input. Hippocampus. 2002;12:291–303. doi: 10.1002/hipo.1112. [DOI] [PMC free article] [PubMed] [Google Scholar]
Stahl J.S. Using eye movements to assess brain function in mice. Vision Res. 2004;44:3401–3410. doi: 10.1016/j.visres.2004.09.011. [DOI] [PubMed] [Google Scholar]
Taube J.S. The head direction signal: origins and sensory-motor integration. Annu. Rev. Neurosci. 2007;30:181–207. doi: 10.1146/annurev.neuro.29.051605.112854. [DOI] [PubMed] [Google Scholar]
Taube J.S., Muller R.U., Ranck J.B., Jr. Head-direction cells recorded from the postsubiculum in freely moving rats. I. Description and quantitative analysis. J. Neurosci. 1990;10:420–435. doi: 10.1523/JNEUROSCI.10-02-00420.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
Turner-Evans D., Wegener S., Rouault H., Franconville R., Wolff T., Seelig J.D., Druckmann S., Jayaraman V. Angular velocity integration in a fly heading circuit. eLife. 2017;6:e04577. doi: 10.7554/eLife.23496. [DOI] [PMC free article] [PubMed] [Google Scholar]
Valerio S., Taube J.S. Head Direction Cell Activity Is Absent in Mice without the Horizontal Semicircular Canals. J. Neurosci. 2016;36:741–754. doi: 10.1523/JNEUROSCI.3790-14.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
Vann S.D., Aggleton J.P., Maguire E.A. What does the retrosplenial cortex do? Nat. Rev. Neurosci. 2009;10:792–802. doi: 10.1038/nrn2733. [DOI] [PubMed] [Google Scholar]
Vanni-Mercier G., Magnin M. Single neuron activity related to natural vestibular stimulation in the cat’s visual cortex. Exp. Brain Res. 1982;45:451–455. doi: 10.1007/BF01208606. [DOI] [PubMed] [Google Scholar]
Vélez-Fort M., Bracey E.F., Keshavarzi S., Rousseau C.V., Cossell L., Lenzi S.C., Strom M., Margrie T.W. A Circuit for Integration of Head- and Visual-Motion Signals in Layer 6 of Mouse Primary Visual Cortex. Neuron. 2018;98:179–191.e6. doi: 10.1016/j.neuron.2018.02.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
Voigts J., Harnett M.T. Somatic and Dendritic Encoding of Spatial Variables in Retrosplenial Cortex Differs during 2D Navigation. Neuron. 2020;105:237–245.e4. doi: 10.1016/j.neuron.2019.10.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
von Holst E., Mittelstaedt H. Das Reafferenzprinzip. Naturwissenschaften. 1950;37:464–476. [Google Scholar]
Waespe W., Henn V. Neuronal activity in the vestibular nuclei of the alert monkey during vestibular and optokinetic stimulation. Exp. Brain Res. 1977;27:523–538. doi: 10.1007/BF00239041. [DOI] [PubMed] [Google Scholar]
Whitlock J.R., Pfuhl G., Dagslott N., Moser M.-B., Moser E.I. Functional split between parietal and entorhinal cortices in the rat. Neuron. 2012;73:789–802. doi: 10.1016/j.neuron.2011.12.028. [DOI] [PubMed] [Google Scholar]
Wilber A.A., Clark B.J., Forster T.C., Tatsuno M., McNaughton B.L. Interaction of egocentric and world-centered reference frames in the rat posterior parietal cortex. J. Neurosci. 2014;34:5431–5446. doi: 10.1523/JNEUROSCI.0511-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wolpert D.M., Miall R.C. Forward Models for Physiological Motor Control. Neural Netw. 1996;9:1265–1279. doi: 10.1016/s0893-6080(96)00035-4. [DOI] [PubMed] [Google Scholar]
Zong W., Wu R., Li M., Hu Y., Li Y., Li J., Rong H., Wu H., Xu Y., Lu Y., et al. Fast high-resolution miniature two-photon microscopy for brain imaging in freely behaving mice. Nat. Methods. 2017;14:713–719. doi: 10.1038/nmeth.4305. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Video S1. Rotating mouse and rotating walls, related to Figure 1

Head-restrained mouse rotated under the two-photon microscope. Example trials, rotating either the mouse or the arena wall with visual cues. Inset shows pupil tracking.

Download video file^{(9.9MB, mp4)}

Video S2. Rotating FOV and de-rotated FOV, related to Figure 1

Example of two-photon image sequence obtained while rotating the mouse (left), and after post-processing when images are de-rotated and corrected for brain movement (right).

Download video file^{(31.1MB, mp4)}

Video S3. Example of luminance artifacts during rotation under a two-photon microscope, related to Figure 1

Even minor misalignments of the excitation laser beam will result in major luminance changes within the image during rotation.

Download video file^{(9.6MB, mp4)}

Video S4. Illustration of how minor excitation beam misalignment results in major luminance changes, related to Figure 1

Download video file^{(2.2MB, mp4)}

Video S5. Example of AHV decoding using RSC neurons, related to Figure 5

Download video file^{(1.6MB, mp4)}

Document S1. Figures S1–S13

mmc1.pdf^{(8.2MB, pdf)}

Document S2. Article plus supplemental information

mmc7.pdf^{(20.2MB, pdf)}

Data Availability Statement

•
All data reported in this paper will be shared by the lead contact upon request.
•
Technical drawings of the setup and microscope (Autodesk Inventor files) are available on GitHub (DOI available in the Key resources table).
•
All original code has been deposited on GitHub and is publicly available as of the date of publication (DOI available in the Key resources table).
•
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.

[bib1] Alexander A.S., Nitz D.A. Retrosplenial cortex maps the conjunction of internal and external spaces. Nat. Neurosci. 2015;18:1143–1151. doi: 10.1038/nn.4058. [DOI] [PubMed] [Google Scholar]

[bib2] Angelaki D.E., Cullen K.E. Vestibular system: the many facets of a multimodal sense. Annu. Rev. Neurosci. 2008;31:125–150. doi: 10.1146/annurev.neuro.31.060407.125555. [DOI] [PubMed] [Google Scholar]

[bib3] Angelaki D.E., Ng J., Abrego A.M., Cham H.X., Asprodini E.K., Dickman J.D., Laurens J. A gravity-based three-dimensional compass in the mouse brain. Nat. Commun. 2020;11:1855. doi: 10.1038/s41467-020-15566-5. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib4] Avila E., Lakshminarasimhan K.J., DeAngelis G.C., Angelaki D.E. Visual and Vestibular Selectivity for Self-Motion in Macaque Posterior Parietal Area 7a. Cereb. Cortex. 2019;29:3932–3947. doi: 10.1093/cercor/bhy272. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib5] Bassett J.P., Taube J.S. Neural correlates for angular head velocity in the rat dorsal tegmental nucleus. J. Neurosci. 2001;21:5740–5751. doi: 10.1523/JNEUROSCI.21-15-05740.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib6] Blumer R., Maurer-Gesek B., Gesslbauer B., Blumer M., Pechriggl E., Davis-López de Carrizosa M.A., Horn A.K., May P.J., Streicher J., de la Cruz R.R., Pastor Á.M. Palisade Endings Are a Constant Feature in the Extraocular Muscles of Frontal-Eyed, But Not Lateral-Eyed, Animals. Invest. Ophthalmol. Vis. Sci. 2016;57:320–331. doi: 10.1167/iovs.15-18716. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib7] Bouvier G., Senzai Y., Scanziani M. Head Movements Control the Activity of Primary Visual Cortex in a Luminance-Dependent Manner. Neuron. 2020;108:500–511.e5. doi: 10.1016/j.neuron.2020.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib8] Brooks J.X., Carriot J., Cullen K.E. Learning to expect the unexpected: rapid updating in primate cerebellum during voluntary self-motion. Nat. Neurosci. 2015;18:1310–1317. doi: 10.1038/nn.4077. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib9] Büttner U., Buettner U.W. Parietal cortex (2v) neuronal activity in the alert monkey during natural vestibular and optokinetic stimulation. Brain Res. 1978;153:392–397. doi: 10.1016/0006-8993(78)90421-3. [DOI] [PubMed] [Google Scholar]

[bib10] Chen L.L., Lin L.H., Green E.J., Barnes C.A., McNaughton B.L. Head-direction cells in the rat posterior cortex. I. Anatomical distribution and behavioral modulation. Exp. Brain Res. 1994;101:8–23. doi: 10.1007/BF00243212. [DOI] [PubMed] [Google Scholar]

[bib11] Cho J., Sharp P.E. Head direction, place, and movement correlates for cells in the rat retrosplenial cortex. Behav. Neurosci. 2001;115:3–25. doi: 10.1037/0735-7044.115.1.3. [DOI] [PubMed] [Google Scholar]

[bib12] Cullen K.E. Vestibular processing during natural self-motion: implications for perception and action. Nat. Rev. Neurosci. 2019;20:346–363. doi: 10.1038/s41583-019-0153-1. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib13] Cullen K.E., Taube J.S. Our sense of direction: progress, controversies and challenges. Nat. Neurosci. 2017;20:1465–1473. doi: 10.1038/nn.4658. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib14] Dana H., Chen T.-W., Hu A., Shields B.C., Guo C., Looger L.L., Kim D.S., Svoboda K. Thy1-GCaMP6 transgenic mice for neuronal population imaging in vivo. PLoS One. 2014;9:e108697. doi: 10.1371/journal.pone.0108697. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib15] Fernandez C., Goldberg J.M. Physiology of peripheral neurons innervating semicircular canals of the squirrel monkey. II. Response to sinusoidal stimulation and dynamics of peripheral vestibular system. J. Neurophysiol. 1971;34:661–675. doi: 10.1152/jn.1971.34.4.661. [DOI] [PubMed] [Google Scholar]

[bib16] Gdowski G.T., McCrea R.A. Neck proprioceptive inputs to primate vestibular nucleus neurons. Exp. Brain Res. 2000;135:511–526. doi: 10.1007/s002210000542. [DOI] [PubMed] [Google Scholar]

[bib17] Giovannucci A., Friedrich J., Gunn P., Kalfon J., Brown B.L., Koay S.A., Taxidis J., Najafi F., Gauthier J.L., Zhou P., et al. CaImAn an open source tool for scalable calcium imaging data analysis. eLife. 2019;8:e38173. doi: 10.7554/eLife.38173. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib18] Goldberg J.M., Fernandez C. Physiology of peripheral neurons innervating semicircular canals of the squirrel monkey. I. Resting discharge and response to constant angular accelerations. J. Neurophysiol. 1971;34:635–660. doi: 10.1152/jn.1971.34.4.635. [DOI] [PubMed] [Google Scholar]

[bib19] Guitchounts G., Masís J., Wolff S.B.E., Cox D. Encoding of 3D Head Orienting Movements in the Primary Visual Cortex. Neuron. 2020;108:512–525.e4. doi: 10.1016/j.neuron.2020.07.014. [DOI] [PubMed] [Google Scholar]

[bib20] Guo Z.V., Hires S.A., Li N., O’Connor D.H., Komiyama T., Ophir E., Huber D., Bonardi C., Morandell K., Gutnisky D., et al. Procedures for behavioral experiments in head-fixed mice. PLoS One. 2014;9:e88678. doi: 10.1371/journal.pone.0088678. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib21] Hardcastle K., Maheswaranathan N., Ganguli S., Giocomo L.M. A Multiplexed, Heterogeneous, and Adaptive Code for Navigation in Medial Entorhinal Cortex. Neuron. 2017;94:375–387.e7. doi: 10.1016/j.neuron.2017.03.025. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib22] Holtmaat A., Bonhoeffer T., Chow D.K., Chuckowree J., De Paola V., Hofer S.B., Hübener M., Keck T., Knott G., Lee W.-C.A., et al. Long-term, high-resolution imaging in the mouse neocortex through a chronic cranial window. Nat. Protoc. 2009;4:1128–1144. doi: 10.1038/nprot.2009.89. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib23] Hulse B.K., Jayaraman V. Mechanisms Underlying the Neural Computation of Head Direction. Annu. Rev. Neurosci. 2020;43:31–54. doi: 10.1146/annurev-neuro-072116-031516. [DOI] [PubMed] [Google Scholar]

[bib24] Jacob P.-Y., Casali G., Spieser L., Page H., Overington D., Jeffery K. An independent, landmark-dominated head-direction signal in dysgranular retrosplenial cortex. Nat. Neurosci. 2017;20:173–175. doi: 10.1038/nn.4465. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib25] Keshavarzi S., Bracey E.F., Faville R.A., Campagner D., Tyson A.L., Lenzi S.C., Branco T., Margrie T.W. The retrosplenial cortex combines internal and external cues to encode head velocity during navigation. bioRxiv. 2021 doi: 10.1101/2021.01.22.427789. [DOI] [Google Scholar]

[bib26] Kim T.H., Zhang Y., Lecoq J., Jung J.C., Li J., Zeng H., Niell C.M., Schnitzer M.J. Long-Term Optical Access to an Estimated One Million Neurons in the Live Mouse Cortex. Cell Rep. 2016;17:3385–3394. doi: 10.1016/j.celrep.2016.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib27] Kirkcaldie M.T.K. The Mouse Nervous System. Academic Press; 2012. Chapter 4—The Neocortex; pp. 52–111. [Google Scholar]

[bib28] Knierim J.J., Zhang K. Attractor dynamics of spatially correlated neural activity in the limbic system. Annu. Rev. Neurosci. 2012;35:267–285. doi: 10.1146/annurev-neuro-062111-150351. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib29] Lasker D.M., Han G.C., Park H.J., Minor L.B. Rotational responses of vestibular-nerve afferents innervating the semicircular canals in the C57BL/6 mouse. J. Assoc. Res. Otolaryngol. 2008;9:334–348. doi: 10.1007/s10162-008-0120-4. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib30] Laurens J., Angelaki D.E. A unified internal model theory to resolve the paradox of active versus passive self-motion sensation. eLife. 2017;6:129. doi: 10.7554/eLife.28074. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib31] Laurens J., Abrego A., Cham H., Popeney B., Yu Y., Rotem N., Aarse J., Asprodini E.K., Dickman J.D., Angelaki D.E. Multiplexed code of navigation variables in anterior limbic areas. bioRxiv. 2019 doi: 10.1101/684464. [DOI] [Google Scholar]

[bib32] Lenschow C., Copley S., Gardiner J.M., Talbot Z.N., Vitenzon A., Brecht M. Sexually Monomorphic Maps and Dimorphic Responses in Rat Genital Cortex. Curr. Biol. 2016;26:106–113. doi: 10.1016/j.cub.2015.11.041. [DOI] [PubMed] [Google Scholar]

[bib33] Liu B., Tian Q., Gu Y. Robust vestibular self-motion signals in macaque posterior cingulate region. eLife. 2021;10:e64569. doi: 10.7554/eLife.64569. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib34] Lopez C., Blanke O. The thalamocortical vestibular system in animals and humans. Brain Res. Brain Res. Rev. 2011;67:119–146. doi: 10.1016/j.brainresrev.2010.12.002. [DOI] [PubMed] [Google Scholar]

[bib35] Mallory C.S., Hardcastle K., Campbell M.G., Attinger A., Low I.I.C., Raymond J.L., Giocomo L.M. Mouse entorhinal cortex encodes a diverse repertoire of self-motion signals. Nat. Commun. 2021;12:671. doi: 10.1038/s41467-021-20936-8. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib36] McNaughton B.L., Barnes C.A., O’Keefe J. The contributions of position, direction, and velocity to single unit activity in the hippocampus of freely-moving rats. Exp. Brain Res. 1983;52:41–49. doi: 10.1007/BF00237147. [DOI] [PubMed] [Google Scholar]

[bib37] McNaughton B.L., Chen L.L., Markus E.J. “Dead reckoning,” landmark learning, and the sense of direction: a neurophysiological and computational hypothesis. J. Cogn. Neurosci. 1991;3:190–202. doi: 10.1162/jocn.1991.3.2.190. [DOI] [PubMed] [Google Scholar]

[bib38] McNaughton B.L., Mizumori S.J.Y., Barnes C.A., Leonard B.J., Marquis M., Green E.J. Cortical Representation of Motion during Unrestrained Spatial Navigation in the Rat. Cereb. Cortex. 1994;4:27–39. doi: 10.1093/cercor/4.1.27. [DOI] [PubMed] [Google Scholar]

[bib39] Medrea I., Cullen K.E. Multisensory integration in early vestibular processing in mice: the encoding of passive vs. active motion. J. Neurophysiol. 2013;110:2704–2717. doi: 10.1152/jn.01037.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib40] Mehlman M.L., Winter S.S., Valerio S., Taube J.S. Functional and anatomical relationships between the medial precentral cortex, dorsal striatum, and head direction cell circuitry. I. Recording studies. J. Neurophysiol. 2019;121:350–370. doi: 10.1152/jn.00143.2018. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib41] Mergner T., Huber W., Becker W. Vestibular-neck interaction and transformation of sensory coordinates. J. Vestib. Res. 1997;7:347–367. [PubMed] [Google Scholar]

[bib42] Mimica B., Dunn B.A., Tombaz T., Bojja V., Whitlock J.R. Efficient cortical coding of 3D posture in freely behaving rats. Science. 2018;362:584–589. doi: 10.1126/science.aau2013. [DOI] [PubMed] [Google Scholar]

[bib43] Niell C.M., Stryker M.P. Highly selective receptive fields in mouse visual cortex. J. Neurosci. 2008;28:7520–7536. doi: 10.1523/JNEUROSCI.0623-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib44] Pnevmatikakis E.A., Giovannucci A. NoRMCorre: An online algorithm for piecewise rigid motion correction of calcium imaging data. J. Neurosci. Methods. 2017;291:83–94. doi: 10.1016/j.jneumeth.2017.07.031. [DOI] [PubMed] [Google Scholar]

[bib45] Pnevmatikakis E.A., Soudry D., Gao Y., Machado T.A., Merel J., Pfau D., Reardon T., Mu Y., Lacefield C., Yang W., et al. Simultaneous Denoising, Deconvolution, and Demixing of Calcium Imaging Data. Neuron. 2016;89:285–299. doi: 10.1016/j.neuron.2015.11.037. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib46] Preston-Ferrer P., Coletta S., Frey M., Burgalossi A. Anatomical organization of presubicular head-direction circuits. eLife. 2016;5:e14592. doi: 10.7554/eLife.14592. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib47] Rancz E.A., Moya J., Drawitsch F., Brichta A.M., Canals S., Margrie T.W. Widespread vestibular activation of the rodent cortex. J. Neurosci. 2015;35:5926–5934. doi: 10.1523/JNEUROSCI.1869-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib48] Roy J.E., Cullen K.E. Selective processing of vestibular reafference during self-generated head motion. J. Neurosci. 2001;21:2131–2142. doi: 10.1523/JNEUROSCI.21-06-02131.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib49] Sasaki R., Angelaki D.E., DeAngelis G.C. Dissociation of Self-Motion and Object Motion by Linear Population Decoding That Approximates Marginalization. J. Neurosci. 2017;37:11204–11219. doi: 10.1523/JNEUROSCI.1177-17.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib50] Sharp P.E. Multiple spatial/behavioral correlates for cells in the rat postsubiculum: multiple regression analysis and comparison to other hippocampal areas. Cereb. Cortex. 1996;6:238–259. doi: 10.1093/cercor/6.2.238. [DOI] [PubMed] [Google Scholar]

[bib51] Sharp P.E., Tinkelman A., Cho J. Angular velocity and head direction signals recorded from the dorsal tegmental nucleus of gudden in the rat: implications for path integration in the head direction cell circuit. Behav. Neurosci. 2001;115:571–588. [PubMed] [Google Scholar]

[bib52] Sigl-Glöckner J., Maier E., Takahashi N., Sachdev R., Larkum M., Brecht M. Effects of Sexual Experience and Puberty on Mouse Genital Cortex revealed by Chronic Imaging. Curr. Biol. 2019;29:3588–3599.e4. doi: 10.1016/j.cub.2019.08.062. [DOI] [PubMed] [Google Scholar]

[bib53] Sikes R.W., Vogt B.A., Swadlow H.A. Neuronal responses in rabbit cingulate cortex linked to quick-phase eye movements during nystagmus. J. Neurophysiol. 1988;59:922–936. doi: 10.1152/jn.1988.59.3.922. [DOI] [PubMed] [Google Scholar]

[bib54] Skaggs W.E., Knierim J.J., Kudrimoti H.S., McNaughton B.L. A model of the neural basis of the rat’s sense of direction. Adv. Neural Inf. Process. Syst. 1995;7:173–180. [PubMed] [Google Scholar]

[bib56] Stackman R.W., Taube J.S. Firing properties of rat lateral mammillary single units: head direction, head pitch, and angular head velocity. J. Neurosci. 1998;18:9020–9037. doi: 10.1523/JNEUROSCI.18-21-09020.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib55] Skaggs W., McNaughton B., Gothard K. Advances in neural information processing systems. Morgan-Kaufmann; 1993. An Information-theoretic approach to deciphering the hippocampal code; pp. 1030–1037. [Google Scholar]

[bib57] Stackman R.W., Clark A.S., Taube J.S. Hippocampal spatial representations require vestibular input. Hippocampus. 2002;12:291–303. doi: 10.1002/hipo.1112. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib58] Stahl J.S. Using eye movements to assess brain function in mice. Vision Res. 2004;44:3401–3410. doi: 10.1016/j.visres.2004.09.011. [DOI] [PubMed] [Google Scholar]

[bib59] Taube J.S. The head direction signal: origins and sensory-motor integration. Annu. Rev. Neurosci. 2007;30:181–207. doi: 10.1146/annurev.neuro.29.051605.112854. [DOI] [PubMed] [Google Scholar]

[bib60] Taube J.S., Muller R.U., Ranck J.B., Jr. Head-direction cells recorded from the postsubiculum in freely moving rats. I. Description and quantitative analysis. J. Neurosci. 1990;10:420–435. doi: 10.1523/JNEUROSCI.10-02-00420.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib61] Turner-Evans D., Wegener S., Rouault H., Franconville R., Wolff T., Seelig J.D., Druckmann S., Jayaraman V. Angular velocity integration in a fly heading circuit. eLife. 2017;6:e04577. doi: 10.7554/eLife.23496. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib62] Valerio S., Taube J.S. Head Direction Cell Activity Is Absent in Mice without the Horizontal Semicircular Canals. J. Neurosci. 2016;36:741–754. doi: 10.1523/JNEUROSCI.3790-14.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib63] Vann S.D., Aggleton J.P., Maguire E.A. What does the retrosplenial cortex do? Nat. Rev. Neurosci. 2009;10:792–802. doi: 10.1038/nrn2733. [DOI] [PubMed] [Google Scholar]

[bib64] Vanni-Mercier G., Magnin M. Single neuron activity related to natural vestibular stimulation in the cat’s visual cortex. Exp. Brain Res. 1982;45:451–455. doi: 10.1007/BF01208606. [DOI] [PubMed] [Google Scholar]

[bib65] Vélez-Fort M., Bracey E.F., Keshavarzi S., Rousseau C.V., Cossell L., Lenzi S.C., Strom M., Margrie T.W. A Circuit for Integration of Head- and Visual-Motion Signals in Layer 6 of Mouse Primary Visual Cortex. Neuron. 2018;98:179–191.e6. doi: 10.1016/j.neuron.2018.02.023. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib66] Voigts J., Harnett M.T. Somatic and Dendritic Encoding of Spatial Variables in Retrosplenial Cortex Differs during 2D Navigation. Neuron. 2020;105:237–245.e4. doi: 10.1016/j.neuron.2019.10.016. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib67] von Holst E., Mittelstaedt H. Das Reafferenzprinzip. Naturwissenschaften. 1950;37:464–476. [Google Scholar]

[bib68] Waespe W., Henn V. Neuronal activity in the vestibular nuclei of the alert monkey during vestibular and optokinetic stimulation. Exp. Brain Res. 1977;27:523–538. doi: 10.1007/BF00239041. [DOI] [PubMed] [Google Scholar]

[bib69] Whitlock J.R., Pfuhl G., Dagslott N., Moser M.-B., Moser E.I. Functional split between parietal and entorhinal cortices in the rat. Neuron. 2012;73:789–802. doi: 10.1016/j.neuron.2011.12.028. [DOI] [PubMed] [Google Scholar]

[bib70] Wilber A.A., Clark B.J., Forster T.C., Tatsuno M., McNaughton B.L. Interaction of egocentric and world-centered reference frames in the rat posterior parietal cortex. J. Neurosci. 2014;34:5431–5446. doi: 10.1523/JNEUROSCI.0511-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib71] Wolpert D.M., Miall R.C. Forward Models for Physiological Motor Control. Neural Netw. 1996;9:1265–1279. doi: 10.1016/s0893-6080(96)00035-4. [DOI] [PubMed] [Google Scholar]

[bib72] Zong W., Wu R., Li M., Hu Y., Li Y., Li J., Rong H., Wu H., Xu Y., Lu Y., et al. Fast high-resolution miniature two-photon microscopy for brain imaging in freely behaving mice. Nat. Methods. 2017;14:713–719. doi: 10.1038/nmeth.4305. [DOI] [PubMed] [Google Scholar]

PERMALINK

Mapping vestibular and visual contributions to angular head velocity tuning in the cortex

Eivind Hennestad

Aree Witoelar

Anna R Chambers

Koen Vervaeke

Summary

Graphical abstract

Highlights

Introduction

Results

Rotation-selective neurons in the RSC

Figure 1.

Many rotation-selective neurons are biased by head direction

Figure 2.

A large fraction of rotation-selective neurons encode AHV

Figure 3.

AHV can be decoded from neural activity in the RSC

Figure 4.

AHV tuning in the RSC depends on sensory transduction in the vestibular organs

Figure 5.

AHV is widespread in cortical circuits

Figure 6.

The sensory origin of AHV tuning is dependent on cortical area

Figure 7.

Discussion

Limitations of the study

STAR★Methods

Key resources table

Resource availability

Lead contact

Materials availability

Experimental model and subject details

Method details

Rotation arena

Commutator

Pupil tracking camera

Mouse body camera

Lick port

Arena wall and roof

Light-shield

Two-photon microscope

Control and acquisition software

Surgery

Water restriction

Animal training and habituation

Two-photon Imaging

Allocentric rotation protocol

Angular velocity protocol

Intrinsic imaging

Quantification and statistical analysis

Image registration

Image segmentation

Signal and event extraction

Quantification of rotation selectivity

Rotation selective cells

Rotation selectivity Index

Spatial clustering

Classification of head direction tuning

Head direction tuning curves

Classification of HD

Response reliability

Statistical model

Optimization of parameters

Classification of tuned cells

Decoding

Comparing cortical areas and rotation conditions

Model of vestibular nerve activity

Pupil movement analysis

Registration of FOVs across brain regions

Acknowledgments

Author contributions

Declaration of interests

Footnotes

Supplemental information

Data and code availability

References

Associated Data

Supplementary Materials

Data Availability Statement