Effect of facet inclination and location on TMJ loading during bruxism: An in-silico study

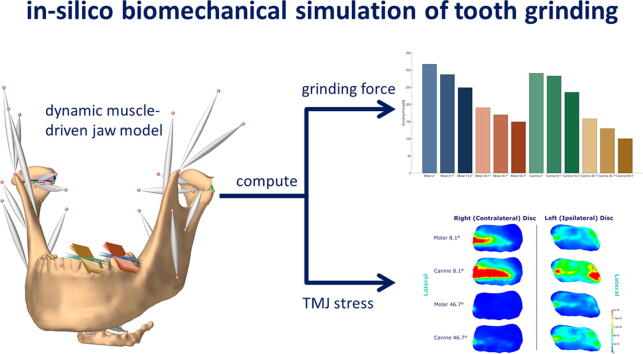
Graphical abstract

Highlights

• •Sheds new light on the important potential connection between tooth grinding and temporomandibular joint loading
• •Demonstrates a larger effect of grinding inclination than grinding position on TMJ loading
• •Creates a novel computer simulation of TMJ disc stress during dynamic tooth grinding tasks
• •Uses state-of-the-art in silico methods for a highly multidisciplinary investigation, which is not feasible in vivo
• •Presents a tracking simulation approach to work around the highly complicated recording of masticatory muscle EMG acquisition

Abstract

Introduction

Functional impairment of the masticatory region can have significant consequences that range from a loss of quality of life to severe health issues. Increased temporomandibular joint loading is often connected with temporomandibular disorders, but the effect of morphological factors on joint loading is a heavily discussed topic. Due to the small size and complex structure of the masticatory region in vivo investigations of these connections are difficult to perform.

Objectives

We propose a novel in silico approach for the investigation of the effect of wear facet inclination and position on TMJ stress.

Methods

We use a forward-dynamics tracking approach to simulate lateral bruxing on the canine and first molar using 6 different inclinations, resulting in a total of 12 simulated cases. By using a computational model, we control a single variable without interfering with the system. Muscle activation pattern, maximum bruxing force as well as TMJ disc stress are reported for all simulations.

Results

Muscle activation patterns and bruxing forces agree well with previously reported EMG findings and in vivo force measurements. The simulation results show that an increase in inclination leads to a decrease in TMJ loading. Wear facet position seems to play a smaller role with regard to bruxing force but might be more relevant for TMJ loading.

Conclusion

Together these results suggest a possible effect of tooth morphology on TMJ loading during bruxism.

Introduction

The masticatory region has a complex composition and a multitude of elements that need to work in unison, which makes investigation of its biomechanics a difficult endeavor. Previous literature often connects increased temporomandibular joint (TMJ) loading with temporomandibular joint disorders (TMD), but due to the small size and complex structure of the joint in vivo investigations are exceedingly difficult [1], [2]. For example, the effect of morphological or occlusal factors on TMJ loading have been a frequent subject of debate [3], [4], [5], [6], [7]. Another highly debated topic is the potential role of sleep bruxism in the onset of TMD [8], [9]. While previous literature has not found a direct connection between sleep bruxism and increased myofascial pain [3], [10], the potential connection between sleep bruxism and increased joint loads has not been investigated in vivo.

Investigating the connection between occlusal factors and/or morphological changes of the masticatory structures with joint loading remains possible through biomechanical reasoning. One such example is the report of a relationship between an anterior edge-to-edge-bite/crossbite with a reduced eminence height and deep bite with an increased ratio between eminence steepness and postglenoid process height [5]. While wear facets alone cannot be used to distinguish myofascial TMD patients from volunteers [11], the potential influence of wear facet position and/or inclination on TMJ stress in an isolated fashion is relevant, since particular bruxing positions or inclinations might lead to increased joint loading and consequently could represent a risk factor for the onset of TMD, especially arthralgia and degenerative joint diseases.

Apart from ethical considerations of TMJ load investigations, it is virtually impossible to find a study cohort that only differs in a single morphological variable or is large enough to capture the effect of a single variable with a multitude of changing factors present. In addition, recording of muscle activation patterns of the masticatory region through electromyography (EMG) is highly challenging, because this small region encompasses many muscles that partly overlap each other or are not accessible with surface electrodes. Hence, EMG of the masticatory region is commonly only collected for the masseter and temporalis muscles and, at times, for the submental region as a whole [10], [12]. While the masseter and temporalis undoubtably play a major role in bite force creation, bruxing tasks must facilitate a complex activation pattern to guide the mandible downwards along the wear facet simultaneously with force creation.

In silico investigations, such as musculoskeletal modeling [13] and finite-element simulation [14], [15], have become an important tool in advanced scientific research. For analysis of bruxism, an in silico investigation allows for the investigation of TMJ loading and the controlled alteration of a single variable, while keeping the rest of the morphology stable and are therefore one of the few tools appropriate for an investigation of the potential connection between TMJ stress and tooth morphology. Moreover, sophisticated tracking approaches allow for the computation of muscle excitation patterns, without the need for EMG acquisition. Previous in silico investigations have mostly focussed on static bruxing tasks in the closed mouth position [16], [17], [18], [19]. For example, Commisso et al., (2014) investigated cyclic and sustained loading, mimicking bruxing activity, and investigated the effect of static clenching tasks on the TMJ disc [20]. They report that sustained clenching induces shear stresses that are high enough to create damage to the TMJ disc. These previous modeling studies provide valuable insights into the possible role of static clenching in the development of TMD. However, bruxing movements are dynamic in nature and it can be expected that the combination of loads together with movement is required to characterize the mechanical forces that may underlie TMD.

The goal of the current study was to investigate a possible effect of bruxing position and inclination on maximum bruxing force, muscle activation patterns and TMJ stress, using our previously developed high-resolution model of the masticatory region and forward-dynamics tracking approach. We computed muscle activation patterns and joint stresses for 12 different cases. Overall, this project uses state of the art computational methods for an in-silico investigation of a complex dental research question that is not feasible for direct in vivo examination.

Material and methods

The model was built from high-resolution data from a symptom-free, male volunteer. Ethics approval was obtained from the institutional review board of the Medical University of Vienna (Nr. 1190/2017) and written informed consent was obtained. Data acquisition and model creation have been described in previous publications [21], [22]. In short, a single full skull CT scan (Siemens™ Sensation 4; resolution: 0.3 × 0.3 × 0.5 mm) was collected to define bone contours and a full skull MRI dataset was used to define muscle paths. Moreover, high resolution TMJ MRI volumes were collected to allow for precise segmentation of the TMJ discs. MRI scans were acquired using a TSE-T1 sequence on a Siemens Magneton 3 T machine using a 64-channel head coil, allowing for a resolution of 0.17 mm and a slice thickness of 1 mm. The biomechanical computer model was built using the ArtiSynth toolkit (www.artisynth.org) [23]. Muscles were modeled as Hill-type actuators [24] and bones were represented as rigid bodies. Using a novel approach, we modeled the TMJs as a combination of a finite element (FE) disc, using a Mooney-Rivlin-Material taken from literature (C1 = 9 · 10⁵Pa and C2 = 9 · 10²Pa) [25], and two elastic foundation contact (EF) layers, representing articular cartilage. We based our elastic modulus on previous literature values for an articular cartilage Mooney–Rivlin material [25] and estimated E using 6 · C1 [26]. EF contact has previously shown to be a valuable tool for the investigation of cartilage layers bonded to bone [27], [28], but the combination of EF layers with a FE body is a novel approach. The TMJ disc mesh included a similar number of tetrahedral elements as our previous investigation, but with increased mesh quality. Four axial springs were used to model the biomechanical workings of the TMJ capsule. Three connect the disc and the condyle anteriorly, medially, laterally and one connects the skull and disk posteriorly [22]. To spread the attachment out over multiple nodes and increase stability of the simulations a distributed FEM attachment was used, in accordance with previous literature [29].

Since it is prohibitively challenging to collect reliable muscle activation patterns during a bruxing task, we aimed to solve this problem by using a forward-dynamics tracking approach that incorporates reaction force tracking. A detailed explanation and theoretical description of the optimization method can be found in [30]

Briefly, we set up our optimization problem in a way that kinematics and kinetic goals can be incorporated as quadratic optimization goals, as follows:

$${\mathbf{\Phi }}_v\left(\mathit{a}\right)=\frac{1}{2}{\Vert \overline{\mathit{v}}-{\mathit{H}}_v\mathit{a}\Vert }^2{\mathbf{\Phi }}_c(\mathit{a})=\frac{1}{2}{\Vert \overline{\mathit{c}}-{\mathit{H}}_c\mathit{a}\Vert }^2$$ (1)

where ${\mathbf{\Phi }}_v$ and ${\mathbf{\Phi }}_c$ are the quadratic optimization goals that try to minimize the difference between a movement and/or reaction force (i.e.: bruxing force) goal, $\overline{\mathit{v}}$ or $\overline{\mathit{c}}$, and the movement and/or force created by a set of muscle activations, represented by ${\mathit{H}}_v\mathit{a}$ and ${\mathit{H}}_c\mathit{a}$.

At each time-step we compute the optimal, in terms of the optimization function, muscle activation vector $\mathit{a}$ using the optimization equation:

$$\underset{\mathit{a}}{\min }{w}_v{\mathbf{\Phi }}_v\left(\mathit{a}\right)+w_c{\mathbf{\Phi }}_c\left(\mathit{a}\right)+\frac{w_a}{2}{\mathit{a}}^T\mathit{a}+\frac{w_d}{2}{\Vert {\mathit{a}}_{i-1}-\mathit{a}\Vert }^2$$ (2)

subject to $0\le \mathit{a}\le 1$

where $w_v$, $w_c$, $w_a$ and $w_d$ are the respective weights for each cost term (typically $w_d<w_a\ll w_v$, $w_c)$. The $l^2$ norm regularization term ${\frac{w_a}{2}\mathit{a}}^T\mathit{a}$ is used to solve the muscle load sharing problem. To prevent the solution from oscillating between two possibly feasible states, caused by the multitude of muscles in the small area, we added a damping term, penalizing fast changes in muscle activation patterns. The weights of the regularization term and damping term were set to 0.00025 and 0.00005, respectively.

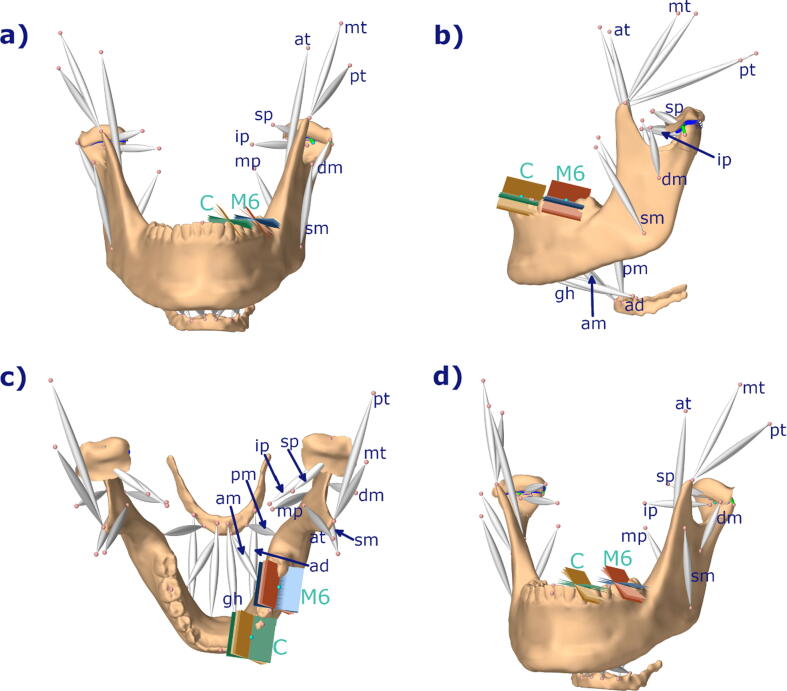
To investigate the effect of bruxing location and tooth inclination on tooth and TMJ loading we simulated left lateral bruxing movements with a movement goal of 3 mm excursion along the wear facet. A lateral movement of 3 mm was chosen, since it lies in between the mean values for lateral excursion for first molar and canine bruxing [31]. Tooth wear facets were represented by a planar, bilateral constraint (Fig. 1). A second, static movement goal was added at the condyle to penalize non-physiological separation of the TMJ structures. The laterotrusion goal was weighted with 1 and the static goal was assigned weights of 1 for the medio-lateral, 0.75 for the anterior-posterior and 0.75 for the inferior-superior directions. The in silico investigations were performed for tooth contact at the position of the first molar as well as the canine, using a time step of 0.002 s, which was the largest timestep that ensured success of the simulations. Bruxing force was ramped up and down for 0.05 s, without movement, at the start and end of the simulation and the task itself was simulated over a 0.4 s time frame. To investigate the effect of facet inclination, mean values and standard deviation from literature were used [31]. Values were reported relative to the axis-orbital-plane, consequently we used previously recorded data to define the axis-orbital-plane of the model and defined it as 0° inclination. The mean values for the inclination of the wear facets on the canine and first molar were simulated as starting points, representing the main lateral guidance and the center of mastication, respectively. Additionally, simulations with ± one standard deviation were performed to depict a full range of physiological variance. To further isolate the effect of bruxing position and inclination, we simulated bruxing at both teeth with the appropriate inclination values and the values of the other tooth, leading to 12 simulation cases (Fig. 1). The maximum achievable bruxing force for all 12 set-ups was identified and von Mises stress of the TMJ discs was recorded, together with the computed muscle excitation patterns.

Fig. 1.

Overview of modeling set-up used; a) frontal view; b) side view, c) top view, d) oblique view; blue: molar 2°, 8.1°, 14.2°; red: molar 38.1°, 46.7°, 55,4°; green: canine 2°, 8.1°, 14.2°; brown: canine 38.1°, 46.7°, 55.3°; mp: medial pterygoid, ip: inferior head of lateral pterygoid, sp: superior head of lateral pterygoid, at: anterior temporalis, mt: medial temporalis, pt: posterior temporalis, dm: deep masseter, sm: superficial masseter, pm: posterior mylohyoid, ad: anterior digastric, am: anterior mylohyoid, gh: geniohyoid; all muscles occur on both sides; C: canine, M6: first molar; tooth inclinations taken from [31] and represent mean inclination values for canine and first molar plus ± one standard deviation.

Results

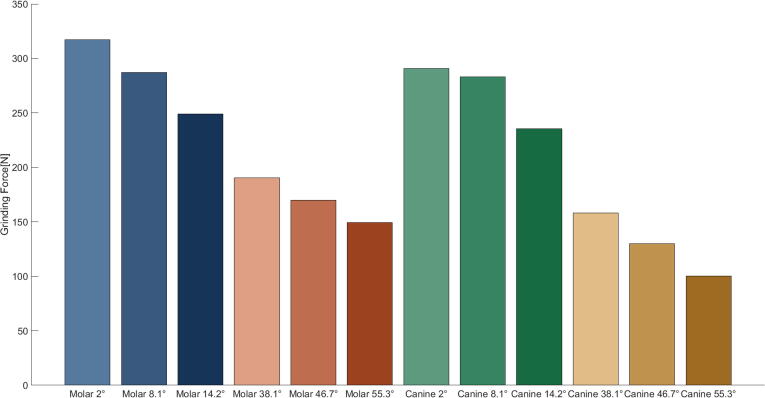
Mean bruxing forces, over the duration of the bruxing task, are reported in Fig. 2. In general, the molar tooth contact position allowed for the highest bruxing forces, with a max value of 317.24 N for 2° inclination. Moreover, the bruxing force decreased with increasing facet inclination. Changes in inclination lead to relatively large differences in mean bruxing force, while changes in bruxing contact position only had a minor influence on bruxing force (Table 1).

Fig. 2.

Maximum achievable mean bruxing force over the duration of the simulation.

Table 1.

Maximum achievable mean bruxing force during a laterotrusive bruxing task and differences between position and inclination in Newton. Bruxing force for mean inclinations for canine and molar are reported.

	Molar	Canine	Difference
8.1°	287.12	283.26	3.86
46.7°	169.95	129.98	39.97
Difference	117.17	153.28

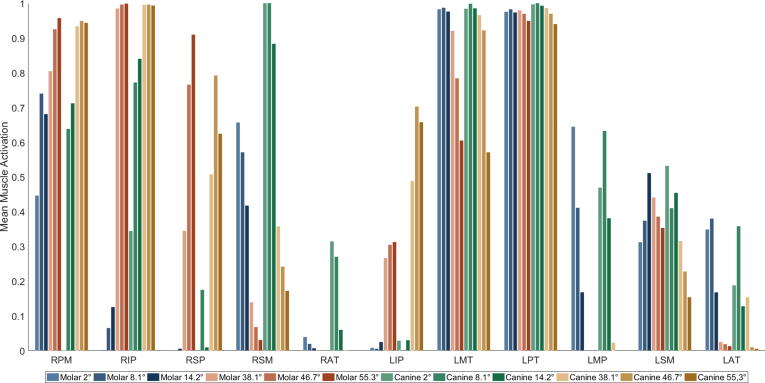
Mean muscle activations, over the duration of the bruxing task, can be seen in Fig. 3. For clarity, only muscles with an activation larger than 20% are shown. The medial and posterior compartments of the temporal muscle on the ipsilateral side (LMT, LPT) are strongly activated during all simulated cases. The ipsilateral anterior compartment (LAT) is mostly activated during the shallower simulations. Ipsilateral medial pterygoid (LMP) activation is present during the shallower sets of cases, while the ipsilateral superficial masseter (LSM) is activated for all cases. The ipsilateral inferior head of the lateral pterygoid muscle (LIP) is activated for the steeper cases. Moreover, the contralateral inferior and superior heads of the lateral pterygoid (RIP, RSP) are strongly activated for the steeper simulation cases. Contralateral superficial masseter (RSM) activation decreases with increasing facet inclination. Additionally, contralateral activation of the posterior mylohyoid muscle (RPM) occurs in all cases, except for the 2° canine bruxing case.

Fig. 3.

Mean muscle excitation of muscles with excitation higher than 20%; right side is contralateral; RPM: right posterior mylohyoid, RIP: right inferior head of lateral pterygoid, RSP: right superior head of lateral pterygoid, RSM: right superficial masseter, RAT: right anterior temporalis, LIP: left inferior head of lateral pterygoid, LMT: left middle compartment of temporal muscle, LPT: left posterior compartment of temporal muscle, LMP: left medial pterygoid, LSM: left superficial masseter, LAT: left anterior compartment of temporalis.

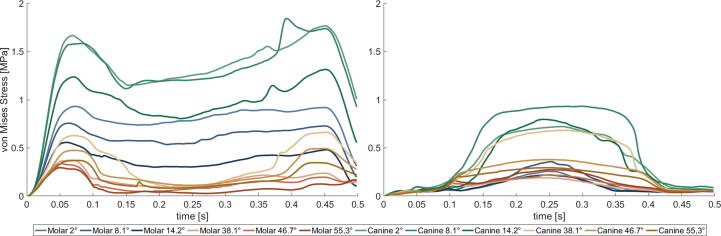
Fig. 4 shows the mean von Mises stress of the intermediate zone of both discs over the course of the bruxing task. Generally speaking, higher stresses occur in the contralateral disc. Stress values show a trend for higher values on the canine compared to the molar and decreasing stresses with increasing steepness. Fig. 5 gives a visual comparison of TMJ disc stress at the most lateral position of the bruxing movement.

Fig. 4.

Mean von Mises stress of intermediate zone of right, contralateral (left picture) and left, ipsilateral TMJ disc (right picture) during laterotrusive bruxing to the left side.

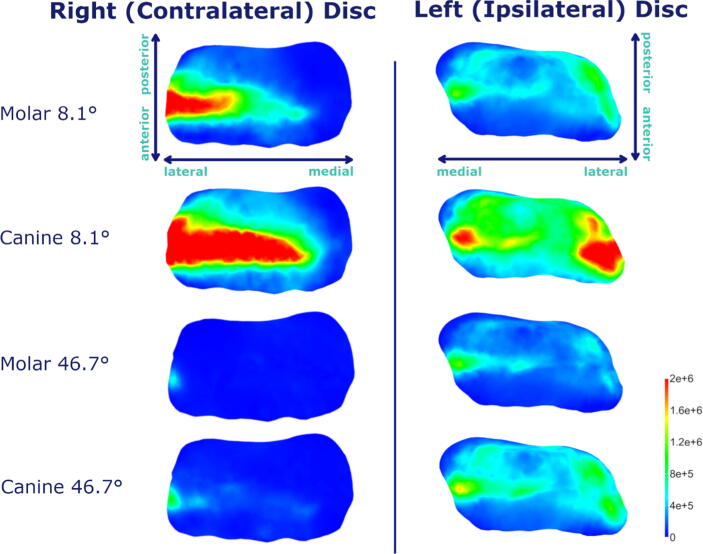
Fig. 5.

Von Mises stress plots for mean inclinations at both bruxing positions at the most lateral position (t = 0.25) during laterotrusive bruxing to the left side; axes orientations shown for first row are the same for all subsequent rows.

Discussion

This paper presents the first ever dynamic in silico investigation of bruxism biomechanics. We used a detailed, dynamic computer model of the masticatory region, including FEM discs, combined with a forward-dynamics tracking approach to compute muscle activation patterns for lateral bruxing movements. Simulations are used to investigate the effect of wear facet inclination and position on bruxing force magnitude and TMJ stress. The reported simulations generated plausible bruxing movements and loads, and muscle contraction patterns that conform with experimental observations were reported.

The highest bruxing forces were measured for the shallower set of molar simulations. This is a reasonable observation since a shallower facet leads to bruxing forces that are more parallel to the force vectors of the closing muscles and hence these strong muscles can be highly activated. Nishigawa et al. (2001) used an instrumented splint to measure bruxing force during sleep bruxism at the first molar position [32]. Their reported value of 200 ± 127 N agrees well with the range of 250–320 N computed for our shallow molar simulations. The achievable bruxing force seems to be strongly dependent on facet inclination, while similar inclinations produced comparable bruxing forces for both positions. In our case, bruxing force describes the force created in the normal direction of the facets and hence with steeper facets the overall force vector points more outwards instead of upwards, leading to a shift in muscle recruitment away from pure activation of closing muscles to include additional auxiliary muscle activation to achieve a more lateral bruxing force. Therefore, reduced bruxing force magnitudes are an expected consequence.

To predict muscle forces, our optimization procedure includes goals for jaw movement and tooth contact force and uses a minimum energy assumption [33] to resolve the force sharing problem among agonist muscles. Given the multitude of mandibular muscles in the small area it is hard to validate the muscle activation patterns predicted by the model with experimental data in detail. Nevertheless, the patterns observed are largely consistent with available published muscle data. According to Miller (1991) a laterotrusive movement is governed by activation of contralateral masseter, temporalis and lateral pterygoid muscle activation, combined with ipsilateral masseter, temporalis and digastric muscle activation [34]. Our results generally agree with these observations, except for the digastric muscle. However, digastric muscle activation is commonly measured using a single submental EMG measurement, which cannot adequately differentiate between different submental muscles. Therefore, our observation of mylohyoid muscle activation is consistent with these submental recordings [35]. In addition, submental muscle activation could be associated with floor-of-mouth stiffening and tongue bracing during sleep recordings [36]. A previous EMG study with changes in steepness of lateral canine tooth-guidance reports results comparable to our set of steep canine simulations [6]. They state a decrease of ipsilateral anterior and posterior temporalis activation with increasing steepness, which agrees with our reported results. While we did not observe a lot of anterior compartment activation, we do see a clear inclination dependent decrease of medial temporalis activation. Huang et al. only separated the temporal muscle into an anterior and posterior part, possibly explaining this slight discrepancy. A decrease in masseter activation with increased steepness was reported, which can be seen in our set of steeper simulations at both locations. Furthermore, they report an increase of contralateral activation of the inferior head of the contralateral lateral pterygoid muscle for steeper inclinations. While the inferior head of the contralateral lateral pterygoid muscle is strongly activated in all steep simulations a clear increase cannot be seen. The contralateral medial pterygoid was not strongly recruited in any simulation, despite its medial angulation. Overall, it seems that facet inclination has a greater influence on the muscle activation pattern than tooth contact position (molar vs. canine). Moreover, we see an increase in activation of the inferior head of the contralateral lateral pterygoid with increasing steepness. A trend of decreasing closing muscle activation with increasing steepness (contralateral superficial masseter, medial compartment of temporal muscle) can be observed and might be the reason for decreased joint loads for steeper simulations, in a similar fashion to the decreasing maximum bruxing force.

Additionally, Huang et al. 2006 included mid-incisor traces for lateral grinding under normal tooth conditions as well as an increased grinding facet inclination [6]. They reported that an increased facet inclination led to a decreased amount of lateral movement, increased amount of mouth opening, and decreased amount of protrusion of the mid incisor motion. All these observations agree with our computed mid incisor traces.

Our investigation suggests a higher mechanical load on the contralateral disc, especially for shallower simulation cases. The increased loading might be associated with the missing tooth support on the contralateral side during the laterotrusive bruxing movement. Generally, the intermediate zone of both discs is loaded the most. For the ipsilateral disc, the area of highest stresses is located close to the lateral pole for all inclinations as well as facet positions. For the contralateral side, the stress is again highest in the intermediate zone but more spread through the zone. The high loading of the lateral pole is of special interest, since literature often reports it to be the main zone for disc degeneration [17], [37], [38], [39], [40]. Bruxing on the canine seems to lead to higher disc stress compared to molar bruxing using the same inclination. This could be caused by the longer distance between the facet and the TMJ, resulting in a longer moment arm. On the ipsilateral disc even steep canine simulations seem to produce increased disc stress compared to all molar cases.

Since high TMJ loading is often associated with the development of TMD [2], the findings of this study have potential clinical implications. According to our results a strong protective effect on the TMJ can be seen for steep inclinations of the wear facet and a smaller effect for wear facet positions closer to the TMJ. While in theory this would suggest a steep molar guidance to be the most beneficial set-up to reduce TMJ loading, tooth steepness cannot be chosen arbitrarily. For example, during mastication molars are used to break down food using high forces and a grinding motion. Consequently, very steep surfaces would be detrimental for proper masticatory motion and force application [41]. Since steepness seems to have a larger effect on loading than position, our results suggest that canine guidance could be the preferred lateral guidance when designing splints or prosthodontic restorations. The investigation of the effect of lateral guidance on TMJ status would be an interesting topic for a future clinical investigation.

Our in silico approach does involve assumptions and limitations that are worth noting: 1) the model is designed from the morphology of a single subject; 2) there exists substantial uncertainty regarding the mechanical properties for articular, disc and muscle tissue represented in the model, and 3) the optimization procedure for predicting muscle patterns includes assumptions regarding how muscle force is shared among agonist muscles. More specifically, our simulations mimic bruxing on a single tooth which neglects the complex nature of tooth abrasion. Consequently, a next step should be to simulate group bruxing involving multiple teeth. Moreover, an interesting future step would be to investigate tooth contact on the mediotrusive side instead of the laterotrusive. Another limitation of the simulations is that we prescribe motion, which was not directly measured. This is an inherent limitation of our approach since we change wear facet inclination and position independently by keeping the rest of the system the same. To measure kinematic data, one would have to mechanically change the occlusal surfaces of a volunteer to capture the kinematics, which is not feasible with keeping the vertical dimension from a patient-safety perspective. We tried to diminish the effect of the prescribed kinematics by using a tracking approach that includes the motion as an optimization goal and hence allows the simulations to deviate slightly from the prescribed motion, while minimizing the overall error of all goals associated with the bruxing task. Hence, small deviations of the mandibular movement are possible if they lead to a “better” (e.g., smoother) muscle activation pattern. Moreover, the amount of lateral excursion was made consistent across all conditions and was chosen to lie in the range of measured excursions [31]. The current model does not include a full representation of the articular capsule and hence rather large mandibular distractions are possible. To prevent this a second movement target at the condyle was added that only allows for small condylar distractions. Our computed muscle activation patterns, mid-incisor traces as well as bruxing forces agree well with previous literature [6], [32], [34], which helps to corroborate our simulation results. Lastly, while current in silico models are a valuable tool for the comparative investigation of soft tissue stresses, the computed values should be interpreted carefully. Because measurements of in vivo tissue stiffnesses cannot currently be made, and the patient-specific nature of the approach infers a rather large amount of anatomical variation, one should not use the presented values as thresholds [42]. Rather, the presented study should be considered a comparative investigation of TMJ loading relative to bruxing position as well as wear facet inclination. The presented information still is of high relevance and could lead to better informed clinical decision making in the future.

Conclusion

In conclusion, the presented work used an innovative in silico approach to isolate the effect of wear facet inclination and position on muscle activation patterns and TMJ loading; an investigation not feasible for in vivo studies. The examination suggests that increased inclination leads to a decreased loading of the TMJ, especially on the contralateral side. While wear facet position plays a smaller role on bruxing force, canine bruxing simulations did compute higher loading of the TMJ compared to molar simulations with the same inclination. These results suggest an effect of the tooth morphology on TMJ loading and motivate future investigations into the connection between tooth shape and mandibular biomechanics.

Compliance with Ethics Requirements

All procedures followed were in accordance with the ethical standards of the responsible committee on human experimentation (institutional and national) and with the Helsinki Declaration of 1975, as revised in 2008 (5). Informed consent was obtained from all patients for being included in the study.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.