Moving beyond the conventional stratified analysis to estimate an overall treatment efficacy with the data from a comparative randomized clinical study

Abstract

For a two-group comparative study, a stratified inference procedure is routinely used to estimate an overall group contrast to increase the precision of the simple two-sample estimator. Unfortunately, most commonly used methods including the Cochran-Mantel-Haenszel statistic for a binary outcome and the stratified Cox procedure for the event time endpoint do not serve this purpose well. In fact, these procedures may be worse than their two-sample counterparts even when the observed treatment allocations are imbalanced across strata. Various procedures beyond the conventional stratified methods have been proposed to increase the precision of estimation when the naive estimator is consistent. In this paper, we are interested in the case when the treatment allocation proportions vary markedly across strata. We study the stochastic properties of the two-sample naive estimator conditional on the ancillary statistics, the observed treatment allocation proportions and/or the stratum sizes, and present a biased-adjusted estimator. This adjusted estimator is asymptotically equivalent to the augmentation estimators proposed under the unconditional setting. Moreover, this consistent estimation procedure is also equivalent to a rather simple procedure, which estimates the mean response of each treatment group first via a stratum-size weighted average and then constructs the group contrast estimate. This simple procedure is flexible and readily applicable to any target patient population by choosing appropriate stratum weights. All the proposals are illustrated with the data from a cardiovascular clinical trial, whose treatment allocations are imbalanced.

1 |. INTRODUCTION

In a comparative randomized study, suppose that we are interested in estimating an overall group difference, ie, θ, between a treatment and a control via their individual population parameters, ie, τ₂ and τ₁, respectively. For example, τ is the mean value of the study subject’s outcome variable and θ = τ₂ – τ₁. Assume that the study utilizes a M : 1 random treatment allocation rule for assigning patients to the treatment and control groups. Although the primary analysis of the study is generally based on a two-sample empirical counterpart $\widehat{\theta }$ of $\theta$, a stratified inference procedure is often utilized to increase the estimation precision for $\widehat{\theta }$.^1,2 Moreover, when the observed allocation proportions of patients assigned to either arm vary substantially across strata, a stratified estimator ${\widehat{\theta }}_S$ has been generally perceived as less biased than $\widehat{\theta }$.

Unfortunately, a number of routinely used stratified procedures cannot be guaranteed to either increase the precision or reduce the bias for estimating θ, especially when θ is nonlinearly related to τ₁ and τ₂. As an example, consider a simple case where the outcome is a binary variable and θ is the odds ratio (OR) of the event rates ${\tau }^{\prime }s$, that is,

$$\theta =\frac{{\tau }_2/\left(1-{\tau }_2\right)}{{\tau }_1/\left(1-{\tau }_1\right)}.$$

The two-sample empirical counterpart is

$$\widehat{\theta }=\frac{{\widehat{\tau }}_2/\left(1-{\widehat{\tau }}_2\right)}{{\widehat{\tau }}_1/\left(1-{\widehat{\tau }}_1\right)},$$

where ${\widehat{\tau }}_j$ is the observed empirical counterpart of τ_j, j = 1, 2. For a large randomized study, $\widehat{\theta }$ is consistent for θ. Now, suppose that one considers a stratified inference procedure with K strata to estimate θ. Let the observed stratum sizes be n₁, n₂, …, n_K and $n={\Sigma }_{k=1}^K{n}_k$. For the jth group in the kth stratum, let the group size be n_jk, the true event rate be ${\tau }_{jk},{\widehat{\pi }}_k=n_{2k}/n_k$ and ${\widehat{w}}_k=n_k/n,j=1,2;k=1,\dots ,K$. A commonly used stratified estimate for θ is based on the Cochran-Mantel-Haenszel (CMH) statistics,³ which results in

$${\widehat{\theta }}_S=\frac{{\sum }_{k=1}^K{\widehat{\tau }}_{2k}\left(1-{\widehat{\tau }}_{1k}\right){\widehat{\pi }}_k\left(1-{\widehat{\pi }}_k\right){\widehat{w}}_k}{{\sum }_{k=1}^K\left(1-{\widehat{\tau }}_{2k}\right){\widehat{\tau }}_{1k}{\widehat{\pi }}_k\left(1-{\widehat{\pi }}_k\right){\widehat{w}}_k},$$

where ${\widehat{\tau }}_{jk}$ is the observed empirical counterpart of τ_jk Note that, even when n_k → ∞ and ${\widehat{\pi }}_k\to M/(M+1),k=1,\dots ,K$, ${\widehat{\theta }}_S$ converges to

$${\theta }_S=\frac{{\Sigma }_{k=1}^K{\tau }_{2k}\left(1-{\tau }_{1k}\right)w_k}{{\Sigma }_{k=1}^K\left(1-{\tau }_{2k}\right){\tau }_{1k}{w}_k},$$

where w_k, the limit of ${\widehat{w}}_k$, is the mixing proportion of the kth stratum in the study population. In general, θ_S ≠ θ, and therefore, ${\widehat{\theta }}_S$ is an inconsistent estimator. Moreover, θ_S is not a simple weighted average of the stratum-specific OR’s as usually interpreted by the practitioners. Here, the kth weight is proportional to (1 − τ_2k)τ_1kw_k, a rather complex form of the underlying stratum-specific event rates.

In survival analysis, a stratified inference procedure, which is routinely used for comparing two groups, is to estimate the hazard ratio (HR) θ under a two-sample proportional hazards model.⁴ Here, the outcome variable is the time to a specific event. The corresponding stratified method is the stratified Cox procedure,^4,5 which suffers from the same limitation of the CMH method for the binary outcome. More details will be given in Section 4 of this paper.

Alternatives to the aforementioned conventional stratified procedures have been studied extensively when the simple estimator $\widehat{\theta }$ is consistent. For this case, the goal is mainly to increase the estimation precision of $\widehat{\theta }$ with the baseline covariate information.^6–10 The performance of such alternative estimation procedures are assessed under an “unconditional” setting by considering all possible realizations of the estimator generated from the random sampling in the study. Now, suppose that (i) ${\widehat{\pi }}_k^{\prime }\text{s}$, the observed proportions of study patients assigned to the treatment group, vary substantially across strata, and/or (ii) ${\widehat{w}}_k^{\prime }\text{s}$, the observed proportions of the patients in each stratum, are substantially different from the underlying $w_k^{\prime }\text{s}$. Then, generally, for the case with a practical sample size, the observed naive estimate $\widehat{\theta }$ would not be close to θ. It is not clear, however, how to empirically quantify the bias of $\widehat{\theta }$. One possible approach to handle this problem would be based on a conditional inference principle via ancillary statistics for the treatment difference θ.¹¹ For the present case, both the empirical proportions of patients assigned to the treatment $\left\{{\widehat{\pi }}_k,k=1,\dots ,K\right\}$ and the empirical proportions of the strata $\left\{{\widehat{w}}_k,k=1,\dots ,K\right\}$ are ancillary statistics. The distribution of ($\widehat{\theta }$ – θ) conditional on such ancillary statistics would be more “relevant” and informative than its unconditional counterpart to study the stochastic behavior of $\widehat{\theta }$.^12,13 Specifically, we consider realizations of $\widehat{\theta }$ generated from the random sampling in the study, but $\left\{\left({\widehat{\pi }}_k,{\widehat{w}}_k\right),k=1,\dots ,K\right\}$ of each realized sample would be the same as its observed counterparts. By doing so, the individual realizations in the aforementioned conditional sample space are obtained under the experimental condition similar to the observed one. In this paper, using this procedure, one can empirically quantify the bias of $\widehat{\theta }$ and then obtain a consistent estimator for θ by modifying $\widehat{\theta }$. It is interesting to note that the aforementioned modified estimator is identical or asymptotically equivalent to the augmentation estimators proposed by Zhang et al,⁶ Wei and Zhang,¹⁴ Tsiatis et al,¹⁵ and Tian et al¹⁰ under the unconditional setting. Moreover, the aforementioned modified estimator is also equivalent to a rather simple estimator obtained via a mixture estimation procedure across strata. Specifically, for the aforementioned example for θ being the OR, we first estimate the overall event rate for the control arm using a weighted average of stratum-specific event rate estimates, where the weight for the kth stratum-specific estimate is w_k, the target proportion of patients from the kth stratum. Similarly, we estimate the overall event rate for the treated arm. Then, we construct the OR estimate with these two overall event rate estimates. The details are given in Sections 2 and 3. In Section 4, we apply the proposal to the case with the censored event time observations. All the procedures are illustrated with the data from a comparative randomized cardiovascular clinical trial.

2 |. MODIFYING THE NAIVE ESTIMATOR $\widehat{\theta }$ IN THE PRESENCE OF TREATMENT ALLOCATION IMBALANCE

Using the notations in the introduction for the general case, that is, let τ_j and ${\widehat{\tau }}_j$ be the population mean and its empirical counterpart of the subject’s outcome variable for the jth group, respectively, and let τ_jk and ${\widehat{\tau }}_{jk}$ be the corresponding quantities in the kth stratum, k = 1, … , K;j = 1, 2. Let θ = g(τ₁, τ₂) and $\widehat{\theta }=g\left({\widehat{\tau }}_1,{\widehat{\tau }}_2\right)$, where g(·, ·) is a given smooth function. For example, g(τ₁, τ₂) = τ₁ – τ₂, if we are interested in the mean difference, and log(τ₁/τ₂), if we are interested in the log ratio of two means. With a random assignment allocation rule and the random sampling assumption of subjects in each group and stratum, for large n_k, k = 1, … , K, it is straightforward to show that the joint distribution of $(\widehat{\theta }-\theta )$ and ${\left({\widehat{w}}_1-w_1,\dots ,{\widehat{w}}_K-w_K,{\widehat{\pi }}_1-\stackrel{-}{\pi },\dots ,{\widehat{\pi }}_K-\stackrel{-}{\pi }\right)}^{\prime }\text{s}$ approximately normal with mean 0 and covariance matrix $\widehat{\Sigma }$ given in the Appendix A, where $\stackrel{-}{\pi }={\Sigma }_{k=1}^K{\widehat{w}}_k{\widehat{\pi }}_k$. Heuristically, it follows that the conditional distribution of

$$(\widehat{\theta }-\theta )\mid \left\{\left({\widehat{w}}_k-w_k,{\widehat{\pi }}_k-\stackrel{-}{\pi }\right),k=1,\dots ,K\right\}$$

is approximately normal with a mean of

$${\widehat{b}}_{\pi w}={\dot{g}}_1\left({\tau }_1^{†},{\tau }_2^{†}\right)\underset{k=1}{\overset{K}{{{\displaystyle \sum }}^{\text{}}}}{\widehat{\tau }}_{1k}\left(\frac{{\widehat{w}}_k\left(1-{\widehat{\pi }}_k\right)}{1-\stackrel{-}{\pi }}-w_k\right)+{\dot{g}}_2\left({\tau }_1^{†},{\tau }_2^{†}\right)\underset{k=1}{\overset{K}{{{\displaystyle \sum }}^{\text{}}}}{\widehat{\tau }}_{2k}\left(\frac{{\widehat{w}}_k{\widehat{\pi }}_k}{\stackrel{-}{\pi }}-w_k\right)$$

and a variance of

$${\widehat{\sigma }}_{\pi w}^2=\underset{k=1}{\overset{K}{{{\displaystyle \sum }}^{\text{}}}}\left\{{\dot{g}}_2{\left({\tau }_1^{†},{\tau }_2^{†}\right)}^2{w}_k^2{\widehat{\sigma }}_{2k}^2+{\dot{g}}_1{\left({\tau }_1^{†},{\tau }_2^{†}\right)}^2{w}_k^2{\widehat{\sigma }}_{1k}^2\right\},$$ (1)

where

$${\tau }_j^{†}=\underset{k=1}{\overset{K}{{{\displaystyle \sum }}^{\text{}}}}{w}_k{\widehat{\tau }}_{jk},j=1,2,$$

${\dot{g}}_j\left({\tau }_1,{\tau }_2\right)$ is the partial derivative of g(τ₁,τ₂) with respect to τ_j and ${\widehat{\sigma }}_{jk}^2$ is a consistent estimator for the variance of ${\widehat{\tau }}_{jk},j=1,2$. Note that the aforementioned large sample normal approximation is not straightforward. The theoretical justification of this approximation to the conditional distribution is given in Appendix A. The aforementioned conditional distribution shows that $\widehat{\theta }$ is in general not root n consistent for θ, when there are treatment allocation imbalances within individual strata or ${\widehat{w}}_k^{\prime }\text{s}$ are different from $w_k^{\prime }\text{s}$. An obvious consistent estimator for θ by directly adjusting $\widehat{\theta }$ is

$${\widehat{\theta }}_{\pi w}=\widehat{\theta }-{\widehat{b}}_{\pi w}.$$

Note that ${\widehat{\theta }}_{\pi w}$ is a sum of $\widehat{\theta }$ and a linear combination of $({\widehat{w}}_k-w_k)$ and $({\widehat{\pi }}_k-\stackrel{-}{\pi })$ , k = 1, …, K and is asymptotically equivalent to the augmentation estimators proposed and discussed in Zhang et al,⁶ Moor and van der Laan,⁸ and Tian et al.¹⁰ Note also that the augmentation procedures in the literature do not have ${\widehat{w}}_k-w_k$, k = 1, … , K, as one of the augmented terms. On the other hand, from the semiparametric efficiency argument, it is a trivial extension to do so, when w_k, k = 1, … , K are known. Note that one of the fundamental principles for conducting a randomized clinical trial is to define and characterize the study population in which the treatment effect is to be estimated. For the present case, this means the mixture proportions w_ks should be prespecified in the study protocol. As a result, unconditionally, ${\widehat{\theta }}_{\pi w}$ minimizes the asymptotic variance of the sum of $\widehat{\theta }$ and any linear combination of {$({\widehat{w}}_k-w_k)$, $({\widehat{\pi }}_k-\stackrel{-}{\pi })$, k = 1, … , K}. However, all the augmented estimators were developed to improve efficiency over the naive estimator $\widehat{\theta }$, under an unconditional setting for which the naive estimator $\widehat{\theta }$ is consistent.

When w_k for the study population is unknown, one may consider an adjusted estimator ${\widehat{\theta }}_{\pi }$ based on the conditional distribution of $\widehat{\theta }-\theta$ given $\left\{{\widehat{\pi }}_k-\stackrel{-}{\pi },k=1,\dots ,K\right\}$ only. Specifically, ${\widehat{\theta }}_{\pi }=\widehat{\theta }-{\widehat{b}}_{\pi }$, where

$${\widehat{b}}_{\pi }={\dot{g}}_1\left({\tau }_{1\pi }^{†},{\tau }_{2\pi }^{†}\right)\underset{k=1}{\overset{K}{{{\displaystyle \sum }}^{\text{}}}}{\widehat{w}}_k{\widehat{\tau }}_{1k}\left(\frac{1-{\widehat{\pi }}_k}{1-\stackrel{-}{\pi }}-1\right)+{\dot{g}}_2\left({\tau }_{1\pi }^{†},{\tau }_{2\pi }^{†}\right)\underset{k=1}{\overset{K}{{{\displaystyle \sum }}^{\text{}}}}{\widehat{w}}_k{\widehat{\tau }}_{2k}\left(\frac{{\widehat{\pi }}_k}{\stackrel{-}{\pi }}-1\right).$$

The variance of ${\widehat{\theta }}_{\pi }$ can be estimated consistently by

$${\widehat{\sigma }}_{\pi }^2={\widehat{\sigma }}_{\pi w}^2+n^{-1}\underset{k=1}{\overset{K}{{{\displaystyle \sum }}^{\text{}}}}{\widehat{w}}_k{\left\{{\dot{g}}_2\left({\tau }_{1\pi }^{†},{\tau }_{2\pi }^{†}\right)\left({\widehat{\tau }}_{2k}-{\widehat{\tau }}_2\right)+{\dot{g}}_1\left({\tau }_{1\pi }^{†},{\tau }_{2\pi }^{†}\right)\left({\widehat{\tau }}_{1k}-{\widehat{\tau }}_1\right)\right\}}^2,$$ (2)

where

$${\tau }_{j\pi }^{†}=\underset{k=1}{\overset{K}{{{\displaystyle \sum }}^{\text{}}}}{\widehat{w}}_k{\widehat{\tau }}_{jk}.$$

It is interesting to note that ${\widehat{\sigma }}_{\pi }^2$ is greater than ${\widehat{\sigma }}_{\pi w}^2$ due to the sampling variation from $\left\{{\widehat{w}}_k,k=1,\dots ,K\right\}$. This adjusted estimator would not be unbiased under the conditional setting with the additional conditioning event, {$\left({\widehat{w}}_k-w_k\right),k=1,\mathrm{...},K$}. It is important to note that there is no general rule on the choice of ancillary statistics. This topic has been discussed extensively in the literature. In practice, the choice of the ancillary statistics would be made on a case-by-case basis. For our present case, the choice of the ancillary statistics, ie, $\left\{{\widehat{\pi }}_k\right\}$ and $\left\{{\widehat{w}}_k\right\}$, was similar to those in the conditional inference for analyzing multiple 2 × 2 tables.¹⁶ The choice of the ancillary statistic $\left\{{\widehat{\pi }}_k\right\}$ only was also discussed by Senn¹² and Pocock et al.¹³

As an example, consider the data from a cardiovascular trial “Valsartan in acute myocardial infarction (VALIANT) study”¹⁷ to illustrate the aforementioned estimation procedures. There were three arms in this study, the patients in the first group were treated by ARB valsartan, the second group was with ACE inhibitor captopril, and the third one was a combination of these two drugs. For illustration, we consider the time to the first hospitalization or death as the endpoint and compare the monotherapy (combing two treatment groups) with the combo therapy. The study enrolled a total of 14 703 patients, who were equally assigned to three arms. The median follow-up time was 24.7 months after randomization. For the entire study, there is no difference with respect to the endpoint considered here. In Figure 1, we show the Kaplan-Meier curves for this endpoint for two comparators. On the other hand, with the data from 302 patients in Australia, the monotherapy somehow appears to be statistically significantly better than its combo counterpart (see Figure 2). Note that Australia was the only country among 24 countries participated in the VALIANT study, whose patients tend to have better outcomes for the monotherapy than those for the combo therapy.

FIGURE 1.

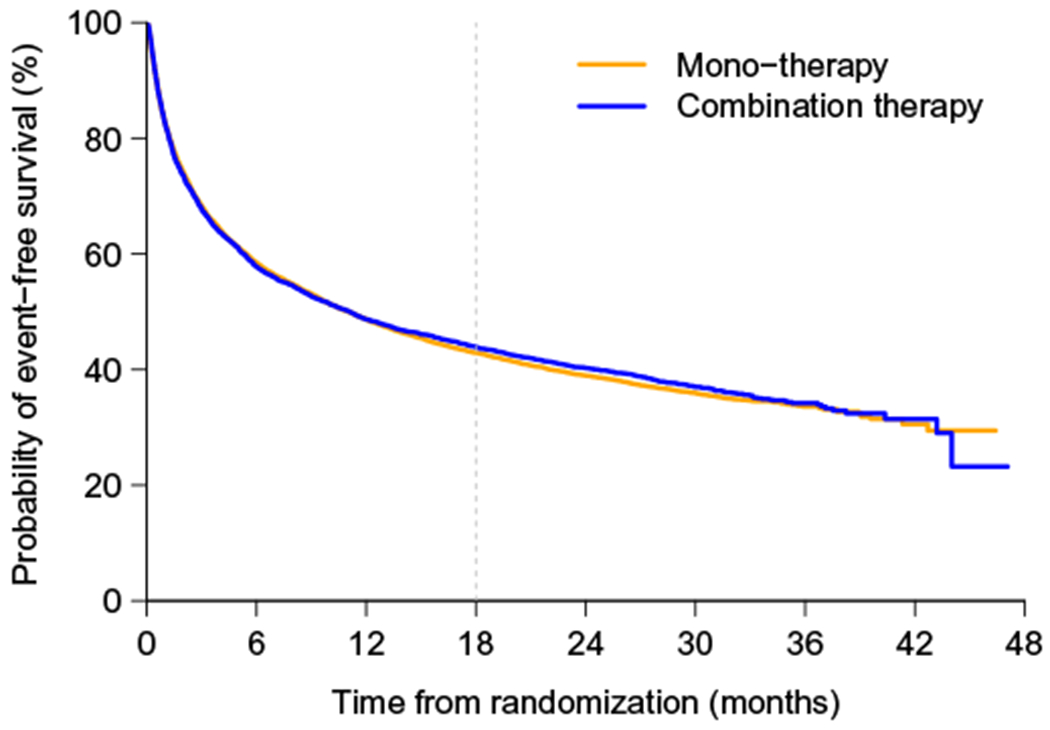
The survival curves for entire VALIANT study by arms: monotherapy and combo therapy arms [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 2.

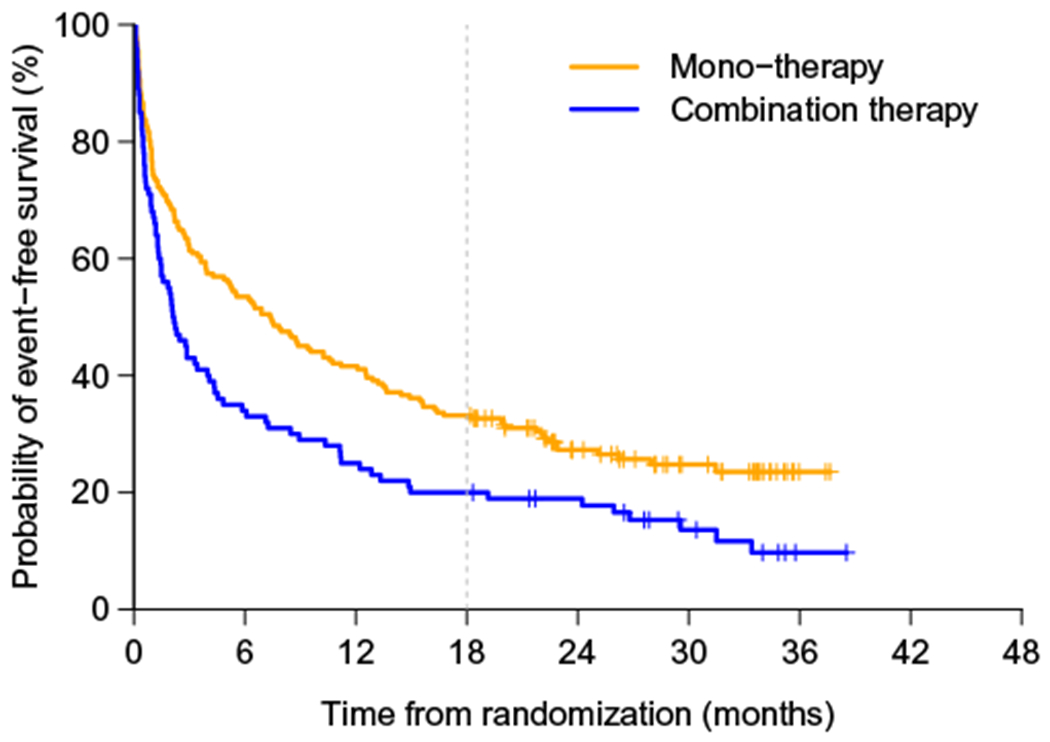
The survival curves for Australian patients in Valsartan in acute myocardial infarction study by arms: monotherapy and combo therapy arms [Colour figure can be viewed at wileyonlinelibrary.com]

We will discuss the case with an event time as the endpoint in Section 4. Here, let us consider the outcome from the aforementioned study to be a binary, either the patient had event by or at month 18. Note that there were no censored observations in the study before month 18. There are two important patient’s covariates, which are related to this binary endpoint, BMI and history of diabetes. For simplicity, we dichotomize BMI with a cutoff value of 25 and create four strata (ie, 1: low BMI and no diabetic history; 2: low BMI and with diabetic history; 3: high BMI and no diabetic history; 4: high BMI and with diabetic history). Table 1 shows the number of 302 Australian patients assigned to each treatment group with respect to the four strata, whose sizes $\left({\widehat{w}}_1,{\widehat{w}}_2,{\widehat{w}}_3,{\widehat{w}}_4\right)=(0.24,0.06,0.54,0.16)$. Note that, if the randomization scheme worked well, the treatment allocation ratio (mono vs combo) would be around 2:1. From Table 1, it seems that there is a nontrivial treatment allocation imbalance with respect to these two factors.

TABLE 1.

Stratified event rate of death or hospitalization up to 18 months in Australia region of Valsartan in acute myocardial infarction Study

Stratification Factors		Australia Data (# of events / # of patients)		${\widehat{\pi }}_k$	OR
BMI	History of Diabetes	Mono-therapy	Combo-therapy
1 < 25	No	43/60	8/13	0.82	0.63
< 25	Yes	9/10	6/8	0.56	0.33
≥ 25	No	65/108	44/54	0.67	2.91
≥ 25	Yes	18/24	22/25	0.49	2.44

Abbreviations: BMI, body mass index; OR, odds ratio.

The naive estimate $\widehat{\theta }$ for the log(OR) of two event rates (combo vs mono) at month 18 is 0.69 with a standard error of 0.29. Therefore, the corresponding estimator of OR is 1.99 with a 95% confidence interval (CI) of (1.12, 3.51) in favor of monotherapy. The corresponding CMH estimate is 1.83 with a 95% CI of (1.03, 3.25). Using the empirical strata weights $\left\{{\widehat{w}}_i\right\}$, the bias adjusted estimate $\exp ({\widehat{\theta }}_{\pi })$ is 1.73 with a 95% CI of (0.96, 3.12) for OR. The CI includes one, suggesting that the group difference is not statistically significant based on the bias adjusted estimator. If we assume that the true mixing proportions for the Australia substudy are identical to the observed proportions in the entire VALIANT study, ie, (w₁, w₂, w₃, w₄) = (0.24, 0.04, 0.53, 0.19), then ${\widehat{\theta }}_{\pi w}$ for OR becomes 1.75 with a slightly different 95% CI of (0.97, 3.13), also indicating an insignificant treatment effect.

3 |. A SIMPLE CONSISTENT STRATIFIED ESTIMATOR FOR θ WITH TWO GROUP-SPECIFIC WEIGHTED AVERAGES OF THE STRATUM MEAN OUTCOMES

Under a stratification setting with K strata, the mean of the outcome τ_j can be rewritten as ${\Sigma }_{k=1}^K{w}_k{\tau }_{jk}$ and can be estimated consistently with ${\tau }_j^{†}={\Sigma }_{k=1}^K{w}_k{\widehat{\tau }}_{jk}$, j = 1, 2. It follows that

$${\widehat{\theta }}_{\text{new}}=g\left({\tau }_1^{†},{\tau }_2^{†}\right)$$

is a consistent estimator unconditionally or conditionally on $\left\{{\widehat{\pi }}_k,k=1,\dots ,K\right\}$ and/or $\left\{{\widehat{w}}_k,k=1,\dots ,K\right\}$. It is interesting to note that this new estimator is asymptotically equivalent to the bias-adjusted estimator ${\widehat{\theta }}_{\pi w}$ conditional on $\left({\widehat{\pi }}_1,\dots ,{\widehat{\pi }}_K\right)$ and $\left({\widehat{w}}_1,\dots ,{\widehat{w}}_K\right)$. This equivalence is due to the fact that

$${\tau }_1^{†}-{\widehat{\tau }}_1=-\underset{k=1}{\overset{K}{{{\displaystyle \sum }}^{\text{}}}}{\widehat{\tau }}_{1k}\left(\frac{{\widehat{w}}_k\left(1-{\widehat{\pi }}_k\right)}{1-\stackrel{-}{\pi }}-w_k\right),$$

$${\tau }_2^{†}-{\widehat{\tau }}_2=-\underset{k=1}{\overset{K}{{{\displaystyle \sum }}^{\text{}}}}{\widehat{\tau }}_{2k}\left(\frac{{\widehat{w}}_k{\widehat{\pi }}_k}{\stackrel{-}{\pi }}-w_k\right),$$

and

$$g\left({\widehat{\tau }}_1,{\widehat{\tau }}_2\right)-g\left({\tau }_1^{†},{\tau }_2^{†}\right)\approx {\dot{g}}_1\left({\tau }_1^{†},{\tau }_2^{†}\right)\left({\widehat{\tau }}_1-{\tau }_1^{†}\right)+{\dot{g}}_2\left({\tau }_1^{†},{\tau }_2^{†}\right)\left({\widehat{\tau }}_2-{\tau }_2^{†}\right)={\widehat{b}}_{\pi w}.$$

Because of this equivalence, the variance of ${\widehat{\theta }}_{\text{new}}$ can be estimated by ${\widehat{\sigma }}_{\pi w}^2$ given in (1). Note also that, when {w_k, k = 1, … , K} is not known, ${\widehat{\theta }}_{\text{new}}$ can be replaced by

$${\widehat{\theta }}_{\text{new}\pi }=g\left({\tau }_{1\pi }^{†},{\tau }_{2\pi }^{†}\right),$$

with ${\tau }_{j\pi }^{†}={\Sigma }_{k=1}^K{\widehat{w}}_k{\widehat{\tau }}_{jk}$, j = 1, 2. For this case, the resulting ${\widehat{\theta }}_{\text{new}\pi }$ is asymptotically equivalent to ${\widehat{\theta }}_{\pi }$ discussed in Section 2. Consequently, the variance of ${\widehat{\theta }}_{\text{new}\pi }$ can be approximated by ${\widehat{\sigma }}_{\pi }^2$ given in (2).

Considering the estimator ${\widehat{\theta }}_{\text{new}\pi }$ with ${\widehat{w}}_k$ as the weights, first, ${\tau }_{j\pi }^{†}$ estimates the mean response of the subjects in arm j by a weighted average with the observed proportion of the stratum size as the weight. One then constructs a group contrast measure with these two resulting treatment group-specific estimators. Note that this estimation procedure for the between-group difference is constructed in a rather different way from the conventional stratified counterparts. For the conventional stratification methods, we first estimate the stratum specific group contrasts and then empirically combine them across strata, whose weights may not have clinical or physical interpretation. Moreover, the conventional stratified methods for the case with a nonlinear g(τ₁, τ₂) may not increase the estimation efficiency and introduce nontrivial bias, as discussed in the previous section. Since ${\widehat{\theta }}_{\text{new}}$ or ${\widehat{\theta }}_{\text{new}\pi }$ is asymptotically equivalent to its augmentation estimation procedure, this estimator is always more efficient than $\widehat{\theta }$ asymptotically.

As an estimator for the marginal mean response, ${\tau }_j^{†}$ not only serves as the building block for adjusting the bias of the naive estimator but also provides important reference level in interpreting the group contrast measure θ. For example, although both $\left({\tau }_1^{†},{\tau }_2^{†}\right)=(0.050,0.095)$ and (0.500, 0.667) yield the same OR of 2.0, they may have quite different implications in practice. The conventional stratified estimator and the estimators ${\widehat{\theta }}_{\pi w}$ and its corresponding equivalent augmented counterparts do not have the benchmark value from the control arm for assisting clinical decision making.

In the VALIANT example, the estimated event rate is ${\tau }_{1\pi }^{†}=0.67$ with a 95% CI of (0.61, 0.74) for monotherapy and ${\tau }_{2\pi }^{†}=0.77$ with a 95% CI of (0.72, 0.83) for combo therapy based on the observed stratum sizes. Note that, if we are interested in a different group contrast measure, for instance, the event rate difference as θ, these values are readily available from this simple new procedure to make inferences.

4 |. APPLICATION TO THE CASE WITH THE EVENT TIME OUTCOME VARIABLE

The most commonly used stratification estimation procedure is based on the stratified Cox model.⁵ Here, the parameter of interest is the overall HR by assuming that the two hazard functions are proportional of each other over the entire study time. As discussed extensively in the statistical and medical literature, the HR estimate is difficult to interpret especially when the proportional hazards (PHs) assumption is violated.^18,19 The stratified Cox procedure follows the same approach as other conventional stratified methods for analyzing noncensored outcomes. That is, for each stratum, we assume that the PH assumption is plausible. We then obtain the HR estimate for each stratum and combine those estimates. The resulting estimator is asymptotically equivalent to linearly combining the log-transformed stratum-specific HR estimators over K strata. The weight of the combination is proportional to the inverse of the variance estimate for the log-transformed stratum-specific HR estimate. However, even when PH assumption holds within each stratum, the PH assumption for entire study population is violated, if the survival distributions are not identical across strata in the control group and two groups have different survival distributions in at least one stratum (see Appendix B). Consequently, the combined HR estimator from the stratified Cox procedure cannot be interpreted as the HR for the entire population. Now, the question is whether we can apply the marginal treatment effect method discussed in Section 3 to deal with the HR. Unfortunately, since the hazard function is not a probability measure, the overall hazard function cannot be expressed as a weighted average of stratum-specific hazard functions. The simple estimation approach discussed in Section 3 cannot be applied to the case using HR as the group contrast.

There are several alternative summary measures to quantify survivorship for each treatment group. For example, one may consider the median survival time. However, it is in general not a weighted average of stratum-specific median failure times either. Two other alternatives are the event rate and restricted survival time at a specific time point.^18,19

For the t-year event rate τ_j, j = 1, 2, we can use the same approach discussed in Section 3. That is, we estimate τ_j by

$${\tau }_j^{†}=\underset{k=1}{\overset{K}{{{\displaystyle \sum }}^{\text{}}}}{w}_k{\widehat{\tau }}_{jk}\hspace{1em}\text{ or }\hspace{1em}{\tau }_{j\pi }^{†}=\underset{k=1}{\overset{K}{{{\displaystyle \sum }}^{\text{}}}}{\widehat{w}}_k{\widehat{\tau }}_{jk},$$

where ${\widehat{\tau }}_{jk}={\widehat{S}}_{jk}(t)$ and ${\widehat{S}}_{jk}(\cdot )$ is the Kaplan-Meier estimator for the survival function of the kth stratum in the jth group. Then, ${\widehat{\theta }}_{\text{new}}=g\left({\tau }_1^{†},{\tau }_2^{†}\right)$ and ${\widehat{\theta }}_{\text{new}\pi }=g\left({\tau }_{1\pi }^{†},{\tau }_{2\pi }^{†}\right)$ are unbiased for estimating θ even when there are markedly observed treatment allocation imbalance.

As an example, we also consider the substudy analysis for Australia in VALIANT study. The estimated event rate (death or hospitalization) at t = 1000 days is 0.88 in the combo therapy group and 0.77 in the monotherapy group. The naive estimate of the OR of two event rates is 2.33 with a 95% CI of [1.39, 3.93], suggesting that the event rate by t = 1000 days for patients receiving monotherapy is significantly lower than that for combo therapy. Recall that there are four strata defined by BMI and diabetic history with the stratum size, ie, $\left({\widehat{w}}_1,{\widehat{w}}_2,{\widehat{w}}_3,{\widehat{w}}_4\right)=(0.24,0.06,0.54,0.16)$. With the aforementioned simple procedure, the adjusted event rate is 0.87 in the combo therapy group and 0.77 in the monotherapy group. The resulting estimator ${\widehat{\theta }}_{\text{new}}$ of the log(OR) is 0.65 (standard error: 0.40). Therefore, the estimated OR is 1.92 (95% CI: 0.88 to 4.22). It is smaller than the unadjusted counterpart of 1.99 and the p-value based on the Wald test using this new log(OR) estimator is 0.103.

The second alternative is the t-year mean survival time (t-MST) up to time point t or coined as the restrictive mean survival time. That is, E{min(T, t)} for survival time T, which is the area under the survival function up to the time point t.^18,19 In contrast to the survival probability at a single time point, the t-MST is proportional to the average survival probability over the entire interval [0, t] and thus a better global summary of the survival profile in a patient population. It also can be interpreted as the life expectancy before time t. The corresponding parameter summarizing the treatment effect is g(τ₁, τ₂), a contrast between t-MSTs from two groups, where τ_j is the t-MST in group j. For instance, g(τ₁, τ₂) can be the ratio of two t-MSTs. The parameter g(τ₁, τ₂) can be estimated by replacing τ_j by the area under the Kaplan-Meier curves in group j. Unlike Cox regression for estimating HR, this estimation procedure for treatment effect based on t-MST does not rely on any strong model assumption such as the PH assumption. Furthermore, as the survival probability, the t-MST is also additive in that the overall t-MST is a weighted average of stratum-specific t-MST and thus a suitable summary of survival distribution in stratified analysis. For the aforementioned VALIANT study, the area under the Kaplan-Meier curves for the monotherapy and combo therapy arms are ${\widehat{\tau }}_1=395$ days and ${\widehat{\tau }}_2=260$ days up to t = 1000 days, respectively. That means, in the future, if we treat the patient with the new treatment up to 1000 days, we expect on average, the patient receiving monotherapy will have 395 event-free days, and 260 event-free days for patients receiving combo therapy. If we let θ be the log-transformed ratio of two t-MSTs at 1000 days, $\text{exp}(\widehat{\theta })=1.52$ with a 95% CI of (1.12, 2.05) and a p-value less than 0.01.

Now, for a stratified analysis with respect to the t-MST measure, we first estimate this parameter with a weighted sum of stratum-specific t-MSTs, that is,

$${\tau }_j^{†}=\underset{k=1}{\overset{K}{{{\displaystyle \sum }}^{\text{}}}}{w}_k{\widehat{\tau }}_{jk}\hspace{1em}\text{ or }\hspace{1em}{\tau }_{j\pi }^{†}=\underset{k=1}{\overset{K}{{{\displaystyle \sum }}^{\text{}}}}{\widehat{w}}_k{\widehat{\tau }}_{jk},$$

where ${\widehat{\tau }}_{jk}={\int }_0^t{\widehat{S}}_{jk}(u)du$. The variance of ${\tau }_j^{†}$ can be estimated by ${\widehat{\sigma }}_j^2={\Sigma }_{k=1}^K{w}_k^2{\widehat{\sigma }}_{jk}^2$, where

$${\widehat{\sigma }}_{jk}^2=n_{jk}^{-1}\underset{0}{\overset{t}{\int }}{\left(\underset{s}{\overset{t}{\int }}{\widehat{S}}_{jk}(u)du\right)}^2\frac{d\left\{-\log ({\widehat{S}}_{jk}(s))\right\}}{{\widehat{S}}_{jk}(s){\widehat{G}}_{jk}(s)}$$

and ${\widehat{G}}_{jk}(\cdot )$ is the Kaplan Meier estimator for survival function of the censoring time in stratum k of group j. Furthermore, the variance of ${\widehat{\theta }}_{\text{new}}=g\left({\tau }_1^{†},{\tau }_2^{†}\right)$ can be estimated by ${\dot{g}}_1{\left({\tau }_1^{+},{\tau }_2^{+}\right)}^2{\widehat{\sigma }}_1^2+{\dot{g}}_2{\left({\tau }_1^{+},{\tau }_2^{+}\right)}^2{\widehat{\sigma }}_2^2$. For the aforementioned numerical example,${\tau }_1^{†}=394$ days and ${\tau }_2^{†}=280$ days based on observed $\left\{{\widehat{w}}_k,k=1,2,3,4\right\}$. The log-ratio of these two, ${\widehat{\theta }}_{\text{new }}=0.34$ (standard error: 0.16). Thus, the estimated ratio is 1.41 with a 95% CI of (1.03, 1.92). Although, statistically, the monotherapy is significantly better than the combo, the CI of the ratio of two t-MSTs is shifted toward the null value of one. Similar analysis can be conducted to estimate the difference in t-MST by letting g(τ₁, τ₂) = τ₁ − τ₂. In this example, the proposed new estimator of the difference is ${\widehat{\theta }}_{\text{new }}=114$ (standard error: 47) days with a 95% CI of (22, 206) days compared with the naive estimator of 135 (95% CI: 46 to 223) days. Note that, if we are willing to assume that the censoring time is independent of stratum, then we also may estimate ${\tau }_j^{†}$ and ${\tau }_{j\pi }^{†}$ based on weighted Kaplan-Meier estimator with observations in the stratum k of group j weighted by w_k/n_jk and ${\widehat{w}}_k/n_{jk}$, respectively.

5 |. NUMERICAL STUDY

In this section, we performed an extensive simulation study to investigate the finite sample performance of the proposed estimators under different settings. In order to mimic realistic settings, we simulated the data based on the VALIANT study. Specifically, we considered four strata with (w₁, w₂, w₃, w₄) = (0.242, 0.045, 0.526, 0.187), the proportions of the aforementioned four strata defined by BMI and diabetic history in the entire VALIANT study. The randomization allocation ratio was 1:2, ie, M = 2. The binary response was a Bernoulli random variable with the incidence rate (τ₁₁, τ₁₂, τ₁₃, τ₁₄) = (0.717, 0.900, 0.602, 0.750) and (τ₂₁, τ₂₂, τ₂₃, τ₂₄) = (0.615, 0.750, 0.815, 0.880) depending on the stratum indexed by 1,2,3, and 4 and treatment arm indexed by 1 and 2. These incidence rates were chosen to be identical to their observed counterparts in Australian data. Under this model, the true marginal incidence rate was 0.671 in arm 1 and 0.776 in arm 2, suggesting a log(OR) of −0.530.

In the first setting, the data were generated conditional on the observed imbalances in Australian data, where $\left({\widehat{w}}_1,{\widehat{w}}_2,{\widehat{w}}_3,{\widehat{w}}_4\right)={(0.241,0.060,0.536,0.162)}^{\prime }$ and $\left({\widehat{\pi }}_1,{\widehat{\pi }}_2,{\widehat{\pi }}_3,{\widehat{\pi }}_4\right)=(0.178,0.444,0.333,0.510)$ with $\stackrel{-}{\pi }=0.331$. For each set of simulated data, we obtained four estimators for log(OR): the naive estimator $\widehat{\theta }$, the bias corrected estimator ${\widehat{\theta }}_{\pi w}$, the stratified ${\widehat{\theta }}_{\text{new}}$, and the CMH estimator ${\widehat{\theta }}_S$. Based on 10 000 simulations, their performance was summarized by empirical bias, standard error, and the coverage probability of two one-sided 97.5% CIs in Table 2. In this setting, the naive estimator was downwardly biased by 0.172, resulting OR estimates 16% lower than the true value. On the other hand, both ${\widehat{\theta }}_{\pi w}$ and ${\widehat{\theta }}_{\mathrm{new}}$ were almost unbiased, suggesting satisfactory bias correction. While CMH estimator aims for a different parameter, it was actually less biased than the naive estimator conditional on this specified randomization allocation ratios across strata. The CMH estimator was also downwardly biased with a bias of −0.089. To interpret the size of biases, we may use the true parameter value as well as the standard error of the naive estimate as references. The bias of the naive estimator was 32% of the true log(OR) and 59% of the standard error. As a result, the coverage probabilities were 99.5% and 93.6% for lower and upper one-sided CIs, respectively. Considering the nominal level of 97.5%, the downward bias of the naive estimator resulted in conservativeness of the lower one-sided CI but sacrificed the coverage level of the upper one-sided CI. On the other hand, the coverage levels of the CIs based on ${\widehat{\theta }}_{\pi w}$ and ${\widehat{\theta }}_{\mathrm{new}}$ were fairly close to the nominal level of 97.5%. The coverage probabilities were 98.7% and 96.4% for lower and upper one-sided CIs based on CMH estimator, respectively, also due to the bias of CMH estimator. To examine the proposed method under more balanced setting, we generated additional data conditional on the observed imbalances in Great Britain data, where n = 723,$\left({\widehat{w}}_1,{\widehat{w}}_2,{\widehat{w}}_3,{\widehat{w}}_4\right)={(0.272,0.035,0.570,0.123)}^{\prime }$ and $\left({\widehat{\pi }}_1,{\widehat{\pi }}_2,{\widehat{\pi }}_3,{\widehat{\pi }}_4\right)={(0.315,0.320,0.320,0.382)}^{\prime }$. It can be seen from Table 2 that, with this relatively balanced allocation, the naive estimator was almost unbiased with a bias being only −0.014, which was negligible, comparing with either the true log(OR) or the standard error of the naive estimator. As a result, the coverage levels of two one-sided 97.5% CIs were close to 97.5%. In this case, both ${\widehat{\theta }}_{\pi w}$ and ${\widehat{\theta }}_{\mathrm{new}}$ were also unbiased with standard errors similar to that of the naive estimator. Therefore, there was no real sacrifice in using the bias corrected estimators when there was no bias. Estimating the bias correction term only slightly increased the standard error of the estimator, approximately 1% in this case. Interestingly, the CMH estimator was also almost unbiased in this case. If the sample size increased, the balance between two arms should be improved and we investigated such a case by generating data conditional on the observed imbalances in USA data, where $n=3894,\left({\widehat{w}}_1,{\widehat{w}}_2,{\widehat{w}}_3,{\widehat{w}}_4\right)={(0.196,0.048,0.511,0.245)}^{\prime }$ , and $\left({\widehat{\pi }}_1,{\widehat{\pi }}_2,{\widehat{\pi }}_3,{\widehat{\pi }}_4\right)={(0.336,0.257,0.330,0.335)}^{\prime }$. The results were also summarized in Table 2. The bias of the naive estimator was −0.052, which indeed is substantially smaller than that conditioning on the imbalances of Australia data and less than 10% of the true log(OR). However, the bias was still big relative to the standard error of the naive estimator, which also decreased with the increasing sample size. As a result, the coverage levels of the two one-sided CIs were 99.7% and 91.1%, away from the nominal level of 97.5%. In this case, the bias correction in either ${\widehat{\theta }}_{\pi w}$ or ${\widehat{\theta }}_{\mathrm{new}}$ was still needed. Therefore, the large sample size does not necessarily solve all the concerns of bias.

TABLE 2.

Conditional inferences for binary outcomes: $\left({\widehat{w}}_1,{\widehat{w}}_2,{\widehat{w}}_3,{\widehat{w}}_4\right)={(0.242,0.059,0.536,0.162)}^{\prime }$ and $\left({\widehat{\pi }}_1,{\widehat{\pi }}_2,{\widehat{\pi }}_3,{\widehat{\pi }}_4\right)={(0.178,0.444,0.333,0.510)}^{\prime }$ in Australia;$\left({\widehat{w}}_1,{\widehat{w}}_2,{\widehat{w}}_3,{\widehat{w}}_4\right)={(0.272,0.035,0.570,0.123)}^{\prime }$ and $\left({\widehat{\pi }}_1,{\widehat{\pi }}_2,{\widehat{\pi }}_3,{\widehat{\pi }}_4\right)={(0.315,0.320,0.320,0.382)}^{\prime }$ in Britain; $\left({\widehat{w}}_1,{\widehat{w}}_2,{\widehat{w}}_3,{\widehat{w}}_4\right)={(0.196,0.048,0.511,0.245)}^{\prime }$ and $\left({\widehat{\pi }}_1,{\widehat{\pi }}_2,{\widehat{\pi }}_3,{\widehat{\pi }}_4\right)={(0.336,0.257,0.330,0.335)}^{\prime }$ in USA. Bias stands for the empirical bias. ESE stands for the empirical standard errors. CP1 and CP2 stand for the empirical coverage levels of upper and lower 97.5% confidence intervals, respectively

Country	n	θ	Bias	ESE	CP1	CP2
Australia	302	$\widehat{\theta }$	−0.172	0.291	0.995	0.936
		${\widehat{\theta }}_{\pi w}$	−0.025	0.307	0.972	0.975
		${\widehat{\theta }}_{\text{new}}$	−0.018	0.308	0.970	0.976
		${\widehat{\theta }}_S$	−0.089	0.294	0.987	0.964
GBR	723	$\widehat{\theta }$	−0.014	0.180	0.978	0.976
		${\widehat{\theta }}_{\pi w}$	−0.005	0.182	0.972	0.975
		${\widehat{\theta }}_{\text{new}}$	−0.005	0.182	0.972	0.975
		${\widehat{\theta }}_S$	0.011	0.178	0.971	0.984
USA	3894	$\widehat{\theta }$	−0.052	0.079	0.997	0.911
		${\widehat{\theta }}_{\pi w}$	−0.001	0.080	0.973	0.975
		${\widehat{\theta }}_{\text{new}}$	0.000	0.080	0.972	0.977
		${\widehat{\theta }}_S$	−0.059	0.079	0.997	0.898

In the second set of simulations, the data were generated unconditionally, ie, the patients were randomly assigned to arm 1 and 2 with probability of π = 1/3 and 1 – π = 2/3, respectively. For each simulated dataset of n = 302, 723, and 3894, we calculated the aforementioned four estimators for log(OR). The randomization ensured that except ${\widehat{\theta }}_S$, all other three estimators should be asymptotically unbiased and the associated conventional inferences were valid. Based on 10 000 simulated datasets, we summarized the performance of these estimators by their empirical bias, standard error, and coverage probability of one-sided 97.5% CIs in Table 3. We also calculated the bias of the naive estimator conditional on the realized treatment allocation at each of the simulated dataset, ie, conditional on $\widehat{\mathbf{w}}$ and $\widehat{\pi }$, using

$$b_{\pi w}=\underset{k=1}{\overset{K}{{{\displaystyle \sum }}^{\text{}}}}\frac{{\tau }_{1k}}{{\tau }_1\left(1-{\tau }_1\right)}\left(\frac{{\widehat{w}}_k\left(1-{\widehat{\pi }}_k\right)}{1-\stackrel{-}{\pi }}-w_k\right)-\underset{k=1}{\overset{K}{{{\displaystyle \sum }}^{\text{}}}}\frac{{\tau }_{2k}}{{\tau }_2\left(1-{\tau }_2\right)}\left(\frac{{\widehat{w}}_k{\widehat{\pi }}_k}{\stackrel{-}{\pi }}-w_k\right).$$

TABLE 3.

Unconditional inferences for binary outcomes:(w₁, w₂, w₃, w₄) = (0.242, 0.045, 0.526, 0.187)′ and π = 1/3. (τ₁₁, τ₁₂, τ₁₃, τ₁₄) = (0.717, 0.900, 0.602, 0.750) and (τ₂₁, τ₂₂, τ₂₃, τ₂₄) = (0.615, 0.750, 0.815, 0.880). Bias stands for the empirical bias. ESE stands for the empirical standard errors. CP1 and CP2 stand for the empirical coverage levels of upper and lower 97.5% confidence intervals, respectively. $\widehat{P}\left(\left|b_{\pi w}\right|>SE/3\right)$ is the empirical probability that the absolute bias is greater than one third of the standard error of the naive estimator

n	θ	Bias	ESE	CP1	CP2	$\widehat{P}\left(\left|b_{\pi w}\right|>SE/3\right)$
302	$\widehat{\theta }$	−0.013	0.289	0.974	0.978	0.108
	${\widehat{\theta }}_{\pi w}$	−0.013	0.286	0.972	0.975
	${\widehat{\theta }}_{\text{new}}$	−0.011	0.286	0.972	0.975
	${\widehat{\theta }}_S$	−0.012	0.286	0.976	0.979
723	$\widehat{\theta }$	−0.008	0.184	0.976	0.976	0.118
	${\widehat{\theta }}_{\pi w}$	−0.008	0.181	0.976	0.976
	${\widehat{\theta }}_{\text{new}}$	−0.008	0.181	0.976	0.976
	${\widehat{\theta }}_S$	−0.005	0.182	0.976	0.978
3894	$\widehat{\theta }$	−0.001	0.079	0.975	0.976	0.119
	${\widehat{\theta }}_{\pi w}$	−0.001	0.077	0.974	0.975
	${\widehat{\theta }}_{\text{new}}$	−0.001	0.077	0.974	0.975
	${\widehat{\theta }}_S$	0.004	0.078	0.973	0.980

We examined the proportion that this absolute bias was greater than 1/3 of the standard error of the naive estimator. There was approximately 11% chance that the conditional bias of the naive estimator exceeded one third of its standard error regardless of the sample size n, which would either inflate the coverage level of the one-sided 97.5% confidence interval to ≥ 98.9% or deflate the level to ≤ 94.8%. This result highlighted the fact that, while the bias adjustment may not be needed for majority of the cases, there was a nontrivial probability that the random imbalances are big enough to negatively affect the validity of statistical inference based on the naive estimator and bias correction was desirable. The slightly smaller standard error of two bias corrected estimators was due to the fact that the correction of conditional bias reduced the unconditional variance of the naive estimator.

We also noted that the CHM stratified estimator was almost unbiased and the empirical coverage levels of the associated 97.5% confidence intervals were acceptable. Indeed, the log-transformed CHM estimator converged to log(θ_S) = −0.524, very close to the marginal log(OR) = −0.530 of our interest. This was not a coincidence: θ_S was in general very similar to the marginal OR. If we considered the case where all the arm-stratum response rates τ_ij were within the interval [0.6, 0.9], then the biggest difference between log(θ_S) and log(OR) is 0.079, when {θ_S, OR} = (0.382, 0.353).

Next, we considered survival time as the primary endpoint, which was generated from log normal distributions, whose parameters were estimated based on Australia data. Specifically, the survival time followed LN(4.96, 2.15²), LN(3.90, 1.77²), LN(5.67, 2.30²), and LN(5.15, 1.76²) at stratum 1, 2, 3, and 4 of arm 1, respectively. Similarly, the survival time followed LN(5.02, 2.62²), LN(4.69, 2.23²), LN(4.48, 1.83²), and LN(4.14, 1.77²) at stratum 1, 2, 3, and 4 of arm 2, respectively. Under this model, the t-MST at t = 1000 days was 336, 156, 455, and 340 days at the four strata of arm 1 and 370, 302, 237, and 185 days at the four strata of arm 2. The marginal t-MST was 391 days at arm 1 and 262 days at arm 2 with a ratio of 1.49, whose log-transformation was the parameter to be estimated. Furthermore, the censoring time was generated uniformly from the interval [540, 1170] days.

As in the binary case, we conducted three sets of simulations conditional on $\widehat{\mathbf{w}}$ and $\widehat{\pi }$ observed in Australia, Great Britain, and USA data, separately. For each simulated dataset, we calculated the naive estimator $\widehat{\theta }$, the bias adjusted estimator ${\widehat{\theta }}_{\pi w}$, and the proposed stratified estimator ${\widehat{\theta }}_{\text{new}}$. In this simulation, we extrapolated the Kaplan Meier curve to t = 1000 days, when the largest survival time in a stratum is censored before 1000 days. The finite sample performance based 10 000 simulated data was summarized by their empirical bias, standard error, and coverage level of two one-sided 97.5% CIs in Table 4. In this setting, the naive estimator was 0.067 away from the true parameter, ie, over-estimated the ratio by approximately 7%. On the other hand, both ${\widehat{\theta }}_{\pi w}$ and ${\widehat{\theta }}_{\text{new}}$ were almost unbiased, suggesting satisfactory bias correction. Furthermore, while the CIs based on the naive estimator were either too conservative or too liberal, those based on ${\widehat{\theta }}_{\pi w}$ and ${\widehat{\theta }}_{\text{new}}$ had appropriate coverage level. For more balanced setting based on the Great Britain data, the naive estimator was almost unbiased. In this case, all three estimators performed similarly well. For the simulation study based on the observed imbalance from the USA data, the bias of the naive estimator was less than 50% of that conditional on the Australia data due to increased sample size. However, it was clear that the bias correction based on either ${\widehat{\theta }}_{\pi w}$ or ${\widehat{\theta }}_{\text{new}}$ was still needed based on the coverage level of one-sided CIs.

TABLE 4.

Conditional inferences for survival outcomes: $\left({\widehat{w}}_1,{\widehat{w}}_2,{\widehat{w}}_3,{\widehat{w}}_4\right)=(0.242,0.059,0.536,0.162)$ and $\left({\widehat{\pi }}_1,{\widehat{\pi }}_2,{\widehat{\pi }}_3,{\widehat{\pi }}_4\right)=(0.178,0.444,0.333,0.510)$ in Australia; $\left({\widehat{w}}_1,{\widehat{w}}_2,{\widehat{w}}_3,{\widehat{w}}_4\right)=(0.272,0.035,0.570,0.123)$ and $\left({\widehat{\pi }}_1,{\widehat{\pi }}_2,{\widehat{\pi }}_3,{\widehat{\pi }}_4\right)=(0.315,0.320,0.320,0.382)$ in Britain; and $\left({\widehat{w}}_1,{\widehat{w}}_2,{\widehat{w}}_3,{\widehat{w}}_4\right)=(0.196,0.048,0.511,0.245)$ and $\left({\widehat{\pi }}_1,{\widehat{\pi }}_2,{\widehat{\pi }}_3,{\widehat{\pi }}_4\right)=(0.336,0.257,0.330,0.335)$ in USA. Bias stands for the empirical bias. ESE stands for the empirical standard errors. CP1 and CP2 stand for the empirical coverage levels of upper and lower 97.5% confidence intervals, respectively

Country	n	θ	Bias	ESE	CP1	CP2
Australia	302	$\widehat{\theta }$	0.067	0.149	0.945	0.990
		${\widehat{\theta }}_{\pi w}$	0.003	0.161	0.967	0.961
		${\widehat{\theta }}_{\text{new}}$	0.006	0.160	0.966	0.962
GBR	723	$\widehat{\theta }$	0.002	0.093	0.980	0.976
		${\widehat{\theta }}_{\pi w}$	0.000	0.093	0.976	0.969
		${\widehat{\theta }}_{\text{new}}$	0.000	0.094	0.977	0.970
USA	3894	$\widehat{\theta }$	0.029	0.041	0.907	0.997
		${\widehat{\theta }}_{\pi w}$	0.000	0.042	0.976	0.974
		${\widehat{\theta }}_{\text{new}}$	−0.000	0.042	0.976	0.976

Finally, we generated survival time unconditionally with the patients being randomly assigned to two arms. The sample sizes used were 302, 723, and 3894. Table 5 showed that the three estimators had similar estimation biases, variances, and coverage probabilities. We also examined the proportion that the absolute bias of the naive estimator was greater than one third of the standard error of the naive estimator. There were approximately 8% chances that the conditional bias of the naive estimator was greater than one third of its standard error. This result also supported the claim that there was oftentimes a need of bias correction due to imperfect randomization.

TABLE 5.

Unconditional inferences for survival outcomes: (w₁, w₂, w₃, w₄) = (0.242, 0.045, 0.526, 0.187) and π = 1/3. Bias stands for the bias. ESE stands for the empirical standard errors. CP1 and CP2 stand for the empirical coverage levels of upper and lower 97.5% confidence intervals, respectively. $\widehat{P}\left(\left|b_{\pi w}\right|>SE/3\right)$ is the empirical probability that the absolute bias is greater than one third of the standard error of the naive estimator

n		Bias	ESE	CP1	CP2	$\widehat{P}\left(\left|b_{\pi w}\right|>SE/3\right)$
302	$\widehat{\theta }$	0.004	0.149	0.976	0.972	0.081
	${\widehat{\theta }}_{\pi w}$	0.003	0.148	0.970	0.965
	${\widehat{\theta }}_{\text{new}}$	0.004	0.148	0.969	0.965
723	$\widehat{\theta }$	0.001	0.097	0.975	0.972	0.081
	${\widehat{\theta }}_{\pi w}$	0.000	0.096	0.974	0.970
	${\widehat{\theta }}_{\text{new}}$	0.000	0.096	0.974	0.970
3894	$\widehat{\theta }$	0.000	0.041	0.978	0.974	0.084
	${\widehat{\theta }}_{\pi w}$	0.000	0.040	0.977	0.975
	${\widehat{\theta }}_{\text{new}}$	0.000	0.040	0.977	0.974

6 |. REMARKS

The conventional stratified analysis, for example, the CMH, has been perceived as an analytic approach to increase the precision of the inference procedure about the between-group-difference in a comparative study. If the between-group-difference θ is quantified with a contrast via the group mean values of the primary study outcome (eg, the odds ratio of a binary endpoint), the parameter or estimand for which the conventional stratified procedure estimates can be quite different from our target parameter θ. This is the first topic we emphasized in this paper. Using the data from a randomized clinical study, the simple naive estimator $\widehat{\theta }$ is asymptotically unbiased “unconditionally.” That is, the sample space of $\widehat{\theta }$ consists of all realizations generated from the random treatment assignment rule utilized in this study. For this case, the two-sample estimator $\widehat{\theta }$ is consistent and the “efficiency augmentation method” with the stratification factors would improve the variance of $\widehat{\theta }$. However, when the treatment assignment rule, by chance, results in a nontrivial imbalance in the number of patients between two comparative groups across strata, it is not clear how to justify that the conventional stratified methods or the aforementioned augmentation procedure would reduce bias. In fact, we did not know how to quantify the potential bias. In this paper, we use a “conditional argument” to quantify the bias of $\widehat{\theta }$ and derive an adjusted estimator ${\widehat{\theta }}_{\pi w}$, which would be closer to θ than $\widehat{\theta }$ stochastically. To our pleasant surprise, this ${\widehat{\theta }}_{\pi w}$ is asymptotically equivalent to an augmented estimator “unconditionally.” This connection further enhances our understanding of the efficiency augmentation procedure via the perspective of conditional bias correction. Moreover, in our paper, we find that ${\widehat{\theta }}_{\pi w}$ is also asymptotically equivalent to a very simple intuitive estimator ${\widehat{\theta }}_{\text{new}}$, which is based on the weighted average of the stratum-specific means, where the weights are the mixture proportions of the strata. The present paper sheds light on the potential utility of stratification procedures when there is an imbalance between two groups in the numbers of patients across strata and proposes a simple intuitively interpretable inference procedure. This proposed that marginal treatment effect approach is rather flexible, which can handle the case when the target patient population is different from the study population. For example, in a cardiovascular clinical study, the majority of study patients is male. The target future population may be evenly divided with respect to gender. Unlike the new proposal, it is difficult to figure out the overall treatment difference for the target population with the conventional stratified analysis.

The choice of the stratification factors is important. If we overly stratify the study, that is, some factors are not related or mildly related to the outcome, the precision of the stratified inference procedure can be worse than the naive two-sample estimate. Therefore, as a general principle, we suggest to select stratification factors having the strongest association with the outcome and maintain reasonable number of patients within each stratum. In practice, it is desirable to automatically select the stratification factors based on the observed data to avoid subjectivity in the analysis. Recently, Tian et al¹⁰ and Bloniarz et al²⁰ generalized the augmentation method originally proposed by Zhang et al⁶ to efficiently select relevant baseline covariates among a set of prespecified candidates under an unconditional setting for adjusting the consistent two-sample estimator. It is not clear how to apply this idea to handle the case when there is a potential imbalance with respect to a large set of stratification factors to avoid overstratification. Further research on appropriate selection of stratification factors is warranted. Lastly, we want to emphasize that theoretical properties of the proposed estimators are derived under the standard assumption that the sample size goes to infinity, whereas the number of strata is fixed.

Abbreviations:

CMH

Cochran-Mantel-Haenszel

OR

odds ratio

VILIANT study

Valsartan in acute myocardial infraction study

HR

hazard ratio

PH

proportional hazards

t-MST

t-year mean survival time

APPENDIX A

ASYMPTOTIC PROPERTIES OF THE NAIVE ESTIMATOR CONDITIONAL ON OBSERVED ALLOCATION IMBALANCES

Firstly, we assume that the observed data consist of n i.i.d observations (Y_i, R_i, X_i), i = 1, … , n, where Y_i is the response; R_i = 1 or 2 is the treatment indicator for group 1 and 2, respectively; and X_i takes values 1, 2, … , K, representing the stratum of the ith subject. Without loss of generality, let $\widehat{\theta }=g\left({\widehat{\tau }}_1,{\widehat{\tau }}_2\right)$, where ${\widehat{\tau }}_j$ is the observed mean response in arm j and ${\widehat{\tau }}_{jk}$ is the observed mean response in arm j of stratum k, j = 1, 2; k = 1, … , K. Our goal is to derive the limiting distribution of

$$n^{1/2}(\widehat{\theta }-\theta ),$$

conditional on

$${\widehat{w}}_k-w_k,{\widehat{\pi }}_k-\stackrel{-}{\pi },k=1,\dots ,K,$$

where $n={\Sigma }_{k=1}^K{n}_k$.

To this end, we first have the expansion

$$\left(\begin{array}{c}\widehat{\theta }-\theta \\ {\widehat{w}}_1-w_1\\ ⋮\\ {\widehat{w}}_K-w_K\\ {\widehat{\pi }}_1-\stackrel{-}{\pi }\\ ⋮\\ {\widehat{\pi }}_K-\stackrel{-}{\pi }\end{array}\right)=n^{-1}\underset{i=1}{\overset{n}{{{\displaystyle \sum }}^{\text{}}}}\left(\begin{array}{c}\frac{{\dot{g}}_2\left({\tau }_1,{\tau }_2\right)I\left(R_i=2\right)\left(Y_i-{\tau }_2\right)}{\pi }+\frac{{\dot{g}}_1\left({\tau }_1,{\tau }_2\right)I\left(R_i=1\right)\left(Y_i-{\tau }_1\right)}{1-\pi }\\ I\left(X_i=1\right)-w_1\\ ⋮\\ I\left(X_i=K\right)-w_K\\ \frac{\left\{I\left(X_i=1\right)-w_1\right\}\left\{I\left(R_i=2\right)-\pi \right\}}{w_1}\\ ⋮\\ \frac{\left\{I\left(X_i=K\right)-w_K\right\}\left\{I\left(R_i=2\right)-\pi \right\}}{w_K}\end{array}\right)+\left(\begin{array}{c}{\xi }_{\theta }\\ 0\\ {\xi }_{\pi }\end{array}\right),$$

where π = pr(R_i = 2) and $\left|{\xi }_{\theta }\right|+\left|{\xi }_{\pi }\right|=o\left(n^{-1/2}\right)$ almost surely. Let

$$U_n=n^{-1/2}\underset{i=1}{\overset{n}{{{\displaystyle \sum }}^{\text{}}}}{U}_i\text{ and }{V}_n=n^{-1/2}\underset{i=1}{\overset{n}{{{\displaystyle \sum }}^{\text{}}}}{V}_i,$$

where

$$U_i=\frac{{\dot{g}}_2\left({\tau }_1,{\tau }_2\right)I\left(R_i=2\right)\left(Y_i-{\tau }_2\right)}{\pi }+\frac{{\dot{g}}_1\left({\tau }_1,{\tau }_2\right)I\left(R_i=1\right)\left(Y_i-{\tau }_1\right)}{1-\pi }$$

and

$$V_i=\left(\begin{array}{c}I\left(X_i=1\right)-w_1\\ ⋮\\ I\left(X_i=K\right)-w_K\\ \frac{\left\{I\left(X_i=1\right)-w_1\right\}\left\{I\left(R_i=2\right)-\pi \right\}}{w_1}\\ ⋮\\ \frac{\left\{I\left(X_i=K\right)-w_K\right\}\left\{I\left(R_i=2\right)-\pi \right\}}{w_K}\end{array}\right).$$

By central limit theorem, ${\left(U_n,V_n^{\prime }\right)}^{\prime }$’ converges weakly to ${\left(U_0,V_0^{\prime }\right)}^{\prime }$, a multivariate normal with mean 0 and a variance-covariance matrix

$$\sum =\left(\begin{array}{ccc}{\sigma }_{\theta }^2& D_{\theta w}^{\prime }& D_{\theta \pi }^{\prime }\\ D_{\theta w}& {\text{Σ}}_{ww}& 0\\ D_{\theta \pi }& 0& {\text{Σ}}_{\pi \pi }\end{array}\right),$$

where

$${\sigma }_{\theta }^2=\frac{{\dot{g}}_2\left({\tau }_1,{\tau }_2\right){\sigma }_{Y2}^2}{\pi }+\frac{{\dot{g}}_1\left({\tau }_1,{\tau }_2\right){\sigma }_{Y1}^2}{1-\pi }$$

$$\begin{array}{c}{\sigma }_{Yj}^2=\mathrm{var}\left(Y_i\mid R_i=j\right),D_{\theta w}={\left(d_{w1},\dots ,d_{wK}\right)}^{\prime },D_{\theta \pi }={\left(d_{\pi 1},\dots ,d_{\pi K}\right)}^{\prime },\\ d_{wk}={\dot{g}}_2\left({\tau }_1,{\tau }_2\right)w_k\left({\tau }_{2k}-{\tau }_2\right)+{\dot{g}}_1\left({\tau }_1,{\tau }_2\right)w_k\left({\tau }_{1k}-{\tau }_1\right),\\ d_{\pi k}={\dot{g}}_2\left({\tau }_1,{\tau }_2\right)(1-\pi )\left({\tau }_{2k}-{\tau }_2\right)-{\dot{g}}_1\left({\tau }_1,{\tau }_2\right)\pi \left({\tau }_{1k}-{\tau }_1\right),\\ {\text{Σ}}_{ww}=\left(\begin{array}{ccc}{w}_1\left(1-w_1\right)& \cdots & -w_1{w}_K\\ \cdots & \cdots & \cdots \\ -w_K{w}_1& \cdots & w_K\left(1-w_K\right)\end{array}\right)\end{array}$$

and

$${\text{Σ}}_{\pi \pi }=\pi (1-\pi )\left(\begin{array}{ccc}\left(1-w_1\right)/w_1& \cdots & -1\\ \cdots & \cdots & \cdots \\ -1& \cdots & \left(1-w_K\right)/w_K\end{array}\right)$$

It follows from the work of Steck,²¹ as n → ∞, U_n|V_n = v converges weakly to a limiting distribution in the sense that for any sequence {v_n} such that v_n ∈ A_n, the range of V_n, and lim_{n → ∞}v_n = v,

$$\underset{u}{\sup }\left|F_n^{v_n}(u)-F^v(u)\right|=o(1),$$

where $F_n^{v_n}(u)$ is the cumulative distribution function of U_n conditional on V_n = v_n and F^v(u) is the cumulative distribution function of U₀ conditional on V₀ = v. Furthermore, since $\left|{\xi }_{\theta }\right|+\left|{\xi }_{\pi }\right|=o\left(n^{-1/2}\right)$ almost surely, for any ${\delta }_n={\left({\delta }_{nw}^{\prime },{\delta }_{n\pi }^{\prime }\right)}^{\prime }\to \delta$,

$$\begin{array}{c}P\left\{n^{1/2}(\widehat{\theta }-\theta )\le u\mid n^{1/2}\left({\widehat{w}}_k-w_k\right)={\delta }_{nw},n^{1/2}\left({\widehat{\pi }}_k-\stackrel{-}{\pi }\right)={\delta }_{n\pi }\right\}\\ =P\left\{U_n\le u-n^{1/2}{\xi }_{\theta }\mid V_n={\left({\delta }_{nw}^{\prime },{\delta }_{n\pi }^{\prime }-n^{1/2}{\xi }_{\pi }^{\prime }\right)}^{\prime }\right\}\\ =F_n^{{\tilde{v}}_n}\left(u-n^{1/2}{\xi }_{\theta }\right)\\ =F^{\delta }\left(u-n^{1/2}{\xi }_{\theta }\right)+o(1)\\ =F^{\delta }(u)+o(1),\end{array}$$

where ${\tilde{v}}_n={\left({\delta }_{nw}^{\prime },{\delta }_{n\pi }^{\prime }-n^{1/2}{\xi }_{\pi }^{\prime }\right)}^{\prime }\to \delta$. Therefore, the conditional distribution $n^{1/2}(\widehat{\theta }-\theta )\mid n^{1/2}\left({\widehat{w}}_k-w_k\right),n^{1/2}\left({\widehat{\pi }}_k-\stackrel{-}{\pi }\right)$ converges to the normal distribution with a mean b_θ and variance ${\sigma }_{\text{adj }}^2$. Next, we will derive the explicit expression for mean b_θ and variance ${\sigma }_{\text{adj}}^2$. We first note that the variance-covariance matrices Σ_ππ and Σ_ww are singular, the conditional distribution U₀|V₀ is the same as that only conditioning on the components corresponding to (w₁, … ,w_K−1, π₁, … , π_K−1)′. Let ${\tilde{D}}_{\theta \pi }{\tilde{D}}_{\theta w},{\tilde{\Sigma }}_{ww}$, and ${\tilde{\Sigma }}_{\pi \pi }$ be the associated covariance vectors and variance matrices

$$\begin{array}{l}\begin{array}{c}{b}_{\theta }=n^{1/2}\left({\widehat{w}}_1-w_1,\dots ,{\widehat{w}}_{K-1}-w_{K-1}\right){\tilde{\Sigma }}_{\theta w}^{-1}{\tilde{D}}_{\theta \pi }+n^{1/2}\left({\widehat{\pi }}_1-\stackrel{-}{\pi },\dots ,{\widehat{\pi }}_{K-1}-\stackrel{-}{\pi }\right){\tilde{\Sigma }}_{\pi \pi }^{-1}{\tilde{D}}_{\theta \pi }\\ =n^{1/2}{\left(\begin{array}{c}{\widehat{w}}_1-w_1\\ ⋮\\ {\widehat{w}}_{K-1}-w_{K-1}\end{array}\right)}^{\prime }\left\{{\dot{g}}_2\left({\tau }_1,{\tau }_2\right)\left(\begin{array}{c}{\tau }_{21}-{\tau }_{2K}\\ ⋮\\ {\tau }_{2(K-1)}-{\tau }_{2K}\end{array}\right)+{\dot{g}}_1\left({\tau }_1,{\tau }_2\right)\left(\begin{array}{c}{\tau }_{11}-{\tau }_{1K}\\ ⋮\\ {\tau }_{1(K-1)}-{\tau }_{1K}\end{array}\right)\right\}+n^{1/2}{\left(\begin{array}{c}{\widehat{\pi }}_1-\stackrel{-}{\pi }\\ ⋮\\ {\widehat{\pi }}_{K-1}-\stackrel{-}{\pi }\end{array}\right)}^{\prime }\left\{\frac{{\dot{g}}_2\left({\tau }_1,{\tau }_2\right)}{\pi }\left(\begin{array}{c}{w}_1\left({\tau }_{21}-{\tau }_{2K}\right)\\ ⋮\\ w_{K-1}\left({\tau }_{2(K-1)}-{\tau }_{2K}\right)\end{array}\right)-\frac{{\dot{g}}_1\left({\tau }_1,{\tau }_2\right)}{1-\pi }\left(\begin{array}{c}{w}_1\left({\tau }_{11}-{\tau }_{1K}\right)\\ ⋮\\ w_{K-1}\left({\tau }_{1(K-1)}-{\tau }_{1K}\right)\end{array}\right)\right\}\\ \end{array}\\ =n^{1/2}\left[{\dot{g}}_2\left({\tau }_1,{\tau }_2\right)\underset{k=1}{\overset{K}{{{\displaystyle \Sigma }}^{\text{}}}}\left\{{\widehat{w}}_k-w_k+\frac{{\widehat{w}}_k\left({\widehat{\pi }}_k-\stackrel{-}{\pi }\right)}{\stackrel{-}{\pi }}\right\}{\tau }_{2k}+{\dot{g}}_1\left({\tau }_1,{\tau }_2\right)\underset{k=1}{\overset{K}{{{\displaystyle \Sigma }}^{\text{}}}}\left\{{\widehat{w}}_k-w_k-\frac{{\widehat{w}}_k\left({\widehat{\pi }}_k-\stackrel{-}{\pi }\right)}{1-\stackrel{-}{\pi }}\right\}{\tau }_{1k}\right]+o_p(1),\end{array}$$

which is asymptotically equivalent to $n^{1/2}\left({\widehat{\theta }}_{\pi w}-\widehat{\theta }\right)$. It is clear that the bias of $\widehat{\theta }$ can then be consistently estimated by ${\widehat{b}}_{\pi w}$.

For the conditional variance, we first have

$${\sigma }_{\pi w}^2={\sigma }_{\theta }^2-{\tilde{D}}_{\theta w}^{\prime }{\tilde{\Sigma }}_{ww}^{-1}{\tilde{D}}_{\theta w}-{\tilde{D}}_{\theta \pi }^{\prime }{\tilde{\Sigma }}_{\pi \pi }^{-1}{\tilde{D}}_{\theta \pi }.$$

Since

$$\begin{array}{c}{\tilde{D}}_{\theta w}^{\prime }{\tilde{\Sigma }}_{ww}^{-1}{\tilde{D}}_{\theta w}={\tilde{D}}_{\theta w}^{\prime }\left\{{\dot{g}}_2\left({\tau }_1,{\tau }_2\right)\left(\begin{array}{c}{\tau }_{21}-{\tau }_{2K}\\ ⋮\\ {\tau }_{2(K-1)}-{\tau }_{2K}\end{array}\right)+{\dot{g}}_1\left({\tau }_1,{\tau }_2\right)\left(\begin{array}{c}{\tau }_{11}-{\tau }_{1K}\\ ⋮\\ {\tau }_{1(K-1)}-{\tau }_{1K}\end{array}\right)\right\}\\ =\underset{k=1}{\overset{K}{{{\displaystyle \Sigma }}^{\text{}}}}{w}_k{\left\{{\dot{g}}_2\left({\tau }_1,{\tau }_2\right)\left({\tau }_{2k}-{\tau }_2\right)+{\dot{g}}_1\left({\tau }_1,{\tau }_2\right)\left({\tau }_{1k}-{\tau }_1\right)\right\}}^2,\end{array}$$

$$\begin{array}{l}{\tilde{D}}_{\theta w}^{\prime }{\tilde{\Sigma }}_{ww}^{-1}{\tilde{D}}_{\theta w}={\tilde{D}}_{\theta w}^{\prime }\left\{\frac{{\dot{g}}_2\left({\tau }_1,{\tau }_2\right)}{\pi }\left(\begin{array}{c}{w}_1\left({\tau }_{21}-{\tau }_{2K}\right)\\ ⋮\\ w_{K-1}\left({\tau }_{2(K-1)}-{\tau }_{2K}\right)\end{array}\right)-\frac{{\dot{g}}_1\left({\tau }_1,{\tau }_2\right)}{1-\pi }\left(\begin{array}{c}{w}_1\left({\tau }_{11}-{\tau }_{1K}\right)\\ ⋮\\ w_{K-1}\left({\tau }_{1(K-1)}-{\tau }_{1K}\right)\end{array}\right)\right\}\\ =\frac{{\dot{g}}_2{\left({\tau }_1,{\tau }_2\right)}^2}{\pi }\underset{k=1}{\overset{K}{{{\displaystyle \Sigma }}^{\text{}}}}{w}_k\left({\tau }_{2k}^2-{\tau }_2^2\right)+\frac{{\dot{g}}_1{\left({\tau }_1,{\tau }_2\right)}^2}{1-\pi }\underset{k=1}{\overset{K}{{{\displaystyle \Sigma }}^{\text{}}}}{w}_k\left({\tau }_{1k}^2-{\tau }_1^2\right)-\underset{k=1}{\overset{K}{{{\displaystyle \Sigma }}^{\text{}}}}{w}_k{\left\{{\dot{g}}_2\left({\tau }_1,{\tau }_2\right)\left({\tau }_{2k}-{\tau }_2\right)+{\dot{g}}_1\left({\tau }_1,{\tau }_2\right)\left({\tau }_{1k}-{\tau }_1\right)\right\}}^2,\end{array}$$

and ${\sigma }_{Yj}^2={\Sigma }_{k=1}^K{w}_k\left({\sigma }_{Yjk}^2+{\tau }_{jk}^2\right)-{\tau }_j^2$, we have

$${\sigma }_{\text{adj}}^2=\frac{{\dot{g}}_2{\left({\tau }_1,{\tau }_2\right)}^2}{\pi }\underset{k=1}{\overset{K}{{{\displaystyle \Sigma }}^{\text{}}}}{w}_k{\sigma }_{Y2k}^2+\frac{{\dot{g}}_1{\left({\tau }_1,{\tau }_2\right)}^2}{1-\pi }\underset{k=1}{\overset{K}{{{\displaystyle \Sigma }}^{\text{}}}}{w}_k{\sigma }_{Y1k}^2,$$

where ${\sigma }_{Yjk}^2=\mathrm{var}(Y_i|R_i=j,X_i=k)$. Furthermore, the conditional variance of $\widehat{\theta }$ − θ can be consistently estimated by ${\widehat{\sigma }}_{\pi w}^2={\Sigma }_{k=1}^K\left\{{\dot{g}}_2{\left({\tau }_1^{†},{\tau }_2^{†}\right)}^2{\widehat{w}}_k^2{\widehat{\sigma }}_{2k}^2+{\dot{g}}_1{\left({\tau }_1^{†},{\tau }_2^{†}\right)}^2{\widehat{w}}_k^2{\widehat{\sigma }}_{1k}^2\right\}$. In the aforementioned derivation, we used the fact that

$${\tilde{\Sigma }}_{ww}\left(\begin{array}{c}{\tau }_{j1}-{\tau }_{jK}\\ ⋮\\ {\tau }_{j(K-1)}-{\tau }_{jK}\end{array}\right)=\left(\begin{array}{c}{w}_1\left({\tau }_{j1}-{\tau }_j\right)\\ ⋮\\ w_{K-1}\left({\tau }_{j(K-1)}-{\tau }_j\right)\end{array}\right)$$

and

$${\tilde{\Sigma }}_{\pi \pi }\left(\begin{array}{c}{w}_1\left({\tau }_{j1}-{\tau }_{jK}\right)\\ ⋮\\ w_{K-1}\left({\tau }_{j(K-1)}-{\tau }_{jK}\right)\end{array}\right)=\pi (1-\pi )\left(\begin{array}{c}{\tau }_{j1}-{\tau }_j\\ ⋮\\ {\tau }_{j(K-1)}-{\tau }_j\end{array}\right),j=1,2.$$

APPENDIX B

INCOMPATIBILITY OF PH ASSUMPTION IN THE ENTIRE STUDY AND WITHIN STRATUM

Assume that the PH assumption holds within each of the K strata. Let S_jk(t) denote the survival function in the kth stratum of arm j,j = 1, 2. Then, we have

$$S_{2k}(t)=S_{1k}{(t)}^{r_0},$$

for k = 1, …, K and a common HR r₀. Furthermore, the marginal survival function for the entire study population is

$$S_j(t)=\underset{k=1}{\overset{K}{{{\displaystyle \Sigma }}^{\text{}}}}{w}_k{S}_{jk}(t),$$

for arm j, where w₁ + ⋯ + w_K = 1, w_k ∈ (0, 1), k = 1, … , K. If the PH assumption holds for the marginal survival function, then S₂(t) = S₁(t)^r for a constant r, ie,

$${\left\{\underset{k=1}{\overset{K}{{{\displaystyle \Sigma }}^{\text{}}}}{w}_k{S}_{1k}(t)\right\}}^r=\underset{k=1}{\overset{K}{{{\displaystyle \Sigma }}^{\text{}}}}{w}_k{S}_{1k}{(t)}^{r_0}.$$

Taking derivative with respect to t for both sides at t = 0, we obtain that

$$r=\frac{r_0\underset{k=1}{\overset{K}{{{\displaystyle \sum }}^{\text{}}}}{w}_k{S}_{1k}{(0)}^{r_0-1}{f}_{1k}(0)}{\underset{k=1}{\overset{K}{{{\displaystyle \sum }}^{\text{}}}}{w}_k{f}_{1k}(0){\left(\underset{k=1}{\overset{K}{{{\displaystyle \sum }}^{\text{}}}}{w}_k{S}_{1k}(0)\right)}^{r-1}}=r_0.$$

Without loss of generality, we assume that r₀ ≥ 1, otherwise we always can switch two groups of interest to ensure that the HR is greater than or equal to 1. Under this assumption,

$$S_2(t)=\underset{k=1}{\overset{K}{\Sigma }}{w}_k{S}_{1k}{(t)}^{r_0}\ge {\left(\underset{k=1}{\overset{K}{\Sigma }}{w}_k{S}_{1k}(t)\right)}^{r_0}=S_1{(t)}^{r_0},$$

for 0 < S_1k(t) < 1 due to the convexity of the function x^r₀. The equality holds only when S₁₁(t) = ⋯ = S_1K(t) or r₀ = 1. Thus, the PH model with a HR of r₀ is not true for the entire study population unless S₁₁(t) = ⋯ = S_1K(t), ie, the survival distributions are the same across strata or r₀ = 1, ie, there is no difference in survivorship in any stratum.