FLINO: a new method for immunofluorescence bioimage normalization

Abstract

Motivation

Multiplexed immunofluorescence bioimaging of single-cells and their spatial organization in tissue holds great promise to the development of future precision diagnostics and therapeutics. Current multiplexing pipelines typically involve multiple rounds of immunofluorescence staining across multiple tissue slides. This introduces experimental batch effects that can hide underlying biological signal. It is important to have robust algorithms that can correct for the batch effects while not introducing biases into the data. Performance of data normalization methods can vary among different assay pipelines. To evaluate differences, it is critical to have a ground truth dataset that is representative of the assay.

Results

A new immunoFLuorescence Image NOrmalization method is presented and evaluated against alternative methods and workflows. Multiround immunofluorescence staining of the same tissue with the nuclear dye DAPI was used to represent virtual slides and a ground truth. DAPI was restained on a given tissue slide producing multiple images of the same underlying structure but undergoing multiple representative tissue handling steps. This ground truth dataset was used to evaluate and compare multiple normalization methods including median, quantile, smooth quantile, median ratio normalization and trimmed mean of the M-values. These methods were applied in both an unbiased grid object and segmented cell object workflow to 24 multiplexed biomarkers. An upper quartile normalization of grid objects in log space was found to obtain almost equivalent performance to directly normalizing segmented cell objects by the middle quantile. The developed grid-based technique was then applied with on-slide controls for evaluation. Using five or fewer controls per slide can introduce biases into the data. Ten or more on-slide controls were able to robustly correct for batch effects.

Availability and implementation

The data underlying this article along with the FLINO R-scripts used to perform the evaluation of image normalizations methods and workflows can be downloaded from https://github.com/GE-Bio/FLINO.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Revealing true biology from experimental error and noise has always been a challenge. It is especially challenging for high content data generated from microarrays (Johnson, 2007; Leek, 2012; Zhang, 2018), RNA-sequencing and more recently, multiplexed immunofluorescence (MxIF) bioimaging, where tissue sections are repeatedly stained and/or imaged, followed by single-cell segmentation and generation of millions of data-points for spatial cell biomarker analysis (Gerdes et al., 2013; Kennedy-Darling et al., 2021). Evolving standards in RNA sequencing now allow robust batch correction and comparison across studies (Anders and Huber, 2010; Birmingham, 2009; Espin-Perez, 2018; Maza, 2016, Evans, 2018; Mortazavi, 2008; Robinson and Oshlack, 2010). Such standards do not yet exist for MxIF bioimaging and the field is quickly evolving with novel methods being proposed (Andrews and Rutherford, 2016; Chang, 2020; Van Eycke, 2017), but there are limited comparisons of methods (Ahmed Raza, 2016; Caicedo, 2017) and evaluation in context of a biological ground truth.

Generating MxIF bioimages is a complex multiple step process. Experimental variability, can arise from the tissue slide preparation, including initial histological processing and antigen retrieval. Furthermore, multiround immunofluorescence staining and imaging of tissue slides can introduce additional biases including tissue loss, deformation, tissue autofluorescence, nonspecific staining and sample degradation over time due to handling. Preanalytical conditions such as storage temperature, decalcification and time to formalin fixation can result in protein, RNA and DNA degradation (Bass et al., 2014). Depending on sample dimensions, the duration of sample fixation in formalin can lead to under- or over-fixation, which can affect protein integrity and result in reduced sensitivity (Forest, 2019; Magaki, 2019; van Seijen, 2019). Engel and Moore (2011) identified 15 preanalytic variables (fixation delay, fixative type, fixative concentration, pH and buffer, time in fixative, reagents and conditions of dehydration, clearing reagent and temperature, paraffin-embedding temperature and duration, and condition of slide drying and storage) that can impact an immunohistochemistry test. Particularly in the last 10 years, there is an increasing amount of control over these preanalytical factors in the clinical and research setting (Engel et al., 2014), but older samples (>10–20 years), important where long-term outcome of patients is desirable, may have been processed under more variable conditions, as well as undergoing aging and oxidation over time.

Typically tissue analysis is conducted as single sections on slides, or multiple patient cores (∼50 to 250) spread across one or more tissue microarrays. To avoid signal bias, an ideal study design includes random distribution of patient samples in batches (if working with a large number of single sections), or randomly distributed patient cores across multiple slides. Control tissue sections or cell lines are also highly desirable to ensure technical robustness and potentially improve quantitation but are often not used. Methods have been developed that attempt to identify negative control cells from within a sample for each marker and use their intensity levels to determine the background signal to be used to remove intraimage variation (Chang et al., 2020).

One requirement when comparing normalization methods and workflows is the need for a ground truth dataset. One approach is to generate and use simulated data images with a known ground truth to judge and compare methods and workflows (Svoboda, 2009; Ulman, 2016; Watabe, 2015; Wiesmann, 2013, 2017; Wiesner, 2019). A drawback of the simulated data approaches is the reliance on a theoretical error model. Selecting an error model that represents the batch and processing errors of the sample preparation and bioimaging pipeline is not trivial. Some experimental errors are systematic while others are random. Therefore, one must select and tune a theoretical error model to properly model both systematic and random error contributions observed in the actual assay.

A multiyear retrospective study on biomarkers of recurrence in stages II and III colorectal cancer using tissue samples from multiple sites provided the impetus to evaluate both historical and new methods of normalization. In previous studies, we have routinely applied a median normalization method to correct MxIF bioimages. The method is robust, fast and simple to implement, but had not previously been benchmarked against other methods. In this article, we performed a benchmarking analysis that compared it with alternative normalization methods and workflows. We first assembled a list of normalization methods from the literature (Bullard, 2010; Hicks, 2018; Maza, 2013; Robinson and Oshlack, 2010; Tarazona, 2011, 2015). Next, we devised an approach that allowed us to test and evaluate each normalization method against the same ground truth for a fair apple-to-apple comparison. Finally, we performed testing of the methods and workflows across different scenarios including 24 biomarkers that were multiplexed across three tissue microarray slides, and including slides with and without control samples. Our findings show the performance of each and suggest the power of a new grid-based object workflow [immunoFLuorescence Image NOrmalization (FLINO)] to reliably normalize MxIF bioimages.

2 Materials and methods

2.1 Overview of bioimage normalization workflows

Translating raw immunofluorescent bioimages into quantitative biological features is a multistep process that typically involves a normalization step to correct for systematic errors (i.e. batch effect) and offsets between images between and of the same slide. Figure 1 presents the bioimaging workflow steps including the preprocessing of raw images, aggregating pixels from the images into objects, filtering objects on quality metrics, normalizing objects across slides, correcting the images and finally segmenting the corrected images into biological relevant features for downstream analysis. Raw image preprocessing includes field-of-view (FOV) illumination correction, distortion correction, image registration across multiple rounds of staining and imaging and autofluorescence removal. Each of these preprocessing steps can introduce systematic errors into the slide images above those that originate from the tissue slide preparation, staining and microscope imaging process steps.

Fig. 1.

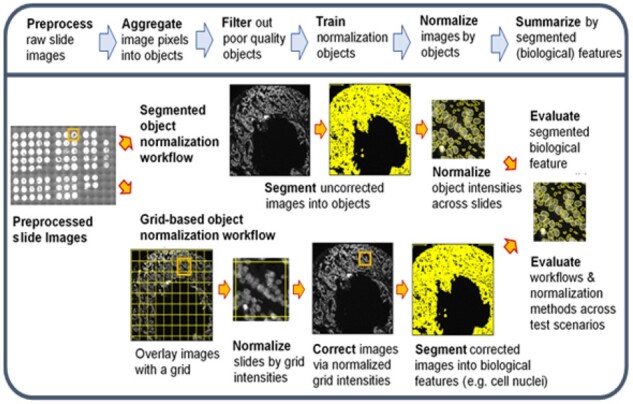
Overview of the workflows for normalizing bioimages and intensities of biological features across virtual slides

Two normalization workflows are illustrated in Figure 1 that are conducted after the raw MxIF images have undergone preprocessing: a segmented object workflow and a grid-based object workflow. Both workflows begin by aggregating individual pixels into objects. The intensity value for an object is defined as the mean of the pixel intensities contained within the object. The segmented object normalization workflow uses one or more image channels (e.g. nuclear staining intensity such as DAPI) to delineate objects and consequentially classify pixels as either belonging to a specific object or external to all objects (i.e. background). The grid-based approach aggregates all image pixels into grid objects defined by a regularly spaced grid. The grid size can range from the size of one pixel up to aggregating all pixels of the entire image into one grid.

The grid-based object workflow is unbiased and does not exclude bioimage regions unlike the segmented object workflow. Immunofluorescence staining of antigen targets are distributed according to actual protein expression and not necessarily limited to segmented objects. Another major difference is that the step of normalizing the bioimages across the staining channels occurs prior to segmenting pixels into cell objects for the grid-based object workflow. A third difference between the two workflows is that the number of segmented objects per bioimage may vary due to tissue and cell density variations while the grid-based object workflow will have a constant number of objects across all bioimages.

An evaluation step is conducted at the end of the two normalization workflows (right side in Fig. 1). This step is the primary objective of our benchmarking effort in evaluating and comparing multiple normalization methods. We developed an approach for this evaluation step that utilized virtual slides based on real DAPI staining and imaging data along with a metric to quantify the error. This allowed us to judge each method and normalization workflow against an empirical ground truth versus a theoretically derived one. DAPI was selected as the marker to evaluate the normalization workflows because DAPI staining of a tissue slide is repeatedly refreshed and reimaged in each round of the MxIF workflow. DAPI is a very useful marker and is used for image registration and to access if the same underlying nuclear structures are present throughout all rounds of staining and imaging. The nuclear structures that DAPI stains become the empirical ground truth and each round of DAPI staining and imaging becomes a virtual slide.

2.2 Tissue samples and generation of bioimages

Full details on the tissue samples and generation of bioimages including each round of staining and imaging within the MxIF workflow (Supplementary Tables S1 and S2) is available in Supplementary Material, but briefly: Tissue samples from deidentified stage III colorectal cancer (CRC) patients were obtained from Beaumont Hospital/RCSI, Dublin, Ireland, Queen’s University Belfast, Northern Ireland and Paris Descartes University, Paris, France. Three tissue microarray (TMA) blocks were constructed comprising of 79 patient tumor cores and 6 formalin-fixed, paraffin-embedded cell pellets (i.e. cell lines). Formalin-fixed, paraffin-embedded cell pellets of cell lines (HeLa, HCT116 XIAP-KO, MCF7, JURKAT) were included in the three TMAs. The TMA slides underwent multiplexed immunofluorescence (MxIF) microscopy at GE Global Research. A detailed description of the multiplexed microscopy technique and single-cell analysis has been described previously (Gerdes, 2013). The platform used herein (Cell DIVE^TM, Leica Microsystem) allows for an iterative staining, imaging (on a IN Cell 2200) and a chemical dye inactivation workflow for over 60 biomarkers on a single tissue section with automated calibration scripts providing objective centration and focus, blank glass subtraction, distortion correction and field flattening. Postprocessing of the images includes autofluorescence subtraction, registration with baseline DAPI and region stitching. The TMAs were stained with 24 biomarkers (iterative staining steps with two biomarkers stained per round), including apoptosis pathway markers, BAK, BAX, BCL2, Bclxl, SMAC, XIAP, APAF, Caspases and MCL1; Immune cell/response markers: CD3, CD4, CD8, CD45, FOXP3, PD1, HLA1; Epithelial cell markers: PCK26, NaKATPase, cytoplasmic S6 and functional markers: CA9, Glut 1 and Ki67 (see Supplementary Table S1 for more details). All antibodies underwent extensive validation prior to multiplexing (workflow described in supplementary data of Gerdes et al. (2013) and Berens et al. (2019), starting with evaluation of staining sensitivity and specificity of the primary–secondary clones compared to isotype controls in a multi-tissue array containing 15 cancer types (MTU481, Pantomics, CA). This was followed by simulation of the dye inactivation process for up to 10 times and evaluation of staining performance, and finally direct conjugation of each antibody which is necessary for the multiplexed staining process and avoidance of cross-reactivity issues. Staining patterns for all biomarkers was compared and verified against known positive and negative controls or cell types, data from the Human Protein Atlas and/or prior staining data by the research team. DAPI is refreshed and imaged in each staining/imaging round and used for image registration.

2.3 Normalization methods

We assembled a list of normalization methods and workflows from the literature that are summarized in Table 1 and described in greater detail in Supplementary Material and Supplementary Table S3. Median normalization is defined (Equation 1) as an additive transformation shifting the intensity of all objects within an image to a global median without changing the spread in the intensity distribution of objects within the image. For example, the normalized intensity of object j found in image k ($I_{k,j}^{\mathrm{norm}}$) is equal to the raw intensity of object j in image k ($I_{k,j}^{\mathrm{raw}}$) shifted by the differences in the median intensity for all objects across all images ($\mathrm{Median}\left(I^{\mathrm{raw}}\right)$) minus the median intensity of all objects within image k ($\mathrm{Median}\left(I_k^{\mathrm{raw}}\right)$).

$$I_{k,j}^{\mathrm{norm}}=\mathrm{ }{I}_{k,j}^{\mathrm{raw}}+\left[\mathrm{Median}\left(I^{\mathrm{raw}}\right)-\mathrm{Median}\left(I_k^{\mathrm{raw}}\right)\right]$$ (1)

Table 1.

List of normalization methods that were evaluated

Normalization Method
• Median normalization
• Q50 and Q75: 50% and 75% quantile normalization
• SQUA: smooth quantile normalization (Hicks, 2018)
• UQUA: upper quartile normalization (Bullard, 2010)
• MRN: median ratio normalization (Maza, 2013)
• TMM: trimmed mean of the M-values (Robinson and Oshlack, 2010; Tarazona, 2011, 2015)

The quantile normalization methods (e.g. Q50, Q75) scale the raw intensity values by means of a multiplicative transformation (Equation 2). The normalized intensity of object j found in image k is equal to the raw intensity of object j multiplied by the ratio of the quantile intensity for all objects across all images ($\mathrm{Quantile}\left(I^{\mathrm{raw}}\right)$) divided by the quantile intensity of all objects within image k ($\mathrm{Quantile}\left(I_k^{\mathrm{raw}}\right)).$  

$$I_{k,j}^{\mathrm{norm}}=\mathrm{ }{I}_{k,j}^{\mathrm{raw}}\frac{\mathrm{Quantile}\left(I^{\mathrm{raw}}\right)}{\mathrm{Quantile}\left(I_k^{\mathrm{raw}}\right)}\mathrm{ }$$ (2)

We implemented both the median and quantile normalization methods as a function in R because of their simplicity. For all other normalization methods listed in Table 1 including Smooth Quantile Normalization, Median Ratio Normalization and Trimmed Mean of the M-values, we downloaded their implementation in R packages from Bioconductor.org that included: qsmooth (Hicks, 2018), fCI (Tang, 2016) and NOISeq (Tarazona, 2011, 2015).

2.4 Virtual slides and ground truth definition

To benchmark multiple normalization methods, we defined a metric to quantify the differences between a set of evaluation objects across a series of virtual slides. We utilized 14 rounds of DAPI restaining and imaging of the same physical TMA slide to represent our ground truth. We abstracted the individual rounds of DAPI staining and imaging to represent virtual slides. Each virtual TMA slide is the exact same 85 physical samples that have undergone a set of experimental conditions that introduce both random variation and systematic offsets between the virtual slides. Some of the systematic offsets introduced by lab technicians were known and electronically recorded. For example, the exposure time for the DAPI imaging was changed in a known amount between the virtual slides (rounds of imaging). The exposure time was either 20, 50 or 100 milliseconds for specific virtual slides which introduces known systematic offsets between the virtual slide images. Supplementary Table S2 presents the details for each virtual slide. A second known batch effect was the time of consecutive processing of the physical TMA slide; this was electronically captured via time stamps. The last virtual slide was stained and imaged 43 days after the staining and imaging of the first virtual slide. The time interval between staining of each virtual slide was not equivalent and ranged up to a maximum of 14 days. There are other batch effects that occurred in the empirically derived virtual slide data. For example, the DAPI stain on the physical slide is refreshed for each round with several changes in the chemical lot of DAPI solution used over the course of the 14 staining rounds.

Evaluation objects (EO) were defined and used to compute the differences across the virtual slides. The virtual slides are the same physical slide and thus contain the same physical samples, and consequently contain the same evaluation objects. The exact same evaluation objects were used to quantify and compare the performance for all methods and for both the segmented object and grid-based object workflows.

Overall, there were 297 430 nuclei objects generated by segmenting the DAPI images from the first TMA slide. A subset of these can be selected to become evaluation objects by prefiltering objects of lower quality prior to normalization. First, we filtered out the smallest and largest segmented nuclei objects. The area of the DAPI segmented nuclei objects ranged from 62 to 14 500 pixels² (Supplementary Table S4). The 10% and 90% quantiles from the distribution of all nuclei object areas were selected as the tolerances to filter by object size. Next, we filtered out objects that were not of sufficient image quality. Image correlation metrics (Bello, 2008) that measure alignment of a cell object’s pixels between rounds of successive DAPI staining was used to characterize an object’s image quality. Objects with less than 90% correlation across all 14 rounds of DAPI staining and imaging were filtered out. Filtering for both size and image quality resulted in 144 315 ground truth evaluation objects being selected out of all 297 430 nuclei objects.

2.5 Metrics to quantify and compare methods and workflows

We utilized the coefficient of variation (CV) as a metric to quantify the error in the intensity value for an individual evaluation object across the multiple rounds of staining and imaging (i.e. virtual slides). The intensity of an evaluation object is the mean of image pixel intensities contained within each evaluation object’s boundaries. We define EO[i, k] to be the intensity for the ith evaluation object for the kth virtual slide. The coefficient of variation for the ith evaluation object EO-CV(i) is defined (equation 3) to equal to the standard deviation ($\sigma )$ of the intensity distribution for the ith evaluation object across the N_s virtual slides divided by the mean ($\mu$) of the same distribution.

$$\begin{array}{c}EO-CV(i)=\frac{\sigma }{\mu }\\ \sigma =\sqrt{\frac{{\sum }_{k=1}^{N_s}{\left(EO\left[i,k\right]-\mu \right)}^2}{N_s} } \mu =\frac{{\sum }_{k=1}^{N_s}EO\left[i,k\right]}{N_s}\end{array}$$ (3)

Each evaluation object represents the same physical nuclei therefore the variance in the intensity is a result of systematic offset errors and random measurement noise. The EO-CV metric quantifies the variance in the intensity value of the evaluation object across the virtual slides that includes both contributions from systematic errors that in principle can be eliminated by a normalization method and random errors that cannot. A perfect normalization method would remove all experimental batch effects and the CV for the evaluation object would approach a limiting value that is dependent only upon the standard deviation of the measurement noise relative to the true intensity of the object and the number of slides being normalized. Under the condition of normalizing an infinite number of slides, the CV limit is the standard deviation of the measurement noise divided by the object’s true intensity value.

The mean of the EO-CV(i) distribution (MEO-CV) across all evaluation objects (N_E = 144 315) is what we used to quantify the performance of a normalization method under a given test scenario.

$$\text{MEO}-\text{CV}=\frac{{\sum }_{i=1}^{N_E}\text{EO}-\text{CV}\left(\mathrm{i}\right)}{N_E}\mathrm{ }$$ (4)

2.6 Test scenarios to evaluate normalization methods and workflows

We applied each normalization method and then computed its MEO-CV metric for each of 29 test scenarios. Each test scenario involved correcting the images from a specified subset of the 14 virtual slides. Details of each test scenario are presented in Supplementary Table S6. We applied both biased selection as well as random selection to define the virtual slide subsets for the test scenarios. For example, we forced the creation of test cases correcting virtual slides across and within known imaging exposure times. We created test cases that considered correcting virtual slides that were stained and imaged consecutively over a short period of time and other cases that were generated over weeks of time. Finally, we forced the cases of correcting 2, 3, 10 and 14 virtual slides. We also used random selection to generate some of the test cases at correcting 2 and 3 virtual slides.

3 Results

3.1 Comparing normalization methods in a segmented object workflow

We began our evaluation by first comparing the performance of each normalization method to correct the systematic error (i.e. batch effects) across the virtual slide images. We used all 297 430 nuclei objects for the segmented object normalization workflow. Unless otherwise noted, we ran 29 test scenarios (Supplementary Table S6) for each normalization method in which 2, 3, 10 or 14 virtual slides were corrected. Figure 2A presents the performance and comparison of multiple normalization methods (see Supplementary Fig. S3 and Supplementary Table S7 for results of all normalization comparisons). We found all six normalization methods reduced the slide-to-slide error (ANOVA P-value < 1E−16) for the evaluation objects as quantified by the MEO-CVs across the 29 test scenarios. All methods performed better in log space versus absolute space except for the SQUA method (Supplementary Table S7). The trimmed mean of the M-values (TMM) and median ratio normalization (MRN) methods applied in log space performed the best reducing the slide-to-slide error by approximately 10-fold and were found not to be statistically different from each other (Wilcoxon rank sum test with Bonferroni correction P-value = 0.93). Figure 2B and C presents one example of a test scenario involving the correction of 14 virtual slides before and after normalization respectively. The full distributions of DAPI intensities for the segmented nuclei objects pre- (Fig. 2B) and post- (Fig. 2C) normalization is presented in Supplementary Figure S4.

Fig. 2.

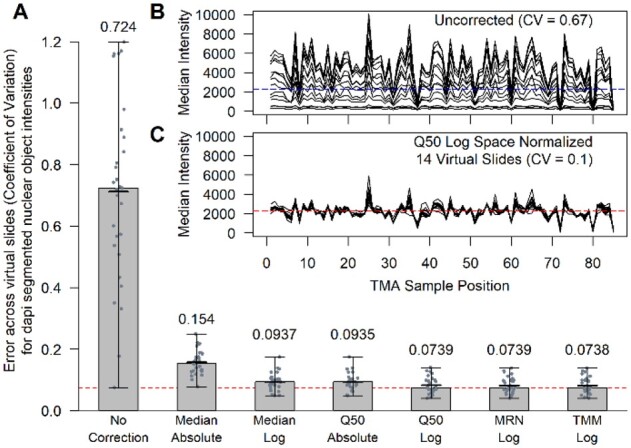
Performance of normalization methods for DAPI-segmented nuclei objects. (A) The bar chart presents the performance of six normalizations across 29 test scenarios relative to the uncorrected case (left most bar). The horizontal red dashed line in the bar chart located at 0.0738 is achieved by the TMM method when applied in log space (right most bar). The height of each bar represents the median of the MEO-CVs across the 29-test scenarios. Within each bar, there is a vertical line segment that represents the range in the 29 test values. The mean of the test cases is represented by a thicker horizontal line segment that is near the height of each bar. The two inset line plots (B, C) present 14 lines each representing a different virtual slide. The y axis is the median of the evaluation objects within each of the 85 TMA sample positions. The upper line plot (B) presents the uncorrected data, and the lower line plot (C) presents the data after normalizing using the 50% Quantile (Q50) method in log space. The horizontal dashed lines represent the global median intensity of all evaluation objects across all sample positions and virtual slides pre (B) and post (C) normalization, respectively

3.2 Impact of filtering objects prior to image normalization

We next evaluated the approach of filtering low image quality cell objects prior to inputting them into the bioimage normalization method. Our hypothesis was that by prefiltering objects of lower image quality prior to normalization would subsequently improve the slide-to-slide error correction. Surprisingly, we learned that the best performance in error correction was achieved by using all 297 430 nuclei objects when performing normalization (Supplementary Fig. S5). The image quality metric we used for filtering was the object’s pixel correlation across all 14 rounds of DAPI staining and imaging. If the correlation of pixels is low, then there is either blurring, tissue movement, or even tissue loss that has occurred across the imaging rounds. Moderate to low quality objects still provide good information when correcting errors and offsets. For example, very slight tissue movement or very slight image blurring can lead to a reduction in an object’s pixel correlation and thus its assessed imaging quality. However, the object’s mean intensity value computed as the mean of the pixel values within the object’s boundaries, can remain relatively constant. Therefore, it may be a blurry object, but its intensity value is still informative from the perspective of normalizing bioimages.

3.3 Evaluating a grid-based object workflow to normalize bioimages

We evaluated a grid-based object normalization approach to determine if it could achieve the same level of performance to normalizing segmented objects (e.g. nuclei) directly. We started by first understanding how the grid size impacted the normalization performance. Evaluations were conducted on grid sizes that ranged from an entire FOV (2560 × 2160 pixels²) down to a square grid size of 16 (15 × 15 pixels²). The median area for the nuclei segmented objects is 203 pixels (Supplementary Table S4) which is approximately equal to the area of a grid size of 16 (Supplementary Table S5). We found that a grid size of 32 produced the best performance, achieving a median value of 0.0741 for the MEO-CVs across the 29-test scenarios (Supplementary Fig. S6A). A grid size of 32 had a 9.2% improvement versus using the whole image (Wilcoxon rank sum test with Bonferroni correction P-value = 4.7E−05). Furthermore, using a grid size of 32 had only a slight reduction of 0.4% in the MEO-CVs versus the TMM method applied directly to the nuclei objects (0.0741 versus 0.0738, P-value = 0.092). Thus, the unbiased grid-based approach can achieve similar performance (see Supplementary Fig. S7 comparing distributions) as the TMM method applied directly to the segmented nuclei objects.

Supplementary Figure S6B presents the quantile normalization using quantiles that ranged from 50% up to 100% (Q50 to Q100). The 75% quantile (Q75) achieved the best performance. The Q50 method had a 42% loss in performance as did the MRN and TMM methods when applied to the grid objects. In contrast, when normalizing segmented nuclei objects directly, the Q50, MRN and TMM methods achieved the best performance (Fig. 2A, Supplementary Fig. S3).

3.4 Using on-slide controls to normalize bioimages

We next wanted to evaluate the use of on-slide tissue and cell-line control samples. To assess their use in normalization, we conducted a series of virtual slide normalization simulations that used different numbers of control samples to correct either two or three virtual TMA slides. There were 27 test scenarios in all. For each of these we performed random selections of control samples from each virtual TMA slide. As illustrated in Figure 3A, the randomly selected control samples for each virtual slide were constrained such that a randomly selected sample used as a control on one virtual TMA slide could not be selected and used as a control on any other virtual slide.

Fig. 3.

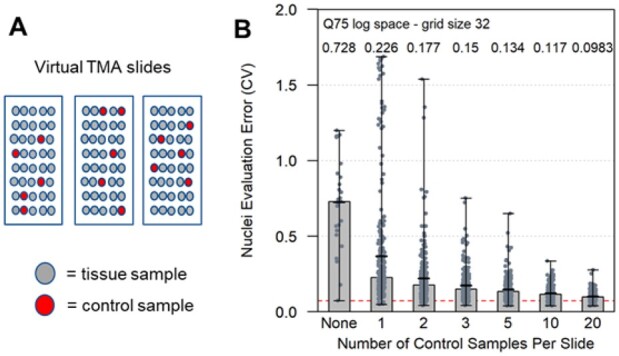
The effect of control sample number on error correction of TMA slide images. A limited number (1, 2, 3, 4, 10 or 20) of control samples and their images were used to normalize virtual TMA slide images. Each normalization was performed 10 times in which TMA samples were randomly selected and used as controls for normalization. The random selection of control samples for each virtual slide was constrained such that a randomly selected sample used as a control on one virtual TMA slide could not be selected and used as a control on any other virtual slide. An example is illustrated (A) in which five control samples are randomly selected from three virtual TMA slides. The bar chart (B) presents the performance of applying the Q75 normalization method in log space to the grid objects of size 32 from the control samples on each virtual slide. After normalizing the images, the evaluation of nuclei objects across all 85 samples from the virtual TMA slides was used to compute the MEO CVs. The computed performance was based on 27 testing scenarios that involved either 2 or 3 virtual slides. The ‘None’ case (left most bar) is the uncorrected data with a median value of 0.728. This value is slightly different than the uncorrected data presented in Figure 2 that included two additional test scenarios. The horizontal red dashed line is located at 0.0738 in the bar chart

Figure 3B presents the results and shows that ten or more on-slide controls are required for robust normalization. Relying on five or less control samples can be detrimental. In other words, by relying on only a few controls there is an unacceptable probability that the error in the data will increase after normalization relative to the original uncorrected data. Even with five controls, the probability that the controls would be of limited value in reducing the batch effects between slides is still relatively high as indicated by the range observed in our simulations (Fig. 3B). Using ten to twenty controls reduces the range to a more acceptable level but comes with the cost of reducing the number of available positions for experimental samples within the TMA. Our simulations show that by using 5 control samples, the median of MEO-CVs that is achieved across the 270 (27 × 10) test simulation runs was 0.134 which is 36% higher in error than when using 20 control samples.

3.5 Demonstration of grid-based object normalization performance

We applied the grid-object normalization workflow to 24 multiplexed biomarkers imaged on each of three TMA slides. As an exemplar, Figure 4 presents the median image intensity for the staining of the BCL2 associated X, apoptosis regulator (BAX) protein across 85 samples that includes both CRC tissues and cell lines. The BAX staining intensity for slide A3 (Fig. 4A) is distinctly lower than the corresponding slides A1 and A2 for the uncorrected images of each of the four cell lines. BAX is a member of the Bcl-2 protein family and is proapoptotic (Oltvai, 1993). A decrease in BAX staining may indicate less sensitivity to apoptosis when comparing different cell lines. However, each individual cell line sample on each physical slide is from the same paraffin-embedded cell pellet. Furthermore, a reduction in BAX protein levels is unlikely to occur proportionally across four cell lines under physiological culture growing conditions. This reduction in BAX intensity for slide A3 versus the other two slides is purely an experimental artifact (i.e. slide to slide batch effect). To prevent false biological discoveries, it is critical to remove this artifact from the data prior to downstream analysis. We applied the grid-based object normalization workflow with grids of 32 pixels in size and the Q75 method applied in log space. The normalized data presented in Figure 4A shows approximately equivalent BAX staining intensity across the three slides and the relative proportions across the four cell lines is now constant across the three slides. Figure 4B presents the uncorrected and normalized images of the BAX staining across the three slides for the HeLa cell line. Supplementary Table S10 summarizes the performance of the grid-based object normalization workflow assessed by four cell lines across 24 independent fluorescently labelled antibody markers that were analyzed on the same slides. We finally applied Uniform Manifold Approximation and Projection (UMAP) to visualize the high-dimensional data before and after normalization. The UMAP plots (Supplementary Fig. S8) clearly show a batch effect between the three slides with serial tissue slices prior to normalization which is then eliminated after the grid normalization method is applied. This provides a clear demonstration of the ability of the grid-based object normalization workflow to reduce the batch effects for fluorescently labelled antibody markers in addition to DAPI in real data.

Fig. 4.

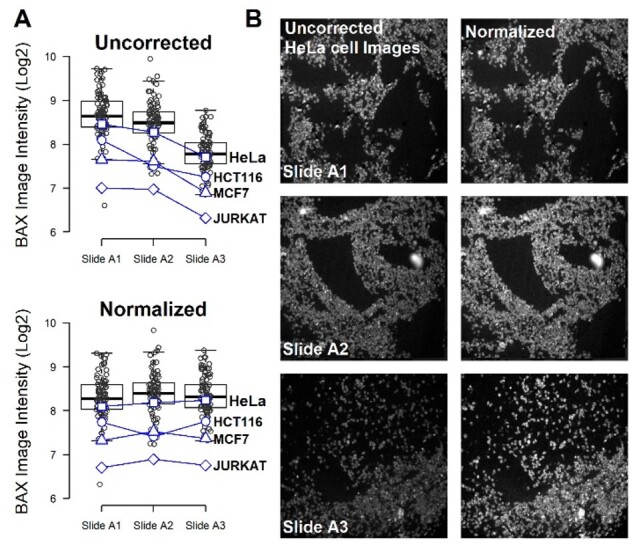
Application of grid-object normalization to BAX staining of three physical TMA slides that include 85 CRC tissues and cell lines. (A) The median BAX staining intensity of each image for each of the three slides is presented uncorrected and normalized by applying the grid-based object workflow with grids of 32 pixels in size and the 75% quantile (Q75) method in log space. The intensity of four cell lines, HeLa (square), HCT116 (circle), MCF7 (triangle) and Jurkat (diamond) is shown for the three TMA slides. (B) The images for the HeLa cell line across the three slides is presented before and after normalization

4 Discussion

The main goal of our work was to both evaluate published normalization methods and test a new normalization method for correction of experimental errors and batch variation between multiplexed immunofluorescence bioimages. The biggest initial challenge we faced was simply defining a ground truth to judge all the methods against. Without a ground truth, the value of any comparative analysis becomes limited. We generated a ground truth dataset from multiround staining and imaging of the same marker in the same tissue with each round representing a ‘virtual slide’ image. These virtual slides consist of the same physical tissue, include actual batch processing errors and noise, and serve as the ground truth necessary to compare multiple methods and workflows.

Our virtual slide ground truth approach does have its limitations when it comes to approximating batch effects in epitope-antibody staining and imaging. For example, there may be significant differences between antibody permeability arising from differences in slide section thickness, access to binding sites and difference in binding affinities, or off target binding and background staining. These potential limitations of our virtual slide approach still need to be further studied and understood. Nevertheless, we are encouraged by our results at applying the grid-object normalization workflow to 24 independent fluorescently labelled antibody markers.

We examined the unbiased grid-based object workflow to normalize images prior to segmenting the bioimages into cell objects. When compared to the workflow of normalizing segmented cell objects directly, we found the differences in performance (0.4%) to be statistically insignificant (P-value > 0.05). With the performance being almost equivalent, the grid-based object workflow has the additional advantage of performing normalization of the bioimages across the staining channels prior to segmenting pixels into cell objects. This can improve global intensity thresholding for segmentation, identifying cell type classification and performing unsupervised clustering based on cell marker intensity levels.

We found that filtering of objects prior to bioimage normalization did not improve performance in error correction. Most normalization methods that we evaluated (TMM, MRN, median, Q50, Q75) are robust to the presence of outlier and experimental artifact object values. In a situation where you have potentially lower quality information which can be randomly distributed across both high and low values, the use of the median tends not to be impacted by the presence of outlier data.

This use of quality control samples becomes increasingly important to normalization approaches when the slides cannot be balanced. Unbalanced situations can occur if there are significant mean differences between slides such as tissue type, tissue morphology, cell type, cell density, cancer stage and other factors impacting protein expression. In that case, it may be more appropriate to redesign the TMA slides to be more balanced for types of samples. For the case of balanced TMA slides, we found that normalizing across all samples achieves improved performance relative to normalizing based on a small number of quality control tissues or cell lines. Suboptimal performance (36% loss) was achieved with five controls per slide. We found that relying on only one or two controls on a slide had an unacceptable probability of amplifying errors upon normalization. Consequently, the normalized data were further from the ground truth than the original uncorrected data. Using ten to twenty controls per slide improved the performance but with a cost of having a portion of the TMA being devoted to control samples. However, one further benefit of having a larger number of control samples available is the ability to set aside some of them to validate if the normalization process itself is introducing biases into the data.