Reference-Free Traction Force Microscopy Platform Fabricated via Two-Photon Laser Scanning Lithography Enables Facile Measurement of Cell-Generated Forces

Abstract

Cells sense and respond to the physical nature of their microenvironment by mechanically probing their surroundings via cytoskeletal contractions. The material response to these stresses can be measured via traction force microscopy (TFM). Traditional TFM platforms present several limitations including variable spatial resolution, difficulty in attaining the full three-dimensional (3D) deformation/stress profile, and the requirement to remove or relax the cells being measured to determine the zero-stress state. To overcome these limitations, we developed a two-photon, photochemical coupling approach to fabricate a new TFM platform that provides high-resolution control over the 3D placement of fluorescent fiducial markers for facile measurement of cell-generated shear and normal components of traction forces. The highly controlled placement of the 3D marker array provides a built-in, zero stress state eliminating the need to perturb the cells being measured while also providing increased throughput. Using this platform, we discovered that the magnitude of cell-generated shear and normal force components are linked both spatially and temporally. The facile nature and increased throughput of measuring cell-generated forces afforded by this new platform will be useful to the mechanotransduction community and others.

Graphical Abstract

INTRODUCTION

Traction force microscopy (TFM) has become the standard method to measure cell-generated forces and investigate the role these forces play in mediating cell behavior. TFM has been implemented to investigate the influences of cytoskeletal tension and/or traction forces in regulating cell proliferation,^1–3 differentiation,^4–9 migration,^10–12 nuclear polarization,¹³ nuclear deformation,^14–16 and reaction to drugs.¹⁷ Although cell-generated shear components of traction are usually measured, the magnitude of the out-of-plane, normal components can reach 50% of in-plane, shear components.^12,18 Normal components of traction play an important role in cellular processes including leukocyte extravasation¹⁹ and may also influence cell fate via nuclear deformation and chromatin remodeling.^14,15,20,21 Accordingly, the ability to accurately and easily measure out-of-plane, normal components, along with shear components, is of great interest to many areas of research.

The most common platform capable of measuring out-of-plane, normal tractions utilizes protein- or peptide-functionalized elastomeric materials, usually polyacrylamide, containing embedded micro- or nanometer-sized fluorescent spheres that act as fiducial markers to measure material deformation.^18,22,23 These platforms are straightforward to fabricate and characterize and provide high-resolution traction measurements through the use of densely packed fluorescent spheres.²⁴ A limitation of this approach is the lack of control over fiducial marker placement and spacing. This lack of control can induce a number of spacing-related issues.²⁵ For example, markers may be too close together to be accurately resolved or too far apart as to create unusable regions, together inducing regionally biased resolution in material deformation measurements and subsequent force/stress calculations. Random marker placement also necessitates acquisition of a zero-stress state reference image to be registered with the deformation images for displacement measurements, requiring physical removal of the cells being examined or chemical perturbation to relax their cytoskeletal tension. This necessity hinders long-term cell studies and prevents subsequent cellular analyses.

To overcome some of these limitations, several reference-free platforms have been generated using micromolding and other high-resolution fabrication techniques.^17,26–29 The most commonly implemented method in this category utilizes micromolded pillar arrays to approximate cellular tractions based on the deflection of pillars in response to cell-generated tension. The reference position of the surface of the pillars is approximated based on the location of the pillar base. Pillar-based methods greatly facilitate measures of cell-induced shear components but are limited to two-dimensional (2D) measures. Reference-free platforms capable of measuring out-of-plane deformations implement patterned arrays of fluorescent fiducial markers on the surface of an elastomeric substrate with high spatial resolution and fidelity. The patterned marker surface array can serve as a built-in, implied, zero-stress reference state. The implied reference provides the ability to measure cell-induced material deformation using a single three-dimensional (3D) image acquisition, without physically removing or chemically perturbing the cells, thereby enabling facile use of standard cell analysis techniques, including immunofluorescence labeling, in combination with TFM.^26,30

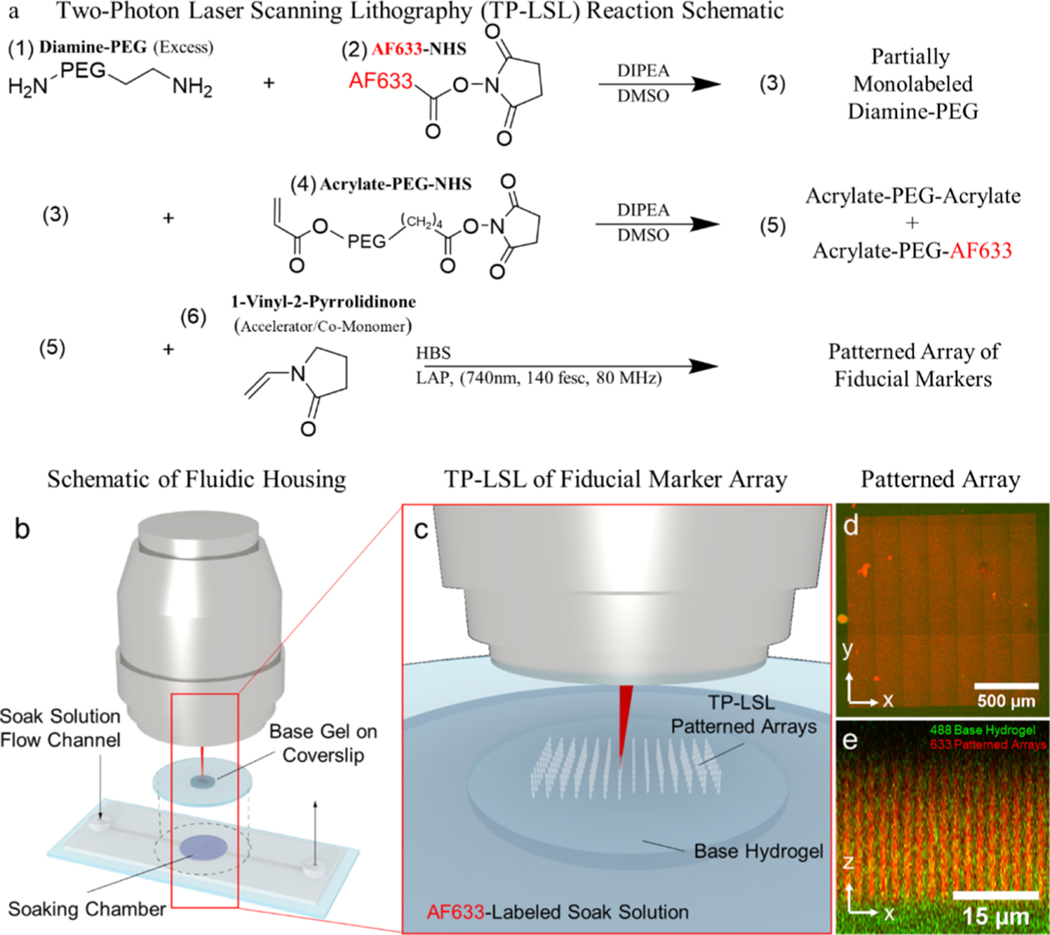
We developed an alternative reference-free platform using a photolithographically patterned hydrogel containing a built-in, implied reference state to measure the complete 3D material deformation profile induced by cells. The platform allows for continuous capture of material deformation without chemically relaxing or physically removing the cells. This facilitates temporal measurements of the same cell population over extended time as well as the ability to analyze a relatively large cell population providing higher throughput. The platform utilizes a 3D array of fluorescent fiducial markers embedded in a base hydrogel. Two-photon laser scanning lithography (TP-LSL)^31–36 is implemented to photocouple fluorescently labeled, poly(ethylene glycol) monoacrylate macromers into a base hydrogel composed of poly(ethylene glycol) diacrylate (PEGDA) (Figure 1). The resulting markers are ellipsoidal in shape with a 3D profile dictated by the point spread function of the pulsed laser. Reference positions for displaced markers are approximated using linear fits of surrounding nondisplaced markers resulting in a digital reconstruction of the zero-stress state. We demonstrate that using this implied reference state allows facile measurement of shear and normal components of cell-generated tractions using a single volumetric image stack. Using this platform, we quantified material deformation profiles and forces induced by individual human umbilical vein endothelial cells (HUVECs) as well as small HUVEC clusters. Consistent with a previous study, we observe that the extent of the shear component of traction generated by individual cells is positively correlated with increased spreading.³⁷ We further demonstrate that the normal component induced by individual cells follows a similar trend and that shear and normal components are tightly linked both in magnitude and temporally. Cell clusters display weaker correlations of shear and normal components of tractions with increased area, but the magnitude of shear and normal components are still tightly linked. We also demonstrate the ability to generate single-cell patterns via a second round of TP-LSL to photocouple PEG monoacrylates functionalized with integrin-binding peptide, arginine-glycine-aspartic acidserine (RGDS), to the hydrogel surface to control cell shape and spreading.

Figure 1.

Fabrication of the reference-free TFM platform. (a) Fluorophore-labeled PEG used to fabricate fiducial markers is synthesized by coupling a diamine-PEG to either an acrylate and a fluorophore or two acrylates using NHS esters. (b,c) Resulting acrylated-PEG species are photocoupled into a preformed hydrogel by soaking the hydrogel in a solution containing the PEG species, a radical generating photoinitiator (LAP), and a comonomer (NVP). (d,e) Resulting fiducial markers are patterned in large arrays within the upper ~20 μm of the base hydrogel.

RESULTS

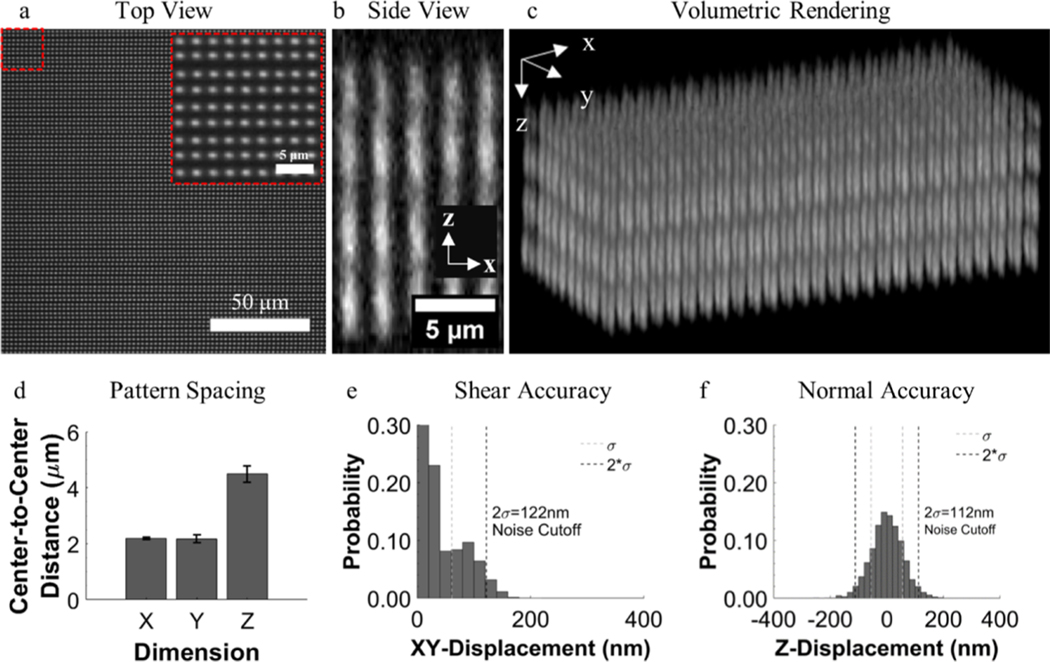
The platform consists of a base PEGDA hydrogel containing an embedded array of ellipsoidal fluorescent fiducial markers with Gaussian-like intensity profiles (Figure 2a–c). We chose PEGDA because of its protein-repulsive properties, biological inertness, and ease of chemical and mechanical manipulation. The size, shape, and intensity profile of the patterned fiducial markers are dictated by the numerical aperture of the objective as well as the intensity of the focused laser beam. Using a 740 nm, 140 fs pulse width, Ti:S laser operating at 80 MHz with a fluence of 3.7 nJ μm⁻² focused through a 1.2 numerical aperture water immersion objective resulted in ellipsoidal features with full-width, half maximum dimensions of 0.84 ± 0.11 μm in XY and 3.73 ± 0.30 μm in Z. Marker spacing was prescribed in the X-direction by a digital mask (2.12 μm), in Y by an automated image tiling step size (2.12 μm), and in Z by an automated Z-stepping size for the objective turret motor (3.5 μm). The center-to-center marker spacing varied slightly from the dictated values as the spacing precision was dependent on the mode of stepping (image-guided galvometers vs stage motor vs objective turret motor). A spacing in X of 2.19 ± 0.04 μm, Y of 2.17 ± 0.14 μm, and Z of 4.50 ± 0.30 μm was typically achieved (Figure 2d), with a corresponding 2D fiducial marker density of 0.21 markers μm⁻² in XY and 3D density of 0.05 markers μm⁻³.

Figure 2.

Characteristics of the fiducial marker array. (a) Single view field of a patterned region with an inset demonstrating the consistency of the patterns. (b) Profile view and (c) volumetric rendering of a patterned region demonstrating the intensity profile of fiducial markers through the Z-direction that allows for centroid localization based on intensity fluctuations. (d) Mean spacing between fiducial markers in the patterned array. (e,f) Histograms demonstrating the accuracy of reference lines as a true reference, displayed as the probability of measuring fiducial marker displacement in a nondeformed marker array.

To determine the accuracy of using reference line fitting to establish marker centroid positions, the deviation of fiducial marker centroids in nonstressed hydrogels, without cells, was measured (Figure 2e,f; Figure S1), as well as in nondeformed regions sufficiently far enough away from cells as to not be displaced. The value representing two standard deviations from the mean displacement magnitude in each patterned region was used to characterize the accuracy and to set a lower limit threshold of displacement magnitude, which would reliably yield displacements of the correct orientation. Displacements falling below the threshold were treated as noise and suppressed. The threshold value was updated for each patterned region to account for possible variability. Typical accuracies were 127 ± 17 nm in the XY plane and 140 ± 22 nm in Z.

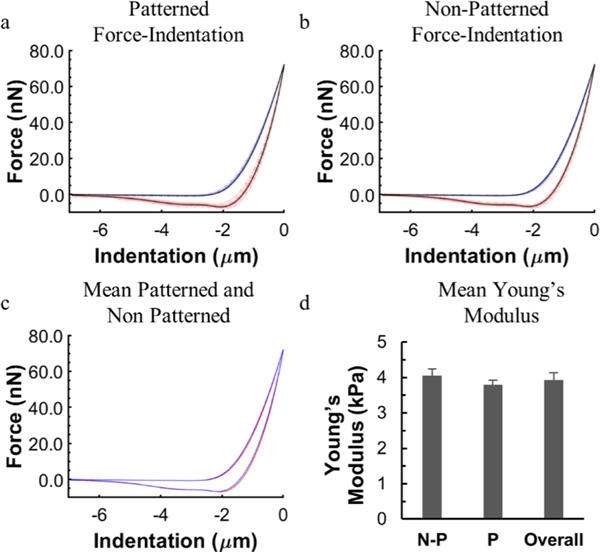
To quantify stiffness of the hydrogels for traction force calculations, nanoindentation experiments were performed using a Bruker Bioscope Catalyst BioAFM (Figure 3). All curve fitting was performed using the Bruker NanoScope Analysis (see the Supporting Information). Of particular interest was whether addition of fluorescent fiducial markers had a measurable impact on hydrogel elasticity. The surface moduli for the patterned and nonpatterned hydrogels were 3.79 ± 0.12 and 4.05 ± 0.18 kPa, respectively. Although this difference was statistically significant, the functional impact of the difference was ignored because of its low magnitude. To account for the possibility that the observed differences were simply due to local variations in surface elasticity of the base hydrogel, a Young’s modulus of 3.9 kPa representing an average of all measures and which is within 5% of all measured means was used for traction calculations.

Figure 3.

Nanoindentation of PEGDA hydrogels to measure surface elasticity. Force indentation curves of (a) patterned and (b) nonpatterned hydrogels. Blue lines indicate approach, red lines indicate retraction, and black lines represent the average profile. (c) Overlay of the average indentation curves shows minimal difference between patterned and nonpatterned hydrogels. (d) Average Young’s modulus determined from a Hertzian contact model for nonpatterned (N-P), patterned (P), and all regions (overall). n = 129 (66 patterned, and 63 nonpatterned).

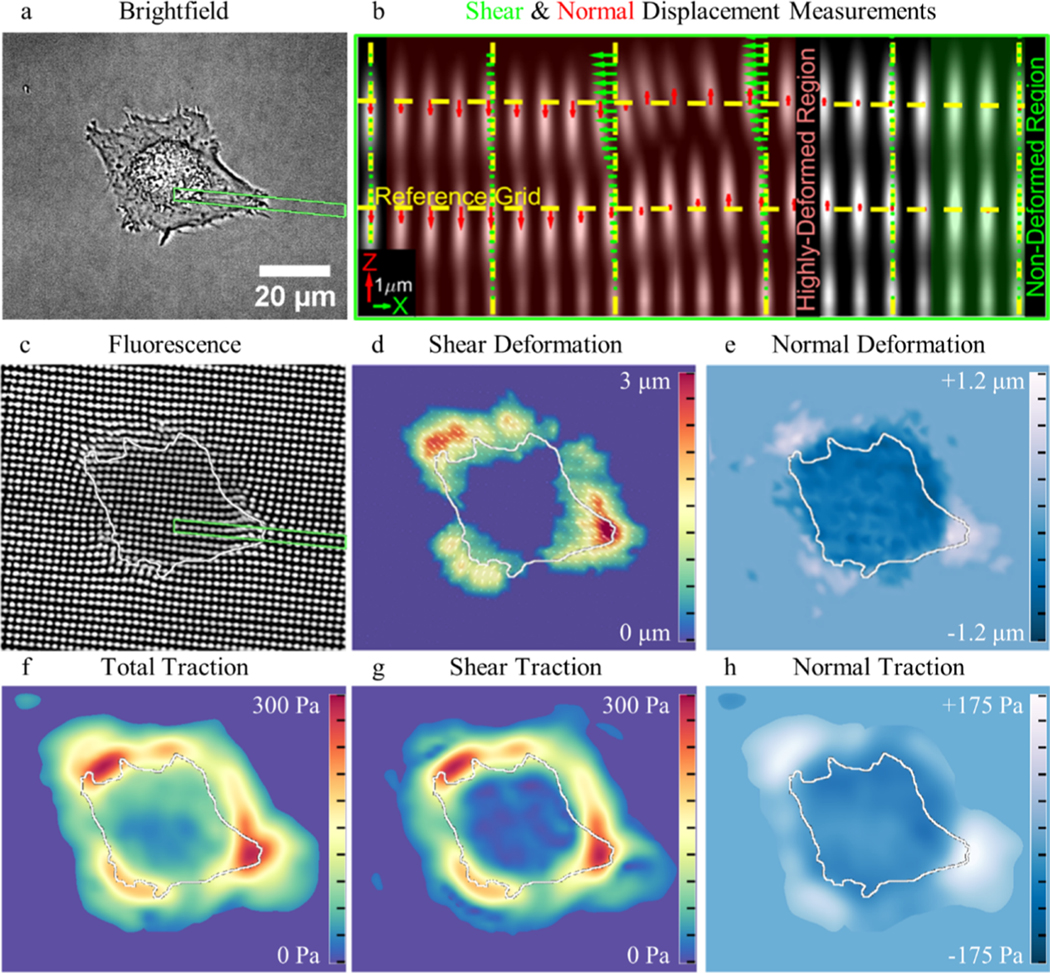
To approximate the zero-stress state marker positions for a displacement data set, we interpolated reference positions for displaced markers from linear fits of nondisplaced markers within the same row or column (Figure 4b; see the Supporting Information). For any given marker, the intersection of linearfits of nondisplaced markers in the X-direction (rows) and in the Z-direction (columns) provided the 3D, nonstressed, reference coordinates needed to measure marker displacement. The reference lines running axially (Z-direction) through the hydrogel were used to measure the shear displacement in the XY plane. A depth of 12 μm into the hydrogel, from the surface, was sufficient to reach nondisplaced markers with XY coordinates that represented the zero-stress state location of displaced markers. To measure normal marker displacement, linear reference fits parallel to the hydrogel surface (X-direction) were used. A dilation of the cell boundary in XY of 8.13 μm was sufficient to encompass, on average, >90% of all hydrogel deformation, so all markers beyond the boundary were designated nondisplaced for fitting reference lines. To convert marker displacements to surface tractions, we implemented a 3D TFM algorithm which utilizes a linear elastic material model with Young’s modulus of 3.9 kPa and ν = 0.2 (Figure 4f–h).³⁸ A Poisson’s ratio of 0.2 was chosen as it accurately describes small hydrogel surface deformations.^39–41 Prior to conversion, unfiltered deformation data were interpolated to a grid spacing equal to the sampling density of the fiducial marker arrays, which served as the input to the TFM code.

Figure 4.

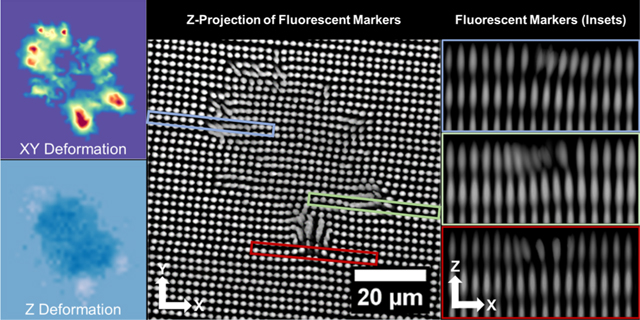
Measuring 3D cell-induced hydrogel deformation and tractions. (a) Brightfield image of a HUVEC seeded on the surface of a patterned gel. (b) XZ profile view of the inset [green box in (a)] demonstrates how reference lines are used to measure shear and normal fiducial marker displacement. (c) Z-projection of the fluorescent markers below the adherent HUVEC demonstrates a clear representation of the measured displacements. Heatmaps of (d) shear and (e) normal deformation. Surface tractions are displayed as (f) total magnitude, (g) magnitude of shear component of tractions, and (h) normal component of tractions.

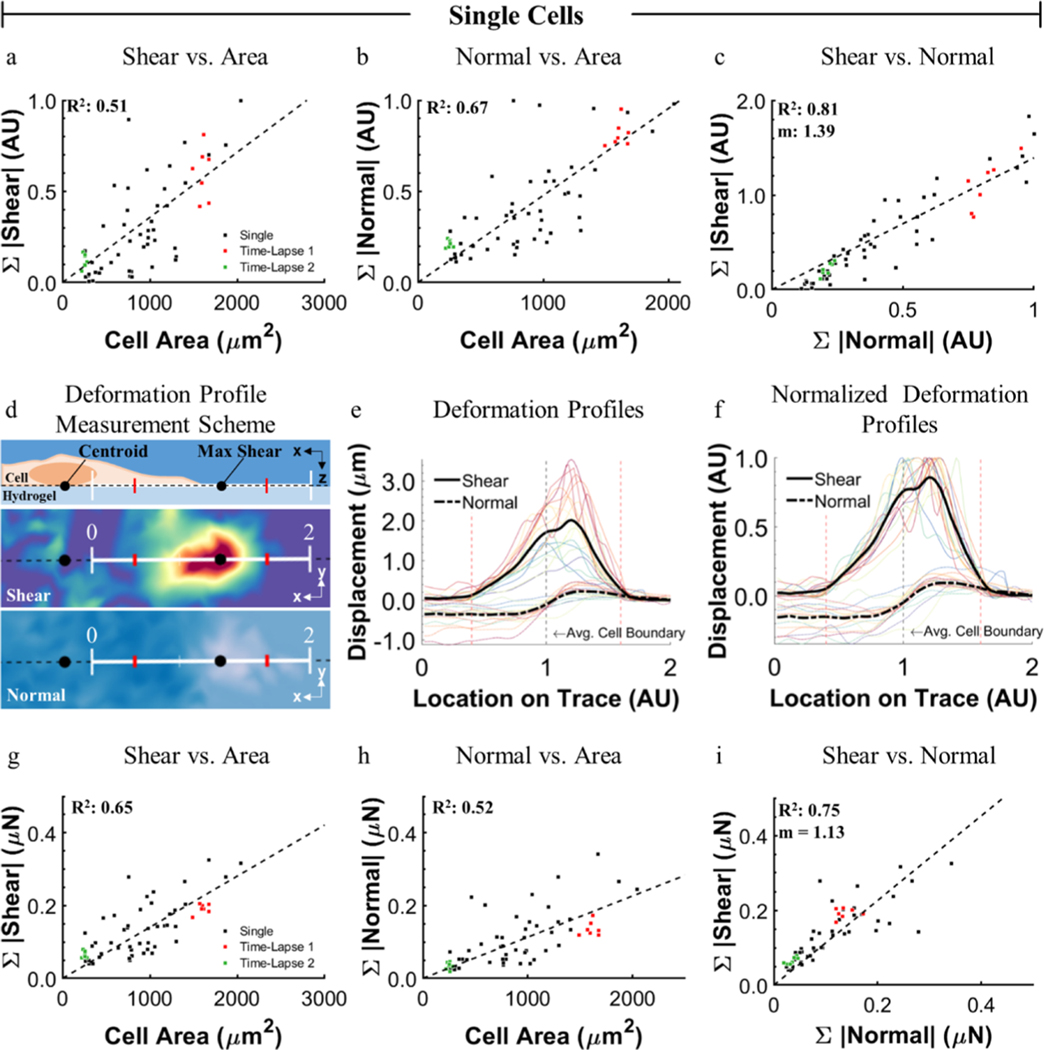
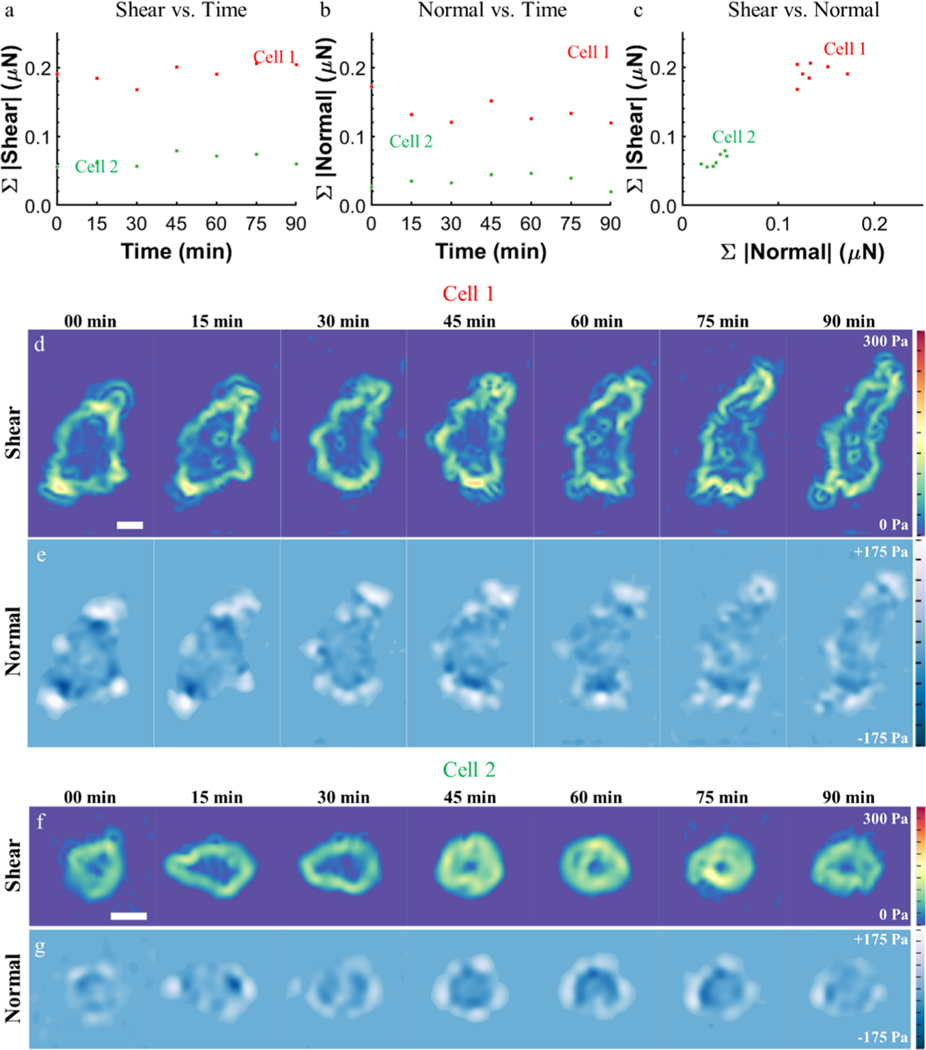
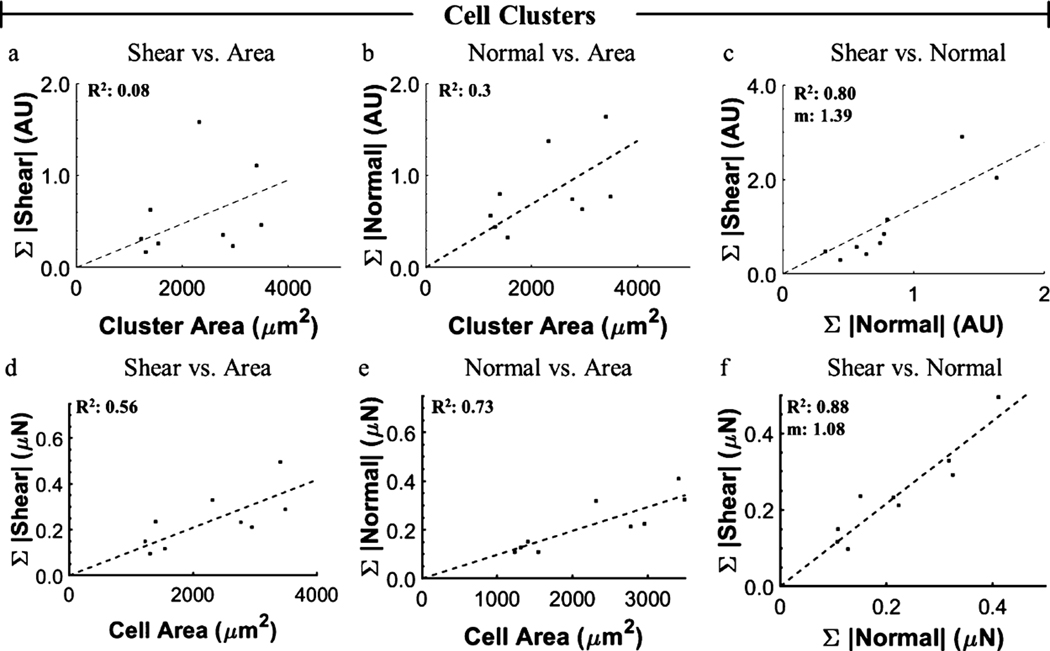
Using this new platform, many cells can be measured without concern for maintaining positional accuracy to collect a nonstressed, reference state image, thereby allowing for higher throughput. To demonstrate this, data were collected from more than 50 individual cells and 9 cell clusters over a 24 h period, including several time-lapse studies. As metrics to describe the total material deformation induced by a cell, surface displacements were interpolated to a grid spacing matching the sampling density of the original marker arrays. The sum of the displacement magnitudes in the XY plane and in Z are referred to as the sum of shear displacement and sum of normal displacement, respectively. To validate the platform, we reproduced a previously reported trend of linearly increased shear with increased cell spreading (Figure 5a).³⁷ As the platform allows facile measurement of normal components, we also examined this relationship and demonstrated that normal deformation and force follow similar linear trends with increased cell spreading (Figure 5b,h). To further investigate the relationship between shear and normal traction components, we examined their relative magnitude, spatial distribution, and temporal behavior. We found a positive correlation between shear and normal deformation and traction components for all cells measured, where the slope of a linear regression was 1.39 and 1.13 for the deformation and forces, respectively (Figure 5c). This prompted us to investigate how the normal and shear components were related spatially. The largest material deformation occurs at the cell periphery with shear components oriented toward the cell interior, upward normal components occurring distally, and downward normal components proximally (Figure 5d–f). The relative spatial organization of shear and normal components suggests a rotational moment occurring about the location of maximum shear, likely at focal adhesions, as has been previously reported.^12,18,42 The observed trends in displacement data held true for the converted traction data (Figure 5g–i). Time-lapse studies (Figure 6, Movies S1 and S2) demonstrate that the shear and normal traction components vary with time (Figure 6a,b) but that the relative ratio of shear to normal components stays nearly constant (Figure 6c), indicating that normal and shear components are linked in magnitude even temporally. We applied the same analysis to cell clusters (Figure 7). Interestingly, although small clusters did not always exhibit the same spatial distribution of shear and normal components as observed in individual cells (Figure S2), the overall ratio of shear to normal was consistent with that of individual cells with a linear regression slope of 1.39 and 1.08 for deformation and forces, respectively (Figure 7c). In addition, we observed the highest magnitude of the in-plane component of cellular tractions at the periphery of cell clusters, suggesting that cell–cell junctions propagate cell–matrix loads between cells in a cluster, consistent with previous studies.^43–45

Figure 5.

Magnitudes and distributions of cell-induced hydrogel deformations and forces. Positive linear correlations exist between both (a) shear and (b) normal deformation with increased cell spreading for individual single cells. Black markers represent different individual cells and red and green markers are time-lapse measures of specific cells. (c) Strong linear correlation was observed between the sum of shear and normal deformation magnitudes (normalized to highest normal magnitude). n = 60 data points for (a–c). The distribution of shear and normal deformation was measured along a trace from the cell center through the maximum shear. (d) Lengths of the profiles were normalized so that the proximal and distal locations where the magnitude of shear was 20% of the maximum occurred at 0.4 and 1.6 (red ticks). (e,f) 22 profiles of shear and normal deformation, with the average plotted in black. The transition from negative to positive normal deformation occurs at the cell boundary, with maximum shear coinciding with maximum positive normal deformation. (g–i) Calculated shear and normal traction components corresponding to (a–c), respectively.

Figure 6.

Time-lapse, cell-induced hydrogel traction measurements. The sum of (a) shear and (b) normal components of traction for a well-spread cell (cell 1) and a spreading cell (cell 2) over 90 min at 15 min intervals. (c) Although shear and normal traction magnitudes vary with time, their magnitudes are linearly correlated at all time points. Heatmaps of (d,f) shear stress and (e,g) normal stress for cell 1 and cell 2. SB = 20 μm. See Movies S1 and S2.

Figure 7.

Magnitudes and distributions of cell cluster-induced hydrogel deformations and forces. Cell clusters (n = 9) displayed similar trends between (a) shear and (b) normal deformation with spread area, as well as (c) shear vs normal, that was observed for individual cells. (a,b) are normalized to the highest value measured in the individual, single-cell data in the respective category (i.e., shear or normal). Shear and normal data in (c) are normalized to the highest normal deformation measured in individual cells. (d–f) Calculated forces corresponding to (a–c), respectively.

A common technique often coupled with TFM is micro-contact printing,^6,9,46,47 which provides control over adhesion ligand availability and subsequently cell spreading and shape. Using TP-LSL, the same control can be achieved at the hydrogel surface. The protein-repulsive nature of PEG provides a nonadhesive background for patterning cells. We implemented a second round of TP-LSL to photocouple an RGDS-functionalized PEG monoacrylate macromer to the surface of the TFM platform to generate arrays of single-cell patterns (Figure 8). We demonstrate the ability to culture adipose-derived stem cells on 50 μm diameter circular patterns and elongated, obround patterns which induced a high-tension state with strain concentrated at the rounded narrow ends.^6,46,47

Figure 8.

Fabrication of single-cell pattern arrays. (a) Fluorescent image of an array of circle and obround patterns composed of an (red) acrylated RGDS peptide on top of (green) TFM fiducial markers. (b–d) Z-projections of several permutations of ASCs adhered to patterns demonstrate that a variety of deformation profiles can be imposed on the cells using two-photon lithography to augment TFM studies.

DISCUSSION

We developed a reference-free platform containing a built-in, implied, zero-stress state that allows complete capture of cell-induced 3D material deformation and force profiles. The platform tracks material deformation as a function of centroid displacement of photolithographically patterned fluorescent fiducial markers embedded in a base hydrogel. The ability to capture both the reference state and displaced state in a single image stack greatly facilitates data collection allowing for a large cell population to be analyzed in a single experiment, thereby increasing throughput. It is important to note that circumventing the need for a reference image is not a new concept. A number of platforms exist that contain a built-in reference state achieved through implementing regular arrays of fiducial markers.^{26,28,29,48–51} To achieve reference-free functionality, this platform uses a new approach to approximate the zero-stress state positions of fiducial markers. Developing the methodology to analyze displacements in this platform required characterizing the precision of the laser scanning microscope used for multiphoton chemical coupling. To minimize error, patterning dimensions that had the most consistent and predictable spacing of rows of markers were identified and linear fits of individual rows in these dimensions were used to determine reference locations of displaced markers (see the Supporting Information). Linear fits of columns through the Z-dimension accurately predict X and Y reference positions, and similarly, linear fits of rows through the X-dimension accurately predict Y and Z reference positions. The intersection of these two independent fits provides the 3D nonstressed, reference position for every marker in the data set.

As an example of this platform’s potential applications, we measured the 3D deformation profiles induced by HUVECs. Cells generate both in-plane and out-of-plane traction components, inducing 3D deformation in the underlying material. The spatial distribution, relative magnitude, and temporal linking suggest that both the in-plane and out-of-plane deformation are linked and may be a direct or indirect product of myosin-mediated cell contractility. On the basis of the distribution of normal material deformations beneath adherent cells, we expect that normal deformation may be, at least in part, the result of the cellular cortex pressing into the hydrogel perhaps because of the mechanisms described previously in Dictyostelium cells.¹² However, we discovered that normal deformation was most commonly either near or coincident with large shear deformation, which may also suggest that some component of normal deformation is simply the material response of the hydrogel to a high-magnitude shear. This is reinforced by the cell cluster data, where the spatial distribution of measured deformation did not follow the same pattern as individual cells (Figure S2), although the linear relationship between shear and normal deformation and forces held. Although it is clear that cells are responsible for generating normal force, it is unclear how it may be translated into the cell and what role, if any, this force plays in determining cell behavior. However, recent studies have shown that adhesion sites under the nucleus are compressed⁵² and that force applied to the nucleus results in nuclear deformation and chromatin remodeling which can impact cell fate.^14,15,20,21 We also presented material displacement data converted to tractions. Several strategies exist for this conversion that are applicable to the workflow presented here; the method we used was found to be most compatible with our existing code.^18,38 Regardless of the methodology used to convert these data, other studies suggest that describing cellular tension in terms of material displacement yield useful information on their own.^17,53

Although the ubiquitous RGDS ligand was used in this study, essentially any desired peptide or protein which can be functionalized with a compatible acrylate-PEG linker can be coupled to or patterned on the surface in a similar manner. In this way, the platform affords control over cell area, shape, focal adhesion distribution, and other physical aspects which have demonstrated roles in mechanotransduction pathways. In addition, digital masks, rather than physical masters, are used to control pattern geometry allowing new and interesting patterns to be implemented quickly.^54–59

Traction forces have recently been used to distinguish the response between diseased and normal airway smooth muscle cells to bronchoconstrictor drugs in a high-throughput manner, demonstrating the potential of cellular traction as a metric for drug screening applications.¹⁷ Also, another reference-free approach recently demonstrated the ability to simultaneously measure cell-generated tractions and the phosphorylation state of paxillin by combining TFM with traditional immunofluorescence labeling.^26,30 Similar applications may be possible with the TFM platform described here which could potentially aid throughput of such investigations.

There are a couple of considerations to keep in mind when determining the proper marker spacing when using this platform which include the level of tension generated by the cells being measured and the hydrogel elasticity. The fluorescent markers are composed of the same material as the base hydrogel and therefore deform with the base hydrogel in response to cellular tractions. If spaced too close to each other, the markers may begin to overlap in cases of high substrate deformation, making accurate centroid detection difficult. This can be avoided by either increasing the marker spacing or increasing the hydrogel elasticity. Increasing marker spacing lowers resolution while increasing hydrogel elasticity leads to lower deformations. For the cell types used here, HUVECs and ASCs, cultured on a 4 kPa hydrogel, we determined that a 2.12 μm spacing in X,Y provided enough spacing to avoid marker overlap while providing sufficient resolution to describe the traction profiles. An approach to decrease marker spacing includes the incorporation of additional marker colors which has been implemented in bead-based and reference-free TFM platforms to increase resolution.^24,26

With regard to fabrication time, although multiphoton lithography provides high-resolution, 3D control over photoinitiation events, it is a serial process limited by the speed in which photocoupling occurs. In this study, a write speed of 1.25 mm² h⁻¹ was achieved and has since been improved to 1.9 mm² h⁻¹ using a piezo-actuated z-axis stage controller. This current write speed allows fabrication of a 2.2 mm² array of fiducial markers that extends 30 μm into the hydrogel, from the surface (nine layers of markers spaced at 3.5 μm) in 70 min.

CONCLUSIONS

In summary, a new TFM platform was developed that offers complete control over 3D fiducial marker placement to simplify measurement of cell-induced normal and shear material deformation in individual cells, cell clusters, and patterned cells.