Flexible filtering by neural inputs supports motion computation across states and stimuli

Summary

Sensory systems flexibly adapt their processing properties across a wide range of environmental and behavioral conditions. Such variable processing complicates attempts to extract mechanistic understanding of sensory computations. This is evident in the highly constrained, canonical Drosophila motion detection circuit, where the core computation underlying direction selectivity is still debated despite extensive studies. Here, we measured the filtering properties of neural inputs to the OFF motion-detecting T5 cell in Drosophila. We report state- and stimulus-dependent changes in the shape of these signals, which become more biphasic under specific conditions. Summing these inputs within the framework of a connectomic-constrained model of the circuit demonstrates that these shapes are sufficient to explain T5 responses to various motion stimuli. Thus, our stimulus- and state-dependent measurements reconcile motion computation with the anatomy of the circuit. These findings provide a clear example of how a basic circuit supports flexible sensory computation.

Graphical Abstract

eTOC Blurb

Kohn, Portes et al. measure state and stimulus dependent high temporal resolution responses of neural inputs to the Drosophila T5 motion detector. They show that simple linear summation of excitatory adaptive neural input signals is sufficient to explain direction selective responses across conditions.

Introduction

To operate in diverse environmental and behavioral conditions, sensory neurons must encode signals across a broad range of input statistics. This requires a number of forms of adaptation, including stimulus- and state-dependent changes in gain and tuning^1,2. Although sensory adaptation has been studied extensively, it has generally been difficult to explore its implications for computations performed across a full neural circuit. Here we take advantage of the extensively characterized Drosophila visual motion detection circuity to reveal how adaptive changes in the processing properties of sensory inputs affect the output of a motion detector. Our results reveal how modifications of temporal selectivity due to both behavioral state and input statistics impact motion detection, and clarify a fundamental computation underlying direction selectivity.

Some of the adaptive effects we report, in particular those associated with state changes, likely involve modulation of cellular and/or synaptic function. Others, such as those associated with stimulus statistics, could reflect dynamic changes in cellular properties or could arise from nonlinearities without requiring dynamic changes. Following convention^1,2, we use the term “adaptation” in either case as a catch-all to describe state- and stimulus-dependent changes in sensory processing.

Across taxa, neural circuits for motion detection are especially sensitive to both behavioral state and sensory statistics in different natural environments^3,4. Motion detection circuits in Drosophila provide an ideal model for understanding the impact of adaptation on neural circuitry. The physiological properties of both the neural inputs and the outputs of fly motion detecting ON and OFF pathways have been extensively characterized^5,6,7. Moreover, unlike in most other model systems, the Drosophila motion circuit connectome has been well-defined by electron microscopy reconstruction^8,9. Despite these detailed descriptions, however, the core computation underlying direction selectivity is still uncertain, and recently proposed models are in disagreement^10,11,12,13. A number of studies have highlighted the fact that, as in vertebrate systems, circuit elements change their response properties in different behavioral states^10,14,15,16 and for different stimuli^17,18. However, the relationship between adaptive sensory encoding and motion computation has not been explicitly investigated.

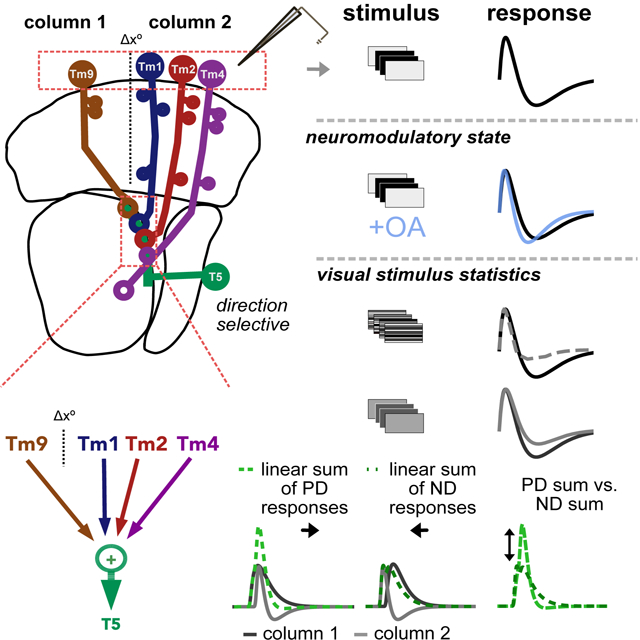
To address this question, we recorded the responses of the primary neural inputs to T5 OFF motion sensing neurons for stimuli with different visual statistics and in the presence of a behaviorally relevant neuromodulator. In addition to previously described frequency tuning¹⁰ and contrast gain adaptation^17,18 (Figure 1A, left and center), we found that these neural inputs display state- and stimulus-dependent changes in the shapes of their temporal filtering properties, including instances of strong biphasic responses (Figure 1A, right). This previously unappreciated aspect of sensory dynamics can have profound consequences on circuit function. For instance, linearly combining two spatially separated inputs, when one is biphasic, can enhance direction selective responses (Figure 1B). To investigate the consequences of this biphasic tuning on T5 responses, we incorporated our measurements into a model based on the Drosophila optic lobe connectome and summation of the measured responses of neural inputs. When adjusted to account for the differences in shape of neural input filters in response to different motion stimuli, our model resolves discrepancies between previously reported T5 responses across conditions^11,12. Our results highlight the flexible nature of this stereotyped circuit and show that changes in the shape of neural input filters are necessary and sufficient to explain direction selective responses in the context of diverse stimuli and states. More generally, our work illustrates how a neural circuit can optimize the computation it performs in response to statistical features of the sensory environment and changes in behavior.

Figure 1: Neural input adaptation and motion detection in the Drosophila OFF Pathway.

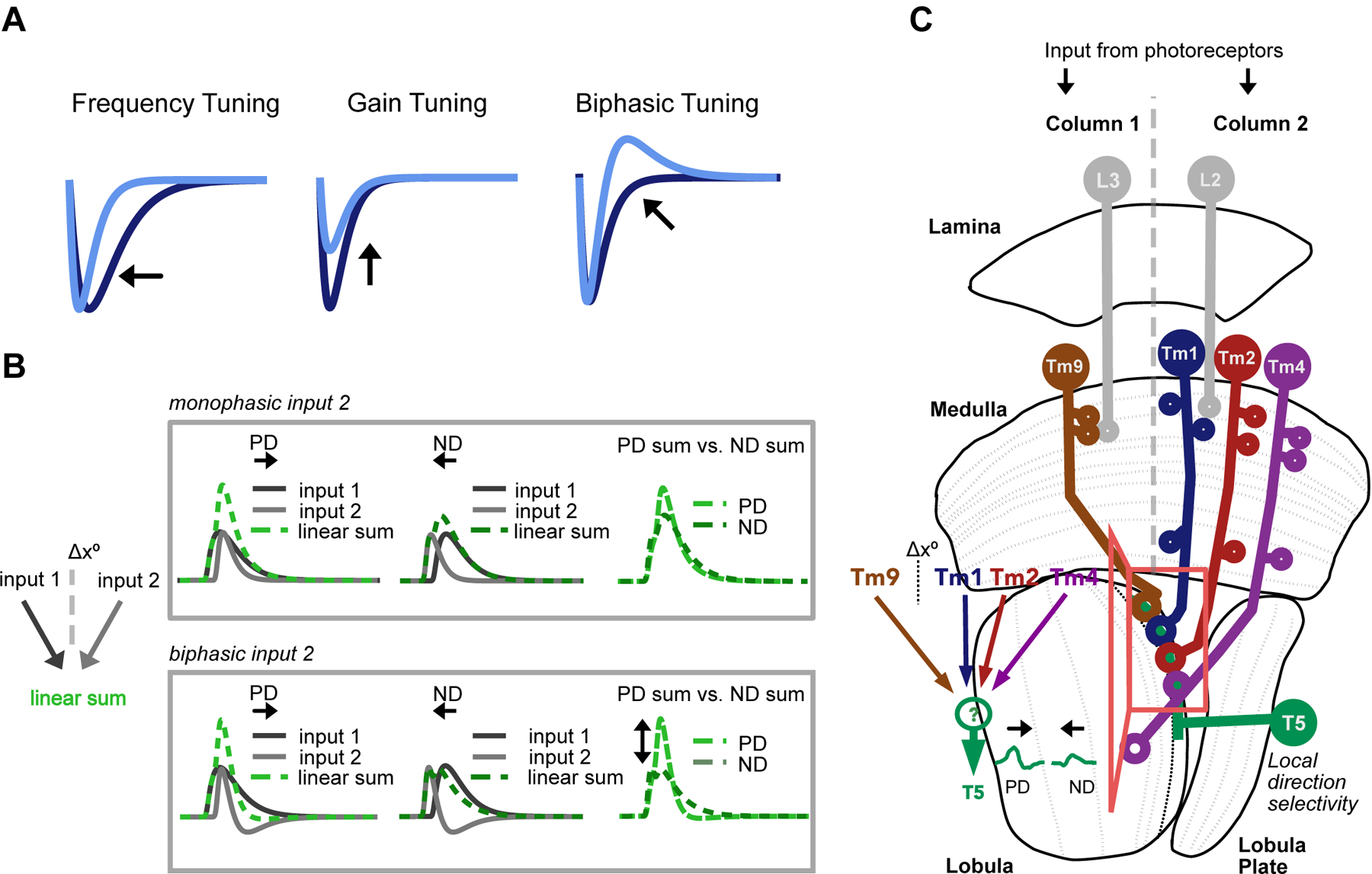
A. The temporal processing properties of sensory neurons, here represented by idealized temporal filters, have been shown to be stimulus and/or state dependent, varying in frequency, gain, and biphasic tuning (which can also affect frequency tuning). B. Filter shape can have a strong effect on the output of a motion detector. The linear combination of two excitatory inputs spatially offset by Δx°, one of which is biphasic (bottom, input 1 is monophasic, while input 2 is biphasic), can effectively suppress ND responses, generating an output that is more direction selective than the sum of two monophasic inputs (top). C. Schematic of the feed-forward Drosophila OFF motion pathway circuit Inset: T5 cells receive the majority of their input from columnar Tm1, Tm2, Tm4 and Tm9. Using the spatial distribution of synaptic inputs to T5 dendrites in the lobula, Shinomiya et al.⁹ infer the spatial structure of inputs in the medulla: Tm1/Tm2/Tm4 are postsynaptic to lamina monopolar cell L2 and look at the same point in space. They are spatially offset (Δx°) from Tm9, which is postsynaptic to L3. Voltage responses in T5 are direction selective, depolarizing more strongly to motion in the preferred direction (PD) than to motion in the opposite, null direction (ND). The mechanisms underlying the emergence of these signals in T5 are debated.

Results

Octopamine changes both the frequency tuning and the shape of temporal filters of neural inputs to T5

OFF motion-sensing T5 neurons compare changes in luminance at neighboring points in space to generate direction selective signals. Such spatial displacement of neural inputs to T5 was inferred from averaged weighted visuospatial distribution of synapses onto the dendrites of these neurons from connectomic data⁹. This analysis concluded that T5 receives what can be considered as “columnar” inputs (i.e. corresponding to one pixel in the field of view of the animal) from medulla cells Tm1, Tm2, and Tm4 in one column and from Tm9 cells in an offset, neighboring column (Figure 1C)^9,10,19,20. These four neurons make up the majority of feed-forward, columnar inputs to T5. Their response properties are critical in shaping the direction selective properties of T5 cells. T5 also receives input from the inhibitory wide-field neuron CT1. However, while CT1 exhibits compartmentalized responses compatible with it acting at the columnar level²¹, it has not been shown experimentally to affect motion detection. We therefore focused our investigation on columnar feed-forward inputs, which have previously been shown to affect motion detection²⁰. Specifically, we asked to what extent the responses properties of these neural inputs depend on stimulus and state, and measured the responses of Tm1/Tm2/Tm4/Tm9 in the absence/presence of a neuromodulator known to affect motion signals, as well as to different types of stimuli. We used whole-cell patch clamp electrophysiology to obtain high-temporal resolution measurements of these response properties, as important aspects might be overlooked when using lower temporal resolution imaging techniques^10,11,22.

We started our analysis by measuring the processing properties of each of these cell types in response to a Gaussian white noise stimulus^10,23,24,25. This standard approach allowed us to extract linear spatiotemporal filters and associated nonlinearities via reverse correlation from cellular responses to a stimulus consisting of 5° horizontal flickering bars, each showing independently generated Gaussian white noise (Figure 2 and Figure S1). As expected, the linear temporal filters of OFF-pathway inputs Tm1/Tm2/Tm4/Tm9 consist primarily of a negative lobe, indicating a sign-inversion between contrast polarity and cellular response (Figure 2A). In the frequency domain, Tm1/Tm2/Tm4 exhibit clear band-pass filtering properties^10,20 (Figure 2B). These band-pass properties correspond to the slight biphasic character of their linear temporal filters, which have shallow second positive lobes. In contrast to results obtained with calcium imaging, which determined that Tm9 is low-pass^10,20,26, we find that Tm9 also exhibits band-pass filtering properties, albeit weaker than the other columnar inputs. This discrepancy is most likely due to differences in the temporal resolution of calcium imaging and electrophysiology techniques.

Figure 2: Octopamine changes both the frequency tuning and the shape of temporal filters of neural inputs to T5.

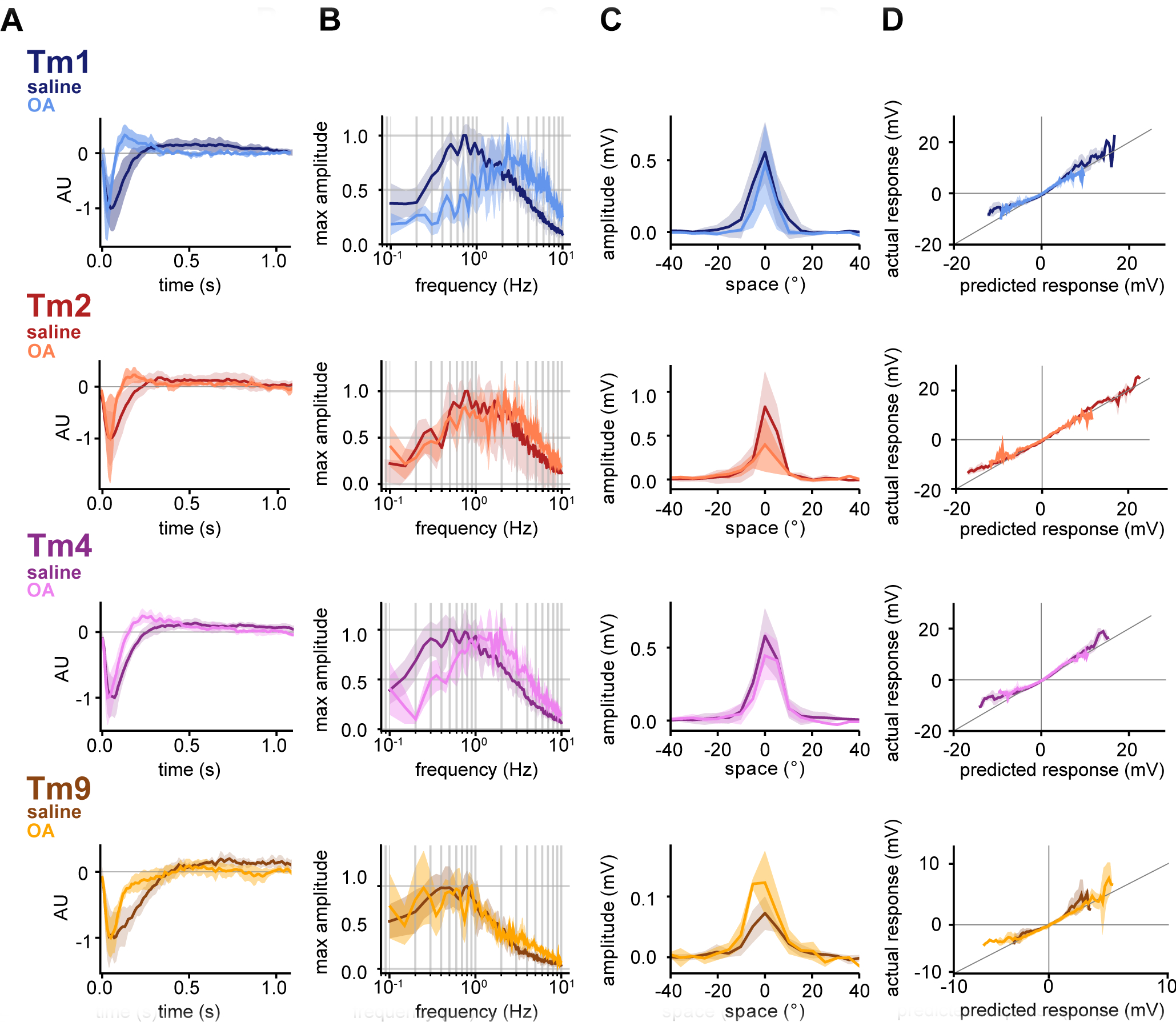
A. Normalized mean temporal filters extracted via white noise analysis in saline (darker colored lines, Tm1 (n=8), Tm2 (n=5), Tm4 (n=6), and Tm9 (n=7)) and in the presence of OA (lighter colored lines, Tm1 (n=4), Tm2 (n=5), Tm4 (n=4), and Tm9 (n=4)). Filters extracted in OA are faster, with a narrower first lobe for all four neurons and the emergence of a sharp second lobe in the case of Tm1/Tm2/Tm4. Shaded area represents standard deviation. B. Normalized mean frequency tuning of temporal filters from A, when linearly convolved with sine waves of increasing temporal frequency. All four Tm neurons are band-pass. Tm9 shows lower temporal frequency optimum than Tm1/Tm2/Tm4. Tm1/Tm2/Tm4 filters in the presence of OA shift their tuning to higher frequencies, while Tm9 tuning changes only slightly. C. Mean spatial receptive fields extracted from spatiotemporal filters with full width at half maximum (FWHM) of 10.8° for Tm1, 8.2° for Tm2, 11.3° for Tm4 and 15.3° for Tm9 when fit with Gaussians (see STAR Methods), with no significant differences in OA. Spatiotemporal filters were extracted in response to white noise presented as 5° horizontal bars. D. Static nonlinearities show partial rectification, with no differences between saline and OA conditions. See also Figures S1 and S2.

The spatial components of our linear spatiotemporal receptive fields show Tm1/Tm2/Tm4/Tm9 to have narrow spatial receptive fields, with only limited surround inhibition. An additional subset of Tm9 cells responded across a much wider region of the screen (Figure S1), as previously reported^13,26. Tm9 responses fall naturally into two distinct populations based on their spatial receptive fields; however, with regards to their temporal properties, the two types of Tm9 responses are not distinct from each other (Figure S1). In terms of nonlinear processing properties, the extracted static nonlinearities show partial rectification^22,24. All four T5 inputs respond linearly for small deflections in their membrane potential, but nonlinearly at the upper and lower boundaries of their dynamic ranges, with greater-than-linear depolarization amplitudes, and less-than-linear hyperpolarization amplitudes (Figure 2D).

We then performed the same analysis in the presence of the neuromodulator octopamine (OA), which mediates a locomotion-induced shift in the tuning of T4 and T5, as well as downstream partners, towards faster frequencies of motion^10,15,16. Bath application of OA or an OA agonist was previously shown to increase the kinetics of the responses of inputs to motion detectors^10,27. Thus, we specifically focused on its effect on the waveforms of cellular responses of neural inputs to T5. We found that while the application of OA had strong effects on the temporal filters of Tm1/Tm2/Tm4 (Figure 2A). In addition to inducing faster temporal filter peaks, which manifests in the frequency domain as a shift toward higher frequencies (Figure 2B), OA induces a biphasic character in the temporal filters of Tm1/Tm2/Tm4, with a sharp, positive second lobe emerging (Figure 2A). Correspondingly, responses are more band-pass in the frequency domain (Figure 2B). In the case of Tm9, the temporal filter becomes narrower, but does not present the biphasic character that the other Tm neurons acquire in OA.

Stimulus dependence can elicit changes in response shape similar to those produced by octopamine

Neuromodulator-mediated adaptive changes in the processing properties of neurons, corresponding to different brain states, have been described in all sensory systems^28,29. Furthermore, neurons across sensory systems exhibit another form of adaptation that depends on the statistics of a particular sensory stimulus^{1,30,31,32,33,34}. This stimulus-dependent adaptation may arise from nonlinearities inherent to the system rather than “true” dynamical changes, and is also widespread^1,2. Thus, we next asked whether the shape changes seen in the presence of OA can also be induced by probing cells with different visual stimuli. To answer this question, we recorded the responses of Tm1/Tm2/Tm4/Tm9 to another type of visual stimulus: full-field, high contrast brightness decrements of varying durations from a mean of grey. These “flash” responses in Tm1/Tm2/Tm4 are clearly biphasic (Figure 3A). We compared these responses to predictions made from white noise filters extracted in saline conditions. The responses of Tms to high contrast flashes of 20/40/80/160 ms did not match the output of our LN spatiotemporal white noise filters convolved with same stimuli (Figure 3A, see STAR Methods). Discrepancies appeared in both the shape and amplitude of the responses. More specifically, we found Tm1 and Tm4 flash responses to be more biphasic than corresponding white noise filter predictions across the four flash durations, and to have higher amplitudes than white noise filter predictions. Tm2 flash responses are more similar to the white noise prediction, but also display a more biphasic response for 40 ms flashes. In addition, Tm1/Tm2/Tm4 white noise filter predictions of 20 and 40 ms flashes underestimate actual amplitudes of responses to flash stimuli, highlighting nonlinearities in gain at these shorter time scales. While the gain of the excitatory lobes of all Tm cell flash responses increases with flash duration, the amplitude of the negative lobe remains constant across stimulus duration. Tm9 flash responses are larger in amplitude than white noise predictions for all flash durations, and repolarization kinetics are slower.

Figure 3: High contrast flashes elicit biphasic responses in T5 inputs.

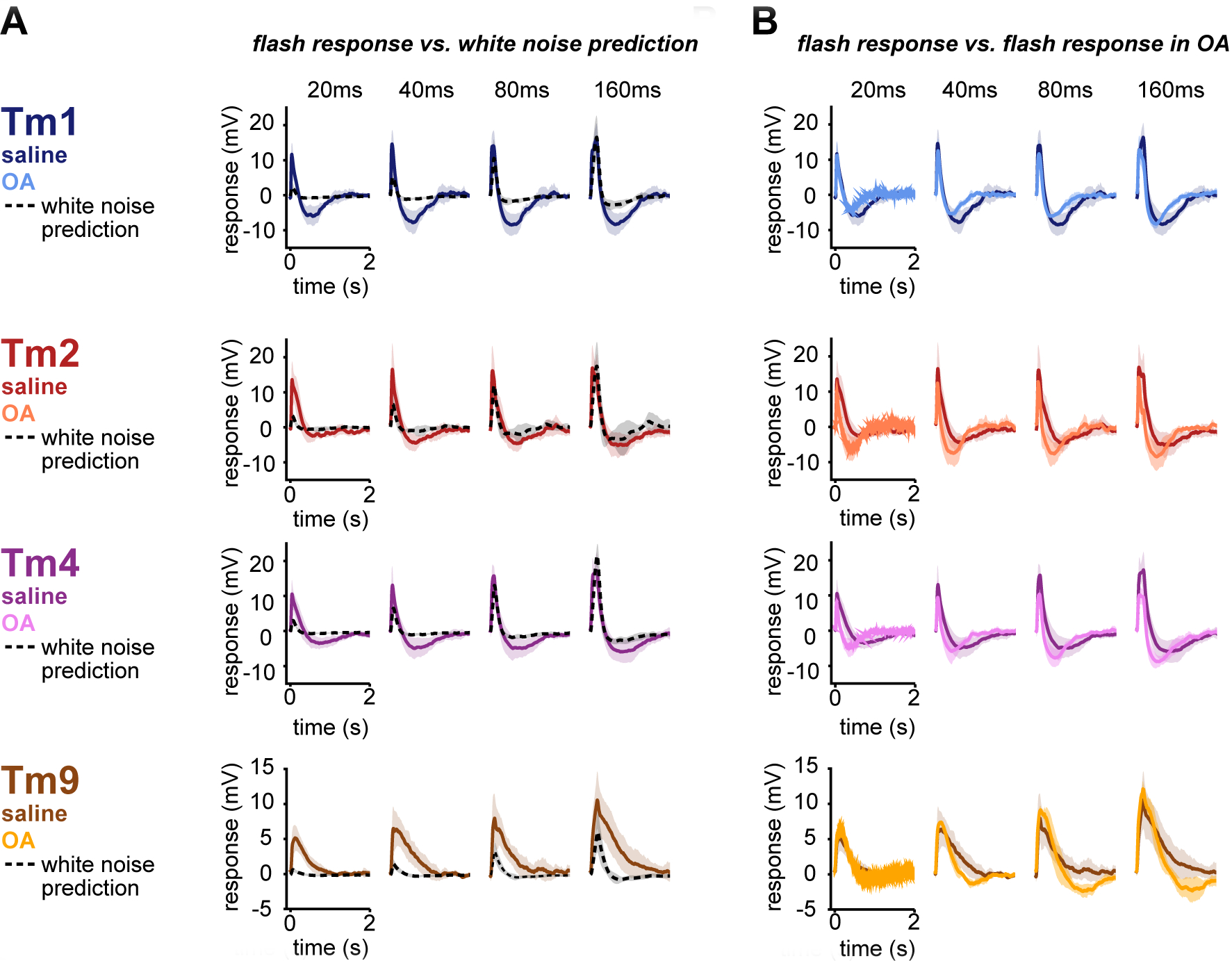
A. Mean Tm responses to 20/40/80/160 ms high contrast flashes in saline (colored lines, Tm1 (n=5–6), Tm2 (n=5), Tm4 (n=6–7), and Tm9 (n=4–6)) are biphasic. Mean white noise filter predictions for the same 20/40/80/160 flashes (black, dashed lines) do not match the corresponding flash responses. Shaded area represents standard deviation. B. Responses to 20/40/80/160 ms high contrast flashes return to baseline more quickly and, in most instances, are more biphasic in OA (Tm1 (n=4–5), Tm2 (n=3), Tm4 (n=5–6), and Tm9 (n=3), lighter colored lines) than in saline (darker colored lines, same as in A). See also Figure S3.

These experiments demonstrate that linear filters combined with a static nonlinearity are poor approximators of Tm cell responses to high contrast flashes. This is consistent with a form of adaptation that likely reflects the inherent nonlinear properties of the system, and for which statistical models, such as linear-nonlinear models that depend on the stimulus ensemble used to generate them, do not provide a complete description. As such, we refer to these apparent changes in processing properties, which are revealed by the use of multiple types of stimuli and which occur on the same time scale as the response itself, as “stimulus dependent” in the rest of this paper.

We next asked how state-dependent changes interact with stimulus-dependent changes in the temporal processing properties of columnar T5 inputs, and assessed the effect of OA on responses to the same flash stimuli (Figure 3B). The addition of OA only minimally increased the already biphasic nature of Tm1/Tm2/Tm4 flash responses, but did increase the kinetics of the responses. OA once again exerted a minimal effect on Tm9, rendering its monophasic flash responses to be slightly biphasic. Although the filters extracted in response to white noise in OA have a biphasic character, they are still not sufficient to predict flash responses in OA (Figure S3B).

Signal statistics affect the shape of T5 input responses

Across sensory systems, the shape and gain of neural temporal filters are sensitive to the statistical properties of stimuli^{1,30,31,32,33,34}. In blowfly lamina monopolar cells (LMCs), which are correlates of the main inputs to the transmedullary cells that we focused on in this study, the biphasic character of responses increases when the signal to noise ratio (SNR) of a stimulus is increased^35,36. Our results so far fit this framework, since Gaussian noise can be considered low SNR as compared to high contrast flashes. To further explore this question, we varied our stimuli with this property in mind.

In a flash stimulus regime, lowering contrast should equate to lowering the SNR of the stimulus and therefore, according to our hypothesis, decrease the biphasicness of the responses. We found that Tm1/Tm2/Tm4 responses to flashes in low-contrast flashes, starting at the same mean luminance level, indeed lost their biphasic character, and more closely matched the white-noise filter predictions, both in terms of amplitude and waveform (Figure S3A). In the case of Tm9, which is only minimally biphasic to white noise, response shape did not change significantly at different contrasts. Similar to saline conditions, low contrast flashes recorded in the presence of OA produced less biphasic responses than high contrast (Figure S3B); however, low contrast flashes in OA do maintain a slight biphasic character. These results reveal a trend where high contrast (high SNR) flash responses are more biphasic than white noise predictions, while low contrast (low SNR) flash responses are more comparable to white noise predictions.

These results do not preclude the possibility that contrast alone drives shape changes of Tm responses. To explore this possibility, we altered the contrast step size of the noise stimulus. We used high and low contrast ternary noise (Figure S3C, top) consisting of random transitions between the mean luminance of the projector and fixed contrast increments/decrements of either high or low contrast, with the same temporal properties as the white noise. We found that Tm1 filters extracted from both low and high contrast ternary noise have similar shapes to each other (Figure S3D–E, top), as well as to the Tm1 filter extracted from white noise. While we did not see a change in the shapes of filters, we found that the amplitude of the temporal filter increased with decreasing contrast. This gain change corresponds to an amplification of smaller signals, allowing the cell to produce the same amplitude responses in different contrast regimes^17,18. Similar to Tm1, filters extracted from Tm2 and Tm4 responses to the high contrast ternary stimulus (Figure S3C–E, middle, bottom) did not differ significantly in shape from filters extracted from the white noise stimulus, but had lower gains. These experiments demonstrate that increases or decreases in contrast do not change the biphasic character of Tm responses in the context of a noise stimulus. Thus, contrast alone cannot account for changes in response shape. Rather, we hypothesize that specific aspects of signal statistics, such as information content in the stimulus, drive stimulus dependent changes in shape of the responses of these cells.

The temporal responses of columnar T5 inputs move through a stimulus- and state- dependent parameter space

The similarities between shape changes in the temporal responses of T5 columnar inputs to either high contrast flashes or to responses measured in the presence of OA is consistent with a continuum of responses between states and stimuli (Figure 4A). To compare all stimuli and state conditions on a similar temporal timescale, we describe a “parameter space” of responses for each of the inputs to T5, using parameterized responses (Figure S4, see STAR Methods).

Figure 4: Tm1, Tm2, Tm4 and Tm9 temporal responses move within a parameter space.

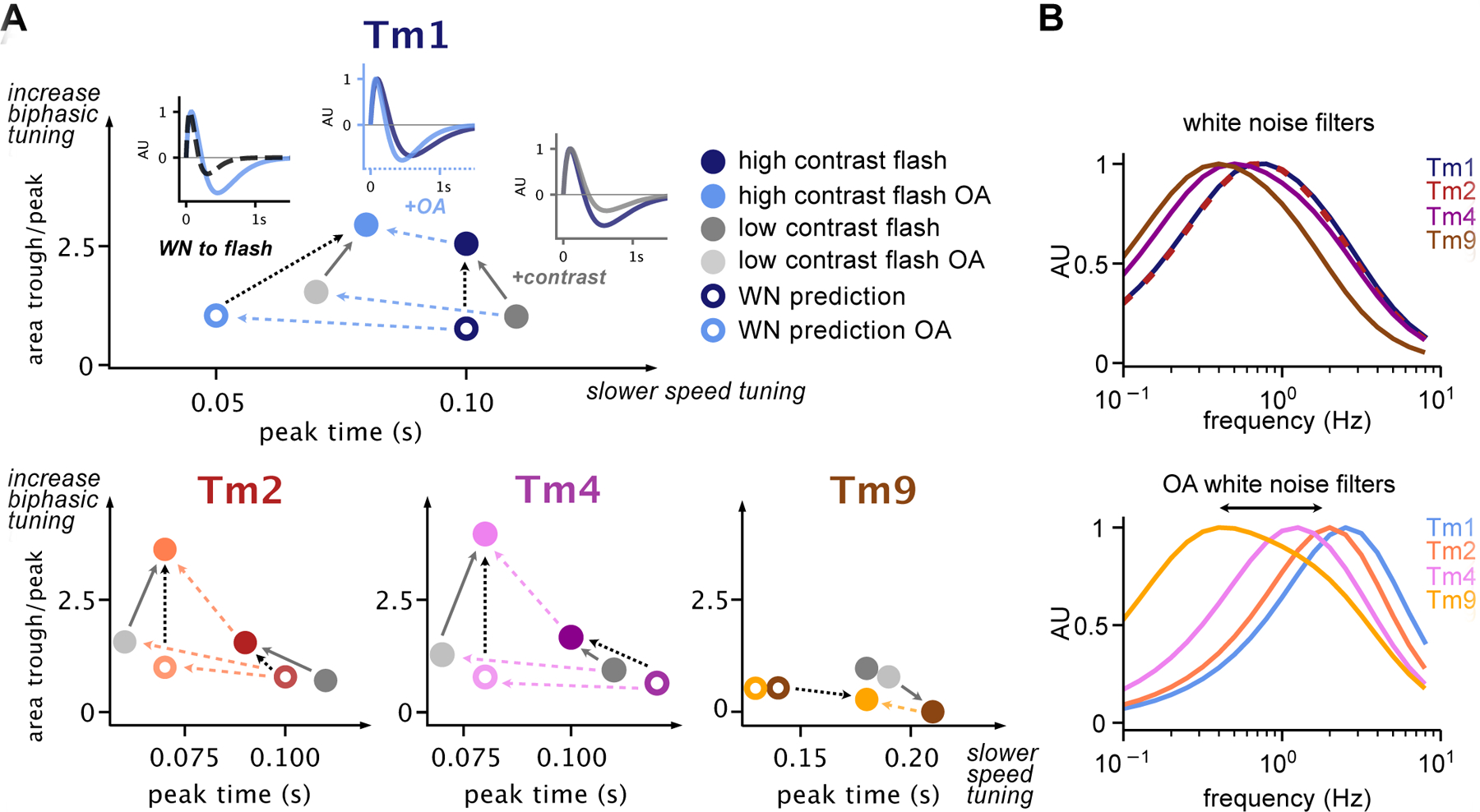
A. ratio of the area of the peak lobe with respect to the trough lobe (biphasic tuning) as a function of peak time (speed tuning) of parameterized responses of Tm1, Tm2, Tm4 and Tm9 to 160 ms flashes across conditions, including high contrast and high contrast OA (solid colored filled circles), low contrast and low contrast OA (grey filled circles), and baseline and OA white noise filter predictions for 160 ms stimuli (colored circles). For Tm1, example traces are included in insets comparing (i) White noise OA prediction and high contrast flash in OA, (ii) high contrast flashes with and without OA, and (iii) low and high contrast flashes. Solid grey, dashed black and dashed blue lines indicate corresponding trends in biphasic and speed tuning driven by OA or stimulus. B. Frequency tuning of parameterized filters obtained in saline (top) and in OA (bottom). Tm1/Tm2/Tm4 filters in OA become more band-pass (respond to a narrower range of frequencies), and shift their peaks to higher frequencies. Additionally, Tm1/Tm2/Tm4/Tm9 become more distinct in the frequency range each cell responds to. See also Figure S4.

We focused on responses to a 160 ms flash stimulus, either measured directly or predicted from white noise filters across all Tm cells, in the absence and the presence of OA. Plotted together, it is clear that Tm1/Tm2/Tm4 exhibit a wide range of responses, while Tm9 shows somewhat fewer changes across stimuli (Figure S4C). To better visualize how different conditions affect these responses, we plotted the ratio of the area of the trough by the area of the peak as a function of peak time, roughly representing the extent of a filter’s biphasic character as a function of speed of response (Figure 4A). The 2D space occupied by the Tm neurons within these plots illustrates the span of the diversity of responses within cell types and reveals global trends: responses shift toward being faster and more biphasic in the presence of OA, and move from being less to more biphasic between both noise/flash stimuli and low/high contrast flashes. This analysis also reveals another stimulus-dependent effect: high contrast flash responses are faster than low contrast, once again indicating that high contrast flash stimuli can elicit changes in Tm responses similar to those seen in OA. In the case of white noise filters, the effect of OA is particularly clear in the frequency domain (Figure 4B). OA shifts peak responses of Tm1/Tm2/Tm4 towards higher frequencies so that their frequency tuning curves are spread further from each other, and thus across a broader spectrum of frequencies, than in saline conditions. Tm9 changes are mainly restricted to the single axis of speed tuning.

Our high temporal resolution electrophysiological recordings of Tm1/Tm2/Tm4/Tm9 under different stimuli and neuromodulatory conditions reveal a highly adaptive circuit with the ability to display changes in temporal filter shape and kinetics across a wide range of parameters. We next investigated the computational consequences of these stimulus- and state-dependent properties of neural input on the output of the circuit.

A sum of columnar inputs predicts T5 flash responses

In order to determine whether state- and stimulus-dependent processing properties of T5 inputs could explain responses at the level of T5, we used our measured responses to predict T5 voltage responses¹². In response to stationary high contrast flashing bars, T5 displays asymmetric hyperpolarizing responses: for any particular T5 cell, flashing bars on the side of the spatial receptive field corresponding to the leading edge of the cell’s preferred direction of motion elicit only a depolarizing response. Bars on the opposite side of the receptive field, however, cause a depolarization followed by a hyperpolarization. One potential model to explain this functional property uses a combination of direct columnar excitation and inhibition; however, since no such columnar inhibitory input has been found by connectome studies⁹, we instead hypothesized that the strongly biphasic nature of the temporal responses of Tm1/Tm2/Tm4 to flashes could explain T5 responses without the need for a direct inhibitory input. Because Tm1/Tm2/Tm4 have similar processing properties (Figure 3) and look at the same point in space⁹, we asked whether a single biphasic excitatory columnar input combined with Tm9 via linear regression could capture the dynamics of the T5 response, including asymmetric hyperpolarization.

We used our measured responses of Tm1 and Tm9 to predict T5 responses to stationary high contrast flashing bars without additional manipulation. To compare our data with existing T5 data, we first convolved the white-noise extracted linear temporal filter of each cell type with a 1D stimulus of length 20/40/80/160 ms^12,37. Using linear regression with positivity constraints, we fit these predicted responses to T5 flash responses collected by Gruntman et al.¹². As expected from their shape, we find that the white noise filter predictions were able to capture the depolarizing responses, but failed to capture asymmetric hyperpolarization (Figure 5A, top).

Figure 5: The sum of adaptive columnar inputs predicts T5 flash responses.

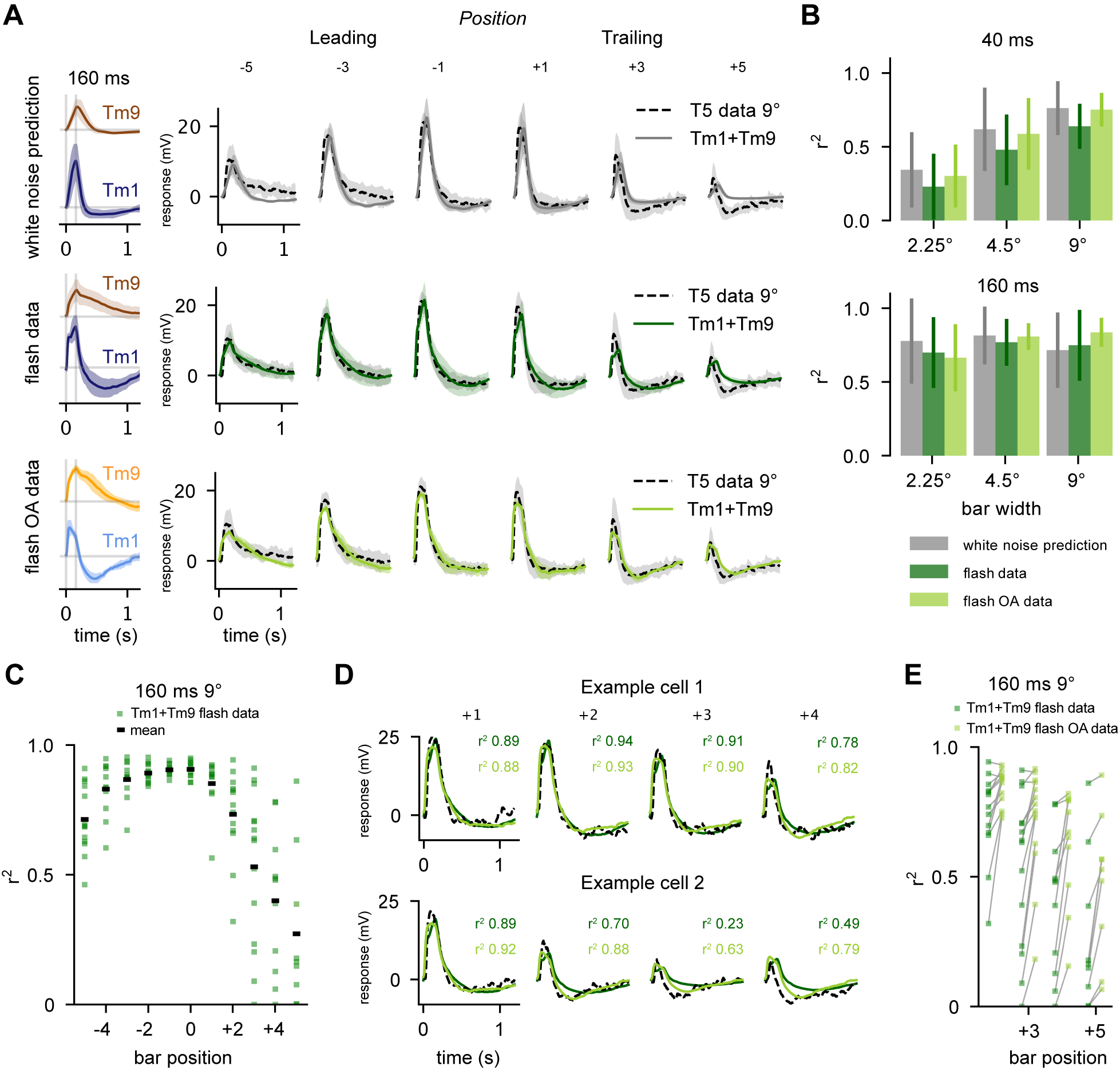
A.Top: White noise extracted filters are convolved with 160 ms stimulus and then fit with linear regression to T5 electrophysiological recordings from Gruntman et al. [6] for the 160 ms, 9° bar condition, at various positions in the receptive field of T5 (data dashed line, fit solid grey line). T5 average traces shown for bar position from “Leading” edge (−5, −3, −1) and “Trailing” edge (+1, +3, +5). Middle: Average Tm1 and Tm9 responses to 160 ms flashes are fit via linear regression to each T5 recording from Gruntman et al. [6] for the 160 ms, 9° bar condition (data dashed line, fit solid dark green line) Bottom: Same as Middle using Tm1 and Tm9 160 ms flashes in the presence of OA (data dashed line, fit solid line). Linear regression using flash responses and flash responses recorded in OA provides a good fit to T5 data. This is especially evident in the trailing edge (bar positions +3 and +5). B. Aggregate r² values (square of sample correlation coefficient, see STAR Methods) across bar positions for linear regression fits of Tm1+Tm9 to Gruntman et al.¹² recordings of T5 (conditions: 40 and 160 ms presentations of 2.25°, 4.5°, and 9° bars). Error bars depict standard deviation C. Distribution of r² values across bar positions for fits to individual T5 responses to 160 ms, 9° bars. D. Example traces of fits to two single cells from C (T5 data, black dashed line; fits using saline flashes, dark green; fits using OA flashes, light green). E. Using the highly biphasic Tm1/Tm9 flashes recorded in OA improves the r² of fits on the trailing edge of the T5 receptive field, where asymmetric hyperpolarization is most evident. See also Figure S5.

We next asked if our flash responses, which were obtained from an experimental paradigm more similar to the single-position bar flashes of Gruntman et al., could predict response properties of T5 more accurately than our white noise filters. We find that a weighted sum of Tm1 and Tm9 responses derived from flash stimuli do better at reproducing measured T5 responses to single-position bar flashes (Figure 5A, middle), but still fall short of capturing both the extent and the kinetics of T5’s asymmetric hyperpolarization at the trailing edge of the T5 receptive field. Since Tm1 flash responses obtained in OA conditions have faster kinetics and larger second lobes, we also ran the linear regression using flash responses of Tm1 and Tm9 obtained in the presence of OA. In this case, the linear regression provides a near perfect fit with T5 data (Figure 5A, bottom).

It was puzzling that the flash responses recorded in OA provided such a good fit in the linear regression, as Gruntman et al.¹² acquired these data in regular saline and not in OA-supplemented saline. It is, however, conceivable that endogenous state modulation occurred during T5 recordings. This was hinted at by the apparent variability in the amplitude and kinetics of the asymmetric hyperpolarization in T5 responses across different cells¹². To investigate this, we performed linear regression on individual T5 cells, instead of the average of all recordings, using flash responses recorded in either saline or saline with OA. For a subset of T5 with slower and less salient hyperpolarization, the saline linear regression provided a good fit (Figure 5C and D top). For a different set of T5 cells, the OA linear regression provided a better fit (Figure 5D bottom). This indicates that the diversity of responses in the T5 data largely accounts for the distribution of our r² values (Figure 5C). In these cases, performing the linear regression using the OA flash responses often increased the r² value substantially (Figure 5E). Although we performed this analysis using Tm1 and Tm9 to predict 9° 160 ms T5 flashes, these results stand across flash durations and widths as well as using other combinations of Tm inputs (Figure S5A–B).

In all conditions, the coefficients output by this linear regression show distinct separation between Tm1 and Tm9 (Figure S5C), similar to that seen in the electron-microscopy (EM) data. In addition, the weighted spatiotemporal receptive fields constructed by linearly combining Tm1 and Tm9 fits are tilted in space-time, indicating direction selectivity. The tilt is more prominent when these are constructed from flash responses, both in saline and OA. In agreement with this, the same linear regression fits predict the profile of T5 responses to moving bars from Gruntman et al.¹², as well as direction selectivity (Figure S5D, see STAR Methods).

These results demonstrate that including a biphasic input to T5 within the framework of this model is sufficient to explain measured output response properties such as spatially asymmetric hyperpolarization, which was previously proposed to emerge from an unsubstantiated direct inhibitory input. Thus, accounting for stimulus and state dependence of inputs to T5 is critical to understanding the response properties of this hardwired circuit across conditions.

A connectome-based model captures T5 direction selectivity across stimuli and states

Motivated by the linear regression, we built a model of T5 direction selectivity that is faithful to the anatomy of the circuit and takes into account our experimental measurements of Tm response properties. We imposed the following overarching constraints: (1) T5 receives inputs from Tm9 in one ommatidial column, and Tm1/Tm2/Tm4 from an adjacent column, (2) all four T5 inputs are excitatory (cholinergic), and (3) the response properties of the transmedullary inputs vary with stimulus or state, as we demonstrated. We captured the first constraint by separating the center of the receptive field of Tm9 by 5° from the rest of the Tm cells (Figure 6A). The second constraint was satisfied by requiring all cells to provide positive input to T5. Additionally, we used the relative synaptic counts of Tm1/Tm2/Tm4/Tm9 from the connectome as synaptic weights to constrain the relative contribution of each cell type to T5 responses⁹. For the third constraint, when constructing the four inputs to T5, we matched their response properties with the stimulus presented to our model, such as moving sine waves^11,12 or high contrast moving bars¹².

Figure 6: Low-parameter, connectome-based model is sufficient to capture OFF pathway direction selectivity in the context of different stimuli and states.

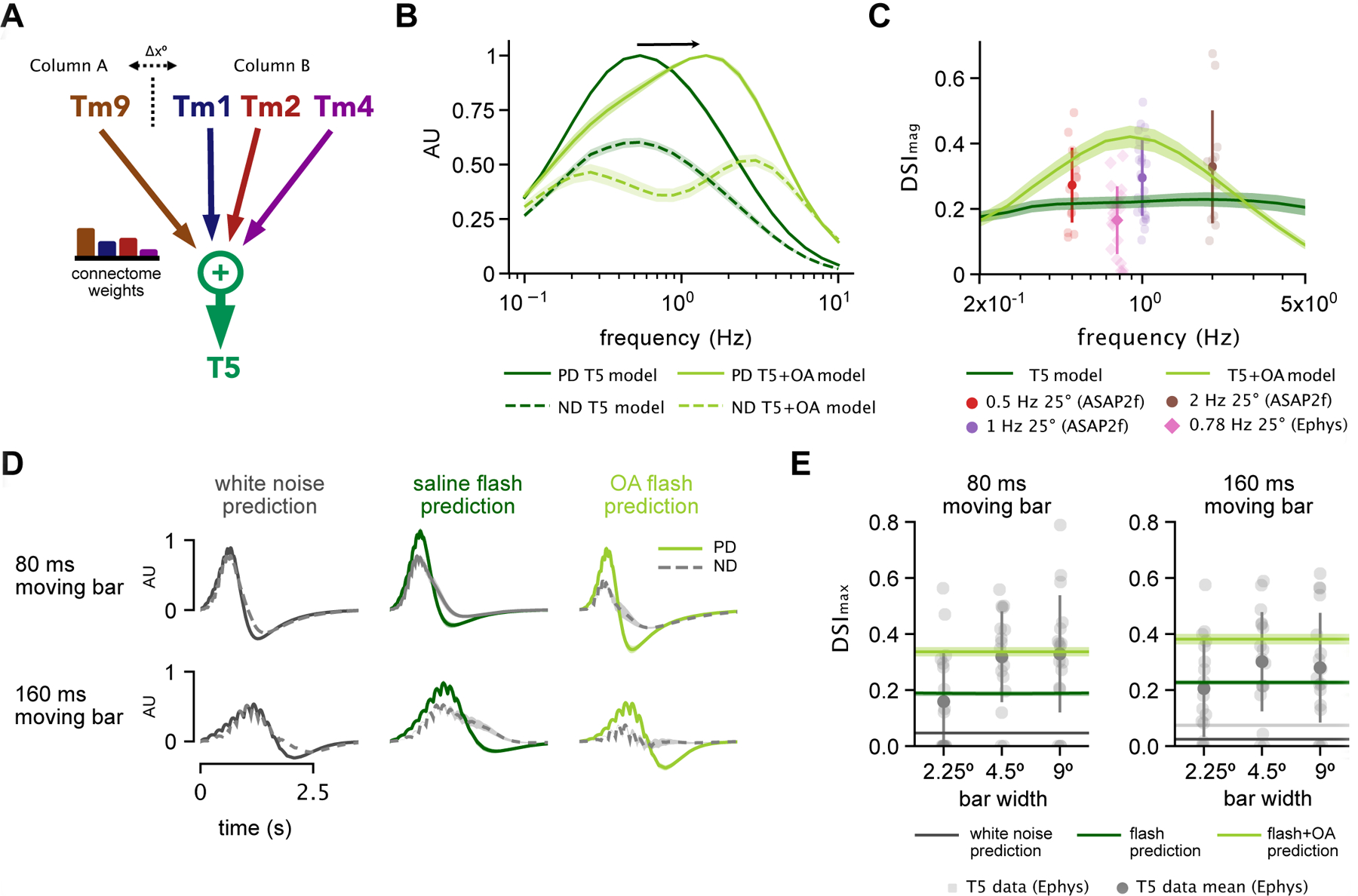
A. Schematic of model framework constructed with Tm9 spatially offset from Tm1/Tm2/Tm4 by Δx = 5°. Connectome weights refer to weighted visuospatial distribution of synaptic inputs⁹. B. Preferred direction (PD) and null direction (ND) frequency tuning of model to sine waves using parameterized spatiotemporal filters extracted in saline alone (dark green) vs. those extracted in the presence of OA (light green). C. Direction selectivity index (DSI_mag = (|PD| − |ND|)/(|PD| + |ND|), see STAR Methods) for model using saline-derived filters with n=20 samples of published EM weights from [16] across various frequencies (dark green) compared to output using OA-derived filters (light green). Experimental voltage-imaging (ASAP2f) T5 DSI data shown from¹¹ (circles), and T5 electrophysiology data from¹² (diamonds). D. Example PD and ND model output traces for an 80 ms and a 160 ms moving bar stimulus, with inputs based on white noise predictions (left, black), flash responses recorded in saline (middle, dark green) and OA (right, light green). E. Using flash response-based inputs, model DSI falls within the range of T5 electrophysiology data reported by Gruntman et al.¹² for moving bars. Direction selectivity index (DSI_max = (max(PD) − max(ND)) / (max(PD) + max(ND), see STAR Methods) increases when using OA-based flash responses due to their strong biphasic nature. See also Figure S6.

We first modeled T5 responses to sine waves. To describe the response of each T5 input to this stimulus, we used the temporal and spatial filters of Tms extracted from white noise analysis, as well as their associated static nonlinearities (see STAR Methods). These filters accurately predicted measured responses of Tm cells to sine waves (Figure S6), making them appropriate descriptors of cellular responses in this particular stimulus regime. Output from this model in response to sine waves matched T5 data from previous studies, in that it predicted maximum preferred direction (PD) tuning just below 1 Hz (Figure 6B)^10,15. The direction selectivity index (DSI) for the output of the model also fell within the range of experimentally calculated DSIs from two recent studies: Wienecke et al.¹¹, using voltage-imaging, and Gruntman et al.¹², using electrophysiology (Figure 6C). We then asked how the enhanced biphasic character and shifted frequency tuning of filters extracted in the presence of OA affected model output. In this case, our model predicted a broadening and a shift in T5 PD frequency tuning toward faster frequencies (Figure 6B) that matched previous measurements of T5¹⁰ and LPTC¹⁶ tuning in the presence of OA or the OA agonist chlordimeform (CDM). Furthermore, using OA-derived filters increased DSI (Figure 6C). Using white noise filters, these results show that combining input Tm responses linearly with EM connectome weights is sufficient to achieve the direction selective response of T5 cells to sine waves across studies, and that the biphasic character and faster kinetics introduced by the neuromodulator can enhance direction selectivity while adjusting frequency tuning. Notably, randomizing weights within columns (randomizing Tm1/Tm2/Tm4 weights while maintaining the relative ratio with respect to Tm9) increased variance and produced slightly lower DSI, while completely randomizing weights of Tms caused the model to perform poorly (Figure S6F). This indicates that while there is some flexibility in terms of the ratios of input from Tm1/Tm2/Tm4 from one column, maintaining the anatomical ratio of Tm9 input to combined Tm1/Tm2/Tm4 input is important for producing direction selectivity.

We next modeled T5 response to moving high contrast bars. The results of our linear regression analysis showed that strongly biphasic Tm responses best predicted T5 flashing bar responses. As expected, the characteristic white noise filters for Tms did not capture the DSI of T5 responses to moving bars (Figure 6D left, E). We therefore constructed a corollary model of T5 based on parameterized Tm flash responses (see STAR Methods). The increased biphasic nature of the flash responses allowed the model to achieve direction selectivity for moving bar stimuli in the range of T5 recorded electrophysiology data¹² (Figure 6D middle, E). In this case, the negative lobe from strongly biphasic Tm inputs cancels out depolarizations in lieu of direct inhibition. Correspondingly, flash responses obtained in the presence of OA increased the model’s DSI when used as inputs (Figure 6E). These results demonstrate that the increased biphasic character of Tm cells, which occurs both as the result of changes to stimulus or the presence of a neuromodulator, can produce direction selectivity on par with that seen in T5 electrophysiology recordings.

Our state- and stimulus-dependent measurements of the response properties of neural inputs to T5, when considered within the framework of a simple model grounded in connectomic data, are therefore necessary and sufficient to explain T5 direction selective signals across experimental paradigms. Our approach not only highlights encoding flexibility but also reconciles anatomy and function in a canonical Drosophila circuit.

Discussion

In this study, we demonstrate that the response properties of neurons in the Drosophila OFF motion pathway are shaped by both visual stimulus statistics and a behaviorally relevant neuromodulator. Our results demonstrate that neurons in the Drosophila visual system operate within a stimulus- and state-dependent space of temporal filtering parameters, and are underdescribed by the filters commonly used in Drosophila motion circuit models. Incorporating these state- and stimulus-dependent properties into an anatomically constrained model of the motion circuit based on input summation explains the direction selective response of T5 across conditions. By measuring the relationship between stimulus, state, and the response properties of inputs to a motion detector, and incorporating these adaptive signals in an anatomically constrained model, we also clarify the core computation for direction selectivity.

Stimulus- and state-dependent changes in filtering properties highlight circuit flexibility

Previous work has demonstrated changes in frequency tuning¹⁰ and contrast gain adaptation^17,18 at the level of T5 inputs. Here, using methods with high temporal resolution, we characterize changes in response shape; namely the biphasic character that they can acquire, in response to both specific stimuli or state.

This property has been previously demonstrated in blowfly LMCs, the main inputs to the transmedullary cells that we focused on in this study. Both van Hateren³⁵ and Srinivasan et al.³⁶ have shown that the biphasic character of LMC responses is dependent on the signal-to-noise ration (SNR) of the stimulus. These studies provide a rationale for differences across conditions. A monophasic, or low-pass, filter acts as an integrator, extracting slow temporal components of a visual scene. This is useful when visual information is noisy (low SNR), because increases in the redundancy of information translate into increases in reliability. A biphasic, or band-pass, filter, however, is advantageous in high SNR conditions because it acts as a differentiator and decreases correlations, thereby reducing redundancy and efficiently conveying changes in the visual scene³⁸.

When comparing responses across stimuli in stimulus regimes, our recordings of Tm1/Tm2/Tm4 are compatible with these hypotheses regarding SNR. The temporal filters of these three neurons have less biphasic shapes in response to temporally unstructured stimuli that have the characteristics of noise, both white and ternary, which we consider to correspond to a low SNR regime. Responses to low contrast flashes, which can also be considered low SNR, are also close to monophasic and are well predicted by white noise filters. On the other hand, high contrast (high SNR) flashes produce strong biphasic responses. The properties of Tm1/Tm2/Tm4 are therefore similar to, and likely inherited from their LMC input (primarily L2, Figure 1C). Similar effects of changing stimulus mean and variance on neural filtering properties are ubiquitous across sensory systems^{1,30,31,32,33,34}. It will be important for future work to explicitly characterize the effects of stimulus SNR on the responses of Tms and their presynaptic partners, as well as determine the circuit/intrinsic mechanisms underlying them.

Interestingly, we find that the addition of OA also produces a more biphasic character in the white noise-extracted temporal filtering properties of Tm1/Tm2/Tm4, similar to the waveform changes seen in response to high contrast flashes. More biphasic, differentiator-like responses may be beneficial during locomotion, a state also associated with arousal³⁹ or attention⁴, where OA would possibly prime the motion vision circuit to respond to more salient moving stimuli. Furthermore, columnar inputs to T5 express receptors for many neuromodulators other than OA⁴⁰, suggesting that state-dependent modulation of motion detection likely plays an even more heterogeneous role, with multiple neuromodulators acting in concert at any given time.

In addition to changes in filter shapes, we observed OA-dependent shifts in the kinetics of the temporal filters of Tm1/Tm2/Tm4 towards faster speeds. Locomotion, through the release of OA, has previously been shown to broaden and shift the tuning of Drosophila motion detector outputs toward higher frequencies^15,16. This mechanism is thought to tune motion pathways to the increased frequencies of motion that flies experience as a result of self-motion during locomotion. Our findings corroborate the hypothesis that octopaminergic modulation of frequency tuning in this circuit is inherited in part from upstream elements¹⁰. In addition, our high temporal resolution data shows that Tm1/Tm2/Tm4 have similar temporal response dynamics to one another in saline, but acquire different kinetics in the presence of OA. This broadens the range of temporal frequencies collectively encoded by these three neurons (Figure 4C, right), an effect that we see in the output of our model, and which should enable a fly to respond to motion over the broader range of frequencies it might encounter while walking or flying. Thus, while Tm1/Tm2/Tm4 might appear to have redundant roles, the differential effect of OA on these three T5 inputs highlights a functional relevance in the context of changing behavioral states. Finally, in contrast to Tm1/Tm2/Tm4, we find the temporal filtering properties of Tm9 to be less affected by either stimulus statistics or by the presence of OA, showing that adaptation need not affect all input elements of circuit to influence output tuning.

We focused here on changes in temporal dynamics; however, it is likely that additional processing properties of Tm neurons, such as in their spatial receptive fields, are sensitive to both stimulus and state. Integrating changes in these processing properties could hypothetically fine-tune the motion-selective outputs across conditions. In addition, we find two distinct classes of Tm9 cells with different sizes of receptive field, as has been previously reported²⁶. Although larger spatial receptive fields may not contribute directly to direction selectivity, further characterization of this heterogeneity may provide insight into diverse T5 responses.

Accounting for stimulus and state dependence clarifies circuit mechanisms

Although direction selectivity has been investigated since the 1950s, the mechanisms underlying motion detection in the invertebrate visual lobe are still being debated^6,7. In the OFF pathway, one debate concerns the linearity of the summation of inputs to directionally selective T5 neurons. Wienecke et al.¹¹ argue that the response of T5 axonal terminals to stationary and moving sine waves suggests linear summation, whereas Gruntman et al.¹², who studied responses to flashed and moving bars, argue for nonlinear summation. Neither of the studies had access to the waveforms of the actual inputs to T5, which we measure here. On the basis of this additional knowledge, our modeling work supports linear summation of adaptive input signals. Additionally, although T5 responses show apparent suppression in some regions of the visual field, we find that this does not require an inhibitory input. Instead, the biphasic character of the Tm1/Tm2/Tm4 responses in specific stimulus regimes can reproduce the data without direct inhibition. Furthermore, we found that the model could account for direction selectivity when not only the identity but also the strengths of its connections were determined directly from the connectome data⁹. It should be stressed that we are not proposing that inhibition plays no role in the directionally selective OFF pathway. For example, the wide-field inhibitory cell CT1^9,21 may provide wide-field gain normalization^18,41. Such normalization could enhance direction selectivity, but we argue that it is not necessary for producing it.

More generally, the clarification of the computation underlying direction selectivity is a direct consequence of our state- and stimulus-dependent measurements combined with the anatomical constraint imposed by the connectome. When underdescribed, these parameters can lead to diverse algorithms to account for what is ultimately the result of adaptive encoding.

STAR Methods

RESOURCE AVAILABILITY

Lead Contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Rudy Behnia (rb3161@columbia.edu).

Materials Availability

This study did not generate any new unique reagents.

Data and Code Availability

Custom Python code used for modeling and analysis is freely available at GITHUB LINK TBD. All source code used for visual stimulation is available on GitLab

(https://gitlab.com/rbehnialab/motyxia2/whitenoise)

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Fly Genetics

Flies were reared on standard molasses-based medium at 25°C- 28°C. We used the following drivers to target each medulla cell input to T5: R74G01-Gal4 (Tm1), otd-Gal4 (Tm2, gifted by the Desplan Lab⁴²), R35H01-Gal4 (Tm4), and R24C08-Gal4 (Tm9). Drivers were expressed homozygously in a w+ background along with a a cytosolic variant of UAS–GFP (a gift from G.Turner). All experimental animals were collected approximately 24 hours post-eclosion.

METHOD DETAILS

Electrophysiology

Flies were anesthetized on ice for approximately 30 seconds, or until movement ceased. Legs were then amputated below the coxa-femur joint, and flies were gently mounted in a custom stainless-steel/3D-printed holder before being secured in place with epoxy resin. A window was cut in the cuticle on the caudal side of the head to expose the medulla, where the cell bodies of Tm cells could be visualized. Dorsal and anterior trachea and fat deposits were gently removed, and 1% protease in physiological saline (see below) was applied to the exposed brain for 90 seconds to remove the glial sheath.

During recording, the eyes of the fly remained face down under the holder, and remained dry while viewing the visual stimuli, while the upper part of the preparation, including the exposed brain, was covered with saline. The saline composition was as follows (in mM): 103 NaCl, 3 KCl, 5 n- tri(hydroxymethyl) methyl-1Aminoethane-sulphonic acid, 8 trehalose, 10 glucose, 26 NaHCO3, 1 NaH2PO4, 1.5 CaCl2, and 4 MgCl2, adjusted to 270 mOsm. The pH of the saline was equilibrated near 7.3 when bubbled with 95%O2/5%CO2. Saline was perfused continuously over the preparation at 2 mL/min using a gravity perfusion system. To record in OA conditions, the physiological saline solution was switched to a physiological saline solution containing 10 μM OA via a Y-perfusion manifold.

Patch-clamp electrodes (resistance 8–12 MΩ) were pressure-polished and filled with internal solution composed of the following (in mM): 125 potassium aspartate, 10 HEPES, 1 KCl, 4 MgATP, 0.5 Na3GTP, and 1 EGTA, 13 biocytin hydrazide, pH 7.3, adjusted to 265 mOsm. Recordings were obtained under visual control using an Olympus BX51 with 60X water-immersion objective mounted on a Scientifica Universal Motorized Stage, and the preparation was visualized using transmitted infrared illumination. Membrane potential was measured in current-clamp mode using a Multiclamp 700B amplifier, and electrophysiology data were collected using AxoGraph and analyzed using Python 3.6.

Stimulus Presentation

We built visual stimuli using our own custom extension of the Allen Brain Institute’s retinotopic-mapping package⁴³. Each stimulus was warped and projected onto a flat screen aligned with the left eye. To correctly warp the stimulus, we assumed the eye was a sphere and measured the size of the screen, distance of the eye to the screen, the angle of the eye center relative to the plane that the screen lay in, and the position of the eye within the screen. Using this information, we mapped pixels to their corresponding visual degrees. We added an indicator that was synced to the presentation of each stimulus and detected via a photodiode in order to sync our stimulus to our electrophysiological recordings. For stimulus presentation, we used the PsychoPy package⁴⁴. Stimuli were displayed using a Texas Instrument Lightcrafter 4500 in monochrome mode (green) running at 180 Hz. The mean luminance of the projector was 1.39 W / m², while the max luminance was 4.37 W / m². Due to the difficulty of maintaining a patched cell for significant durations of time under multiple conditions, the total duration time of each recording varied from 5 minutes to 25 minutes depending on the health of the individual cell. Recordings were discarded if access to the cell became poor, or if the cell became overly unstable in its responses.

• White noise stimulus: (Figure 2) our white noise stimulus consisted of a 120 second presentation of 5° horizontal bars flickering at 60 Hz with luminance values randomly drawn from a truncated Gaussian distribution. The stimulus was therefore changing across one spatial dimension and one time dimension, allowing for the extraction of two-dimensional spatiotemporal filters via white noise reverse correlation. The stimulus was randomly generated for each presentation.

• Full field flashes: (Figure 3, Figure S2) OFF flashes of 20 ms, 40 ms, 80 ms and 160 ms with 10 second intervals were repeated for four sweeps per recording. While we conducted repeat sweeps within the same stimulus length condition, we randomized between presentations of different length flashes. High contrast OFF flashes consisted of light decrements from the mean luminance of the projector to its minimum output, corresponding to a Weber contrast of −1 (Figure 3A), while low contrast OFF flashes consisted of light decrements from the mean luminance of the projector corresponding to a Weber contrast of −0.1 (Figure S3A, B).

• Ternary noise: (Figure S3C–E) The ternary noise stimulus consisted of a 120 second presentation of 5° horizontal bars flickering at 60Hz with luminance values randomly sampled from Weber contrast steps of −1, 0, or 1 (high contrast condition) from the mean luminance of the projector, or −0.1, 0, or 0.1 (low contrast condition) from the mean luminance of the projector.

• Drifting gratings: (Figure S6) Drifting grating stimulus consisted of 0.5 Hz, high contrast drifting square waves of spatial wavelengths ranging from 2.5°, 10°, 12.5°, 25°, 40°, 50°, 80°, 100°, 125°, and 200°. Gratings were presented for 10 seconds each, in order of increasing spatial frequency.

Reverse correlation for extraction of white noise filters

We extracted spatiotemporal white noise filters and static nonlinearities via the reverse correlation method as described in Behnia et al.²⁴ and elsewhere^10,17,23,45. All “white-noise filter” predictions in this study are linear-nonlinear (LN) predictions, as cell response predictions combine white noise (linear) filters with static nonlinearities.

To extract white noise filters for each cell, we selected continuous responses to white noise over a window of time up to 300 seconds depending on recording stability. Across white noise samples for all 4 cell types, the average duration was 157 seconds. The shortest duration was 40 seconds, and the longest duration was 300 seconds. Traces were downsampled to 100 Hz, and filters were extracted for a duration of 5 seconds. Spatiotemporal filter properties were not significantly affected by different downsampling factors, or by increasing or decreasing filter duration.

All spatiotemporal filters were space-time separable: thus, after a 2D spatiotemporal filter was extracted via reverse correlation, we extracted a characteristic 1D temporal filter by selecting the temporal trace at the spatial location with the highest amplitude. These 1D temporal filters were averaged across individual recordings to get a characteristic temporal filter for each cell type (Figure 2A). Cells that displayed a spatial response to stimuli near the edge of our screen were eliminated from analyses. In order to characterize each temporal filter in frequency space, we convolved each 1D temporal filter with 1D sine waves of varying temporal frequencies from 0.1 to 10 Hz with an arbitrary amplitude of 1. The maximum steady-state amplitude of the convolved response at each frequency constituted a frequency tuning curve. These tuning curves were normalized and averaged across individual recordings to get a characteristic frequency tuning curve for each cell type (Figure 2B).

We extracted a characteristic 1D spatial receptive field by selecting the spatial profile at the time point with the highest amplitude. These 1D spatial receptive fields were averaged across individual recordings to get a characteristic spatial filter for each cell type (Figure 2C). As the white noise stimulus consisted of 5° horizontal bars, these spatial receptive fields have a resolution of 5°.

In order to obtain static nonlinearities, 2D white noise filters were convolved in time and summed in space to obtain (1D) linear predictions in time that could be compared with the (1D) recorded responses. The predicted and actual responses were binned by amplitude and averaged within each bin across recordings (Figure 2D). Bin size did not significantly affect static nonlinearity shape. For stimuli that cause small deflections, such as white noise, the static nonlinearity only slightly improved fits (Figure S1). The contribution of the static nonlinearity is more prominent with stimuli that cause large deflections, such as high contrast flashes. In this case, the negative components of responses have lower amplitudes than the positive components (Figure S2). Furthermore, reduced dynamic range in the presence of OA likely prevents cells from reaching response amplitudes at which nonlinear processing effects are seen.

In order to compare flash responses to predictions based on extracted white noise filters, each spatiotemporal white noise filter was convolved in time with a 2D flash stimulus of the appropriate duration and summed across space. The resulting 1D linear prediction in time was then transformed via the static nonlinearity, resulting in a LN prediction. These LN predictions were then averaged (Figure 3A, S3A). The same approach was used to compare drifting grating data with white noise filter predictions (Figure S6).

Parameter Fitting

We parameterized both extracted white noise filters and flash responses in order to compare Tm cell changes across conditions. A band-pass filter responds strongly to stimuli within a certain frequency range, and attenuates stimuli with frequencies outside of this range. We define a biphasic filter, or response, to mean that there are two distinct “lobes” in the filter or response. The strength of a biphasic filter’s band-pass properties, or the amount it attenuates frequencies outside of its peak sensitivity, is dependent on the ratio of positive to negative lobes in the shape of filter. As our temporal filters show two distinct lobes, we fit them using a biphasic function (see below).

Parameterization of White Noise Filters

Spatial receptive fields in all scenarios were fit to a Gaussian function $g(x)=e^{-{(x-\mu )}^2/2{\sigma }^2}$. The mean temporal filters for Tm1, Tm2, Tm4 and Tm9 were similarly fit with a biphasic function in time t:

$$f(t)=\frac{1}{{\tau }_1^2}t\cdot e^{-t/{\tau }_1}-c\cdot \frac{1}{{\tau }_2^2}t\cdot e^{-t/{\tau }_2}$$ (1)

The two lobes of the biphasic function are determined by constants τ₁ and τ₂. For parameterizing temporal filters from our white noise analysis, we set c = 1. This constrained the convolution of the above function with a constant stimulus to integrate to zero, thus fitting the band-pass character of recorded cells. Recording responses to long, 10 s flashes of light confirmed that these neurons are indeed band-pass, as their responses return to baseline during the course of the stimulation (Figure S2A, B). These parameterizations did not adversely affect the tuning properties of the filters for each cell type (Figure S4). For parameterized flash responses, c was unconstrained. All functions were parameterized using scipy.optimize.curve_fit.

We derived frequency tuning curves for parameterized white noise filters by convolving them with 1D sine waves of varying temporal frequencies varying from 0.1 to 10 Hz. The tuning curve consisted of the maximum amplitude of the steady state response at each frequency (Figure 4C). These frequency tuning curves were identical to tuning curves derived analytically via transfer functions (not shown). The full width half max (FWHM) and peak frequency was calculated numerically (Figure 4D). To compare flashes with white noise filters in the same parameter regime, we generated white noise filter LN predictions of 160 ms flashes (Figure 4A,B) and plotted them alongside parameterized 160 ms flash responses. For Tm9, we parameterized spatial properties based on the population with narrower receptive fields, as these more closely matched the EM receptive field prediction from⁹. Across cell types, we did not find center-surround structure in the spatial receptive fields extracted from our white noise stimulus (Figure 2C).

Linear Regression

In order to determine if our electrophysiological recordings of Tm1, Tm2, Tm4 and Tm9 could match electrophysiological recordings of T5, we applied linear regression of Tm1 and Tm9 flash responses to recorded T5 responses from Gruntman et al.¹². The authors of this paper recorded individual T5 cell responses to static vertical bar flashes of width 2.25°, 4.5° and 9° at different spatial locations, and for a duration of 40 ms and 160 ms, for a total of six conditions. T5 traces from Gruntman et al.¹² were accessed via https://figshare.com/collections/Simple_integration_paper_data_and_code/3955843.

We required coefficients to be strictly positive so as to maintain the sign of the input, and also did not fit an intercept under the assumption that all T5 recordings were preprocessed such that they had a baseline of zero. Regression was done using the scikitlearn LASSO module (since it allows positive weight constraints), with α = 0.0001 (α = 0 equivalent to a simple linear regression). We first applied linear regression to the average T5 responses for each bar location and condition (Figure 5A–C, S5). We then applied linear regression to individual T5 traces for each T5 cell, for each bar location and condition (Figure 5D–F).

As input to the linear regression, we used: (1) Tm1 and Tm9 white noise LN predictions for 40 ms and 160 ms flashes, as well as (2) measured Tm1 and Tm9 response to 40 ms and 160 ms flashes, and (3) measured Tm1 and Tm9 response to 40 ms and 160 ms flashes in the presence of OA (Figure 5A,B). None of these inputs were parameterized.

Since our linear regression did not use an intercept term, we used the square of the sample Pearson correlation coefficient r² as our measure of goodness of fit, instead of the coefficient of determination R^{2 46}. r² values were averaged across spatial locations for each condition and linear regression fit (Figure 5B).

Gruntman et al.¹² also recorded T5 responses to moving bars consisting of 20/40/80/160 ms consecutive flashes, across 2.25°, 4.5° and 9° widths. In order to predict the T5 response to moving bars, we summed the weighted Tm1 and Tm9 flash responses with appropriate time delays for the preferred direction and (opposite) null direction. The regression coefficients fit to the static T5 data were used for each matching condition (e.g. the coefficients from the 160 ms, 9° static condition were used to predict the response to the 160 ms, 9° moving bar condition, etc.). Both the PD and ND summed traces were then scaled by a single “gain factor” obtained by a separate linear regression on the combined PD and ND traces (Figure S5D). Notably, the DSI values of the T5 moving bar data were well matched by our Tm1+Tm9 flash data in both baseline and OA conditions. This motivated us to build the connectome-constrained model.

Model Construction

We built our framework for T5 based on established EM connectivity and an assumption of positivity for all Tm1, Tm2, Tm4 and Tm9 inputs onto T5. Specifically, Tm1/Tm2/Tm4 were centered and Tm9 was offset by Δx = 5°^10,47. The output of each of these cells was assigned a positive (cholinergic) connection weight proportional to EM synapse counts before being summed (Figure 6A, see below).

In order to construct a white noise model of T5 based on LN predictions for each cell type Tm1, Tm2, Tm4 and Tm9, 2D spatiotemporal receptive fields for each cell were constructed by taking the outer product of the parameterized gaussian spatial receptive field g (x) and the temporal filter f (t):

$$D(x,t)=g(x)\otimes f(t)$$ (2)

A given 2D stimulus in space-time S(x, t) is convolved with each spatiotemporal receptive field in time (but not in space), and then summed over space to give a 1D time course for each cell Tm1, Tm2, Tm4, Tm9. In discrete time this is:

$$y[t]=\sum _x\sum _{\tau }D[x,\tau ]S[x,t-\tau ]$$ (3)

Finally, the mean of the static nonlinearities extracted via white noise analysis for each cell were parameterized by a softplus function:

$$h(y)=c\text{log}\left(1+e^{{(ay+b)}^k}\right)+d$$ (4)

where a determines the sharpness of the “bend,” b translates the softplus curve along the x-axis, the multiplicative factor c controls the angle/slope, d determines offset along the y-axis, and the exponent k increases the curvature. The LN output of each cell was then normalized based on the numerical frequency tuning curve (so that the maximum possible gain across all frequencies was 1). Finally, Tm1, Tm2, Tm4 and Tm9 were scaled in a relative manner determined by the ratio of synapse counts from EM connectome data (see below)⁹.

In order to construct a flash model of T5 based on the flash responses of Tm1, Tm2, Tm4 and Tm9, we parameterized responses to 20/40/80/160 ms flashes and constructed spatiotemporal receptive fields by taking the outer product with parameterized spatial receptive fields derived from white noise spatial filters with a spatial resolution of 2.25°. In order to simulate responses to moving bars, we summed temporal responses at each location with appropriate temporal delays for the PD and ND directions. We did not explicitly model bar width (as we had Tm responses to full field flashes but not to different bar widths), hence the predictions for each model in Figure 6E are the same across the x-axis. Like the white noise model, relative scaling between Tm1, Tm2, Tm4 and Tm9 was determined by the ratio of synapse counts from connectome data (see below)⁹. Spatial receptive fields were those extracted from white noise. We did not include static nonlinearities, as our recorded flash responses already represent the nonlinear processing properties of each cell.

Direction Selectivity Index

In order to match measurements of direction selectivity between our model output and those used in the T5 datasets, we use two metrics that we call DSI_max and DSI_mag.

Wienecke et al. 2018¹¹, inspired by⁴⁸, use the “peak-to-trough” response to calculate DSI_mag:

$${\text{DSI}}_{\text{mag }}=\frac{\left|PD\right|-\left|ND\right|}{\left|PD\right|+\left|ND\right|}$$ (5)

where |PD| represents the response magnitude to motion in the preferred direction, and response magnitude was calculated as 95th percentile minus 5th percentile. This works well to characterize steady-state responses to sine waves, and this metric is used in Figure 6C for both the Wienecke et al.¹¹ T5 sine wave data and the Gruntman et al.¹² T5 sine wave data. However, this measure is less amenable to transient flash responses. DSI_mag ASAP2f values (Figure 6C) were provided by Wienecke et al.¹¹. DSI_mag values for T5 electrophysiology sine wave data from¹² were calculated using average peak and average trough values for both PD and ND traces.

Gruntman et al.^{12, 37} use the following metric to describe their flash responses:

$${\text{DSI}}_{\text{max}}=\frac{\text{max}(PD)-\text{max}(ND)}{\text{max}(PD)}$$ (6)

where each response max is defined as the 0.995 quantile within the stimulus presentation window. However, this does not take into account the ND amplitude in the denomenator, and is possibly susceptible to spuriously large DSI values due to noise⁴⁸. We therefore use the following DSI_max for flash responses:

$${\text{DSI}}_{\text{max}}=\frac{\text{max}(PD)-\text{max}(ND)}{\text{max}(PD)+\text{max}(ND)}$$ (7)

Connectome Data

T5 synapse-level connectomic data was accessed from the comprehensive electron-microscopy (EM) reconstruction of inputs to T4 and T5 cells in the Drosophila optic lobe by Shinomiya et al.⁹. Detailed data from twenty reconstructed T5 cells is available, with synapse counts for each presynaptic cell Tm1, Tm2, Tm4, and Tm9 from various columns (https://flyem.dvid.io/fib19-grayscale accessed June 2020; the updated link is ␣http://emdata.janelia.org/optic-lobe/). For a given T5 cell, we summed the synapse counts for each input (e.g. the synapse counts of Tm9 from column “K” and Tm9 column “C” were summed) and calculated the relative ratio of each of the four cell types. As reported in the study, Tm9 cells were consistently clustered on the leading edge of a given T5 cell, while Tm1/Tm2/Tm4 cell synapses were clustered in the center of T5 dendrites. We therefore made the reasonable assumption that all synapse counts for each cell from various columns should be treated as a single offset (Tm9) or centered unit (Tm1,Tm2,Tm4). Twenty model instances were generated with these relative weight ratios, and the average PD tuning, ND tuning and DSI tuning were calculated (Figure 6B–C). The same approach was applied to flash models (Figure 6D–E). While a wide range of relative weight combinations confer direction selectivity on T5, we found that EM-based synaptic counts provide good fits across multiple models, suggesting that they are a reasonable estimation of synaptic weights in this system.

In order to assess dependence on EM weight ratios, we randomized weight ratios “within column” by fixing the Tm9 value at 0.45 (the EM mean for Tm9) while generating 20 random values each for Tm1/Tm2/Tm4 such that they summed to 0.55. This leads to an increase in overall variance and decrease in DSI (Figure S6F, middle). We also randomized all ratios for Tm1, Tm2, Tm4 and Tm9 i.e. “between columns;” this led to a large increase in variance and a degradation in DSI (Figure S6F, right).

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, Peptides, and Recombinant Proteins
Octopamine hydrochloride	Millipore Sigma	68631
Protease from Streptomyces griseus	Millipore Sigma	P5147
Deposited Data
FlyEM Optic Lobe Data	Janelia FlyEM Project [6]	http://emdata.janelia.org/
T5 responses to flashing bars	Reiser Lab, Janelia [12]	https://doi.org/10.25378/janelia.c.4771805.v1
T5 responses to sine waves	Clandinin Lab, Stanford University [11]	NA
Tm1, Tm2, Tm4, and Tm9 responses to mutiple stimuli +/− OA	This paper	link TBD
Experimental Models: Organisms/Strains
D. melanogaster: R71G04-Gal4	Bloomington Drosophila Stock Center	RRID:BDSC_39868
D. melanogaster: R35H01-Gal4	Bloomington Drosophila Stock Center	RRID:BDSC_49922
D. melanogaster: R24C08-Gal4	Bloomington Drosophila Stock Center	RRID:BDSC_48050
D. melanogaster: otd-Gal4	Desplan Lab, NYU [42]	NA
Software and Algorithms
Python 3.6	Python Software Foundation	https://www.python.org
SciPy	SciPy	https://github.com/scipy/scipy
Sklearn	Scikit-learn	https://scikit-learn.org
AxoGraph	AxoGraph Scientific	https://axograph.com/; RRID:SCR_014284
Stimulus Software	This paper	https://gitlab.com/rbehnialab/motyxia2/-/tree/whitenoise
Retinotopic Mapping Package	Allen Institute [43]	https://github.com/zhuangjun1981/retinotopic_mapping
Analysis Pipeline	This paper	github link TBD
DataJoint	DataJoint	https://docs.datajoint.org/python/
Multiclamp Commander Software v2.2.2	Axon Moleulcar Devices	https://support.moleculardevices.com/s/article/Axon-MultiClamp-700B-Commander-Download-page
Other
Patch clamp amplifier	Axon Molecular Devices MultiClamp700B	https://www.moleculardevices.com/products/axon-patch-clamp-system/amplifiers/axon-instruments-patch-clamp-amplifiers; RRID:SCR_018455
Universal Motorized Stage for Microscopes	Scientifica	https://www.scientifica.uk.com/products/scientifica-universal-motorised-stage
DLP	Texas Instruments DLP LightCrafter 4500	https://www.ti.com/tool/DLPLCR4500EVM; DLPLCR4500EVM

Highlights:

• Neural inputs to Drosophila motion detector T5 are state and stimulus dependent

• Their temporal responses are more biphasic in certain conditions

• T5 responses can be explained by linear summation of state/stimulus-dependent input

• A biologically constrained model predicts T5 motion responses across conditions