Mendelian Randomization: Concepts and Scope

Abstract

Mendelian randomization (MR) is a method of studying the causal effects of modifiable exposures (i.e., potential risk factors) on health, social, and economic outcomes using genetic variants associated with the specific exposures of interest. MR provides a more robust understanding of the influence of these exposures on outcomes because germline genetic variants are randomly inherited from parents to offspring and, as a result, should not be related to potential confounding factors that influence exposure–outcome associations. The genetic variant can therefore be used as a tool to link the proposed risk factor and outcome, and to estimate this effect with less confounding and bias than conventional epidemiological approaches. We describe the scope of MR, highlighting the range of applications being made possible as genetic data sets and resources become larger and more freely available. We outline the MR approach in detail, covering concepts, assumptions, and estimation methods. We cover some common misconceptions, provide strategies for overcoming violation of assumptions, and discuss future prospects for extending the clinical applicability, methodological innovations, robustness, and generalizability of MR findings.

Mendelian randomization (MR) was developed as a method to help provide a robust understanding of environmentally modifiable influences on disease (Davey Smith and Ebrahim 2003). It was proposed to offer a more reliable strategy than conventional observational epidemiological studies that have traditionally been plagued by issues such as confounding (in which a common cause of an exposure X and outcome Y may distort the association between X and Y), reverse causation (in which Y—or the disease process leading to Y—influences X) and other forms of bias, thus resulting in potentially misleading causal inference (Davey Smith and Ebrahim 2002). The clearest examples are shown through observational epidemiological studies that have indicated an apparent causal effect that has later failed to be confirmed in large-scale randomized controlled trials (RCTs) (Davey Smith et al. 2020). The proposed protective effects of vitamin and antioxidant supplements on cardiovascular disease (CVD) (Rimm et al. 1993; Myung et al. 2013), β-carotene on lung cancer (Menkes et al. 1986; Heinonen et al. 1994), and selenium on prostate cancer (Yoshizawa et al. 1998; Lippman et al. 2009) are noteworthy examples. Such spurious findings from observational studies have had negative consequences, including the launch of expensive trials based on inadequate evidence, and increased uptake of nutritional supplements in the general population, some of which have subsequently been found to have adverse effects (Heinonen et al. 1994; Lippman et al. 2009).

MR uses genetic variants robustly associated with exposures to strengthen inference regarding their potential causal influence on a particular outcome (Davey Smith and Ebrahim 2003; Davey Smith and Hemani 2014). The online “MR Dictionary” (Lawlor et al. 2019) offers a full description and definitions of terminology specific to MR, which will be useful to refer to as we elaborate on the concepts and scope of the approach in this paper.

The MR approach draws on Mendel's laws of segregation and independent assortment, whereby genetic variants are allocated independently of environment and other genetic factors (except those in close physical proximity to the variant of interest, which tend to be inherited together through linkage disequilibrium [LD]) (Davey Smith et al. 2020). Based on the premise that the random inheritance of genetic variants from parents to offspring is reflected at a population level, genetic variants can identify groups that differ, on average, by a modifiable exposure. Here, group membership should not be associated with a range of behavioral, social, and physiological factors that may confound observational associations (Davey Smith et al. 2007). By design, genetic associations should therefore be largely free from confounding, thus any difference in outcomes between genetically defined groups can be directly attributed to the exposure.

The association between an outcome and a genetic variant known to proxy a particular risk factor mimics the link between the outcome and the proposed risk factor, and can be used to estimate this relationship with less confounding and bias than conventional epidemiological approaches. Other qualities of (germline) genetic variants that make them useful in causal inference analysis are that they (1) can be robustly associated with modifiable exposures (i.e., can serve as genetic proxies); (2) are fixed at conception and not influenced by disease processes (i.e., are less susceptible to reverse causation); and (3) are subject to relatively little measurement error and typically have long-term effects (i.e., are less liable to the underestimation of the exposure–outcome association, referred to as regression dilution bias) (Davey Smith and Ebrahim 2004).

Exposures of interest are typically modifiable and so evidence of causality can—in principle—be used to infer that intervening on an exposure will lead to a change in the outcome under investigation. Making such inference depends on considering it reasonable to accept the principle of gene–environment equivalence: that perturbation of a phenotype by either a (hypothetical) change in genotype or by environmental change would produce the same downstream effect on an outcome (Ames 1999; West-Eberhard 2003; Ebrahim and Davey Smith 2008; Davey Smith 2012a). For example, under this assumption, we would anticipate genotypic influence on circulating cholesterol level would lead to the same effect on coronary heart disease (CHD) as would a similar change in cholesterol level induced by dietary influences. Although many exposures can be closely proxied by genetic variation, for others it is unlikely that genetic variation will mimic environment exactly, for example, in capturing aspects of years of education (Davies et al. 2019b). Gene–environment equivalence is a fundamental principle in MR that also brings to the fore the issue of the time-depth of the exposure that is being examined, because genetic variants that influence a phenotype will do so over an extended period. We will come back to the issue of time, discussed at length in the MR literature since its inception (Davey Smith and Ebrahim 2003, 2004; Holmes et al. 2017).

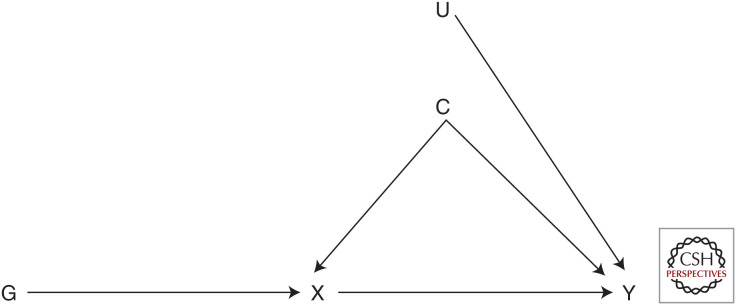
Within a causal inference framework, MR can be implemented as a form of instrumental variable (IV) analysis in which the genetic variants serve as proxies or IVs for the modifiable factors of interest (Fig. 1; Lawlor et al. 2008). If we suppose X and Y are the exposure and outcome of interest, C is a set of variables that affects X and Y (i.e., potential confounding factors), and U is a further set of variables that affect Y, we can use a further variable G (the genetic variant of interest) as an IV to establish the causal effect of X on Y if it satisfies the following assumptions (Hernan and Robins 2020):

1. G is robustly associated with X (“relevance”);

2. G does not share common causes (C and U) with Y (“independence” or “exchangeability”); and

3. G affects Y exclusively through its effect on X (“exclusion restriction”).

Figure 1.

Directed acyclic graph for Mendelian randomization analysis. The genetic variant (G) is associated with the exposure of interest (X); there are no confounders (C, U) of the association between genetic variant (G) and outcome (Y); and the genetic variant (G) does not affect the outcome (Y) except through its effect on the exposure (X).

These assumptions are described in more detail in the section “Assumptions of Mendelian Randomization” and “Instrumental Variable Analysis.”

SCOPE OF MENDELIAN RANDOMIZATION

MR has been used to:

• appraise the causal relevance of both endogenous (e.g., blood pressure, low-density lipoprotein [LDL] cholesterol) and exogenous exposures (e.g., alcohol, smoking),

• confirm and uncover causal effects for known risk factors of clinical relevance,

• establish the causal role of behavioral traits,

• evaluate causality in relation to social and economic factors,

• assess life-course effects,

• elucidate intergenerational influences,

• characterize difficult to measure environmental exposures,

• proxy for modifiers of environmental exposure (e.g., metabolism or detoxification),

• mimic drug targets,

• evaluate the role of modifiable mediators between upstream exposures and disease outcomes, and

• evaluate the effects of genetic liability to a particular disease.

A selection of studies in Table 1 shows how MR has been previously used across a wide variety of contexts.

Table 1.

A selection of Mendelian randomization studies with different applications

Application	Exposure(s)	Outcome(s)	Conclusions	References
Clinical	Vitamin D	Multiple sclerosis (MS)	Lower 25-hydroxyvitamin D has a causal effect on increased MS susceptibility	Mokry et al. 2015
	Metabolic factors	Pancreatic cancer	Causal role of body mass index (BMI) and fasting insulin in pancreatic cancer etiology	Carreras-Torres et al. 2017
	C reactive protein (CRP)	Coronary heart disease (CHD)	CRP concentration is unlikely to be an important causal factor in CHD	Wensley et al. 2011
Behavioral	Cannabis use	Schizophrenia	Some evidence for a small causal effect of cannabis initiation on schizophrenia risk	Gage et al. 2017
	Alcohol intake	Vascular disease	Alcohol increases blood pressure and stroke risk across the distribution of intake	Chen et al. 2008; Millwood et al. 2019
	Smoking heaviness	Anxiety and depression	Limited support for a causal role of smoking heaviness in depression and anxiety	Bjorngaard et al. 2013; Taylor et al. 2014
	BMI and smoking	COVID-19	Elevated BMI and smoking increase susceptibility to severe COVID-19 and sepsis	Ponsford et al. 2020
Socioeconomic	Education	Myopia	More years in education contributes to increased risk of myopia	Cuellar-Partida et al. 2016; Mountjoy et al. 2018
	Height and BMI	Socioeconomic position	Earlier findings suggesting that height and BMI may influence aspects of socioeconomic position may be biased by family-level dynastic effects	Tyrrell et al. 2016a; Brumpton et al. 2020
	Age at menarche	Education	Positive causal effect of age at menarche on time spent in education	Gill et al. 2017
	Education	Cardiovascular disease (CVD)	BMI, systolic blood pressure and smoking mediate a substantial proportion of the protective effect of education on the risk of CVD	Carter et al. 2019
Environmental	Copper and zinc	Ischemic heart disease (IHD)	Protective effect of copper and detrimental effect of zinc on IHD	Kodali et al. 2018
	Arsenic metabolism	Skin lesions	Evidence for a causal relationship between arsenic metabolism and skin lesion risk	Pierce et al. 2013
	Malaria	Stunting	Use of genetic variation for sickle cell trait to demonstrate increased risk of stunting following malaria	Kang et al. 2013
Lifecourse	Childhood adiposity	Type 1 diabetes (T1D)	Support for an effect of childhood adiposity on T1D risk	Censin et al. 2017
	Age at menarche	BMI	Evidence that earlier age at menarche causes higher BMI in later life may be confounded by prepubertal BMI	Bell et al. 2018; Gill et al. 2018
	Childhood body size	Coronary artery disease (CAD), type 2 diabetes (T2D), breast and prostate cancer	Whereas the causal effect of childhood body size on CAD and T2D risk is largely mediated by adulthood body size, smaller childhood body size might increase the risk of breast cancer regardless of body size in adulthood	Richardson et al. 2020b
Intergenerational	Maternal BMI and glucose	Birth weight	Maternal BMI and blood glucose levels causally related to higher offspring birthweight	Tyrrell et al. 2016b
	Maternal alcohol intake	Education	Causal adverse effect of alcohol intake during pregnancy on offspring educational attainment	Zuccolo et al. 2013
	Parental education	Offspring education	Similar effect of paternal and maternal family environmental influences on offspring educational attainment	Kong et al. 2018; Wang et al. 2021a
Drug targets	Niemann–Pick C1-Like 1 (NPC1L1) and HMG-CoA reductase (HMGCR)	CHD	Validation of ezetimibe and statin use for reducing risk of CHD using drug targets in NPC1L1 and HMGCR	Ference et al. 2015
	HMGCR	Bone mineral density (BMD)	LDL-C lowering effect of HMGCR on increased BMD suggests repurposing opportunity for statins	Li et al. 2020
	HMGCR and proprotein convertase subsilisin-kexin type 9 (PCSK9)	T2D	Statins and PCSK9 inhibitors prescribed for reducing risk of CHD may increase risk of T2D	Ference et al. 2016
	Angiotensin-converting enzyme (ACE)	T2D	Causal protective effect of ACE inhibitors on T2D risk	Pigeyre et al. 2020
	Interleukin 6 receptor (IL-6R)	COVID-19	Potential role of IL-6R blockage in COVID-19 severity	Bovijn et al. 2020
Molecular traits	DNA methylation	BMI	DNA methylation changes are predominantly the consequence of adiposity, rather than the cause	Wahl et al. 2017
	Tissue-specific gene expression	Cardiovascular traits	Identified a number of tissue-specific effects at several genomic regions on cardiovascular traits	Taylor et al. 2019
	Proteins	Cardiovascular, cancer, and autoimmune outcomes	Among results was the finding of an independent role for IL18R1 and IL1RL2 on atopic dermatitis risk	Sun et al. 2018
Disease liability	Schizophrenia risk	Reproductive success	Increased genetic liability for schizophrenia does not confer a fitness advantage but does increase mating success	Lawn et al. 2019
	Coronary artery disease (CAD) risk	Metabolites	Genetic variants that influence CAD risk in adults are associated with large perturbations in metabolite levels in childhood	Battram et al. 2018
	Atopy	Glioma	Limited evidence for an effect of atopic disease liability on risk of glioma	Disney-Hogg et al. 2018

When the basic principles of MR were initially formalized there were few examples of genetic variants that had robust associations with potentially modifiable exposures, and it was recognized that the future potential of MR would depend upon identifying such associations (Davey Smith and Ebrahim 2003). There has been very substantial progress in this area. Improvements and cost reductions in array-based genotyping techniques, complemented by DNA sequencing and imputation of information from human genome reference sets, have led to a dramatic increase in our understanding of the genetic contribution to disease risk. Such improvements have also permitted the widespread use of genome-wide association studies (GWAS), which have been successful at detecting replicable associations between common genetic variants and a host of traits in a hypothesis-free approach.

The establishment of GWAS consortia, each focused on investigating different complex traits and diseases, has encouraged numerous population-based studies to contribute genetic data for meta-analysis (Table 2). This has in turn increased sample sizes for the discovery and robust replication of GWAS findings. Many of these consortia have also made their GWAS summary data publicly available, which, aided by data resources hosting such summary data (Richardson et al. 2020a), have catalyzed the development of summary data-based MR studies (described in more detail in the section “MR Methods”).

Table 2.

Selection of studies and consortia used for genome-wide association analysis

Genetic consortia	Approximate sample size	Approximate number of contributing studies	Summary data available for download
Cohorts for Heart and Aging Research in Genomic Epidemiology (CHARGE)	60,000	10	Yes, via dbGAP
Early Growth Genetics (EGG) and Early Genetics and Lifecourse Epidemiology (EAGLE)	170,000	40	Yes
			egg-consortium.org, www.eagle-consortium.org
Meta-Analyses of Glucose and Insulin-related traits Consortium (MAGIC)	130,000	55	Yes
			www.magicinvestigators.org
DIAbetes Genetic Replication And Meta-analysis (DIAGRAM)	150,000	40	Yes
			www.diagram-consortium.org
Genetic Investigation of Anthropometric Traits (GIANT)	340,000	60	Yes
			portals.broadinstitute.org/collaboration/giant/index.php/GIANT_consortium
UCL–LSHTM–Edinburgh–Bristol (UCLEB) (cardiometabolic traits)	40,000	12	No
			Contact UCLEB steering committee
Coronary ARtery DIsease Genome-wide Replication and Meta-analysis (CARDIoGRAM) plus the Coronary artery Disease (C4D) genetics consortium	190,000	50	Yes
			www.cardiogramplusc4d.org
Genetic Associations and Mechanisms in Oncology (GAMe-On)	500,000	33	Yes, via dbGAP
Reproductive Genetics (ReproGen)	330,000	85	Yes
			www.reprogen.org
Psychiatric Genomics Consortium (PGC)	600,000	>50	Yes
			www.med.unc.edu/pgc
Social Science Genetic Association Consortium (SSGAC)	1,000,000	100	Yes
			www.thessgac.org

Genetic studies	Approximate sample size	Number with genetic data available	Availability of data
UK Biobank	500,000	500,000	Data shared with bona fide researchers on project approval; genetic summary data freely available: gwas.mrcieu.ac.uk, www.nealelab.is/uk-biobank
China Kadoorie Biobank (CKB)	500,000	110,000	Period of exclusive use for the CKB collaborative team, after which data will be made available to the wider research community; data access requests of all bona fide researchers will be considered
Million Veteran Program	1,000,000	300,000	Available to Veteran Affairs–affiliated investigators
Biobank Japan (BBJ)	270,000	200,000	Data access to bona fide researchers requires collaboration and research visits to BBJ; genetic summary data freely available
			jenger.riken.jp/en
HUNT	70,000	70,000	Available to investigators affiliated with a Norwegian research institute
FinnGen	500,000	180,000	Data access available to consortium partners only; genetic summary data freely available
			www.finngen.fi/en/access_results
23andMe	>8,000,000	>8,000,000	Collaboration requests but individual data cannot be distributed, shared, or sold to third parties

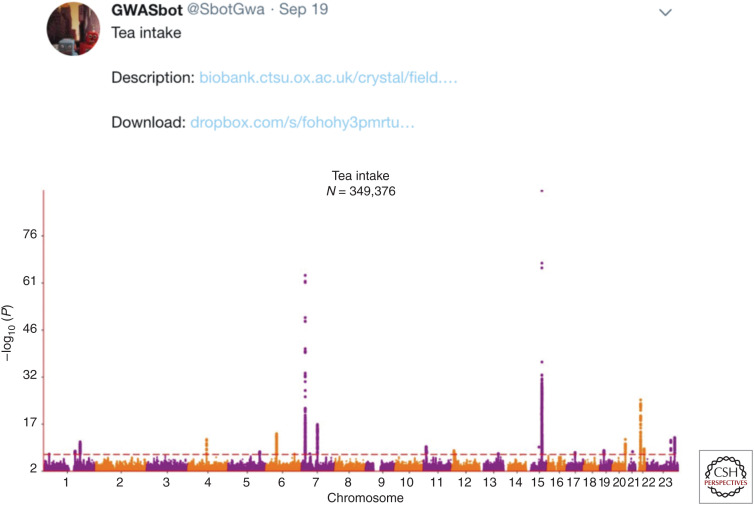
The recent availability of massive genotyped and phenotyped data sets, including biobank resources (Table 2), has added considerably to GWAS efforts. GWAS of phenotypic data from these resources are increasingly performed in an automated fashion, with summary statistics made freely available online (Fig. 2). Efforts such as these have uncovered a host of genetic variants related to a range of traits, which may leverage greater explanatory power by acting as stronger genetic proxies or instruments in MR (Dudbridge 2020).

Figure 2.

Manhattan plot from the “GWASbot” displaying genetic association signals for tea intake from the UK Biobank.

ASSUMPTIONS OF MENDELIAN RANDOMIZATION AND INSTRUMENTAL VARIABLE ANALYSIS

The key assumption of MR is that of gene–environment equivalence, as discussed above. When using the properties of germline genetic variants to strengthen causal inference, the confidence that a particular modifiable exposure is implicated in the causation of a disease can be enhanced by identifying the direction and magnitude of the effect. This can be estimated through IV analysis. The large majority of MR studies are now implemented within an IV framework, and therefore the IV assumptions are central to MR analysis.

Relevance Assumption: The Genetic Variant Must Be Robustly Associated with the Exposure

The most common method of deriving genetic instruments in recent MR studies is via GWAS, whereby single-nucleotide polymorphisms (SNPs) that pass genome-wide significance (p < 5 × 10⁻⁸) are typically considered for inclusion. However, it is important that the strength of the instrument is tested separately to appraise the relevance assumption, which is often done by means of the proportion of variance explained (r²) and the related F-statistic, which additionally takes into account the size of the sample under investigation. Increasingly, multiple genetic variants are found to be independently associated with traits investigated in GWAS and these may be combined in genetic risk scores or through meta-analysis approaches to explain more variation in the trait (Dudbridge 2020). This in turn can be used to increase power, obtain more precise causal estimates and minimize risk of weak instrument bias (i.e., uncertainty in the SNP-exposure association that can bias causal estimates) (Pierce and Burgess 2013).

Independence/Exchangeability Assumption: There Are No Confounders of the Association between the Genetic Variant and Outcome

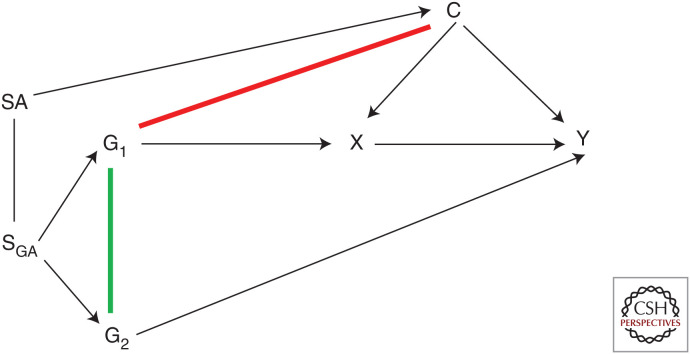
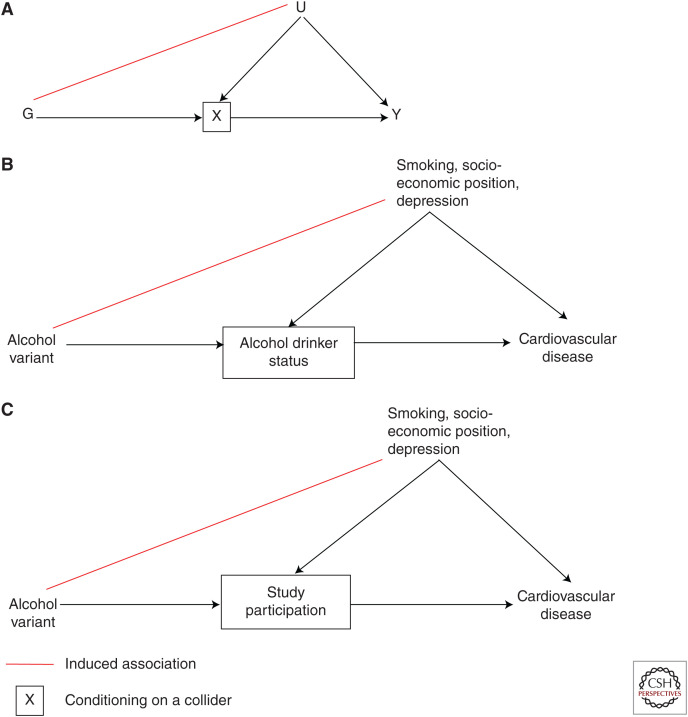
Because genetic variants are randomized at conception, they should be allocated independent of environmental and other genetic variants excluding those in LD. This means that at a family level, genetic associations should be largely free from conventional confounding. Although MR was explicitly introduced in 2003 within a parent–offspring design, data availability did not generally allow use of such designs at the time. It was suggested, however, that population-based studies with appropriate control for population stratification could approximate the parent–offspring design (Davey Smith and Ebrahim 2003; Davey Smith et al. 2020). Concerns about potential violation of this assumption at a population level relate to confounding by ancestry or population stratification, which can influence variation in both allele frequency and disease risk in population(s) being investigated (Fig. 3). Approaches to limit spurious associations generated because of population groups include use of genetic associations derived from homogeneous populations or with adequate control for population structure (e.g., through principal components analysis or linear mixed models) (Loh et al. 2015). However, the independence assumption can also be violated by dynastic effects (when parental genotypes directly affect offspring phenotypes), or by assortative mating (when individuals select a partner based on a particular phenotype). These biases will likely differ depending on the exposure(s), outcome(s), and population(s) under study.

Figure 3.

Violation of the independence and exclusion restriction assumptions caused by shared ancestry or population structure. Shared ancestry (SA) can confound the relationship between shared genetic ancestry (S_GA) and a potential confounder (C), violating the Mendelian randomization (MR) assumption of independence/exchangeability by inducing an association between a genetic instrument, G₁ and C (red line). S_GA can also induce an association between the genetic instrument (G₁) and another genetic variant (G₂) (green line), thus violating the MR assumption of exclusion restriction.

It is impossible to prove the independence assumption in an MR study because, although attempts can be made to account for ancestry and examine how genetic variants relate to measured confounders, associations with unknown confounders cannot be demonstrated. In addition, whereas previous recommendations have been to assess associations between the genetic instrument and a wide range of factors that could bias exposure–outcome associations (Davey Smith et al. 2007), these associations are likely to be indicators of confounding by ancestry (Fig. 3) or horizontal pleiotropy (Fig. 4), rather than reflecting conventional confounding.

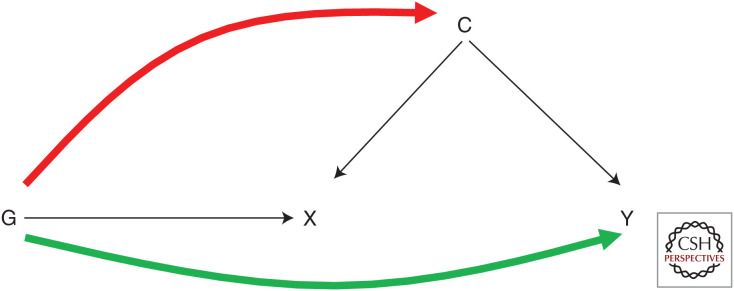
Figure 4.

Correlated and uncorrelated pleiotropy. Uncorrelated pleiotropy occurs when G affects X and Y through separate mechanisms (green line). Correlated pleiotropy occurs when G affects X and Y through a shared confounder (C) (red line).

Exclusion Restriction Assumption: The Genetic Variant Should Only Influence the Outcome of Interest via the Exposure

Pleiotropy is the phenomenon whereby a genetic variant influences multiple traits, and is a major threat to the exclusion restriction assumption. However, it is important to make the distinction between vertical and horizontal pleiotropy (Davey Smith and Hemani 2014; Hemani et al. 2018a). Vertical (or mediated) pleiotropy occurs when the genetic variant (G) is associated with the outcome (Y) because G affects Y entirely through the exposure (X). This fulfils the exclusion restriction assumption and is the essence of the MR approach. Horizontal (unmediated or biological) pleiotropy occurs when G affects both X and Y but through different pathways. This can yield biased estimates in MR if a genetic instrument influences the outcome via a mechanism other than the exposure of interest (Verbanck et al. 2018). Such pleiotropy can be direct, as in the path from G to Y (uncorrelated pleiotropy), or can be indirect (e.g., when G affects X and Y through a shared confounder, U [correlated pleiotropy]) (Fig. 4; Morrison et al. 2020). The latter may occur in cases of misspecifying the primary phenotype, such as when a genetic variant is used to proxy for a trait secondary to the trait with which it is directly associated.

Although it is not possible to prove that the exclusion restriction assumption holds in any MR study, various sensitivity analyses can be applied to uncover deviations from the assumption.

Use a Functional Polymorphism for the Exposure of Interest

One method of ensuring that the genetic variant is unlikely to influence the outcome via another pathway is to use a SNP that has known biological function or is located in a gene that directly codes for the exposure of interest. For example, variants within or near the protein-encoding locus for C-reactive protein (CRP) are known to alter serum levels of CRP and are likely to have a predominant influence on any outcomes via this pathway (Timpson et al. 2011).

Although SNPs serve as valid instruments in some situations, in other cases their use is limited if variants do have a pleiotropic effect that cannot be directly estimated. This may be particularly problematic if a variant

• is associated with multiple biomarkers on separate biological pathways (e.g., genetic variants influencing the branched-chain α-ketoacid dehydrogenase (BCKD) enzyme are associated with different branch chain amino acids [Lotta et al. 2016]);

• disrupts the normal function of the exposure (e.g., an IL6R variant increases circulating interleukin 6 [IL-6] but reduces aspects of IL-6 signaling and that appears to decrease risk of CHD [Swerdlow et al. 2012]); and

• is associated with multiple dependent traits on overlapping pathways, and if those traits have different roles in disease (e.g., ALDH2 is associated with both alcohol consumption and acetaldehyde level, a known carcinogen, which makes it difficult to disentangle the effects of alcohol and acetaldehyde on risk of esophageal carcinoma [Lewis and Davey Smith 2005]).

For a detailed description of these scenarios and other applied examples, see Holmes et al. (2017). Although functional SNP analyses may therefore appear plausible, they can have their drawbacks and many of the sensitivity analyses used for evaluating pleiotropy cannot be applied with a single SNP (see the section “Methods for Assessing and Accounting for Horizontal Pleiotropy”). In cases where a single SNP is used, it is recommended that associations between the SNP and a wide range of traits are investigated, as described below.

Assess Associations between Genetic Variants and Other Factors

The presence of associations between genetic variants and other factors may reveal violations to the independence and/or exclusion restriction assumption. A common approach to appraise this is to assess whether the genetic variants used to instrument the exposure (and those variants in LD with the genetic instrument) have been associated with other phenotypes in GWAS, for example, by searching PhenoScanner (Staley et al. 2016). Although this may highlight genetic variants with horizontal pleiotropy, it can also pick up vertical pleiotropy (e.g., a SNP related to body mass index [BMI] may appear in a GWAS of blood pressure via its influence on BMI). In addition, truly horizontal pleiotropic SNPs may not be detected by this method if the GWAS of the phenotype on the pleiotropic path is absent or underpowered. As such, it is not sufficient to simply exclude the variants that appear in other GWAS as a way to assess the exclusion restriction assumption.

Conduct Stratified Analysis in a Subgroup of the Population in Which the Genetic Variant Is Not Associated with the Exposure of Interest

In some instances, conducting a stratified analysis can provide evidence against the possibility of horizontal pleiotropy. When a genetic variant is not related to the exposure of interest in a particular subgroup of the population, this variant should also not be associated with the outcome of interest in this subgroup (given an absence of the association with the exposure). For example, ALDH2, coding for aldehyde dehydrogenase 2, is a common polymorphism in East Asian populations that has been used as a genetic instrument for alcohol consumption (Lewis and Davey Smith 2005; Chen et al. 2008; Millwood et al. 2019). In East Asian populations, in which women are much less likely to drink alcohol than men, this polymorphism is not strongly associated with alcohol intake among women (Chen et al. 2008). This approach has been used to assess the presence of pleiotropy and evaluate a causal relationship between alcohol consumption and increased blood pressure (Chen et al. 2008) and risk of vascular disease (Millwood et al. 2019). For example, if the effects of alcohol consumption on blood pressure and vascular disease are causal, we would expect to find evidence of association between variation in ALDH2 and the outcomes in East Asian men, but not East Asian women. Any association observed between ALDH2 and the outcomes in East Asian women, in the absence of alcohol intake, would indicate pleiotropy. Such an approach can be considered a negative control design (Lipsitch et al. 2010; Davey Smith 2012b) and models built on this approach can detect and adjust for the pleiotropic effects and provide valid estimates in such instances (Cho et al. 2015; Spiller et al. 2019) (see the section “Methods for Assessing and Accounting for Horizontal Pleiotropy”). However, genetic variants that are not associated with the exposure in a subgroup of a population may be uncommon, and so such direct assessment of pleiotropy is often not possible.

Do Not Condition on the Exposure to Assess Exclusion Restriction

Although it may seem intuitive to assess whether statistical adjustment for the exposure leads to attenuation of the gene–outcome relationship, this is not a recommended approach for testing the exclusion restriction assumption. This is because adjusting for the exposure may induce collider bias, in which another factor that causes the exposure becomes correlated with the genetic instrument by conditioning on the exposure in this manner (Fig. 5; Cole et al. 2010). Stratifying by sex is not problematic in this context because biological sex is not caused by other factors. It is, however, a potential problem in instances where genetic effects are investigated within other subsets of the population, for example, if we were to stratify on alcohol drinker status itself (Gage et al. 2016). Bias induced through adjustment for the exposure may be exacerbated by potential measurement error in the exposure, in addition to introducing collider bias (VanderWeele et al. 2012).

Figure 5.

Collider bias. (A) Generalizable directed acyclic graph (DAG). (B) Collider bias induced from stratifying on exposure. (C) Collider bias induced from stratifying on study participation (e.g., caused by selection or loss to follow-up).

More advanced methods have been developed to assess violation of the exclusion restriction, including techniques that explicitly model and adjust for pleiotropy, and those that are naturally robust to pleiotropy (Hemani et al. 2018a). These are described in more detail in the next section.

MR Methods

Direct Genotype Associations

The simplest MR approach to evaluate the presence of a causal relationship is to assess the association between a genetic variant known to influence or modify an exposure and the outcome of interest. However, this does not allow for the magnitude of causal effect to be estimated, which is most often the estimate of interest, especially when considering the translational implications and clinical utility of findings. In addition, multiple pathways can often explain the association between a genetic variant and a particular outcome, so more knowledge of the exposure of interest and its association with the genetic variant is generally required for a valid interpretation (Holmes et al. 2017).

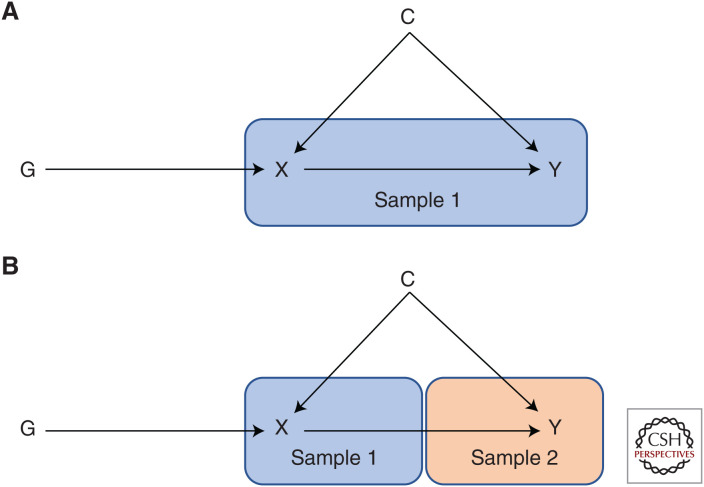
Original Applications of One-Sample Mendelian Randomization

In the pre-GWAS era, most examples of applied MR were conducted within one data set (i.e., in which genetic variants, exposures, and outcomes of interest are obtained from individuals in the same sample) (Fig. 6A). In such a scenario, the causal effect of the exposure on the outcome can typically be estimated using two-stage least-squares (2SLS) regression (Angrist and Imbens 1995a). In the first stage, the exposure is regressed on the genetic instrument and in the second stage the outcome is regressed against the predicted values from the first stage regression. The effect estimate can then be interpreted as the change in the outcome per unit increase in the exposure. The genetic instrument used in one-sample analysis can be a SNP, multiple SNPs, or a genetic risk score (i.e., a summation of risk alleles for each individual) that can be unweighted or weighted to give those genetic variants with the strongest effect on the exposure more weight (Dudbridge 2020).

Figure 6.

One-sample and two-sample Mendelian randomization (MR) study designs. (A) One-sample MR uses a data set in which genotype, exposure, and outcome have been assessed. (B) Two-sample MR uses a genetic data set in which the exposure has been measured (to derive SNP-exposure estimates, sample 1) and a second genetic data set in which the outcome has been measured (to derive SNP-outcome estimates, sample 2).

Studies with more individual-level data may also permit an assessment of associations between genetic variants and confounders of the exposure–outcome relationship to interrogate the independence and exclusion restriction assumptions. Additional approaches to evaluate violation of the exclusion restriction assumption in one-sample MR include the Sargan test (Sargan 1958), which evaluates heterogeneity of the individual SNP estimates, and IV approaches, which can estimate the causal effect in the presence of invalid (e.g., pleiotropic) instruments (Kang et al. 2016; Windmeijer et al. 2019).

Early one-sample MR studies suffered the limitation of low power because few large data sets with relevant genotypic and phenotypic data were available. To counteract this, a number of MR studies were conducted using meta-analysis of causal estimates obtained from independent studies, which was greatly aided by the existence of large genetic consortia (Tyrrell et al. 2016a). However, the development of two-sample MR analysis has vastly improved the scope of MR applied to large-scale data sets.

Development of Two-Sample Mendelian Randomization

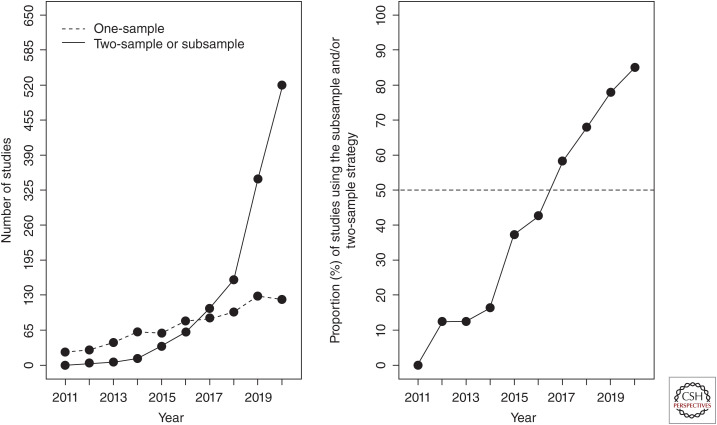
It is possible to use MR to estimate causal effects in which genetic associations with the exposure and the outcome have been estimated in different samples (Fig. 6B). This approach, now known as two-sample MR (Pierce and Burgess 2013), has greatly increased both the scope and popularity of MR analysis (Fig. 7). Although the initial extended exposition of MR in 2003 (Davey Smith and Ebrahim 2003) included examples of what is now called two-sample MR, the rise in popularity in recent years is attributed to the public availability of GWAS summary data, as well as the development of methods to harmonize and integrate data sets and compute causal estimates when the SNP–exposure and SNP–outcome associations come from different studies (Hemani et al. 2018b).

Figure 7.

Number of empirical one- and two-sample Mendelian randomization (MR) papers in PubMed from 2011–2020. Figure has been adapted and updated since that produced by Hartwig et al. (2016). We performed a literature search from 1 January 2011 to 31 December 2020 using the terms “Mendelian randomization” or “Mendelian randomisation” to identify the proportion of Mendelian randomization papers using the two-sample design.

The two-sample approach eliminates the requirement to have access to raw genetic data on individuals within a study and also makes performing MR less time consuming. In terms of data requirements, all that is needed are the details of the genetic association between the variant(s) and the trait from the exposure GWAS (sample one) and the outcome GWAS (sample two). This typically includes information on the effect and other allele, effect allele frequency, effect estimate, and standard error from both GWAS. In addition, the development of web software and code for summary-level data makes MR very straightforward to implement (see the section “Novel Informatic Tools”). It also increases the scope of MR analyses, with a wealth of data on exposures and outcomes available for interrogation, which may be infeasible or expensive to measure in the same set of individuals. Furthermore, a series of methods have been developed within this setting in recent years to assess and correct for potential pleiotropy (see the section “Methods for Assessing and Accounting for Horizontal Pleiotropy”).

The simplest approach for using summary-level data in an MR framework is to derive a Wald ratio for a SNP. This is the effect estimate for the SNP–outcome association (from sample 2) divided by the coefficient of the SNP–exposure association (from sample 1), with the standard error of the Wald ratio often approximated by the delta method (Thomas et al. 2007). In the presence of multiple genetic instruments, a meta-analysis approach (usually inverse-weighted [IVW] meta-analysis) may be used to combine Wald ratio estimates of the causal effect obtained from different SNPs (Dudbridge 2020). The point estimates from an IVW MR are equivalent to a weighted linear regression of the SNP–outcome associations on SNP–exposure associations when the intercept is constrained to zero. The effect estimates obtained should also be equivalent to the effect estimated in 2SLS when sample sizes are large, SNPs independent, and there is limited heterogeneity in the Wald ratios.

One- versus Two-Sample MR

Despite its ease of application, there are various limitations of the two-sample MR that also require consideration. These have been discussed in detail elsewhere (Haycock et al. 2016; Zheng et al. 2017) and are also summarized in Table 3. In part because of these limitations, and also because of the recent availability of large-scale genotyped and phenotyped data sets (Table 1), there has been a recent resurgence of one-sample MR. Major benefits of the one-sample MR approach are the flexibility to perform rigorous MR, and the ability to assess the independence and exclusion restriction assumptions through assessment of individual-level confounders.

Table 3.

Comparison of strengths and limitations of one-sample and two-sample Mendelian randomization (MR)

	One-sample MR	Two-sample MR
Strengths	Flexibility of the analytical strategy in terms of regression models that can be performed as well as covariates and participants that can be included/excluded	Improved sample size and power
		Flexibility and enhanced power to perform an array of sensitivity analyses (e.g., pleiotropy-robust methods)
	Permits thorough evaluation of confounders to test above assumption	Less time-consuming and easier to implement
	Allows for comparison with observational estimates in same study (e.g., through Durbin-Wu-Hausman test)	Can evaluate causal relationships between a range of exposure and outcomes, which might not be possible in a single sample setting
	Can model interactions, survival time, and other analyses (including MR analysis of nonlinear effects)	Unable to thoroughly evaluate individual-level confounding factors
		Assumes the two samples are exchangeable. Examples of where this is difficult to assert are where the samples are heterogeneous in terms of age, sex distributions or ancestry
Limitations	Traditionally low power and therefore imprecise causal estimates	Potential for selection bias caused by study sampling
		Weak instrument bias is toward null
	Potential for selection bias caused by study sampling	Winner's curse in which the discovery GWAS used to estimate the SNP-trait association may overestimate the effect of the genetic instrument relative to the exposure
	Weak instrument bias is toward observational estimate	Relative rigidity of the summary data available, which is limited by the original GWAS model performed (e.g., adjustment for unwanted covariates and a lack of available data on subgroups of interest (e.g., sex-specific estimates)
	Winner's curse in which the sample in the discovery GWAS is the same as that used for MR, which can lead to overestimation of the strength of association of the genetic instrument with the exposure	SNP–exposure and SNP–outcome associations should be coded relative to the same effect allele, also known as “harmonization,” which is nontrivial in the situation of palindromic SNPs (i.e., G/C and A/T SNPs) and in the absence of information on allele frequencies
	Need to have access to individual-level genetic and phenotypic data	Assumes no overlap between samples, which could bias estimates if this is not true
		Direct comparison with observational estimates not as straightforward
		Unable to model interactions, survival time, and other analyses (including nonlinear analyses)

However, weak instrument bias may threaten the estimation of causal effects in one-sample data sets (Burgess and Thompson 2011), in which uncertainty in the SNP–exposure association could bias the causal estimate (Table 3). Importantly, where weak instruments will bias causal estimates in the direction of the null in a two-sample setting, weak instrument bias will be toward the observational association in a one-sample setting (Zheng et al. 2017). In addition, selection bias caused by winner's curse could lead to biased causal estimates if the genetic variants were discovered in the same sample under investigation. This is a phenomenon that occurs in GWAS by using a P-value cut-off that can lead to chance overestimation of the effect size of SNPs with the strongest genetic signals in the GWAS discovery sample (Garner 2007).

Whereas two-sample methods can be used for one-sample MR analysis (Minelli et al. 2021), these may produce biased estimates and type 1 error rate inflation (i.e., incorrectly rejecting the null hypothesis of no association), something learned from two-sample MR analyses when genetic consortia have overlapping samples (Burgess et al. 2016a). It is advised that the covariance between the SNP–exposure and SNP–outcome association estimates are taken into account and that external weights be used where possible to minimize the risk of bias. Specifically, genetic variants can be weighted by the magnitude of their association with the exposure in an independent data set (Burgess and Thompson 2013), in what could be described as a “one-and-a-half sample MR” design.

Extensions to the Basic MR Approach

Other Methods

A series of developments have been made to extend the application of MR to

• consider the prevailing direction of causality between two traits (bidirectional MR);

• evaluate intermediates on the causal pathway between exposures and outcomes (two-step, network, or mediation MR);

• assess the causal role of closely related traits and to establish independent effects of each (multivariable MR); and

• evaluate combined causal effects of risk factors (factorial MR or exposure interactions).

Descriptions, directed acyclic graphs (DAGs), and applied examples for each of these methods are outlined in Table 4.

Table 4.

Extensions to the basic Mendelian randomization (MR) approach

Novel Informatic Tools

The recent widespread availability of GWAS summary data for a range of traits, with large data repositories and bioinformatic resources for performing MR, provides a powerful and user-friendly way of investigating causal relationships between many different traits (Richardson et al. 2020a). For example, MR-Base is a platform that has retrospectively collected GWAS data sets for more than 20,000 traits, as well as protein-, methylation-, and expression-quantitative trait loci (pQTL, mQTL, and eQTL) statistics for tens of thousands of molecular markers (Hemani et al. 2018b). Together with its web-based interface, which allows the user to explore a range of causal relations, there is an accompanying R package (TwoSampleMR), which allows for LD pruning of genetic instruments in the exposure GWAS, the identification of SNPs and tagging SNPs for each instrument in the outcome GWAS, the careful harmonization of summary statistics between exposure and outcome GWAS, as well as the use of sensitivity analyses to promote evaluation of the MR assumptions.

Methods for Assessing and Accounting for Horizontal Pleiotropy

Violation of the exclusion restriction assumption via horizontal pleiotropy is a major threat to the validity of MR analyses and so various methods have been developed in recent years to try to overcome this. These methods (1) can test for potential pleiotropy (e.g., heterogeneity and outlier tests); (2) can directly model and correct for pleiotropy (e.g., MR Egger regression [Bowden et al. 2015]) and MR-TRYX [Cho et al. 2020]); or (3) are “naturally robust” to pleiotropy (e.g., mode and median estimators [Bowden et al. 2016a; Hartwig et al. 2017]). These typically use IV estimates as the basis of the sensitivity analyses and can be used to explore how robust MR findings are to the assumption that the genetic instruments used have no horizontal pleiotropic effects.

If the estimate obtained for a causal effect is of a consistent magnitude across multiple independent variants, then pleiotropy is less likely to be a concern. However, often effect estimates are not consistent across independent instruments, with some “outlying” variants having an observed association with the outcome that is substantially different to that expected given their association with the exposure. If the instrument is valid, it should have an effect on the outcome that is proportional to the effect on the exposure. Formal tests for examining heterogeneity include Sargan's test for 2SLS and Cochran's Q statistic, Rucker's Q, and likelihood ratio tests in two-sample MR (Bowden et al. 2018b; Hemani et al. 2018a). For detecting outliers, the following approaches can be considered: leave-one-out analysis, Cook's distance, studentized residuals, Q-contribution, and the MR-PRESSO global and outlier tests (Verbanck et al. 2018).

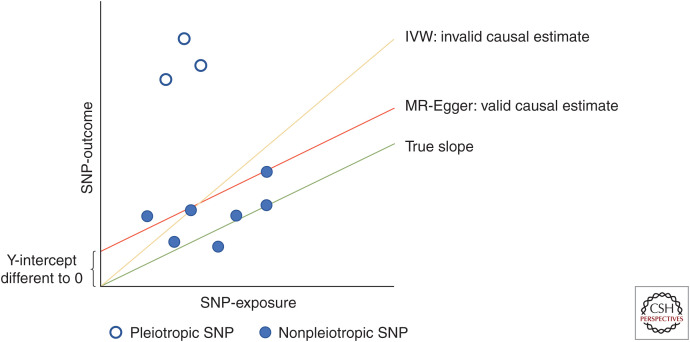
Graphical assessment is also helpful for assessing potential pleiotropy. Heterogeneity can be visualized in scatter plots (Fig. 8), in which estimates derived from each genetic variant do not align with the regression line (i.e., do not converge to the same causal estimate), or in forest plots in which there is clear variation in the causal estimates obtained from each variant. Funnel plot displays of MR estimates of individual genetic variants against their precision will show asymmetry if some variants have unusually strong effects, indicative of pleiotropy. Leave-one-out plots can be used to assess the influence of individual outliers; and the Galbraith radial plot can be considered in place of the scatter plot for detecting outliers and influential data points (Bowden et al. 2018a).

Figure 8.

Inverse-variance weighted (IVW) and Mendelian randomization (MR)-Egger regression.

Whereas random variation could result in different effects estimated by the individual variants, the presence of heterogeneity in the causal effect estimated by individual SNPs could also indicate horizontal pleiotropy. The simplest method of accounting for this is with the use of a random effects IVW meta-analysis model (Dudbridge 2020). However, this approach can only be used where horizontal pleiotropy is “balanced” (i.e., where the random effects have zero weighted mean) (Hemani et al. 2018a). The first method developed for assessing and counteracting the extent of “unbalanced” or “directional” pleiotropy was the application of the Egger regression technique to MR analysis (Bowden et al. 2015). This approach, first introduced in the context of small-study bias within meta-analysis, allows the intercept of the weighted linear regression line of the SNP–outcome on the SNP–exposure association to vary freely (Fig. 8). Directional pleiotropy can be tested by assessing the extent to which the intercept deviates when it is not constrained to the origin (as in IVW), and the gradient of the line can be used to provide a causal estimate in the presence of directional pleiotropy using the MR-Egger approach. It is important to report both estimates.

Additional pleiotropy-robust approaches include the modal and median based estimators that both avoid the contribution of some invalid instruments (Bowden et al. 2016a; Hartwig et al. 2017). Both of these methods can be viewed as implicit outlier correction techniques, because they only allow certain more “reliable” SNPs to contribute to the overall estimate. Use of a weighted approach for both of these methods is typically advocated to maximize statistical power.

Additional methods intended to account for pleiotropy include direct outlier removal (e.g., MR-PRESSO [Verbanck et al. 2018], generalized summary MR [GSMR] [Zhu et al. 2018], and Cook's distance [Corbin et al. 2016]), outlier penalization (e.g., MR-TRYX [Cho et al. 2020]), “no-relevance point” approaches including negative controls (Gage et al. 2017), generalized gene–environment interaction models (MR GxE [Spiller et al. 2019]), pleiotropy-robust MR (van Kippersluis and Rietveld 2018), and techniques that attempt to directly model pleiotropic pathways including multivariable MR (Burgess and Thompson 2015), structural equation modeling (SEM) (Evans et al. 2019), and the direction of causation approach (MR-DOC) (Evans et al. 2019; Hwang et al. 2020). These methods are described in more detail elsewhere (Hemani et al. 2018a; Burgess et al. 2019; Slob and Burgess 2020).

It should be emphasized that while these approaches can relax or bypass the exclusion restriction assumption of conventional MR analysis, they in turn come with their own assumptions (Table 5; Hemani et al. 2018a). In addition, these approaches are typically less well powered than the IVW approach. As such, methods for assessing and accounting for pleiotropy should be viewed as sensitivity analyses to conventional approaches such as IVW.

Table 5.

Additional assumptions of Mendelian randomization (MR) sensitivity analyses

Approach	Assumption	Description	References
Inverse-variance weighted (IVW) and MR-Egger regression	No measurement error (NOME)	There is no measurement error in the association between the single-nucleotide polymorphism (SNP) and the exposure	Bowden et al. 2016b
MR-Egger regression	Instrument strength independent of direct effect (InSIDE)	The strength of the SNP–exposure association should not correlate with the strength of the pleiotropy effect	Bowden et al. 2015
Modal estimator	Zero modal pleiotropy assumption (ZEMPA)	The most common causal effect estimate is a consistent estimate of the true causal effect, even if the majority of instruments are invalid	Hartwig et al. 2017
Median estimator	Simple median = the causal effect is provided by the median SNP estimate	Simple median = at least 50% of the instruments are valid (i.e., not pleiotropic)	Bowden et al. 2016a
	Weighted median = the causal effect is provided by the weighted median SNP estimate	Weighted median = at least 50% of the weight in the analysis stems from variants that are valid instruments (i.e., not pleiotropic)

COMMON MISCONCEPTIONS

With rising popularity of the MR approach, which is now becoming a common element of GWAS papers, there are a number of common misconceptions that require debunking to ensure that the findings from MR analysis are interpreted appropriately.

There Are Three Assumptions on Which MR Relies for Estimating Causal Effects

Although there are three core IV assumptions that apply to many MR studies (relevance, independence, and exclusion restriction), additional assumptions are needed to quantify the effect or to consider that the study is informative about effects that may be produced by manipulation of the exposure. The latter is made under the gene–environment equivalence assumption already discussed.

Another assumption in instrumental variable analysis that is relevant for effect estimation, is the assumption of homogeneity (Swanson 2017). This assumption relates to assessing whether the causal effect obtained in MR is uniform across the population, and so represents an average treatment effect (ATE). For example, if investigating the effect of BMI on CVD, we would assume that a kg/m² increase in BMI would elevate risk of CVD irrespective of the person's gender or age. The homogeneity assumption can also be replaced by the less stringent monotonicity assumption, which assumes that an increase in the number of risk alleles will never lower the likelihood of exposure (Swanson and Hernán 2018) (e.g., a BMI genetic risk score should not increase BMI for some individuals and decrease it for others). If this assumption holds, then estimation of a local average treatment effect (LATE) among those individuals whose exposure level is affected by their genotype is possible. Such assumptions must be made for the effect estimate obtained from any MR analysis to be interpreted as the causal effect of the exposure on the outcome. Although they cannot be explicitly tested, the assumptions can be interrogated through various means. One possibility is to estimate causal effects in different subpopulations and to evaluate whether the estimated effects differ. Alternatively, as nonhomogeneity in the genetic variant–exposure association would lead to nonhomogeneity in the genetic variant–outcome association, evaluating the variance of exposure and outcome groups by genotype would provide a test for the presence and degree of violation of this assumption (Mills et al. 2020). Large GWAS allow variance to be characterized well, and so can be interrogated to investigate this (Young et al. 2018).

An instance in which it is difficult to obtain relevant treatment effects from MR estimates is in the presence of binary exposures (Burgess and Labrecque 2018). As the assumptions of homogeneity and monotonicity are less likely to hold when interpreting causal estimates with binary exposures using MR, it is often simpler to report on the existence and direction (rather than the magnitude) of the causal effect (Burgess and Labrecque 2018). If these assumptions can be made, there are options for causal estimation with a binary exposure that allow estimates to be converted onto a more clinically meaningful scale. In one-sample data with timed events, it may be possible in principle to estimate the causal effect of a binary exposure, but this has not yet been demonstrated. Even if these assumptions can be made, interpretation is to the liability to the binary exposure, rather than the binary exposure itself (Davey Smith 2019; Richmond and Davey Smith 2019).

Interpretation of causal effects on binary outcomes is also challenging (Palmer et al. 2008). Although it is empirically possible to calculate causal estimates in a similar manner to those for continuous variables, for example, with use of the log odds scale, the MR effect estimate may only be approximate in the case of a binary outcome (Burgess et al. 2016c). This is because the “noncollapsibility” of odds ratios means that these estimates may not be constant across strata, and so cannot be used to obtain a precise causal effect (Greenland et al. 1999). Alternatively, analyses can be conducted on the risk difference scale, which reduces the risk of bias caused by noncollapsibility.

As mentioned, whereas sensitivity analyses may relax some of the core IV assumptions (e.g., exclusion restriction in the case of pleiotropy-robust methods), they impose their own set of (albeit weaker) assumptions (Table 5). Two-sample MR also imposes additional assumptions to the one-sample MR approach, including exchangeability of the two samples (i.e., whether they are both drawn from the same underlying population), as well as the assumption that the two samples are nonoverlapping (Lawlor 2016).

MR Is Analogous to a Randomized Controlled Trial

An analogy has often been made between an MR study and an RCT, in which genotypes are said to randomize participants into different levels of exposure or treatment, independent of confounding (Davey Smith and Ebrahim 2005). In particular, it is this random allocation of genetic variants from parents to offspring that can be viewed as analogous to an RCT (Davey Smith and Ebrahim 2003; Davey Smith et al. 2020). Often this analogy is useful, particularly when it is possible to scale causal effect estimates to that of interventions, for example, in the case of (retrospectively) predicting the null effect of selenium on risk of prostate cancer using MR (RR 1.01 [95% CI 0.89, 1.13] per 114 µg/L in MR vs. RR 1.04 [95% CI 0.91, 1.19] per 114 µg/L in RCT) (Yarmolinsky et al. 2018). However, the analogy is not perfect because RCTs typically involve interventions of short duration, whereas an individual's genotype could reflect lifelong exposures, time-dependent or critical period effects, as well as potential developmental compensation that may arise over time (Davey Smith and Ebrahim 2003; Holmes et al. 2017). Causal estimates obtained from MR analyses may therefore differ in magnitude to those seen or anticipated in an RCT, although can also be useful in providing added value regarding life-course effects. For example, knowledge that cholesterol lowering in earlier life is likely to be important for preventing CVD (Ference et al. 2014). However, in MR analysis conducted at a population, rather than family-level, the analogy with RCTs is only approximate (Davey Smith and Ebrahim 2003), as described below.

Genetic Variants Are Not Influenced by Confounding Factors

Under Mendel's laws of segregation and independent assortment, it is assumed that genetic variants should be inherited independently of other genetic and environmental factors. Although population-level genetic variants are typically much less associated with many potential confounders than directly measured exposures (Davey Smith et al. 2007), the random inheritance of genetic variants from parents to offspring does not guarantee that genetic variants and confounders will be independent in samples of unrelated individuals. For example, an obvious violation of this is created because of population stratification that can introduce confounding of genotype–disease associations by factors related to subpopulation group membership within the overall population. This might occur even within groups of relatively homogeneous ancestry, as a result of underlying substructure (Abdellaoui et al. 2019; Haworth et al. 2019; Lawson et al. 2020), or also at the family level, for example, caused by assortative mating (Hartwig et al. 2018). One potential violation of the second IV assumption is that of “dynastic” or “genetic nurture” effects, in which parental genotypes affect the offspring via the environment that parents create for their offspring by affecting the parental phenotype (Davies et al. 2019; Brumpton et al. 2020). As a result, a genetic instrument in the offspring will be correlated with the environment created by the parents. One solution to this problem is to perform MR analysis between siblings who have a shared family background and whose genotype differences will not be confounded by parental or family factors (within-family MR) (Davies et al. 2019a; Brumpton et al. 2020). In the initial presentation of MR, it was suggested that the most robust form would be within families (Davey Smith and Ebrahim 2003) and with increasing sources of data for family-based studies, this approach offers potential for elucidating causal effects for those traits that are most likely to be influenced by dynastic effects (e.g., socioeconomic and behavioral factors).

The Exclusion Restriction Assumption Is Violated because of Pleiotropy

The exclusion restriction assumption is sometimes referred to as the “no pleiotropy assumption,” although it can be violated in a number of other ways, including timing effects, interactions, reverse causation, collider bias, and LD, as previously described (VanderWeele et al. 2014).

In particular, the following sources of collider bias may induce spurious associations between a genetic variant and factors other than the exposure of interest that may influence the outcome (Fig. 5):

• The use of instruments generated from a GWAS that adjusts for another phenotype;

• Ascertainment bias in case-control studies;

• Selection and loss to follow-up bias in cohort studies;

• Survival bias when investigating later-life outcomes; and

• Evaluation of disease progression in a case-only setting.

When there are only moderate effects of a phenotype on selection, bias is generally small (Gkatzionis and Burgess 2019). However, where collider bias is likely to exist, it is recommended that sensitivity and simulation studies are carried out to evaluate the extent to which bias might distort estimates (Hughes et al. 2019). In addition, alternative approaches such as inverse-probability weighting, modeling competing risks, adjusting for index event bias (Dudbridge et al. 2019; Mahmoud et al. 2020), and the use of negative control outcomes (Sanderson et al. 2021) can also be considered.

Another way in which the exclusion restriction may be violated is when genetic instruments are in LD with other variants that have an effect on the outcome not via the exposure. In this instance, genetic colocalization approaches (Giambartolomei et al. 2014) may be used that attempt to evaluate whether two traits share the same causal variant at a particular locus, and thus contribute to evaluation of whether the exclusion restriction assumption is likely to hold.

Reverse Causation Is Not an Issue for MR

Because germline genotypes are fixed at conception, they cannot be influenced by reverse causation, and therefore it is often claimed that reverse causation is not an issue for MR. Although this is true, a scenario in which reverse causation might pose a problem for MR is where the genetic instruments for two traits (X and Y), G_X and G_Y, are not well characterized (Table 4; Davey Smith and Hemani 2014). If trait X influences trait Y, then a GWAS with adequate statistical power will identify a genetic variant with its primary influence of trait X as being associated with trait Y (for example, the CHRNA5 variant related to smoking intensity has been identified at genome-wide significance in relation to lung cancer [Amos et al. 2008]). This will lead to spurious conclusions if this variant were then used as a genetic instrument for trait Y (e.g., that lung cancer causes smoking), that is, by misspecifying the primary phenotype. One way to minimize this problem is to ensure that the two sets of instruments are independent of each other by excluding the genetic variants that they have in common. However, this may also increase the risk of type II error if variants are excluded from the genetic instruments that reflect vertical pleiotropy (e.g., if the CHRNA5 variant were removed from both the smoking and lung cancer instruments). In situations where an outcome Y influences trait X, for example, developing coronary heart disease increases CRP levels, it may be possible to investigate the number of “cases” of the outcome in the sample used to run the exposure GWAS. Here, a low prevalence of the outcome in the exposure sample would minimize risk of such a reverse signal. Another approach that can be used in this context is the Steiger method applied to MR (Hemani et al. 2017b). This has been developed to investigate whether the genetic variants being used to instrument trait X are more strongly correlated with trait Y than X, in which case they will be excluded from the instrument for X.

One way in which this kind of reverse causation can be leveraged within an MR study is with the notion of “reverse MR” (Holmes and Davey Smith 2019). Here, a disease-associated genetic risk score would be expected to associate with causes of the disease (e.g., a genetic risk score for lung cancer would be associated with smoking because the CHRNA5 variant is included in the score). If the outcome of interest cannot plausibly cause the exposure being considered (for example, in a subgroup in which the outcome is not prevalent, e.g., among young study participants in the case of lung cancer), then this situation can be used to confirm causal exposures. This principle has been applied to investigate perturbations in proteins and metabolites in relation to later cardiometabolic disease risk (Battram 2018; Bell et al. 2020; Ritchie et al. 2021). However, alternative scenarios such as pleiotropy, a causal effect of disease liability, or early stages of disease that influence the exposure (e.g., prediagnostic cholesterol lowering in cancer [Ahn et al. 2009]) also need to be considered.

OVERCOMING LIMITATIONS

Limitations of the MR approach have been discussed extensively elsewhere (Davey Smith and Ebrahim 2003, 2004; Davey Smith and Hemani 2014; VanderWeele et al. 2014; Haycock et al. 2016; Zheng et al. 2017; Davey Smith et al. 2020). Although some of the early concerns of the MR approach such as a lack of genetic instruments, horizontal pleiotropy, and low power have been ameliorated with larger data sets and novel methods, some limitations remain and new constraints have been recognized.

Lack of Reliable Polymorphisms for Studying Modifiable Exposures of Interest

Genetic instruments extracted from a single gene with a well-understood biological function, and therefore most likely to meet the MR assumptions, are not available for all exposures. Although the proliferation of GWAS has increased the availability of genetic variants to use as potential instruments, the role of the variants identified often requires careful consideration to assess their validity in MR. Polygenic influences on most phenotypes imply individual SNPs of small effect size, each with a marginal contribution to the variance explained in a trait. This is both a threat to the exclusion restriction assumption and can lead to problems of weak instruments, unless the variants can be combined into a genetic risk score or applied in large sample sizes.

The use of genetic variants may sometimes lead to counterintuitive results. For example, while it would be expected that longer-term IL-6 levels would elevate the risk of CHD (Danesh et al. 2008), genetic variation in the IL-6 receptor that increases circulating IL-6 levels has actually been found to decrease risk of CHD (Swerdlow et al. 2012). This can be explained because carriers of this polymorphism exhibit higher circulating IL-6 levels but reduced membrane-bound IL-6, with reduced IL-6 signaling, which in turn reduces risk of CHD (Swerdlow et al. 2012). Similarly, if genetic polymorphisms are associated with multiple aspects of a single trait, for example, variation in CHRNA5 that is associated with different dimensions of smoking behavior (e.g., number of puffs per cigarette, depth of inhalation) (Lassi et al. 2016), this can also lead to problems in the interpretation of causal effects for any particular dimension of the trait.

A further limitation posed by a lack of understanding of genetic variants is that of “contamination” of the instrument by variants associated with traits “upstream” from the trait of interest, leading to misspecification of the primary phenotype (Davey Smith and Hemani 2014). This is a particular concern as GWAS sample sizes increase, because it increases the power to detect genetic variants that act indirectly on the trait of interest. For example, genetic variants with a primary influence on BMI appear among the top hits in GWAS of C-reactive protein (Dehghan et al. 2011), but should not be used as instruments for CRP levels. This has already been discussed within the context of a bidirectional relationship, in which genetic variants that influence the exposure through reverse cause may be picked up. In addition, it may reintroduce confounding if genetic variants associated with confounders are picked up as genetic variants for the exposure. For example, genetic variants identified in relation to drinking behavior have been found to be strongly related to socioeconomic factors (Rosoff et al. 2021). This may lead to confounding in MR studies if the genetic variants used to instrument the exposure (here drinking behavior) are primarily associated with factors upstream from the exposure (e.g., educational attainment) and may explain the opposite genetic correlations observed for alcohol quantity and intake frequency (which are differentially associated with educational attainment) in relation to various health outcomes in a recent study (Marees et al. 2020). Multivariable MR can be used in this instance to estimate the “true” effect of the phenotype being investigated, for example, accounting for educational attainment to estimate direct effects of drinking behavior, but this requires knowing the structure of the underlying phenotypes.

Horizontal Pleiotropy

There is a clear trade-off between including more variants in a genetic instrument to maximize variance explained in the exposure and the increased risk of pleiotropy by including more poorly characterized variants. However, the potential advantage of including more variants is the ability to use the suite of approaches already described. These approaches relax the exclusion restriction assumption but each has its own sets of assumptions (Table 5). If results are largely consistent across methods that have orthogonal biases (Munafo et al. 2020), there can be more confidence in drawing robust conclusions. Alternatively, in the presence of inconsistent results across methods, a Bayesian model averaging framework may be used as a basis for efficient estimation in the presence of pleiotropy (Shapland et al. 2020).

Lack of Independent Instruments

Although it is not necessary that a genetic variant used to instrument a modifiable exposure of interest in MR should be the causal variant for that trait, it is important to assess whether multiple SNPs used in the instrument are likely to be tagging the same causal variant. This is because including correlated variants will typically lead to erroneous precision in the causal estimate obtained. LD-based clumping or pruning can be used to exclude variants in strong LD, which can ensure independence of the instruments. Another approach is to use a weighted generalized linear regression method that takes into account correlation of multiple nonindependent SNPs (Burgess et al. 2016b). This approach is particularly useful when assessing causality of molecular phenotypes (e.g., DNA methylation, gene expression, protein levels) that are often characterized by few independent instruments in cis (genetic variants located close to the target locus/gene). A method that is often used in conjunction with MR when there is, for example, one independent variant to instrument a molecular trait in cis, is the approach of genetic colocalization mentioned previously. Alternatively, the inclusion of trans instruments (genetic variants more distal to the target locus/gene) in the MR analysis can be considered, although it is more likely that these variants will violate the exclusion restriction criteria via horizontal pleiotropy.

Need for Optimal Precision

A failure to recognize the importance of both sample size and instrument strength in MR studies for the detection of expected effects has in the past led to uninformative findings that lack adequate precision to support or reject hypotheses about causal effects. Genotyping in large-scale epidemiological studies as well as the availability of GWAS summary statistics has vastly improved the power of MR studies and has revealed an increasing number of genetic variants that explain a larger proportion of trait variance. Nonetheless, it is recommended that power calculations for MR studies be conducted a priori (Brion et al. 2013). Equivalence testing may also be used to evaluate observed effects within a priori defined equivalence bounds, to distinguish effects that are large enough in magnitude to be deemed robust.

It is important to recognize that several of the extensions of the conventional MR approach, such as factorial MR, multivariable MR, sensitivity analyses such as MR-Egger, and within-family MR analyses all suffer from precision constraints that should be taken into consideration. This can be evaluated through additional tests, for example, with the Sanderson-Windmeijer conditional F-statistic in the case of multivariable MR, which can be used to assess instrument strength for multiple exposures when estimated jointly (Sanderson et al. 2019, 2020). Furthermore, precision can be limited in specific contexts, for example, when evaluating intergenerational causal effects that have previously been limited to studies with genetic data available in two generations (Lawlor et al. 2017). In this context, new structural equation model (SEM) approaches have been developed that allow effects of parental exposures on offspring outcomes to be inferred without having to have intergenerational genetic data, and which leverage power from large GWAS summary data in a two-sample approach (Evans et al. 2019; Hwang et al. 2020).

Weak Instrument Bias

Methods to overcome potential weak instrument bias in MR include the use of SIMEX-corrected estimates when the assumption of no measurement error (NOME) cannot be met (Bowden et al. 2016b), the use of robust-adjusted profile scores (Zhao et al. 2018; Wang et al. 2021b), as well as a weak instrument and pleiotropy robust estimation method for use in multivariable MR (Sanderson et al. 2020).

Winner's Curse

It is recommended that the GWAS discovery sample is independent of the sample(s) used to conduct the MR analysis (Haycock et al. 2016). Ideally, the genetic variants used as instruments in an MR analysis will also have been replicated in an independent sample to further minimize risk of Winner's curse. However, there is a clear trade-off between maximizing sample sizes of GWAS for discovery of genetic variants and avoiding the problem of Winner's curse by retaining a sample for replication and implementation of the MR approach. In the largest data sets, it may be possible to perform a split-sample (Angrist and Krueger 1995b) or jackknife analysis (Angrist et al. 1999), whereby the data set is partitioned to avoid problems of sample overlap and Winner's curse.

Canalization and Time-Varying Effects

The notion of canalization or developmental compensation is a potential limitation of MR for which there is no simple empirical assessment (Davey Smith and Ebrahim 2003). It refers to the buffering of genetic effects during development that may bias MR estimates and vitiate gene–environment equivalence (i.e., that perturbations caused by genotype have the same downstream effects as if they were caused by modifiable exposures) (Davey Smith 2012a). Canalization is a widespread phenomenon in gene knockout studies (Davey Smith and Ebrahim 2003), although it is currently unclear whether the generally small phenotypic differences induced by common functional polymorphisms are sufficient to induce compensatory responses. A related consideration is the often-stated assumption that genetic variants have lifelong effects, which has been used previously to explain large point estimates obtained from MR compared with other epidemiological approaches (Ference et al. 2012). There are clear examples of MR in which exposures are time limited, and in which canalization is therefore less likely to be an issue. For example, when assessing causal effects of exposures in utero, the maternal genetic variants being used as instruments will only have an effect on the offspring via mechanisms during the intrauterine period (Lawlor et al. 2017), and when assessing causal effects of exposures that occur predominantly in adulthood (e.g., alcohol consumption, childbearing), the genetic variants will only have an effect after the developmental stage in which canalization is most likely to occur.

Although it is often difficult to model such time-varying effects in MR, they can bias causal estimates (Labrecque and Swanson 2019) and may have implications for determining optimal timing of interventions. New GWAS studies have started to reveal genetic variants with distinct timing effects (Couto Alves et al. 2019) that may be leveraged to investigate time varying effects in an MR context. For example, a recent multivariable MR study used genetic variants with distinct effects on body size in childhood and adulthood to separate the causal effects of this trait at two stages of the life course on risk of chronic disease (Richardson et al. 2020b).

FUTURE PROSPECTS

Although the scope of MR has grown massively in recent years, there are several priority research areas that have not yet been fully evaluated. With increasing methodological and bioinformatic innovation, there is great potential to make progress in these areas. However, subject-specific knowledge, methodological insight, and improved reporting of MR findings are required to ensure the robustness and reproducibility of findings.

Extending Clinical Applicability

Identifying Factors Underlying Disease Progression

To date, the majority of GWAS have sought to identify genetic variants associated with risk of disease occurrence. Such variants are informative for disease prevention, but not necessarily for treatment aimed at influencing disease progression because the same genetic factors will not necessarily influence both disease onset and progression of the disease (Davey Smith et al. 2017; Paternoster et al. 2017). In 2017, just 8% of genetic association hits in the GWAS Catalog had attempted to identify variants associated with disease progression or severity, and most with modest sample size (Paternoster et al. 2017). Nonetheless, an increasing number of progression GWAS are being carried out, in studies such as the Genetics and Subsequent Coronary Heart Disease Consortium (GENIUS-CHD; CHD, n > 270 k cases) (Patel et al. 2019), the Breast Cancer Association Consortium (BCAC; breast cancer, n > 47 k cases) (Escala-Garcia et al. 2019), and the Prostate Cancer Association Group to Investigate Cancer Associated Alterations in the Genome consortium (PRACTICAL; prostate cancer, n > 45 k cases) (Szulkin et al. 2015), which should allow MR studies of progression to be conducted.

However, determining true causal effects on disease progression using MR in case-only data sets is made more challenging because of the issue of collider bias (Paternoster et al. 2017; Hughes et al. 2019). In particular, when a group of participants are selected based on certain characteristics (e.g., presence of disease), this will introduce a spurious association between independent risk factors influencing selection that will then distort the relationships between each risk factor and disease progression (Fig. 5). This is a threat to both conventional observational associations and to studies of genetic influences, with confounding being reintroduced that can lead to violation of the MR assumptions. Methods for alleviating such biases are currently in development (Dudbridge et al. 2019; Hughes et al. 2019; Mahmoud et al. 2020). These methods attempt to estimate the bias adjustment factor based on estimates for the association of genetic variants with both incidence and progression.

Drug Trials

Whereas RCTs remain the gold standard approach for testing the efficacy and safety of a new drug, RCTs can be complemented by MR in terms of prioritizing drug targets, predicting the outcome of trials and optimizing trial design (Ference et al. 2021; Schmidt et al. 2021). Human genetic evidence is a strong predictor of drug success (Nelson et al. 2015) and MR studies of proteins and metabolites are becoming fundamental in drug discovery and development (Ference et al. 2021; Gill et al. 2021; Holmes et al. 2021; Schmidt et al. 2021). In particular, cis-acting variants may serve as genetic proxies for protein drug targets, and selection of such variants may be optimized to evaluate the potential causal relationships between those drug targets and a range of diseases (Sun et al. 2018; Zheng et al. 2019; Schmidt et al. 2020). A promising application of MR is in the prioritization of targets for disease prevention, for example, revealing the role of PCKS9 inhibitors for reducing LDL cholesterol (Ference et al. 2016), as well as deprioritizing interventions based on null results from MR, for example, showing that CRP concentration is unlikely to be a causal factor in CHD (Wensley et al. 2011). MR can also indicate potential side effects of drugs, including the elevated risk of type 2 diabetes with use of some lipid-lowering drugs (Ference et al. 2012), which has also been shown in the case of statin trials (Swerdlow et al. 2015). MR has also been used to identify potential repurposing opportunities of existing drugs (Li et al. 2020). Most recently, genetic variation in IL6R has been associated with lower risk of hospitalization from COVID-19, which is in line with findings from IL-6R therapeutic inhibition trials (Bovijn et al. 2020). In addition to predicting the consequences of pharmacotherapy, MR has the potential to be used to optimize trial design, for example, in relation to segmenting patients who are most likely to benefit from the drug or giving insights into the timing of drug initiation (Ference et al. 2012, 2021). However, this typically requires the availability of prospective data sets of target populations with genetic data available (Schmidt et al. 2021).

Scaling up Feasibility Trials Using MR to Robustly Infer Causal Effects on Clinical End Points

A novel application of MR has recently been proposed that may enhance the value of feasibility studies of interventions (Sandu et al. 2019). This approach uses MR to predict causal effect of these interventions on long-term clinical outcomes via short-term intermediate biomarkers. Feasibility trials are small-scale studies that aim to assess the practicality and acceptability of implementing an intervention in a clinical setting. These are not usually powered to evaluate effects on clinical outcomes and are not typically followed up for enough time to assess long-term outcomes. However, intermediate measures may be collected that can serve as surrogate end points in such studies. These measures may lie on the causal pathway to clinical outcomes and MR can be used in this context to appraise the causal effect of those intermediate measures altered by the intervention on long-term outcomes, using a larger study base to the feasibility study in question to bolster power. Whereas these intermediate biomarkers serve as surrogate end points, which are well known to have limitations (Prentice 1989), the advantage of using MR in this context is that it is possible to explore both expected and unanticipated effects of manipulating an intermediate trait on a range of outcomes, including relatively rare ones, and with larger sample sizes. Furthermore, the approach may be used to uncover other causal intermediates that could validate choice of surrogate markers for use in future feasibility studies.

Uncovering Molecular Mechanisms

Building on the success of GWAS and the availability of cost-effective and robust technologies is the scaling up of other -omic technologies within population health. This is largely concerned with understanding how gene regulatory mechanisms or gene products influence health-related outcomes and is useful for investigating the molecular pathways that may underpin causal effects. In particular, such -omic measures are influenced by many environmental and endogenous factors and so can be considered as intermediate phenotypes through which causal effects may be investigated (Davey Smith and Hemani 2014).

Of particular utility are large-scale -omic scans for formulating novel hypotheses on biological processes underpinning complex traits and diseases. However, in contrast to germline genetic variation, -omic signatures are largely phenotypic, and are therefore subject to the same potential problems of confounding and reverse causation that afflict conventional epidemiology (Relton and Davey Smith 2010). MR is being increasingly applied to elucidate causality for a range of molecular data, including epigenetics, transcriptomics, gene expression, metabolomics, and proteomics (Porcu et al. 2021). For this, approaches such as two-step, network, and multivariable MR are of particular utility for determining whether these markers lie on the causal pathway between risk factors and disease (Table 4). Such approaches are being applied in increasingly complex and innovative ways, to consider the causal nature of a large number of molecular markers (Wahl et al. 2017), integrating several types of -omics data to evaluate molecular pathways (Mendelson et al. 2017), as well as considering the tissue-specific nature of causal effects (Taylor et al. 2019; Richardson et al. 2020c).

Increasing Ethnic Diversity in MR Studies

Approximately two-thirds of all previous GWAS have been performed in individuals of European ancestry (Duncan et al. 2019). Differences in allele frequencies and LD patterns between populations threaten the validity of identified genetic variants and therefore transferability of MR findings to other populations (Martin et al. 2017; Duncan et al. 2019). Although restricting GWAS and MR analysis to more homogeneous ancestries can help to reduce the threat of population stratification, other approaches such as Bayesian mixture model analysis can be taken to overcome this limitation while ensuring greater diversity in genetic studies (Loh et al. 2015). Greater diversity is important as it allows for improved causal inference of risk factors and the clinical translation of genetic findings in other ethnic groups. Furthermore, allowing for diversity in MR studies can help to identify genetic variants that are typically rare in Europeans, where more common variation in other ethnic groups can bolster the power of MR for determining causal effects (Kang et al. 2013; Millwood et al. 2019). Some large-scale, non-European biobanks are available for genetic analysis (Table 2), with a recent GWAS of ∼200,000 individuals in Biobank Japan identifying a number of novel loci important for elucidating biology in East Asian populations (Ishigaki et al. 2020).

Methodological Innovations

A number of methodological extensions of the original MR approach have been discussed throughout this review and an increasing number are being developed. In particular, several recently developed whole-genome-based approaches, including Genetic Instrumental Variable regression (GIV) (DiPrete et al. 2018) and Causal Analysis Using Summary Effect estimates (CAUSE) (Morrison et al. 2020), are seemingly less vulnerable to environmental confounders that are correlated with genes than many of the methods already described (Figs. 3 and 4). Whereas the previously outlined methods are specifically designed to account for horizontal pleiotropy of the genetic instruments, GIV and CAUSE make use of full GWAS data to also account for other sources of bias. For example, if the primary phenotype has been misspecified, the Instrument Strength Independent of Direct Effect (InSIDE) assumption of the MR-Egger sensitivity analysis is likely to be violated, and so the CAUSE method may be used as an additional test to determine the presence of correlated pleiotropy in this instance.

Although the range of methods now available allows for rigorous analysis and robust causal inference to be made, it can be difficult to navigate the various approaches and appraise their relative strengths and limitations. However, it has been emphasized that the best choice of method can often be context specific (Koellinger and de Vlaming 2019). More generally, applying a number of approaches each with orthogonal biases can be helpful in “triangulating” evidence if the estimates obtained from the approaches converge on a similar causal estimate (Munafo et al. 2020).

Automation

The development of bioinformatic platforms and software supports the systematic application of MR (Hemani et al. 2018b; Richardson et al. 2020a). There is scope to automate MR analyses to evaluate a multitude of causal relationships in a time-efficient manner. This can aid in the accelerated identification, prioritization, and evaluation of intervention targets, for example, through phenome-wide association studies (MR-PhEWAS) (Millard et al. 2015; Richardson et al. 2019), and the examination of causality in increasingly complex networks with the integration of molecular data (Hemani et al. 2017a). However, limitations of these agnostic approaches include the multiple testing burden imposed as well as the possibility of false positives, which require careful follow-up in terms of evaluating patterns of bias and ensuring robustness of findings to the various assumptions. Although machine learning and Bayesian model algorithms have been developed to help select the most appropriate model for evaluation (Hemani et al. 2017a; Dudbridge 2020; Howey et al. 2020; Shapland et al. 2020; Zuber et al. 2020), users should be careful that the use of automation and data repositories do not trivialize the analysis being conducted and interpretation of results (Burgess and Davey Smith 2019).

Improving Reproducibility and Reporting of MR Results

The relative ease at which MR analysis can now be performed can also threaten the design, conduct, and reporting of the approach. This may lead to spurious and/or nonreproducible results and may encourage data fishing or the selective cherry-picking of findings, which can lead to study bias in the literature. Guidelines that describe and emphasize the importance of analytical choice considerations and appraise the transparency of MR reporting should help to maintain and improve the quality of MR studies being performed (Davies et al. 2018; Burgess et al. 2019; Davey Smith et al. 2019). Code sharing and improved reproducibility of findings, for example, emulating recommendations in GWAS to provide independent replication before publication, should also be encouraged.

CONCLUSIONS

This paper provides an overarching summary of the Mendelian randomization approach, which uses genetic variants reliably related to modifiable exposures to provide a more robust understanding of the influence of these exposures on disease-relevant outcomes. The development of computational tools and availability of large GWAS data sets has enabled the automation of MR analyses for evaluating a multitude of causal relationships in a time-efficient manner, predominantly via the two-sample MR approach. This has led to the rapid expansion of MR publications and is accelerating the identification, prioritization, and evaluation of intervention targets, the detection of novel causal relationships and the integration of molecular data to examine causality in increasingly complex networks. However, as MR is increasingly easy to implement, it may lead to the proliferation of poorly thought-out and conducted studies. It is therefore important that anyone applying the approach is well versed in its assumptions and limitations. We have discussed the current state of the field, highlighting current best practice methodology, methods of assessing the MR assumptions, attempts to overcome potential pitfalls, and some exciting future prospects. Several of the other papers in this collection elaborate on some of the novel methodological approaches, including multivariable MR and the use of MR for assessing mediation (Sanderson 2021), polygenic MR methods for assessing pleiotropy (Dudbridge 2020), as well as within-family MR methods (Hwang et al. 2020). Other papers describe the application of the approach for extending clinical applicability (Ference et al. 2021; Schmidt et al. 2021) and uncovering molecular mechanisms (Porcu et al. 2021).