eQuilibrator 3.0: a database solution for thermodynamic constant estimation

Moritz E Beber; Mattia G Gollub; Dana Mozaffari; Kevin M Shebek; Avi I Flamholz; Ron Milo; Elad Noor

doi:10.1093/nar/gkab1106

. 2021 Nov 29;50(D1):D603–D609. doi: 10.1093/nar/gkab1106

eQuilibrator 3.0: a database solution for thermodynamic constant estimation

Moritz E Beber ^1,^2,^b, Mattia G Gollub ³, Dana Mozaffari ^4,⁵, Kevin M Shebek ⁶, Avi I Flamholz ⁷, Ron Milo ⁸, Elad Noor ^9,^b,^✉

PMCID: PMC8728285 PMID: 34850162

Abstract

eQuilibrator (equilibrator.weizmann.ac.il) is a database of biochemical equilibrium constants and Gibbs free energies, originally designed as a web-based interface. While the website now counts around 1,000 distinct monthly users, its design could not accommodate larger compound databases and it lacked a scalable Application Programming Interface (API) for integration into other tools developed by the systems biology community. Here, we report on the recent updates to the database as well as the addition of a new Python-based interface to eQuilibrator that adds many new features such as a 100-fold larger compound database, the ability to add novel compounds, improvements in speed and memory use, and correction for Mg²⁺ ion concentrations. Moreover, the new interface can compute the covariance matrix of the uncertainty between estimates, for which we show the advantages and describe the application in metabolic modelling. We foresee that these improvements will make thermodynamic modelling more accessible and facilitate the integration of eQuilibrator into other software platforms.

INTRODUCTION

The field of thermodynamics started in the midst of the industrial revolution as an effort to improve mechanical engines (1). The phenomenal success of the theory to describe the relationships between energy, heat, and work and to provide accurate predictions of what is feasible, inspired countless other scientific endeavors, including molecular dynamics and even economics (2–4). Curiously, until recently, thermodynamic reasoning was relatively underutilized in metabolic modelling. We have identified four major reasons for this. The knowledge gap—equilibrium constants for most biochemical reactions have not been measured. The computation gap—thermodynamic constraints tend to make metabolic models more complicated. For example, Flux Balance Analysis (FBA) with thermodynamic constraints turns from a standard Linear Problem to an NP-complete Mixed-Integer one (MILP) (5,6). The motivation gap—it is not clear to everyone that using thermodynamics in models is actually necessary or even useful. The accessibility gap—adding thermodynamics to an existing model is laborious. It involves tasks such as: mapping identifiers, adjusting the ΔG′° values to the aqueous conditions, and annotating charged molecules correctly—to name but a few.

One of the major breakthroughs in bridging the knowledge gap was suggested by Lydersen et al. (7), who adapted the group contribution method (which can computationally predict molecular Gibbs energies) to organic chemistry. Decades later, Joback et al. (8) and Mavrovouniotis et al. (9) eventually implemented this idea for the context of biochemical reactions. This data-driven approach decomposes a compound into a list of predefined chemical groups, each of which is assumed to contribute a fixed amount to the compounds’ Gibbs energy of formation. These group contributions are estimated by regression against measurements of reaction Gibbs energies, thus enabling estimation of thermodynamic potentials for the majority of reactions in central carbon metabolism (10).

In the last decade, several improvements to the accuracy and coverage of this method have been proposed and implemented (11–14). Nevertheless, some estimates cannot be performed using group contributions since certain molecular structures still do not have any experimental data and therefore reactions in which they appear are outside the scope of the methods. Furthermore, some structures seem to violate the assumption of independence between groups and tend to greatly increase the error of the estimates. In the end, although increasing accuracy by improving the method itself or by gathering more experimentally-derived equilibrium constants is still definitely worthwhile, one could argue that the current state-of-the-art has reached a sufficient level for many applications.

Similarly, the complexity gap has changed from a hard barrier to a minor inconvenience. Increasingly faster computers and powerful MILP solvers (such as IBM CPLEX and Gurobi which offer free academic licenses) made it possible to solve large problems using personal computers, a task which was inconceivable only a decade ago.

The motivation gap is harder to overcome due to a chicken-and-egg problem. Since other technical issues delayed the application of thermodynamic models, it was difficult to demonstrate the usefulness of these models and therefore convince the scientific community that they are worth investing in. Nevertheless, several methods that take advantage of thermodynamic data already exist. Some exploit thermodynamic principles to constrain reaction directionality and metabolite concentrations (5,15,16). Others use thermodynamic driving forces as a proxy for pathway efficiency (17,18). More recently, probabilistic methods combining thermodynamic parameters have been suggested for parameter estimation (19) and flux sampling (20). These algorithms have the potential to improve the flux predictions produced by flux analysis (21–23), and assist in the design of new metabolic pathways (18). However, one of the toughest barriers computational approaches need to overcome is gaining the trust of experimental biologists, and it appears that a few cracks are forming already. For instance, thermodynamic driving forces were used to show how glycolysis is passively regulated (24), and predictions based on thermodynamic enzyme efficiency (25) have proven to fit quite well with experimental data from Z. mobilis (26).

It seems that the time has come to address the accessibility gap. In recent years, a plethora of software tools have facilitated the reconstruction, validation, and analysis of genome-scale metabolic models and made them a community standard which is applied in thousands of scientific projects every year (27). In 2012, we launched the first version of the eQuilibrator website, which aimed to broaden access to thermodynamic parameters and thermodynamic reasoning about metabolism (28). eQuilibrator provides a simple search-focused interface for quickly finding the Gibbs energy change of a biochemical reaction, and is now used by ∼1000 distinct users every month. However, eQuilibrator was designed to be used for single reactions. Therefore, it is inefficient at querying lists of reactions and does not account for correlations between multiple estimates. In this paper, we present a new Python package which is aimed at both novice and expert programmers that want to add thermodynamic parameters to their models.

RESULTS

The Python package equilibrator-api, which is freely available on the Python Package Index and on conda-forge, significantly lowers the barrier to thermodynamic modelling in multiple use-cases. In fact, some of the thermodynamic analyses mentioned in the previous section have used an early version of this package to obtain the necessary thermodynamic constants. For example, a recent study (22) tested the hypothesis that an upper limit exists on the total Gibbs energy dissipation rate of cellular metabolism using estimates generated by equilibrator-api. Since this analysis required standard Gibbs energy estimates for thousands of reactions, this would have been untractable using the web interface. Genome-scale metabolic models with annotated metabolites, that use any of the standard chemical identifiers contained in MetaNetX, can make use of dedicated functions that provide a mapping to eQuilibrator compounds with thermodynamic information. These compounds can then be used by constraint-based and sampling frameworks, such as multiTFA (6) and Probabilistic Thermodynamic Analysis (PTA) (20). In the case of specific pathway models, such as ones designed for metabolic engineering and contain novel reactions, our framework provides additional tools for assessing the feasibility of the pathway (17,18).

Furthermore, since the launch of eQuilibrator in 2012 (28) we added a list of new features: a hundred times larger compound database, the ability to locally add new compounds to the database, calculating the full covariance matrix for the uncertainty between estimates, support for multi-compartment reactions, changing magnesium ion concentrations, tools for analysing whole pathways, and general improvements in speed and memory use. Moreover, we now base all estimates on the component contribution method (13), which required developing a way to calculate component contribution estimates for new reactions on-the-fly. The basis for these calculations is provided in the supplementary section S1. Please note, that some of these features are not yet accessible through the online version of eQuilibrator, namely the larger database, adding new compounds, the covariance matrix, and multi-compartment reactions.

Below, we expand on some of these new features, and the benefits they provide to our users.

Covariance matrix

One of the advantages provided by the new system is the ability to compute the covariance matrix for the uncertainty of multiple estimates (a feature currently supported only in the Python package). In some cases, standard transformed formation (Δ_fG′°) or reaction (Δ_rG′°) energy estimates have large uncertainties when taken individually. However, uncertainties might be highly correlated, e.g., when reactions share a common compound or compounds share a common chemical group. Ignoring these correlations usually overestimates the uncertainty and may violate the first law of thermodynamics (13). In contrast to per-reaction and per-compound uncertainties, the covariance matrix describes the joint uncertainty precisely.

The general formula for the standard Gibbs energy of a set of reactions, given their mean 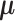Inline graphic and covariance 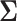is

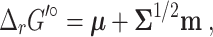(1)

where 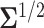Inline graphic is a square root of 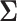. 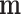can either be a standard multivariate normal random variable in case of random sampling applications or an optimization variable bounded within a desired confidence level for constraint-based approaches. Importantly, this formulation ensures that the computed Gibbs energies are consistent with the first law of thermodynamics, relieving the need for computationally more challenging constraints such as Gibbs energy balance (22) (see supplementary section S2 for more details).

This formulation of the uncertainty has already been available in a development version of eQuilibrator for some time and was successfully applied in both statistical and constraint-based contexts: In PTA (20) it is used to detect thermodynamic inaccuracies in metabolic models, to predict occurrences of substrate channeling, as well as to estimate metabolite concentrations and reaction fluxes with a sampling algorithm. Moreover, multiTFA (6) shows that accounting for covariance reduces the ranges of reaction energies also in constraint-based models.

Expanding the scope of compounds

A frequent request from eQuilibrator users was adding compounds that are not present in the KEGG database (29). We therefore modified eQuilibrator to use MetaNetX (30), a database that aggregates chemicals that are relevant for metabolic models from multiple online databases, including KEGG (29), ChEBI (31), BiGG(32), ModelSEED(33), Swiss Lipids(34) (see Figure 1). This expanded the repertoire from ∼10 000 to ∼1 000 000 compounds which can be accessed using identifiers from various namespaces. As a result, eQuilibrator can now be used with metabolic models from different sources (e.g., SEED or BiGG models) directly, without the need to map all compounds to KEGG identifiers in advance.

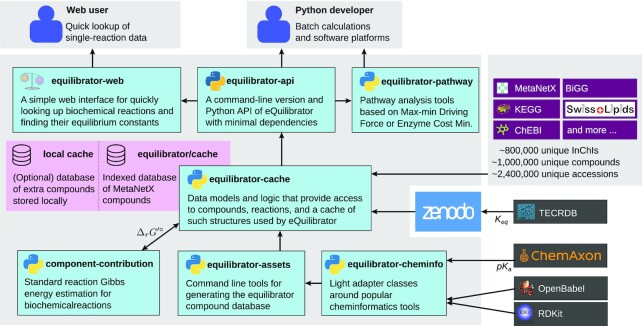
Figure 1. — The design of the eQuilibrator 3.0 suite. At the core, the `equilibrator-cache` Python package defines and manages the database of all compounds, denoted *equilibrator/cache*. All compound identifiers and names come from MetaNetX, which aggregates several popular compound repositories. The `component-contribution` package is responsible for handling training data, group decomposition, Legendre transforms (for pH, pMg and ionic strength adjustments), and the final estimation of Gibbs energies for new compounds and reactions. Some scripts required for rebuilding the database and adding new compounds to a local database are stored in `equilibrator-assets`. All data relevant for running the eQuilibrator packages is stored in Zenodo and is freely available. This includes the experimental data used to train the component contribution method, which comes mainly from NIST TECR database (46). The `equilibrator-api` package exposes nearly all functions relevant for users with sufficient programming skills, and is required for running eQuilibrator in batch mode (e.g. on an entire metabolic model). Some advanced features (namely pathway profiling using Max–min Driving Force analysis (17) or Enzyme Cost Minimization (47)) are available through a separate package called `equilibrator-pahtway`. For non-programmers, the web interface provides quick and easy access to eQuilibrator estimates, but is only designed to deal with a single reaction at a time.

Inline graphic — The design of the eQuilibrator 3.0 suite. At the core, the `equilibrator-cache` Python package defines and manages the database of all compounds, denoted *equilibrator/cache*. All compound identifiers and names come from MetaNetX, which aggregates several popular compound repositories. The `component-contribution` package is responsible for handling training data, group decomposition, Legendre transforms (for pH, pMg and ionic strength adjustments), and the final estimation of Gibbs energies for new compounds and reactions. Some scripts required for rebuilding the database and adding new compounds to a local database are stored in `equilibrator-assets`. All data relevant for running the eQuilibrator packages is stored in Zenodo and is freely available. This includes the experimental data used to train the component contribution method, which comes mainly from NIST TECR database (46). The `equilibrator-api` package exposes nearly all functions relevant for users with sufficient programming skills, and is required for running eQuilibrator in batch mode (e.g. on an entire metabolic model). Some advanced features (namely pathway profiling using Max–min Driving Force analysis (17) or Enzyme Cost Minimization (47)) are available through a separate package called `equilibrator-pahtway`. For non-programmers, the web interface provides quick and easy access to eQuilibrator estimates, but is only designed to deal with a single reaction at a time.

The eQuilibrator website was originally designed to provide pre-calculated Gibbs energy values for a large database of biochemical reactions. Advanced users often want to calculate ΔG values for molecules and reactions not found in the database (even after the expansion to MetaNetX). For example, metabolic pathway engineering often utilizes promiscuous enzymes to generate novel reactions, producing pathways with compounds not found in MetaNetX (35–39).

Previously, this would have required users to add their compounds to the database and rerun the component-contribution method – a considerable effort. To reduce the amount of time it takes to estimate ΔG values of reactions with novel compounds we have extended the equilibrator-assets package, which is responsible for generating the compound database, to enable users to directly add new entries to a local version of the compound database (i.e. a local cache as depicted in Figure 1). The new compounds can be specified using the IUPAC International Chemical Identifier (InChI) or the Simplified Molecular Input Line Entry System (SMILES). These compounds can then be used directly with the equilibrator-api package, allowing for seamless integration of new compounds in thermodynamic analyses (40). See the documentation at https://equilibrator.readthedocs.io for more details.

Multi-compartment reactions

The standard calculation for reaction Gibbs energies assumes that all reactants are in the same aqueous compartment, with a constant pH, pMg, ionic strength and temperature (41). However, most genome-scale metabolic models describe more than one compartment, usually separated by a lipid membrane, and contain many transport reactions that span compartments with different aqueous conditions. Furthermore, the membrane between each two compartments can be associated with an electrostatic potential ΔΦ (in units of volts) which affects the thermodynamics of charged ions travelling between them. When a reaction involves transport of metabolite species between compartments with different hydrogen ion activity or electric potential, we add the following term to its Δ_rG′°:

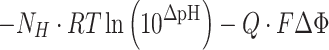(2)

where R is the gas constant, T is the temperature, F is Faraday’s constant (the total electric charge of one mole of electrons –96.5 kC mol⁻¹), ΔpH is the difference in pH between initial and final compartment, N_H is the net number of hydrogen ions transported from initial to final compartment, and Q is the stoichiometric coefficient of the transported charges (41,42). Note that RTln (10^ΔpH) is the energy difference between the compartments specifically for protons (due to their concentration gradient), and FΔΦ is the energy difference relevant to all charges (including protons).

In prior versions of eQuilibrator, adjusting the standard Gibbs energy of multi-compartment biochemical reactions, such as ones facilitated by membrane transporters, had to be performed as a post-processing step. For example, the vonBertalanffy extension in the COBRA toolbox (43) performs such additional calculations as part of its pipeline. In eQuilibrator 3.0, we add functions to facilitate the adjustments required for multi-compartment reactions as part of our Python package. See supplementary section S3 for an example.

Adjusting estimates to different pMg values

Since ions are abundant in the cytosol and can bind metabolites to varying degrees, ion concentrations have a large effect on biochemical thermodynamics (41). The concentration of protons (H⁺), commonly expressed as the pH, is the most dramatic example of this phenomenon. However, this is not the only case. Magnesium ions (Mg^{2 +}) bind to many common biochemical moieties, especially phosphate, and have been shown to play a significant role in the thermodynamics of glycolysis (44). For example, the dissociation constants for ATP and ADP are low enough for them to be in their complex forms Mg · ATP^{2 −} and Mg · ADP⁻ at a physiological intracellular pMg of 3 (which is defined similarly to pH, i.e. it corresponds to a concentration of 10⁻³ M—or 1 mM—of Mg^{2 +}).

Every compound can be seen as an ensemble of pseudoisomers, molecules only differing in protonation or magnesium binding state. In a biochemical context, where all compounds are assumed to be in a buffered aqueous environment, we do not distinguish between pseudoisomers and refer to the entire ensemble as a metabolite. Note that this assumption does not hold for transport reactions across membranes, which may selectively transport only specific pseudoisomers. For single compartment reactions it is thus convenient to discuss the standard transformed Gibbs energy of formation Δ_fG′° which groups together all pseudoisomers into one formation energy. It can be obtained using a Boltzmann-weighted mixture of its constituent pseudoisomers:

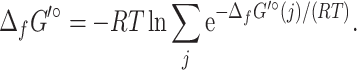(3)

The standard transformed Gibbs energies of formation Δ_fG′°(j) for each pseudoisomer j at given biochemical conditions can be calculated using the Legendre transformation

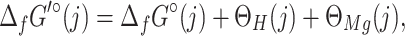(4)

where

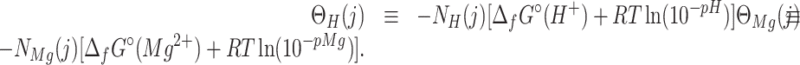The first term—Δ_fG°(j)—is the chemical standard Gibbs energy of formation of the pseudoisomer. The second term—Θ_H(j)—describes the contribution of protons to the Gibbs energy as a function of the pH. N_H(j) is the number of protons associated to this pseudoisomer, and Δ_fG°(H⁺) is the standard formation energy of a proton, defined to be 0 in this framework (41). Similarly, the effect of the concentration of Mg^{2 +} ions (quantified as pMg) can be taken into account by adding the term Θ_Mg(j). Similar to the case of protons, N_Mg(j) is the number of Magnesium ions associated to this pseudoisomer, and Δ_fG°(Mg^{2 +}) is the standard formation energy of Magnesium ions, equal to −455.3 kJ/mol.

Affinity to Mg^{2 +} varies between compounds and pseudoisomers. The presence of certain chemical moieties, such as phosphate groups, tends to increase the binding affinity (45), while increasing the protonation state tends to decrease the affinity. Unfortunately, the availability of affinity constants for Mg^{2 +} is much lower than for H⁺. In eQuilibrator, we used Δ_fG′°(j) for magnesium-bound pseudoisomers collected by Vojinović and von Stockar (44) and affinities predicted by Du et al. (14). For all other pseudoisomers, we assumed that their affinity is weak and has negligible effect on thermodynamics.

After populating the database with magnesium-bound pseudoisomers, we computed the root mean square error (RMSE) for all reactions from the NIST TECR database (46). When taking magnesium into account, the RMSE improved slightly from 2.99 to 2.93.

In the online version of eQuilibrator, pMg can be adjusted in the same way as pH and ionic strength, by entering the value in the proper text field. Similarly, the Python package contains a new p_mg variable that can be set directly, along with p_h and ionic_strength, as explained in the documentation at https://equilibrator.readthedocs.io.

Upgrades to the eQuilibrator website

Compared to its original version (28), the eQuilibrator website has undergone several major updates. As mentioned earlier, the backend method for estimating reaction Gibbs energies was changed to component contribution (13). This method provides a consistent set of reaction energies, without compromising the accuracy of reactions and compounds with direct experimental data. More recently, we added the ability to adjust the pMg as well as an option to plot ΔG′ as a function of pMg. A more comprehensive list of changes can be found on the website itself at https://equilibrator.weizmann.ac.il/static/classic_rxns/updates.html.

Besides improvements to the core search function, the website now offers tools for pathway analysis based on two methods: Max-min Driving Force (MDF) (17) and Enzyme Cost Minimization (47). Both these methods aim to provide a quantitative scoring system that can be used to rank natural or engineered metabolic pathways – either to assist in the design process for metabolic engineers, or for understanding the design principles that govern the evolution of metabolic pathways. MDF is a purely thermodynamic-based approach that assumes driving forces are maximized within the constraints imposed by metabolite concentration bounds and the necessary coupling between adjacent reactions. ECM uses a convex optimization approach to find the optimal distribution of enzyme and metabolite concentrations, where the pathway flux is maximized. Both algorithms are also available in the Python package named equilibrator-pathway.

Complete code refactoring

In order to extend the eQuilibrator framework to new uses-cases (such as those described above) a complete code refactoring was required—creating separate packages for each distinct function. The original code was designed exclusively for a single workflow: starting with analysing the chemical structures (group decompositions), reverse-transforming the measured equilibrium constants to chemical Gibbs energies (48), solving the linear regression problems to find the group contribution energies, and using the solutions to estimate formation energies for all compounds in the KEGG database. This long procedure was not useful for users who only wanted to apply component-contribution on a list of their own reactions.

Therefore, we have redesigned the entire component-contribution package, moved it to a new Git repository, and integrated it completely into a larger framework denoted eQuilibrator 3.0 suite (see Figure 1). In addition, we raised the coding standards, e.g. by running automated tools for coverage, unit-testing, and documentation (available on equilibrator.readthedocs.io). We also facilitated the installation of the packages by submitting them to the Python Package Index (https://pypi.org) and conda-forge (https://conda-forge.org).

Following this refactoring, Python users can easily install the equilibrator packages on their own computer using a simple command (with full support for Windows OS, MacOS, and Linux). The improved documentation and software stability facilitate this further, even for novice programmers. Furthermore, proper versioning enables researchers to easily trace back changes and reproduce their results generated by older versions of the software.

DISCUSSION

The eQuilibrator 3.0 suite marks a major shift in the focus of our software which has so far been mainly geared for single reaction searches or small biochemical networks (pathways) and exposed via a web interface. Now, we reach out to a larger audience, including modellers who want to populate genome-scale metabolic networks with thermodynamic parameters as well as metabolic engineers who want to scan a large set of parameters for their designs. In addition, the software package can now be more easily integrated into other Python-based frameworks and pipelines such as COBRApy (49,50), MEMOTE (51), ModelSEED (52) and CarveMe (53). Furthermore, in supplementary section S1.4, we show how one can efficiently store a set of pre-calculated matrices that can be used to calculate the final estimates (including full uncertainty matrices). This can facilitate building compound databases for frameworks that are not based on Python, or that rely on mathematical calculations that are not yet supported within the eQuilibrator codebase.

The major improvements that we introduce in this work are: (i) an API supported by a refactored codebase that is more suited to modelling applications and integration into other software, (ii) improvements in speed and memory use, (iii) correction for Mg^{2 +} ions, (iv) multi-compartment reactions, (v) access to the full covariance matrix for uncertainty modelling, (vi) cross-databases identification of molecules and reactions with a larger pool of compounds (provided by MetaNetX) and the ability to add novel compounds. We continue to support community-driven development and open source standards, by publishing all the code under the permissive MIT license and making it available on GitLab. All other raw data needed for the algorithm is licensed under a Creative Commons 4.0 license, and stored on www.zenodo.org.

We are open to suggestions for what could be added to eQuilibrator in future via discussions in GitLab issues and we welcome contributions from the community. For example, new features already under consideration include temperature adjustment based on separate entropy/enthalpy estimates, a fully automated script for populating SBML (Systems Biology Markup Language) models with thermodynamic parameters (including multi-compartment reactions), and integration with common platforms and use-cases such as support for Thermodynamic-based Flux Analysis (16) in COBRApy.

We believe that eQuilibrator 3.0 is a substantial step forward in closing the accessibility gap and hope that together with other recent advances (16,17,19,20,47) will bring forth the golden age of thermodynamics in the field of metabolic modelling.

DATA AVAILABILITY

The source code for all the Python packages mentioned in this manuscript can be found at https://gitlab.com/equilibrator. All relevant data and models are stored on Zenodo, and are linked to from the repository (Training data - https://doi.org/10.5281/zenodo.3978439; Compound database - https://doi.org/10.5281/zenodo.4128542; Model parameters - https://doi.org/10.5281/zenodo.4013788; Group definitions - https://doi.org/10.5281/zenodo.4010929). The documentation can be found at https://equilibrator.readthedocs.io.

The eQuilibrator suite depends on several open-source packages, such as: OpenBabel (54), RDKit, NumPy, SciPy, Pandas, Pint, and SQLAlchemy.

In addition, estimating acid-base dissociation constants was done using Marvin Calculator, Calculator version 21.13.0, ChemAxon (www.chemaxon.com), under an academic license. Marvin Calculator is also required for adding new compounds to a local database.

Supplementary Material

gkab1106_Supplemental_File

Click here for additional data file.^{(276KB, pdf)}

ACKNOWLEDGEMENTS

Dedicated to the memory of Arren Bar-Even (1980–2020). We thank Jörg Stelling for a helpful discussion on the effect of magnesium ions.

Contributor Information

Moritz E Beber, Novo Nordisk Foundation Center for Biosustainability, Technical University of Denmark, Kemitorvet, 2800 Kongens Lyngby, Denmark; Unseen Biometrics ApS, Fruebjergvej 3, 2100 København Ø, Denmark.

Mattia G Gollub, Department of Biosystems Science and Engineering and SIB Swiss Institute of Bioinformatics, ETH Zürich, Basel 4058, Switzerland.

Dana Mozaffari, Department of Biosystems Science and Engineering and SIB Swiss Institute of Bioinformatics, ETH Zürich, Basel 4058, Switzerland; Institute of Chemical Sciences and Engineering, EPFL, Lausanne 1015, Switzerland.

Kevin M Shebek, Department of Chemical and Biological Engineering, Chemistry of Life Processes Institute, and Center for Synthetic Biology, Northwestern University, Evanston, IL 60208, USA.

Avi I Flamholz, Division of Biology and Biological Engineering, California Institute of Technology, Pasadena, CA 91125, USA.

Ron Milo, Department of Plant and Environmental Sciences, Weizmann Institute of Science, Herzl 234, Rehovot 7610001, Israel.

Elad Noor, Department of Plant and Environmental Sciences, Weizmann Institute of Science, Herzl 234, Rehovot 7610001, Israel.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

M.E.B. was partly supported by Horizon 2020—Research and Innovation Framework Programme [686070 (DD-DeCaF)]; M.G.G. was supported by the Swiss National Science Foundation Sinergia project [177164]; K.M.S. was supported by the U.S. Department of Energy, Office of Science, Office of Biological and Environmental Research [DE-SC0018249]. Funding for open access charge: Research budget.

Conflict of interest statement. None declared.

REFERENCES

1. Carnot S. Réflexions sur la puissance motrice du feu et sur les machines propres à développer atte puissance. 1824; Bachelier Libraire. [Google Scholar]
2. Jinich A., Rappoport D., Dunn I., Sanchez-Lengeling B., Olivares-Amaya R., Noor E., Even A.B., Aspuru-Guzik A.. Quantum chemical approach to estimating the thermodynamics of metabolic reactions. Sci. Rep.-UK. 2014; 4:7022. [DOI] [PMC free article] [PubMed] [Google Scholar]
3. Jinich A., Flamholz A., Ren H., Kim S.-J., Sanchez-Lengeling B., Cotton C. A.R., Noor E., Aspuru-Guzik A., Bar-Even A.. Quantum chemistry reveals thermodynamic principles of redox biochemistry. PLoS Comput. Biol. 2018; 14:e1006471. [DOI] [PMC free article] [PubMed] [Google Scholar]
4. Georgescu-Roegen N. The Entropy Law and the Economic Process. 1999; Harvard University Press. [Google Scholar]
5. Henry C.S., Broadbelt L.J., Hatzimanikatis V.. Thermodynamics-based metabolic flux analysis. Biophys. J. 2007; 92:1792–1805. [DOI] [PMC free article] [PubMed] [Google Scholar]
6. Mahamkali V., McCubbin T., Beber M.E., Noor E., Marcellin E., Nielsen L.K.. multiTFA: a Python package for multi-variate thermodynamics-based flux analysis. Bioinformatics. 2021; 37:3064–3066. [DOI] [PMC free article] [PubMed] [Google Scholar]
7. Lydersen A. Lydersen A.L. Estimation of critical properties of organic compounds by the method of group contributions. University of Wisconsin, Engineering Experiment Station. Report no. 3. 1955; University of Wisconsin. [Google Scholar]
8. Joback G.K., Reid C.R.. Estimation of pure-component properties from group-contributions. Chem. Eng. Commun. 1987; 57:233–243. [Google Scholar]
9. Mavrovouniotis L.M., Bayol P., Lam M. T.-K., Stephanopoulos G., Stephanopoulos G.. A group contribution method for the estimation of equilibrium constants for biochemical reactions. Biotechnol. Tech. 1988; 2:23–28. [Google Scholar]
10. Feist A.M., Henry C.S., Reed J.L., Krummenacker M., Joyce A.R., Karp P.D., Broadbelt L.J., Hatzimanikatis V., Palsson B.. A genome-scale metabolic reconstruction for Escherichia coli K-12 MG1655 that accounts for 1260 ORFs and thermodynamic information. Mol. Syst. Biol. 2007; 3:121. [DOI] [PMC free article] [PubMed] [Google Scholar]
11. Jankowski M.D., Henry C.S., Broadbelt L.J., Hatzimanikatis V.. Group contribution method for thermodynamic analysis of complex metabolic networks. Biophys. J. 2008; 95:1487–1499. [DOI] [PMC free article] [PubMed] [Google Scholar]
12. Noor E., Bar-Even A., Flamholz A., Lubling Y., Davidi D., Milo R.. An integrated open framework for thermodynamics of reactions that combines accuracy and coverage. Bioinformatics. 2012; 28:2037–2044. [DOI] [PMC free article] [PubMed] [Google Scholar]
13. Noor E., Haraldsdóttir H.S., Milo R., Fleming R. M.T.. Consistent estimation of Gibbs energy using component contributions. PLoS Comput. Biol. 2013; 9:e1003098. [DOI] [PMC free article] [PubMed] [Google Scholar]
14. Du B., Zhang Z., Grubner S., Yurkovich J.T., Palsson B.O., Zielinski D.C.. Temperature-dependent estimation of Gibbs energies using an updated group contribution method. Biophys. J. 2018; 114:2691–2702. [DOI] [PMC free article] [PubMed] [Google Scholar]
15. Holzhótter H.-G. The principle of flux minimization and its application to estimate stationary fluxes in metabolic networks. Eur. J. Biochem. 2004; 271:2905–2922. [DOI] [PubMed] [Google Scholar]
16. Salvy P., Fengos G., Ataman M., Pathier T., Soh K.C., Hatzimanikatis V.. pyTFA and matTFA: a Python package and a Matlab toolbox for thermodynamics-based flux analysis. Bioinformatics. 2019; 35:167–169. [DOI] [PMC free article] [PubMed] [Google Scholar]
17. Noor E., Bar-Even A., Flamholz A., Reznik E., Liebermeister W., Milo R.. Pathway Thermodynamics Highlights Kinetic Obstacles in Central Metabolism. PLOS Comput. Biol. 2014; 10:e1003483. [DOI] [PMC free article] [PubMed] [Google Scholar]
18. Hädicke O., Kamp A.v., Aydogan T., Klamt S.. OptMDFpathway: Identification of metabolic pathways with maximal thermodynamic driving force and its application for analyzing the endogenous CO2 fixation potential of Escherichia coli. PLoS Comput. Biol. 2018; 14:e1006492. [DOI] [PMC free article] [PubMed] [Google Scholar]
19. Lubitz T., Liebermeister W.. Parameter balancing: consistent parameter sets for kinetic metabolic models. Bioinformatics. 2019; 35:3857–3858. [DOI] [PMC free article] [PubMed] [Google Scholar]
20. Gollub M.G., Kaltenbach H.-M., Stelling J.. Probabilistic thermodynamic analysis of metabolic networks. Bioinformatics. 2021; 37:2938–2945. [DOI] [PMC free article] [PubMed] [Google Scholar]
21. Noor E. Removing both internal and unrealistic energy-generating cycles in flux balance analysis. 2018; arXiv doi:13 March 2018, preprint: not peer reviewedhttps://arxiv.org/abs/1803.04999.
22. Niebel B., Leupold S., Heinemann M.. An upper limit on Gibbs energy dissipation governs cellular metabolism. Nat. Metab. 2019; 1:125. [DOI] [PubMed] [Google Scholar]
23. Saldida J., Muntoni A.P., Martino D.D., Hubmann G., Niebel B., Schmidt A.M., Braunstein A., Milias-Argeits A., Heinemann M.. Unbiased metabolic flux inference through combined thermodynamic and 13C flux analysis. 2020; bioRxiv doi:29 June 2020, preprint: not peer reviewed 10.1101/2020.06.29.177063. [DOI]
24. Park J.O., Tanner L.B., Wei M.H., Khana D.B., Jacobson T.B., Zhang Z., Rubin S.A., Li S.H.-J., Higgins M.B., Stevenson D.M.et al.. Near-equilibrium glycolysis supports metabolic homeostasis and energy yield. Nat. Chem. Biol. 2019; 15:1001–1008. [DOI] [PMC free article] [PubMed] [Google Scholar]
25. Flamholz A., Noor E., Bar-Even A., Liebermeister W., Milo R.. Glycolytic strategy as a tradeoff between energy yield and protein cost. Proc. Natl. Acad. Sci. U.S.A. 2013; 110:10039–10044. [DOI] [PMC free article] [PubMed] [Google Scholar]
26. Jacobson T.B., Adamczyk P.A., Stevenson D.M., Regner M., Ralph J., Reed J.L., Amador-Noguez D.. 2H and 13C metabolic flux analysis elucidates in vivo thermodynamics of the ED pathway in Zymomonas mobilis. Metab. Eng. 2019; 54:301–316. [DOI] [PubMed] [Google Scholar]
27. Carey M.A., Dräger A., Beber M.E., Papin J.A., Yurkovich J.T.. Community standards to facilitate development and address challenges in metabolic modeling. Mol. Syst. Biol. 2020; 16:e9235. [DOI] [PMC free article] [PubMed] [Google Scholar]
28. Flamholz A., Noor E., Bar-Even A., Milo R.. eQuilibrator – the biochemical thermodynamics calculator. Nucleic Acids Res. 2012; 40:D770–D775. [DOI] [PMC free article] [PubMed] [Google Scholar]
29. Kanehisa M., Araki M., Goto S., Hattori M., Hirakawa M., Itoh M., Katayama T., Kawashima S., Okuda S., Tokimatsu T.et al.. KEGG for linking genomes to life and the environment. Nucleic Acids Res. 2008; 36:D480–D484. [DOI] [PMC free article] [PubMed] [Google Scholar]
30. Moretti S., Tran V., Mehl F., Ibberson M., Pagni M.. MetaNetX/MNXref: unified namespace for metabolites and biochemical reactions in the context of metabolic models. Nucleic Acids Res. 2021; 49:D570–D574. [DOI] [PMC free article] [PubMed] [Google Scholar]
31. Hastings J., Owen G., Dekker A., Ennis M., Kale N., Muthukrishnan V., Turner S., Swainston N., Mendes P., Steinbeck C.. ChEBI in 2016: improved services and an expanding collection of metabolites. Nucleic Acids Res. 2016; 44:D1214–D1219. [DOI] [PMC free article] [PubMed] [Google Scholar]
32. King Z.A., Lu J., Dräger A., Miller P., Federowicz S., Lerman J.A., Ebrahim A., Palsson B.O., Lewis N.E.. BiGG Models: a platform for integrating, standardizing and sharing genome-scale models. Nucleic Acids Res. 2016; 44:D515–D522. [DOI] [PMC free article] [PubMed] [Google Scholar]
33. Henry C.S., DeJongh M., Best A.A., Frybarger P.M., Linsay B., Stevens R.L.. High-throughput generation, optimization and analysis of genome-scale metabolic models. Nat. Biotechnol. 2010; 28:977–982. [DOI] [PubMed] [Google Scholar]
34. Aimo L., Liechti R., Hyka-Nouspikel N., Niknejad A., Gleizes A., Götz L., Kuznetsov D., David F.P., van der Goot F.G., Riezman H., et al.. The SwissLipids knowledgebase for lipid biology. Bioinformatics. 2015; 31:2860–2866. [DOI] [PMC free article] [PubMed] [Google Scholar]
35. Schwander T., Borzyskowski L. S.V., Burgener S., Cortina N.S., Erb T.J.. A synthetic pathway for the fixation of carbon dioxide in vitro. Science. 2016; 354:900–904. [DOI] [PMC free article] [PubMed] [Google Scholar]
36. Jeffryes J.G., Colastani R.L., Elbadawi-Sidhu M., Kind T., Niehaus T.D., Broadbelt L.J., Hanson A.D., Fiehn O., Tyo K.E.J., Henry C.S.. MINEs: open access databases of computationally predicted enzyme promiscuity products for untargeted metabolomics. J. Cheminformatics. 2015; 7:44. [DOI] [PMC free article] [PubMed] [Google Scholar]
37. Hadadi N., Hafner J., Shajkofci A., Zisaki A., Hatzimanikatis V.. ATLAS of biochemistry: a repository of all possible biochemical reactions for synthetic biology and metabolic engineering studies. ACS Synth. Biol. 2016; 5:1155–1166. [DOI] [PubMed] [Google Scholar]
38. Delépine B., Duigou T., Carbonell P., Faulon J.-L.. RetroPath2.0: A retrosynthesis workflow for metabolic engineers. Metab. Eng. 2018; 45:158–170. [DOI] [PubMed] [Google Scholar]
39. Moriya Y., Shigemizu D., Hattori M., Tokimatsu T., Kotera M., Goto S., Kanehisa M.. PathPred: an enzyme-catalyzed metabolic pathway prediction server. Nucleic Acids Res. 2010; 38:W138–W143. [DOI] [PMC free article] [PubMed] [Google Scholar]
40. Scheffen M., Marchal D.G., Beneyton T., Schuller S.K., Klose M., Diehl C., Lehmann J., Pfister P., Carrillo M., He H.et al.. A new-to-nature carboxylation module to improve natural and synthetic CO2 fixation. Nat. Catal. 2021; 4:105–115. [Google Scholar]
41. Alberty A.R. Biochemical thermodynamics. Biochim. Biophys. Acta - Protein Struct. Mol. Enzymol. 1994; 1207:1–11. [DOI] [PubMed] [Google Scholar]
42. Haraldsdóttir H.S., Thiele I., Fleming R.M.T.. Quantitative assignment of reaction directionality in a multicompartmental human metabolic reconstruction. Biophys. J. 2012; 102:1703–1711. [DOI] [PMC free article] [PubMed] [Google Scholar]
43. Fleming R.M.T., Thiele I.. von Bertalanffy 1.0: a COBRA toolbox extension to thermodynamically constrain metabolic models. Bioinformatics. 2011; 27:142–143. [DOI] [PMC free article] [PubMed] [Google Scholar]
44. Vojinović V., Stockar U.V.. Influence of uncertainties in pH, pMg, activity coefficients, metabolite concentrations, and other factors on the analysis of the thermodynamic feasibility of metabolic pathways. Biotechnol. Bioeng. 2009; 103:780–795. [DOI] [PubMed] [Google Scholar]
45. Alberty A.R. Thermodynamics of the hydrolysis of adenosine triphosphate as a function of temperature, pH, pMg, and ionic strength. J. Phys. Chem. B. 2003; 107:12324–12330. [Google Scholar]
46. Goldberg R.N., Tewari Y.B., Bhat T.N.. Thermodynamics of enzyme-catalyzed reactions–a database for quantitative biochemistry. Bioinformatics. 2004; 20:2874–2877. [DOI] [PubMed] [Google Scholar]
47. Noor E., Flamholz A., Bar-Even A., Davidi D., Milo R., Liebermeister W.. The protein cost of metabolic fluxes: prediction from enzymatic rate laws and cost minimization. PLoS Comput. Biol. 2016; 12:e1005167. [DOI] [PMC free article] [PubMed] [Google Scholar]
48. Alberty A.R. Legendre transforms in chemical thermodynamics. Pure Appl. Chem. 1997; 69:2221–2230. [Google Scholar]
49. Ebrahim A., Lerman J.A., Palsson B.O., Hyduke D.R.. COBRApy: constraints-based reconstruction and analysis for Python. BMC Syst. Biol. 2013; 7:74. [DOI] [PMC free article] [PubMed] [Google Scholar]
50. Lloyd C.J., Ebrahim A., Yang L., King Z.A., Catoiu E., O’Brien E.J., Liu J.K., Palsson B.O.. COBRAme: a computational framework for genome-scale models of metabolism and gene expression. PLOS Comput. Biol. 2018; 14:e1006302. [DOI] [PMC free article] [PubMed] [Google Scholar]
51. Lieven C., Beber M.E., Olivier B.G., Bergmann F.T., Ataman M., Babaei P., Bartell J.A., Blank L.M., Chauhan S., Correia K.et al.. MEMOTE for standardized genome-scale metabolic model testing. Nat. Biotechnol. 2020; 38:272–276. [DOI] [PMC free article] [PubMed] [Google Scholar]
52. Seaver S.M.D., Liu F., Zhang Q., Jeffryes J., Faria J.P., Edirisinghe J.N., Mundy M., Chia N., Noor E., Beber M.et al.. The ModelSEED Biochemistry Database for the integration of metabolic annotations and the reconstruction, comparison and analysis of metabolic models for plants, fungi and microbes. Nucleic Acids Res. 2020; 1:D575–D588. [DOI] [PMC free article] [PubMed] [Google Scholar]
53. Machado D., Andrejev S., Tramontano M., Patil K.R.. Fast automated reconstruction of genome-scale metabolic models for microbial species and communities. Nucleic Acids Res. 2018; 46:7542–7553. [DOI] [PMC free article] [PubMed] [Google Scholar]
54. O’Boyle N., Morley C., Hutchison G.. Pybel: a Python wrapper for the OpenBabel cheminformatics toolkit. Chem. Cent. J. 2008; 2:5. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

gkab1106_Supplemental_File

Click here for additional data file.^{(276KB, pdf)}

Data Availability Statement

The eQuilibrator suite depends on several open-source packages, such as: OpenBabel (54), RDKit, NumPy, SciPy, Pandas, Pint, and SQLAlchemy.

[B1] 1. Carnot S. Réflexions sur la puissance motrice du feu et sur les machines propres à développer atte puissance. 1824; Bachelier Libraire. [Google Scholar]

[B2] 2. Jinich A., Rappoport D., Dunn I., Sanchez-Lengeling B., Olivares-Amaya R., Noor E., Even A.B., Aspuru-Guzik A.. Quantum chemical approach to estimating the thermodynamics of metabolic reactions. Sci. Rep.-UK. 2014; 4:7022. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B3] 3. Jinich A., Flamholz A., Ren H., Kim S.-J., Sanchez-Lengeling B., Cotton C. A.R., Noor E., Aspuru-Guzik A., Bar-Even A.. Quantum chemistry reveals thermodynamic principles of redox biochemistry. PLoS Comput. Biol. 2018; 14:e1006471. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B4] 4. Georgescu-Roegen N. The Entropy Law and the Economic Process. 1999; Harvard University Press. [Google Scholar]

[B5] 5. Henry C.S., Broadbelt L.J., Hatzimanikatis V.. Thermodynamics-based metabolic flux analysis. Biophys. J. 2007; 92:1792–1805. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B6] 6. Mahamkali V., McCubbin T., Beber M.E., Noor E., Marcellin E., Nielsen L.K.. multiTFA: a Python package for multi-variate thermodynamics-based flux analysis. Bioinformatics. 2021; 37:3064–3066. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B7] 7. Lydersen A. Lydersen A.L. Estimation of critical properties of organic compounds by the method of group contributions. University of Wisconsin, Engineering Experiment Station. Report no. 3. 1955; University of Wisconsin. [Google Scholar]

[B8] 8. Joback G.K., Reid C.R.. Estimation of pure-component properties from group-contributions. Chem. Eng. Commun. 1987; 57:233–243. [Google Scholar]

[B9] 9. Mavrovouniotis L.M., Bayol P., Lam M. T.-K., Stephanopoulos G., Stephanopoulos G.. A group contribution method for the estimation of equilibrium constants for biochemical reactions. Biotechnol. Tech. 1988; 2:23–28. [Google Scholar]

[B10] 10. Feist A.M., Henry C.S., Reed J.L., Krummenacker M., Joyce A.R., Karp P.D., Broadbelt L.J., Hatzimanikatis V., Palsson B.. A genome-scale metabolic reconstruction for Escherichia coli K-12 MG1655 that accounts for 1260 ORFs and thermodynamic information. Mol. Syst. Biol. 2007; 3:121. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B11] 11. Jankowski M.D., Henry C.S., Broadbelt L.J., Hatzimanikatis V.. Group contribution method for thermodynamic analysis of complex metabolic networks. Biophys. J. 2008; 95:1487–1499. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B12] 12. Noor E., Bar-Even A., Flamholz A., Lubling Y., Davidi D., Milo R.. An integrated open framework for thermodynamics of reactions that combines accuracy and coverage. Bioinformatics. 2012; 28:2037–2044. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B13] 13. Noor E., Haraldsdóttir H.S., Milo R., Fleming R. M.T.. Consistent estimation of Gibbs energy using component contributions. PLoS Comput. Biol. 2013; 9:e1003098. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B14] 14. Du B., Zhang Z., Grubner S., Yurkovich J.T., Palsson B.O., Zielinski D.C.. Temperature-dependent estimation of Gibbs energies using an updated group contribution method. Biophys. J. 2018; 114:2691–2702. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B15] 15. Holzhótter H.-G. The principle of flux minimization and its application to estimate stationary fluxes in metabolic networks. Eur. J. Biochem. 2004; 271:2905–2922. [DOI] [PubMed] [Google Scholar]

[B16] 16. Salvy P., Fengos G., Ataman M., Pathier T., Soh K.C., Hatzimanikatis V.. pyTFA and matTFA: a Python package and a Matlab toolbox for thermodynamics-based flux analysis. Bioinformatics. 2019; 35:167–169. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B17] 17. Noor E., Bar-Even A., Flamholz A., Reznik E., Liebermeister W., Milo R.. Pathway Thermodynamics Highlights Kinetic Obstacles in Central Metabolism. PLOS Comput. Biol. 2014; 10:e1003483. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B18] 18. Hädicke O., Kamp A.v., Aydogan T., Klamt S.. OptMDFpathway: Identification of metabolic pathways with maximal thermodynamic driving force and its application for analyzing the endogenous CO2 fixation potential of Escherichia coli. PLoS Comput. Biol. 2018; 14:e1006492. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B19] 19. Lubitz T., Liebermeister W.. Parameter balancing: consistent parameter sets for kinetic metabolic models. Bioinformatics. 2019; 35:3857–3858. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B20] 20. Gollub M.G., Kaltenbach H.-M., Stelling J.. Probabilistic thermodynamic analysis of metabolic networks. Bioinformatics. 2021; 37:2938–2945. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B21] 21. Noor E. Removing both internal and unrealistic energy-generating cycles in flux balance analysis. 2018; arXiv doi:13 March 2018, preprint: not peer reviewedhttps://arxiv.org/abs/1803.04999.

[B22] 22. Niebel B., Leupold S., Heinemann M.. An upper limit on Gibbs energy dissipation governs cellular metabolism. Nat. Metab. 2019; 1:125. [DOI] [PubMed] [Google Scholar]

[B23] 23. Saldida J., Muntoni A.P., Martino D.D., Hubmann G., Niebel B., Schmidt A.M., Braunstein A., Milias-Argeits A., Heinemann M.. Unbiased metabolic flux inference through combined thermodynamic and 13C flux analysis. 2020; bioRxiv doi:29 June 2020, preprint: not peer reviewed 10.1101/2020.06.29.177063. [DOI]

[B24] 24. Park J.O., Tanner L.B., Wei M.H., Khana D.B., Jacobson T.B., Zhang Z., Rubin S.A., Li S.H.-J., Higgins M.B., Stevenson D.M.et al.. Near-equilibrium glycolysis supports metabolic homeostasis and energy yield. Nat. Chem. Biol. 2019; 15:1001–1008. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B25] 25. Flamholz A., Noor E., Bar-Even A., Liebermeister W., Milo R.. Glycolytic strategy as a tradeoff between energy yield and protein cost. Proc. Natl. Acad. Sci. U.S.A. 2013; 110:10039–10044. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B26] 26. Jacobson T.B., Adamczyk P.A., Stevenson D.M., Regner M., Ralph J., Reed J.L., Amador-Noguez D.. 2H and 13C metabolic flux analysis elucidates in vivo thermodynamics of the ED pathway in Zymomonas mobilis. Metab. Eng. 2019; 54:301–316. [DOI] [PubMed] [Google Scholar]

[B27] 27. Carey M.A., Dräger A., Beber M.E., Papin J.A., Yurkovich J.T.. Community standards to facilitate development and address challenges in metabolic modeling. Mol. Syst. Biol. 2020; 16:e9235. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B28] 28. Flamholz A., Noor E., Bar-Even A., Milo R.. eQuilibrator – the biochemical thermodynamics calculator. Nucleic Acids Res. 2012; 40:D770–D775. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B29] 29. Kanehisa M., Araki M., Goto S., Hattori M., Hirakawa M., Itoh M., Katayama T., Kawashima S., Okuda S., Tokimatsu T.et al.. KEGG for linking genomes to life and the environment. Nucleic Acids Res. 2008; 36:D480–D484. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B30] 30. Moretti S., Tran V., Mehl F., Ibberson M., Pagni M.. MetaNetX/MNXref: unified namespace for metabolites and biochemical reactions in the context of metabolic models. Nucleic Acids Res. 2021; 49:D570–D574. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B31] 31. Hastings J., Owen G., Dekker A., Ennis M., Kale N., Muthukrishnan V., Turner S., Swainston N., Mendes P., Steinbeck C.. ChEBI in 2016: improved services and an expanding collection of metabolites. Nucleic Acids Res. 2016; 44:D1214–D1219. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B32] 32. King Z.A., Lu J., Dräger A., Miller P., Federowicz S., Lerman J.A., Ebrahim A., Palsson B.O., Lewis N.E.. BiGG Models: a platform for integrating, standardizing and sharing genome-scale models. Nucleic Acids Res. 2016; 44:D515–D522. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B33] 33. Henry C.S., DeJongh M., Best A.A., Frybarger P.M., Linsay B., Stevens R.L.. High-throughput generation, optimization and analysis of genome-scale metabolic models. Nat. Biotechnol. 2010; 28:977–982. [DOI] [PubMed] [Google Scholar]

[B34] 34. Aimo L., Liechti R., Hyka-Nouspikel N., Niknejad A., Gleizes A., Götz L., Kuznetsov D., David F.P., van der Goot F.G., Riezman H., et al.. The SwissLipids knowledgebase for lipid biology. Bioinformatics. 2015; 31:2860–2866. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B35] 35. Schwander T., Borzyskowski L. S.V., Burgener S., Cortina N.S., Erb T.J.. A synthetic pathway for the fixation of carbon dioxide in vitro. Science. 2016; 354:900–904. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B36] 36. Jeffryes J.G., Colastani R.L., Elbadawi-Sidhu M., Kind T., Niehaus T.D., Broadbelt L.J., Hanson A.D., Fiehn O., Tyo K.E.J., Henry C.S.. MINEs: open access databases of computationally predicted enzyme promiscuity products for untargeted metabolomics. J. Cheminformatics. 2015; 7:44. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B37] 37. Hadadi N., Hafner J., Shajkofci A., Zisaki A., Hatzimanikatis V.. ATLAS of biochemistry: a repository of all possible biochemical reactions for synthetic biology and metabolic engineering studies. ACS Synth. Biol. 2016; 5:1155–1166. [DOI] [PubMed] [Google Scholar]

[B38] 38. Delépine B., Duigou T., Carbonell P., Faulon J.-L.. RetroPath2.0: A retrosynthesis workflow for metabolic engineers. Metab. Eng. 2018; 45:158–170. [DOI] [PubMed] [Google Scholar]

[B39] 39. Moriya Y., Shigemizu D., Hattori M., Tokimatsu T., Kotera M., Goto S., Kanehisa M.. PathPred: an enzyme-catalyzed metabolic pathway prediction server. Nucleic Acids Res. 2010; 38:W138–W143. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B40] 40. Scheffen M., Marchal D.G., Beneyton T., Schuller S.K., Klose M., Diehl C., Lehmann J., Pfister P., Carrillo M., He H.et al.. A new-to-nature carboxylation module to improve natural and synthetic CO2 fixation. Nat. Catal. 2021; 4:105–115. [Google Scholar]

[B41] 41. Alberty A.R. Biochemical thermodynamics. Biochim. Biophys. Acta - Protein Struct. Mol. Enzymol. 1994; 1207:1–11. [DOI] [PubMed] [Google Scholar]

[B42] 42. Haraldsdóttir H.S., Thiele I., Fleming R.M.T.. Quantitative assignment of reaction directionality in a multicompartmental human metabolic reconstruction. Biophys. J. 2012; 102:1703–1711. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B43] 43. Fleming R.M.T., Thiele I.. von Bertalanffy 1.0: a COBRA toolbox extension to thermodynamically constrain metabolic models. Bioinformatics. 2011; 27:142–143. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B44] 44. Vojinović V., Stockar U.V.. Influence of uncertainties in pH, pMg, activity coefficients, metabolite concentrations, and other factors on the analysis of the thermodynamic feasibility of metabolic pathways. Biotechnol. Bioeng. 2009; 103:780–795. [DOI] [PubMed] [Google Scholar]

[B45] 45. Alberty A.R. Thermodynamics of the hydrolysis of adenosine triphosphate as a function of temperature, pH, pMg, and ionic strength. J. Phys. Chem. B. 2003; 107:12324–12330. [Google Scholar]

[B46] 46. Goldberg R.N., Tewari Y.B., Bhat T.N.. Thermodynamics of enzyme-catalyzed reactions–a database for quantitative biochemistry. Bioinformatics. 2004; 20:2874–2877. [DOI] [PubMed] [Google Scholar]

[B47] 47. Noor E., Flamholz A., Bar-Even A., Davidi D., Milo R., Liebermeister W.. The protein cost of metabolic fluxes: prediction from enzymatic rate laws and cost minimization. PLoS Comput. Biol. 2016; 12:e1005167. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B48] 48. Alberty A.R. Legendre transforms in chemical thermodynamics. Pure Appl. Chem. 1997; 69:2221–2230. [Google Scholar]

[B49] 49. Ebrahim A., Lerman J.A., Palsson B.O., Hyduke D.R.. COBRApy: constraints-based reconstruction and analysis for Python. BMC Syst. Biol. 2013; 7:74. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B50] 50. Lloyd C.J., Ebrahim A., Yang L., King Z.A., Catoiu E., O’Brien E.J., Liu J.K., Palsson B.O.. COBRAme: a computational framework for genome-scale models of metabolism and gene expression. PLOS Comput. Biol. 2018; 14:e1006302. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B51] 51. Lieven C., Beber M.E., Olivier B.G., Bergmann F.T., Ataman M., Babaei P., Bartell J.A., Blank L.M., Chauhan S., Correia K.et al.. MEMOTE for standardized genome-scale metabolic model testing. Nat. Biotechnol. 2020; 38:272–276. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B52] 52. Seaver S.M.D., Liu F., Zhang Q., Jeffryes J., Faria J.P., Edirisinghe J.N., Mundy M., Chia N., Noor E., Beber M.et al.. The ModelSEED Biochemistry Database for the integration of metabolic annotations and the reconstruction, comparison and analysis of metabolic models for plants, fungi and microbes. Nucleic Acids Res. 2020; 1:D575–D588. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B53] 53. Machado D., Andrejev S., Tramontano M., Patil K.R.. Fast automated reconstruction of genome-scale metabolic models for microbial species and communities. Nucleic Acids Res. 2018; 46:7542–7553. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B54] 54. O’Boyle N., Morley C., Hutchison G.. Pybel: a Python wrapper for the OpenBabel cheminformatics toolkit. Chem. Cent. J. 2008; 2:5. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

eQuilibrator 3.0: a database solution for thermodynamic constant estimation

Moritz E Beber

Mattia G Gollub

Dana Mozaffari

Kevin M Shebek

Avi I Flamholz

Ron Milo

Elad Noor

Abstract

INTRODUCTION