Predictive encoding of motion begins in the primate retina

Abstract

Predictive motion encoding is an important aspect of visually guided behavior that allows animals to estimate the trajectory of moving objects. Motion prediction is understood primarily in the context of translational motion, but the environment contains other types of behaviorally salient motion correlation such as those produced by approaching or receding objects. However, the neural mechanisms that detect and predictively encode these correlations remain unclear. We report here that four of the parallel output pathways in the primate retina encode predictive motion information, and this encoding occurs for several classes of spatiotemporal correlation that are found in natural vision. Such predictive coding can be explained by known nonlinear circuit mechanisms that produce a nearly optimal encoding, with transmitted information approaching the theoretical limit imposed by the stimulus itself. Thus, these neural circuit mechanisms efficiently separate predictive information from nonpredictive information during the encoding process.

To survive, animals must collect information from the environment that can be used to guide their future actions. Most important to behavior are those aspects of past experience that allow an animal to reliably estimate salient features of the environment in the future, that is, predictive information. Making reliable estimates of the future is challenging for at least two reasons. First, most of the information that is available in the environment is not useful for making predictions, and distinguishing this predictive information from nonpredictive information can be challenging¹. Second, neurons are limited in the amount of information they can transmit in the time spans that are relevant to behavior. Thus, to effectively utilize their limited signaling capacity, neural circuits must discard nonpredictive information and preferentially transmit predictive information during the encoding process^1–3.

Understanding how neural circuits separate predictive and nonpredictive information is a fundamental problem in computational and systems neuroscience. Making progress on this question has been challenging, in part because some experimental contexts contain several types of salient information, making it difficult to determine the type of information that should be predicted¹. For this reason, visual motion provides an ideal experimental framework for studying predictive encoding because the type of information to be estimated is straightforward. Behaviorally relevant motion produces correlations between two or more points in space and time^4–9, and neural circuits must utilize these correlations to estimate, on the basis of the past positions of an object, where that object is likely to be in the future—a function we refer to as predictive motion encoding^10–14.

We studied predictive motion encoding in parasol and smooth monostratified ganglion cells, retinal output neurons that project to brain regions that contribute to motion processing in primates^15–17. Responses from these cells were measured to different classes of spatiotemporal correlation that occur during visual motion^6,18 and with distinct behavioral relevance¹⁹. We report that these cells encode predictive information about motion correlations in their spike outputs. The encoding of this information about future motion is nearly optimal—neural responses represent virtually all the predictive information available in the stimuli. Further experiments show that this predictive encoding is present at the synaptic output of diffuse bipolar cells and emerges downstream of horizontal cells in the outer retina. Thus, the primate visual system begins predicting and encoding future motion trajectories at the second visual synapse.

Results

Primate ganglion cells encode motion correlations.

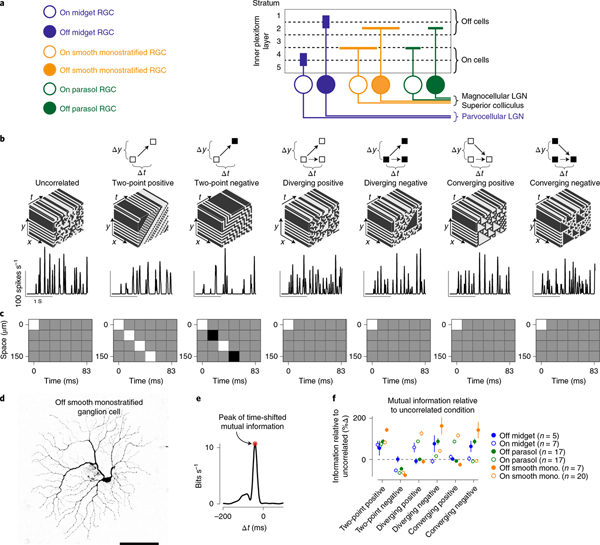
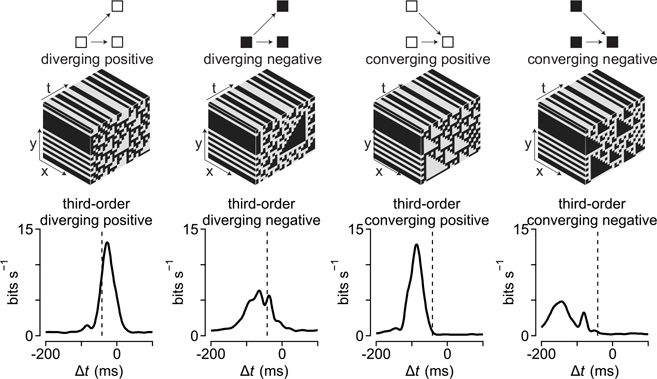
Motion in natural environments produces correlations between two or more points in space and time^5,18,20,21. In primates, sensitivity to two-point motion correlations arises in the retina²², but sensitivity to three-point (higher-order) spatiotemporal correlations is thought to first occur in the visual cortex⁴. To determine whether the primate retina encoded these higher-order correlations, we measured the spike outputs of ganglion cells—the retinal output neurons—to several classes of stimuli containing correlations between three points in space and time^4,5,8,9,18. Two general classes of three-point correlations were tested: (1) diverging correlations that consisted of a point in space that separated to two points in space at a later time, and (2) converging correlations where two points in space merged to a single point at a later time (Fig. 1). These types of correlation can arise when objects approach (diverging correlations) or recede away from (converging correlations) an observer^{4–6,8,18,23,24}. These three-point correlations were further subdivided into positive or negative on the basis of the parity of the correlated points—that is, whether the diverging or converging points were brighter (positive parity) or dimmer (negative parity) than the mean intensity. For the sake of clarity, we refer to the contrast (that is, triangle contrast) of the predominant diverging or converging points rather than to the parity.

Fig. 1 |. Ganglion cells show sensitivity to higher-order correlations.

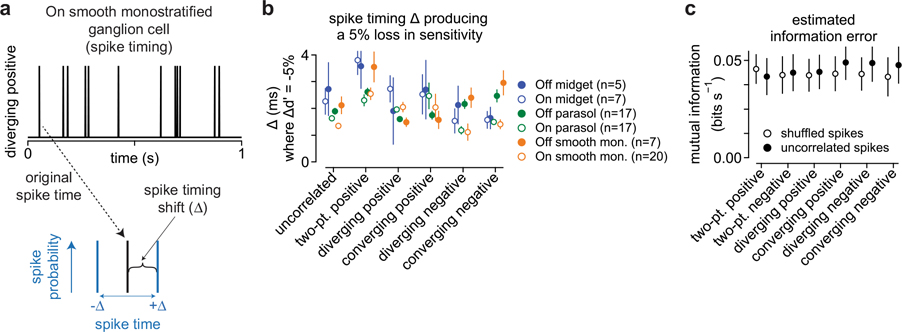
a, Stratification pattern and central projections of the macaque retinal ganglion cells (RGC) recorded as part of this study. Parasol and smooth monostratified cells stratify in similar regions of the neuropil and project to brain nuclei involved in motion processing. LGN, lateral geniculate nucleus b, Top, Example space–time plots for seven of the stimulus classes used in the study. Bottom, Spike rate (in spikes s⁻¹) as a function of the time for these stimuli in an On-type smooth monostratified ganglion cell. c, Autocorrelation for the stimulus types showing space (y axis) as a function of time (x axis). Correlation values ranged between −1 (black) and 1 (white) with gray values equal to zero. d, Morphology from an Off-type smooth monostratified ganglion cell recorded as part of this study. Scale bar, 0.1 mm. e, Example time-shifted mutual information curve showing mutual information (y axis) as a function of time shift (x axis). Shaded region indicates peak value of the information curve used in comparing encoding between stimulus conditions. f, Peak values for the time-shifted mutual information for six types of motion correlation relative to the information for the uncorrelated stimulus. Data are shown for several ganglion cell types. mono., monostratified. Circles and error bars indicate mean ± s.e.m.

The three-point motion stimuli lacked two-point spatiotemporal correlations (Fig. 1c)^4,18. Thus, if the cells were insensitive to these three-point correlations, their encoding of these stimuli should be similar to encoding of a stimulus lacking spatiotemporal correlations (uncorrelated condition; Fig. 1). We compared information encoding across stimulus types by estimating the amount of information that a cell’s response in one interval of time encoded about the stimulus in another interval of time—the time-shifted mutual information (bin width, 16.7 ms; Methods; Fig. 1e and Extended Data Fig. 1). This method measures the amount of information that can be obtained about a stimulus from neural responses—a stimulus that produces increased information rates relative to the uncorrelated condition indicates that neural responses encode more information about that stimulus. We first compared the peak values of the information curves across stimulus conditions and cell types, and we later analyzed the temporal properties of these curves (Fig. 1e,f).

We measured the responses of six different ganglion cell types to these stimuli—midget, parasol and smooth monostratified cells that each come in On and Off subtypes that prefer increments or decrements in light intensity, respectively²⁵. Smooth monostratified and parasol ganglion cells showed peak information rates that were ~twofold (100%) higher relative to the uncorrelated stimulus for three-point motion stimuli in which the stimulus contrast was aligned with the contrast polarity of the cell—positive triangle contrasts for On cells and negative triangle contrasts for Off cells (Fig. 1f; P ≤ 0.02; Wilcoxon signed rank test). These increased information rates for the three-point motion correlations indicate that smooth monostratified and parasol cells encode these correlations in their spike outputs. These data indicate that sensitivity to three-point correlations is not entirely cortical in origin, but occurs in the retina⁴. We next investigated the dependence of this encoding on spike timing.

Information encoding occurs with high temporal precision.

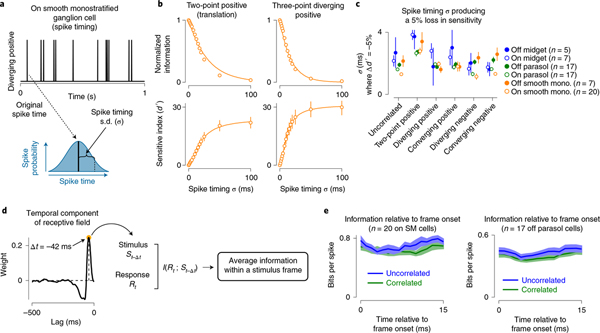
The analysis presented in Fig. 1 calculated the time-shifted mutual information for a time window corresponding to the stimulus update rate (Δt, 16.7 ms). However, many neurons can encode stimulus features on timescales of only a few milliseconds^26–32. To determine the relationship between spike timing and the encoding of motion correlations, we calculated the mutual information between the stimulus and spike response of a cell after randomly varying spike times. Spikes were binned in 1-ms intervals and the timing of each spike was determined by drawing a random value from a Gaussian distribution with a mean centered at the time of the original spike and s.d. between 0 and 100 ms (Fig. 2 and Methods).

Fig. 2 |. Information encoding occurs on short timescales.

a, Example spike train for a 1-s portion of a stimulus containing diverging positive correlations (top). To measure the relationship between spike timing and information transmission, each spike was randomly shifted in time. Time shifts were drawn from a Gaussian distribution with a mean corresponding to the timing of the original spike and a s.d. (σ, bottom). The process was repeated for each spike train in each cell at several s.d. (0–100 ms). b, Normalized information (top) and sensitivity index (d′, bottom) as a function of the s.d. of spike timing (x axis) across On smooth monostratified ganglion cells (n = 20). Solid lines show either a single-exponential fit (top) or a sigmoidal (bottom) to the data. Circles and error bars indicate mean ± s.e.m. c, Spike timing s.d. at which the sensitivity index increased by 5% relative to the condition with spike time unaltered (σ, 0 ms). Data are shown across six stimulus conditions and six ganglion cell types. Information encoding degraded at short timescales for both the uncorrelated stimulus and motion correlations, indicating that encoding occurred at a much finer time scale than the temporal structure of the stimuli. Number of cells in the population are indicated in parentheses. Circles and error bars indicate mean ± s.e.m. d, The receptive field of each neuron was determined from the uncorrelated stimulus and the temporal component was used to determine the delay in visual processing (left). The measured delay was then used to align the stimulus and response, and the average information in each stimulus frame was determined (bin width, 1 ms; right). e, Information per spike as a function of time following the onset of each stimulus frame. Information did not vary significantly across time bins for any of the cell types (P ≥ 0.31, Kruskal–Wallis one-way analysis of variance). Shaded regions indicate mean ± s.e.m. In each cell, frame onset was corrected for the time lag from presenting stimuli at the level of photoreceptors and the peak of the temporal component of the receptive field measured with uncorrelated noise as in d. Solid lines and shading indicate mean ± s.e.m.

Spike timing could affect information across a range of timescales. If information encoding were determined solely by the statistics of the stimulus, information should decrease only when the variation in spike timing exceeded the update interval of the stimulus itself (16.7 ms). However, if encoding occurred on finer timescales, information should decrease rapidly with fine-grained changes in spike timing. Our analysis supported the latter premise that these primate ganglion cell types encoded information on relatively fine timescales. Encoded information decayed rapidly after shifting spike timing by only a few milliseconds (Fig. 2b, top). This decline continued such that, at time shifts of 50 ms, information about the stimulus was almost completely degraded.

To determine the threshold at which variation in spike timing significantly degraded information, we calculated the sensitivity index (d′) between the original and shifted spike trains (Methods). Lower d′ values indicate that the information content of the shifted condition was similar to the original spike train, whereas larger index values indicate that information between the two spike trains is more distinct (that is, degraded). The sensitivity index increased rapidly at time shifts between 1 and 20 ms, consistent with a rapid degradation in information. We defined a significant change in information as a 5% increase in d′ relative to the saturating amount. Across cells and stimulus conditions, this threshold was reached in <4 ms (Fig. 2c). This high sensitivity of information to variations in spike timing was also observed when a Bernoulli distribution rather than a Gaussian distribution was used to shift spike timing, indicating that encoding these motion stimuli requires a high amount of temporal precision (Extended Data Fig. 2).

To determine whether spike timing near frame transitions contained more information than spikes occurring in the middle of a frame, we normalized frame timing relative to the measured lag from the photoreceptors. We then calculated the encoded information relative to the onset of each stimulus frame (Fig. 2d,e). We found that information did not vary significantly across time bins for any of the cell types, which further indicates that information encoding occurred on much finer timescales than the update rate of the stimulus.

Encoding timescales match stimulus correlation structure.

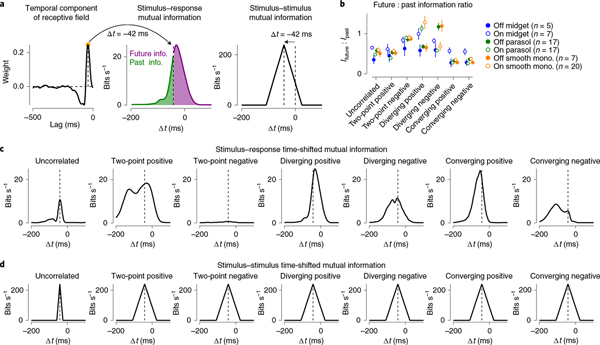
The correlations inherent to visual motion mean that the motion trajectory leading up to a particular time (t ≤0) provides information about the likely trajectory of motion at later time points (t >0). This information can then be used to estimate motion trajectories and to guide behavior^3,10,33–35. The motion stimuli used in our study, because of their correlation structure, contained this type of predictive information within a time window of around 50 ms (Fig. 3). To determine whether the timescales of encoding match the timecourse of available information in the stimulus, we calculated the mutual information between a cell’s spike output and the stimulus at different time lags relative to the stimulus presentation (Extended Data Fig. 1). We then compared these results to the measured mutual information between the stimulus and itself at the same time lags. The temporal profile of information available in the stimulus was shifted to account for the time lag between the presentation of the stimulus at the level of the photoreceptors and the ganglion cell output (~30–50 ms; Fig. 3a). This time lag was calculated directly from the spatiotemporal receptive field measured for each cell (Methods).

Fig. 3 |. Timescales of encoding match higher-order correlations.

a, The spatiotemporal receptive field was measured for the uncorrelated stimuli in each cell. The peak (On cells) or trough (Off cells) of the temporal receptive field was used as the measure of lag in visual processing and was defined as t = 0 for subsequent measures of past and future information. b, Ratio of future-to-past information for six primate ganglion cell types across the seven stimulus classes used in this study. This ratio was <1 for several stimulus classes because the temporal filter was not symmetrical between past and future points relative to the peak (that is, strongly biphasic) as in a. Circles and error bars indicate mean ± s.e.m. c, Information rate (bits s⁻¹) as a function of the time delay (ms) for seven stimulus classes in an On smooth monostratified ganglion cell. d, Information that each stimulus class contains about itself as a function of the time delay. The peak was shifted relative to the measured lag for signal transmission from the photoreceptors to the ganglion cell output. Information decayed linearly as a function of time shift due to stochastic elements in the stimuli.

Ganglion cell encoding of the stimulus closely matched the timecourse of the information contained within the stimulus itself (Fig. 3). For the uncorrelated noise condition, which contained information about itself only within the window of a single frame (~16.7 ms), the cell encoded stimulus information in a relatively short time window. These time windows became broader for encoding of motion stimuli, indicating that the timecourse over which the cell encoded these stimuli depended on the timecourse of available information contained within the motion stimuli. Furthermore, the first- and second-order statistics were identical for the uncorrelated stimulus and the stimuli containing three-point correlations, as all of these stimuli lack pairwise spatiotemporal correlations (Fig. 1c). Thus, any differences in information encoding between the uncorrelated stimulus and the three-point correlation stimuli must occur because the ganglion cells were sensitive to higher-order statistics contained in those stimuli.

In addition to tracking the correlation structure in the stimuli, encoding was shifted to future (that is, positive) time lags for two-point positive and diverging correlations (Fig. 3b,c). This shift indicates that the cell’s response at a given time predicts the pattern of motion at future time points. This pattern in which a cell’s responses anticipate subsequent motion is characteristic of predictive motion encoding^10,11,13.

The observed displacement in the time-shifted mutual information towards future time lags could arise from the effects of motion correlations on the retinal circuit, but could also arise from other aspects of the stimulus. To distinguish between these possibilities, we extracted the motion correlations from the stimulus and used these correlations in calculating the time-shifted mutual information (Extended Data Fig. 3). This analysis showed the same pattern of predictive motion encoding as we observed in Fig. 3. Thus, the predictive displacement in the time-shifted mutual information for pairwise and diverging correlations arises from the motion correlations in the stimulus.

This predictive encoding did not occur for all motion correlations tested. It was not present for converging correlations, as encoded information was not shifted to positive time lags for these stimuli (Fig. 3). These differences in encoding could not arise from differences in available information, which was identical for all of the motion stimuli at all time shifts (Fig. 3d). Thus, the differences in encoding of these stimuli reflect a selectivity for predictive information in pairwise and diverging correlations^22,24. In the next section, we further investigate this relationship between stimulus classes by determining how closely cellular encoding of predictive information in these stimuli approximates an optimal encoding.

Predictive encoding nearly optimal for motion correlations.

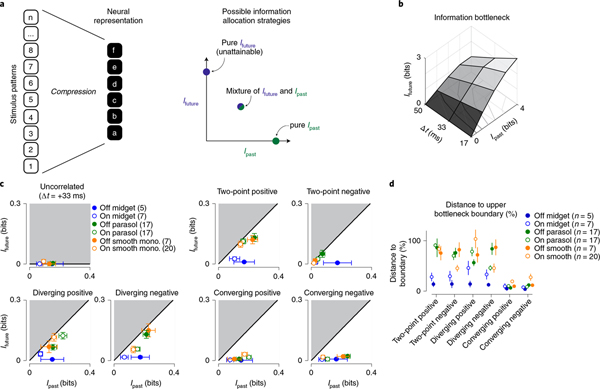
A single neuron cannot encode all the information available in a sensory input. Thus, the encoding scheme adopted by a neuron creates a compressed representation in which much of the information in the incoming stimulus is discarded (that is, lossy compression; Fig. 4a). Further, on the basis of this compression scheme, one can determine the maximal amount of predictive information that can be encoded given the amount of information encoded about the past stimulus trajectory². The predictive information in neural responses can then be compared to this optimal encoding (Fig. 4b).

Fig. 4 |. Encoding of predictive information is nearly optimal for certain stimulus classes.

a, Left, a potential lossy information encoding scheme that could be used to represent components of a high-dimensional stimulus in the neural output. Right, this neural representation can allocate bandwidth for encoding information about the past stimulus history (I_past) and information that can be used to anticipate future motion (I_future). b, Information bottleneck boundary for available past and future information at three future time lags for the stimulus containing spatiotemporal correlations. c, Encoding of predictive information (I_future; y axis) versus past information (I_past; x axis) for the seven stimulus classes. The black solid line indicates the theoretical boundary for predictive information and the shaded region defines the theoretically unattainable values. Predictive information was nearly optimal for two-point positive, diverging positive and diverging negative correlations. Cellular representations of converging correlations lacked similar predictive information. d, Encoded future information (I_future) in six cell types relative to the theoretical maximum value defined by the information bottleneck. Values are given as a percentage of the boundary value for the six stimulus classes used in this study. Number of cells in the population are indicated in parentheses. Circles and error bars indicate mean ± s.e.m.

The results of this analysis are shown in Fig. 4c. The solid black line delineates the boundary for optimal predictive encoding (I_future) as a function of the information about the past stimulus trajectory (I_past). The shaded regions to the upper left define values for predictive information that are not theoretically attainable. Indeed, the entire predictive domain of the curve was unattainable for the uncorrelated noise stimulus, which lacked predictive information, and this was also reflected in a lack of measured predictive information (Fig. 4c, upper left).

For the motion correlations, which contained predictive information, the relationship between cellular encoding of this information and the optimal boundary varied both with cell type and stimulus type. As indicated by the data in Fig. 3, ganglion cells encoded predictive information for two-point correlations and three-point diverging correlations. Further, this encoding was nearly ideal for smooth monostratified and parasol ganglion cells, which captured between 70% and 100% of the available predictive information for stimulus parities aligned with the cells’ preferred contrast polarity (Fig. 4c). This indicates that the spike output of these cells retains most of the predictive information contained in these stimuli. Midget (parvocellular-projecting) ganglion cells, however, encoded relatively less predictive information in their spike outputs to these stimuli. In these cells, mean values were between 38% and 80% of the limit for the two-point and diverging correlations; predictive encoding was particularly low for Off midget cells. Thus, predictive encoding varied with cell type.

Unlike the two-point and diverging motion correlations, cellular encodings of converging motion correlations fell far off the optimal boundary (Fig. 4c). Parasol and smooth monostratified cells encoded less than 50% of the available predictive information for these stimuli. This lack of strong predictive encoding for converging correlations is consistent with our previous work demonstrating a preference for approaching motion in these cell types. Approaching motion, which produces diverging correlations on the retina, elicited significantly larger responses than receding motion, which produces converging correlations²⁴. The data presented in the current study go further to indicate these neurons encode predictive information about diverging correlations that could be utilized to anticipate future motion trajectories.

Predictive encoding is nearly optimal at low contrast.

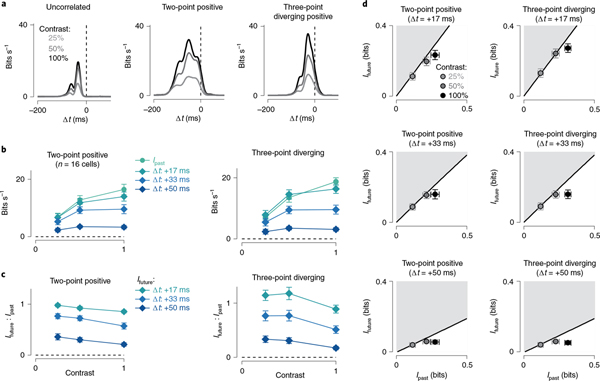
Due to noise introduced in retinal processing, decreasing the contrast of a stimulus diminishes the signal-to-noise ratio and limits the amount of encoded information³⁶. To determine whether encoding of predictive information was also diminished at low contrast (that is, low signal-to-noise ratio), we calculated past and future information encoded in the same cell at three different stimulus contrasts (contrasts: 0.25, 0.5, 1.0).

The relative amount of information encoded about the past and future varied with stimulus contrast (Fig. 5). Past information gradually increased with contrast and showed only weak saturation at the highest contrast level (Fig. 5b). Future information showed a greater degree of saturation relative to past information. This saturation was more pronounced at times farther into the future such that, for the longest lag (+50 ms), the encoded information depended only weakly on contrast. This saturation in future information resulted in a higher ratio of future-to-past information encoding at lower contrasts—a trend that again was strongest for time lags farther into the future (Fig. 5c). Thus, these cells encoded the greatest relative amount of predictive information at low contrast, when the signal-to-noise ratio was lowest.

Fig. 5 |. Ganglion cells optimally encode future information at low contrast.

a, Information rate (bits s⁻¹) as a function of the time delay (ms) for three stimulus classes in an On smooth monostratified ganglion cell. Results are shown at three different contrasts for each stimulus class. b, Relationship between encoded information as a function of stimulus contrast. Results are shown for past information and three future time lags. Diverging correlations were positive parity for On cells and negative parity for Off cells, here and below. c, Ratio of future (I_future) to past (I_past) information as a function of contrast in the same cells as in b (n = 16 cells). d, Encoding of predictive information (I_future; y axis) versus past information (I_past; x axis) (n = 16 parasol and smooth monostratified cells). Measurements were taken at three different stimulus contrasts and three time lags. Circles and error bars indicate mean ± s.e.m.

We next asked whether the greater saturation in future information affected the relationship between cellular encoding and the optimal boundary defined by the information bottleneck. This relationship varied with stimulus contrast and time lag. At a time lag of +17 ms, encoding of future information was near the optimal boundary at all contrasts (Fig. 5d, top). At later time lags, however, the lowest contrast stimulus maintained a position near the optimal boundary, but the higher contrasts separated from this boundary. These data indicate that, at low contrast, parasol and smooth monostratified cells encode nearly all of the available future information for pairwise and diverging correlations. Further, these cells most optimally encoded predictive motion information at low contrast, when the signal-to-noise ratio was the lowest. We return to the implications of these results in the Discussion.

Predictive motion encoding arises early in visual pathway.

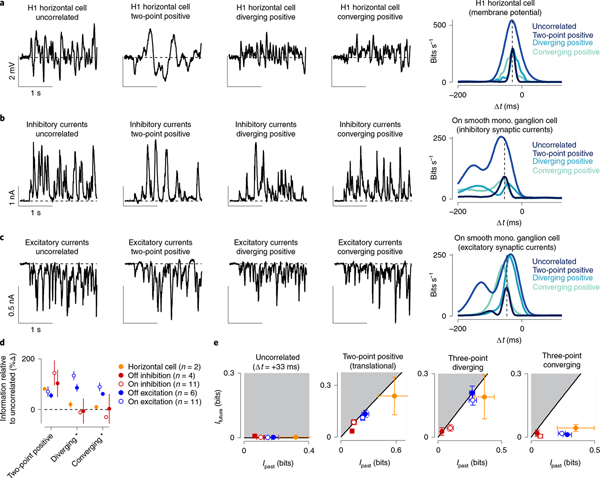
The encoding of spatiotemporal correlations in ganglion cells indicates that information about these correlations must be present in the signals from cone photoreceptors. Ganglion cells also showed a selectivity for these motion correlations relative to the uncorrelated stimulus and showed predictive encoding for a subset of these correlations. Where in the circuit does such selectivity arise? To answer this question, we assayed three different points in the circuit: (1) the voltage responses of horizontal cells in the outer retina, (2) amacrine cell inhibitory synaptic outputs and (3) diffuse bipolar cell excitatory synaptic outputs (Fig. 6). We performed horizontal cell recordings in whole-cell, current-clamp, and inhibitory and excitatory synaptic currents were measured in whole-cell, voltage-clamp (Methods).

Fig. 6 |. Information encoding varies with retinal processing stage.

a, Membrane potential in an H1 horizontal cell for four of the stimulus classes (left) and mutual information for the stimuli in the same cell (right). Peak information was similar between the uncorrelated condition and the three-point motion conditions, but was much higher for the two-point condition. b, Same as a for the inhibitory synaptic currents in an On smooth monostratified ganglion cell. These currents showed a similar pattern observed in the horizontal cell, with a high information rate for the two-point motion correlations and smaller rates for the other stimulus classes. c, Excitatory synaptic currents for the same cell as in b. Here, the pattern shifted, with three-point motion correlations producing higher information rates relative to the uncorrelated condition and with predictive shifts toward positive time lags for the two-point and diverging motion stimuli. d, Mutual information for two-point, diverging and converging motion correlations relative to the information for the uncorrelated stimulus. Diverging and converging correlation data are shown for stimulus parities aligned with a cell’s preferred contrast—positive parities for On-type cells and negative parities for Off-type cells. e, Encoding of predictive information (I_future; y axis) versus past information (I_past; x axis) for the four stimulus classes. The black solid line indicates the theoretical boundary for predictive information and the shaded region defines theoretically unattainable values (n: horizontal cells, 2; Off inhibition, 4; On inhibition, 11; Off excitation, 6; On excitation, 15). Circles and error bars indicate mean ± s.e.m.

Horizontal cells receive excitatory synaptic inputs directly from cone photoreceptors and thus provide a window into neural processing early in the visual stream. We recorded the membrane potential of H1 horizontal cells to our stimulus set and computed the time-shifted mutual information between each cell’s membrane potential and the stimulus (Methods). Pairwise correlations produced higher mutual information values than the uncorrelated stimulus (Fig. 6a,d). Three-point correlations, however, showed similar information values to the uncorrelated control condition, indicating that horizontal cells lacked selectivity for these correlations.

A similar pattern was observed in the inhibitory synaptic input from amacrine cells to the ganglion cells (Fig. 6b). However, inhibitory input to these cells arises from the opposite polarity pathway (that is, crossover inhibition), so the stimuli were not aligned with the preferred contrast polarity of these amacrine cells (Methods). Nonetheless, the absence of selectivity to three-point correlations in horizontal cells and amacrine cells and the presence of this selectivity in ganglion cells indicates that information about three-point correlations is transmitted through the retina with high gain.

Unlike horizontal and amacrine cells, the diffuse bipolar cell synaptic output showed both selectivity for two-point and three-point motion correlations and also predictive encoding of these correlations (Fig. 6c). For excitatory synaptic currents, motion correlations produced peak information rates that were higher than the uncorrelated condition. Further, two-point and three-point diverging correlations shifted information rates towards future time lags just as was observed in the ganglion cell spike outputs. These results indicate that the selective sensitivity to three-point correlations emerges at some point between the synaptic inputs and synaptic outputs of diffuse bipolar cells.

We also estimated the efficiency with which these circuit components encoded predictive information using the information bottleneck model (Fig. 6e). Indeed, the pattern of information in the excitatory synaptic inputs mirrored that observed in the spike outputs of parasol and smooth monostratified ganglion cells—encoding of predictive information approached the optimal boundary for both pairwise motion and diverging motion correlations. Inhibitory synaptic input also approached the boundary for these stimuli, but the overall magnitude of encoded future information was lower (Methods). Further, future information encoding in H1 horizontal cells fell away from the boundary, indicating that this nearly ideal encoding of future information emerges primarily in the diffuse bipolar cell circuitry. We next investigated the contribution of neural mechanisms in diffuse bipolar cells to the prioritized encoding of predictive motion information.

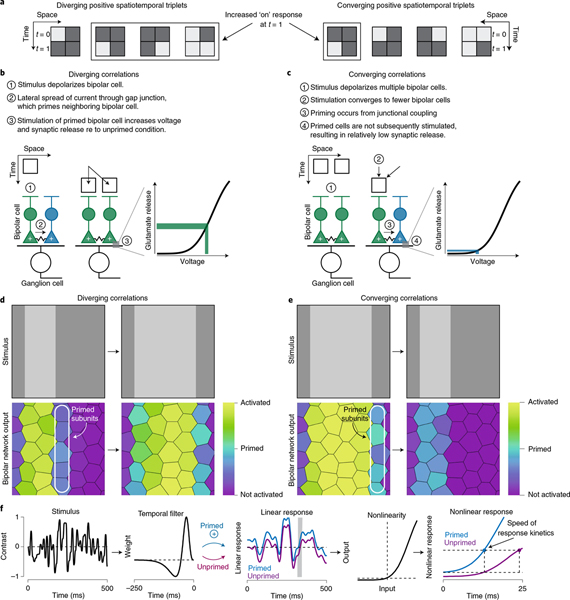
Circuit nonlinearities favor predictive information encoding.

Our physiological recordings indicated that predictive encoding of motion largely arose in the bipolar cells that provided synaptic inputs to smooth monostratified and parasol ganglion cells (Fig. 6). Two known mechanisms in diffuse bipolar cells could contribute to encoding predictive motion information—electrical coupling and nonlinear synaptic release. Electrical coupling occurs in both the On- and Off-type bipolar cells of the primate retina^37–39 and the input–output relationships of these cells are also strongly rectified (that is, nonlinear)^22,24,40,41. Together these components could work to enhance encoding of future information by increasing cellular responsiveness to correlated stimuli through electrical coupling and by discarding weaker responses from uncorrelated stimuli with the output nonlinearity.

We tested this hypothesis using a computational model of the bipolar cell subunits on the basis of direct excitatory synaptic input recordings from parasol and smooth monostratified ganglion cells^22,24. In this model, the shape of the output nonlinearity was modified by shifting the threshold at which an input begins to produce subunit responses (Fig. 7 and Methods). Model outputs were estimated to the motion stimuli (contrast, 0.5). Past and future information were calculated for the model across a range of thresholds. To determine whether electrical coupling between bipolar cells could contribute to encoding predictive information, we compared the subunit model with a model that was identical except that model subunits shared a portion of their responses through coupling (coupled subunit model).

Fig. 7 |. Subunit coupling and high output thresholds favor encoding of predictive information.

a, Model in which an output threshold was placed at the output of the model bipolar cell subunits. Left, the stimulus (contrast, 0.5) was filtered by receptive field subunits. Subunit outputs were passed through an output threshold and then pooled at the level of the model ganglion cell at the ganglion cell output to determine circuit response. Right, encoded information as a function of response threshold. Curves are shown for past information, total future information and future information at three time lags. b, The coupled subunit model was identical to the model in a except that model subunits were coupled and shared a portion of their responses before the output threshold. c, Left, distribution of model subunit responses (bottom), which served as input to the thresholded input–output nonlinearity (top). Right, shapes of subunit input–output relationships at three different threshold amounts. d, Ratio of total future information to past information (I_future:I_past) for the two models as a function of threshold. e, Ratio of future-to-past information as a function of stimulus contrast for the two models at a threshold of 0.6. The coupled subunit model showed higher ratios at all contrasts.

We calculated the ratio of encoded future-to-past information to determine whether the output threshold or coupling would bias encoding of predictive information. The coupled model showed a higher proportion of future versus past information encoded for all of the stimuli when the output threshold was in the range of ~0.5–0.75. Thus, subunit coupling biased encoding of predictive information, but only when combined with a moderately high output threshold (Fig. 7d). Further, the coupled subunit model outperformed the model lacking coupling at all contrasts tested, indicating that coupling would enhance predictive motion encoding across a broad range of stimulus conditions (threshold, 0.6; Fig. 7e).

These modeling results support the hypothesis that known properties of diffuse bipolar cells—electrical coupling and input–output nonlinearities—shape the type of information that these cells encode (Fig. 8). In summary, the correlations inherent in visual motion cause sequential stimulation of neighboring bipolar cells. As the motion excites a bipolar cell, a portion of the current from that cell passes to its neighbors. This shared current means that the neighboring cells will depolarize more as the motion stimulus passes through their receptive fields than if coupling were absent. Similar potentiation from electrical coupling will not occur for stimuli lacking spatiotemporal correlations or for two-point negative correlations, as sequential depolarization of neighboring neurons is required for this mechanism to be effective (Figs. 1 and 3).

Fig. 8 |. Proposed mechanisms contributing to predictive motion encoding.

a, Space–time plots showing the four enforced triplets for diverging and converging positive correlations. In On-type cells, three of the four diverging triplets will produce an increased response at t = 1 relative to t = 0, while this would occur for only one of the four converging triplets. Thus, the diverging correlations will produce responses that are more likely to exceed the bipolar cell output threshold. Most of the converging triplets will produce weaker responses at t = 1, meaning that these correlations are more likely to be discarded by the bipolar cell output nonlinearity. b, Diverging correlations first depolarize a few bipolar cells and depolarization spreads to neighboring bipolar cells through electrical coupling. This spreading activation primes cells at the leading edge of the motion such that subsequent activation of these cells increases depolarization of their synaptic terminals. This results in an increase in the voltage of the terminal that, along with the shape of the output nonlinearity, produces a much larger synaptic output relative to the unprimed condition. c, Converging correlations first activate many bipolar cells and then activate fewer of these cells. This pattern of activation does not take advantage of bipolar cell priming. d,e, Model bipolar cell network output for the diverging (d) and converging (e) stimuli. Bipolar cells at the leading edge of the diverging stimulus are primed through electrical coupling and then subsequently stimulated, engaging the mechanisms described in b. However, for converging correlations, primed bipolar cells are not subsequently stimulated. f, Subunit priming speeds response kinetics. A Gaussian stimulus was convolved with a temporal filter and subunit priming was simulated by increasing the result by 10%. Primed and unprimed responses (right) were then generated after passing inputs from the linear filtering stage through an output nonlinearity. Priming quickened response kinetics relative to the unprimed condition. Responses shown for the shaded region of the linear response.

Response thresholds contribute by discarding weak responses, which, due to the effects of network coupling, tend to lack strong spatiotemporal correlations. Thus, these mechanisms bias transmission of correlated inputs which, in the case of motion stimuli, contain information about the probable future trajectory of a moving object. Furthermore, our modeling results extend previous work on these neural mechanisms to demonstrate that they bias neural networks to both pairwise and higher-order motion correlations^22,40.

Discussion

Principles of efficient encoding have greatly enhanced our understanding of neural systems^42–48, but classical applications of this paradigm do not provide a method for distinguishing different bits of information on the basis of their behavioral relevance¹. The information bottleneck provides a framework for assigning priority to different bits of information on the basis of their salience to behavior—at a minimum, predictive information should be prioritized during encoding as only such information can be used to guide an animal’s behavior^1–3,10,34. Yet, prediction can be difficult to study, as the stimulus properties that should be predicted can often be difficult to identify and control.

Visual motion provides a straightforward setting in which to study predictive coding, as the stimulus property that should be predicted is clear—one must use information about the past locations of an object to estimate where it is likely to be at some point in the future. Here, we found that four ganglion cell pathways in the primate retina effectively encode predictive information about visual motion (Fig. 3). Application of the information bottleneck technique showed that these cells selectively discard nonpredictive information and represent as much predictive information as possible given their overall encoding capacity for pairwise and diverging motion correlations in their spike outputs (Fig. 4). Further, the mechanisms that likely contributed to predictive motion encoding were distinct from those proposed previously (Figs. 7 and 8)^11–14.

We identified two distinct neural mechanisms that could contribute to motion prediction within the receptive field center of these ganglion cells—electrical coupling and nonlinear synaptic release in retinal bipolar cells (Fig. 7). These mechanisms work together to encode predictive information and discard nonpredictive information available in the incoming visual inputs. Electrical coupling between neighboring bipolar cells selectively enhances the response of the bipolar cell network to correlated inputs that contain predictive information. The output thresholding mechanism present in bipolar cell synaptic outputs then discards the weaker uncorrelated components of the input that lack predictive information (Fig. 8)^22,24,40. In this way, bipolar cell networks selectively funnel predictive information to postsynaptic ganglion cells.

The encoding of predictive information by smooth monostratified and parasol ganglion cells was nearly optimal (Figs. 4 and 6). Initiating these predictive computations early in the visual stream allows the primate retina to provide a more refined representation of visual motion to downstream brain regions^{22,24,25,49,50}. Indeed, smooth monostratified and parasol ganglion cells send axonal projections to brain regions that are critical to motion detection in primates—the superior colliculus and the magnocellular layers of the lateral geniculate body^15–17. These brain regions show sensitivity for some of the motion correlations studied in the present work. For example, the superior colliculus contributes to processing of several types of motion, including approaching motion that produces diverging correlations¹⁷. Further, lesioning of the magnocellular lateral geniculate body devastates an animal’s ability to determine the direction of lateral motion, which produces both pairwise and higher-order spatiotemporal correlations¹⁶. Thus, predictive information from the retina can be used by these brain regions to estimate visual motion.

Efficient versus predictive encoding.

Our study shows how early visual circuits can use correlations in incoming stimuli to predict future motion. In the literature, ‘prediction’ is used in at least two different ways that are, in many ways, diametrically opposed to each other. In the context of efficient neural coding, prediction is a tool for compressing incoming sensory signals—neurons discard information that is predictable from past inputs and principally encode only those features that vary from that prediction. Thus, the encoding of stimulus features depends inversely on their likelihood of occurring in the environment^{46–48,51,52}.

The second definition of predictive coding, consistent with the use in the present study, indicates that stimulus information should be encoded on the basis of its salience to animal behavior^1–3,10,34. In this model, the information that can be used to estimate future states of the environment carries the greatest importance for guiding animal behavior and, thus, should be prioritized during neural encoding—this information is also termed predictive information.

Distinguishing between these hypotheses can be difficult as both models can make similar predictions for empirical data. For example, the results of our experiment to test encoding at different stimulus contrasts can be interpreted to support both models (Fig. 5). At low contrast, the ratio of encoded future-to-past information was greater than at high contrast. Classical efficient coding predicts that, as the signal-to-noise ratio increases, as with increasing contrast, the circuit should increasingly decorrelate the input. This decorrelation would remove some of the correlations in the stimulus needed to predict the future motion trajectory^42–47. Thus, the relative amount of future information would decrease at high contrast.

In the context of the second model, predictive future information is prioritized and thus encoding approaches the information bottleneck boundary at low contrast. At high contrast, the circuit more readily encodes information about the past and the ratio of future-to-past information decreases^3,10,33,34. While both models can explain these results, the latter model in which future information is prioritized during encoding is consistent with the neural mechanisms that likely contribute to predictive motion encoding in the primate retina—electrical coupling and nonlinear input–output functions of the diffuse bipolar cell networks.

Information that can be used to predict the future position of a moving object contains stronger spatiotemporal correlations than past information that is nonpredictive. Electrical coupling and nonlinear synaptic transmission in the bipolar cell network produces stronger responses to correlated versus uncorrelated stimuli^22,24,40. Thus, due to electrical coupling, at low contrast the more strongly correlated future information will drive the bipolar cell network harder than nonpredictive information about the past that has weaker correlations. The weaker uncorrelated stimuli will then be discarded by the synaptic output nonlinearity whereas the stronger predictive information will be transmitted. Furthermore, stimuli with weaker correlations (for example, nonpredictive past information) will have a better chance of making it through the output nonlinearity at higher contrasts, which would explain the decrease in the ratio of future-to-past information at high contrast.

However, efficient coding and predictive coding are not mutually exclusive hypotheses. Neural circuits can remove predictable correlations in sensory inputs (that is, efficient coding) while still preserving information needed to predict the trajectory of a moving object (that is, predictive coding). Indeed, theoretical and empirical evidence indicates that removal of redundant information and encoding of information about the future are both critical components of neural coding in dynamic environments^34,51.

A classic example of efficient coding is the difference-of-Gaussians receptive field structure in the early visual system, which discards the low spatial frequencies that are common in nature; removing this predictable structure through decorrelation allows visual circuits to encode surprising features that vary from the prediction^43,44. However, this decorrelation of the spatial frequency information does not eliminate the phase information in the input image. This is a critical distinction because spatial frequency information is a statistical measure of an ensemble of natural images and, as such, is biased toward the average image. The phase information, however, is specific to individual images and can be used to identify features in those images. Thus, neural mechanisms could utilize this phase information in estimating future states of the environment (that is, predictive coding) while simultaneously removing redundant spatial frequency information through decorrelation (that is, efficient coding).

Motion sensitivity arises early in the primate visual stream.

The asymmetrical distribution of bright and dark intensities in nature produce correlations between three or more points in space and time during visual motion^5,18,20,21. Indeed, behavioral studies have shown that humans and other animals utilize these higher-order correlations in estimating motion direction^4,8,9,53. Sensitivity to these correlations arises early in the visual stream of some species⁵⁴. In humans and nonhuman primates, this sensitivity was thought to arise first in the visual cortex⁴. Our findings indicate, however, that sensitivity to higher-order spatiotemporal correlations arises much earlier than previously thought—it is present in the synaptic outputs of diffuse bipolar cells at the second synapse of the visual stream. Thus, it appears that both flies and primates, with visual systems that evolved independently, use a similar strategy of extracting and encoding these correlations early in visual processing^4,23,54. Further, the mechanisms identified here are also engaged during approaching motion, indicating that this behaviorally salient motion would also produce predictive encoding²⁴.

The common structure of natural scenes indicates that many sighted animals are faced with the problem of estimating motion from spatiotemporal correlations. Moreover, motion estimation is one of many prediction problems that animals must solve to survive and reproduce. The neural mechanisms supporting motion prediction identified in this work—subunit pooling and nonlinear thresholding—are features shared across vertebrate evolution in the retina and other brain regions. Thus, future studies may shed light on how these and other neural mechanisms contribute to predictive encoding throughout the brain.

Methods

These experiments were done using an in vitro preparation of macaque monkey retina from three different macaque species (Macaca fascicularis, Macaca mulatta and Macaca nemestrina) of either sex. Tissues were obtained from terminally anesthetized animals that were made available through the Tissue Distribution Program of the National Primate Research Center at the University of Washington. All procedures were approved by the University of Washington Institutional Animal Care and Use Committee.

Cellular recordings were performed in a whole-mount retinal preparation. To aid with cellular visualization, horizontal cell recordings were made with pigment-epithelium removed, and all other recordings were done with the pigment-epithelium intact. Recordings were performed from macular, midperipheral, and peripheral retina (2–8 mm, 10–30° foveal eccentricity). Data were acquired at 10–kHz using a Multiclamp 700B amplifier (Molecular Devices), Bessel filtered at 3–kHz (900–CT, Frequency Devices), digitized using an ITC-18 analog-digital board (HEKA Instruments) and acquired using the Symphony acquisition software package (http://symphony-das.github.io).

Recordings were performed using borosilicate glass pipettes containing Ames medium for extracellular spike recordings from ganglion cells. Current-clamp recordings from horizontal cells were performed using an intracellular solution containing: 123 mM K-aspartate, 10 mM KCl, 10 mM HEPES, 1 mM MgCl₂, 1 mM CaCl₂, 2 mM EGTA, 4 mM Mg-ATP and 0.5 mM Tris-GTP. Whole-cell voltage-clamp experiments were performed to measure the excitatory synaptic currents generated from bipolar cell input or the inhibitory synaptic currents from amacrine cell input. Excitatory and inhibitory synaptic currents were isolated by holding ganglion cells at the chloride (about −70 mV) or cation (0 mV) reversal potential, respectively. These voltage-clamp recordings were performed using an intracellular solution containing: 105 mM Cs methanesulfonate, 10 mM TEA-Cl, 20 mM HEPES, 10 mM EGTA, 2 mM QX-314, 5 mM Mg-ATP and 0.5 mM Tris-GTP, pH ~7.3 with CsOH.

Midget, parasol and smooth monostratified ganglion cells were targeted for recording under infrared illumination on the basis of somatic size and shape. Cell type was confirmed on the basis of a combination of light response properties, receptive field measurements and confocal imaging of cellular morphology.

Visual stimuli.

Visual stimuli were generated using the Stage software package (http://stage-vss.github.io) and displayed on a customized digital light projector designed specifically for studying visual processing in Old World primates^24,55. All stimuli in this work were updated at 60 Hz. Stimuli were presented at medium to high photopic light amounts with average L/M-cone photoisomerization rates (R*) of ~1.5 × 10⁴ −5.0 × 10⁵ s⁻¹. Contrast values are given in Michaelson contrast. ‘Glider’ stimuli with distinct spatiotemporal correlations were generated as described in Jonathan Victor’s previous work^7,18. Recordings were performed for ~40 min in each cell to obtain the data needed for the information-theoretic analysis (37.8 ± 19.6 min; mean ± s.d.; n = 89 cells).

Mutual information calculations.

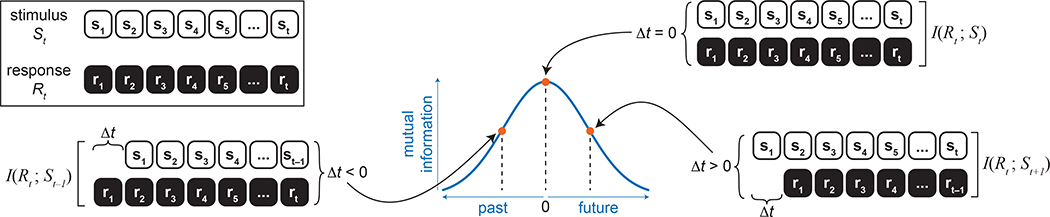
Mutual information quantifies how much knowing the response (R) of a neuron can reduce the uncertainty about a presented stimulus (S). Neural responses were binned at the stimulus presentation rate (update rate, 60 Hz; bin width, 16.7 ms) for all analyses with the exception of the data in Fig. 2, which were binned at 1 kHz (bin width, 1 ms). We estimated the amount of information that cellular responses at a particular time (r_t) provided about the stimulus at time, t′ (s_t′), where t′ = t +Δt using equation (1).

$$I\left(R_t;S_{t^{\prime }}\right)=\sum _{s_t{}^{\prime }\in S_t{}^{\prime }}\sum _{r_t\in R_t}P\left(s_{t^{\prime }},r_t\right){\log }_2\left[\frac{P\left(s_{t^{\prime }},r_t\right)}{P_R\left(r_t\right)P_S\left(s_{t^{\prime }}\right)}\right]$$ (1)

where P_R(r) is the distribution of responses in a single cell, P_S(s) is the stimulus distribution and $P\left(s_{t^{\prime }},r_t\right)$ is the joint distribution of stimuli presented at time t′ and responses r observed at time t. In other words, responses were fixed in time, the stimulus was shifted for each time bin between ±0.5 s and the mutual information was computed at each of these time shifts^{10,30,56–59}.

Response levels were determined by either counting the number of spikes occurring in a time bin (extracellular recordings) or distributing analog responses across six levels (current-clamp and voltage-clamp recordings). Varying the number of response levels between four and eight for the analog data did not noticeably affect the information computations, so we used a value near the center of that range. These mutual information calculations required converting the spatial dimensions of our stimuli into a single value for each time bin. We did this by first identifying the four spatial regions of the stimulus that were centered over the receptive field. Each of the 16 possible stimulus patterns for those four regions was assigned a value between 0 and 15.

To correct for inflation error in our mutual information calculations, stimulus and response data were subsampled randomly at fractions of 0.5–1.0. Information was calculated 50 times for each fraction and information was extrapolated for an infinite number of samples^10,60. Inflation error was estimated as the s.d. of the information calculated for data subsampled at a fraction of 0.5 divided by $\sqrt{2}$. An error value below 0.02 was a criterion for inclusion in our study and, in all cases, error values were <6 × 10⁻³ bits per spike (ref. ¹⁰).

On a conceptual level, the time-shifted mutual information analysis provides an important behavioral constraint on the efficient encoding of motion in the primate retina. As part of this work, we have carefully characterized the spatiotemporal correlations in the stimuli used in this study, such that we know precisely how these correlations influence our calculations (Figs. 1 and 3). We then use this knowledge to directly compute how these correlations can be used to infer the future stimulus trajectory (Figs. 4, 5 and 6).

Correlations in the neural response that are produced by stimulus correlations mean that the information values we report constitute a reasonable lower bound on the actual information encoded by these neurons. As mentioned above, the stimulus entropy is four bits for each time bin as the stimulus can take on 2⁴ (which equals 16) possible states with equal probability. Accounting for some of the temporal correlations by analyzing several time bins would greatly increase the number of states that the stimulus could take, increasing the stimulus entropy. If, for example, three time bins were used to account for a 50 ms window, the stimulus entropy would increase to 12 bits (2¹², which equals 4,096 possible states). Further, the information encoded by the neurons is likely to be redundant between successive time bins because of these stimulus correlations, and this redundancy in the neural responses would increase the mutual information. Thus, our information estimates for neural encoding of the spatiotemporal correlations are certainly an underestimate relative to the uncorrelated control stimulus.

However, the amount of data from each cell that is required to perform this analysis is prohibitive. For information-theoretic analyses to work properly, a good rule of thumb is to obtain at least ten times as many data samples as the number of states in the joint probability matrix $\left(P\left(s_{t^{\prime }},r_t\right)\right)$^10,60. For the four-bit stimulus example, the probability matrix would comprise 16 rows for the stimulus states and, in our recordings, at most eight columns for the possible response states (16 × 8). Our rule of thumb would then dictate that we obtain at least 1,280 samples, requiring about 21 s of recording time for each stimulus class—a very reasonable proposition. If, however, we used three neighboring time bins, the joint probability matrix would be 4,096 × 512 and we would need 20,971,520 samples or more than 242 days of continuous recording for each stimulus class from each cell, which is not physically possible in the lifespan of a typical experiment. Thus, a full treatment of the stimulus correlations was not possible.

Despite this, the relative information encoding at past and future time lags provided strong evidence of predictive encoding for some stimulus types. The correlation structure was identical between the different classes of spatiotemporal correlation (Fig. 3). Thus, if these correlations affected our calculations in a mysterious way that was not taken into account, these effects should be the same for all of our motion correlations. However, we observed very different time-dependent encoding behaviors for these stimuli—predictive encoding for some stimuli, but not for others (Figs. 3 and 4). Moreover, this asymmetry was not observed in horizontal cells, but emerged first in bipolar cells (Fig. 6). These findings lend further support to the premise that our calculations constitute a close approximation of the information encoded by the cells under study.

Information bottleneck calculations.

We used the information bottleneck method to determine the optimal encoding/compression schemes for the stimuli used in this study². The idea is that the past stimulus, S_past, can be compressed into a representation (Z) that retains sufficient information that can be used to estimate future motion trajectories (S_future). The optimal mapping between S_past and its compressed representation Z was determined by solving equation (2):

$$\underset{S_{\text{past}}\to Z}{\max }\left[I\left(Z;S_{\text{future}}\right)-\lambda I\left(Z;S_{\text{past}}\right)\right]$$ (2)

where the Lagrangian multiplier, λ, determines how much information is retained about the past stimulus. Varying the value of λ reflects different tradeoffs between representing the greatest possible amount of information about the future and producing a more compressed representation. Large values of λ exemplify the former case and, thus, poor representations of future information are strongly penalized. For small λ values, the goal is to achieve compression and we are, thus, more likely to ignore disparities in how Z represents future information⁵⁷.

Given the relatively low dimensionality of our stimuli (16 possible states on a single frame), solving equation (2) for each of the possible compression schemes was a computationally tractable problem. Thus, we computed I(Z; S_future) and I(Z; S_past) for every possible stimulus mapping in Z. This process was repeated for three future time lags of +17, +33 and +50 ms. Detailed methods for computing the bottleneck are given elsewhere^2,61. Briefly, the algorithm was initialized with Z ≡ S_past and Z was modified by merging different combinations of the 16 possible stimulus states. Mutual information I(Z; S_future) and I(Z; S_past) was calculated from the corresponding joint probability matrices, P(s_future, z) and P(s_past, z) for each of the possible mergings using equation (1).

Computing the temporal lag in visual processing.

We calculated the spatiotemporal receptive fields of our cells to estimate the temporal lag between the presentation of light stimuli at the level of the cone photoreceptors and the output of the retinal neurons in our study. Receptive fields were determined from the average stimulus preceding a spike⁶²:

$$F=\frac{1}{n_{\text{sp}}}{X}^{\top }R$$ (3)

where X is a matrix with the rows containing time samples and the columns containing the spatiotemporal sequence in the previous 0.5 s. R is a column vector containing the spike counts in the corresponding time bins of X and n_sp is the spike count. The time lag was then defined as the time bin at which the spatiotemporal filter (F) reached a maximum (On-type cells) or minimum (Off-type cells).

Stimulus autocorrelation calculations.

To confirm that the three-point motion stimuli lacked net two-point spatiotemporal correlations, we calculated the autocorrelation functions of these stimuli. Stimulus autocorrelation for a stimulus sequence, X, was determined by first subtracting the mean stimulus (μ) and then taking the outer product of the result with itself.

$$C_{XX}=(X-\mu ){(X-\mu )}^{\top }$$ (4)

where X is a matrix in which the rows are time points and the columns are the spatiotemporal sequence of contrasts occurring in the preceding second.

Low information rates for inhibitory synaptic inputs.

Our inhibitory synaptic recordings showed relatively modest time-shifted mutual information values for higher-order motion correlations, yet amacrine cells receive synaptic input directly from bipolar cells, and bipolar cell output showed sensitivity to these correlations (Fig. 6). This apparent discrepancy likely arose from the fact that parasol and smooth monostratified cells primarily receive inhibitory synaptic inputs from amacrine cells with the opposite contrast polarity. For example, an Off-type amacrine cell provides the dominant inhibitory synaptic inputs to On-type parasol ganglion cells^63,64. However, for our synaptic input recordings, we only recorded three-point correlations in which the contrast aligned with the preferred contrast polarity of the recorded ganglion cells. This ensured that we could obtain the large amount of data required for our analysis from each of the needed stimulus classes while also maintaining the stability of our whole-cell recordings.

We expect diverging and converging correlations that are opposite in polarity to the preferred contrast of the inhibitory amacrine cell will poorly drive predictive encoding. For example, three-point correlations that are positive contrasts would hyperpolarize Off-type bipolar cells such that the correlations contained in the stimulus would not exceed the threshold for synaptic release and would, thus, be discarded. Instead, these Off bipolar cells would depolarize most strongly at switches from positive to negative contrasts, similar to the response pattern expected for the uncorrelated stimuli. Such a response pattern would contain little information about the past motion trajectory of a positive-contrast stimulus. Indeed, this same pattern of relatively weak encoded information was observed in the ganglion cells to diverging and converging correlations that were of nonpreferred contrast polarity (Figs. 1 and 3). Thus, we expect that inhibitory inputs to stimuli aligned with the preferred contrast polarity of these amacrine cells would show a similar pattern to our excitatory synaptic input recordings.

Sensitivity index calculations.

We evaluated a cell’s ability to accurately detect a change in information using the sensitivity index (d′), which measures the amount of overlap between the information distributions in the original spike train and after shifting spike timing:

$$d^{\prime }=\frac{{\mu }_{\text{original}}-{\mu }_{\text{shifted}}}{\sqrt{\frac{1}{2}\left({\sigma }_{\text{original}}^2+{\sigma }_{\text{shifted}}^2\right)}}$$ (5)

where μ_original and μ_shifted are the mean of the original and shifted information distributions and ${\sigma }_{\text{original}}^2$ and ${\sigma }_{\text{shifted}}^2$ are the variances of those distributions, respectively. We defined an increase in discriminability (d′) of threshold of 5% as a significant degradation in information relative to the original spike train. The value of 5% was on the basis of the threshold originally proposed by Fisher that has become generally accepted in statistical analyses⁶⁵.

Computational model.

To understand the origins of predictive motion encoding in primate retina, we modeled the diffuse bipolar cells that provide excitatory synaptic input to parasol and smooth monostratified ganglion cells. A lattice of model bipolar cells was created with a mean spacing of 32 μm^66–68 and spatiotemporal filtering of stimulus inputs was based upon direct physiological measurements²⁴.

The stimulus (S) was convolved with each model bipolar cell’s spatiotemporal receptive field (F) to determine the cell’s response (R) before the output thresholding stage.

$$R(t)={\int }_0^t\text{d}\tau \int {\text{d}}^{2}xF(\mathbf{x},\tau )S(\mathbf{x},t-\tau )$$ (6)

where x is a vector of spatial contrast values and τ is the temporal shift. Noise in the bipolar responses was simulated by adding Poisson fluctuations to the resulting bipolar cell responses on the basis of our previous estimate of noise in the diffuse bipolar cells at photopic mean light amounts²².

Coupling between bipolar cells was also modeled according to previous measurements²² and using equation (7). The response of each bipolar cell following coupling was determined by adding the change due to coupling to the response before coupling (R₀).

$$R_i(t)=R_{0i}(t)+\left[\sum _{j=1}^{n}g\left(R_{0i}(t)-R_{0j}(t)\right)\exp \left(-d_{i,j}/\lambda \right)\right]$$ (7)

where g is the coupling gain or portion of the response shared between bipolar cells, λ is the coupling length constant, d_i,j is the pairwise Euclidean distance between the ith and jth cells and n is the total number of bipolar cells in the model.

Responses in the model bipolar cell network were then normalized, and output thresholding was then applied by setting values below the threshold equal to zero, and renormalizing the outputs between 0 and 1. A piecewise nonlinear function (that is, ReLU) was then applied to the thresholded responses:

$$R(t)=\{\begin{array}{ll}R(t),\hfill & \text{if}R(t)>0\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$$ (8)

Effect of spike timing on information encoding.

To ensure that this low tolerance for variation in spike timing was not a result of using a Gaussian distribution, we repeated this analysis using a Bernoulli distribution to shift spike timing. Each spike was shifted either forward or backward in time by a given value (±Δ) and mutual information was recomputed. The change in mutual information was then calculated as was done for the original analysis. The results of this analysis were similar to the analysis performed using a Gaussian distribution to jitter spike timing—information was degraded significantly when spikes were jittered by only 1–4 ms for all of the cell types and conditions (compare Fig. 2c and Extended Data Fig. 2b). This analysis further supports the premise that these neurons encode information on timescales much shorter than a single frame presentation.

We estimated the error in our information calculations using two independent methods. First, we randomly shuffled spike times for the full trace and computed the mutual information between the stimulus and shuffled responses. This was done 50 times for each cell and our error estimate was the average information calculated across these independent trials. We also estimated the error by calculating the mutual information between the correlated stimuli and the spike times obtained from the uncorrelated stimulus in the same cell. Again, the estimate of information error was obtained by taking the average of 50 different random combinations of the stimulus sequence and the uncorrelated spikes. Both of these techniques produced similarly low error rates of <0.05 bits s⁻¹ (Extended Data Fig. 2c).

Information calculations for local motion correlations.

We performed an alternative analysis to determine the time-shifted mutual information in our cells. For this analysis, the stimulus was collapsed to a single value in each time bin by directly computing the motion correlations as described previously⁶. Briefly, the strength of spatiotemporal correlations in each time bin C(t) was determined from the product of contrasts at points in space and time that corresponded to the space and time lags in the motion stimulus and subtracting the spatially reversed contrast values as described in equation (9) for three-point correlations⁶⁹.

$$\begin{gathered} C(t)=\sum _{i=1}^n[S\left(y_i,t-{\tau }_1\right)S\left(y_i,t-{\tau }_2\right)S\left(y_{i+1},t-{\tau }_3\right) \\ -S\left(y_{i+1},t-{\tau }_1\right)S\left(y_{i+1},t-{\tau }_2\right)S\left(y_i,t-{\tau }_3\right)] \end{gathered}$$ (9)

where τ_x represents the time shift associated with a spatial shift in the correlation⁶.

This approach did not provide a means to compare information in the motion stimuli to the uncorrelated control stimulus, so we did not use it as our primary information measure. However, the technique did serve as another demonstration that the cells under study show predictive encoding for triplet diverging motion correlations. Mutual information for diverging correlations was shifted to future time lags while converging correlations were shifted to time lags in the past (Extended Data Fig. 3). Further, this shift to past time lags was particularly prominent for the negative-contrast converging correlations (Extended Data Fig. 3, right).

Statistics and reproducibility.

Statistical methods were not used to predetermine sample sizes, but our sample sizes are similar to those reported in previous publications^24,25. The effects described in the work were consistent across cells and the sample sizes for all cells was sufficient to demonstrate repeatability of the effects described.

In each area of the tissue, contrast sensitivity was measured in parasol ganglion cells. A peak-to-trough spike rate of 25 spikes s⁻¹ to a 5% contrast modulation was required for inclusion of the parasol cells or surrounding cells in this study. No data were excluded from the present study.

Data randomization and blinding.

This study did not involve any traditional experimental groups. All experiments were performed from the same organisms and data were pulled randomly from a database without selection by investigators. This study did not involve traditional experimental groups that could be blinded. All data were pulled from a database and analyzed with the same code without selection. In this way, the investigators were blind to the measurements calculated in each cell type.

Analysis and statistics.

We performed all statistical analyses in MATLAB (v.R2020b, Mathworks). Mutual information calculations were written in C (Apple Clang v.12.0) and compiled and run in MATLAB. Final figures were created in MATLAB (v.R2020b), Igor Pro (v.8) and Adobe Illustrator (Creative Cloud, v.2021). All data are reported as the mean ± s.e.m. unless otherwise stated. Data were not assumed to be normally distributed and, thus, statistical significance was determined using the Wilcoxon signed rank test for paired samples and the Mann–Whitney U-test for unpaired samples. To determine whether information encoding varied significantly as a function of time relative to stimulus onset, the Kruskal–Wallis test was used.

Reporting Summary.

Further information on research design is available in the Nature Research Reporting Summary linked to this article.

Extended Data

Extended Data Fig. 1 |. Overview of time-shifted mutual information calculations.

To quantify the amount of information that a neuron’s response at a particular time (R_t) contained about the past and future stimulus trajectory (S_t+Δt), we computed the time-shifted mutual information. The stimulus sequence was shifted relative to the response and mutual information was computed between the stimulus and response for each time shift (Δt). This was done for time shifts between ± 0.5 seconds.

Extended Data Fig. 2 |. Information encoding occurs on short timescales.

a, Example spike train for a one-second portion of a stimulus containing diverging positive correlations (top). To measure the relationship between spike timing and information transmission, each spike was randomly shifted forward or backward in time (±Δ, bottom). The process was repeated for each spike train in each cell at several time shifts (0–100 ms). b, Spike timing shift at which the sensitivity index increased by 5% relative to the condition with spike time unaltered (Δ, 0 ms). Data are shown across six stimulus conditions and six ganglion cell types. Number of cells in the population are indicated in parentheses. c, Error in information estimates determined by randomly shuffling spike times (open circles) or by using the spike times from the uncorrelated traces in the same cell (closed circles). Error estimates were not significantly different between these techniques (p-value: two-positive, 0.40; two-negative, 0.78; diverging positive, 0.11; converging positive, 0.34; diverging negative, 0.47; converging negative, 0.78; two-sided Wilcoxon signed rank test; n = 73 cells). Circles and error bars indicate mean ± SEM.

Extended Data Fig. 3 |. Local motion signals show temporally shifted profiles.

Local motion signals show temporally shifted profiles. Third-order spatiotemporal correlations were extracted directly from stimulus sequences. The time-shifted mutual information profile for diverging correlations showed shifts toward future time points, whereas converging information was shifted toward past time lags.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.