Abstract
We here propose an analysis pipeline for inferring the distribution of fitness effects (DFE) from either patient-sampled or experimentally-evolved viral populations, that explicitly accounts for non-Wright-Fisher and non-equilibrium population dynamics inherent to pathogens. We examine the performance of this approach via extensive power and performance analyses, and highlight two illustrative applications - one from an experimentally-passaged RNA virus, and the other from a clinically-sampled DNA virus. Finally, we discuss how such DFE inference may shed light on major research questions in virus evolution, ranging from a quantification of the population genetic processes governing genome size, to the role of Hill-Robertson interference in dictating adaptive outcomes, to the potential design of novel therapeutic approaches to eradicate within-patient viral populations via induced mutational meltdown.
Subject terms: Population genetics, Evolutionary genetics
Introduction
Characterizing the underlying demographic histories and selective pressures shaping the evolutionary trajectories of both extant and extinct species is a focal point of population genetics. When the organism in question is a virus, this demographic history will include the infection (and, when applicable, compartmentalization) dynamics of within-host populations (Jensen 2021). With regards to selection, a major focus of the human pathogen literature is on positive selection, be it identifying mutations conferring drug resistance or underlying immune-evasion (see review of Irwin et al. 2016a). However, despite receiving less attention in this literature, it is well-understood that regardless of the organism in question, most new fitness-impacting mutations have deleterious effects (e.g., Crow 1993; Lynch et al. 1999; Bank et al. 2014b; and see reviews of Eyre-Walker and Keightley 2007; Bank et al. 2014a). The removal of these deleterious mutations via purifying selection is expected to reduce the effective population size to an extent largely dictated both by recombination rates and the strength of selection (Charlesworth et al. 1993; Charlesworth 2013; and see review of Charlesworth and Jensen 2021). Furthermore, linkage to this abundant input of deleterious mutations may impact the fixation probabilities of alleles at other genomic sites, including reducing the likelihood of adaptive fixations (Hill and Robertson 1966; Pénisson et al. 2017).
Yet, in order to quantify how deleterious mutations impact the evolutionary trajectory of a population, it is necessary to understand the shape of the distribution of fitness effects (DFE) of new mutations entering the population (i.e., the selective effects characterizing newly arising mutants). Herein lies a challenge, as the accurate estimation of the DFE is a difficult task. There are three general approaches for such inference. The most direct is achieved via site-directed mutagenesis - measuring the fitness effect, one at a time or in combination, of an artificially created mutation(s) on an otherwise wildtype background under set environmental conditions (e.g., Fowler et al. 2010; Hietpas et al. 2011, 2012; Bank et al. 2014b). As this method is experimentally demanding, the DFE can generally only be obtained for a highly localized genomic region, and the approach is only feasible in certain experimentally tractable organisms. In order to characterize genome-wide effects, mutation accumulation (MA) studies are also used to experimentally infer the DFE. By allowing mutations to accumulate over time - generally under minimal selection - the fitness of the resulting lines can be compared allowing for inference of underlying selective effects (e.g., Lynch et al. 2016; Long et al. 2018). As opposed to the directed-mutagenesis approach, MA lines may obtain poor inference of the most strongly deleterious classes of mutations, as they would not be expected to segregate in the population. Relatedly, by directly tracking individual allele frequencies over time in these experimental lines, selective effects may be inferred based on observed per-generation allele frequency changes; namely, by first determining if the extent of change is consistent with genetic drift alone, and, if not, fitting a selection coefficient to match the degree of change (e.g., Foll et al. 2014; Ferrer-Admetlla et al. 2016).
While these experimental approaches have provided major insights into the general shape of the DFE, they are naturally restricted to laboratory settings. As such, a final class of methods has been developed to estimate the DFE from natural population polymorphism data - both for common single time-point (e.g., Keightley and Eyre-Walker 2007; Schneider et al. 2011; Tataru et al. 2017) as well as for time-sampled data (e.g., Malaspinas et al. 2012; Mathieson and McVean 2013; Acevedo et al. 2014; Foll et al. 2015; Sohail et al. 2021). The earliest class of approach relies on synonymous sites in coding regions to estimate the demographic effects, and conditional on that inferred history, a DFE is fit to the observed data from non-synonymous sites. As such, these methods rely on the neutrality of the former, which has been called into question in many organisms (e.g., Chamary and Hurst 2005; Zeng and Charlesworth 2010; Lawrie et al. 2013; Choi and Aquadro 2016; Jackson et al. 2017), including in viruses (e.g., Canale et al. 2018). Equally importantly, these methods neglect the fact that levels and patterns of variation at synonymous sites may be shaped by their linkage to directly selected non-synonymous sites - this neglect of these background selection effects may result in serious mis-inference of the demographic history (Zeng 2013; Ewing and Jensen 2016). In order to account for these factors, more recent methods have been developed to jointly infer the demographic history simultaneously with the underlying DFE, without making assumptions about the selective effects of any particular class of sites. For example, the approximate Bayesian (ABC) approach recently proposed by Johri et al. (2020) was shown to obtain accurate DFE inference using single time-point datasets, while uniquely accounting for the effects of background selection and the potential non-neutrality of synonymous sites (and see Johri et al. 2021). Importantly, background selection expectations are themselves incorporated into the inference procedure; as such, the full DFE of newly arising mutations is estimated, even if, for example, the strongly deleterious mutations comprising the most deleterious class are not themselves sampled as polymorphic sites.
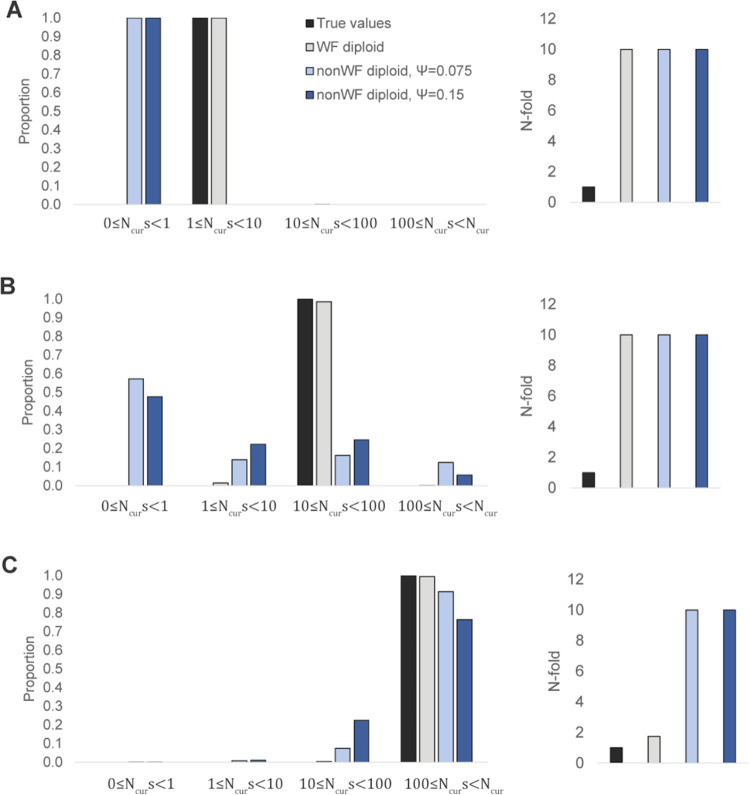
With such estimators now at hand - which have previously only been applied to model organisms (e.g., Drosophila melanogaster) - we here examine the utility of these DFE inference procedures for the study of viruses. In order to do so, we have modified the framework of Johri et al. (2020) to account for the violation of common Wright-Fisher assumptions inherent to viruses - namely, highly skewed progeny distributions (Irwin et al. 2016b; Matuszewski et al. 2018; Sackman et al. 2019; and see Vahey and Fletcher 2019). Owing both to the reduction in effective population size (increasing the effects of genetic drift / decreasing the efficacy of selection) as well as changing expectations in the shape of the site frequency spectrum, such progeny skew is known to result in potential mis-inference of both the DFE and demography. For the sake of illustration, Fig. 1 presents the results of a commonly used estimator of the DFE together with population size change (DFE-alpha; Keightley and Eyre-Walker 2007) - an approach designed neither to account for background selection effects nor skewed progeny distributions - when applied to populations characterized by differing levels of progeny skew. As shown, in the absence of a violation of progeny distribution assumptions, DFE inference is correct, but the inference of population size is incorrect. Namely, and consistent with previous results, population growth is inferred for these constant-sized populations, owing to the left-skewed frequency spectra being generated by the unaccounted for background selection effects (Ewing and Jensen 2016; Johri et al. 2021). With the addition of progeny skew, DFE inference also becomes incorrect for the weakly and moderately deleterious classes, with a bias towards under-estimation owing to the increased effects of genetic drift under these models. For the strongly deleterious class, inference remains largely accurate, as purifying selection is sufficiently strong relative to genetic drift.
Fig. 1. Effects of progeny-skew and background selection on the inference of demography and the DFE, using the DFE-alpha approach (Keightley and Eyre-Walker 2007).
The left panels show the inference of the DFE while the right panels show the inference of fold-change in population size. Inference is shown when 30% of new mutations are neutral, and the remainder are: (A) weakly deleterious, (B) moderately deleterious, and (C) strongly deleterious. Estimates are shown only for the selected classes. Black bars depict true values, gray bars show inference in the absence of progeny skew (thus no violation of the assumption), and the blue bars correspond to populations with levels of progeny skew characterized by ψ = 0.075 (light blue) and ψ = 0.15 (dark blue).
To provide examples of how DFE inference may be more accurately performed in organisms characterized by progeny skew - as well as to highlight the generality of the approach - we present estimates, together with the necessary power analyses, for two viruses of critical public health concern: a patient-sampled DNA virus (human cytomegalovirus (HCMV)), and an experimentally-passaged RNA virus (influenza A virus (IAV)). Finally, we discuss how inferred DFEs may be utilized to generate appropriate null expectations, against which patterns of positive selection (e.g., resistance evolution) may be better characterized, as well as how these estimates may be leveraged in the design of novel therapeutics.
Methods
Data
Influenza A virus (IAV)
Published control line data was taken from Renzette et al. (2014) and Foll et al. (2014). In brief, viruses were serially passaged in MDCK cells, with a multiplicity of infection (MOI) of 0.01 for the initial infection. Viral titers were determined by plaque assay per passage in order to maintain a constant MOI. Here we analyzed 13 passages in total in which high-throughput Illumina sequencing was performed. For each control replicate analyzed, we down-sampled all sites to a coverage of 1000 for the calculation of per-site allele frequencies, only bi-allelic SNPs were retained, and only SNPs >2% frequency were considered in order to eliminate false-inference owing to sequencing errors. For the PB2 segment chosen, a mean of 518 SNPs was observed across control line replicates, with a minimum of 48 and maximum of 980 SNPs after filtering.
Human cytomegalovirus (HCMV)
Published patient data (patient_B103) was taken from Renzette et al. (2013). In brief, serial specimens were collected from HCMV-infected patients at the University of Minnesota Medical Center or the University of Massachusetts Memorial Health Center, amplification was performed and quantified, and whole genomes were sequenced on Illumina technology. For this study, we chose the urine sample collected at 6-months post-birth from a congenitally infected infant. We aligned the sequence reads from the sample to the Merlin strain reference genome (Ref Seq ID: NC_006273). Whole-genome alignments were generated using the Burrows Wheeler Aligner v.0.7.17 mem algorithm (Li and Durbin 2009). Reads were sorted using SAMtools v.1.9 (Li et al. 2009), and duplicates were marked using sambamba v. 0.7.1 (Tarasov et al. 2015). Based on the genomic scan of Renzette et al. (2013), we chose a genomic region with little evidence of positive selection. Namely, we considered nucleotide positions 62,500–86,000 (23,500 nucleotides length) representing a 10th portion of the total genome size.
We used Freebayes v.1.3.2-dirty (Garrison and Marth 2012) for variant calling. SNP calls were only made if the mapping quality of the read was ≥30 and the Phred score for base quality ≥20. Further, we required that each SNP was supported with no fewer than one read for each sequencing direction. We discarded SNPs for which we detected evidence for strand bias in the supporting reads, down-sampled all sites to 100 in order to estimate allele frequencies from allele counts, and only SNPs with frequencies ≥2% were considered. This filtering resulted in 449 SNPs for the region analyzed.
Simulations
We conducted forward-in-time simulations using the SLIM version 3 software package (Haller and Messer 2019). DFE estimation was based on Johri et al. (2020), with an extension to account for skewed progeny distributions. Functional genomic elements of 2314 bp and 23500 bp, for IAV and HCMV respectively, were simulated under a variety of discrete DFEs comprising four fixed bins representing effectively neutral (0≤|2Nes|<1; referred to as f0), weakly deleterious (1≤|2Nes|<10; referred to as f1), moderately deleterious (10≤|2Nes|<100; referred to as f2) and strongly deleterious/lethal mutations (100≤|2Nes|≤2Ne; referred to as f3). Ne was assumed to be 176 for the experimentally passaged IAV data as previously estimated by Foll et al. (2014), based on time-sampled neutral allele frequency change. For HCMV, we used the inferred size of 104 haploid individuals for the purpose of scaling selection coefficients (Renzette et al. 2013). Selection coefficients were sampled uniformly within each bin of the DFE, and the shape of the DFE was proportionally varied by each class of mutation (f0, f1, f2, f3), such that Σi fi = 1. In order to perform ABC, fi were sampled uniformly such that f0 ∈ [0, 1], f1 ∈ [0, 1 − f0] and f2 ∈ [0, 1 − f0 − f1].
IAV simulations
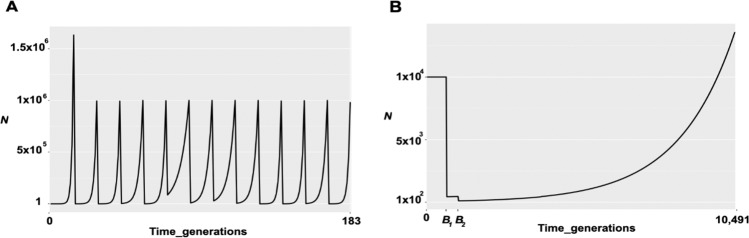
We simulated a population that grew from a single virion to N = 1 × 106 and then experienced twelve population bottlenecks that varied in intensity, corresponding to the experimental passaging as described in Table 1 of Foll et al. (2014). After each bottleneck, the population grew exponentially, reaching a size of 106 in 13 generations. Given that this was an experimental population, these demographic details are well-characterized. In total, the full 183 generations of the experiment were simulated (Fig. 2A). A constant progeny skew value of (ψ) = 6.7% every generation was imposed, as previously estimated by Sackman et al. (2019).
Fig. 2. Graphical representation of the demographic models of IAV and HCMV.
A IAV: in which the population size changes correspond to the experimental passaging. B HCMV: in which the size changes correspond to the initial infection and subsequent compartmentalization.
As previous experiments measured the neutral mutation rate (e.g., Sanjuán et al. 2010), rather than the total mutation rate (that is, including the range of newly arising deleterious mutations), we first simulated 200 different parameter combinations of f0, f1, f2, and f3, for mutation rates of 1 × 10−5, 1 × 10−4 and 1 × 10−3. As 1 × 10−3 was most consistent with the observed statistics, this total rate was fixed for subsequent analysis (Supplementary Table 1). Drawing from these prior distributions, 500 points (i.e., parameter combinations) were sampled. For each parameter combination, we conducted 100 replicates in order to characterize both the mean and variance of summary statistics. In order to match the empirical data, 1000 individuals were sampled, and alleles >2% frequency were considered in the simulated data.
HCMV simulations
Following an initial burn-in period of 10 N generations, we considered a four-stage demographic model characterizing a single patient infection, following Renzette et al. (2013) and Pokalyuk et al. (2017): (1) a neutral equilibrium ancestral population of size N, (2) an initial infection bottleneck (B1) from the mother to the plasma of the fetus, leading to an instantaneous population reduction to size N2, (3) a subsequent population size recovery to size N and, (4) a final bottleneck (B2) representing infection from the plasma into the urine compartment, leading to a second reduction to size N3, followed by population size recovery to the initial N (Fig. 2B). As previously inferred, N = 1 × 104, N2 = 433, and N3 = 100. A recombination rate of 1 × 10−7/site/generation (Renzette et al. 2015) and ψ = 6.7% (Sackman et al. 2019) were assumed. Based on the previous estimate of the neutral mutation rate from segregating variation of 2 × 10−7/site/generation (Renzette et al. 2015), simulations were conducted spanning total mutation rates of 1 × 10−7, 1 × 10−6, and 1 × 10−5/site/ generation, in order to infer the total rate that matched the observed data (Supplementary Table 2). Using the best matching 1 × 10−5, 500 replicates were simulated for each DFE draw. In order to mirror the empirical data, 100 individuals were sampled, and alleles >2% frequency were considered for downstream power and performance analyses. Importantly, by simulating data that matches the empirical sampling, we can directly account for the differences in inference power attained in the down-sampled read-depth of 100 in HCMV, relative to that of 1000 in IAV.
DFE-alpha, and an evaluation of the effects of unaccounted for background selection and progeny skew
Inference was performed using DFE-alpha 2.16 (Keightley and Eyre-Walker 2007) using the folded and pooled site frequency spectrum (SFS). Under this approach, the SFS of segregating neutral mutations was used to infer the demographic history (2-epoch size change), and the SFS at directly selected sites was used to infer the DFE conditional on that inferred history. For the first step, both the current population size and the time of change (with an initial value of 50 generations) were allowed to vary. When inferring the DFE, the initial value of mean s and β were assumed to be −0.1 and 0.5 respectively, where s is the selection coefficient and β is the shape parameter of the assumed gamma distribution of s. The inferred DFE was scaled with respect to the current population size (N2 in DFE-alpha).
The approach was evaluated by simulating N = 10,000 diploid individuals in SLiM 3.1 (Haller and Messer 2019) under constant population size, with mutation rate = 1 × 10−5 per site/generation and the recombination rate = 1 × 10−8 per site/generation. A 10 kb region was simulated with 30% of all mutations being neutral (i.e., s = 0), and the remainder of the sites experiencing three different deleterious DFEs: (a) a uniform distribution between 1 ≤ Ns < 10 (weakly deleterious); (b) a uniform distribution between 10 ≤ Ns < 100 (moderately deleterious); and (c) a uniform distribution between 100 ≤ Ns < N (strongly deleterious). Simulations were run for 10N generations and 50 diploid individuals were sampled with 10 replicates for each evolutionary scenario. In order to test the effect of progeny-skew on DFE inference, populations with ψ = 0.075 and ψ = 0.15 were also simulated.
Calculation of summary statistics and ABC
For the entire genomic elements simulated, the mean and variance of the following statistics were calculated: number of segregating sites (S), nucleotide site diversity (π), Watterson’s θ, Tajima’s D, and Fay and Wu’s H (both absolute and normalized), using the Python package pylibseq 0.2.3 (Thornton 2003). While all summary statistics were used for inference in IAV, HCMV inference was only based on a subset of statistics (S, π, Watterson’s θ, Tajima’s D), owing to the lack of information needed to unfold the SFS. ABC inference was performed using the “abc” package in R (Csillery et al. 2012) When a large number of summary statistics are used, it can be difficult to find sufficient number of simulations that match the observed data and thus ABC methods suffer from the curse of dimensionality. In order to deal with this issue, one can use larger acceptance rates and then perform linear local adjustment to correct for the discrepancy between the simulated and observed summary statistics by weighting the accepted simulations accordingly. In the “abc” package, this discrepancy can be accounted for by using ridge regression (that assumes a linear relationship between the parameters and statistics) or by using neural nets (that can account for non-linear relationships between the parameters and statistics) which can also reduce the dimensionality, and thus deal with multicollinearity (i.e., highly correlated statistics). Neural net was used to perform inference in IAV, owing to superior performance over ridge regression in this parameter space. Conversely, for the HCMV parameter space, ridge regression performed better (e.g., absolute error in performance of ABC using ridge regression vs neural net was 0.137 vs 0.157 for f0; 0.155 vs 0.176 for f1; 0.047 vs 0.044 for f2; and 0.031 vs 0.026 for f3 respectively). A 50-fold cross-validation procedure was employed to choose the appropriate tolerance levels, such that 1 randomly chosen simulation was excluded and its parameters were inferred using n−1 simulations, where n is the total number of simulations. A tolerance of 0.05, and weighted medians of the posterior distribution, were used to determine point estimates of the inferred parameters.
Results
The DFE of newly arising mutations was inferred from experimental populations of a reassorting RNA virus (IAV), as well as from a patient-population of a recombining DNA virus (HCMV). The DFE was modeled as a discrete distribution with four fixed bins - the effectively neutral, mildly deleterious, moderately deleterious, and strongly deleterious classes of mutation (see Methods). By varying the proportion of each class of mutations referred to as f0, f1, f2, and f3, respectively, all possible DFE shapes could be considered for their respective fit to the observed data. In addition, the history of population size change, and progeny skew, was directly and uniquely accounted for in this inference scheme. As both of these neutral processes additionally act to shape levels and patterns of variation, their frequent neglect in such analyses has been shown to lead to a serious mis-inference of the contribution of selection (e.g., Teshima et al. 2006; Thornton and Jensen 2007; Mathew and Jensen 2015; Harris et al. 2018; Sackman et al. 2019, and see Jensen et al. 2019).
Inference of the DFE in IAV
The genome of IAV is composed of eight segments (for a total length of ~13 kb) that can be exchanged by reassortment (Palese and Young 1982; Dadonaite et al. 2019). From an infected cell, IAV progeny release occurs every ~6 h and previous estimates suggest a mutation rate of 2.3 × 10−5 per site/cell infection cycle (Parvin et al. 1986; Sanjuán et al. 2010; Abdoli et al. 2013). Though the IAV population in question has a large census size (N), the effective population size (Ne) has been inferred to be only on the order of 103 (Foll et al. 2014, 2015; and see Poon et al. 2016) - a disparity that likely owes to a combination of factors including strong purifying and positive selection, severe bottlenecks, as well as progeny skew. This observation is consistent with the general notion that Ne is much more strongly constrained than N across organisms, suggesting an upper-bound to the efficacy of natural selection (Lynch 2007; Lynch and Trickovic 2020).
In order to directly compare results with the time-sampled approaches of Foll et al. (2014) and Ferrer-Admetlla et al. (2016), we utilized the same experimentally passaged dataset (see Methods). As we here focused on characterizing the neutral and deleterious DFE distribution, we sought to minimize the effects of positive selection. As such, we used the control lines from each experiment (that is, passaged in the absence of drug treatment), as well as the PB2 segment (2,314nt in length) as scant evidence of positive selection has been observed in this region (Renzette et al. 2014; Foll et al. 2014). Given that the populations under consideration in IAV were of oscillating size owing to experimental passaging (Fig. 2A), it was first necessary to assess the performance of the statistical inference scheme under this rather unique demographic history. Helpfully, the census population sizes at each passage are known experimentally, allowing many aspects of this model to be fixed when performing inference.
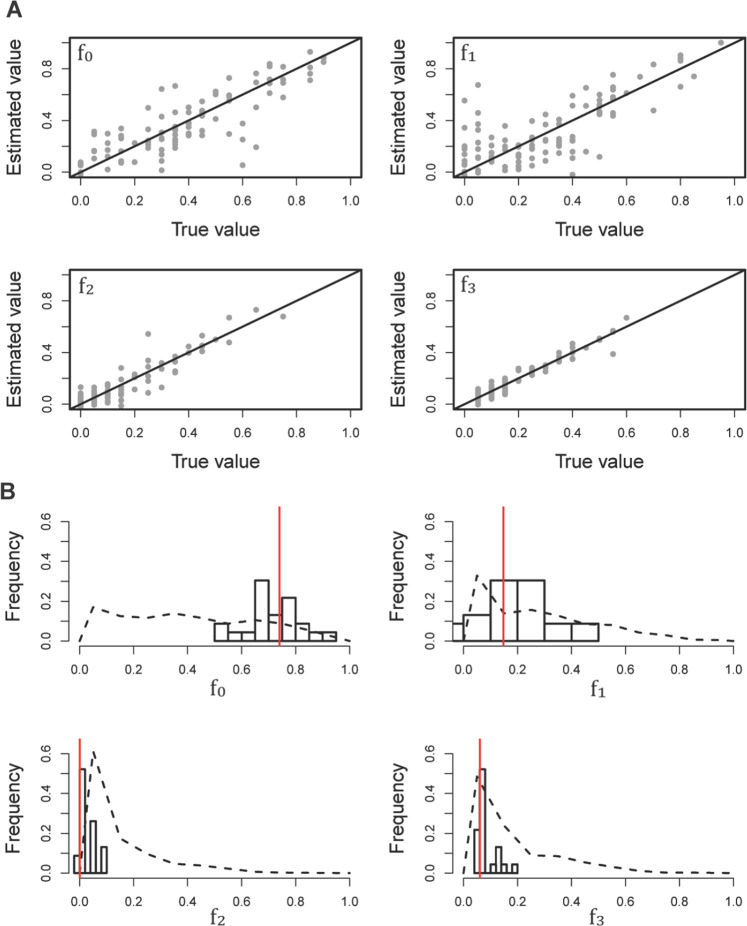
In addition, the degree of progeny skew (ψ) has been previously inferred to be ~7% (Sackman et al. 2019), and was here treated as a fixed parameter. This skew is expected to result in an excess of both rare as well as high-frequency alleles relative to the standard Wright-Fisher expectation, resulting in a U-shaped frequency spectrum (Eldon and Wakeley 2006; Eldon et al. 2015; Blath et al. 2016; Matuszewski et al. 2018). As purifying selection is also expected to result in a higher proportion of rare alleles, inferring an accurate DFE could therefore be challenging under this model. However, this combination of summary statistics was found to enable reasonably accurate inference of all four parameters of the DFE (f0, f1, f2, and f3; Fig. 3A). Moderately and strongly deleterious mutations were estimated with the highest accuracy with mean absolute errors of 0.037 and 0.028, respectively, while the proportion of mildly deleterious and neutral mutations were associated with the largest variance (absolute errors of 0.107 and 0.093, respectively).
Fig. 3. Inference of the DFE in the IAV population.
A Power and performance analyses concerning the inference of the DFE in an oscillating population size model mirroring that of the experimental IAV populations in question. The black diagonal lines represent the points at which estimated parameters match their true values, where f0 is the proportion of new mutations in the neutral class, f1 is the proportion of the weakly deleterious class, f2 is the proportion of the moderately deleterious class, and f3 is proportion of the strongly deleterious/lethal class. B Posterior estimates of the parameters of the DFE in an experimental population of IAV. Dashed lines indicate the distribution of sampled priors, the histograms present the posterior distribution, and the red vertical lines show the point estimates calculated as the weighted median.
With this statistical performance quantified under the appropriate demographic model, we evaluated the experimental data. Thirteen experimental replicate lines were used to obtain means and standard deviations of all statistics utilized in the ABC method. In order to first fit an accurate total mutation rate (that is, including strongly deleterious mutations not observed in MA lines, and not expected to have contributed to divergence as measured by phylogenetic estimates), we simulated a range of mutation rates. We found the that the summary statistics obtained from simulations on the order of 10−3 per site/generation to be highly consistent with the observed data (see Supplementary Table 1).
Using this inferred mutation rate, the estimated DFE is characterized by a strong skew towards the neutral class of mutations, with f0 = 0.78, f1 = 0.16, f2 ~ 0, and f3 = 0.06 (Fig. 3B). These estimates are similar to the DFE inferred using an alternative Markov model-based approach (Ferrer-Admetlla et al. 2016), and the general bi-modal shape of the DFE is also consistent with the mutational effects estimated by Visher et al. (2016) using genome-wide data. Though it may at first seem peculiar that more than 90% of mutations are inferred to be neutral or weakly deleterious, and that only ~6% of mutations are strongly deleterious, it is worth reiterating that this analysis is based on control lines without any selective challenge. Further, the segment analyzed (PB2), which is thought to play a primary role in the genome packing process (Muramoto et al. 2006), was chosen as it appeared to be evolving in a relatively neutral manner. As such, this inferred DFE likely reflects largely biophysical constraints on potential amino acid changes (see Discussion). For example, the whole-genome DFE inferred by Visher et al. (2016) referenced above estimated greater density in the strongly deleterious class, likely owing in part to the inclusion of more strongly constrained segments across the genome, as well as their directed mutagenesis approach (as opposed to the mutation-accumulation data considered here).
Inference of the DFE in HCMV
HCMV is a linear DNA virus with a genome size nearly 20x that of IAV (~236 kb; Dolan et al. 2004). HCMV presents a high level of genetic diversity relative to other DNA viruses (Renzette et al. 2011, 2015; and see Sackman et al. 2018; Jensen and Kowalik 2020), despite a slowly replicating process of ~24 h that includes encoding a polymerase with proofreading capacity (Nishiyama et al. 1983). Additionally, HCMV compartmentalizes within a host, and diversifies strongly between compartments (Renzette et al. 2013). Furthermore, previous studies have suggested important roles of both purifying and background selection, as well as episodic positive selection, in shaping HCMV genetic diversity (Renzette et al. 2016, 2017; Hage et al. 2017).
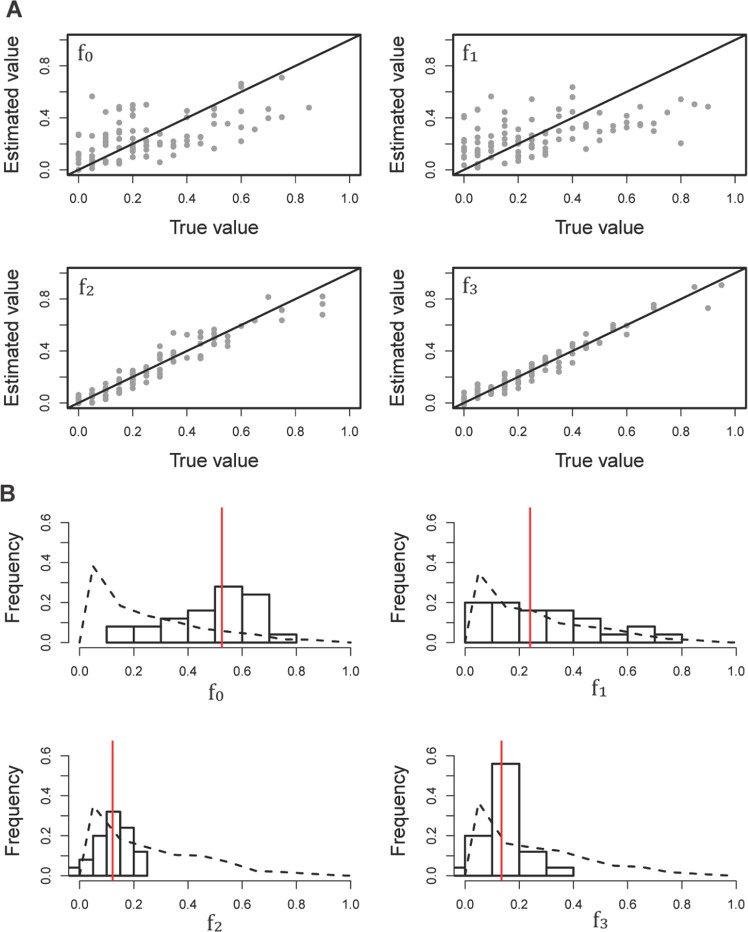
The genetic data available from HCMV represents a within-patient population sample collected from the urine of a congenitally infected infant (see Methods). The population has previously been inferred to have experienced multiple bottlenecks - corresponding to the initial infection and subsequent compartmentalization (Renzette et al. 2011, 2013). As such, it was again necessary to evaluate whether the DFE could be accurately inferred under such a complex demographic history. The specific demographic history (Fig. 2B) inferred by Renzette et al. (2011) was fixed for HCMV, while the four parameters of the DFE were varied in order to perform power and performance simulations within the ABC framework. Under this demographic model, HCMV populations experience extremely rapid recent growth post-infection, which is expected to result in a strong excess of rare alleles, potentially mimicking the effects of purifying selection. As observed in our cross-validation (Fig. 4A), our estimate of the proportion of strongly (absolute error: 0.030) and moderately (absolute error: 0.047) deleterious mutations is quite accurate, however the method performs less accurately when distinguishing between neutral (absolute error: 0.138) and mildly deleterious mutations (absolute error: 0.151), likely owing to this conflation of processes contributing to rare alleles.
Fig. 4. Inference of the DFE in the HCMV population.
A Power and performance analyses concerning the inference of the DFE under an infection scenario mirroring that previously inferred for the HCMV population in question. The black diagonal lines represent the points at which estimated parameters match their true values, in which f0 is the proportion of new mutations in the neutral class, f1 is the proportion of the weakly deleterious class, f2 is the proportion of the moderately deleterious class, and f3 is the proportion of the strongly deleterious/lethal class. B Posterior estimates of the parameters of the DFE in a patient population of HCMV. Dashed lines indicate the distribution of sampled priors, the histograms present the posterior distributions, and the red vertical lines show the point estimates defined as the weighted median.
Turning to the empirical data, a total mutation rate of 1 × 10−5 provided a good match of the simulated summary statistics to the observed data (Supplementary Table 2), and was thus fixed in subsequent inference. We inferred the four parameters corresponding to the DFE of new mutations in HCMV to be f0 = 0.51, f1 = 0.24, f2 = 0.12, and f3 = 0.13 (Fig. 4B). It should be noted that because our method has less accuracy under this demographic model for estimating f0 and f1, the underlying posterior distributions are fairly broad. However, inference confidently suggests that ~70% of all new mutations are neutral or weakly deleterious, with the remaining being moderately and strongly deleterious.
Discussion
We here provide an example of estimating the DFE from both patient-sampled as well as passaged viral populations, using a commonly studied RNA (IAV) and DNA (HCMV) virus for the purposes of illustration. To do so, we suggest a modification of the joint approximate Bayesian estimator of Johri et al. (2020) in order to account for the non-Wright-Fisher replication dynamics of viruses. It should be noted that there are currently no standard methods for inferring the DFE for such populations; thus, although our proposed method assumed a fixed measure of progeny skew, it is nonetheless a first step towards incorporating such life history traits of microbial organisms. As the inference of selection may be strongly confounded by demography, we conducted performance analyses under the strongly non-equilibrium experimental (IAV) and infection (HCMV) histories known for these samples, thereby quantifying uncertainty in the resulting DFE estimates. These two examples indicate the broader applicability of this framework for the study of pathogen evolution.
The DFE estimates provided by this analysis speak to a number of points of evolutionary interest. Firstly, estimates suggest that ~90% of new mutations in the PB2 segment of the experimental IAV population are neutral or weakly deleterious. This large fraction probably partly owes to the fact that inference was performed on control populations evolved in the absence of any experimental challenge, and that the segment itself was chosen for its lack of evidence of strongly selected sites in earlier studies. As such, the fraction of strongly deleterious sites inferred likely represents a biophysical/biochemical constraint on potential amino acid changes (e.g., Shakhnovich 2006; Zeldovich et al. 2007). For comparison, in the patient population of HCMV - in which the population is, at a minimum, exposed to immune pressures - the fraction of neutral and weakly deleterious sites was estimated at 70%, with nearly a third of all mutations in the genomic region under study being inferred to experience strong purifying selection. Accounting for this full DFE, as well as the diversity-reducing effects of progeny skew, also suggests somewhat faster mutation rates than have been estimated using phylogenetic approaches or MA lines - both of which will disproportionately measure neutral mutation rates at the neglect of strongly deleterious rates.
Secondly, inter-virus comparisons of this sort will allow for a consideration of the effects, and evolution, of recombination and mutation rates themselves. For example, as HCMV frequently recombines (Renzette et al. 2016), while IAV rather reassorts between segments, Hill-Robertson effects (Hill and Robertson 1966; and see Muller 1964; Felsenstein 1974) may be expected to differ substantially between these two example viruses. Specifically, as recombination breaks up linkage effects allowing natural selection to more efficiently purge deleterious variants, HCMV might be expected to better tolerate a higher deleterious input (as here inferred, and see Lynch et al. 1995; Charlesworth and Charlesworth 1998).
Thirdly, these comparisons also allow for an examination of genome size determinants, which itself tends to scale inversely with mutation rate (e.g., Drake 1991; Lynch 2010; and see Gago et al. 2009; Bradwell et al. 2013). In our examples, the per-site mutation rate in the smaller IAV genome (~13 kb) is expected to be larger than HCMV (~236 kb), as has long been known. Specifically, given that selection acts on the genome-wide input of deleterious variants (Kimura 1967), the smaller IAV genome would be expected to survive a higher per-site input than the larger HCMV genome. Notably, given the DFE and mutation rates estimated here, as well as the genome sizes, the expected per-replication deleterious mutational input of moderately and strongly deleterious variants is roughly similar between the two viruses (on the order of 1-2 deleterious mutations per genome/replication). However, owing to multiple differences in polymerase and proof-reading activity amongst viruses, accumulating larger numbers of examples will be important in order to determine the generality of this genome-wide input.
Finally, the underlying shape of the DFE has important clinical implications as well. This particularly relates to the concept of mutational meltdown (Lynch and Gabriel 1990; Gabriel et al. 1993; Lynch et al. 1993), the ability to induce it in viral populations (e.g., Lynch et al. 1995; Bank et al. 2016; Jensen et al. 2020), and the specific outcome of lethal mutagenesis (e.g., Crotty et al. 2001; Bull et al. 2007; Wylie and Shakhnovich 2012; and see review of Matuszewski et al. 2017). In short, high mutation rates can overwhelm the ability of natural selection to purge deleterious variants, even in large recombining populations, and this increasing deleterious load can result in a snowball effect leading towards ultimate extinction. This transition to mutation-driven rather than genetic drift-driven meltdown occurs when the deleterious mutation rate is ~1 per individual per generation (Lynch et al. 1993) - similar to the numbers for IAV and HCMV reported here. However, the shape of the underlying DFE is critical in understanding the likelihood of meltdown, the required therapeutic increase in mutation rates necessary to induce it, and the expected time to within-host viral extinction. Promisingly, and further supporting the result that IAV and HCMV may reside near a mutational boundary - hence making them particularly susceptible to therapeutic meltdown - recent results have demonstrated that experimentally increasing mutation rates in IAV using the mutation-inducing drug favipiravir can indeed induce meltdown dynamics and ultimate extinction (Baranovich et al. 2013; Bank et al. 2016; Ormond et al. 2017; Goldhill et al. 2018). Similar investigations have been suggested, and are currently underway, as a novel treatment strategy for SARS-CoV2 (Sheahan et al. 2020; Jensen and Lynch 2020; Santiago and Caballero 2020; Jensen et al. 2020). Future characterizations of the DFE across viruses currently posing critical public health threats, of the variety presented here, will be essential for further exploring meltdown as a generally applicable therapeutic.
Data accessibility
Full simulation and summary statistic results are available on GitHub: https://github.com/AYMoralesArce/sims_DFE_virus
Supplementary information
Acknowledgements
This work was funded by U.S. National Institutes of Health Grants R01GM135899 and R35GM139383 to JDJ, as well as an Arizona State University Center for Evolution and Medicine postdoctoral fellowship to AMA.
Author contributions
AMA, PJ, and JDJ conceived of and designed the study, interpreted the results, and wrote the manuscript. AMA and PJ conducted the simulations and wrote the analysis scripts. JDJ obtained research funding.
Competing interests
The authors declare no competing interests.
Footnotes
Associate editor: Louise Johnson
This work is dedicated to the memory of Bill Hill (1940–2021).
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Ana Y. Morales-Arce, Parul Johri
Supplementary information
The online version contains supplementary material available at 10.1038/s41437-021-00493-y.
References
- Abdoli A, Soleimanjahi H, Tavassoti Kheiri M, Jamali A, Jamaati A. Determining influenza virus shedding at different time points in Madin-Darby canine kidney cell line. Cell J. 2013;15(2):130–135. [PMC free article] [PubMed] [Google Scholar]
- Acevedo A, Brodsky L, Andino R. Mutational and fitness landscapes of an RNA virus revealed through population sequencing. Nature. 2014;505:686–690. doi: 10.1038/nature12861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bank C, Ewing GB, Ferrer-Admettla A, Foll M, Jensen JD. Thinking too positive? Revisiting current methods of population genetic selection inference. Trends Genet. 2014;30(12):540–546. doi: 10.1016/j.tig.2014.09.010. [DOI] [PubMed] [Google Scholar]
- Bank C, Hietpas RT, Wong A, Bolon DN, Jensen JD. A Bayesian MCMC approach to assess the complete distribution of fitness effects of new mutations: uncovering the potential for adaptive walks in challenging environments. Genetics. 2014;196(3):841–852. doi: 10.1534/genetics.113.156190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bank C, Renzette N, Liu P, Matuszewski S, Shim H, Foll M, et al. An experimental evaluation of drug-induced mutational meltdown as an antiviral treatment strategy. Evolution. 2016;70(11):2470–2484. doi: 10.1111/evo.13041. [DOI] [PubMed] [Google Scholar]
- Baranovich T, Wong S-S, Armstrong J, Marjuki H, Webby RJ, Webster RG, et al. T-705 (favipiravir) induces lethal mutagenesis in influenza a H1N1 viruses. Vitr J Virol. 2013;87(7):3741–3751. doi: 10.1128/JVI.02346-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blath J, Cronjäger MC, Eldon B, Hammer M. The site-frequency spectrum associated with Ξ-coalescents. Theor Popul Biol. 2016;110:36–50. doi: 10.1016/j.tpb.2016.04.002. [DOI] [PubMed] [Google Scholar]
- Bradwell K, Combe M, Domingo-Calap P, Sanjuán R. Correlation between mutation rate and genome size in riboviruses: mutation rate of bacteriophage Qβ. Genetics. 2013;195(1):243–251. doi: 10.1534/genetics.113.154963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bull JJ, Sanjuán R, Wilke CO. Theory of lethal mutagenesis for viruses. J Virol. 2007;81(6):2930–2939. doi: 10.1128/JVI.01624-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Canale A, Venev S, Whitfield T, Caffrey D, Marasco W, Schiffer C, et al. Synonymous mutations at the beginning of the influenza A virus hemagglutinin gene impact experimental fitness. J Mol Biol. 2018;430:1098–1115. doi: 10.1016/j.jmb.2018.02.009. [DOI] [PubMed] [Google Scholar]
- Chamary J, Hurst LD. Evidence for selection on synonymous mutations affecting stability of mRNA secondary structure in mammals. Genome Biol. 2005;6:R75. doi: 10.1186/gb-2005-6-9-r75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth B, Morgan MT, Charlesworth D. The effect of deleterious mutations on neutral molecular variation. Genetics. 1993;134:1289–1303. doi: 10.1093/genetics/134.4.1289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth B, Charlesworth D. Some evolutionary consequences of deleterious mutations. Genetica. 1998;102-103:3–19. [PubMed] [Google Scholar]
- Charlesworth B. Background Selection 20 Years on. J Heredity. 2013;104(2):161–171. doi: 10.1093/jhered/ess136. [DOI] [PubMed] [Google Scholar]
- Charlesworth B, Jensen JD. The effects of selection at linked sites on patterns of genetic variability. Annu Rev Ecol Evol Syst. 2021;52:177–197. doi: 10.1146/annurev-ecolsys-010621-044528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi JY, Aquadro CF. Recent and long term selection across synonymous sites in Drosophila ananassae. J Mol Evol. 2016;83:50–60. doi: 10.1007/s00239-016-9753-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crotty S, Cameron CE, Andino R. RNA virus error catastrophe: direct molecular test by using ribavirin. Proc Natl Acad Sci USA. 2001;98(12):6895–6900. doi: 10.1073/pnas.111085598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crow JF. Mutation, mean fitness, and genetic load. In: Futuyma D, Antonovics J, editors. Oxford Surveys in Evolutionary Biology. Oxford, UK: Oxford Univ Press; 1993. pp. 3–42. [Google Scholar]
- Csilléry K, François O, Blum MGB. ABC: an R package for approximate Bayesian computation (ABC) Meth Ecol Evol. 2012;3(3):475–479. doi: 10.1016/j.tree.2010.04.001. [DOI] [PubMed] [Google Scholar]
- Dadonaite B, Gilbertson B, Knight ML, Trifkovic S, Rockman S, Laederach A, et al. The structure of the influenza A virus genome. Nat Microbiol. 2019;4(11):1781–1789. doi: 10.1038/s41564-019-0513-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dolan A, Cunningham C, Hector RD, Hassan-Walker AF, Lee L, Addison C, et al. Genetic content of wild-type human cytomegalovirus. J Gen Virol. 2004;85:1301–1312. doi: 10.1099/vir.0.79888-0. [DOI] [PubMed] [Google Scholar]
- Drake JW. A constant rate of spontaneous mutation in DNA-based microbes. Proc Natl Acad Sci USA. 1991;88(16):7160–4. doi: 10.1073/pnas.88.16.7160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eldon B, Wakeley J. Coalescent processes when the distribution of offspring number among individuals is highly skewed. Genetics. 2006;172(4):2621–2633. doi: 10.1534/genetics.105.052175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eldon B, Birkner M, Blath J, Freund F. Can the site-frequency spectrum distinguish exponential population growth from multiple-merger coalescents? Genetics. 2015;199(3):841–856. doi: 10.1534/genetics.114.173807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ewing G, Jensen JD. The consequences of not accounting for background selection in demographic inference. Mol Ecol. 2016;25:135–41. doi: 10.1111/mec.13390. [DOI] [PubMed] [Google Scholar]
- Eyre-Walker A, Keightley PD. The distribution of fitness effects of new mutations. Nat Rev Genet. 2007;8(8):610–618. doi: 10.1038/nrg2146. [DOI] [PubMed] [Google Scholar]
- Felsenstein J. The evolutionary advantage of recombination. Genetics. 1974;78(2):737–756. doi: 10.1093/genetics/78.2.737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferrer-Admetlla A, Leuenberger C, Jensen JD, Wegmann D. An approximate Markov model for the Wright-Fisher diffusion and its application to time series data. Genetics. 2016;203:831–46. doi: 10.1534/genetics.115.184598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foll M, Poh Y-P, Renzette N, Ferrer-Admetlla A, Shim H, Malaspinas A-S, et al. Influenza virus drug resistance: a time-sampled population genetics perspective. PLoS Genet. 2014;10(2):e1004185. doi: 10.1371/journal.pgen.1004185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foll M, Shim H, Jensen JD. A Wright-Fisher ABC-based approach for inferring per-site effective population sizes and selection coefficients from time-sampled data. Mol. Ecol Res. 2015;15:87–98. doi: 10.1111/1755-0998.12280. [DOI] [PubMed] [Google Scholar]
- Fowler DM, Araya CL, Fleishman SJ, Kellog EH, Stephany JJ, et al. High-resolution mapping of protein sequence-function relationships. Nat Methods. 2010;7:741–6. doi: 10.1038/nmeth.1492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gabriel W, Lynch M, Burger R. Muller’s ratchet and mutational meltdowns. Evolution. 1993;47(6):1744–57. doi: 10.1111/j.1558-5646.1993.tb01266.x. [DOI] [PubMed] [Google Scholar]
- Gago S, Elena SF, Flores R, Sanjuán R. Extremely high mutation rate of a hammerhead viroid. Science. 2009;323:1308. doi: 10.1126/science.1169202. [DOI] [PubMed] [Google Scholar]
- Garrison E, Marth G. Haplotype-based variant detection from short-read sequencing. arXiv. 2012;1207:3907. [Google Scholar]
- Goldhill DH, Te Velthuis AJW, Fletcher RA, Langat P, Zambon M, Lackenby A, Barclay WS. The mechanism of resistance to favipiravir in influenza. Proc Natl Acad Sci USA. 2018;115(45):11613–11618. doi: 10.1073/pnas.1811345115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hage E, Wilkie GS, Linnenweber-Held S, Dhingra A, Suárez NM, Schmidt JJ, et al. Characterization of human cytomegalovirus genome diversity in immunocompromised hosts by whole-genome sequencing directly from clinical specimens. J Infect Dis. 2017;215(11):1673–1683. doi: 10.1093/infdis/jix157. [DOI] [PubMed] [Google Scholar]
- Haller BC, Messer PW. SLiM3: forward genetic simulations beyond the Wright-Fisher model. Mol Biol Evol. 2019;36:632–37. doi: 10.1093/molbev/msy228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris RB, Sackman A, Jensen JD. On the unfounded enthusiasm for soft selective sweeps II: examining recent evidence from humans, flies, and viruses. PLoS Genet. 2018;14:e1007859. doi: 10.1371/journal.pgen.1007859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hietpas R, Jensen JD, Bolon DNA. Experimental illumination of a fitness landscape. Proc Natl Acad Sci USA. 2011;108:7896–7901. doi: 10.1073/pnas.1016024108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hietpas R, Roscoe B, Jiang L, Bolon DNA. Fitness analyses of all possible point mutations for regions of genes in yeast. Nat Protoc. 2012;7:1382–1396. doi: 10.1038/nprot.2012.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill WG, Robertson A. The effect of linkage on limits to artificial selection. Genet Res. 1966;8(3):269–294. [PubMed] [Google Scholar]
- Irwin KK, Renzette N, Kowalik TF, Jensen JD. Antiviral drug resistance as an adaptive process. Virus Evol. 2016;2:1–10. doi: 10.1093/ve/vew014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Irwin KK, Laurent S, Matuszewski S, Vuilleumier S, Ormond L, Shim H, et al. On the importance of skewed offspring distributions and background selection in virus population genetics. Heredity. 2016;117(6):393–399. doi: 10.1038/hdy.2016.58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson BC, Campos JL, Haddrill PR, Charlesworth B, Zeng K. Variation in the intensity of selection on codon bias over time causes contrasting patterns of base composition evolution in Drosophila. Genome Biol Evol. 2017;9:102–23. doi: 10.1093/gbe/evw291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen JD, Payseur BA, Stephan W, Aquadro CF, Lynch M, Charlesworth D, Charlesworth B. The importance of the Neutral Theory in 1968 and 50 years on: a response to Kern and Hahn 2018. Evolution. 2019;73:111–14. doi: 10.1111/evo.13650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen JD, Kowalik TF. A consideration of within-host human cytomegalovirus genetic variation. Proc Natl Acad Sci USA. 2020;117(2):816–817. doi: 10.1073/pnas.1915295117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen JD, Lynch M. Considering mutational meltdown as a potential SARS-CoV- 2 treatment strategy. Heredity. 2020;124(5):619–620. doi: 10.1038/s41437-020-0314-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen JD, Stikeleather RA, Kowalik TF, Lynch M. Imposed mutational meltdown as an antiviral strategy. Evolution. 2020;74:2549–2559. doi: 10.1111/evo.14107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen JD (2021) Studying population genetic processes in viruses: from drug-resistance evolution to patient infection dynamics. In: Bamford, D.H. and Zuckerman, M. (eds.), Encyclopedia of virology, 4th edn, vol. 5, Oxford Academic Press, San Diego, CA USA, pp 227–232
- Johri P, Charlesworth B, Jensen JD. Toward an evolutionarily appropriate null model: jointly inferring demography and purifying selection. Genetics. 2020;215(1):173–192. doi: 10.1534/genetics.119.303002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johri P, Riall K, Becher H, Excoffier L, Charlesworth B, Jensen JD. The impact of purifying and background selection on the inference of population history: problems and prospects. Mol Biol Evol. 2021;38:2986–3003. doi: 10.1093/molbev/msab050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keightley PD, Eyre-Walker A. Joint inference of the distribution of fitness effects of deleterious mutations and population demography based on nucleotide polymorphism frequencies. Genetics. 2007;177(4):2251–2261. doi: 10.1534/genetics.107.080663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura M. On the evolutionary adjustment of spontaneous mutation rates. Genet Res. 1967;9:23–34. [Google Scholar]
- Lawrie DS, Messer PW, Hershberg R, Petrov DA. Strong purifying selection at synonymous sites in D. melanogaster. PLoS Genet. 2013;9:e1003527. doi: 10.1371/journal.pgen.1003527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H, Durbin R. Fast and accurate short read alignment with Burrows-Wheeler transform. Bioinformatics. 2009;25(14):1754–1760. doi: 10.1093/bioinformatics/btp324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H, Handsaker B, Wysoker A, Fennell T, Ruan J, Homer N, et al. The sequence alignment/map format and SAMtools. Bioinformatics. 2009;25(16):2078–2079. doi: 10.1093/bioinformatics/btp352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long H, Sung W, Kucukyildirim S, Williams E, Guo S, Patterson C, et al. Evolutionary determinants of genome-wide nucleotide composition. Nat Ecol Evol. 2018;2:237–240. doi: 10.1038/s41559-017-0425-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M, Gabriel W. Mutation load and the survival of small populations. Evolution. 1990;44(7):1725–37. doi: 10.1111/j.1558-5646.1990.tb05244.x. [DOI] [PubMed] [Google Scholar]
- Lynch M, Bürger R, Butcher D, Gabriel W. The mutational meltdown in asexual populations. J Hered. 1993;84(5):339–344. doi: 10.1093/oxfordjournals.jhered.a111354. [DOI] [PubMed] [Google Scholar]
- Lynch M, Conery J, Burger R. Mutational meltdowns in sexual populations. Evolution. 1995;49(6):1067–80. doi: 10.1111/j.1558-5646.1995.tb04434.x. [DOI] [PubMed] [Google Scholar]
- Lynch M, Blanchard J, Houle D, Kibota T, Schultz S, Vassilieva L, Willis J. Spontaneous deleterious mutation. Evolution. 1999;53:645–663. doi: 10.1111/j.1558-5646.1999.tb05361.x. [DOI] [PubMed] [Google Scholar]
- Lynch M (2007) The origins of genome architecture (1st ed.). Sinauer Associates Inc., Sunderland, MA USA
- Lynch M. Scaling expectations for the time to establishment of complex adaptation. Proc Natl Acad Sci USA. 2010;107:16577–82. doi: 10.1073/pnas.1010836107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M, Ackerman MS, Gout J-F, Long H, Sung W, Thomas WK, Foster PL. Genetic drift, selection and the evolution of the mutation rate. Nat Rev Genet. 2016;17(11):704–714. doi: 10.1038/nrg.2016.104. [DOI] [PubMed] [Google Scholar]
- Lynch M, Trickovic B. A theoretical framework for evolutionary cell biology. J Mol Biol. 2020;432(7):1861–1879. doi: 10.1016/j.jmb.2020.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malaspinas A-S, Malaspinas O, Evans SN, Slatkin M. Estimating allele age and selection coefficients from time-serial data. Genetics. 2012;192:599–607. doi: 10.1534/genetics.112.140939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathew L, Jensen JD. Evaluating the ability of the pairwise joint site frequency spectrum to co-estimate selection and demography. Front Genet. 2015;6:268. doi: 10.3389/fgene.2015.00268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathieson I, McVean G. Estimating selection coefficients in spatially structured populations from time series data of allele frequencies. Genetics. 2013;193:973–84.. doi: 10.1534/genetics.112.147611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matuszewski S, Ormond L, Bank C, Jensen JD. Two sides of the same coin: a population genetics perspective on lethal mutagenesis and mutational meltdown. Virus Evol. 2017;3:1–5. doi: 10.1093/ve/vex004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matuszewski S, Hildebrandt ME, Achaz G, Jensen JD. Coalescent processes with skewed offspring distributions and nonequilibrium demography. Genetics. 2018;208:323–338. doi: 10.1534/genetics.117.300499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muller HJ. The relation of recombination to mutational advance. Mutat Res/Fundamental Mol Mechanisms Mutagenesis. 1964;1(1):2–9. doi: 10.1016/0027-5107(64)90047-8. [DOI] [PubMed] [Google Scholar]
- Muramoto Y, Takada A, Fujii K, Noda T, Iwatsuki-Horimoto K, Watanabe S, et al. Hierarchy among viral RNA (vRNA) segments in their role in vRNA incorporation into influenza A virions. J Virol. 2006;80:2318–25. doi: 10.1128/JVI.80.5.2318-2325.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishiyama Y, Maeno K, Yoshida S. Characterization of human cytomegalovirus-induced DNA polymerase and the associated 3′-to−5′, exonuclease. Virology. 1983;124(2):221–231. doi: 10.1016/0042-6822(83)90339-2. [DOI] [PubMed] [Google Scholar]
- Ormond L, Liu P, Matuszewski S, Renzette N, Bank C, Zeldovich K, et al. The combined effect of oseltamivir and favipiravir on influenza A virus evolution. Genome Biol Evol. 2017;9:1913–24. doi: 10.1093/gbe/evx138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palese P, Young J. Variation of influenza A, B, and C viruses. Science. 1982;215(4539):1468–1474. doi: 10.1126/science.7038875. [DOI] [PubMed] [Google Scholar]
- Parvin JD, Moscona A, Pan WT, Leider JM, Palese P. Measurement of the mutation rates of animal viruses: influenza A virus and poliovirus type 1. J Virol. 1986;59(2):377–383. doi: 10.1128/jvi.59.2.377-383.1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pénisson S, Singh T, Sniegowski P, Gerrish P. Dynamics and fate of beneficial mutations under lineage contamination by linked deleterious mutations. Genetics. 2017;205(3):1305–1318. doi: 10.1534/genetics.116.194597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pokalyuk C, Renzette N, Irwin KK, Pfeifer SP, Gibson L, Britt WJ, et al. Characterizing human cytomegalovirus reinfection in congenitally infected infants: an evolutionary perspective. Mol Ecol. 2017;26(7):1980–1990. doi: 10.1111/mec.13953. [DOI] [PubMed] [Google Scholar]
- Poon LLM, Song T, Rosenfeld R, Lin X, Rogers MB, Zhou B, et al. Quantifying influenza virus diversity and transmission in humans. Nat Genet. 2016;48(2):195–200. doi: 10.1038/ng.3479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renzette N, Bhattacharjee B, Jensen JD, Gibson L, Kowalik TF. Extensive genome-wide variability of human cytomegalovirus in congenitally infected infants. PLoS Path. 2011;7(5):e1001344. doi: 10.1371/journal.ppat.1001344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renzette N, Gibson L, Bhattacharjee B, Fisher D, Schleiss MR, Jensen JD, Kowalik TF. Rapid intrahost evolution of human cytomegalovirus is shaped by demography and positive selection. PLoS Gen. 2013;9(9):e1003735. doi: 10.1371/journal.pgen.1003735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renzette N, Caffrey DR, Zeldovich K, Liu P, Gallagher G, Aiello D, et al. Evolution of the influenza A virus genome during development of oseltamivir resistance in vitro. J Virol. 2014;88:272–81. doi: 10.1128/JVI.01067-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renzette N, Pokalyuk C, Gibson L, Bhattacharjee B, Schleiss MR, Hamprecht K, et al. Limits and patterns of cytomegalovirus genomic diversity in humans. Proc Natl Acad Sci USA. 2015;112(30):E4120–E4128. doi: 10.1073/pnas.1501880112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renzette N, Kowalik TF, Jensen JD. On the relative roles of background selection and genetic hitchhiking in shaping human cytomegalovirus diversity. Mol Ecol. 2016;25:403–13. doi: 10.1111/mec.13331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renzette N, Pfeifer SP, Matuszewski M, Kowalik TF, Jensen JD. On the analysis of intra-host and inter-host viral populations: human cytomegalovirus as a case study of pitfalls and expectations. J Virol. 2017;91:e01976–16. doi: 10.1128/JVI.01976-16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sackman AM, Pfeifer SP, Kowalik TF, Jensen JD. On the demographic and selective forces shaping patterns of human cytomegalovirus variation within hosts. Pathogens. 2018;7:16. doi: 10.3390/pathogens7010016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sackman AM, Harris RB, Jensen JD. Inferring demography and selection in organisms characterized by skewed offspring distributions. Genetics. 2019;211(3):1019–1028. doi: 10.1534/genetics.118.301684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanjuán R, Nebot MR, Chirico N, Mansky LM, Belshaw R. Viral mutation rates. J Virol. 2010;84(19):9733–9748. doi: 10.1128/JVI.00694-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santiago E, Caballero A. The value of targeting recombination as a strategy against coronavirus diseases. Heredity. 2020;125:169–172. doi: 10.1038/s41437-020-0337-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneider A, Charlesworth B, Eyre-Walker A, Keightley PD. A method for inferring the rate of occurrence and fitness effects of advantageous mutations. Genetics. 2011;189:1427–37. doi: 10.1534/genetics.111.131730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shakhnovich E. Protein folding thermodynamics and dynamics: where physics, chemistry, and biology meet. Chem Rev. 2006;106:1559–88. doi: 10.1021/cr040425u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheahan T, Sims A, Zhou S, Graham R, Pruijssers A, Agostini M, et al. An orally bioavailable broad-spectrum antiviral inhibits SARS-CoV-2 in human airway epithelial cell cultures and multiple coronaviruses in mice. Sci Transl Med. 2020;12:eabb5883. doi: 10.1126/scitranslmed.abb5883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sohail MS, Louie RHY, McKay MR, Barton JP. MPL resolves genetic linkage in fitness inference from complex evolutionary histories. Nat Biotechnol. 2021;39:472–479. doi: 10.1038/s41587-020-0737-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tarasov A, Vilella AJ, Cuppen E, Nijman IJ, Prins P. Sambamba: fast processing of NGS alignment formats. Bioinformatics. 2015;31(12):2032–2034. doi: 10.1093/bioinformatics/btv098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tataru P, Mollion M, Glémin S, Bataillon T. Inference of distribution of fitness effects and proportion of adaptive substitutions from polymorphism data. Genetics. 2017;207(3):1103–1119. doi: 10.1534/genetics.117.300323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teshima KM, Coop G, Przeworski M. How reliable are empirical genome scans for selective sweeps? Genome Res. 2006;16:702–12. doi: 10.1101/gr.5105206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornton K. libsequence: a C++ class library for evolutionary genetic analysis. Bioinformatics. 2003;19(17):2325–2327. doi: 10.1093/bioinformatics/btg316. [DOI] [PubMed] [Google Scholar]
- Thornton K, Jensen JD. Controlling the false positive rate in multi-locus genome scans for selection. Genetics. 2007;175:737–50. doi: 10.1534/genetics.106.064642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vahey MD, Fletcher DA. Low-fidelity assembly of influenza a virus promotes escape from host cells. Cell. 2019;176:281–94. doi: 10.1016/j.cell.2018.10.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Visher E, Whitefield SE, McCrone JT, Fitzsimmons W, Lauring AS. The mutational robustness of influenza A virus. PLoS Pathog. 2016;12:e1005856. doi: 10.1371/journal.ppat.1005856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wylie CS, Shakhnovich EI. Mutation induced extinction in finite populations: lethal mutagenesis and lethal isolation. PLoS Comput Biol. 2012;8:e1002609. doi: 10.1371/journal.pcbi.1002609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeldovich KB, Chen P, Shakhnovich EI. Protein stability imposes limits on organism complexity and speed of molecular evolution. Proc Natl Acad Sci USA. 2007;104(41):16152–57. doi: 10.1073/pnas.0705366104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng K, Charlesworth B. Studying patterns of recent evolution at synonymous sites and intronic sites in Drosophila melanogaster. J Mol Evol. 2010;70:116–28. doi: 10.1007/s00239-009-9314-6. [DOI] [PubMed] [Google Scholar]
- Zeng K. A coalescent model of background selection with recombination, demography and variation in selection coefficients. Heredity. 2013;110:363–71. doi: 10.1038/hdy.2012.102. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Full simulation and summary statistic results are available on GitHub: https://github.com/AYMoralesArce/sims_DFE_virus