Bayesian-based optimized deep learning model to detect COVID-19 patients using chest X-ray image data

Abstract

Coronavirus Disease 2019 (COVID-19) is extremely infectious and rapidly spreading around the globe. As a result, rapid and precise identification of COVID-19 patients is critical. Deep Learning has shown promising performance in a variety of domains and emerged as a key technology in Artificial Intelligence. Recent advances in visual recognition are based on image classification and artefacts detection within these images. The purpose of this study is to classify chest X-ray images of COVID-19 artefacts in changed real-world situations. A novel Bayesian optimization-based convolutional neural network (CNN) model is proposed for the recognition of chest X-ray images. The proposed model has two main components. The first one utilizes CNN to extract and learn deep features. The second component is a Bayesian-based optimizer that is used to tune the CNN hyperparameters according to an objective function. The used large-scale and balanced dataset comprises 10,848 images (i.e., 3616 COVID-19, 3616 normal cases, and 3616 Pneumonia). In the first ablation investigation, we compared Bayesian optimization to three distinct ablation scenarios. We used convergence charts and accuracy to compare the three scenarios. We noticed that the Bayesian search-derived optimal architecture achieved 96% accuracy. To assist qualitative researchers, address their research questions in a methodologically sound manner, a comparison of research method and theme analysis methods was provided. The suggested model is shown to be more trustworthy and accurate in real world.

1. Introduction

COVID-19, a novel form of Coronavirus, has wreaked havoc on the global health system, claiming thousands of lives and wreaking havoc on millions more [1,2]. Coronavirus (SARS-COV-2) invaded the human body for the first time in December 2019, and it spreads mostly via droplets created by infected individuals when they talk or cough. Due to the droplets’ inability to travel long distances, they cannot transmit from human to human without coming into close touch [3,4]. COVID-19 has been identified as the organ of the community of coronaviruses [5,6]. COVID-19 infection is spreading every day owing to a lack of rapid diagnosis technologies. This illness will claim a staggering number of lives worldwide. The respiratory system and lungs are the primary routes of transmission for the virus. People have already been afflicted by a variety of other ailments because of global climate change, and the consequence of COVID-19 is incalculable. Almost every country on Earth has been infected with the virus at this point. On May 30, 2021, the WHO revealed that the virus has confirmed over 170 million infections and killed over 3.5 million people [7].

By 2020, COVID-19's exponential spread would have driven the World Health Organization (WHO) into declaring a global pandemic. COVID-19's flu virus may be spread in a variety of ways including in dirty and congested places [[8], [9], [10]]. Governments have enacted new regulations to address overpopulation and regional overpopulation. Governments and healthcare organizations have done so by implementing infection control systems in this manner [[11], [12], [13]]. Several nations are currently developing vaccinations against COVID-19. Among these, vaccines Pfizer, Moderna, Sputnik V, Sinovac, and AstraZeneca have been approved and are being used in many nations [[14], [15], [16]]. According to clinical data, it has been said that the widely used vaccinations have attained effectiveness and are safe to use without causing major adverse effects. Nonetheless, a vast industrial scale is necessary to make the vaccine in sufficient quantity to cover the whole world's population. Additional study is needed to determine the duration of protection and the vaccines' efficacy, especially against newly discovered viral types. Additional studies are needed to develop an effective screening procedure for diagnosing and isolating viral cases. Numerous countries' health professionals and scientists are seeking to strengthen their treatment plans and testing capability by introducing multifunctional testing in order to halt the spread of the virus and to protect people from the fatal infection [17].

Mostly, all projected models will need chest X-ray or CT data from patients as the primary input parameter, which can be obtained exclusively from diagnostic centers [18,19]. Thus, each patient must make an in-person visit to the diagnostic center to confirm the presence of COVID-19 in his or her body. Most households in underdeveloped nations lack access to private transport. Additionally, individuals living in rural regions must drive a considerable distance to access a diagnostic center. As a result, individuals must use public transportation to the diagnostic center for COVID-19 testing. This will increase susceptibility to the propagation of COVID-19, among other things [20].

Artificial Intelligence (AI) approaches have been used intensively in medical domain to diagnose diseases based on the chest scans, e.g. Pneumonia [[21], [22], [23], [24], [25]]. Recognition techniques used range from Bayesian to Deep Learning (DL). Recently, DL has been shown to be beneficial and successful for classifying images to detect COVID-19. DL techniques are composed of multi-layer neural networks that are very competent of identifying image's deep patterns without requiring the images to be preprocessed in any way. Various advancements in Convolutional Neural Network (CNN) during the subsequent years greatly reduced the error rate in image categorization competitions [[26], [27], [28], [29]].

The primary goal of this study is to characterize the COVID-19 feature detected in chest X-ray images based on Bayesian optimized deep learning model. The following are the primary contributions of this study:

• 1)A novel DL model for recognizing COVID-19 based on the chest X-ray images is proposed.
• 2)Bayesian optimization is a technique used in place of sweeping hyperparameters throughout an experiment.
• 3)By identifying suitable network hyperparameters and training choices for CNN, the proposed approach improves recognition efficiency.
• 4)The proposed model has been trained, optimized, and tested using a real dataset. This dataset is large compared to the literature and balanced which support the results to be trusted by domain expert.
• 5)Load the optimal DL network discovered during optimization and its accuracy of validation.

The following sections are utilized throughout the remainder of this work. The second portion deals with comparable studies beforehand. Section 3 describes the key characteristics of the dataset. Section 4 shows in a methodological approach of the proposed DL model. Section 5 discusses the testing results, and Section 6 presents the conclusion and future work.

2. Related works

This section will review the most recent literature on chest x-ray scans used to diagnose COVID-19 and compiles information on the application of machine learning and deep learning to picture categorization. The classification step of an image is separated into three stages: pre-processing, extraction, and recognition. Recently, researchers used deep learning algorithms to explore and evaluate chest X-ray images to discover COVID-19. Using deep learning algorithms, images are pre-processed using the CNN network to extract higher-quality and deep features that are then fed into a classifier (e.g., SoftMax) for image categorization. In [30], Authors used a hybrid chest X-ray radiography (CXR) images model to utilize a decision-tree (DT) classifier based on DL to detect COVID-19. This classifier tested a set of three binary DTs made using the Torch library by making comparisons. For the third DT, the decision tree managed to accurately classify whether an X-ray image was healthy or unhealthy, with 95% accuracy.

Wang et al. [31] created a transfer learning (TL) approach based on DL models to diagnose COVID-19. A chest X-ray dataset of 565 COVID-19 and 537 healthy is used in the proposed model. The suggested DL technique had a diagnosis accuracy of 96.7%. Additionally, they used deep features and machine learning classification to establish an effective diagnostic approach for enhancing the DL model's accuracy. The authors concluded that their suggested strategy improved the COVID-19's classification accuracy and diagnostic performance. However, the authors made no attempt to compare their findings to those of previous comparable investigations.

Chowdhury et al. [32] used chest X-ray images to construct new framework based on CNN. The study utilized a chest X-ray dataset of 219 COVID-19, 1345 pneumonia, and 1341 healthy patients. The authors employed a convolution in the parallel stack to collect and extend the essential features to achieve a detection accuracy of 96.6% in their suggested dilated technique. In [33], three deep TL models including AlexNet, GoogleNet, and ResNet were used on a dataset of X-ray scans with four distinct class types. The chest X-ray dataset include 79 healthy, 69 COVID-19, and 79 + 79 bacterial/viral pneumonia patients. The study was spread out into three different situations to minimize memory usage and overall execution time. DL can assess the 100% of the data correctness using the newest TL model.

In [34], authors devised and successfully validated a deep CNN, known as DeTraC, for identifying COVID-19 patients from their chest X-ray scans. The dataset for chest X-rays contains the following numbers: 11 SARs, 105 COVID-19, and 80 healthy patients. They suggested a decomposition approach to inspect for detect anomalies in the dataset by identifying class borders and using that information to acquire for high accuracy of 93%. The authors of [35] proposed a DL model that had the three layers of patient layer, cloud layer, and hospital layer. The study used a chest X-rays dataset of 250 COVID-19 and 500 healthy patients. A patient data collection was obtained from the patient layer with the use of wearable devices and a phone app. A neural network-based DL algorithm was used to find COVID-19 utilizing the patient X-ray scans. The suggested model obtained a high-level accuracy of 97.9%.

Authors in [36] developed a DL-based approach to identify COVID-19 from chest X-ray scans, based on four different TL models. Their dataset contains 184 COVID-19 and 5000 healthy patients. The approach used image augmentation to construct a new version of the COVID-19 images, which resulted in an increased number of samples and was eventually able to reach a higher accuracy. ResNet-101 and ResNet-151 were used [37] to construct a model with fusion effects, and the weight ratio of the produced model was dynamically enhanced. The chest X-ray dataset consists of 8851 healthy, 140 COVID-19, and 9576 pneumonia patients. To organize and standardize the chest X-ray images, their recognition was based on three distinct recognitions including normal, COVID-19, and pneumonia. The study achieved 96% accuracy.

In [38], Khan and Aslam used pre-trained DL models (i.e. VGGNet, ResNet, and DenseNet) to expand the diagnostic capabilities of their imaging systems and built a whole new image processing architecture based on normal utilizing TL models. The used chest X-rays dataset had 195 COVID-19 and 862 healthy patients. In this suggested model, there were two steps like preprocessing and data augmentation followed by transfer learning. The results demonstrated a perfect level of 99% accuracy. CNN and machine learning classifiers [39] were used in order to build a model where many tests were done using CNN in order to identify the COVID-19 from chest X-ray pictures. The best accuracy of the proposed DL model was above 98% compare to the machine learning algorithms. The chest X-ray dataset contained 4292 pneumonia, 225 COVID-19, and 1583 healthy patients. The system achieved a remarkable level of accuracy with 98.5% of accuracy. They ultimately determined that the proposed CNN system could identify COVID-19 patients from a small number of cases, without any preprocessing and with the least possible number of layers.

A deep learning algorithm based on the ResNet CNN model was used to identify COVID-19 [40]. In their proposed technique, thousands of images were used in the pre-trained phase to distinguish significant items, and a different number of images in the retrained phase were utilized to search for abnormalities in chest X-ray data. The COVID-19 chest X-ray dataset has 154 COVID-19 and 5828 healthy patients. The study achieved an accuracy of 72%.

As shown in Table 1 , most published research for COVID-19 diagnosis has employed chest X-ray data to diagnose COVID-19 which highlighted the critical role of chest X-ray image analysis as an indispensable tool for physicians and radiographers. However, these studies used different and imbalance datasets, and they extracted insufficient features from images. As a result, the classification outcomes were not accurate nor intended [41,42]. The majority of the studies discussed before relied heavily on mathematical analysis and transfer learning to reliably diagnose COVID-19 infection. There is little research on using CNN with balanced data with optimization technique to identify COVID-19 in X-ray imaging. As a result, more research on deep learning with simplified efficiency criteria may be conducted. According to the literature evaluation conducted for this study, it is recommended that chest scans be used to balanced data to diagnose COVID-19. The new paradigms are generally more effective and efficient in combating the COVID-19 epidemic.

Table 1.

Most data of published studies were imbalanced COVID-19 datasets.

References	Dataset
	COVID-19	Pneumonia	Normal
Wang et al. [31]	565	–	537
Chowdhury et al. [32]	219	1345	1341
Loey et al. [33]	69	bacterial = 79	79
		virus = 79
Abbas et al. [34]	105 SARS = 11	–	80
El-Rashidy et al. [35]	250	–	500
Minaee et al. [36]	184	–	5000
Wang et al. [37]	140	9576	8851
Khan and Aslam [38]	195	–	862
Sekeroglu and Ozsahin [39]	225	4292	1583
Che Azemin et al. [40]	154	–	5828

3. Dataset

COVID-19 patients are anticipated to undergo a variety of rigorous data gathering procedures. Not only the sample structure inside a collection, but also their distribution across classes, has a substantial impact on the model that will be created. Color, geometry, and pattern have a direct influence on the performance of intelligent computer-aided prototypes. Additionally, a consistent and robust model requires an equal number of samples that cover all conceivable situations or occurrences for each class.

This paper conducted its experiments based on two publicly available X-ray datasets. The first dataset is COVID-19 Radiography dataset1 published by Rahman et al. [43,44]. The collection includes 3616 COVID-19, 10,192 normal, 6012 lung opacity, and 1345 viral Pneumonia cases. The second public X-ray dataset is a Chest X-Ray Images.2 The collection [45] contains 5863 images of patients with Pneumonia/Normal lung function.

By integrating the COVID-19 radiography dataset with chest X-ray dataset, we developed a new dataset. By eliminating low-quality and redundant images, the combined dataset comprises 10,848 (3616 COVID-19, 3616 Normal cases, and 3616 Pneumonia) scans. The resulting dataset is balanced as illustrated in Fig. 1 . We split our dataset to three sets, as shown in Fig. 2 . To demonstrate the suggested model using a publicly available dataset, we created a model that does X-ray categorization. The diagnostic engine uses this X-ray classifier to determine whether an X-ray image is associated with COVID-19. To assess the classifier, we employ two datasets of COVID-19, normal, and Pneumonia. The new dataset is a massive archive including an unusually diverse population of COVID-19 patients.

Fig. 1.

The proposed dataset structures.

Fig. 2.

The proposed COVID-19 dataset split.

4. Proposed model

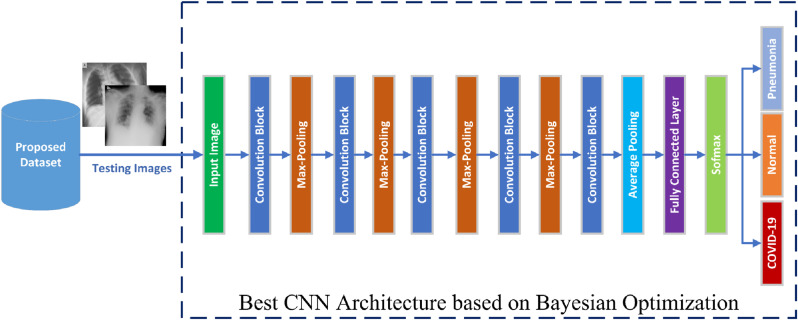
Fig. 3 illustrates the proposed classification model for detecting COVID-19 patients. The train and validation set are utilized throughout training and tuning procedures. The proposed model consists of two main parts: initial CNN architecture and the Bayesian optimizer. The proposed Bayesian optimizer has three main steps: selection of hyperparameters, calculation of fitness function, and tuning of hyperparameters. The CNN architecture extracts deep features and followed by a classifier. Fig. 4 illustrates the suggested recognition model topology. The testing data will be used to assess the optimized model. After tweaking the CNN hyperparameters using Bayesian optimizer, the optimizer picks the optimum hyperparameters to be used in the testing stage.

Fig. 3.

The proposed COVID-19 X-ray classification model for training.

Fig. 4.

The proposed COVID-19 X-ray classification model for testing.

The test procedure will be utilized to find the optimal of hyperparameters in CNN model. During the first iteration of the search, we train the CNN using the default hyperparameters. Then, we adjust our CNN model's hyperparameters to approximate the objective function using the validation loss, which serves as our fitness function. Then, we get a fresh set of hyperparameters by using the projected improvement acquisition function. This Bayesian function specifies whether the next set of hyperparameters is created randomly or using the fitness model. We update the CNN architecture to match the hyperparameters once they are obtained. CNN is trained and used to calculate the validation loss using the training technique. After that, the Bayesian process is updated to provide a more precise estimate of the objective function. This method is done 30 times in total. The model with the lowest loss will be chosen after 30 iterations. This is the procedure technique of Bayesian-optimized CNN model of tuning hyperparameters.

4.1. Choosing of hyperparameters in Bayesian optimizer

It is required to decide which hyperparameters are optimized before commencing the optimization. The innovative concept here is to construct a neural network to assist the diagnosis of COVID-19 by chaining an extractive feature backbone CNN network. To acquire the best model, four hyperparameters were chosen for optimization in the Optimization stage of the hyperparameter:

• 1)Initial learning rate (μ): rely on dataset size and network depth. To compute Stochastic Gradient Descent (SGD) with μ: $\Delta Q_{i+1}=Q_i+\mathrm{\mu *E}\left({\text{Q}}_{\text{i}}\right)$ where the hyperparameter $Q$ which minimizes error rate $E\left(Q_i\right)$ with estimated step size $\mathrm{\mu }$.
• 2)SGD with momentum: Momentum adds inertia to hyperparameter changes by including a contribution proportionate to the prior iteration's change in the current update. This leads in more consistent parameter updates and a decrease in the noise associated with stochastic gradient descent. The momentum term rises for dimensions with identical gradients and decreases for dimensions with varying gradients. To compute SGD with momentum: $\Delta Q_{i+1}=\Omega Q_i+\mathrm{\mu *E}\left({\text{Q}}_{\text{i}}\right)$ where the momentum term $\Omega$ is usually set to 0.8–1.
• 3)Depth of the network stage: This option checks the network depth. The network comprises three sections with the same convolution layers each with depth $D$. The total number of convolutionary layers is $3\ast D$. Later on, in the script, the goal function takes the number of convolution filters in each layer to $1/\sqrt{D}$. As a consequence, the number of parameters and the calculation quantity needed for each iteration are almost same for varied section depths.
• 4)L2 regularization: By include a regularization β term for the weights in the loss function, overfitting is minimized, i.e., $E_r=E+\mathrm{\beta }\mathrm{\Omega }\left(\text{Q}\right)$, where $\text{Q}$ is the weight vector, $\mathrm{\beta }$ is the regularization coefficient, and the regularization function is $\mathrm{\Omega }\left(\text{Q}\right)$ = $\frac{1}{2}{\text{ Q}}^{\text{t}}\text{Q}$.

4.2. Tuning of hyperparameters in Bayesian optimizer

In the broadest sense, optimization is the process of identifying a position that decreases a real-valued function known as the fitness function. Bayesian optimization is a term that refers to one of these processes. Bayesian optimization utilizes an internal Gaussian process model of the goal function and trains the model using optimal solution evaluations. One novel feature of Bayesian optimization is the method's use of an acquisition function to select the next point to assess. The acquisition function may be used to strike a compromise between sampling at sites with low-modeled goal functions and investigating regions that have not yet been well modeled.

One of the most challenging aspects of any Deep Learning project is determining the optimal combination of hyperparameters that decreases or increases the fitness function, given the variety of neural network topologies available today. When considering the high number of criteria, creating a static search space might be a big difficulty. The goal of this study was based on constructed with a fitness function and a search space comprising the hyperparameters such as the depth of network layer, and the learning rate. Thus, we were able to find the optimal hyperparameter design, taking the goal function stated above and the hyperparameters of interest into account.

The Bayes theorem is at the heart of Bayesian optimization. According to Bayes's theorem $P\left(H|F\right)=P\left(H\right)xP\left(F\right|H)$, $H$ is the hypothesis in this case. Hypothesis is independent features. $F$ is the proof or evidence. proof is the target variable. The probability of the hypothesis $H$ given the evidence $F$. $H$ and $F$ must be different events. The prior probability is denoted by $P\left(H\right)$. $P\left(F\right|H)$ denotes the probability. The posterior probability is denoted by $P\left(H\right|F)$. The objective function is the real or true function that we are attempting to estimate via Bayesian optimization. By sampling points from the hyperparameter. space, Bayesian optimization optimizes this function without knowing its gradient. It attempts to estimate the objective function using the results of evaluating the function at these sample locations. The surrogate function is this estimate of the objective function. Keep in mind that the classification error is being utilized as an objective function. The following method is described in Bayesian terms: 1) Fit the objective function to a Gaussian probability model. The objective function of this investigation is classification error. 2) Identify the optimal hyperparameters parameters for the Gaussian process. 3) Transform the objective function using these hyper-parameters. 4) Apply the new findings to the Gaussian model. Finally, Repeat Steps 2–4 until the maximum number of iterations has been achieved.

To optimize CNN model and to evaluate various hyperparameter in CNN configurations based on Bayesian techniques. Bayesian statistics is a critical methodology in statistics that is especially useful when analyzing a series of data dynamically. Rapid, efficient, urgent, and adaptive Deep Learning trials. Table 2 shows the four (Initial learning rate, SGD with momentum, depth of the network, and L2 regularization) tuning hyperparameter used in DL training generated by the Bayesian tuning algorithm.

Table 2.

The proposed hyperparameters from the Bayesian optimization for DL training.

Hyperparameter	Range	Function	Data type
Initial learning rate	[0.001 1]	Logarithmic	Real number
SGD with momentum	[0.8 1]	None	Real number
Depth of the network	[15]	none	Integer number
L2 regularization	[10−10 0.001]	Logarithmic	Real number

4.3. Proposed CNN Architecture

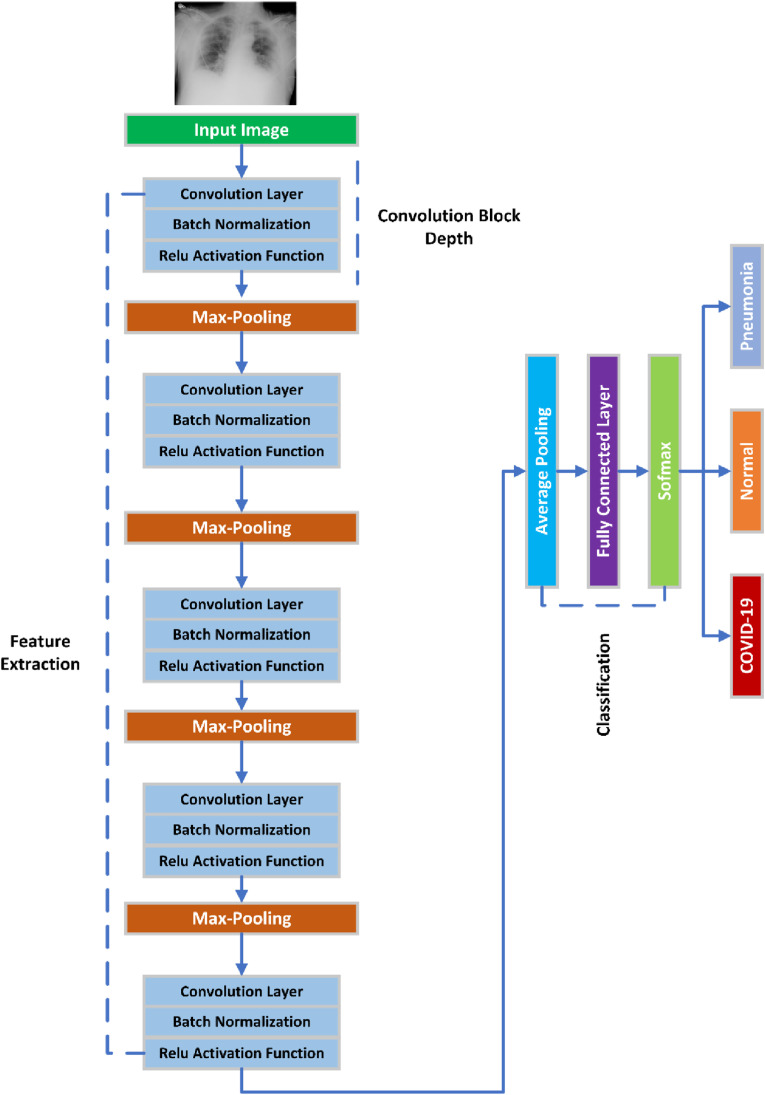
As seen in Fig. 5 , proposed CNN architecture consists of two stages: feature extraction and learning classifier or classification. The objective of feature extraction stage is to extract significant characteristics from the data. Convolutional layers perform feature extraction in CNN. A learning predictor stage is used to train the system to categories data based on the characteristics extracted by the feature extraction layer. The classifier for learning is composed of one or more fully connected layers. Each layer has a certain number of nodes. Each layer employs a variety of non-linear activation functions to learn complicated function mappings from source to destination.

Fig. 5.

Proposed custom CNN architecture for COVID-19 classification.

Assume layer $c$ is convolutional, we have a set of $sxs$ square neuron nodes followed by a convolutional layer. If we employ a $fxf$ filter, the outcome of the convolutional layer will be $(s-f+1)(s-f+1)$, which results in $k$-feature maps. The convolutional layer functions as a feature vector, capturing characteristics from the inputs. Convolution retrieves picture features such as edges, lines, and corners. To calculate the output of convolution function in equation (2):

$$G_i^c=B_i^c+\sum _{x=1}^s\sum _{y=1}^s{W}_i{Q}_{\left(i+x\right)\left(j+y\right)}^{c-1}$$ (2)

where $B_i^b$ is a bias and $W_i$ is the mask of volume $f\times f$.), the input of layer $c-1$ The convolution operation then applies its activation function as specified in formula (3):

$$Out=\Omega \left(G_i^c\right)$$ (3)

where $\Omega (.)$ is referred to as non-linearity, and the function used to generate non-linearity in DTL comes in a variety of flavors, including tanh, sigmoid, and Rectified Linear Units (ReLU). In our technique, we use ReLU as the activation function in equation (4) to facilitate the training phase.:

$$Re\left(d\right)=\max \left(0,d\right)$$ (4)

Bayesian optimization uses historical data to choose the optimal hyperparameters for assessment. In machine learning models and simulations, Bayesian optimization has been applied [46,47]. It assists in devising the time-consuming job of optimizing a large number of parameters. It has been used in several trials to determine the optimal set of gait characteristics. Our paper presents a unique CNN model that is trained entirely from scratch, rather than using the TL technique.

5. Results

We trained our deep learning model on a GPU using TensorFlow and MATLAB (2021a) based on Nvidia. We implement the proposed CNN model using the recommended training configuration (batch norm decay = 0.2, weight decay = 0.001, and dropout = 0.6). To avoid the overfitting concerns associated with deep nets, we use the dropout strategy [48]. The early-stopping is permitted if no decrease in correctness is observed. The starting learning rate is set from the domain [0.001–1] with a batch size of 64 and the learning rate is automatically reduced. This resulted in a shorter preparation time without sacrificing efficiency. They observed that model output increased as more samples were used in 10-fold cross-validation [49]. SGDM [50] has been selected as our optimizer strategy for enhancing CNN detection performance. Validation accuracy is a categorization score used to evaluate the effectiveness of the learning approach throughout the procedure. It makes it possible to identify overfitting as a possible cause. If evaluation and training are inaccurate, overfitting has already occurred. The proposed CNN model update training configuration parameters. To achieve the highest degree of model efficiency, an efficient balance between classes must be found.

The dataset was divided into three scenarios. 1) Scenario 1: the data are split to 60% for training, 10% for validation, and 30% for testing; 2) Scenario 2: the data are split into 70% for training, 10% for validation, and 20% for testing); 3) Scenario 3: the data are split into 80% for training, 10% for validation, and 10% for testing. Our dataset is balanced, so it is sufficient to measure the model accuracy, i.e., accuracy = ($C_{TP}$ +$C_{TN}$)/(($C_{TP}$ +$C_{FP}$)+($C_{TN}$ +$C_{FN}$)), where $C_{TP}$ is the quantity of properly labelled, $C_{FN}$ is the number of incorrectly labelled, $C_{TN}$ is the number of instances of the remaining categories that are properly named, and $C_{FP}$ is the total number of incorrectly labelled classes in the remaining classes. The confusion matrices for three groups of labels (COVID-19, Normal, and Pneumonia) have also been reported.

Scenario 1

Table 3 shows the results of optimizing CNN hyperparameters (depth of the network, initial learning rate, SGD with momentum, and L2 regularization) based on the Bayesian technique. The maximum number of objective function evaluations is 30 iterations. The best estimated CNN hyperparameters are: depth of the network = 2, initial learning rate = 0.010518, SGD with momentum = 0.83379, and L2 regularization = 1.606e-05 in all layers). Fig. 6 (a) shows an overall accuracy of 95.1% of the best CNN model to detect COVID-19 patients. Fig. 6(b) shows a graph between the function evaluation and minimum objective. The goal, shown on the x-axis as min objective against the total number of function evaluations on the y-axis.

Scenario 2

Table 4 shows the result of optimizing CNN hyperparameters: depth of the network, initial learning rate, SGD with momentum, and L2 regularization based on Bayesian technique. The maximum objective function evaluations are 30 iterations. Best estimated CNN hyperparameters model is (depth of the network = 1, initial learning rate = 0.042721, SGD with momentum = 0.84845, and L2 regularization = 5.3403e-07). Fig. 7 (a) shows an overall accuracy of 95.2% of the best CNN model to classify COVID-19 patients. Fig. 7(b) shows a graph between the function evaluation and minimum objective. The goal, shown on the x-axis as min objective against the total number of function evaluations on the y-axis.

Scenario 3

Table 5 shows the result of optimizing CNN hyperparameters (Depth of the network, Initial learning rate, SGD with momentum, L2 regularization) based on Bayesian technique. The maximum objective function evaluations are 30 iterations. Best estimated CNN hyperparameters model is (Depth of the network = 2, Initial learning rate = 0.0104, SGD with momentum = 0.80281, L2 regularization = 1.7329e-08). Fig. 8 (a) shows the overall accuracy = 96.0% of the best CNN model to classify COVID-19 dataset. Fig. 8(b) shows a graph between the function evaluation and minimum objective. The goal, shown on the x-axis as min objective against the total number of function evaluations on the y-axis.

Table 3.

The outcomes of Bayesian-based tuned CNN model for scenario 1.

Iter	Objective	depth	Learn rate	Momentum	L2Regularize	Iter	Objective	depth	Learn rate	Momentum	L2Regularize
1	0.26593	5	0.56005	0.89236	2.5293e-08	16	0.077562	2	0.010068	0.813	8.9211e-10
2	0.12835	2	0.45045	0.9174	2.0423e-10	17	0.21422	1	0.88155	0.80601	9.464e-07
3	0.1819	5	0.045905	0.86003	0.0030503	18	0.31671	1	0.95217	0.97863	0.00024883
4	0.12558	2	0.22518	0.85151	5.6765e-05	19	0.12281	1	0.010019	0.83885	6.3628e-08
5	0.076639	2	0.013965	0.87512	7.0055e-10	20	0.099723	2	0.040626	0.83333	2.1794e-10
6	0.094183	1	0.04873	0.88431	1.491e-10	21	0.067405	2	0.01063	0.84146	0.001894
7	0.091413	1	0.010025	0.88907	7.0909e-09	22	0.20314	5	0.011115	0.97862	7.4731e-05
8	0.061865	3	0.010232	0.91538	1.2663e-10	23	0.09603	1	0.012718	0.97888	4.3264e-09
9	0.1542	3	0.010113	0.97821	2.7617e-10	24	0.083102	3	0.011089	0.80001	2.0768e-08
10	0.092336	2	0.010307	0.91339	3.3622e-06	25	0.19852	3	0.99239	0.81422	3.1124e-10
11	0.10619	3	0.010329	0.89705	2.5414e-10	26	0.11357	2	0.016571	0.81267	0.008776
12	0.069252	2	0.010099	0.83021	1.0997e-08	27	0.085873	2	0.010446	0.81777	1.2133e-10
13	0.083102	2	0.010003	0.80689	9.7536e-07	28	0.36011	1	0.073301	0.97775	0.0050097
14	0.075716	1	0.010273	0.80193	7.0922e-05	29	0.070175	3	0.010102	0.83679	3.7223e-05
15	0.038781	2	0.010104	0.83095	7.9384e-06	30	0.066482	2	0.010518	0.83379	1.606e-05

Fig. 6.

(a) Confusion matrix of Scenario-1. (b) plot of the number of function evaluations vs min objective.

Table 4.

The outcomes of Bayesian-based tuned CNN in scenario 2.

Iter	Objective	depth	Learn rate	Momentum	L2Regularize	Iter	Objective	depth	Learn rate	Momentum	L2Regularize
1	0.17359	5	0.56005	0.89236	2.5293e-08	16	0.39151	1	0.85309	0.80126	0.0047163
2	0.086796	2	0.45045	0.9174	2.0423e-10	17	0.097876	1	0.048194	0.81467	1.1155e-10
3	0.19668	5	0.045905	0.86003	0.0030503	18	0.065559	1	0.015893	0.92199	3.0676e-07
4	0.09603	2	0.22518	0.85151	5.6765e-05	19	0.089566	1	0.20578	0.83616	1.0967e-10
5	0.66759	2	0.96209	0.97666	1.0098e-10	20	0.057248	1	0.055434	0.81781	6.2685e-06
6	0.0988	2	0.69253	0.82806	2.3652e-08	21	0.057248	2	0.010601	0.90455	4.7382e-06
7	0.051708	1	0.045746	0.89761	1.5974e-08	22	0.047091	1	0.060467	0.91755	2.3564e-10
8	0.064635	1	0.027362	0.80004	0.000474	23	0.090489	1	0.043747	0.8017	5.659e-07
9	0.051708	1	0.017239	0.90674	0.00070454	24	0.064635	1	0.029504	0.91162	1.0623e-06
10	0.17452	1	0.91842	0.87403	1.1245e-10	25	0.065559	1	0.010295	0.83171	0.0034166
11	0.11634	5	0.010243	0.80031	0.0015368	26	0.075716	1	0.010218	0.81136	0.00069518
12	0.045245	1	0.1452	0.90559	5.8502e-10	27	0.038781	1	0.042721	0.84845	5.3403e-07
13	0.073869	1	0.53902	0.8108	1.3185e-10	28	0.043398	1	0.010106	0.87598	0.00042163
14	0.057248	1	0.019588	0.90257	2.3604e-10	29	0.15605	4	0.25799	0.81222	1.2145e-10
15	0.3518	1	0.55331	0.90567	0.0022727	30	0.056325	1	0.065363	0.83903	1.1961e-05

Fig. 7.

(a) Confusion matrix of Scenario-2. (b) plot of the number of function evaluations vs min objective.

Table 5.

The outcomes of Bayesian-based tuned CNN in scenario-3.

Iter	Objective	Depth	Learn rate	Momentum	L2 Regularize	Iter	Objective	Depth	Learn rate	Momentum	L2 Regularize
1	0.073869	5	0.56005	0.89236	2.5293e-08	16	0.031394	1	0.3408	0.80021	2.085e-08
2	0.084026	2	0.45045	0.9174	2.0423e-10	17	0.061865	1	0.14746	0.80107	1.7148e-09
3	0.14681	5	0.045905	0.86003	0.0030503	18	0.1265	2	0.20049	0.97991	6.7533e-09
4	0.079409	2	0.22518	0.85151	5.6765e-05	19	0.34441	5	0.71311	0.97992	2.8196e-09
5	0.10249	4	0.57092	0.80002	5.0694e-05	20	0.065559	1	0.36462	0.80086	4.6695e-08
6	0.17359	5	0.60652	0.88909	2.5798e-08	21	0.13758	3	0.93362	0.84857	5.843e-09
7	0.078486	2	0.27832	0.87092	2.719e-07	22	0.056325	1	0.010313	0.84758	3.5044e-07
8	0.084026	2	0.64306	0.81325	5.4379e-09	23	0.054478	1	0.056957	0.92869	4.5579e-09
9	0.064635	3	0.020184	0.90189	1.1136e-10	24	0.048015	1	0.086999	0.81024	1.8238e-06
10	0.073869	1	0.99879	0.85691	3.9481e-10	25	0.056325	1	0.066059	0.97703	1.1357e-10
11	0.087719	3	0.082862	0.97899	1.7582e-07	26	0.028624	1	0.0104	0.80281	1.7329e-08
12	0.1145	1	0.30907	0.96899	4.8241e-09	27	0.058172	1	0.010883	0.80102	8.7027e-09
13	0.068329	3	0.022298	0.80173	1.6709e-08	28	0.037858	1	0.010189	0.88753	1.5256e-06
14	0.033241	3	0.016754	0.80022	2.0167e-06	29	0.2096	5	0.92303	0.80051	2.6785e-07
15	0.63343	4	0.39236	0.97969	4.2755e-06	30	0.058172	1	0.011612	0.97707	1.0257e-07

Fig. 8.

(a) Confusion matrix of Scenario-3. (b) plot of the number of function evaluations vs min objective.

6. Discussion

The comparative assessments of related work are given in Table 6 . It is quite obvious that the suggested methodology achieved a decent classification accuracy in identifying COVID-19 compared to the other strategies presented in the literature. However, the research by revealed a greater accuracy than this research. This could be owing to a much lower number of photos and unbalanced data utilized in their dataset for assessing the framework efficiency. The difficulty in comparing COVID-related research is that the majority of studies employed various datasets and the split of the dataset into train, validation, and test sets is not publicly accessible. The proposed CNN model is the best model to classify our COVID-19 dataset with small number of network size and the best hyperparameter selected. Most of previous work used transfer learning models like VGGNet, GoogleNet, and ResNet, those models have high deep CNN depth with large number of parameters. Three ablation experiments were conducted to determine the effect of Bayesian optimization on our CNN model as illustrated in Table 7 . In the first ablation investigation, we compared Bayesian optimization against three scenarios. We employed convergence plots, accuracy to compare the three scenarios. We discovered that the best architecture achieved by Bayesian search had a 96% accuracy.

Table 6.

Comparison of the performance of several approaches in terms of accuracy.

References	Method	Class	Dataset			Accuracy
			COVID-19	Pneumonia	Normal
Wang et al. [31]	TL	2	565	–	537	96.7%
Chowdhury et al. [32]	CNN	3	219	1345	1341	96.5%
Loey et al. [33]	TL	4	69	bacterial = 79	79	100%
				virus = 79
Abbas et al. [34]	DeTraC	3	105 SARS = 11	–	80	93.1%
El-Rashidy et al. [35]	DL	2	250	–	500	97.9%
Minaee et al. [36]	TL	2	184	–	5000	98%
Wang et al. [37]	ResNet	3	140	9576	8851	96.1%
Khan and Aslam [38]	TL	2	195	–	862	99.3%
Sekeroglu and Ozsahin [39]	CNN	3	225	4292	1583	98.5%
Che Azemin et al. [40]	ResNet	2	154	–	5828	71.9%
Proposed Method		3	3616	3616	3616	96%

Table 7.

Comparison of the performance of several scenarios in terms of accuracy.

Scenarios	Depth of network	Learning rate	Momentum	L2Regularization	Accuracy
Scenario-1	2	0.010518	0.83379	1.606e-05	95.1%
Scenario-2	1	0.042721	0.84845	5.3403e-07	95.2%
Scenario-3	1	0.0104	0.80281	1.7329e-08	96%

The issue with comparing COVID-related research is that most studies employed distinct datasets and the split of the dataset into train, validation, and test sets is not publicly accessible. As a consequence, we trained and evaluated other researchers' techniques on our dataset in order to compare them to ours. Although the datasets were comparable in type, the distribution of data and the assessment process were distinct in each instance. Several studies use cross-validation, while others divided the whole dataset into a train, validation, and test set. Three kinds of X-rays were included in the datasets: normal, pneumonia, and COVID-19 [32,34,37,39]. Normal and COVID-19 X-rays were included in the datasets having two classes [31,35,36,38,40]. Notably, the suggested model is assessed using the COVID-19 Radiology Database scale. Given the global prevalence of positive COVID-19 cases, one may argue that the database is insufficiently big. However, we believe that this is a non-issue. Because the performance of CNN networks increases as the number of samples utilized in the development process increases, in this scenario, just computation time and physical hardware need to be considered. Another critical point to remember is that by the time positive COVID-19 cases are found using X-ray pictures, the infection may have progressed dramatically. In other words, whereas X-ray pictures are a valuable tool for confirming positive COVID-19 instances, they may not be clinically meaningful for early diagnosis. In this regard, our paper presents a unique CNN model that was trained entirely from scratch, rather than using a transfer learning technique. Additionally, rather of employing pre-trained CNNs, the suggested architecture's completely linked layers were investigated, analyzed, and employed for the COVID-19 infection detection job. Our research incorporates novel elements in this regard. Additionally, the suggested model is based on the end-to-end learning approach and does not use a bespoke feature extraction engine. Therefore, a model that is efficient, quick, and dependable was constructed, and encouraging results were obtained.

7. Conclusion

In this study, we offer a new classifier for chest X-ray images using convolutional neural network models (CNNs) based on Bayesian optimization. The suggested model is composed of two distinct components. The first one used CNN to extract features and do classification. The second component is a Bayesian optimizer that is used to modify CNN hyperparameters in accordance with the goal function. The proposed COVID-19 dataset contains 10,848 images (3616 COVID-19, 3616 Normal cases, and 3616 Pneumonia). We compared Bayesian optimization to three different ablation situations in the first ablation research. We compared the three situations using convergence charts and accuracy. We observed that the optimum architecture obtained by Bayesian search was 96% accurate. The findings indicated that the best CNN model is the most successful in identifying balanced COVID-19 pictures when compared to other models assessed on a smaller dataset. This research was compared to previous research using COVID-19 x-ray images. The model outperformed all existing classifiers in terms of predictive power and significance. X-ray analysis is sufficiently promising to permit extrapolation and generalization. In the future, we want to contribute our findings to other machine learning and deep learning projects. Despite its high accuracy rates, the suggested study should be replicated on a larger scale since it has the potential to be used in other medical applications.

Funding

This research received no external funding

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Declaration of competing interest

On behalf of all authors, the corresponding author states that there is no conflict of interest.