Adapting Urban Transport Planning to the COVID-19 Pandemic: An Integrated Fermatean Fuzzy Model

Abstract

The critical worldwide problem of adapting urban transport planning to COVID-19 is for the first time comprehensively addressed and solved in this study. It primarily aims to help transport planners increase the resilience of transport systems. Firstly, a multi-level decision-making hierarchy structure based on four main criteria and 17 sub-criteria is introduced for relevant stakeholders to provide a practical framework for assessing existing transport plans. Then, a three-stage integrated Fermatean fuzzy model for adapting urban transport planning to the pandemic is presented. The model hybridizes the method based on the removal effects of criteria (MEREC) and combined compromise solution (CoCoSo) method into a unique methodological framework under the Fermatean fuzzy environment. A case study provides decision-making guidelines on how to adapt transport plans to COVID-19 in the real-world context of Belgrade, Serbia. The research findings show that the pandemic significantly changed the priorities of transport planning strategies and measures. “Non-motorized travel” is now the best alternative since its numerous short-term measures lead to better transport service. The major advantages of the introduced model are higher flexibility and a more precise fusion of experts’ preference information. The integrated Fermatean fuzzy model could be used for adapting other emerging problems to COVID-19.

1. Introduction

Sustainable transport planning relies on making all transport modes sustainable and widely available in a multimodal transport system (European Commission, 2020). It also supports new sustainable mobility services and measures to reduce traffic congestion and pollution in urban areas. Environmentally sustainable and socially resilient cities are a desirable outcome but the COVID-19 pandemic lead to reconsiderations regarding previous assumptions, criteria, and plans for mobility development (Kesselring and Freudendal-Pedersen, 2021; Miskolczi et al., 2021).

Regardless of the level of development, the travel characteristics of people in urban areas have changed under COVID (Khavarian-Garmsir et al., 2021). Some studies show that mobility is reduced by up to 90% (Muhammad et al., 2020). A survey conducted in Switzerland showed a 60% reduction in the number of trips and mileage (Molloy et al., 2020). Due to the specific way of spreading, the strongest reduction effect was felt in the public transport systems. In Hong Kong, 40% of the respondents stated that they would avoid the use of public transport (Kwok et al., 2020). Users avoid public transport, assessing it as unsafe, and decide to use passenger cars and active transport modes (De Vos, 2020). In the study conducted in Tampere, Finland, the reduction in the number of public transport users during the COVID-19 pandemic is about 70% (Tiikkaja and Viri, 2021). A similar study in Budapest, Hungary, reported that the demand for public transport decreased by approximately 80%, while car usage increased in the range from 43% to 65% (Bucsky, 2020). In a study in the City of Santander, Spain, data showed a reduction of 76% in total mobility, with a decline in public transport of 93% (Aloi et al., 2020). Research in the Netherlands during COVID-19 showed a significant decrease in the use of public transport (about 90%) and lower use of passenger cars (about 80%) (de Haas et al., 2020). A study in Seoul, South Korea, explored variation in subway transport demand during the COVID-19 pandemic and found that the daily count of passengers decreased by 40% (Park, 2020). Similar studies were conducted in some cities in Sweden and revealed that in Stockholm the decrease in public ridership was 60%, while in the county of Västra Götaland it was 40% (Jenelius and Cebecauer, 2020). Research in Turkey also showed that one of the basic preventive measures of COVID-19 is to avoid using public transport (Yıldırım et al., 2021). It should be noted that differences in presented results are partly a consequence of different measures and restrictions to prevent the spread of COVID-19 that varied from country to country. In addition to the fact that a reduction of passengers contributes to large losses in public transport systems, some studies pointed out that extra measures to provide a high level of hygiene in vehicles generated additional costs (Eisenmann et al., 2021). From sustainability and resilience points of view (De Iuliis et al., 2021), a few studies that explored the effects of COVID-19 on mobility showed that multimodality in transport should be pursued, instead of focusing on a single transport mode (Benita, 2021).

Mobility patterns and user behavior are obviously changing during the COVID-19 pandemic. The changes are proved to be in the number of total and commuter trips (Beck and Hensher, 2020), distances of conducted trips (Abdullah et al., 2020), and modal split (Bucsky, 2020). Some researches have shown the so-called modal shift (i.e., the decline in the use of public transport) is followed by an increase in passenger car use and the use of active transport modes (Beck and Hensher, 2020; De Vos, 2020). Although the trip distances decreased during the COVID-19 pandemic (Abdullah et al., 2020), it was discovered that there is no intense shift from passenger car use to non-motorized types of movement. The changes in travel characteristics suggest that all three sustainability aspects (i.e., economic, social, and environmental) should be involved in system planning to mitigate the negative effects on the transport system (Shokouhyar et al., 2021).

There is a great probability that a part of travelers who shifted to passenger cars instead of public transport will find it difficult to get used to the old travel patterns (de Haas et al., 2020). Changes in traveler behavior in the pandemic additionally support the opportunity to promote sustainable means of transport. However, the question of the share of passenger cars in modal split remains, having in mind its individual character (Mouratidis and Papagiannakis, 2021). Even though there are studies that analyzed the changes in the transport system during the various phases of the pandemic (Shakibaei et al., 2021), it is very hard to fully predict the influence of COVID-19 on the future development of transport systems. In this situation, decision-makers are thinking about ways to adapt previously proposed transport planning strategies and measures. Because of the uncertainty about the duration of the pandemic, some studies recommended new approaches in transport policymaking that account for COVID-19 (Zhang, 2020). However, collaboration between different stakeholders (e.g., city authorities, operators, etc.) is strongly needed to transfer knowledge into practical action strategies and adapt existing transport plans. Also, transport planning strategies and measures need to be comprehensively assessed through some multi-criteria decision-making (MCDM) tool since the sustainability of the transport system has to be observed through a prism of social, economic, and environmental development. As a result, it is important to help transport planners choose the most effective measures and define priorities that would contribute to adapting the plans quickly to the “new normal”, by reconsidering plans and policies that lead to future financial programs.

This study aims to help transport planners increase the resilience of the transport system and reduce its vulnerability to COVID-19 by providing a straightforward methodological framework. The major question of adapting transport planning to COVID-19 is comprehensively addressed for the first time in the study. In addition, it aims to explore related key decision criteria to offer a practical framework to follow up. Thus, the study suggests an integrated Fermatean fuzzy model for adapting urban transport planning to the pandemic with a real-life case study of Belgrade, Serbia. The three-stage model hybridizes the method based on the removal effects of criteria (MEREC) and combined compromise solution (CoCoSo) method into a unique methodological framework under the Fermatean fuzzy environment. The formulated model is based on Yager T-norm and T-conorm to attain a more flexible methodological framework as well as enable a more precise aggregation of vague, unreliable, and inexact decision-making preference information under the Fermatean fuzzy environment.

1.1. The Motivation for Using Fermatean Fuzzy Sets

Recently, Senapati and Yager (2020) developed the concept of Fermatean fuzzy sets (FFSs). FFSs are the novel generalization of intuitionistic fuzzy sets (IFSs) (Atanassov, 1983) and Pythagorean fuzzy sets (PyFSs) (Yager, 2013a,b). FFSs provide a more general perspective for fuzzy sets since the sum of cubes of membership and non-membership degrees of FFSs is in the unit interval (Shahzadi and Akram, 2021). They give experts more freedom in expressing their beliefs about membership grades (Senapati and Yager, 2019b; Yang et al., 2021). FFSs are more flexible and efficient than IFSs and PyFSs to handle uncertain information. Therefore, using FFSs to represent decision-making uncertainties when adapting transport planning to the COVID-19 pandemic provides an advanced evaluation of main and sub-criteria importance, a more accurate appraisal of experts’ reputation, and an efficient assessment of investigated alternatives. FFS-based models have already been applied for solving MCDM problems in civil engineering (Senapati and Yager, 2019a, 2020), logistics (Keshavarz-Ghorabaee et al., 2020), and medicine (Akram et al., 2020; Garg et al., 2020). Unfortunately, no previous research provided an FFS-based MCDM model for transport planning.

1.2. The Motivation for Using MEREC

Keshavarz-Ghorabaee et al. (2021) developed the MEREC based on the concept of causality to determine objective weights of evaluation criteria in an MCDM problem and confirmed its consistency with other state-of-the-art objective weighting methods. This method uses the removal effect of each criterion on the overall performance of alternatives for calculating criteria weights. Also, it utilizes a logarithmic function to measure the overall and partial performances of the alternatives. The MEREC assigns greater weights to the criteria that have higher effects on alternatives’ performances. Its calculation process is forthright, logical, and methodical. To the best of the authors’ knowledge, none of the previous studies utilized this innovative criteria weighting method for solving real-world decision-making problems. Moreover, the traditional MEREC may not be able to cope with a multi-level decision-making hierarchy since its hierarchical form is not attainable. Also, its integration with other decision-making method(s) into a unique methodological framework is still missing. Finally, the MEREC, as one of the latest criteria weighting methods, has not been extended under the Fermatean fuzzy environment. To fill these research gaps, this study develops the Fermatean fuzzy hierarchical MEREC and utilizes it to determine the importance of main and sub-criteria for comparing different strategies for adapting transport planning to COVID-19.

1.3. The Motivation for Using CoCoSo Method

The CoCoSo is one of the newest MCDM methods introduced by Yazdani et al. (2018, 2019b). This method is based on the combinatory perspective (Mi and Liao, 2020). It integrates simple additive weighting and exponentially weighted product models (Zavadskas et al., 2021). This MCDM method can obtain the best alternative without counterintuitive phenomena and division by zero problems (Torkayesh et al., 2021a). Also, the deletion or addition of alternatives has a minimum impact on final results (Cui et al., 2021). The original CoCoSo method is highly effective in the ranking of alternatives with deterministic parameters (Kieu et al., 2021; Khan and Haleem, 2021; Torkayesh and Simic, in press). It has been extended under various uncertain environments, such as grey (Yazdani et al., 2019a), hesitant fuzzy linguistic term (Wen et al., 2019b), interval rough (Erceg et al., 2019), probabilistic linguistic term (Wen et al., 2019a), triangular fuzzy (Ecer and Pamucar, 2020), interval-valued (Maghsoodi et al., 2020), neutrosophic soft (Peng and Smarandache, 2020), picture fuzzy (Švadlenka et al., 2020), Pythagorean fuzzy (Peng et al., 2020), rough (Yazdani et al., 2020), interval-valued intuitionistic fuzzy (Alrasheedi et al., 2021), interval-valued fuzzy soft (Peng et al., 2021), intuitionistic fuzzy soft (Peng and Garg, in press), and single-valued neutrosophic (Rani and Mishra, in press). However, this exceptional MCDM method has not been extended before using FFSs so it may lead to erroneous decisions under contradictory decision-making environments. Also, the extension with FFSs can significantly improve the practicality of the CoCoSo method under uncertain real-life decision-making environments. On the other hand, real-life applications of the CoCoSo method in the transportation engineering area are scarce; e.g., last-mile delivery mode evaluation (Švadlenka et al., 2020) and automotive passenger vehicle selection (Biswas et al., 2020). To the best of the authors’ knowledge, this exceptional MCDM method has neither been applied for transport planning. To fill these research gaps, we formulate the Fermatean fuzzy CoCoSo method and apply it to rank alternative strategies for adapting transport planning to COVID-19.

1.4. Contributions of the Study

The theoretical and practical contributions of this study to the present body of knowledge are as follows:

• i)The critical worldwide problem of adapting transport planning to COVID-19 is for the first time comprehensively addressed and solved in this study. Also, a multi-level decision-making hierarchy structure based on four main criteria and 17 sub-criteria is introduced for relevant stakeholders to provide a practical framework for assessing and adapting existing transport plans to COVID-19 in a real-world context.
• ii)This is the first study that formulates an integrated Fermatean fuzzy methodological framework based on the hierarchical MEREC and CoCoSo methods with very flexible Yager norms. Besides, different from the available MCDM models for transport planning or COVID-19 analysis that mostly equally appraise experts, the proposed group decision-making model can account for their experience, domain expertise, and impact. As a result, the integrated Fermatean fuzzy model offers to researchers and practitioners a more precise fusion of experts’ preference information.
• iii)A case study of Belgrade confirms the effectiveness of the integrated Fermatean fuzzy model and provides valuable decision-making guidelines. The research findings show that the pandemic significantly changed the priorities of transport planning strategies and measures. The external aspect is recognized as a crucial main criterion. “Non-motorized travel” is now the best alternative for Belgrade since its numerous short-term measures lead to better transport service.
• iv)Even though this study primarily aims to adapt available transport plans to COVID-19, the integrated Fermatean fuzzy model can be applied to solve other emerging pandemic-related MCDM problems.

This research is structured as follows: Section 2 provides a review of related state-of-the-art research. Section 3 defines the investigated problem. Section 4 presents the integrated Fermatean fuzzy model for adapting transport planning to the COVID-19 pandemic. Section 5 provides the results and discussion. Section 6 presents the conclusions and indicates possible future research directions.

2. Literature Review

The literature review is organized into three sub-sections. The first sub-section overviews available MCDM approaches for transport planning. The second sub-section surveys state-of-the-art MCDM approaches for COVID-19 analysis. The third sub-section presents identified research gaps.

2.1. Multi-Criteria Decision-Making Approaches for Transport Planning

MCDM has a special role in the early stages of transport infrastructure planning and improvement of service quality. A summary of the available MCDM approaches for transport planning is presented in Table 1 .

Table 1.

Summary of the available multi-criteria decision-making approaches for transport planning.

Author(s) and year	Research focus	GDM	Parameter type	SA	CA	Method(s)	Country	(Main) criteria	Sub-criteria	Alt.
Barbosa et al. (2017)	PT indicator evaluation	Yes	Deterministic	No	No	AHP	Brazil	10	30	−
Nassereddine and Eskandari (2017)	PT system evaluation	Yes	Deterministic	Yes	No	AHP, PROMETHEE	Iran	6	−	5
Awasthi et al. (2018)	Urban mobility project evaluation	Yes	Fuzzy	Yes	No	TOPSIS, VIKOR, GRA	Luxemburg	4	31	3
Barfod (2018)	Transport project appraisal	No	Deterministic	No	No	SMARTER	Denmark	3	8	4
Güner (2018)	Bus route assessment	Yes	Deterministic	No	Yes	AHP, TOPSIS	Turkey	2	9	10
Lee (2018)	Advanced PT mode evaluation	Yes	Deterministic	No	No	AHP	Korea	4	13	3
Ullah et al. (2018)	Transp. fuel technology selection	No	Deterministic	Yes	No	AHP	Pakistan	4	12	3
Li et al. (2019)	Clean energy vehicle selection	Yes	Deterministic	No	No	AHP, VIKOR	China	5	20	4
Moslem et al. (2019)	PT quality evaluation	Yes	Fuzzy	No	No	AHP	Turkey	3	11	−
Broniewicz and Ogrodnik (2020)	Expressway section selection	No	Deterministic	No	Yes	AHP, TOPSIS	Poland	13	−	6
Dogan et al. (2020)	Vehicle corridor selection	Yes	IVIF	Yes	Yes	AHP, TOPSIS	Turkey	6	15	5
Hamurcu and Eren (2020a)	Electric bus selection	Yes	Deterministic	Yes	No	AHP, TOPSIS	Turkey	6	−	6
Hamurcu and Eren (2020b)	PT project evaluation	Yes	Fuzzy	No	No	AHP, TOPSIS	Turkey	4	14	3
Li et al. (2020)	Rail transit quality evaluation	Yes	PyF	No	Yes	SE, MULTIMOORA	China	5	26	5
Pérez-Dominguez et al. (2020)	Transport performance evaluative	Yes	PyF	No	Yes	CODAS	Mexico	25	−	6
Seker and Aydin (2020)	PT system selection	Yes	IVIF	Yes	Yes	AHP, CODAS	Turkey	5	18	4
Duleba et al. (2021)	Commuter modal split estimation	Yes	Deterministic	Yes	No	BWM	Hungary	−	−	6
Morfoulaki and Papathanasiou (2021)	Mobility measure evaluation	Yes	Deterministic	No	No	PROMETHEE	Greece	2	−	10
Rao (2021)	Rail transit system indicators	Yes	Deterministic	No	No	DEMATEL, ANP	ROC (Taiwan)	3	7	−
Our study	Adapting transport planning to COVID-19	Yes	Fermatean fuzzy	Yes	Yes	H-MEREC, CoCoSo	Serbia	4	17	5

Analytic Hierarchy Process: AHP, Analytic Network Process: ANP, Best-Worst Method: BWM, COmbinative Distance-based ASsessment: CODAS, Combined Compromise Solution: CoCoSo, Comparative Analysis: CA, COronaVIirus Disease-2019: COVID-19, DEcision MAking Trial and Evaluation Laboratory: DEMATEL, Grey Relational Analysis: GRA, Group Decision-Making: GDM, Hierarchical MEthod based on the Removal Effects of Criteria: H-MEREC, Interval-Valued Intuitionistic Fuzzy: IVIF, Multi-Objective Analysis by Ratio Analysis plus the Full Multiplicative Form: MULTIMOORA, Preference Ranking Organization METHod for Enrichment Evaluations: PROMETHEE, Public Transport: PT, Pythagorean Fuzzy: PyF, Sensitivity Analysis: SA, Shannon Entropy: SE, Simple Multi-Attribute Rating Technique Exploiting Ranks: SMARTER, Technique for Order of Preference by Similarity to Ideal Solution: TOPSIS, VIšeKriterijumska Optimizacija i kompromisno Rešenje: VIKOR.

Barbosa et al. (2017) identified objective and subjective indicators that determine a user's opinion of the service quality of urban public transport. Nassereddine and Eskandari (2017) estimated the service quality of public transport systems from the passengers' point of view. Awasthi et al. (2018) performed a sustainability evaluation of urban mobility projects in situations under limited or no quantitative information. Several studies applied MCDM approaches to make consensus among different stakeholders on the future development of transport systems (Barfod, 2018; Moslem et al., 2019). Güner (2018) assessed the quality of bus transit routes from the passengers’ point of view. Lee (2018) investigated appropriate advanced public transport modes for specific city types. Ullah et al. (2018) appraised three gaseous alternatives for the road transport sector from aspects in the context of sustainable development. Li et al. (2019) prioritized clean-energy vehicle alternatives by taking into account electricity, gas, ethanol, and methanol propulsions.

Broniewicz and Ogrodnik (2020) ranked the most favorable route variants according to environmental criteria. Dogan et al. (2020) assessed suitable corridors for operating autonomous vehicles as public transport. Hamurcu and Eren (2020a) evaluated the introduction of new technologies in transport, like electric vehicle technology for buses. Hamurcu and Eren (2020b) prioritized alternative public transport projects based on sustainability. Li et al. (2020) explored the passenger satisfaction level of public transportation systems to improve their competitiveness. Pérez-Dominguez et al. (2020) analyzed alternatives of public transport lines to provide a comprehensive evaluating method. Seker and Aydin (2020) assessed sustainable public transportation systems for public university campuses in metropolitan areas.

Recently, Duleba et al. (2021) suggested a new approach for modal split estimation by ranking mode choice alternatives. Morfoulaki and Papathanasiou (2021) evaluated the most important sustainable mobility measures that should be implemented in urban areas. Rao (2021) defined key sustainability indicators of transportation systems and examined their causality and correlation.

2.2. Multi-Criteria Decision-Making Approaches for COVID-19 Analysis

The worldwide effect of the COVID-19 pandemic has attracted the large attention of researchers in various fields. Table 2 provides the widespread overview of the available MCDM approaches for COVID-19 analysis.

Table 2.

Summary of the available multi-criteria decision-making approaches for COVID-19 analysis.

Author(s) and year	Research focus	GDM	Parameter type	SA	CA	Method(s)	Country	(Main) criteria	Sub-criteria	Alt.
Belhadi et al. (2020)	Adapting waste management	Yes	IVF	Yes	No	LCA, LCC, AHP, VIKOR	Morocco	4	17	5, 5
Biswas and Das (2020)	SC barrier evaluation	Yes	Fuzzy	No	No	AHP	India	5	−	−
Kaya (2020)	Development impact assessment	Yes	Deterministic	Yes	Yes	MAIRCA	OECD	8	−	33
Ocampo and Yamagishi (2020)	Lockdown protocol evaluation	Yes	IF	No	No	DEMATEL	Philippines	13	−	−
Ali Shah et al. (2021)	Adapting waste management	Yes	Fuzzy	No	No	DEMATEL, ANP, VIKOR	Pakistan	3	9	7
Bait et al. (2021)	Locating indicator evaluation	Yes	Deterministic	No	No	AHP, TOPSIS	Ghana	7	34	−
Deng and Kong (2021)	Rescue scheme selection	Yes	IVIF	No	No	TOPSIS	IE	4	−	3
Ecer and Pamucar (2021)	Insurance company evaluation	Yes	IF	Yes	Yes	MARCOS	Turkey	7	−	10
Hezer et al. (2021)	Safety level evaluation	No	Deterministic	Yes	Yes	TOPSIS, VIKOR, COPRAS	World	6	−	100
Ilyas et al. (2021)	Supplier risk evaluation	No	Det., fuzzy	No	Yes	BWM, TOPSIS	Morocco	4	11	−
Kumar et al. (2021)	SC risk evaluation	Yes	Fuzzy	No	No	BWM	India	9	−	−
Lin et al. (2021)	Smart hospital asset selection	Yes	Deterministic	No	No	AHP	ROC (Taiwan)	5	15	4
Manupati et al. (2021)	Adapting waste disposal	Yes	Fuzzy	Yes	Yes	VIKOR	India	4	10	9
Ortiz-Barrios et al. (2021)	Preparedness level assessment	Yes	Deterministic	No	Yes	AHP, TOPSIS	Colombia	8	29	7
Pamučar et al. (2020)	Adapting healthcare system	Yes	Fuzzy	Yes	Yes	LBWA, MACBETH, RAFSI	Serbia	5	−	4
Marti and Puertas (in press)	Vulnerability assessment	No	Deterministic	No	No	TOPSIS	EU	3	−	29
Qarnain et al. (in press)	Adapting energy consumption	Yes	Deterministic	No	No	BWM, DEMATEL	India	4	17	−
Rathore and Gupta (in press)	Occupational safety assessment	Yes	Fuzzy	Yes	No	Delphi, AHP, TOPSIS	India	5	15	5
Sharma et al. (in press)	SC survivability evaluation	Yes	Deterministic	No	No	SWARA	IE	6	18	−
Our study	Adapting transport planning to COVID-19	Yes	Fermatean fuzzy	Yes	Yes	H-MEREC, CoCoSo	Serbia	4	17	5

Analytic Hierarchy Process: AHP, Analytic Network Process: ANP, Best-Worst Method: BWM, Combined Compromise Solution: CoCoSo, Comparative Analysis: CA, COmplex PRoportional Assessment: COPRAS, COronaVIirus Disease-2019: COVID-19, DEcision MAking Trial and Evaluation Laboratory: DEMATEL, Group Decision-Making: GDM, Hierarchical MEthod based on the Removal Effects of Criteria: H-MEREC, Illustrative Example: IE, Interval-Valued Fuzzy: IVF, Interval-Valued Intuitionistic Fuzzy: IVIF, Intuitionistic Fuzzy: IF, Level Based Weight Assessment: LBWA, Life Cycle Assessment: LCA, Life Cycle Costing: LCC, Measurement of Alternatives and Ranking according to COmpromise Solution: MARCOS, Measuring Attractiveness by a Categorical-Based Evaluation Technique: MACBETH, Multi Attribute Ideal Real Comparative Analysis: MAIRCA, Organisation for Economic Co-operation and Development: OECD, Preference Ranking Organization METHod for Enrichment Evaluations: PROMETHEE, Ranking of Alternatives through Functional mapping of criterion sub-intervals into a Single Interval: RAFSISensitivity Analysis: SA, Step-wise Weight Assessment Ratio Analysis: SWARA, Supply Chain: SC, Technique for Order of Preference by Similarity to Ideal Solution: TOPSIS, VIšeKriterijumska Optimizacija i kompromisno Rešenje: VIKOR.

Belhadi et al. (2020) compared various management strategies for infectious solid waste and wastewater flows to reveal the best available treatment technologies during the COVID-19 pandemic. Biswas and Das (2020) identified essential barriers to supply chain management in the manufacturing sector during the lockdown. Kaya (2020) ranked the sustainability performance of numerous countries worldwide to quantify the negative effect of COVID-19 on their development level. Ocampo and Yamagishi (2020) appraised relaxation protocols for a lockdown exit strategy to offer guidelines for relevant government bodies. Ali Shah et al. (2021) prioritized thermal, thermochemical, and biochemical waste-to-energy treatment options to accelerate sustainable development in the post-COVID-19 world. Bait et al. (2021) assessed criteria for locating manufacturing plants for the textile industry based on the COVID-19 impact. Deng and Kong (2021) explored the humanitarian rescue process and evaluated emergency plans under multiple criteria. Ecer and Pamucar (2021) assessed the performances of insurance companies in health services during COVID-19. Hezer et al. (2021) analyzed regional safety levels worldwide in terms of COVID-19. Ilyas et al. (2021) prioritized pandemic-related risks for supplier selection in the automotive industry. Kumar et al. (2021) identified and prioritized risk mitigation strategies for perishable food supply chains during the pandemic. Lin et al. (2021) researched a hospital evaluation system and performed smart asset categorization in the COVID-19 context. Manupati et al. (2021) analyzed health care waste disposal techniques for the effective treatment of medical wastes during COVID-19. Ortiz-Barrios et al. (2021) compared the preparedness level of companies from the electrical appliance sector. Pamučar et al. (2020) ranked strategic guidelines for the reorganization of healthcare systems based on the prediction of disease spread.

Recently, Marti and Puertas (in press) analyzed the vulnerability of countries to the present health crisis. Qarnain et al. (in press) examined energy efficiency in residential buildings to determine energy conservation factors during pandemic times. Rathore and Gupta (in press) evaluated hospitals and health management systems based on safety risk factors among healthcare workers. Sharma et al. (in press) proposed factors for enhancing the survivability of sustainable supply chains in COVID-19.

2.3. Research Gaps

There is a scarcity of transport planning studies in the COVID-19 context that provide straightforward and flexible decision-making tools for relevant stakeholders (Table 1, Table 2). Besides, the available deterministic, fuzzy, intuitionistic fuzzy, and/or Pythagorean fuzzy MCDM approaches for transport planning (Table 1) or COVID-19 analysis (Table 2) could generate and recommend erroneous decisions to researchers and practitioners since they are unable to handle higher levels of uncertainties and provide freedom in expressing decision-making preferences, especially under a contradictory decision-making environment such as the COVID-19 pandemic. On the other hand, FFSs are an advanced type of fuzzy technique (De Iuliis et al., 2019), which can handle higher levels of incompleteness or impreciseness by assigning fuzzy parameters from a much larger domain than IFSs and PyFSs. As a result, an FFS-based decision-making approach is fully applicable under the contradictory COVID-19 environment in which the sum and quadratic sum of membership and non-membership degrees of experts’ reputation, main and sub-criteria importance, and/or transport plans could exceed 1. Unfortunately, no previous research provided an FFS-based model for transport planning and/or COVID-19 analysis, as can be seen from Tables 1-2.

The MEREC, as one of the newest criteria weighting methods, has neither been applied in a real-world context nor been integrated with other decision-making methods into a unique methodological framework. Besides, its hierarchical form, as well as extension into the Fermatean fuzzy environment, are still missing. On the other hand, the CoCoSo method, which is a very popular and influential MCDM tool, has neither been applied for transport planning nor been extended before using FFSs. As a result, this study also aims to provide an integrated Fermatean fuzzy methodological framework based on the hierarchical MEREC and CoCoSo methods with very flexible Yager norms as well as approve its effectiveness in the real-world context of adapting transport plans for Belgrade.

3. Problem Definition

Belgrade is the capital of Serbia and the third-largest city in South-East Europe with a residential population of 1.65 million inhabitants. As one of the oldest cities in Europe, Belgrade joined Green Cities in August 2018 to build a better and more sustainable future for its residents (EBRD, 2021). Two important Pan-European transport corridors, Corridor X and Corridor VII intersect in Belgrade. The total number of daily person trips generated in Belgrade is more than 3 million with a very high share of public transport that makes it a typical “public transport city”.

In recent years, two very important transport plans were adopted in Belgrade: 1) Transport master plan (EBRD, 2017), 2) Sustainable urban mobility plan (EPC, 2020). Both plans relied on data that did not take into account the effects of the COVID-19 pandemic. Since travel patterns have changed and it is uncertain if they will ever go back to the previous state, there is a necessity to adapt the plans.

Travel data show that the motorization rate increased from 191 to 306 passenger cars per 1000 inhabitants in the period from 2000 to 2017. It is expected that the motorization rate will grow further to 429 passenger cars per 1000 inhabitants in 2033, which presents an average annual growth rate of 3.5% (Fig. 1 ). Close to 65% of trips last under 30 minutes, 15.8% last under 10 minutes, and 9.5% last longer than one hour. Modal split shows that almost 50% of all trips are executed by public transport, while around 24% by passenger cars. The share of bicycle trips is below 1% in the modal split (EBRD, 2017).

Fig. 1.

The trend of motorization rate.

Development scenarios for 2021, 2027, and 2033 indicate that the current trends will lead to an increase in traffic congestion and produce negative environmental impacts. It is expected for public transport use to decrease to 43%, while passenger cars use shall increase to 34% (EBRD, 2017). Compared to 2021, the average traffic congestion on the entire network will increase by 18% and 37% in 2027 and 2033, respectively.

The Sustainable urban mobility plan for Belgrade (EPC, 2020) was adopted in 2020. It was based on the Transport master plan of Belgrade as well as the European Green Deal and the Sustainable and Smart Mobility Strategy (European Commission, 2019, 2020). This plan defines a number of measures to make Belgrade a better place to live. The measures aim to improve the quality and sustainability of the transport system by increasing the share of non-motorized modes of travel and the use of public transport. However, this plan did not take into account the impact of the COVID-19 pandemic.

According to one small survey conducted in Belgrade (SKGO, 2020), COVID-19 contributed to an additional increase in the use of passenger cars, where more than 36% of people stated that they used it more. Additionally, the increase in the use of walking (by 49%) and cycling (by 30%) was reported. On the other hand, about a 50% decrease in the use of public transport was identified.

All previously presented facts show that the situation in traffic can become even more unfavorable and stress out the importance of adapting to the changes of travel behavior since the additional increase in passenger car use can significantly reduce the efficiency of the transport system. It is essential to take into account the impact of the COVID-19 pandemic in changing the priorities defined by the Sustainable urban mobility plan for Belgrade.

This study defines several alternatives for adapting transport planning to COVID-19 in Belgrade. They represent strategies that put a priority on different measures. It would be ideal to provide the simultaneous implementation of all strategies. However, this is not possible due to different limitations (e.g., economic, organizational, etc.). Alternative strategies were constructed around measures proposed by the Sustainable urban mobility plan for Belgrade as well as changes in the travel characteristics caused by the COVID-19 pandemic.

3.1. Definition of Alternatives

• i)
  Non-motorized travel (A ₁) − Development of non-motorized modes of transport (e.g., walk and bikes) and micro-mobility. This alternative includes the following measures:

  • •
    improvement of the pedestrian infrastructure,
  • •
    improvement of connections with other transport modes,
  • •
    development of pedestrian and integrated streets, super-blocks, and spaces,
  • •
    development of the bicycle network (e.g., paths, lanes, parking lots),
  • •
    improvement of the existing cycling infrastructure,
  • •
    implementation of public bicycle systems,
  • •
    transport of bicycles in public transport vehicles,
  • •
    promotion of cyclo (cycling) tourism to realize EuroVelo routes and Bike-and-Bed,
  • •
    development of micro-mobility.
• ii)
  Service quality improvement in public transport (A ₂) − Improving the quality of service in the public transport system. This alternative includes the following measures:

  • •
    development and improvement of the structure and efficiency of the entire urban public transport system,
  • •
    development and improvement of high-capacity rail sub-systems of the public passenger transport,
  • •
    development of public transport sub-systems related to passengers’ river transport.
• iii)
  Mobility management (A ₃) − Promoting transport policies that will try to mitigate the increased number of passenger cars. This alternative includes the following measures:

  • •
    development of the Mobility-as-a-service (MaaS) concept,
  • •
    work from home,
  • •
    car sharing,
  • •
    carpooling,
  • •
    parking management,
  • •
    e-mobility services,
  • •
    promotion of greater use of Park-and-Ride and Bike-and-Ride systems.
• iv)
  Transport infrastructure development (A ₄) − Satisfying the increased number of passenger car users through investment in the infrastructure. This alternative includes the following measures:

  • •
    construction of subway,
  • •
    completion of inner ring,
  • •
    completion of external highway tangents,
  • •
    the old Sava bridge and the tunnel connection between the Sava and Danube slopes
  • •
    construction of public garages,
  • •
    construction of parking lots to implement the Park-and-Ride system on perimeter terminals,
  • •
    other reconstructions of the street network.
• v)
  Intelligent transport systems (A ₅) − Investing in real-time traffic management and driver assistance systems to enable the maximum utilization of the existing capacities. In this way, the efficiency of the transport system is improved by applying modern technological solutions. This alternative includes the following measures:

  • •
    adaptive traffic management system,
  • •
    advanced driver assistance systems (ADAS).

3.2. Definition of Criteria

1) Environmental aspect (MC₁):

• •Air pollution (C ₁) − Assessment of how an alternative affects air pollution.
• •Noise (C ₂) − Assessment of how an alternative affects noise.
• •Eco-friendliness (C ₃) − Refers to the extent to which the construction and operation of a specific alternative can affect the natural environment of a city.
• •Land use impact (C ₄) − Land consumption per population for necessary infrastructure.

2) Economic aspect (MC₂):

• •Community cost (i.e., investment cost) (C ₅) − Costs of infrastructure, equipment, and facilities.
• •Operator cost (i.e., operational and maintenance costs) (C ₆) − Costs required to maintain and operate solutions proposed by an alternative.
• •User cost (i.e., affordability for potential users) (C ₇) − Assessment whether an alternative is affordable for all categories of transport system users.

3) Social aspect (MC₃):

• •Travel time (C ₈) − Whether an alternative provides a shorter travel time.
• •User accessibility (C ₉) − Assessment of how easy it is for users to access and use an alternative.
• •Spatial coverage (C ₁₀) − The geographical coverage of a city by an alternative.
• •Interconnectivity (i.e., connectivity to other transport modes) (C ₁₁) − It refers to how well a specific alternative is connected with other transport networks.
• •New users (i.e., the intensity of attracting new users) (C ₁₂) − The power of an alternative to attract new users.

4) External aspect (MC₄):

• •Political support (C ₁₃) − The probability that an alternative will be supported by politicians.
• •Public support (C ₁₄) − The probability that an alternative will be supported by the general public, including non-governmental organizations.
• •Congestion reduction (C ₁₅) − Impact on city congestion reduction by an alternative.
• •Resource efficiency (C ₁₆) − Non-renewable resource consumption in the production and use of vehicles and transport facilities.
• •Safety (C ₁₇) − The degree to which transport system users can be protected from an accident.

The main criteria are environmental, economic, social, and external. Sub-criteria are defined so that they cover all important effects in the main criteria domains. As a result, this study differentiates four main criteria and 17 sub-criteria for adapting transport planning to the COVID-19 pandemic. Fig. 2 presents a hierarchical three-level structure of the investigated decision-making problem.

Fig. 2.

Three-level decision-making hierarchy structure for adapting transport planning to COVID-19.

4. Methodology

This section provides some preliminaries and presents the integrated Fermatean fuzzy model for adapting transport planning to the COVID-19 pandemic.

4.1. Preliminaries

FFSs are a novel extension of IFSs and PyFSs. Compared to IFSs and PyFSs, FFSs provide a more general perspective for two-dimensional (i.e., membership and non-membership) information since the sum of cubes of membership and non-membership degrees of FFSs is in the unit interval (Fig. 3 ).

Fig. 3.

The relationships between intuitionistic, Pythagorean, and Fermatean fuzzy sets.

Definition 1

(Atanassov, 1986). An intuitionistic fuzzy set A defined on a non-empty set X is an object having the form $A=\left\{〈x,{\alpha }_A\left(x\right),{\beta }_A\left(x\right)〉|x\in X\right\},$ where ${\alpha }_A\left(x\right)\in \left[0,1\right]$ and ${\beta }_A\left(x\right)\in \left[0,1\right]$ are the degree of membership and the degree of non-membership of the element x in the set A, respectively, and $0\le {\alpha }_A\left(x\right)+{\beta }_A\left(x\right)\le 1$ for every x∈X (Fig. 3).

Definition 2

(Yager, 2013). A Pythagorean fuzzy set P defined on a non-empty set X is an object having the form $P=\left\{〈x,{\alpha }_P\left(x\right),{\beta }_P\left(x\right)〉|x\in X\right\},$ where ${\alpha }_P\left(x\right)\in \left[0,1\right]$ and ${\beta }_P\left(x\right)\in \left[0,1\right]$ are the degree of membership and the degree of non-membership of the element x in the set P, respectively, and $0\le {\left({\alpha }_P\left(x\right)\right)}^2+{\left({\beta }_P\left(x\right)\right)}^2\le 1$ for every x∈X (Fig. 3).

Definition 3

(Senapati and Yager, 2019a, 2020). A Fermatean fuzzy set $\tilde{F}$ in a universe X is an object having the form of:

$$\tilde{F}=\{〈x,\alpha \widetilde{{}_F}\left(x\right),\beta \widetilde{{}_F}\left(x\right)〉|x\in X\},$$ (1)

where $\alpha \widetilde{{}_F}\left(x\right)\in [0,1]$ is the degree of membership of the element x in the set $\tilde{F},$ $\beta \widetilde{{}_F}\left(x\right)\in [0,1]$ is the degree of non-membership of the element x in the set $\tilde{F},$ and $\alpha \widetilde{{}_F}\left(x\right)$ and $\beta \widetilde{{}_F}\left(x\right)$ satisfy the condition (Fig. 3):

$$0\le {\left(\alpha \widetilde{{}_F}\left(x\right)\right)}^3+{\left(\beta \widetilde{{}_F}\left(x\right)\right)}^3\le 1,\forall x\in X.$$ (2)

The degree of indeterminacy of the element x in the set $\tilde{F}$ is:

$${\pi }_{\tilde{F}}\left(x\right)=\sqrt[3]{1-{\left(\alpha \widetilde{{}_F}\left(x\right)\right)}^3-{\left(\beta \widetilde{{}_F}\left(x\right)\right)}^3},\forall x\in X.$$ (3)

If X has only one element, then $\tilde{F}=\left\{〈x,\alpha \widetilde{{}_F}\left(x\right),\beta \widetilde{{}_F}\left(x\right)〉\right|x\in X\}$ is called a Fermatean fuzzy number (FFN) in which ${\alpha }_{\tilde{F}},{\beta }_{\tilde{F}}\in [0,1],$ and $0\le {\alpha }_{\widetilde{{}_F}}^3+{\beta }_{\widetilde{{}_F}}^3\le 1.$ For convenience, an FFN is denoted by $\tilde{F}=({\alpha }_{\tilde{F}},{\beta }_{\tilde{F}}).$

Definition 4

(Garg et al., 2020). Let $\tilde{F}=({\alpha }_{\tilde{F}},{\beta }_{\tilde{F}}),$ ${\tilde{F}}_1=({\alpha }_{{\tilde{F}}_1},{\beta }_{{\tilde{F}}_1}),$ and ${\tilde{F}}_2=({\alpha }_{{\tilde{F}}_2},{\beta }_{{\tilde{F}}_2})$ be three FFNs, the operational parameter η>0, and τ>0. The Yager T-norm and T-conorm operations of FFNs are defined as follows:

(a) Addition “⊕”

$$\begin{array}{c}\begin{array}{ccc}{\tilde{F}}_1\oplus {\tilde{F}}_2\hfill & =& (\sqrt[3]{\min [1,{({\alpha }_{{\tilde{F}}_1}^{3\eta }+{\alpha }_{{\tilde{F}}_2}^{3\eta })}^{1/\eta }]},\hfill \end{array}\hfill \\ \sqrt[3]{1-\min \{1,{[{(1-{\beta }_{{\tilde{F}}_1}^3)}^{\eta }+{(1-{\beta }_{{\tilde{F}}_2}^3)}^{\eta }]}^{1/\eta }\}}),\hfill \end{array}$$ (4)

(b) Multiplication “⊗”

$$\begin{array}{c}\begin{array}{ccc}{\tilde{F}}_1\otimes {\tilde{F}}_2\hfill & =& (\sqrt[3]{1-\min \{1,{[{(1-{\alpha }_{{\tilde{F}}_1}^3)}^{\eta }+{(1-{\alpha }_{{\tilde{F}}_2}^3)}^{\eta }]}^{1/\eta }\}},\hfill \end{array}\hfill \\ \sqrt[3]{\min [1,{({\beta }_{{\tilde{F}}_1}^{3\eta }+{\beta }_{{\tilde{F}}_2}^{3\eta })}^{1/\eta }]}),\hfill \end{array}$$ (5)

(c) Scalar multiplication

$$\tau \tilde{F}=(\sqrt[3]{\min [1,{\left(\tau {\alpha }_{\tilde{F}}^{3\eta }\right)}^{1/\eta }]},\sqrt[3]{1-\min \{1,{\left[\tau {(1-{\beta }_{\tilde{F}}^3)}^{\eta }\right]}^{1/\eta }\}}),$$ (6)

(d) Power

$${\tilde{F}}^{\tau }=(\sqrt[3]{1-\min \{1,{\left[\tau {(1-{\alpha }_{\tilde{F}}^3)}^{\eta }\right]}^{1/\eta }\}},\sqrt[3]{\min [1,{\left(\tau {\beta }_{\tilde{F}}^{3\eta }\right)}^{1/\eta }]}),$$ (7)

Definition 5

(Senapati and Yager, 2019a, 2020). Let $\tilde{F}=({\alpha }_{\tilde{F}},{\beta }_{\tilde{F}})$ be an FFN. The complement is defined as follows:

$${\tilde{F}}^c=({\beta }_{\tilde{F}},{\alpha }_{\tilde{F}}).$$ (8)

Definition 6

(Keshavarz-Ghorabaee et al., 2020). Let $\tilde{F}=({\alpha }_{\tilde{F}},{\beta }_{\tilde{F}})$ be an FFN. The positive score function is defined as follows:

$$\mathit{score}\left(\tilde{F}\right)=1+{\alpha }_{\tilde{F}}^3-{\beta }_{\tilde{F}}^3.$$ (9)

Definition 7

(Garg et al., 2020). Let ${\tilde{F}}_l=({\alpha }_{{\tilde{F}}_l},{\beta }_{{\tilde{F}}_l})$ (l=1, ..., p) be a number of FFNs, the operational parameter η>0, and γ=(γ ₁, ..., γ_p)^T be the weight vector of them, with γ_l∈[0, 1] and $\sum _{l=1}^p{\gamma }_l=1.$ A Fermatean fuzzy Yager weighted average (FFYWA) operator is defined as follows:

$$\begin{array}{c}\mathit{FFYW}{A}_{\gamma }({\tilde{F}}_1,...,{\tilde{F}}_l,...,{\tilde{F}}_p)=\underset{l=1}{\stackrel{p}{\oplus }}\left({\gamma }_l{\tilde{F}}_l\right)\hfill \\ =(\sqrt[3]{\min [1,{\left({\sum }_{l=1}^p{\gamma }_l{\alpha }_{{\tilde{F}}_l}^{3\eta }\right)}^{1/\eta }]},\sqrt[3]{1-\min \{1,{\left[{\sum }_{l=1}^p{\gamma }_l{(1-{\beta }_{{\tilde{F}}_l}^3)}^{\eta }\right]}^{1/\eta }\}}).\hfill \end{array}$$ (10)

and a Fermatean fuzzy Yager weighted geometric (FFYWG) operator is defined as follows:

$$\begin{array}{c}\mathit{FFYW}{G}_{\gamma }({\tilde{F}}_1,...,{\tilde{F}}_l,...,{\tilde{F}}_p)=\underset{l=1}{\stackrel{p}{\otimes }}{\tilde{F}}_l^{{\gamma }_l}\hfill \\ =(\sqrt[3]{1-\min \{1,{\left[{\sum }_{l=1}^p{\gamma }_l{(1-{\alpha }_{{\tilde{F}}_l}^3)}^{\eta }\right]}^{1/\eta }\}},\sqrt[3]{\min [1,{\left({\sum }_{l=1}^p{\gamma }_l{\beta }_{{\tilde{F}}_l}^{3\eta }\right)}^{1/\eta }]}).\hfill \end{array}$$ (11)

4.2. Integrated Fermatean Fuzzy Model for Adapting Transport Planning to the COVID-19 Pandemic

Fig. 4 presents the flowchart of the integrated Fermatean fuzzy model for adapting transport planning to COVID-19. The model has three stages. The first stage differentiates the experts by taking into account their experience, domain expertise, and impact. In the second stage, the new Fermatean fuzzy hierarchical MEREC determines the importance of main and sub-criteria. In the third stage, the novel Fermatean fuzzy CoCoSo method prioritizes alternatives.

Fig. 4.

The flowchart of the integrated Fermatean fuzzy model for adapting transport planning to COVID-19.

Let A={A ₁, …, A_i, …, A_m} (m≥2) be a finite set of alternatives, MC={MC ₁, …, MC_t, …, MC_q} (t≥2) be a finite set of main criteria, and C={C ₁, …, C_j, …, C_n} (n≥2) be a finite set of sub-criteria. Let us denote by B₁ the set of sub-criteria from MC ₁, by B₂ the set of sub-criteria from MC ₂, and so on, until B_q being the set of sub-criteria from MC_q, where $|{\mathrm{B}}_t|\ge 2$ (t=1, ..., q), ${\mathrm{B}}_1\cup \cdots \cup {\mathrm{B}}_q=\mathrm{C},$ and ${\mathrm{B}}_l\cap {\mathrm{B}}_{l^{\prime }}=\varnothing$ $(l,l^{\prime }=1,...,q|l\ne l^{\prime }).$ Suppose that D={D ₁, …, D_e, …, D_k} (k≥2) is a set of experts. The stages and encompassed steps of the integrated Fermatean fuzzy model for adapting transport planning to the COVID-19 pandemic are given in the following:

Stage 1: Fermatean fuzzy expert reputation rating.

Step 1.1.Construct the expert reputation matrix$\tilde{\mathrm{Y}}={\left[{\tilde{Y}}_l^e\right]}_{3\times k}:$

$$\begin{array}{ccc}\hfill \tilde{Y}& =& \left[\begin{array}{ccccc}({\alpha }_{{\tilde{Y}}_1^1},{\beta }_{{\tilde{Y}}_1^1})& \cdots & ({\alpha }_{{\tilde{Y}}_1^e},{\beta }_{{\tilde{Y}}_1^e})& \cdots & ({\alpha }_{{\tilde{Y}}_1^k},{\beta }_{{\tilde{Y}}_1^k})\\ ({\alpha }_{{\tilde{Y}}_2^1},{\beta }_{{\tilde{Y}}_2^1})& \cdots & ({\alpha }_{{\tilde{Y}}_2^e},{\beta }_{{\tilde{Y}}_2^e})& \cdots & ({\alpha }_{{\tilde{Y}}_2^k},{\beta }_{{\tilde{Y}}_2^k})\\ ({\alpha }_{{\tilde{Y}}_3^1},{\beta }_{{\tilde{Y}}_3^1})& \cdots & ({\alpha }_{{\tilde{Y}}_3^e},{\beta }_{{\tilde{Y}}_3^e})& \cdots & ({\alpha }_{{\tilde{Y}}_3^k},{\beta }_{{\tilde{Y}}_3^k})\end{array}\right],\hfill \end{array}$$ (12)

where ${\tilde{Y}}_1^e=({\alpha }_{{\tilde{Y}}_1^e},{\beta }_{{\tilde{Y}}_1^e}),$${\tilde{Y}}_2^e=({\alpha }_{{\tilde{Y}}_2^e},{\beta }_{{\tilde{Y}}_2^e}),$ and ${\tilde{Y}}_3^e=({\alpha }_{{\tilde{Y}}_3^e},{\beta }_{{\tilde{Y}}_3^e})$ are FFNs that represent the self-appraisal of the experience, the domain expertise, and the impact of the expert D_e (e=1, ..., k), respectively. Table 3 provides the five-point Fermatean fuzzy linguistic scale to distinct experts in accordance with their experience, expertise, and impact.

Table 3.

Five-point Fermatean fuzzy linguistic scale to distinct experts.

Experience (years)	Domain expertise	Impact	Fermatean fuzzy number
7.5<	Poor	Negligible	(0.10, 0.95)
[7.5, 15)	Fair	Minor	(0.30, 0.75)
[15, 22.5)	Good	Moderate	(0.55, 0.50)
[22.5, 30)	Very good	Significant	(0.75, 0.30)
≥30	Excellent	Major	(0.95, 0.10)

Step 1.2.Calculate the aggregated expert reputation:

$$\begin{array}{c}{\tilde{\Phi }}_e=\frac{1}{3}({\tilde{Y}}_1^e\oplus {\tilde{Y}}_2^e\oplus {\tilde{Y}}_3^e)=(\sqrt[3]{\min [1,{\left(\frac{1}{3}{\sum }_{l=1}^3{\alpha }_{{\tilde{Y}}_l^e}^{3\eta }\right)}^{1/\eta }]},\hfill \\ \sqrt[3]{1-\min \{1,{\left[\frac{1}{3}{\sum }_{l=1}^3{(1-{\beta }_{{\tilde{Y}}_l^e}^3)}^{\eta }\right]}^{1/\eta }\}}),e=1,\cdots ,k,\hfill \end{array}$$ (13)

where ${\tilde{\Phi }}_e=({\alpha }_{{\tilde{\Phi }}_e},{\beta }_{{\tilde{\Phi }}_e})$ is the Fermatean fuzzy aggregated (i.e., average) reputation of the expert D_e and η>0 is the operational parameter.

Step 1.3.Determine the expert reputation:

$${\delta }_e=\frac{1+{\alpha }_{{\tilde{\Phi }}_e}^3-{\beta }_{{\tilde{\Phi }}_e}^3}{{\sum }_{l=1}^k(1+{\alpha }_{{\tilde{\Phi }}_l}^3-{\beta }_{{\tilde{\Phi }}_l}^3)},e=1,\cdots ,k,$$ (14)

where $\delta ={\left({\delta }_1,\dots ,{\delta }_e,\dots ,{\delta }_k\right)}^T$ represents the reputation vector of the experts, with ${\delta }_e\in \left[0,1\right]$ (e=1, …, k), and $\sum _{e=1}^k{\delta }_e=1.$

Stage 2: Fermatean fuzzy hierarchical MEREC.

Step 2.1.Construct the main and sub-criteria decision matrices.

(i) The main criteria decision matrices ${\tilde{\mathrm{V}}}^e={\left[{\tilde{V}}_{it}^e\right]}_{m\times q}:$

$$\begin{array}{c}{\tilde{\mathrm{V}}}^e=\left[\begin{array}{ccccc}({\alpha }_{{\tilde{V}}_{11}^e},{\beta }_{{\tilde{V}}_{11}^e})& \cdots & ({\alpha }_{{\tilde{V}}_{1t}^e},{\beta }_{{\tilde{V}}_{1t}^e})& \cdots & ({\alpha }_{{\tilde{V}}_{1q}^e},{\beta }_{{\tilde{V}}_{1q}^e})\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ ({\alpha }_{{\tilde{V}}_{i1}^e},{\beta }_{{\tilde{V}}_{i1}^e})& \cdots & ({\alpha }_{{\tilde{V}}_{it}^e},{\beta }_{{\tilde{V}}_{it}^e})& \cdots & ({\alpha }_{{\tilde{V}}_{iq}^e},{\beta }_{{\tilde{V}}_{iq}^e})\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ ({\alpha }_{{\tilde{V}}_{m1}^e},{\beta }_{{\tilde{V}}_{m1}^e})& \cdots & ({\alpha }_{{\tilde{V}}_{mt}^e},{\beta }_{{\tilde{V}}_{mt}^e})& \cdots & ({\alpha }_{{\tilde{V}}_{mq}^e},{\beta }_{{\tilde{V}}_{mq}^e})\end{array}\right],\hfill \\ e=1,\cdots ,k,\hfill \end{array}$$ (15)

where ${\tilde{V}}_{it}^e=({\alpha }_{{\tilde{V}}_{it}^e},{\beta }_{{\tilde{V}}_{it}^e})$ (i=1, ..., m; t=1, ..., q; e=1, ..., k) is an FFN that represents the assessment of the alternative A_i under the main criterion MC_t given by the expert D_e.

(ii) The sub-criteria decision matrices ${\tilde{\mathrm{W}}}^e={\left[{\tilde{W}}_{ij}^e\right]}_{m\times n}:$

$$\begin{array}{c}{\tilde{\mathrm{W}}}^e=\left[\begin{array}{ccccc}({\alpha }_{{\tilde{W}}_{11}^e},{\beta }_{{\tilde{W}}_{11}^e})& \cdots & ({\alpha }_{{\tilde{W}}_{1j}^e},{\beta }_{{\tilde{W}}_{1j}^e})& \cdots & ({\alpha }_{{\tilde{W}}_{1n}^e},{\beta }_{{\tilde{W}}_{1n}^e})\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ ({\alpha }_{{\tilde{W}}_{i1}^e},{\beta }_{{\tilde{W}}_{i1}^e})& \cdots & ({\alpha }_{{\tilde{W}}_{\mathit{ij}}^e},{\beta }_{{\tilde{W}}_{\mathit{ij}}^e})& \cdots & ({\alpha }_{{\tilde{W}}_{in}^e},{\beta }_{{\tilde{W}}_{in}^e})\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ ({\alpha }_{{\tilde{W}}_{m1}^e},{\beta }_{{\tilde{W}}_{m1}^e})& \cdots & ({\alpha }_{{\tilde{W}}_{mj}^e},{\beta }_{{\tilde{W}}_{mj}^e})& \cdots & ({\alpha }_{{\tilde{W}}_{mn}^e},{\beta }_{{\tilde{W}}_{mn}^e})\end{array}\right],\hfill \\ e=1,\cdots ,k,\hfill \end{array}$$ (16)

where ${\tilde{W}}_{\mathit{ij}}^e=({\alpha }_{{\tilde{W}}_{\mathit{ij}}^e},{\beta }_{{\tilde{W}}_{\mathit{ij}}^e})$ (i=1, ..., m; j=1, ..., n; e=1, ..., k) is an FFN that represents the assessment of the alternative A_i under the sub-criterion C_j given by the expert D_e.

The main and sub-criteria decision matrices are defined by using a Fermatean fuzzy linguistic assessment scale. Table 4 gives the nine-point Fermatean fuzzy linguistic scale to present alternative assessment preferences of experts.

Table 4.

Nine-point Fermatean fuzzy linguistic scale to assess alternatives under main and sub-criteria.

Linguistic term	Fermatean fuzzy number
Extremely low	(0.10, 0.975)
Very low	(0.20, 0.90)
Low	(0.30, 0.80)
Medium low	(0.40, 0.65)
Medium	(0.55, 0.50)
Medium high	(0.65, 0.40)
High	(0.80, 0.30)
Very high	(0.90, 0.20)
Extremely high	(0.975, 0.10)

Step 2.2. Determine the aggregated main and sub-criteria decision matrices.

(i) The aggregated main criteria decision matrix $\tilde{\Theta }$ $={\left[{\tilde{\Theta }}_{it}\right]}_{m\times q}:$

$$\begin{array}{c}{\tilde{\Theta }}_{it}=\mathit{FFYW}{G}_{\delta }({\tilde{V}}_{it}^1,...,{\tilde{V}}_{it}^e,...,{\tilde{V}}_{it}^k)=\underset{e=1}{\stackrel{k}{\otimes }}{\left({\tilde{V}}_{it}^e\right)}^{{\delta }_e}\hfill \\ =(\sqrt[3]{1-\min \{1,{\left[{\sum }_{e=1}^k{\delta }_e{(1-{\alpha }_{{\tilde{V}}_{it}^e}^3)}^{\eta }\right]}^{1/\eta }\}},\sqrt[3]{\min [1,{\left({\sum }_{e=1}^k{\delta }_e{\beta }_{{\tilde{V}}_{it}^e}^{3\eta }\right)}^{1/\eta }]}),\hfill \\ i=1,\cdots ,m;t=1,\cdots ,q,\hfill \end{array}$$ (17)

where ${\tilde{\Theta }}_{it}=({\alpha }_{{\tilde{\Theta }}_{it}},{\beta }_{{\tilde{\Theta }}_{it}})$ is the Fermatean fuzzy aggregated assessment of the alternative A_i under the main criterion MC_t given by the experts.

(ii) The aggregated sub-criteria decision matrix $\tilde{\Psi }$ $={\left[{\tilde{\Psi }}_{\mathit{ij}}\right]}_{m\times n}:$

$$\begin{array}{c}{\tilde{\Psi }}_{ij}=FFYW{G}_{\delta }({\tilde{W}}_{ij}^1,...,{\tilde{W}}_{ij}^e,...,{\tilde{W}}_{ij}^k)=\underset{e=1}{\stackrel{k}{\otimes }}{\left({\tilde{W}}_{ij}^e\right)}^{{\delta }_e}\hfill \\ =(\sqrt[3]{1-min\{1,{\left[{\sum }_{e=1}^k{\delta }_e{(1-{\alpha }_{{\tilde{W}}_{ij}^e}^3)}^{\eta }\right]}^{1/\eta }\}},\sqrt[3]{min[1,{\left({\sum }_{e=1}^k{\delta }_e{\beta }_{{\tilde{W}}_{ij}^e}^{3\eta }\right)}^{1/\eta }]}),\hfill \\ i=1,\cdots ,m;j=1,\cdots ,n,\hfill \end{array}$$ (18)

where ${\tilde{\Psi }}_{\mathit{ij}}=({\alpha }_{{\tilde{\Psi }}_{\mathit{ij}}},{\beta }_{{\tilde{\Psi }}_{\mathit{ij}}})$ is the Fermatean fuzzy aggregated assessment of the alternative A_i under the sub-criterion C_j given by the experts.

Step 2.3.Determine the normalized decision matrix$\tilde{\mathrm{H}}={\left[{\tilde{H}}_{\mathit{ij}}\right]}_{m\times n}:$

$$\begin{array}{c}{\tilde{H}}_{ij}=\{\begin{array}{c}{\tilde{\Psi }}_{ij}=({\alpha }_{{\tilde{\Psi }}_{ij}},{\beta }_{{\tilde{\Psi }}_{ij}})|C_j\in {\mathrm{C}}^{-}\hfill \\ {\left({\tilde{\Psi }}_{ij}\right)}^c=({\beta }_{{\tilde{\Psi }}_{ij}},{\alpha }_{{\tilde{\Psi }}_{ij}})|C_j\in {\mathrm{C}}^{+}\hfill \end{array},\hfill \\ i=1,\cdots ,m;j=1,\cdots ,n,\hfill \end{array}$$ (19)

where ${\tilde{H}}_{\mathit{ij}}=({\alpha }_{{\tilde{H}}_{\mathit{ij}}},{\beta }_{{\tilde{H}}_{\mathit{ij}}})$ denotes the Fermatean fuzzy normalized aggregated assessment of the alternative A_i under the sub-criterion C_j given by the experts, ${\mathrm{C}}^{+}\subseteq \mathrm{C}$ is the set of benefit sub-criteria, ${\mathrm{C}}^{-}\subseteq \mathrm{C}$ is the set of cost sub-criteria, and ${\mathrm{C}}^{+}\cup {\mathrm{C}}^{-}=\mathrm{C}.$

Step 2.4.Calculate the overall performance of each alternative.

(i) The overall performance under the main criteria:

$$\begin{array}{c}{O}_i=\mathit{ln}\{1+\left[\frac{1}{q}\sum _{t=1}^q\left|\mathit{ln}(1+{\alpha }_{{\tilde{\Theta }}_{it}}^3-{\beta }_{{\tilde{\Theta }}_{it}}^3)\right|\right]\},\hfill \\ i=1,\cdots ,m,\hfill \end{array}$$ (20)

where O_i represents is the overall performance of the alternative A_i under the main criteria.

(ii) The overall performance under the sub-criteria:

$$\begin{array}{c}{P}_{it}=\mathit{ln}\{1+\left[\frac{1}{\left|{\mathrm{B}}_t\right|}\sum _{j\in {\mathrm{B}}_t}\left|\mathit{ln}(1+{\alpha }_{{\tilde{H}}_{ij}}^3-{\beta }_{{\tilde{H}}_{ij}}^3)\right|\right]\},\hfill \\ i=1,\cdots ,m;t=1,\cdots ,q,\hfill \end{array}$$ (21)

where P_{i t} represents is the overall performance of the alternative A_i under the sub-criteria of the main criterion MC_t.

Step 2.5.Calculate the partial performance of each alternative.

(i) One-by-one main criterion removal:

$$\begin{array}{c}{O}_{it}^{\text{'}}=ln\{1+\left[\frac{1}{q}\sum _{l\in \mathrm{C}|l\ne t}\left|ln(1+{\alpha }_{{\tilde{\Theta }}_{il}}^3-{\beta }_{{\tilde{\Theta }}_{il}}^3)\right|\right]\},\hfill \\ i=1,\cdots ,m;t=1,\cdots ,q,\hfill \end{array}$$ (22)

where $O_{it}^{\prime }$ presents the partial performance of the alternative A_i under the main criteria when the main criterion MC_t is removed.

(ii) One-by-one sub-criterion removal:

$$\begin{array}{c}{P}_{i\mathit{tj}}^{\text{'}}=\mathit{ln}\{1+\left[\frac{1}{\left|{\mathrm{B}}_t\right|}\sum _{l\in {\mathrm{B}}_t|l\ne j}\left|\mathit{ln}(1+{\alpha }_{{\tilde{H}}_{ij}}^3-{\beta }_{{\tilde{H}}_{ij}}^3)\right|\right]\},\hfill \\ i=1,\cdots ,m;t=1,\cdots ,q;j=1,\cdots ,n|j\in {\mathrm{B}}_t,\hfill \end{array}$$ (23)

where $P_{itj}^{\prime }$ denotes the partial performance of the alternative A_i under the sub-criteria of the main criterion MC_t when the sub-criterion C_j is removed.

Step 2.6.Calculate the removal effect for each main and sub-criterion.

(i) The main criterion removal effect:

$${\xi }_t=\sum _{i=1}^m\left|O_{it}^{\prime }-O_i\right|,t=1,\dots ,q,$$ (24)

where ${\xi }_t$ is the removal effect of the main criterion MC_t.

(ii) The sub-criterion removal effect:

$$\begin{array}{c}{\upsilon }_j=\sum _{i=1}^m|P_{i\mathit{tj}}^{\text{'}}-P_{it}|,\hfill \\ t=1,\cdots ,q;j=1,\cdots ,n|j\in {\mathrm{B}}_t,\hfill \end{array}$$ (25)

where ${\upsilon }_j$ is the removal effect of the sub-criterion C_j.

Step 2.7. Determine the main and sub-criteria importance.

(i) The main criteria importance:

$${\theta }_t=\frac{{\xi }_t}{\sum _{l=1}^q{\xi }_l},t=1,\dots ,q,$$ (26)

where $\theta ={\left({\theta }_1,\dots ,{\theta }_t,\dots ,{\theta }_q\right)}^T$ is the importance vector of the main criteria, with ${\theta }_t\in \left[0,1\right]$ (t=1, …, q), and $\sum _{t=1}^q{\theta }_t=1.$

(ii) The sub-criteria local importance:

$${\omega }_j=\frac{{\upsilon }_j}{\sum _{l|l,j\in {\mathrm{B}}_t}{\upsilon }_l},j=1,\dots ,n,$$ (27)

where $\omega ={\left({\omega }_1,\dots ,{\omega }_j,\dots ,{\omega }_n\right)}^T$ is the local importance vector of the sub-criteria, with ${\omega }_j\in \left[0,1\right]$ (j=1, …, n), and $\sum _{j\in {\mathrm{B}}_t}{\omega }_j=1.$

Step 2.8.Determine the sub-criteria global importance:

$${\omega }_j^{*}={\omega }_j{\theta }_t,t=1,\dots ,q;j=1,\dots ,n|j\in {\mathrm{B}}_t$$ (28)

where sub-criterion global importance is obtained by multiplying sub-criterion local importance with the corresponding main criteria importance, ${\theta }_t={\theta }_t^{*}$ (t=1, ..., q) is the global importance in the first (i.e., main criteria) level of the hierarchy, and ${\omega }^{*}={\left({\omega }_1^{*},\dots ,{\omega }_j^{*},\dots ,{\omega }_n^{*}\right)}^T$ is the global importance vector of the sub-criteria, with ${\omega }_j^{*}\in \left[0,1\right]$ (j=1, …, n), and $\sum _{j=1}^n{\omega }_j^{*}=1.$

Stage 3: Fermatean fuzzy CoCoSo method.

Step 3.1.Determine two comparability sequences for each alternative.

(i) Fermatean fuzzy Yager weighted average comparability sequence:

$$\begin{array}{c}{\tilde{Q}}_i=\mathit{FFYW}{A}_{\omega }({\tilde{H}}_{i1},...,{\tilde{H}}_{ij},...,{\tilde{H}}_{in})=\underset{j=1}{\stackrel{n}{\oplus }}\left({\omega }_j^{*}{\tilde{H}}_{ij}\right)\hfill \\ =(\sqrt[3]{\min [1,{\left({\sum }_{j=1}^n{\omega }_j^{*}{\alpha }_{{\tilde{H}}_{ij}}^{3\eta }\right)}^{1/\eta }]},\sqrt[3]{1-\min \{1,{\left[{\sum }_{j=1}^n{\omega }_j^{*}{(1-{\beta }_{{\tilde{H}}_{ij}}^3)}^{\eta }\right]}^{1/\eta }\}}),\hfill \\ i=1,...,m,\hfill \end{array}$$ (29)

where ${\tilde{Q}}_i=({\alpha }_{{\tilde{Q}}_i},{\beta }_{{\tilde{Q}}_i})$ is the Fermatean fuzzy Yager weighted average comparability sequence for the alternative A_i.

(ii) Fermatean fuzzy Yager weighted geometric comparability sequence:

$$\begin{array}{c}{\tilde{U}}_i=\mathit{FFYW}{G}_{\omega }({\tilde{H}}_{i1},...,{\tilde{H}}_{ij},...,{\tilde{H}}_{in})=\underset{j=1}{\stackrel{n}{\otimes }}{\left({\tilde{H}}_{ij}\right)}^{{\omega }_j^{*}}\hfill \\ =(\sqrt[3]{1-\min \{1,{\left[{\sum }_{j=1}^n{\omega }_j^{*}{(1-{\alpha }_{{\tilde{H}}_{ij}}^3)}^{\eta }\right]}^{1/\eta }\}},\sqrt[3]{\min [1,{\left({\sum }_{j=1}^n{\omega }_j^{*}{\beta }_{{\tilde{H}}_{ij}}^{3\eta }\right)}^{1/\eta }]}),\hfill \\ i=1,...,m,\hfill \end{array}$$ (30)

where ${\tilde{U}}_i=({\alpha }_{{\tilde{U}}_i},{\beta }_{{\tilde{U}}_i})$ is the Fermatean fuzzy Yager weighted geometric comparability sequence for the alternative A_i.

Step 3.2. Calculate three appraisal scores for each alternative.

(i) The first strategy:

$$\begin{array}{c}{S}_i^{\left(1\right)}=\frac{2+{\alpha }_{{\tilde{Q}}_i}^3+{\alpha }_{{\tilde{U}}_i}^3-{\beta }_{{\tilde{Q}}_i}^3-{\beta }_{{\tilde{U}}_i}^3}{{\sum }_{l=1}^m(2+{\alpha }_{{\tilde{Q}}_l}^3+{\alpha }_{{\tilde{U}}_l}^3-{\beta }_{{\tilde{Q}}_l}^3-{\beta }_{{\tilde{U}}_l}^3)},\hfill \\ i=1,...,m,\hfill \end{array}$$ (31)

where $S_i^{\left(1\right)}$ is the appraisal score of the alternative A_i based on the arithmetic mean strategy.

(ii) The second strategy:

$$\begin{array}{c}{S}_i^{\left(2\right)}=\frac{1+{\alpha }_{{\tilde{Q}}_i}^3-{\beta }_{{\tilde{Q}}_i}^3}{\underset{1\le l\le m}{\min }[1+{\alpha }_{{\tilde{Q}}_l}^3-{\beta }_{{\tilde{Q}}_l}^3]}+\frac{1+{\alpha }_{{\tilde{U}}_i}^3-{\beta }_{{\tilde{U}}_i}^3}{\underset{1\le l\le m}{\min }[1+{\alpha }_{{\tilde{U}}_l}^3-{\beta }_{{\tilde{U}}_l}^3]},\hfill \\ i=1,...,m,\hfill \end{array}$$ (32)

where $S_i^{\left(2\right)}$ is the appraisal score of the alternative A_i based on the relative score (to the worst value) strategy.

(iii) The third strategy:

$$\begin{array}{c}{S}_i^{\left(3\right)}=\frac{1+\lambda ({\alpha }_{{\tilde{Q}}_i}^3-{\beta }_{{\tilde{Q}}_i}^3)+(1-\lambda )({\alpha }_{{\tilde{U}}_i}^3-{\beta }_{{\tilde{U}}_i}^3)}{\lambda \underset{1\le l\le m}{\max }[1+{\alpha }_{{\tilde{Q}}_l}^3-{\beta }_{{\tilde{Q}}_l}^3]+(1-\lambda )\underset{1\le l\le m}{\max }[1+{\alpha }_{{\tilde{U}}_l}^3-{\beta }_{{\tilde{U}}_l}^3]},\hfill \\ i=1,...,m,\hfill \end{array}$$ (33)

where $S_i^{\left(3\right)}$ is the appraisal score of the alternative A_i based on the balanced compromise strategy and $\lambda \in \left[0,1\right]$ is the balancing parameter.

Step 3.3.Aggregate three appraisal score strategies and rank the alternatives:

$$\begin{array}{c}{Z}_i=\sum _{g=1}^3\sqrt{\frac{1}{2}[{\left(\frac{S_i^{\left(g\right)}}{\underset{1\le l\le m}{\max }{S}_l^{\left(g\right)}}\right)}^2+{\left(\frac{m-R_i^{\left(g\right)}}{m}\right)}^2]},\hfill \\ i=1,...,m,\hfill \end{array}$$ (34)

where Z_i represents the assessment score of the alternative A_i and $R_i^{\left(g\right)}$ is the rank of the alternative A_i under the appraisal score strategy g (g=1, 2, 3). The best alternative has the highest assessment score. The detailed nomenclatures for the indices, parameters, sets, matrices, and variables are provided in Appendix A.

5. Results and Discussion

5.1. Experimental Results

This sub-section presents the results of the integrated Fermatean fuzzy model for adapting transport planning to COVID-19 in the real-life context of Belgrade. The online questionnaire approach via Google Forms is utilized to collect experts’ self-appraisals of their reputation indicators as well as assessments of six alternatives under four main and 17 sub-criteria.

Stage 1: Fermatean fuzzy expert reputation rating.

Step 1.1. Five transport planning experts participated in the online questionnaire. The information about them is given in Table 5 . The five-point Fermatean fuzzy linguistic scale presented in Table 3 is used to distinct the transport planning experts. Table 6 provides FFNs that represent the qualifications, experience, and domain expertise of the experts.

Table 5.

The information about the transport planning experts.

Expert	Experience (years)	Domain expertise	Impact	Occupation	Gender
D1	14	Very good	Significant	Industry	Male
D2	45	Very good	Minor	Academia	Male
D3	20	Very good	Moderate	Industry	Male
D4	45	Very good	Significant	Industry	Male
D5	13	Excellent	Significant	Industry	Male

Table 6.

Fermatean fuzzy experience, domain expertise, impact, and aggregated reputation of the experts.

Expert	Experience (years)	Domain expertise	Impact	Aggregated reputation
D1	(0.30, 0.75)	(0.75, 0.30)	(0.75, 0.30)	(0.7170, 0.4950)
D2	(0.95, 0.10)	(0.75, 0.30)	(0.30, 0.75)	(0.8514, 0.4799)
D3	(0.55, 0.50)	(0.75, 0.30)	(0.55, 0.50)	(0.6724, 0.4481)
D4	(0.95, 0.10)	(0.75, 0.30)	(0.75, 0.30)	(0.8610, 0.2629)
D5	(0.30, 0.75)	(0.95, 0.10)	(0.75, 0.30)	(0.8514, 0.4799)

Step 1.2. A Fermatean fuzzy aggregated reputation of an expert is calculated by using Eq. (13), the operational parameter $\eta =3,$ and three corresponding FFNs (Table 6, Columns 2−4). For example, according to Table 6, the Fermatean fuzzy experience, domain expertise, and impact of expert one are (0.30, 0.75), (0.75, 0.30), and (0.75, 0.30), respectively. As a result, the Fermatean fuzzy aggregated reputation of expert one is:

$$\begin{array}{c}{\tilde{\Phi }}_1=(\sqrt[3]{min[1,{\left(\frac{0.{30}^{3·3}+0.{75}^{3·3}+0.{75}^{3·3}}{3}\right)}^{1/3}]},\hfill \\ \sqrt[3]{1-min\{1,{\left[\frac{1}{3}({(1-0.{75}^3)}^3+{(1-0.{30}^3)}^3+{(1-0.{30}^3)}^3)\right]}^{1/3}\}})\hfill \\ =(0.7170,0.4950).\hfill \end{array}$$

Step 1.3. Based on the Fermatean fuzzy aggregated reputations (Table 6, Column 5) and Eq. (14), the following reputation vector of five transport planning experts is determined: δ=(0.1758, 0.2124, 0.1711, 0.2284, 0.2124)^T. According to this vector, it can be seen that the fourth expert has the highest reputation; i.e., δ ₄=0.2284. He has 45 years of experience, very good domain expertise, and a significant impact on transport planning in Belgrade.

Stage 2: Fermatean fuzzy hierarchical MEREC.

Step 2.1. Five transport planning experts used Fermatean fuzzy linguistic variables from Table 4 to assess five alternatives for adapting transport planning to COVID-19 under four main criteria. Their assessments of the alternatives in the Belgrade context are given in Table 7 . The main criteria decision matrices are constructed based on the experts’ input and with the help of Eq. (15). They are provided in Table B.1 (Appendix B).

Table 7.

Transport planning experts’ assessments of the alternatives under the main criteria.

Alternative	Expert	Main criterion
		MC1: Environmental	MC2: Economic	MC3: Social	MC4: External
A1: Non-motorized travel	D1	Extremely high	Very low	Medium	Very high
	D2	High	Medium	Medium	Medium
	D3	Extremely high	High	Medium	Medium
	D4	Very high	Medium	Medium high	Medium high
	D5	Medium	Medium low	Very high	Medium high
A2: Service quality improvement in public transport	D1	Low	Extremely high	Very high	Very high
	D2	High	Very high	Very high	Very high
	D3	High	Medium low	Medium high	Very high
	D4	Very high	Medium low	Medium high	Medium
	D5	Very high	Medium high	Very high	Very high
A3: Mobility management	D1	Very high	Medium high	High	High
	D2	High	Very high	High	Very high
	D3	Extremely high	Medium high	Medium high	High
	D4	High	Medium	Medium high	Medium high
	D5	Very high	Medium high	Very high	High
A4: Transport infrastructure development	D1	Very high	Extremely high	Extremely high	Extremely high
	D2	High	Very high	Very high	Very high
	D3	Medium	High	High	Very high
	D4	Very high	Low	Medium	Medium high
	D5	Very high	Medium high	Very high	Very high
A5: Intelligent transport systems	D1	Medium	High	Very high	Very high
	D2	Medium high	High	High	High
	D3	Medium	High	High	Very high
	D4	Medium	Medium	Medium high	Medium high
	D5	Medium low	Medium low	Very high	Very high

Table 8 provides the experts’ assessments of the alternatives for adapting transport planning to COVID-19 in Belgrade under 17 sub-criteria. Then, five sub-criteria decision matrices, one for each expert, are constructed with the help of Eq. (16) and given in Table B.2.

Table 8.

Transport planning experts’ assessments of the alternatives under the sub-criteria.

Alternative	Expert	Sub-criterion
		C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11	C12	C13	C14	C15	C16	C17
A1: Non-motorized travel	D1	EL	VL	VH	VL	L	L	ML	ML	MH	MH	ML	MH	VL	VL	MH	MH	MH
	D2	EL	EL	EH	H	H	H	H	H	H	H	H	H	MH	H	H	VH	VH
	D3	EL	EL	H	M	H	ML	H	H	ML	M	H	H	ML	M	VH	L	H
	D4	ML	ML	L	VL	ML	M	H	MH	H	H	H	MH	MH	H	MH	MH	M
	D5	VL	EL	VH	VH	MH	ML	EL	MH	MH	H	MH	M	MH	MH	VH	VH	VH
A2: Service quality improvement in public transport	D1	VH	VH	VH	H	VH	VH	H	MH	H	VH	VH	H	M	MH	EL	ML	H
	D2	L	L	H	VH	VH	VH	H	H	H	H	VH	H	VH	H	H	H	H
	D3	L	L	MH	M	VH	H	M	MH	H	M	MH	ML	H	MH	VH	M	H
	D4	M	ML	M	MH	MH	MH	MH	ML	M	MH	M	MH	M	MH	M	ML	H
	D5	VL	ML	ML	ML	MH	EH	EH	MH	MH	H	H	H	L	H	M	MH	H
A3: Mobility management	D1	EL	EL	VL	L	ML	ML	ML	L	H	H	VH	VH	VL	VL	EH	VL	EH
	D2	L	L	H	MH	MH	H	MH	MH	H	H	MH	MH	H	H	MH	H	H
	D3	L	L	H	M	H	M	M	ML	M	L	M	H	H	H	H	M	H
	D4	VL	VL	ML	ML	ML	ML	M	MH	MH	ML	M	H	ML	MH	MH	VL	MH
	D5	VL	VL	VH	VH	ML	ML	ML	VH	H	H	H	H	VH	H	VH	VH	VH
A4: Transport infrastructure development	D1	EH	EH	EL	VH	EH	EH	VH	VH	VH	VH	VH	VH	VH	VH	ML	L	MH
	D2	H	H	L	H	VH	VH	H	VH	VH	VH	H	H	VH	VH	VH	H	VH
	D3	EH	VH	H	H	VH	VH	H	VH	H	L	ML	VH	VH	VH	VH	M	VH
	D4	H	H	L	VH	VH	H	MH	H	M	MH	H	H	H	H	H	M	MH
	D5	H	VH	H	MH	VH	VH	H	VH	MH	MH	MH	H	VH	VH	VH	H	VH
A5: Intelligent transport systems	D1	VH	H	H	H	H	H	H	ML	M	H	H	H	M	M	H	M	MH
	D2	ML	ML	MH	MH	MH	H	MH	H	H	H	H	MH	H	H	H	H	H
	D3	M	M	M	VL	H	MH	ML	H	M	H	M	H	MH	MH	VH	M	H
	D4	VL	VL	VH	L	MH	M	H	MH	M	ML	ML	M	L	M	M	VL	L
	D5	MH	H	MH	M	VH	VH	M	MH	MH	MH	H	VH	M	M	H	VH	VH

Extremely Low: EL, Very Low: VL, Low: L, Medium Low: ML, Medium: M, Medium High: MH, High: H, Very High: VH, Extremely High: EH.

Step 2.2. The aggregated main criteria decision matrix is presented in Table 9 . It is determined with the help of Eq. (17) by taking into account the reputation vector of the transport planning experts and five main criteria decision matrices (Table B.1). For example, the Fermatean fuzzy assessments of the non-motorized travel alternative (A ₁) under the environmental main criterion (MC ₁) given by experts one, two, three, four, and five are (0.975, 0.10), (0.80, 0.30), (0.975, 0.10), (0.90, 0.20), and (0.55, 0.50), respectively. As a result, the Fermatean fuzzy aggregated assessment of the alternative A ₁ under the main criterion MC ₁ given by five transport planners is calculated as follows:

$${\tilde{\Theta }}_{11}=(\sqrt[3]{1-\min \{1,{[0.1758{(1-{0.975}^3)}^3+\cdots +0.2124{(1-{0.55}^3)}^3]}^{1/3}\}},$$

$$\begin{array}{c}\sqrt[3]{\min [1,{(0.1758·0.{10}^{3·3}+\cdots +0.2124·0.{50}^{3·3})}^{1/3}]})\hfill \\ =(0.7752,0.4214).\hfill \end{array}$$

Table 9.

The aggregated main criteria decision matrix.

Main criterion	Alternative
	A1: Non- motorized travel	A2: Service quality impr. in public transport	A3: Mobility management	A4: Transport infrastructure development	A5: Intelligent transport systems
MC1: Environmental	(0.7752, 0.4214)	(0.7372, 0.6595)	(0.8484, 0.2746)	(0.7860, 0.4115)	(0.5451, 0.5618)
MC2: Economic	(0.5276, 0.7481)	(0.6344, 0.5874)	(0.6659, 0.4380)	(0.6834, 0.6791)	(0.6551, 0.5533)
MC3: Social	(0.6332, 0.4715)	(0.7675, 0.3613)	(0.7450, 0.3641)	(0.7699, 0.4247)	(0.7837, 0.3441)
MC4: External	(0.6439, 0.4567)	(0.7783, 0.4244)	(0.7726, 0.3460)	(0.8129, 0.3397)	(0.7951, 0.3422)

The Fermatean fuzzy assessments of the alternatives under the sub-criteria (Table B.2) are aggregated by using Eq. (18) as well as experts’ reputations from Step 1.3. Table 10 provides the aggregated sub-criteria decision matrix.

Table 10.

The aggregated sub-criteria decision matrix.

Sub-criterion	Alternative
	A1: Non-motorized travel	A2: Service quality imp. in public transport	A3: Mobility management	A4: Transport infrastructure development	A5: Intelligent transport systems
C1: Air pollution	(0.2529, 0.9323)	(0.4843, 0.8000)	(0.2405, 0.8933)	(0.8322, 0.2861)	(0.5492, 0.7683)
C2: Noise	(0.2515, 0.9352)	(0.4709, 0.7324)	(0.2405, 0.8933)	(0.8485, 0.2746)	(0.5698, 0.7683)
C3: Eco-friendliness	(0.7244, 0.6790)	(0.6409, 0.5537)	(0.6370, 0.7475)	(0.5249, 0.8359)	(0.6986, 0.4247)
C4: Land use impact	(0.5794, 0.8140)	(0.6483, 0.5525)	(0.5738, 0.6740)	(0.7877, 0.3417)	(0.5379, 0.7720)
C5: Community cost	(0.6035, 0.6732)	(0.7583, 0.3653)	(0.5354, 0.6163)	(0.9068, 0.1958)	(0.7386, 0.3676)
C6: Operator cost	(0.5207, 0.6822)	(0.8010, 0.3417)	(0.5229, 0.6178)	(0.8717, 0.2565)	(0.7196, 0.4296)
C7: User cost	(0.6274, 0.8228)	(0.7281, 0.4194)	(0.5221, 0.5916)	(0.7704, 0.3463)	(0.6451, 0.5418)
C8: Travel time	(0.6624, 0.5378)	(0.6282, 0.5536)	(0.6036, 0.6701)	(0.8674, 0.2570)	(0.6624, 0.5378)
C9: User accessibility	(0.6711, 0.5360)	(0.7027, 0.4310)	(0.7146, 0.4199)	(0.7229, 0.4303)	(0.6214, 0.4729)
C10: Spatial coverage	(0.7222, 0.4184)	(0.7239, 0.4195)	(0.6335, 0.6714)	(0.6742, 0.6579)	(0.6743, 0.5525)
C11: Interconnectivity	(0.6933, 0.5369)	(0.7289, 0.4293)	(0.6706, 0.4553)	(0.7039, 0.5353)	(0.6628, 0.5560)
C12: New users	(0.6802, 0.4324)	(0.6929, 0.5354)	(0.7731, 0.3442)	(0.8263, 0.2866)	(0.7136, 0.4306)
C13: Political support	(0.5595, 0.7463)	(0.6140, 0.6755)	(0.6370, 0.7475)	(0.8674, 0.2570)	(0.578, 0.6809)
C14: Public support	(0.6393, 0.7424)	(0.7077, 0.3784)	(0.6770, 0.7420)	(0.8674, 0.2570)	(0.6174, 0.4760)
C15: Cong. reduction	(0.7539, 0.3633)	(0.6116, 0.8043)	(0.7505, 0.3664)	(0.7564, 0.5359)	(0.7428, 0.4256)
C16: Resource eff.	(0.6810, 0.6578)	(0.5724, 0.5908)	(0.5794, 0.8140)	(0.6196, 0.6619)	(0.6145, 0.7645)
C17: Safety	(0.7302, 0.4293)	(0.8000, 0.3000)	(0.7861, 0.3440)	(0.7665, 0.3618)	(0.6779, 0.6791)

Step 2.3. The normalized decision matrix is presented in Table B.3 (Appendix B). It is determined based on the aggregated sub-criteria decision matrix (Table 10) with the help of Eq. (19). As can be seen from Fig. 2, air pollution (C ₁), noise (C ₂), land use impact (C ₄), community cost (C ₅), operator cost (C ₆), user cost (C ₇), and travel time (C ₈) belong to the set of the cost sub-criteria. The other 10 sub-criteria belong to the set of the benefit sub-criteria.

Step 2.4. Firstly, the overall performance of each alternative for adapting transport planning to COVID-19 under the main criteria is computed based on Eq. (20) and the aggregated main criteria decision matrix (Table 9). Then, as defined in Eq. (21), overall performances of the alternatives under the environmental, economic, social, and external sub-criteria are calculated by taking into account the corresponding FFNs from Table 10. The obtained values are shown in Table 11 .

Table 11.

The overall alternative performance under the main and the sub-criteria.

Alternative	Main criteria	Sub-criteria
		Environmental	Economic	Social	External
A1	0.2120	0.3247	0.1582	0.1694	0.1920
A2	0.1889	0.1798	0.4069	0.1853	0.1991
A3	0.2846	0.2897	0.0735	0.1694	0.2445
A4	0.2390	0.5411	0.6787	0.3224	0.2810
A5	0.1961	0.2214	0.2621	0.1419	0.1452

Step 2.5. Partial performances of the assessed alternatives are comprehensively provided in Table B.4 (Appendix B). They are calculated by performing one-by-one main criterion removal and one-by-one sub-criterion removal by using Eq. (22) and Eq. (23), respectively.

Steps 2.6−2.8. Firstly, removal effects of the main and the sub-criteria on performances of five alternatives are calculated (Table 12 ). Main criteria removal effects are determined by employing Eq. (24) based on the corresponding overall and partial performances from Table 11 and Table B.4, respectively. Sub-criteria removal effects are computed similarly with the help of Eq. (25). Secondly, the removal effects are normalized by using Eqs. (26)−(27) to obtain the objective importance of the main criteria and the sub-criteria. Lastly, sub-criterion global importance is obtained by multiplying its local importance (Table 12, Column 3) with the importance of a corresponding main criterion, as defined in Eq. (28). As a result, the importance vector of the main criteria affects the importance vector of the sub-criteria. The obtained global importance vector of the sub-criteria can be found in Table 12.

Table 12.

The removal effect and importance of the main and sub-criteria.

Criterion	Removal effect	Local importance	Global importance
MC1: Environmental	0.2569	0.2482	−
C1: Air pollution	0.4653	0.3399	0.0844
C2: Noise	0.4592	0.3355	0.0833
C3: Eco-friendliness	0.1998	0.1460	0.0362
C4: Land use impact	0.2445	0.1786	0.0443
MC2: Economic	0.1368	0.1322	−
C5: Community cost	0.5382	0.3943	0.0521
C6: Operator cost	0.5150	0.3773	0.0499
C7: User cost	0.3116	0.2283	0.0302
MC3: Social	0.3052	0.2949	−
C8: Travel time	0.2353	0.2572	0.0758
C9: User accessibility	0.1684	0.1841	0.0543
C10: Spatial coverage	0.1253	0.1370	0.0404
C11: Interconnectivity	0.1519	0.1660	0.0490
C12: New users	0.2340	0.2558	0.0754
MC4: External	0.3362	0.3248	−
C13: Political support	0.1871	0.1915	0.0622
C14: Public support	0.1851	0.1894	0.0615
C15: Congestion reduction	0.2526	0.2585	0.0840
C16: Resource effciency	0.1275	0.1305	0.0424
C17: Safety	0.2248	0.2301	0.0747

Stage 3: Fermatean fuzzy CoCoSo method.

Step 3.1. Two comparability sequences for each alternative for adapting transport planning to COVID-19 in Belgrade are determined based on the global importance vector of the sub-criteria (Table 12, Column 5) and the normalized decision matrix (Table B.3). Very flexible Fermatean fuzzy Yager aggregation operators are employed to aggregate the related decision information. More detailed, Fermatean fuzzy Yager weighted average comparability sequences are calculated by utilizing the FFYWA operator defined in Eq. (29), while Fermatean fuzzy Yager weighted geometric comparability sequences are computed by using the FFYWG operator defined in Eq. (30). The obtained values are shown in Table 13 .

Table 13.

The comparability sequences of the alternatives for adapting transport planning to COVID-19.

Alternative	Comparability sequence
	FFYWA	FFYWG
A1: Non-motorized travel	(0.7969, 0.5305)	(0.7079, 0.6252)
A2: Service quality improvement in public transport	(0.7042, 0.5700)	(0.6419, 0.6764)
A3: Mobility management	(0.7712, 0.5189)	(0.7054, 0.6501)
A4: Transport infrastructure development	(0.7423, 0.6230)	(0.5840, 0.7826)
A5: Intelligent transport systems	(0.6961, 0.5801)	(0.6472, 0.6408)

Fermatean Fuzzy Yager Weighted Average: FFYWA, Fermatean Fuzzy Yager Weighted Geometric: FFYWG.

Step 3.2. Three appraisal scores for the alternatives for adapting transport planning to COVID-19 in Belgrade are given in Table 14 . FFNs from Table 13 that represent two comparability sequences are taken into account to calculate the arithmetic mean strategy, the relative score (to the worst value) strategy, and the balanced compromise strategy for each alternative by using Eqs. (31)−(33). Also, it is adopted that the balancing parameter of the third appraisal score strategy λ is 0.5.

Table 14.

The appraisal score strategies, assessment scores, and ranks of the alternatives for adapting transport planning to COVID-19.

Alternative	Appraisal score strategy						Assessment score	Final rank
	Arithmetic mean		Relative score		Balanced compromise
	Value	Rank	Value	Rank	Value	Rank
A1	0.224	1	2.730	1	1.000	1	2.717	1
A2	0.192	4	2.346	4	0.859	4	1.870	4
A3	0.217	2	2.650	2	0.971	2	2.420	2
A4	0.171	5	2.022	5	0.765	5	1.604	5
A5	0.195	3	2.400	3	0.871	3	2.038	3

Step 3.3. The assessment score of each alternative is obtained by aggregating the corresponding value and rank of three appraisal score strategies from Table 14, as defined in Eq. (34). Then, five investigated alternatives for adapting transport planning to COVID-19 are ranked according to the decreasing values of the assessment scores. The generated ranks are provided in the last column of Table 14. Based on the results, the best alternative is “non-motorized travel” (A ₁) since it has the highest assessment score. The complete ranking order is as follows: A ₁ (non-motorized travel) $\succ$ A ₃ (mobility management) $\succ$ A ₅ (intelligent transport systems) $\succ$ A ₂ (service quality improvement in public transport) A ₄ $\succ$ (transport infrastructure development).

5.2. Ranking Discussion

Due to the specific situation caused by the COVID pandemic, the transport planning experts recognized the external aspect (MC ₄) as a crucial main criterion with an importance of 0.3248. In this way, they acknowledged the importance of taking into account the factors that affect the probability of realization of a certain planning alternative; i.e., aspects of political and public support. The social (MC ₃) and environmental (MC ₁) aspects have very close importance. The social aspect emphasizes the importance of providing conditions to perform the basic life activities of transport system users (Mouratidis, 2021). It is highly rated with importance of 0.2949. This is fully in line with the current situation since the COVID pandemic emphasizes the importance of human life and health. The environmental aspect, which is based on the impact of the proposed alternative on the environment, has also gained importance (Koehl, in press). In some countries, the situation with lockdown due to the pandemic has shown a significant reduction in air pollution caused by traffic (Xiang et al., 2020), which has further drawn attention to this effect. The economic aspect (MC ₂) is the last with importance of only 0.1322. Therefore, the cost of an alternative solution loses its importance under COVID-19 (OECD, 2021). The rank of the economic criterion shows that the adaptation of transport planning measures to specific situations should be kept in mind (Simic et al., 2021). No matter how much this main criterion has lost importance under the COVID-19 pandemic, the costs can be minimized with good planning and investments in the resilience of the transport system.

As for the sub-criteria, air pollution (C ₁) and congestion reduction (C ₁₅) are the two most important since they are strongly correlated to the problem of increased passenger car use under the COVID-19 pandemic (Eisenmann et al., 2021). On the other hand, the least important sub-criteria are user cost (C ₇) and eco-friendliness (C ₃) with the global importance of 0.0302 and 0.0362, respectively.

The rankings of the investigated alternatives can be explained as follows:

• •The highest priority is given to “non-motorized travel” (A ₁), as a direct result of COVID-19. This finding is fully in line with Dalkmann and Turner (2020) who outlined that walking and cycling are currently the safest options to avoid exposure. This decision expresses the importance of short-term measures that could lead to better transport service (like pop-up bike lanes), which is the opposite of long-term solutions that were emphasized in the existing transport plans of Belgrade (like the construction of subway lines). Also, the COVID-19 pandemic affected the increased importance of the criteria related to health improvement. This is supported by the promotion of non-motorized travel modes and additionally contributes to the reduction of the negative environmental impacts (Koehl, in press). Increased passenger car use, as a direct consequence of the fear of COVID-19, significantly affects the sustainability of the transport system and reduces the quality of life.
• •The increased importance of “mobility management” (A ₃) comes as a result of incorporated measures that enable avoiding the necessity to travel (e.g., from home to work or school) and the MaaS concept. Work from home is an especially visible alternative in common practice (Hensher et al., 2021). Besides, a significant number of companies will continue to utilize remote working after the COVID-19 pandemic since it offers cost reduction. When it comes to the MaaS concept, it is recognized that the increase in the number of transport alternatives for users is very important (Hensher, 2020).
• •“Intelligent transport systems” (A ₅) is not recognized as something that could bring significant effects under the COVID-19 pandemic. However, it is important for the traditional efficiency improvement of the transport system in Belgrade. The rank of this alternative is in between its orientation towards improving the service level of car users (as a negative characteristic) and COVID-19 safe transport by passenger cars (as a positive characteristic).
• •“Service quality improvement in public transport” (A ₂) is ranked very low since public transport presents the most unsafe transport mean due to the possibility to get infected. Public transport is highly sensitive to the impact of COVID-19 (Hörcher et al., in press). Also, people doubt the personal responsibility and behavior of other passengers regardless of various preventive measures in public transport (Gkiotsalitis and Cats, 2021).
• •“Transport infrastructure development” (A ₄) is the worst alternative since fast solutions are expected following the rapid spread of COVID-19. These mostly long-term measures are not recognized as a priority in the current situation, as outlined by Falk et al. (2020).

5.3. Sensitivity Analyses

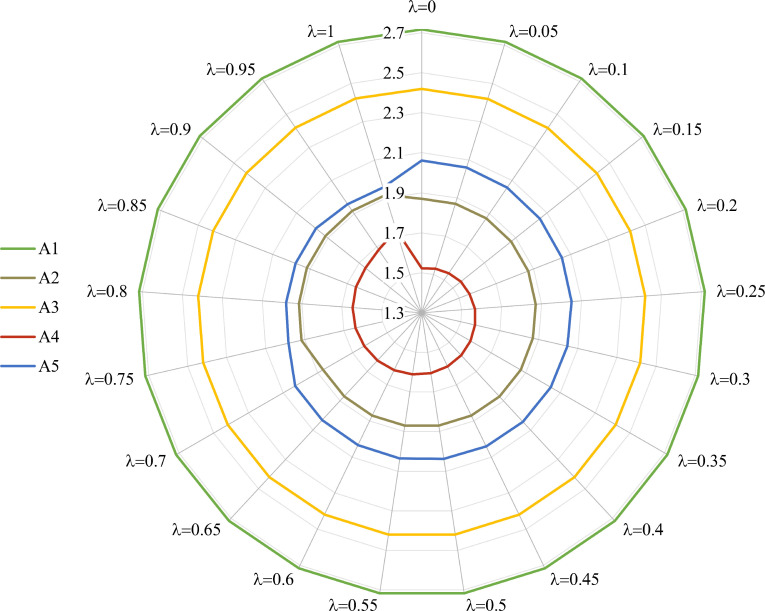
The first sensitivity analysis investigates how the balancing parameter λ∈[0, 1] influences the solutions of the proposed integrated Fermatean fuzzy model. In the base scenario, the balancing parameter was set to 0.5. The values of this built-in parameter are changed from λ=0 to λ=1 with the increment of 0.05 to comprehensively analyze its impact. Fig. 5 shows the assessment scores of the alternatives in twenty additional scenarios as well as their values when λ=0.5. According to Fig. 5, it is found that “non-motorized travel” (A ₁) is the best alternative under all balancing parameter values since it has the highest assessment score. The performed variations of the parameter λ do not produce any notable change in the ranks of five alternatives for adapting transport planning to COVID-19 in Belgrade. Therefore, the results indicate that the initial ranks are highly robust to changes in the balancing parameter.

Fig. 5.

The sensitivity analysis to changes in the balancing parameter.

The second sensitivity analysis explores how the reputation of the transport planning experts influences the results of the proposed integrated Fermatean fuzzy model. The scenarios are generated by changing the reputation of the most influential expert while adjusting the reputations of the other transport planning experts as follows:

$${\delta }_e^{\prime }=(1-{\delta }_l^{\prime })\frac{{\delta }_e}{(1-{\delta }_l)},e=1,\dots ,k|e\ne l,$$ (35)

where ${\delta }_e^{\prime }$ represents the adjusted reputation of the expert D_e, ${\delta }_l^{\prime }$ is the adjusted reputation of the most influential expert D_l, ${\delta }_e$ is the original reputation of the expert D_e, and ${\delta }_l$ is the original reputation of the most influential expert D_l.

In the base scenario (scenario 0), the reputation vector of the transport planning experts is determined based on the newly-proposed Fermatean fuzzy expert reputation rating approach as well as the experts’ self-appraisals of their experience, domain expertise, and impact on transport planning in Belgrade; i.e., the reputations are δ ₁=0.1758, δ ₂=0.2124, δ ₃=0.1711, δ ₄=0.2284, and δ ₅=0.2124 (Fig. 6 ). Therefore, the fourth expert is the most influential one. One-hundred additional reputation scenarios are simulated by reducing its reputation with a rate of 1% while adjusting the reputations of the other four transport planning experts by utilizing Eq. (35). The simulated expert reputation scenarios are presented in Fig. 6.

Fig. 6.

The simulated expert reputation scenarios.

Fig. 7 shows the assessment scores of the five alternatives in 100 simulated reputation scenarios. As can be seen from Fig. 7, “non-motorized travel” (A ₁) remains dominant over other possible alternatives for adapting transport planning to COVID-19 in Belgrade. Also, compared to the base scenario, there is no change in the ranks of the five assessed alternatives through all 100 simulated expert reputation scenarios. It can be outlined that the initial results (scenario 0) are highly robust to changes in the reputation of the transport planning experts.

Fig. 7.

The sensitivity analysis to changes in the reputation of the transport planning experts.

According to the results of both sensitivity analyses, it can be concluded that the integrated Fermatean fuzzy model is highly robust. Also, “non-motorized travel” (A ₁) stands out as the best alternative for adapting transport planning in Belgrade.

5.4. Comparative Analysis

The comparative analysis of the proposed model with the Fermatean fuzzy TOPSIS (Senapati and Yager, 2020), WASPAS (Keshavarz-Ghorabaee et al., 2020), and WPM (Senapati and Yager, 2019b) methods is performed to check its reliability and consistency.

Obtained comparison results are depicted in Fig. 8 . The integrated Fermatean fuzzy model, FFS-TOPSIS, and FFS-WASPAS generate the same ranking order of the alternatives. On the other hand, the FFS-WPM produces a slightly different ranking order by giving higher priority to “service quality improvement in public transport” (A ₂) than “intelligent transport systems” (A ₅). However, this approach also puts A ₁ and A ₃ in the first two positions. As a result, it can be outlined that the integrated Fermatean fuzzy model is highly reliable.

Fig. 8.

The comparison of different Fermatean fuzzy approaches.

The major differences between the integrated Fermatean fuzzy model and three existing FFS-based approaches are provided in Table 15 . As can be seen from this table, the advantages of the introduced model are as follows:

• 1)High flexibility in real-life applications with FFN operations based on Yager norms and two build-in parameters; i.e., the parameter η offers fine-tuning of the FFYWA and the FFYWA operators, the parameter λ balances of the appraisal score strategies, while Yager T-norm and T-conorm operations provide advanced integration of uncertain information.
• 2)Expert reputation rating in the group decision-making context by taking into account reputation indicators such as experience, domain expertise, and impact to support precise aggregation of multi-expert input preferences of alternatives and criteria.
• 3)The objective weighting of main criteria and sub-criteria in a multi-level decision-making hierarchy based on the concept of causality when their importance is not equal or fully known in advance.

Table 15.

The characteristic of different Fermatean fuzzy approaches.

Characteristic	Approach
	IFFM (our study)	FFS-TOPSIS	FFS-WASPAS	FFS-WPM
Uncertain environment	Fermatean fuzzy	Fermatean fuzzy	Fermatean fuzzy	Fermatean fuzzy
Operations	Yager T-norm and T-conorm	Algebraic	Algebraic	Algebraic
Group decision-making	Yes	No	Yes	No
Expert reputation rating	Yes	No	No	No
Main criteria weighting	Yes (objective)	No	No	No
Sub-criteria weighting	Yes (objective)	No	No	No
Alternative ranking	Yes	Yes	Yes	Yes
Build-in parameter(s)	Two	No	One	No
Flexibility	High	Low	Medium	Low

Fermatean fuzzy set: FFS, Integrated Fermatean fuzzy model: IFFM, Technique for the Order Preference by Similarity to Ideal Solution: TOPSIS, Weighted Aggregated Sum Product ASsessment: WASPAS, Weighted Product Model: WPM.

5.5. Implications

It should be kept in mind that the COVID-19 pandemic was impossible to predict, and in line with that, future transport plans should be characterized by higher flexibility. Also, the measures that are an integral part of development strategies should be periodically reviewed since the pandemic affects the constant change of travel patterns.

The research findings show that the existing transport plans should be adapted in line with the circumstances of COVID-19. In contrast to the priorities of the existing plans that were given to the long-term measures (e.g., the construction of the subway and completing the road network), the focus of revised plans should be placed on the short-term project measures that are primarily focused on the development and encouragement of non-motorized transport modes. City authorities should initially focus on the top-ranked alternatives. The presented results can implicitly aid relevant stakeholders to adapt existing transport plans to COVID-19 as well as in any future disruption event.

The practical importance of the integrated Fermatean fuzzy model is reflected in the following: a) It offers the possibility to test and analyze different scenarios for the development of transport systems and strategically direct the changes towards best improvements in line with primal opportunities; b) Transport planners are provided with an effective tool to review the priorities of certain development strategies, both in regular situations and emergencies (such as COVID-19).

6. Conclusions

This study presents the integrated Fermatean fuzzy model for adapting transport planning to the COVID-19 pandemic. The multi-stage model hybridizes the MEREC and CoCoSo methods into a unique methodological framework under the Fermatean fuzzy environment. The first stage differentiates experts by considering their experience, domain expertise, and impact. In the second stage, the new Fermatean fuzzy hierarchical MEREC determines the importance of main and sub-criteria. In the final stage, the novel Fermatean fuzzy CoCoSo method prioritizes alternatives. The comparative analysis approved the high reliability of the integrated Fermatean fuzzy model. Also, two sensitivity analyses confirmed its high robustness for adapting existing transport plans to COVID-19.

Compared to the available FFS-based approaches, the advantages of the integrated Fermatean fuzzy model are as follows: (1) Two build-in parameters (i.e., the operational parameter η and the balancing parameter λ), as well as FFN operations based on Yager norms, provide higher decision-making flexibility; (2) The ability to take into account the experience, domain expertise, and impact when determining the reputation vector of experts; and (3) Removal effects of each main and sub-criterion can be considered to determine their importance when this information is not known in advance. As a result, the introduced model offers to researchers and practitioners advanced decision support.

A case study of Belgrade provides decision-making guidelines on how to assess and adapt existing transport plans to the COVID-19 pandemic in a real-world context. The research findings show that “non-motorized travel” is now the best alternative while the external aspect is recognized as a crucial main criterion. The investments in infrastructure and public transport should be put on hold until further developments related to the pandemic are clearer. The focus should be given to the active transport modes and mobility management. The results suggest a close relationship between alternative strategies of infrastructure improvements for the active transport modes and strategies that involve e-mobility, carpooling, and work from home. Therefore, COVID-19 has led to a significant change in the priority of transport planning strategies and measures. As a result, it is strongly recommended to revise existing transport plans due to significant changes in user behavior and adapt them to the effect of COVID-19.

There are also some limitations of this study because the integrated Fermatean fuzzy model is applied only in the Belgrade context. As a result, the provided practical findings may not be directly applicable to general settings. Thus, it is important to employ the introduced model to other cities worldwide and adapt their transport plans to the COVID-19 pandemic. Secondly, the formulated model is unable to account for the subjective importance of main and sub-criteria since the Fermatean fuzzy hierarchical MEREC only provides their objective importance. Popular subjective criteria weighting methods are the analytic hierarchy process (Saaty, 1977), best-worst method (Rezaei, 2015), and step-wise weight assessment ratio analysis (Keršuliene et al., 2010). However, their Fermatean fuzzy extensions are not yet available. Extension of some of the aforementioned approaches to the Fermatean fuzzy environment and integration into the presented methodological framework based on the hierarchical MEREC and CoCoSo methods can help surpass this limitation. Thirdly, another important future direction is to consider the impacts of future events through the concept of stratification (Torkayesh et al. 2021b) to determine even more reliable results. Fourthly, the introduced model can be integrated with data mining and machine learning algorithms to tackle large-scale decision-making problems with a high number of criteria and alternatives for the COVID-19 pandemic issues. Finally, another important extension area is to use the integrated Fermatean fuzzy model to solve other complex decision-making problems like sustainable policy selection, green supplier selection, carbon footprint evaluation, smart city development, sustainability assessment, etc.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A

Notation
i	Index of the alternatives, i=1, …, m
t	Index of the main criteria, t=1, …, q
j	Index of the sub-criteria, j=1, …, n
e	Index of the experts, e=1, …, k
g	Index of the appraisal score strategy, g=1, 2, 3
l	Auxiliary index
Sets
A	Set of the alternatives
MC	Set of the main criteria
C	Set of the sub-criteria
Bt, t∈MC	Set of the sub-criteria from the main criteria MCt
D	Set of the experts
C+	Set of the benefit sub-criteria
C−	Set of the cost sub-criteria
$\tilde{F}$	Fermatean fuzzy set
Parameters
m	Number of the alternatives
q	Number of the main criteria
n	Number of the sub-criteria
k	Number of the experts
η	Operational parameter of the FFYWA and the FFYWG operators, η>0
λ	Balancing parameter of the third appraisal score strategy, λ∈[0, 1]
Matrices
$\tilde{\mathrm{Y}}$	Expert reputation matrix
${\tilde{\mathrm{V}}}^e,$e∈D	Main criteria decision matrix by the expert De
${\tilde{\mathrm{W}}}^e,$e∈D	Sub-criteria decision matrix by the expert De
$\tilde{\Theta }$	Aggregated main criteria decision matrix
$\tilde{\Psi }$	Aggregated sub-criteria decision matrix
$\tilde{\mathrm{H}}$	Normalized decision matrix
Variables
${\alpha }_{\tilde{F}}$	Degree of membership in the Fermatean fuzzy set $\tilde{F},$${\alpha }_{\tilde{F}}$∈[0, 1]
${\beta }_{\tilde{F}}$	Degree of non-membership in the Fermatean fuzzy set $\tilde{F},$${\beta }_{\tilde{F}}$∈[0, 1]
${\pi }_{\tilde{F}}$	Degree of indeterminacy in the Fermatean fuzzy set $\tilde{F},$${\pi }_{\tilde{F}}$∈[0, 1]
${\tilde{Y}}_1^e,$e∈D	Fermatean fuzzy self-appraisal of the experience of the expert De
${\tilde{Y}}_2^e,$e∈D	Fermatean fuzzy self-appraisal of the domain expertise of the expert De
${\tilde{Y}}_3^e,$e∈D	Fermatean fuzzy self-appraisal of the impact of the expert De
${\tilde{\Phi }}_e,$e∈D	Fermatean fuzzy aggregated reputation of the expert De
δe, e∈D	Reputation of the expert De, δe∈[0, 1]
${\tilde{V}}_{it}^e,$i∈A, t∈MC, e∈D	Fermatean fuzzy assessment of the alternative Ai under the main criterion MCt given by the expert De
${\tilde{W}}_{\mathit{ij}}^e,$i∈A, j∈C, e∈D	Fermatean fuzzy assessment of the alternative Ai under the sub-criterion Cj given by the expert De
${\tilde{\Theta }}_{it},$i∈A, t∈MC	Fermatean fuzzy aggregated assessment of the alternative Ai under the main criterion MCt given by the experts
${\tilde{\Psi }}_{\mathit{ij}},$i∈A, j∈C	Fermatean fuzzy aggregated assessment of the alternative Ai under the sub-criterion Cj given by the experts
${\tilde{H}}_{\mathit{ij}},$i∈A, j∈C	Fermatean fuzzy normalized assessment of the alternative Ai under the sub-criterion Cj given by the experts
$O_i,$i∈A	Overall performance of the alternative Ai under the main criteria
$P_{it},$i∈A, t∈MC	Overall performance of the alternative Ai under the sub-criteria of the main criterion MCt
$O_{it}^{\prime },$i∈A, t∈MC	Partial performance of the alternative Ai under the main criteria when the main criterion MCt is removed
$P_{itj}^{\prime },$i∈A, t∈MC, j∈C	Partial performance of the alternative Ai under the sub-criteria of the main criterion MCt when the sub-criterion Cj is removed
${\xi }_t,$t∈MC	Removal effect of the main criterion MCt
${\upsilon }_j,$j∈C	Removal effect of the sub-criterion Cj
θt, t∈MC	Importance of the main criterion MCt, θt∈[0, 1]
ωj, j∈C	Local importance of the sub-criterion Cj, ωj∈[0, 1]
${\omega }_j^{*},$j∈C	Global importance of the sub-criterion Cj, ${\omega }_j^{*}$∈[0, 1]
${\tilde{Q}}_i,$i∈A	Fermatean fuzzy Yager weighted average comparability sequence for the alternative Ai
${\tilde{U}}_i,$i∈A	Fermatean fuzzy Yager weighted geometric comparability sequence for the alternative Ai
$S_i^{\left(1\right)},$i∈A	Appraisal score of the alternative Ai based on the arithmetic mean strategy
$S_i^{\left(2\right)},$i∈A	Appraisal score of the alternative Ai based on the relative score strategy
$S_i^{\left(3\right)},$i∈A	Appraisal score of the alternative Ai based on the balanced compromise strategy
$R_i^{\left(g\right)},$i∈A, g=1, 2, 3	Rank of the alternative Ai under the appraisal score strategy g
Zi, i∈A	Assessment score of the alternative Ai

Appendix B

Table B.1.

The main criteria decision matrices.

Alternative	Expert	Main criterion
		MC1: Environmental	MC2: Economic	MC3: Social	MC4: External
A1: Non-motorized travel	D1	(0.975, 0.10)	(0.20, 0.90)	(0.55, 0.50)	(0.90, 0.20)
	D2	(0.80, 0.30)	(0.55, 0.50)	(0.55, 0.50)	(0.55, 0.50)
	D3	(0.975, 0.10)	(0.80, 0.30)	(0.55, 0.50)	(0.55, 0.50)
	D4	(0.90, 0.20)	(0.55, 0.50)	(0.65, 0.40)	(0.65, 0.40)
	D5	(0.55, 0.50)	(0.40, 0.65)	(0.90, 0.20)	(0.65, 0.40)
A2: Service quality improvement in public transport	D1	(0.30, 0.80)	(0.975, 0.10)	(0.90, 0.20)	(0.90, 0.20)
	D2	(0.80, 0.30)	(0.90, 0.20)	(0.90, 0.20)	(0.90, 0.20)
	D3	(0.80, 0.30)	(0.40, 0.65)	(0.65, 0.40)	(0.90, 0.20)
	D4	(0.90, 0.20)	(0.40, 0.65)	(0.65, 0.40)	(0.55, 0.50)
	D5	(0.90, 0.20)	(0.65, 0.40)	(0.90, 0.20)	(0.90, 0.20)
A3: Mobility management	D1	(0.90, 0.20)	(0.65, 0.40)	(0.80, 0.30)	(0.80, 0.30)
	D2	(0.80, 0.30)	(0.90, 0.20)	(0.80, 0.30)	(0.90, 0.20)
	D3	(0.975, 0.10)	(0.65, 0.40)	(0.65, 0.40)	(0.80, 0.30)
	D4	(0.80, 0.30)	(0.55, 0.50)	(0.65, 0.40)	(0.65, 0.40)
	D5	(0.90, 0.20)	(0.65, 0.40)	(0.90, 0.20)	(0.80, 0.30)
A4: Transport infrastructure development	D1	(0.90, 0.20)	(0.975, 0.10)	(0.975, 0.10)	(0.975, 0.10)
	D2	(0.80, 0.30)	(0.90, 0.20)	(0.90, 0.20)	(0.90, 0.20)
	D3	(0.55, 0.50)	(0.80, 0.30)	(0.80, 0.30)	(0.90, 0.20)
	D4	(0.90, 0.20)	(0.30, 0.80)	(0.55, 0.50)	(0.65, 0.40)
	D5	(0.90, 0.20)	(0.65, 0.40)	(0.90, 0.20)	(0.90, 0.20)
A5: Intelligent transport systems	D1	(0.55, 0.50)	(0.80, 0.30)	(0.90, 0.20)	(0.90, 0.20)
	D2	(0.65, 0.40)	(0.80, 0.30)	(0.80, 0.30)	(0.80, 0.30)
	D3	(0.55, 0.50)	(0.80, 0.30)	(0.80, 0.30)	(0.90, 0.20)
	D4	(0.55, 0.50)	(0.55, 0.50)	(0.65, 0.40)	(0.65, 0.40)
	D5	(0.40, 0.65)	(0.40, 0.65)	(0.90, 0.20)	(0.90, 0.20)

Table B.2.

The sub-criteria decision matrices.

Alternative	Expert	Sub-criterion
		C1: Air pollution	C2: Noise	C3: Eco-friendliness	C4: Land use impact	C5: Comm. cost	⋅⋅⋅	C17: Safety
A1: Non-motorized travel	D1	(0.10, 0.975)	(0.20, 0.90)	(0.90, 0.20)	(0.20, 0.90)	(0.30, 0.80)	⋅⋅⋅	(0.65, 0.40)
	D2	(0.10, 0.975)	(0.10, 0.975)	(0.975, 0.10)	(0.80, 0.30)	(0.80, 0.30)	⋅⋅⋅	(0.90, 0.20)
	D3	(0.10, 0.975)	(0.10, 0.975)	(0.80, 0.30)	(0.55, 0.50)	(0.80, 0.30)	⋅⋅⋅	(0.80, 0.30)
	D4	(0.40, 0.65)	(0.40, 0.65)	(0.30, 0.80)	(0.20, 0.90)	(0.40, 0.65)	⋅⋅⋅	(0.55, 0.50)
	D5	(0.20, 0.90)	(0.10, 0.975)	(0.90, 0.20)	(0.90, 0.20)	(0.65, 0.40)	⋅⋅⋅	(0.90, 0.20)
A2: Service quality improvement in public transport	D1	(0.90, 0.20)	(0.90, 0.20)	(0.90, 0.20)	(0.80, 0.30)	(0.90, 0.20)	⋅⋅⋅	(0.80, 0.30)
	D2	(0.30, 0.80)	(0.30, 0.80)	(0.80, 0.30)	(0.90, 0.20)	(0.90, 0.20)	⋅⋅⋅	(0.80, 0.30)
	D3	(0.30, 0.80)	(0.30, 0.80)	(0.65, 0.40)	(0.55, 0.50)	(0.90, 0.20)	⋅⋅⋅	(0.80, 0.30)
	D4	(0.55, 0.50)	(0.40, 0.65)	(0.55, 0.50)	(0.65, 0.40)	(0.65, 0.40)	⋅⋅⋅	(0.80, 0.30)
	D5	(0.20, 0.90)	(0.40, 0.65)	(0.40, 0.65)	(0.40, 0.65)	(0.65, 0.40)	⋅⋅⋅	(0.80, 0.30)
A3: Mobility management	D1	(0.10, 0.975)	(0.10, 0.975)	(0.20, 0.90)	(0.30, 0.80)	(0.40, 0.65)	⋅⋅⋅	(0.975, 0.10)
	D2	(0.30, 0.80)	(0.30, 0.80)	(0.80, 0.30)	(0.65, 0.40)	(0.65, 0.40)	⋅⋅⋅	(0.80, 0.30)
	D3	(0.30, 0.80)	(0.30, 0.80)	(0.80, 0.30)	(0.55, 0.50)	(0.80, 0.30)	⋅⋅⋅	(0.80, 0.30)
	D4	(0.20, 0.90)	(0.20, 0.90)	(0.40, 0.65)	(0.40, 0.65)	(0.40, 0.65)	⋅⋅⋅	(0.65, 0.40)
	D5	(0.20, 0.90)	(0.20, 0.90)	(0.90, 0.20)	(0.90, 0.20)	(0.40, 0.65)	⋅⋅⋅	(0.90, 0.20)
A4: Transport infrastructure development	D1	(0.975, 0.10)	(0.975, 0.10)	(0.10, 0.975)	(0.90, 0.20)	(0.975, 0.10)	⋅⋅⋅	(0.65, 0.40)
	D2	(0.80, 0.30)	(0.80, 0.30)	(0.30, 0.80)	(0.80, 0.30)	(0.90, 0.20)	⋅⋅⋅	(0.90, 0.20)
	D3	(0.975, 0.10)	(0.90, 0.20)	(0.80, 0.30)	(0.80, 0.30)	(0.90, 0.20)	⋅⋅⋅	(0.90, 0.20)
	D4	(0.80, 0.30)	(0.80, 0.30)	(0.30, 0.80)	(0.90, 0.20)	(0.90, 0.20)	⋅⋅⋅	(0.65, 0.40)
	D5	(0.80, 0.30)	(0.90, 0.20)	(0.80, 0.30)	(0.65, 0.40)	(0.90, 0.20)	⋅⋅⋅	(0.90, 0.20)
A5: Intelligent transport systems	D1	(0.90, 0.20)	(0.80, 0.30)	(0.80, 0.30)	(0.80, 0.30)	(0.80, 0.30)	⋅⋅⋅	(0.65, 0.40)
	D2	(0.40, 0.65)	(0.40, 0.65)	(0.65, 0.40)	(0.65, 0.40)	(0.65, 0.40)	⋅⋅⋅	(0.80, 0.30)
	D3	(0.55, 0.50)	(0.55, 0.50)	(0.55, 0.50)	(0.20, 0.90)	(0.80, 0.30)	⋅⋅⋅	(0.80, 0.30)
	D4	(0.20, 0.90)	(0.20, 0.90)	(0.90, 0.20)	(0.30, 0.80)	(0.65, 0.40)	⋅⋅⋅	(0.30, 0.80)
	D5	(0.65, 0.40)	(0.80, 0.30)	(0.65, 0.40)	(0.55, 0.50)	(0.90, 0.20)	⋅⋅⋅	(0.90, 0.20)

Table B.3.

The normalized decision matrix.

Sub-criterion	Alternative
	A1: Non-motorized travel	A2: Service quality imp. in public transport	A3: Mobility management	A4: Transport infrastructure development	A5: Intelligent transport systems
C1: Air pollution	(0.9323, 0.2529)	(0.8000, 0.4843)	(0.8933, 0.2405)	(0.2861, 0.8322)	(0.7683, 0.5492)
C2: Noise	(0.9352, 0.2515)	(0.7324, 0.4709)	(0.8933, 0.2405)	(0.2746, 0.8485)	(0.7683, 0.5698)
C3: Eco-friendliness	(0.7244, 0.6790)	(0.6409, 0.5537)	(0.6370, 0.7475)	(0.5249, 0.8359)	(0.6986, 0.4247)
C4: Land use impact	(0.8140, 0.5794)	(0.5525, 0.6483)	(0.6740, 0.5738)	(0.3417, 0.7877)	(0.7720, 0.5379)
C5: Community cost	(0.6732, 0.6035)	(0.3653, 0.7583)	(0.6163, 0.5354)	(0.1958, 0.9068)	(0.3676, 0.7386)
C6: Operator cost	(0.6822, 0.5207)	(0.3417, 0.8010)	(0.6178, 0.5229)	(0.2565, 0.8717)	(0.4296, 0.7196)
C7: User cost	(0.8228, 0.6274)	(0.4194, 0.7281)	(0.5916, 0.5221)	(0.3463, 0.7704)	(0.5418, 0.6451)
C8: Travel time	(0.5378, 0.6624)	(0.5536, 0.6282)	(0.6701, 0.6036)	(0.2570, 0.8674)	(0.5378, 0.6624)
C9: User accessibility	(0.6711, 0.5360)	(0.7027, 0.4310)	(0.7146, 0.4199)	(0.7229, 0.4303)	(0.6214, 0.4729)
C10: Spatial coverage	(0.7222, 0.4184)	(0.7239, 0.4195)	(0.6335, 0.6714)	(0.6742, 0.6579)	(0.6743, 0.5525)
C11: Interconnectivity	(0.6933, 0.5369)	(0.7289, 0.4293)	(0.6706, 0.4553)	(0.7039, 0.5353)	(0.6628, 0.5560)
C12: New users	(0.6802, 0.4324)	(0.6929, 0.5354)	(0.7731, 0.3442)	(0.8263, 0.2866)	(0.7136, 0.4306)
C13: Political support	(0.5595, 0.7463)	(0.6140, 0.6755)	(0.6370, 0.7475)	(0.8674, 0.2570)	(0.578, 0.6809)
C14: Public support	(0.6393, 0.7424)	(0.7077, 0.3784)	(0.6770, 0.7420)	(0.8674, 0.2570)	(0.6174, 0.4760)
C15: Cong. reduction	(0.7539, 0.3633)	(0.6116, 0.8043)	(0.7505, 0.3664)	(0.7564, 0.5359)	(0.7428, 0.4256)
C16: Resource eff.	(0.6810, 0.6578)	(0.5724, 0.5908)	(0.5794, 0.8140)	(0.6196, 0.6619)	(0.6145, 0.7645)
C17: Safety	(0.7302, 0.4293)	(0.8000, 0.3000)	(0.7861, 0.3440)	(0.7665, 0.3618)	(0.6779, 0.6791)

Table B.4.

The partial performance of the alternatives for adapting transport planning to COVID-19.

Criterion	Alternative
	A1: Non- motorized travel	A2: Service quality imp. in public transport	A3: Mobility management	A4: Transport infrastructure development	A5: Intelligent transport ystems
MC1: Environmental	0.1429	0.1664	0.1934	0.1681	0.1929
C1: Air pollution	0.2131	0.1071	0.1853	0.4165	0.1694
C2: Noise	0.2122	0.1254	0.1853	0.4020	0.1726
C3: Eco-friendliness	0.3129	0.1609	0.2567	0.4531	0.1733
C4: Land use impact	0.2697	0.1566	0.2688	0.4504	0.1667
MC2: Economic	0.1457	0.1783	0.2479	0.2378	0.1741
C5: Community cost	0.1347	0.2919	0.0492	0.4219	0.1435
C6: Operator cost	0.1109	0.2531	0.0457	0.4859	0.1688
C7: User cost	0.0783	0.3202	0.0539	0.5835	0.2319
MC3: Social	0.1835	0.1160	0.2243	0.1735	0.1181
C8: Travel time	0.1446	0.1717	0.1561	0.1643	0.1164
C9: User accessibility	0.1458	0.1452	0.1253	0.2839	0.1198
C10: Spatial coverage	0.1236	0.1400	0.1609	0.3193	0.1193
C11: Interconnectivity	0.1413	0.1397	0.1370	0.2963	0.1222
C12: New users	0.1332	0.1575	0.1082	0.2578	0.0977
MC4: External	0.1794	0.1176	0.2165	0.1561	0.1148
C13: Political support	0.1456	0.1859	0.2170	0.2038	0.1224
C14: Public support	0.1653	0.1551	0.2282	0.2038	0.1243
C15: Cong. reduction	0.1373	0.1409	0.1936	0.2431	0.0943
C16: Resource eff.	0.1869	0.1960	0.1760	0.2729	0.1025
C17: Safety	0.1464	0.1321	0.1851	0.2285	0.1449