Abstract
The distribution of fitness effects (DFE) for new mutations is one of the most theoretically important but difficult to estimate properties in population genetics. A crucial challenge to inferring the DFE from natural genetic variation is the sensitivity of the site frequency spectrum to factors like population size change, population substructure, genome structure, and nonrandom mating. Although inference methods aim to control for population size changes, the influence of nonrandom mating remains incompletely understood, despite being a common feature of many species. We report the DFE estimated from 326 genomes of Caenorhabditis elegans, a nematode roundworm with a high rate of self-fertilization. We evaluate the robustness of DFE inferences using simulated data that mimics the genomic structure and reproductive life history of C. elegans. Our observations demonstrate how the combined influence of self-fertilization, genome structure, and natural selection on linked sites can conspire to compromise estimates of the DFE from extant polymorphisms with existing methods. These factors together tend to bias inferences toward weakly deleterious mutations, making it challenging to have full confidence in the inferred DFE of new mutations as deduced from standing genetic variation in species like C. elegans. Improved methods for inferring the DFE are needed to appropriately handle strong linked selection and selfing. These results highlight the importance of understanding the combined effects of processes that can bias our interpretations of evolution in natural populations.
Keywords: mutation, distribution of fitness effects, self-fertilization, linked selection, site frequency spectrum
Introduction
Understanding the distribution of fitness effects (DFE) of new mutations is necessary to characterize the role of mutation in the evolutionary process and to determine the full impact that mutations have on the fitness of individuals and populations. The DFE influences the rate and trajectory of adaptive evolution (Orr 2000; Good et al. 2012), the maintenance of genetic variation (Charlesworth et al. 1995), the evolution of sex and recombination (Peck et al. 1997), the fate of small populations (Schultz and Lynch 1997), the molecular clock (Ohta 1992), the rate of decay of fitness due to Muller's Ratchet (Loewe 2006), and the evolution of the mutation rate itself (Kondrashov 1995; Lynch 2008). Understanding the DFE also is necessary for accurate characterization of the genetic basis of complex traits, including human disease (Eyre-Walker 2010), and has been sought for decades (Eyre-Walker and Keightley 2007; Boyko et al. 2008; Kousathanas and Keightley 2013; Charlesworth 2015; Kim et al. 2017; Tataru et al. 2017). Any dynamic model of evolution must either define the DFE explicitly and assume its distribution or ignore the varying effects of mutations. Despite these fundamental roles, the DFE is a challenging property to estimate (Eyre-Walker and Keightley 2007; Charlesworth 2015).
The DFE defines the probability that a new mutation will alter organismal survival or reproduction by a given magnitude. Following common practice, we restrict our consideration of the DFE to new deleterious mutations that reduce fitness relative to the ancestral state. This DFE can be quantified in two basic ways: (1) from direct experimental measurement of fitness effects of new mutations or mutation panels (Thatcher et al. 1998; Sanjuán et al. 2004; DePristo et al. 2007) or (2) from indirect inference using the site frequency spectrum (SFS) of genetic variants in populations (Loewe et al. 2006; Keightley and Eyre-Walker 2007; Boyko et al. 2008). Using the SFS-based approach, population genomic data have been used to infer the DFE for many organisms (Boyko et al. 2008; Kousathanas and Keightley 2013; Charlesworth 2015; Kim et al. 2017; Tataru et al. 2017). With rare exceptions, these taxa are predominantly or obligately outcrossing. The SFS approach benefits from the large number of mutations, accessible with genome sequencing methods, that have experienced a fairly long evolutionary history in the natural environment. However, the utility of the SFS approach depends on the ability of analytical methods to use the observed standing genetic variation to correctly infer the effects of new mutations.
An accurate inference of the DFE allows one to understand the evolutionary trajectory that mutations will follow, because the selection coefficient conferred by any given mutation (s) combines with the effective size of the population in which it arose (Ne) to determine the efficacy of selection (Nes) on that variant. The accuracy of the SFS inference method is challenged, however, by its sensitivity to nonequilibrium demography, population structure, and nonrandom mating (Eyre-Walker 2006). Demographic changes like population size expansions or contractions that mimic some effects of natural selection can lead to mischaracterization of the DFE (Eyre-Walker and Keightley 2007). Population size changes and cryptic population structure should largely be accounted for with existing methods that contrast two sets of loci: one set presumed to be selectively neutral (e.g., fourfold degenerate sites in coding sequences) and thus reflecting neutral demographic change, vs a second set presumed to experience the direct effects of selection (e.g., zerofold degenerate sites in coding sequences) in addition to the selectively neutral effects of demography (Keightley and Eyre-Walker 2007).
Nonrandom mating, of which self-fertilization is the most extreme form, presents a more difficult problem. Inbreeding reduces the effective recombination rate (Nordborg 1997), which exacerbates the effects of selection at linked loci (Felsenstein 1974; Charlesworth and Wright 2001; Cutter and Payseur 2013). With reduced recombination, individual variants may no longer have independent evolutionary trajectories, as the fitness effects of their nearby genomic neighbors can play a role in changing the allele frequency of a focal variant (Hill-Robertson interference; Hill and Robertson 1966). How Hill-Robertson interference affects inference of the DFE from the SFS cannot easily be predicted a priori. Furthermore, self-fertilization also exposes more variants as homozygous in the population, erasing possible effects of additivity in heterozygotes. In outcrossing taxa, selection against deleterious alleles typically occurs in heterozygotes, because recent deleterious mutations will be present as rare alleles that almost always occur in a heterozygous state. Excess homozygosity caused by self-fertilization thus means that selection on homozygous genotypes will be a major driver of allele frequency change with potentially profound implications for inference of the DFE from variant frequencies. Few studies have inferred the DFE in nonobligately outcrossing organisms (Arunkumar et al. 2015; Huber et al. 2018), motivating deeper investigation into the impact of extreme selfing on DFE estimation.
Here, we report the DFE estimated from the SFS of a globally distributed collection of Caenorhabditis elegans, a nematode roundworm with a 99 to 99.9% rate of self-fertilization (Cutter et al. 2019). In this species, the rate of recombination varies along the holocentric chromosomes with low recombination in the central third of autosomes that also are gene-dense and enriched for essential genes (C. elegans Sequencing Consortium 1998; Cutter et al. 2009; Rockman and Kruglyak 2009). These features stand in stark contrast to the genomes of many outcrossing taxa (e.g., Drosophila and mammals), in which regions of low recombination are depleted of genes, especially essential genes. In C. elegans, genome architecture combines with selfing to cause strong linked selection (Cutter and Payseur 2003; Andersen et al. 2012; Thomas et al. 2015; Crombie et al. 2019). Selfing and linked selection in C. elegans contribute to a nearly 100-fold reduced polymorphism relative to the hyperdiversity of obligately outcrossing congeners [e.g., Caenorhabditis remanei and Caenorhabditis brenneri; (Cutter et al. 2013; Dey et al. 2013)]. This influence also is observed within the genome: nucleotide diversity in low-recombination regions is fivefold lower than in high-recombination regions (Rockman and Kruglyak 2009; Andersen et al. 2012; Thomas et al. 2015; Lee et al. 2021). We estimate the homozygous DFE for C. elegans by the maximum likelihood method implemented in the DFE-alpha software (Keightley and Eyre-Walker 2007; Eyre-Walker and Keightley 2009). Further, we evaluate the robustness of the inferred DFE from simulated data that matches the genome architecture and life history of C. elegans to understand how the joint effects of self-fertilization, genome structure, and natural selection influence estimates of the DFE.
Materials and methods
Caenorhabditis elegans genome-wide variant data
The C. elegans genome-wide variant data were acquired from the C. elegans Natural Diversity Resource 20200815 release (Cook et al. 2017). These data were generated by aligning Illumina short reads from each strain to the WS276 N2 reference genome (Lee et al. 2018) and then calling variants using the GATK4 (v4.1.4.0) HaplotypeCaller function and recalled using the GenomicsDBImport and GenotypeGVCFs functions (Poplin et al. 2018). Variants were annotated using SnpEff (v4.3.1) (Cingolani et al. 2012). These processes and pipelines are described on the C. elegans Natural Diversity Resource Release page under the “Methods/Pipelines” tab. This site also includes links to all GitHub repositories for pipelines to reproduce these data. To generate the site frequency spectra, we filtered the CeNDR VCF to contain the recently described 328 strain set (Lee et al. 2021), but two strains were removed. The strain ECA701 was removed because of high levels of residual heterozygosity, and the strain JU1580 was removed because it was found to be in the JU1793 isotype in the 20200815 CeNDR release. The final strain list contained 326 strains (Supplementary Table S1).
Generation of swept and divergent strain sets
The variants for all spectra were polarized using the XZ1516 strain as the ancestor, so this strain is not included in any spectra. For each SFS, we further pruned the VCF to contain only sites with no missing genotype data and with allele frequencies greater than 0%. We generated 18 SFS that encompass three different subsets of C. elegans strains, three different genomic regions, and two different site class comparisons. For the three different subsets of C. elegans strains, we used (1) the entire population sample (n = 325, 326 minus XZ1516), (2) the subset of “swept” strains (n = 273), and (3) the subset of “divergent” strains (n = 52). We classified a strain as “swept” if any of chromosomes I, IV, V, or X contained greater than or equal to 30% of the same haplotype (Andersen et al. 2012). Any strains not among the swept strains were classified as “divergent” (Supplementary Table S1). The chromosome scale selective sweeps cause the most significant population structure effects across this strain set with limited additional contribution of geography (Andersen et al. 2012; Lee et al. 2021).
Chromosome regions and generation of site frequency spectra
Caenorhabditis elegans chromosomes have distinct recombination domains where arms recombine more than centers (Rockman and Kruglyak 2009). In our analyses, we separately analyzed (1) the whole genome, (2) high recombination chromosome arms, or (3) low recombination chromosome centers, as defined previously (Rockman and Kruglyak 2009). Population diversity summary statistics were calculated for all three sets of strains (Table 1). For the two different site class comparisons within coding sequences, we used (1) Fourfold vs zerofold degenerate sites only or (2) Fourfold vs the combination of zerofold degenerate sites and sites annotated as causing high or moderate deleterious effects as predicted by SnpEff (Cingolani et al. 2012). The R package SeqinR (Charif and Lobry 2007) was used to parse gene positions and a custom script was used to classify the degeneracy of each nonvariant site as zero- or fourfold degenerate. We generated BED files (Quinlan and Hall 2010) of zero- and fourfold degenerate sites using a custom AWK script that categorizes the alleles as ancestral or derived, into specific chromosomal regions, and by their predicted SnpEff effects. For inferring derived states, we used the highly diverged strain XZ1516 as the outgroup because the most closely related species to C. elegans, Caenorhabditis inopinata, is too far diverged to be useful as an outgroup (Kanzaki et al. 2018; Lee et al. 2021). We then used vcfanno (Pedersen et al. 2016) to append these annotations to the original VCF file (Danecek et al. 2011). The annotated variant data was extracted from the VCF to a tab-separated file using BCFtools (Li 2011). This file was used to generate the 18 site-frequency spectra (Supplementary Files S1–S18).
Table 1.
Caenorhabditis elegans datasets used to generate SFS for DFE inference
| Dataset | Num. strains | Chromosome region | θπ | θW |
|---|---|---|---|---|
| Full | 325 | Whole | 0.001766758 | 0.003413565 |
| Arms | 0.002579272 | 0.004665253 | ||
| Centers | 0.00098359 | 0.00220825 | ||
| Swept strains | 273 | Whole | 0.001150452 | 0.001427463 |
| Arms | 0.002060343 | 0.002270279 | ||
| Centers | 0.00062137 | 0.000932747 | ||
| Divergent strains | 52 | Whole | 0.002795314 | 0.003263276 |
| Arms | 0.004194129 | 0.004985293 | ||
| Centers | 0.002097188 | 0.002181485 |
Simulation of site frequency spectra with SLiM
We used SLiM v2.1 (Haller and Messer 2019) to conduct forward-in-time simulations mimicking key features of C. elegans genome structure and life history. We simulated a single population with nonoverlapping generations. Population size was constant in a given simulation with 99.9% of reproduction occurring via self-fertilization, as well as a comparison set of simulations with full outcrossing (N = 50,000 for outcrossing simulations and N = 500,000 in selfing populations; see Supplementary Table S1). We generated a 24 Mb genome to represent the coding fraction of 100 Mb C. elegans genome, divided into six 4 Mb chromosomes comprising 1.44 Mb left and right arms and a 1.12 Mb center region (C. elegans Sequencing Consortium 1998). Recombination varied between the arms and centers of each chromosome, scaled to account for including only coding sequences in simulations: 2.35 × 10−7 crossovers per base pair per generation in arms, 4.96 × 10−8 crossovers per base pair per generation in centers (Rockman and Kruglyak 2009). This recombination profile leads to a map length for each chromosome of ∼73cM, somewhat longer than C. elegans chromosomes. Consequently, the effects of linked selection will be weaker in the simulations than expected for C. elegans populations and conservative with respect to the influence of selfing. We simulated mutations to arise at a uniform rate across the genome (3.3 × 10−9 mutations per base pair per generation, or approximately 0.08 mutations per simulated genome per generation), with 75% of mutations subject to selection and the remaining 25% neutral to match the incidence of replacement- and synonymous sites in coding sequences (Saxena et al. 2019). Of the 75% of mutations with fitness effects, simulation sets created either all selected mutations as deleterious or as 99.9% deleterious plus 0.1% beneficial. Beneficial mutations had a gamma-distributed DFE with mean selection coefficient s = 0.01, shape parameter β = 0.3, and additive effects (h = 0.5). The deleterious mutational effects followed a mixture of two gamma distributions to best match the theoretical expectation for biologically realistic DFEs: many small effect deleterious mutations with few more recessive deleterious mutations of larger effect (Eyre-Walker and Keightley 2007). Most of this mixture distribution (95%) was defined by a gamma distribution made up of many nearly neutral deleterious mutations with mean s = −0.001, shape β = 0.3, and dominance, h = 0.3. The remaining 5% of the distribution of deleterious fitness effects came from a gamma distribution comprising mutations with strong and more recessive effects to imitate the existence of recessive lethals with mean s = −0.01, β = 0.3, and h = 0.2. We also conducted a second set of simulations with a more extreme DFE for deleterious mutations: a single gamma distribution with s = −0.161, β = 2.13, and h = 0.3 to serve as an example from a more severely deleterious distribution of mutations, similar to that inferred from the empirical C. elegans dataset.
DFE inference with DFE-alpha
We used DFE-alpha (Keightley and Eyre-Walker 2007) to infer the DFE by maximum likelihood from both the empirical and simulated datasets. We then compared the DFE derived from the empirical and simulated datasets to test for deviations between the inferred DFEs that might result from inaccurate or oversimplified genomic architectures and evolutionary parameters. We then conducted a second set of simulations that used DFE parameters inferred from the empirical data as input for the simulations, re-estimated the simulated DFE, and tested whether we could accurately recover this underlying DFE. We also compared the DFE inferred for polymorphisms linked to different chromosome regions (arms vs centers). We used DFE-alpha with the two-epoch model and the folded SFS, as recommended by the DFE-alpha documentation and also as is commonly used across empirical applications of the method. Input configuration files are archived with the data in the GitHub repository below. We also averaged the SFS across three sampling points in the simulations, at generations 4N, 4.5N, and 5N prior to applying the inference approach as performed previously (Messer and Petrov 2013).
Results
We estimated the distribution of deleterious fitness effects from the genomes of 325 strains of C. elegans, using DFE-alpha. All subsets of the data showed that the highest densities in the inferred distributions are for strongly deleterious mutations, with mutations of weakest effect being the second most prevalent. For analyses using only the zerofold degenerate sites designated as the selected class of sites, 62.5% of mutations fall into the most severely deleterious class and 17.3% into the weakest, nearly neutral deleterious class (whole genome; Figure 1A). Chromosome arms and centers have qualitatively similar profiles but with arms exhibiting a somewhat greater density of highly deleterious mutations (Figure 1). We also inferred the DFE using a more sophisticated categorization of selected sites beyond simply zerofold degenerate positions of coding sequences. In this approach, we predicted deleterious functional effects of variants (SnpEff, see Methods), including stop-gained, splice-site, and nonsynonymous variants. The overall profile for the DFE in these cases exhibited decreased weight in the strongest deleterious class (49.7% of mutations for the whole genome) at the expense of more sites of weakly deleterious effects being inferred (23.2% for the whole genome; Figure 1B). Again, chromosome arms showed a greater relative weight in the most deleterious class compared to chromosome centers.
Figure 1.
DFE inference for C. elegans based on coding sequence polymorphism from genomes of 325 strains. Site frequency spectra of polymorphisms derive from the whole genome (purple) or separately for coding sequences in chromosome arms (blue) and centers (red), defined by recombination rate boundaries (Rockman and Kruglyak 2009). The neutral and selected classes for site frequency spectra provided to DFE-alpha correspond to fourfold degenerate sites and zerofold degenerate sites, respectively (A). An alternative selected site class also included the sites characterized as having variants exerting high or moderate fitness effects by SnpEff (B). All estimated parameters of the inferred DFE are listed in Table 2. Error bars indicate 95% confidence intervals, estimated from 5000 bootstrap replicates.
To assess the reliability of these DFE inferences from standing variation under extreme selfing, we conducted a series of forward-time simulations that mimic C. elegans genome architecture and reproduction. Inference of the DFE from simulated data sets, where the true input DFE is known, resulted in different inferred estimates than expected from the input mixture gamma distribution (Figure 2A; Supplementary Table S2). This inferred distribution comprised almost entirely nearly neutral mutations (−Nes = 0–1), regardless of linkage to chromosome arms or centers (Figure 2A). These results also differed starkly from what we observed for the empirical C. elegans results. Our second set of simulations used a more strongly deleterious input DFE, similar to, but more extreme than, the DFE inferred from the C. elegans data. In our simulations with high selfing, DFE-alpha was better able to estimate the input DFE for this mutational spectrum that was weighted toward strongly deleterious mutations (Figure 2B). Curiously, however, it showed a U-shaped distribution with excess density in the nearly neutral class relative to the input (Figure 2B), reminiscent of the pattern observed in the empirical analysis of C. elegans genomes (Figure 1). For both input distributions that contained some beneficial mutations, DFE-alpha’s demographic inference algorithm struggled to capture the influence of the joint effects of selfing and linked selection as evidenced by the N2 coefficient reaching its maximum value of N2 = 1000 (Supplementary Table S2).
Figure 2.
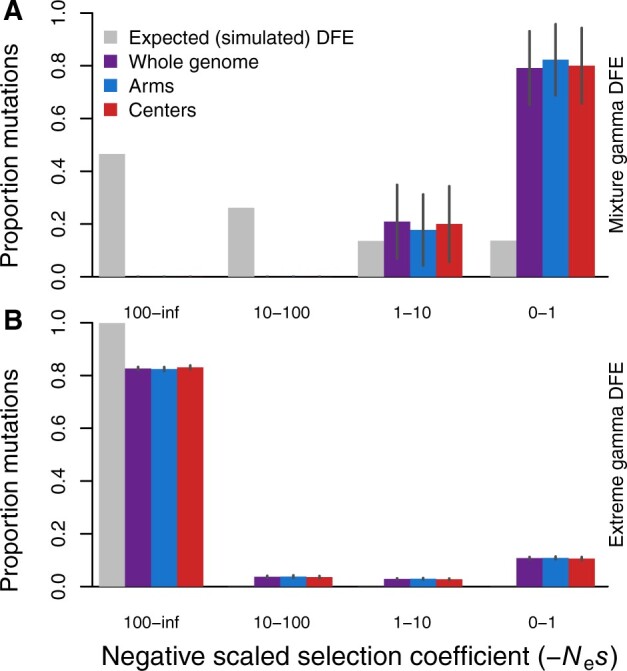
Distributions of deleterious fitness effects for simulations mimicking C. elegans genome structure and selfing reproductive mode (99.9% selfing). (A) The inferred DFEs for deleterious mutations (colored bars) from simulations with an input DFE (gray bars) of a mixture gamma distribution (β = 0.3 for 95% mutations with mean s = −0.001 and h = 0.3 plus 5% with mean s = −0.01 and h = 0.2). (B) Inferred DFEs for a more extreme, deleterious gamma distribution of mutational input (β = 2.13, mean s = −0.161, h = 0.3), similar to that of the inferred DFE from the empirical data. Larger values of −Nes are more deleterious; simulation census size N = 500,000; selfing rate 99.9%; SFS are averaged over generations 4N, 4.5N, and 5N. All estimated parameters of the inferred DFE are listed in Supplementary Table S2. Error bars indicate 95% confidence intervals.
To further elucidate the impact and potential biases introduced by selfing on our DFE inferences, we contrasted simulations that differed only in reproductive mode: 99.9% selfing (Figure 2) vs 100% outcrossing (Figure 3). We found that the inferred DFE much more accurately matches the known input DFE for the simulations under a regime of full outcrossing (Figure 3) as opposed to high selfing. Both the mixture gamma DFE and the extreme DFE that we simulated matched well to the input mutational spectra under a regime of pure outcrossing, compared to the extremely poor match to the mixture DFE for highly selfing populations (Figure 2 cf. Figure 3). Nevertheless, the gene dense and low recombining chromosome centers exhibited an inferred DFE shifted toward weaker fitness effects even in these purely outcrossing simulations. DFE-alpha’s demographic estimation algorithm also struggled with the low-recombination chromosome centers. The N2 coefficient, representing the population size in the second epoch of a two-epoch demographic model (not to be confused with the N2 strain of C. elegans), reached its maximum allowed value of 1000 for the chromosome centers (Supplementary Table S2). Despite the simulations modeling a stable population, the N2 coefficient for arm regions implicated a demographic correction for an approximate fourfold population expansion (Supplementary Table S2). These observations indicate that DFE-alpha is able to subsume the expansion-mimicking effects of linked selection within the N2 coefficient for high recombination arm regions but does less well for low recombination center regions, even in the case of pure outcrossing.
Figure 3.
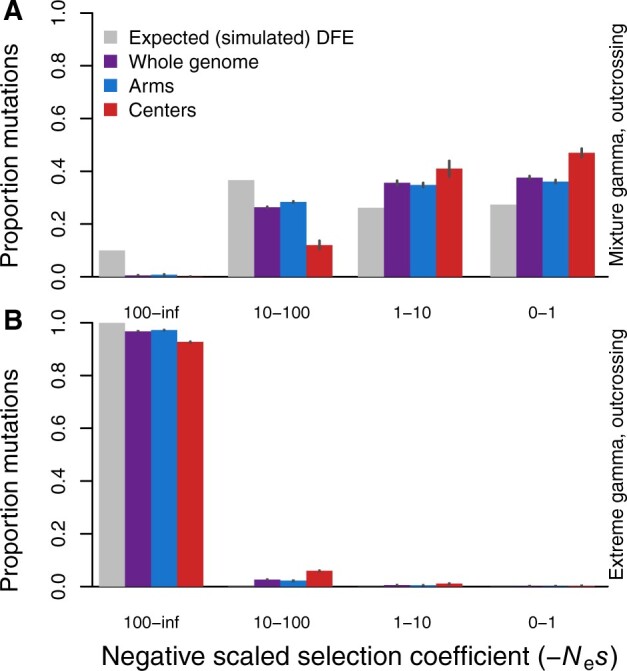
DFE inferences from simulations of fully outcrossing individuals. Genetic properties are otherwise equivalent to the selfing simulations shown in Figure 2, but with census size N = 50,000 instead of 500,000 (hence the difference in expectation of the gray bars from Figure 2). Panel (A) shows results of simulations using the mixture gamma distribution while panel (B) corresponds to simulations of an input DFE that includes greater incidence of highly deleterious mutations. SFS are averaged over generations 4N, 4.5N, and 5N. All estimated parameters of the inferred DFE are listed in Supplementary Table S2. Error bars indicate 95% confidence intervals.
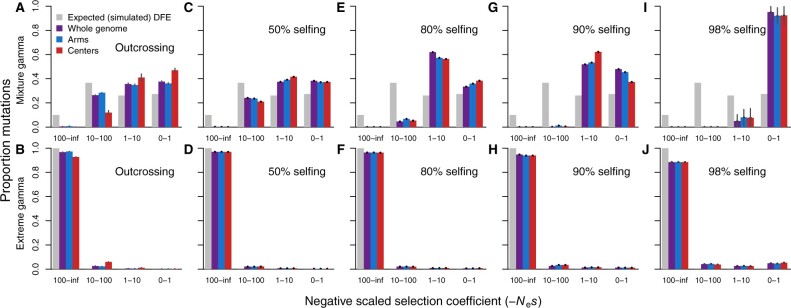
To explore how extreme the amount of selfing must be in order to compromise the ability of DFE-alpha to infer the DFE, we conducted further simulations using selfing rates of 98, 90, 80, and 50%. Under 98% selfing, the DFE inferred by DFE-alpha was still as poorly inferred as our results for 99.9% selfing, particularly for the mixture gamma DFE (Figure 4, top panels). With a less extreme selfing rate of 90% selfing or below, we found the DFE inference to approach the true input distribution, albeit with a bias toward overestimating the incidence of weak-effect mutations (Figure 4). The severity of mis-inference also clearly is sensitive to the underlying simulated DFE, with more accurate inferences for the more extreme simulated DFE (Figure 4).
Figure 4.
DFE inference from simulated datasets across a range of self-fertilization rates shows strong influence of selfing rate and distribution of mutational effects. Top row results (A, C, E, G, and I) show DFE inferred with DFE-alpha from simulations using the mixture gamma distribution. Bottom row results (B, D, F, H, and J) show DFE inferences from simulations using the extreme gamma distribution. Panels show increasing selfing rate left to right, from outcrossing (A,B) to 50% selfing (C, D), 80% selfing (E,F), 90% selfing (G, H), and 98% selfing (I, J). All simulation parameters as in the main text, Figure 2, and Figure 3, except N = 50,000 instead of 500,000. Error bars are 95% confidence intervals.
We hypothesized that a subset of C. elegans strains might contribute to a perturbed DFE because they are hypothesized to have experienced selective sweeps that impacted large portions of the genome (Andersen et al. 2012). Whether or not strains show evidence of chromosome-scale selective sweeps also forms the primary axis of genetic structure for this global sample of C. elegans (Andersen et al. 2012; Lee et al. 2021), so partitioning our analysis for “swept” and nonswept “divergent” strain sets separately also allows us to explore the potential influence of population genetic structure within the full sample. When we compared the DFE inferred using data from the 273 “swept” strain subset to the DFE inferred using data from the 52 nonswept “divergent” strain subset, we did not observe a drastic difference in DFE shapes for the whole genome analyses (Figure 5). Qualitatively, both subsets of the data showed the largest proportion of deleterious mutations in the strongest selection class and the second most abundant mutations to be in the weakest selection class (Figure 5). For chromosome centers, however, the swept strain subset showed a less strongly “U-shaped” distribution, instead having the second most weight for intermediate effect deleterious mutations (−Nes = 10–100; Figure 5B). Using the SFSs that included sites specified by SNPeff further exacerbated the DFE shift toward weaker fitness effects in chromosome centers for swept strains (Figure 5, C and D). This pattern of weaker mutational effects inferred for the strains and genomic regions most impacted by selective sweeps suggests that linked selection influences the DFE inference.
Figure 5.
DFE inferences from subsets of C. elegans strains. (A, C) DFEs based on 273 “swept” strains with >30% of the genome showing strong influence of linked selection (Andersen et al. 2012). (B, D) DFEs based on 52 “divergent” strains with no evidence of selective sweeps across their genomes (see Methods). Panels (A) and (B) show inferences that used only zero- vs fourfold sites whereas C and D include sites designated as exerting high or moderate effects by SnpEff in the selected class. All estimated parameters of the inferred DFE are listed in Table 2. Error bars indicate 95% confidence intervals calculated from 5000 bootstrap replicates.
We also hypothesized that the presence or absence of beneficial mutational input might complicate inference of the DFE in the context of selfing-induced homozygosity and linked selection because DFE-alpha only infers the DFE for deleterious mutations. Therefore, we tested whether the inclusion or exclusion of beneficial mutations in the simulations impacted the inferred DFE under high selfing. We observed that the presence of beneficial mutations most strongly influenced the fraction of mutations in the weak and intermediate fitness effect classes (−Nes = 0–1 and 1–10), shifting the inferred DFE toward a greater density of weakly deleterious effects relative to simulations that lacked any beneficial mutations (Figure 6). The pattern for chromosome centers contrasted with chromosome arms and the whole genome when only deleterious mutations were present, exhibiting a more even distribution across all greater deleterious effect classes but still retaining a large proportion of mutations in the nearly neutral class (Figure 6B). Finally, we tested whether DFE inferences using the unfolded SFS might better match the expected DFE but found no clear improvement relative to the performance of DFE-alpha using the folded SFS (Supplementary Figure S1).
Figure 6.
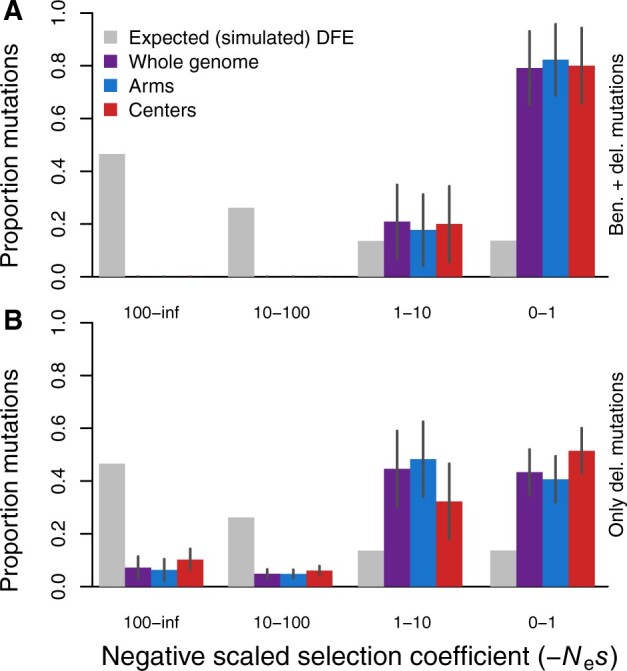
The DFE inferred from simulations with both deleterious and beneficial mutations (A, as in Figure 2A), or with deleterious mutations only (B). Simulation parameters as in Figure 2. SFS are averaged over generations 4N, 4.5N, and 5N. All estimated parameters of the inferred DFE are listed in Supplementary Table S2. Error bars indicate 95% confidence intervals.
Discussion
Population genomic data, in principle, provide a rich collection of allelic variation from which to infer the DFE for mutational input into populations. Accurate estimation of the DFE from such data can be complicated by population demography that differs from equilibrium, due to growth or decline in population size, although methods implemented in inference algorithms attempt to minimize such demographic biases (Keightley and Eyre-Walker 2007; Boyko et al. 2008; Tataru et al. 2017). The influence of nonrandom mating on DFE inference, however, remains incompletely understood. Our exploration of the DFE for deleterious mutations in C. elegans, using genome sequences for 326 wild isolates combined with biologically motivated simulations, demonstrated that extreme self-fertilization can compromise accurate inference of the DFE.
Based on naive application of DFE-alpha to infer C. elegans’ DFE, one would conclude that mutational effects exert predominantly strong deleterious consequences on fitness. However, we showed that, when simulating conditions that mimic C. elegans’ genome architecture and its extreme 99.9% selfing mode of reproduction, the same inference algorithm does not always recover the input DFE. This discrepancy is not a general problem with the method, as simulations under random mating do successfully recover the input DFE. This contrast highlights the bias that a highly selfing mating regime coupled with linked selection can cause for inferred DFEs.
Demographic model-fitting plays an important role in inferring the DFE, as s is scaled by Ne. And yet, as we saw in many cases, estimates of the N2 parameter that aims to capture the effective population size in the current population were often capped at the maximum rescaling allowed by the method, especially in low-recombination chromosome centers (see diverged strains in Table 2). One interpretation of these capped N2 parameter values is that accurate estimation of the other model parameters cannot be assumed to be reliable, as we observe in mismatches between simulated input and estimated DFEs. This capping of the N2 parameter at its maximum value even emerged in simulations of demographic stability in purely outcrossing populations for the low-recombination chromosome center regions, despite settling on an intermediate value for high-recombination arm regions (Supplementary Table S2). With empirical data, one might interpret such values of N2 as representing a large population expansion, but our simulations modeled populations of constant size. We can therefore conclude that the N2 demographic parameter of DFE-alpha can serve to account for the biasing effects of linked selection, but does so successfully only when linked selection is not too strong or recombination is not too restricted.
Table 2.
Inferred parameters of the DFE for the empirical C. elegans dataset using DFE-alpha
| Dataset | Genome portion | SNP set | Population size after first epoch, in 2-epoch mode (N2, relative to N1 = 100) | Duration of epoch after first population size change (t2) | Weighted recent effective population size (Nw, Eyre-Walker and Keightley 2009) | Mean selection coefficient (Es) | Shape parameter (b) |
|---|---|---|---|---|---|---|---|
| Empirical full strain set | Whole | 4-0-fold | 1000 | 299.23 | 225.06 | −40.42 | 0.17 |
| Arms | 1000 | 245.70 | 204.04 | −124.88 | 0.16 | ||
| Centers | 1000 | 298.62 | 224.83 | −22.36 | 0.15 | ||
| Whole | 4-0-fold, high-moderate | 1000 | 299.23 | 225.06 | −6.80 | 0.17 | |
| Arms | 1000 | 245.70 | 204.04 | −20.83 | 0.16 | ||
| Centers | 1000 | 298.62 | 224.83 | −2.95 | 0.15 | ||
| Empirical swept strain set | Whole | 4-0-fold | 1000 | 679.00 | 359.09 | −6.63 | 0.20 |
| Arms | 1000 | 628.18 | 342.59 | −197.65 | 0.14 | ||
| Centers | 1000 | 501.51 | 299.61 | −0.72 | 0.26 | ||
| Whole | 4-0-fold, high-moderate | 1000 | 679.00 | 359.09 | −1.45 | 0.20 | |
| Arms | 1000 | 628.18 | 342.59 | −29.71 | 0.13 | ||
| Centers | 1000 | 501.51 | 299.61 | −0.18 | 0.28 | ||
| Empirical diverged strain set | Whole | 4-0-fold | 307 | 140.07 | 142.22 | −546.09 | 0.13 |
| Arms | 372 | 143.18 | 147.62 | −321.05 | 0.15 | ||
| Centers | 1000 | 1814.82 | 636.79 | −16.75 | 0.14 | ||
| Whole | 4-0-fold, high-moderate | 307 | 140.07 | 142.22 | −71.53 | 0.13 | |
| Arms | 372 | 143.18 | 147.62 | −50.33 | 0.15 | ||
| Centers | 1000 | 1814.82 | 636.79 | −2.37 | 0.13 |
The mean selection coefficient (Es) is not scaled by effective population size (i.e., not Nes). Mean (absolute) selection coefficients greater than 1 reflect the long tail of a leptokurtic gamma distribution. See Keightley and Eyre-Walker (2007) for explanation and further interpretation. Note that the DFE-alpha approach caps N2 at 1000, reflecting the poor ability to estimate the DFE in these cases due to poor fit during the rescaling.
Previous results, using an alternative inference method, indicated that a scaled additive model could be applied for the case of 97% selfing in Arabidopsis (Huber et al. 2018). Similarly, work in self-compatible Eichhornia plants found that the DFE could be recovered adequately with 98% selfing (Arunkumar et al. 2015). These findings further imply that accurate DFE inference under selfing may be sensitive to genomic and evolutionary parameters (e.g., genome size and architecture of selected sites, recombination and mutation rates, and the DFE itself, including beneficial mutations). We observed that the shape of the underlying DFE, in particular, strongly impacts our ability to correctly infer it under selfing, suggesting that our mixture gamma distribution used in combination with regions of lower recombination poses especially difficult conditions for DFE-alpha. Both of the studies in plants benefited from calibrating their analysis of selfing populations with a close outgroup that is fully outcrossing. Although C. elegans lacks a known outgroup that would be appropriate to use in this way, future analysis of the DFE for the selfing Caenorhabditis briggsae in combination with its close outcrossing relative Caenorhabditis nigoni is promising for this comparative approach.
Our simulations show that the extreme selfing of species like C. elegans interacts with the shape of the DFE such that some distributions show a greater disparity between the DFE input by mutation and the output DFE inferred from polymorphism. This discrepancy depends on at least two factors: the nature of the underlying DFE (weighted toward more strongly negative effects vs weighted toward more nearly neutral effects), and linkage between beneficial and deleterious variants. Dominance plays little role in the evolutionary fate of mutations in highly selfing populations, because new mutations become homozygous after only a few generations. As a consequence, selfing is thought to more effectively purge recessive large-effect mutations as compared to nearly additive weak-effect mutations (Charlesworth and Charlesworth 1998). This differential purging might induce the DFE inferred from polymorphism data to show an abundance of variants with nearly neutral deleterious effects, as we have seen for our simulations of high selfing leading to poor recovery of the underlying DFE when that underlying distribution contained mutations over a wide range of effects (Figure 2A). Only under a simulated DFE where the vast majority of mutations entering the population are highly deleterious does the DFE inference appropriately recover the underlying distribution (Figure 2B), likely because few or no weakly deleterious mutations are segregating in the population at all. Indeed, our selfing simulations and C. elegans analysis both show high densities of mutations in either the highest or the lowest deleterious fitness class of mutations and few mutations of intermediate effect (Figures 1 and 2).
The effect of linkage between selected variants on the DFE inference is detectable from both our empirical and simulation datasets. Comparison of our “swept” vs “divergent” empirical data subsets reveal a pattern of weaker mutational effects inferred for the strains and genomic regions most impacted by selective sweeps (i.e., chromosome centers in swept strains). Considering chromosome arm and center regions separately also reflects the stark difference in recombination rate and gene density found between these regions in the C. elegans genome (C. elegans Sequencing Consortium 1998; Cutter et al. 2009; Rockman and Kruglyak 2009). This chromosomal heterogeneity leads to profound effects of linked selection in chromosome centers (Cutter and Payseur 2003; Andersen et al. 2012; Crombie et al. 2019), which we hypothesized might influence DFE inference. Indeed, we found that the inferred DFE tended to shift toward weaker-effect mutations in chromosome centers. To some extent, this effect was apparent even in simulated genomes with full outcrossing. However, we observed the most substantial differences between arm and center regions in our analysis of the subset of C. elegans data from strains that show selective sweeps that span nearly two-thirds of the genome. DFE-alpha can therefore account for modest perturbations due to linked selection within its demographic correction by approximating this influence as a reduction in effective population size (Keightley and Eyre-Walker 2007). The magnitude of effects from linked selection in C. elegans (Cutter and Payseur 2003; Andersen et al. 2012; Thomas et al. 2015), however, appear too extreme to be adequately accounted in this way.
Furthermore, inclusion or exclusion of beneficial mutations in our simulations also greatly impacted the inferred DFE. The distribution inferred in all of our scenarios by DFE-alpha is that of deleterious mutations only, yet for the same input deleterious DFE, we can observe different inferences based on the presence or absence of beneficial mutations entering the population. In the presence of linkage between deleterious and beneficial variants, the inferred DFE for deleterious mutational effects is shifted to a more weakly deleterious distribution overall (Figure 6A cf. Figure 6B). The difference in inference between simulated arms and centers of the genome also clearly shows this pattern of a greater weight for weakly deleterious mutations in the lower-recombining regions of the chromosome centers.
We conclude that the disparities between mutational input and the DFE inferred from site frequency spectra are caused by linked selection that is exacerbated by selfing. The consequences of linked selection are even further exacerbated by C. elegans’ genome structure with gene-dense and low recombination chromosome centers. The impact of linked selection on the DFE inference is not due to underlying mutational differences along chromosomes, as centers and arms did not differ in selective effects of mutations in our simulations. The correction for demographic change implemented in DFE-alpha does not seem able to accommodate the degree of linked selection resulting from the extreme selfing experienced by C. elegans, since this correction only modulates the effective population size in an attempt to accommodate the presence of nonstandard population conditions. The high values of the N2 parameter (the effective population size during the second epoch estimated by DFE-alpha and used for scaling the selection coefficient; see Table 2), capped at 1000 estimated during the DFE inference, may reflect this poor fit to the demographic model due to selfing and linked selection and thus the poor inferences of the DFE. Such an inability to fully account for the effects of strong linked selection conforms with the fact that the influence of selection on a genomic region is imperfectly approximated by a scaled effective population size (Kaiser and Charlesworth 2009; Neher 2013). Similar to Messer and Petrov (2013), we find that this bias causes genomic regions most impacted by linked selection to show an inferred DFE of weaker fitness effects. This problem is likely to be especially acute for populations that experience high rates of selfing.
As we strive to understand more about the role of deleterious mutations in evolution and the prevalence and distribution of their fitness effects, inferring the DFE in well-characterized model systems are an essential first step toward a comprehensive understanding of the mutational process and the impacts of selection, demography, and genomic architecture on the fate of new mutations. We emphasize the difficulties that can be encountered when applying existing methods for inferring the DFE to nonstandard population conditions, in particular for the extreme of nonrandom mating reflected by the high selfing of C. elegans. This challenge highlights the need for integration of empirical and theoretical approaches, and new methods, to account for perturbing effects of linked selection and nonrandom mating to generate a fuller understanding of the mutational processes that underlie the evolution of populations in the wild.
Data availability
All data and code necessary for confirming the conclusions presented in the article are archived at the following GitHub repository or contained in the supplemental materials. SFS data from C. elegans strains, scripts for generating these SFS, input scripts for SLiM simulations, and parameter files and analysis scripts for DFE-alpha inferences are archived on GitHub at: https://github.com/Thatguy027/SFS_Invariant_Sites.
Supplementary material is available at GENETICS online.
Supplementary Material
Acknowledgments
The authors are grateful to three anonymous reviewers for their constructive input.
Funding
K.J.G. was funded by EMBO long-term fellowship ALTF2-2016 and Swiss National Science Foundation Ambizione grant #PZ00P3_185952. A.D.C. is supported by a Discovery Grant from the Natural Sciences and Engineering Research Council (NSERC) of Canada. C.F.B. and E.C.A. were supported by NIH award R01GM107227.
Conflicts of interest
The authors declare that there is no conflict of interest.
Literature cited
- Andersen EC, Gerke JP, Shapiro JA, Crissman JR, Ghosh R, et al. 2012. Chromosome-scale selective sweeps shape Caenorhabditis elegans genomic diversity. Nat Genet. 44:285–290. doi:10.1038/ng.1050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arunkumar R, Ness RW, Wright SI, Barrett SCH. 2015. The evolution of selfing is accompanied by reduced efficacy of selection and purging of deleterious mutations. Genetics. 199:817–829. doi:10.1534/genetics.114.172809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boyko AR, Williamson SH, Indap AR, Degenhardt JD, Hernandez RD, et al. 2008. Assessing the evolutionary impact of amino acid mutations in the human genome. PLoS Genet. 4:e1000083.doi:10.1371/journal.pgen.1000083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- C. elegans Sequencing Consortium 1998. Genome sequence of the nematode C. elegans: a platform for investigating biology. Science. 282:2012–2018. doi:10.1126/science.282.5396.2012. [DOI] [PubMed] [Google Scholar]
- Charif D, Lobry JR, 2007. SeqinR 1.0–2: a contributed package to the R project for statistical computing devoted to biological sequences retrieval and analysis. In: Bastolla U, Porto M, Roman HE, Vendruscolo M, editors. Structural Approaches to Sequence Evolution: molecules, Networks, Populations. Berlin, Heidelberg: Springer Berlin Heidelberg. p. 207–232. [Google Scholar]
- Charlesworth B. 2015. Causes of natural variation in fitness: evidence from studies of Drosophila populations. Proc Natl Acad Sci USA. 112:1662–1669. doi:10.1073/pnas.1423275112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth B, Charlesworth D. 1998. Some evolutionary consequences of deleterious mutations. Genetica, 102, 10.1023/A:1017066304739 [DOI] [PubMed] [Google Scholar]
- Charlesworth D, Charlesworth B, Morgan MT. 1995. The pattern of neutral molecular variation under the background selection model. Genetics, 141, 1619–1632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth D, Wright SI. 2001. Breeding systems and genome evolution. Curr Opin Genet Dev. 11:685–690. [DOI] [PubMed] [Google Scholar]
- Crombie TA, Zdraljevic S, Cook DE, Tanny RE, Brady SC, et al. 2019. Deep sampling of Hawaiian Caenorhabditis elegans reveals high genetic diversity and admixture with global populations. Elife, 8, e50465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cingolani P, Platts A, Wang LL, Coon M, Nguyen T, et al. 2012. A program for annotating and predicting the effects of single nucleotide polymorphisms, SnpEff: SNPs in the genome of Drosophila melanogaster strain w1118; iso-2; iso-3. Fly (Austin). 6:80–92. doi:10.4161/fly.19695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cook DE, Zdraljevic S, Roberts JP, Andersen EC. 2017. CeNDR, the Caenorhabditis elegans natural diversity resource. Nucleic Acids Res. 45:D650–D657. doi:10.1093/nar/gkw893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cutter AD, Dey A, Murray RL. 2009. Evolution of the Caenorhabditis elegans genome. Mol Biol Evol. 26:1199–1234. doi:10.1093/molbev/msp048. [DOI] [PubMed] [Google Scholar]
- Cutter AD, Payseur BA. 2003. Rates of deleterious mutation and the evolution of sex in Caenorhabditis. J Evol Biol. 16, 812–822. [DOI] [PubMed] [Google Scholar]
- Cutter AD, Jovelin R, Dey A. 2013. Molecular hyperdiversity and evolution in very large populations. Mol Ecol. 22:2074–2095. doi:10.1111/mec.12281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cutter AD, Morran LT, Phillips PC. 2019. Males, outcrossing, and sexual selection in Caenorhabditis nematodes. Genetics. 213:27–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cutter AD, Payseur BA. 2013. Genomic signatures of selection at linked sites: unifying the disparity among species. Nat Rev Genet. 14:262–274. doi:10.1038/nrg3425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danecek P, Auton A, Abecasis G, Albers CA, Banks E, et al. ; 1000 Genomes Project Analysis Group. 2011. The variant call format and VCFtools. Bioinformatics. 27:2156–2158. doi:10.1093/bioinformatics/btr330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DePristo MA, Hartl DL, Weinreich DM. 2007. Mutational reversions during adaptive protein evolution. Mol Biol Ecol. 24, 1608–1610. [DOI] [PubMed] [Google Scholar]
- Dey A, Chan CKW, Thomas CG, Cutter AD. 2013. Molecular hyperdiversity defines populations of the nematode Caenorhabditis brenneri. Proc Natl Acad Sci USA. 110:11056–11060. doi:10.1073/pnas.1303057110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eyre-Walker A. 2006. The genomic rate of adaptive evolution. Trends Ecol Evol. 21:569–575. doi:10.1016/j.tree.2006.06.015. [DOI] [PubMed] [Google Scholar]
- Eyre-Walker A. 2010. Evolution in health and medicine Sackler colloquium: genetic architecture of a complex trait and its implications for fitness and genome-wide association studies. Proc Natl Acad Sci USA. 107(Suppl. 1):1752–1756. doi:10.1073/pnas.0906182107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eyre-Walker A, Keightley PD. 2007. The distribution of fitness effects of new mutations. Nat Rev Genet. 8:610–618. doi:10.1038/nrg2146. [DOI] [PubMed] [Google Scholar]
- Eyre-Walker A, Keightley PD. 2009. Estimating the rate of adaptive molecular evolution in the presence of slightly deleterious mutations and population size change. Mol Biol Evol. 26:2097–2108. [DOI] [PubMed] [Google Scholar]
- Felsenstein J. 1974. The evolutionary advantage of recombination. Genetics, 78, 737–756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Good BH, Rouzine IM, Balick DJ, Hallatschek O, Desai MM. 2012. Distribution of fixed beneficial mutations and the rate of adaptation in asexual populations. PNAS, 109, 4950–4955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haller BC, Messer PW. 2019. SLiM 3: forward genetic simulations beyond the wright–fisher model. Mol Biol Evol. 36:632–637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill WG, Robertson A. 1966. The effect of linkage on limits to artificial selection. Genet Res. 8:269–294. [PubMed] [Google Scholar]
- Huber CD, Durvasula A, Hancock AM, Lohmueller KE. 2018. Gene expression drives the evolution of dominance. Nat Commun. 9:2750. doi:10.1038/s41467-018–05281-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaiser VB, Charlesworth B. 2009. The effects of deleterious mutations on evolution in non-recombining genomes. Trends Genet. 25, 9–12. [DOI] [PubMed] [Google Scholar]
- Kanzaki N, Tsai IJ, Tanaka R, Hunt VL, Liu D, et al. 2018. Biology and genome of a newly discovered sibling species of Caenorhabditis elegans . Nat Commun. 9, 3216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keightley PD, Eyre-Walker A. 2007. Joint inference of the distribution of fitness effects of deleterious mutations and population demography based on nucleotide polymorphism frequencies. Genetics. 177:2251–2261. doi:10.1534/genetics.107.080663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim BY, Huber CD, Lohmueller KE. 2017. Inference of the distribution of selection coefficients for new nonsynonymous mutations using large samples. Genetics. 206:345–361. doi:10.1534/genetics.116.197145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kondrashov AS. 1995. Modifiers of mutation-selection balance: general approach and the evolution of mutation rates. Genet Res. 66:53–69. [Google Scholar]
- Kousathanas A, Keightley PD. 2013. A comparison of models to infer the distribution of fitness effects of new mutations. Genetics. 193:1197–1208. doi:10.1534/genetics.112.148023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee RYN, Howe KL, Harris TW, Arnaboldi V, Cain S, et al. 2018. WormBase 2017: molting into a new stage. Nucleic Acids Res. 46:D869–D874. doi:10.1093/nar/gkx998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee D, Zdraljevic S, Stevens L, Wang Y, Tanny RE, et al. 2021. Balancing selection maintains hyper-divergent haplotypes in Caenorhabditis elegans. Nat Ecol Evol. 5:794–807. doi:10.1038/s41559-021–01435-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H. 2011. A statistical framework for SNP calling, mutation discovery, association mapping and population genetical parameter estimation from sequencing data. Bioinformatics. 27:2987–2993. doi:10.1093/bioinformatics/btr509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loewe L. 2006. Quantifying the genomic decay paradox due to Muller’s ratchet in human mitochondrial DNA. Genet Res. 87:133–159. doi:10.1017/S0016672306008123. [DOI] [PubMed] [Google Scholar]
- Loewe L, Charlesworth B, Bartolomé C, Nöel V. 2006. Estimating selection on nonsynonymous mutations. Genetics. 172:1079–1092. doi:10.1534/genetics.105.047217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M. 2008. The cellular, developmental and population-genetic determinants of mutation-rate evolution. Genetics. 180:933–943. doi:10.1534/genetics.108.090456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Messer PW, Petrov DA. 2013. Population genomics of rapid adaptation by soft selective sweeps. Trends Ecol Evol. 28:659–669. doi:10.1016/j.tree.2013.08.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neher R. 2013. Genetic Draft, Selective Interference, and Population Genetics of Rapid Adaptation. Annu Rev. 44, 195–215. [Google Scholar]
- Nordborg M. 1997. Structured coalescent processes on different time scales. Genetics. 146:1501–1514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohta T. 1992. The nearly neutral theory of molecular evolution. Annu Rev Ecol Syst. 23:263–286. [Google Scholar]
- Orr HA. 2000. Adaptation and the cost of complexity. Evolution, 54, 13–20. [DOI] [PubMed] [Google Scholar]
- Peck JR, Barreau G, Heath SC. 1997. Imperfect genes, Fisherian mutation and the evolution of sex. Genetics. 145:1171–1199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedersen BS, Layer RM, Quinlan AR. 2016. Vcfanno: fast, flexible annotation of genetic variants. Genome Biol. 17:118. doi:10.1186/s13059-016–0973-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poplin R, Ruano-Rubio V, DePristo MA, Fennell TJ, Carneiro MO, et al. 2018. Scaling accurate genetic variant discovery to tens of thousands of samples. bioRxiv 201178.
- Quinlan AR, Hall IM. 2010. BEDTools: a flexible suite of utilities for comparing genomic features. Bioinformatics. 26:841–842. doi:10.1093/bioinformatics/btq033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rockman MV, Kruglyak L. 2009. Recombinational landscape and population genomics of Caenorhabditis elegans. PLoS Genet. 5:e1000419. doi:10.1371/journal.pgen.1000419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanjuán R, Moya A, Elena SF. 2004. The distribution of fitness effects caused by single-nucleotide substitutions in an RNA virus. PNAS, 101, 8396–8401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saxena AS, Salomon MP, Matsuba C, Yeh S-D, Baer CF. 2019. Evolution of the mutational process under relaxed selection in Caenorhabditis elegans. Mol Biol Evol. 36:239–251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schultz ST, Lynch M. 1997. Mutation and extinction: the role of variable mutational effects, synergistic epistasis, beneficial mutations, and degree of outcrossing. Evolution. 51:1363–1371. doi:10.1111/j.1558–5646.1997.tb01459.x. [DOI] [PubMed] [Google Scholar]
- Tataru P, Mollion M, Glémin S, Bataillon T. 2017. Inference of distribution of fitness effects and proportion of adaptive substitutions from polymorphism data. Genetics. 207:1103–1119. doi:10.1534/genetics.117.300323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thatcher JW, Shaw JM, Dickinson WJ. 1998. Marginal fitness contributions of nonessential genes in yeast. PNAS, 95, 253–257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas CG, Wang W, Jovelin R, Ghosh R, Lomasko T, et al. 2015. Full-genome evolutionary histories of selfing, splitting, and selection in Caenorhabditis. Genome Res. 25:667–678. doi:10.1101/gr.187237.114. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data and code necessary for confirming the conclusions presented in the article are archived at the following GitHub repository or contained in the supplemental materials. SFS data from C. elegans strains, scripts for generating these SFS, input scripts for SLiM simulations, and parameter files and analysis scripts for DFE-alpha inferences are archived on GitHub at: https://github.com/Thatguy027/SFS_Invariant_Sites.
Supplementary material is available at GENETICS online.