Abstract
Background
Multi-segment foot models (MFMs) for assessing three-dimensional segmental foot motions are calculated via various analytical methods. Although validation studies have already been conducted, we cannot compare their results because the experimental environments in previous studies were different from each other. This study aims to compare the kinematics, repeatability, and reproducibility of five MFMs in the same experimental conditions.
Methods
Eleven healthy males with a mean age of 26.5 years participated in this study. We created a merged 29-marker set including five MFMs: Oxford (OFM), modified Rizzoli (mRFM), DuPont (DFM), Milwaukee (MiFM), and modified Shriners Hospital for Children Greenville (mSHCG). Two operators applied the merged model to participants twice, and then we analysed two relative angles of three segments: shank-hindfoot (HF) and hindfoot-forefoot (FF). Coefficients of multiple correlation (CMC) and mean standard errors were used to assess repeatability and reproducibility, and statistical parametric mapping (SPM) of the t-value was employed to compare kinematics.
Results
HF varus/valgus of the MiFM and mSHCG models, which rotated the segment according to radiographic or goniometric measurements during the reference frame construction, were significantly more repeatable and reproducible, compared to other models. They showed significantly more dorsiflexed HF and plantarflexed FF due to their static offset angles. DFM and mSHCG showed a greater range of motion (ROM), and some models had significantly different FF points of peak angle.
Conclusions
Under the same conditions, rotating the segment according to the appropriate offset angle obtained from radiographic or goniometric measurement increased reliability, but all MFMs had clinically acceptable reliability compared to previous studies. Moreover, in some models, especially HF varus/valgus, there were differences in ROM and points of peak angle even with no statistical difference in SPM curves. Therefore, based on the results of this study, clinicians and researchers involved in the evaluation of foot and ankle dysfunction need an understanding of the specific features of each MFM to make accurate decisions.
Supplementary Information
The online version contains supplementary material available at 10.1186/s13047-021-00508-1.
Keywords: Multi-segment foot model, Foot kinematics, Repeatability, Reproducibility
Background
There are various multi-segment foot models (MFMs) for assessing three-dimensional foot motion in clinical gait analysis [1]. Each MFM differs not only in the location of the markers on the foot and how the foot segments are defined, but also in the way they are calibrated for the foot’s reference position and coordinate system [2].
Majority of MFMs construct the reference frame using three or more markers placed on each segment identified in the static standing trial. After the static calibration, relative angles of the segments while walking are calculated [3–5]. This is a general marker-based method of performing motion analysis that builds segments by skin-mounted markers, but it is significantly affected by marker-placement errors among sessions or evaluators [5–10]. Some models subtract the static offset values from walking trials [11]. This can increase repeatability and reproducibility, but the omission of anatomical information is a concern [12]. Meanwhile, a few models rotate some coordinate systems according to radiographic and/or goniometric measurements during the reference frame construction [13, 14]. This could be less affected by marker-placement errors and reflect actual bone anatomy. However, this requires subjects to be exposed to radiation, and some measurements are difficult to acquire from radiographic images such as the shank and hindfoot in the transverse plane, and the forefoot in the coronal plane [13].
Previous studies using various MFMs for specific foot deformities can be reviewed and compared by researchers and clinicians [1]; however, these comparisons are limited because it is difficult to understand the special feature of each MFM and its relative differences from other MFMs. Although repeatability studies have already been conducted individually for each model, multiple factors such as the demographic characteristics of the subjects, laboratory environment, operators, statistical analysis, and test intervals were still different, which could have affected their outcomes [5, 7–10, 14–16].
Di Marco, Rossi [12] conducted a comparative study on four MFMs. They identified the most repeatable and reproducible model only in the sagittal plane and the kinematic differences between treadmill and over-ground walking without comparing MFMs. Nicholson, Church [17] also verified, via a comparative study of five MFMs using an amalgamated model, that the MFMs had moderate to low variability as assessed by standard deviations, and that using the same normative data for each model is important when comparing findings between laboratories. However, they did not consider the shank coordinate system that affects the foot kinematics and did not include some methods of applying offset angles, such as radiographic measurements. Consequently, these previous studies have limitations in comparing MFMs simultaneously.
Therefore, this study aimed to compare the kinematics, inter-session repeatability, and inter-evaluator reproducibility among five MFMs of healthy males during walking with all their markers simultaneously in the same experimental conditions with various analytical methods.
Methods
Study design
This is a cross-sectional study to analyse the differences in repeatability and reproducibility of five MFMs applied to normal healthy males.
Participants
Eleven healthy male volunteers with a mean age of 26.5 years participated in this study. The inclusion criteria were as follows: 1) no soft tissue injuries of both feet and ankles within one year from the experimental date, 2) no history of fracture or surgery on both lower extremities, 3) no abnormal findings on both feet radiographs including arthritic changes, 4) no pain during gait. The institutional review board of Seoul National University Hospital approved this study, and all participants provided informed consents prior to participation.
Multi-segment foot models
We selected five MFMs which have been validated and used in clinical articles [1]: DuPont foot model (DFM) [3], modified Rizzoli foot model (mRFM) [4], Oxford foot model (OFM) [5], Milwaukee foot model (MiFM) [13], and modified Shriners Hospital for Children Greenville foot model (mSHCG) [14]. We created a merged 28-marker set using nine 8-mm spheres on the shank and twenty 4-mm spheres on the foot (Fig. 1 and Additional file 1). To apply the merged set, we slightly modified the marker placements of mRFM. It attaches the markers on the second metatarsal head and base, but the other models attach these markers between the second and third metatarsal heads and bases. Since it was difficult to place them separately due to their positional difference of only a few millimeters, we placed the markers between the second and third metatarsal heads and bases only. Although hallux is an important segment to be considered during gait, it was excluded because it was too small to allow for the successful attachment of the markers of all the models.
Fig. 1.
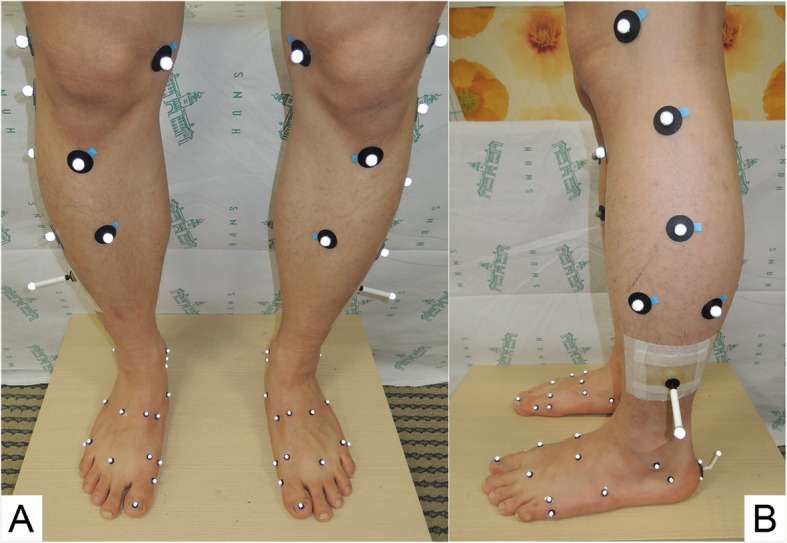
Anterior (A) and lateral (B) view of a merged 28-marker set
Data acquisition and post-processing
Two physical therapists with 8 years of experience participated in attaching the merged set to all subjects. A preliminary analysis was done prior to this study to have an appropriate level of experience with other foot models in two subjects. They individually applied the merged 28-marker set to the participants and repeated it after one or two weeks to analyse inter-trial and inter-session repeatability and inter-evaluator reproducibility. To prevent offset angles from influencing foot positioning during static calibration, we maintained the participants’ feet in a fixed position during the first and second visit. Specifically, we marked two parallel straight lines on the ground using masking tape at 30 cm apart, and the center of the subject’s heel and the second toe were placed on the line. After the static calibration, the subjects walked at a self-selected speed along an 8-m walkway. Kinematic data were captured using 12 cameras with a 3D optical motion capture system (Motion Analysis Co., Santa Rosa. CA) and Cortex 1.3.0 software (Motion Analysis Co., Santa Rosa. CA) at a sampling rate of 120 Hz. Visual3D Professional v6.01.36 (C-Motion, Inc.) was used for post-processing and building the five models. According to the original paper of each MFM, the Euler/Cardan angle sequence of OFM, MiFM, and mSHCG was sagittal-coronal-transverse, while DFM and mRFM used the sagittal-transverse-coronal sequence. All kinematic data were time-normalized to 100% of the gait cycle (1% interval between time points), and three representative walking trials were chosen from each session. To use unified terminology, we defined “tibia and shank” as “shank,” “calcaneus and hindfoot” as “hindfoot,” and “metatarsus and forefoot” as “forefoot.” Then, we analysed two relative angles between three segments: shank-hindfoot (HF) and hindfoot-forefoot (FF). We indicated the tracking markers constituting the segments of each model in Additional file 1. To assist understanding of the tri-planar motions, superscripts were used: i.e., HF motion in the sagittal, coronal, and transverse planes were abbreviated as HFsag, HFcor, and HFtrans, respectively.
Radiographic and goniometric measurements
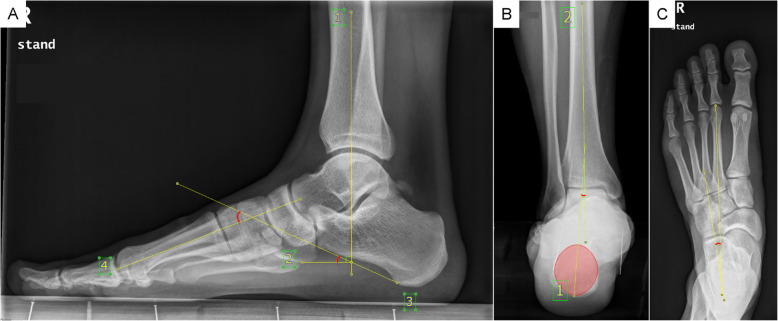
DFM, mRFM, and OFM used the general marker-based method without subtracting the static offset from the corresponding value of the walking trials, while MiFM used a method of rotating each segment in the medial/lateral, anterior/posterior, and longitudinal axes from radiographic measurements. Thus, the participants underwent three weight-bearing X-ray scans of the dorsoplantar foot, lateral view of the foot and ankle, and heel alignment view (Fig. 2). Two evaluators (physical therapists) individually collected the radiographic measurements according to the original papers’ methods and applied it to each segment rotation [18, 19]. Furthermore, mSHCG rotated the HF segment in the anterior/posterior axis according to goniometric measurements of the HF varus/valgus, and provided options of rotating the FF and HF segments to the pitch angles measured from the radiographic images, or constructing the segments with the markers only. Accordingly, we selected Option 2 for the HF, a radiograph for calcaneal pitch, and Option 3 for the FF, a marker-based FF pitch [14]. The goniometric measurement of HF valgus/varus was taken between the calcaneal axis and the line perpendicular to the floor during weight bearing standing. To reduce the effect of foot posture, we placed the participants’ feet in a fixed position similar to static calibration. Moreover, to minimize the influence of the evaluator’s angle of view during measurement, they were asked to measure the angle with their eyes at the subject’s ankle height.
Fig. 2.
Radiographic measurements from the lateral view (A), posterior view (B), and standing A/P (C)
Statistical analysis
Coefficients of multiple correlations (CMC) [20] and experimental errors (σ) [21] were calculated to assess inter-trial and inter-session repeatability and inter-evaluator reproducibility. Inter-trial CMC was calculated from two strides processed by one evaluator in the second session and analysed by the averaged data from three strides for each session. To determine inter-evaluator CMC, the averaged data from the second session were selected. Moreover, the inter-trial errors (σtrial), inter-session errors (σsess) of each evaluator, and inter-evaluator errors (σeval) were calculated for each model. These were expressed as the mean standard deviation of 0 to 100 points of the whole gait cycle. The Kruskal-Wallis test and Bonferroni correction were performed to find differences in the range of motion (ROM) (α = 0.05). When we analysed CMC and ROM, SPSS statistics 25.0 for windows (SPSS Inc., Chicago, IL) was used. To compare the kinematics of five models, statistical parametric mapping (SPM) [22] of the t-value from the post-hoc unpaired t-test (α = 0.01) was employed using MATLAB (R2019a, The MathWorks, Inc., Natick, MA). SPM of the t-value was used for identifying the difference between continuous curves, which can be calculated using open-source SPM1d code (www.spm1D.org).
Results
Repeatability and reproducibility
The inter-trial CMCs of HF and FF were greater than 0.886 in all models (see Table 1). In the sagittal plane, the inter-session and inter-evaluator CMCs of all segments were greater than 0.840 in all models. In HFcor repeatability, the CMCs of DFM, OFM, and mRFM were less than 0.660, whereas those of MiFM and mSHCG were greater than 0.793. For OFM, the averaged inter-session and inter-evaluator CMCs were lower in HFcor (0.424 and 0.410, respectively) than in HFtrans (0.810 and 0.791, respectively). Similarly, this was also observed in FFcor (0.467 and 0.612, respectively), when compared to FFtrans (0.931 and 0.846, respectively). The repeatability and reproducibility of FF were generally greater than HF in all planes, but in FFtrans, the reproducibility of mRFM and mSHCG (0.332 and 0.441, respectively) were lower than their repeatability (0.735 and 0.735, respectively).
Table 1.
Repeatability and reproducibility of five multi-segment foot models
| Model | Plane | Shank - Hindfoot | Hindfoot - Forefoot | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Inter-trial | Inter-session | Inter- evaluator | Inter-trial | Inter-session | Inter- evaluator | ||||||||||||
| evaluator A | evaluator B | evaluator A | evaluator B | ||||||||||||||
| CMC | σtrial | CMC | σsess | CMC | σsess | CMC | σeval | CMC | σtrial | CMC | σsess | CMC | σsess | CMC | σeval | ||
| DFM | Sagittal | 0.959 | 1.2 | 0.903 | 2.0 | 0.950 | 1.6 | 0.934 | 2.0 | 0.967 | 0.9 | 0.869 | 1.8 | 0.958 | 1.2 | 0.920 | 1.7 |
| Coronal | 0.926 | 1.2 | 0.554 | 2.5 | 0.584 | 2.0 | 0.652 | 3.1 | 0.929 | 1.1 | 0.696 | 2.1 | 0.606 | 1.8 | 0.733 | 2.9 | |
| Transverse | 0.895 | 1.3 | 0.461 | 3.0 | 0.777 | 2.1 | 0.627 | 3.5 | 0.886 | 1.2 | 0.618 | 2.3 | 0.850 | 1.7 | 0.837 | 2.3 | |
| mRFM | Sagittal | 0.957 | 1.2 | 0.957 | 1.8 | 0.952 | 1.7 | 0.944 | 2.2 | 0.983 | 0.7 | 0.971 | 1.3 | 0.947 | 1.2 | 0.929 | 1.7 |
| Coronal | 0.923 | 1.0 | 0.194 | 2.8 | 0.660 | 1.8 | 0.401 | 3.4 | 0.931 | 0.6 | 0.862 | 1.3 | 0.835 | 1.3 | 0.862 | 1.8 | |
| Transverse | 0.943 | 0.9 | 0.807 | 2.1 | 0.838 | 1.7 | 0.778 | 2.3 | 0.968 | 0.6 | 0.746 | 1.8 | 0.723 | 1.9 | 0.332 | 2.7 | |
| OFM | Sagittal | 0.966 | 1.0 | 0.946 | 1.6 | 0.960 | 1.3 | 0.962 | 1.6 | 0.982 | 0.5 | 0.934 | 1.0 | 0.941 | 1.0 | 0.924 | 1.2 |
| Coronal | 0.923 | 0.8 | 0.327 | 2.2 | 0.520 | 2.0 | 0.410 | 3.1 | 0.961 | 0.6 | 0.481 | 2.6 | 0.453 | 2.0 | 0.612 | 3.4 | |
| Transverse | 0.953 | 0.8 | 0.752 | 2.1 | 0.867 | 1.5 | 0.791 | 2.0 | 0.988 | 0.5 | 0.931 | 1.2 | 0.930 | 1.1 | 0.846 | 1.8 | |
| mSHCG | Sagittal | 0.962 | 1.1 | 0.960 | 1.6 | 0.962 | 1.4 | 0.971 | 1.7 | 0.981 | 0.8 | 0.926 | 1.9 | 0.840 | 2.4 | 0.871 | 2.7 |
| Coronal | 0.929 | 1.0 | 0.836 | 1.7 | 0.897 | 1.4 | 0.742 | 2.7 | 0.924 | 0.8 | 0.873 | 1.5 | 0.663 | 1.6 | 0.720 | 2.0 | |
| Transverse | 0.946 | 0.6 | 0.734 | 1.9 | 0.881 | 1.2 | 0.827 | 1.9 | 0.974 | 0.6 | 0.672 | 1.9 | 0.797 | 1.7 | 0.441 | 3.1 | |
| MiFM | Sagittal | 0.968 | 1.1 | 0.933 | 1.9 | 0.946 | 1.6 | 0.952 | 2.0 | 0.987 | 0.7 | 0.968 | 1.2 | 0.978 | 1.0 | 0.965 | 1.4 |
| Coronal | 0.940 | 0.8 | 0.859 | 1.3 | 0.793 | 1.4 | 0.898 | 1.8 | 0.902 | 0.8 | 0.702 | 1.4 | 0.771 | 1.2 | 0.848 | 1.6 | |
| Transverse | 0.971 | 0.4 | 0.939 | 0.8 | 0.654 | 1.7 | 0.728 | 2.9 | 0.936 | 0.6 | 0.873 | 1.0 | 0.931 | 0.9 | 0.628 | 1.8 | |
Coefficients of multiple correlations (CMC) and mean standard errors (σ) of inter-trial (σtrial), inter-session (σsess), and inter-evaluator (σeval) of relative motions of the shank-hindfoot and hindfoot-forefoot in five multi-segmental foot models
With respect to the averaged σ, σtrial of all models were less than 1.3° for both HF and FF (Table 1). HFcor, DFM, OFM, and mRFM showed σsess ranging from 1.8° to 2.8° and σeval ranging from 3.1° to 3.4°, whereas MiFM and mSHCG showed σsess ranging from 1.3° to 1.7° and σeval of 1.8° and 1.7°, respectively. FF σsess ranged from 0.9° to 2.6° among all models, which was generally lower than that of HF, and σeval ranged from 1.2° to 3.4°, which was higher than σsess. All averaged σ of all models did not exceed 3.5°.
Kinematics
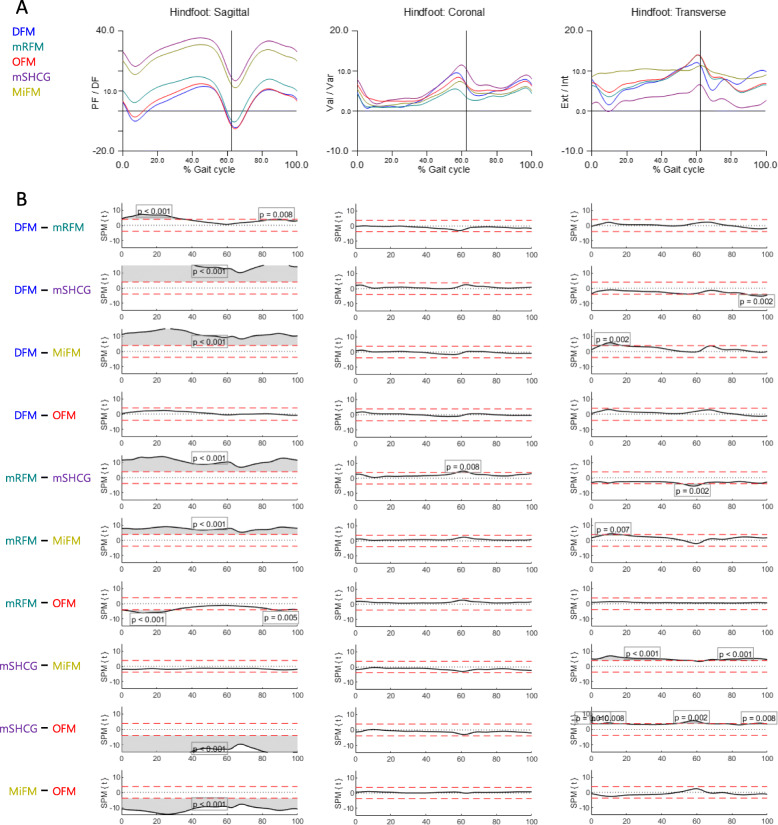
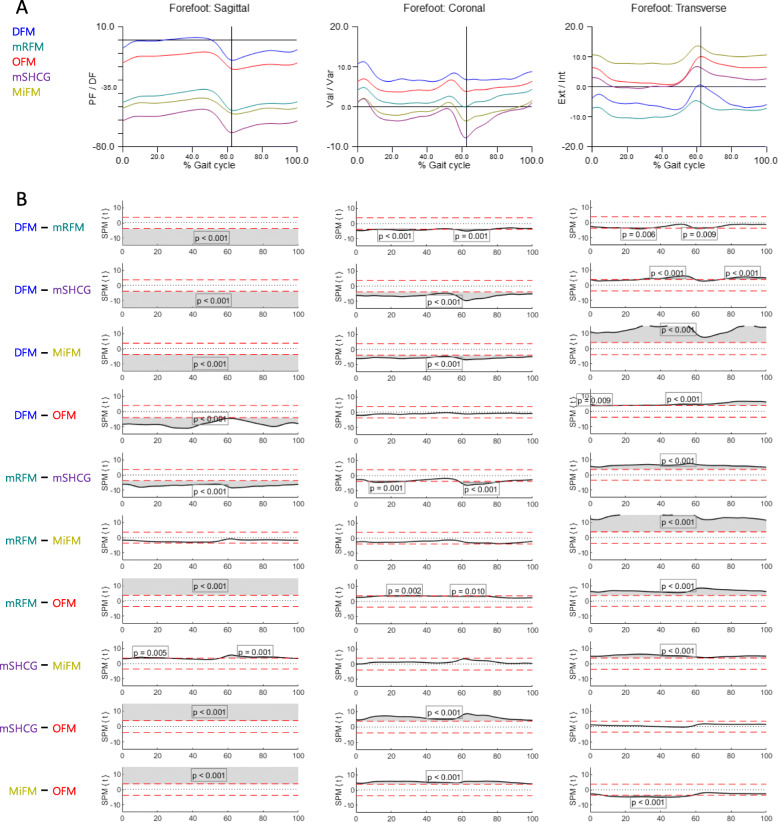
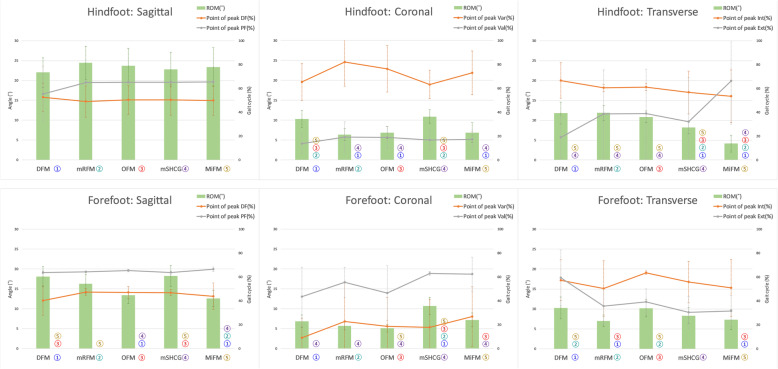
Figures 3 and 4 show the mean kinematics for each model and SPM curves acquired from the post-hoc unpaired t-test of MFMs. In HFsag, MiFM and mSHCG were more dorsiflexed than DFM, OFM, and mRFM in the whole cycle due to static offset angles, and there were no differences in ROM among MFMs (Figs. 3 and 5). In HFcor, all SPM curves showed no significant differences except for mRFM-mSHCG, but the DFM and mSHCG had significantly greater ROMs. In HFtrans, MiFM and mSHCG showed significantly reduced ROM than the others. The SPM curves of HF for DFM-OFM were not statistically different in all planes. In contrast to HFsag, FFsag of MiFM, mSHCG, and mRFM were more plantarflexed than those of DFM and OFM in the whole cycle (Fig. 4). In addition, there were significant differences in overall SPM curves for FF kinematics between the models in all planes. With respect to the point of peak angle, each model was significantly different in FFsag and FFtrans, and some MFMs had standard deviations greater than the mean in HFtrans and FFcor (Fig. 5).
Fig. 3.
The hindfoot kinematics of five multi-segment foot models. A Average graphs for each model (% gait cycle). B Differences among the models were visualized by statistical parametric mapping of the t-values from the post-hoc unpaired t-test (α = 0.01)
Fig. 4.
The forefoot kinematics of five multi-segment foot models. A Average graphs for each model (% gait cycle). B Differences among the models were visualized by statistical parametric mapping of the t-values from the post-hoc unpaired t-test (α = 0.01)
Fig. 5.
Mean and standard deviations of ROM and the point of peak angle of each MFM. Each MFM was numbered with a different color, and the number of MFM with significant differences in ROM was indicated next to the graph of each MFM. There were significant differences in ROM between MFMs in all motions except “Hindfoot: Sagittal,” and the the peak angle time showed large deviations in the coronal and transverse planes
Discussion
In this study, we investigated the kinematic differences, repeatability, and reproducibility of five MFMs that are widely used in the clinical gait analysis and obtained several meaningful results.
According to classifications suggested by Garofalo, Cutti [20], the inter-session repeatability and inter-evaluator reproducibility of all five MFMs in our study ranged from “very good” to “excellent” in the sagittal plane [7–9, 15]. In general gait analysis, the reliability decreased from the sagittal to the coronal, and transverse planes [23, 24], but the reliability of the coronal plane was lower than that of the transverse plane for HF in the OFM and mRFM models [7, 9]. Furthermore, the OFM, DFM, and mRFM models, which have a marker-based analysis, showed a lower repeatability of HF in the coronal plane than in the transverse plane compared to MiFM and mSHCG, which use offset angles. There may be more variables such as the influence of the Euler/Cardan angle sequence [25]; however, we consider that the horizontal variation in the placement of the two posterior heel markers had a major impact on the marker-based analysis of coronal HF motion. Thus, clinicians or researchers using only marker-based analysis should consider using a calcaneal marker placement device [26] or establish a more precise criterion for locating these markers and sticking them carefully.
McGinley, Baker [27] stated in their review that in common clinical situations, an error of 2° or less was highly likely to be acceptable. Errors between 2° and 5° were also likely to be regarded as reasonable but may require consideration in data interpretation. Schwartz, Trost [21] introduced experimental errors in the lower extremities (excluding the multi-segmented foot), and the mean σeval ranged from 1.2 to 5.3°. In a study that applied σ to MFM, Deschamps, Staes [8] reported that mean σsess ranged between 0.9° and 5.0°, while the mean σeval ranged between 2.8° and 7.6°. Saraswat, MacWilliams [14] verified that mean σsess and σeval were less than 6.0°. In our study, MiFM and mSHCG showed lower σ than other models in motion analysis with offset angles, but the σtrial, σsess, and σeval of all MFMs did not exceed 3.5°. This indicated that the highest σ in our study was lower than those of previous studies. Therefore, we believe that rotating the segments by the offset angles obtained from radiographic and/or goniometric measurements increased reliability, and consequently avoided the effects of marker-placement errors. However, any model used in our study would be clinically acceptable.
MiFM and mSHCG showed greater HF dorsiflexion and FF plantarflexion compared to other models because they reflected the pitch angles of the calcaneus and FF [13, 14]. Additionally, we verified a close affinity in HF for all planes between OFM and DFM, which corresponds with the findings of Nicholson, Church [17]. However, the CMCs for DFM of HFtrans were lower than those for OFM. This suggests that the DFM, by using markers on the medial/lateral malleolus to coordinate the HF segment, was more variable in the transverse plane than the OFM, which applies markers on the medial/lateral calcaneus.
Although most MFMs showed no statistical differences in HF varus/valgus SPM curves except for the toe-off of mRFM-mSHCG, DFM and mSHCG showed significantly increased ROM. In the HF external/internal rotation, there were also similarities in kinematics and ROM in DFM, mRFM, and OFM; however, MiFM and mSHCG showed inconsistent kinematics and decreased ROM compared to the other models. In addition, the point of peak angle showed large deviations in some motions and significant differences in FF. We think that these dissimilarities were not due to the offset angle but to the different local coordinate system and marker placement for each MFM. In particular, soft tissue artifacts that occur differently in each model due to the marker placement discrepancy even within the same segment also had a critical influence [28, 29]. In previous studies, the wand marker, which was used for mSHCG, reflected only 40–70% of the actual axial hip rotation when attached to the lateral thigh [30]. Similarly, the three markers on the lateral shank, which were used for DFM, can rotate themselves by moving with the calf muscle, creating excessive rotation in the proximal segments [17]. In other words, the sensitivity to motion was different for each MFM due to the influence of differences in the segment coordination and the marker type and location. Hence, these factors must be considered when comparing clinical studies using different MFMs.
We obtained meaningful results by comparing the kinematic characteristics of the five models, but it was impossible to find a model that accurately depicts actual foot motions. To compare MFMs with actual foot movements, the influence of STA must be considered. Although there was a study that measured rear, mid, and forefoot kinematics and ROM through an invasive in vivo study using bone pins [31], it could not be compared with our results because the subjects and experimental environments were different. In addition, valuable studies have been conducted to quantify the STA between the skin-mounted marker and the bone to identify the location most affected by STA [32–34]. They reported that the medial malleolus [32], lateral malleolus [34], navicular [32, 33], medial calcaneus [32], lateral calcaneus [33], and posterior aspect of the proximal calcaneus [34] were significantly affected by STA during maximum plantarflexion. In particular, Schallig, Streekstra [34] reported that, in a study with a computed tomography scan, RFM that utilized the posterior aspect of the proximal calcaneus marker as a tracking marker was significantly affected by STA, compared to OFM, which used the proximal calcaneal marker only in the anatomical coordinate system. In summary, although we could not compare the bone movement in five models, further studies are needed to find a model that most accurately reflects actual foot movement.
Some limitations should be considered when appreciating these results. First, only young adult men were analysed in this study. The biomechanics of the elderly, children, and females may differ from those of young males. Second, although the number of subjects in this study was small, it is similar to that of other studies [7, 8, 15, 17]. Further research is required to investigate the implications of the findings to a wider population. Finally, we applied some slight modifications of marker placements to mRFM, OFM, and mSHCG for convenience. This could affect the FF kinematics of mRFM and those of HF of OFM and mSHCG.
Conclusion
Rotating the segment according to the appropriate offset angle obtained from radiographic or goniometric measurements increased reliability. However, even with kinematic similarities, ROMs and the point of peak angle were different for each MFM. Therefore, it was impossible to define an MFM close to the actual foot and ankle motions in this study, but it is important to consider that different MFMs have different reliability and sensitivity to motion when understanding clinical findings. Clinicians and researchers involved in the evaluation of foot and ankle dysfunction need an understanding of the specific features of each MFM to make accurate decisions. Based on the results of this study, further studies are needed to determine which model closely reflects the actual foot and ankle motions.
Supplementary Information
Additional file 1. Table. Names and anatomical landmarks of a 28-merged marker set.
Acknowledgements
Not applicable.
Abbreviations
- MFMs
Multi-segment foot models
- DFM
DuPont foot model
- mRFM
Modified Rizzoli foot model
- OFM
Oxford foot model
- MiFM
Milwaukee foot model
- mSHCG
Modified Shriners Hospital for Children Greenville foot model
- HF
The relative motion of shank-hindfoot
- FF
The relative motion of hindfoot-forefoot
- CMC
Coefficients of multiple correlations
- σ
Experimental errors
- σtrial
Inter-trial errors
- σsess
Inter-session errors
- σeval
Inter-evaluator errors
- SPM
Statistical parametric mapping
Authors’ contributions
Hyo Jeong Yoo conducted original draft and wrote the manuscript, analysed and interpreted data, conducted statistical analysis. Hye Sun Park analysed and interpreted data, conducted writing and revising the manuscript. Dong-Oh Lee, Seong Hyun Kim, Gil Young Park, and Tae Jun Cho conducted writing and revising the manuscript. Dong Yeon Lee supervised the study, interpreted data, conducted writing and revising the manuscript. All authors participated in reviewing and editing the manuscript, and approved the final manuscript.
Funding
This study was supported by a grant (NRF-2017M3A9E2063104) from the Bio & Medical Technology Development Program of the National Research Foundation (NRF) funded by the Ministry of Science & ICT, Republic of Korea.
Availability of data and materials
The datasets used and/or analysed during the current study are available from the corresponding author on reasonable request.
Declarations
Ethics approval and consent to participate
The institutional review board of Seoul National University Hospital (H-1010-047-335) approved this study, and all participants provided informed consents prior to participation.
Consent for publication
Not applicable.
Competing interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Footnotes
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Leardini A, Caravaggi P, Theologis T, Stebbins J. Multi-segment foot models and their use in clinical populations. Gait Posture. 2019;69:50–59. doi: 10.1016/j.gaitpost.2019.01.022. [DOI] [PubMed] [Google Scholar]
- 2.Novak AC, Mayich DJ, Perry SD, Daniels TR, Brodsky JW. Gait analysis for foot and ankle surgeons-- topical review, part 2: approaches to multisegment modeling of the foot. Foot Ankle Int. 2014;35(2):178–191. doi: 10.1177/1071100713511435. [DOI] [PubMed] [Google Scholar]
- 3.Henley J, Richards J, Hudson D, Church C, Coleman S, Kerstetter L, et al. Reliability of a clinically practical multi-segment foot marker set/model. In: MR HGF, et al., editors. In Foot and ankle motion analysis: clinical treatment and technology. In Foot and ankle motion analysis: clinical treatment and technology. Boca Raton: CRC Press; 2008. pp. 445–463. [Google Scholar]
- 4.Portinaro N, Leardini A, Panou A, Monzani V, Caravaggi P. Modifying the Rizzoli foot model to improve the diagnosis of pes-planus: application to kinematics of feet in teenagers. J Foot Ankle Res. 2014;7(1):754. doi: 10.1186/s13047-014-0057-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Stebbins J, Harrington M, Thompson N, Zavatsky A, Theologis T. Repeatability of a model for measuring multi-segment foot kinematics in children. Gait Posture. 2006;23(4):401–410. doi: 10.1016/j.gaitpost.2005.03.002. [DOI] [PubMed] [Google Scholar]
- 6.Caravaggi P, Benedetti MG, Berti L, Leardini A. Repeatability of a multi-segment foot protocol in adult subjects. Gait Posture. 2011;33(1):133–135. doi: 10.1016/j.gaitpost.2010.08.013. [DOI] [PubMed] [Google Scholar]
- 7.Wright CJ, Arnold BL, Coffey TG, Pidcoe PE. Repeatability of the modified Oxford foot model during gait in healthy adults. Gait Posture. 2011;33(1):108–112. doi: 10.1016/j.gaitpost.2010.10.084. [DOI] [PubMed] [Google Scholar]
- 8.Deschamps K, Staes F, Bruyninckx H, Busschots E, Jaspers E, Atre A, Desloovere K. Repeatability in the assessment of multi-segment foot kinematics. Gait Posture. 2012;35(2):255–260. doi: 10.1016/j.gaitpost.2011.09.016. [DOI] [PubMed] [Google Scholar]
- 9.Seo SG, Lee DY, Moon HJ, Kim SJ, Kim J, Lee KM, Chung CY, Choi IH. Repeatability of a multi-segment foot model with a 15-marker set in healthy adults. J Foot Ankle Res. 2014;7(1):24. doi: 10.1186/1757-1146-7-24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kim EJ, Shin HS, Lee JH, Kyung MG, Yoo HJ, Yoo WJ, Lee DY. Repeatability of a multi-segment foot model with a 15-marker set in normal children. Clin Orthop Surg. 2018;10(4):484–490. doi: 10.4055/cios.2018.10.4.484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Leardini A, Benedetti MG, Berti L, Bettinelli D, Nativo R, Giannini S. Rear-foot, mid-foot and fore-foot motion during the stance phase of gait. Gait Posture. 2007;25(3):453–462. doi: 10.1016/j.gaitpost.2006.05.017. [DOI] [PubMed] [Google Scholar]
- 12.Di Marco R, Rossi S, Racic V, Cappa P, Mazza C. Concurrent repeatability and reproducibility analyses of four marker placement protocols for the foot-ankle complex. J Biomech. 2016;49(14):3168–3176. doi: 10.1016/j.jbiomech.2016.07.041. [DOI] [PubMed] [Google Scholar]
- 13.Kidder SM, Abuzzahab FS, Harris GF, Johnson JE. A system for the analysis of foot and ankle kinematics during gait. IEEE Trans Rehabil Eng. 1996;4(1):25–32. doi: 10.1109/86.486054. [DOI] [PubMed] [Google Scholar]
- 14.Saraswat P, MacWilliams BA, Davis RB. A multi-segment foot model based on anatomically registered technical coordinate systems: method repeatability in pediatric feet. Gait Posture. 2012;35(4):547–555. doi: 10.1016/j.gaitpost.2011.11.022. [DOI] [PubMed] [Google Scholar]
- 15.Long JT, Eastwood DC, Graf AR, Smith PA, Harris GF. Repeatability and sources of variability in multi-center assessment of segmental foot kinematics in normal adults. Gait Posture. 2010;31(1):32–36. doi: 10.1016/j.gaitpost.2009.08.240. [DOI] [PubMed] [Google Scholar]
- 16.Arnold JB, Mackintosh S, Jones S, Thewlis D. Repeatability of stance phase kinematics from a multi-segment foot model in people aged 50 years and older. Gait Posture. 2013;38(2):349–351. doi: 10.1016/j.gaitpost.2012.11.010. [DOI] [PubMed] [Google Scholar]
- 17.Nicholson K, Church C, Takata C, Niiler T, Chen BP, Lennon N, et al. Comparison of three-dimensional multi-segmental foot models used in clinical gait laboratories. Gait Posture. 2018;63:236–241. doi: 10.1016/j.gaitpost.2018.05.013. [DOI] [PubMed] [Google Scholar]
- 18.Johnson JE, Lamdan R, Granberry WF, Harris GF, Carrera GF. Hindfoot coronal alignment: a modified radiographic method. Foot Ankle Int. 1999;20(12):818–825. doi: 10.1177/107110079902001212. [DOI] [PubMed] [Google Scholar]
- 19.Ness ME, Long J, Marks R, Harris G. Foot and ankle kinematics in patients with posterior tibial tendon dysfunction. Gait Posture. 2008;27(2):331–339. doi: 10.1016/j.gaitpost.2007.04.014. [DOI] [PubMed] [Google Scholar]
- 20.Garofalo P, Cutti AG, Filippi MV, Cavazza S, Ferrari A, Cappello A, Davalli A. Inter-operator reliability and prediction bands of a novel protocol to measure the coordinated movements of shoulder-girdle and humerus in clinical settings. Med Biol Eng Comput. 2009;47(5):475–486. doi: 10.1007/s11517-009-0454-z. [DOI] [PubMed] [Google Scholar]
- 21.Schwartz MH, Trost JP, Wervey RA. Measurement and management of errors in quantitative gait data. Gait Posture. 2004;20(2):196–203. doi: 10.1016/j.gaitpost.2003.09.011. [DOI] [PubMed] [Google Scholar]
- 22.Pataky TC, Robinson MA, Vanrenterghem J. Vector field statistical analysis of kinematic and force trajectories. J Biomech. 2013;46(14):2394–2401. doi: 10.1016/j.jbiomech.2013.07.031. [DOI] [PubMed] [Google Scholar]
- 23.Growney E, Meglan D, Johnson M, Cahalan T, An K-N. Repeated measures of adult normal walking using a video tracking system. Gait Posture. 1997;6(2):147–162. doi: 10.1016/S0966-6362(97)01114-4. [DOI] [Google Scholar]
- 24.Kadaba MP, Ramakrishnan HK, Wootten ME, Gainey J, Gorton G, Cochran GV. Repeatability of kinematic, kinetic, and electromyographic data in normal adult gait. J Orthop Res. 1989;7(6):849–860. doi: 10.1002/jor.1100070611. [DOI] [PubMed] [Google Scholar]
- 25.Grood ES, Suntay WJ. A joint coordinate system for the clinical description of three-dimensional motions: application to the knee. J Biomech Eng. 1983;105(2):136–144. doi: 10.1115/1.3138397. [DOI] [PubMed] [Google Scholar]
- 26.Deschamps K, Roosen P, Birch I, Dingenen B, Bruyninckx H, Desloovere K, Aertbelien E, Staes F. A novel device for standardizing marker placement at the calcaneus. J Am Podiatr Med Assoc. 2014;104(1):43–49. doi: 10.7547/0003-0538-104.1.43. [DOI] [PubMed] [Google Scholar]
- 27.McGinley JL, Baker R, Wolfe R, Morris ME. The reliability of three-dimensional kinematic gait measurements: a systematic review. Gait Posture. 2009;29(3):360–369. doi: 10.1016/j.gaitpost.2008.09.003. [DOI] [PubMed] [Google Scholar]
- 28.Nester CJ, Liu AM, Ward E, Howard D, Cocheba J, Derrick T. Error in the description of foot kinematics due to violation of rigid body assumptions. J Biomech. 2010;43(4):666–672. doi: 10.1016/j.jbiomech.2009.10.027. [DOI] [PubMed] [Google Scholar]
- 29.Peters A, Sangeux M, Morris ME, Baker R. Determination of the optimal locations of surface-mounted markers on the tibial segment. Gait Posture. 2009;29(1):42–48. doi: 10.1016/j.gaitpost.2008.06.007. [DOI] [PubMed] [Google Scholar]
- 30.Lamoreux LW. Errors in thigh axial rotation measurements using skin mounted markers. J Biomech. 1992;25:769. doi: 10.1016/0021-9290(92)90486-K. [DOI] [Google Scholar]
- 31.Lundgren P, Nester C, Liu A, Arndt A, Jones R, Stacoff A, Wolf P, Lundberg A. Invasive in vivo measurement of rear-, mid- and forefoot motion during walking. Gait Posture. 2008;28(1):93–100. doi: 10.1016/j.gaitpost.2007.10.009. [DOI] [PubMed] [Google Scholar]
- 32.Tranberg R, Karlsson D. The relative skin movement of the foot: a 2-D roentgen photogrammetry study. Clin Biomech. 1998;13(1):71–76. doi: 10.1016/S0268-0033(97)00052-1. [DOI] [PubMed] [Google Scholar]
- 33.Shultz R, Kedgley AE, Jenkyn TR. Quantifying skin motion artifact error of the hindfoot and forefoot marker clusters with the optical tracking of a multi-segment foot model using single-plane fluoroscopy. Gait Posture. 2011;34(1):44–48. doi: 10.1016/j.gaitpost.2011.03.008. [DOI] [PubMed] [Google Scholar]
- 34.Schallig W, Streekstra GJ, Hulshof CM, Kleipool RP, Dobbe JGG, Maas M, Harlaar J, van der Krogt MM, van den Noort JC. The influence of soft tissue artifacts on multi-segment foot kinematics. J Biomech. 2021;120:110359. doi: 10.1016/j.jbiomech.2021.110359. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Additional file 1. Table. Names and anatomical landmarks of a 28-merged marker set.
Data Availability Statement
The datasets used and/or analysed during the current study are available from the corresponding author on reasonable request.