Abstract
X-ray induced acoustic computed tomography (XACT) provides X-ray absorption based contrast with acoustic detection. For its clinical translation, XACT imaging often has a limited field of view. This can result in image artifacts and overall loss of quantification accuracy. In this article, we aim to demonstrate model-based XACT image reconstruction to address these problems. An efficient matrix-free implementation of the regularized LSQR (MF-LSQR) based minimization scheme and a non-iterative model back-projection (MBP) scheme for computing XACT reconstructions have been demonstrated in this paper. The proposed algorithms have been numerically validated and then employed to perform reconstructions from experimental measurements obtained from an XACT setup. While the commonly used back-projection algorithm produces limited-view and noisy artifacts in the region of interest, model-based LSQR minimization overcomes these issues. The model based algorithms also reduce the ring artifacts caused due to the non-uniformity response of the multichannel data acquisition. Using the model-based reconstruction algorithms, we are able to obtain reasonable XACT reconstructions for acoustic measurements of up to 120° view. Although the MBP is more efficient than the model-based LSQR algorithm, it provides only the structural information of the region of interest. Overall, it has been demonstrated that the model-based image reconstruction yields better image quality for XACT than the standard back-projection. Moreover, the combination of model-based image reconstruction with different regularization methods can solve the limited view problem for XACT imaging (in many realistic cases where the full-view dataset is unavailable) and hence pave the way for the future clinical translation.
Keywords: X-ray induced acoustic tomography (XACT), model-based image reconstruction, Biomedical imaging, regularization, least-squares problem, model back-projection
I. INTRODUCTION
EVER since their discovery, X-rays have been instrumental in biomedical research. X-rays are not only used for imaging and revealing tissue morphology through computerized tomography (CT) scans [1]–[3], but also for treating tumors with radiation therapy [4],[5]. However, an excess of X-ray exposure may lead to DNA mutations that can cause cancer [6], and hence, regular CT scans can be harmful. Therefore an imaging modality that induces low radiation exposure of patients is desirable. X-ray induced acoustic computed tomography (XACT) is a contemporary approach for biomedical imaging that employs X-ray excitation and acoustic detection, invented to address the challenges in traditional X-ray imaging. Time-varying X-ray radiation, when absorbed by materials, leads to an increase in local temperature (~mK) causing thermoelastic expansion which generates ultrasound (US) [1]. Unlike X-rays, X-ray induced acoustic (XA) waves are omnidirectional and hence a three-dimensional image can be obtained from pulsed X-ray excitation thus reducing the radiation exposure required for imaging an organ. Due to the low scattering of X-rays in tissue, X-ray induced acoustic computed tomography (XACT) [7]–[10] can facilitate deep imaging and hence has numerous potential clinical applications such as radiation dosimetry [11] and bone density evaluation for osteoporosis assessment [12].
Generation of pressure waves caused by X-ray absorption was first reported in 1983 [13]. The pressure source and hence the pressure waves were hypothesized to carry the information about the internal properties of the material and therefore the collected pressure signals could be employed to study these properties. The first ultrasound emission following X-ray absorption (by water) in a therapeutic setting was demonstrated in 1991 [14]. The ultrasonic transducer used for collecting the XA signal was placed perpendicular to the direction of the X-ray beam. It was reported that with 34 Gy X-ray exposure, detectable XA signals were obtained as far as 13 cm from the beam. These experiments indicated the possible clinical applicability of the X-ray induced ultrasound. The next two decades saw very little research in this field. The interest in X-ray induced ultrasound was revitalized in 2013 when the first XACT image was reported by Xiang et al. [7]. Pulsed X-rays generated from a medical linear accelerator (LINAC) were used to irradiate a chicken breast with a lead rod embedded in it. The XA signals thus produced were collected at multiple positions on a circle by scanning a single transducer. The image reconstruction was performed using the back-projection algorithm and the 2D XACT images were able to locate the lead target in the tissue. They also demonstrated the linear dependence of the XA signal strength on the radiation dose thus spurring the possibility of radiation dosimetry using XACT which can be advantageous for monitoring and planning radiotherapy. The Monte Carlo simulations [15] used in radiation therapy for treatment planning can be coupled with acoustic propagation simulators (k-wave toolbox [16]) to numerically assess the suitability of XACT for dosimetry [17]. A computational study of the efficacy of XACT for dose monitoring for a human prostate was performed in 2014 [18]. In 2016, simulations were performed by Hickling et al. to study the behavior of the radiation induced acoustic waveforms due to variation in the X-ray energy, target material, and its dimensions [19]. The predicted acoustic waveform properties were found to be reasonably consistent with the experimental observations thus implying that the simulation framework can potentially be used in the study of XACT in different radiotherapy settings. Clinical XACT based dosimetry setups typically employ a clinical Linac X-ray system for irradiating the tissue along with a transducer array for collecting the XA signals. A typical Linac used in the clinics has a pulse width of a few microseconds. While X-rays with nanosecond pulse widths have been reported to generate XA signals more efficiently [20], [21], clinical Linacs have also demonstrated to produce detectable XA signals [7], [17]–[19], [22]–[24]. Initial XACT experiments employed heavy metals, which have high X-ray absorption, as targets [7], [20], [21]. In [22], XA signals following X-ray absorption in water were reported and further employed in the back-projection algorithm to image the X-ray energy deposition in water. XACT for imaging relative radiation dose distribution in real biological tissue (veal liver) was first shown by Lei et al. [25]. The potential of XACT for in vivo radiation dosimetry was first demonstrated in [22] and systematic characterization of XACT-based dosimetry was carried out [23]. Another XACT-based dosimetry system was demonstrated by Kim et al. in 2017 [24] where a medical LINAC was used to irradiate a lead sample scanned by a spherically focused transducer to image X-ray energy deposition and later in 2019, an XACT-based imaging device facilitating real-time dosimetry in water was patented [26]. Forghani et al. [27] performed simulations to compare the back-projection (BP) and iterative time-reversal (ITR) algorithms’ potential for absolute dosimetry in 3D XACT. They concluded that ITR reconstructions are quantitatively more accurate as compared to the BP counterparts. However, due to the high computational time associated with the ITR algorithm, it has limited clinical applicability. In a recent numerical study [28], the potential of XACT for tracking the X-ray beam and in vivo dosimetry during stereotactic partial breast irradiation [29] was examined. Wang et al. carried out simulations to demonstrate the feasibility of using a transperineal (planar) ultrasound transducer array for XACT imaging to monitor prostate radiotherapy [30]. They also developed a workflow for simultaneous, real-time XA and US imaging capturing the dose deposition and the movement of the tissue respectively. These results foster the feasibility of the clinical translation of XACT based dosimetry. Clinically used linear accelerators can produce sufficiently strong XA signals for tissue imaging. Therefore, the existing radiotherapy set-ups only need to integrate the coupling medium and a transducer-array (detection grid) to adopt XACT-based dosimetry without significantly affecting existing radiotherapy practices.
XACT has also shown the potential for radiological imaging in clinics. XACT imaging of gold fiducial markers (GFMs) which due to high X-ray absorption properties, are used in the clinics for improving visualization of tumors, was presented in [20]. A simulation study for XACT imaging of the human breast to identify microcalcifications, an indicator for cancer development, was presented by Tang et al [31] demonstrating the possibility of diagnosing breast cancer using XACT. In [32], 3D XACT was demonstrated using an XACT system that uses a pulsed X-ray source and a 96-element arc shaped transducer array for acoustic detection. Reconstructions were achieved by employing the back-projection algorithm driven by a graphics processor unit (GPU) which was found to be about 40-times more efficient than the CPU-based BP [33]. Li et al. carried out a computational study of the feasibility of 3D-XACT using a spherical array of transducers [34] and Robertson et al. demonstrated the first XACT imaging of bone where the acoustic measurements were obtained by scanning a transducer and the image reconstruction was performed using time-reversal [35]. Excitation sources for XACT are typically limited to Linacs and portable pulsed X-ray generator tubes. In a recent study, Choi et al. demonstrated the feasibility of XACT using synchrotron X-ray illumination [36].
Each imaging modality has its advantages and limitations. Integrating the information extracted from multiple complementary imaging modalities can offer a better evaluation and visualization of the region of interest. XACT in combination with US imaging was employed for monitoring the alignment of the X-ray beam with respect to the target during the session [37]. Dual modality imaging systems that employ co-registration of real-time dose deposition obtained from XACT with anatomical US images [38], [39] are also being developed.
XACT typically employs the back-projection-based image reconstruction algorithm which can be implemented only for certain detection geometries (i.e. planar, circular, or spherical) [40]. Unlike the back-projection algorithm, model-based algorithms can incorporate experimental attributes (i.e. acoustic inhomogeneity, finite detector size, etc.) and can perform reconstructions for arbitrary data acquisition geometries. In laser induced photoacoustic imaging modality, model-based algorithms have been demonstrated to ameliorate the limited-view and noisy artifacts associated with conventional back-projection algorithms [41], [42].
XACT-based detection often needs an acoustically matching medium (e.g., water) between the object and the detection grid which is generally achieved by immersing the entire object and the detection grid in water [8]–[10]. For such cases, full-view acoustic measurements can easily be performed. However, for in vivo measurements, acoustic data acquisition is often feasible for a partial view only which leads to artifacts in the back-projection reconstructions. In this paper, we introduce the model-based image reconstruction to solve the limited view problem in XACT imaging. Model-based schemes offer the flexibility to incorporate regularization priors to subdue the noisy and limited-view artifacts and hence are known to produce better reconstructions than the back-projection algorithm [40]. To the best of our knowledge, the results presented in this work are the first demonstration of the model-based XACT.
Model-based reconstruction algorithms rely on an accurate forward model relating the X-ray energy deposition (XED) to the boundary acoustic measurements. Model-based three-dimensional reconstruction problems are computationally demanding. To reduce the dimensionality of the tomographic problem, several set-ups employ circular arrays of detectors and corresponding model-based algorithms have been developed to reconstruct a two-dimensional energy deposition map [41], [44]–[54]. Typically, model-based reconstructions are carried out using a model-matrix, which relates the measurements with the initial pressure source (which is proportional to the XED). For problems aiming at large domain and high-resolution reconstructions as well as high data sampling rates, constructing a model-matrix can be slow and memory intensive. Reconstructions presented in this paper were computed iteratively using the LSQR (least squares with QR-factorization) method, which provides the ability to employ functions for on-the-fly computation of matrix-vector products, effectively avoiding storage of the measurement matrix. Computational efficiency was further improved by using a non-iterative reconstruction scheme (model-back-projection (MBP) [42]) and corresponding results from numerical as well as experimental data have been illustrated in the sequel.
The rest of this paper is structured as follows. Section 2 deals with the mathematical formulation of modeling the forward problem as well as the inverse model-based algorithms associated with XACT. The numerical test cases and phantom XACT experiments are described in sections 3 and 4 respectively and the reconstruction results thus obtained are discussed in section 5. The paper is concluded in section 6.
II. MATHEMATICAL FORMULATION
A. Forward Problem
The forward model deals with the prediction of the acoustic fields due to the thermoelastic expansion of the X-ray energy deposition (XED) in the tissue under the assumptions of thermal confinement and zero acoustic attenuation and is based on [40]:
| (1) |
where Γ(v2β/Cp) is the Gruneisen parameter, v is the speed of sound, β is the volumetric expansion coefficient, Cp is the specific heat at constant pressure and H is the XED distribution; initial pressure source is the product of the Gruneisen parameter and XED. The solution to Eq. (1) is given by: [41]
| (2) |
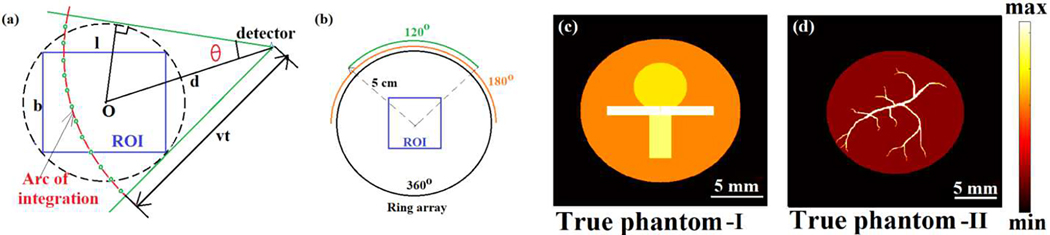
where S′(t) denotes a time-dependent spherical surface centered at a detector (located at such that ). If the pressure source lies in a plane, Eq. (2) reduces to its 2D analog where the integral in Eq. (2) represents the integration of the pressure distribution in the domain of interest on a circular arc of radius vt as demonstrated in Fig. 1(a).
Fig. 1.
(a) Arc of integration for a detector at distance d from the center of the ROI at time t and corresponding range of θ. The quadrature points on the arc are denoted by small circles. (b) Full and limited-view detection geometries, and the cross-sections of the initial pressure sources (c) I and (d) II.
Setting as unity and further solving Eq. (2) can be written as
| (3) |
The region of interest (typically chosen to be a rectangle containing the complete initial pressure source or XED) is discretized into triangular elements (three nodes each) and the initial pressure source is expressed in the nodal basis: . The interpolated value of the initial pressure source (at location ) inside an element e can be written as [55]
| (4) |
with being the linear basis function 39 for the kth node of the element e.
For computation of the integral term, each circular arc is discretized into a sufficiently high number of circular elements as demonstrated in Fig. 1. For ease of computation, the value of the initial pressure source on each of the contributing elements (total Mc elements (say)) has been considered to be constant and equal to the value at its midpoint which is computed using Eq. (4). Therefore the integration in Eq. (2) for the mth detector location and qth time step can be written as:
| (5) |
where denotes the value of the initial pressure source at the midpoint and Δθi denotes the angle subtended by the ith contributing element onto the detector point . The contribution from all the elements is assembled into sparse vector (size: N × 1), such that the desired integral can be expressed as
| (6) |
The vectors are stacked to prepare matrix and the integral vector consisting of the integral contributions for all the Nd detectors can be written as
| (7) |
Similarly the matrices are stacked to prepare matrix V and the integral vector consisting of the integral contributions for all the Nd detectors and at all the time samples can be written as:
| (8) |
Using central difference, the time-derivative in Eq. (3) can be approximated as:
| (9) |
and using Eq. (7), the discrete measurements at all the detectors at the qth time step (t(q) = q Δt), can be expressed as:
| (10) |
Where
| (11) |
Matrices are stacked to prepare matrix M (size: (Nd.Nt) × N) and the complete measurement vector (size: (Nd.Nt) × 1) is written as:
| (12) |
B. Inverse Problem
The inverse problem is to reconstruct the X-ray energy deposition (XED) distribution from the time-domain boundary pressure measurements and corresponding regularized least-squares (LS) problem can be expressed as [41], [42]
| (13) |
where ||.||2 denotes the L2-norm. R is the regularizer matrix with λ being the regularization parameter; for Tikhonov regularization R = R I (I being the identity matrix) and for Laplacian regularization R = R L (L being the incidence matrix; LTL is the discrete Laplacian operator). The LS minimizer to Eq. (13) is given as:
| (14) |
For certain problem settings (with large domain size, fine spatial discretization and high sampling frequency), constructing M requires huge computational time and memory, and hence solving Eq. (14) becomes impractical. Therefore, Eq. (13) is solved iteratively using LSQR algorithm, which utilizes routines computing matrix-vector products and on-the-fly instead of constructing the measurement matrix M.
Algorithm 1.
Matrix-Free Computation of
| procedure Computing ; |
| (initialization by null-vector) |
| for id = 1 to Nd do |
| ; ; |
| end for |
| return |
| end procedure |
Algorithm 2.
Matrix-Free Computation of
| procedure Computing ; |
| (initialization by zero-vector) |
| for id = 1 to Nd do |
| ; ; |
| G ← [NT. ∗ P]; |
| end for |
| return |
| end procedure |
In order to compute and during LSQR iterations efficiently, the following set of quantities were computed and stored in MATLAB cells:
: Each cell contains the spatial element numbers in which the mid-points (quadrature points) of the contributing circular elements for a detector at all the time-samples lie in.
: Each cell contains the elemental interpolation function values corresponding to these quadrature points and elements.
: Each cell contains the time-samples corresponding to these quadrature points.
The algorithms for computing on-the-fly matrix-vector products and are provided in algorithms 1 and 2 respectively. A model back-projection (MBP) reconstruction has been proposed by Ding et al. [42], which is given by:
| (15) |
This solution represents a highly (Tikhonov) regularized reconstruction. It needs to be noted that MBP reconstructions require a single matrix-vector product computation (algorithm 2) and hence are much faster than the iterative model-based reconstruction algorithms.
III. NUMERICAL STUDIES
A. Model-matrix based XACT Algorithm (MB-XACT)
Numerical studies were performed to validate the proposed reconstruction schemes. For the first numerical experiment, we consider a square of side length 2 cm as the region of interest (ROI). A circle of radius 5 cm, concentric with the ROI is considered as the detection array (Fig. 1(b)) with 128 detection-points uniformly distributed on its circumference. The full- and partial-view detection geometries are demonstrated in Fig. 1(b). The pressure source chosen for this study (true phantom-I) is shown in Fig. 1(c).
To simulate the pressure signals (mimicking experimental measurements) the ROI was discretized into triangular elements with a grid resolution of h = 100μm and each arc of integration (Fig. 1(a)) was divided into Nq ≈ 1000 quadrature elements. The numerical acoustic signal at each detector was recorded for a total of 410 time-samples at Fs = 8MHz sampling frequency, and white Gaussian noise was added to obtain signals with 5 dB SNR. To perform the unregularized and Laplacian-regularized reconstructions in the ROI, the model-matrix was constructed with h = 200μm and Nq ≈ 1000, and reconstructions were obtained using Eq. (14).
The model-matrix-based LSQR (MB-LSQR) unregularized (Unreg-LSQR) and Laplacian regularized (Lap-LSQR) reconstructions along with the back-projection reconstructions for phantom-I are shown in Fig. 2 and corresponding computation time (τ) and correlation coefficients (ρ) [56] are provided in Table I. The reconstructions were performed using full-view (360°) as well as partial-view (180° and 120°) detection geometries as demonstrated in Fig. 1(b). As expected, the back-projection algorithm is computationally the most efficient and the structures in the cross-section are reconstructed well. However, not only do the back-projection reconstructions fail to provide the quantitative information of the cross-section, but they also carry limited view as well as noisy artifacts and hence yield low correlation coefficients with respect to the true phantom. For all the test cases, Laplacian regularization helped to reduce the noisy artifacts in the reconstruction and yield smoother images. This is also reflected in the relatively higher ρ values for the Laplacian-regularized reconstructions than their unregularized counterparts. For partial-view (<180°) measurements, the visibility of structures oriented perpendicular to the detection grid is known to be adversely affected [52], [57], as is also evident in Fig. 2(c,f). While for both the 360° and 180° view measurements (Fig. 2(a,b,d,e)), both the unregularized and Laplacian-regularized algorithms reconstruct all the structures of the phantom reasonable well, for the 120° view measurement neither can reconstruct the lower rectangle (oriented normal to the detection grid) due to missing data.
Fig. 2.
Unregularized (a,b,c) and Laplacian-regularized (d,e,f) model-matrix-based reconstructions and back-projection reconstructions (g,h,i) obtained from 360°, 180° and 120° views, respectively.
TABLE I.
Computation time (τ) and reconstruction quality measures – correlation coefficient (ρ) for numerical and contrast to noise ratio (CNR) for XACT experimental studies
| View | MB-XACT | MF-XACT | XACT Experiment | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BP | Unreg-LSQR | Lap-LSQR | MF-LSQR | MBP | MF-LSQR | MBP | BP | |||||||||
| P | τ (s) | P | τ (s) | P | τ (s) | P | τ (s) | P | τ (s) | CNR | τ (s) | CNR | τ (s) | CNR | τ (s) | |
| 360° | 0.42 | 0.3 | 0.93 | 310 | 0.99 | 310 | 0.95 | 45 | 0.49 | 10 | 0.83 | 80 | 0.31 | 42 | 0.35 | 1.1 |
| 180° | 0.07 | 0.2 | 0.93 | 160 | 0.99 | 160 | 0.95 | 35 | 0.39 | 8 | 0.70 | 55 | 0.27 | 27 | 0.30 | 0.7 |
| 120° | 0.06 | 0.2 | 0.92 | 115 | 0.97 | 115 | 0.88 | 29 | 0.33 | 7 | 0.61 | 36 | 0.22 | 16 | 0.27 | 0.5 |
B. Model-matrix free XACT Algorithm (MF-XACT)
In the second numerical experiment, the size of the ROI was chosen to be 2.5cm × 2.5cm; the initial pressure source is depicted in Fig. 1(d). The detection geometry was chosen to be the same as the previous numerical experiment. Due to the sharper structures in the initial pressure source, the measurements were computed at a higher spatial resolution h = 30μm), a higher sampling frequency (Fs = 20MHz), and a higher number of quadrature points (Nq ≈ 2000) than the first numerical experiment. The size of the structures in the ROI decides the frequency content in the signal. Thinner structures result in high frequency content and hence need higher sampling frequencies. Gaussian noise was added to obtain data with 5 dB SNR. For this problem setting, model-based reconstructions were performed with h = 60μm and Nq ≈ 500 without explicitly constructing M.
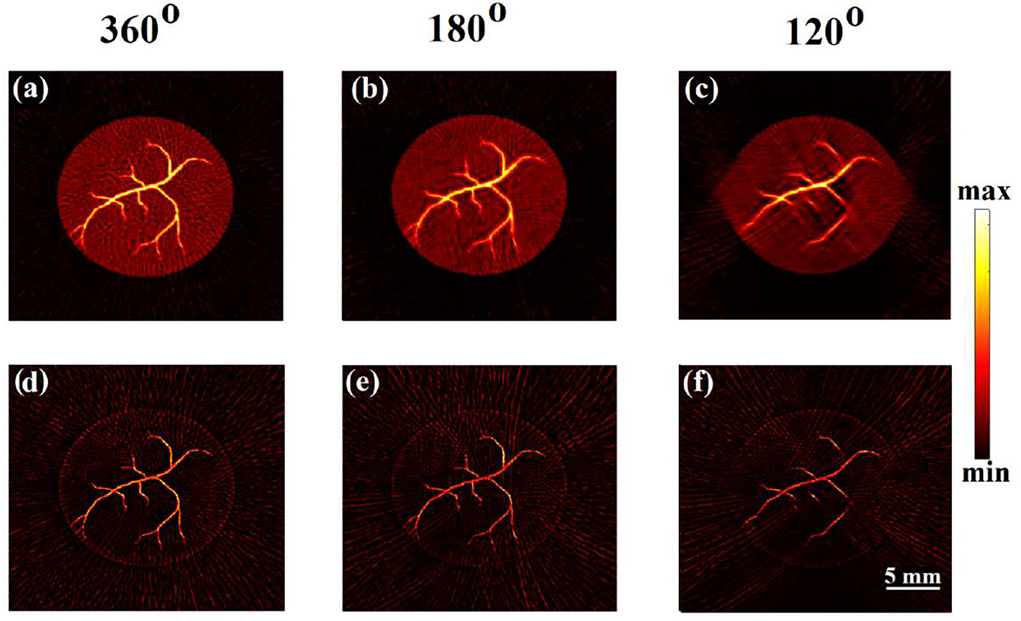
MF-LSQR and MBP reconstructions corresponding to full and partial-view noisy measurements for phantom-II are demonstrated in Fig. 3 and corresponding computation time (τ) and correlation (ρ) with respect to the true phantom are tabulated in Table I. For the 360° and 180° view measurement data, all the structures are reconstructed reasonably well (Fig. 3(a,b,d,e)), but for the 120° view, the structures normal to the detection grid are poorly reconstructed - a trend also observed in numerical experiment-I.
Fig. 3.
Model-matrix free reconstruction results: Laplacian-regularized (first row: a,b,c) and model-back-projection (second row: d,e,f) reconstructions obtained from 360°, 180° and 120° views, respectively.
While both these model-based algorithms are able to provide reasonably good structural information of the phantoms, the MF-LSQR demonstrates better quantitative accuracy than the MBP algorithm which is reflected in lower ρ values for MBP reconstructions with respect to their MF-LSQR counterparts. Moreover, Laplacian regularization enabled MF-LSQR to render smoother reconstructions than the MBP reconstructions which carry streak artifacts. However, it needs to be noted that while MF-LSQR is an iterative algorithm, MBP is not and hence takes less computational time to produce the reconstructions. Both these matrix-free model-based algorithms need to precompute the quantities , , and (as mentioned in section 2.2), which takes about 8, 6.7, and 5.7 seconds respectively for the 360° 180° and 120° view measurement settings. The MF-LSQR algorithm takes about 10–15 LSQR iterations to produce reasonable reconstructions. Each LSQR iteration needs one computation of {, } each which takes ~{1.5, 2} seconds, ~{1.1, 1.5} seconds, and ~{1.0, 1.3} seconds respectively for the 360°, 180° and 120° views. The MBP algorithm requires a single computation and hence takes ~20 folds less time (after computing , , and ) as compared to the MF-LSQR reconstruction algorithm.
Moreover, in section IIIA, the model-based reconstructions require constructing and storing the model-matrix (size: (number of detectors × number of time samples) × number of nodes in the reconstruction domain). For high sampling frequencies, constructing the model matrix can take huge computation time and its storage may demand huge memory. Therefore, the studies performed in section IIIA are carried out for low (8 MHz) sampling frequency.
This section demonstrates the LSQR reconstructions obtained in a model-matrix free approach. This approach does not need the model-matrix explicitly, and hence computations can be performed for higher sampling frequencies.
IV. XACT EXPERIMENTAL VERIFICATION
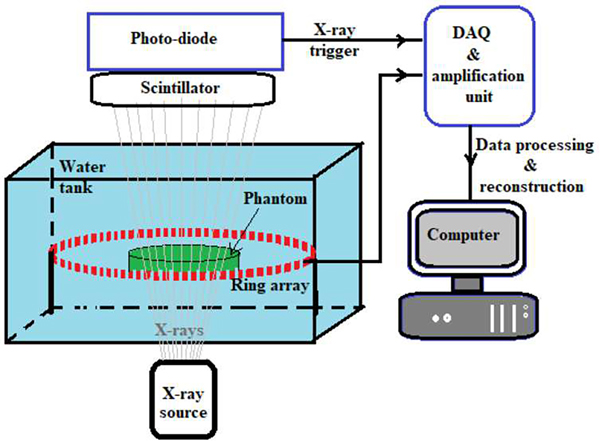
After numerical validation of the proposed model-based algorithms, these schemes were employed to obtain XACT reconstructions from experimental measurements. Fig. 4 shows the schematic of the XACT experimental setup [10].
Fig. 4.
Schematic of XACT experimental setup.
This XACT set up employs a 128-element ring array transducer (radius 5cm; Doppler Electronic Technologies Co. Ltd., Guangzhou, China) with 5 MHz central frequency and 60% bandwidth for sensing the XA waves. A target in ‘T’ shape, made of a 1/64 inch thick lead sheet was fixed at the center of a 3% gelatin water-based phantom. The phantom was placed at the center of the ring-array inside of a water tank and a pulsed X-ray generator (XR200, Golden Engineering, USA) with the tube energy of 150 kVp, pulse repetition rate of 10 Hz, and pulse width of 50 ns, was used to excite the phantom. The X-ray beams emitted from the X-ray generator carried an average dose of ~2.6 mR/pulse with a divergence angle of 40°. The XA waves are sensed by the transducer elements and sent to the amplification and data acquisition unit. The X-ray beams exiting the water tank were converted into visible light photons by a Ce:Lu2SiO5 crystal (MTI Corporation, USA) scintillator which were converted to voltage pulses by an integrated amplified photodetector (APD410C, Thorlab USA) and sent as the trigger pulses to the amplification and data acquisition system. The collected XA signals were averaged over 1500 pulses and the MF-LSQR and MBP-based XACT reconstructions were performed.
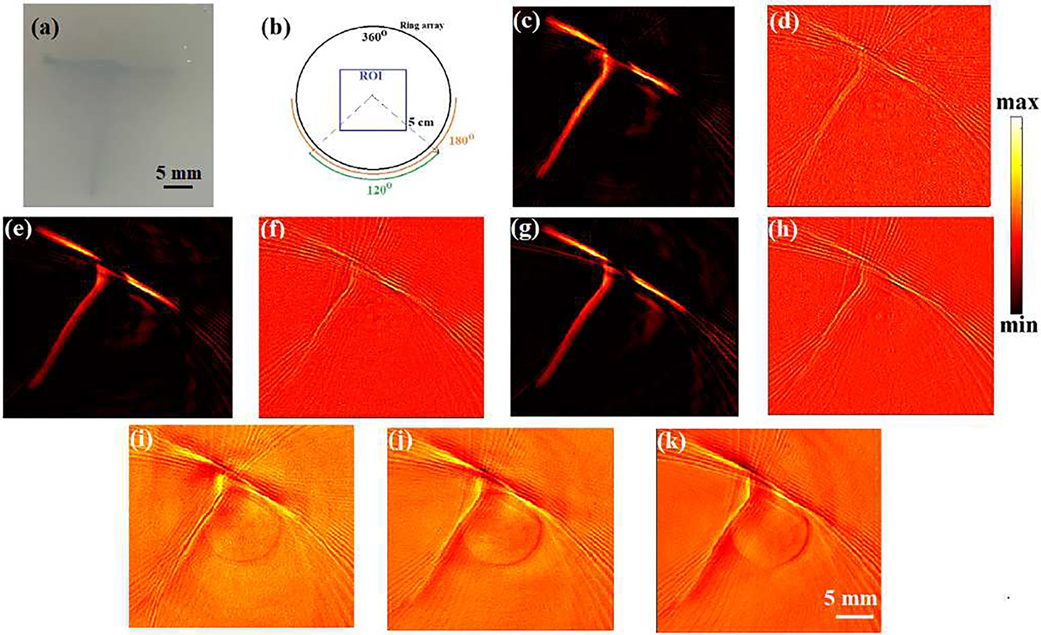
Model-based (MF-LSQR and MBP) and back-projection (BP) algorithms were employed on the full and partial-view (Fig. 5(b)) XACT measurements for reconstructions which are provided in Fig. 5(c–k) and corresponding computation time and contrast-to-noise ratios (CNR) [48] are tabulated in Tab. I. While all the algorithms are able to reconstruct the target, the back-projection reconstructions (MBP (Fig. 5(d,f,h)) and BP (Fig. 5(i,j,k))) carry more noisy artifacts and hence have lower CNRs as compared to their MF-LSQR (Fig. 5(c,e,g)) counterparts. Non-uniform response associated with multichannel data acquisition (DAQ) for ring-array transducers results in vertical lines in the XA sinogram. Vertical lines in sinograms form ring artifacts in reconstructions [58]. Both, the Laplacian and Tikhonov regularizers have a smoothening effect on the reconstructions. Therefore, the Laplacian regularized MF-LSQR and the highly Tikhonov regularized MBP algorithm manage to suppress the ring artifacts up to a certain extent. However, it needs to be noted that severe ring artifacts cannot be corrected simply by using the regularized reconstruction algorithms; additional signal processing can help to correct in such cases [58].
Fig. 5.
XACT experimental reconstruction results: (a) true phantom, (b) full and limited-view measurement geometry, and Laplacian-regularized MF-LSQR (c,e,g), model-back-projection MBP (d,f,h), and traditional back-projection (BP) (i,j,k) reconstructions obtained from 360°, 180° and 120° views, respectively.
The artifacts in the reconstructions can be attributed to the electromagnetic interference in data collection as well as the attenuation and distortion of XA waves due to the finite-shaped lead target. Other possible sources of error include the acoustic reflections due to acoustic mismatch between the target and the background, out-of-plane contribution to the XA signal, as well as inaccuracy in the radius and shape of the ring-array.
V. CONCLUSION
We demonstrated model-based algorithms to perform XACT reconstructions for numerical test cases as well as experimental measurements. The first numerical experiment employed the model-matrix (M) to solve the unregularized as well as Laplacian-regularized least squares problems (Eq. (13)) for low-scale test cases. While both the schemes reconstructed the initial pressure source reasonably well, the unregularized reconstructions were observed to carry noisy artifacts that the Laplacian regularizer was able to ameliorate up to a certain extent. Corresponding back-projection reconstructions carried limited-view and noisy artifacts while also failing to provide quantitative information about the cross-section thus affirming the superiority of the model-based schemes over back-projection.
Construction of the model-matrix can be expensive in terms of computational time and memory, especially for problems associated with a large region of interest, high resolution, and high sampling frequency. To overcome this issue, algorithms for computing matrix-vector products {, } on-the-fly (without storing M) have been developed. These algorithms can be passed as function handles in the MATLAB-based LSQR function to solve Eq. (13) iteratively. This scheme was employed in the second numerical experiment to efficiently compute Laplacian-regularized (MF-LSQR) reconstructions.
For the test cases considered in this paper, the MF-LSQR algorithm produces reasonable reconstructions in ~10–15 LSQR iterations and each LSQR iteration needs one set of {, } computation. In order to further reduce the computational costs, the model-back-projection (MBP) algorithm which produces highly Tikhonov regularized reconstructions, was employed. MBP is a non-iterative scheme and requires a single computation. Therefore, it is computationally much more efficient than the MF-LSQR algorithm. Despite both the MF-LSQR and MBP algorithms being able to reconstruct the structures in the cross-section reasonably well, the MBP reconstructions lacked quantitative accuracy and carried more artifacts as compared to their MF-LSQR counterparts. The MF-LSQR and MBP algorithms were further employed to reconstruct a ‘T’ shaped target (made of lead) embedded in an agar-based phantom from experimental XACT measurements collected by a 128-element ultrasound ring-array and compared with the corresponding BP reconstructions. Both the model-based algorithms produced acceptable reconstructions of the target and were able to significantly reduce the ring artifacts caused by the non-uniformity response of the multichannel data acquisition. The Laplacian regularized MF-LSQR reconstructions carry lesser artifacts than both of the back-projection (MBP and BP) reconstructions.
These results, to the best of our knowledge, are the first model-based XACT reconstructions. While the computationally efficient MBP algorithm can be used to obtain the structural information of the cross-section, MF-LSQR can also be employed in dosimetry-based applications which desire quantitative information of the cross-section.
The results presented in this paper affirm that regularized model-based schemes are advantageous over the conventionally used back-projection algorithms in terms of the quantification accuracy as well as image artifacts. Matrix free implementation of the model-based algorithms potentially enables high resolution and large scale XACT imaging. The algorithms 1 and 2 for computing {, } can be accelerated using GPUs to reduce the reconstruction time.
In comparison to the commonly used back-projection scheme, model-based algorithms not only give the ability to employ regularization to improve the reconstructions but also provide the flexibility to incorporate features such as heterogeneous speed of sound distribution, finite detector shape, etc. which will be addressed in future work. Moreover, the strong acoustic mismatch between bone and soft tissue causes acoustic refraction and reflection at the interface. These corrections also need to be integrated in the model-based algorithms for accurate XACT reconstruction and will be the focus of future studies.
ACKNOWLEDGEMENTS
This work was supported by the National Institute of Health (R37CA240806), American Cancer Society (133697-RSG-19-110-01-CCE). The authors would like to acknowledge the support from UCI Chao Family Comprehensive Cancer Center (P30CA062203).
Biography

Prabodh Kumar Pandey completed his Ph.D. in Physics from Indian Institute of Technology Kanpur, India in 2020 with a focus on photoacoustic and optical tomographic modalities. He joined the School of Computer and Electrical Engineering at University of Oklahoma (OU), Norman, OK, USA, for postdoctoral research and subsequently moved to University of California, Irvine, CA, USA where he is currently working on developing reconstruction algorithms for XACT. He was awarded the Medical Training Research Grant-2021 by the Department of Radiological Sciences, U.C. Irvine. His other research interests include protoacoustic, electro-acoustic and impedance-acoustic tomographic modalities.

Siqi Wang (Member, IEEE) received bachelor’s and master’s degrees in electrical engineering from The University of Oklahoma (OU), Norman, OK, USA, in 2017 and 2019, respectively. He is currently pursuing the Ph.D. degree in biomedical engineering at UC Irvine, Irvine, CA, USA.
During his time at OU, he was a Founding Member of the OU SPIE Student Chapter and served as a Chapter President in the year 2019–2020. Currently, he is working on the development of X-ray-induced acoustic computed tomography systems. Wang’s awards include the SPIE Student Chapter Officer Travel Grant in 2020, the OU Alumni and Foundation Recruitment Fellowship in 2019, and the Mentored Research Fund Award in 2017.

Hari Om Aggrawal received the M.Tech. degree in electrical engineering from the Indian Institute of Technology Kanpur, Kanpur, India, in 2011. He received his Ph.D. degree in 2018 from the Section for Scientific Computing, Department of Applied Mathematics and Computer Science, Technical University of Denmark, Kgs. Lyngby, Denmark. He was a postdoc in the Institute of Mathematics and Image Computing, University of Lübeck, Germany. He is currently working as an independent technical consultant. He is also associated with KITE Medical, Ireland. He received the first best paper award for his work in the Workshop on Biomedical Image Registration (WBIR) 2020. His research interests include image reconstruction in tomographic imaging, image registration, and numerical optimization.

Kristina Bjegovic is a biomedical engineering graduate student working on the application of XACT imaging to real time dosimetry during radiation therapy in Dr. Liangzhong Xiang’s lab at the University of California, Irvine. She received her B.S. in bioengineering from the University of California, San Diego in 2019 and has worked in engineering roles at Siemens Healthineers and Becton Dickinson.

Salime Boucher is the CEO of RadiaBeam Technologies, LLC, a company focused on the development of novel accelerator systems and components for both research and commercial applications. He is an expert in the design, fabrication and application of industrial accelerator systems. He has led or contributed to the development of several accelerator systems and components, including X-band linacs and deflecting cavities, S-band linacs, S-band photoinjector guns, and betatrons. He is also currently developing a robotic radiation therapy system for the recently-developed 4π radiotherapy technique. Mr. Boucher’s previous background includes experience as an engineer with SureBeam Corporation, a manufacturer of linac systems for food irradiation and product sterilization. He also worked for several years at the UCLA Particle Beam Physics Laboratory, where he gained experience in accelerator physics and engineering. Mr. Boucher graduated Magna Cum Laude with a B.S. in Physics from UCLA in 2000 and completed one year of graduate school before deciding to pursue a career in industry.

Liangzhong Xiang (Member, IEEE) is currently a Tenured Associate Professor of radiology and BME. He is also a Core Faculty Member of the Beckman Laser Institute and the Medical Clinic and Chao Family Comprehensive Cancer Center, UC Irvine, USA. His laboratory was the first to report X-ray-induced acoustic computed tomography (XACT), fast proton-induced acoustic imaging (PAI), and electroacoustic tomography (EAT). Dr. Xiang received the NIH MERIT Award (R37) and the Research Scholar Award from the American Cancer Society. He also received the Nancy L. Mergler Faculty Mentor Award in 2017 and the OU Presidential Professorship in 2020. He has served as the Conference Chairs in the AAPM Annual Meetings and the International Conference on Information Optics and Photonics, the SPIE Student Chapter Advisor, an Associate Editor for Medical Physics journal, and a Grant Reviewer for the NIH, DOE, Russian Science Foundation, Helmholtz Association of German Research Centre, and ETH Zurich.
Contributor Information
Prabodh Kumar Pandey, Department of Radiological Sciences, University of California, Irvine, CA, 92697, USA.
Siqi Wang, Department of Biomedical Engineering, University of California, Irvine, CA 92617, USA.
Hari Om Aggrawal, Institute of Mathematics and Image Computing, University of Lübeck, Germany and currently is a freelance technical consultant.
Kristina Bjegovic, Department of Biomedical Engineering, University of California, Irvine, CA 92617, USA.
Salime Boucher, RadiaBeam Technologies, 1717 Stewart St, Santa Monica, CA 90404.
Liangzhong Xiang, Department of Radiological Sciences, University of California, Irvine, CA, 92697, USA; Department of Biomedical Engineering, University of California, Irvine, CA 92617, USA; Beckman Laser Institute, University of California, Irvine, Irvine, CA 92612, USA.
REFERENCES
- [1].Boone JM et al. , “Computed tomography for imaging the breast.” J. of Mammary Gland Biology and Neoplasia, vol. 11, no. 2, pp. 103–111, April. 2006. [DOI] [PubMed] [Google Scholar]
- [2].Momose A, Takeda T, Itai Y, and Hirano K, “Phase–contrast X–ray computed tomography for observing biological soft tissues.” Nature Medicine, vol. 2, no. 4, pp. 473–475, April. 1996. [DOI] [PubMed] [Google Scholar]
- [3].Kalender WA, “X-ray computed tomography”. Phys. Med. Bio, vol. 51, no. 13, R29, June 2006. [DOI] [PubMed] [Google Scholar]
- [4].Brady LW and Perez CA, Perez & Brady’s principles and practice of radiation oncology, Lippincott Williams & Wilkins, May2013. [Google Scholar]
- [5].Podgorsak EB, & Kainz K, “Radiation oncology physics: A handbook for teachers and students.” International Atomic Energy Agency, Vienna, Austria, May 2003. [Google Scholar]
- [6].Dracham CB, Shankar A and Madan R, “Radiation induced secondary malignancies: a review article.” Radiation Oncology Journal, vol. 36, no. 2, pp. 85–94, June 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Xiang L et al. , “X-ray acoustic computed tomography with pulsed x-ray beam from a medical linear accelerator,” Med. Phys, vol. 40, no. 1, January. 2013, Art. no. 010701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Robertson E and Xiang L, “Theranostics with radiation-induced ultrasound emission (TRUE).” J. of Innovative Opt. Health Sci, vol. 11, no. 3, May 2018, Art. no. 1830002. [Google Scholar]
- [9].Samant P, Trevisi L, Ji X, and Xiang L, “X-ray induced acoustic computed tomography. “ Photoacoustics, 100177 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Wang S, “Radiation-Induced Acoustic Imaging System Development and Applications” Master Thesis, Sch. of Computer and Electrical Engg., University of Oklahoma, 2019. [Google Scholar]
- [11].Attix FH, Introduction to radiological physics and radiation dosimetry, Strauss GmbH, Morlenbach, Germany, John Wiley & Sons, September. 2008. [Google Scholar]
- [12].Cadarette S et al. “Development and validation of the osteoporosis risk assessment instrument to facilitate selection of women for bone densitometry,” Cmaj, vol. 162, no. 9, pp. 1289–1294, May 2000. [PMC free article] [PubMed] [Google Scholar]
- [13].Kim KY, and Sachse W, “X-ray generated ultrasound,” Appl. Phys. Lett, vol. 43, no. 12, pp. 1099–1101, December. 1983. [Google Scholar]
- [14].Bowen T et al. , “Observation of ultrasonic emission from edges of therapeutic x-ray beams,” Phys. Med. Biol, vol. 36, no. 4, pp. 537–539, April. 1991. [DOI] [PubMed] [Google Scholar]
- [15].Andreo P, “Monte Carlo techniques in medical radiation physics,” Phys. Med. Biol, vol. 36, no. 7, 861, July. 1991. [DOI] [PubMed] [Google Scholar]
- [16].Treeby BE and Cox BT, “k-Wave: MATLAB toolbox for the simulation and reconstruction of photoacoustic wave fields,” J. Biomed. Opt, vol. 15, no. 2, March 2010, Art. no. 021314. [DOI] [PubMed] [Google Scholar]
- [17].Hickling S, Léger P and Naqa IE, “Simulation and experimental detection of radiation-induced acoustic waves from a radiotherapy linear accelerator,” in 2014 IEEE International Ultrasonics Symposium, pp. 29–32. IEEE, September. 2014. [Google Scholar]
- [18].Hickling S, Hobson M, and Naqa IE., “Feasibility of x-ray acoustic computed tomography as a tool for noninvasive volumetric in vivo dosimetry.” Int. J. of Radiation Oncology Biology Physics, vol. 90, no. 1, September. 2014, Art. no. S843. [Google Scholar]
- [19].Hickling S, Léger P, and Naqa IE, “On the detectability of acoustic waves induced following irradiation by a radiotherapy linear accelerator.” IEEE Trans. Ultra. Ferro. Freq. Cont, vol. 63, no. 5, pp. 683–690, February. 2016. [DOI] [PubMed] [Google Scholar]
- [20].Xiang L, Tang S, Ahmad M, and Xing L, “High resolution x-ray-induced acoustic tomography,” Scientific Reports, vol. 6, May 2016, Art. no. 26118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Tang S et al. , “X-ray-induced acoustic computed tomography with an ultrasound transducer ring-array.” Appl. Phys. Lett, vol. 110, no. 10, pp. 103504, March. 2017. [Google Scholar]
- [22].Hickling S et al. , “Experimental evaluation of x-ray acoustic computed tomography for radiotherapy dosimetry applications,” Med. Phys, vol. 44, no. 2, pp. 608–617, February. 2017. [DOI] [PubMed] [Google Scholar]
- [23].Hickling S, Hobson M, and Naqa IE, “Characterization of x-ray acoustic computed tomography for applications in radiotherapy dosimetry,” IEEE Trans. Rad. Plas. Med. Sci, vol. 2, no. 4, pp. 337–344, February. 2018. [Google Scholar]
- [24].Kim J et al. ,”X-ray acoustic-based dosimetry using a focused ultrasound transducer and a medical linear accelerator.” IEEE Trans. Rad. Plas. Med. Sci, vol. 1, no. 6, pp. 534–540, September. 2017. [Google Scholar]
- [25].Lei H et al. , “Toward in vivo dosimetry in external beam radiotherapy using x-ray acoustic computed tomography: A soft-tissue phantom study validation,” Med. Phys, vol. 45, no. 9, pp. 4191–4200, September. 2018. [DOI] [PubMed] [Google Scholar]
- [26].Kim CH et al. , “ Water dosimetry device using x-ray induced ultrasonic waves,” U.S. Patent Application No. 16/488,236, December. 19, 2019.
- [27].Forghani F et al. , “ Simulation of x-ray-induced acoustic imaging for absolute dosimetry: Accuracy of image reconstruction methods,” Med. Phys, vol. 47, no. 3, pp. 1280–1290, December. 2019. [DOI] [PubMed] [Google Scholar]
- [28].Zheng Y et al. , “ X-ray-induced acoustic computed tomography for guiding prone stereotactic partial breast irradiation: a simulation study,” Med. Phys, vol. 47, no. 9, pp. 4386–4395, May 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Obayomi-Davies O et al. , “ Stereotactic accelerated partial breast irradiation for early-stage breast cancer: rationale, feasibility, and early experience using the cyberknife radiosurgery delivery platform,” Frontiers in Oncology, vol. 6, no. 129, May 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Wang M et al. , “Towards in vivo Dosimetry for Prostate Radiotherapy with a Transperineal Ultrasound Array: A Simulation Study,” IEEE Trans. Rad. Plas. Med. Sci, vol. 5, no. 3, pp. 373–382, May 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Tang S, Yang K, Chen Y, and Xiang L, “X-ray-induced acoustic computed tomography for 3d breast imaging: A simulation study,” Med. Phys, vol. 45, no. 4, pp. 1662–1672, April. 2018. [DOI] [PubMed] [Google Scholar]
- [32].Choi S et al. , “3D X-ray induced acoustic computed tomography: a phantom study.” in Photons Plus Ultrasound: Imaging and Sensing 2020, vol. 11240, pp. 112404R. International Society for Optics and Photonics, February. 2020. [Google Scholar]
- [33].Lee D et al. , “ GPU-accelerated 3D volumetric X-ray-induced acoustic computed tomography.” Biomed. Opt. Exp, vol. 11, no. 2, pp. 752–761, February. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Li Y et al. , “3-D X-Ray-Induced Acoustic Computed Tomography With a Spherical Array: A Simulation Study on Bone Imaging.” IEEE Trans. Ultra. Ferro. Freq. Cont, vol. 67, no. 8, pp. 1613–1619, April. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Robertson E et al. , “X-ray-Induced Acoustic Computed Tomography (XACT): Initial Experiment on Bone Sample.” IEEE Trans. Ultra. Ferro. Freq. Cont, vol 68, no. 4, pp. 1073–1080 October. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Choi S et al. , “Synchrotron X-ray induced acoustic imaging.” Sci. Rep, vol 11, no. 1, pp. 1–7 February. 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Zhang W et al. ,” Real-time monitoring the alignment of x-ray beam relative to treatment target during radiation treatment based on ultrasound and x-ray acoustic dual-modality imaging.” in Photons Plus Ultrasound: Imaging and Sensing 2018, vol. 10494, pp. 104940E. International Society for Optics and Photonics, March. 2018. [Google Scholar]
- [38].Zhang W et al. , “Dual-Modality X-Ray-Induced Radiation Acoustic and Ultrasound Imaging for Real-Time Monitoring of Radiotherapy.” BME Frontiers, vol. 2020, May 2020, Art. no. 9853609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Oraiqat I et al. , “An ionizing radiation acoustic imaging (iRAI) technique for realtime dosimetric measurements for FLASH radiotherapy.” Med. Phys vol. 47, no. 10, pp. 5090–5101, October. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Xu M and Wang LV, “Universal back-projection algorithm for photoacoustic computed tomography,” Phys. Rev. E, vol. 71, no. 1, January. 2005, Art. No. 016706. [DOI] [PubMed] [Google Scholar]
- [41].Buehler A et al. , “Model-based optoacoustic inversions with incomplete projection data,” Med. Phys vol. 38, no, 3, pp. 1694–1704, March. 2011. [DOI] [PubMed] [Google Scholar]
- [42].Ding L, Razansky D, and Dean-Ben XL, “Model-based reconstruction of large three-dimensional optoacoustic datasets,” IEEE Trans. Med. Imag. vol. 29, no. 9, pp. 2931–2940, March. 2020. [DOI] [PubMed] [Google Scholar]
- [43].Dean-Ben XL, Ntziachristos V and Razansky D, “Acceleration of optoacoustic model-based reconstruction using angular image discretization,” IEEE Trans. Med. Imag. vol. 31, no. 5, pp. 1154–1162, February. 2012. [DOI] [PubMed] [Google Scholar]
- [44].Rosenthal A, Jetzfellner T, Razansky D, and Ntziachristos V, “Efficient framework for model-based tomographic image reconstruction using wavelet packets,” IEEE Trans. Med. Imag. vol. 31, no. 7, pp. 1346–1357, February. 2012. [DOI] [PubMed] [Google Scholar]
- [45].Lutzweiler C, Dean-Ben XL and Razansky D, “Expediting model-based optoacoustic reconstructions with tomographic symmetries,” Med. Phys vol. 41, no. 1, January. 2014, Art. no. 013302. [DOI] [PubMed] [Google Scholar]
- [46].Ding L et al. , “Efficient non-negative constrained model-based inversion in optoacoustic tomography,” Phys. Med. Biol, vol. 60, no. 17, pp. 6733–6750, August. 2015. [DOI] [PubMed] [Google Scholar]
- [47].Han Y et al. , “Sparsity-based acoustic inversion in cross-sectional multiscale optoacoustic imaging,” Med. Phys vol. 42, no. 9, pp. 5444–5452, September. 2015. [DOI] [PubMed] [Google Scholar]
- [48].Ding L et al. , “Image reconstruction in cross-sectional optoacoustic tomography based on non-negative constrained model-based inversion,” in Proc. European Conference on Biomedical Optics, Optical Society of America, 2015, Art. no. 953919. [Google Scholar]
- [49].Ding L, Dean-Ben XL and Razansky D, “Real-time model-based inversion in cross-sectional optoacoustic tomography,” IEEE Trans. Med. Imag. vol. 35, no. 8, pp. 1883–1891, March. 2016. [DOI] [PubMed] [Google Scholar]
- [50].Lutzweiler C, “High-throughput sparsitybased inversion scheme for optoacoustic tomography,” IEEE Trans. Med. Imag. vol. 35, no. 2, pp. 674–684, October. 2015. [DOI] [PubMed] [Google Scholar]
- [51].Dean-Ben XL, Mercep E and Razansky D, “Hybrid-array-based optoacoustic and ultrasound (opus) imaging of biological tissues,” Appl. Phys. Lett. vol. 110, no. 20, May 2017, Art. no. 203703. [Google Scholar]
- [52].Dean-Ben XL, Ding L and Razansky D, “Dynamic particle enhancement in limited-view optoacoustic tomography,” Opt. Lett, vol. 42, no. 4, pp. 827–830, February. 2017. [DOI] [PubMed] [Google Scholar]
- [53].Biton S et al. , “Optoacoustic model-based inversion using anisotropic adaptive total-variation regularization,” Photoacoustics, vol. 16, December. 2019, Art. no. 100142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Yang H et al. , “Soft ultrasound priors in optoacoustic reconstruction: Improving clinical vascular imaging,” Photoacoustics, vol 19, March. 2020, Art. no. 100172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Jin JM, The finite element method in electromagnetics, Hoboken, NJ, USA, John Wiley & Sons, 2015. [Google Scholar]
- [56].Klose A, “Optical tomography based on the equation of radiative transfer,” PhD thesis, Dept. of Phys., Freie Universitat Berlin, Germany, 2002. [Google Scholar]
- [57].Dean-Ben XL and Razansky D, “On the link between the speckle free nature of optoacoustics and visibility of structures in limited-view tomography,” Photoacoustics, vol 4, no. 4, pp. 133–140, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Eldib M, Wang S and Xiang L,” Ring artifact and non-uniformity correction method for improving XACT imaging.” in SPIE: Medical Imaging 2021: Physics of Medical Imaging vol. 11595, pp. 1159552. International Society for Optics and Photonics, February. 2021. [Google Scholar]