Higher-order effects, continuous species interactions, and trait evolution shape microbial spatial dynamics

Significance

Persistently diverse microbial communities are one of biology’s great puzzles. Using a modeling framework that accommodates high mutation rates and a continuum of species traits, we studied microbial communities in which antagonistic interactions occur via the production of, inhibition of, and vulnerability to toxins (e.g., antibiotics). Mutation size and mobility enhanced microbial diversity and temporal persistence to extraordinarily high levels. These findings—including the discovery that the duration of the transient phase in community assembly provides a guide to equilibrial diversity—highlight the potentially critical role that antagonistic interactions play in promoting the diversity of bacterial systems. Such interactions, together with resource-driven interactions and spatial structure, may drive the enigmatic levels of biodiversity seen in microbial systems.

Abstract

The assembly and maintenance of microbial diversity in natural communities, despite the abundance of toxin-based antagonistic interactions, presents major challenges for biological understanding. A common framework for investigating such antagonistic interactions involves cyclic dominance games with pairwise interactions. The incorporation of higher-order interactions in such models permits increased levels of microbial diversity, especially in communities in which antibiotic-producing, sensitive, and resistant strains coexist. However, most such models involve a small number of discrete species, assume a notion of pure cyclic dominance, and focus on low mutation rate regimes, none of which well represent the highly interlinked, quickly evolving, and continuous nature of microbial phenotypic space. Here, we present an alternative vision of spatial dynamics for microbial communities based on antagonistic interactions—one in which a large number of species interact in continuous phenotypic space, are capable of rapid mutation, and engage in both direct and higher-order interactions mediated by production of and resistance to antibiotics. Focusing on toxin production, vulnerability, and inhibition among species, we observe highly divergent patterns of diversity and spatial community dynamics. We find that species interaction constraints (rather than mobility) best predict spatiotemporal disturbance regimes, whereas community formation time, mobility, and mutation size best explain patterns of diversity. We also report an intriguing relationship among community formation time, spatial disturbance regimes, and diversity dynamics. This relationship, which suggests that both higher-order interactions and rapid evolution are critical for the origin and maintenance of microbial diversity, has broad-ranging links to the maintenance of diversity in other systems.

Understanding the origin and maintenance of species diversity is a long-standing biological question, and understanding diversity through the lens of species interactions has been deemed key (1–5). Natural communities possess high species diversity, often much higher than expected from a “simple” Darwinian interpretation of species interactions (6). Extraordinary levels of diversity exist in several macroscopic systems (e.g., coral reefs and tropical forests), but remarkable levels of diversity also exist in microscopic systems among microbial communities. High levels of diversity in microbial systems are especially intriguing given the ubiquity of antagonistic interactions among microbes, such as the production of antibiotics/toxins against one another (7–11).

Theoretical and empirical studies have explored microbial interactions with the goal of understanding the mechanisms of species coexistence in hyper-diverse microbial systems. Major examples include models with 1) mutualistic and cross-feeding interactions (12), 2) resource-based competitive interactions (13), 3) a combination of mutualistic and competitive interactions (13–16), 4) stochastic spatiotemporal processes (17, 18), and 5) antagonistic interactions because of toxin production (6, 19, 20).

Previous studies focusing on the mutualistic, cross-feeding, and resource-based competitive interactions (points 1 to 3 above) have demonstrated that positive interactions arising from resource exchange can affect key criteria governing the relationship between community diversity and stability. Examples of such criteria are that species richness is inversely related to the strength of random pairwise interactions in stable communities (2), and communities constructed with random pairwise interactions feature an upper bound on diversity (21–23). Additional key findings from the resource-based framework are that cooperative (metabolic) interactions can arise spontaneously in complex microbial communities (24) and that a cooperative versus competitive dichotomy of microbial communities may exist, depending on conditions (25). Sometimes, the interactions arising from resource exchange allow systems to bypass classic stability–diversity relationships (13, 14). Collectively, these results have tremendously improved our understanding of the factors influencing the development and persistence of microbial community diversity. However, resource-based perspectives fail to account for a major class of well-known antagonistic interactions that exist among microbes, mediated through bacterial toxins or antibiotics (also termed as bacteriocins and related compounds). Toxin-based interactions are ubiquitous in both natural microbial communities and controlled settings (7–10), are found in all known phyla of bacteria, come in diverse forms, and play a central yet usually underappreciated role in shaping microbial community structure (11).

Here, we focus on modeling microbial communities structured by antagonistic interactions among antibiotic/toxin-producing, sensitive, and resistant species. Prior research in this area has relied on the framework of cyclic dominance (also termed nontransitive systems or rock-paper-scissors systems) and related techniques in evolutionary game theory (7, 19, 20, 26–28). Early models using cyclic dominance explored community stabilization, increased coexistence, and maintenance of diversity in spatially structured environments (19, 26, 29, 30). However, because these models focused on pairwise interactions, they generally did not account for other kinds of interactions that occur when intermixed species coexist at very small spatial scales (6, 9, 10, 31–33). For example, real microbial species are routinely involved in multispecies interaction systems including so-called “higher-order interactions” in which the interactions between two species can be modulated by other species (34, 35). One simple example of such a behavior occurs when an antibiotic produced by one species that inhibits the growth of a competing (sensitive) species can be attenuated by a third species that can degrade the antibiotic (20, 36, 37). Here, the third species modulates the interaction between the antibiotic-producing and antibiotic-sensitive species without impacting either of them directly (34), thus creating a higher-order interaction.

Models using cyclic dominance with higher-order interactions for a small number of static (i.e., nonevolving) species have demonstrated increased stability and diversity in both spatially structured and well-mixed communities (6, 19, 20, 26, 29, 38), and findings from such models have been verified empirically (20). In contrast, horizontal gene transfer and mutation blur the boundaries among microbial strains and species, reflecting the continuous nature of phenotypes in microbial assemblages. Scaling up analytic models of cyclic dominance to species-rich scenarios is not possible because the incorporation of more than a few discrete species makes the dynamics extremely complex and hard to interpret using equation-based approaches (20).

Despite its prominence in modeling studies, pure cyclic dominance, in which there is a “closed” loop of dominance, is rare in nature (39–42). In contrast, rapid evolution routinely leads to model systems featuring semicyclic or noncyclic patterns in which higher-order interactions, such as those involving antibiotic-producing, sensitive, and resistant species, are common (35, 40). Therefore, the notion of pure cyclic dominance used in earlier studies of antagonistic microbial dynamics needs to be supplemented with evolving, “mixed” patterns of dominance in order to better model microbial community interactions.

Prior studies of community-level eco-evolutionary dynamics, which have explored the evolution of species interactions abstractly or the specific traits that determine such interactions (43–45), focused on niche-based food web models (i.e., those involving resource consumption) rather than the nonresource-based antagonistic interactions that characterize our work. Even when studies did investigate antagonistic interactions and resultant species dynamics, they emphasized very slow mutation regimes and assumed a separation of ecological and evolutionary timescales (46–48). Such assumptions do not work very well for microbial systems in which high mutation rates and extensive horizontal gene transfers are commonplace, creating an overlap of ecological and evolutionary timescales (47–50). These eco-evolutionary feedbacks can affect the nature of trait evolution (48) and even destabilize species interactions (51). Recent models exploring these fast-evolving regimes in antibiotic-mediated antagonistic communities have uncovered mechanisms responsible for de novo assembly of diverse microbial communities with higher-order interactions, but such results are qualitatively different from what is possible when mutation is rare (38, 47). What is needed, then, are studies of community assembly in models in which a large number of species interact in continuous phenotypic space, are capable of rapid mutation, and engage in both direct and higher-order interactions.

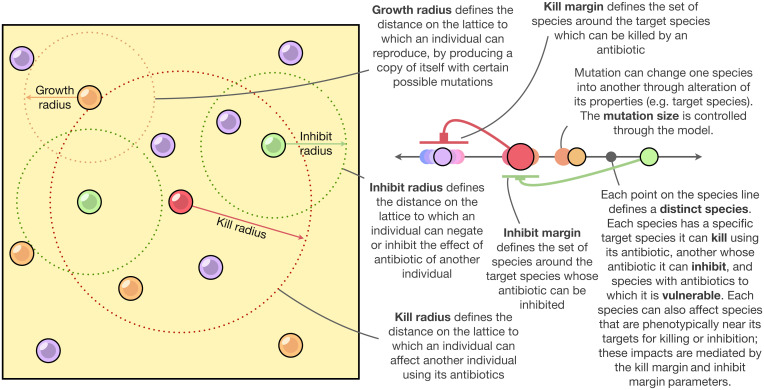
Here, we integrate three major themes concerning the dynamics of microbial communities structured by antagonistic interactions, specifically higher-order interactions, a continuous view of microbial trait space, and an eco-evolutionary perspective on community assembly wherein evolution can happen rapidly. This integrated perspective allows us to explore mixed, rather than strict, patterns of dominance among a large number of biologically realistic species (hundreds to thousands; constrained only by computational power) to study microbial communities of toxin/antibiotic-producing, sensitive, and resistant species. Within an agent-based modeling framework, we use a continuous species parametrization model with a wide range of mutational sizes to explore spatiotemporal community assembly, diversity, and stability (Fig. 1 and SI Appendix, Supplemental Methods). Parameters are defined at a global level and are divided into two categories: spatial (which define rules and properties of spatial interactions) and species level (which define the toxin interactions in the species space). The continuous (phenotypic) species space generalizes intraspecies relationships of toxin production, vulnerability, and resistance that arise randomly in populations through mutation and interspecies relationships.

Fig. 1.

A conceptual representation of the model with descriptions of all the parameters involved. See SI Appendix, Supplemental Methods for details about implementation.

We find that species-level properties, such as constraints on higher-order interactions among species, affect the spatial structure of microbial dynamics more than spatial factors like mobility and the effective distance over which individuals kill or inhibit each other. In contrast, nonspatial metrics of community diversity reflect complex interactions among species-level and spatial parameters, especially mobility and mutation size, plus community formation time (the time it takes to form a stable community; see ref. 38). Our attention to community formation time, which provides an opportunity for characterizing transient dynamics rather than just focusing on stable states or the long-term maintenance of diversity (15, 39, 47), is intentional. It turns out that community formation time is a very good predictor of diversity dynamics, but, this time, duration cannot be estimated well from other parameters, pointing to emergent complex properties of community assembly.

Results

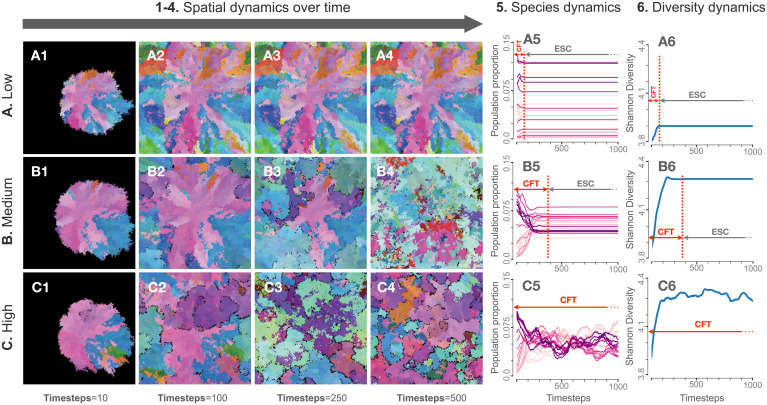
After running 10.49 million simulations across a broad range of parameter combinations, we observed strong differences in spatial heterogeneity among runs. We classified this behavior into three major categories depending only on the observed level of spatial disturbance (low, medium, and high disturbance; Fig. 2 and SI Appendix, Supplemental Methods). These three categories featured both between- and within-category differences in community spatiotemporal dynamics but exhibited similar disturbance regimes within categories (Fig. 2). The continuous trait axis and the mutable nature of traits together allow for the simulation and visualization of hyper-diverse communities, contrasting with the small, fixed number of discrete, immutable species in previous works (6, 20, 27).

Fig. 2.

System dynamics in three example conditions of initial conditions pertaining to different regimes of spatial disturbance behavior (Low, Medium, and High) (A–C). Snapshots of each simulation at different timesteps (10, 100, 250, and 500) are shown in columns 1 through 4. The respective species dynamics (in which different colors represent different species “bins,” SI Appendix, Supplemental Methods) and diversity dynamics are represented in columns 5 and 6, respectively. In columns 5 and 6, the time taken for the simulation to stabilize (i.e., the CFT) is denoted with a vertical red dotted line. The community existing after the system has reached the CFT is termed an eco-evolutionary stable community.

The time that each simulation took to stabilize (i.e., to form a stable community) is termed the community formation time (CFT; SI Appendix, Supplemental Methods and ref. 38), and the community that thus assembled is called an eco-evolutionary stable community. The incorporation of mutations allows for an exploration of community assembly, transient dynamics (such as CFT and its relation to community properties over time), and complex spatial patterns that were not possible using previous frameworks (Fig. 2) (20, 38).

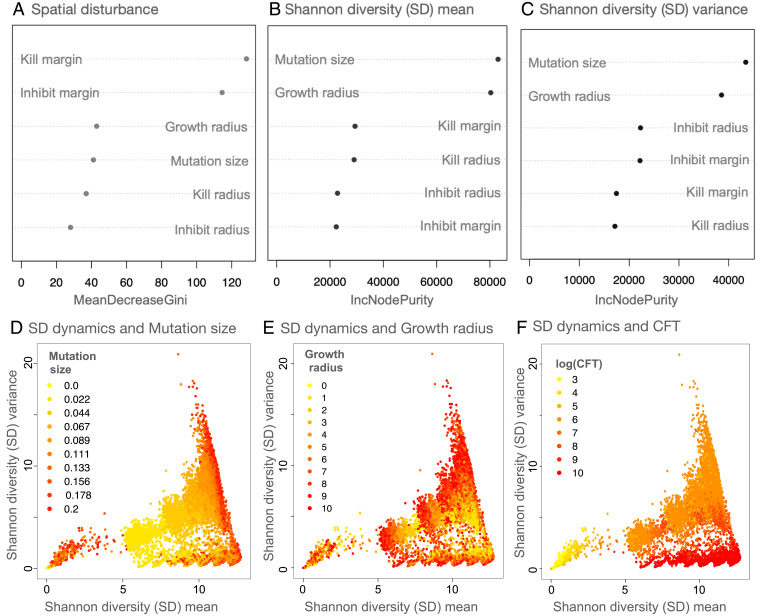
To understand how parameters relate to the spatial disturbance categories, we performed a random forest (RF) classification using the six model parameters (kill radius, inhibit radius, growth radius, kill margin, inhibit margin, and mutation size). The model had an out-of-bag error (OOB) of 10.2% and identified the kill margin and the inhibit margin as the best predictors of the disturbance classification (Fig. 3A). Note that the kill margin and the inhibit margin are global species-specific parameters.

Fig. 3.

Dependence of model dynamics on different parameters and CFT. A shows the variable importance score for all the parameters from an RF classification (with 10,000 trees) on the three categories of spatial disturbance (OOB = 10.2%). B and C denote the variable importance scores from RF regression models (with 10,000 trees) for SD mean and variance, respectively. D, E, and F show the SD mean–variance plots overlaid with mutation size, growth radius, and CFT values of the respective simulations. For A–C, IncNodePurity (used in regression RFs) and MeanDecreaseGini (used in classification RFs) refer to how well a parameter explains the prediction variable in question.

The next most important parameter was the growth radius, which is a proxy for mobility in our model (Fig. 1), followed by mutation size, kill radius, and inhibit radius. These findings showed that, except for the growth radius, other spatial parameters played a minor role in determining the structure of spatial disturbance in the model systems.

To assess nonspatial metrics of community assembly, we performed an RF regression on the Shannon diversity (SD) mean (i.e., mean SD for the period from timestep = 0 to the CFT) and the associated SD variance using the same six simulation parameters (and an associated species bin size of 0.05 for discretizing species; for more details on species binning, see SI Appendix, Supplemental Methods). That RF model explained 68.4% of the variance for the SD mean and 70.2% for the SD variance. Mutation size and growth radius were the two best predictors of both outcome variables (Fig. 3 B and C). Among the less important parameters that affect SD mean and variance, we note that the kill margin and the kill radius play a larger role in determining SD mean, whereas inhibition processes better predict SD variance (Fig. 3 B and C and SI Appendix, Fig. S1).

From a naïve interpretation, one would expect mutation size to be a good predictor of increasing diversity, as a higher mutation size allows for the possibility of greater variation in microbial phenotypic space, and, therefore, the binned SD would be expected to be higher. However, after overlaying the plot of SD mean versus variance with the respective mutation size values, the picture is largely muddled (Fig. 3D). We saw even more mixed results after overlaying the growth radius values on the SD mean–variance plot (Fig. 3E). Overlaying other less important model parameters on the SD mean–variance plot showed no straightforward pattern at all (SI Appendix, Fig. S2).

Interestingly, upon overlaying the SD mean–variance plot with the values of the respective CFTs, a stronger pattern emerged. Note the clustering by color gradient of the points because of CFT in SD mean–variance space (Fig. 3F). Although CFT is not a parameter, it is an emergent outcome of the community assembly process, and exploring it further provided insights into the diversity formation process itself.

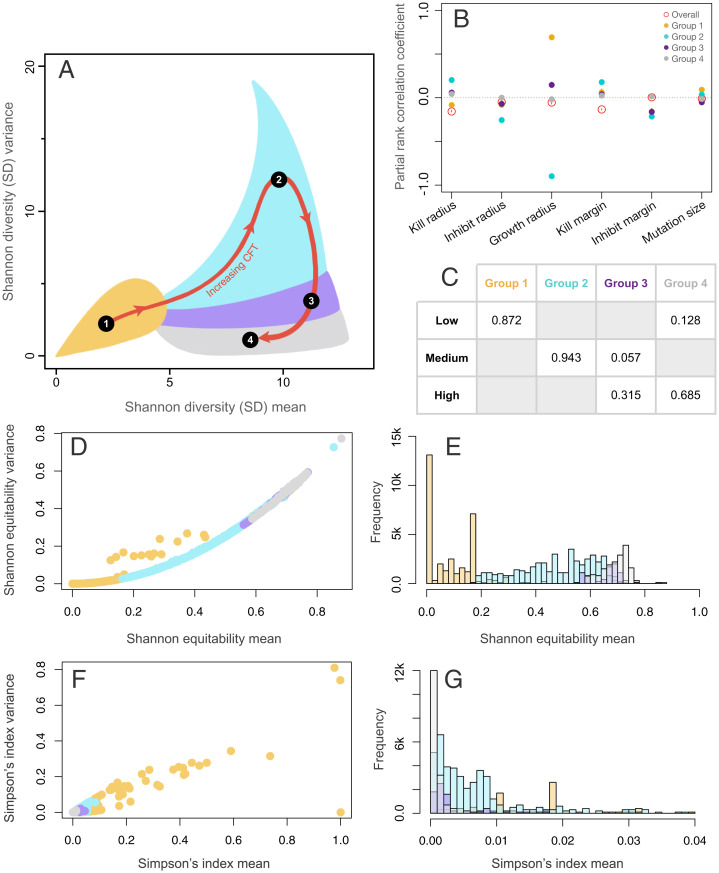
To formally detect clusters in the SD mean–variance plot with respect to CFT, we used k-means clustering optimized for the number of clusters using multiple methods (SI Appendix, Supplemental Methods) and identified four clusters (Fig. 4A and SI Appendix, Fig. S3). These clusters pertain to 1) low SD mean and SD variance, 2) high SD mean and SD variance, 3) high SD mean and medium SD variance, and 4) high SD mean and low SD variance in order of increasing values of CFT.

Fig. 4.

Effects of CFT on the spatial diversity dynamics. A depicts the four optimal clusters (groups) of SD mean–variance space found using k-means clustering (SI Appendix, Fig. S3). B shows the results from the PRCC analyses of the four groups and the overall data. C shows the proportion of spatial disturbance regimes present in different groups. D and F show the distribution of the values of mean and variance of Shannon equitability and Simpson’s index, respectively, for a smaller subsample of the runs with points colored by groups from A. E depicts the group-wise histogram of Shannon equitability, and G depicts the histogram of Simpson’s index (for clarity, only the range between 0 and 0.04 is shown).

On performing RF regression predicting CFT using the six parameters for the whole dataset, we found a low explanation of variance (22.3%), with the kill parameters (kill radius and kill margin) being the strongest predictors. However, upon performing the analysis separately on the four CFT groups, a stronger pattern emerged (SI Appendix, Fig. S4). For group 1, the regression explained 30.2% of the variance with the growth radius being the strongest predictor and other variables playing a smaller part, but, nevertheless, the second and third best predictors are the kill parameters (SI Appendix, Fig. S3A). Group 2 regression explained 90.6% of the variance with the growth radius as the strongest predictor again with other parameters making almost no contributions (SI Appendix, Fig. S4B). For groups 3 and 4, the regression explains 27.2 and 6.0% of the variance, respectively, with the growth radius again having most impact on prediction (SI Appendix, Fig. S4 C and D). This pattern of results is unusual because the overall regression did not show any strong dependence on growth radius (SI Appendix, Fig. S4E).

To explore this dilemma further, we performed a partial rank correlation coefficient (PRCC) analysis on this data pertaining to CFT (Fig. 4B). We found that the sign and strength of the dependence of growth radius for CFT groups vary widely; hence, the RF regression on the whole dataset misses this signal. The growth radius had a strong positive PRCC with CFT in group 1, a very strong negative PRCC with CFT in group 2, a weakly positive PRCC in group 3, and a negligible one in group 4. Other parameters had relatively smaller PRCC values as compared to the growth radius values for groups 1 and 2. The kill radius and kill margin had overall higher PRCC values than the other parameters and thus were identified by the RF algorithm (Fig. 4B and SI Appendix, Fig. S4E). Moreover, on calculating the PRCC of parameters on SD mean and SD variance, we found that the general values are similar for both SD metrics, but what differentiates SD mean and SD variance values the most is the growth radius (SI Appendix, Fig. S1).

To link the dependence of diversity dynamics on CFT with the spatial disturbance regimes, we compared what proportion of the three spatial disturbance regimes (low, medium, and high) fall into the four CFT-classified groups from SD mean–variance space (Fig. 4C). We found that the low disturbance regime was most associated with group 1 and, to a much lesser extent, group 4. The medium disturbance regime was primarily dominated by group 2, with a small contribution from group 3. Lastly, the high disturbance regime was dominated by groups 3 and 4. These results can be interpreted in the light of the Shannon equitability and Simpson’s index values for the simulations (Fig. 4 D–G). Transitioning from groups 1 through 4 reveals an increase in mean Shannon’s equitability (Fig. 4 D and E) and a decrease in mean Simpson’s index (Fig. 4 F and G). One interpretation here is that higher equitability among species (i.e., higher values of Shannon equitability), which can occur when comparatively few species dominate the community (i.e., lower Simpson’s index), results in simulations that take longer to equilibrate (i.e., longer CFTs). For example, communities in group 4 take longer to equilibrate (longer CFTs) because the species in those communities are more nearly equitable with comparatively fewer species whose interactions exercise control over the community. In contrast, group 1 has low equitability, implying a higher level of community dominance by some players, and, therefore, those simulations settle down quickly (low CFTs). Collectively, these results highlight some important connections between temporal spatial patterns and diversity dynamics, especially through the lens of transient phenomena (52, 53).

All the results in this section were performed using a species bin size (for the discretization of species for diversity metrics; SI Appendix, Supplemental Methods) of 0.05, but we repeat the analyses at three other reasonable bin sizes (0.03, 0.07, and 0.09; SI Appendix, Supplemental Methods) and find almost no changes in the structure of the results and their interpretations (SI Appendix, Fig. S5) in any of the cases. The space of SD mean and variance shrinks in scale (SI Appendix, Fig. S5C) as the bin sizes increase, which is expected because increasing bin sizes results in fewer distinct species for analysis. However, the categorization of spatial disturbance remains unaltered because binning does not affect the actual dynamics of the model but only how we quantify those dynamics through discretization. Therefore, the dependence of CFT on parameters remained unaltered (SI Appendix, Fig. S5D). The categorization of SD mean and variance into groups, their relation to spatial disturbance regimes, and their dependence on parameters also varied little (SI Appendix, Fig. S5 A, B, and E).

Discussion

A continuous species model with simple rules for interactions based on antibiotic production, inhibition, and vulnerability can produce a wide array of complex dynamics and generate hyper-diverse, persistent communities. Despite enormous heterogeneity in behavior, certain general patterns in the assembly and stability of these hypothetical microbial communities stand out.

The diversity patterns seen across time were expressed in the form of mean SD and its associated variance. The phase space of these two metrics shows a nonlinear relationship between the metrics. RF regressions revealed that the mutation size and the growth radius were the best predictors of mean SD diversity and its variance (Fig. 3 B and C). In other words, the mutation size and mobility of species jointly determine how diversity dynamics play out in these theoretical communities.

Mobility controls diversity dynamics in numerous previous studies (6, 20, 27, 28). In particular, small amounts of mobility enhance diversity, whereas large amounts of mobility jeopardize it (6, 28). Reduced mobility results in spatially structured populations in which coexistence is easier to maintain as seen in experimental works on competing Escherichia coli strains (26, 54, 55). Recent work has shown that even in cases of high mobility (i.e., well-mixed communities), one can observe coexistence if higher-order interactions such as antibiotic production and degradation are considered (20). This is the case for in vivo experiments with bacterial colonies in the intestines of cocaged mice; these systems can be considered locally well mixed and have high levels of coexistence (30).

High mutation rates, and processes such as horizontal gene transfer (HGT), have been long known to affect diversity in experimental microbial populations, especially during the initial phase of community assembly (56, 57). However, cyclic dominance models have tended to overlook the role of mutations and HGT in coexistence. Such studies have focused instead on the detailed understanding of a small number of discrete species under a low mutation regime (47). Recently, studies have focused on understanding the effects of high mutational regimes in community assembly, which better represent microbial systems (38) and can generate frequent noncyclic interactions (40). Our efforts have considered an array of mutational regimes and characterized the importance of noncyclic patterns of interactions in the assembly and maintenance of microbial communities.

Mutation size and the growth radius (a proxy for mobility) were good predictors of SD mean and SD variance but yielded no discernable patterns in the phase space (Fig. 3 D and E). In contrast, CFT partitioned the space cleanly into four regions with distinct properties (Figs. 3F and 4A). Communities that have low diversity (SD mean) and small fluctuations in diversity (i.e., low SD variance) (group 1) assemble quickly, and mobility enhances diversity and coexistence in this scenario (Fig. 4 A and B). In contrast, mobility negatively affects diversity and coexistence for communities with high diversity (SD mean) and larger fluctuations (high SD variance) (group 2), and these communities assemble slower than group 1. For communities that take a long time to stabilize (groups 3 and 4), diversity is generally high (SD mean), but it fluctuates less, and mobility has a negligible effect.

Mutation sizes were weakly correlated with CFT, as observed previously (38), but exhibited substantial variation in trends due to interactions with other model parameters. For low SD mean and variance (group 1) and high SD mean and variance (group 2), mutation size positively affects CFT (Fig. 4B). This implies that communities with larger mutations take longer to stabilize but only when the diversity outcome corresponds to these two groups (Fig. 4B). If the SD mean is high but the SD variance is low, mutation affects CFT negatively (i.e., higher mutation helps communities converge faster) (Fig. 4B).

Community spatial structure is also important for coexistence (28). However, rather than focusing on the final spatial structure, we examined the degree of spatial disturbance that occurred throughout the assembly process, which provides insight into the extent of mixing/migration that might occur in these communities. The categorization of spatial disturbance regimes was best predicted by species-level parameters (the kill margin and the inhibit margin) rather than by other spatial parameters in our model. This is somewhat surprising, but higher-order interactions are known to influence spatial patterns of coexistence (20). Importantly, we found a strong correspondence between the regimes of spatial disturbance and the groups produced by CFTs. The communities that formed quickly (group 1) tended to have low spatial disturbance (Fig. 4C). Communities that took more time to stabilize and ended up with high diversity through large overall diversity fluctuations (high SD mean and SD variance, group 2) have primarily a medium level of spatial disturbance. The communities that took longest to stabilize were characterized by high diversity (SD mean) and lower average fluctuations in diversity (SD variance) (groups 3 and 4) but have larger spatial disturbances.

All these observations point toward a complex interplay of mutation and mobility, which affects the assembly time of a community (CFT), and, in turn, controls the diversity of the assembled community. Although mobility (or, more broadly, dispersal) is known to enhance diversity in ecological communities in both theoretical (58, 59) and experimental (60, 61) settings, especially at local scales (62), we found that mobility is linked to diversity only in communities with short and intermediate CFT (i.e., those that equilibrated relatively quickly). Mobility enhances diversity and coexistence in group 1 in which a subset of dominant (high relative abundance) species appear to set community dynamics. In this capacity, dispersal would appear to act in the classic disruptive fashion, permitting coexistence where it would otherwise not occur (63, 64). In contrast, in group 2 in which communities are characterized by both high diversity and high fluctuations, mobility has a negative effect on diversity and coexistence in keeping with the capacity for dispersal to homogenize otherwise diverse systems (65, 66). This dichotomy, together with the absence of an important role for mobility in group 4 in which communities are characterized by long-term nonequilibrial dynamics, offers an intriguing target for future integrative research.

The mechanistic light shed upon these patterns by studying the Shannon equitability index (which measures the distribution of relative abundance of species in a community) and Simpson’s index (which measures the distribution of the “dominance” of species in a community) is also worth mentioning. The more equitable a community (higher Shannon equitability), the lower the chance of a particular species dominating the interactions (lower value of Simpson’s index) and, therefore, the longer it takes for the community dynamics to stabilize (longer CFTs) as seen in the behavior of the four groups (Fig. 4 D–G). The importance of species dominance to the maintenance of diversity in this model, which is structured via nonresource-based antagonistic interactions, is intriguingly similar to the critical role that species dominance plays in both real and theoretical communities structured via resource-based competition (67–70).

Collectively, these results demonstrate the rich spatiotemporal dynamics that are possible when large numbers of microbial species with limited but heterogeneous rules for aggressive, inhibitory, and vulnerable interactions live in a common space. Although these findings are focused primarily on nonresource-based antagonistic interactions between microbes, such dynamics may also be relevant for coral communities and other spatially structured systems featuring diverse types of interspecific interactions (71–73).

Our results also point toward the important yet often-overlooked role that transient dynamics play in the behavior and structure of ecological systems (53). Usually, models of ecological dynamics use asymptotically stable behavior or values at stability to explore patterns in the system (53). Admittedly, we have followed this approach in our exploration of how different parameters affect microbial communities’ long-run behavior (i.e., after CFT is reached). In addition, however, we also focused on categorizing spatiotemporal disturbance regimes and connecting these transient phenomena to system diversity. Great opportunities exist for future work investigating temporal diversity dynamics and how they relate to spatial heterogeneity and system processes. Such investigations can shed light on how transient microbial dynamics and assembly history affects the species diversity seen in microbial communities (74).

Even though our model introduced the use of continuous axes for species traits and interactions, we note that the post hoc binning procedure creates a bridge back to the matrix/network framework that has characterized community ecology studies for decades (2, 4, 13, 14, 21, 23). In this case, however, a multilayered network perspective would be necessary to accommodate the different kinds of antibiotic-mediated interactions (production, inhibition, and vulnerability). Future work could also incorporate other important forms of microbial interactions (e.g., mutualism, cross-feeding, resource competition) into the continuous species framework we have developed. Such investigations would allow exploration of how the interplay between resource-based and antagonistic interactions jointly shape diversity dynamics. However, to do this, we need to understand the interrelationships between resource-based and antagonistic interactions across species (11, 75, 76). Such investigations could be highly beneficial by providing a more complete view of how higher-order, intransitive interactions shape community assembly, stability, and diversity in natural systems.

Model

Model Description.

Here, we outline an algorithmic presentation of the model. The parameters of the model and their corresponding symbols are detailed in Table 1. The simulation takes place on a 200 × 200 square lattice with toroidal boundary conditions. This size of this simulation was a tradeoff between being small enough for computational feasibility and large enough to allow interesting dynamics. We found 200 × 200 to be a reasonable range for our computation budget. The model of microbial dynamics on this simulation is split into two parts: the microbial (phenotypic) space and the environment space (Fig. 1). This division of the model is purely for convenience and can easily be reinterpreted when the microbes and the environment are not differentiated. For the microbial phenotypic space, each cell in the lattice represents a single “variant” of microbe and is parameterized by a stateful three-dimensional species vector ${\mathit{R}}^3\mathit{\epsilon } \{\text{Ø}, {[0, 1]}^3\}$, in which $\text{Ø}$ represents a cell that is unoccupied, and [0,1] is a bounded real value that defines the parameters of any occupants. The three elements of the species vector are the species’ vulnerability ($S_v$), the species’ inhibition value ($S_i$), and the species’ antibiotic production value ($S_a$). In the microbial space, neighboring cells do not interact with each other directly but instead affect the environment space, which then affects the microbial space. The environment space is stateless and instead always resets to the most recent effects from the microbial space, or, in other words, no antibiotics remain in the environment between timesteps. This can just be interpreted as diffusion on a less granular timescale. A cell in the environment space is parameterized by a single scalar value ${\mathit{R}}^1\mathit{\epsilon } \{\text{Ø}, \left[0, 1\right]\}$, which represents the antibiotic occupying that cell space ($C_a$) or indicates that the cell contains no antibiotics, represented by $\text{Ø}$.

Table 1.

Brief description of model parameters

Parameter	Type	Definition
Species antibiotic production value ($S_a$)	Species-level, Species-specific	Defines what species are vulnerable to the antibiotic that this individual produces
Species vulnerability value ($S_v$)	Species-level, Species-specific	Defines what antibiotics (and hence species) this individual is vulnerable to
Species inhibition value ($S_i$)	Species-level, Species-specific	Defines the species whose antibiotics this individual can inhibit
Kill radius ($K_r$)	Spatial, Global	Maximum spatial distance of diffusion of the antibiotics produced by an individual
Inhibit radius ($I_r$)	Spatial, Global	Maximum spatial distance of diffusion of the inhibitors to antibiotics of produced by an individual
Growth radius ($G_r$)	Spatial, Global	Maximum spatial distance at which an individual can reproduce by producing a copy of itself with certain possible mutations
Kill margin (${\mathit{\epsilon }}_k$)	Species-level, Global	The total span centered around the specified species antibiotic production value ($S_a$), which can be affected/killed by the antibiotic of a given species
Inhibit margin (${\mathit{\epsilon }}_k$)	Species-level, Global	The total span centered around the specified species inhibition value ($S_i$), whose antibiotic can be inhibited by a given species
Mutation size ($\mathit{\mu }$)	Species-level, Global	Maximum value by which the species-specific parameters can be additively altered during reproduction/copying

Note that our model involves only a phenotypic space for microbial traits. There is no underlying genotypic space, and our phenotypic microbial space abstracts away genotypic changes into expressed phenotypic traits. Doing this in a meaningful way is a very difficult problem, and this is especially true for bacterial toxin-based antagonisms in which the basic nature of the interactions remains at a preliminary level of research and discovery (11, 76–84).

At fixed-interval time steps, the state of the microbial space is updated synchronously in four stages. First, an antibiotic release step occurs, which simulates the process of microbes diffusing antibiotics into the environment. Here, each cell’s antibiotic value ($C_a$) in the environment space is randomly assigned a species’ antibiotic value ($S_a$) of one other cell from the microbial space that is within the antibiotic radius ($K_r$). Note that rewrites of the environment cell are possible during this step, so the order of cell updates is randomized. Second, an inhibition step occurs which handles any inhibiting effects of the antibiotics in the environment space. In this step, for every cell in the microbe space, an inhibition radius ($I_r$) around it is checked for other cells in the environment space which contain an antibiotic value ($C_a$) such that the inhibition value is within a marginal range of the antibiotic value, $I_v–{\mathit{\epsilon }}_i\le C_a\le I_v+{\mathit{\epsilon }}_i$. If this is the case, the cell in the environment space antibiotic value ($C_a$) is made empty, $\text{Ø}$. Third, a kill step occurs when we iterate over every cell, comparing the antibiotic value ($C_a$) in the environment space and the individual vulnerability value ($S_v$) in the microbial space. If the individual vulnerability value ($S_v$) is within the range of the antibiotic value $(C_a$), $C_a-{\mathit{\epsilon }}_a\le S_v\le C_a+{\mathit{\epsilon }}_a$, then the individual is killed and the cell in the microbial space is made empty, $\text{Ø}$. Fourth and last, a growth step occurs when, for every cell in the microbial space that it is not empty, another cell in the microbial space that is within that cell’s growth radius ($G_r$) is randomly selected. If the selected cell is empty, the species vector of the growing microbe cell is copied to the selected cell. The copied parameters are also further modified according to a mutation size ($\mu$). This modification is a noncorrelated additive perturbation of the species’ vector by a uniform value sampled from $U(-\mu , \mu )$, and the value is restricted in the range [0,1] by adding or subtracting 1 if it is outside this range. This ensures that all species have equal likelihood of interactions with other species by putting the species parameters on a three-dimensional toroid. From a theoretical perspective, this growth can be seen as a model of growth probability in which the probability that an individual will reproduce is equal to $E\left(C\right)/F\left(C\right)$ in which $E\left(C\right)$ is the number of empty cells within radius $G_r$ of the current $C$, and $F\left(C\right)=\mathit{floor}\left(2\mathit{\pi } G_r^2\right)$ is equal to the total number of cells within radius $G_r$ of cell $C$.

Model Assumptions.

There are three major assumptions/rules underlying our model implementation. The first is that the model only attends to toxin-based antagonistic interactions. Little evidence is available to characterize the relationship between antagonistic interactions and other forms of microbial interactions (e.g., mutualisms and resource competition) across species (11, 77). Therefore, our aim here was to build a “base” model that allows for the investigation of antagonistic interactions with more nuance and across more dimensions of complexity than was possible in previous work on the subject. The interplay between antagonistic interactions and other types of microbial interactions may be explored in future work as more information becomes available.

The second assumption pertains to the structure of the microbial trait space. Our model represents species traits of “antibiotic production,” “vulnerability,” and “inhibition” as continuous values on a real number line. A chief advantage of this approach is that a continuous trait space makes it easy to introduce mutations that preserve some history of the evolutionary process. Though critical to representations of species evolution, such mutations are difficult to combine with graph-based models of species interactions because it is unclear how mutation would update the graph edges (20). We define the presence or absence of a species interaction using a simple thresholded Euclidean distance (termed a “margin” in our model). In a multispecies context, the larger the margin, the greater the connectivity of the graph of interacting species, and, likewise, the smaller the margin, the sparser the graph.

These distance-based margins assume that the trait space is a uniform, three-dimensional toroid, which has implications for how we deal with changes in trait space. In particular, changing the value of one trait in one species and a second trait in another species by the same value d will result in the interacting edge between those two species remaining unchanged in the graph of interacting species. For example, if species A is vulnerable to species B’s antibiotic and the trait values of vulnerability ($S_v$) in A and antibiotic production ($S_a$) in B each mutate by a value d, species A will remain vulnerable to species B’s antibiotic. This approach, which is mathematically simple compared to alternative representations of trait evolution (SI Appendix, Supplemental Methods and Fig. S6), is a reasonable starting point because the true nature of the relationship between antibiotic production and vulnerability across microbial species is very much unknown (10, 11, 76–84).

In real species, a small genotypic change may or may not correspond to a small change in phenotypic space, and some phenotypes can be independently reached via alternative sets of genotypic mutational processes (including HGTs). To accommodate such phenomena, models of microbial diversity and/or mutational processes often adopt an explicitly phenotypic modeling approach (20, 32). The phenotypic structure of our model allows for such complexity—including the possibility of both small and large phenotypic changes in a single generation, and no specific correlation exists between distance on the phenotypic space along any axis and the (implicit, unmodeled) genetic change from which it results. Modeled in this fashion, phenotypic changes could plausibly represent the outcome of a diverse set of microbial mutational processes, given that the details of such processes affecting antagonistic microbial interactions are still in their infancy (for details see refs. 10, 11, and 76 to 84). We emphasize that we do not model mutations at a genotype level because HGT, which plays a major role in trait evolution in microbes, especially bacteriocins (10, 11, 77), is not easily amenable to such modeling.

For our third assumption, we stipulate that, within a run of our model, mutations only affect species identity (i.e., parameters $S_a, S_v, S_i$ within the continuous trait space). Other parameters (i.e., those governing spatial aspects of interactions, the species breadth [“margin”] of interactions, and mutation size; Table 1) remain constant in a given run. We make this assumption because antagonistic spatial interactions between bacteria (which we emulate via parameters for the kill radius and the inhibit radius) are typically affected by diffusion properties of the toxin compounds, which have similar physical properties within a given class of molecules but can vary across classes of toxins (11). Hence, for computational purposes, we keep the radius parameters constant over a run. Likewise, we keep the margin parameters constant over a run because they govern the generality of the interactions within the fixed kill and inhibit radii. We keep the maximum mutation size constant within runs to facilitate comparisons across different regimes of trait alteration.

Model Implementation.

We implemented the simulation in C++ using the SFML (Simple and Fast Multimedia Library) graphics library for rendering. It is possible to parallelize the updating of substeps of the cells due to the synchronous nature of the model, but we chose to use a simpler sequential algorithm that looped through each cell one at a time. We did, however, parallelize the running of multiple simulations when sweeping parameter spaces. This allowed us to reduce the total computation time required by two orders of magnitude. Each simulation was run for 2,000 timesteps or until stability/stagnation (also termed the CFT). Stagnation/stability was determined by comparing the state of all cells between two consecutive time steps, and if it remained unchanged for a total of five time steps, the simulation was terminated. This helped to quickly remove a large number of simulations that terminated early because of poor parameter settings. Because the simulation was so large, collecting per-cell data across many parameters was not practical. Alternatively, we chose to compute population-level statistics online during each simulation using the SD mean and variance (over time), and then, from the analysis of this lower-granularity data, we selected individual parameter settings to explore population-level statistics. Furthermore, we also built a qualitative application to allow quick classification of simulations, assigning them to a class based on their spatial heterogeneity/disturbance dynamics. Simulations were assigned to one of three classes according to how the spatial dynamics evolved (Fig. 2).

To track population-level statistics, it was necessary to discretize the continuous species space. $l$-discretization (or $l$-binning) assigned individuals to the same species if the three parameters of those individuals had the same integer values after performing a binning transformation on them like so: $\lfloor \frac{S_v}{l}\rfloor$, $\lfloor \frac{S_i}{l}\rfloor$, and $\lfloor \frac{S_a}{l}\rfloor$. When recording the population-level data, we stored the number of individuals per species every time step using a standard 0.05 discretization. Although the choice of 0.05 discretization is arbitrary, we emphasize that the binning only affects the resolution of the statistical analysis and has no influence on the dynamics of the model itself. We found 0.05 to be a small enough value for which the simulation statistics did not blend away but not too small such that there were no measurable statistics (see Data Analysis). For comparison, we repeated the complete set of analyses on system properties at three other reasonable species bin sizes (0.03, 0.07, and 0.09) (see SI Appendix, Fig. S5 for more details).

For every parameter setting, we repeated the simulation 10 times, seeding the pseudorandom number generator with a unique value for each repetition. Every simulation began by assigning every cell vector the all-empty state $\left(-1,-1,-1,-1,-1\right)$ except the center cell, which is assigned a random value in the range $\left[-1, 1\right]$ for the first three elements of its vector. This initial cell represented a randomly created individual. One potential issue was that if the center cell was assigned a random value such that it was vulnerable to its own antibiotic, it would kill itself, and the simulation would terminate immediately. Although this was possible, it was rarely the case, and it did not significantly affect our results because of our use of multiple runs per parameter setting.

Data Analysis.

We ran a total of 10.49 million runs of our model with various parameter initializations and performed data analysis with Python 3.7 and the R statistical language. For these runs, we obtained a manual classification of the size of the spatial disturbance (low, medium, and high). The simulations which stabilized quickly (fewer than 20 time steps) with no further changes in spatial patterns and the ones that had (more or less) stabilized by 20 time steps, except for a small number of point fluctuations in the grid, were categorized as the “low disturbance” regime (Fig. 2 A, 1). The simulations which had not stabilized after 20 time steps but exhibited small waves of diversity replacements which diminished over time were termed as “medium” disturbance. All medium disturbance simulations stabilized before 500 time steps (Fig. 2 B, 1). The remaining simulations did not stabilize even after 500 time steps nor had a reduced amplitude of waves of diversity replacements; these were categorized as the “high” spatial disturbance regime (Fig. 2 C, 1).

We also calculated the mean SD, Shannon equitability, and Simpson’s index over time (until a community stabilized, i.e., reached the CFT) and the variance in each of the three metrics over the same time period. The disturbance classification, SD mean, and SD variance were our three outcomes of interest and are the focus of the results. We later connect the results to the values of Shannon equitability and Simpson’s index.

To understand how parameters affect diversity dynamics, we determined the PRCC of various parameters with respect to the three outcomes of interest using the sensitivity package (85) in R. We also performed RF regressions and classification using the randomForest package (82) in R to identify which parameters were the strongest predictors of the patterns in predicting the outcomes of interest. We optimized the number of parameters available for splitting at each tree node in the RF using OOB (86). Please note that the overlay figures (Fig. 3 D–F and SI Appendix, Fig. S2) have been plotted with pruned samples for better visualization.

For clustering values on the SD mean versus SD variance space with respect to CFT, we used k-means clustering in R and optimized for the number of clusters using the elbow method, the D index, and the Hubert indices (which all yielded similar results) using the package NbClust (87). For each obtained cluster in the SD space, we performed an RF analysis to calculate differences in variable importance scores across these clusters. For each cluster, we also performed PRCC and RF analyses in order to delineate the effects that individual parameters had on the different subsets of the diversity space.

Data Availability

All code and required data to replicate our results are available in the following repository: https://github.com/levifussell/MicroEvo.