Slow expanders invade by forming dented fronts in microbial colonies

Significance

Living organisms never cease to evolve, so there is a significant interest in predicting and controlling evolution in all branches of life sciences. The most basic question is whether a trait should increase or decrease in a given environment. The answer seems to be trivial for traits such as the growth rate in a bioreactor or the expansion rate of a tumor. Yet, it has been suggested that such traits can decrease, rather than increase, during evolution. Here, we report a mutant that outcompeted the ancestor despite having a slower expansion velocity when in isolation. To explain this observation, we developed and validated a theory that describes spatial competition between organisms with different expansion rates and arbitrary competitive interactions.

Abstract

Most organisms grow in space, whether they are viruses spreading within a host tissue or invasive species colonizing a new continent. Evolution typically selects for higher expansion rates during spatial growth, but it has been suggested that slower expanders can take over under certain conditions. Here, we report an experimental observation of such population dynamics. We demonstrate that mutants that grow slower in isolation nevertheless win in competition, not only when the two types are intermixed, but also when they are spatially segregated into sectors. The latter was thought to be impossible because previous studies focused exclusively on the global competitions mediated by expansion velocities, but overlooked the local competitions at sector boundaries. Local competition, however, can enhance the velocity of either type at the sector boundary and thus alter expansion dynamics. We developed a theory that accounts for both local and global competitions and describes all possible sector shapes. In particular, the theory predicted that a slower on its own, but more competitive, mutant forms a dented V-shaped sector as it takes over the expansion front. Such sectors were indeed observed experimentally, and their shapes matched quantitatively with the theory. In simulations, we further explored several mechanisms that could provide slow expanders with a local competitive advantage and showed that they are all well-described by our theory. Taken together, our results shed light on previously unexplored outcomes of spatial competition and establish a universal framework to understand evolutionary and ecological dynamics in expanding populations.

Population dynamics always unfold in a physical space. At small scales, microbes form tight associations with each other, substrates, or host cells (1, 2). At large scales, phytoplanktons and zooplanktons form complex patterns influenced by ecological interactions (3–5) and hydrodynamics (6, 7). Between these two extremes, populations constantly shrink and expand in response to changing conditions, and there is still a great deal to be learned about how spatial structure affects ecology and evolution (8–12). Better understanding of these eco-evolutionary dynamics is essential for management of invasive species (13, 14), controlling the growth of cancer (15), and preserving biodiversity (16, 17).

It is particularly important to understand how natural selection operates at the edge of expanding populations. These expansion frontiers are hot spots of evolution because mutations that arise at the edge can rapidly establish over large areas via allele surfing or sectoring (18–21). Furthermore, numerous studies argue that selection at the expansion front favors faster expanders and therefore makes population control more difficult (22–32). Indeed, organisms that expand faster have a head start on growing into a new territory and may face weaker competition or better access to nutrients. A well-known example is the evolution of cane toads, which increased the expansion speed by fivefold over 50 y (33). Yet, despite substantial empirical evidence across many systems (23–26, 28–32), it has been suggested that the simple intuition of “faster runner wins the race” does not always hold.

Two theoretical studies have found that slower dispersal could evolve in populations with a strong Allee effect, i.e., a negative growth rate at low population densities (34–36). Slow mutants nevertheless can take over the populations because they are less likely to disperse ahead of the front into regions with low densities and negative growth rates. In a different context, both theory and experiments have shown that slow cheaters could invade the growth front of fast cooperators (27, 37). In this system, the production of public goods allowed cooperators to expand faster, but made them vulnerable to the invasion by cheaters.

The examples above show that slower expanders succeed in the presence of a tradeoff between local and global fitness. The global fitness is simply the expansion rate of a given species in isolation, which determines how quickly it can colonize an empty territory. When two species are well-separated in space, their competition is determined solely by the global fitness. In contrast, when the two species are present at the same location, their competition could involve differences in growth rates, production of public goods (38, 39), or secretion of toxins (40). We refer to such local competitive abilities as local fitness. It is natural to assume that slow expanders can win only if they are superior local competitors, but it is not clear a priori if this is actually feasible or how to integrate local and global fitness under various scenarios of spatial competition.

Our interest in the interplay between local and global competition was sparked by an unusual spatial pattern in colonies of Raoultella planticola grown on agar plates. These colonies repeatedly developed depressions or dents along the edge. We found that dents were produced by a spontaneous mutant that expanded slower than the wild type, when in isolation. Thus, we discovered a convenient platform to explore the fate of slower expanders in spatial competition and to elucidate the tension between local and global fitness.

In our experiment, the slower mutant took over the colony either while increasing in frequency homogeneously along the front or while forming pure, mutant-only sectors. When mutant sectors formed, they had an unusual “dented” or “V” shape. To explain this spatial pattern, we developed a theory that describes all possible sector geometries. Our theory unifies local and global competitions without assuming any particular mechanism for growth and dispersal. Although mechanism-free, the theory makes quantitative predictions, which we confirmed experimentally. We also simulated specific microscopic models to demonstrate that the takeover by a mutant with a slower monoculture expansion velocity is generic and could occur due to multiple ecological mechanisms. These simulations further confirmed that sector-shape prediction from geometric theory is universal. Taken together, our results establish a framework to understand evolutionary and ecological dynamics in expanding populations with arbitrary frequency- and density-dependent selection.

Results

Experimental Observation of Slow Mutants Taking Over the Front.

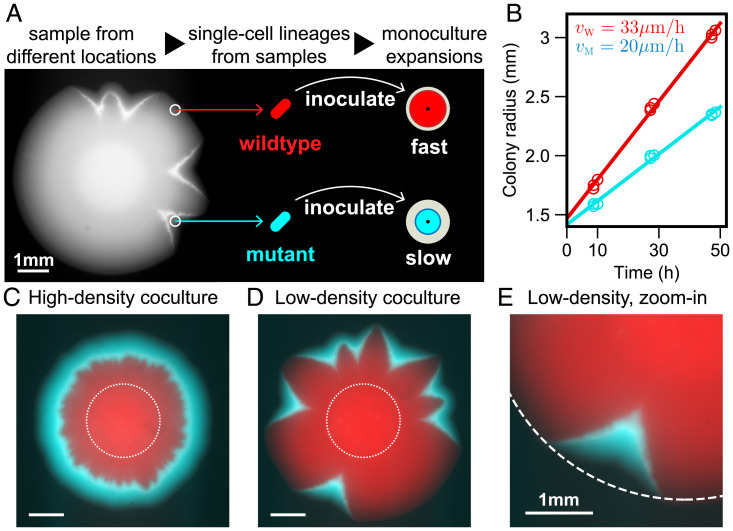
The strains used in our experiment were derived from a soil isolate of R. planticola, a Gram-negative, facultatively anaerobic, nonmotile bacterium that is found in soil and water and can occasionally lead to infections (41, 42). We grew R. planticola on a hard Luria–Bertani (LB) agar plate (1.5% agar) and noticed the formation of V-shaped dents along the front. Such dents were reproducibly observed in biological replicates (SI Appendix, Fig. S1). Suspecting that dents were caused by a mutation, we isolated cells from the smooth parts of the colony edge (wild type) and from the dents (mutant) (Fig. 1A).

Fig. 1.

Slow mutant takes over the front with and without sector formation. (A) We found that wild-type R. planticola colonies develop V-shaped indentations; a bright-field image is shown. We sampled cells from the dents and nondented regions and then developed strains descending from a single cell (Materials and Methods). (B) The mutant expanded more slowly than the wild type when in isolation. The data points come from two technical replicates, and the line is a fit. (C and D) Despite its slower expansion on its own, the mutant wins in coculture. Fluorescence images show the spatial patterns 48 h after inoculation with a 99:1 mixture of the wild type and mutant. A ring of mutant (cyan) outrun and encircled wild type (red) when the mixed inoculant had a high density (${\text{OD}}_{600}$ of ${10}^{-1}$). Mutant sectors emerged and widened over the front when the mixed inoculant had a low density (${\text{OD}}_{600}$ of ${10}^{-3}$). Images are taken 48 h after inoculation, and dotted lines represent initial inoculant droplets. (E) A zoomed image of a V-shaped sector (from the bottom of D). Dotted circle is a fit from wild-type expansion. The advantage of the mutant and its slower expansion away from the wild type is evident from the lateral expansion of the cyan sector.

We first characterized the expansion dynamics of the two strains in isolation by inoculating each culture at the center of a hard agar plate. Both strains formed smooth, round colonies, which expanded at a constant velocity (Fig. 1B and SI Appendix, Fig. S2). The wild type had about 50% larger expansion velocity compared to the mutant. Thus, the evolved strain expanded more slowly when in isolation.

Our observations seemed paradoxical, given numerous observations of invasion acceleration due to genetic changes that increase expansion velocities (33, 43). However, range expansions are known to produce high genetic drift (44, 45) and, therefore, allow for the fixation of deleterious mutations (20, 46–49). So, we next investigated whether the mutant has a selective advantage in competition with the wild type within the same colony.

We competed the two strains by inoculating an agar plate with a drop containing a 99:1 mixture of the wild type and the mutant. We used two wild-type strains (and their respective mutants) with different fluorescent labels, and the spatial patterns were analyzed with fluorescence microscopy (Materials and Methods). After about 48 h of growth, a ring of mutant completely encircled the wild type (Fig. 1C). Only the mutant ring continued to expand, while the expansion of the wild type ceased (SI Appendix, Fig. S3). Thus, the mutant not only localized to the front, but also achieved a greater population size. This is quite different from other microbial systems, where a strain with poor motility localized to the front without suppressing the growth of faster strain and without producing a larger biomass (50, 51). Thus, our experiments strongly suggest that the mutant has a competitive advantage when in contact with the wild type, despite its lower expansion velocity in isolation.

Experimental Observation of Mutants Invading while Forming Dented Fronts.

Our initial competition experiments did not exhibit the dents that sparked our initial interest in the strains. The mutant took over uniformly across the expansion front, producing a rotationally invariant spatial pattern (Fig. 1C). In fact, one might even argue that the success of the mutant could have been entirely due to the transient growth dynamics, and the wild type would prevail if allowed to somehow spatially segregate from the mutant. To address both of these concerns, we sought to alter the experiments so that the mutant and the wild type grow as distinct sectors within the same colony.

In microbial colonies, sectors emerge due to genetic drift at the growing edge. The magnitude of demographic fluctuations varies widely in different systems, depending on the organism, the growth conditions, and the duration of the experiment (52, 53). To test for the effects of sectoring, we needed to increase stochasticity without altering other aspects of the competition. Reducing the cell density of the initial inoculant accomplished this goal. By lowering the inoculant density (from ${10}^{-1}$ ${\text{OD}}_{600}$ to ${10}^{-3}$ ${\text{OD}}_{600}$), we increased the separation between cells that localized to the colony edge following the drying of the inoculation drop. This, in turn, dramatically increased the formation of monoclonal sectors (Fig. 1D).

Sectoring spatially segregated the two strains and, thus, allowed the wild type to take advantage of its higher expansion velocity as a monoculture. Nevertheless, the mutant still outcompeted the wild type (Fig. 1 D and E). The takeover of mutant was robust under different choices of initial density, initial mutant fraction, and fluorescent label (SI Appendix, Figs. S4 and S5). The takeover by the mutant also produced the characteristic V-shaped dents at the colony edge. These dents are the exact opposite of the bulges or protrusions that one usually observes for beneficial mutations (54). Typically, the advantageous mutants have a greater expansion velocity and, therefore, outgrow the ancestors at the front. For our strains, however, the winning mutant had a lower expansion velocity away from the wild type, and this lower expansion velocity produced the opposite of the bulge—the dent.

Mechanism-Free Theory of Sector Geometry.

Our experiments unambiguously demonstrated that a mutant that expands more slowly on its own can indeed outcompete a faster wild type with and without sectoring. Still, we need a careful theoretical description of the spatial dynamics to reconcile the apparent contradiction between the slow global expansion of the mutant and its superior performance in local competition. We could approach this question by simulating a specific ecological mechanism that could be responsible for the tradeoff between local and global fitness. However, it is much more useful to first ask what can be said about spatial competition generically and determine the range of possible sector shapes without relying on any specific mechanism.

One way to understand the origin of the dented fronts is to consider the motion of the sector boundary. The mutant clearly expands further along the sector boundary than it expands outward away from the sector boundary. In other words, the mutant expands faster in the presence of the wild type, and the dented shape of sector is the result of this velocity enhancement of the mutant in the vicinity of the wild type.

To formalize this idea, we followed the approach similar to geometric optics in physics (55–57), which relies on a few standard assumptions. The expansion velocities of the two strains in isolation ($v_W$ and $v_M$) were assumed to be time-independent, both to simplify the calculations and to reflect experimental observation (Fig. 1B). We also assumed, consistent with past studies (58–60), that there is little growth behind the front, so that the spatial pattern remains once established, as in our experiments. Finally, we neglected long-range interactions due to the diffusion of nutrients, toxins, or signaling molecules* (61–63).

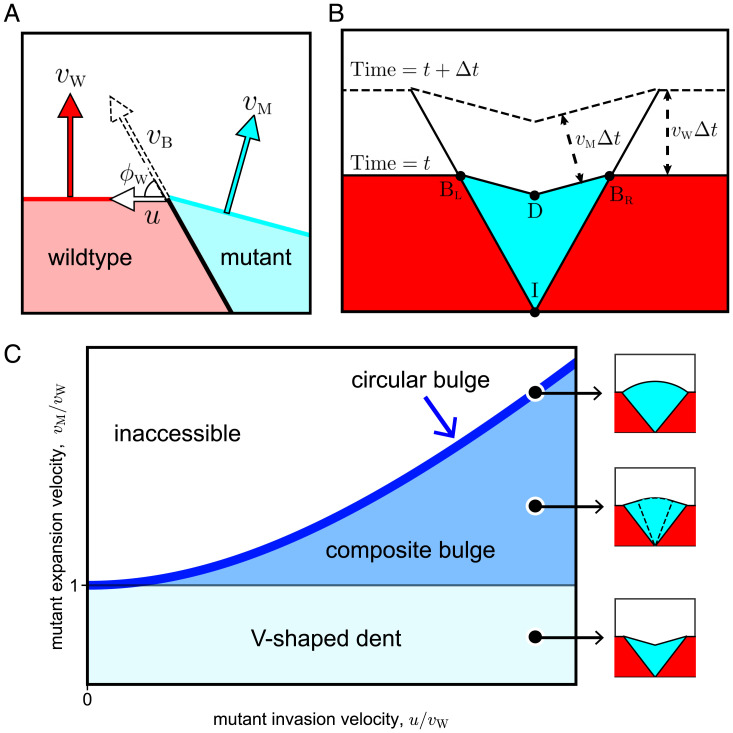
The nontrivial aspect of our work is how we capture the effect of local competition between strains. This can be done in a number of ways. One approach is to consider the velocity of the boundary between the strains $v_B$, which cannot be inferred solely from $v_W$ and $v_M$ because it depends on the interaction between the wild type and the mutant. Another approach, which is equivalent to the first one, is to define a velocity u as the projection of the boundary velocity $v_B$ on the wild-type front. In other words, u is the rate at which the length of the front dominated by the wild type shrinks. The connection between these approaches is illustrated in Fig. 2A.

Fig. 2.

Geometric theory predicts sector shapes as a function of local and global fitness. Flat-front initial conditions are illustrated here, and the corresponding results for circular fronts are shown in SI Appendix. (A) Global fitness of mutant and wild type are defined with speeds $v_W$ and $v_M$, with which their fronts advance away from sector boundary. Local fitness is characterized by movement of mutant along the sector boundary, which advances with speed $v_B$ at angle ${\varphi }_W$ with the wild-type front. We use lateral invasion speed u to describe the local fitness, and the equivalence among $v_B$, ${\varphi }_W$, and u is explained in SI Appendix, section 1. (B) The shape of the mutant sector can be derived from geometric considerations. During a time interval $\mathrm{\Delta }t$, the boundary points ${\text{B}}_L$ and ${\text{B}}_R$ move upward by $v_W\mathrm{\Delta }t$ and laterally outward by $u\mathrm{\Delta }t$. The position of the dent $\text{D}$ is obtained from the requirement that both $\overline{{\text{DB}}_L}$ and $\overline{{\text{DB}}_R}$ shift by $v_M\mathrm{\Delta }t$; the directions of the shifts are perpendicular to $\overline{{\text{DB}}_L}$ and $\overline{{\text{DB}}_R}$, respectively. Point $\text{I}$ labels the origin of the sector. (C) The geometric theory predicts sector shapes as a function of $u/v_W$ and $v_M/v_W$. When $v_M<v_W$ and u > 0, the mutant forms a V-shaped dented front; note that all boundaries are straight lines. When $v_M>v_W$ and $u>\sqrt{v_M^2-v_W^2}$, the mutant forms a bulged front. The shape of the bulge consists of two regions. It is an arc of a circle near the middle and two straight lines near the two boundaries between the mutant and the wild type. The circular region grows and the linear region shrinks as $v_M/v_W$ increases at constant $u/v_W$. The bulge becomes completely circular when $v_M/v_W$ reaches its maximal value of $\sqrt{1+u^2/v_W^2}$ on the boundary of the accessible region. See SI Appendix for derivation and exact mathematical expressions of all sector shapes.

The knowledge of the three velocities $v_W$, $v_M$, and u is sufficient to simulate how the shape of the colony changes with time. In some situations, colony shapes can also be obtained analytically by comparing the position of the front at two times t and $t+\mathrm{\Delta }t$. We derived the equations for sector shapes by requiring that all distances between the corresponding points of the two fronts are given by $\mathrm{\Delta }t$ times the appropriate velocity (Fig. 2B). The details of these calculations are provided in SI Appendix, Fig. S9.

We found that all possible sector shapes fell into three classes. Without loss of generality, we take u to be positive by calling the mutant the strain that invades locally. The shape of the sector is then largely determined by $v_M/v_W$. When this ratio is less than one, sectors have a dented shape. In the opposite case, sectors bulge outward. The exact shape of the front, of course, depends on all three velocities. Overall, there are the two broad classes discussed above and a special limiting case when $u=\sqrt{v_M^2-v_W^2}$, which is discussed below. In all cases, we obtained sector shapes analytically for both circular and flat initial fronts (SI Appendix, Figs. S10 and S11). The latter are summarized in Fig. 2C and are used to test the theoretical predictions.

The geometrical theory provides a concrete way to define local fitness advantage, $u/v_W$, and global fitness advantage, $v_M/v_W-1$. These two types of fitness can take arbitrary values, even with opposite signs. The only condition is that a positive u needs to be larger than $\sqrt{v_M^2-v_W^2}$ when the mutant is faster than the wild type. This constraint arises because, for large $v_M/v_W$, the gaining of new territory due to the large global fitness advantage outpaces the gain in the new territory due to a smaller local fitness advantage. The constraint on u is not relevant to dented fronts, so we relegate this discussion to SI Appendix, Fig. S8.

Experimental Test of the Geometric Theory.

How can we test whether the theory of sector geometry described above indeed applies to our experiments? The theory utilizes three velocities, $v_W,\hspace{0.17em}{v}_M$, and u, to predict the shape of the sector boundary and the sector front. The absolute values of the velocities determine how quickly the colony grows overall, and its shape depends only on two dimensionless parameters: $v_M/v_W$ and $u/v_W$. The first parameter can be obtained from the direct measurements of expansion velocities in monocultures. The second parameter can be inferred by fitting the shape of the sector boundary to the theory. This leaves the shape of the sector front as an independent measurement that can be compared to the theoretical prediction.

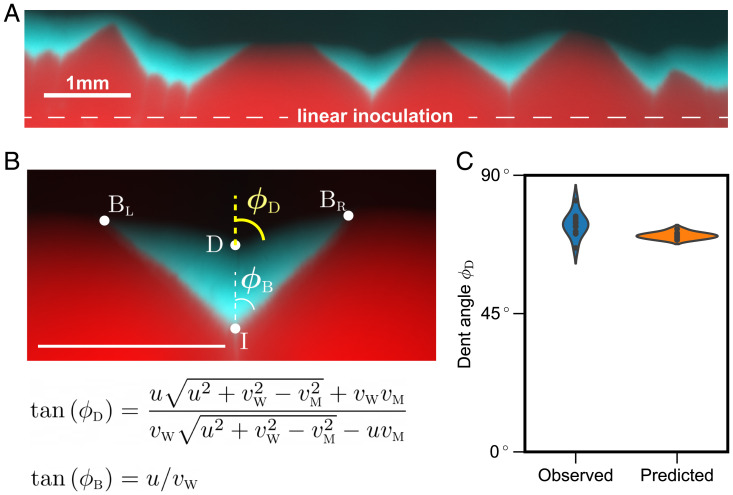
The linear expansion geometry greatly simplifies all the steps involved in testing the theory because the shapes of both the sector boundary and the dent are determined by their opening angles. Qualitative agreement with this theoretical prediction is quite clear from the experimental images (Fig. 3A), which indeed show that mutant sectors are bounded by straight lines on all sides. The opening angle of the sector boundary determines $u/v_W$, and the opening angle of the dent serves as a testable prediction (Fig. 3B).

Fig. 3.

Empirical test of predicted sector shapes. (A) We used linear inoculations with low density and low fraction of the mutant and grew the colonies for 48 h. (B, Upper) Zoom-in image of one of the sectors. The shape of mutant sector is quantified by two opening angles: one between the two sector boundaries $2{\varphi }_B$ and one between the two parts of the expansion front that meet at the dent $2{\varphi }_D$. (B, Lower) The theory predicts ${\varphi }_B$ and ${\varphi }_D$ as functions of the three velocities: $v_W,\hspace{0.17em}{v}_M$, and u. We used ${\varphi }_B$ to determine $u/v_W$ and predict ${\varphi }_D$; $v_M/v_W$ is measured from monoculture expansions. (C) The observed and predicted values of ${\varphi }_D$ are very close to each other.

Our experiments proceeded as follows. We first measured expansion velocities in monocultures by tracking the colony radius as a function of time (Fig. 1B). Then, the data on sector shapes were collected from plates inoculated along a straight line with a low-density (${10}^{-3}$ ${\text{OD}}_{600}$) 99:1 mixture of the wild type and the mutant. After 2 d of growth, five well-isolated sectors were analyzed to determine ${\varphi }_B$ and ${\varphi }_D$ (Materials andMethods). Since each side of the angle can be used, we effectively obtained 10 measurements. Fig. 3C shows that observed ${\varphi }_D$ is ${73.93}^{°}$

(SD = ${3.81}^{°}$, SEM = ${1.21}^{°}$, n = 10). Predicted ${\varphi }_D$ is ${70.39}^{°}$ (SD = ${1.02}^{°}$, SEM = ${0.32}^{°}$, n = 10). This is an excellent agreement, given other sources of variability in our experiment, including variations in velocity between replicates and potential systematic errors in fitting sector shapes. Thus, the geometric theory not only provides an explanation of the sector shape, but also describes it quantitatively.

Another experimental verification of our theory comes from ref. 54, which studied sector shapes in yeast colonies. Instead of dents, their strains produced circular bulges (the special case with $v_M=\sqrt{v_W^2+u^2}$). For this special case, our results fully agree with both their theoretical and experimental findings (equation 12, table 1, and figure S8 in ref. 54). As far as we know, the intermediate case of composite bulge (Fig. 2C) has not been observed yet. Perhaps engineered strains with a tunable tradeoff between local and global fitness would enable the observation of all sector shapes in a single system.

Concrete Mechanisms of Fitness Tradeoff.

The geometric theory integrates local and global competition and quantitatively predicts the shape of mutant sector in our experiment. Yet, the theory does not provide a tangible mechanism behind the takeover by a mutant with a slower monoculture expansion velocity. To show that dented fronts emerge readily under different ecological scenarios, we used the flexible framework of reaction-diffusion models, which are also known as generalized Fisher–Kolmogorov equations (64–66). A general model can be written as:

$$\begin{array}{l}{\partial }_t{n}_W=\left({\nabla }^2\left(D_W{n}_W\right)+r_W{n}_W\right)(1-n_W-n_M),\\ {\partial }_t{n}_M=\left({\nabla }^2\left(D_M{n}_M\right)+r_M{n}_M\right)(1-n_W-n_M).\end{array}$$ [1]

Here, $n_W$ and $n_M$ are the population densities of the wild type and the mutant normalized by the shared carrying capacity; $D_W,\hspace{0.17em}{r}_W$ and $D_M,\hspace{0.17em}{r}_M$ are their respective dispersal and per capita growth rates.

The factor of $(1-n_W-n_M)$ ensures that there is no growth or movement behind the front. In the growth term, this is a standard assumption that ensures finite carrying capacity (66). In the dispersal term, the factor of $(1-n_W-n_M)$ has rarely been studied in mathematical biology because it is specific to microbial range expansions, where there is no movement behind the front (54, 58–60). In SI Appendix, we demonstrate that dented fronts also occur with standard density-independent dispersal and, therefore, could be relevant for range expansions of macroscopic organisms (SI Appendix, section II).

The nonspatial limit of Eq. 1 is obtained by dropping the dispersal term. This limit is analyzed in SI Appendix, section 3. As population grows from any initial condition, the relative abundance of the faster grower increases until the total population density reaches the carrying capacity. At this point, there is no further change in $n_W$ and $n_M$. This neutral coexistence between the two strains ensures that the population is frozen behind the front, and the competition unfolds only at expansion frontier. The simplest spatial model takes all growth and dispersal rates to be independent of population density. It is then easy to show that there is no difference between local and global fitness (SI Appendix, Fig. S6 and ref. 54). Most of the previous work focused on this special case of so-called “pulled” waves (67) and thus could not observe the takeover by the slower expander.

Many organisms, however, exhibit some density dependence in their growth or dispersal dynamics (68–72), which can lead to a tradeoff between local and global fitness. One commonly studied case is found in the interaction between cooperators and cheaters (27, 50, 73, 74). To model this ecological scenario, we take

$$\begin{array}{l}{D}_W=D_M=D,\\ r_W=r\left(1-\alpha \frac{n_M}{n_W+n_M}\right),\hspace{1em}{r}_M=r\left(1-s+\alpha \frac{n_W}{n_W+n_M}\right).\end{array}$$ [2]

The benefit of cooperation is specified by s, which is the difference in the growth rate of cooperators and cheaters when grown in isolation. The benefit of cheating is controlled by α; the growth rate of cheaters increases by up to α, provided cooperators are locally abundant. For simplicity, we chose a symmetric linear dependence of the growth rates on the mutant frequency and assumed that the diffusion constants are equal.

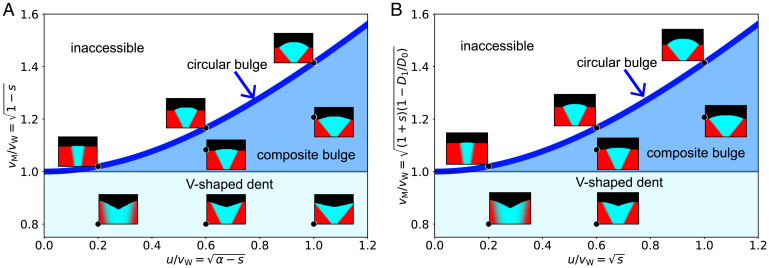
Numerical simulations of this model reproduced a V-shaped dented front (Fig. 4A). The dents flattened when there was no benefit to cooperate (s = 0) and were replaced by bulges when cooperators grew more slowly than cheaters when in isolation (s < 0). We were also able to test whether these transitions in sector shape matched the predictions of the geometric theory. For this comparison between the theory and simulations, we need a mapping between the microscopic parameters of the model and the three velocities that enter our geometric theory. Fortunately, in this model, all three velocities can be calculated analytically: $v_W=2\sqrt{rD(1+s)},\hspace{0.17em}{v}_W=2\sqrt{rD}$, and $u=\sqrt{(\alpha -s)rD}$. Therefore, we could overlay individual simulations on the phase diagram predicted by the geometric theory. The result, shown in Fig. 4A, shows the expected agreement and provides further validation for the geometric theory. The geometric description is generic and should transcend the specifics of the cooperator–cheater model discussed above. To further illustrate that different ecological interactions can produce identical spatial patterns, we simulated a completely different mechanism for the tradeoff between local and global fitness. This time, we assumed that the wild type loses the local competition because it reproduces more slowly than the mutant, but this slower growth is more than compensated by a much higher dispersal rate. This growth–dispersal tradeoff may be common in nature (29, 75–77) and is captured by the following set of parameters:

$$\begin{array}{l}{D}_W=D_M=D_0-D_1\frac{n_M}{n_W+n_M},\\ r_W=r,\hspace{1em}{r}_M=r\left(1+s\right).\end{array}$$ [3]

Fig. 4.

Sector shapes from microscopic simulations recapitulate phase diagram from the geometric theory. (A) Simulation of cooperator–cheater model (Eq. 2) is compared with the geometric theory. By varying s (benefit from cooperation) and α (strength of cheating), we explored sector shapes for different values of $v_M/v_W$ and $u/v_W$. The locations of various sector shapes match the predictions of the geometric theory. In particular, V-shaped dents are observed when a cheater expands more slowly than a cooperator when in isolation (s > 0), but has a sufficiently large advantage from cheating ($\alpha >s$). (B) Simulations of growth–dispersal tradeoff model (Eq. 3) also agree with the geometric theory. Different sector shapes were obtained by varying the growth advantage s and the dispersal disadvantage D₁. See Materials and Methods for simulation parameters.

Here, the growth rates are density-independent, but the dispersal rates change with the local community composition. We chose $D_W=D_M$ to reflect the collective nature of movement in colonies of nonmotile microbes (78, 79), which are pushed outward by mechanical stress generated by all cells behind the front. In addition, this simplifying assumption enables us to calculate the velocities analytically and construct a quantitative phase diagram similar to Fig. 4A. In SI Appendix, we show that dented front can also be observed in models with $D_W\ne D_M$ (SI Appendix, Fig. S7).

Our simulations again exhibited dented fronts and all shape transitions in full agreement with the geometric model (Fig. 4B). Thus, the geometric description is universal, i.e., a wide set of growth–dispersal dynamics converges to it. This universality, however, makes it impossible to determine the specifics of ecological interactions from spatial patterns alone. In other words, the observation of a dented front indicates the existence of a tradeoff between local and global fitness, but does not hint at any specific mechanism that is responsible for this tradeoff. For example, both models (Eqs. 2 and 3) produce identical sector shapes (Fig. 4), and both would provide a perfect fit to our experimental data. Indeed, each model has four parameters, which is more than sufficient to specify the three velocities that control all aspects of spatial patterns. Such fits, of course, would not provide a meaningful insight into the mechanism. To determine the mechanism, one would have to perform a different kind of experiment that could probe population dynamics on the spatial scale of local competition.

Discussion

This study used a simple and well-controlled laboratory microcosm to elucidate the factors that influence spatial competition. We found a stark contradiction to the intuitive expectation that the faster runner wins the race (32). A mutant that expanded more slowly on its own nevertheless took over the expansion front when inoculated with the wild type. This spatial takeover accompanied V-shaped sectors, which are a characteristic signature of the mismatch between local and global competition. To explain these observations, we developed a theory that integrates local and global competition and predicts all possible sector shapes. We then confirmed the validity of the theory using both further experiments and simulations.

Our experimental results unequivocally demonstrate that a mutant that grows more slowly in isolation can nevertheless win in competition. Under low-genetic-drift conditions, the mutant took over the front uniformly across the colony. This outcome can be described by one-dimensional models because the competition occurs primarily along the radial direction. In contrast, stronger genetic drift resulted in sector formation and produced fully two-dimensional growth dynamics. Even under these less favorable conditions, the mutant still outcompeted the wild type.

Previously, slower expanders were found to be successful only in one-dimensional models (34, 36, 37), and only bulged sectors of faster expanders were reported for two-dimensional growth (54). The latter was true even when there was a tradeoff between local and global fitness (80), presumably because local fitness advantage was not sufficiently large. Our experiments not only confirm the predictions of one-dimensional models, but also expand the set of conditions under which the unusual takeover by a slower mutant can be observed. In fact, the slower expanders could be successful in many settings not only because the theory and simulations strongly support this claim, but also because we relied on evolved mutants from natural isolates rather than genetic engineering to obtain the strains.

The observation of dented fronts clearly shows that the existing theoretical understanding of sector growth is incomplete. Previously, it was assumed that the spatial pattern depends only on the mutant and wild-type velocities in monocultures (54). We found, however, that the outcome of the competition also depends on the interaction between the species at sector boundaries. When the mutant expands much faster in the presence of the wild type than in isolation, the boundary velocity could tilt toward the region dominated by the wild type and result in a positive velocity u that describes how quickly the mutant takes over along the wild-type front. Our theory integrated both local and global competition and showed that the sector shapes are completely determined by the three velocities ($v_M,\hspace{0.17em}{v}_W$, and u). These results enabled us to make quantitative inferences from experimental data and test our theory.

The geometric theory is not without limitations. This phenomenological theory cannot predict whether the fast or the slow mutant wins in a given system. To answer that question, one needs to consider a mechanistic model and derive how the invasion velocity u depends on microscopic parameters, which we have done for specific models. The universal nature of the geometric theory also precluded us from identifying the mechanism responsible for the growth dynamics observed in our experiments. We left this fascinating question for future works and, instead, focused on several common tradeoffs between local and global fitness. The simulations of these tradeoffs not only confirmed the validity of the geometric theory, but further highlighted that slower expanders could establish by a wide range of mechanisms.

The geometric theory also relies on a few technical assumptions, such as constant expansion velocities, negligible stochasticity, and the absence of long-range interaction due to chemotaxis or nutrient depletion. Relaxing these assumptions could lead to certain quantitative changes in sector shapes, but the main conclusions, including the existence of the dented front, should not be affected. In particular, the strain that grows more slowly on its own could nevertheless prevail in competition.

Our work opens many directions for further investigation. We clearly showed that the expansion velocity cannot be the sole determinant of the spatial competition. Therefore, it will be important to examine how local interactions influence the eco-evolutionary dynamics during range expansions. Such future work would bring about a more detailed description of ecological and biophysical processes in growing populations. It would also greatly enhance our understanding of the tradeoffs among different life-history traits and shed light on the incredible diversity of successful strategies to navigate spatial environments (29, 75–77). The geometric theory developed here provides a convenient way to integrate these various aspects of population dynamics. It abstracts the main features of spatial growth and should facilitate the analysis of both experiments and simulations.

Materials and Methods

Strains.

Wild-type R. planticola strains were isolated from a soil sample (Massachusetts Institute of Technology [MIT] Killian Court) (81) and were tagged with two different fluorescent proteins, mScarlet-I (red) and mTurquois2 (cyan), by insertion of plasmids pMRE145 and pMRE141, respectively (82). As we grew wild-type colonies on agar plates, they reproducibly developed dents after several days, as shown in Fig. 1A and SI Appendix, Fig. S1. We sampled the cells from either inside the dent or on the smooth edge using inoculation loops, streaked on small plates, and grown in ${30}^{°}\text{C}$ for 2 d. Then, we sampled single colonies, grew them overnight in LB growth medium, and stored as a $-{80}^{°}\text{C}$ glycerol stock.

Growth Media Preparation.

We prepared hard agar plates with 1× LB medium (2.5% weight/volume [wt/vol]; BD Biosciences-US) and 1.5% wt/vol agar (BD Bioscience-US). We also added 1× Chloramphenicol (Cm; 15 mg/L, prepared from 1,000× solution) for constitutive expression of fluorescence. For each agar plate, 4 mL of medium was pipetted into a Petri dish (60 × 15 mm, sterile, with vents; Greiner Bio-one) and was cooled overnight (15 h) before inoculation.

Expansion Experiment.

For each strain, $-{80}^{°}\text{C}$ glycerol stock was streaked on a separate plate and grown for 2 d. Then, a colony from each strain was picked up and put into a 50-mL Falcon Tube filled with 5 mL of liquid medium (1× LB and 1× Cm). Bacterial cultures were grown overnight at ${30}^{°}\text{C}$ under constant shaking at 1,350 rpm (on Titramax shakers; Heidolph). We then diluted and mixed the cultures to desired total density and mutant fraction, measured in optical density (${\text{OD}}_{600}$) using a Varioskan Flash (Thermo Fisher Scientific) plate reader. For circular expansions, we gently placed a droplet of 1.5 µL of inoculant at the center of an agar plate. For linear expansions, we dipped a long edge of a sterile cover glass (24 × 50 mm; VWR) gently into the culture and touched the agar plate with the edge. After inoculation, each colony was grown at ${30}^{°}\text{C}$ for 48 h.

Imaging.

At fixed times after inoculation, each plate was put on a stage of Nikon Eclipse Ti inverted light microscope system. Magnification of 10× was used for whole-colony images, and 40× magnification was used for single-sector images. Fluorescent images were taken by using Chroma filter sets ET-dsRed (49005) and ET-CFP (49001) and a Pixis 1024 charge-coupled device camera.

We used scikit-image (83) for image processing in Python. Images from different fluorescent channels were integrated after background subtraction and normalization by respective maximum intensity. The sector boundaries were identified as the furthest points from the inoculation plane, where both strains’ fluorescence intensities were above respective thresholds. The codes for image analysis are available via GitHub (https://github.com/lachesis2520/dented_front_public).

Numerical Simulation.

Numerical simulations were performed by solving the corresponding partial differential equations on a square grid using a forward-in-time, finite-difference scheme that is second-order accurate in space and first-order accurate in time (84). Python codes are available via GitHub (https://github.com/lachesis2520/dented_front_public).

For cooperator–cheater model simulation, we used the following set of values for parameters $(s,\alpha )$: (–0.04, 0), (–0.36, 0), (–1, 0), (–0.173, 0.187), (–0.457, 0.543), (0.36, 0.4), and (0.36, 0.72).

For growth–dispersal tradeoff model simulation, we used $(s,D_1)$ of (0.04, 0), (0.36, 0), (1, 0), (0.36, 0.147), (1, 0.271), (0.04, 0.385), and (0.36, 0.529).

Data Availability

The dataset, algorithms, and computer codes have been uploaded to the GitHub repository (https://github.com/lachesis2520/dented_front_public) (85).