Functional observability and target state estimation in large-scale networks

Significance

Observing the states of a network is fundamental to our ability to explore and control the dynamics of complex natural, social, and technological systems. The problem of determining whether the system is observable has been addressed by network control researchers over the past decade. Progress on the further problem of actually designing and implementing efficient algorithms to infer the states from limited measurements has been hampered by the high dimensionality of large-scale networks. Noting that often only a small number of state variables in a network are essential for control, intervention, and monitoring purposes, this work develops a graph-based theory and highly scalable methods that achieve accurate estimation of target variables of network systems with minimal sensing and computational resources.

Abstract

The quantitative understanding and precise control of complex dynamical systems can only be achieved by observing their internal states via measurement and/or estimation. In large-scale dynamical networks, it is often difficult or physically impossible to have enough sensor nodes to make the system fully observable. Even if the system is in principle observable, high dimensionality poses fundamental limits on the computational tractability and performance of a full-state observer. To overcome the curse of dimensionality, we instead require the system to be functionally observable, meaning that a targeted subset of state variables can be reconstructed from the available measurements. Here, we develop a graph-based theory of functional observability, which leads to highly scalable algorithms to 1) determine the minimal set of required sensors and 2) design the corresponding state observer of minimum order. Compared with the full-state observer, the proposed functional observer achieves the same estimation quality with substantially less sensing and fewer computational resources, making it suitable for large-scale networks. We apply the proposed methods to the detection of cyberattacks in power grids from limited phase measurement data and the inference of the prevalence rate of infection during an epidemic under limited testing conditions. The applications demonstrate that the functional observer can significantly scale up our ability to explore otherwise inaccessible dynamical processes on complex networks.

Large-scale complex systems, including power grids, neuronal networks, and food webs, are often represented as sets of interconnected dynamical systems and referred to as dynamical networks. Understanding the properties and control principles of dynamical networks allows for the development of intervention strategies that can shape the behavior of these systems to achieve the desired functionality. As formalized by Wiener (1), the fundamental mechanism enabling precise control of a dynamical system is feedback, which involves sensors, signals, and actuators in a closed loop. A sensor provides immediate measurements of a particular variable of the system. As the dynamical network grows large, it becomes prohibitive to implement a sensor for each state variable, be it due to cost or physical constraints. For instance, our ability to measure each of the tens of billions of neurons present in a human brain is physically limited. Likewise, infrastructure and operation costs may impede the placing of sensors in every node of a large technological system. Therefore, the indirect estimation of the unmeasured states is essential for the control of large-scale dynamical networks.

The property of a dynamical system that enables the reconstruction of the entire system state from its control inputs and sensor measurements is called observability (2). In particular, observability constitutes the necessary and sufficient condition that guarantees the existence and enables the design of full-state estimators—such as Luenberger observers (3) and Kalman filters (4). Despite the success of state observers in uncountable engineering applications, high dimensionality is still an obstacle to the direct use of these methods in large-scale dynamical networks (5–7). This calls for different approaches and novel techniques (8–14) to overcome the lack of scalability of existing methods. Based on a graph-theoretic approach to controllability (15), Liu et al. (9) presented an efficient method that, by duality, can be used to determine a minimum set of sensor nodes required to guarantee the observability of complex networks. However, even if a minimum set of sensors is used, the state observer will have the same dimension as the entire network, making its design and implementation computationally expensive in large-scale systems. Moreover, a minimum set of sensor nodes does not guarantee good quality for the full-state reconstruction in higher-order systems (16–20).

For many real-world problems, estimating the entire state vector of a high-dimensional system is not necessary or even desirable (6). It is often sufficient to focus on a particular subset of nodes of interest. For instance, in decentralized control strategies applied to network systems, each controller only requires feedback signals from a fraction of nodes in the neighborhood determined by the corresponding controlled area (21, 22). This is also true for the detection and monitoring of unforeseen failures and cyberattacks, which find several applications in supply networks (23), power grids (24, 25), and autonomous vehicle coordination (26). Similarly, in biomedical applications, estimation (diagnosis) and control (intervention) often require monitoring of a reduced set of variables in the respective networks (27, 28). Examples include regulatory network states associated with cancer (10) and brain network states associated with Parkinson’s disease (29) and epilepsy (30).

These practical problems motivate the concept of functional observability (31, 32), which characterizes the existence of a functional observer capable of reconstructing a targeted subset of state variables from a limited number of sensors—even when the network is not completely observable. Functional observability can be related to the concept of target controllability (33–37), which establishes the conditions for the existence of a controller capable of steering a targeted subset of state variables and has been applied to problems of drug target identification (38). However, despite the duality between (complete) controllability and observability (2), such duality does not hold between target controllability and functional observability. This is the case because as we show, the state estimation of a subset of variables requires a stronger condition than the dual condition to the control of a subset of variables. Even though the design of functional observers is a problem that dates back to the 1970s (39–41), previous studies on functional observability (31, 32, 42) were based on numerical rank-based conditions, without explicitly taking advantage of the network topology, and thus do not lead to scalable algorithms applicable to large-scale networks.

In this paper, we develop a graph-theoretic characterization of functional observability and the associated algorithms for sensor placement and observer design, making it possible to accurately estimate the target states of a large-scale dynamical network using minimal sensing and computational resources. The contributions of this work are threefold. First, we propose the concept of structural functional observability, which can be seen as a generalization of Lin’s structural observability (15). This allows us to rigorously establish graph-theoretic conditions for functional observability equivalent to the original rank-based conditions (32). Second, based on the proposed theory, two highly scalable algorithms are developed to solve the sensor placement and observer design problems. The first algorithm determines a minimal set of sensors placed on a dynamical network to ensure functional observability with respect to a given set of target nodes. After the sensor placement is decided, the second algorithm designs a minimum-order functional observer whose output converges asymptotically to the target states, achieving accurate estimation. Third, we demonstrate the advantages of the proposed methods with two concrete applications: the cybersecurity of power grids and the monitoring of epidemic spreading. In power grids, we show that the proposed functional observers can be implemented as active detectors of cyberattacks, effectively providing state estimates that allow for cross-validation among different information sources and the detection of fake measurement data in real time. In epidemics such as the COVID-19 pandemic, we demonstrate that the proposed functional observer can infer the fraction of infected population in areas where testing is limited from the data collected in areas with sufficient testing; moreover, our algorithms can also guide the optimal allocation of limited testing resources.

Results

Complete and Functional Observability of Dynamical Systems.

A general linear dynamical system can be written as

$$\begin{array}{l}\{\begin{array}{l}\dot{\text{x}}=A\mathit{x}+B\mathit{u},\hfill \\ \mathit{y}=C\mathit{x},\hfill \end{array}\hfill \end{array}$$ [1]

where $\mathit{x}\in {\mathbb{R}}^n$ is the vector of state variables, $\mathit{u}\in {\mathbb{R}}^p$ accounts for the control inputs or environmental influences, and $\mathit{y}\in {\mathbb{R}}^q$ represents the direct measurement from available sensors in the system. Matrix A, which is referred to as the system matrix, encompasses the nodal dynamics and network interactions—and can thus correspond to an adjacency matrix, a Laplacian matrix, or more generally, a Jacobian matrix of the system. The system is completely observable if it is possible to reconstruct the entire state trajectory $\mathit{x}(t)$ from the input vector $\mathit{u}(t)$ and measurement vector $\mathit{y}(t)$. Complete observability is guaranteed when the $nq\times n$ observability matrix

$$\mathcal{O}={\left[\begin{array}{ccccc}{C}^{\mathrm{T}}& {(CA)}^{\mathrm{T}}& {(C{A}^2)}^{\mathrm{T}}& \dots & {(C{A}^{n-1})}^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}}$$ [2]

has full rank (43) [i.e., $\text{rank}(\mathcal{O})=n$]. Under this rank condition, there exist straightforward methods to design a full-state observer. Such observer is an auxiliary dynamical system whose states converge asymptotically to those of the original system (Eq. 1) when taking y and u as inputs, providing an estimation of the state vector $\mathit{x}$. Since the direct measurement $\mathit{y}$ already contains q linear combinations of state $\mathit{x}$, only $(n-q)$ state variables are required to be reconstructed, which can be accomplished by a reduced-order state observer that we refer to as the Luenberger observer (3) (Materials and Methods has details).

In practice, it is often unnecessary to estimate the entire state vector x. Instead, only a lower-dimensional function $\mathit{z}=F\mathit{x}\in {\mathbb{R}}^r$ is of interest, where r can be much smaller than n. Given the desirable F, functional observability characterizes the system property that enables the reconstruction of $\mathit{z}$ from $\mathit{u}$ and $\mathit{y}$ (31). The system is functionally observable if and only if (32, 44)

$$\text{rank}\left[\begin{array}{c}\mathcal{O}\\ F\end{array}\right]=\text{rank}\left(\mathcal{O}\right);$$ [3]

that is, if and only if the row space $\text{row}(F)$ is a subspace of the observable space $\text{row}(\mathcal{O})$. Clearly, complete observability is a special case of functional observability for F = I. However, the condition in Eq. 3 only guarantees the theoretical existence of a functional observer (32). It does not readily lead to an algorithm to design a functional observer (31, 44), for which two additional conditions must be satisfied (40):

$$\text{rank}\left[\begin{array}{c}C\\ CA\\ F_0\\ F_{0}A\end{array}\right]=\text{rank}\left[\begin{array}{c}C\\ CA\\ F_0\end{array}\right],$$ [4]

$$\text{rank}\left[\begin{array}{c}\lambda F_0-F_{0}A\\ CA\\ C\end{array}\right]=\text{rank}\left[\begin{array}{c}CA\\ C\\ F_0\end{array}\right],$$ [5]

where $F_0\in {\mathbb{R}}^{r_0\times n}$ and Eq. 5 must hold for every eigenvalue λ of A. If a triple (A, C, F) satisfies Eq. 3, then there exists some matrix F₀ whose row space contains that of F [i.e., $\text{row}(F_0)\supseteq \text{row}(F)$] that satisfies Eqs. 4 and 5 for the triple $(A,C,F_0)$ (31). A functional observer of order $r_0\ge r$ can be designed systematically after such a matrix F₀ is determined (Materials and Methods). Finding a matrix F₀ with the minimum number of rows r₀ satisfying these conditions is then a crucial problem since the functional observer order is directly related to the computational costs of its design and real-time simulation (as demonstrated below).

Structural Functional Observability.

The rank-based conditions (Eqs. 3–5) are not numerically stable and computationally efficient for the design of functional observers for large-scale systems. Here, we adopt a graph-theoretic approach that explicitly leverages the network structure of the dynamical system. The system matrix A can be structurally represented as a corresponding inference graph $\mathcal{G}(A)$ whose nodes are the internal state variables $\mathcal{X}=\{x_1,\dots ,x_n\}$. The links in $\mathcal{G}(A)$ capture the interaction pattern among state variables: there is a link from x_j to x_i on the graph $\mathcal{G}(A)$ if A_ij is nonzero. A node x_j on graph $\mathcal{G}(A)$ is a sensor node if $C_{ij}\ne 0$ for some i, and a node x_k is a target node if $F_{ik}\ne 0$ for some i. The sets of all sensor and target nodes are denoted $\mathcal{S}$ and $\mathcal{T}$, respectively. We assume that each sensor or target is only related to one internal state variable, meaning that each row of C or F has only one nonzero entry. Throughout, the terms nodes and links are used exclusively in connection with inference graphs and are not to be confused with the vertices and edges, which are the corresponding terms used for the network systems. Fig. 1A illustrates the representation of the inference graph $\mathcal{G}(A)$ and the set of nodes estimated by a minimum-order functional observer for the indicated sensor and target nodes in a 10-dimensional system.

Fig. 1.

Structural functional observability of dynamical systems. (A) System matrix A and corresponding inference graph $\mathcal{G}(A)$. The set of state variables $\mathcal{X}=\{x_1,\dots ,x_{10}\}$ is represented by nodes on the graph, where the set of sensor nodes $\mathcal{S}=\{x_5,x_8\}$ (defined by C) is marked in blue and the set of target nodes $\mathcal{T}=\left\{x_{10}\right\}$ (defined by F) is marked in red. In this example, the system is unobservable [$\text{rank}(\mathcal{O})=9<n$], but it is functionally observable [$\text{rank}{[{\mathcal{O}}^{\mathrm{T}}\hspace{0.17em}\hspace{0.17em}{F}^{\mathrm{T}}]}^{\mathrm{T}}=\text{rank}(\mathcal{O})$], enabling the design of a functional observer. We show the minimum-order matrix F₀ such that $(A,C,F_0)$ satisfies Eqs. 4 and 5. Nonzero elements in F₀ determine the minimum set of auxiliary nodes (highlighted in orange) whose states also have to be estimated by a functional observer in order to estimate the state of the target node. The number of rows of F₀ is the order of the functional observer: $r_0=2$. (B) Example of a system that is observable and hence functionally observable. Since the system is completely observable, a Luenberger observer can be designed. However, while such Luenberger observer has order $n-q=8$ because it estimates the state of every unmeasured node, a functional observer can estimate the target node x₁₀ with the much smaller order $r_0=2$. (C) Minimum sensor set for functional observability. For the same graph and target set as in B, the sensor node x₅ is a minimum sensor set required for the functional observability of x₁₀. However, the absence of sensor node x₈ increases the functional observer order to $r_0=7$. (D) Functional observability in a strongly connected graph. Due to the stronger connectivity, the functional observer order increases to $r_0=5$ (compared with B) while remaining smaller than the Luenberger observer order $n-q=8$. Differences between graphs are indicated by the pink links.

A system given by the triple (A, C, F) is said to be structurally functionally observable if there exists a functionally observable triple $(\tilde{A},\tilde{C},\tilde{F})$, which shares the same structure as (A, C, F). We define that triples (A, C, F) and $(\tilde{A},\tilde{C},\tilde{F})$ have the same structure if, according to the representation described above, they share the same inference graph $\mathcal{G}(A)$, sensor set $\mathcal{S}$, and target set $\mathcal{T}$. Thus, structural functional observability is purely determined by the state interaction structure encoded by graph $\mathcal{G}(A)$, the sensor node set $\mathcal{S}$, and the target node set $\mathcal{T}$—which are all independent of the specific numerical entries of (A, C, F). In fact, if a triple (A, C, F) is structurally functionally observable, a system that shares the same structure as (A, C, F) is functionally observable with probability one.

This structural approach allows us to establish a graph-theoretic characterization of functional observability:

A system (A, C, F) is structurally functionally observable if and only if 1) there exists a direct path from every target node to some sensor node and 2) no target node is an element of a minimal subset of nodes with a dilation.

A rigorous proof of this theorem is given in SI Appendix, section 2. This result can be seen as a significant generalization of Lin’s theory of structural controllability and, by duality, of structural observability (15). Note that when F = I (or equivalently, $\mathcal{T}=\mathcal{X}$), our definition of structural functional observability reduces to Lin’s structural observability. The latter states that a pair (A, C) is structurally observable if and only if 1$\prime$) there exists a direct path from every state node to some sensor node and 2$\prime$) the corresponding graph has no dilations. More background on structural observability is presented in SI Appendix, section 1. We further illustrate this characterization in Fig. 1A, where the inference graph has no dilations due to the presence of self-links and thus satisfies conditions 2 and 2$\prime$ for structural functional and complete observability, respectively. However, because node x₉ does not have a direct path to a sensor node, condition 1$\prime$ for structural observability is not satisfied for the pair (A, C). Nevertheless, condition 1 is satisfied for structural functional observability of the triple (A, C, F) since one can identify a path from the target node x₁₀ to a sensor node (x₅ or x₈), hence rendering (A, C, F) structurally functionally observable.

The above result lays a foundation for the functional observer design in large-scale dynamical networks. To enable the algorithm development, we further investigate two main design problems:

• 1)How do we select the minimum set of sensor nodes $\mathcal{S}$ such that a triple (A, C, F) is structurally functionally observable?
• 2)Given a structurally functionally observable triple (A, C, F), how do we determine the minimum-order matrix F₀ such that Eqs. 4 and 5 are satisfied for $(A,C,F_0)$ ? (In other words, what is the minimum set of “auxiliary” state nodes that must be estimated along with the target nodes so that the systematic functional observer design is possible?)

The examples in Fig. 1 B–D illustrate that both questions are intertwined and inherently related to the structure of $\mathcal{G}(A)$.

In the following sections, we assume that no target node is an element of a minimal subset of nodes with a dilation. A sufficient condition for this latter assumption is that every target node has a self-link. The importance of including self-links in dynamical networks models, especially for state control and estimation applications, has been thoroughly discussed in the literature (7, 45, 46). Indeed, dilations are not found in a broad range of dynamical networks, including diffusively coupled systems. Our assumptions can be satisfied for applications in networks of coupled oscillators (47–49), power grids (50, 51), neuronal systems (52, 53), combustion networks (18, 54), regulatory networks (55, 56), consensus problems (21), and multigroup epidemiological models (57).

Minimum Sensor Placement for Functional Observability.

According to the theory and assumptions discussed above, the minimal sensor placement problem is to determine a minimum set $\mathcal{S}$ such that there is a direct path in $\mathcal{G}(A)$ from every target node to some sensor node. We show that the minimum sensor placement problem can be formulated as a set cover problem. For each candidate sensor node, let ${\mathcal{R}}_i$ denote the set of target nodes that have a direct path to the state node $x_i\in \mathcal{X}$. By this definition, the minimal sensor placement amounts to identifying the minimal sensor set $\mathcal{S}$ such that the union of the sets ${\mathcal{R}}_i$ for all $x_i\in \mathcal{S}$ covers the target set $\mathcal{T}$ (i.e., ${\cup }_{x_i\in \mathcal{S}}{\mathcal{R}}_i\supseteq \mathcal{T}$). This is an NP-hard problem (58), to which we provide an approximate but highly scalable solution via Algorithm 1 (Materials and Methods), where a breadth-first search determines ${\mathcal{R}}_i$ for each node $x_i\in \mathcal{X}$ and a greedy algorithm solves the set cover problem. Owing to the submodularity of the problem (59), this approximation is guaranteed to be near optimal.

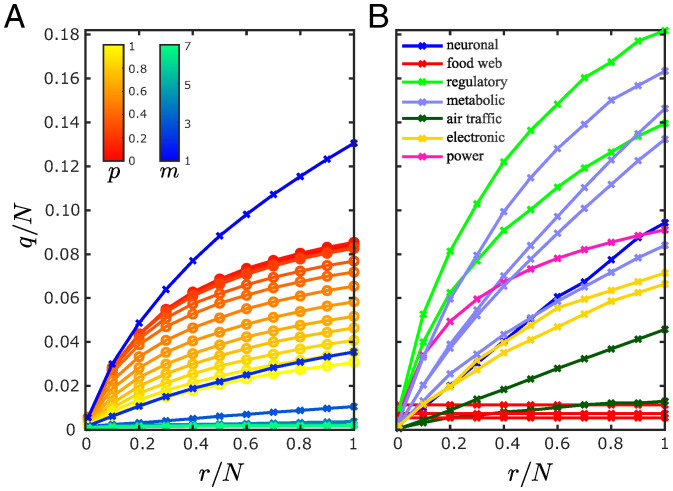
Fig. 2 illustrates the application of Algorithm 1 to randomly generated small-world (SW) and scale-free (SF) networks as well as a selection of real-world networks. As expected, the results show that a smaller number of target nodes tends to require a smaller number of sensor nodes to guarantee the functional observability of a system. Fig. 2A shows, however, that the relation between the minimum set of sensor nodes and the number of target nodes depends on the network structure, where the number of sensor nodes can be substantially smaller if the network connectivity is larger (i.e., higher parameters p and m in SW and SF networks, respectively). Similar conclusions are also noted for the real-world networks shown in Fig. 2B. As r approaches n, the minimum number of sensor nodes tends to the number required for complete observability. For example, in the metabolic networks analyzed, complete observability requires monitoring 8 to 16% of all metabolites, which is consistent with previous findings (11). However, complete observability is often unnecessary for many biomedical applications since the number of biomarkers (e.g., target nodes whose activity is altered by a disease) is usually much smaller than the network size ($r\ll N$) (27). If only 1% of the metabolites are biomarkers, then functional observability can be guaranteed by placing sensors in only 0.17 to 0.24% of the state nodes. Moreover, SI Appendix, Fig. S3 shows that, for the same metabolic networks, around 78 to 85% of all metabolites are observable from a single optimally placed sensor node. This means, in particular, that in applications where all target nodes belong to this set of observable nodes, functional observability can be achieved with even fewer sensor nodes than shown in Fig. 2B (where the targets were randomly chosen). In addition to their significance for biological and ecological networks, these results are also relevant for cyber–physical systems in engineering applications (e.g., power grids and transportation networks), where the monitoring and detection of potential failures or cyberattacks are often required to be conducted in specific nodes.

Fig. 2.

Minimum sensor placement in large-scale networks. Minimum number of sensors q as a function of the number of target nodes r (normalized by the network size N) in (A) randomly generated directed SW and SF networks and (B) real-world networks. Each data point is an average over 100 realizations of randomly selected target nodes. The minimum set of sensor nodes $\mathcal{S}$ is determined using Algorithm 1. The SW and SF networks were generated with $N={10}^4$ vertices, where each vertex is a three-dimensional subsystem (i.e., $n=3N$), while vertices in the real-world networks are assumed to be one-dimensional subsystems (i.e., n = N). The SW networks were generated using the Newman–Watts model, where p is the probability of adding a new edge, and the SF networks were generated using the Barabási–Albert model, where m is the number of existing vertices a new vertex is connected to. Materials and Methods has more details on the network datasets and models.

Minimum-Order Functional Observer Design.

After the sensor nodes have been selected, we need to further choose a matrix F₀ to enable the design of a functional observer. The theoretical problem of finding a minimum-order F₀ that satisfies Eqs. 4 and 5 was solved in the past decade (31). However, a direct numerical implementation of the method (42) is not scalable for high-dimensional systems because it iteratively uses singular value decomposition (SVD) to construct a matrix F₀ that satisfies Eq. 4 and is followed by a combinatorial search to augment the number of rows of F₀ in order to satisfy Eq. 5 (SI Appendix, section 4). We circumvent these issues by adopting the structural approach described in the previous sections, in which we convert the rank-based conditions (Eqs. 4 and 5) into equivalent graph-theoretic ones. This is achieved by first noting that, if the corresponding graph of a dynamical system has a self-link in every target node (as assumed throughout), then Eq. 4 implies Eq. 5 with probability one for triples $(A,C,F_0)$ sharing the given structure (SI Appendix, corollary 1). In light of this, only Eq. 4 needs to be considered to determine F₀, and hence the combinatorial search is no longer needed. We thus propose Algorithm 2 (Materials and Methods) as a highly scalable solution to determine matrix F₀ with the smallest order possible by adding suitable rows to F in such a way that Eq. 4 is satisfied. In Algorithm 2, instead of invoking SVD, the rank condition in Eq. 4 is verified by computing the maximum matching set of an associated bipartite graph. The algorithm is shown to have a computational complexity of order $O(n^{2.5})$ (Materials and Methods), which is a substantial improvement compared with the complexity of order $O(n^{2.5})$ of the numerical procedure in ref. 42.

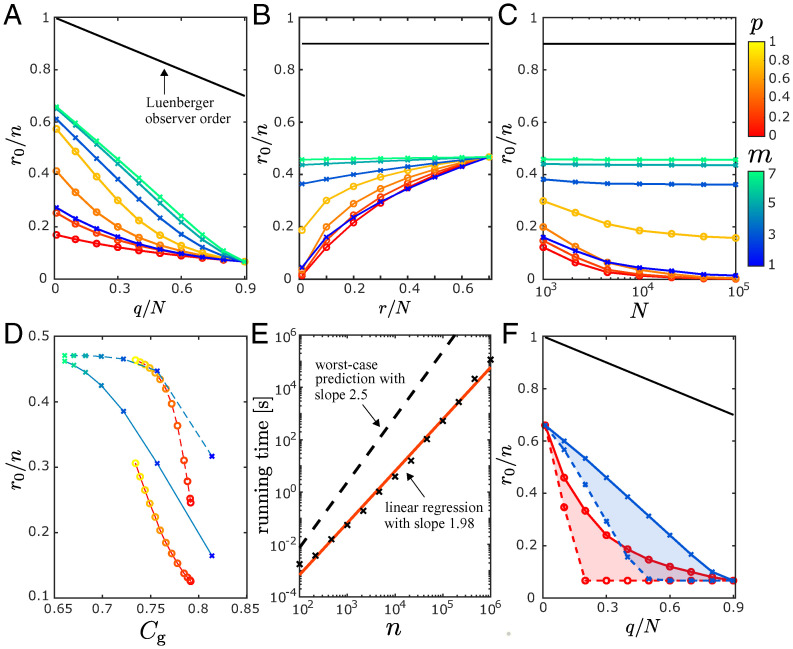
Fig. 3 A and B illustrates the minimum order of the functional observer for randomly generated networks, determined by Algorithm 2, as a function of the numbers of sensor and target nodes. On average, a larger sensor set $\mathcal{S}$ leads to a lower order r₀, whereas a larger target set $\mathcal{T}$ results in a higher order r₀. We note that, overall, functional observers are of much lower order compared with the corresponding Luenberger observers. This leads to a significant improvement in computation efficiency and scalability when designing and implementing observers in large-scale networks. For a fixed number of target nodes, Fig. 3C shows that the functional observer order normalized by the system dimension, $r_0/n$, tends to decrease as the network size increases (in SF networks, $r_0/n$ exhibits weaker dependency on N as m increases). This means that the order reduction gained by the functional observer compared with the Luenberger observer increases with the network size. The extent of this gain depends, however, on other system properties, including the structure of the inference graph $\mathcal{G}(A)$, the choice of target nodes in $\mathcal{T}$, and how sensor nodes in $\mathcal{S}$ are placed. In particular, directed links, self-links, and clustering in $\mathcal{G}(A)$ tend to lead to a larger order reduction in the functional observer design for the random model networks considered. This is illustrated in Fig. 3D, where it is shown for both directed and undirected networks that the functional observer order decreases sharply as a function of the generalized clustering $C_{\text{g}}$, which is defined to account for both clustering and self-links (Materials and Methods). Interestingly, although directed graphs require a larger minimum set of sensor nodes to guarantee the structural functional observability of a system compared with undirected graphs [which only require one sensor node (45)], directed graphs allow the design of functional observers of smaller orders. This result also highlights that Algorithm 2 brings computational improvement for both directed and undirected network applications compared with existing ones. Furthermore, Fig. 3E illustrates how the running time of Algorithm 2 scales with the network size, showing that it does not surpass our worst-case prediction.

Fig. 3.

Minimum-order functional observer design in large-scale networks. (A–C) Minimum functional observer order r₀ (normalized by the system dimension $n=3N$) as a function of the normalized number of sensor nodes q / N (A), the normalized number of target nodes r / N (B), and the network size N (C). The results are shown for random placement of sensor and target nodes in directed SW and SF networks (color coded by the respective parameters p and m). The other parameters are set to $(N,r)=({10}^4,0.1N)$ for A, $(N,q)=({10}^4,0.3N)$ for B, and $(q,r)=(0.3N,100)$ for C. The black lines indicate the Luenberger observer order $(n-q)$ for comparison. (D) Normalized order $r_0/n$ in directed (solid lines) and undirected (dashed lines) SW and SF networks as a function of the generalized clustering of the corresponding undirected graph (Materials and Methods), color coded by p and m for $(N,q,r)=({10}^4,0.3N,0.1N)$. (E) Running time of Algorithm 2 as a function of n in directed SW networks for $(q,r,p)=(0.3N,0.1N,0.2)$. The simulations were implemented in MATLAB, and each network realization was run on a single core of an Intel Xeon Processor E7-8867 v4 at 2.4 GHz. (F) Normalized order $r_0/n$ as a function of q / N in undirected SW (red; p = 0) and SF (blue; m = 3) networks for randomly (solid lines) and optimally (dashed lines) placed sensors, where $(N,r)=(100,0.1N)$. In all panels, each data point corresponds to an average over 100 independent realizations of the network, target placement, and sensor placement (except for the optimal placement in F).

The results shown in Fig. 3 A–E concern sensors and targets randomly placed in the inference graph. The sensor placement, in particular, was implemented by first finding the minimum set of sensor nodes for functional observability and then, increasing q with randomly placed sensor nodes. As shown in Fig. 3F for undirected networks, the functional observer order r₀ decreases on average as the number of sensors increases, even if the placement is random. However, r₀ can be further reduced by optimizing the placement of the additional sensors. This is a computationally demanding bilevel optimization problem, which—for illustration purposes only—we solve using a (nonscalable) greedy algorithm (Materials and Methods). Fig. 3F shows that such optimization indeed leads to a functional observer with a consistently smaller order compared with the average order for randomly placed sensors. Even though this specific result is illustrated in a lower-dimensional setting, we extrapolate from Fig. 3C that this optimal sensor placement can be relevant for systems of any dimension.

Comparative Analysis of the Observers.

Fig. 4 compares the performances of the functional observer and Luenberger observer when estimating the target variables of a large-scale network. For the target state evolution illustrated in Fig. 4A, which is representative of a trajectory starting away from equilibrium, the transients of the target state estimation error $\left|\right|\mathit{z}(t)-\widehat{\mathit{z}}\prime (t)\left|\right|$ are presented in Fig. 4B for both observers initialized with unknown initial conditions (SI Appendix, section 4). It can be seen that the functional and Luenberger observers have similar dynamical behavior and that their estimates converge to the target states of the system. Statistical analysis further reveals that the two observers perform asymptotically close to each other even under the effects of modeling errors in the system matrix A (Fig. 4C). (Note that if the system were functionally, but not completely, observable, then the target estimation error is only guaranteed to converge for the functional observer.)

Fig. 4.

Comparative performance of the observers for target state estimation in large-scale networks. (A) Dynamical evolution of the target vector $\mathit{z}(t)=F\mathit{x}(t)$, where each color represents a different target variable $z_i(t)$. (B) Dynamical evolution of the target state estimation error $\left|\right|\mathit{z}(t)-\widehat{\mathit{z}}\prime (t)\left|\right|$, where $\mathit{z}(t)$ is the “true vector value” of the target state and $\widehat{\mathit{z}}\prime (t)$ is the estimated target state provided by the functional (blue) or Luenberger (orange) observer initialized with random estimates. (C) Histogram of the steady-state estimation error $\left|\right|\mathit{z}(t_{\text{f}})-\widehat{\mathit{z}}\prime (t_{\text{f}})\left|\right|$ for $t_{\text{f}}=4$ s, where both observers are designed using a system matrix $\tilde{A}$ for different modeling errors σ. Here, each matrix entry is drawn from a uniform distribution as ${\tilde{A}}_{ij}\sim \mathcal{U}[(1-\frac{\sigma }{2})A_{ij},(1+\frac{\sigma }{2})A_{ij}]$. (D) Running time of the design algorithms (Left) and simulation time of the observer dynamics (Right) as a function of the network size N (computer specifications are in Fig. 3E). The color code in C and D is the same as in B. In all panels, the results are shown for directed SW networks with randomly selected sensor and target nodes. The undeclared parameters are set as $(N,n,p,q,r)=({10}^3,3N,0.2,0.3N,0.1N)$, where each parameter choice in C and D corresponds to 100 realizations of the network, sensor and target selection, and modeling errors (σ = 0 in D). SI Appendix, section 4 has details on the simulations.

Overall, the numerical results show that the considerable order reduction demonstrated here for the functional observer design does not compromise its efficacy. Fig. 4D, on the other hand, shows that such order reduction significantly reduces the computational costs both in the design (Algorithm 2) and in real-time simulations of the functional observer. This computational advantage of functional observers makes them superior or even indispensable to observe large-scale networks, especially when continual redesign of the observer is expected due to the evolution of the system’s equilibrium and/or network structure.

Cyberattack Detection in Power Grids.

The control of man-made technological systems, such as power grids, supply networks, interconnected autonomous vehicles, and swarms of robots, is supported by sensing and communication infrastructure. Decentralized control strategies (60), such as wide-area control in power grids (22), are important to maintain system stability and in particular, mitigate the impact of perturbations that could lead to large-scale failures (61). However, such control strategies rely on resilient communication networks between spatially distributed components, which are arguably more vulnerable to potential failures and cyberattacks than the physical systems themselves. Indeed, there have been growing threats to cybersecurity, including cyberattacks to supervisory control and data acquisition systems, which led to the massive 2015 power outages in Ukraine (62), the 2000 Maroochy Water Services breach in Australia (63), the 2010 Stuxnet computer worm attack on Iran’s nuclear program (64), and communication outages in the western United States power grid in March 2019 (65).

Two common types of cyberattacks are denial of service attacks (e.g., via signal jamming) and deception attacks (e.g., via data corruption) (66). Depending on the specifics of the attack, modeling of the physical system dynamics and transmitted data can still be used to design observers capable of recovering lost data through state estimation. Crucially, state estimation can also be used to detect deception attacks (23, 67, 68), which is significant because such attacks are designed to evade detection. We now show, in the context of power grids, how functional observers can be implemented for cyberattack detection and data recovery and the extent of their computational efficiency improvement compared with the traditional full-state estimators.

The power-grid dynamics can be modeled as a structure-preserving network of coupled first- and second-order Kuramoto oscillators (50, 51). In this model, the generators dynamics are governed by the so-called swing equation,

$$\frac{2H_i}{{\omega }_{\text{R}}}{\ddot{\varphi }}_i+\frac{D_i}{{\omega }_{\text{R}}}{\dot{\varphi }}_i=P_i+{\displaystyle \sum _{j=1,j\ne i}^N{K}_{ij}}\sin ({\varphi }_j-{\varphi }_i),$$ [6]

for $i=1,\dots ,n_{\text{g}}$, and the dynamics of load buses and generator terminals are described as first-order phase oscillators,

$$\frac{D_i}{{\omega }_{\text{R}}}{\dot{\varphi }}_i=P_i+{\displaystyle \sum _{j=1,j\ne i}^N{K}_{ij}}\sin ({\varphi }_j-{\varphi }_i),$$ [7]

for $i=n_{\text{g}}+1,\dots ,N$, where $n_{\text{g}}$ is the number of generators, $n_{\text{l}}$ is the number of load buses, $N=2n_{\text{g}}+n_{\text{l}}$ is the number of oscillators (vertices), and $n=N+n_{\text{g}}$ is the system dimension. Here, ${\varphi }_i(t)$ is the phase angle of oscillator i at time t relative to the frame rotating at reference frequency ${\omega }_{\text{R}}$, and H_i and D_i are the inertia and damping constants, respectively. In addition, $K_{ij}=V_i{V}_j{B}_{ij}$, where B_ij is the susceptance of the transmission line connecting buses i and j and V_i and V_j are the voltage magnitudes at these buses. If there is no line connecting buses i and j, K_ij = 0. The power injection P_i represents power generation for $P_i>0$ and power consumption for $P_i<0$.

We illustrate our framework on the IEEE-118 benchmark system given by the diagram in Fig. 5A and parameters in Materials and Methods. Fig. 5A, Inset shows a zoomed-in representation of the corresponding inference graph of the power-grid model (Eqs. 6 and 7) around an equilibrium point. We assume that the power grid is equipped with phasor measurement units (PMUs) randomly placed on a subset of load and generator terminal buses, comprising the set of sensor nodes $\mathcal{S}\subseteq \{{\varphi }_{n_{\text{g}}+1},\dots ,{\varphi }_N\}$. The PMU measurements are transmitted to a control center in real time to support automated control actions, human decision making, and cyberattack detection. We assume the system initially operates in steady state when, taking advantage of an otherwise inconsequential perturbation at time t = 1 s (Fig. 5B), a deception cyberattack tampers with the measured data ${\varphi }_{\text{a}}(t)$ from one of the sensors, transmitting instead false data ${\tilde{\varphi }}_{\text{a}}(t)$ to the control center for t > 1 s. For illustration purposes, in Fig. 5C, we assume that the false data are copied from the measurements of some neighboring vertex j [i.e., ${\tilde{\varphi }}_{\text{a}}(t)=\{{\varphi }_j(t):K_{\text{a}j}>0\}$].

Fig. 5.

Deception attack detection in a power grid. (A) Diagram of the IEEE-118 network, which comprises 118 buses with $n_{\text{g}}=54$ generators (black circles), each connected to a terminal bus (gray circles), and $n_{\text{l}}=64$ loads (gray squares). PMUs are randomly placed in $\left|\mathcal{S}\right|=n_{\text{g}}/3$ load and generator terminal buses (blue symbols). The deception attack tampers with the transmitted measurement ${\overline{\varphi }}_{\text{a}}(t)$ from the highlighted PMU (red circle). Inset illustrates the inference graph of the dynamical system, where each generator bus (vertex) is represented by two state nodes (phase ${\varphi }_i$ and frequency ${\dot{\varphi }}_i$ in Eq. 6) and each generator terminal and load bus is represented by a single state node (phase ${\varphi }_i$ in Eq. 7). Links with state nodes outside the highlighted neighborhood are omitted. (B) Dynamics of the oscillators’ phases ${\{{\varphi }_i(t)\}}_{i=1}^N$ and the generators’ frequencies ${\{{\dot{\varphi }}_i(t)\}}_{i=1}^{n_{\text{g}}}$ over time t. An additive perturbation, drawn from the Gaussian distribution $\mathcal{N}(0,0.01)$, is applied to each generator’s phase in steady state at t = 1 s. (C) Functional observer-based detection of a deception attack, where the transmitted measurement ${\overline{\varphi }}_{\text{a}}(t)$ of the terminal’s phase ${\varphi }_{\text{a}}(t)$ (blue solid line) is replaced by the false data ${\tilde{\varphi }}_{\text{a}}(t)$ (red solid line). The data are reconstructed with the state estimates ${\widehat{\varphi }}_{\text{a}}^{(\ell )}(t)$ provided by different functional observers (colored dashed lines), where the shaded window illustrates a time of detection $t_{\text{d}}=0.5$ s. (D) Histogram of the RMSE between the transmitted measurement ${\overline{\varphi }}_{\text{a}}(t)$ and the state estimates ${\widehat{\varphi }}_{\text{a}}^{(\ell )}(t)$ provided by the functional observers $\ell =1,\dots ,100$ as a function of $t_{\text{d}}$. The histograms are shown for the system under attack (red) and not under attack (blue), where an estimate of the statistical properties of the latter can be inferred from training data. Each histogram comprises 10,000 data points corresponding to 100 independent realizations of the system perturbations with 100 functional observers designed for each realization. The contoured histogram at $t_{\text{d}}=1$ s represents the hardest to detect attack (smallest median value) for the simulated perturbations. (E) Running time of the observer design as a function of the observer order. The results are color coded for functional (blue scale) and Luenberger (red scale) observers as the number of sensors $\left|\mathcal{S}\right|$ is varied for 100 independent realizations, where the placement of the attack and PMUs is random in each realization and each data point is an average over 100 observers. In all simulations, the observers were designed to estimate the target node ${\varphi }_{\text{a}}$ using the system model (Eqs. 6 and 7) linearized around the equilibrium point and ${\widehat{\varphi }}_{\text{a}}^{(\ell )}(t)={\varphi }_{\text{a}}(t)$ for t < 1 s (Materials and Methods has details).

We show that this cyberattack can be successfully detected by designing functional observers and cross-validating the transmitted measurements ${\overline{\varphi }}_{\text{a}}(t)$ against the state estimates ${\widehat{\varphi }}_{\text{a}}^{(\ell )}(t)$ of each observer $\ell$. This cross-validation takes place during the short transient dynamics that follow the perturbation, where ${\overline{\varphi }}_{\text{a}}(t)\leftarrow {\tilde{\varphi }}_{\text{a}}(t)$ if there is an attack and ${\overline{\varphi }}_{\text{a}}(t)\leftarrow {\varphi }_{\text{a}}(t)$ otherwise. Since one has no access to the true state estimation error ${\varphi }_{\text{a}}(t)-{\widehat{\varphi }}_{\text{a}}^{(\ell )}(t)$, such cross-validation is performed statistically, relying on the state estimation of multiple functional observers designed from distinct ${\mathcal{S}}^{(\ell )}\subset \mathcal{S}$, with cardinality $\left|{\mathcal{S}}^{(\ell )}\right|=\left|\mathcal{S}\right|/2$, as shown in Fig. 5C. To cross-validate the state estimates against the transmitted data, we use the root-mean-square error (RMSE) index:

$$\text{RMSE}=\sqrt{\frac{1}{t_{\text{d}}}{\displaystyle {\int }_1^{t_{\text{d}}+1}|}|{\overline{\varphi }}_{\text{a}}(t)-{\widehat{\varphi }}_{\text{a}}^{(\ell )}(t)|{|}^{2}dt},$$ [8]

where $t_{\text{d}}$ is the time of detection window defined as the time it takes to reliably detect an attack after it is launched. Clearly, the performance of the detection method depends on $t_{\text{d}}$ (shaded window in Fig. 5C), which is also a lower bound of the time interval under which the system is left unprotected waiting for a decision.

Fig. 5D shows that, after a short period of time ($\approx$ 0.25 s), the separation between the histograms corresponding to the attacked and unattacked systems becomes statistically significant so that reliable detection can be made. Since the separation between the two histograms becomes more pronounced as time increases, the detection becomes more accurate when a larger detection window is allowed. While the histograms show an aggregate representation of attacks under different perturbation scenarios, the same conclusions hold for individual attacks. In our simulations, reliable detection can be achieved even in the hardest to detect attack among all realizations, as illustrated by the contoured histogram for $t_{\text{d}}=1$ s. The asymptotic convergence of the functional observer is guaranteed if the perturbed state remains in the attraction basin of the given equilibrium. For larger perturbations crossing into the basin of a different equilibrium, the functional observer has to be redesigned around the new equilibrium. Thus, the extent to which the designed observer remains valid upon large perturbations is ultimately determined by the basin stability of the nonlinear system, which can be assessed numerically as proposed in refs. 69 and 70.

In applications with a constantly changing operation point, such as smart power grids, algorithms for the design of controllers and observers have to be sufficiently fast so that they can be implemented in real time following a change of the equilibrium operation point. Moreover, the statistical significance of the cyberattack detection method increases with the number of implemented observers. Thus, the method can be used statistically only if, in addition, the algorithms for the observer design are fast enough to allow for a sufficiently large number of observers to be implemented in real time. To that end, Algorithm 2 provides a fast and scalable solution for the design of minimum-order functional observers. Fig. 5E shows for the IEEE-118 system that the functional observer usually has a much smaller dimension than the Luenberger observer as the number of PMUs increases, leading to a running time reduction by a factor of up to a hundred. This example illustrates for a small power grid the results anticipated in Figs. 3 and 4, and we expect that the computational gain of the functional observers will increase as the network size increases (Fig. 4D).

Estimation of Epidemic Spreading under Limited Testing.

Motivated by the unprecedented impact of the COVID-19 pandemic, recent studies have highlighted the importance of epidemiological models for the design of containment measures. Such models are useful for understanding the growth patterns and scaling laws governing the epidemic spreading (71, 72) as well as for developing control strategies (73–75), which ultimately support policy-making decisions (76). For instance, these models can inform decisions on social distancing and quarantine measures, which cannot be taken lightly as they generally involve social and economic costs. The quality of the model predictions (and thus their ability to inform decisions) is strongly dependent on the state of the epidemic in a population, which is often only partially known due to limitations in testing and reporting. This is especially the case for a new and rapidly evolving pandemic since it takes time to mobilize medical resources and ramp up testing capacity. In particular, as illustrated in the early stages of the COVID-19 pandemic, the testing capacity can vary widely across cities even within the same country. Therefore, it is important to develop the ability to infer as much information as possible from the available incomplete data. Previous work has shown that state estimators can provide meaningful estimates of the true state of the number of infected, susceptible, and recovered individuals in an epidemic when sufficient data are available (74, 77).

Here, we show that, for target estimation, functional observers can be designed to provide reliable information using reduced testing data compared with full-state estimators. As the underlying dynamics in this case are inherently nonlinear, this will give us the opportunity to demonstrate that the methods established here for linear systems are also informative for nonlinear ones. We illustrate this application for the estimation of the infected population in a set of “target cities” (where testing is inadequate) from the known case fatality rate in a set of “sensor cities” (where sufficient testing is conducted). To this end, consider the multigroup model of the spreading of an infectious disease mediated by the air transportation network (57):

$$\begin{array}{l}\{\begin{array}{l}{\dot{S}}_i=-{\beta }_i\frac{S_i{I}_i}{P_i}-{\displaystyle \sum _{j=1,j\ne i}^N{K}_{ji}}\frac{S_i}{P_i}+{\displaystyle \sum _{j=1,j\ne i}^N{K}_{ij}}\frac{S_j}{P_j},\hfill \\ {\dot{I}}_i={\beta }_i\frac{S_i{I}_i}{P_i}-\gamma I_i-{\displaystyle \sum _{j=1,j\ne i}^N{K}_{ji}}\frac{I_i}{P_i}+{\displaystyle \sum _{j=1,j\ne i}^N{K}_{ij}}\frac{I_j}{P_j},\hfill \\ {\dot{R}}_i=(1-\eta )\gamma I_i,\hfill \\ {\dot{D}}_i=\eta \gamma I_i,\hfill \end{array}\hfill \end{array}$$ [9]

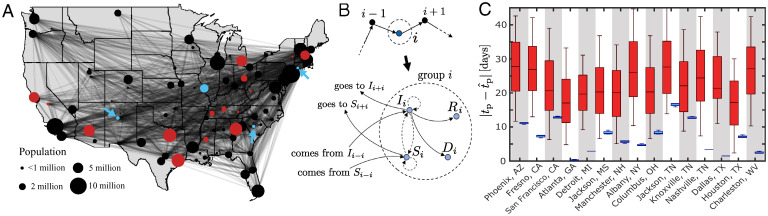
for $i=1,\dots ,N$, where N is the number of groups and $(S_i,I_i,R_i,D_i)$ are the susceptible, infected, recovered, and dead (SIRD) individuals of group i with population size $P_i=S_i+I_i+R_i+D_i$. Parameters γ and η are the recovery and fatality rates, respectively; β_i is the contact rate in group i; and K is the adjacency matrix of the transportation network, where K_ij describes the number of individuals traveling from group j to i daily. As indicated in Fig. 6A, we assume each group to be a city in the United States and matrix K to describe the air traffic between the cities’ airports, while $({\beta }_i,\gamma ,\eta )$ and K are chosen for illustration purposes to reflect the early stages of the COVID-19 epidemic (Materials and Methods). The epidemiological model (Eq. 9) can be represented as an inference graph, where each state variable is a node and links represent linear and nonlinear interactions between variables, as illustrated by Fig. 6B.

Fig. 6.

Target state estimation in epidemics. (A) US air transportation network, where vertices represent cities and edges represent the direct flights. The target (red) and sensor (blue) cities are highlighted. (B) Network flow between three cities (Upper) and the corresponding inference graph (Lower) of the dynamical system (Eq. 9). The dynamics are taken into account by expanding each vertex i as a set of SIRD state nodes, where links represent the linear (solid lines) and nonlinear (dashed lines) interactions between the state variables in the differential equations. (C) Box plot of the error between the time $t_{\text{p}}$ of the epidemic peak in each target city and the predicted peak time ${\widehat{t}}_{\text{p}}$. The red bars show predictions from free-run simulations, while the blue bars show predictions given by the estimates of the designed functional observer, both for 100 independent realizations with arbitrary initial conditions. The bottom, middle, and top of each box represent the 25th, 50th (median), and 75th percentiles of the sample, respectively; the whiskers mark the 5th and 95th percentiles. For illustration purposes, this example assumed an outbreak initiated in Miami, Florida, and its spreading dominated by domestic air transportation. Materials and Methods has simulation and modeling details.

Within the idealized model model described by Eq. 9, if the exact state of the epidemic is known at a given time, subsequent containment measures to “flatten the curve” could be designed based on a free-run simulation of the model. Unfortunately, this would not be the case in practice even if an accurate model was available because as noted above, there are limitations on how precise the data are on the number of infected individuals in a population. This is illustrated in Fig. 6C (red) for the predicted epidemic peaks in a set of 15 target cities. We circumvent this limitation by designing a functional observer that provides more reliable estimates of the number of infected individuals.

A salient property of this problem is that the epidemiological model (Eq. 9) is nonlinear. Our algorithms are not guaranteed to determine a minimum set of sensors and a minimum-order functional observer if the system is nonlinear. Notwithstanding, in many applications, Algorithms 1 and 2 can still be used to identify a small set of sensor nodes $\mathcal{S}$ (relative to the number of state variables) and a small order matrix F₀ (compared with that of a full-state observer) for the design of the corresponding nonlinear functional observer. In particular, it can be shown that the nonlinear functional observer for the system in Eq. 9 satisfies the theoretical conditions for asymptotic convergence of the state estimates (SI Appendix, section 5).

To design the functional observer, let a city i be a sensor (target) city if $D_i\in \mathcal{S}$ (if $I_i\in \mathcal{T}$) is a sensor (target) node. Given the specified set of target cities, Fig. 6A highlights the selected set of four sensor cities for functional observability as provided by Algorithm 1. We then design the nonlinear functional observer based on the inference graph associated with Eq. 9 and the sets $\mathcal{S}$ and $\mathcal{T}$ using Algorithm 2 (SI Appendix, section 5). Fig. 6C (blue) shows the estimated time of the epidemic peaks as provided by the designed nonlinear functional observer. Clearly, there is a great improvement in the estimation accuracy (i.e., a smaller deviation between realizations of different initial conditions), which highlights the observer’s resilience to false initial predictions. Note that this functional observer is designed in a situation where the system is unobservable but is functionally observable. This highlights a fundamental advantage of our approach: when the conventional full-state estimators are not applicable, our approach may still provide high-quality estimates of the nonlinear system’s state from sparse measurement data.

Discussion

In large-scale complex networks, it often is physically impossible to ensure complete observability or computationally prohibitive to design full-state observers. This poses fundamental challenges to our ability to observe, understand, and control network processes. Yet, many practical applications only require the observation of a small subset of key variables, which we formalize by introducing the notion of structural functional observability. This work establishes graph-theoretical conditions for functional observability, enabling direct application to large-scale network systems. In particular, the resulting theory allows us to devise highly scalable algorithms to optimally allocate sensors and design functional observers for accurate estimation of a target subset of all state variables.

Observability and controllability are dual properties in control theory (2), which lead to the natural question of what would be the dual of functional observability. By parallelism, one might be tempted to assume that a notion of “target observability” for the given target set could be defined as the target controllability condition (33) for the pair $(A^{\mathrm{T}},C^{\mathrm{T}})$. However, we argue that—in contrast with the target controllability condition for controller design—such a notion of target observability does not lead to the design of an observer capable of estimating the state of the target nodes. Crucially, target estimation in this sense can only be accomplished with functional observability, which is a stronger condition than target observability. Indeed, based on the observability Gramian, we can show that the initial condition of the target nodes is uniquely reconstructable from measurements if and only if Eq. 3 is satisfied (SI Appendix, section 3). This leads us to a fundamental conclusion: despite not being strictly dual, functional observability and target controllability are mirror properties in terms of their functionalities.

Applications of the results presented here may include cybersecurity in the decentralized control of infrastructure and multiagent systems; state estimation for epidemic and ecosystem management from incomplete observation; and identification of biomarkers for prognosis, diagnosis, and treatment. In biomedical and ecological applications, for example, assessment of the state of the system must not interfere significantly with the system dynamics in order to avoid mispredictions and adverse effects. Our results provide a framework under which variables of interest can be estimated from indirect measurements, avoiding variables that interfere with the system’s function and control actions. They also provide an alternative to reduce the computational costs associated with sensing, communication, and data processing in infrastructure, supply, and technological networks that require real-time feedback control (78).

This work also leads to fundamental questions worth pursuing in future research. First, because our theory allows a decision on whether the system is functionally observable or not from the graph structure of the model alone, it is natural to consider how to design functional observers when specific parameters of the system are unknown. This could be addressed by combining our graph-based methods with machine learning techniques to enable data-driven state estimation by functional observers. Second, while here we considered the sensor placement problem and functional observer design in a preexisting cyber–physical network, combining these approaches with the codesign of the communication (and/or physical) layers of the system can lead to further improved resilience against attacks and failures. In particular, the transition to renewable energy is leading to highly heterogeneous networks that integrate conventional synchronous generators, converter-based distributed generation units (solar and wind), flexible alternating current (AC) transmission systems, and high-voltage direct current transmission systems. To ensure the functional observability and stable operation of future power systems, detailed models of these critical components (79) can be incorporated in the codesign of the communication network for wide-area monitoring, protection, and control systems (80). Third, it would be interesting to examine the estimation accuracy, convergence rate, and stability of functional observers in large-scale systems under modeling uncertainties, measurement noise, and round-off errors. A systematic study of the theoretical performance of functional observers in the presence of bounded modeling and measurement errors is still an open problem in the literature, which may be approached in a framework dual to the problem of robust control (81). Finally, our application example to epidemics illustrates how the modeling of the system structure can be used to design functional observers in nonlinear systems. Deriving conditions that allow our methods to be extended to more general nonlinear systems with guarantees of optimality is left for future work.

Materials and Methods

Observer Design.

Both the Luenberger and the functional observer are auxiliary dynamical systems that can be designed under the following structure:

$$\begin{array}{l}\{\begin{array}{l}\stackrel{.}{\mathit{w}}=N\mathit{w}+J\mathit{y}+H\mathit{u},\hfill \\ \widehat{\mathit{z}}=D\mathit{w}+E\mathit{y},\hfill \end{array}\hfill \end{array}$$ [10]

where $(N,J,H,D,E)$ are design matrices with consistent dimension. In a properly designed Luenberger observer, $\widehat{\mathit{z}}$ converges asymptotically to the $(n-q)$ unmeasured states of the system (Eq. 1), while in a properly designed functional observer, $\widehat{\mathit{z}}$ converges asymptotically to ${\mathit{z}}_0=F_0\mathit{x}$. The initial state $\mathit{w}(0)$ of the observer can be assigned arbitrarily, and the initial state $\mathit{x}(0)$ is unknown.

Despite sharing the same equations (Eq. 10), the Luenberger and functional observers have very different orders (defined by the dimension of vector $\mathit{w}$) and involve very different design procedures. In what follows, the design procedure for each observer is presented using the linear transformation

$$P^{-1}AP=\left[\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right],\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}PB=\left[\begin{array}{c}{B}_1\\ B_2\end{array}\right],\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{F}_{0}P=\left[\begin{array}{cc}{F}_1& F_2\end{array}\right],$$ [11]

where $P=[C^{†}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{C}^{\perp }]$ is the transformation matrix, $C^{†}$ is the Moore–Penrose inverse of C, and $C^{\perp }$ is the orthogonal complement of the row space of C.

If (A, C) is observable, then a stable Luenberger observer (with arbitrary stable poles) can be designed by defining $N=A_{22}-E{A}_{12},\hspace{0.17em}J=A_{21}-E{A}_{11}+NE,\hspace{0.17em}H=B_2-E{B}_1$, and $D=I_{n-q}$, where E is a design matrix that can be found using any pole-placement algorithm such that $(A_{22}-E{A}_{12})$ is Hurwitz. Note that $\mathit{w}\in {\mathbb{R}}^{n-q}$.

If (A, C, F) is functionally observable and $(A,C,F_0)$ satisfies Eqs. 4 and 5 for some $\text{row}(F_0)\supseteq \text{row}(F)$, then a stable functional observer (with arbitrary stable poles) can be designed as follows (40, 41). 1) Compute $N_1=(\mathrm{\Phi }{\mathrm{\Omega }}^{†}{A}_{12}+F_2{A}_{22})F_2^{†}$ and $N_2=(\mathrm{\Omega }{\mathrm{\Omega }}^{†}-I_q)A_{12}{F}_2^{†}$, where $\mathrm{\Omega }=A_{12}{F}_2^{\perp }$ and $\mathrm{\Phi }=-F_2{A}_{22}{F}_2^{\perp }$. 2) Find Z using any pole-placement algorithm such that $N=N_1-Z{N}_2$ is Hurwitz. 3) Compute $T=[T_1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{T}_2]$, where $T_1=\mathrm{\Phi }{\mathrm{\Omega }}^{†}+Z(I_q-\mathrm{\Omega }{\mathrm{\Omega }}^{†})$ and T₂ = F₂. 4) Compute D = I_r, $J=T_1{A}_{11}+T_2{A}_{21}-N{T}_1$, H = TB, and $E=F_1-D{T}_1$. Note that $\mathit{w}\in {\mathbb{R}}^{r_0}$.

In this paper, we use the linear-quadratic regulator as a pole-placement algorithm, which requires solving the algebraic Riccati equation $X^{\mathrm{T}}P+PX-PY{R}^{-1}{Y}^{\mathrm{T}}P+Q=0$ for P. For the Luenberger observer design, let $E\leftarrow P,\hspace{0.17em}X\leftarrow A_{22}^{\mathrm{T}}+\alpha I$, and +

$Y\leftarrow A_{12}^{\mathrm{T}}$. For the functional observer design, let $Z\leftarrow P,\hspace{0.17em}X\leftarrow N_2^{\mathrm{T}}+\alpha I$, and $Y\leftarrow N_1^{\mathrm{T}}$. In both cases, we define $\alpha =-100$, $Q={10}^{-3}·I$, and R = I, which leads to observers with minimum estimation energy ($R\gg Q$). The diagonal terms in X guarantee that Z and E are designed to have the rightmost eigenvalues equal to α. This ensures that their dynamics are dominated by the same slowest eigenvalue, allowing a consistent comparison of the observers’ performance despite their different orders.

Minimum Sensor Placement Algorithm.

Algorithm 1 provides an approximate solution to the minimum sensor placement problem in polynomial time. The key steps are as follows. First, a breadth-first search is run for each target node (for loop), allowing us to determine the sets of target nodes ${\mathcal{R}}_i\subseteq \mathcal{T}$ that have a direct path to each state node $x_i\in \mathcal{K}\subseteq \mathcal{X}$ in $\mathcal{G}(A)$, where $\mathcal{K}$ is a set of candidate nodes for sensor placement. Note that a breadth-first search has a complexity of order $O(n+|\mathcal{E}|)$ (82), where $\left|\mathcal{E}\right|$ is the cardinality of the set of links $\mathcal{E}$ in $\mathcal{G}(A)$, and can be run in parallel for each $x_i\in \mathcal{T}$. Second, a greedy algorithm is used (while loop) to find an approximation of the minimum set of sensor nodes such that structurally functional observability is guaranteed. In the worst-case scenario, the greedy search has a complexity of order $O(n^2)$.

Algorithm 1:

Minimum sensor placement

input: inference graph $\mathcal{G}(A^{\mathrm{T}})$, target set $\mathcal{T}$, candidate set $\mathcal{K}$

output: sensor set $\mathcal{S}$

initialize ${\mathcal{R}}_i\leftarrow \varnothing ,\hspace{0.17em}\forall i=1,\dots ,\left|\mathcal{K}\right|$;

for all $x_i\in \mathcal{T}$

starting at node x_i in graph $\mathcal{G}(A^{\mathrm{T}})$, find the set of reachable nodes $\mathcal{R}{\prime }_i\subseteq \mathcal{X}$ using a breadth-first search algorithm;

for all $x_j\in \mathcal{K}$

 if $x_j\in \mathcal{R}{\prime }_i$, then ${\mathcal{R}}_j\leftarrow {\mathcal{R}}_j\cup \left\{x_i\right\}$;

end

end

initialize $\mathcal{S}\leftarrow \varnothing$.

do

for all $x_i\in \mathcal{K}\backslash \mathcal{S}$, compute gain

$$\mathrm{\Delta }(x_i)=\left|{\displaystyle \underset{j:x_j\in \mathcal{S}\cup \left\{x_i\right\}}{\cup }{\mathcal{R}}_j}\right|-\left|{\displaystyle \underset{j:x_j\in \mathcal{S}}{\cup }{\mathcal{R}}_j}\right|;$$ [12]

 add the element with the highest gain

$$\mathcal{S}\leftarrow \mathcal{S}\cup \{\arg \underset{{}_{x_i}}{\max }\mathrm{\Delta }(x_i)|x_i\in \mathcal{K}\backslash \mathcal{S}\};$$ [13]

while ${\cup }_{j:x_j\in \mathcal{S}}{\mathcal{R}}_j\ne \mathcal{T}$.

Minimum-Order Functional Observer Design Algorithm.

For cases where (A, C, F) is functionally observable, Algorithm 2 provides a scalable solution to the problem of determining F₀ of minimum order such that Eq. 4 is satisfied for the triple $(A,C,F_0)$ (SI Appendix, corollary 2). In this algorithm, we avoid numerical computation of the rank condition in Eq. 4, which is numerically unstable and computationally demanding for high-dimensional matrices [e.g., numerical rank computation based on SVD methods has a complexity of order $O(n^3)$]. Instead, we compute the structural (or generic) rank of a matrix by finding the maximum matching of the corresponding bipartite graph of such a matrix. This is a highly scalable alternative since the maximum matching problem can be solved by the Hopcroft–Karp algorithm, which has a complexity of order $O(\sqrt{n_b}|{\mathcal{E}}_b|)$, where n_b and $\left|{\mathcal{E}}_b\right|$ are the numbers of nodes (columns and rows) and links (nonzero entries) in the bipartite graph (matrix). SI Appendix, Fig. S2 presents an illustrative example of Algorithm 2, where it becomes clear how we take advantage of the structural properties of a dynamical system to augment F₀ at every iteration until Eq. 4 is satisfied.

Algorithm 2:

Minimum-order functional observer design

input: functionally observable triple (A, C, F)

output: functional observer matrices $(F_0,N,J,H,D,E)$

initialize $F_0\leftarrow F,\hspace{0.17em}{r}_0\leftarrow \text{rank}(F_0),\hspace{0.17em}{\mathcal{M}}_1\leftarrow \varnothing ,\hspace{0.17em}{\mathcal{M}}_2\leftarrow \varnothing$;

do

update $G\leftarrow {[C^{\mathrm{T}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{(CA)}^{\mathrm{T}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{F}_0^{\mathrm{T}}]}^{\mathrm{T}}$;

build a bipartite graph $\mathcal{B}(\mathcal{V},\mathcal{V}\prime ,{\mathcal{E}}_{\mathcal{V},\mathcal{V}\prime })$, where $\mathcal{V}=\{v_1,\dots ,v_{2q+r_0}\}$ is a set of nodes with each element corresponding to a row of G, $\mathcal{V}\prime =\{v{\prime }_1,\dots ,v{\prime }_n\}$ is the set of nodes with each element corresponding to a column of G, and ${\mathcal{E}}_{\mathcal{V},\mathcal{V}\prime }$ is the set of undirected links $(v_i,v{\prime }_j)$ defined by the nonzero entries G_ij of G;

find the maximum matching set ${\mathcal{E}}_m$ associated with $\mathcal{B}(\mathcal{V},\mathcal{V}\prime ,{\mathcal{E}}_{\mathcal{V},\mathcal{V}\prime })$ (e.g., via the Hopcroft–Karp algorithm);

for all $v{\prime }_i\in \mathcal{V}\prime$, if $v{\prime }_i$ and each of its second neighbors are connected to a link in ${\mathcal{E}}_m$, then update the set of right-matched nodes ${\mathcal{M}}_1\leftarrow {\mathcal{M}}_1\cup \left\{v{\prime }_i\right\}$;

define the set of candidate nodes $\mathcal{K}={\mathcal{M}}_2\backslash {\mathcal{M}}_1$, where $v{\prime }_j\in {\mathcal{M}}_2$ if ${[F_{0}A]}_{ij}$ is a nonzero entry for some i;

draw an element $v{\prime }_k\in \mathcal{K}$ and update $F_0\leftarrow {[F_0^{\mathrm{T}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{(F\prime )}^{\mathrm{T}}]}^{\mathrm{T}}$ ($r_0\leftarrow r_0+1$), where $F\prime \in {\mathbb{R}}^{1\times n}$ and ${[F\prime ]}_{1j}=1$ if j = k and ${[F\prime ]}_{1j}=0$ otherwise;

while $\mathcal{K}\ne \varnothing$;

compute the functional observer matrices $(N,J,H,D,E)$ for a triple $(A,C,F_0)$.

Algorithm 2 finds the minimum-order F₀ in $O((r_0-r){\sqrt{n}}_b|{\mathcal{E}}_b|)$ time, where n_b and $\left|{\mathcal{E}}_b\right|$ are the numbers of nodes and links in $\mathcal{B}$, respectively. This follows from F₀ being determined with $(r_0-r)$ recursive iterations, in which a maximum matching algorithm of $O(\sqrt{n_b}|{\mathcal{E}}_b|)$ is run at each iteration. This complexity order can be estimated as a function of n in a worst-case scenario in which one has a single sensor node (q = 1) and a single target node (r = 1), but, in order to satisfy Eq. 4, all other unmeasured nodes must be estimated, resulting in $r_0=n-q\approx n$ and hence $r_0-r\approx n$. Since there are at most $n_b=2q+r_0+n\approx 2n$ nodes in $\mathcal{B}$, let $\left|{\mathcal{E}}_b\right|=n_b{k}_{\text{avg}}$, where $k_{\text{avg}}$ is the average node degree in $\mathcal{B}$. Thus, the complexity order is $O(n^{2.5})$ if we assume that $k_{\text{avg}}\ll n$. Note that, being a worst-case scenario, this is still a very conservative estimate since usually $r_0\ll n$ (Fig. 3). This estimate should be contrasted with the complexity order of $O(n^4)$ in the worst-case scenario for the procedure in ref. 42, which requires computation of the rank condition via SVD in approximately n iterations (SI Appendix, section 4).

Optimal Sensor Placement for Minimum-Order Functional Observers.

Given a functionally observable triple (A, C, F), one may be interested in how to optimally place additional sensor nodes in a network such that the functional observer order r₀ is minimized. This is a bilevel optimization problem

$$\underset{{}_{\mathcal{S}\subseteq \mathcal{K}\backslash \mathcal{T},\left|\mathcal{S}\right|\le q}}{\min }\hspace{0.17em}\underset{{}_{F_0\in {\{0,1\}}^{n\times n}}}{\min }J(\mathcal{S},F_0),\hspace{0.17em}\hspace{0.17em}\text{s}.\text{t}.\hspace{0.17em}\text{Eqs}.\hspace{0.17em}\mathbf{3}\hspace{0.17em}\text{and}\hspace{0.17em}\mathbf{4}.$$ [14]

where $\mathcal{K}$ is a set of candidate nodes for sensor placement and $J(\mathcal{S},F_0)$ is a cost function that returns the minimum order $r_0=\text{rank}(F_0)$ of a functional observer. However, finding F₀ depends on $\mathcal{S}$ (which defines matrix C in Eqs. 3 and 4) and is “embedded” in a lower-level optimization task that requires, for instance, use of Algorithm 2. This is a hard-to-solve problem, but, for illustration purposes, in Fig. 3F we implement a (nonscalable) greedy algorithm that recursively adds elements to $\mathcal{S}$ by letting $\mathcal{S}\leftarrow \mathcal{S}\cup \{\arg {\max }_{x_i}\mathrm{\Delta }(x_i)|x_i\in \mathcal{K}\backslash \mathcal{S}\}$ until $\left|\mathcal{S}\right|=q$, where $\mathrm{\Delta }(x_i)=J(\mathcal{S}\cup \{x_i\})-J(\mathcal{S}),\forall x_i\in \mathcal{K}\backslash \mathcal{S}$, and $J(\mathcal{S})$ is the order of F₀ returned by Algorithm 2 for this set $\mathcal{S}$.

Generation of Complex Dynamical Networks.

For the generation of the N-vertex complex networks used in Figs. 2–4, we explore the following parameters: $m\in \{1,2,\dots ,7\}$ for Barabási–Albert SF networks (83) and k = 2 and $p\in [0,1]$ for Newman–Watts SW networks (84). Parameter m is the number of edges of each vertex iteratively added to the network, k is the number of nearest neighbors in a ring graph, and p is the probability of adding a new edge. For each of these undirected networks, a directed model is generated by randomly assigning a single direction to each edge.

Since we are concerned with dynamical networks, we consider that each vertex in an SW or SF network is a dynamical system of possibly more than one dimension. For illustration purposes, we assume that each vertex of a network generated from these models is a three-dimensional subsystem with the following general structure:

$$A_{\text{v}}=\left[\begin{array}{ccc}-1& -1& 0\\ 1& -1& 0\\ 1& 0& -1\end{array}\right].$$ [15]

To include the effects of heterogeneity in the vertex dynamics of the dynamical networks generated, we let the dynamics of each subsystem be defined by $A_i={\lambda }_i{A}_{\text{v}}$ for ${\lambda }_i\sim \mathcal{U}[2,5]$, where $i=1,\dots ,N$ and $\mathcal{U}[a,b]$ is a uniform distribution in the interval $[a,b]$. Thus, the system matrix A describing the whole dynamical network is given by $A=\text{diag}({\lambda }_1,\dots ,{\lambda }_N)\otimes A_{\text{v}}-L\otimes M$, where ⊗ is the Kronecker product operator, L is the Laplacian matrix of the generated network, and $M\in {\{0,1\}}^{3\times 3}$ is defined by $M_{ij}=1$ if $i=j=2$ and 0 otherwise. The term $L\otimes M$ means that the second state variable of all subsystems is diffusively coupled according to L. Note that A has dimension $n=3N$, which is also the number of nodes in $\mathcal{G}(A)$.

The generalized clustering of the inference graph $\mathcal{G}(A)$, studied in Fig. 3D, is defined as ${\text{C}}_{\text{g}}=\frac{1}{n}{\displaystyle {\sum }_{i,j,k}A{\prime }_{ij}A{\prime }_{jk}A{\prime }_{ki}}/k_i^2$, where k_i is the node degree of node x_i in $\mathcal{G}(A\prime )$ and $A\prime =(A+A^{\mathrm{T}})/2$. Note that the diagonal entries a_ii are included to account for self-edges, which distinguishes $C_{\text{g}}$ from the standard clustering coefficient, and that the computation is effectively done for the undirected counterpart of $\mathcal{G}(A)$.

For the results presented in Figs. 3 and 4, the target and sensor nodes were chosen randomly among the first state variable of each subsystem (vertex) A_i, under the condition that the sets of sensor nodes and target nodes are nonoverlapping (i.e., $\mathcal{S}\cap \mathcal{T}=\varnothing$). That is, F_ij or C_ij is a nonzero entry only if $(j+2)/3$ is integer, and thus $\mathcal{S}\cup \mathcal{T}$ can have at most N state nodes. This procedure is relaxed in Fig. 2, where all state variables are candidates for sensor placement (i.e., $\mathcal{K}=\mathcal{X}$).

Real-World Networks Datasets.

For the real-world networks used in Fig. 2B, we take several adjacency matrices $A_{\text{adj}}$ available in different real-world datasets (described in SI Appendix, section 6). For each real-world network, we define the system matrix A as the Laplacian matrix of $A_{\text{adj}}$ in order to model the energy/information flow in such systems as diffusive processes.

Parameters of the IEEE-118 Power-Grid Model.

The IEEE-118 system is derived from a representation of the US Midwest system with 118 buses, 54 generators, and 186 lines (85). The network parameters K_ij and generator’s mechanical power P_i are computed from the nominal AC power flow solution, the generator and load dynamical parameters H_i and D_i are estimated following the method provided in ref. 51, and the nominal frequency $w_{\text{R}}$ is 60 Hz. The power flow equations were numerically solved using the MATPOWER toolbox (85). The initial conditions were set, for all i, assuming that the power system is in a synchronized steady state ${\dot{\varphi }}_i(0)=0$, with ${\varphi }_i(0)$ determined by the power flow solution.

Parameters of the Epidemic Spreading Model.

The parameters in Eq. 9 were set as $(\beta ,\gamma ,\eta )=(0.4,0.16,0.01)$ in order to mimic the coronavirus spreading in each group according to results reported in ref. 72, where here, β is the average value of β_i. We define the contact rate of each group as ${\beta }_i\sim \mathcal{N}(\beta ,0.01)$ to account for group heterogeneity in the simulation. The air transportation network defined by K describes the traffic of passengers according to the TranStats database for international and domestic flights (https://www.transtats.bts.gov/). Multiple airports belonging to the same city are combined into a single group (vertex) i with a population P_i given by the corresponding city’s population. In Fig. 6, the epidemic peak time $t_{\text{p}}$ is determined by numerically integrating Eq. 9 with the initial conditions $I_j(0)={10}^3$ and $S_j(0)=P_j-{10}^3$ if j is the index for Miami, Florida, and $I_j(0)=0$ and $S_j(0)=P_j$ otherwise. The predicted peak time ${\widehat{t}}_{\text{p}}$ is determined based on the free-run simulations and functional observer estimations, both initialized with a false guess of the outbreak in a randomly selected city k. That is, $I_j(0)=1$ and $S_j(0)=P_j-1$ if j = k and $I_j(0)=0$ and $S_j(0)=P_j$ otherwise.

Data Availability

Codes and data have been deposited in GitHub (https://github.com/montanariarthur/FunctionalObservability).