Self-assembly of photonic crystals by controlling the nucleation and growth of DNA-coated colloids

Significance

Assembling optical metamaterials from DNA-coated colloids has been a central goal of programmable self-assembly for decades. Despite significant advances in expanding the structural diversity of colloidal crystals, a lack of understanding of the crystallization pathways has hindered the realization of programmable metamaterials. In this paper, we combine experiments and theory to develop a complete understanding of the crystallization dynamics. We show that the nucleation and growth kinetics of DNA-coated colloids are fundamentally different from those of atoms or small molecules, owing to an effective friction that arises from transient DNA hybridization. By incorporating this effective friction into classical theories, we predict the absolute rates of nucleation and growth with quantitative accuracy, enabling the design of protocols for making photonic crystals.

Abstract

DNA-coated colloids can self-assemble into an incredible diversity of crystal structures, but their applications have been limited by poor understanding and control over the crystallization dynamics. To address this challenge, we use microfluidics to quantify the kinetics of DNA-programmed self-assembly along the entire crystallization pathway, from thermally activated nucleation through reaction-limited and diffusion-limited phases of crystal growth. Our detailed measurements of the temperature and concentration dependence of the kinetics at all stages of crystallization provide a stringent test of classical theories of nucleation and growth. After accounting for the finite rolling and sliding rates of micrometer-sized DNA-coated colloids, we show that modified versions of these classical theories predict the absolute nucleation and growth rates with quantitative accuracy. We conclude by applying our model to design and demonstrate protocols for assembling large single crystals with pronounced structural coloration, an essential step in creating next-generation optical metamaterials from colloids.

By encoding specific short-range interactions, DNA molecules grafted to colloidal particles can be used to direct the self-assembly of complex, crystalline materials (1–3). This general approach to crystal engineering is a triumph of synthetic self-assembly and has yielded a vast diversity of crystal structures with programmable stoichiometries, composition, and crystallographic symmetries from both nanometer-(4–10) and micrometer-scale particles (11–17). Although the breadth of such structures has increased dramatically over time, experiments using optical-scale colloidal particles have produced relatively small, polycrystalline structures due to poorly understood crystallization kinetics. Realizing the ultimate goal of assembling colloidal metamaterials, such as photonic crystals, thus requires new experimental methodologies and theoretical models to understand and achieve control over the dynamics of self-assembly.

Colloidal crystals are widely believed to self-assemble via classical nucleation and growth, following dynamical pathways analogous to those of atoms and simple molecules. According to classical nucleation theory (CNT), a crystalline nucleus spontaneously forms from a metastable fluid by surmounting a free-energy barrier (18). Subsequent growth then occurs by the addition of free particles to the nucleus. A central challenge in programmable self-assembly of colloids is to understand whether this framework quantitatively describes the crystallization dynamics of micrometer-sized colloidal particles. On the one hand, colloidal particles can be thought of as “model atoms” that interact via an effective interaction potential that is averaged over all of the molecular degrees of freedom (19). On the other hand, the effective interaction arises from the transient formation and rupture of very real DNA duplexes that link neighboring particles together, whose kinetics may dramatically influence the rates of local rearrangements within a colloidal assembly (13, 20, 21). Such dynamical considerations are crucially important, as numerous examples of colloidal self-assembly have shown that the thermodynamically stable phase that one would predict on the basis of the effective interactions alone is not always accessible, and that these systems are prone to becoming arrested as a colloidal gel instead (22, 23).

Here we quantify the nucleation and growth dynamics of DNA-programmed crystallization in a binary mixture of colloidal particles. By monitoring the self-assembly of hundreds of isolated crystals simultaneously, we show that a modified version of CNT—which takes into account the finite rate at which bound particles roll or slide over one another at the crystal interface—quantitatively describes the observed temperature and concentration dependence of the nucleation barrier, as well as the absolute nucleation rate. Furthermore, our model of the friction-mediated attachment kinetics successfully captures the dynamics of the initial reaction-limited phase of crystal growth, which occurs before large crystals ultimately enter into a deterministic, diffusion-limited growth regime. With this understanding of the crystallization dynamics, we accurately predict the extremely narrow temperature window—less than $0.1{ }^{°}\text{C}$—in which large, faceted single crystals can be grown. We then use this knowledge to design and demonstrate a protocol for assembling millions of single crystals of DNA-coated particles that exhibit a pronounced photonic response, thereby overcoming a critical hurdle to using DNA-programmed assembly to build optical metamaterials (17, 24–26).

Results

Quantifying Crystallization Pathways.

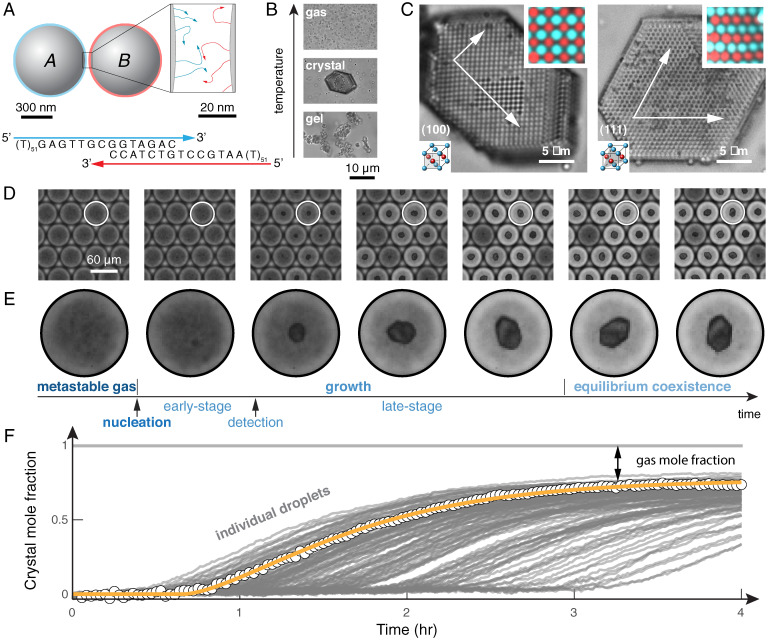
We follow the full dynamic pathways to crystallization using optical microscopy and droplet-based microfluidics. Hybridization of complementary DNA strands grafted to colloidal particles (Fig. 1A) induces a short-range attraction whose strength can be tuned by adjusting the temperature (Fig. 1B). Just below the melting temperature, the colloids assemble into a binary alloy that is isostructural to copper–gold (CuAu-FCC; Fig. 1C) (11). Inspired by the work of Fraden and coworkers (27), Galkin and Vekilov (28), and others (29), we combine equal amounts of both particle species inside monodisperse, 100-pL-volume droplets, in order to image and quantify hundreds of crystallization experiments running in parallel—one experiment per droplet (Fig. 1D). Because the number of free particles decreases as a crystal grows, the droplets become brighter after the initial nucleation event (Fig. 1E), enabling us to follow the entire dynamic evolution by quantifying the concentration of free particles, and thus the mole fraction of the crystal phase, from measurements of the transmitted intensity (Fig. 1F). Importantly, we are able to track many instances of nucleation and growth within a single experiment, enabling precise quantification of the behavior of both individual crystals and the ensemble of many crystals (30). Furthermore, this experiment can be repeated at many temperatures by heating the system to the gas phase and then quenching to a new temperature (see SI Appendix, sections 1–3 for experimental details).

Fig. 1.

DNA-coated colloids follow a dynamic pathway to crystallization characterized by three distinct regimes: nucleation, growth, and equilibrium coexistence. (A) A binary mixture of 600-nm-diameter colloidal particles that interact by direct hybridization of complementary DNA sequences. (B) The resultant interactions are temperature dependent, forming a colloidal gas phase at high temperature, an ordered crystal phase at intermediate temperature, and a disordered gel phase when quenched to low temperatures. (C) The binary mixture forms crystals with a copper–gold lattice structure. Bright-field and fluorescence micrographs (Top Insets) show the (100) and (111) planes (Bottom Insets), as well as the crystal facets. (D) Micrographs of water droplets containing DNA-coated particles show the dynamics of nucleation and growth, as seen in the time series. (E) Time-lapse micrographs of a single droplet show the full dynamic pathway to crystallization, which proceeds through multiple stages: 1) nucleation from a metastable gas; 2) early-stage growth; 3) detection of a crystal followed by late-stage growth; and, 4) eventually, equilibrium coexistence between crystal and gas. (F) We extract the crystal mole fraction as a function of time for each droplet individually. Points show data for a single droplet, and the orange curve shows a model of growth described in the main text (Eq. 2). The crystal mole fraction is defined as the number of particles in the crystal, $N_{\text{c}}$, divided by the total number of particles per droplet. Gray lines show trajectories of other droplets in the same experiment. Data are for a colloid concentration of 1% (vol/vol).

The transition from a metastable, disordered gas to an ordered crystal is a complex dynamic process that follows a sequence of stages (Fig. 1E). First, we observe a metastable fluid at short times during which there are no visible stable nuclei. After some waiting time, which varies widely from droplet to droplet (Fig. 1F), we observe the spontaneous emergence of small crystallites. Next, the nucleated crystals grow in size as particles from the gas phase adsorb to the growing crystal surface. Eventually, the crystals stop growing. The observation that crystals nucleate at a variety of times (Fig. 1F) suggests some underlying stochasticity and hints at the presence of a free-energy barrier between the gas and crystal phases. In contrast, following nucleation, crystal growth is consistent from droplet to droplet, suggesting that growth is nearly deterministic. Similarly, all crystals stop growing at the same crystal mole fraction, indicating that the crystals eventually equilibrate with a dilute gas phase. Thus, from a single experiment, we quantify the kinetics of both nucleation and growth, as well as the thermodynamic driving force, which we can then dissect to construct a quantitative model of the dynamic crystallization process.

Crystal Nucleation.

To study the nucleation behavior, we measure the survival probability—the fraction of droplets that have not yet formed a crystal—as a function of time for a variety of temperatures (Fig. 2A) and three nominal colloid concentrations. After accounting for random concentration variations between the droplets, which vary by roughly $\pm 5\%$ of the mean concentration, we find that the survival probabilities are characterized by an exponential decay at long times, suggesting that a single rate, $k_{\text{n}}({\rho }_0,T)$, controls nucleation at each temperature T and concentration ρ₀. This rate most likely describes homogeneous nucleation, since the colloidal particles are repelled from the oil–water interface by a polymeric surfactant and are nearly density matched to the solvent, implying that sedimentation plays an insignificant role during the initial nucleation process. We also observe a lag period with a soft shoulder at short times, which we attribute to the fact that the crystals must grow to a threshold size before they are detected by our image analysis methods. Indeed, the survival probability for each quench can be well fitted by a simple first-passage model to determine the nucleation rate $k_{\text{n}}$ (Fig. 2B) and the mean lag time, ${\tau }_{\text{lag}}$, which is discussed further below (see SI Appendix, section 7A for details). Both of these quantities vary by several orders of magnitude within a temperature range of roughly $0.5{ }^{°}\text{C}$ for all three concentrations.

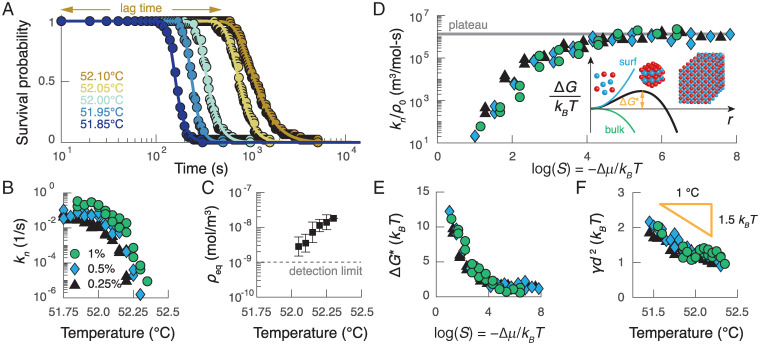
Fig. 2.

The kinetics of nucleation can be predicted by a modified version of CNT. (A) The survival probability for a colloid concentration of 0.25% (vol/vol) as a function of time for different temperatures (colors). Points show data, and curves show fits of the model described in the main text. (B) The measured nucleation rate $k_{\text{n}}$ as a function of temperature at three different particle volume fractions: 0.25% (black triangles), 0.50% (blue diamonds), and 1.00% (green circles). At the lowest temperatures, the nucleation rate plateaus; at higher temperatures, the nucleation rate decreases superexponentially with temperature. (C) Average measurements of the equilibrium gas density as a function of temperature. The error bars represent the SD of the measurements for all three colloid concentrations and two independent experimental trials. (D) The nucleation rate divided by the initial colloid concentration as a function of the supersaturation S. Inset illustrates the free-energy barrier as a function of the cluster radius that results from the classical theory of nucleation. (E) The inferred barrier height $\mathrm{\Delta }{G}^{*}$ as a function of supersaturation. (F) The inferred surface tension γ as a function of temperature for the experiments in B. The surface tension decreases with increasing temperature as expected given the temperature dependence of DNA hybridization; d is the colloid diameter.

We analyze our measurements of the homogeneous nucleation rate within the framework of CNT, which has been used to describe nucleation in a variety of systems, including molten metals, simple liquids, protein solutions, and colloidal suspensions (31). CNT predicts that a single free-energy barrier separates a metastable fluid from a globally stable crystal, resulting in a nucleation rate of the form $k_{\text{n}}=k_{\text{n},0}({\rho }_0,T)\exp \left(-\mathrm{\Delta }{G}^{*}/k_{\text{B}}T\right)$, where $k_{\text{n},0}({\rho }_0,T)$ is the nucleation rate prefactor, ρ₀ is the initial gas number density, and T is the absolute temperature. The height of the nucleation barrier, $\mathrm{\Delta }{G}^{*}$, is determined by a competition between the temperature-dependent interfacial free energy and the thermodynamic driving force for assembling the bulk crystal phase, $\mathrm{\Delta }\mu$. To determine $\mathrm{\Delta }\mu$, we use the measured equilibrium gas number density, ${\rho }_{\text{eq}}$, from each quench (Fig. 2C), to calculate the supersaturation, $S(T)\equiv \exp (-\mathrm{\Delta }\mu /k_{\text{B}}T)\simeq {\rho }_0/{\rho }_{\text{eq}}(T)$ .

Analyzing the temperature and concentration dependence of our measured nucleation rates yields estimates of the free-energy barrier height and the surface free energy for DNA-programmed crystallization. Plotting the measured nucleation rates as a function of the supersaturation reveals two distinct regimes predicted by CNT: a barrier-dominated regime at low supersaturation, and a temperature-independent plateau at high supersaturation, where the free-energy barrier is negligibly small relative to $k_{\text{B}}T$ (Fig. 2D). Assuming that the nucleus is roughly spherical and has the same crystallographic symmetry as the bulk crystal, CNT predicts a barrier height of the form $\mathrm{\Delta }{G}^{*}=16\pi \gamma {(T)}^3/3{\rho }_{\text{c}}^2{(\log S)}^2$, where $\gamma (T)$ is the interfacial free-energy density and ${\rho }_{\text{c}}$ is the number density of the crystal. Taking the plateau value of $k_n/{\rho }_0$ to be equal to the nucleation rate prefactor, we find that $\mathrm{\Delta }{G}^{*}$ decreases from ∼10 $k_{\text{B}}T$ at the lowest supersaturations to near 0 $k_{\text{B}}T$ above $\log S\approx 5$ (Fig. 2E). These calculations suggest that the critical nucleus contains on the order of 10 colloidal particles under the conditions in which the free-energy barrier is rate limiting. We highlight that this estimate of a 10-particle critical nucleus is consistent with homogeneous nucleation due to short-range attractions and strong driving forces ($\mathrm{\Delta }\mu >k_{\text{B}}T$). Furthermore, the surface free energies that we obtain from all temperatures and concentrations collapse onto a single curve, which decreases linearly with increasing temperature (Fig. 2F). Importantly, both the magnitude and the temperature dependence of $\gamma (T)$ are consistent with independent estimates of the surface tension based on either the binding free energy between DNA-coated colloids (19, 32) or the equilibrium gas density shown in Fig. 2C (see SI Appendix, section 7B for details). This agreement between experiment and calculation provides a strong justification for modeling nucleation with CNT.

Our measurements of the nucleation rates at high supersaturation, where the nucleation rate is determined solely by the nucleation rate prefactor, reveal two additional interesting results. First, the nucleation rate prefactor is a very weak function of temperature. We hypothesize that any temperature dependencies are undetectable given the narrow temperature window of our experiment, which is only $0.5{ }^{°}\text{C}$ wide; for example, we estimate that the self-diffusion coefficient of the particles increases by only 1% from 51.75 ${}^{°}$C to 52.25 ${}^{°}$C, which is below the precision of our measurements of the nucleation rate. Second, and more surprisingly, the nucleation rate prefactor scales linearly with the initial gas density. This observation contrasts with other examples of nucleation in which the nucleation rate prefactor is diffusion limited and scales as $V_{\text{drop}}{\rho }_{0}D/{\lambda }^2\propto {\rho }_0^{5/3}$, where $V_{\text{drop}}$ is the droplet volume, D is the self-diffusion constant, and λ is the mean free path between particles in the gas phase (31).

The linear dependence of the nucleation rate prefactor on the initial gas density suggests that the pathway to forming a critical nucleus is fundamentally different for DNA-coated colloids, as compared to atoms, molecules, or other colloidal suspensions. We understand this unique functional dependence by considering the specific attachment kinetics for micrometer-sized DNA-coated particles. When a particle from the gas phase attaches to a crystalline nucleus, it must first “roll” on the surface of the cluster before settling at a metastable position within the emerging lattice. This process can be slowed dramatically by the transient formation and rupture of DNA linkages (13, 20, 21). We model this effect by introducing an unstable intermediate state in which a colloidal particle is adsorbed onto the nucleus but not yet maximally coordinated in the emerging crystalline lattice (see SI Appendix, section 6B for details). In this model, an adsorbed particle either rolls to a metastable position in the crystalline lattice with rate κ, where ${\kappa }^{-1}$ is the characteristic time for a colloid to move a distance equal to its own radius, or detaches from the nucleus with a rate proportional to $K{(S)}^{-1}$, where K(S) is the equilibrium constant for an adsorbed particle in a non-crystalline-lattice position. The net rate of attachment of a single particle to the emerging crystalline lattice is thus

$$k_{\text{att}}(S)=\frac{\kappa }{1+K{(S)}^{-1}+\kappa {\lambda }^2/D}.$$ [1]

When adsorbed single particles are highly unstable, the prefactor reduces to $k_{\text{n},0}\simeq \kappa K(1)V_{\text{drop}}{\rho }_0$, reproducing the linear dependence of the nucleation rate on the colloid density observed in our experiments. This model also predicts the absolute nucleation rate at high supersaturation to within an order of magnitude of our measurements using independent estimates of $\kappa \simeq 0.1 {\text{s}}^{-1}$ (13), $D\simeq {10}^{-12} {\text{m}}^2\hspace{0.17em}\mathbf{·}\hspace{0.17em}{\text{s}}^{-1}$, and $K(1)\simeq {10}^{-3}$ for a critical nucleus, providing further support of this interpretation (see SI Appendix, section 6B for details). In contrast, the assumption of a diffusion-limited prefactor overestimates the nucleation rates by at least four orders of magnitude. Therefore, it appears that, while the interactions between particles can be accurately described by an effective potential that averages over the molecular degrees of freedom, capturing the dynamics of nucleation requires incorporating the effective friction that results from transient bridge formation, an effect that is exclusive to the colloidal length scale. We point out that, although we describe this process as “rolling,” a term first coined by Pine and coworkers (13), our model is agnostic as to whether or not the relative motion is due to rolling or sliding.

Crystal Growth.

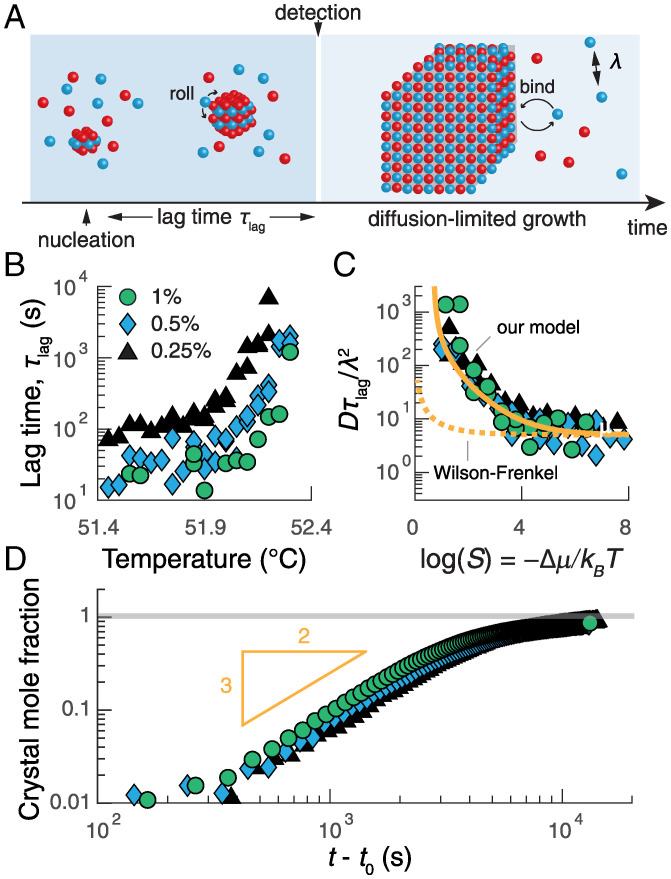
We now turn to analyzing the growth stage of the crystallization pathway. We study the earliest stage of growth by analyzing the mean lag time between the formation of a critical nucleus and the moment that a postcritical cluster is detected (Figs. 1E and 3A). Based on the resolution of our imaging setup and the specifics of our crystal detection algorithm, we estimate that this smallest detectable cluster contains on the order of 50 to 200 colloidal particles. From the survival probabilities shown in Fig. 2A, we find that the lag times vary over several orders of magnitude and are temperature and concentration dependent (Fig. 3B). When rescaled by the characteristic timescale for diffusion-limited collisions and plotted against the thermodynamic driving force, the lag times collapse onto a single curve (Fig. 3C) that provides an independent test of our rolling-limited attachment model presented above in Eq. 1. Specifically, the mean early-stage growth rate, which is proportional to ${\tau }_{\text{lag}}^{-1}$, is predicted to have the approximate form $D(1-2S^{-1})/{\lambda }^2[2+S^{-1}K{(1)}^{-1}]$ (see SI Appendix, section 6D for details). Fitting this expression to the data in Fig. 3C, we obtain $K(1)\approx 0.01$, which supports our hypothesis that individual adsorbed particles are unstable at noncrystalline lattice positions and that early-stage growth is reaction limited. Moreover, this model also accurately accounts for the observed variation in lag times up to $\log (S)\approx 5$, whereas the standard Wilson–Frenkel law for crystal growth (33) predicts a measurable supersaturation dependence only when $\log (S)\mathrm{\lesssim }1$ (Fig. 3C).

Fig. 3.

The growth kinetics are reaction limited just after nucleation and become diffusion limited as the crystal grows larger. (A) An illustration of the stages of growth following the formation of a critical cluster. (B) The inferred average lag time for early-stage growth ${\tau }_{\text{lag}}$ as a function of temperature for three colloid concentrations: 0.25% (black triangles), 0.5% (blue diamonds), and 1% (vol/vol) (green circles). (C) The same lag times in B rescaled by the diffusion coefficient D and the mean-free path λ as a function of the measured supersaturation S. The solid orange curve shows a fit of SI Appendix, Eq. S22, which is described in the text; the dashed orange curve shows the predictions of the Wilson–Frenkel model (33). (D) The average crystal mole fraction as a function of the time since nucleation exhibits power-law growth with an exponent of roughly 3/2, consistent with predictions of diffusion-limited growth (SI Appendix, section 6D). Data in D are for temperatures at which mostly single crystals nucleate and grow: 52.15 ${}^{°}$C, 52.25 ${}^{°}$C, and 52.3 ${}^{°}$C for 0.25%, 0.5%, and 1%, respectively; t₀ is the nucleation time for a given droplet.

Once a crystal grows large enough, the situation changes, and the growth dynamics become limited by the diffusion of particles to the crystal–vapor interface. Assuming a roughly spherical crystal with radius R, our model predicts that growth enters this regime when $d^2/\lambda R\mathrm{\lesssim }{k}_{\text{att}}{\lambda }^2/D$, after which the crystal mole fraction should increase as the 3/2 power of the time. Replotting our measurements of the crystal mole fraction versus the time since nucleation for three shallow quenches reveals a power-law dependence with an exponent of roughly 3/2, as predicted (Fig. 3D; see SI Appendix, section 6D for details). The growth rate then decreases exponentially as the crystal approaches its equilibrium size. Furthermore, by fitting the late-stage growth data for individual crystals to the integrated form of the deterministic, diffusion-limited growth law (Fig. 1F and SI Appendix, Fig. S15)

$$\frac{d{N}_{\text{c}}(t)}{dt}\simeq 4\pi R(t)D_{\text{eff}}\left[{\rho }_0-\frac{N_{\text{c}}(t)}{V_{\text{drop}}}-{\rho }_{\text{eq}}\right],$$ [2]

where $N_{\text{c}}$ is the number of particles in the crystal phase, we obtain an effective diffusion constant, $D_{\text{eff}}$, that agrees quantitatively with predictions from the Stokes–Einstein equation (34) in droplets with single crystals (SI Appendix, Fig. S16). Taken together, these results demonstrate that our theoretical framework captures the functional dependences and the absolute rates of the distinct rate-limiting steps at all stages of growth in a self-consistent manner.

Assembling Single Crystals.

We are now in a position to apply our quantitative understanding of the crystallization dynamics in order to grow large colloidal crystals. Our specific aim is to assemble a single crystal per droplet with high probability, as this is an essential step in developing practical technologies based on colloidal crystallization. In general, one should expect single crystals to form under conditions where nucleation is much slower than growth, since the addition of particles to a growing crystal at constant volume lowers the supersaturation elsewhere in the droplet and thus reduces the rate of subsequent nucleation events (35, 36). Single crystals should therefore assemble when the nucleation rate, $k_{\text{n}}$, is fast enough that nucleation occurs during the experiment, but slow enough that it is rare to observe two nuclei form within a time ${\tau }_{\text{g}}$, which represents the typical growth time required to suppress additional nucleation events. Because the nucleation rate decreases rapidly with decreasing concentration, we reach ${\tau }_{\text{g}}$ soon after entering the diffusion-limited phase of growth (see SI Appendix, section 8A for details).

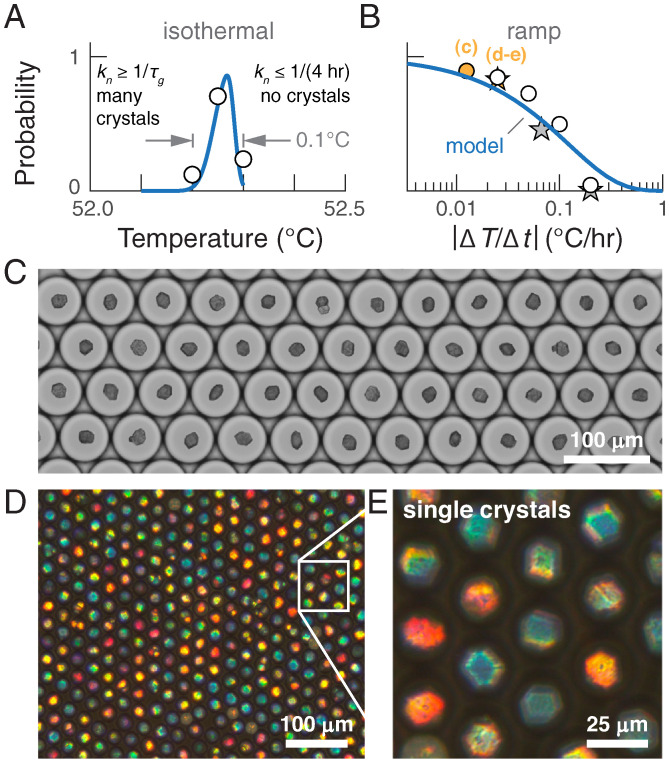
Theoretical predictions suggest that forming single crystals with high probability using an isothermal protocol is intractable. Fig. 4A compares the theoretical predictions of the probability of forming a single crystal per droplet, using $k_{\text{n}}({\rho }_0,T)$ and ${\tau }_{\text{g}}({\rho }_0)$ calculated from our model of the crystallization pathway, to the fraction of single crystals obtained at different temperatures. While the close agreement between the theory and experiments confirms our intuition that the crystal morphology depends on a balance of nucleation and growth, we find that the temperature window within which we can grow single crystals with high probability is less than $0.1{ }^{°}\text{C}$ wide. Unfortunately, sustained temperature precision and accuracy on this scale is difficult to achieve with conventional hardware, and, consequently, we observe polycrystals in most of our isothermal experiments. An analysis of the full distributions of the number of crystals per droplet is presented in SI Appendix, Fig. S17.

Fig. 4.

A temperature ramp protocol yields large single crystals of DNA-coated colloids without the need for high-accuracy temperature control. (A) The probability of forming a single crystal within a droplet held at a constant temperature for 4 h as a function of temperature. Points show experimental measurements, and the curve shows our model prediction, described in the text. (B) The probability of forming a single crystal within a drop that is cooled at a constant rate $\mid \mathrm{\Delta }T/\mathrm{\Delta }t\mid$. The circles show experimental measurements, and the curve shows our model prediction for 600-nm-diameter particles at a concentration of 0.5% (vol/vol); stars show experimental measurements for 400-nm-diameter particles at 1% (vol/vol). (C) An optical micrograph of the temperature ramp experiment for 600-nm-diameter particles at a ramp rate of 0.1 ${}^{°}$C/8 h (orange circle in B), showing that greater than 85% of the droplets contain a single, well-faceted crystal. (D and E) Transmission optical micrographs showing that single crystals self-assembled from 400-nm-diameter colloids exhibit strong structural coloration when imaged through crossed polarizers. Crystals in D and E are formed from 1% colloids at a ramp rate of 0.1 ${}^{°}$C/4 h (orange star in B). The different colors reflect different orientations of the single crystals with respect to the optical axis of illumination and the orientation of the polarizer, and not different crystal structures.

An alternative strategy is to perform the self-assembly in a temperature ramp in which the temperature decreases linearly with time (9). To predict the efficacy of this scheme, we compute the probability of forming a single crystal as a function of the ramp rate, $|\mathrm{\Delta }T/\mathrm{\Delta }t|$, assuming the same competition between $k_{\text{n}}$ and ${\tau }_{\text{g}}$ as above (Fig. 4B; see SI Appendix, section 8B for details). Encouragingly, our theory suggests that a ramp rate of $0.025{ }^{°}\text{C/h}$ or slower is sufficient to guarantee a single crystal fraction of 75% in our droplet system. This prediction is borne out by a set of linear annealing experiments conducted at a range of ramp rates, which yield fractions of single crystals that closely match our predictions (Fig. 4C; see SI Appendix, section 4 for details and SI Appendix, Fig. S18 for additional experiments and predictions capturing the influence of the droplet volume). Both the higher yield and the greater flexibility in choosing the ramp rate represent dramatic improvements compared to an isothermal protocol.

Building on our ability to predict the efficacy of such a nontrivial experimental protocol from our quantitative understanding of the crystallization dynamics, we conclude by demonstrating a ramp protocol that produces an array of photonic crystals from DNA-coated colloids, thus realizing a longstanding goal of programmable self-assembly. Assuming that reducing the particle diameter by 33% minimally affects the parameters in our model, we choose a ramp rate that is predicted to yield primarily single crystals from 400-nm-diameter particles at a concentration of 1% (vol/vol). Fig. 4 D and E shows representative micrographs of the crystals that form. As predicted, 82% of the droplets contain single crystals, which are each assembled from about 30,000 particles. Most strikingly, the crystals exhibit pronounced structural coloration, a photonic property that arises from the precise, periodic arrangement of the wavelength-sized colloidal particles. This experimental demonstration of DNA-programmed assembly of photonic single crystals at optical length scales is enabled only through our detailed understanding of the dynamic pathways that govern crystallization.

Discussion

Our findings from these experiments are broadly twofold. First, we have demonstrated that the complete crystallization pathway can be understood in terms of classical theories of nucleation and growth, provided that a model of rolling-limited attachment kinetics is included to account for the finite rates of formation and rupture of the DNA linkages. With this modification, our model predicts both the absolute nucleation and growth rates to within an order of magnitude of their measured values, a level of agreement between theory and experiment that stands in stark contrast with previous attempts to describe colloidal systems using CNT (37). Our results thus establish a precise description of the temperature and concentration dependencies of the nucleation barrier, surface tension, and growth laws for micrometer-sized DNA-grafted colloids. In particular, our quantification of the strong temperature dependence of the nucleation barrier may explain why forming large faceted crystals with these particles has been historically challenging (2). More broadly, because of the large dynamic range of our measurements, our ability to suppress heterogeneous nucleation by eliminating impurities, and our ability to account for the relevant kinetics across multiple length scales, we believe that our experiments are among the most direct tests of CNT to date in any molecular or colloidal system. Furthermore, given the generality of our modeling approach, we anticipate that our models of nucleation and growth could also be applied to other material platforms in which colloidal interactions arise from transient bridge formation, like polymer-grafted nanoparticles (38).

Second, we have applied these insights to predict the morphologies of crystals that form under various conditions and experimental protocols, culminating in the assembly of millions of large, well-faceted single crystals that exhibit pronounced structural coloration. This achievement points the way toward the rational design of experimental protocols for guiding DNA-programmed colloidal self-assembly and hints at further practical applications of forming colloidal crystals in droplets. Unlike in a bulk system, where the large variation in nucleation times leads to a broad distribution of crystal sizes, droplets enable the growth of single crystals with a specified, uniform size. With an optimally tuned experimental protocol, droplets can be used to selectively self-assemble different crystal morphologies and sizes, following a size-limiting mechanism similar in spirit to the finite pool mechanism of self-limiting assembly within living cells (39). Furthermore, by using noninvasive methods to permanently cross-link the DNA-coated colloids once crystallized (40, 41) and then dissolving the droplet interface, it may be possible to use droplet-nucleated crystals to seed the continued growth of larger single crystals in bulk (42). Finally, we note that other methods to soften the sharp temperature dependence of the nucleation rate, such as adding free DNA oligomers to compete with the binding of the grafted DNA strands (12), could be employed to increase the maximum temperature ramp rate for growing single crystals, thereby shortening the duration of the assembly process. Taken together, our results promise that the long-standing goals of programming the complete self-assembly pathway to prescribed crystal structures (3, 43), and then extending this technology to build more complex structures (44), may finally be within reach.

Materials and Methods

Synthesizing DNA-Coated Colloids.

Colloidal particles are functionalized with DNA using a combination of strain-promoted click chemistry and physical grafting, following a modified version of the methods described by Pine and coworkers (45). In brief, polystyrene-block-poly(ethylene oxide) (PS-b-PEO) copolymers are functionalized with an azide group, the azide-modified PS-b-PEO is adsorbed onto the surface of polystyrene colloidal particles, and then dibenzocyclooctyne-modified DNA is attached to the PS-b-PEO via click chemistry. After the reaction, the particles are washed five times in deionized (DI) water via centrifugation and resuspension and stored at 1% (vol/vol). A detailed protocol is provided in SI Appendix.

Fabricating the Microfluidic Device.

The microfluidic drop maker is fabricated via standard photolithographic techniques. A glob of SU8 (SU-8 2075, MicroChem) roughly the size of a quarter is poured onto a silicon wafer (3-76-024-V-B, Silicon Materials Inc.). The wafer is then spun at 500 rpm with a spin coater at a ramp rate of 100 rpm/s for 5 s, and then 1500 rpm at a ramp rate of 300 rpm/s for 60 s, which leads to a thickness of around 80 $\mathrm{\mu }$m. Next, the wafer is placed onto a 65 ${}^{°}$C hot plate for 3 min and then a 95 ${}^{°}$C hot plate for 5 min. A photomask (Output City) with the pattern of our microfluidic device is placed on top of the wafer, which is then moved to a Manual Mask Aligner System (ABM-USA) and exposed to UV light for 46 s. The mask is removed, and the wafer is washed with isopropanol and propylene glycol methyl ether to remove the undeveloped photoresist. The wafer is then dried with an air brush and placed on a 65 ${}^{°}$C hot plate for 3 min and a 95 ${}^{°}$C hot plate for 20 min. Next, the wafer is placed in a glass Petri dish with propylene glycol methyl ether and shaken back and forth for 10 min to remove any photoresist. Finally, the wafer is sprayed with isopropanol and dried with an air brush.

The master is a negative of the actual device and acts as a mold. Thirty grams of polydimethylsiloxane (PDMS) and 3 g of cross-linker (1673921, Dow Chemical Company) are mixed using a Thinky AR-250 planetary centrifugal mixer for 3 min. A plastic Petri dish is lined with aluminum foil, and the microfluidic device master is placed face up in the dish. The mixed PDMS is then poured onto the master and placed in a vacuum desiccator for 30 min to remove any bubbles from the solution. The dish is placed in a 70 ${}^{°}$C oven overnight. The wafer is removed from the dish, the foil is peeled off, and a hobby knife is used to cut away the excess PDMS and separate it fully from the master. A coring tool (69039-07, Electron Microscopy Sciences) is then used to punch holes into all the device inlets and outlets. A glass slide (2947-75X50, Corning) and the PDMS chip are placed into an oxygen plasma cleaner (Zepto, Diener Electronic) for 45 s. The PDMS chip is then laid down onto the glass slide and held with uniform pressure for 30 s.

Droplet Making.

Syringe pumps are used to operate the microfluidic device to produce monodisperse droplets containing colloidal suspensions. The channels of the microfluidic device are made hydrophobic by flushing them with Aquapel (B004NFW5EC, Amazon), leaving it for 30 s, and then flushing them out again with air to remove the Aquapel. The channels are flushed with HFE-7500 oil (3M) and then air. Flow rates are controlled by three 3-mL syringes independently with syringe pumps (98-2662, Harvard Apparatus) connected to the device via tubing (06417-11, Cole-Palmer) that is slightly larger in diameter than the holes, to ensure a snug fit. HFE-7500 with 2% RAN fluorosurfactant (008-FluoroSurfactant-5wtH-20G, RAN Biotechnologies) is fed into the oil inlet, 1 M NaCl in 1xTE buffer is fed into one aqueous inlet, and DNA-coated particles suspended at twice the desired volume fraction in DI water are fed into the other aqueous inlet. The particles are loaded into the tube by using a reverse flow rate and never enter the syringe body. Flow rates of 800 $\mathrm{\mu }$L/h for the oil phase and 400 $\mathrm{\mu }$L/h for each of the aqueous phases are used to obtain droplets with diameters of roughly 60 $\mathrm{\mu }$m which are collected in an Eppendorf tube via outlet tubing.

Sample Chamber.

Sample chambers comprise a rectangular capillary filled with colloidal suspension that is glued to a glass coverslip. A 100-$\mathrm{\mu }$m-tall, 2-mm-wide glass rectangular capillary (5012, VitroCom) is cut to 3 cm in length with a glass scoring pen and held suspended in place with a pair of clamping tweezers. Approximately 2 μL to 3 μL of the droplet emulsion is transferred into the capillary via a micropipette that has been snipped at the tip to have a wider inlet. HFE 7500 with 2% RAN is used to fill the rest of the volume. Ultraviolet (UV) glue is applied in a thin 3-cm line on a glass slide that the capillary is then placed onto and gently pressed flat. UV glue is then used to seal the two sides of the capillary tube, taking care not to introduce bubbles inside the capillary. The capillary and slide are placed under a UV lamp for 30 s, and then foil is used to cover all but the glue at the ends of the capillary to avoid UV damage of the DNA-coated particles. The sample is placed capillary side down on an acrylic frame with a rectangular hole with a small amount of immersion oil fixing the slide to the acrylic. A drop of immersion oil is placed on the glass slide, and a Peltier unit with a central hole and sapphire window attached to it via thermal paste is placed against the slide, with the capillary force from the oil keeping the assembly together with no downward pressure from clamps.

Imaging.

Bright-field microscope images and videos are obtained using a Nikon Ti2 microscope with a 10× magnification, 0.45 NA objective, and a Phantom v9.1 digital camera connected to a computer. The condenser is roughly 2/3 closed. The Nikon Perfect Focus System is used to maintain a constant focal plane, which is set to roughly 10 $\mathrm{\mu }$m above the bottom of the droplets. Fluorescence images are obtained using a Leica SP8.

Crystallization Experiment.

For the droplet-based experiments, a temperature protocol is carried out automatically using a programmable temperature controller (TC-720, TE Technology, Inc.). The system is held above the melting temperature for 20 min and then dropped in temperature. A custom MATLAB script reads the images as they come in to determine the fraction of droplets that have nucleated crystals over time. If over 90% of the droplets have a crystal within 1 h of quenching, then the quench will finish, and the system will go to a temperature above the melting temperature. Otherwise, the temperature is held for a total of 4 h before remelting. After the system has been melted for 20 min, a new quench is performed at a temperature 0.05 ${}^{°}$C higher than the previous one. This process is continued until fewer than 10% of the droplets nucleate by the end of 4 h.

Data Availability

Data are available upon request from the corresponding authors.