EFAMIX, a tool to decompose inline chromatography SAXS data from partially overlapping components

Abstract

Small‐angle X‐ray scattering (SAXS) is an established technique for structural analysis of biological macromolecules in solution. During the last decade, inline chromatography setups coupling SAXS with size exclusion (SEC‐SAXS) or ion exchange (IEC‐SAXS) have become popular in the community. These setups allow one to separate individual components in the sample and to record SAXS data from isolated fractions, which is extremely important for subsequent data interpretation, analysis, and structural modeling. However, in case of partially overlapping elution peaks, inline chromatography SAXS may still yield scattering profiles from mixtures of components. The deconvolution of these scattering data into the individual fractions is nontrivial and potentially ambiguous. We describe a cross‐platform computer program, EFAMIX, for restoring the scattering and concentration profiles of the components based on the evolving factor analysis (EFA). The efficiency of the program is demonstrated in a number of simulated and experimental SEC‐SAXS data sets. Sensitivity and limitations of the method are explored, and its applicability to IEC‐SAXS data is discussed. EFAMIX requires minimal user intervention and is available to academic users through the program package ATSAS as from release 3.1.

1. INTRODUCTION

Accurate determination of structural parameters and three‐dimensional (3D) shape analysis of biological macromolecules using small‐angle X‐ray scattering (SAXS) ¹ requires purified monodisperse solutions. ² However, biological samples are often present as mixtures of individual components, which complicates SAXS data analysis. By coupling a chromatographic separation step with the SAXS measurements, for example, using inline size‐exclusion chromatography–SAXS (SEC‐SAXS), it becomes possible to separate the contributions of the individual components present in the system. ³ Although chromatography is extremely useful when dealing with mixtures, analysis of the data becomes not trivial when the sample components do not separate well providing a peak overlap in the chromatography trace. The SAXS data represent volume‐fraction‐weighted scattering contributions from an evolving mixture of components eluting from the column, and, if the components are overlapping, no direct separation is possible. The analysis of such SAXS data requires a decomposition procedure to assess the number of components and to further restore their scattering patterns from the experimental data.

Several chemometric algorithms are available that can deal with such a separation task; in particular, multivariate curve resolution with alternating least squares (ALS) ⁴ , ⁵ and evolving factor analysis (EFA). ⁶ , ⁷ These algorithms have successfully been applied for SEC‐SAXS data ⁸ , ⁹ , ¹⁰ SAXS studies of amyloid systems, ¹¹ transient complexes, ¹² folding processes, ¹³ equilibrium oligomeric mixtures, ¹⁴ ion‐exchange chromatography (IEC)‐SAXS data, and time‐resolved studies. ¹⁵ In the latter case, ALS method was coupled with Tikhonov's regularization. ¹⁶ There are also approaches allowing for ab initio 3D shape reconstruction of unknown intermediate in an evolving system with two or three components ¹⁷ and for systems with two‐component monomer–oligomer equilibrium. ¹⁸

An interactive processing of chromatography SAXS data also can be performed for example, using graphical interfaces like the program CHROMIXS ¹⁹ from the package ATSAS ²⁰ as well as other programs like DATASW, ²¹ DELA, ²² and the US‐SOMO high‐performance liquid chromatography (HPLC)‐SAXS module. ²³ The results may depend on the available angular ranges in SAXS data, on the signal‐to‐noise ratio, and on the degree of peak overlap and comparisons of the results from different approaches are often useful. Comparisons of the results obtained by interactive and automated decompositions may provide useful cross‐checks, especially for complicated cases with overlapping peaks.

Here, we present a program EFAMIX for restoring the scattering and concentration profiles of individual components from multiple SAXS data curves utilizing EFA, singular value decomposition (SVD) ²⁴ and the rotation matrix ⁷ approaches. An EFA‐based approach with the “explicit” rotation matrix was earlier implemented in the program BioXTAS RAW data. ⁹ EFAMIX requires minimum user intervention for the analysis and provides an option for an automated estimation of the components. Our method helps to resolve overlapping peaks in SEC‐SAXS profiles, and it can also be applicable to IEC‐SAXS data with a moderate degree of salt buffer gradient. The performance of EFAMIX is illustrated in several simulated and experimental data sets.

2. EFA AND ROTATION MATRIX METHOD

2.1. The general concept of EFA

EFA is a model‐free approach for analyzing matrices of one‐dimensional multicomponent data where a sequential but incomplete separation of components is observed. A typical example is given by the SAXS spectra sequentially recorded from solutions during the elution from a chromatographic column with an overlap of peaks.

In SAXS, one‐dimensional scattering intensity curves I(s) are measured as functions of momentum transfer s = 4πsinθ/λ, where 2θ is the scattering angle and λ is the X‐ray wavelength. A set of multiple SAXS data profiles is described by a matrix A = {A _ik } = {I ^(k)(s _i )}, (i = 1,…, N; k = 1,…, K), where N is the number of experimental points, K is the number of SAXS curves, for example, the total number of time frames in a SEC‐SAXS data set. With SVD, this matrix can be represented as A = USV ^T , where the matrix S is diagonal, and the columns of the orthogonal matrices U and V are the eigenvectors of the matrices AA ^T and A ^T A, respectively. The matrix U yields a set of left singular vectors, that is, orthonormal basic curves U ^(k) (s _i ), that spans the column space of matrix A, whereas the diagonal of S contains their associated singular values in descending order (the larger the singular value, the more significant the corresponding U‐vector). The number of significant singular vectors (nonrandom curves with significant singular values) yields the number of independent curves required to represent the entire data set by their linear combinations, that is, the number of individual components in the mixtures.

EFA employs the SVD decomposition of the SAXS data set for finding the component start and end points during the system evolution (the so‐called concentration windows of the components). Each component is not present outside its concentration time window, and its concentration is therefore equal to zero. It is also assumed that the components elute after each other, that is, the first component present in the system will be the first to disappear, the second component will disappear next, and so on.

The fundamental idea of EFA is to follow the rank of the data matrix A as a function of the number of measurements taken into account. The assessment is conducted by performing SVD on the data matrix with increasing size. For this, forward and backward EFAs are normally done to determine when a component appears/disappears from the system (for SEC‐ or IEC‐SAXS, this defines the points corresponding to the appearance of an extra component in the time frames in the elution peaks). Forward EFA consists of SVD repeatedly carried out on a portion of the matrix A, A _m , where A _m is defined as the first m columns of A. For the backward EFA, last m columns of A are used (also with sequentially increasing m). From the plots of significant singular values versus the profile numbers (e.g., time frames) of SAXS data sets, one can assess the “concentration windows” of the components by the moments when the corresponding singular values of them start to rise above the baseline or decrease approaching the baseline.

The next step of the EFA analysis is the determination of a rotation matrix that is needed for the transformation of the significant singular vectors into the concentration matrix and the scattering profiles of the components. Given that the data matrix is A = IC, where the columns of the matrix I represent the scattering profiles of the components, the concentration matrix C is expressed as C = (U ^T I) ⁻¹ SV ^T  = RV ^T , where R is a rotation matrix. The latter one is unknown but can be found using the information about the concentration windows of the components obtained in the previous step from the evolving plots. Taking only the portion of the vectors and matrix C outside of the concentration window range, one column of the matrix R can be sequentially restored after the other. ⁷ Having found the elements of matrix R, the columns of matrix C can easily be calculated. Using this approach, the concentration matrix C is evaluated non‐iteratively and without assumptions. The last step of EFA is the calculation of matrix I that can be done using the Moore–Penrose pseudoinverse of matrix C multiplied by the data matrix A.

2.2. EFA implementation and the scheme of the search

EFA is implemented in the program EFAMIX included in the ATSAS package (http://www.embl-hamburg.de/biosaxs/software.html). ²⁰ EFAMIX is freely available to academic users, together with other ATSAS programs from its 3.1 release. On the input, EFAMIX requires SAXS data sets in ASCII format with the files corresponding to measured frames enumerated in ascending order and the full or relative path to the file directory. The following parameters need to be specified by the user:

1. the expected number of components in the system (for practical reasons, from two to four components are allowed),

2. a subset of the sample data frames that will be processed by the EFA (i.e., the start and end frame numbers containing the sample signal),

3. a subset of the buffer data frames to calculate the average buffer signal (if not specified, a region of the data sets before the first sample frame is selected), and

4. the angular s‐axis range (by default EFAMIX includes all experimental data points, but in practice, it is convenient to discard any unstable/parasitic scattering at very low angles near the beamstop, which can be distorted by a small, but essential drift of the recording system which may produce relatively large error when subtracting the buffer scattering) as well as noisy data points at high angles where the curves emerge to the atomic scattering background (the maximum useful s‐value can be assessed, for example, by the program SHANUM ²⁵ ).

The number of components to use for the EFA may be deduced from the shape of the elution profile or independently assessed by the module SVDPLOT of the programs PRIMUS ²⁶ and/or POLYSAS ²⁷ using the nonparametric statistical test for random oscillation of significant singular vectors due to Wald–Wolfowitz. ²⁸ On the output, EFAMIX yields the restored scattering curves of the individual components, their concentration profiles, and the fits to the experimental data for each time frame.

EFAMIX is written in Fortran and utilizes the subroutines from the open‐source Fortran library LAPACK for SVD matrix decomposition (www.netlib.org/lapack/). Two algorithms are of interest in this library. The first one, DGESVD, is close to the classical procedure of Golub and Reinsh ²⁴ (the input matrix A is converted to the upper bidiagonal matrix by a sequence of Hausholder transformations followed by diagonalization by QR algorithm). ²⁴ , ²⁹ The second procedure, DGESDD, uses the divide‐and‐conquer algorithm (adaptive block partitioning of the matrix). This algorithm is two to four times faster than the previous one with similar computational accuracy and will be applied in the next version of EFAMIX after thorough testing. To solve the redundant system of linear equations (from which the elements of the rotation matrix R are recovered), EFAMIX uses a linear least‐squares method also based on the SVD. ²⁹ This method is numerically stable since the solution is obtained by orthogonal transformations. In addition, the singular decomposition allows one to stabilize the solution by implicit computation of the Moore–Penrose pseudoinverse matrix, limiting the spectrum of singular values (the diagonal of the matrix S), sorted in descending order, by the ratio $\frac{S_{\min }}{S_{\max }}\ge \sqrt{M\bullet N}\bullet \mathrm{EPS}$, where EPS is the machine precision, in our case 1.12 × 10⁻¹⁶. Currently, EFAMIX does not use the nonnegative least‐squares method because the imposed constraints may lead to several local minima in the search.

A detailed scheme of the search for the peak decomposition of inline chromatography SAXS data can be found in Supporting Information.

3. APPLICATIONS OF EFAMIX TO SIMULATED AND PRACTICAL CASES

3.1. Applications to the simulated SEC‐SAXS data sets of oligomeric mixtures

The method was first tested on the simulated SEC‐SAXS curves from protein mixtures. In the examples presented in Figures 1, 2, 3 and Figures [Link], [Link], we generated SEC‐SAXS data sets from two‐component monomer–dimer mixtures of bovine serum albumin (BSA) with different degrees of peak overlap (emulating different SEC columns (Figure 2), different concentrations ratios in the mixture (Figure [Link], [Link]), and different signal‐to‐noise levels (Figure 1). The theoretical scattering curves from monomeric and dimeric BSA models (PDB ID: 4F5S) were calculated using CRYSOL, ³⁰ and subsequently, 100 scattering curves were generated as their linear combinations weighted by the volume fractions from the concentration profiles of the components. The latter were represented by Gaussian (symmetric peaks; Figures 1, 2, and [Link], [Link]), and the exponential–Gaussian hybrid (EGH) functions (asymmetric peaks; Figure 3) shifted relative to each other. Similar to the elution peaks from the SEC column, the dimer species appeared first followed by the monomer species (Figures 1, 2, 3).

FIGURE 1.

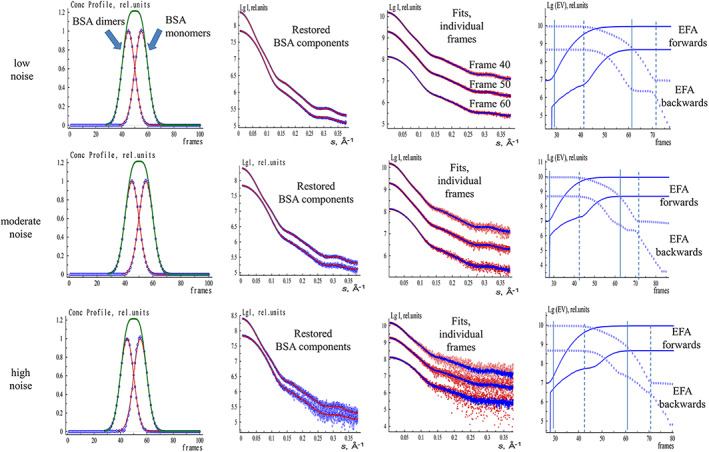
EFAMIX deconvolution of synthetic SEC‐SAXS data from BSA monomer–dimer mixture (both components have equal fractions). The concentration profiles are modeled by Gaussian functions. From left to right, Column 1—concentration profiles of the components restored by EFAMIX (blue), theoretical (ideal) profiles of the components (red), and the overall theoretical concentration profile (green); Column 2—scattering profiles of the components restored by EFAMIX (blue) and the theoretical (ideal) scattering profiles calculated by CRYSOL (red); Column 3—the individual frames of SEC‐SAXS data (frames number 40, 50, and 60; red) and the fits provided by EFAMIX decomposition (blue); Column 4—plots of the forward EFA (solid lines) and the backward EFA (circles) for the first two significant singular values, and the appearance and disappearance of the first and the second components are shown by solid and dashed vertical lines, respectively. The noise level of Poisson type added to the data corresponds to the following numbers of photons around the beamstop with subsequent radial averaging: from the top to the bottom, Row 1 (low noise)—10⁴ photons, Row 2 (moderate noise)—10³ photons, Row 3 (high noise)—10² photons. BSA, Bovine serum albumin; EFA, evolving factor analysis; SEC‐SAXS, size‐exclusion chromatography–small‐angle X‐ray scattering

FIGURE 2.

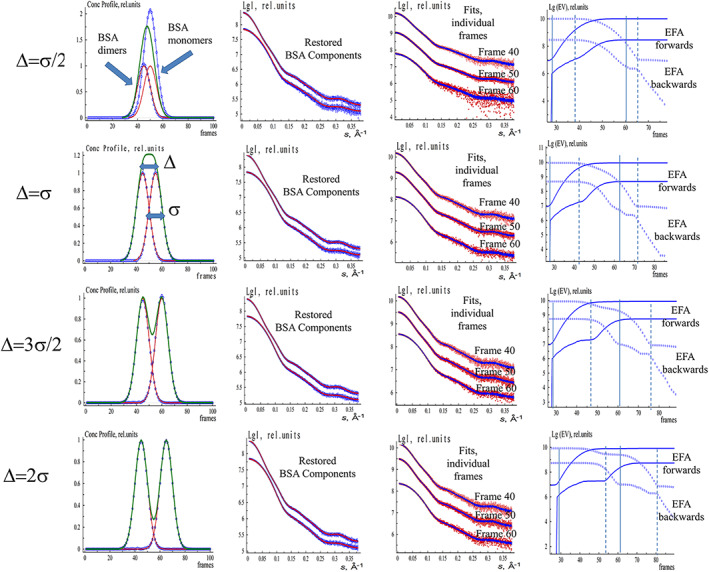
EFAMIX deconvolution of synthetic SEC‐SAXS data from BSA monomer–dimer mixture (both components have equal fractions) with different peak overlap (Δ). The concentration profiles are modeled by Gaussian functions. The notations and color schemes are as in Figure 1. BSA, Bovine serum albumin; EFA, evolving factor analysis; SEC‐SAXS, size‐exclusion chromatography–small‐angle X‐ray scattering

FIGURE 3.

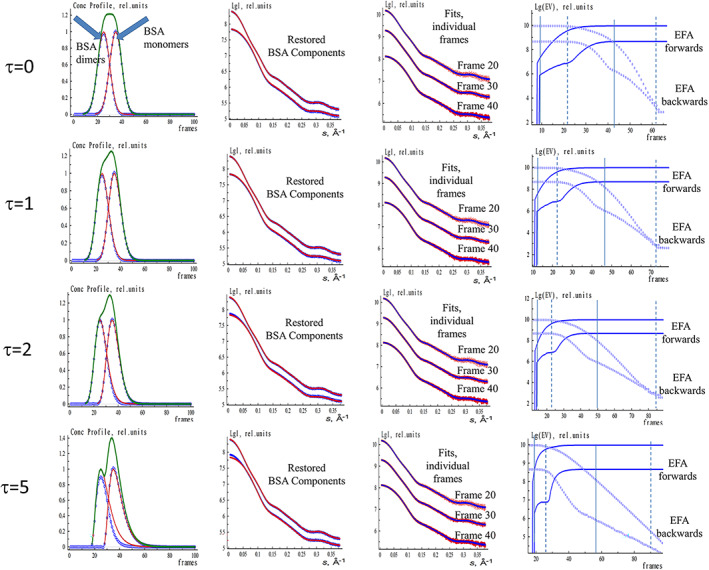
EFAMIX deconvolution of synthetic SEC‐SAXS data from BSA monomer–dimer mixture (both components have equal fractions) with different concentration profile asymmetry (τ). The concentration profiles are modeled by EGH functions. The notations and color schemes are as in Figure 1. BSA, Bovine serum albumin; EFA, evolving factor analysis; EGH, exponential–Gaussian hybrid; SEC‐SAXS, size‐exclusion chromatography–small‐angle X‐ray scattering

As any experimental data contain noise, one has to add it in a proper way to the theoretical data sets. The modern 2D pixel detectors (e.g., Pilatus, Eiger.) are considered counters of single photons, and the recorded signals obey Poisson (counting) statistics. The buffer subtraction step is not required during the noise simulation procedure as the sum of two Poisson‐distributed random variables will also have Poisson distribution. At the same time, one has to take into account the error propagation during the azimuthal averaging of 2D data. We have employed the algorithm for the generation of Poisson pseudorandom noise as described in References 31, 32 A 2D detector with the number of pixels 2500 × 2500 was assumed to calculate the error propagation during the azimuthal averaging. To obtain one‐dimensional scattering curves with different signal‐to‐noise ratios, we scaled the original curves (which are linear combinations of theoretical component curves weighted by their volume fractions) by a factor corresponding to the standard deviations of Poisson noise of 1, 3, and 10% in the maximum intensity region (the initial part of the one‐dimensional curve). Considering such curves as mathematical expectations of intensity, pseudorandom realizations of Poisson noise were calculated for each detector pixel. Finally, the intensities were azimuthally averaged over the detector plane. These noise levels can be defined as low noise (corresponds to 10⁴ photon counts at the region close to the beamstop of the 2D detector), moderate noise (10³ photons), and high noise (10² photons).

The generated SEC‐SAXS data sets were analyzed using EFAMIX. The scattering signals of BSA monomers and dimers were restored together with their concentration profiles and compared to calculated scattering curves of the initial monomeric and dimeric BSA X‐ray crystal structures.

As seen from Figures 1 and 2 and Figures [Link], [Link], in the case of Gaussian (symmetric) concentration profiles, EFAMIX successfully decomposed the simulated data and restored the information about the individual components with the accuracy influenced by the degree of the peak overlap, ratios of peak positions, and the noise level in the data. At low noise levels (with photon counts 10³ and 10⁴), the restored concentration profiles and scattering curves of the components perfectly coincided with the theoretical (ideal) values. For the higher noise level (photon count 10²), the restored concentration profiles contained some artifacts and the scattering curves from the components became noisier at higher angles. Interestingly, the overall quality of the data decomposition was still satisfactory, also at high noise. These simulations demonstrated the efficiency of EFA for the analysis of SEC‐SAXS data from two‐component systems with symmetric concentration profiles even for significant peak overlap and for high noise levels in the SAXS data.

In practice, the elution peaks may be somewhat asymmetric with a sharper rise on the leading edge and an elongated tail on the falling edge. These profiles can be modeled using asymmetric EGH functions with the additional “relaxation time” parameter. ³³ This “tailing” may cause systematic deviations for EFA peak decomposition even at low noise levels for two‐component systems as can be seen from Figure 3. For highly overlapping peaks, a decomposition is still possible for a moderate asymmetry of the concentration profiles (when the relaxation parameter τ of the EGH function does not exceed the value of 2). At higher profile asymmetries, the component peaks display significantly overlapping concentration windows leading to systematic deviations in the EFA results (τ = 5 row in Figure 3).

The shape of the proteins may also influence the results of the decomposition process but in a rather moderate way. EFAMIX was applied to a synthetic SEC‐SAXS data set from a mixture of elongated dimers and tetramers of fibrinogen (Figure S5) and restored reasonably well the components even at high noise levels (with photon counts 10²).

One can also estimate the concentration ratio threshold of the successful decomposition for the two‐component mixtures with one major and one minor component. Figures S3 and S4 display the EFAMIX results for BSA monomer–dimer mixtures with 1:5 and 5:1 concentration ratio, respectively. As demonstrated in Figures S3 and S4, it is possible to restore the dimers when they represent a minor fraction in the mixture but is more problematic to recover the monomeric component if the dimer scattering dominates the signal. One is still able to resolve the components if their concentration ratios are about 1:5/1:7 while the ratio exceeding 1:10 appears to be a limit of the EFA decomposition. Peak separation distance also plays a role. The distance between the overlapped peaks of the concentration profiles of the components in all test cases was at least two times the individual peak width; for smaller separations, the peak decomposition may become ambiguous as can be seen in Figure 2 where the different degree of peak overlap (Δ) was considered.

Subsequently, we generated simulated SEC‐SAXS data from three‐ and four‐component mixtures of BSA (monomer–dimer–tetramer and monomer–dimer–tetramer–octamer mixture equilibria, respectively;) Figures S6 and S7). The elution peaks appeared and disappeared sequentially with the higher molecular weight species and ending with the lower oligomers or monomers. EFAMIX could successfully decompose the three‐component system at low, moderate, and high noise levels (with photon counts of 10⁴ 10³, and 102; Figure S6). For the four‐component system, the reconstruction was possible at relatively low noise level (with photon counts of 10⁴ and 10³), whereas at higher noise levels (photon counts 10²), only the information about the largest species (tetramers/octamers) could be restored (Figure S7). Hence, the EFA method can be useful for the analysis of SEC‐SAXS data from three‐ and four‐component systems, but the noise threshold, after which the reconstruction becomes unreliable, is decreasing with the number of components in the system.

To further check the quality of our approach, we also simulated a realistic SEC‐SAXS data set using the IMSIM and IM2DAT tools ³⁴ of ATSAS. Here, two‐dimensional (2D) scattering patterns for BSA monomer–dimer mixtures (corresponding to the concentration profile with overlapped peaks as in Figure 1) were simulated by IMSIM for an experimental setup with Pilatus 6 M detector positioned at the distance of 3.0 m from the sample with the flux of the upcoming beam of 10¹² photons/sec, the exposure time of 1 second and the protein concentration of 1 mg/ml (at the peak maximum). After that, the 2D images were transformed into 1D scattering curves by radial averaging with IM2DAT, and the buffer signal was subtracted from each individual frame. Finally, EFAMIX was applied to the generated SEC‐SAXS data set and successfully restored the scattering curves of the components and the corresponding concentration profiles (Figure S8). These results further reveal the efficiency of EFA for simulated SEC‐SAXS data sets emulating real experimental conditions.

3.2. Applications of EFAMIX to the experimental SEC‐SAXS data sets

After validation on simulated data, the method was applied to a number of experimental SEC‐SAXS data sets collected from samples containing particles of various sizes at different concentrations. Some of these examples are presented below to illustrate the capacity of the method to restore the scattering curves and concentration profiles of the individual components in protein mixtures. The X‐ray synchrotron scattering data were recorded on the P12 beamline of the EMBL ³⁵ , ³⁶ at the storage ring PETRA III (DESY, Hamburg) using the inline SEC setup.

The first SEC‐SAXS data set, from a monomeric BSA sample, produced a single elution peak (Figure 4a). The restored EFAMIX scattering profiles contained only one significant component, and the crystal structure of BSA (PDB ID: 4F5S) neatly fits the experimental curve from this component. The second SEC‐SAXS data set, also from a standard protein often used for molecular mass calibration, glucose isomerase (GI), yields the elution profile with a symmetric single peak (Figure 4b). The EFAMIX decomposition of the data also yielded only one significant component, and the curve computed from the crystallographic model of GI (PDB ID: 1OAD) fits the restored scattering signal. These results demonstrate that for systems with a single component, EFAMIX reliably distinguishes the useful scattering signal from the noise component.

FIGURE 4.

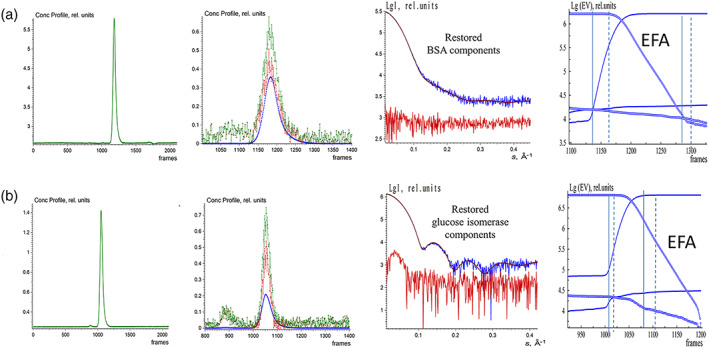
EFAMIX deconvolution of experimental SEC‐SAXS data from BSA (a) and glucose isomerase (b); calculations were performed within a two‐component approximation. Column 1—Elution profiles of SEC‐SAXS data obtained by chromatography inline X‐ray scattering (CHROMIXS) (green). Column 2—Restored concentration profiles of the components, the blue and red curves are individual components, and the green curve is the overall concentration profile. Column 3—Restored scattering profiles of the components (blue and red curves, respectively); the fits from the crystallographic models (brown; BSA: 4F5S.pdb, Glucose isomerase: 1OAD.pdb) to the restored scattering profiles by EFAMIX from the most significant component (blue). Column 4—Plots of the forward EFA (solid lines) and the backward EFA (circles) for which the notations and color schemes are the same as in Figure 1. BSA, Bovine serum albumin; EFA, evolving factor analysis; SEC‐SAXS, size‐exclusion chromatography–small‐angle X‐ray scattering

The third SEC‐SAXS data set, from a Class II pyruvate aldolase, ³⁷ yielded a skewed elution peak pointing to the potential presence of two significant components (Figure 5a). Indeed, the SVD analysis pointed to the presence of two significant components and the EFAMIX decomposition produced two distinct components, where the curve from the smaller species was well reproduced by the hexamer crystal structure of the enzyme (PDB ID: 6R62). The larger species likely correspond to an octameric protein as the ratio of Porod volumes ³⁸ estimated for the two restored scattering curves is about 1.3. We have additionally checked the stability of the EFAMIX solutions by taking only the odd‐ or even‐numbered SEC‐SAXS data frames into the analysis, and the restored solutions did not significantly differ from the results obtained using the full SEC‐SAXS data set.

FIGURE 5.

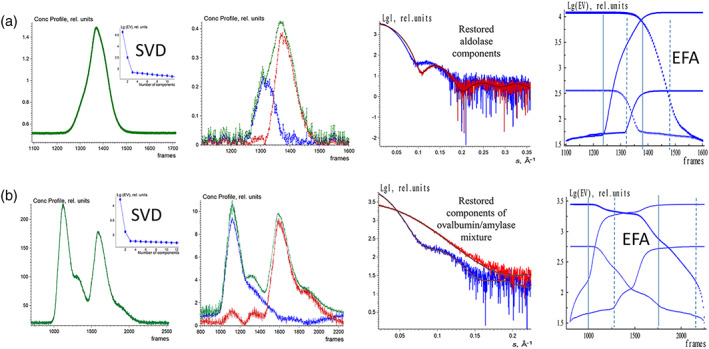
EFAMIX deconvolution of experimental SEC‐SAXS data from aldolase (a) and the mixture of ovalbumin with β‐amylase (b); calculations were performed within a two‐component approximation. Column 1—Elution profiles of SEC‐SAXS data obtained by CHROMIXS (green). The insets contain the singular values of SVD decomposition of SEC‐SAXS data (after buffer subtraction) in descending order. Column 2—Restored concentration profiles of the components, the blue and red curves are individual components, and the green curve is the overall concentration profile. Column 3—Restored scattering profiles of the components and the fits (brown curves) from the crystallographic models (aldolase hexamer: 6R62.pdb; ovalbumin monomer: 1OVA.pdb; β‐amylase tetramer: 1FA2.pdb) to the restored scattering profiles by EFAMIX (blue and red, respectively). Column 4—Plots of the forward EFA (solid lines) and the backward EFA (circles) for which the notations and color schemes are the same as in Figure 1. EFA, evolving factor analysis; SEC‐SAXS, size‐exclusion chromatography–small‐angle X‐ray scattering; SVD, singular value decomposition

The fourth SEC‐SAXS data set was obtained from a preprepared mixture of two proteins, ovalbumin and β‐amylase. The elution profile from this solution showed two partially overlapping peaks (Figure 5b). Although a small shoulder after the first peak was observed, the SVD analysis of the data revealed only two significant components in the system. EFAMIX was also able to decompose the profile and fit the entire SEC‐SAXS data set by a linear combination of two components. The restored scattering curves were in a good agreement with the theoretical curves calculated from the crystallographic structures of the two proteins, monomeric ovalbumin PDB ID: 1OVA (MW = 42 kDa) and tetrameric β‐amylase PDB ID: 1FA2 (MW = 223 kDa). Thus, the method produces robust and stable solutions for the experimental SEC‐SAXS data sets with two distinct components even in the case of partially overlapping elution profiles. The linear Guinier plots ³⁹ of the restored components further confirm the adequate separation (Figure S9).

3.3. Applications of EFAMIX to simulated and experimental IEC‐SAXS data sets

During IEC, the sample from the column is eluted by flowing a buffer with an increasing salt concentration. The main challenge in IEC‐SAXS data deconvolution analysis is to take into account the changing background scattering from the buffer due to the salt gradient. Formally, the evolving background may violate the assumptions of the EFA method (the presence of nonoverlapping areas in the concentration contours of the components), but in practice, the extent of this violation depends on the degree of the gradient.

We first simulated IEC‐SAXS data from a BSA monomer–dimer mixture (the same as in Figure 1) and introduced a buffer gradient as an increasing constant term to the scattering data frames. We selected the case with a relatively high noise level (with photon counts 10²) and tested two buffer gradients of 12 and 25% difference levels (the relative difference in buffer signal before and after the elution peak of the sample). In practice, the buffer gradient with 12% of difference level would correspond to the addition of 1.2 M of NaCl. As can be seen from Figure S10, EFAMIX can successfully decompose IEC‐SAXS data with the presence of 12% buffer gradient but starts to have difficulties at a 25% buffer gradient. In the latter case, only the dimeric component can be restored correctly, whereas the restored scattering curve from the monomeric species has a systematic deviation from the theoretical curve at higher angles. These results demonstrate that EFA can be applicable for IEC‐SAXS data sets with a moderate degree of gradient in the buffer scattering.

We have then applied the EFA to an experimental IEC‐SAXS data set obtained for the monoclonal antibody (mAb) IgG1 after papain digestion. Here, IgG1 is separated into the fragment crystallizable (Fc) domain, as well as the two identical fragment antigen‐binding (Fab) domains. All these domains have molecular mass around 50 kDa and can therefore not be separated with SEC. However, due to the different surface charge, a separation through IEC is possible, whereby the Fc domain elutes before the Fab domain on a ProPac WCX‐10 column. This is a weak cation‐exchange column designed specifically for high‐resolution, high‐efficiency analysis of mAbs (Figure 6). The relative buffer difference (estimated as a ratio between the sample signal at the maximum of the elution peak minus the buffer background after elution peak to the sample signal minus the buffer background before the elution peak) is rather high (about 35%). We have therefore applied EFAMIX to extract separately the scattering curves from the Fc domain only (the first elution peak) and the Fab domain only (the second elution peak), and the result is presented in Figure 6. In each case, EFAMIX found a single significant component present in the system (the second component had a negligible intensity signal), and the restored scattering profiles from these components were compared to the curves obtained by manual subtraction in CHROMIXS using the buffer signals before and after the elution peak. The two results overlap with each other at lower angles, but the curves restored by EFAMIX differ from CHROMIXS results at higher angles. Interestingly, the crystallographic structures of Fc and Fab domains of IgG1 provide better fits to the EFAMIX curves. The EFAMIX decomposition appears therefore to be less influenced by artifacts of the buffer changing background while the manual data processing by CHROMIXS yields a more biased subtraction. This result indicates that EFAMIX can also be utilized on the IEC data with moderately varying background level.

FIGURE 6.

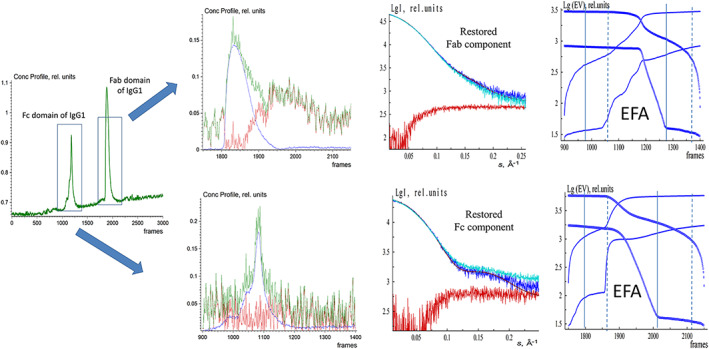
EFAMIX deconvolution of experimental IEC‐SAXS data from Fc and Fab domains of IgG1. From left to right, Column 1—the elution profile of IEC‐SAXS data (green) obtained by CHROMIXS (the first elution peak corresponds to the Fc domain of IgG1, and the second elution peak belongs to the Fab domain of IgG1). Column 2—Restored concentration profiles of the components (Row 1 corresponds to the first elution peak from the Fc domain of IgG1 and Row 2 to the second elution peak from the Fab domain of IgG1), the blue and red curves are individual components, and the green curve is the overall concentration profile. Column 3—Restored scattering profiles of the components (blue and red, respectively), the fits (brown curves) from the Fc and Fab domains of IgG1 crystallographic structure (1HZH.pdb), and the comparison with the curve obtained by manual subtraction in CHROMIXS (cyan) using the buffer signals before and after the elution peak. Column 4—Plots of the forward EFA (solid lines) and the backward EFA (circles) for which the notations and color schemes are the same as in Figure 1. EFA, evolving factor analysis; Fab, fragment antigen‐binding; Fc, fragment crystallizable; IEC‐SAXS, ion‐exchange chromatography–small‐angle X‐ray scattering

4. DISCUSSION AND CONCLUSIONS

EFA is a general method for the analysis of multiple data sets described by a systematic and evolving order of individual components. The technique involves no assumptions about the number of components, their shapes, or the separation between the components. EFA approach is of general value and was already successfully applied in analytical and solution chemistry, in particular for HPLC with photodiode array detection and ultraviolet spectrometry. The implementation of the method for the analysis of SEC‐SAXS data also showed its high potential and permitted not only to decompose the signals from oligomeric equilibrium protein mixtures ⁹ , ⁴⁰ but also to characterize domain movements of an enzyme involved in allosteric activation. ⁸

It is known from the literature on chemometric separation of matrices for mixtures that the separation is unambiguous if there are nonoverlapping areas in the contours of the component spectra (which is not always the case with SAXS) or in the contours of the concentration profiles (the EFA principle relies on this). Chromatographic separation, as a minimum, provides nonoverlapping initial sections of the concentration curves, and this should be sufficient for a successful decomposition. The same is valid for the tailed sections of the concentration curves, but even in the case of their overlap, the full‐range profiles are employed as they contain useful information that improves the data set statistics.

In this study, we implemented EFA in a general‐purpose program EFAMIX for SAXS data analysis and explored the sensitivity of the method with respect to the noise level of the data and to the number of components in the systems with overlapping elution peaks. Using the simulated SEC‐SAXS data sets, it was shown that for two‐component systems with symmetric (Gaussian‐like) concentration profiles (e.g., monomer–dimer equilibrium mixture), EFA is able to deconvolute the SEC‐SAXS data and restore the concentration profiles and scattering patterns of the individual components even if significant noise levels present in the data. At higher noise levels, EFA reconstruction becomes unstable, and for the systems with a higher number of components, this noise threshold steadily decreases. Interestingly, the scattering signals from larger molecular weight species can still be restored while these from the smaller molecular weight species start to display artifacts and systematic deviations from the expected signals. Expectedly, EFA does show limitations when applied to systems with significantly asymmetric concentration profiles or when the peaks overlap too much (the distance between peak maxima is smaller than twice the individual peak width). Such cases may arise for example at nonoptimal pressures and flow rates in an SEC column or due to structural heterogeneity within a sample where specific conformational states have a tendency to interact differently with an SEC column matrix.

The method was then applied to experimental SEC‐SAXS and IEC‐SAXS data sets from several standard proteins and yielded robust solutions compatible with the theoretical curves calculated from known crystallographic structures. In particular, it was possible to describe an unusual oligomeric mixture of pyruvate aldolase consisting of hexamers and octamers. For IEC‐SAXS data, we demonstrated that, despite the changing background due to varying salt amount in the eluent, EFA is still applicable for moderate salt buffer gradients.

The proposed method implemented in the program EFAMIX (available in the ATSAS 3.1 release) requires minimal user intervention and is therefore potentially applicable in automated pipelines. It can be used for the analysis of various SEC‐SAXS data sets and also IEC‐SAXS runs with a moderate salt buffer gradient.

5. MATERIALS AND METHODS

5.1. Sample preparation

For the preparation of monomeric BSA, the following pre‐purification protocol was applied (as described in Graewert et al., ⁴¹ and refer to SASBDB ⁴² entry SASDFQ8):

All procedures were performed at 4°C. Protein powder (Sigma Aldrich, A7030) consisting of BSA monomers, dimers, trimers, and higher MW species was made to approximately 25 mg/ml in 25 mM HEPES, 50 mM NaCl, 5 mM urea, 1% v/v glycerol, and pH 7. Approximately 200 μl of sample was loaded onto a Superdex 200 Increase 10/300 column (GE Healthcare, now Cytiva) equilibrated in the same buffer (flow rate = 0.4 ml/min). Fractionated aliquots corresponding to the highest absorbing peak (estimated using UV A280 and UV A245 nm) were pooled and concentrated (30 kDa centrifuge spin filter) to a final concentration of 8.8 mg/ml, and the concentration was determined from triplicate UV A280 measurements using an E0.1% of 0.646 (= 1 g/l) calculated from the amino acid sequence (ProtParam). Approximately 75 μl aliquots were snap‐frozen in liquid nitrogen then stored at −80°C.

GI from Streptomyces rubiginosus was provided as an ammonium sulfate precipitate (crystalline suspension) from Hampton Research (HR7‐102) at 33 mg/ml. For the SEC‐WAXS measurements, the sample was diluted in GI mobile phase (50 mM Tris, 100 mM NaCl, 1 mM MgCl2, 1% v/v glycerol, and pH = 7.5), dialyzed extensively against the buffer. For the SEC‐SAXS/MALLS run, the concentration was adjusted to 10.3 mg/ml.

A sample of Class II pyruvate aldolase (HpcH/HpaI aldolase, UniProt ID A5VH82; amino acids 2–251, plus an N‐terminal 6‐His tag) was kindly provided by Isabel Bento (EMBL Hamburg) and prepared as described in Mardsen et al. ³⁷

Ovalbumin from hen egg was purchased from GE Healthcare (now Cytiva, GE‐28‐4038‐42 [HMV kit]), and β‐amylase from sweet potato was purchased from Sigma Aldrich (A8781). The powders of both samples were dissolved in the mixture buffer (20 mM Tris, 150 mM NaCl, and 5% glycerol). The final concentration was approximately 15 mg/ml. The samples were filtered through 0.2 μm centrifugal filter units (Millipore) prior to loading onto the respective SEC column. Equal volumes of the two samples were mixed together for the final sample.

For the papain digestion study, a mAb formulation (a recombinant human IgG1) manufactured by Chugai Pharmaceutical was used. To analyze the Fab as well as Fc domains of IgG1, a papain digestion was performed and the subunits separated on a ProPac WCX‐10 column (Thermo Fisher Scientific; particle size: 10um; id: 4.0 mm; length: 25 cm). For this, the formulation buffer of IgG1 was exchanged for digestion buffer (100 mM Tris–HCl, 20 mM EDTA 2Na, 20 mM cysteine, and pH 7.4). The protein concentration was set to 1 mg/ml. Papain was added with a final concentration of 0.01 mg/ml. After an incubation for 2 hr at 37°C, the reaction was stopped by the addition of 28 mM iodoacetamide. The buffer was again exchanged, this time against mobile phase A (25 mM MES and pH 6.1). The sample was further concentrated to 5 mg/ml, and 100 μl was injected onto the column for the IEC‐SAXS/MALLS run.

5.2. SAXS measurements

SAXS data sets were acquired at EMBL's P12 beamline at PetraIII in Hamburg, Germany ³⁵ using an incident beam size of 200 × 110 μm² (full width at half maximum). The eluent of the employed chromatography column was passed through a 1.7‐mm quartz capillary held under vacuum (1.0‐mm capillary was used for the Class II pyruvate aldolase). The SAXS data were recorded on a Pilatus 6 M area detector (Dectris) at a sample to detector distance 3 m and the wavelength λ = 0.124 nm (X‐ray energy 10 keV). Series of individual 1‐s exposure X‐ray data frames were measured from the continuously flowing column eluate across one column volume. The 2D SAXS intensities were reduced to I(s) versus s using the integrated analysis pipeline SASFLOW. ⁴³ The s‐axis was calibrated with silver behenate, and the resulting profiles were normalized for exposure time and sample transmission.

For the ovalbumin–β‐amylase experiment, the chromatography setup as described in Reference 36 was employed; for the other experiments, the HPLC setup ⁴¹ was used. In all cases, the eluent from the column was split so that half the stream was directed to the SAXS capillary and the other portion further analyzed with various detectors: in the former case with the TDA from Malvern and in the latter cases with the Wyatt light scattering devices.

IEC was performed in a similar manner as the SEC runs. A linear gradient was programmed to increase the amount of NaCl by increasing the amount of IEC buffer B (25 mM MES, pH 6.1, and 1 M NaCl). Change in ionic strength of the mobile phase leads to elution of the different subunits, Fab and Fc, at different time points.

The various mobile phases and columns are listed in Table S1.

CONFLICT OF INTEREST

The authors declare no competing interests.

AUTHOR CONTRIBUTIONS

Petr V Konarev: Conceptualization (equal); formal analysis (equal); investigation (equal); methodology (equal); software (equal); writing – original draft (equal); writing – review and editing (equal). Melissa A Graewert: Formal analysis (equal); investigation (equal); writing – review and editing (equal). Cy M Jeffries: Formal analysis (equal); investigation (equal); writing – review and editing (equal). Masakazu Fukuda: Investigation (equal); writing – review and editing (equal). Taisiia A Cheremnykh: Investigation (equal); writing – review and editing (equal). Vladimir V Volkov: Formal analysis (equal); investigation (equal); methodology (equal); writing – review and editing (equal). Dmitri I Svergun: Conceptualization (equal), methodology (equal), formal analysis (equal), investigation (equal), writing – review and editing (equal), supervision.

Supporting information

Appendix S1 Supporting Information

Figure S1 EFAMIX deconvolution of synthetic SEC‐SAXS data from BSA monomer–dimer mixture (the main fraction is dimeric, the concentration ratio is 2:1). The notations and color schemes are as in Figure 1

Figure S2 EFAMIX deconvolution of synthetic SEC‐SAXS data from BSA monomer–dimer mixture (the main fraction is monomeric, the concentration ratio is 1:2). The notations and color schemes are as in Figure 1

Figure S3 EFAMIX deconvolution of synthetic SEC‐SAXS data from BSA monomer–dimer mixture (the main fraction is dimeric, the concentration ratio is 5:1). The notations and color schemes are as in Figure 1

Figure S4 EFAMIX deconvolution of synthetic SEC‐SAXS data from BSA monomer–dimer mixture (the main fraction is monomeric, the concentration ratio is 1:5). The notations and color schemes are as in Figure 1

Figure S5 EFAMIX deconvolution of synthetic SEC‐SAXS data from fibrinogen (PDB ID: 3GHG) dimer–tetramer mixture (elongated particles). From left to right, Column 1—concentration profiles of the components restored by EFAMIX (blue), theoretical (ideal) profiles of the components (red), the overall theoretical concentration profile (green); Column 2—scattering profiles of the components restored by EFAMIX (blue) and the theoretical (ideal) scattering profiles (red); Column 3—the individual frames of SEC‐SAXS data (frames number 40, 50 and 60, from top to the bottom, respectively) (red) and the fits provided by EFAMIX decomposition (blue). The noise level of Poisson type added to the data corresponds to the following numbers of photons near the beamstop with subsequent radial averaging: from the top to the bottom, Row 1(low noise)—10⁴ photons, Row 2 (moderate noise)—10³ photons, Row 3 (high noise)—10² photons. Column 4—The plots of the forward EFA (solid lines) and the backward EFA (circles) for which the notations and color schemes are the same as in Figure 1

Figure S6 EFAMIX deconvolution of synthetic SEC‐SAXS data from BSA monomer–dimer–tetramer mixture (three‐component system). Column 3—The individual frames of SEC‐SAXS data (frames number 40, 50, and 60). The other notations and color schemes are as in Figure 1

Figure S7 EFAMIX deconvolution of synthetic SEC‐SAXS data from BSA monomer–dimer–tetramer–octamer mixture (four‐component system). Column 3—The individual frames of SEC‐SAXS data (frames number 30, 50, 70, and 90). The other notations and color schemes are as in Figure 1

Figure S8 EFAMIX deconvolution of synthetic “most realistic” SEC‐SAXS data from BSA monomer–dimer mixture (both components have equal fractions) generated using IMSIM and IM2DAT tools from the program package ATSAS

Figure S9 Guinier plots of the components restored by EFAMIX: aldolase hexamers and octamers, ovalbumin monomers, β‐amylase tetramers, BSA monomers, glucose isomerase tetramers (SEC‐SAXS data), and Fc and Fab domains of IgG1 (IEX‐SAXS data)

Figure S10 EFAMIX deconvolution of synthetic IEC‐SAXS data from BSA monomer–dimer mixture (the main fraction is dimeric) with a constant buffer gradient. From left to right, Column 1—concentration profiles of the components restored by EFAMIX (blue), theoretical (ideal) profiles of the components (red), the overall theoretical concentration profile (green); Column 2—scattering profiles of the components restored by EFAMIX (blue) and the theoretical (ideal) scattering profiles (red); Column 3—the individual frames of SEC‐SAXS data (frames number 40, 50 and 60) (red) and the fits provided by EFAMIX decomposition (blue). The noise level of the Poisson type added to the data corresponds 10² photons on the detector. Row 1—IEC‐SAXS data with 12% relative buffer difference before and after the elution peak, Row 2—IEC‐SAXS data with 25% relative difference. Column 4—The plots of the forward EFA (solid lines) and the backward EFA (circles) for which the notations and color schemes are the same as in Figure 1

Konarev PV, Graewert MA, Jeffries CM, Fukuda M, Cheremnykh TA, Volkov VV, et al. EFAMIX, a tool to decompose inline chromatography SAXS data from partially overlapping components. Protein Science. 2022;31:269–282. 10.1002/pro.4237