Abstract
Many macromolecules form helical assemblies to carry out their functions. Helical reconstruction from electron microscopic images is a powerful approach for solving high‐resolution structures of such assemblies. Determination of the symmetry parameters of the helical assemblies is a prerequisite step in helical reconstruction. The most widely used method for deducing the symmetry is through Fourier–Bessel indexing the diffraction pattern of the helical assemblies. This method, however, often leads to incorrect solutions, due to intrinsic ambiguities in indexing helical diffraction patterns. Here, we present Python‐based Helix Indexer (PyHI), which provides a graphical user interface (GUI) to guide the users through the process of symmetry determination. Diffraction patterns can be read into the program directly or calculated on the fly from two‐dimensional class averages of helical assemblies. PyHI allows deducing the Bessel orders of diffraction peaks by using both the amplitudes and phases of the diffraction data. Based on the Bessel orders of two unit vectors, the Fourier space lattice is constructed with minimal user inputs. The program then uses a refinement algorithm to optimize the Fourier space lattice, and subsequently generate the helical assembly in real space. The program provides both a publication‐quality graphic representation of the helical assembly and the symmetry parameters required for subsequent helical reconstruction steps.
Keywords: cryo‐EM, helical reconstruction, helical symmetry, indexing
1. INTRODUCTION
Formation of large helical assemblies is a common mechanism by which molecules gain unique properties and functions absent in individual components. The critical roles of such assemblies in biology are exemplified by the DNA double helix and microtubules, which are essential for storing the genetic information and regulating the shape and mechanical properties of the cell, respectively. Recently, more and more proteins are found to form helical assemblies in their physiological or pathological states, such as large helical complexes of signaling proteins and β‐amyloids. Helical reconstruction from electron microscope (EM) data is a powerful approach for solving the structures of helical assemblies, critical for understanding the mechanisms and functions of the assemblies. The invention of the iterative helical real‐space reconstruction (IHRSR) algorithm and its recent implementation in various software packages have led to high‐resolution cryo‐EM structures of many helical assemblies. 1 , 2 , 3 , 4
One critical initial step in helical reconstruction is to determine the symmetry parameters of the helical assembly. As discussed in detail previously, helical assemblies without rotational point group symmetry can be described with one‐start helices. 1 Parameters that characterize the symmetry of such helices include the rise and twist of each subunit, from which the pitch of the helix and the number of subunits per turn can also be deduced. More complicated helices may possess Cn rotational point group symmetry, such as C2 (twofold) and C3 (threefold), along the helical axis (or referred to as the z‐axis). In addition, a twofold symmetry axis perpendicular to the helix axis may exist, leading to dihedral symmetry such as D1, D2, and D3. Several methods have been developed for deducing the symmetry. 5 , 6 , 7 , 8 There is also an online server with a browser‐based user interface dedicated for this purpose (http://rico.ibs.fr/helixplorer/). One of the most used methods is the Fourier–Bessel indexing process based on analyses of the Fourier transform of the helical assembly. The Fourier transform can be calculated from one segment of the helix or two‐dimensional (2D) class averages of many segments. Alternatively, the average of the Fourier transforms of many individual segments can be used. The image of the amplitudes of the Fourier transform of vertically aligned helices (also called the power spectrum) shows evenly spaced horizontal layer lines with strong intensities (Figure 1). 9 The horizontal and vertical axes crossing at the origin of the power spectrum are referred to as the equator and meridian, respectively (Figure 1a). The reciprocal of the distance between the neighboring layer lines is the repeat distance of the helix. 9 In general, average power spectra are of higher quality and easier to interpret than those calculated from single helical segments or 2D class averages, as the latter may suffer from artifacts and loss of information.
FIGURE 1.
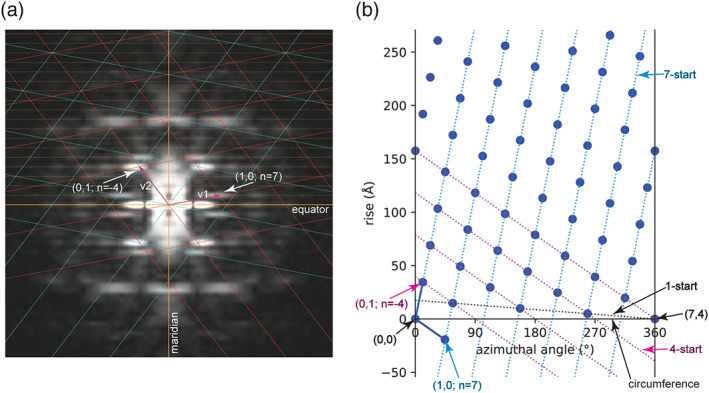
Power spectrum and two‐dimensional (2D) lattices of a helical assembly. (a) A 2D lattice (red) consistent with peaks in the power spectrum is drawn based on the two unit vectors v1 (Bessel order 7) and v2 (Bessel order −4). The lattice in cyan is the mirror image of the red lattice. Layer lines are represented by dashed lines in orange. For simplicity, the bottom halves of the two lattices are not drawn to completion, because they are the mirror images of the top halves. Likewise, layer lines in the bottom half of the power spectrum are omitted. (b) Real space lattice generated from the Fourier space lattice in (a). The two blue solid lines are the two real space unit vectors. The first vector ends at the lattice point (1, 0), which specifies the spacing of the right‐handed seven‐start helical family (blue dashed lines), because the Bessel order of the Fourier space vector v1 is 7. The second vector ends at the lattice point (0, 1), which specifies the spacing of the left‐handed four‐start helical family (magenta dashed lines), because the Bessel order of the Fourier space vector v2 is −4. The circumferential vector of the helical assembly begins and ends at lattices points (0, 0) and (4, 7), respectively. The simplest description of the helical assembly is the one‐start helix indicated by the black dashed line. The rise (along the helical axis) and twist (azimuthal angle difference) between two consecutive lattice points in this one‐start helix are the required parameters for helical reconstruction with IHRSR
The diffraction peaks in layer lines can be described with Bessel functions. 9 , 10 A Bessel function in the helical formalism has an argument 2𝜋Rr, where R is the distance of the first peak from the meridian in reciprocal space and r is the radius of the helix in real space. There is a direct relationship between the value of 2𝜋Rr and the Bessel order n. 11 For example, the Bessel orders n is 1 when 2𝜋Rr = 1.8, while the Bessel order n is 2 when 2𝜋Rr = 3.1. For Bessel orders larger than 10, 2𝜋Rr is approximately equal to n + 2. The assignment of Bessel orders of peaks in power spectra of biological helical samples containing large number of atoms is, however, often more difficult. A major issue is that the effective helix radius r for each diffraction peak could be different due to varied contributions of atoms distributed at different radial positions. 6 , 12 With the Bessel orders known, one method for deducing the symmetry parameters is the selection rule specified by the following equation: 9 , 10 , 11
| (1) |
where l is the layer‐line number and n is the Bessel order. m is an integer, which could be zero, positive or negative. The numbers t and u mean that the helix contains exactly u subunits in t turns. The symmetry of a helix is solved by finding a pair of t and u that satisfy the equation with all the l and n. A drawback of this method is that the selection rule could have multiple solutions, only one of which is correct. 8 In addition, defining helical symmetry in terms of t and u is less meaningful when considering that a small change in the twist per subunit in a helix could result in dramatic changes to t and u. 8 , 13
A second method for indexing is by treating a helical assembly as a 2D crystal rolled into a cylinder. 7 , 8 , 11 , 14 The diffraction patterns of helical assemblies are therefore similar to those of 2D crystals, except that the diffraction peaks from helical assemblies are elongated, appearing as layer lines instead of discrete spots. As a result, a reciprocal 2D lattice, also named the (n, l) plot, can describe the diffraction pattern of helical assemblies. This lattice can be constructed from two unit vectors with Miller indices (1, 0) and (0, 1), which define the reciprocal unit cell. 7 , 8 , 14 The Bessel orders n of a lattice point with the miller index of (h, k) is given by:
| (2) |
where n 10 and n 01 are the Bessel orders of the two unit vectors. This simple linear relationship greatly constrains the Bessel orders of all the layer‐line peaks, reducing the difficulty in their assignment. In addition, the Bessel order n of any point in the reciprocal lattice specifies the n‐start number of the helical family that gives raise to this diffraction peak. 7 , 8 , 14 Positive and negative Bessel orders correspond to right‐handed and left‐handed helices, respectively. For example, the Bessel order 7 of the first unit vector comes from the right‐handed seven‐start helical family in Figure 1b, which has seven helices that pass through the circumference. Likewise, the Bessel order −4 of the second unit vector corresponds to the left‐handed four‐start helical family (Figure 1b). The real space 2D lattice can be generated with the two real space unit vectors converted from the reciprocal space unit vectors. 1 A circumferential vector must be chosen between two lattice points such that the n‐start numbers of the two principle helical families defined by the two unit vectors are equal to their respective Bessel orders (Figure 1b). 7 The helix can then be generated by rolling up the 2D lattice into a cylinder to join the beginning and end of the circumferential vector. This method provides a graphic representation of the helical structure and contains all the symmetry parameters required for the subsequent helical reconstruction steps using IHRSR or RELION helical reconstruction. 1 , 7 , 13
Regardless the methods used, the indexing process remains one of the most difficult tasks in helical reconstruction. The intrinsic ambiguity in the indexing of power spectra makes it often very difficult to choose the correct one from multiple potential solutions. Choosing incorrect solutions would lead to wrong structures. 3 , 15 , 16 The method based on the 2D crystal analogy requires accurate construction of both the Fourier space and real space lattices, which is not easy to carry out manually. In this article, I present the Python‐based Helix Indexer (PyHI) program that provides a user‐friendly graphic interface to guide the user from assigning the Bessel orders to using the 2D crystal method to construct the lattices, making it easier to determine a range of possible symmetry parameters. The program generates high‐quality graphic representations of the lattices that can both help understand the helical structure and be used in publication.
2. RESULTS AND DISCUSSION
2.1. Visual inspection of images and identifying layer lines
The PyHI program allows loading of power spectrum in the MRC format, a commonly used file format in cryo‐EM, 17 or other image formats such as tiff, jpeg, and png. Average power spectra calculated from many aligned filaments often show better signal‐to‐noise ratio and less artifacts, helpful for identifying layer lines and diffraction peaks. However, phases of the peaks, which are useful for resolving the ambiguity in assigning the Bessel orders (see details below), are lost in this case. Alternatively, images of individual helical segments or 2D class averages (as MRC stacks) can be loaded. The helix should be centered and aligned vertically, which can be done by using the “align img” function and further fine‐tuning with the “rotate img” and “shift img” spin‐boxes. PyHI calculates the Fourier transform of the displayed 2D image on the fly and displays the power spectrum containing the amplitude of each pixel of the Fourier transform (Figure 2a), while the phases are stored internally and can be used later. The “class number:” box in the control area allows quick scrolling through different 2D class averages and selection of the best one for indexing. The program provides tools for zooming, panning, as well as adjustment of the contrast and colormap of the displayed images. In addition, various interpolation algorithms can be applied through the image adjustment tool in the toolbar to smoothen the power spectrum image for visual inspection.
FIGURE 2.
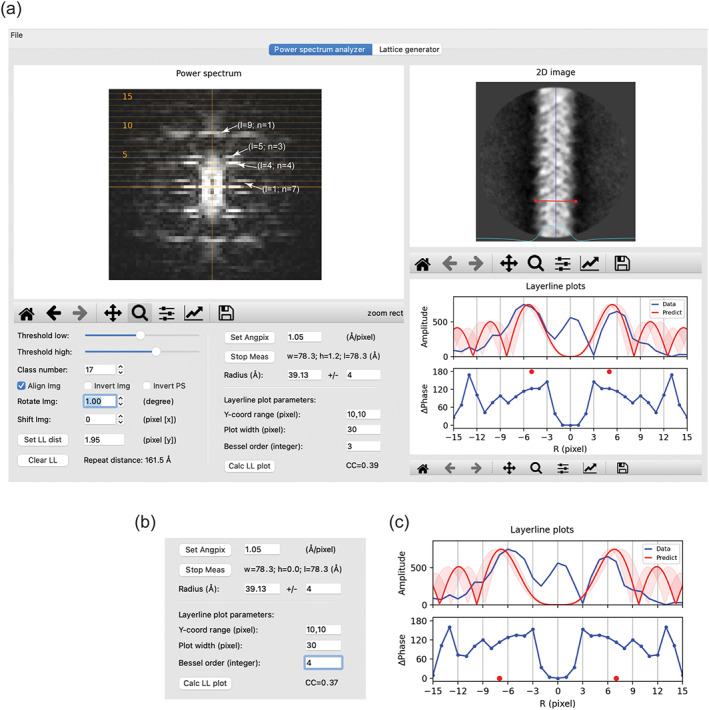
The “power spectrum analyzer” tab. (a) Overview of the user interface. One of the two‐dimensional (2D) class averages of the MAVS filament in the MRC stack format and its power spectrum are shown. The 2D image is centered and vertically aligned by checking the “align img” checkbox. The blue vertical line in the 2D image window serves as an indicator of the centering and alignment. The cyan curve represents the horizontal one‐dimensional (1D) profile of the 2D image, useful for finding the left and right boundaries of the helix when measuring the radius. Layer lines are drawn as dotted lines, with every fifth line labeled. The distance between layer lines is set to 1.95 pixel. The plots of amplitude and phase difference in the “layer‐line plots” window are generated with the parameters in the “layer‐line plot parameter” area. Note that the “Y‐coord range” should be specified in pixel, not the number of layer lines. The theoretical amplitude plot with Bessel order 3 (red) is shown for comparison. The range of radius of 4 Å specified in the ± input box is reflected by the semi‐transparent trace in the plot. The red dots indicate that the expected phase difference between the two peaks related by mirror symmetry along the meridian should be 180°. (b,c) The theoretical amplitude plot with Bessel order 4 matches the data plot reasonably well. However, the predicted phase difference is 0°, inconsistent with the data
The coordinates of the mouse pointer in the power spectrum image are displayed in the toolbar. This information allows the distance between layer lines (in pixel) to be estimated. Layer lines can be plotted on the image by inputting the number of the distance and clicking either “Set LL dist” or “Draw LL” (which toggles between “Draw LL” and “Clear LL” upon mouse click) (Figure 2a). The repeat distance of the helical assembly, which is the reciprocal of the layer‐line distance, is automatically calculated and displayed at the bottom of the control area. If the power spectrum is calculated form 2D images of the helix as in Figure 2a, the center of the power spectrum is the origin for the equator and meridian. The program uses the center as the default origin when drawing the equator, meridian, and layer lines. However, if a power spectrum image is loaded directly, the center of the image may not be the origin. In this case, the origin can be manually set by mouse clicking the correct position while holding the Option (MacOS) or Alt (Windows and Linux) key. With the origin correctly set, the user can iteratively change the layer‐line distance and draw layer lines in order to reach the optimal fit to the data.
In the example shown in Figure 2a, the image size of the 2D class averages of MAVS filaments is 300 × 300 pixel and the pixel size is 1.05 Å/pixel. The layer lines drawn with the distance of 1.95 pixel fit the data very well. The repeat distance is therefore 300 × 1.05/1.95 = 161.5 Å.
2.2. Determining the Bessel orders of peaks in the power spectrum
The radius of the helix is required for determining the Bessel orders of the peaks in the power spectrum. The radius can be measured by clicking the “measure” button followed by clicking the left and right edges of the helix (Figure 2a). The radius can also be manually set in the “radius of helix” box. The measured radius of the MAVS filament is ~40 Å. It is important to note that the “effective” radius of helices that gives rise to the diffraction peaks is often different from this measured radius based on the outer edges. 6 , 18 To deal with this issue, the user can input the ± range of the set radius into the box next to the radius box, which makes the program draw the Bessel plots according to this range (Figure 2a). This range should be taken into consideration when estimating the Bessel order of the diffraction peaks in the following process.
The major peaks in the power spectrum can be indexed through the following procedure. As an example, to determine the Bessel order of the first peak on layer‐line 5, the user can plot the amplitude of the pixels on this layer line as a function of R, the distance from the meridian, in the “layer‐line plots” window (Figure 2a). The program shows the theoretically calculated plot based on the helix radius range and a trial Bessel order for comparison. In Figure 2a, the first pair of peaks of the calculated plot with Bessel order 3 match those of the data plot quite well, suggesting that the Bessel order of the peaks is 3. However, as shown in Figure 2b,c, the plot calculated from Bessel order 4 also appears to match the data plot well. This ambiguity can be resolved by considering the plot below that shows the phase difference between each pair of pixels with equal distance from the meridian. In theory, with the helix well centered and vertically aligned, these phase differences for Bessel functions of even and odd Bessel orders should be 0 and 180°, respectively. 8 , 11 Figure 2 shows that all the pixel pairs within the major peak pair (pixels 4/−4, 5/−5, 6/−6, 7/−7 from the meridian) have phase differences close to 180° rather than 0°, strongly suggesting that the Bessel orders of the two peaks in this layer line are odd numbers. The Bessel orders 3 and −3 are therefore the correct solution.
As pointed out previously, out‐of‐plane tilt of filaments alters both peak positions and phases in power spectra, which could mislead the assignment of Bessel orders. 7 , 8 , 11 , 16 Position of peaks on layer lines far away from the equator are affected by out‐of‐plane tilt more than those close to the equator. On the other hand, the effect of out‐of‐plane tilt on the phase relationship depends on the Bessel order, with higher order peaks affected more than lower order peaks. For example, the first pair of peaks in layer‐line 9 in Figure 2a are located slightly away from the meridian, suggesting the Bessel orders 1 and −1, respectively. A different 2D class average as shown in Figure 3, however, shows a single peak centered on the meridian, incorrectly indicting the Bessel order 0. In addition, the phase differences for peaks on layer‐line 5 are ~60°, raising ambiguity on whether their Bessel orders are even or odd. In this regard, it is advantageous to be able to scroll through different 2D class averages to check for inconsistency and choose the best power spectrum for indexing.
FIGURE 3.
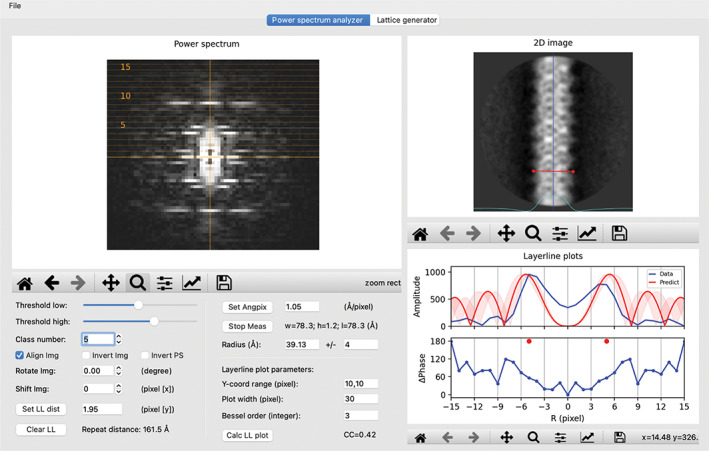
Effect of out‐of‐plane tilt on the power spectrum. The image and power spectrum of a different two‐dimensional (2D) class average from the MAVS filament data are shown. Out‐of‐plane tilt reduces the phase difference of the two peaks on layer‐line 5. It also causes the first peak on layer‐line 9 to sit on the meridian, indicating Bessel order 0, which is incorrect
2.3. Setting the unit vectors and generating the lattice in Fourier space
With the layer lines drawn and the Bessel orders of the major peaks in the power spectrum indexed, the user can go to the “lattice generator” tab to construct the Fourier space lattice. The power spectrum chosen in the “power spectrum analyzer” tab is automatically displayed in this tab (Figure 4). The display settings are largely the same, except that the power spectrum can be symmetrized for easier recognition of the diffraction pattern by checking the “sym” checkbox. The first task here is to choose two peaks in the power spectrum to define the two unit vectors. In Figure 4, unit vector 1 lands on the peak of Bessel order 7 on layer‐line 1, set by mouse clicking on the peak while holding the command/control key. Similarly, unit vector 2 is set to the peak of Bessel order −4 on layer‐line 4, by clicking on the peak while holding the Shift key. These actions trigger drawing of the Fourier space lattice in red, which should generate the lattice points accounting for one half of the major peaks in the power spectrum. The second half the peaks should be accounted for by the lattice in cyan, which is the mirror image of the red lattice. Alternatively, unit vectors 1 and 2 could be set to the peak of Bessel order −7 on layer‐line 1 and the peak of Bessel order 4 on layer‐line 4, respectively. The resulting 2D lattices in red and cyan would be swapped relative to the ones shown in Figure 4. The real space lattices from these two alternative schemes have opposite hand. Either one of these indexing schemes could be correct, because the handedness of helix cannot be determined at this stage. For a given power spectrum, there are multiple alternative ways of designating the unit vectors that give rise to the same set of lattice points. For example, in Figure 5, unit vector 2 is set to the peak of the Bessel order 3 on layer‐line 5, while unit vector 1 is the same as in Figure 4. The lattice points generated from this setting are identical to those in Figure 4.
FIGURE 4.
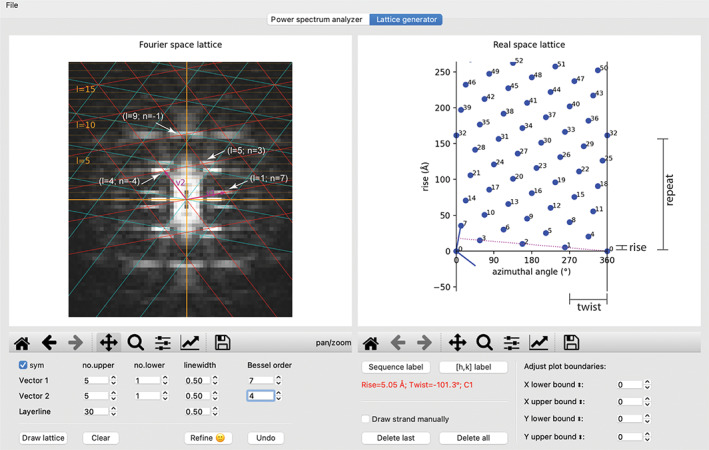
The “lattice generator” tab. The same power spectrum as in Figure 2 is shown, except that it has been symmetrized by checking the “sym” checkbox. A refined Fourier space lattice and the associated real space lattice are shown in the left and right windows, respectively. The dotted line in the right panel represents the one‐start helix that connects all the subunits in the helical assembly. The calculated point group, rise, and twist per subunit of this helix are displayed with red text in the control area
FIGURE 5.
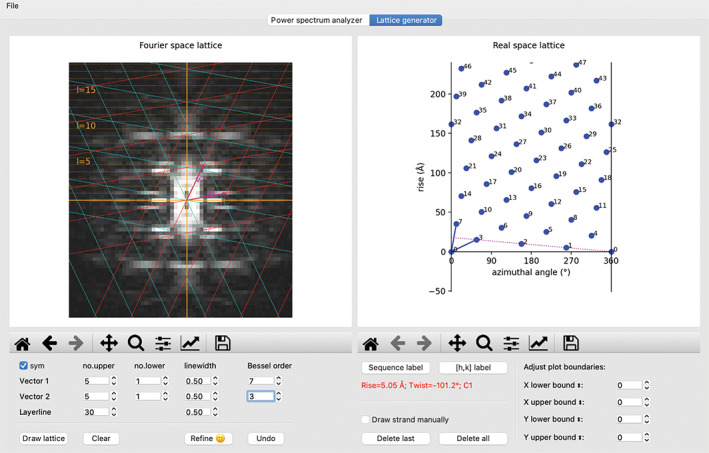
An alternative indexing scheme leading to the same real space lattice as in Figure 4
The two unit vectors can be adjusted iteratively to improve the match between the lattice points and the peaks. The number of layer lines and lattice lines displayed can be increased or decreased based on the number of peaks in the power spectrum. The match between the lattice points and the peaks does not need to be perfect at this stage, as it can be improved by the following refinement routine. In addition, some peaks may deviate from the lattice because they originate from diffractions of atoms located at different radii as mentioned above. 6 , 18
2.4. Refine the parameters and generating the real space lattice
To refine the manually set Fourier space lattice, the user needs to first set the Bessel orders of the two unit vectors by changing the numbers in the “Bessel order” input boxes (Figure 4). The input numbers are always positive integers. The program internally switches the sign of the number if the vector lands on the left side of the meridian and therefore has a negative Bessel order. Clicking the “refine” button triggers the refinement routine that optimizes the Fourier space lattice as described in the method section. The user can check again whether the lattice points overlap with the diffraction peaks. In Figure 4, the two unit vectors match the two chosen peaks well. Another example is the peak on layer‐line 5, which is also predicted correctly by the lattice, with Bessel order (7‐4) = 3 based on Equation (2).
It should be noted that the lattice drawn based on the 2D crystal analogy of helical diffraction assumes a simple linear relationship between the Bessel order and the distance of the diffraction peaks from the meridian. This linear relationship is, however, an approximation. For example, the first maxima of a Bessel function with the Bessel order 1 is 1.8, while the first maxima of a Bessel function of the Bessel order 2 is 3.1 rather than 3.6. This is another reason that the lattice points may not align perfectly with the diffraction peaks even when the indexing scheme is correct.
The refinement routine automatically draws the plot of the real space lattice, with the horizontal and vertical axes corresponding to the circumference and the helical axis, respectively (Figures 4 and 5). Each dot in the plot represents one asymmetric unit in the helical assembly. In addition, the program automatically calculates and displays the point group symmetry, rise/subunit, and twist/subunit of the simplest helical family that can represent the entire helical assembly (Figures 4 and 5). If the helical assembly does not have rotational point group symmetry, the simplest helical family is the one‐start helix that passes through all the subunits in the real space lattice. A dotted strand line is drawn on the plot to indicate this one‐start helix. If there is a rotational point group symmetry such as C2 and C3, the program detects it based on subunit arrangement in the real space lattice. In this case, multiple strand lines are drawn to reflect the point group symmetry. This type of rotational point group symmetries can also be deduced from the greatest common factor of all Bessel orders in the power spectrum. 7 For example, a common factor 2 (all even Bessel orders) indicates the presence of the C2 symmetry in the helical assembly. PyHI does not automatically identify the dihedral symmetry Dn. However, the presence of the Dn symmetry constraints the phases of all pixels along the layer lines to be 0 or 180°, provided that the helix has no out‐of‐plane tilt. 7 PyHI prints the phases of the pixels in the terminal window when drawing layer‐line plots to help the user decide whether Dn needs be considered. Cn should be used if unsure, and the presence of Dn may become clear when the three‐dimensional (3D) reconstruction reaches high resolution. The point group symmetry, twist, and rise per subunit are the parameters needed by the subsequent 3D helical reconstruction with programs such as IHRSR and RELION. 1 , 13 In Figure 4, the strand line connecting subunits 1 and 2 represents the one‐start helix of the MAVS filament. The rise and twist per subunit are 5.05 Å and −101.3°, respectively, very close to the refined results. 1
3. CONCLUSION
The PyHI program is designed to make the 2D lattice method for indexing power spectrum more accessible to non‐experts. The graphic user interface provides both a platform for learning Fourier–Bessel indexing and generating high‐quality graphics for publication. Future development will be directed at more automatic decision making by the program and further reducing required user inputs.
4. MATERIALS AND METHODS
4.1. Example data
The helical filament dataset of the protein MAVS (EMPIAR entry ID: 10,031; link: https://www.ebi.ac.uk/pdbe/emdb/empiar/entry/10031/) was used as the example. RELION was used for manually picking of filaments and calculating 2D class averages following the helical reconstruction procedure as described in detail in Reference 1. The 2D class averages in the MRC stack format were loaded into PyHI to illustrate how the program works.
4.2. Python code
The program is a Python script that runs under Python version 3.7. The script depends on the following Python libraries: Mrcfile 1.1.2, 19 numpy 1.18.3, 20 matplotlib 3.3.1, 21 Pillow 7.2.0 (https://pillow.readthedocs.io/en/stable/), PyQt5 5.15.0 (https://pypi.org/project/PyQt5/), SciPy 1.4.1, 22 and mplsursors 0.4 (https://mplcursors.readthedocs.io/en/stable/). These libraries can be installed on modern operating systems with standard Python library management tools such as Python Package Installer (PIP; https://pip.pypa.io/en/stable/) and anaconda (https://docs.conda.io/en/latest/). The script can be freely downloaded from Github (https://github.com/xuewuzhang-UTSW/PyHI). A brief video demonstration on how to use the program is provided at: https://youtu.be/KxAeo90CIt4.
4.3. Overall organization of the user interface
The user interface is designed to guide the user through the indexing process. The procedure starts with loading an image file using the menu bar item “File.” Both a single image of a filament segment in the MRC format and MRC stacks of 2D class averages can be loaded. Power spectra in various image formats can also be loaded. The graphics window contains two tabs, named “power spectrum analyzer” and “lattice generator,” respectively. The “power spectrum analyzer tab” is for displaying the 2D image and power spectrum, as well as plotting one‐dimensional plots that facilitate the determination of the Bessel orders of the peaks in the power spectrum. The “lattice generator” tab is dedicated for drawing the reciprocal and real space lattices, based on the assignment of the Bessel orders from the first tab. The names of the buttons and input fields are in general self‐explanatory. Additional help messages for many of them are provided, which can be shown by placing the mouse pointer on top of the buttons or input boxes. Images and plots generated in the program can be saved in various formats such as PDF and png. The parameters derived from the program, such as Bessel orders of the unit vectors, the rise, and twist the helix, can be saved as a formatted text file and reloaded for convenience.
4.4. “Power spectrum analyzer” tab
The 2D image is displayed in the “2D class average” window the in the “power spectrum analyzer” tab. The user interface provides tools for switching, rotating, zooming, panning, as well as adjusting contrast and color map of the displayed images. The program reads the pixel size from the MRC file, required for converting the rise per subunit from pixel to angstrom. If this information from the MRC header is absent or incorrect, it can be set manually with the “Set Angpix” button. The Fourier transform of the currently displayed 2D image is calculated automatically. The amplitude of the Fourier transform is displayed in the “power spectrum” window. If a power spectrum image is loaded, it is displayed in the same window, while the “2D class average” window will remain blank. This tab provides all the functions for determining the layer‐line distance and Bessel orders of the diffraction peaks. These functions are described in detail in Section 2.
4.5. “Lattice generator” tab
The power spectrum image is also displayed in the “Fourier space lattice” window in the “lattice generator” tab. The power spectrum of a helical segment is expected to show approximate mirror symmetry along both the meridian and equator. Power spectra calculated from 2D class averages, however, often deviate substantially from such symmetry. Checking the “sym” checkbox in the control area below the image window symmetrizes the displayed power spectrum, making it visually easier to interpret. With the layer lines set in the “power spectrum analyzer” tab, a Fourier space lattice can be drawn by clicking the “Draw lattice” button in the control area. The two unit vectors are set arbitrarily at this point and therefore need to be adjusted by the user (see below).
With both the Fourier space lattice drawn and the Bessel orders of the two unit vectors set, the user can then click the “refine” button to refine the Fourier space lattice, which also triggers the generation of the real space lattice on the right side of this tab. Each point in the real space plot represents one asymmetric unit in the helical assembly. The point group, rise/subunit, and twist/subunit of the simplest helical family are calculated automatically and displayed. One line is drawn in the plot to indicate this helical family. The Miller indexes and the sequential numbers along the vertical direction of the lattice points can be toggled on and off by clicking the “[h, k] label” and “sequence label” buttons. With the “Draw strand” box checked, mouse clicks, while holding the command (MacOS) or control (Windows and Linux) key, on two neighboring subunits trigger drawing a strand line linking these two points and calculation of the twist and rise between them.
4.6. Generation of the Fourier space and real space lattices
The two unit vectors in Fourier space are colored magenta and labeled v1 and v2, respectively. The user sets the two vectors by clicking on the desired peaks on the power spectrum while holding the command/control and shift key, respectively. The program automatically limits the end of the vectors to layer lines. In addition, it limits the angle of the first unit vector (v1) to the range of 0–90°, while the angle of vector 2 is larger than vector 1 and smaller than 180°. As a result, vector 1 always ends in the upper right quadrant of the power spectrum and has a positive Bessel order, whereas vector 2 could end in either the upper right or left quadrant and have either a positive or negative Bessel order. Linear combinations of the two unit vectors generates the Fourier space lattice (shown in red), which should account for half of the major peaks in the power spectrum. The other half of the peaks is the mirror image of the first half, which are accounted for by the lattice in cyan that is mirror‐symmetric to the red lattice.
The angles of the two unit vectors in Fourier space are converted to the angles of the unit vectors in real space as described previously: 1
| (3) |
| (4) |
where a 1 and a 2 are the angles of the real space unit vectors, whereas a*1 and a*2 are the angles of the Fourier space unit vectors. The meaning of these equations is that the first unit vector in real space is perpendicular to the second unit vector in Fourier space, and vice versa. The negative sign in the two equations causes mirror operations of the two unit vectors along the horizontal circumference in real space. These operations make the calculated values consistent with the convention that the positive and negative Bessel orders correspond to right‐handed and left‐handed strand families, respectively, 10 without changing the absolute values of the rise and twist per subunit. The length l of the real space unit vectors is given by:
| (5) |
where l* is the length of the corresponding reciprocal space unit vector. a 12 is the angle between the two unit vectors. With the two unit vectors known, the real space lattice is determined, which is drawn in the form of blue dots that represent individual asymmetric units in the helical assembly.
4.7. Method for refining the Fourier space and real space lattices
The lattice points in the Fourier space must sit on layer lines. The program automatically enforces this by rounding the y‐coordinates, y*1 and y*2, to the closest layer line when the user manually sets the two unit vectors by mouse clicks. The x‐coordinates of the lattice points are the distances from the meridian, which have a linear relationship with the associated Bessel orders. The refinement algorithm enforces this relationship by setting the initial trial x‐coordinates of the two unit vectors, x 1i and x 2i , with the following equations:
| (6) |
| (7) |
where x* u1 and x* u2 are the x‐coordinates of the two unit vectors manually set by the user. n 1 and n 2 are the Bessel orders of the two unit vectors. These equations set x* i1 by taking into consideration of both x* u1 and x* u2, while x* i2 is tied to x* i1 based on the linear relationship between the x‐coordinates and the Bessel orders.
As described in Section 1, the Bessel orders of the two unit vectors in Fourier space determine the n‐start numbers of the corresponding strand families in real space. According to this relationship, it can be shown that the (0, 0) and (n 1, −n 2) lattice points in real space are the start and end points of the circumferential vector, respectively. For example, in Figure 1, the Bessel orders of the two unit vectors are 7 and −4, respectively. With the (0, 0) and (7, 4) lattice points defining the circumferential vector, the helical assembly correctly contains a right‐handed seven‐start and a left‐handed four‐start strand family. Therefore, the y‐coordinate of the (n 1, −n 2) lattice point in real space must be 0. The coordinates of the real space unit vectors are determined by the coordinates of the Fourier space vectors according to Equations ((3), (4), (5)). The problem is simplified to finding the optimal value of x*1, because x*2 is tied to x*1 as in Equation (7) and y*1 and y*2 are fixed. The refinement routine uses a minimization algorithm from SciPy that that minimizes the y‐coordinate of the (n 1, −n 2) lattice point in real space by varying x*1 in the range of 0.5‐ to 1.5‐fold of its initial value x* i1. If executed successfully, the coordinates of the two unit vectors in Fourier space would satisfy all the rules described above, resulting in the 2D lattices in both the Fourier space and real space consistent with the data.
CONFLICT OF INTEREST
The author declares no conflict of interest.
ACKNOWLEDGMENT
The author is grateful to Judith Short, Sjors Scheres, Xiao‐Chen Bai and two anonymous reviewers for discussions and suggestions.
Zhang X. Python‐based Helix Indexer: A graphical user interface program for finding symmetry of helical assembly through Fourier–Bessel indexing of electron microscopic data. Protein Science. 2022;31:107–117. 10.1002/pro.4186
Funding information National Cancer Institute, Grant/Award Number: CA220283; Welch Foundation, Grant/Award Number: I‐1702
REFERENCES
- 1. He S, Scheres SHW. Helical reconstruction in RELION. J Struct Biol. 2017;198:163–176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Egelman EH. A robust algorithm for the reconstruction of helical filaments using single‐particle methods. Ultramicroscopy. 2000;85:225–234. [DOI] [PubMed] [Google Scholar]
- 3. Desfosses A, Ciuffa R, Gutsche I, Sachse C. SPRING—An image processing package for single‐particle based helical reconstruction from electron cryomicrographs. J Struct Biol. 2014;185:15–26. [DOI] [PubMed] [Google Scholar]
- 4. Scheres SHW. Amyloid structure determination in RELION‐3.1. Acta Cryst D. 2020;76:94–101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Sachse C. Single‐particle based helical reconstruction—How to make the most of real and Fourier space. AIMS Biophys. 2015;2:219–244. [Google Scholar]
- 6. Egelman EH. Three‐dimensional reconstruction of helical polymers. Arch Biochem Biophys. 2015;581:54–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Coudray N, Lasala R, Zhang Z, Clark KM, Dumont ME, Stokes DL. Deducing the symmetry of helical assemblies: Applications to membrane proteins. J Struct Biol. 2016;195:167–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Toyoshima C. Structure determination of tubular crystals of membrane proteins. I. Indexing of diffraction patterns. Ultramicroscopy. 2000;84:1–14. [DOI] [PubMed] [Google Scholar]
- 9. Cochran W, Crick F, Vand V. The structure of synthetic polypeptides. I. The transform of atoms on a helix. Acta Crystallogr. 1952;5:581–586. [Google Scholar]
- 10. Klug A, Crick F, Wyckoff H. Diffraction by helical structures. Acta Crystallogr. 1958;11:199–213. [Google Scholar]
- 11. Stewart M. Computer image processing of electron micrographs of biological structures with helical symmetry. J Electron Microsc Tech. 1988;9:325–358. [DOI] [PubMed] [Google Scholar]
- 12. Egelman EH. Reconstruction of helical filaments and tubes. Methods Enzymol. 2010;482:167–183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Egelman EH. The iterative helical real space reconstruction method: Surmounting the problems posed by real polymers. J Struct Biol. 2007;157:83–94. [DOI] [PubMed] [Google Scholar]
- 14. Toyoshima C, Unwin N. Three‐dimensional structure of the acetylcholine receptor by cryoelectron microscopy and helical image reconstruction. J Cell Biol. 1990;111:2623–2635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Egelman E, Wang F. Cryo‐EM is a powerful tool, but helical applications can have pitfalls. Soft Matter. 2021;17:3291–3293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Egelman EH. Ambiguities in helical reconstruction. Elife. 2014;3:e04969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Cheng A, Henderson R, Mastronarde D, et al. MRC2014: Extensions to the MRC format header for electron cryo‐microscopy and tomography. J Struct Biol. 2015;192:146–150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. DiMaio F, Yu X, Rensen E, Krupovic M, Prangishvili D, Egelman EH. Virology. A virus that infects a hyperthermophile encapsidates A‐form DNA. Science. 2015;348:914–917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Burnley T, Palmer CM, Winn M. Recent developments in the CCP‐EM software suite. Acta Cryst D. 2017;73:469–477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Harris CR, Millman KJ, van der Walt SJ, et al. Array programming with NumPy. Nature. 2020;585:357–362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Hunter JD. Matplotlib: A 2D graphics environment. IEEE Ann Hist Comput. 2007;9:90–95. [Google Scholar]
- 22. Virtanen P, Gommers R, Oliphant TE, et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat Methods. 2020;17:261–272. [DOI] [PMC free article] [PubMed] [Google Scholar]


