Visual Motion and Decision-Making in Dyslexia: Reduced Accumulation of Sensory Evidence and Related Neural Dynamics

Abstract

Children with and without dyslexia differ in their behavioral responses to visual information, particularly when required to pool dynamic signals over space and time. Importantly, multiple processes contribute to behavioral responses. Here we investigated which processing stages are affected in children with dyslexia when performing visual motion processing tasks, by combining two methods that are sensitive to the dynamic processes leading to responses. We used a diffusion model which decomposes response time and accuracy into distinct cognitive constructs, and high-density EEG. Fifty children with dyslexia (24 male) and 50 typically developing children (28 male) 6-14 years of age judged the direction of motion as quickly and accurately as possible in two global motion tasks (motion coherence and direction integration), which varied in their requirements for noise exclusion. Following our preregistered analyses, we fitted hierarchical Bayesian diffusion models to the data, blinded to group membership. Unblinding revealed reduced evidence accumulation in children with dyslexia compared with typical children for both tasks. Additionally, we identified a response-locked EEG component which was maximal over centro-parietal electrodes which indicated a neural correlate of reduced drift rate in dyslexia in the motion coherence task, thereby linking brain and behavior. We suggest that children with dyslexia tend to be slower to extract sensory evidence from global motion displays, regardless of whether noise exclusion is required, thus furthering our understanding of atypical perceptual decision-making processes in dyslexia.

SIGNIFICANCE STATEMENT Reduced sensitivity to visual information has been reported in dyslexia, with a lively debate about whether these differences causally contribute to reading difficulties. In this large preregistered study with a blind modeling approach, we combine state-of-the art methods in both computational modeling and EEG analysis to pinpoint the stages of processing that are atypical in children with dyslexia in two visual motion tasks that vary in their requirement for noise exclusion. We find reduced evidence accumulation in children with dyslexia across both tasks, and identify a neural marker, allowing us to link brain and behavior. We show that children with dyslexia exhibit general difficulties with extracting sensory evidence from global motion displays, not just in tasks that require noise exclusion.

Introduction

It has long been suspected that visual processing relates to the reading difficulties characterizing developmental dyslexia (e.g., Hinshelwood, 1896; Lovegrove et al., 1980). One visual function that develops atypically in those with dyslexia is visual motion processing: an important ability contributing to scene segmentation, depth perception and object recognition (Braddick et al., 2003). Difficulties in global motion tasks requiring integration over space and time have been widely reported in dyslexia (Benassi et al., 2010). Typically, participants are required to detect or discriminate coherently moving signal dots among randomly moving noise dots (Newsome and Paré, 1988). In this “motion coherence” task, dyslexic individuals tend to have elevated psychophysical thresholds, requiring higher proportions of signal dots to perform at the same level of accuracy as those without dyslexia (Benassi et al., 2010). The nature of the relationship is still being debated, with some researchers proposing a causal relationship between motion sensitivity and reading ability (Boets et al., 2011; Gori et al., 2016; but see Olulade et al., 2013; Goswami, 2015; Joo et al., 2017; Piotrowska and Willis, 2019).

Atypical global motion processing in dyslexia may reflect reduced sensitivity to rapid temporal information originating from deficiencies in the magnocellular system (Livingstone et al., 1991; Stein and Walsh, 1997; Stein, 2001, 2019) or related dorsal stream (Hansen et al., 2001; Braddick et al., 2003), which are particularly specialized for motion perception (Livingstone and Hubel, 1988). Alternative accounts suggest that dyslexic individuals have difficulty filtering out the randomly moving noise dots in motion coherence tasks (“noise exclusion”) (Sperling et al., 2006; Conlon et al., 2012) or difficulties integrating over space and time (Raymond and Sorensen, 1998; Hill and Raymond, 2002; Benassi et al., 2010).

Despite focusing on the sensory parameters of visual motion stimuli, these accounts give little consideration to the dynamic processes leading to atypical behavioral responses in dyslexia, and particularly, whether decision-making processes are affected. Here we explicitly modeled the decision-making process using a popular cognitive model of accuracy and response time (RT): the diffusion model (Stone, 1960; Ratcliff, 1978; Evans and Wagenmakers, 2020). The decision is modeled as a noisy evidence accumulation process from a starting point toward one of two decision bounds (Fig. 1). This modeling approach will help identify the locus of atypical processing in dyslexia, with two further advantages: (1) the resulting parameters may be more sensitive to group differences than accuracy or RT alone (Stafford et al., 2020); and (2) the parameters relate well to neural measures (Kelly and O'Connell, 2013; Turner et al., 2015; Manning et al., 2021a). Accordingly, we combined the diffusion model with a neural measure sensitive to the dynamic processes contributing to behavioral responses (EEG), bridging brain and behavior.

Figure 1.

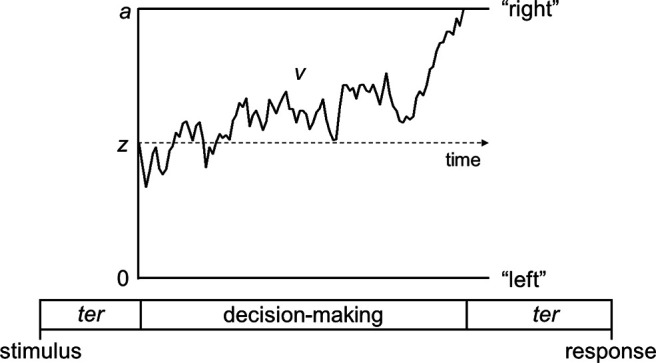
Schematic representation of the decision-making process in the diffusion model for a trial with rightward motion. Decision-making process represented as a noisy accumulation of evidence from a starting point, z, toward one of two decision bounds. In our motion tasks, the decision bounds correspond to left and right responses. Boundary separation, a, represents the width between the two bounds and reflects response caution. Wider decision boundaries reflect that more evidence is required before making a decision (i.e., more cautious responses). Drift rate, v, reflects the rate of evidence accumulation, which depends on both the individual's sensitivity to a stimulus and the stimulus strength. Nondecision time, ter, is the time taken for sensory encoding processes before the decision-making process and response generation processes after a bound is reached.

The diffusion model was recently applied to motion coherence performance in children with varying reading abilities (O'Brien and Yeatman, 2021). Poorer reading was related to lower drift rates, wider decision bounds, and more intra-individual variability in starting point and nondecision time. Therefore, poor readers accumulated motion evidence more slowly and responded more cautiously than good readers.

Here, we used diffusion models to identify the processing stages affected in children with dyslexia across two global motion tasks. The first task was a standard motion coherence task (comparable to O'Brien and Yeatman, 2021). The second task was a direction integration task not used before with dyslexic individuals, whereby dot directions are sampled from a Gaussian distribution, with difficulty manipulated via the SD of the distribution. In this task, the optimal strategy is to average over all dots, with no noise exclusion requirement. The reason for presenting both tasks to children with dyslexia was to determine whether differences in model parameters are found for both motion tasks, suggesting a general motion-processing deficit (i.e., magnocellular/dorsal deficit) (Stein, 2001; Braddick et al., 2003), or whether differences in model parameters are found particularly for the motion coherence task, reflecting noise exclusion difficulties (Sperling et al., 2006; Conlon et al., 2012).

Materials and Methods

Preregistration

We preregistered our inclusion criteria and analysis plan before completing data collection and before commencing analyses (https://osf.io/enkwm). When analyzing the data, we used a blind modeling approach to ensure that modeling decisions were not biased by our hypotheses. Our preregistered primary research questions and hypotheses were as follows:

1. Do children with dyslexia have reduced drift rates in a motion coherence task compared with typically developing children?

We hypothesized that children with dyslexia would have reduced drift rates in the motion coherence task compared with typically developing children, in line with the results of O'Brien and Yeatman (2021) and reports of reduced motion coherence sensitivity in dyslexic individuals (Benassi et al., 2010).

2. Do children with dyslexia have reduced drift rates in a direction integration task compared with typically developing children?

If children with dyslexia show difficulties with all global motion tasks (in line with impaired magnocellular/dorsal stream functioning) (Stein, 2001; Braddick et al., 2003), then we would expect children with dyslexia to have a reduced drift rate in this task as well. Instead, if the performance of children with dyslexia in a motion coherence task is limited solely by difficulties with noise exclusion (Sperling et al., 2006; Conlon et al., 2012), we would expect to see no difference between children with and without dyslexia in this task, as it does not require segregating signal dots from randomly moving noise dots.

3. Do children with dyslexia show increased boundary separation?

We hypothesized that children with dyslexia would have wider boundary separation compared with typically developing children in both tasks, following O'Brien and Yeatman (2021).

4. Do children with dyslexia show increased nondecision time?

We hypothesized no group differences in overall nondecision time in either task, following O'Brien and Yeatman (2021).

Participants

We collected data from 50 children with dyslexia and 60 typically developing children who met our inclusion criteria. Specifically, participants were required to be 6-14 years (inclusive) of age, have verbal and/or performance IQ (PIQ) scores >70 (measured using the Wechsler Abbreviated Scales of Intelligence, Ed 2 [WASI-2]) (Wechsler, 2011), and to have normal or corrected-to-normal acuity, as measured using a Snellen acuity chart (with binocular acuities of 6/9 or better for children 6-8 years of age and 6/6 or better for children 9-14 years of age). Children in the dyslexia group were required to have a dyslexia diagnosis (or be in the process of obtaining one, n = 1), and to have a reading and spelling composite score of ≤89, which was computed by averaging the standard scores for the spelling subtest of the Wechsler Individual Achievement Test (WIAT-III) (Wechsler, 2017) and the Phonological Decoding Efficiency subtest of the Test of Word Reading Efficiency (TOWRE-2) (Torgesen et al., 2012). A cutoff of 89 was chosen to correspond to 1.5 SDs below the mean of typically developing children in a similar study (Snowling et al., 2019a,b). Children in the typically developing group were required to have composite scores >89 and to have no diagnosed developmental conditions. Datasets from an additional 4 typically developing children were excluded because of poor visual acuity (n = 1), having a composite score of ≤89 (n = 2), or failing to pass criterion on the task (n = 1), and datasets from an additional 11 children with dyslexia were excluded because of poor visual acuity (n = 2) or having a composite score >89 (n = 9).

We then selected 50 typically developing children to best match the children with dyslexia in terms of age and PIQ using the R MatchIt package (Ho et al., 2011), so that the final dataset included 50 children with dyslexia (24 male) and 50 typically developing children (28 male). As shown in Table 1, the children with dyslexia had slightly higher ages and lower IQ values on average than the typically developing children. EEG data were collected during task performance in 47 typically developing and 44 children with dyslexia (although EEG data were available only in the motion coherence task for one child with dyslexia and one typically developing child). The EEG data from these participants were included in a paper investigating responses locked to the onset of coherent motion in typically developing children and children with autism or dyslexia (Toffoli et al., 2021), and the larger group of 60 typically developing children were used to form the comparison group in an autism study (Manning et al., 2021b).

Table 1.

Demographics of participants included in final dataset^a

	Typically developing (n = 50)	Dyslexia (n = 50)
Age	10.65 (2.34); 6.55-14.98	11.08 (1.87); 7.81-14.53
PIQb	109.26 (11.53); 81-145	99.40 (15.29); 72-141
Verbal IQ	110.60 (8.42); 95-127	98.56 (10.60); 77-118
Full-scale IQ	111.36 (9.02); 89-132	98.70 (12.85); 75-132
TOWRE-2 PDE	111.18 (16.53); 81-153	79.16 (9.45); 51-99
WIAT-Spelling	105.74 (10.21); 80-127	77.86 (7.96); 58-99
Composite score	108.46 (12.15); 89.5-138.0	78.51 (7.46); 54.5-89.0

^aData are mean (SD); range.

^bPIQ, performance IQ.

Apparatus

The tasks were presented on a Dell Precision M3800 laptop (2048 × 1152 pixels, 60 Hz) using the Psychophysics Toolbox for MATLAB (Brainard, 1997; Pelli, 1997; Kleiner et al., 2007). EEG signals were collected using 128-channel Hydrocel Geodesic Sensor Nets connected to Net Amps 300 (Electrical Geodesics) and NetStation 4.5 software. A photodiode attached to the monitor independently verified stimulus presentation timing. Participants used a Cedrus RB-540 response box (Cedrus).

Stimuli

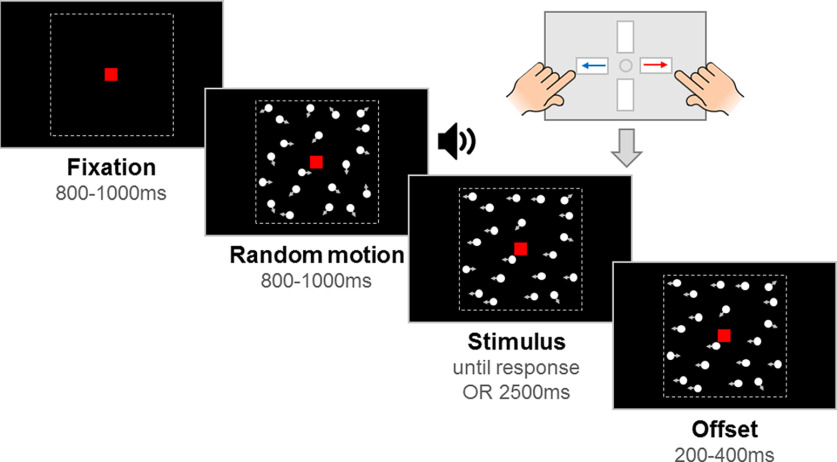
Stimuli were 100 white, randomly positioned dots (diameter 0.19°) moving at 6°/s within a square aperture (10° × 10°) on a black background, with a limited lifetime of 400 ms. Each trial had a fixation period, a random motion period, a stimulus period, and an offset period, with a red fixation square (0.24° × 0.24°) presented throughout (Fig. 2). By presenting random (incoherent) motion before the stimulus period, we could dissociate evoked responses to directional motion from pattern- and motion-onset evoked potentials. The start of the stimulus period was highlighted to participants with an auditory tone. In the motion coherence task, directional motion (leftward or rightward) was introduced in a proportion of “signal” dots, while the remainder of the dots continued to move in random directions. In the direction integration task, the directions of dots in the stimulus phase were distributed according to a Gaussian distribution with a mean leftward or rightward direction. The fixation period, random motion period, and offset period had jittered durations within a fixed range, while the stimulus period was presented until a response or 2500 ms had elapsed. The offset period continued the directional motion to temporally separate motion offset from the response.

Figure 2.

Schematic representation of trial procedure. The trial started with an initial fixation period that was followed by a random motion period consisting of random, incoherent moving dots, which was in turn followed by a stimulus containing leftward or rightward global motion. The child was asked to report the direction using a response box. After the response or after the maximum stimulus duration elapsed (2500 ms), the stimulus remained on the screen for a short offset period. Arrows (indicating movement) and dotted lines (marking the square stimulus region) are presented for illustration only. The stimulus shown here is from the motion coherence task, where a proportion of dots move coherently. In the direction integration task, dot directions were taken from a Gaussian distribution. Figure reproduced from https://osf.io/wmtpx/ under a CC-BY4.0 license.

Experimental task procedure

Children completed motion coherence and direction integration tasks within child-friendly games (based on Manning et al., 2019, 2021a). Using animations, participants were told that fireflies were escaping from their viewing boxes, and they were asked to tell the zookeeper which way the fireflies were escaping. There were 10 “levels” of the game. Levels 1-5 corresponded to one task (either motion coherence or direction integration), and Levels 6-10 corresponded to the other task, with the order of tasks being counterbalanced across participants. Levels 1 and 6 were practice phases, and the remaining four levels for each task were experimental blocks. In the motion coherence task, difficulty was manipulated by varying the proportion of coherently moving dots; and in the direction integration task, difficulty was manipulated by varying the SD of the Gaussian distribution from which the dot directions were sampled.

In the practice phases, four demonstration trials were presented with no random motion phase and an unlimited stimulus phase, so that the experimenter could explain the task. Participants reported stimulus direction using a response box. The first two demonstration trials were “easy” (100% coherence or 1° SD), and the last two were more difficult (75% and 50% coherence, or 10° and 25° SDs). Following the demonstration trials, there were up to 20 criterion trials with a coherence of 95% or an SD of 5°. These trials introduced the random motion phase. Participants were told that the fireflies would be going “all over the place” at first, and that they must wait for an alarm (auditory beep) before deciding which way the fireflies were escaping. A time limit was enforced, with visual feedback presented on the screen if participants did not respond within 2500 ms (“Timeout! Try to be quicker next time!”). Feedback on accuracy was given for responses made within the time limit (“That was correct!”, or “It was the other way that time”). When participants met a criterion of four consecutive correct responses, no more criterion trials were presented. Next, there were eight practice trials of increasing difficulty (motion coherence task: 80%, 70%, 60%, 50%, 40%, 30%, 20%, 10%; direction integration task: 5°, 10°, 15°, 20°, 30°, 40°, 50°, 60°) with feedback as before. Level 1 was repeated for one typically developing child and 2 children with dyslexia who did not meet the criterion of four consecutive correct responses on the first attempt, but passed on the second attempt.

Levels 2-5 and 7-10 each contained 38 trials, with 9 repetitions of each of two difficulty levels (motion coherence task: 30%, 75%; direction integration task: 70°, 30° SD), for each motion direction (leftward, rightward), and an additional 2 catch trials presenting 100% coherent (0° SD) motion. The experimental phase for each task therefore consisted of 152 trials. No trial-by-trial feedback was presented during the experimental phase, apart from a “timeout” message if no response was made within 2500 ms after stimulus onset. At the end of each level, participants were given points for their speed and accuracy in the preceding block (computed by (1/median RT) × the number of correct responses × 2, rounded to the nearest integer). If participants obtained a score <10, a score of 10 points was given to maintain motivation. Trials were presented automatically, although the experimenter could pause and resume trial presentation if necessary. The experimental code can be found here: https://osf.io/fkjt6/.

General procedure

The procedure was approved by the Central University Research Ethics Committee at the University of Oxford. Parents provided written informed consent, and children gave verbal or written assent. All children took part at the University of Oxford apart from one child with dyslexia who was seen at school without EEG. During the experimental tasks, participants sat 80 cm away from the computer screen in a dimly lit room. For children who participated with EEG, we fitted the net before the experiment and ensured that electrode impedances were <50 kΩ. EEG data were acquired at a sampling rate of 500 Hz with a vertex reference electrode.

Children were closely monitored by an experimenter sitting beside them. The experimenter provided general encouragement and task reminders, pausing before the start of a trial if needed (e.g., to remind the child to keep still). Children had short breaks at the end of each “level” and a longer break at the end of the first task (at the end of “level 5”). During the longer break, electrode impedances were reassessed for children wearing EEG nets. Children marked their progress through the levels using a stamper on a record card. The children also completed a Snellen acuity test, the WASI-2, the TOWRE-2, and the spelling subtest of the WIAT-III. The whole session took no longer than 2 h, and children were given a gift voucher to thank them for their time.

Diffusion model analysis

Initially, a blinded analysis was conducted to ensure that modeling decisions were made without being biased by the hypotheses under test. The first author (C.M.) prepared a blinded dataset in which group membership was randomly permuted (see also Dutilh et al., 2017) and one of the authors (N.J.E.) ran diffusion model analysis on this blinded dataset.

Before modeling, trials with RTs <200 ms were removed (corresponding to 0.20% of trials in the typical group and 0.24% of trials in the dyslexia group). Trials without a response (i.e., no response made within the 2500 ms deadline) were modeled as nonterminating accumulation trajectories, with the probability of a nonresponse occurring being the survivor function for the model at the time of the 2500 ms deadline (Ulrich and Miller, 1994; Evans et al., 2018; Howard et al., 2020). These trials accounted for 1.02% of the data in the typical group and 1.26% of the data in the dyslexia group. We fit the data from each task with hierarchical, Bayesian diffusion models with five parameters: (1) average drift rate across difficulty levels v.mean, (2) boundary separation a, (3) nondecision time ter, (4) difference in mean drift rate between difficulty levels v.diff, and (5) starting point z. The stochastic noise within the model (s) was fixed at 0.1 to solve a scaling problem within the model, as per convention (Ratcliff, 1978). There were three hyperparameters for each parameter reflecting the mean (μ) and SD (σ) across the two groups and the difference between groups (δ). Importantly, this parameterization allowed us to explicitly set priors on the differences between groups, which was the key effect of interest within the current study. More specifically, the priors were as follows:

Data level:

$$y_{pi}\sim diffusion\left(a_{p,}{z}_p,Te{r}_p,v_{pi},s\right)$$

Parameters:

$$a_p\sim N_{+}\left({\mathrm{\mu }}_a\pm {\delta }_a,{\sigma }_a\right)$$

$$z_p/a_p\sim T{N}_{0,1}\left({\mathrm{\mu }}_z\pm {\delta }_z,{\sigma }_z\right)$$

$$Te{r}_p\sim N_{+}\left({\mathrm{\mu }}_{Ter}\pm {\delta }_{Ter},{\sigma }_{Ter}\right)$$

$$v_{p1}-v_{p2}\sim N\left({\mathrm{\mu }}_{v.diff}\pm {\delta }_{v.diff},{\sigma }_{v.diff}\right)$$

$$\frac{v_{p1}+v_{p2}}{2}\sim N\left({\mathrm{\mu }}_{v.mean}\pm {\delta }_{v.mean},{\sigma }_{v.mean}\right)$$

$$s=0.1$$

Hyperparameters:

$${\mathrm{\mu }}_a\sim N_{+}\left(0.2,0.2\right)$$

$${\mathrm{\mu }}_z\sim T{N}_{0,1}\left(0.5,0.2\right)$$

$${\mathrm{\mu }}_{Ter}\sim N_{+}\left(0.3,0.3\right)$$

$${\mathrm{\mu }}_{v.diff}\sim N\left(0,0.1\right)$$

$${\mathrm{\mu }}_{v.mean}\sim N\left(0.3,0.3\right)$$

$${\sigma }_a,{\sigma }_z,{\sigma }_{Ter},{\sigma }_{v.diff},{\sigma }_{v.mean}\sim \Gamma \left(1,1\right)$$

$${\delta }_a,{\delta }_z,{\delta }_{Ter},{\delta }_{v.diff},{\delta }_{v.mean}\sim N\left(0,0.01\right)$$

where y reflects the data, and subscripts p and i reflect the participant and difficulty level, respectively. The priors for the μ and σ parameters were based on those used in previous studies implementing hierarchical diffusion models (e.g., Evans and Brown, 2017; Evans and Hawkins, 2019; Evans et al., 2019), and the priors for the δ parameters were based on the “moderately informative priors” used for the differences between conditions in Evans (2019). We used a differential evolution Markov chain Monte Carlo algorithm (Ter Braak, 2006; Turner et al., 2013b) to sample from the posterior with 15 interacting chains, each with 4000 iterations, the first 1500 of which were discarded as burn-in. We also implemented a migration algorithm (see Turner et al., 2013b), where chains were randomly migrated every 14 iterations between iterations 500 and 1100. We calculated Bayes factors (BFs) through the Savage-Dickey ratio. Where we found evidence of group differences, we established the population effect size by dividing the posterior of the group difference (δ) by the posterior of the population SD (σ).

As shown in Table 1, the children with dyslexia were on average slightly older and of lower IQ than the typically developing children. As preregistered, the first author (C.M.) ran a default Bayesian t test using the BayesFactor R package (Morey and Rouder, 2018) which revealed weak, inconclusive evidence for the absence of group differences in age (BF in support of group differences = 0.33) (Jeffreys, 1961). As we know that diffusion model parameters change with age (Manning et al., 2021a), and as we could not conclusively rule out group differences in age, we also ran models which partialled out the effects of age from all of the parameters (using the residuals from the line of best fit between age and each of the parameters), in addition to our standard models. In our preregistered analysis plan, we decided not to control for PIQ as it may relate to both group membership and decision-making in cognitively relevant ways (Dennis et al., 2009). The analysis files were posted on the Open Science Framework before unblinding (https://osf.io/nvwf7/), at which point all models were rerun on the unblinded dataset with correct group membership.

EEG analysis for joint modeling

We ran exploratory analysis on the unblinded dataset to investigate links between drift rate and EEG activity. EEG data were bandpass filtered between 0.3 and 40 Hz in NetStation and then exported for further processing in MATLAB using EEGLAB functions (Delorme and Makeig, 2004). We downsampled each participant's data to 250 Hz and selected only the data between the first fixation onset and the last offset period. We then bandpass-filtered between 0.3 and 40 Hz (because of insufficient attenuation of low frequencies by NetStation filters) (Manning et al., 2019) and used EEGLAB's “clean_artifacts” function to remove bad channels, identify data segments with SDs over 15 and correct them using artifact subspace reconstruction (Chang et al., 2018). Missing channels were then interpolated. We then ran independent components analysis on 3000 ms epochs starting at fixation onset using an Infomax algorithm and subtracted ocular components from the continuous data. Finally, we average rereferenced the data. In line with the behavioral analyses, we excluded triggers for response events made <200 ms or >2500 ms after stimulus onset.

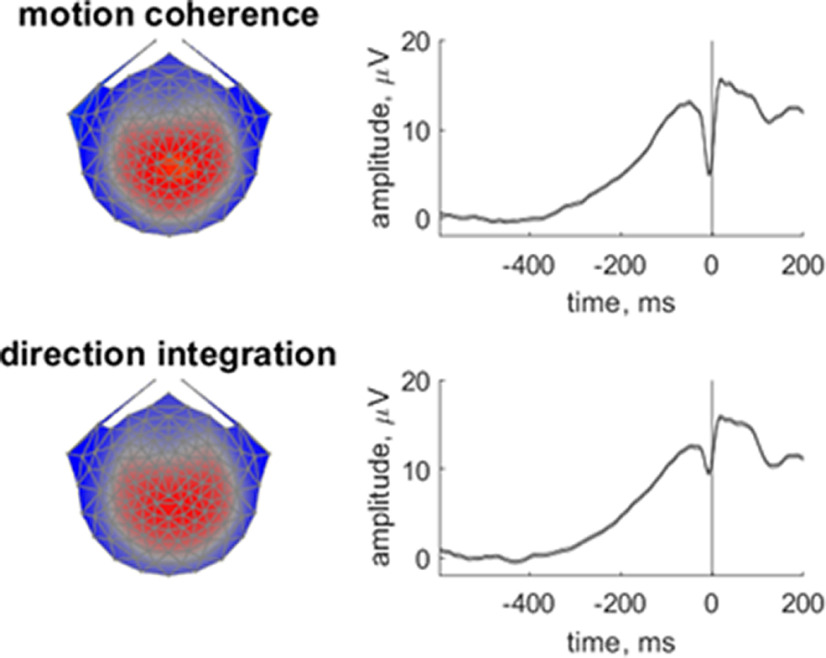
Following previous work, we used a data-driven component decomposition technique to identify spatiotemporally reliable patterns of activity across trials, which has the effect of maximizing signal-to-noise ratio (reliable components analysis) (Dmochowski et al., 2012; Dmochowski and Norcia, 2015; Manning et al., 2019, 2021a). To do this, we epoched each participant's preprocessed continuous data from −600 to 200 ms around each response, and we baselined the data to the last 100 ms of the random motion period. We submitted the baselined epochs for participants in both groups to reliable components analysis for each task separately. The forward-model projections of the weights for the most reliable component for each task (which explained 28.7% and 27.1% of the reliability in the motion coherence and direction integration tasks, respectively) are shown in Figure 3. This component resembled the most reliable component found in our previous work (Manning et al., 2021a), which in turn resembles the centro-parietal positivity (O'Connell et al., 2012; Kelly and O'Connell, 2013). Buildup of activity in this component has been linked to drift rate in typically developing children (Manning et al., 2021a). To investigate links with drift rate in the current dataset, we projected each participant's continuous data through the spatial weights for this component to yield a single component waveform for each participant for each task.

Figure 3.

Scalp topographies and temporal dynamics for the most reliable component in the motion coherence and direction integration tasks. Topographic visualizations of the forward-model projections of the most reliable component (left) reflecting the weights given to each electrode following reliable components analysis on data from all participants pooled across difficulty level, for the motion coherence task (top) and direction integration task (bottom). The waveforms (right) show the temporal dynamics of the component.

In our paradigm, stimulus-locked and response-locked activity overlaps temporally, with the degree of overlap relating to the participant's reaction time. Importantly, the extent of overlap could vary between groups and/or conditions (Ehinger and Dimigen, 2019). Thus, to obtain an EEG measure for inclusion in our model that reflects the decision-making process as purely as possible, and fully separate the contributions of stimulus-locked and response-locked activity, we used a linear deconvolution method to unmix overlapping stimulus-locked and response-locked activity in our component waveform using the Unfold toolbox (Ehinger and Dimigen, 2019). We modeled the continuous waveform for each participant by selecting a time window of −1000 to 1000 ms around each stimulus event or response event. We specified a design matrix with predictors for each difficulty level (difficult, easy) for each event type (stimulus, response). We then time-expanded the design matrix by adding a predictor for each time point sampled (i.e., every 4 ms from −1000 to 1000 ms) for each event type. The reason for this “time-expansion” is that each regressor in the resulting design matrix models the evoked response (either stimulus-locked or response-locked) at a particular point in time (Smith and Kutas, 2015; Ehinger and Dimigen, 2019); this is equivalent to the “finite impulse response” approach to analysis of fMRI timeseries (Henson et al., 2001). The predictors are therefore simply “boxcar” functions at each point in time, rather than information relating to the stimulus display. Having constructed the design matrix, we identified segments with amplitudes >±250 μV using a sliding 2000 ms segment in 100 ms steps, and excluded these segments from the design matrix (motion coherence task: mean 2.36% of data for each participant, range: 0 to 19.50%; direction integration task: mean 2.19% of the data for each participant, range: 0 to 21.17%). We then fit the deconvolution model resulting in regression weights (betas) for each of the 2 event types, 2 difficulty levels, and 500 time points, which we used to construct regression waveforms (see Figs. 4 and 5). Comparing the left and middle columns of Figures 4 and 5 shows that deconvolution led to reduced amplitudes (which is expected as the nondeconvolved waveform contains a mix of overlapping stimulus-locked and response-locked activity).

Figure 4.

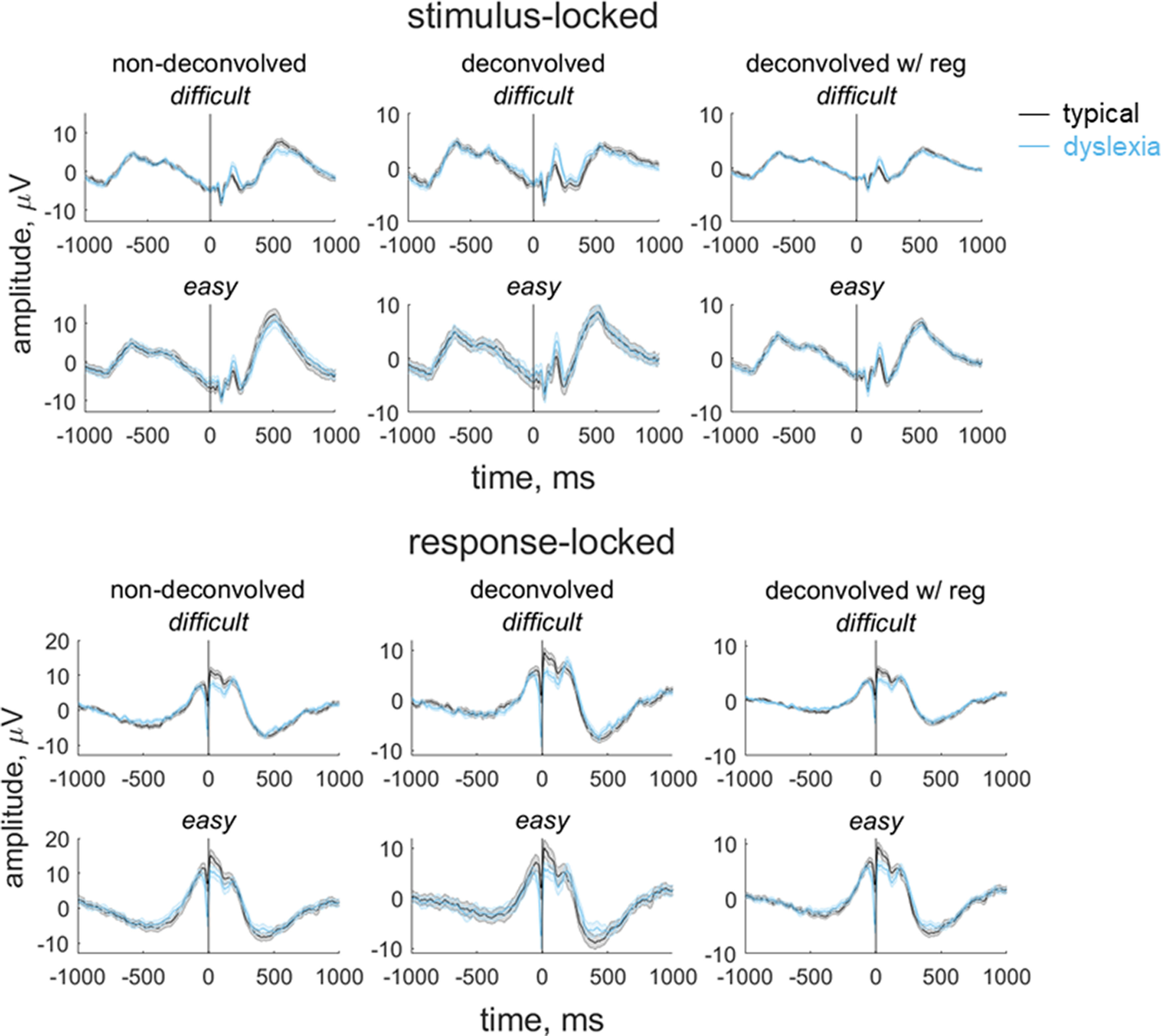
Group average stimulus-locked and response-locked evoked potentials for the motion coherence task. Average (±1 SEM) stimulus-locked (top) and response-locked (bottom) evoked potentials for typically developing children (gray) and children with dyslexia (blue) in the motion coherence task for difficult and easy levels. Left column represents nondeconvolved group average waveforms. Middle column represents deconvolved group average waveforms (without regularization). Right column represents deconvolved group average waveforms with regularization (ridge regression). Vertical line at 0 ms indicates when the stimulus phase started (stimulus-locked) or when the response was made (response-locked).

Figure 5.

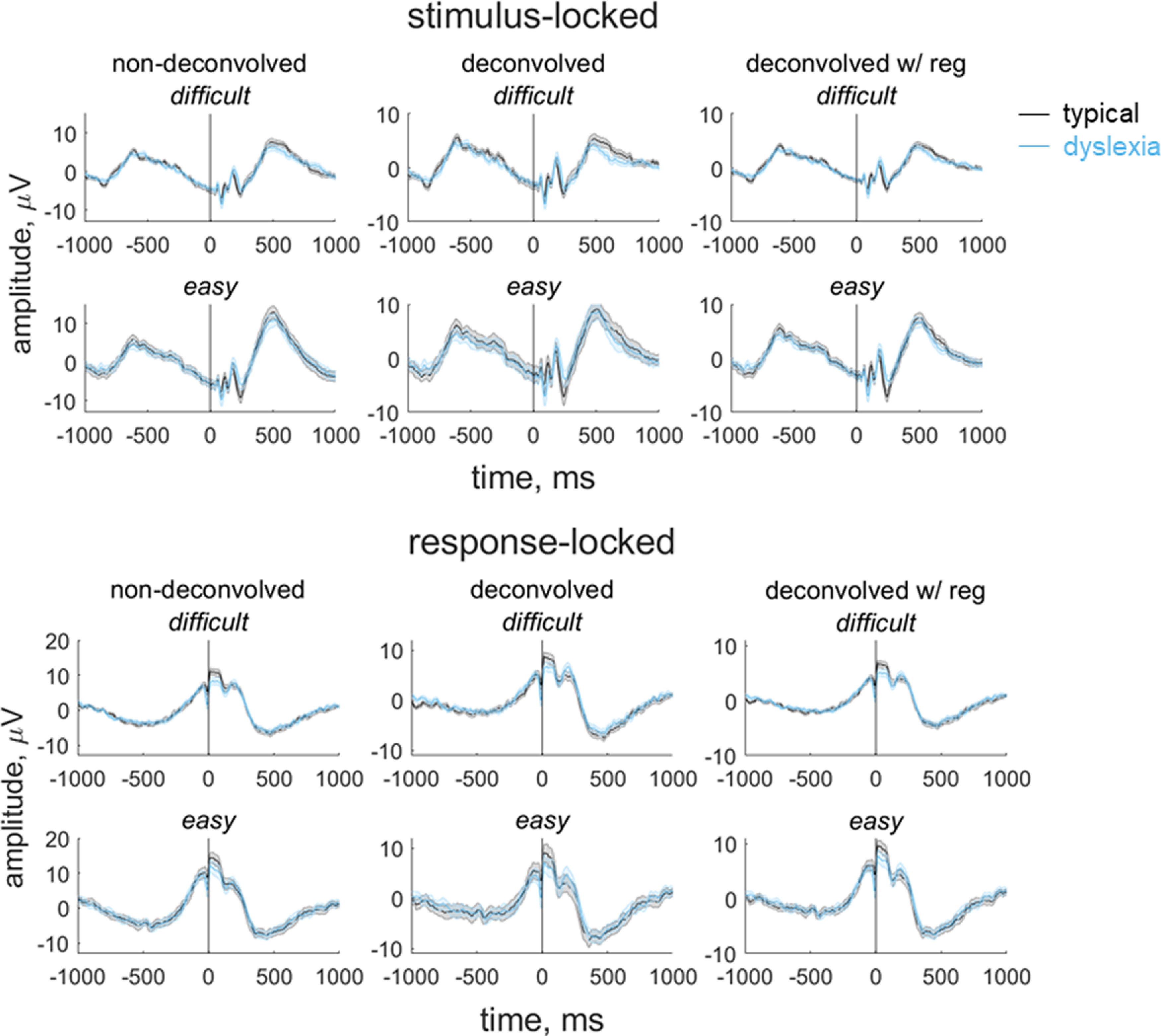
Group average stimulus-locked and response-locked evoked potentials for the direction integration task. Average (±1 SEM) stimulus-locked (top) and response-locked (bottom) evoked potentials for typically developing children (gray) and children with dyslexia (blue) in the direction integration task for difficult and easy levels. Left column represents nondeconvolved group average waveforms. Middle column represents deconvolved group average waveforms (without regularization). Right column represents deconvolved group average waveforms with regularization (ridge regression). Vertical line at 0 ms indicates when the stimulus phase started (stimulus-locked) or when the response was made (response-locked).

The nondeconvolved waveforms showed amplitude differences between difficult and easy levels (Figs. 4 and 5, left column), as to be expected for an EEG measure which reflects the decision-making process. However, these differences across difficulty levels were not evident in the deconvolved waveforms (Figs. 4 and 5, middle column). The fact that the difference between difficulty levels changed as a result of deconvolution could suggest that the overlap between stimulus- and response-locked activity differs between difficulty levels, because of different RT distributions in each difficulty level. However, we found a difficulty level difference in the nondeconvolved waveforms even when matching the RT distributions for the easy and difficult levels, so that difficulty level differences could not be purely attributed to different RT distributions. We therefore suspected that the β estimates may be noisy and that the deconvolution technique was overfitting the noise. Therefore, in the final step where we selected EEG measures for inclusion in the diffusion model, we reran the deconvolution model using a regularization method which penalizes the squared magnitude of the regression coefficients (ridge regression) (Kristensen et al., 2017) to minimize noise. Using this approach retained the difficulty level differences while minimizing the noise in the waveforms (Figs. 4 and 5, right column). Specifically, we found the best regularization parameter for each participant using cross-validation, and then took the mode across all participants and constrained the regularization parameter to ensure that differences in regularization did not contribute to group differences in resulting waveforms. The modal parameter value was 10 for the motion coherence task (5.5 and 10 for the typically developing children and children with dyslexia, separately) and 5 for the direction integration task (5 and 4.5 for the typically developing children and children with dyslexia, separately). We then fit a regression slope to each participant's average deconvolved waveform for each difficulty level between −200 and 0 ms around the time of the response to obtain a slope measure which we entered into the diffusion model and related to drift rate.

To assess the relationship between drift rate and the EEG component discussed above, we used a joint modeling approach (Turner et al., 2013a, 2015, 2016; Evans et al., 2018; Knowles et al., 2019). Specifically, we estimated additional hyperparameters for the correlation between the v.mean parameter and the average of the EEG measure (slope of centro-parietal component activity between −200 and 0 ms before response) over difficulty levels (EEG.mean), and between the v.diff parameter and the difference in the EEG measure between difficulty levels (EEG.diff). Specifically, this meant that the structure of the original hierarchical model (with age partialled out) was only different for the drift rate parameter, which was now a bivariate normal with the EEG measure as follows:

$$\begin{array}{c}\left[v_{p1}-v_{p2},EE{G}_{p1}-EE{G}_{p2}\right]\sim \\ BN\left(\left[{\mathrm{\mu }}_{v.diff}\pm {\delta }_{v.diff},{\mathrm{\mu }}_{EEG.diff}\pm {\delta }_{EEG.diff}\right],\left[{\sigma }_{v.diff}^2,{\sigma }_{v.diff}{\sigma }_{EEG.diff}\mathit{\rho },{\sigma }_{EEG.diff}{\sigma }_{v.diff}\mathit{\rho },{\sigma }_{EEG.diff}^2\right]\right)\end{array}$$

$$\begin{array}{c}\left[(v_{p1}+v_{p2})/2,(EE{G}_{p1}+EE{G}_{p2})/2\right]\sim \\ BN\left(\left[{\mathrm{\mu }}_{v.mean}\pm {\delta }_{v.mean},{\mathrm{\mu }}_{EEG.mean}\pm {\delta }_{EEG.mean}\right],\left[{\sigma }_{v.mean}^2,{\sigma }_{v.mean}{\sigma }_{EEG.mean}\mathit{\rho },{\sigma }_{EEG.mean}{\sigma }_{v.mean}\mathit{\rho },{\sigma }_{EEG.mean}^2\right]\right)\end{array}$$

$${\mathrm{\mu }}_{EEG.diff}\sim N\left(0,0.5\right)$$

$${\mathrm{\mu }}_{EEG.mean}\sim N\left(0,1\right)$$

$${\sigma }_{EEG.diff},{\sigma }_{EEG.mean}\sim \Gamma \left(1,1\right)$$

$${\delta }_{EEG.diff},{\delta }_{EEG.mean}\sim N\left(0,0.01\right)$$

$$\mathit{\rho }\sim U\left(-1,1\right)$$

where ρ refers to the correlation between drift rate and the EEG measure. We again used a differential evolution Markov chain Monte Carlo algorithm with 15 interacting chains to sample from the posterior of the joint model, although because of the greater computational burden of the model, we used 3000 iterations, of which the first 1000 were discarded as burn-in and no migration algorithm was implemented. Furthermore, we estimated two different variants of this joint model: one where the correlations were constrained to be the same across groups, which would allow for the estimation of more precise posteriors because of the limited sample size, and another less constrained version where the correlations were estimated separately for each group.

Data and code availability

Analysis scripts are available at https://osf.io/nvwf7/. Data and output files are available on the United Kingdom Data Service at http://doi.org/10.5255/UKDA-SN-855236.

Results

Diffusion modeling of behavioral data

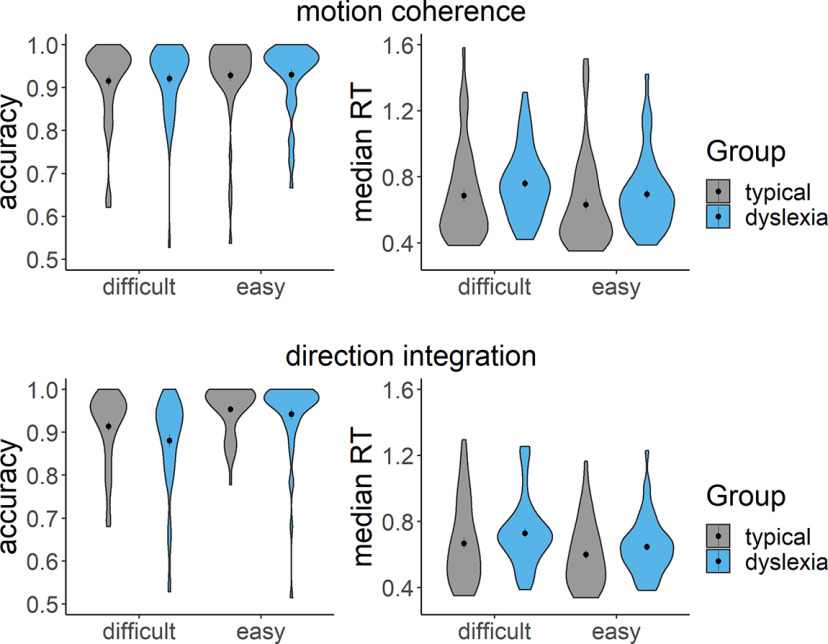
Figure 6 summarizes the accuracy and RT data subjected to diffusion modeling. This figure shows that the children with dyslexia had slightly slower median RTs compared with typically developing children, on average, and were slightly less accurate in the direction integration task, particularly on the difficult trials. However, there was substantial overlap between the groups with considerable variability within each group. These behavioral data were well fit by our diffusion models, as shown by the cumulative density functions in Figure 7. All chains were well converged, as reflected by Gelman-Rubin diagnostic values (Gelman and Rubin, 1992) close to 1 (mean = 1.00, range = 1.00-1.07).

Figure 6.

Accuracy and median RT for correct trials. Violin plots showing the kernel probability density for each group's accuracy (left) and median RT (s) for correct trials (right) for each difficulty level and each task (top: motion coherence; bottom: direction integration). Data for typically developing children and children with dyslexia are presented in gray and blue, respectively. Dots and vertical lines represent the group mean and ±1 SEM.

Figure 7.

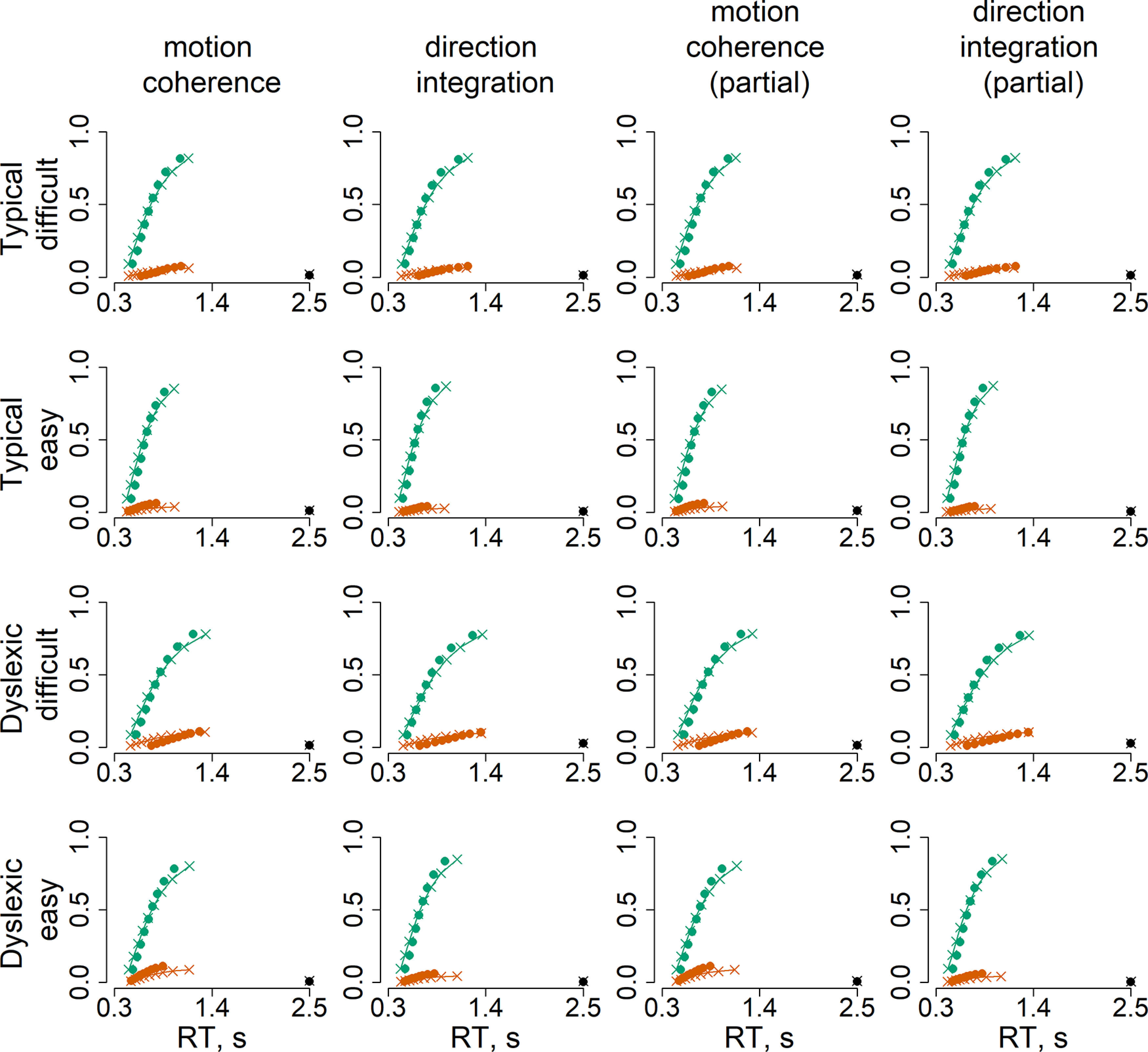
Model fits. Defective cumulative density function plots for each of the four models, for typically developing children (top rows) and children with dyslexia (bottom rows) for difficult and easy levels. Green represents correct responses and red represents error responses, at each of 9 quantiles. Dots represent the observed data. Crosses with connecting lines represent the model fit. The dots and crosses at 2.5 s represent the observed and model predicted misses.

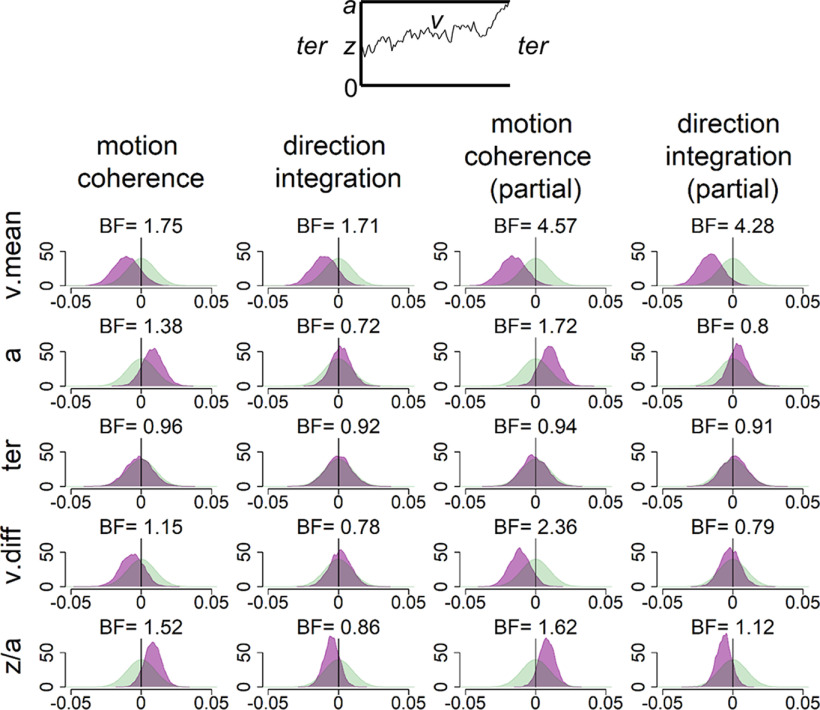
Figure 8 shows the prior and posterior distributions for the group-level parameters that reflect the difference between groups for each of the five parameters (v.mean, a, ter, v.diff, β), along with BFs. BFs >1 reflect more evidence for the alternative hypothesis of group differences compared with the null hypothesis, whereas BFs <1 reflect relatively more evidence for the null hypothesis than the alternative hypothesis. We use the heuristic that BFs between 1/3 and 3 constitute only weak, inconclusive evidence (Jeffreys, 1961).

Figure 8.

Prior and posterior density distributions. Prior (green) and posterior (purple) density distributions for the group-level parameters reflecting group differences in each of the five model parameters (v.mean, mean drift rate across difficulty levels; a, boundary separation; ter, nondecision time; v.diff, difference in mean drift rate between difficulty levels; z/a, relative starting point) for each task. Top inset, Schematic of the model parameters shown. Leftmost columns represent the results of the standard model. Rightmost columns represent the results of the model with age partialled out. Negative values reflect lower parameter values in the dyslexia group compared with the typically developing group. BF, Savage-Dickey BFs in favor of the alternative hypothesis (H₁) over the null hypothesis (H₀). BF > 1 support H₁.

In support of our first hypothesis, children with dyslexia had reduced drift rates in the motion coherence task compared with typically developing children, as shown by the leftward shift in the posterior distribution of v. mean in Figure 8. When age was partialled out, there was moderate evidence in favor of group differences (BF = 4.57, population effect size mean = –0.18, 95% CI: [–0.40, 0.02]). The evidence was weaker when age was not partialled out (BF = 1.75). Interestingly, the same pattern was found in support of our second hypothesis, with children with dyslexia also showing reduced drift rates in the direction integration task compared with typically developing children. Again, there was moderate evidence for group differences when age was controlled for (BF = 4.28, population effect size mean = –0.21, 95% CI: [–0.45, 0.02]), but weak evidence when age was not controlled for (BF = 1.71).

Our third hypothesis was that children with dyslexia would show increased boundary separation. Although children with dyslexia did have slightly higher boundary separation compared with typically developing children (indicated by a small rightward shift in the posterior distribution of a in Fig. 8), particularly in the motion coherence task, the evidence remained inconclusive, even when controlling for age. Our final hypothesis was that there would be no group differences in nondecision time (ter) in either task. Figure 8 shows little difference between the groups in this parameter, but the BFs are close to 1, suggesting inconclusive evidence. Therefore, more data would be required to make firm conclusions regarding these hypotheses.

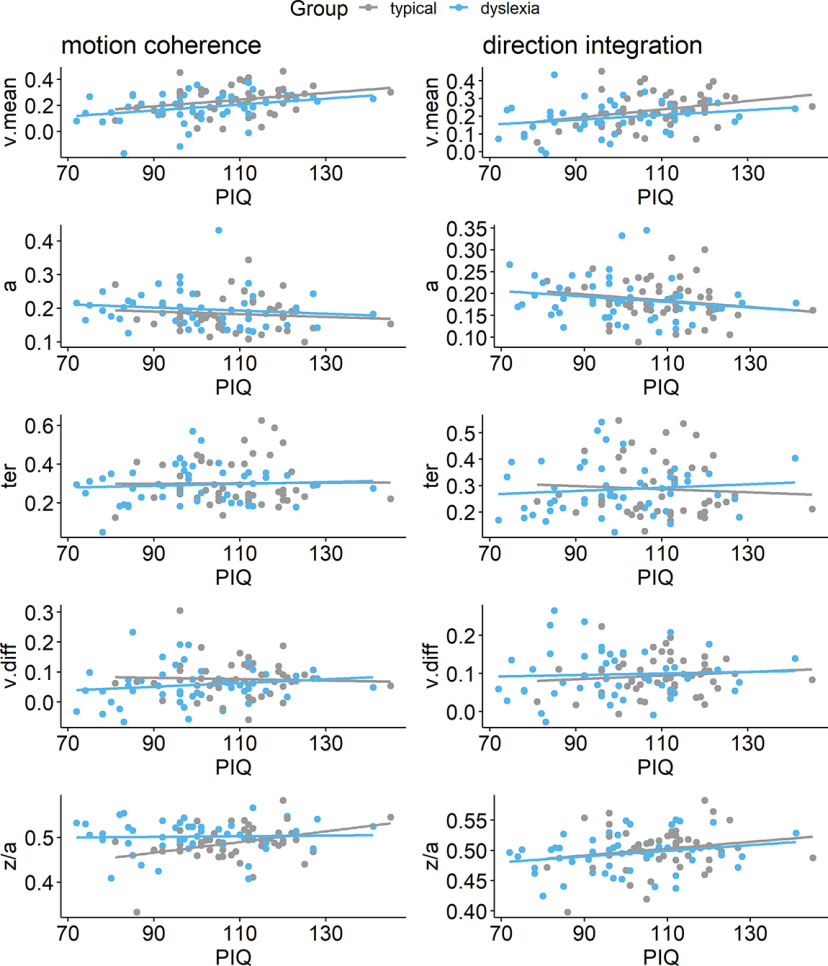
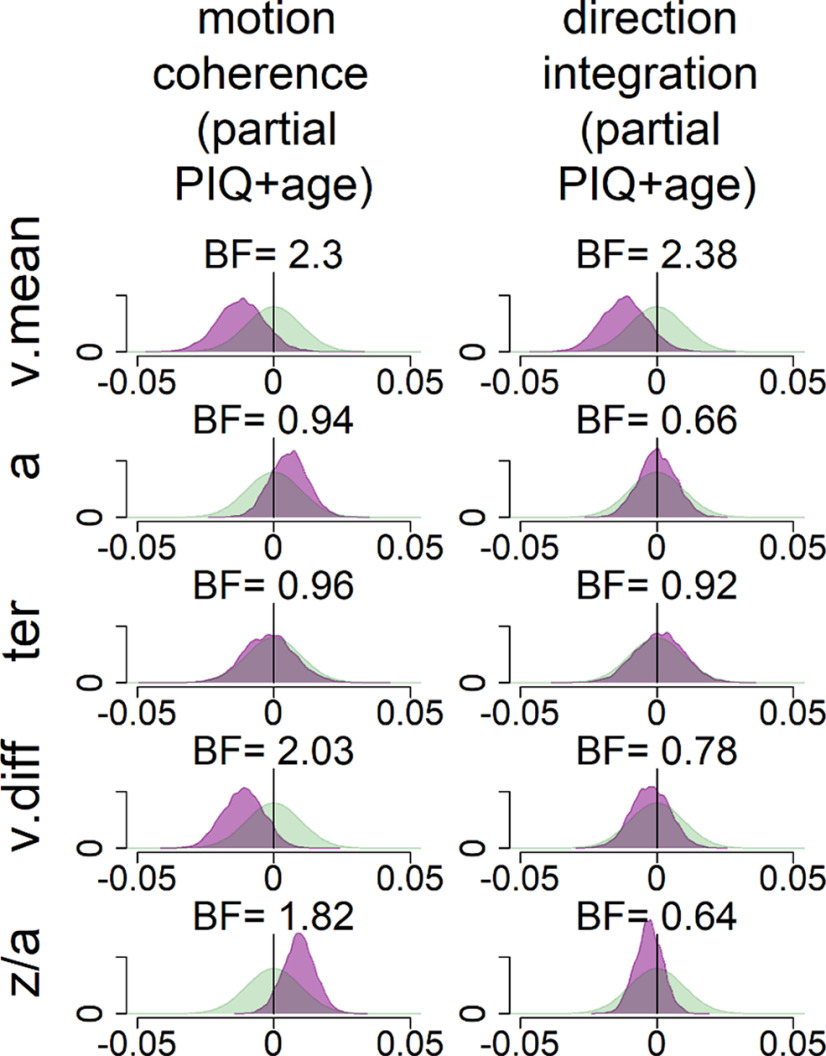
These preregistered analyses did not control for PIQ because it could be meaningfully related to both decision-making parameters and group membership, and investigating its contribution to both was beyond the scope of our multilevel modeling approach. However, as there was an indication of a relationship between PIQ and drift rate (Fig. 9), and as both PIQ and drift rate differed between the groups, we investigated these links further with an exploratory analysis, which partialled out the effects of both age and PIQ (Fig. 10). In brief, BFs of 2.3 and 2.38 in the two tasks continue to provide weak evidence for group differences in mean drift rate when both age and PIQ are controlled for.

Figure 9.

Scatterplots plotting individual parameter estimates against PIQ. Maximum likelihood estimates contained within the posterior for each participant's mean drift rate across difficulty levels (v.mean), boundary separation (a), nondecision time (ter), difference in drift rate between difficulty levels (v.diff), and starting point (z/a), plotted as a function of PIQ, for the motion coherence task (left column) and direction integration task (right column). Gray represents typically developing children. Blue represents children with dyslexia.

Figure 10.

Exploratory analyses: prior and posterior density distributions for model with age and PIQ partialled out. While our preregistered analysis did not control for PIQ, we conducted an exploratory analysis to investigate whether group differences in drift rate were still apparent when controlling for PIQ. The figure shows prior (green) and posterior (purple) density distributions for the group-level parameters reflecting group differences in each of the five model parameters (v.mean, mean drift rate across difficulty levels; a, boundary separation; ter, nondecision time; v.diff, difference in mean drift rate between difficulty levels; z/a, relative starting point) for each task, when both age and PIQ and their interaction are partialled out. Negative values reflect lower parameter values in the dyslexia group compared with the typically developing group. BF, Savage-Dickey BFs in favor of the alternative hypothesis (H₁) over the null hypothesis (H₀). BF > 1 support H_1. As in Figure 8, the posterior distribution for v.mean is shifted leftwards, reflecting lower mean drift rate in the dyslexia group than the typically developing group. The corresponding BFs are smaller in these analyses, indicating weaker evidence for group differences. As we reflect on in Discussion, the decision to partial out PIQ should not be taken lightly, as PIQ seems to contribute to both decision-making variables (drift rate) and group differences, so it is likely that partialling out PIQ removes some of the variance related to the group differences we are interested in.

Joint modeling of EEG and behavioral data

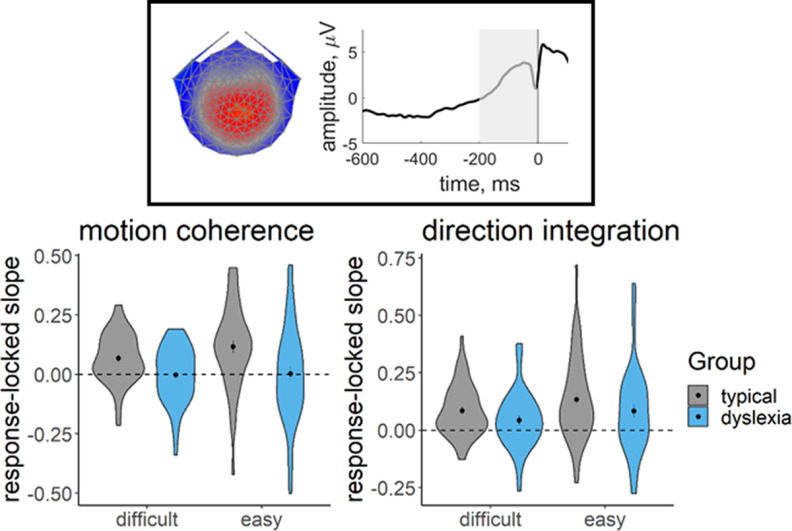
Figure 11 shows the distribution of slope measures that were extracted from each participant's deconvolved (with regularization) response-locked waveform, which were used in joint modeling to explore links between EEG and model parameters. While there was considerable between-participants variability, the children with dyslexia had shallower slopes than the typical children, on average. A Bayesian repeated-measures ANOVA in JASP (JASP Team, 2020) showed that, in the motion coherence task, the best model of EEG slope measures included the within-participants factor of difficulty level, the between-participants factor of group, and an interaction term. When averaging across models, there was strong evidence for including a main effect of group (BF_incl = 14.70) and a group by difficulty level interaction (BF_incl = 4.65). Yet in the direction integration task, the best model of EEG slope measures included only the within-participants factor of difficulty, with inconclusive evidence for including a main effect of group (BF_incl = 0.70) or a group by difficulty level interaction (BF_incl = 0.49). Therefore, it seems that the buildup of activity in the centro-parietal component is clearly reduced in children with dyslexia in the motion coherence task, but the reduction is not compelling in the direction integration task.

Figure 11.

EEG slope measure extracted for inclusion in the joint model. Violin plots showing the kernel probability density for the EEG slope measure extracted for inclusion in the joint model for each group (gray represents typically developing; blue represents dyslexia) for each difficulty level. The extracted measure was the slope of a linear regression line fitted to each participant's deconvolved (with regularization) response-locked waveform, from 200 ms before the response to the response (see shaded area of schematic response-locked waveform in inset). Dotted line indicates a flat slope. Dots and vertical lines represent the group mean and ±1 SEM.

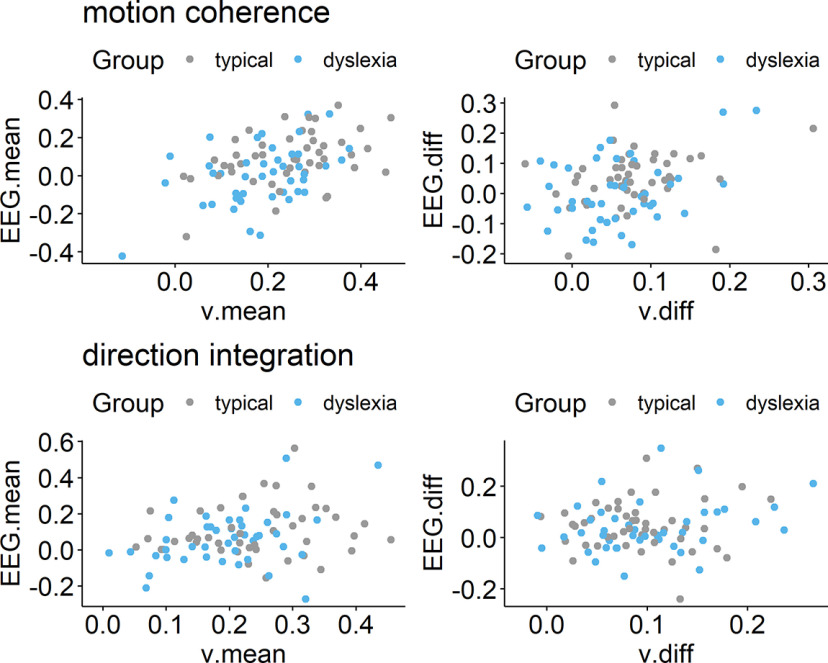
Next, we established whether this EEG measure was related to drift rate across the whole sample, estimating a single correlation for both groups, with the effects of age partialled out. For both tasks, the EEG measure was positively related to the mean drift rate across difficulty levels, although the evidence was only weak in the case of the direction integration task (motion coherence: posterior mean r = 0.44, 95% credible intervals (CI) = [0.26, 0.6], BF = 8869.49; direction integration: posterior mean r = 0.25, CI = [0.03, 0.45], BF = 1.65). The posterior means were in the direction of a positive relationship between the difference in EEG measure and the difference in drift rate between difficulty levels, although the evidence was inconclusive with relatively more evidence for the null hypothesis (motion coherence: posterior mean r = 0.22, CI = [–0.02, 0.44], BF = 0.73; direction integration: posterior mean r = 0.17, CI = [–0.08, 0.4], BF = 0.43; for scatterplots, see Fig. 12).

Figure 12.

Scatterplots showing relationship between drift rate and EEG. Left panels, Maximum likelihood estimates contained within the posterior for each participant's mean drift rate across difficulty levels (v.mean) plotted against the slope of EEG activity averaged across difficulty levels (EEG.mean) for the motion coherence (top) and direction integration (bottom) tasks. Right panels, Estimates for each participant's difference in drift rate between difficulty levels (v.diff) plotted against the difference in slopes of EEG activity between the two difficulty levels (EEG.diff), for each task. Gray represents typically developing children. Blue represents children with dyslexia.

Next, we fit joint models in which we estimated a separate correlation coefficient between drift rate and the EEG measure for the children with dyslexia and typical children (Fig. 13). Our intention was not to explicitly test for differences in correlations between groups, but rather to see if the previous findings seem to hold for each group; any separation between the groups below is intended to merely describe our estimated posterior distributions. A positive correlation can be seen for both groups in the motion coherence task for the mean drift rate across difficulty levels (typical: posterior mean r = 0.41, CI = [0.13, 0.63], BF = 7.45; dyslexia: posterior mean r = 0.43, CI = [0.15, 0.64], BF = 12.75). The posterior means were in the direction of a positive relationship for the difference in drift rate between difficulty levels, but the evidence was inconclusive with relatively more evidence for the null hypothesis (typical: posterior mean r = 0.18, CI = [–0.2, 0.51], BF = 0.39; dyslexia: posterior mean r = 0.20, CI = [–0.12, 0.49], BF = 0.46). The strength of correlations was weaker in the direction integration task, particularly for the typical children, for whom the BFs suggested moderate evidence for no relationship (mean drift rate across difficulty levels: posterior mean r = 0.10, CI = [–0.22, 0.4], BF = 0.29; difference between difficulty levels: posterior mean r = 0.04, CI = [–0.31, 0.38], BF = 0.24). The strength of the correlations in children with dyslexia was slightly stronger than in the typical children, with the mean drift rate across difficulty levels showing weak evidence for a relationship, although the difference in drift rate between difficulty levels showed weak evidence for no relationship (mean drift rate across difficulty levels: posterior mean r = 0.34, CI = [0.04, 0.58], BF = 2.59; difference between difficulty levels: posterior mean r = 0.24, CI = [–0.09, 0.53], BF = 0.61).

Figure 13.

Posterior density plots showing the correlation between drift rate and the EEG measure. Inset, Schematic representation of the drift rate parameter (v; left) and EEG measure (slope of response-locked waveform from −200 to 0 ms around the response; right) that were correlated in the joint model, where ρ represents the correlation. Posterior density plots in the left column reflect the correlation between the mean drift rate across difficulty levels (v.mean) and the mean EEG slope measure across difficulty levels (EEG.mean). Posterior density plots in the right column reflect the correlation between the difference in drift rate between difficulty levels (v.diff) and the difference in EEG slope measure between difficulty levels (EEG.diff). Top row, Plots for the motion coherence task. Bottom row, Plots for the direction integration task. Orange distribution represents the correlation across all participants. Gray and blue distributions represent separate correlations estimated for typical children and children with dyslexia, respectively.

Discussion

We analyzed the performance of children with dyslexia and typical children in two global motion tasks using diffusion modeling, to identify the processing stages that are altered in dyslexia. In both the motion coherence and direction integration tasks, children with dyslexia accumulated sensory evidence more slowly than typical children, on average, once controlling for age. Moreover, we found a neural correlate of this evidence accumulation process that was attenuated in dyslexia in the motion coherence task, thus linking brain and behavioral measures with a latent model parameter.

The finding of reduced evidence accumulation for children with dyslexia during the motion coherence task echoes O'Brien and Yeatman (2021) and helps to explain previous reports of elevated motion coherence thresholds in dyslexia (Benassi et al., 2010). Importantly, the current study goes further by showing that reduced evidence accumulation is also found in a direction integration task that does not require segregating signal dots from noise dots. This result suggests that dyslexic individuals have general difficulties with extracting global motion information, rather than solely difficulties with noise exclusion (in contrast to Sperling et al., 2006; Conlon et al., 2012), in line with reports of atypical performance in an illusory motion task without noise exclusion requirements (Gori et al., 2015, 2016). These general difficulties could reflect reduced temporal and/or spatial integration of motion signals (Raymond and Sorensen, 1998; Hill and Raymond, 2002; Benassi et al., 2010). This conclusion does not negate the possibility that dyslexic individuals face additional difficulties when segregating signal from noise, as we suggested based on stimulus-locked analyses using a similar dataset (Toffoli et al., 2021).

By supplementing our diffusion modeling analysis with EEG, we identified a neural index of reduced evidence accumulation in dyslexia. Specifically, we used a data-driven component decomposition technique to find a centro-parietal component previously linked to decision-making (O'Connell et al., 2012; Kelly and O'Connell, 2013; Manning et al., 2021a), and then “unmixed” overlapping stimulus- and response-locked activity. In the motion coherence task, we found that children with dyslexia showed a shallower buildup in the response-locked centro-parietal component compared with typical children, and the gradient of the buildup was positively correlated with drift rate in the joint model. While the EEG analysis was exploratory, the results are consistent with an earlier study of typically developing children (Manning et al., 2021a) and follow our hypothesized pattern (https://osf.io/enkwm). Similarly, Stefanac et al. (2021) reported reduced centro-parietal buildup in children with dyslexia compared with chronological and reading age-matched controls. Yet, in our direction integration task, we found no compelling evidence for reduced centro-parietal buildup in children with dyslexia, and the evidence for a relationship between this EEG measure and drift rate was weaker. This suggests that the magnitude of the centro-parietal positivity and its association with drift rate may be group- and task-dependent, to some extent (see also Lui et al., 2021).

Alongside reductions in drift rate, we hypothesized that children with dyslexia would show wider boundary separation compared with typically developing children, reflecting more cautious responses, and no differences in nondecision time. We found some evidence for increased boundary separation in children with dyslexia in the motion coherence task, but this was inconclusive. There was also inconclusive evidence for group differences in nondecision time. These results are not at odds with O'Brien and Yeatman (2021) but suggest that more data are required to reach a firm conclusion regarding these parameters. Seemingly, any group differences in these parameters are more subtle than group differences in drift rate. We note that the inferential method used by O'Brien and Yeatman (2021) differed from our own: while they also fit a hierarchical Bayesian model, they then extracted point estimates of diffusion model parameters for each individual to draw statistical inferences. Importantly, this means that O'Brien and Yeatman (2021) ignored the uncertainty in the individual-level parameters, which can inflate the evidence in favor of the winning model (Boehm et al., 2018; Evans and Wagenmakers, 2019).

Together with the results from stimulus-locked analyses using a similar dataset (Toffoli et al., 2021), our results suggest that early sensory encoding of motion information is not altered in children with dyslexia. While differences in drift rate cannot completely tease apart sensory and decision-making processes, in the current study we found no evidence of group differences in nondecision time, a measure that includes the time taken for sensory encoding. Moreover, Toffoli et al. (2021) showed that early peaks reflecting motion-specific processing were similar in children with dyslexia and typically developing children, with differences arising only after ∼430 ms following stimulus onset, specifically in the motion coherence task. The current analyses suggest that differences in dyslexia arise because of the efficiency with which evidence is extracted from global motion stimuli and integrated toward a decision bound, which is often attributed to parietal areas (Shadlen and Newsome, 1996, 2001; Hanks et al., 2006; de Lafuente et al., 2015). Without a comparable form task, it is unclear from the current study whether reduced evidence accumulation is restricted to tasks that tax the dorsal stream. However, we suggest that, within the magnocellular/dorsal stream, early sensory processing is unaffected in dyslexia with group differences emerging only at later processing stages, including those involved in decision-making. While this conclusion contrasts studies indicating early alterations of the magnocellular pathway in dyslexia (Livingstone et al., 1991; Stein and Walsh, 1997; Stein, 2001, 2019; Giraldo-Chica et al., 2015; Perani et al., 2021), the global motion tasks used in the current study are not ideally placed to isolate magnocellular processes (Skottun and Skoyles, 2006, 2008; Skottun, 2011, 2016). Future work will be required to determine how specific reduced evidence accumulation in dyslexia is to visual motion processing. Slower responses have been reported in dyslexia for other tasks (Nicolson and Fawcett, 1994; Catts et al., 2002), which could reflect pervasive reduced evidence accumulation, and reduced global integrative processes have been reported in static tasks in children with dyslexia (Franceschini et al., 2017a). However, slowed responses could arise for different reasons (e.g., increased nondecision time, wider boundary separation), so diffusion model decompositions on various tasks are required.

A number of future research directions emerge. What cognitive skills other than magnocellular/dorsal stream processing contribute to reduced drift rate in dyslexia? General processing speed is a unique predictor of word reading and comprehension (Christopher et al., 2012); and RAN is a recognized independent contributor to variation in reading ability, complementing phonological skills (e.g., O'Brien and Yeatman, 2021). Future work will need to establish the extent to which reduced processing speed and slower RAN associate with reduced drift rate in dyslexia. Additionally, PIQ varied across our two groups and was associated with drift rate. Exploratory models revealed that, even when controlling for both age and PIQ, there was still relatively more evidence for group differences in drift rate than no group differences. Yet the evidence was weaker than in models controlling only for age. Importantly, partialling out differences in PIQ could remove some of the variance related to the group differences we are interested in, as atypical development could lead to both dyslexia and reduced IQ (Dennis et al., 2009). Indeed, PIQ has been shown to strongly predict reading skills, independently of phonological skills (O'Brien and Yeatman, 2021). Future work will need to investigate the contribution of processing speed and PIQ to decision-making across the spectrum of reading abilities. Future research will also be required to explain the considerable between-participants variability in model and EEG parameters in children with and without dyslexia.

By combining diffusion modeling and EEG measures that are sensitive to the multiple processes contributing to motion perception, we have uncovered differences between children with dyslexia and typically developing children that could not be observed in behavioral responses alone. Moreover, diffusion modeling allows motion sensitivity to be measured without confounding speed-accuracy tradeoffs. Given that reduced behavioral sensitivity to motion has been reported in a range of other disorders (Braddick et al., 2003; Chen et al., 2003; McKendrick and Badcock, 2004), we suggest that diffusion modeling may provide a useful framework to identify convergence and divergence across different conditions, with implications for understanding the development of these conditions and their relationship to other cognitive processes.

Future work should establish whether differences in evidence accumulation of motion information contribute causally to the reading difficulties experienced by children with dyslexia. Some studies have suggested a causal relationship between motion perception and reading difficulties (e.g., Kevan and Pammer, 2009; Boets et al., 2011; Qian and Bi, 2015; Gori et al., 2016; Lawton, 2016; Ebrahimi et al., 2019), so it would be interesting to know whether evidence accumulation processes can be trained to improve reading ability. In support of this possibility, action video game training has been shown to improve motion perception by acting on the evidence accumulation phase (Green et al., 2010) and action video game training has also been linked to improved reading skills in children with dyslexia (Franceschini et al., 2013, 2017b; Bertoni et al., 2019, 2021; Franceschini and Bertoni, 2019). Such causal links will need to be investigated in future work using training or intervention designs.