Noninvasive measurements of spin transport properties of an antiferromagnetic insulator

Nitrogen-vacancy centers offer an alternative way to detect spin diffusive transport in an antiferromagnet.

Abstract

Antiferromagnetic insulators (AFIs) are of substantial interest because of their potential in the development of next-generation spintronic devices. One major effort in this emerging field is to harness AFIs for long-range spin information communication and storage. Here, we report a noninvasive method to optically access the intrinsic spin transport properties of an archetypical AFI α-Fe₂O₃ via nitrogen-vacancy (NV) quantum spin sensors. By NV relaxometry measurements, we successfully detect the frequency-dependent dynamic fluctuations of the spin density of α-Fe₂O₃ along the Néel order parameter, from which an intrinsic spin diffusion constant of α-Fe₂O₃ is experimentally measured in the absence of external spin biases. Our results highlight the significant opportunity offered by NV centers in diagnosing the underlying spin transport properties in a broad range of high-frequency magnetic materials such as two-dimensional magnets, spin liquids, and magnetic Weyl semimetals, which are challenging to access by the conventional measurement techniques.

INTRODUCTION

Advanced materials are integral to both scientific research and modern technology, enabling a wide range of emerging applications. Antiferromagnetic (AF) insulators (AFIs), a group of scientifically intriguing and technologically relevant materials, promise to bring new functionalities, such as high-density magnetic memory, ultrafast data processing speeds, and robust strategies, against malignant perturbations to develop transformative spin-based information technologies (1–3). Many of these advantages derive from their exchange-enhanced magnon bandgaps reaching into a terahertz regime and the vanishing net magnetization of the Néel order, which enable opportunities for outperforming their ferromagnetic counterparts (4–8).

Recent efforts have pursued effective control and manipulation of the Néel orientation in a range of AFIs (9–14). Building on the excellent spin coherence and reduced energy dissipation channels, AFIs naturally stand out as an attractive solid-state medium to support long-range, energy-efficient transmission of spin information (15–17). In the present state of the art, spin transport in AFIs is typically investigated via transport measurements in a nonlocal geometry, in which two patterned heavy metal strips with a large spin-orbit coupling serve as a spin injector and detector via the spin Hall effect and inverse spin Hall effect, respectively. The AFI embedded between the two metallic contacts provides the spin transport channel (15, 16, 18, 19). The characteristic spin diffusion length is obtained by measuring the spatially dependent variation of the longitudinal (relative to the magnetic order) spin accumulation. An essential element in the nonlocal measurement scheme is an external spin bias established by either electrical spin Hall injection or temperature gradient (20–22), which is usually sensitive to interfacial/surface conditions and is challenging to be precisely controlled in miniaturized spintronic devices.

Here, we report a noninvasive measurement technique that takes advantage of nitrogen-vacancy (NV) centers in diamond to reveal the intrinsic spin transport properties of the archetypical AFI α-Fe₂O₃ (10, 15, 19). We show explicitly that NV centers offer a novel platform to probe AF spintronics, which, despite the enormous promise and expectation, is still in its infancy because of the sparse experimental approaches available. By measuring dynamic fluctuations of the spin density along the Néel order parameter, NV centers provide an alternative way to extract the intrinsic spin diffusion constant of α-Fe₂O₃ in the absence of external spin stimuli. We emphasize that the probing frequency of the NV quantum sensing platform is well below the magnon band minimum, suggesting that this approach can be extended naturally to many other high-frequency magnetic systems, such as two-dimensional magnets (23, 24), spin liquids (25), and magnetic Weyl semimetals (26, 27), whose spin transport behaviors are challenging to access by conventional magnetic resonance techniques.

RESULTS

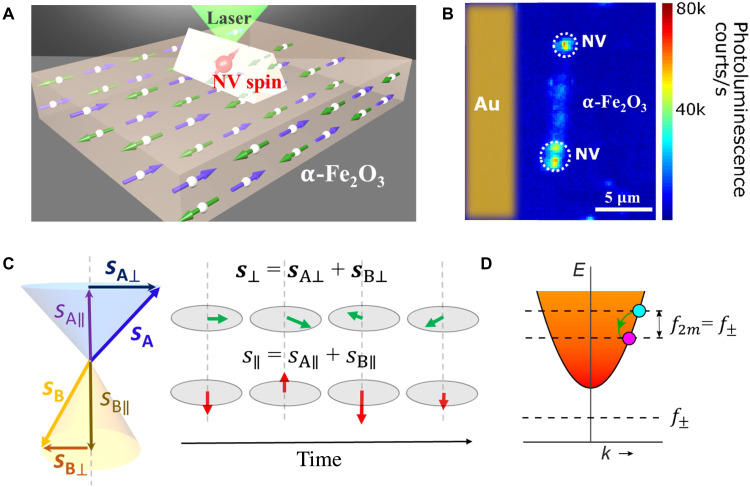
We first briefly review the pertinent quantum-mechanical properties of NV centers. An NV center is formed by a nitrogen atom adjacent to a carbon atom vacancy in one of the nearest neighboring sites of a diamond crystal lattice (28). The negatively charged NV state has an S = 1 electron spin and serves as a three-level qubit system. Because of their excellent quantum coherence, single-spin sensitivity, and functionality in a broad temperature range (28, 29), NV centers promise to be a transformative tool in exploring magnetic and electric properties in a variety of quantum materials with unprecedented field sensitivity and nanoscale spatial resolution (30–32). In our measurements, we transferred patterned diamond nanobeams containing individually addressable NV centers on the surface of an α-Fe₂O₃ crystal, as illustrated in Fig. 1A. The diamond nanobeam has the shape of an equilateral triangular prism with dimensions of 500 nm by 500 nm by 10 μm to ensure nanoscale proximity between NV centers and the sample studied (33–35). A 200-nm-thick Au stripline was fabricated on the α-Fe₂O₃ crystal to provide microwave control of the NV spin states (36). An external magnetic field H was applied and aligned to the NV axis. A photoluminescence (PL) image shows two individual NV centers positioned on top of the α-Fe₂O₃ crystal (Fig. 1B), demonstrating the single-spin addressability of the measurement platform.

Fig. 1. Quantum sensing of time-dependent longitudinal spin fluctuations in an antiferromagnet by NV centers.

(A) Schematic of a single NV spin contained in a patterned diamond nanobeam locally probing the longitudinal spin noise generated by an α-Fe₂O₃ crystal. (B) A PL image showing a diamond nanobeam containing two individually addressable NV spins positioned on top of an α-Fe₂O₃ crystal. (C) Left: Spin configuration of a Néel vector of a bipartite antiferromagnet. s_A and s_B represent the spin density of the two AF sublattices. s_A⊥ (s_B⊥) and s_A∥ (s_B∥) are the transverse and longitudinal components, respectively. Right: Schematic of the time-dependent fluctuations of the longitudinal and transverse spin density s_∥ and s_⊥ of the Néel order. (D) Sketch of the magnon dispersion and the magnon density of α-Fe₂O₃ in the uniaxial AF phase, which falls off as 1/energy (1/E), as indicated by the fading colors. The full expression of the dispersion curve is given by 2πf_k = $\sqrt{{\mathrm{\nu }}^2{k}^2+{\mathrm{\Delta }}^2}$ ± Δ_B, where f_k is the frequency of a magnon at a certain wave vector k, ν is the magnon velocity, Δ is the magnon gap, and Δ_B is the frequency gap between the two degenerate magnon modes set by the external magnetic field. In the low field regime, Δ_B is negligible compared with the AF magnon bandgap Δ. The longitudinal spin fluctuations are associated with two-magnon scattering processes, which are coupled with an NV center through dipolar interaction. f_± corresponds to the NV electron spin resonance frequencies, and f_2m represents the frequency of longitudinal spin fluctuations.

α-Fe₂O₃ exhibits a characteristic Morin phase transition at a critical temperature (T_M) of ~263 K, where it changes from an easy-plane, canted AFI to a conventional uniaxial AFI with an easy axis along the [0001] crystalline orientation (15, 17). We first focus on the uniaxial AF state with a temperature below T_M. Figure 1C illustrates the time-dependent fluctuations of the transverse and longitudinal spin density s_⊥ and s_∥ of the Néel vector of α-Fe₂O₃ at thermal equilibrium. The dynamical opening angle of the two sublattices is exaggerated for clarity. The local fluctuations of s_⊥(t) and s_∥(t) generate the magnetic noise δB_⊥(t) and δB_∥(t), respectively. Such magnetic noise can be understood by invoking the Holstein-Primakoff transformation: s_⊥ ∝α⁺(α), s_∥ ∝ s − α⁺α, with α⁺(α) being the magnon creation (annihilation) operator (37). In an intuitive picture, the transverse spin noise δB_⊥(t) is related to one-magnon scattering processes (34, 38, 39), i.e., the creation or annihilation of magnons, which vanish at frequencies below the magnon band minimum. The longitudinal spin noise δB_∥(t) is related to two-magnon scattering processes, where a magnon with frequency f + f_2m can undergo a transition to another magnon with frequency f (or vice versa), emitting magnetic noise at frequency f_2m as illustrated in Fig. 1D (38, 39). Microscopically, the time-dependent fluctuations of the longitudinal spin density s_∥ reflect spin transport via Brownian motion and naturally connect to the intrinsic spin diffusion constant D through the conventional diffusion equation (in the absence of an external magnetic field) (38, 40)

$${\mathrm{\partial }}_t{s}_{\parallel }-D{\nabla }^2{s}_{\parallel }=-\frac{1}{{\mathrm{\tau }}_s}{s}_{\parallel }$$ (1)

where τ_s is the coarse-grained spin relaxation time. Figure 1D illustrates the magnon band structure of α-Fe₂O₃ in the uniaxial AF phase and the generation of longitudinal spin noise. In contrast to the transverse counterpart with a minimum frequency determined by the magnon bandgap, the frequency of the longitudinal spin noise starts from zero and extends to the available magnon band energy (38), which can be addressed by NV centers in the low gigahertz frequency regime.

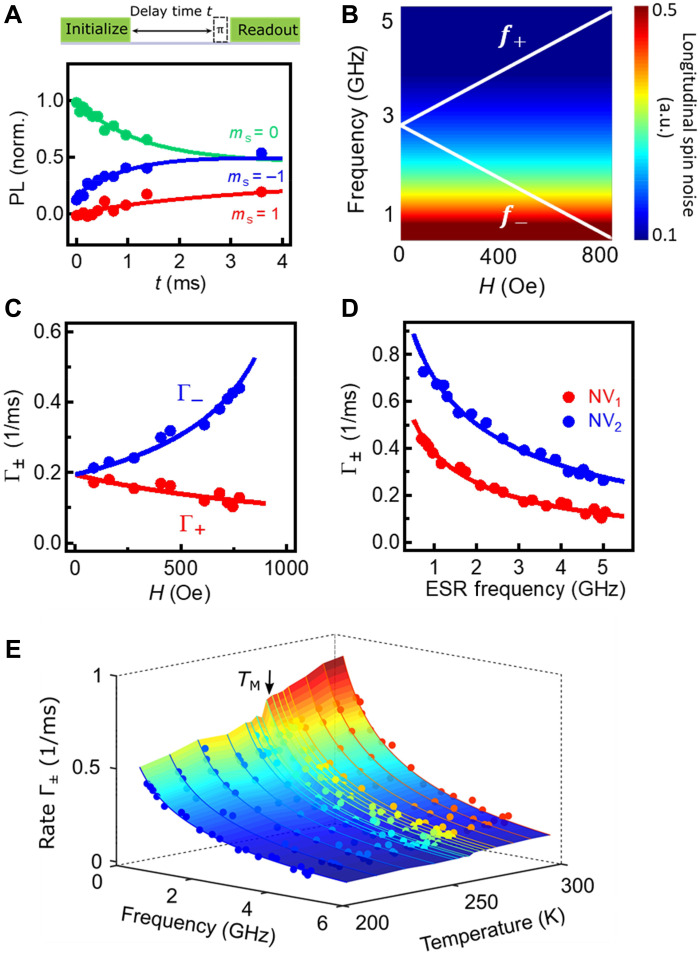
We used NV relaxometry measurements (28, 34, 41, 42) to detect the longitudinal spin noise generated by the α-Fe₂O₃ crystal. Figure 2A (top) shows the optical and microwave measurement sequence. A 3-μs-long green laser pulse is first applied to initialize the NV spin to the m_s = 0 state. Spin fluctuations in the α-Fe₂O₃ crystal couple to the NV centers through dipolar interactions. Longitudinal spin noise at frequencies f_± induces NV spin transitions from the m_s = 0 to the m_s = ±1 states, leading to an enhancement in the NV relaxation rates Γ_±. Here, f_± and Γ_± correspond to the NV electron spin resonance (ESR) frequencies and NV relaxation rates of the m_s = 0⟷±1 transitions, respectively. Compared with the m_s = 0 state, the optically excited m_s = ±1 states are more likely to be trapped by a dark pathway through an intersystem crossing and back to the m_s = 0 ground state, exhibiting a reduced PL. After delay time t, we measure the occupation probabilities of the NV spin at the m_s = 0 and the m_s = ±1 states by applying a microwave π pulse on the corresponding ESR frequencies and measuring the spin-dependent PL during the first ~600 ns of the green laser readout pulse. By measuring the integrated PL intensity as a function of the delay time t and fitting the data with a three-level model (34), NV relaxation rates can be quantitatively obtained (see section S1 for details).

Fig. 2. Local measurements of longitudinal spin fluctuations in α-Fe₂O₃ by NV relaxometry.

(A) Top: Optical and microwave sequence for NV relaxometry measurements. Bottom: A set of NV relaxation data measured with H = 745 Oe. The curves are fitted to a three-level model to extract the NV relaxation rate. (B) Calculated longitudinal spin noise spectrum. a.u., arbitrary units. The white curves correspond to the characteristic NV ESR frequencies f_± = 2.87 ± $\tilde{\mathrm{\gamma }}$H/2π. (C) Obtained spin relaxation rates Γ_± of NV₁ as a function of H. The red and blue points correspond to Γ₊ and Γ₋, respectively. The curves are fitting to Eq. 3. (D) Spin relaxation rates Γ_± of NV₁ (red dots) and NV₂ (blue dots) measured as a function of the NV ESR frequency, which are in agreement with the theoretical model (red and blue curves). The NV₁ and NV₂ were set at two different distances to the surface of the α-Fe₂O₃ crystal. (E) NV relaxation rates Γ_± measured as a function of temperature and NV ESR frequencies, from which the temperature dependence of the diffusive constant is extracted. The solid lines are the fitting curves to the theory.

Invoking perturbation theory, the measured NV relaxation rate Γ_± induced by the spin noise longitudinal to the Néel order parameter at the NV ESR frequencies f_± can be expressed as follows (43)

$${\mathrm{\Gamma }}_{\pm }(f_{\pm })=\frac{{\mid \tilde{\mathrm{\gamma }}\mathrm{\delta }{B}_{\parallel }(f_{\pm })\mid }^2}{2}$$ (2)

where ∣δB_∥(f_±)∣² is the spectral density of the longitudinal spin noise that is projected transversely to the NV orientation, and $\tilde{\mathrm{\gamma }}$ is the gyromagnetic ratio of the NV spin. According to the fluctuation-dissipation theorem, ∣δB_∥(f_±)∣² is related to the imaginary part of the longitudinal dynamic spin susceptibility χ′′, which can be further expressed as a function of the intrinsic spin diffusion constant D via Eq. 1. In the high temperature limit appropriate for our NV measurements, Γ_± can be written as (see section S2 for details) (38)

$${\mathrm{\Gamma }}_{\pm }(f_{\pm })=\frac{{(\mathrm{\gamma }\tilde{\mathrm{\gamma }})}^2{k}_{\mathrm{B}}T}{2\mathrm{\pi }{f}_{\pm }}\int f(\mathbf{k},d)\mathrm{\chi }″(D)d\mathbf{k}$$ (3)

where γ is the gyromagnetic ratio of the magnetic sample, k_B is the Boltzmann constant, T is the temperature, k is the wave vector of magnons, and f(k, d) is the transfer function describing the magnetic fields generated at the NV site (38, 43). By setting the frequency to an arbitrary value in Eq. 3, we calculate the longitudinal spin noise spectrum as shown in Fig. 2B. Qualitatively, the NV relaxation rate induced by the longitudinal spin noise is higher (lower) at a lower (higher) ESR frequency, corresponding to a smaller (larger) energy difference invoked in the two-magnon process discussed above.

In our experiments, we used two NV centers (NV₁ and NV₂) with different NV-to-sample distances (d₁ = 250 ± 6 nm and d₂ = 185 ± 5 nm; see section S3 for details) to perform the NV relaxometry measurements. Figure 2A (bottom) shows a set of spin relaxation data measured on NV₁ when H = 745 Oe and T = 200 K. The measured PL intensity corresponding to the m_s = 0 (±1) state decreases (increases) as a function of the delay time, indicating a relaxation of the NV spin to a mixture of the m_s = 0 and the m_s = ±1 states. Figure 2C shows the extracted NV spin relaxation rate Γ_± as a function of H. The measured magnetic field dependence of Γ_± is in agreement with the calculated magnetic noise spectrum, as shown in Fig. 2B.

To quantitatively determine the intrinsic spin diffusion constant of the α-Fe₂O₃ crystal, we fit the NV ESR frequency dependence of the measured relaxation rates Γ_± to Eq. 3. The agreement between the experimental results and the theoretical model, as shown in Fig. 2D, provides strong evidence that we are indeed probing the spin noise generated by the longitudinal spin fluctuation. The intrinsic spin diffusion constant D of α-Fe₂O₃ is obtained to be (8.9 ± 0.5) × 10⁻⁴ m²/s at 200 K, from which the spin conductivity is calculated to be (6.6 ± 0.4) × 10⁶ S/m (see section S4 for details). We highlight that the measurements by two NV centers (NV₁ and NV₂) set at different distances to the sample surface give the same spin diffusion constant of the α-Fe₂O₃ crystal, which is independent of the details of the NV quantum spin sensors. Taking the measured spin diffusion constant and the magnon velocity v ~ 30 km/s (44), we get momentum scattering time of ~3 ps and a magnon mean free path of ~90 nm for α-Fe₂O₃. Using spin relaxation time τ_s = 10 ns, which is suggested by a rough estimation in (45), the spin diffusion length λ = $\sqrt{D{\mathrm{\tau }}_s}$ of α-Fe₂O₃ is estimated to be 3 μm at 200 K, in agreement with values reported by the nonlocal spin transport measurements (15, 17). Note that the magnon mean free path is orders of magnitude smaller than the estimated spin diffusion length, confirming the diffusive nature of AF magnons in α-Fe₂O₃. Figure 2E plots a three-dimensional map of the NV relaxation rates Γ_± as a function of ESR frequency and temperature. The variation of the NV relaxation rate agrees well with the theoretical model, from which the intrinsic spin diffusion constant at individual temperatures is extracted. Note that the magnon spectrum of α-Fe₂O₃ is generally gapped on both sides of the Morin transition. Below the Morin transition temperature, the magnon gap is dominated by the exchange energy and the uniaxial magnetic anisotropy in the low field regime. Above the Morin transition temperature, the magnon gap is significantly reduced because of the small basal plane anisotropy of α-Fe₂O₃. Nevertheless, the minimal magnon energies of α-Fe₂O₃ in both cases are larger than the NV ESR frequencies in the magnetic field range of our study (46); therefore, the measured NV relaxation rates are driven by the longitudinal spin fluctuations of α-Fe₂O₃, and our theoretical model and analysis remain valid in the entire temperature range of study.

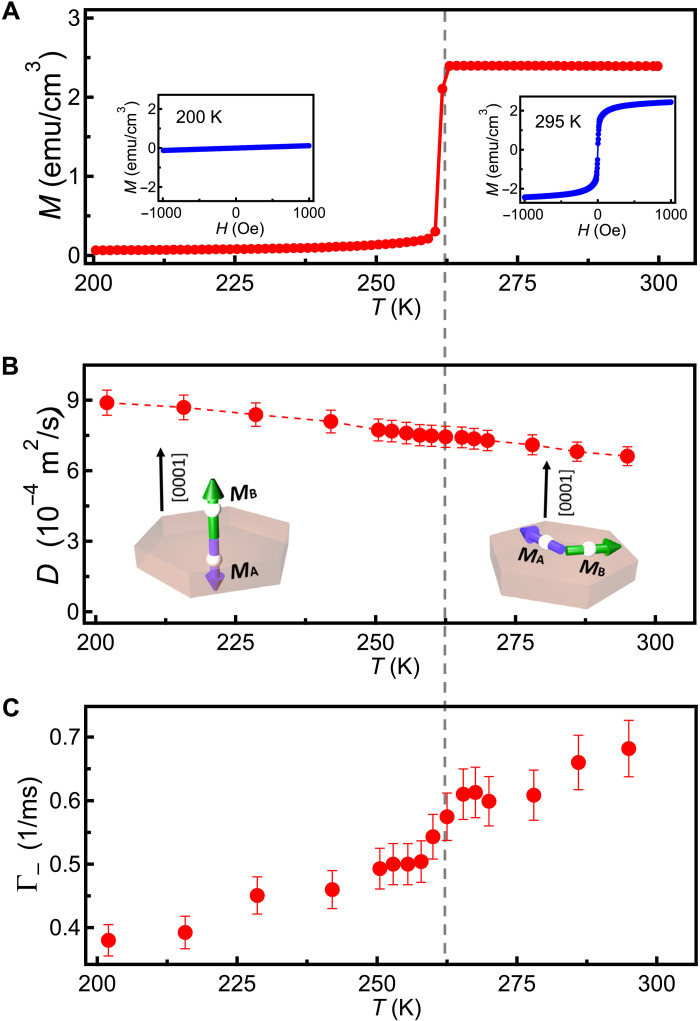
Recently, nonlocal spin transport behaviors have been studied in α-Fe₂O₃ crystals (films) in both the easy-plane and uniaxial AFI phases (15, 19). Next, we investigate the temperature dependence of the intrinsic spin diffusion constant of α-Fe₂O₃. In particular, we are interested in revealing the variation of spin diffusion constant across the Morin phase transition. Figure 3A shows a temperature dependence of the magnetization of the α-Fe₂O₃ crystal measured by vibrating sample magnetometer. The external magnetic field is set to be 1000 Oe, perpendicular to the [0001] crystalline axis. Above the Morin transition temperature (T_M ~ 263 K), a weak canted magnetic moment exists in the (0001) magnetic easy plane, which is confirmed by a field-dependent magnetization curve as shown in the inset. When T < T_M, there is a near absence of a ferromagnetic moment. Figure 3B shows the temperature dependence of the spin diffusion constant D measured between 200 and 300 K, which exhibits a gradual decrease from (8.9 ± 0.5) × 10⁻⁴ to (6.6 ± 0.4) × 10⁻⁴ m²/s. Notably, D smoothly varies across the Morin transition temperature. Theoretically, the intrinsic spin diffusion constant is determined by the magnon velocity v ~ $\frac{J_{\mathrm{s}}a}{\mathrm{\hslash }}$ (J_s is the exchange constant, a is the lattice constant, and ℏ is the reduced Planck constant) (47) and the momentum relaxation time τ as follows: D = $\frac{v^2\mathrm{\tau }}{3}$ (45). Momentum relaxation time τ in magnetic crystals (films) is determined by disorder, phonons, and Umklapp scattering (21). As the temperature increases, the inelastic scattering rate also increases, leading to a reduced τ and a spin diffusion constant as shown in Fig. 3B. Above the Morin transition temperature, a small canted magnetic moment emerges in the easy-plane AF phase of α-Fe₂O₃. While the canted magnetic moment induces variations in the magnon band structure, we note that AF spin transport in equilibrium state is mainly driven by thermal magnons governed by the exchange interaction, and the variation of magnetic anisotropies and Dzyaloshinskii-Moriya interaction can be treated as small corrections on the thermal energy scale (46). This is consistent with our observation that the spin diffusion constant extracted from our NV relaxometry measurements exhibits a smooth variation across the Morin phase transition.

Fig. 3. Temperature-dependent spin diffusion constant and magnetic phase transition of α-Fe₂O₃ probed by NV relaxometry.

(A) Temperature dependence of the magnetization of the α-Fe₂O₃ crystal with an external magnetic field of 1000 Oe applied perpendicular to the [0001] crystalline axis. Insets: Field-dependent magnetization of the α-Fe₂O₃ crystal when T = 200 and 295 K. The dashed line represents the Morin transition temperature of α-Fe₂O₃. (B) Intrinsic spin diffusion constant D measured as a function of temperature between 200 and 300 K. Insets: Schematic views of the magnetic order of α-Fe₂O₃ below and above the Morin transition temperature. M_A and M_B illustrate the magnetic moment of the two AF spin sublattices. (C) NV relaxation rate Γ₋ measured as a function of temperature. The external magnetic field H is set to be 683 Oe, corresponding to an NV ESR frequency f₋ of 0.96 GHz.

Last, we remark that NV relaxometry could be further used to reveal the intrinsic magnetic phase transition of α-Fe₂O₃. Figure 3C plots the temperature-dependent NV relaxation rate Γ₋ measured between 200 and 300 K. As discussed above, the magnetic stray field δB_∥ generated by the fluctuating longitudinal spin density of α-Fe₂O₃ interacts with the NV spin S through Zeeman coupling δB_∥∙S, leading to an enhancement of NV relaxation rates. The measured Γ₋ increases with increasing temperature, indicating that the magnetic noise scales with the magnon density. Across the Morin transition temperature (T_M ~ 263 K), the Néel order rotates from the magnetic easy-plane to the easy-axis direction accompanied by a change of the component of the produced stray field δB_∥ that is projected transversely to the NV axis, leading to a variation of the NV relaxation. In a macro-spin picture, the measured NV relaxation rate should follow a step-like jump in a narrow temperature window across the Morin phase transition. However, in real experiments, magnetic domains could be formed in the α-Fe₂O₃ sample, especially when close to the first-order phase temperature. Note that the spatial sensitivity of our measurement technique is determined by the NV-to-sample distance, which is about 200 nm in this study. We expect that magnetic domains with dimensions comparable to (smaller than) this length scale are formed when close to the Morin transition regime, leading to a gradual variation of the measured NV relaxation rates (see the details of the numerical analysis in section S5).

DISCUSSION

In summary, we have demonstrated NV centers as a local probe of intrinsic spin transport properties of a proximal AFI. In contrast to existing measurement platforms that involve integrating materials into the device structure, NV centers access the spin diffusion constant noninvasively by probing the local (equilibrium) longitudinal spin fluctuations in the time domain, which obviates the requirement of an external spin bias. We highlight that this merit is of particular relevance when it comes to investigating spin transport in high-frequency magnetic materials, whose coherent spin resonances are challenging to excite. In addition, the presented NV relaxometry method does not depend on the form of created NV centers in diamond, which can be naturally extended to many other NV measurement schemes. By using scanning NV microscopy or diamond nanopatterns with shallowly implanted NV centers (31, 32), we expect that the spatial resolution of the presented NV quantum sensing platform could ultimately reach the nanometer scale, offering new opportunities to reveal emergent spin transport in a broad class of material systems.

MATERIALS AND METHODS

Sample information

The α-Fe₂O₃ crystal with dimensions of 0.5 mm by 5 mm by 5 mm was obtained commercially from the company SurfaceNet and was orientated with $\left[11\overline{2}0\right]$ out of the sample plane. The crystal structure and surface morphology of the α-Fe₂O₃ crystal have been characterized by x-ray diffraction and atomic force microscopy, as shown in fig. S1. The Morin transition temperature was characterized to be ~263 K by temperature-dependent magnetometry measurements. Above the Morin transition temperature, α-Fe₂O₃ behaves as an easy-plane antiferromagnet, exhibiting a weak canted magnetic moment (M_s ∼ 2 emu/cm³) in (0001) plane because of the Dzyaloshinskii-Moriya interaction. Below the Morin transition temperature, the sign of the anisotropy field along the [0001] axis changes, and α-Fe₂O₃ behaves as a uniaxial antiferromagnet with an easy axis along the [0001] crystalline orientation.

Device fabrication

Diamond nanobeams were fabricated by a combination of top-down etching and angled etching processes (33). Acid cleaning (48) was performed before and after the fabrication processes to ensure a pristine diamond surface. Patterned diamond nanobeams containing individually addressable NV centers were transferred onto the surface of an α-Fe₂O₃ crystal using a tungsten tip performed on a micromechanical transfer stage (fig. S2A). The out-of-plane orientation of the NV axis was experimentally confirmed to be the same (within experimental errors) before and after the transfer process, excluding the possibility of rotation or tilting of diamond nanobeams. The NV orientation is obtained by magnetic field alignment. We measured the NV PL as a function of the position of the permanent magnet, and the external magnetic field aligns with the NV axis when the NV centers emit the maximum PL. The NV spin state was controlled by microwave currents flowing a 5-μm-wide and 200-nm-thick Au on-chip stripline patterned on the α-Fe₂O₃ crystal. The distance between the diamond nanobeam and the Au stripline is about 3 μm, ensuring a sufficiently large microwave field applied at the NV site (fig. S2B). The angle between the NV axis and the surface normal for the two NV centers (NV₁ and NV₂) positioned on top of the α-Fe₂O₃ crystal is 59°.

NV measurements

NV measurements were performed in a closed-loop optical cryostat with a working temperature from 4 to 350 K. We optically addressed individual NV centers using a home-built scanning confocal microscope. A 532-nm continuous laser (Hubner Photonics) was used for optical excitation of the NV centers. Laser pulses for optical initialization and readout of NV centers were generated by an acoustic-optical modulator in a double-pass configuration. Microwave signals used for driving NV centers were generated by Rohde & Schwarz signal generators (SGS100a and SMB100A). The microwave currents were delivered to microwave switches (Mini-Circuits ZASWA-2-50DRA+), a microwave combiner (Mini-Circuits ZB3PD-63-S+), and an amplifier with +50-dB amplification (Mini-Circuits ZHL-25 W-63+) and, lastly, sent to the on-chip Au stripline via a printed circuit board. NV PL was detected by an avalanche photo diode (Excelitas SPCM-AQRH-13). The trigger pulses to the optical modulator and photon counting were generated by a programmable pulse generator (Spincore, PBESR-PRO-500). The external magnetic field was generated by a cylindrical NdFeB permanent magnet attached to a scanning stage. The magnitude and the orientation of the magnetic field can be controlled by moving the position of the permanent magnet. Extended NV relaxometry measurements are presented in section S6 to show the direct comparison between the longitudinal and transverse spin fluctuations.

Supplementary Materials

This PDF file includes:

Supplementary Text

Sections S1 to S6

Figs. S1 to S9

References