Predicting individual neuron responses with anatomically constrained task optimization

Summary

Artificial neural networks trained to solve sensory tasks can develop statistical representations that match those in biological circuits. However, it remains unclear whether they can reproduce properties of individual neurons. Here, we investigated how artificial networks predict individual neuron properties in the visual motion circuits of the fruit fly Drosophila. We trained anatomically-constrained networks to predict movement in natural scenes, solving the same inference problem as fly motion detectors. Units in the artificial networks adopted many properties of analogous individual neurons, even though they were not explicitly trained to match these properties. Among these properties was the split into ON and OFF motion detectors, which is not predicted by classical motion detection models. The match between model and neurons was closest when models were trained to be robust to noise. These results demonstrate how anatomical, task, and noise constraints can explain properties of individual neurons in a small neural network.

eTOC

Mano et al. show that in Drosophila’s well-characterized motion circuits, many properties of individual neurons can be predicted by an anatomically-matched artificial neural network that is trained to detect visual motion in the presence of noise.

Introduction

Biological neural networks (BNNs) have evolved through natural selection to perform tasks that promote survival, but it is often unclear how their properties relate to the tasks they perform. Recent work in sensory systems has shown that artificial neural networks (ANNs) optimized to perform ethologically-relevant tasks often develop stimulus representations similar to those in BNNs. For instance, ANNs trained to categorize visual objects possess intermediate representations similar to those in the hierarchical processing steps in primate visual cortex ¹. Similarly, representations of temperature in zebrafish are similar to those in artificial neural networks trained to navigate thermal gradients ². These comparisons between ANNs and BNNs test a hypothesis about the goal of the biological circuit: is optimizing a network to perform a task under specific constraints sufficient to account for properties of the biological network?^3–5 These prior studies drew connections between clusters of nodes or layers in an ANN and the heterogeneous response properties of groups neurons in regions of the brain. In this study, in contrast, we show that nodes in a trained ANN can have properties that correspond to individual neurons in a biological circuit. To do this, we apply connectomic constraints to small ANNs to create an a priori correspondence between specific ANN nodes and individual neurons in the biological network. In this framework, we compare the task-optimized ANN to the evolved BNN to show how optimization and constraints—especially noise—account for properties of individual neurons in a biological circuit.

We focus on the fruit fly Drosophila’s motion detection circuits (Figure 1A), which are critical to the fly’s visual navigation behaviors ^6–9. These circuits are well-studied, so that anatomical connectivity has been measured ^10–13, along with many functional properties of neurons in the circuit ^{7, 9, 14–31}. These motion circuits have evolved two types of motion detectors: T4 neurons, which are selective for moving light edges (ON-edges), and T5 neurons, which are selective for moving dark edges (OFF-edges). T4 and T5 neurons are arranged so that at each location in visual space there are one leftward and one rightward sensitive T4 neuron and one leftward and one rightward sensitive T5 neuron. Each T4 and T5 neuron receives excitatory and inhibitory input from neurons that signal visual intensity in 3 spatially-separated locations (Figure 1A) ^{10, 11, 18}.

Figure 1. Non-canonical measured properties of primary motion detecting neurons in Drosophila.

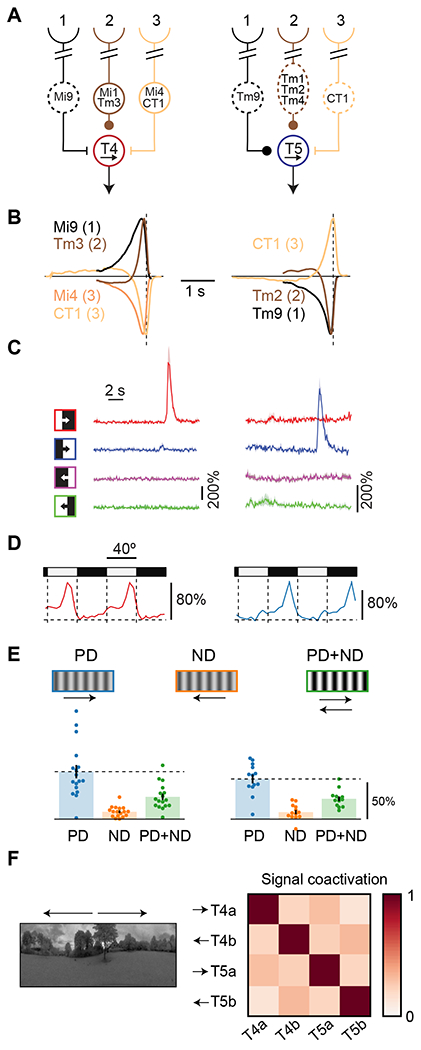
A) Connectivity schematic of the three spatially separated inputs to T4 and T5 neurons, two parallel, primary motion detectors in Drosophila’s visual system. Dashed lines indicate that a cell is in the OFF pathway. Round synapses indicate excitatory connections, while bars indicate inhibitory synapses.

B) For each cell immediately upstream of T4 and T5, we plot the linear model prediction of the calcium response to an impulse of light signed by their input to T4 and T5. Neurons in position 2 show fast dynamics compared to the neurons in flanking positions. Inputs from position 3 have the opposite influence on T4 and T5 from neurons in positions 1 and 2. Data from ^24,37.

C) Traces of T4 and T5 calcium responses to light and dark edges moving in the preferred (rightward) and null (leftward) directions. Data from ³⁰.

D) Mean calcium responses of T4 and T5 neurons to a stationary square wave stimulus as a function of position, showing preferential responses at edges of specific polarity. Data from ³⁰.

E) Mean calcium responses of T4 and T5 neurons to preferred direction (PD) and null direction (ND) drifting sinusoid gratings, as well as to their sum (PD+ND). The addition of null direction motion suppresses calcium responses in T4 and T5, a form of opponent suppression in primary motion detectors. Data from ²⁹.

F) T4 and T5 calcium signals in response to naturalistic stimuli tend to be non-coactive. Arrows indicate the direction selectivity of the different neuron classes. Data from ²⁸.

Textbook models for motion estimation, including the Hassenstein-Reichardt correlator model and the motion energy model ^{32, 33}, may be largely derived from first principles ^{34, 35} and suggest that temporal delays, spatially separated inputs, and nonlinear processing are critical to motion detection ³⁶. These models specify a minimum set of conditions to arrive at direction-selective signals, but they fail to account for many of the features measured in the fly’s motion circuits. In particular: (1) The three spatially-separated inputs to T4 and T5 are organized such that the central signal is fast, while the two flanking signals are slow ^{18, 24, 37} (Figure 1B). Moreover, when local luminance changes, one flanking signal has the opposite influence on the downstream motion detector compared to the other two spatial locations ^{10,16, 27}. (2) Horizontal motion detection is organized into four parallel pathways, consisting of light and dark moving edge detectors in both horizontal directions ⁷ (Figure 1C), a split not present in or explained by classical models. (3) Although T4 and T5 neurons are direction-selective, they also respond to specific stationary light or dark edges ³⁰ (Figure 1D), an unexpected result for cells that detect visual motion. (4) T4 and T5 neurons show opponent suppression: they respond less to the sum of null and preferred direction motion stimuli than to preferred direction motion stimuli alone. This phenomenon runs counter to predictions of common, classical motion detection models ²⁹ (Figure 1E). (5) Last, the four neurons that encode horizontal motion have signals that tend to be non-coactive when presented with moving natural scenes, so that their signals are decorrelated ²⁸ (Figure 1F), a property not addressed by classical models of motion detection. Since classical models do not account for this suite of qualitative properties of identified neurons in the fly’s motion circuits, we asked whether they could be explained by optimizing a network to detect motion under the anatomical constraints of the fly’s motion circuits.

In this study, we developed a set of three shallow, convolutional ANN models with direct correspondences between analogous ANN units and BNN neurons. We trained these models to predict the velocity or direction of moving natural scenes, and then examined their solutions and response properties. The trained models accounted for many response properties of individual neuron types measured in the fly’s motion circuits, including those listed above (Figure 1). Therefore, the task of predicting natural scene velocity, combined with anatomical constraints from the circuit connectivity, was sufficient to reproduce circuit properties not accounted for by classical models. Moreover, the presence of noise during training was instrumental in generating artificial units with these properties. These results show that many unexplained properties of individual neurons in this small neural network are consistent with a system optimized for motion detection in the presence of noise.

Results

Detecting motion in natural scenes

Our goal is to relate optimized ANNs to the evolved circuits in the fly. To make this comparison, we set up a problem for the artificial networks to solve that is similar to problem solved by the fly (Figure 2A–C). As the fly navigates its environment, the direction-selective neurons T4 and T5 receive luminance information from three neighboring points in space and use that to infer the direction and speed of visual motion ^{34, 35, 38, 10, 11, 18}.

Figure 2. Models predicted velocities of naturalistic training data.

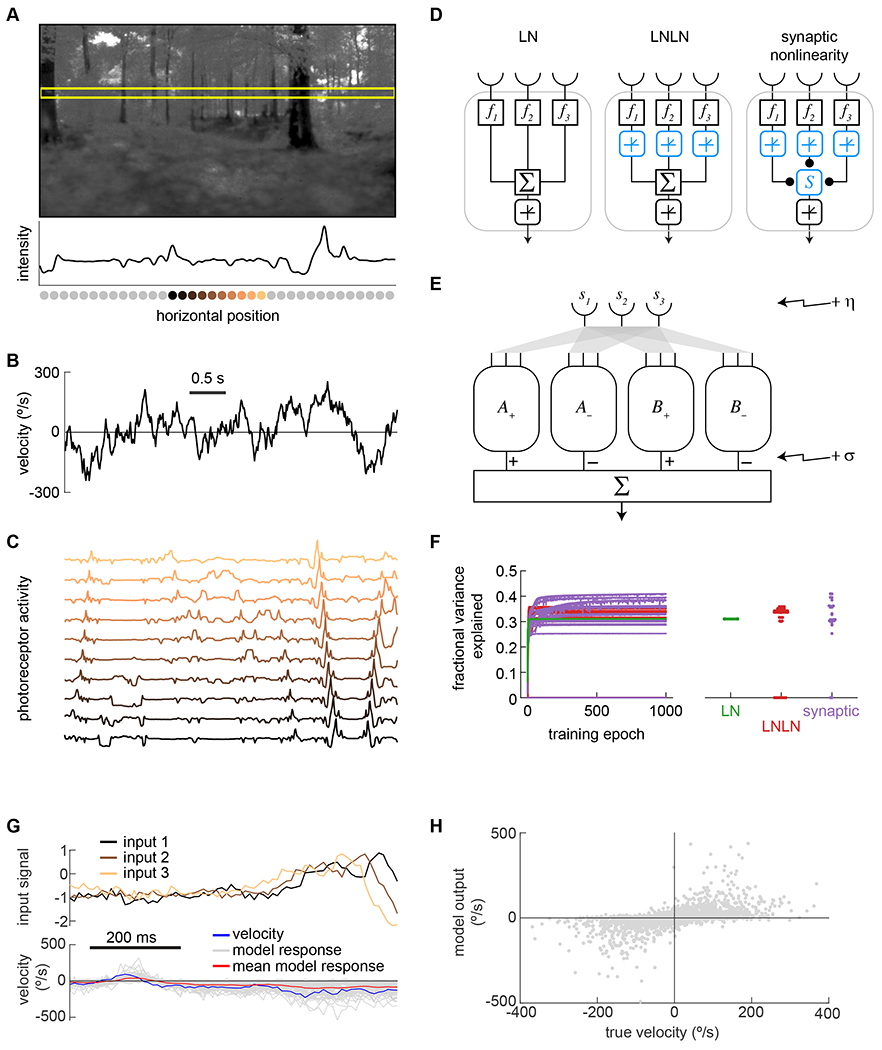
A) Panoramic natural scene from database ³⁹ Horizontal yellow box shows a 1-dimensional cut through the scene. The luminance trace of that cut is shown below the image, with the positions of simulated photoreceptors below the x-axis.

B) Dynamic velocities traces were drawn from a Gaussian distribution with a correlation time of 200 ms (see Methods).

C) Scenes were translated at the assigned velocities in order to generate a trace of inputs that mirrored the ommatidial inputs of a fly (see Methods). Each trace represents the activity of a photoreceptor located at the position of the photoreceptor in (A) with matching color.

D) Three different shallow network unit types were tested: a linear-nonlinear unit (LN), an LNLN unit, and a unit combining inputs using a biophysical nonlinearity (see Methods).

E) In the models, two units were each paired with a mirror symmetric version of themselves (A₊ with A₋, B₊ with B₋), and signals from the units were subtracted. A and B units had the same architecture but were trained with independent weights. The model output was the sum of these differences. Noise was added at the front-end of the model (η) and at the back end σ, see Methods).

F) Models containing the three different unit types were trained to predict the scene velocity from ommatidial signal traces. The training converged (left) and the fully-trained models predicted 30-40% of the variance in the velocity (right). These traces show results for training with η = σ = 1/8.

G) Example traces of inputs and outputs of an LN model trained as in (F), as compared to the true input velocity (blue). Different model outputs (gray) are for different spatial locations in images, with the same velocity trace. The mean value of the model responses is plotted in red.

H) Scatter plot of individual instantaneous model outputs against the true velocity.

To simulate naturalistic inputs to fly motion detectors, we rigidly translated panoramic natural scenes ³⁹ using stochastic yaw rotational velocities (Figure 2A). The rigid translation of panoramic scenes ignores the occlusions and the different angular velocities that arise from an animal translating through the world, but it mimics scenes generated by an animal purely rotating in the world. Flies use motion detection circuitry to stabilize their orientation in the face of angular perturbations ^{40, 41}, and rigid translation of natural scenes has been useful in other studies of motion detection ^{38, 42–47}.

The stochastic velocities for scene motion were drawn from a zero-mean Gaussian distribution with standard deviation of 100°/s and a correlation half-life of 200 ms (Figure 2B, see Methods). These turning rates are typical of walking flies ^{48, 49}. For this study, it is critical that stimuli do not have a constant velocity over time, since that would allow stimuli far in the past to inform current velocity estimates ³⁵. The correlation time of 200 ms matches timescales for turns during walking ^{48, 49}, and ensures that recent information is most useful to infer the current visual velocity.

We approximated the optical filtering of scenes by the fly ommatidia. To do this, we generated discrete signals with separation of 5°, each spatially filtered with a two-dimensional Gaussian that roughly matched the acceptance angles of ommatidial optics ⁵⁰. For each random velocity trace, this created sets of 72 ommatidial signals from 360° horizontal strips across scenes (Figure 2C). Such signals were obtained from random elevation and azimuthal positions on randomly chosen panoramic images. The task for the ANN (and for the fly eye) is to infer the velocity or direction of motion (latent variables) from this suite of ommatidial luminance signals.

Shallow neural networks for motion detection

We defined three basic types of units for motion detection that incorporated varying degrees of biophysical detail (Figure 2D). All unit types received inputs over time from three neighboring ommatidia, matching the three spatial inputs to T4 and T5 ¹⁰. The units linearly filter these inputs in time with three distinct kernels that are learned through training. The three unit types are distinguished by the nonlinearity that combines the three spatially-offset inputs (see Methods).

The first unit type employs a linear-nonlinear (LN) processing step, so that the temporally filtered signals are summed and then acted upon by a threshold-linear rectifier (Figure 2D, left). A nonlinearity is required to generate direction-selective signals ^{33, 36}. This unit type is related to the motion energy model and is similar to models describing motion detection in mouse retina ^{51, 52}, mammalian cortex ^53–56, and the fly motion detecting neurons ^{16, 17}. We call this the linear-nonlinear (LN) unit.

The second unit type employs an additional threshold-linear rectifier after each ommatidial signal is filtered in time, but before the three signals are summed and thresholded again (Figure 2D, middle). This rectification of the signals from each spatial location mimics rectification observed in the calcium and voltage signals of medulla interneurons upstream of motion detectors ^{15, 57, 58}. Because this model employs two sequential stages of linear-nonlinear processing, we call this the LNLN unit.

The third unit type also rectifies the filtered ommatidial signals, but uses a synaptic nonlinearity to combine the three filtered, rectified signals (Figure 2D, right). This synaptic nonlinearity considers each of the three inputs to be synaptic conductances with associated reversal potentials, which are learned though training. The nonlinearity is the sum of weighted conductances divided by the sum of unweighted conductances (see Methods). This is similar to other biophysically realistic models for T4 and T5 direction-selectivity ^{19, 21, 29, 59, 60}. Such conductance models can explain properties of wide-field motion detectors in the fly ⁶¹. The nonlinearity here assumes a pseudo-steady-state response, consistent with T4 measurements ¹⁹. We call this the synaptic nonlinearity unit.

These three unit classes are nested. That is, the LN unit is a special case of the LNLN unit, and the LNLN unit is a special case of the synaptic nonlinearity unit. Thus, progressing from LN to LNLN to synaptic nonlinearity adds more parameters. In principle, the more complex units can only perform better, since each could still obtain the solution of the simpler units.

These three unit types were each placed into models with architecture that matched the circuitry in the fly eye (Figure 2E). The three model classes consisted of multiple units of the same type, and the weights in each unit were optimized through training on the naturalistic dataset we defined. In this architecture, each (+) unit was paired with a (−) unit constrained to be mirror symmetric in space, and the two resulting signals were subtracted. This differencing reflects the subtraction of oppositely tuned motion signals that occurs in the fly eye downstream of T4 and T5 ^{62, 63}. Two pairs of symmetric units were trained (A₊/A₋ and B₊/B/₋ unless otherwise noted. In all three model classes, the temporal filters were free parameters, as were weights and biases before rectifications.

We scaled the training images so that each set of 72 ommatidial signals had zero mean and unit variance. This roughly matches the contrast computation and normalization that occurs upstream of motion detection in flies ^{26, 64, 65,66, 67}.

Last, we added two sources of noise to the models (Figure 2E, see Methods). First, we imposed additive noise at the input signals, after contrast computation. This front-end noise reflects noise measured in photoreceptors and lamina cells ^{68, 69}. Second, we included multiplicative noise at the output of each unit in the model before signals were subtracted to generate the overall signal. This back-end noise represents intrinsic noise in the circuit ⁷⁰, which could arise from variability in T4 and T5 signals ^{19, 21}. We varied both the front-end and back-end noise to investigate how noise affects the solutions found by optimizing these models.

Training models

We used TensorFlow ⁷¹ to train these three model classes using gradient descent from different random initializations (Figure 2F, see Methods). The models were trained to use the preceding 300 ms of visual data to predict the instantaneous scene velocity. During training, the models were optimized by adjusting the temporal filter weights, biases applied with each nonlinearity, and additional weighting parameters in the LNLN and synaptic nonlinearity model. The different models all converged on solutions, but the LNLN and synaptic nonlinearity models converged more slowly and the solutions varied more in their performance (Figure 2F). We evaluated model performance on a hold-out dataset, which was independent of the training data. Model output depended on the scene, but gave reasonable velocity estimates over many scenes (Figure 2G, H).

Trained models possess features of fly motion detectors

When we trained the three model classes to predict image velocity in the presence of noise, the trained models showed many of the non-canonical properties of the fly’s motion detectors (Figure 3). Most importantly, the paired units in all three models could be classified as ‘T4-like’ or ‘T5-like’, based on whether they responded most to light or dark flashes. We evaluated the properties of trained models in a noise-free regime, corresponding to a bright visual stimulus and responses averaged over many trials (see Methods).

Figure 3. Models trained to predict naturalistic velocities possess many properties of the biological circuit.

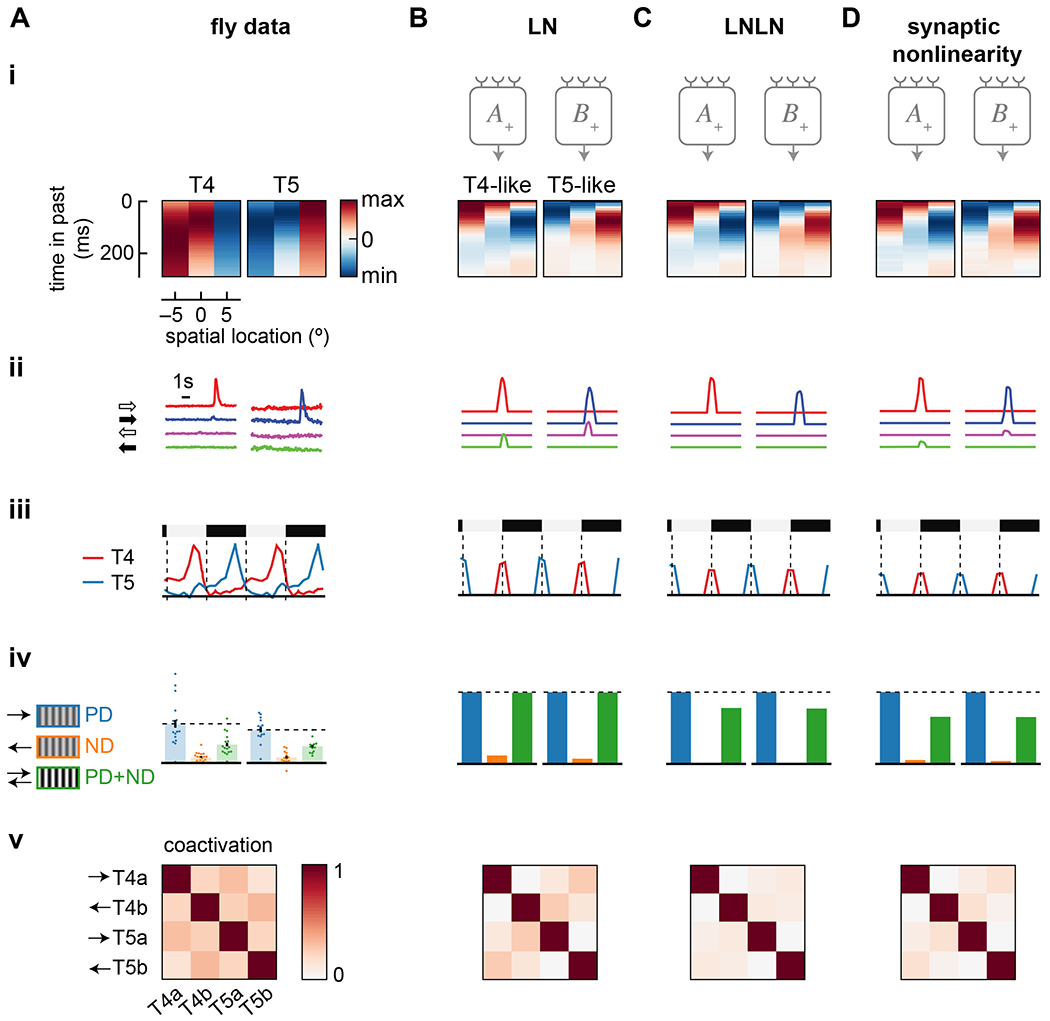
Data shown includes: (i) Spatiotemporal receptive fields composed of time traces of the filters of the 3 spatially separated inputs to T4 and T5 or to T4- and T5-like units. Each input filter is normalized. (ii) Responses to light and dark edges moving left and right. (iii) Responses to stationary square waves. For model responses, the full vertical extent of the dashed lines is the amplitude of responses to the preferred moving edge in (ii). (iv) Relative responses to preferred and null direction sinusoids, and their sum. (v) Coactivation of units in response to naturalistic stimuli.

A) Data from the fly, as in Figure 1.

B) As in (A), but for a trained LN model.

C) As in (A), but for a trained LNLN model.

D) As in (A), but for a trained synaptic nonlinearity model. All three models were trained with noise values of η = σ = 1.

See also Figure S1.

All three trained models had units with similar temporal filters, with relative dynamics and polarities similar to those in cells upstream of T4 and T5 (Figure 3(i)). The ANN filters are faster than measured ones, which include filtering by optical indicators ⁷². However, like T4 and T5 cells (Figure 1B), all trained units had high-pass filters on the center input, and slower, lowpass filters on the flanking inputs. The central inputs in the T4-like and T5-like units were sensitive to positive and negative derivatives, respectively, just as in T4 and T5 cells. Both T4- and T5-like units had a positively-signed filter on one side and a negatively-signed filter on the other, in the pattern of T4 and T5 cells.

In all trained units, the temporal filter f₃ (rightmost filter in Figure 3(i)) in the T4- and T5-like units had a small initial response of the opposite sign to its delayed response. This feature was not observed in the cells proposed to correspond to input 3 (Figure 1A) ^{24, 37} or in voltage responses in T4 or T5 ^{19, 21}. In the learned f₃ filters, the prolonged, second lobe had a larger integral than the initial lobe by factors of 10 to 15. Thus, the second lobe tended to dominate the initial lobe.

The pattern of temporal filtering in the trained units led to strong direction- and edge polarity-selectivity (Figure 3(ii)). Each unit responded much more strongly to a single direction and a single edge type (ON-edges vs. OFF-edges) than to any other combination. The ON- vs. OFF-edge selectivity of each unit corresponded to the sign of the central derivative filter, just as in the fly’s circuitry. The direction-selectivity corresponded to the signs and shapes of the two flanking filters. The LNLN model was more selective than the LN model, responding exclusively to one edge type, while the synaptic nonlinearity showed intermediate selectivity. Critically, all three models generated ON- and OFF-edge direction-selective units, even though no such constraint was imposed on them.

Several other features of the fly motion circuits were also reproduced. All three models showed stationary edge responses that matched empirical response patterns in T4 and T5 (Figure 3(iii)). Moreover, the units in the LNLN and synaptic nonlinearity models showed opponent suppression as observed in T4 and T5 (Figure 3(iv)). (The LN units are mathematically incapable of generating this opponent suppression ²⁹.) In trained models, units were not very coactive when presented with natural scenes, with coactivation decreasing from LN to LNLN to synaptic nonlinearity models (Figure 3(v)). Last, all three trained models, but especially the LNLN and synaptic nonlinearity models, responded to signal strength and different sinusoidal temporal frequencies with tuning comparable to neurons and behaviors downstream of T4 and T5 ^{9, 73–75} (Figure S1).

When trained to predict natural scene velocities, these models adopt many properties of T4 and T5 circuits that are not explained by classical models of motion detection. Thus, this training regime is sufficient to account for many properties of neurons found in this circuit. Optimized solutions depend not only on the loss function, but also on constraints on the network. To understand how constraints affected model solutions, we next investigated how model architecture, loss functions, training data, and noise all affect the trained solutions. Since the LN model is readily interpretable and reproduces many circuit properties, we focus on that model for the remainder of this study, except to probe opponent suppression.

ANN solutions do not depend strongly on the loss function or training data

First, we asked how optimized solutions depend on the loss function. We had initially trained models to estimate the true image velocity (Figure 3). This objective for model motion detectors has been used previously with some success ^{38, 44}, but fly motion detectors might instead have evolved predict some other function of the true velocity. To investigate how a different loss function affects solutions, we trained the LN model to predict only the direction of motion (Figure 4AB, see Methods). In this case, the units in the trained models looked largely identical to the initial training, becoming direction and edge polarity selective, sensitive to stationary edges, and showing little coactivity between units.

Figure 4. Effects of model loss function, training, architecture, and noise.

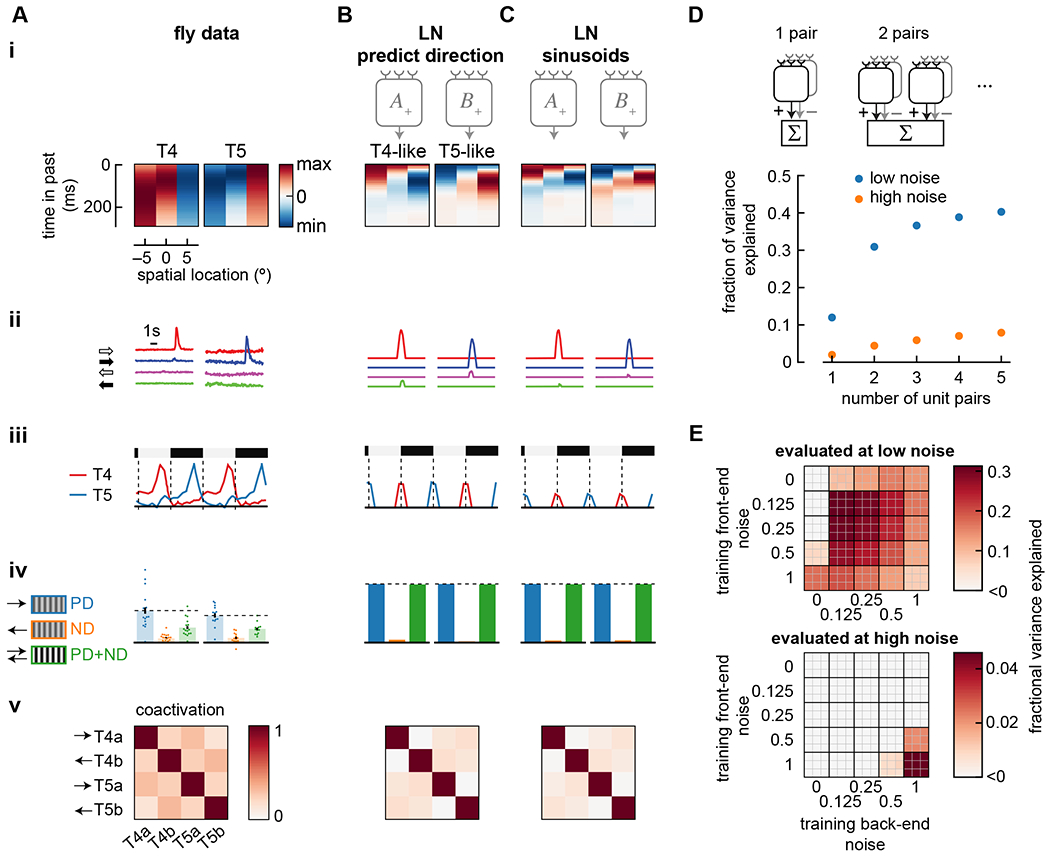
A) Summary of properties measured in T4 and T5 (from Figure 1). Data shows false color time traces of 3 spatially separated input filters (i), responses to light and dark edges moving left and right (ii), responses to stationary square waves (iii), responses to preferred and null direction sinusoids, and their sum (iv), and coactivation of units in response to naturalistic stimuli (v).

B) As in (A), but showing the results of an LN model with an alternate loss function, in which it was trained to predict direction of motion rather than predict velocity of motion. Compare with Figure 3B. Model was trained with noise of η = σ = 1.

C) As in (A), but showing the results of an LN model trained on sinusoidal gratings instead of natural scenes. Compare with Figure 3B. Model was trained with noise of η = σ = 1.

D) The number of mirror-symmetric, subtracted unit pairs was swept from one to five (top), while measuring the fraction of variance explained for LN models trained and evaluated in high and low noise conditions. All unit pairs received inputs from the same 3 spatial locations. Throughout the rest of this study, two pairs were used.

E) Fraction of variance explained by models trained at a variety of front- and back-end noise levels, then tested at low noise (top) and high noise (bottom). The top 9 models are shown as a 3x3 grid at the coordinate of a specific parameter set. Low noise evaluation used parameters η = σ = 0.125; high noise evaluation used parameters η = σ = 1.

See also Figures S2 and S3.

We wondered whether the mirror symmetry imposed on unit pairs in the model would arise naturally through training. We therefore trained a set of four units without the mirror symmetry pairing, using 12 independent temporal filters, 3 for each unit. After training, the best performing solutions always included two, subtracted mirror-symmetric unit pairs (Figure S2). This finding likely reflects the mirror symmetry imposed in our training dataset, which match the natural world’s visual mirror symmetries.

Next, we asked whether the division into ON- and OFF-edge detector units (Figure 3) depended on asymmetries in light and dark in natural scenes. These natural scene asymmetries have been hypothesized to account for a variety of asymmetries in fly behavior ^{38, 43, 76} and differences between T4 and T5 ⁴⁴. To investigate this dependence, we trained the models with the same velocity distribution, but instead of photographs as the visual input we used sinusoidal gratings, which are light-dark symmetric. Interestingly, the two unit pairs in each model still became sensitive to ON- and OFF-edges (Figure 4C). To test whether this split into ON- and OFF-edge selective channels depended on the precise nonlinearity we used, we changed the nonlinearity from threshold-linear to a saturating, sigmoid function. This had little effect on the optimized solution (Figure S2). Thus, when estimating motion in scenes that contains both positive and negative contrasts and when there are two unit pairs available to optimize, models naturally segregate into ON- and OFF-edge selective units.

Largest marginal performance improvement comes from adding the second detector pair

We wanted to better understand why flies have two primary motion detector types (i.e., T4 and T5 neurons), rather than 1 or 3. We therefore created and trained LN models with different numbers of unit pairs, ranging from 1 to 5 (Figure 4D). Increasing the number of unit pairs increased model performance under low- and high-noise training conditions, but the largest improvement in performance came from increasing from 1 to 2 unit pairs with low-noise training. If the cost of adding additional units in biological systems is high, this result may explain why flies have only two elementary motion detector types.

Training with high noise is more robust to changes in noise

We next asked how noise during training affected the structure of solutions. To investigate this, we trained LN models under a range of front-end noise and back-end noise conditions. Then we evaluated how well models performed under conditions that were different from their training noise level. The best-performing models in a particular noise regime were the ones trained under that same noise regime (Figure 4E). However, when models trained in high noise regimes were tested in low noise, they still performed reasonably well, while models trained in low noise regimes performed very poorly in high noise. The high-noise trained model performed evenly over many noise regimes (Figure S2D).

Overall, the high-noise trained models performed worse because the injected noise made their task much more difficult (Figure S3). Importantly, the high-noise trained units were far more direction-selective to sinusoids than low-noise trained units (Figure S3E), better matching the strong direction-selectivity to sinusoids of T4 and T5 cells ^{7, 9, 16, 17}. We therefore investigated the properties of the high- and low-noise trained solutions.

Training noise strongly affects direction-selectivity and edge-polarity-selectivity

The noise amplitude at both the front- and back-end substantially changed the learned solutions (Figure 5). First, the front-end noise amplitude dramatically changed the temporal extent of the learned filters (Figure 5(i)). When more noise was added, the filters were extended, presumably to average signals over time. The correlation time scale in the velocity limits the usefulness of averaging more than ~200 ms in the past ³⁵. With less front-end noise, less averaging was required, and using only the most recent measurements of intensity produced the best estimate of the current velocity.

Figure 5. High training noise yields slower filter dynamics and stronger selectivity to moving edges.

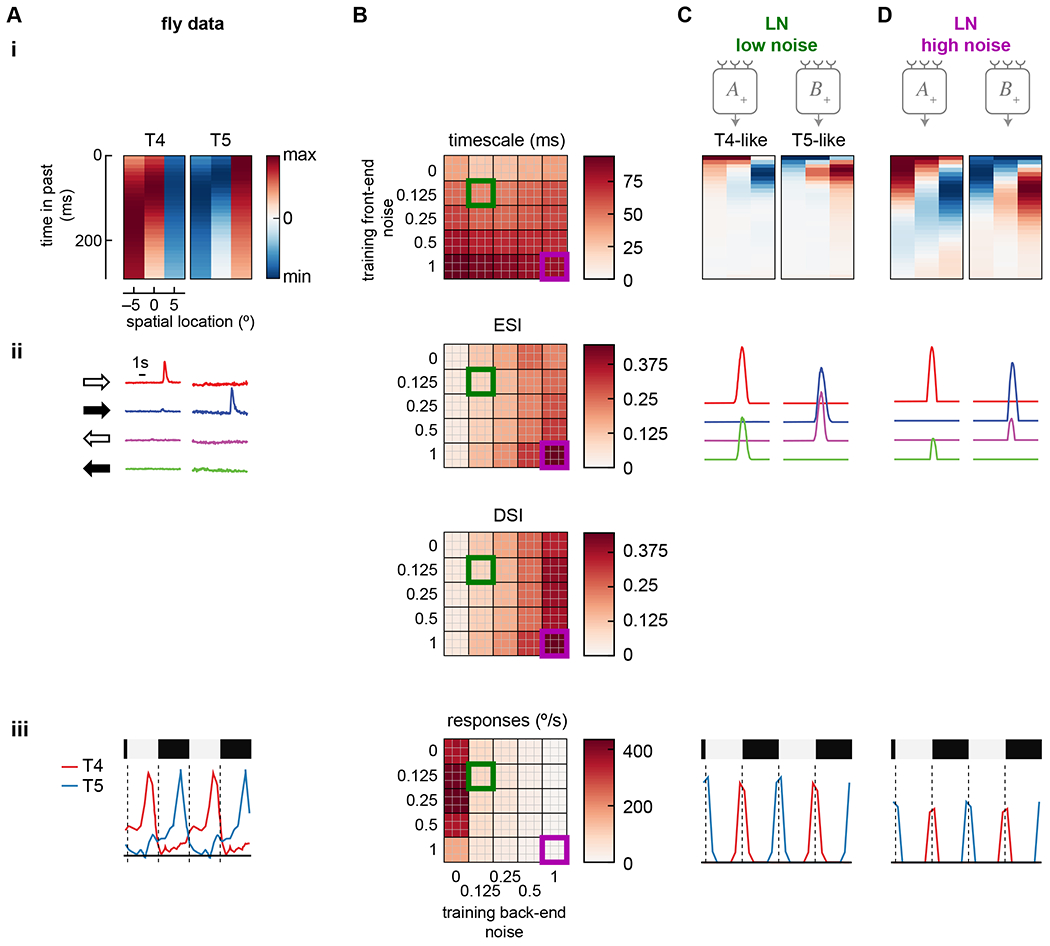
A) Summary of properties measured in T4 and T5 (from Figure 1). Data shows false color time traces of 3 spatially separated input filters (i), responses to light and dark edges moving left and right (ii), and responses to stationary square waves (iii).

B) Summary responses of models trained with different levels of front-end and back-end noise. Top 9 performing models of 50 trained are shown for each condition, measuring the center-of-mass of the filters (i), the ESI and DSI of the light and dark moving edge responses of each unit (ii, top and bottom), and the responses to stationary square waves of the units (iii).

C) Example traces of a low-noise trained model (green square in (B)). Shown are filters for each unit (i), traces of responses to left and right moving light and dark edges (ii), and responses to stationary square wave stimuli (iii).

D) As in (C) but with the high-noise trained model (purple square in (B)).

Second, the back-end noise strongly influenced the degree of edge polarity- and direction-selectivity in the individual LN units (Figure 5(ii)). In the high noise case, the T4- and T5-like units were more edge- and direction-selective. In the low noise case, both units responded strongly to light edges in one direction and dark edges in the other, with a slight imbalance that was direction-selective; this pattern is unlike T4 and T5 responses. This pattern reflects that the units responded strongly to spatial gradients and only mildly to direction. With low back-end noise, large unit responses could be subtracted, leaving only the small difference as an estimate of motion. When back-end noise was added, this computational strategy was no longer viable, since the subtraction of unit responses could no longer reliably negate the non-directional components of the responses. As a result, the individual units converged on solutions that were robust to noise by being more direction-selective even before subtraction.

Last, adding back-end noise to the system made the units less selective for stationary edges (Figure 5(iii)). The spatial pattern of responses to stationary edges matched those in T4 and T5, but when more back-end noise was added, the units responded less strongly. The back-end noise prevents precise cancellation of the signals from stationary scenes, making it advantageous for the model to respond less to such stimuli.

Increased noise increases opponency and sparsity

To evaluate the effects of noise on opponency and sparsity, we performed the same sweep of front- and back-end noise (Figure 6(i)). We first measured unit opponent suppression as the degree to which the mean response decreased when a null-direction sinusoid was added to a preferred-direction sinusoid. In the case of LN models, the response to the sum can never be less than the response to the preferred-direction sinusoid alone ²⁹. But as training noise increased, the response to the sum became closer to the response to the preferred direction sinusoid alone (Figure 6CD(i)).

Figure 6. High training noise yields strong opponency and channel decorrelation.

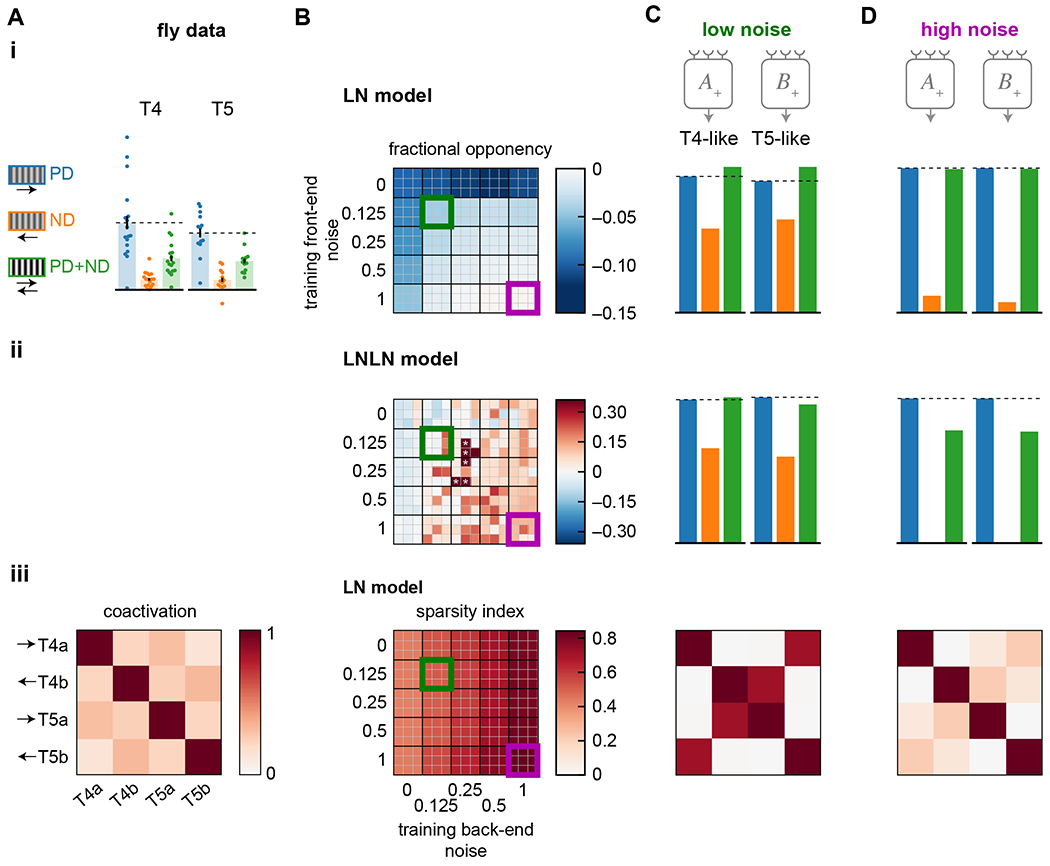
A) Summary of properties measured in T4 and T5 (from Figure 1). Data shows responses to preferred and null direction sinusoids (PD, ND) and their sum (PD+ND) (i), and coactivation of units in response to naturalistic stimuli (iii).

B) Summary responses of models trained with different levels of front-end and back-end noise. The top 9 performing models of 50 trained are shown for each condition. Data shown is the opponency of LN models (i) and LNLN models (ii), where asterisks denote models with opponency near 1, out of the false color range. The sparsity index is shown for the LN model units in response to naturalistic stimuli (iii). The sparsity index is 1 when the coactivation matrix is the identity matrix and is 0 when all elements in the matrix are 1.

C) Example responses from a low-noise training protocol (green box in (B)). Opponency is shown for the LN model (i) and LNLN model (ii), while a coactivation matrix is shown for an LN model responding to naturalistic stimuli (iii).

D) As in (C) but for a high-noise training protocol (purple box in (B)).

When we trained the LNLN model with different noise levels, opponent suppression increased with increasing noise (Figure 6(ii)). Opponent suppression in T4 and T5 cells in Drosophila has been hypothesized to cancel out ‘common mode’ correlations, leaving a larger dynamic range for motion signals ²⁹. When noise is added during training, it makes the unit signals more direction-selective, and the opponent suppression could reflect that additional direction-selectivity.

Last, we examined how training noise affected the decorrelation of the signals among units in an LN model (Fig 6(iii)). As back-end noise was increased during training, optimized LN units became less coactivated by the naturalistic stimuli. This seems linked to the increased direction- and edge-selectivity of the units under larger back-end noise (Figure 5(ii)): only one unit at a time would be active because only one edge type at a time moves through the model receptive field.

Discussion

This study demonstrates the potential for fine-grained, neuron-level mapping between task optimized ANNs and real neural circuits. Results show that an optimized model for visual motion detection accounts for measured neural properties in the Drosophila motion detection circuits that are not predicted by textbook models for motion detection ^{32, 33}. Anatomical constraints from the real circuit were key to developing correspondence between ANN and BNN. Robustness to noise was critical to generating artificial networks that matched the measured properties.

Importantly, our results were not built into the fitting routine or model architecture. One can imagine other solutions that might have performed well in the training. For instance, splitting the A₊/A₋ and B₊/B₋ unit pairs into fast and slow motion channels instead of ON- and OFF-edge channels would cover a wider range of input velocities. Alternatively, the ON- and OFF-edge segregation need not be complete, as in the low-noise optimizations, where units were not strongly edge- or directi on-selective (Figure 5). Last, the two flanking filters do not need to have opposite signs and be delayed with respect to the center filter: if all three filters had single lobes with the same sign and have delays of τ, 2τ, and 3τ, they could sum above threshold only for motion in one direction. However, these counterfactual solutions did not occur in the optimized models. This leads us to interpret these features in fly motion detectors as having evolved to optimize performance in motion detection, and suggests that we have identified crucial constraints on the circuit.

Loss functions and optimization

In this study, we used loss functions that minimized error in predicting the velocity or direction of a moving natural scene. How realistic are these tasks? Motion detectors in flies generate graded responses that depend on direction and speed ³⁶, so these tasks are reasonable starting points. But future studies could incorporate more realistic tasks, such as training a motion detector to act as the input for an agent-based model that attempts to stabilize its course or approach objects. Such a task would require incorporating knowledge of locomotor control ⁷⁷. More simply, one could also incorporate known downstream circuitry, such as the shunting mechanisms that perform gain control in spatial integration of T4 and T5 units ^{61, 78}. Such studies could generate new hypotheses about the evolutionary origin of motion detection. Here, the simplest loss functions were sufficient to generate many of the features in the fly’s circuits.

Our study used gradient descent to optimize the models. We examined the best performing models from a suite of initializations, since models could become trapped in local optima. How might optimization occur in the fly’s visual circuit? It seems likely that optomotor circuit structure and function is genetically determined to a large degree, and optimized over generations of natural selection. Gradient descent can become stuck in local optima with shallow and minimally-parameterized networks like ours ⁷⁹. Optimization algorithms similar to natural selection can optimize models efficiently and avoid local optima ⁸⁰. Our results show that one may think productively about these visual circuits as solutions to an optimization problem, solved by evolution.

Influence of noise

The model features that matched biology did not arise from the task and network structure alone, but depended critically on noise in the system. The back-end noise made units more direction-selective by penalizing large, correlated responses from opposing units. Thus, the noise had an effect similar to adding an explicit sparsity constraint. Sparsity is commonly observed in neural systems ⁸¹, and non-coactivity of parallel motion detectors has previously been hypothesized to organize their response properties ²⁸. Here, we can see one advantage of the sparse solution: the non-coactivation of the units makes the system more robust to multiplicative noise. Interestingly, the common technique of dropout training, in which only stochastic subsets of weights are updated during each learning iteration, is equivalent to injecting certain types of training noise ⁸². This means that many ANNs trained using dropout techniques are already implicitly trained to be robust to noise. By adding noise explicitly, we control this constraint and can more easily relate it to biological sources.

Sources of noise

Given the influence of noise on the model solutions (Figs. 4, 5, 6), it is important to ask how the injected noise relates to noise in the fly’s visual circuits. Front-end noise could be attributed to fluctuations in photoreceptor signals or signals in downstream cells. Photoreceptor signal-to-noise ratio (SNR) depends strongly on the absolute light intensity, as well as on temperature ^{69, 83}. In bright light, the SNR of photoreceptors in flies can be ~10, while in dim light, the signal-to-noise ratio can decrease to ~0.1 (ratio of powers).

Less is known about noise deeper in the visual system. Studies in locust suggest that SNR can decrease in neurons further from the periphery ⁸⁴. Electrical recordings of T4 and T5 responses to strong stimuli show relatively little trial to trial variability (SNR of ~10, mean/std) but higher variability between cells (SNR of ~2, mean/std) ^{19, 21}. The larger variance between cells could reflect long timescale gain fluctuations. Noise within a cell could also be amplified by expansive nonlinearities that transform voltage into synaptic release. Synaptic transmission might also decrease SNR, since it’s metabolically expensive to transmit high SNR signals ⁸⁵. With careful measurements of the noise characteristics of T4 and T5, one could add more accurate, spectrally-matched noise to training procedures.

Although we trained models with noise at specific levels, the biological circuit is likely exposed to varying levels of noise, dependent on stimulus and internal state. Since models trained under high-noise are more generalized (Figure 4E, Supp. Figure S2), training in high-noise may be most similar to optimization under a range of different noise levels.

Structure of delays in 3-input motion detectors

The optimized models showed a fast central input and delayed flanking inputs with opposite signs (Figure 3). This configuration appears in the fly motion detectors (Figure 1A) and has also been suggested to explain cortical direction-selective signals ⁸⁶. This functional organization emerged with all three unit types and both loss functions (Figure 4). It has a clear orientation in space-time, suggestive of motion energy-like processing ^{16, 17}. This opposite-delayed-flanks weighting structure also appears in a completely different optimization task, in which a network is trained to preserve similarity under translation of images ⁸⁷. Thus, this spatiotemporal weighting structure in motion detection appears to solve several different optimization problems. This could also serve the fly’s visual system well, since neurons downstream to T4 and T5 are specialized to detect visual flow ^{6, 63}, looming stimuli ⁸⁸, and likely other visual features.

ON- and OFF-edge detectors and natural scenes

In this study, ON- and OFF-edge selective detectors emerged naturally as solutions to the task of detecting motion. This did not depend strongly on the loss function, training data, or form of the nonlinearity (Figure 4, S2). Units must remain near the nonlinear threshold in order to generate direction-selective signals, and there is a benefit to tuning units to ON- and OFF-edges over alternative configurations. If a system did not contain both ON- and OFF-edge selective units, it would suffer by not responding to roughly half of all inputs. This logic could explain parallels in motion computation among species^{89, 90}, including the split into ON- and OFF-edge motion detectors in flies and in mouse retina ^{91, 92} and evidence for edge polarity-selective motion detection in primate cortex ^{30, 76, 93–96}. Flies, zebrafish, and humans all treat light and dark signals asymmetrically, potentially improving performance in naturalistic motion computation ^{38, 43, 44, 76, 94, 97}. This suggests additional benefits to pathway splitting not explored here. Another powerful explanation for sensory splitting into ON and OFF pathways is based on preserving stimulus information under metabolic constraints ^{98, 99}, but that logic does not seem to map onto the optimization task here, in which the model infers a latent variable and there is no obvious analogue to a metabolic constraint.

Stationary edge responses

Prior experiments have measured T4 and T5 responses to flashes ^{17, 19, 21, 23, 25, 28} or stationary sinusoids ¹⁰⁰, which are consistent with classical models ³³. Our results shed light on T4 and T5 responses to stationary edges of specific polarities (Figure 1D) ³⁰. Our results (Figure 5(ii,iii)) suggest that models best predict motion when units respond to stationary edges and have partner units to cancel this signal. This approach is limited by system noise, which results in reduced responses to stationary edges. The biological responses to stationary edges may reflect the emphasis on spatial gradients in the low-noise solutions.

Circuit features neglected in these models

Our models neglected many known features of the circuit, which could have important effects on the learned solutions. We summarize here some important simplifications made in this study. (1) We represented the processing upstream of medulla interneurons as simple spatiotemporal filtering, when in fact complex, nonlinear processing takes place upstream of medulla interneurons ^{69, 101–103}. (2) Interneurons upstream of T4 and T5 have different receptive field shapes, including center-surround organization ^{14, 24, 58, 102}, which could influence response properties in trained models. (3) In our training data, we assumed perfect contrast normalization, when in fact there are dynamics and spatial scales for normalization ^{66, 67}. (4) Our units have only one neuron at each of three spatially separated inputs, but there are multiple input neurons at some positions ^{10, 11, 13} and they may interact nonlinearly ¹⁸. (5) Our models are feedforward, but the true circuits have lateral interactions and feedback ^{10, 11, 13}. (6) Early temporal and spatial processing integrates signals differently under different noise regimes ^{64, 65, 104}, while our model did not include adaptation. These features are likely to impact the performance of the biological circuit. However, the simplifications in this study were sufficient to generate trained models with features of the biological circuit.

Performance optimization

This work adds to a suite of models that show how constraints and optimization contribute to sensory processing. Some of these models have been fit directly to predict data ^{105, 106}, while ours and others ^{1, 2, 107} have been optimized to perform specific tasks. Our work is closest to two prior approaches. In fitting retinal responses to a convolutional neural network, other studies have found that the best-fitting models have units that respond similarly to the progression of cell types in the retina ^{105, 106}. These studies included temporal processing, as ours did, but had weaker anatomical constraints, using 3 layers of units, without specifying a priori how units in each layer were connected. The artificial networks were fit to recorded retinal outputs, so features of the artificial network can reflect circuit components but do not provide information about the tasks performed by the biological circuit.

A different approach used detailed connectomic data to investigate the fly motion circuits by training a network to detect the position of an object in a movie ¹⁰⁷. That study employed more detailed connectivity, encompassing more than 40 neuron types arrayed over a large swath of visual space, and used a separate network to interpret the outputs of the fly eye. It obtained direction-selective signals in model T4 and T5 neurons when using measured synaptic connectivity with manually imposed signs and delays. In the present study, we focused on a small number of inputs to T4 and T5 and fit both temporal processing and synaptic weighting. This allowed us to interpret how processing properties in a shallow, feedforward ANN compared to those measured in neurons in the biological circuit.

There are many properties one could measure in a circuit, and comparisons with task-optimized models allow one to evaluate how such properties relate to a specific task or constraint. This study argues that when strong anatomical constraints are included in performance optimized models, there can be a close correspondence between the model units and the analogous individual neurons.

STAR Methods

RESOURCE AVAILABILITY

Lead Contact

Further information and requests for code or data should be directed to and will be fulfilled by the lead contact, Damon A. Clark (damon.clark@yale.edu).

Materials availability

This study did not generate new unique reagents.

Data and code availability

Python and Matlab code to train all models in this paper and generate all figures in this paper is available at http://www.github.com/ClarkLabCode/T4T5TrainingCode. Code is in Matlab (Mathworks, Natick, MA), Python, and several Python libraries ^{71, 108–110}. The natural image database used in this study has DOI https://doi.org/10.4119/unibi/2689637 and is available at https://pub.uni-bielefeld.de/rc/2689637/2693616.

METHOD DETAILS

Training data

We wanted to train neural networks to predict velocity traces v(t) from simulated visual input signals over space and time. To create velocity traces with the statistical properties similar to fly rotation, we first drew samples from a Gaussian distribution with mean of 0°/s and standard deviation of 100°/s. These samples were placed in a 1-dimensional vector with a sample rate of 100 Hz. To create autocorrelations in the trace, this vector was convolved with an exponential filter h(t) = K exp(−t/τ) where τ = 0.2/log 2 s and K was chosen so that the variance remained unchanged under filtering. This resulted in a velocity trace with an autocorrelation half-life of 200 ms and a standard deviation of 100 °/s (as in the original trace). This trace corresponds to an auto-regressive Gaussian process of order 1, which is a discrete time approximation of an Ornstein-Uhlenbeck process. These scales are comparable to those in walking flies ^{48, 49}. The final traces contained 101 elements each, corresponding to 1.01 seconds of simulated time.

After creating the velocity traces, we constructed corresponding matrices of simulated photoreceptor activation values. Conceptually, for each 101-element velocity trace, we needed a 3x101 element photoreceptor matrix that corresponds to the activations of the three inputs to our models. In order to efficiently generate and use these 3x101 element matrices, we generated 72x101 element matrices corresponding to a full 360 degrees of photoreceptor activities, spaced 5 degrees apart⁵⁰. These 72 photoreceptors observed natural scenes rotating at the speed specified by the 101-element velocity trace. These matrices can be used in convolution operations to quickly simulate the behavior of many model motion detectors.

To generate these 72x101 matrices, we took a dataset of natural scenes ³⁹ and selected 241 images of natural environments, excluding indoor and architectural scenes. These scenes were panoramic captures of 360x97.5 degrees sampled at around 2.6 pixels per degree. For each velocity trace, we selected a natural scene image at random. We convolved these images with a 5 degree FWHM gaussian filter, approximating the acceptance angle of fly photoreceptors ⁵⁰. We converted the velocity trace into a position trace by integrating over time. These positions were used as offsets when converting the images in the spatially filtered dataset from 927x251 pixels to 72x20x101 elements representing the activations of an array of 72x20 photoreceptors at 101 points in time. The 20 rows of photoreceptors were spaced every 5° in elevation. Each row of photoreceptors had an associated set of signal traces s_n,t where n represents the azimuthal location and t represents time. Each set of s_n,t was treated independently in further processing by duplicating the corresponding velocity traces such that the responses of all rows of photoreceptors could be used to predict the same velocity trace. For each velocity trace and photoreceptor matrix generated in this manner, we also created a paired trace with the entire spatial structure reversed (and negated velocities), in order to ensure that the dataset was balanced with respect to the direction of motion. Finally, the input images were mean subtracted and scaled so that the set of spatially filtered signals s_n,t had a mean of zero and a unit variance, computed over all signals in a row and over time. In total, we created 8664 velocity traces and corresponding 72x101 element photoreceptor matrices, divided into a 6346 trace training set and a 2318 trace test set.

To generate the sinusoidal training data (Figure 4), we substituted the natural scenes with sinusoidal gratings with wavelengths chosen from a uniform distribution ranging from 20° to 90°. All other processing steps were identical.

Model definitions

Our models consisted of multiple units whose outputs were summed to generate the model predictions. We defined (+) and (−) versions of each unit type, corresponding to mirror symmetric units that were added and subtracted to generate the final model outputs. To obtain the unit outputs, we filtered signals, s_t, in time by convolving them with filters, f_t, with 30 elements, corresponding to 300 ms in time. We define this convolution as ${(\mathit{f}\ast \mathit{s})}_t={\sum }_{\tau =0}^{29}{f}_{\tau }{s}_{t-\tau }$.

The mirror symmetric LN units were defined as:

$$\begin{gathered} u_{k+,t}=\varphi \left({\left({\mathit{f}}_{k,1}\ast {\mathit{s}}_1\right)}_t+{\left({\mathit{f}}_{k,2}\ast {\mathit{s}}_2\right)}_t+{\left({\mathit{f}}_{k,3}\ast {\mathit{s}}_3\right)}_t+b_k\right) \\ {u}_{k-,t}=\varphi \left({\left({\mathit{f}}_{k,1}\ast {\mathit{s}}_3\right)}_t+{\left({\mathit{f}}_{k,2}\ast {\mathit{s}}_2\right)}_t+{\left({\mathit{f}}_{k,3}\ast {\mathit{s}}_1\right)}_t+b_k\right) \end{gathered}$$

Where s_i are the input signals, and all parameters (f_k,i and b_k) are identical for both units in the pair, and the pairs are indexed by k. The activation function ϕ is everywhere a rectified linear unit (ReLU):

$$\varphi (x)=\{\begin{array}{c}x\text{if}x>0\\ 0\text{if}x\le 0\end{array}$$

The mirror symmetric LNLN units were defined as:

$$\begin{gathered} u_{k+,t}=\varphi \left(w_{k,1}\varphi \left({\left({\mathit{f}}_{k,1}\ast {\mathit{s}}_1\right)}_t+b_{k,1}\right)+w_{k,2}\varphi \left({\left({\mathit{f}}_{k,2}\ast {\mathit{s}}_2\right)}_t+b_{k,2}\right)+w_{k,3}\varphi \left({\left({\mathit{f}}_{k,3}\ast {\mathit{s}}_3\right)}_t+b_{k,3}\right)+b_{k,4}\right) \\ {u}_{k-,t}=\varphi \left(w_{k,1}\varphi \left({\left({\mathit{f}}_{k,1}\ast {\mathit{s}}_3\right)}_t+b_{k,1}\right)+w_{k,2}\varphi \left({\left({\mathit{f}}_{k,2}\ast {\mathit{s}}_2\right)}_t+b_{k,2}\right)+w_{k,3}\varphi \left({\left({\mathit{f}}_{k,3}\ast {\mathit{s}}_1\right)}_t+b_{k,3}\right)+b_{k,4}\right) \end{gathered}$$

As above, all the parameters are the same for both units in the pair. Each w_k,i is a scalar free parameter.

For the synaptic nonlinearity, we followed previous work to create a nonlinearity that treats input LN lines as conductances in the membrane of a postsynaptic cell, and then computes the steady state voltage, given weighting parameters that are equivalent to reversal potentials in a real cell ^{19, 29, 59, 111}. This approximates the membrane time constants as being much smaller than typical variations in inputs ¹⁹:

$$\begin{gathered} S_{k,t}({\mathit{s}}_1,{\mathit{s}}_2,{\mathit{s}}_3) \\ =\frac{w_{k,1}\varphi \left({\left({\mathit{f}}_{k,1}\ast {\mathit{s}}_1\right)}_t+b_{k,1}\right)+w_{k,2}\varphi \left({\left({\mathit{f}}_{k,2}\ast {\mathit{s}}_2\right)}_t+b_{k,2}\right)+w_{k,3}\varphi \left({\left({\mathit{f}}_{k,3}\ast {\mathit{s}}_3\right)}_t+b_{k,3}\right)}{1+\varphi \left({\left({\mathit{f}}_{k,1}\ast {\mathit{s}}_1\right)}_t+b_{k,1}\right)+\varphi \left({\left({\mathit{f}}_{k,2}\ast {\mathit{s}}_2\right)}_t+b_{k,2}\right)+\varphi \left({\left({\mathit{f}}_{k,3}\ast {\mathit{s}}_3\right)}_t+b_{k,3}\right)} \end{gathered}$$

We then defined our two units as:

$$\begin{gathered} u_{k+,t}=\varphi (S_{k,t}({\mathit{s}}_1,{\mathit{s}}_2,{\mathit{s}}_3)+b_{k,4}) \\ {u}_{k-,t}=\varphi (S_{k,t}({\mathit{s}}_3,{\mathit{s}}_2,{\mathit{s}}_1)+b_{k,4}) \end{gathered}$$

Where the second activation function could correspond to a calcium nonlinearity acting on the membrane voltage ^{17, 29, 59}.

Our model output is R_t, which weights the two pairs of units by the scalars a_k as follows:

$$R_t=a_1(u_{1+,t}-u_{1-,t})+a_2(u_{2+,t}-u_{2-,t})$$

This arrangement of units within models gave us three models: the LN model using two pairs of LN units, the LNLN model using two pairs of LNLN units, and the synaptic nonlinearity model using two pairs of synaptic nonlinearity units. When we examined additional units in Figure 4, we added the additional pairs with new weight parameters.

Noise in the models

We added noise to the models at two stages. First, we added front end noise by adding random samples from a zero-mean Gaussian distribution to each element in the matrices s_n,t. Since the standard deviation of these matrices was unity, the standard deviation of the added noise controlled the relative amplitude of signal and noise. Second, we multiplied the output of each model unit u_k±,t by random draws from a lognormal distribution for each point in time. The lognormal distribution was chosen such that its mean was 1, and its standard deviation determined the relative size of the output noise. The output noise was chosen to be multiplicative rather than additive so that the models could not escape the noise by producing very large unit outputs and then rescale them with the model weights after the addition of noise. The standard deviations for both these sources varied according to the experiment.

Training protocols

All models were trained in Python using TensorFlow ⁷¹. Due to the convolution operations employed by our neural network models, for each 72×101× [batch size] input to our model, the output was a set of 70×72×[batch size] velocities corresponding to a set of 72×[batch size] true velocities. We duplicated these true velocities to create tensors of 70×72×[batch size]. To train the models, we chose the loss function to be the mean squared error between the true input velocity and the individual model outputs, R_t (not averaged over space). In the case of models trained to predict the direction of motion (Figure 4B), we converted the velocity trace into a binary direction trace, and the loss function became the cross-entropy of the true direction with a sigmoid function acting on the model output, R_t. The primary analyzed models each had two unit types with three filters each (180 parameters). In the LN model, each of the two LN unit pairs had one additional bias term associated with the threshold nonlinearity. In the LNLN model, each of the LNLN units had four additional bias terms associated with the four threshold nonlinearities, and three additional weight parameters for the three rectified input arms. For the synaptic nonlinearity model, the additional parameters were the same as for the LNLN model.

To train our models, we used the Adam optimizer with an initial learning rate of 0.03 and learning rate decay such that the final learning rate was 0.0027. We trained for 1000 epochs with a batch size of 128. For each set of model hyperparameters (model type, direction prediction, input and output noise, etc.), we trained 50 instantiations of that model. Each instantiation had a different initial set of weights drawn from a “Glorot” distribution ¹¹². For analysis, we chose the 9 highest performing models for each set of hyperparameters as evaluated by the coefficient of determination in the training dataset. Multiple training runs from the same initialization tended to arrive at the same solution, suggesting that in our training regime, the stochasticity of initialization affects solutions more than stochasticity in training protocol.

Stimuli for comparison with biological data

To compare model responses to those measured in fly visual circuits, we created several visual stimuli to present to our models. First, to obtain the effective linear filters of the inputs to the synaptic model, we stimulated the model with independent, Gaussian noise to each input, with zero mean and unit variance, then extracted the kernels from the unit output, using standard methods ¹¹³.

To make comparisons with responses to edges (Figure 1C), we created light and dark edges expanding over time so that the image, m, over space and time, was:

$$m(x,t)=\pm 2\left(H(x\pm vt)-\frac{1}{2}\right)$$

where H(x) is the Heaviside step function and we used all combinations of ± to make light and dark edges moving in both directions.

The stimulus velocity v was 30°/s. These images were spatially filtered to create the input signals s_n,t.

To compare responses to different stationary edges (Figure 1D), we created a light and dark square wave with an image over space of:

$$m(x)=\text{sign}\left(\sin \left(\frac{2\pi x}{\lambda }\right)\right)$$

where the wavelength λ was chosen to be 80°. These images were spatially filtered to create the input signals s_n,t.

To compare responses to sinusoids moving the preferred and null directions and to their sum (Figure 1E), we created images as follows:

$$\begin{gathered} m_{PD}(x,t)=\frac{1}{2}\sin (kx-\omega t) \\ {m}_{ND}(x,t)=\frac{1}{2}\sin (kx+\omega t) \\ {m}_{PD+ND}(x,t)=\frac{1}{2}\sin (kx-\omega t)+\frac{1}{2}\sin (kx+\omega t) \end{gathered}$$

The spatial frequency was chosen to be k = 2π/60 deg⁻¹ and ω = 2π s⁻¹. In sweeps of spatial and temporal frequency (Supp. Figure 1), the spatial and temporal frequencies were chosen as labeled. When signal strength was swept, the sinusoid amplitude was changed as labeled. As with the other stimuli, these images were spatially filtered.

To compare the degree of coactivation (Figure 1F), we used the natural scenes test (holdout) dataset described above.

In all comparisons of the model with data, we set the noise values in the model to 0, regardless of training regime, unless otherwise noted. Setting the input noise to 0 is the equivalent of having a bright stimulus with high signal to noise, as is typical of experiments. Setting the output noise to 0 is the equivalent of averaging over many trials of the same stimulus (since the multiplicative noise has expected value of 1). Averaging over trials was typical in the comparison data (Figure 1).

Metrics

We summarized properties of models with several metrics (Figs. 5 and 6). Fraction of variance explained was evaluated using the coefficient of determination in the holdout (test) dataset; it could be negative if the model performed worse than uniformly predicting the average velocity in the dataset. We evaluated the timescale of the learned filters by calculating the center of mass (or expected value) of the absolute value of the filters.

We also evaluated the edge selectivity indices (ESIs) and the direction selectivity indices (DSIs) of the models by simulating the responses to the moving edges. We simulated a light edge and a dark edge moving in the positive and negative direction, each as a separate trace. Then, for each unit in the model, we calculated the maximum of the absolute value of the response. For each unit, we averaged the PD and ND max responses across the dark and light edges, and separately averaged the light and dark max responses across the PD and ND edges. Then, for each unit we compute the selectivity index; $ESI=\frac{R_{light}-R_{dark}}{R_{light}+R_{dark}}$, where R_light is the average of the max response to light edges in both preferred and null directions and R_dark is the average of the max response to dark edges in both preferred and null directions. Similarly, $DSI=\frac{R_{PD}-R_{ND}}{R_{PD}+R_{ND}}$ where R_PD is the average of the max response to light and dark edges in the preferred direction while R_ND is the average of the max response to light and dark edges in the null direction. Finally, we computed selectivity index for the model as a whole by taking the mean of the absolute values of the selectivity indices of the individual units.

To summarize the static edge activation as a scalar value for each model, we stimulated the model units with static edges of both polarities centered on the central receptor and found the steady state response. We report the model response as the average of all unit responses to both edges.

In order to measure opponent suppression, we generated a moving sinusoidal grating dataset with PD, ND, and PD+ND stimuli, as described above. We then calculated the space- and time-averaged responses of the individual units our models to these three stimuli. We defined an opponency index of these units as $OI=\frac{R_{PD}-R_{CP}}{R_{PD}+R_{CP}}$ where R_PD and R_CP are the time-averaged unit response to the preferred direction sinusoid grating and the response to the counterphase grating respectively. We then defined the model’s opponency index as the average of the opponency indices of its units.

Finally, we evaluated the sparsity of the coactivation of the model units in response to the test set, naturalistic stimuli, with no noise added. Coactivation between units m and n was defined as $C_{nm}=\frac{1}{T}{\sum }_{t=1}^T\frac{u_{n,t}}{\sqrt{\frac{1}{T}{\sum }_{t=1}^T{u}_{n,t^2}}}\frac{u_{m,t}}{\sqrt{\frac{1}{T}{\sum }_{t=1}^T{u}_{m,t^2}}}$ where u_n,t is the response trace of unit n at time t and u_m,t is defined similarly; T is the length of the trace in time. Averages were taken over the entire test dataset. We defined a sparsity index as the root mean square difference between the coactivation matrix of the model units and the identity matrix and then rescaled it so that a sparsity index of 1 corresponds to the identity matrix and a sparsity of 0 corresponds to all units being 100% coactive.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and algorithms
Matlab 2020a	Mathworks, Natick, MA	https://www.mathworks.com/
Python 3.8	Python Software Foundation	https://www.python.org/
TensorFlow 2.1	71	https://www.tensorflow.org/
NumPy 1.20	108	https://www.numpy.org/
SciPy 1.6	109	https://www.scipy.org/
Matplotlib 3.4	110	https://doi.org/10.5281/zenodo.592536

Highlights.

• Anatomically-constrained neural networks were trained to predict scene velocity

• Trained networks matched properties of neurons in Drosophila’s motion circuits

• Trained networks contained segregated ON and OFF motion channels

• Networks facing noise during training were better predictors of neural responses