CHARMM-GUI Drude Prepper for Molecular Dynamics Simulation Using the Classical Drude Polarizable Force Field

Abstract

Explicit treatment of electronic polarizability in empirical force fields (FFs) represents an extension over a traditional additive or pairwise FF and provides a more realistic model of the variations in electronic structure in condensed phase, macromolecular simulations. To facilitate utilization of the polarizable FF based on the classical Drude oscillator model, Drude Prepper has been developed in CHARMM-GUI. Drude Prepper ingests additive CHARMM protein structures file (PSF) and pre-equilibrated coordinates in CHARMM, PDB, or NAMD format, from which the molecular components of the system are identified. These include all residues and patches connecting those residues along with water, ions, and other solute molecules. This information is then used to construct the Drude FF-based PSF using molecular generation capabilities in CHARMM, followed by minimization and equilibration. In addition, inputs are generated for molecular dynamics (MD) simulations using CHARMM, GROMACS, NAMD, and OpenMM. Validation of the Drude Prepper protocol and inputs is performed through conversion and MD simulations of various heterogeneous systems that include proteins, nucleic acids, lipids, polysaccharides, and atomic ions using the aforementioned simulation packages. Stable simulations are obtained in all studied systems, including 5 μs simulation of ubiquitin, verifying the integrity of the generated Drude PSFs. In addition, the ability of the Drude FF to model variations in electronic structure is shown through dipole moment analysis in selected systems. The capabilities and availability of Drude Prepper in CHARMM-GUI is anticipated to greatly facilitate the application of the Drude FF to a range of condensed phase, macromolecular systems.

INTRODUCTION

Molecular simulations based on empirical force fields (FFs) are widespread and applied to a wide range of chemical, biological, and pharmacological systems. The increase in the number of systems subjected to molecular simulations is associated with a number of driving forces from both the experimental and computational sides. Experimentally, X-ray crystallography, NMR, and, more recently, cryogenic electron microscopy (cryo-EM) are producing an ever increasing number of 3-dimensional structures of a range of macromolecules that can be starting points for molecular simulations.¹ Moreover, solution techniques such as X-ray and neutron scattering, Förster resonance energy transfer (FRET), and other single-molecule experiments yield observables for which molecular simulations offer the potential of producing an atomic level interpretation.^2–4 In addition, the combination of quantum mechanical or machine learning models in conjunction with molecular mechanics (QM/MM or ML/MM) methods offers the ability to understand data from various kinetic experiments at an atomic and electronic level.^{5, 6}

Computational drivers leading to the increased use of molecular simulations include both hardware and software contributions. Ever increasing accessibility to multicore CPU and GPU technologies,⁷ as well as specialized simulation hardware⁸ allow for accessibility to more molecular systems for extended simulation times by a larger number of researchers including experimentalists interested in applying simulations to accentuate their experimental portfolios. Software developments include programs used for performing simulations, tools for the preparation of simulation systems, algorithms to access larger timescales and ensembles, and the energy functions and FFs used in the molecular simulations. Simulation programs undergoing developments to take advantage of ongoing changes in hardware include GROMACS,⁹ GROMOS,¹⁰ CHARMM,¹¹ AMBER,¹² NAMD,¹³ GENESIS¹⁴, TINKER,¹⁵ OpenMM,¹⁶ and LAMMPS,¹⁷ among others. These programs include a range of advanced simulation algorithms including free energy methods and enhanced sampling approaches including temperature and Hamiltonian replica exchange methods and a wide collection of meta dynamics approaches, many of which are implemented in the PLUMED package.¹⁸ In the area of simulation system preparation, most commercially available software packages, such as MOE (Chemical Computing Group), Maestro (Schrödinger), and Discovery Studio (BIOVIA) include system preparation capabilities, while there are academic tools such as CHARMM-GUI and MDWeb,¹⁹ among others. In particular, CHARMM-GUI (https://www.charmm-gui.org), developed in the Im laboratory with contributions from a number of other groups, allows for the preparation of highly heterogeneous biomolecular systems and is recently expanding into non-traditional biological systems such as polymers and materials.^20–26

Essential to the accuracy of molecular simulations is the quality of empirical FFs from which the energies and/or forces driving the sampling of conformational space are obtained. In other words, the FF accuracy, in the limit of full sampling of the partition function, dictates the quality and utility of the simulation outcomes. In the context of biological and pharmacological systems, a number of additive or pairwise FFs are available, including AMBER,^27–31 CHARMM,^32–37 OPLS,^38–40 and GROMOS,^41–43 among others. These FFs dominate the molecular simulation landscape due to their computational efficiency with a satisfactory level of accuracy. While these FFs continue to undergo improvements, there is evidence that inherent limitations in the underlying potential energy function, notably the additive approximation for the treatment of electrostatic interactions, ultimately place an upper limit in their accuracy^44–47 with recent examples being the treatment of disordered proteins.^{48, 49}

To overcome these limitations, FFs that explicitly include the treatment of electronic polarization have been introduced and are now starting to be more widely used in application studies. Methods used to treat polarizability include induced dipole,^50–53 fluctuating charge,^54–58 and classical Drude oscillator (or charge-on-spring) models.^59–61 Of these, the AMOEBA⁵² and Drude polarizable FFs are the most comprehensive. The AMOEBA FF includes proteins,⁵² nucleic acids,⁵³ and small molecules.^{62, 63} The Drude FF, developed in the MacKerell laboratory in collaboration with Roux and coworkers, includes nucleic acids,^{64, 65} lipids,⁶⁶ proteins,⁶⁷ carbohydrates,^68–71 ions,^{72, 73} and organic molecules⁶¹ with halogens⁷⁴ and methods to automate the prediction of electrostatic parameters using machine learning.⁷⁵ In addition to the explicit treatment of polarizability, the Drude FF also accounts for the anisotropic features of hydrogen bond acceptors via the inclusion of virtual “lone pair” particles and a non-diagonal polarizability tensor. The accuracy of nonbonded interactions is improved through shielded short-range electrostatic interactions via Thole scaling⁷⁶ and the use of atom pair-specific Lennard-Jones parameters (e.g., NBFIX in CHARMM nomenclature).⁷⁷ A particular advantage of the Drude model is the use of an explicit particle to treat the electronic degrees of freedom allowing for steric polarization effects to be modeled, a property that has been used to improve the treatment of Mg²⁺ and halogens.^{74, 78} The Drude model is computationally efficient, having only a 3–4 fold overhead over the additive model, such that molecular dynamics (MD) simulations up to and beyond 1 μs are possible.^{61, 79} This contrasts the AMOEBA polarizable FF, which is slower by over an order of magnitude.^{80, 81}

In this work, we describe Drude Prepper (https://www.charmm-gui.org/input/drude) in CHARMM-GUI that provides molecular systems and input scripts for simulations using the Drude polarizable FF. Drude Prepper takes equilibrated systems prepared and simulated with the CHARMM additive FF as inputs and converts them for use with the Drude FF. Current capabilities detailed and validated in this paper include the necessary conversions of the coordinate and “protein structure files” (PSF) required for polarizable simulations, as well as inputs for MD simulations using CHARMM,⁸² NAMD,⁸³ OpenMM,⁸⁴ and GROMACS,⁸⁵ all of which have been extended to treat the Drude FF and allow for MD simulations to be performed on a range of CPU and GPU platforms. It should be noted that the term “PSF” is historical in nature and that a PSF may be created for any class of molecule. The remainder of the paper describes the additive to Drude polarizable FF conversion algorithms and their application to a range of macromolecular systems. The latest versions of the CHARMM Drude polarizable FF can be obtained separately through MacKerell lab website (http://mackerell.umaryland.edu/charmm_ff.shtml). The Drude FF versions used for this study are summarized in Supporting Information Table S1.

METHODS

Conversion of Additive FF PSF to Drude FF PSF

The foundation of the generation of molecules in CHARMM is based on a combination of desired residues and patches of chemical entities to build all necessary atom connectivity information (i.e., PSF) required for the energy and force calculations, as well as other molecular manipulations. Residues are the fundamental chemical entities such as amino acids, nucleotides, monosaccharides, and lipids. The patch capability in CHARMM is a unique tool that manipulates these residues. For example, there are patches to link amino acid residues or nucleotides to create polypeptides or oligonucleotides, respectively, and patches allow for a nearly endless collection of chemical modifications, including disulfide bonds, changes in protonation states, and chemical modifications of amino acids or nucleotides. In addition, patches can be used as molecular modeling tools such as adding covalent bonds between protein residues and metals to assure that the chelation state of the metal is maintained throughout an MD simulation. This approach contrasts with other programs in which the final chemical entity must be input directly into the program. Indeed, the residue and patching capabilities in CHARMM allow for an infinite number of chemical connectivities to be readily created, with a prime example being the ability to create a wide range of poly- and oligosaccharides by simply listing the desired monosaccharides followed by the list of patches creating the various types of glycosidic linkages and chemical modifications. Accordingly, several simulation packages including NAMD and OpenMM allow for CHARMM PSFs to be directly read, directly supplying the information required for molecular simulations with those programs.

The molecular generation tools were initially developed in the context of the CHARMM additive FF. Currently, the CHARMM all-atom additive FF contains over 2,200 residues and 300 patches, representing a near comprehensive collection of chemical coverage with emphasis on biological and pharmacological systems, although now extending significantly beyond that range. To take advantage of this, the Drude FF largely uses the same molecular generation strategy, importantly, maintaining the same residue and atom name nomenclature as in the additive FF except water molecules. Accordingly, it is possible and a good strategy to perform a CHARMM additive PSF to Drude PSF conversion by detecting the residues and patches used in an additive FF PSF and creating the corresponding Drude FF PSF.

Drude Prepper handles this conversion in two steps: 1) detecting the components and patches that comprise an input molecular system and 2) reassembling the components in the context of the Drude FF. The detection of system components is done based on the residue names in each segment (SEGID), e.g., a single polypeptide chain. For example, if all residues in a segment are amino acids, the segment is classified as a protein. DNA and RNA are detected in a similar way, but if the segment contains O2’ atoms, it is classified as RNA, and DNA otherwise. Default patches are then applied to create the respective biopolymers. Special patches applied to each segment are detected by checking for the existence of a certain atom in a residue. For example, an acetylated N-terminus is detected by confirming the presence of a CY atom at the N-terminal residue. In addition, a disulfide bond can be detected by searching for any SG atom bonded to the SG atom of another residue.

Handling carbohydrates is the most demanding task due to the wide variety of glycosidic linkages. To properly recognize the glycosidic linkages between sugar residues, Drude Prepper utilizes Glycan Reader^{86, 87} that recognizes the monosaccharide types and linkages using the atomic coordinates and connectivity information in a PSF. The detected linkage information is passed in the form of a CHARMM stream file. Note that Drude Prepper only supports the sugars that are available in the Drude FF such as general furanoses, pyranoses, hexouronic acids, and other acid moieties.⁸⁸ Additional monosaccharides and linkage types, such as seven-, eight-, nine-carbon sugars, and N/O glycosidic linkages to proteins will be included as they are developed. More generally, Drude Prepper only covers those chemical entities explicitly in the Drude FF, although the coverage is currently quite extensive. On the other hand, there is currently no analog of the CHARMM General Force Field (CGenFF) and associated program,⁸⁹ although efforts towards a Drude General Force Field (DGenFF) are actively ongoing.

Water molecules are detected if a segment contains a residue named TIP3. All other components not described above are classified as “else”, and Drude Prepper issues an error if topologies and parameters for the residues in “else” are not available in the Drude FF. After all components are successfully recognized in the first step, they are reassembled based on the recognized residues and patches in the Drude FF. A mass of 0.4 AMU is subtracted from polarizable atoms (i.e., non-hydrogen atoms) and assigned to the Drude oscillators or particles. Lone pair particles are generated according to the topology of the residues in the Drude FF. While charge is distributed onto the lone pair, no mass is assigned to the lone pair particles as the forces acting on those particles are transformed back to their parent atom as required for propagation of a MD trajectory. The TIP3P^{90, 91} water molecules from the additive PSF are converted to the SWM4-NDP⁹² water model; a more accurate, but computationally more demanding water model SWM6 is also available.⁹³ In addition to creating the scripts to perform molecular simulations in CHARMM, Drude Prepper provides input scripts optimized for simulating the system with the Drude FF using NAMD, GROMACS, and OpenMM. Once the conversion from the additive to Drude FF PSF is complete and the input scripts are created, Drude Prepper then performs initial system minimization using CHARMM. Details of these steps and the input options for the various programs follow.

Drude System Preparation and Simulation Protocols

Drude Prepper creates a collection of CHARMM input and stream files for system setup, minimization, and simulation using the Drude FF. Brief descriptions of these input and stream files are included in Table S2. In addition, input scripts and supporting files for equilibration and production simulations using NAMD, OpenMM, and GROMACS can be found in each program directory from “download.tgz” that can be downloaded at the final step of Drude Prepper. Note that one can modify the inputs to adjust equilibration and production times and the trajectory saving steps for their specific needs. Detailed descriptions of the contents in these input files follow.

CHARMM pre-equilibration with the additive FF:

First, all simulation systems are assumed to be built using Solution Builder or Membrane Builder modules in CHARMM-GUI and are equilibrated using the CHARMM additive FF and the equilibration inputs provided by CHARMM-GUI. We refer this additive FF based equilibration to as “pre-equilibration” in the context of preparing the simulation system for the Drude FF. Using the standard inputs generated by Solution Builder or Membrane Builder, the systems are minimized and equilibrated in the NVT (constant particle number, volume, and temperature) and NPT (constant particle number, pressure, and temperature) ensembles. System sizes are generated to have a minimum of 10 Å buffer of TIP3P water beyond the non-hydrogen atoms of the macromolecules in all directions. A force-switch smoothing function over 10 to 12 Å is applied for Lennard-Jones (LJ) interactions. The particle mesh Ewald (PME)⁹⁴ method is used for long-range electrostatic interactions, and the SHAKE⁹⁵ algorithm is utilized for fixing all bonds including hydrogen atoms. In this study, all pre-equilibration was performed at 303.15 K. The backbone and sidechain heavy atoms were harmonically restrained during this equilibration. The definition of backbone and sidechain heavy atoms are provided in Table S3. It needs to be emphasized that using a well pre-equilibrated system to initiate the Drude FF calculations is recommended, especially in cases where the starting structure is of low resolution, contains externally docked ligands, and/or have homology modeled sections, etc.

CHARMM minimization:

Since the Drude particles are initially assigned the same coordinates as their parent atoms, the initial minimization requires special attention. Drude Prepper performs this minimization using CHARMM in two stages. First, only the Drude particles are minimized with a very strong harmonic restraint with a force constant of 100,000 kcal/mol/Ų applied to all real atoms including hydrogens. 100 steps of adopted basis Newton-Raphson (ABNR) are used in this stage. Next, the strong restraints on all real atoms are removed and only the non-hydrogen atoms (Table S3) are restrained with force constants of 1 kcal/mol/Ų (for backbone atoms) and 0.1 kcal/mol/Ų (sidechain atoms). The full system is minimized for 100 steps of steepest descent (SD) and another 100 steps of ABNR. Long-range electrostatic interactions are computed using PME⁹⁴ summation with a real space cutoff of 12 Å with the nonbond list maintained out to 16 Å in conjunction with an heuristic update, an Ewald splitting parameter (κ) of 0.34 Å⁻¹, a grid spacing of ~1.0 Å, and a sixth-order interpolation of the charge to the grid. The LJ interactions are truncated at 12 Å with a switching function^{96, 97} over 10–12 Å. The isotropic long-range correction (LRC)⁹⁸ is added to the non-bonded interactions that assumes the radial distribution function is unity beyond the real space cutoff. Future versions of Drude Prepper will include the necessary scripts to perform simulations using the LJ-PME treatment of long-range LJ interactions.⁹⁹ The internal geometry of water molecules and covalent bonds involving hydrogen atoms are kept fixed using a separate SHAKE⁹⁵ algorithm called RATTLE/Roll. The minimized coordinates of the system are used to generate the inputs for both equilibration and production in CHARMM or user-selected additional MD platform(s).

CHARMM equilibration & production:

Performing a short MD equilibration is essential prior to production simulations. The MD equilibration involves a 100-ps simulation in the NPT ensemble using a small timestep of 0.5 fs. The simulation is performed with the velocity-Verlet integrator (VV2) developed specifically for the Drude model.⁸² A dual Nose-Hoover^{100, 101} thermostat is used, where the thermostat coupled to Drude particles is set to 1 K and the thermostat for real atoms is set to the target temperature. The friction coefficient is set to 10 ps⁻¹ for the temperature control and the pressure is controlled at 1 atm by a modified Anderson-Hoover barostat.¹⁰² The nonbonded interaction options, the usage of RATTLE/Roll for water molecules, and positional harmonic restraints to the non-hydrogen atoms are the same as in the above CHARMM minimization. To avoid polarization catastrophe, a hard-wall constraint is used with a parent-Drude bond length cutoff of 0.2 Å.^{66, 72} During the equilibration, a trajectory is saved every 2.5 ps for any analysis, and the final coordinate is used to initiate the production simulation. The input for the CHARMM production MD simulation is identical to that used for equilibration except that the integration timestep is set to 1 fs, coordinates are saved every 10 ps, and all positional harmonic restraints are removed.

Equilibration with OpenMM, GROMACS, or NAMD uses the same timestep and positional restraint protocol as in the above CHARMM equilibration with the differences being in the integrators, thermostats, and barostats as described below for the production MD inputs.

NAMD:

The NAMD program⁸³ uses an extended Lagrangian method for integrating Drude particle positions in Langevin dynamics.^{82, 83} For NPT simulation, the temperature is regulated by a dual thermostat⁸² with Drude particles coupled to 1 K with a damping coefficient of 20 ps⁻¹ and real atoms coupled to the thermostat at the target temperature with a friction coefficient of 5 ps⁻¹. The pressure is maintained at 1 atm using the Langevin piston method¹⁰³ with an oscillation period of 50 fs and a decay time of 25 fs. The timestep is set to 1 fs and coordinates are saved every 10 ps for production. PME⁹⁴ summation is used to compute long-range electrostatics with ~1 Å grid spacing and an interpolation order of 6. Non-bonded interactions are calculated with a real space cutoff of 12 Å and a switching distance is set to 10–12 Å for the LJ interactions and the isotropic LJ long-range correction is applied. Note that the force switching is turned off while using the Drude FF and a potential switch is used for the LJ interactions. The pair lists within 16 Å are updated every 10 steps. Constraints are added using SHAKE to keep the covalent bonds involving hydrogen atoms rigid. The Drude hardwall is set to 0.2 Å.

OpenMM:

The OpenMM program¹⁶ has GPU implementation⁸⁴ capability for the Drude FF. An extended Lagrangian dynamics simulation with velocity-Verlet integrator is implemented for treating the motion of atoms and the associated Drude particles. A dual thermostat with specific reference temperatures and friction coefficients for both real atoms and Drude particles is used with the same values as for CHARMM and NAMD. Differently for OpenMM, the pressure is maintained using a Monte Carlo barostat set to 1 atm with a coupling frequency of 100 steps. The timestep is set to 1 fs and coordinates are saved every 10 ps. PME is used for the electrostatic interactions and the LJ interactions are switched over 10 to 12 Å with a long-range isotropic correction. The Ewald error tolerance is set to 0.0001. The SHAKE algorithm is implemented in OpenMM to constrain all covalent bonds that involve hydrogen atoms, and the Drude hardwall is set to 0.2 Å.

GROMACS:

The GROMACS program¹⁰⁴ allows for both GPU and CPU simulations of the Drude polarizable systems.⁸⁵ Parallelization on CPU hardware is currently supported via OpenMP parallelization. The integrator implemented for extended Lagrangian dynamics in Drude systems is the same two-step velocity-Verlet algorithm as implemented in CHARMM. Currently, only NVT simulations are supported in GROMACS for the Drude FF using a dual Nosé-Hoover thermostat. Real atoms are coupled to a thermostat at a target temperature with a coupling constant of 0.1 ps and Drude particles are coupled to a 1 K thermostat with a coupling constant of 0.005 ps. The timestep is set to 1 fs and coordinates are saved every 10 ps. The Drude hard wall constraint is set to a maximum value of 0.2 Å. Bonds involving hydrogen atoms are constrained via LINCS.¹⁰⁵ The short-range LJ potential is switched to zero over 10–12 Å. Electrostatic forces are computed with the smooth PME algorithm⁹⁴ with a real-space cutoff of 12 Å.

Dipole Moment Calculations

Dipole moments of selected moieties were calculated from the trajectories and presented as probability distributions. Both the CHARMM additive and Drude FFs define the topologies such that the molecules can be divided into the groups of atoms with integer charges. While this feature not only facilitates the modular approach to building new chemical entities, it also provides an opportunity to analyze dipole moments of specific moieties in a highly specific way. The dipole moment is calculated from the charges of all the particles in the moiety and their spatial relationship. In the case of the Drude FF, this includes all Drude particles and lone pairs, as well as atoms. Presented in Table S4 is the list of atom definitions for integer charge groups. When the sum of the charges in the moiety equals zero, the dipole moment is orientation independent. However, if the charge does not equal zero, the dipole moment is position dependent. In such cases, the structures from each simulation snapshot were aligned with the crystal structure based on the backbone heavy atoms and the coordinates of the selected particles were translated to define their center of geometry as the origin prior to the dipole moment calculation. This was performed with all groups of integer −1 or +1 (i.e., acidic and basic amino acids), as well as with PRO residues in the Drude FF whose total charge is 0.178.

Simulation Systems

Table 1 summarizes the diverse biomolecular systems used in this study to test Drude Prepper and its simulation protocols, and the respective system images are shown in Figure 1. For each system, we performed pre-equilibration for 1 ns, equilibration for 100 ps, and production for 100 ns, 200 ns, or 5 μs using different MD engines as described.

Table 1.

Simulation system descriptions.

System name	Molecular type	# particles†	Box size (Å3)	Pre-equilibration / Equilibration / Production
Ubiquitin	Protein	41,694	64 × 64 × 64	NAMD / GROMACS / GROMACS
TF-DNA	Protein + DNA	51,026	66 × 66 × 66	CHARMM / NAMD / NAMD
HIV-1 TAR-TAT RBD	Protein + RNA	50,444	69 × 69 × 69	CHARMM / OpenMM / OpenMM
Cas9-sgRNA-DNA	Protein + DNA + RNA	426,781	140 × 140 × 140	OpenMM / OpenMM / OpenMM
LeuT in a POPC bilayer	Protein + Lipid	411,236	155 × 155 × 114	OpenMM / OpenMM / OpenMM
MalT-maltose complex	Protein + Lipid + Carbohydrate	382,991	150.5 × 150.5 × 112.0	OpenMM / OpenMM / OpenMM
E. coli O176-antigen OS	Carbohydrate	198,373	108 × 108 × 108	OpenMM / OpenMM / OpenMM
M. catarrhalis OS	Carbohydrate	12,468	43 × 43 × 43	OpenMM / OpenMM / OpenMM
HA lyase-HA substrate	Protein + Carbohydrate	208,974	110 × 110 × 110	OpenMM / OpenMM / OpenMM

^†Including Drude particles and virtual lone pairs.

Figure 1.

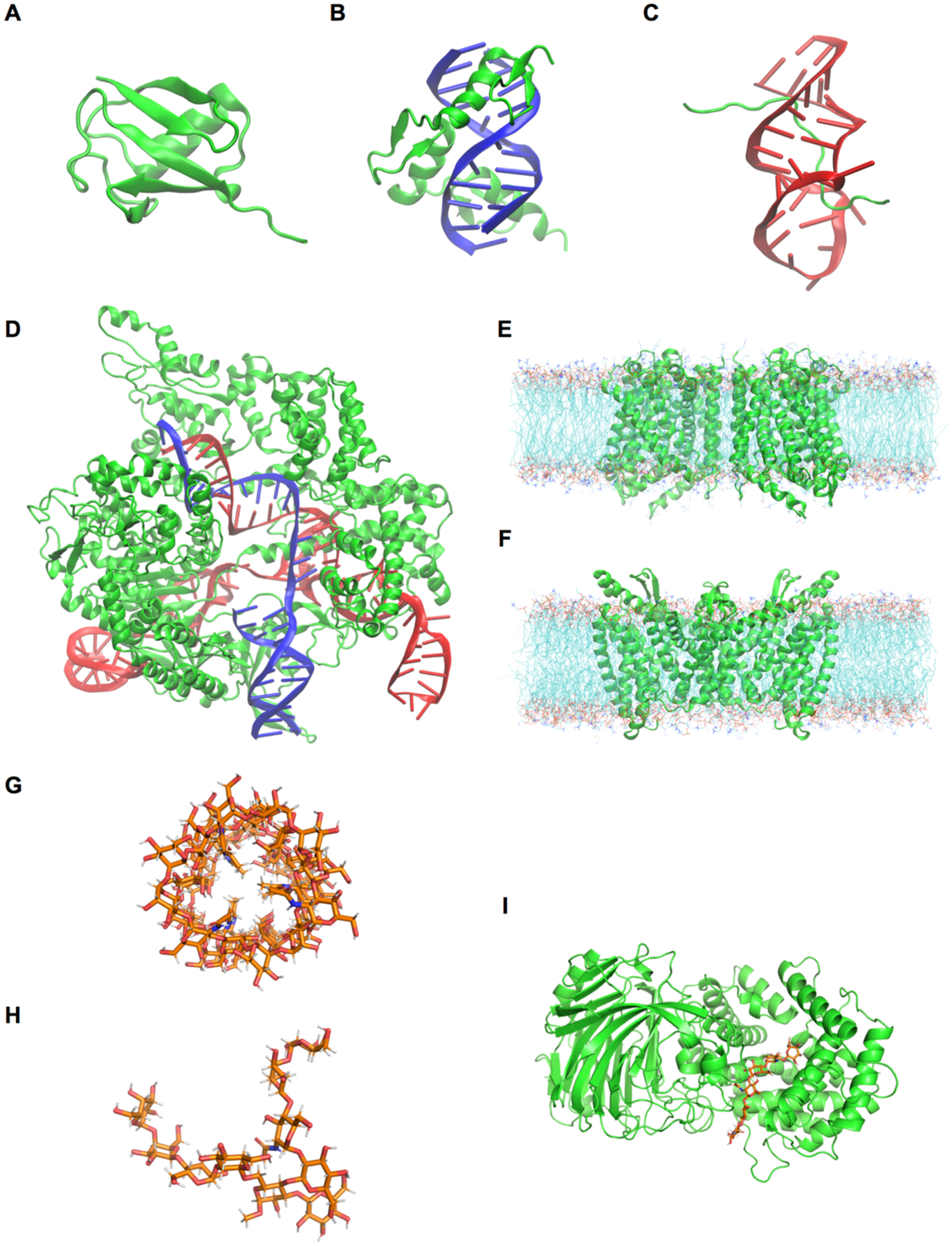
Molecular visualizations of the simulation systems in this study: (A) Ubiquitin, (B) TF-DNA, (C) HIV-1 TAR-TAT RBD, (D) Cas9-sgRNA-DNA. (E) LeuT in a bilayer, (F) MalT-maltose complex in a bilayer, (G) E. coli O176 O-antigen oligosaccharide, (H) M. catarrhalis serotype C oligosaccharide, and (I) HA lyase – HA substrate. Coloring scheme: green cartoon for protein, red cartoon for RNA, blue cartoon for DNA, cyan lines for lipids, and orange sticks for carbohydrates.

Ubiquitin:

Human erythrocytic ubiquitin coordinates were obtained from the 1.8 Å resolution crystal structure (PDB ID 1UBQ).¹⁰⁶ The protein was solvated in a cubic box with 7,921 water molecules. For this system, the protein carries no net charge and simulations were performed without any neutralizing counterions or added salt. The initial box size was 64 × 64 × 64 ų (Figure 1A).

Transcription factor-DNA complex:

A simulation system of a zinc finger transcription factor (TF) binding with a DNA fragment was setup using the 1.6 Å resolution X-ray structure (PDB ID 1AAY).¹⁰⁷ The double strand DNA contains 11 base pairs, and the TF-DNA complex was solvated in a cubic water box containing 9,493 water molecules and 150 mM KCl (including neutralization cations, 28 K⁺ and 25 Cl⁻ ions). The initial box size was 66 Å × 66 Å × 66 ų (Figure 1B).

HIV-1 TAR with Tat RNA binding domain (RBD):

Interaction of human immunodeficiency virus (HIV) trans-activation-response (TAR) RNA element with the trans-activator protein (Tat) is critical towards viral mRNA production.¹⁰⁸ A novel conformational rearrangement in the TAR RNA binding site allows Tat RNA binding domain to recognize it.¹⁰⁹ System construction was initiated from model 1 of the solution NMR structure (PDB ID 6MCE).¹¹⁰ The RNA-peptide complex was solvated in a cubic box of 69 × 69 × 69 ų with TIP3P water and 0.15 M KCl buffer (including neutralization cations, 48 K⁺ and 27 Cl⁻ ions) (Figure 1C).

Cas9-sgRNA-DNA:

The simulation setup for Cas9-sgRNA-DNA complex started with a cryo-EM structure (PDB ID 6O0Z) at 3.3 Å resolution.¹¹¹ The complex was solvated in a cubic box of 140 × 140 × 140 ų. Overall negative charge on the complex was neutralized by adding K⁺ ions to the system along with 150 mM KCl buffer (324 K⁺ and 214 Cl⁻ ions) (Figure 1D).

LeuT in a POPC bilayer:

Leucine transporter LeuT is a 12 transmembrane-helix protein that utilizes established electrochemical potential of Na⁺ ions to facilitate the transport of neutral amino acids. The LeuT protein (PDB ID 3TT1)¹¹² at a resolution of 3.1 Å was embedded in a palmitoyloleoyl-phosphatidylcholine (POPC) bilayer with 290 POPC at the top leaflet and 297 POPC at the bottom leaflet. 53,950 water molecules were added along with 150 mM NaCl (including neutralization ions, 146 Na⁺ and 154 Cl⁻ ions), reaching an initial system size of 155 ×155 ×114 ų (Figure 1E).

MalT-maltose complex in a mixed bilayer of DOPC and DOPE:

MalT, a member of the enzyme IIC family, is a membrane-embedded sugar transport protein that is part of the phosphoenolpyruvate-dependent phosphotransferases.^113–115 The initial simulation system was built using PDB ID 5IWS, 2.55 Å resolution, for MalT from Bacillus cereus.¹¹⁶ To properly recognize the maltose substrate, the PDB structure was downloaded from RCSB not OPM.¹¹⁷ Since PDB:5IWS contains only MalT monomer and a maltose substrate, a dimeric structure was prepared using the “Generation of Biologically Functional Unit” option in PDB Reader & Manipulator.¹¹⁸ In addition, since the protein structure from RCSB is not properly oriented to a membrane whose normal is along the Z-axis and center is at Z = 0, the PPM option of the OPM server¹¹⁷ was used to orient the MalT dimer. Then, the structure was embedded in a 3:1 mixed bilayer of dioleoyl-phosphatidylethanolamine (DOPE) and dioleoyl-phosphatidylcholine (DOPC): 213 DOPE and 71 DOPC at the top leaflet and 228 DOPE and 76 DOPC at the bottom leaflet. 49,355 TIP3P water molecules and 0.15 M KCl (including neutralization ions, 133 K⁺ and 153 Cl⁻) were added to the system, and the initial system size was 150.5 × 150.5 × 112.0 ų (Figure 1F).

Escherichia coli O176 O-antigen oligosaccharide:

O-antigen polysaccharides constitutes part of the lipopolysaccharide molecule present in the outer membrane of Gram-negative bacteria,¹¹⁹ which have diverse chemical compositions even within a single species.¹²⁰ In a previous study, Patel et al. studied the conformational preferences of an Escherichia coli O176 O-antigen oligosaccharide at the atomic level using NMR spectroscopy and MD simulations.¹²¹ An initial structure of ten repeating units of O176 O-antigen structures (Figure 2A) was built by Glycan Modeler²⁴ and immersed at the center of a cubic box (108 × 108 × 108 ų) including 150 mM KCl (112 K⁺ and 112 Cl⁻) (Figure 1G).

Figure 2.

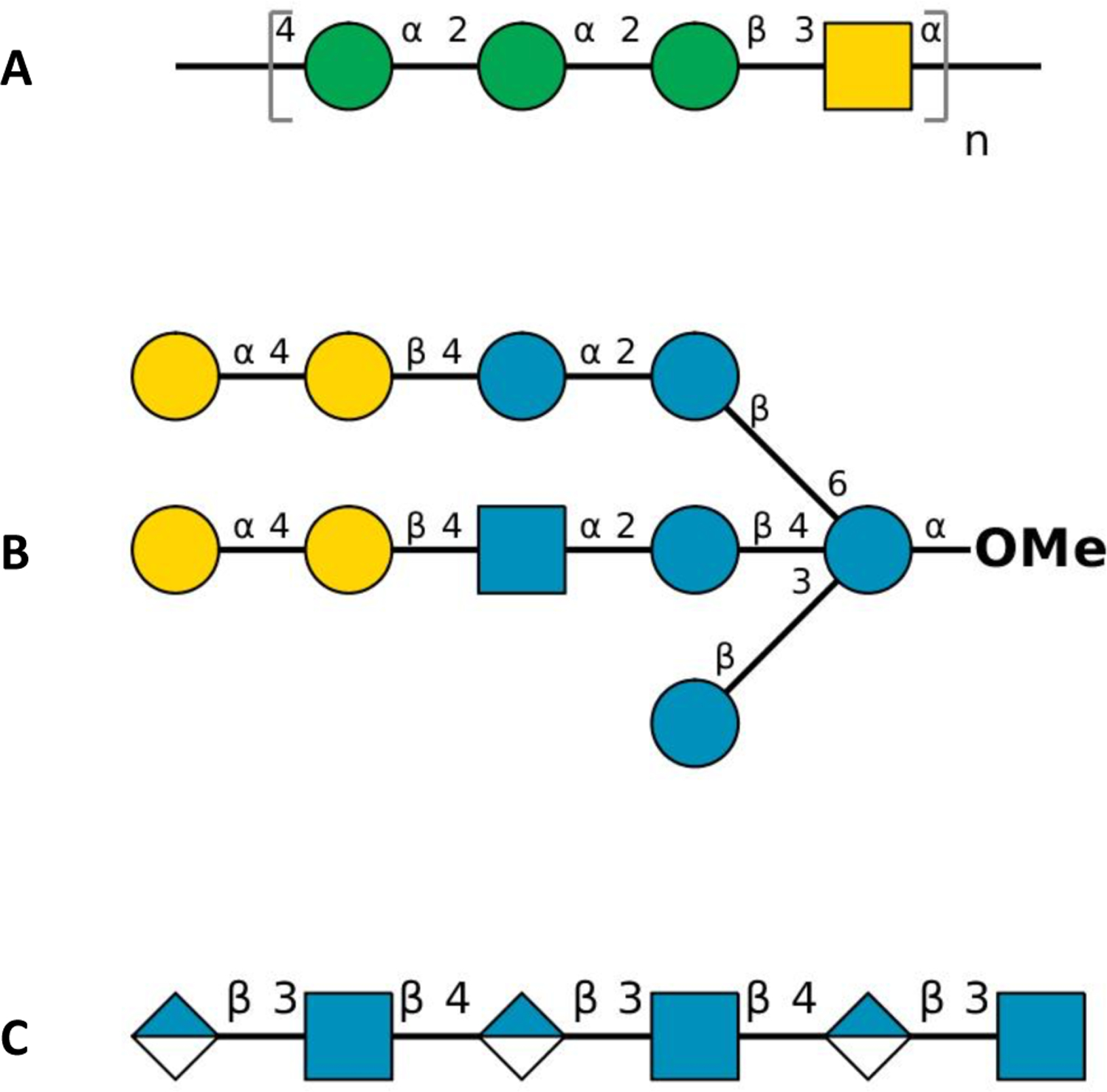
Symbol representation of carbohydrate sequences of (A) E. coli O176 O-antigen repeating unit (n = 10), (B) M. catarrhalis serotype C oligosaccharide, and (C) hyaluronan hexasaccharide in PDB ID 1LOH: blue circle for d-glucose (Glc), green circle for d-mannose (Man), yellow circle for d-galactose (Gal), blue square for N-acetyl-d-glucosamine (GlcNAc), yellow square for N-acetyl-d-galactosamine (GalNAc), and half-filled blue diamond for d-glucuronic acid (GlcA).

Moraxella catarrhalis serotype C oligosaccharide:

Moraxella catarrhalis is a pathogenic Gram-negative bacterium that causes otitis media and sinusitis in children.¹²² In a previous study, all-atom MD simulations were conducted to understand the conformational properties of three major serotypes A, B, and C that are responsible for approximately 95% of the clinical isolates.¹²³ In this work, we built a serotype C oligosaccharide (Figure 2B). Lipid A and two Kdo residues in serotype C were replaced by O-methylation. An initial structure of the oligosaccharide was built by Glycan Modeler and immersed at the center of a cubic box of TIP3P water molecules (43 × 43 × 43 ų) with 150 mM KCl (6 K⁺ and 6 Cl⁻) (Figure 1H).

Hyaluronate lyase in complex with hyaluronan substrate:

Hyaluronate lyase enzymes degrade hyaluronan, which is a linear glycosaminoglycan consisting of a polymer with N-acetylglucosamine (GlcNAc) and glucuronic acid (GlcA) repeating units linked via alternating β1–4 and β1–3 glycosidic bonds.¹²⁴ It is present predominantly as a main polysaccharide component of the host connective tissues including bacterial toxins.¹²⁵ An initial complex structure of hyaluronate lyase enzyme with hexasaccharide hyaluronan substrate (Figure 2C) was set up using PDB ID 1LOH¹²⁵ with a resolution of 2.0 Å. The terminal GlcA ring at the non-reducing end of the substrate was distorted in the crystal structure,¹²⁵ so its coordinates were refined using Glycan Modeler. This initial complex was placed into the center of a cubic box (110 × 110 × 110 ų), solvated with 42,412 TIP3P water molecules and 150 mM KCl (124 K⁺ and 107 Cl⁻ ions including neutralization ions) (Figure 1I).

RESULTS AND DISCUSSION

The unique functionality of CHARMM-GUI is its versatility to allow users with the option to choose widely used simulation packages for their simulations. With Drude MD simulations now supported by CHARMM, NAMD, OpenMM, and GROMACS, we have been able to transfer this feature into Drude Prepper as well. To demonstrate it, MD simulations of various systems in Table 1 were carried out with different MD simulation software. While the pre-equilibration with the additive FF can be performed by using any of the simulation packages, it is recommended to perform the equilibration and production MD simulations with the Drude FF using the same simulation package. In this study, we have performed 1 ns pre-equilibration for each system from which the last coordinates along with the additive PSF file were then used as input data for Drude Prepper. To evaluate the implementation of the Drude model in NAMD, OpenMM, and GROMACS, as well as the conversion of the CHARMM PSF to the data structures required by those programs by Drude Prepper and the consistency of the respective inputs, we performed a single-point energy component analysis on the minimized system coordinates (Table S5). The total energy differences for NAMD, OpenMM, and GROMACS compared to CHARMM were less than ± 0.1 % except the carbohydrate-containing systems, which were less than ± 0.3 %.

Using the input files generated by Drude Prepper, each system was equilibrated for 100 ps followed by 100 or 200 ns production MD simulation, or 5 μs performed in the case of ubiquitin. To evaluate the stability of the systems, root mean square deviations (RMSD) of backbone atoms with respect to the initial structure, root mean square fluctuation (RMSF) of each residue, and radius of gyration (RGYR) of the macromolecules were calculated. The production trajectories were aligned to the backbone atoms of the respective protein, nucleic acid, or carbohydrates segments for these calculations. In addition, given the variation of the electronic structure of the molecules associated with the explicit treatment of polarization in the Drude FF, variations in dipole moments for selected moieties were calculated. The calculation of dipole moments, which can have significant impact on the dynamics and interactions,^{126, 127} was facilitated by the presence of neutral or integer charge group in the Drude FF. For example, the charges of the protein backbone C, O, N, H, Cα, and Hα atoms sum to zero as do charges of the neutral protein sidechains. Definitions of the atoms, Drude particles, and lone pairs included in the different moieties used for the dipole moment calculations are in Table S4. In the case of charged groups, the individual moieties were RMSD aligned based on the non-hydrogen atoms to a reference frame based on the structure used to initiate the MD simulations

Ubiquitin:

The solvated structure of ubiquitin remained stable over 100 ns GROMACS simulation with no systematic structural deviation, as demonstrated by stable backbone RMSD (Figure S1A) and RGYR (Figure S1B). After an initial increase to ~3 Å, the RMSD relaxed back to ~2 Å for the remainder of the 100 ns simulation. The RMSF analysis revealed that the C-terminal residues were very flexible during the simulation, accounting for most of the structural deviation (Figure S1C). We also ran the equilibration and production for the same system using OpenMM to determine if any variations in the structure would occur in an extended long-time MD. The production simulation was carried out for 5 μs and the trajectory was saved every 1 ns. The protein stayed stable over the entire simulation with a backbone RMSD of ~3 Å (Figure 3).

Figure 3.

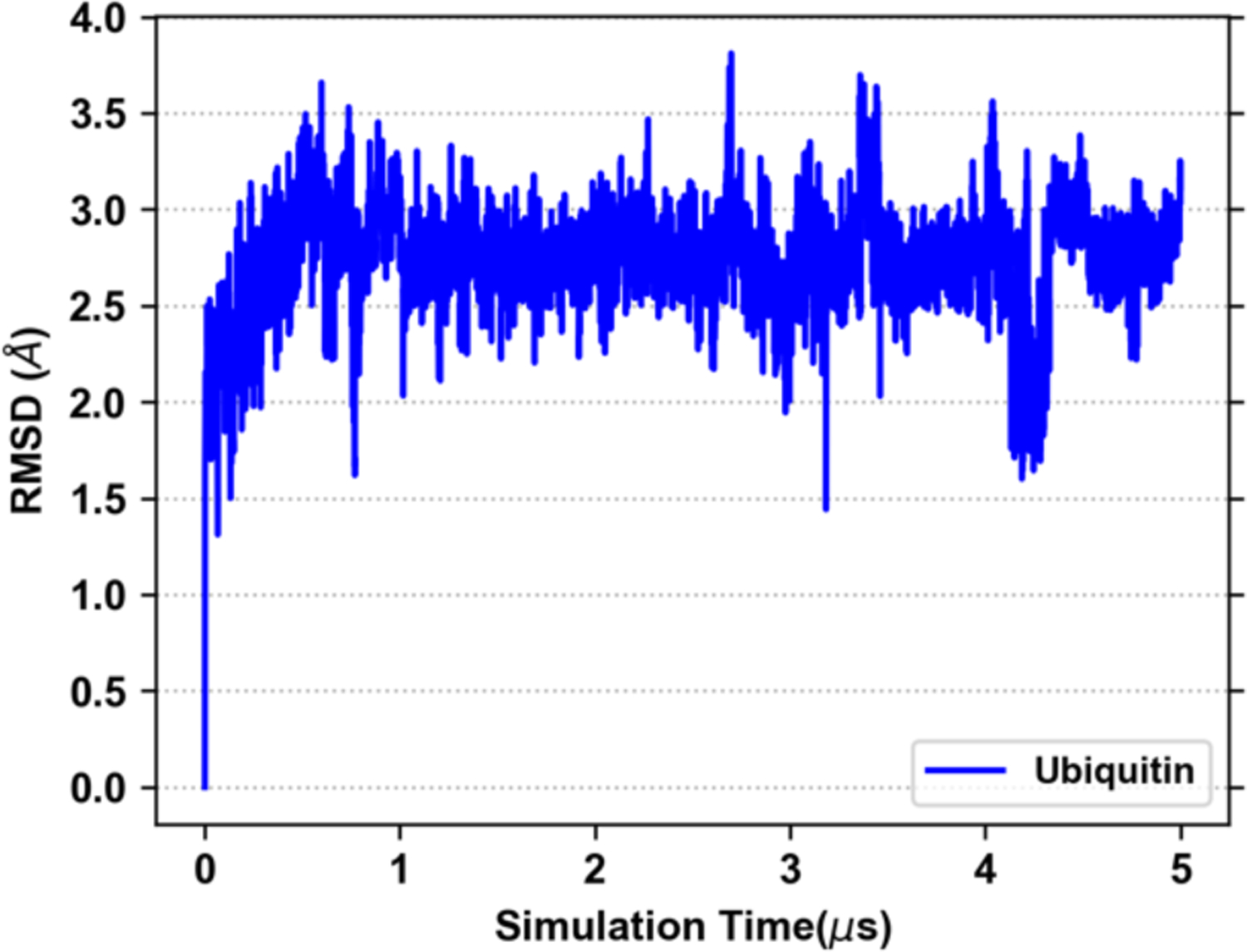
Backbone RMSD of ubiquitin from the 5 μs MD simulation performed using OpenMM.

Transcription factor-DNA complex:

TF proteins modulate the transcription of genetic information from DNA to mRNA by binding specifically to DNA sequences. A model TF-DNA system was simulated with the Zif268 zinc finger TF bound to a 11 base-pair double strand DNA. The TF-DNA interactions were well maintained throughout the 200 ns MD simulation. The heavy atom RMSD of TF protein or DNA was computed by aligning the DNA structure to its initial structure. As illustrated in Figure 4, the DNA structures are very stable with RMSD fluctuating between 2 Å and 3 Å. The protein RMSD increases to ~4.5 Å after 50 ns MD simulation and then decrease to ~3 Å and remains stable out to 200 ns, indicating conformational dynamics of the TF protein.

Figure 4.

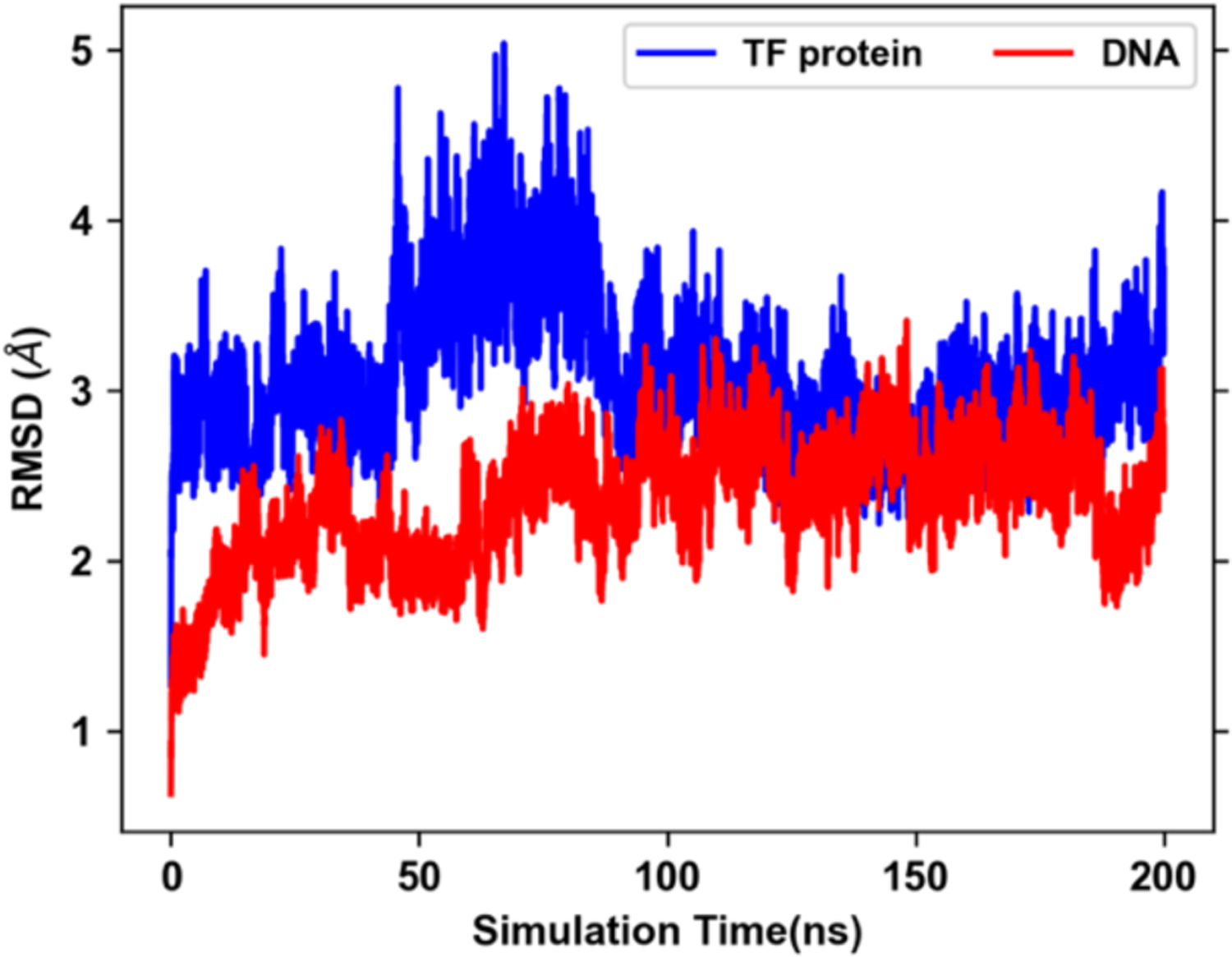
RMSD of TF-protein and DNA heavy atoms after alignment of the DNA structure with respect to the initial structure.

HIV-1 TAR with Tat RBD:

The MD simulation was started with an NMR structure (PDB ID 6MCE) of HIV-1 TAR RNA-Tat RBD peptide complex that contains an arginine sandwich motifs.¹¹⁰ We find that this interaction was short lived during MD simulation as Arg49 and Arg52 lost the initial interactions with the sandwiching nucleobases. The peptide RMSD is higher than the TAR RNA with most deviation coming from exposed N and C termini of the peptide (Figure 5A). However, the TAR RNA over the simulation adapts a conformation with Arg52 sandwiched between two base-pairs (Figure 5B), while Arg49 interacts with two flipped bases. Such interactions stabilize the RMSD during last 50 ns. We find significant standard deviations (up to ±1.5 D) in dipole moments of some nucleobases (Figure 5C). Peptide bond dipole moments also show slight variations in the mean values across the residues (Figure S2).

Figure 5.

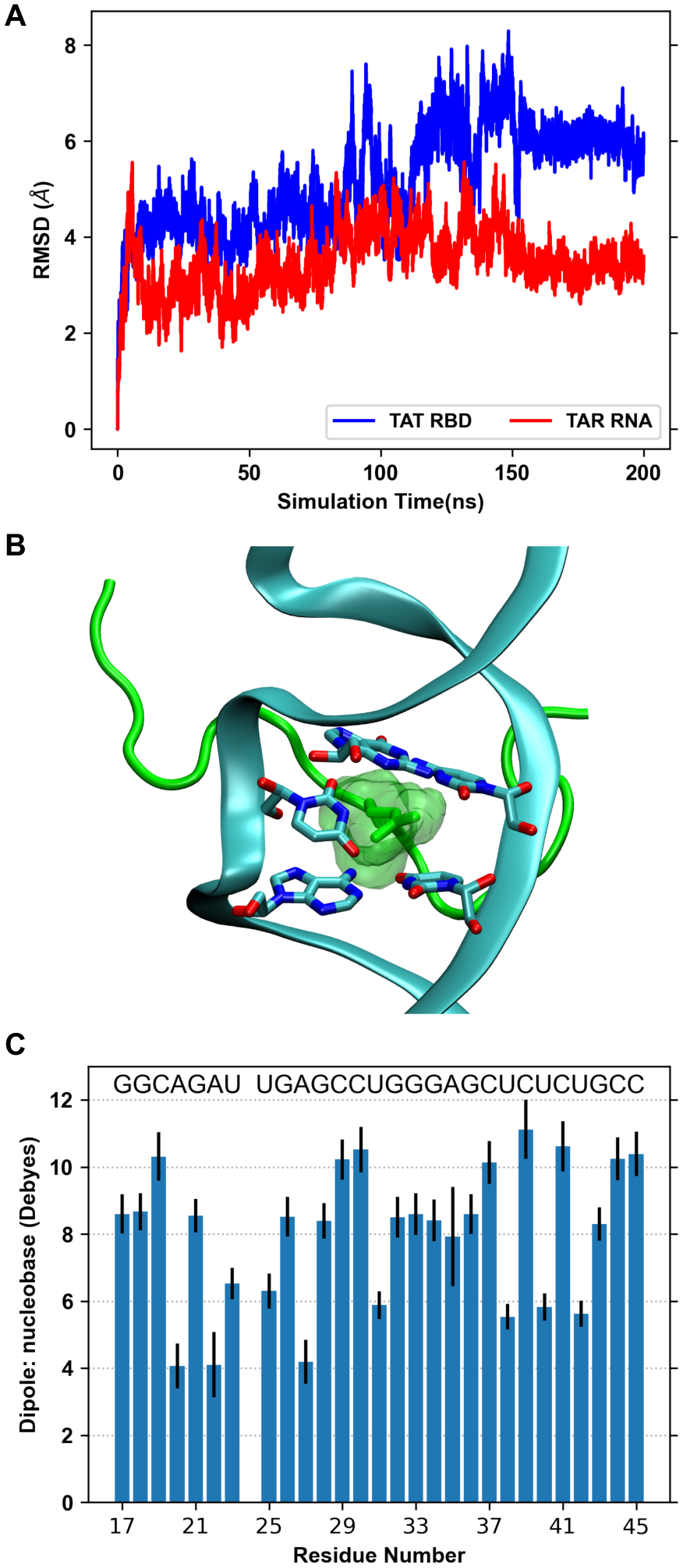
(A) RMSD of HIV-1 TAR RNA and Tat RBD with respect to their initial structure. (B) Snapshot of HIV-1 TAR–TAT RBD complex at 200 ns, showing Arg52 sandwiched between two base-pairs. Protein is shown as green cartoon and RNA is shown as cyan cartoon. (C) Dipole moments of nucleobases of HIV-1 TAR RNA calculated as an average over the 200 ns sampled every 1 ns. The error bars represent one standard deviation.

Cas9-sgRNA-DNA:

This multimolecular complex is the largest of the selected systems in terms of number of atoms including Drude particles and lone pairs (Table 1). The RMSD of Cas9 protein, DNA, and RNA components shows that the complex adapts a stable conformation after 50 ns (Figure 6A). The major conformational change comes from the recognition lobe (Figure 7), which was also observed in previous MD simulations of the complex.²³ The protein RGYR time series shows significant reduction as the recognition lobe and HNH domain tightly wrap around the portion showing interactions between target DNA strand and 5’ end of sgRNA (Figure 6B). We calculated the distributions of dipole moments of amino acid sidechains and nucleobases (Figure 8). Compared to the additive FF, the Drude FF appears to provide broader fluctuations in the dipole moment to respond to the interactions. We find that there are major differences in the mean dipole moments of amino acids such as ASP, GLU, ASN, and GLN. In case of nucleobases, we find that dipole moments are consistently higher with the Drude FF. The creation of sets of atoms whose total charge is an integer in the Drude and CHARMM FFs is critical for the dipole moment comparisons. Such groups include peptide bonds, amino acid sidechains, nucleobases, heads/tails of lipids, etc. The selection definitions for atoms, Drude particles and lone pairs in each group is in Table S4.

Figure 6.

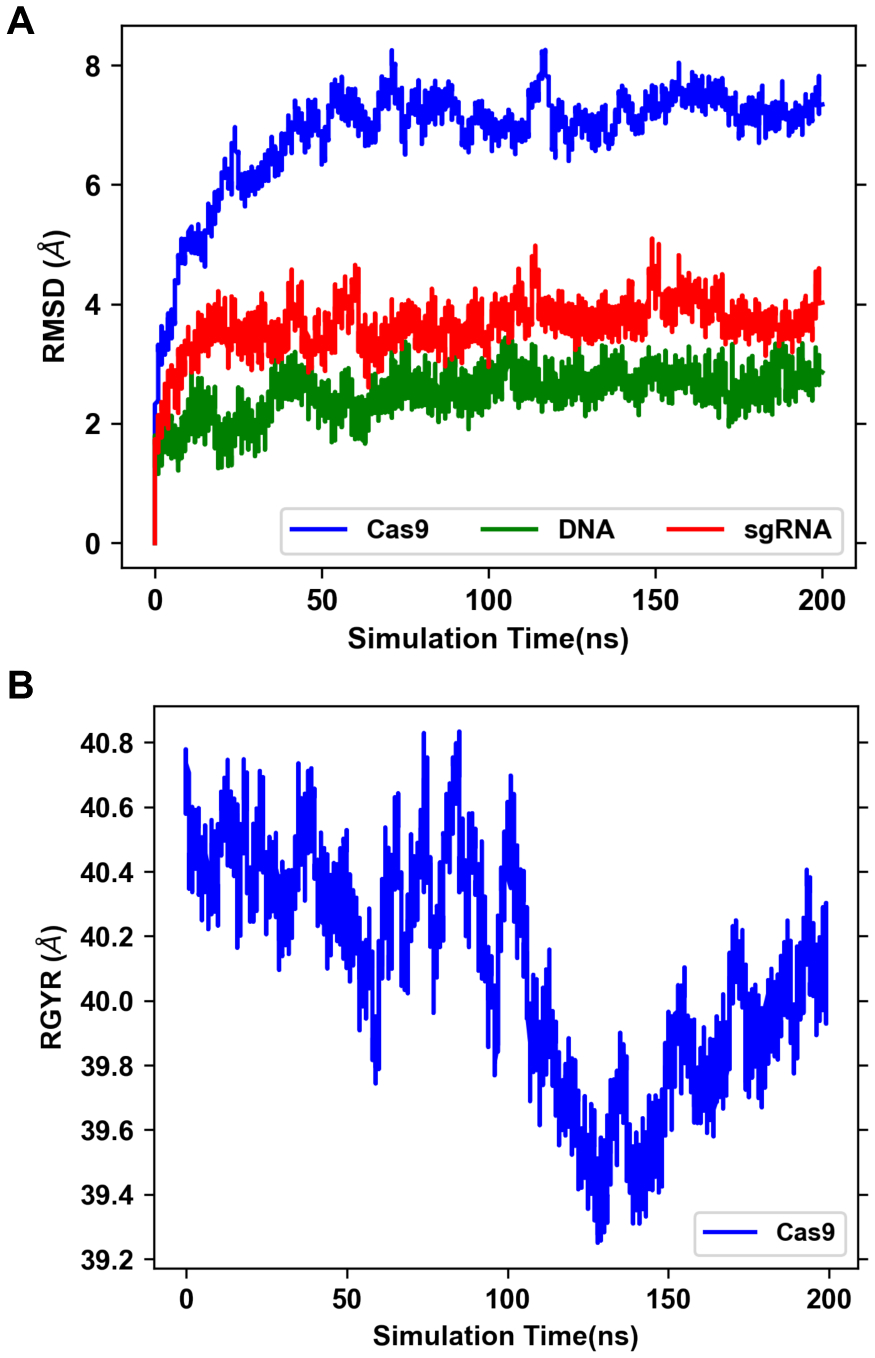
(A) RMSD of different components of Cas9 complex following alignment of each component to its initial structure. (B) RGYR of Cas9 protein.

Figure 7.

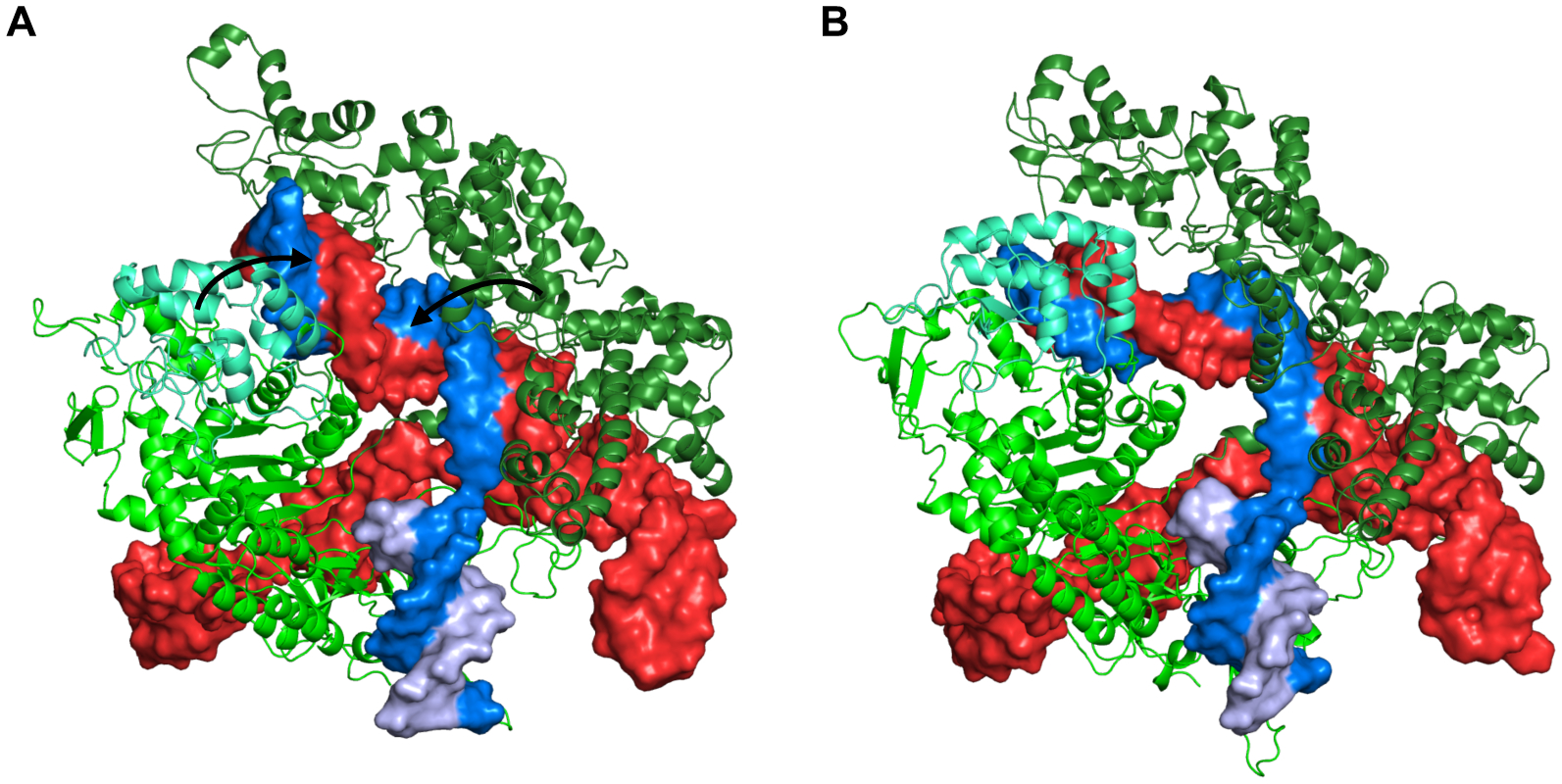
Conformations of Cas9-sgRNA-DNA complex at (A) 0 ns and (B) 200 ns. The protein is shown as green cartoon with the recognition lobe in forest green and the HNH domain in cyan. The polynucleotides are shown as surface with sgRNA in red, target DNA strand in marine blue, and non-target DNA strand in light blue. The arrows in (A) show the movement of the recognition lobe and HNH domain during the simulation that results in a conformation in (B).

Figure 8.

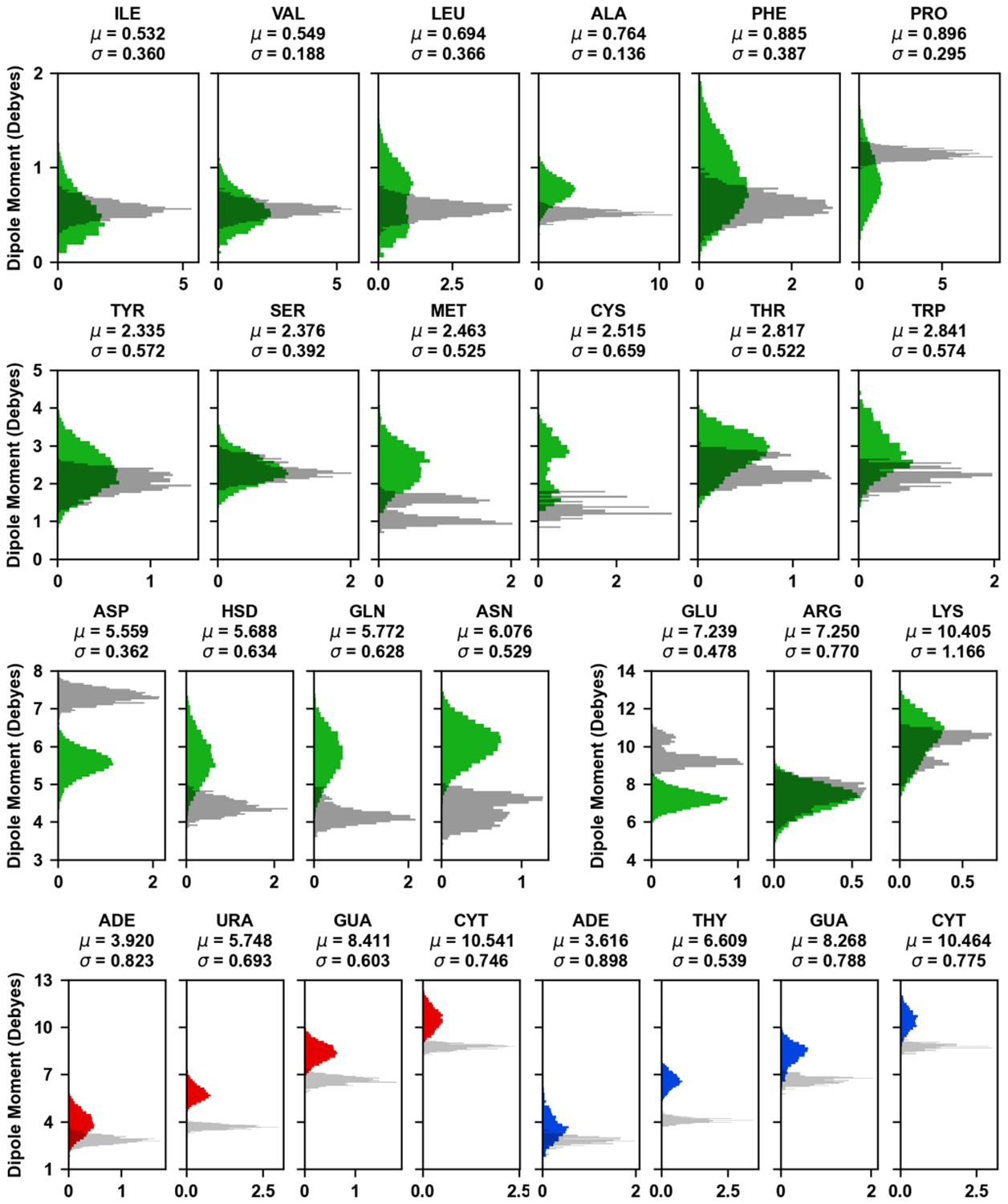
Distributions of dipole moments of amino acid sidechains and nucleobases in the Cas9 complex. The colored histograms correspond to the Drude FF (Cas9 – green; sgRNA – red; DNA – blue) calculated based on 200 ns simulation, while the transparent gray histograms represent the additive FF calculated based on the 1 ns pre-equilibration trajectory. The histograms are normalized and the mean and standard deviation from Drude simulations is shown above each subplot. Comparison of Drude FF dipole moment distributions at 1 ns and 200 ns is presented in Figure S3.

LeuT in a POPC bilayer:

The availability of the high-quality Drude FF parameters for both protein and lipids allows the study of membrane proteins with charge polarization. A LeuT homodimer in an outward-open conformation was embedded in a POPC lipid bilayer and subjected to a 200 ns MD simulations using OpenMM. The overall protein structure is stable during the MD trajectory. The slowly increasing RMSD mainly reflected the conformational changes of extracellular loops (Figure S4).

MalT-maltose complex in a mixed bilayer of DOPC and DOPE:

The Drude FF has also been tested for a protein-carbohydrate complex in a membrane. The MalT homodimer with a maltose in each binding site was embedded in a mixed bilayer of DOPC:DOPE=1:3 (Figure 1F). The distribution of glycosidic torsion angles of maltose (Figure 9A) shows good agreement with that obtained from GFDB (Glycan Fragment Database)¹²⁸ (Figure 9B) that is composed of a glycosidic torsion angle distributions of selected glycan sequences in the PDB. The dipole moments of head and tail groups of DOPC and DOPE lipids were calculated (Figure 10). There is no significant difference in the dipole moments of tail groups between DOPC and DOPE lipids, which is expected as they have identical acyl tails. The phosphatidyl ethanolamine (PE) head group shows a peak at higher dipole moments compared to phosphatidyl choline (PC), indicating that the PE head group is slightly more polar than the PC head group. The calculated dipole moments of lipid tail groups from the Drude simulations show broader distribution compared to the additive FF. In addition, Drude lipid head groups show higher dipole moments than the additive FF lipids.

Figure 9.

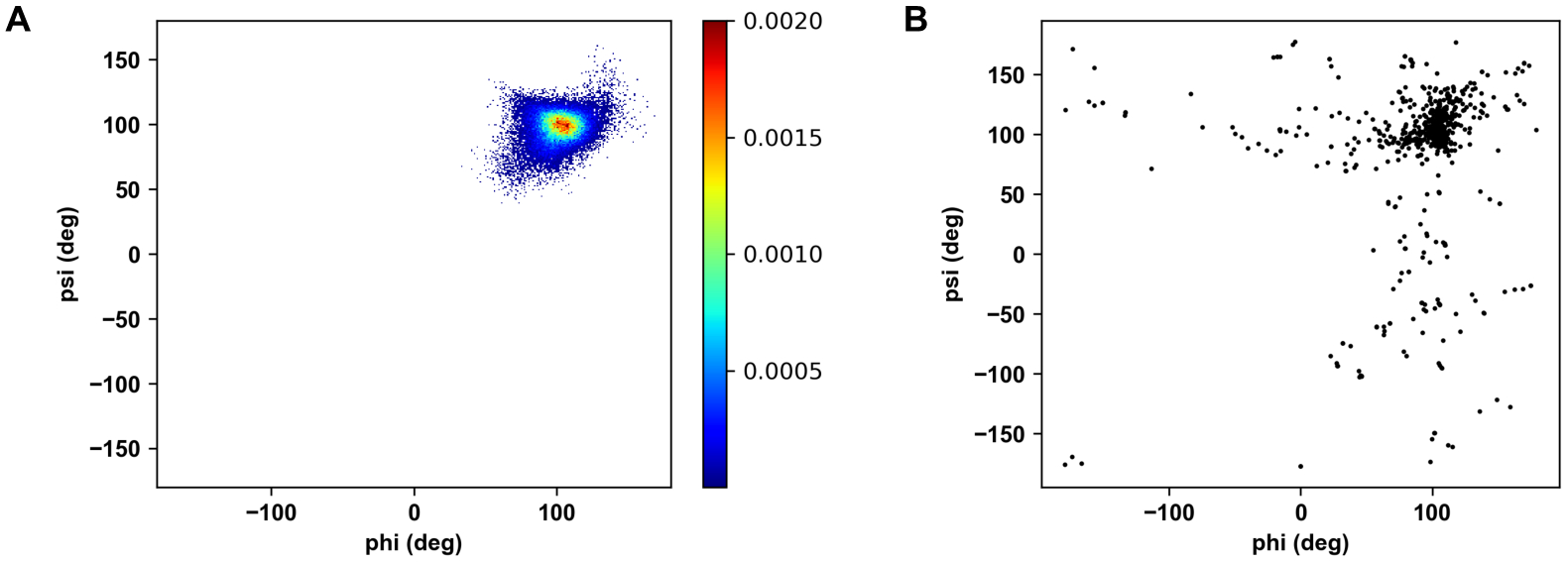
Distributions of glycosidic torsion angles of maltose in (A) MalT-maltose complex simulation and from (B) all PDB maltose structures.

Figure 10.

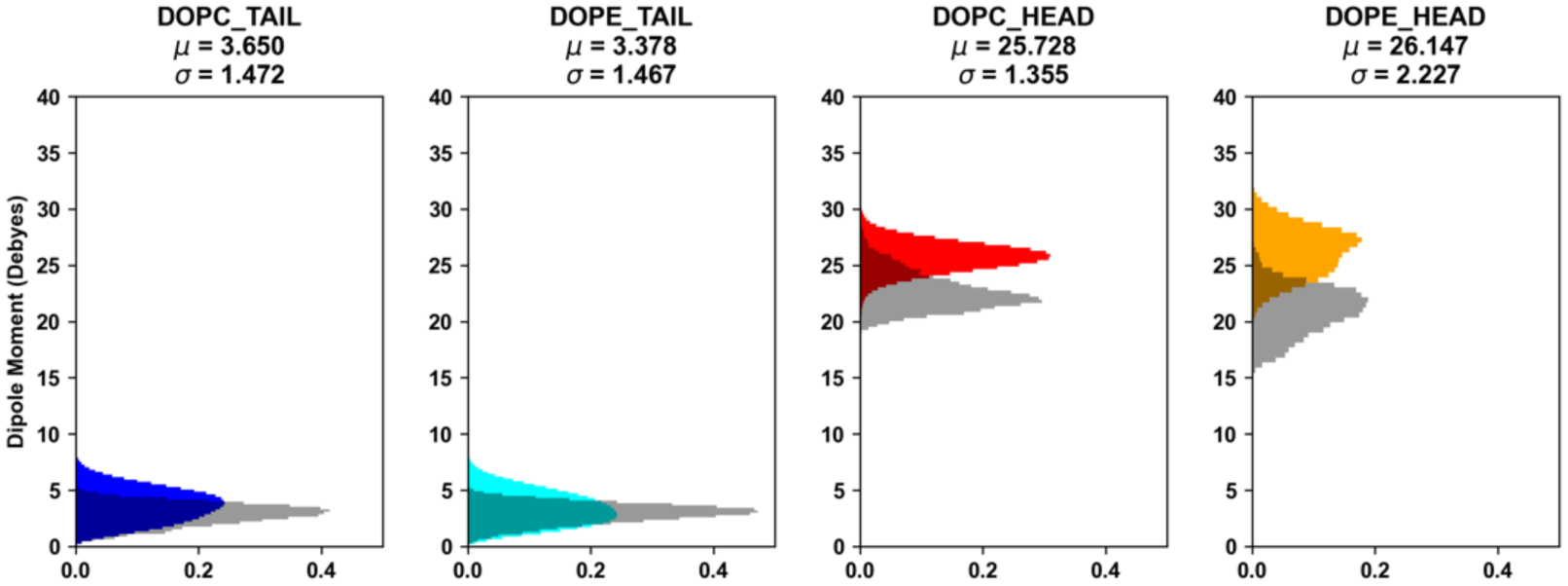
Distributions of dipole moments of membrane lipid head and tail groups over 200 ns simulations. The colored histograms correspond to the Drude FF (DOPC tail – blue; DOPE tail – cyan; DOPC head – red; DOPE head - orange), while the transparent gray histograms represent the additive FF calculated based on the 1 ns pre-equilibration trajectory. The histograms are normalized and the mean and standard deviation from Drude simulations is shown above each subplot.

Escherichia coli O176 O-antigen oligosaccharide:

We also ran a 200 ns simulation of the 10 repeating unit of O176 O-antigen oligosaccharide in solution with the Drude FF to calculate the ϕ/ψ glycosidic torsions, where ϕ = O5′−C1′−On−Cn, ψ = C1′−On−Cn−C (n−1), and n is the linkage position. The O176 O-antigen sequence is [α-d-Man(1→2)α-d-Man(1→2)β-d-Man(1→3)α-d-GlcNAc(1→4)]₁₀ (Figure 2A). The distribution of each glycosidic linkage is presented as a contour plot in Figure 11B. Except the ψ angle distribution of α-d-GlcNAc(1→4)α-d-Man (i.e., B-C in Figure 11A), the glycosidic torsion angles from the Drude simulation agree well with a previous study.¹²¹ Figure 11C shows the dipole moment distribution of each carbohydrate type, revealing large variations of dipole moments with different average values even for αMan and βMan. Note that for the carbohydrates, the charge on the monosaccharide units in the additive FF does not sum to be integer, so it is not possible to calculate well-defined dipole moments for a meaningful comparison.

Figure 11.

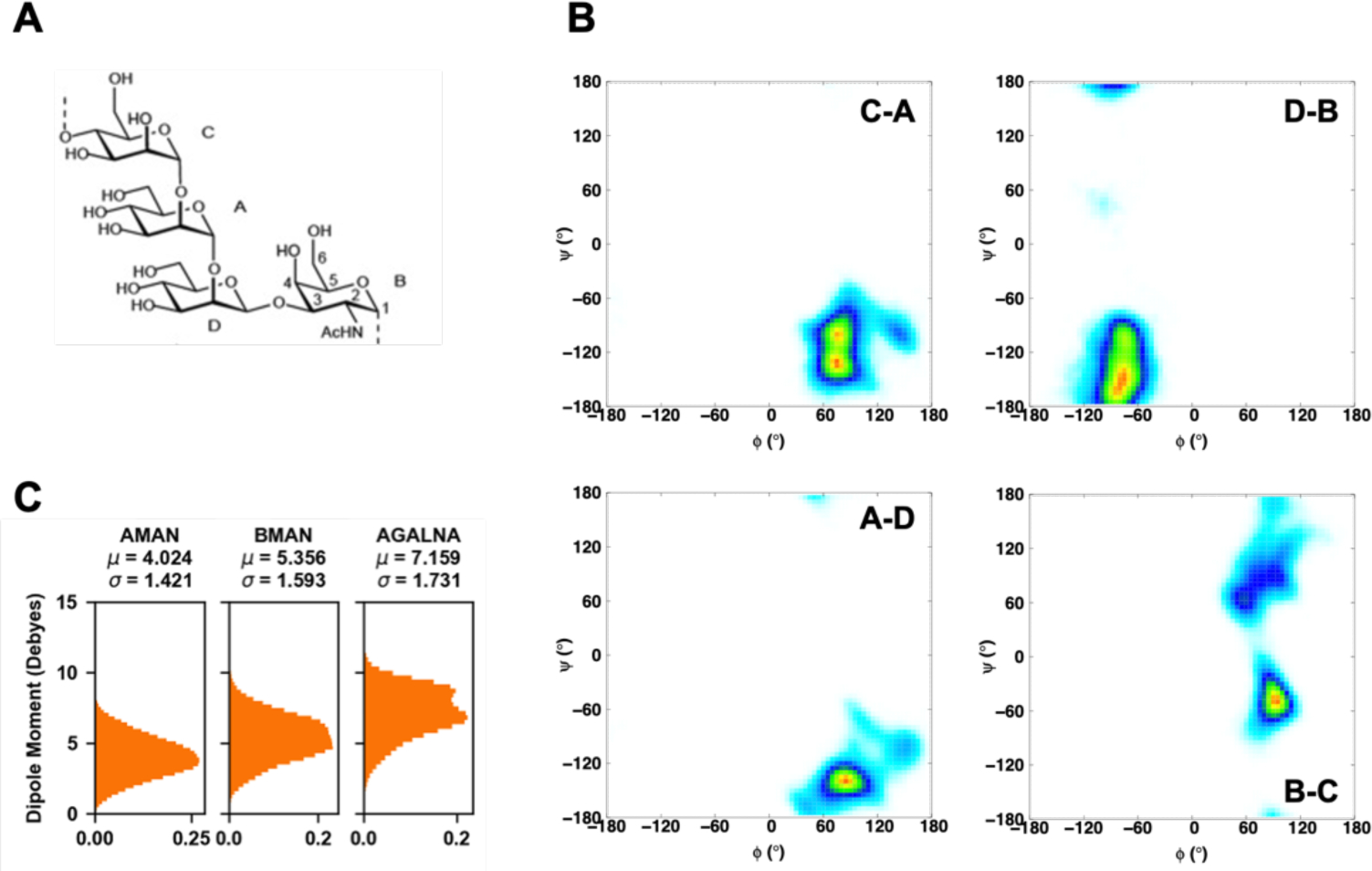
(A) Schematic structure of the repeating units of the O-antigen polysaccharides from E. coli O176. (B) Glycosidic torsion angles ϕ and ψ distributions. ϕ = O5′−C1′−On−Cn, ψ = C1′−On−Cn−C (n−1), where n is the linkage position. The probability range is from white, 0, to blue, 0.1, to green, 0.3, to yellow, 0.7, and to red, 1. (C) Distributions of dipole moments of sugar monomers in the Drude FF.

Moraxella catarrhalis serotype C oligosaccharide:

Previously, we used the CHARMM additive FF to perform 1 μs simulation of symmetric bilayer and solution systems of three serotypes A, B, and C lipooligosaccharides of M. catarrhalis. Here, the Drude FF has been tested with a serotype C oligosaccharide solution system. The distributions of ϕ/ψ glycosidic torsion angles over 200 ns are presented in Figure 12A, and these 2D distributions are consistent with the one in our previous study (Figure S5). In the case of ω torsion angle of β1–6 linkage at the first root residue, gauche–gauche (g−) conformations are dominant, almost identical to our previous study, but trans-gauche (t) conformations have a slightly bigger population. The ratio between rotamer conformations g−:g+:t from the Drude simulation is 58.4:34.7:6.9, which is consistent with the experimental result in that methyl α-d-glucopyranose shows a rotamer conformational ratio of 57:38:5.¹²⁹ Figure 12C shows the dipole moment distribution of each carbohydrate type, again revealing large variations of dipole moments with different average values for different carbohydrate types.

Figure 12.

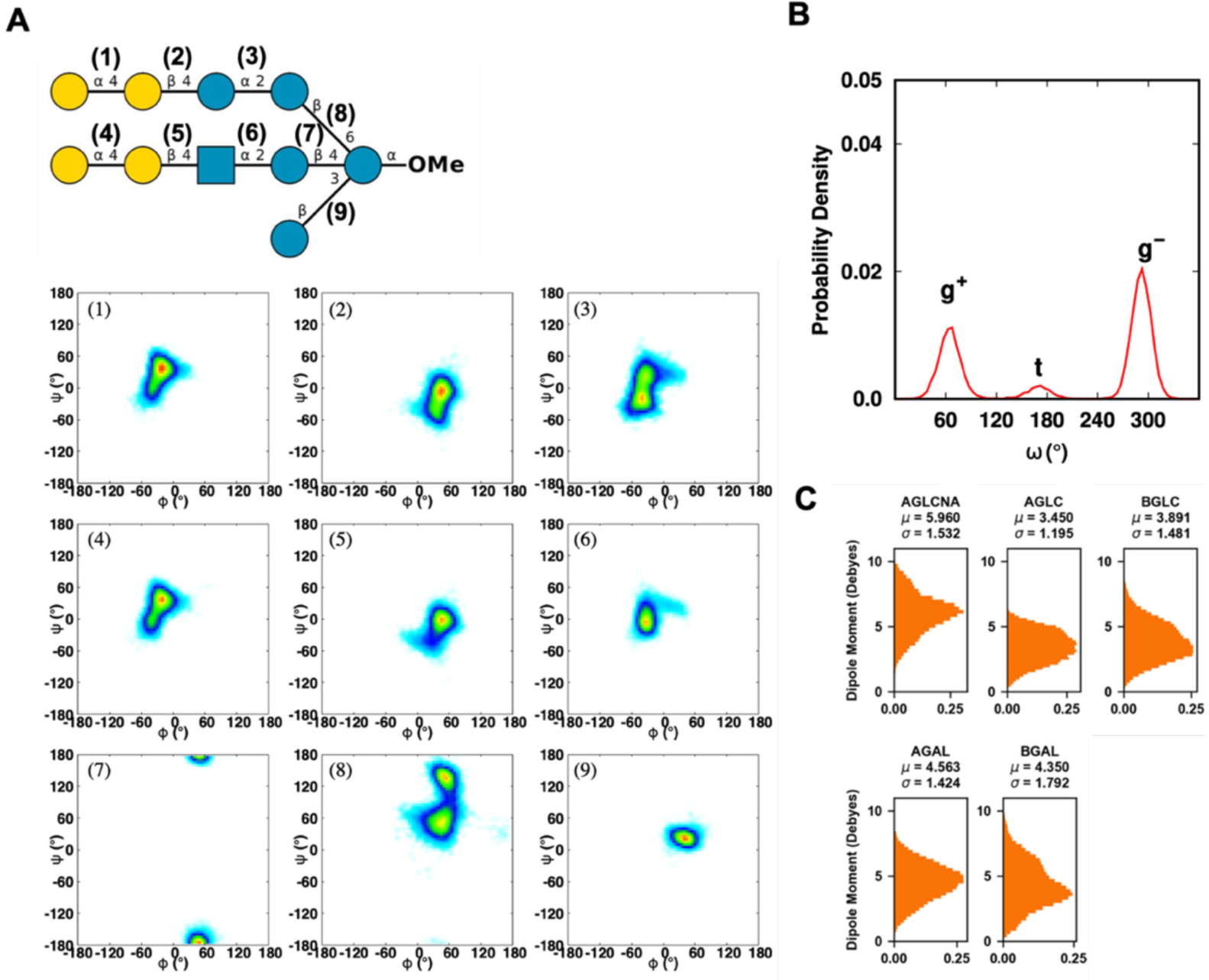
(A) Two-dimensional distributions of ϕ/ψ glycosidic torsion angles of serotype C oligosaccharide of M. catarrhalis. The glycosidic torsion angle definitions are defined in Figure 11. The probability range is from white, 0, to blue, 0.1, to green, 0.3, to yellow, 0.7, and to red, 1. (B) The torsion angle ω is defined as O6-C6-C5-O5, where g+ denotes gauche-trans, g− denotes gauche–gauche, and t denotes trans-gauche. (C) Distributions of dipole moments of sugar monomers.

Hyaluronate lyase in complex with hyaluronan substrate:

Streptococcus pneumoniae hyaluronate lyase enzyme in complex with a hexasaccharide hyaluronan substrate (PDB ID: 1LOH) was simulated for 200 ns with the Drude FF. The overall complex structure was stable during the simulation (Figure 13A). The hexasaccharide substrate remains stably bound in the active site of lyase enzyme. To understand the stability of the substrate binding to the active site, hydrogen bond analysis was carried out. A time-series of the intermolecular hydrogen bonds between the lyase enzyme and the hexasaccharide is shown in Figure 13B. At least more than 3 hydrogen bonds exist in ~80% of the trajectory. Especially, R243 and R300 form these hydrogen bonds with the forth sugar (O61 of GlcA) in ~64% and ~35%, N580 with the second sugar (O2 of GlcA) in ~44%, N290 with the second sugar (O3 of GlcA) in ~34%, E477 with the fifth sugar (O6 of GlcNAc) in ~33%, and D293 with the third sugar (O6 of GlcNAc) in ~23% (Figure 13C,D). This result is well matched with the previous site-directed mutation study showing that R243 and N580 are involved in substrate binding, whereas N349, H399, and Y408 are involved in the catalytic process. The lower number of hydrogen bonds in the later residues are understandable because this enzyme is the Y408F mutant (inactive) form. Clearly, the hyaluronan substrate is stably bound due to the charge complementarity between substrate negative charges and the multiple basic residues lining the cleft surface. Such electrostatic interactions in the binding cleft are well characterized in the Drude simulation, as the dipole moment distributions of amino acids around the substate within 4.5 Å (i.e., substrate-contact residues) are wider than the non-contact protein residues (Figure S6).

Figure 13.

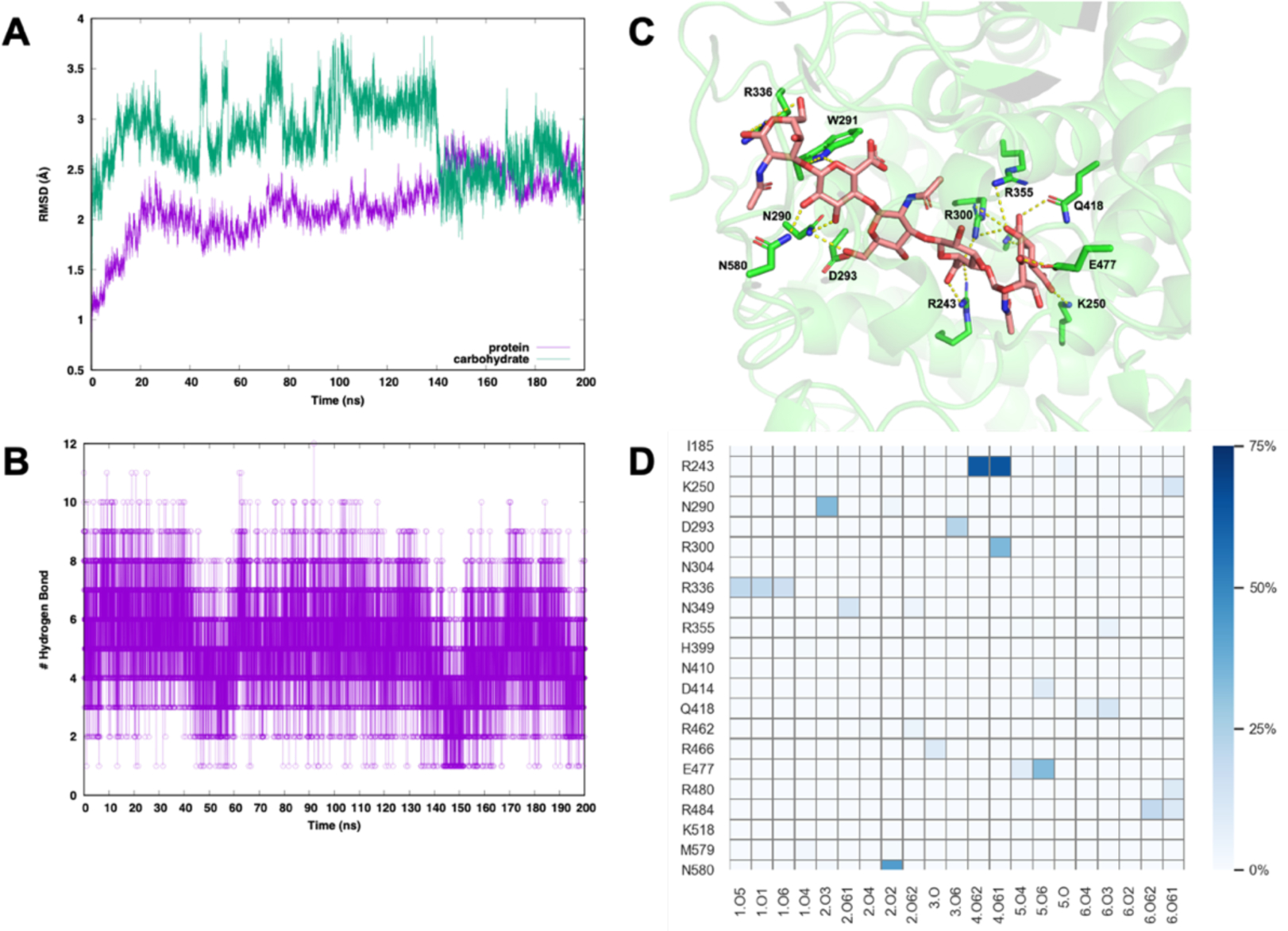
(A) Backbone RMSD of hyaluronate lyase (purple) and hyaluronan substrate (green). (B) The number of hydrogen bonds between a hyaluronan substrate and its enzyme (C) A snapshot of complex structure at 30 ns (D) Hydrogen bonding frequencies between a hyaluronan substrate and its enzyme. The y-axis labels the interacting amino acid residues, and the x-axis labels the interacting atoms of the substrate. The color bar represents the frequency of hydrogen bonding observed in the simulation trajectory.

CONCLUSIONS

In this work, we present Drude Prepper, a new utility in CHARMM-GUI, a web-based tool that will facilitate the use of the Drude FF by the scientific community for studies of a multitude of biomolecular systems. The Drude FF for proteins was first released in 2013 and only a few research groups have been using it as compared to the number of studies using the additive FF. CHARMM-GUI, by providing a simplified platform to diverse users, has played an important role in facilitating the use of the CHARMM additive FF, and we anticipate that the Drude Prepper will give the same access to the CHARMM Drude FF. Here, we have demonstrated the best practices to use Drude Prepper by applying it to various systems including proteins, DNA, RNA, lipids, carbohydrates, atomic ions, and their combinations. Drude Prepper takes the advantage of using the same residue nomenclature as in the CHARMM additive FF to allow for the additive PSF to be readily converted to its Drude counterpart. This avoids the major effort that would be required to build each simulation system from scratch. The inputs generated by Drude Prepper are highly consistent across the four simulation packages (CHARMM, NAMD, OpenMM, and GROMACS), and the energies calculated with the 4 simulation programs with the generated data structures and inputs are in agreement. The inputs for GROMACS are currently available for protein only systems, and there are ongoing efforts to extend the inputs to other classes of molecules. While the analysis of simulations performed in this study demonstrate the applicability of the Drude FF, they also highlight the ability of the Drude FF to provide potentially important information based on dipole moment variations occurring in the simulations.

Data Availability Statement

All the protein structures and molecular dynamics data are available upon request. Drude Prepper can be accessed through the following link: https://www.charmm-gui.org/input/drude.