Is group testing ready for prime-time in disease identification?

Abstract

Large-scale disease screening is a complicated process in which high costs must be balanced against pressing public health needs. When the goal is screening for infectious disease, one approach is group testing in which samples are initially tested in pools and individual samples are retested only if the initial pooled test was positive. Intuitively, if the prevalence of infection is small, this could result in a large reduction of the total number of tests required. Despite this, the use of group testing in medical studies has been limited, largely due to skepticism about the impact of pooling on the accuracy of a given assay. While there is a large body of research addressing the issue of testing errors in group testing studies, it is customary to assume that the misclassification parameters are known from an external population and/or that the values do not change with the group size. Both of these assumptions are highly questionable for many medical practitioners considering group testing in their study design. In this article, we explore how the failure of these assumptions might impact the efficacy of a group testing design and, consequently, whether group testing is currently feasible for medical screening. Specifically, we look at how incorrect assumptions about the sensitivity function at the design stage can lead to poor estimation of a procedure’s overall sensitivity and expected number of tests. Furthermore, if a validation study is used to estimate the pooled misclassification parameters of a given assay, we show that the sample sizes required are so large as to be prohibitive in all but the largest screening programs.

1 |. INTRODUCTION

Developing design strategies to reduce study expense is an important job for the practicing biostatistician. In many settings, measuring biomarkers can be expensive, and design strategies for reducing these costs are needed. In 1943, Dorfman¹ proposed a simple method to make the testing of syphilis feasible in recruits for the US Army. This simple design suggested testing a grouped collection of k samples, and only testing individual samples if the combined sample is positive. Intuitively, this design could provide a tremendous cost reduction in terms of the required number of tests if the disease prevalence is small.

There has been a vast amount of research in group testing since the original Dorfman paper. A majority of this work can be divided into either using group testing for disease screening or for prevalence estimation. Particularly for the application of group testing to screening, there has been lots of work not only in the statistics literature, but also in computer science and applied mathematics (see References 2–6, among others). This is because optimality of group testing algorithms often involves choosing a particular set of group sizes that minimizes the expected number of tests required to identify all cases in a population of individuals. Deriving optimal designs often involves the development of complex algorithms that rely on dynamic programming, mathematical techniques that are usually applied in areas of applied mathematics and computer science, and less often in statistics. There has also been extensive work in prevalence estimation, where participants are tested in groups with no retesting at the individual level. This article will focus on the use of group testing in disease screening.

Although methodological research in this area has expanded, we believe that there has been limited use of these designs as they were originally formulated in the biomedical sciences for disease screening. Some notable exceptions do exist, such as the screening of donated blood for HIV and hepatitis.⁷ More recently, group testing has received increasing attention for SARS-CoV-2 screening. However, the successful implementation of group testing in this area remains unclear at this point.^8–10 We have seen a reluctance by our epidemiological collaborators to use these designs in large-scale studies. In part this is due to our laboratory and epidemiology colleagues not being aware of the advantages of the group testing methodology. However, most often, scientists are afraid that combining different participants in a single sample will decrease the sensitivity of an assay, thereby increasing the likelihood of a false negative on a grouped test. Furthermore, it is perceived that in much of the group testing literature unreasonable assumptions have been made that, in many cases, favor the use of group testing procedures over single testing. The goal of this current article is to provide a balanced view of the research in this area and to provide suggestions for evaluating its feasibility in practical settings.

There are a number of issues that have caused confusion and have made comparisons with individual testing difficult. These include

1. Questions over how to choose a design that appropriately accounts for misclassification.

2. Assumptions of nondifferential misclassification, that is, that the testing errors do not change with the group size.

3. Assumptions that sensitivity and specificity values are known a priori from external sources and can be readily applied to the question at hand.

A careful comparison of group testing with individual testing that takes into account these issues is important in deciding the situations where group testing should be used for disease identification in the biosciences. Although aspects of these issues have been addressed in the statistics literature, there has not been a careful statistical examination of these issues in totality. In what follows, we introduce several case studies that are representative of the types of problems in which group testing is appealing to researchers, but current limitations raise questions about or prevent its use. This is followed by a full discussion of each of the above issues. We then present numerical comparisons to examine the impact of incorrect assumptions regarding the misclassification parameters on a screening procedure and the feasibility of using a validation study to estimate these values.

2 |. CASE STUDIES

2.1 |. Population-based screening for SARS-CoV-2 infection

Coronavirus disease 2019 (COVID-19) caused by the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) was first identified in Wuhan, China in late 2019 and is rapidly spreading worldwide with dramatic impacts on the healthcare and economic landscapes. In the United States, shortages of testing reagents hinder the ability to carry out sufficient screening for infection with SARS-CoV-2 which may ultimately threaten the ability of public health officials to adequately control the spread of the virus. The need for large-scale screening, coupled with scarce testing resources, make this an ideal scenario for implementing group testing to reduce the number of tests required to carry out a screening program.

2.2 |. Large-scale screening for HIV viral load

Monitoring of viral load in individuals diagnosed with HIV is important for determining treatment failure and making informed treatment decisions. Current World Health Organization guidelines recommend viral load testing at 6 and 12 months following initiation of antiretroviral therapy (ART), and annually thereafter.¹¹ These tests are meant to determine if an individual’s viral-load has surpassed a given threshold, potentially indicating treatment failure. Current recommendations define treatment failure as a test measuring a viral load higher than 1000 copies/mL. These recommendations have proven to be cost prohibitive, and continue to be impractical in many low resource settings. For example, in Malawi, a country with over 1 million people living with HIV and over 600 000 taking ART,¹² the annual burden of sufficient viral load monitoring is enormous. In this context, group testing has regularly been considered as a cost saving measure, however concerns over false negative rates are common.^13–15

2.3 |. Stratified cancer screening

Cervical cancer is currently the fourth most common cancer among women,¹⁶ highlighting the need for cheap and effective clinical screening. The most effective indicator of cervical cancer risk is HPV infection, however only a small number of HPV positive women will go on to develop cervical cancer. To minimize unnecessary and invasive follow-up procedures such as colposcopy, it is necessary to develop better tests for triaging HPV infections in order to identify those at greater risk of progressing to cancer. One promising method is methylation testing which captures the methylation of HPV DNA transitioning to precancer.^16–18 Unfortunately, such tests are too expensive to routinely carry out for all HPV positive women. Group testing could offer one way of making such testing feasible.

2.4 |. Biomarker presence in a cohort study

In many cohort studies specimens collected from individual participants are to be screened for a variety of biomarkers. For example, the Connect study is a cohort study funded by the National Cancer Institute planning to enroll 200 000 adults in the United States with the goal of understanding the etiology of cancer through longitudinal assessment of biomarkers, environmental exposure, and the occurrence of cancer precursors. One biomarker of interest in this study is monoclonal gammopathy of undetermined significance (MGUS), a premalignant plasma cell disorder present in about 3% of adults.¹⁹ MGUS is a precursor for multiple myeloma and other blood cancers. Screening all cohort participants for MGUS would add significant costs to the Connect study, a particular concern since it is one of many biomarkers of interest. In theory, this is an ideal case for group testing since the low prevalence of MGUS would result in a large reduction in the number of tests to screen the entire cohort.²⁰ In practice, however, the sensitivity of pooling procedures when screening for MGUS is unknown, and a validation study would be required to characterize test performance for grouped samples and then to assess the feasibility of group testing in this case. When considered for this particular study, the costs of this validation study would have to be considered in light of the, initially unknown, potential savings from a pooling design.

3 |. NOTATION AND DORFMAN PROCEDURE

For a screening program, we assume a population of N individuals for which the presence of a binary characteristic (eg, an infectious disease or an HIV viral load >1000 copies/mL) is represented by random variables x_i, i = 1, 2, …, N. When referring to a population, we mean all potentially tested individuals with similar characteristics including demographics, type and temporality of testing, and selection of the individual samples for testing. We will assume that each member of this population has an identical probability, p, of having said characteristic so that x_i ~ Bernoulli(p), i=1, 2, …, N and that each x_i is independent of the others. For grouping, often a maximum feasible group size will exist which we denote by k_max. The set of possible group sizes is then $\mathcal{K}=\left\{1,2,\dots ,k_{max}\right\}$. For a group of size k, let ${\tilde{y}}^{(k)}$ be a random variable which is 1 if at least one member of the group has the given characteristic and 0 otherwise. Then, since each x_i is independent, ${\tilde{y}}^{(k)}~Bernoulli\left(1-{(1-p)}^k\right)$.¹ Since testing error may make observation of ${\tilde{y}}^{(k)}$ impossible, let y^(k) represent the observed value of this random variable from a test based on a given assay. For the assay of interest, we define the sensitivity and specificity for a grouped test containing k individuals to be $Se(k)=P\left(y^{(k)}=1\mid {\tilde{y}}^{(k)}=1\right)$ and $Sp\text{(}k\text{)}\text{=}P\left(y^{(k)}=0\mid {\tilde{y}}^{(k)}=0\right)$, respectively. We consider that these probabilities may change with the group size, which is referred to as differential misclassification. When the misclassification parameters are constant for any k, we say that there is nondifferential misclassification. Using these definitions, the probability of a positive test is $P\left(y^{(k)}=1\right)=Se(k)P\left({\tilde{y}}^{(k)}=1\right)+(1-Sp(k))P\left({\tilde{y}}^{(k)}=0\right)=Se(k)-(Se(k)+Sp(k)-1){(1-p)}^k$ so that y^(k) ~ Bernoulli(Se(k)−(Se(k)+Sp(k)−1)(1−p)^k).

The first published group testing procedure proposed by Dorfman¹ is a simple two-stage procedure. To implement it, a group size k is chosen and the population is divided into groups of that size. For each group, an initial grouped test is carried out to determine if any of the samples within are positive for the disease. If negative, each sample is assumed to be disease free. If positive, additional samples from each individual in the group are tested to identify those with the disease. If T is the number of tests required to assign a status to an individual, the choice of k is typically made to minimize the expected T (ie, the expected number of tests per person) which is given by

$$\begin{gathered} \text{E}(T\mid p,k,Se(k))=\frac{1}{k}\left[P\left(y^{(k)}=0\right)+(k+1)P\left(y^{(k)}=1\right)\right] \\ =\frac{1}{k}\left[kP\left(y^{(k)}=1\right)+1\right] \\ =Se(k)-(Se(k)+Sp(k)-1){\left(1-p\right)}^k+\frac{1}{k}. \end{gathered}$$

Typically, such designs are optimized with respect to the expected number of tests.

Another important quantity which is not typically accounted for is the overall sensitivity (specificity) of a test defined as the probability that a positive (negative) individual is correctly identified as positive (negative) at the termination of the pooling procedure (eg, for a positive individual, the probability that the test at each stage of a group in which they are a member is positive). For clinicians and researchers, these quantities are the most important since they allow for an understanding of how many false positives and negatives can be expected in a population when using a group testing procedure and have simple individualistic interpretations (since they express the misclassification probabilities for an individual being screened).

Our reason for focusing on the Dorfman procedure here over more complicated designs with more stages is 2-fold. First, it is a simple intuitive design which can easily be implemented and explained to researchers. Second, by requiring only two stages, the Dorfman procedure will typically maximize the overall procedure sensitivity. To see why this is so, note that, even if misclassification probabilities do not change with group sizes(eg, they are nondifferential), group testing will generally lead to smaller sensitivities and larger specificities as a result of repeated testing (eg, repeated testing yields more chances for a mistake). Generally, this means that overall sensitivity will decrease with the number of stages in a group testing procedure.

Much of the more recent group testing literature has focused on alternative schemes, such as those that create smaller subgroups following a positive test prior to individual testing, which generally have a smaller number of expected tests when compared with the Dorfman procedure. However, each additional stage will decrease the overall sensitivity of the screening program and result in an overall sensitivity which is difficult to quantify. The Dorfman procedure, however yields a simple closed form expression for the overall sensitivity. For example, if a single unit test is treated as a gold standard (no misclassification) the overall sensitivity of the Dorfman procedure with initial group size k will be Se(k). It will be very hard, if not impossible, for any reasonable group testing design to have a lower overall sensitivity of the Dorfman procedure.

4 |. TESTING WITH MISCLASSIFICATION AND COMPARISON WITH SINGLE TESTING

Since nearly all of the issues impeding the use of group testing in medical settings involve questions of misclassification, we briefly review the literature related to this issue here. Beginning in the 1970s with the resurgence of research in group testing, methodology for accounting for misclassification was proposed. The idea is that even if a test on a single sample has little or no misclassification, it is natural to think that there may be measurement error induced by the combining of samples across individuals. Graff and Roeloffs (1972)²¹ and Hwang (1976)²² recognized early that the objective function to minimize should not simply be the expected number of tests when tests can be misclassified. Graff and Roeloffs (1972)²¹ proposed a modification of the Dorfman procedure and searched for a design that minimizes total cost as a linear function of the expected number of tests, weighted expected number of good items misclassified as defective, and weighted expected number of defective items misclassified as good. Burns et al (1987)²³ generalized Graff and Roeloffs (1972) results to the situation where the probability of misclassification depends on the proportion of defective items in the group.

Hwang (1976)²² studied a group testing model with the presence of a dilution effect, where a group containing a few defective items may be misidentified as a group containing no such items, especially when the size of the group is large. He calculated the expected cost under the Dorfman procedure in the presence of the dilution effect and derived the optimal group sizes to minimize this cost. Further, Wein and Zenios (1996)²⁴ embedded a group testing model for continuous test outcomes into a dynamic programming algorithm that derives a group testing design to minimize a linear combination of expected cost due to false negatives, false positives, and testing. Malinovsky et al (2016)²⁵ characterized the optimal design in the Dorfman procedure in the presence of nondifferential misclassification by maximizing the ratio between the expected number of correct classifications and the expected number of tests. Using the same criterion and testing procedure, they also characterized a cut-off point of disease prevalence where all individuals should be tested together at the first stage.

Aprahamian et al (2019)²⁶ considered the Dorfman procedure in the population with heterogeneous prevalences^27,28 under the setting of nondifferential misclassification. They investigated two models: in the first one a linear combination of the expected number of false positives, false negatives and total number of tests was minimized; in the second one a linear combination of the expected number of false positives and false negatives was minimized, subject to constraints on the upper bound of the expected total number of tests. In contrast to earlier work, recent authors have argued that the expected number of tests alone should be used and that careful accounting for the number of correct classifications is an unnecessary complication.²⁹ The basis for Hitt et al’s²⁹ argument that misclassification need not be considered in optimal design is based on a comparison of the expected number of tests versus the ratio of the expected number of tests and the expected number of correct classifications. Note that the above citations do not provide an exhaustive list of approaches and many additional works have addressed group testing under misclassification (see, eg, References 30–35)

Many recent papers assume nondifferential misclassification. Specifically, they assume that misclassification does not depend on the size of the group and that there is misclassification for a test used for on a single or individual sample. Although the assumption of nondifferential misclassification may be reasonable for some types of sample pooling, it cannot be generally assumed. Further, misclassification needs to be defined relative to a gold standard. A natural comparison of group testing screening designs is with a design where individuals are tested separately. In many cases, it is reasonable to assume that the assay tested on a single sample is the gold standard. In this case, misclassification for group testing will be relative to single testing with the sensitivity and specificity of the individual test being 1, as it also was assumed earlier by Hwang (1976).²²

5 |. WHAT IS THE OPTIMAL DESIGN?

As can be seen from the previous section, many works have appropriately attempted to account for misclassification for the optimal group testing design for disease identification. Minimizing the expected number of tests has been used as an objective function.²⁹ In other previous works, authors have proposed minimizing a linear combination of the expected number of tests and the rate of correct classification.^21,23,26 However, choosing the coefficients for these terms is subjective and may be difficult to motivate from a medical or public health perspective. Some authors include a cost for incorrect classification^22,24 which may also difficult to motivate from a medical or public health perspective. Although, the criterion proposed by Malinovsky et al²⁵ does not require such specifications, it assigns the same weight for the expected number of tests and the expected number of correct classifications, and therefore can also be subjective.

A larger issue is that none of these cited works have considered the impact of differential misclassification. In this case, an optimization procedure which does not constrain the misclassification parameters may lead to unacceptably low values of sensitivity and/or specificity and overly optimistic estimates of the savings provided by group testing. For example, based on the Dorfman procedure, the expected number of tests per person (or individual) is a decreasing function of the sensitivity. Therefore, if sensitivity is changing with group sizes, the group size minimizing the expected number of tests may result in very low sensitivity. In this work, we address both of these issues by proposing a simple, easy to interpret, optimization problem so that the group size k is chosen to satisfy the following:

$$\begin{gathered} \underset{k\in \mathcal{K}}{\arg \min }\text{E}(T\mid p,k,\mathrm{Se}(k),Sp(k)), \\ \text{subject}\text{to}Se(k)\ge {\delta }_1, \\ \text{subject}\text{to}Sp(k)\ge {\delta }_2, \end{gathered}$$ (1)

where δ₁ and δ₂ are fixed threshold values and, p, Se(k), and Sp(k) are assumed known. Here, the objective function is the expected number of tests per person (or individual) and the misclassification parameters are subject to lower bounds. This has the benefit of being very easy to interpret and explain to nonstatisticians. Furthermore, it ensures that the misclassification parameters are sufficiently high in the final design.

6 |. IMPORTANCE OF CORRECTLY SPECIFYING SE(K) AND SP(K)

Despite the advantages of this approach, a major drawback (which is shared with all previous approaches), is that it relies on the assumption that the parameters Se(k) and Sp(k) are known. In reality, this is almost never the case and researchers are likely to have little a priori information on the magnitude of the misclassification parameters and whether or not they change with the group size. As such, to choose an optimal design and understand its properties, it is essential that researchers first acquire knowledge of the diagnostic performance of the assay for grouped samples. Without such knowledge no claim that group testing is more efficient than individual testing for disease screening can confidently be made. By far the most common approach in the group testing literature is to use estimates of sensitivity and specificity found in the literature. There are a number of issues of concern here. First, the estimates of sensitivity and specificity are often based on studies conducted in other populations. The problem of applying the sensitivity and specificity of an assay in one population when they were estimated in a different population with a different mix of patients has been well recognized in the area of diagnostic medicine.³⁶ Second, the uncertainty in the estimation of sensitivity and specificity is not taken into account in most comparisons.

Misspecification of the sensitivity and specificity can impact the testing procedure in two primary ways. First, even small differences can lead to changes in the optimal choice of design. This is particularly true if the sensitivity changes with the group size, since the expected number of tests typically decreases with the sensitivity. This will result in a poor understanding of the expected number of tests for a given design and may lead to poor decisions regarding the application of a group testing procedure in a given population.

Second, misspecification of the misclassification parameters can lead to choosing a design with very high error rates. For example, if the sensitivity of an assay is decreasing with group size then overestimating the sensitivity by even a small degree can lead to choosing a large group size for which the assumed overall error rate estimate is overly optimistic.

These issues are illustrated in the following example.

6.1 |. Example

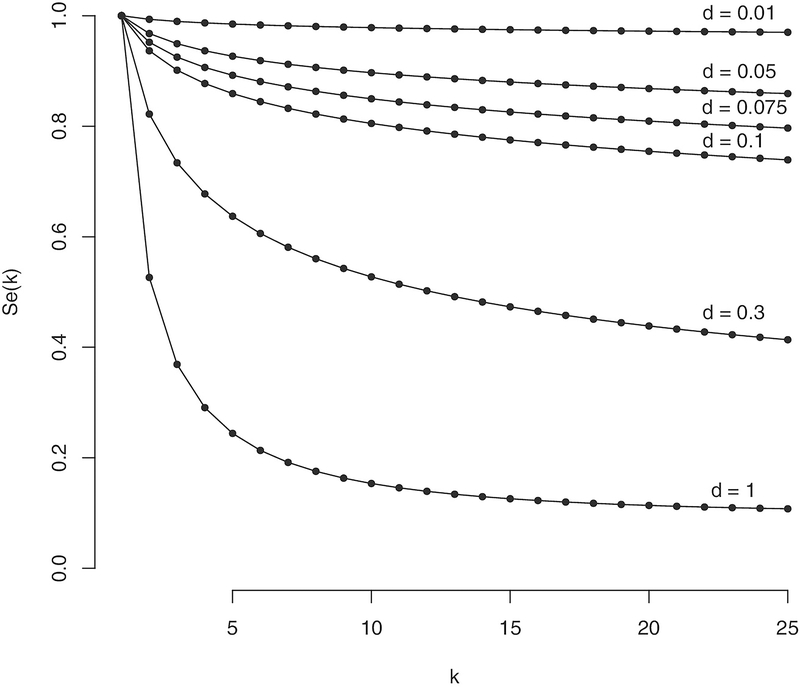
In this section, we explore numerically how misspecification of the sensitivity function, Se(k), when choosing an optimal design can lead to errors in the estimation of a procedure’s overall sensitivity as well as the expected number of tests. We will assume in all cases that Sp(k)=1. While this assumption will not be true in many settings, it is sufficient here to illustrate how poor a priori information regarding the sensitivity function can lead to bad design choices. Furthermore, grouped specificity is often of only secondary interest to researchers as, even if the specificity decreases with the group size, group testing still results in a larger overall specificity than individual testing. This is true since, to ultimately be determined positive, an individual must undergo testing at least two stages, one of which is at the individual level. To illustrate different potential ways the sensitivity might be subject to differential misclassification, we consider the function $Se(k)=f_H(p,k,d)=\frac{p}{1-{(1-p)}^{k^d}}$, due to Hwang (1976),²² for various values of d. This function allows us to model the sensitivity as a function of the group size k using an index parameter d for which the sensitivity decreases as d ranges from 0 to 1. Note that, when d=0, f_H(p, k, 0)=1 indicating that the grouped assay is perfectly sensitive (ie, false negatives do not occur). For d=1, f_H gives the probability of a single unit being positive given there is at least one positive in the group. Plots of f_H for p=0.1 and k =1, 2, …, 25 for various values of d are shown in Figure 1. For our example, we assume that the true assay sensitivity can be represented by taking d=0.075, and will look at designs constructed assuming values of d=0.01, 0.05, 0.1, and 0.3. The value of d=0.075 represents a moderate decay of the sensitivity function as k increases and allows for the comparison of cases when the sensitivity function is both underestimated (eg, d is assumed to be greater than 0.075) and overestimated (eg, d is assumed to be less than 0.075). In this context, underestimation implies that we assume the sensitivity function decreases more quickly with increasing group sizes and reaches a lower point than is true. Likewise, overestimation implies that we assume the sensitivity function decreases more slowly with increasing group sizes and does not decrease as far as what is true.

FIGURE 1.

Plot of sensitivity function, Se(k)=f_H(p, k, d) for p=0.1 for various values of k and d

To find the optimal group size, k_opt, we consider two approaches. The first, for a given p and function Se(k), solves the unconstrained optimization problem

$$\underset{k\in \mathcal{K}}{\arg \min }\text{E}(T\mid p,k,Se(k)),$$

where $\mathcal{K}$ is the set of all possible group sizes and

$$\text{E}(T\mid p,k,Se(k))=\{\begin{array}{ll}1,\hfill & k=1\hfill \\ Se(k)\left[1-{(1-p)}^k\right]+1/k,\hfill & k\ge 2\hfill \end{array}.$$

The second approach enforces a lower bound on the overall sensitivity of a procedure by finding k which satisfies:

$$\begin{gathered} \underset{k\in \mathcal{K}}{\arg \min }\text{E}(T\mid p,k,Se(k)), \\ \text{subject}\text{to}Se(k)\ge \delta \text{,} \end{gathered}$$ (2)

where δ is a fixed threshold value and, again, p and Se(k) are assumed known.

For our numerical comparisons, we set $\mathcal{K}=\{1,2,\dots ,25\}$ and δ = 0.95. Results are shown in Table 1. The table contains estimates for three basic quantities:

• k_opt, the optimal group size chosen for a given optimization procedure;

• Se(k_opt), the sensitivity function evaluated at the optimal group size;

• E(T|k_opt), the expected number of tests for a given procedure based on the optimal group size.

TABLE 1.

Assumed design parameters when the true sensitivity function is Se(k) = f_H(p, k, d = 0.075) and ${\widehat{k}}_{opt}$ is chosen with the assumption that d = 0.01, 0.05, 0.1, or 0.3

		Unconstrained								Constrained
p	d	${\widehat{k}}_{opt}$	kopt	$\widehat{Se}({\widehat{k}}_{opt})$	$Se({\widehat{k}}_{opt})$	Se(kopt)	$\widehat{E}(T\mid {\widehat{k}}_{opt})$	$\widehat{E}(T\mid {\widehat{k}}_{opt})$	E(T|kopt)	${\widehat{k}}_{opt}$	kopt	$\widehat{Se}({\widehat{k}}_{opt})$	$Se({\widehat{k}}_{opt})$	Se(kopt)	$\widehat{E}(T\mid {\widehat{k}}_{opt})$	$\widehat{E}(T\mid {\widehat{k}}_{opt})$	E(T|kopt)
0.01	0	11	12	1	0.836	0.831	0.196	0.178	0.178	11	1	1	0.836	1	0.196	0.178	1
	0.01	11	12	0.976	0.836	0.831	0.193	0.178	0.178	11	1	0.976	0.836	1	0.193	0.178	1
	0.05	12	12	0.884	0.831	0.831	0.184	0.178	0.178	2	1	0.966	0.95	1	0.519	0.519	1
	0.1	13	12	0.775	0.826	0.831	0.172	0.178	0.178	1	1	1	1	1	1	1	1
	0.3	21	12	0.404	0.797	0.831	0.125	0.199	0.178	1	1	1	1	1	1	1	1
0.05	0	5	6	1	0.889	0.877	0.426	0.401	0.399	5	2	1	0.889	0.951	0.426	0.401	0.593
	0.01	5	6	0.984	0.889	0.877	0.423	0.401	0.399	5	2	0.984	0.889	0.951	0.423	0.401	0.593
	0.05	5	6	0.925	0.889	0.877	0.409	0.401	0.399	2	2	0.967	0.951	0.951	0.594	0.593	0.593
	0.1	6	6	0.84	0.877	0.877	0.389	0.399	0.399	1	2	1	1	0.951	1	1	0.593
	0.3	10	6	0.514	0.845	0.877	0.306	0.439	0.399	1	2	1	1	0.951	1	1	0.593
0.1	0	4	4	1	0.906	0.906	0.594	0.562	0.562	4	2	1	0.906	0.952	0.594	0.562	0.681
	0.01	4	4	0.987	0.906	0.906	0.589	0.562	0.562	4	2	0.987	0.906	0.952	0.589	0.562	0.681
	0.05	4	4	0.937	0.906	0.906	0.572	0.562	0.562	2	2	0.968	0.952	0.952	0.684	0.681	0.681
	0.1	4	4	0.877	0.906	0.906	0.552	0.562	0.562	1	2	1	1	0.952	1	1	0.681
	0.3	25	4	0.414	0.797	0.906	0.424	0.779	0.562	1	2	1	1	0.952	1	1	0.681

Note: Results are given for designs chosen based on solving the unconstrained and constrained optimization problems.

For each quantity, an assumed value (eg, the value calculated based on the sensitivity function Se(k)=f_H(p, k, d) for a given d) is indicated by a hat, $\widehat{.}$(eg, $\text{E}\left(T\mid {\widehat{k}}_{opt}\right)$ is the true expected number of tests based on the assumed optimal group size and true sensitivity value and $\widehat{\text{E}}\left(T\mid {\widehat{k}}_{opt}\right)$ is the value believed to be true based on the assumed sensitivity values).

From the results, we see that the unconstrained optimization, which considers only the expected number of tests, often yields very poor assumed overall sensitivity. For examples, with p=0.01 and d assumed to be 0.01, the assumed sensitivity value is 0.976, which is substantially different from the actual sensitivity value of 0.836 which would occur if d=0.075 and k =11 were used. This highlights the fact that such an optimization procedure can do nothing to control the overall sensitivity rates and should be used cautiously, particularly with differential misclassification. While the overall sensitivity values are always much higher when using the constrained procedure, when the assumed sensitivity function overestimates the true values the chosen group size can yield an overall sensitivity value much smaller than is assumed to be true. This can be seen by, again, looking at the example of p=0.01 with d assumed to be 0.01 where the assumed and actual sensitivity values are 0.976 and 0.836, respectively. This highlights a major drawback of the constrained procedure (which is also present in the unconstrained), namely that it cannot overcome poor a priori information concerning the sensitivity function (specifically, overestimation of the sensitivity function).

The differences observed between true and assumed sensitivity tend to decrease sharply as p increases. For example, looking again at an assumed value of d=0.01, we noted above that the assumed and true sensitivity values were 0.976 and 0.836, respectively, when p=0.01. At p=0.1, these values have become 0.987 and 0.906. This is due to the fact that for larger p the expected number of tests decreases rapidly with the group size, regardless of the sensitivity values. Differences between the assumed and true expected number of tests, however, follows the opposite pattern, with the differences increasing with p. For example, with an assumed value of d=0.3, the difference between the true and assumed expected number of tests per person (or individual) increases from 0.199−0.125=0.074 at p=0.01 to 0.779−0.424=0.355 at p=0.1. Such a difference would lead to an overconfidence in the savings provided by group testing which scales linearly with the total number of people to be screened. For the most part, we see that, when the sensitivity function is assumed to have lower values than are true for each group size, the expected number of tests per person is underestimated (as seen in the previous example). Conversely, when the sensitivity function is assumed to have higher values than are true for each group size, the expected number of tests per person (or individual) is overestimated. For example, returning to the case of p=0.01 and an assumed value of d=0.01, the assumed expected number of tests exceeds the true expected number of tests by 0.193−0.178=0.015.

7 |. OPTIMAL DESIGN INCORPORATING ESTIMATION ERROR IN $\widehat{Se(k)}$ AND $\widehat{Sp(k)}$

As seen in the previous example, reliable knowledge of the misclassification parameters and their dependence on k is essential in designing a group testing screening program. In most cases, this will require researchers to first obtain population specific estimates of the sensitivity and specificity. To do this will require a validation study design in which individuals with known disease status (most likely from initial individual screening) are tested in groups of varying group sizes. To date, we are unaware of any literature related to the question of how to best design such studies. However, in practice it is important to consider how large such validation studies would need to be before deciding if group testing is a reasonable approach. Another important question is, given that a validation study of a certain size is to be carried out, how large of a target population for screening is required to see an overall benefit from utilizing group testing. Answers to such questions will vary greatly depending on the underlying population and particular assay being used, but it is reasonable to assume that such considerations will show group testing is not warranted in many situations when such an approach might otherwise be considered.

7.1 |. Example

To estimate Se(k) and Sp(k), a simple validation design is described in Algorithm 1 for an initial sample of size N and a maximum group size k_max. The maximum group size is predetermined by researchers to be the largest possible group size under consideration. Once the misclassification parameters have been estimated, they can be used to find k_opt from the constrained optimization procedure described above in (2) using the estimated sensitivity and specificity values. In this section, our goal is to determine how large of an initial validation sample size, N, would be required to be confident that the bounding criterion in (2) is truly met. Mathematically, for the sensitivity this means we hope to achieve $\varphi (\delta )=\text{P}(\widehat{Se({\widehat{k}}_{opt})}>\delta )>ϵ$ where ϵ is some threshold value. Note that this is conceptually similar to a tolerance interval where we can be assured with a certain probability that a particular value falls within the interval.

Algorithm 1.

Procedure for validation study

for k = 1, 2, …, kmax do

if N/k is an integer then Randomly group units into N/k groups of size k

else Randomly form ⌊N/k⌋ groups of size k and construct a final group with the remaining N − k × ⌊N/k⌋ units and k − N + k × ⌊N/k⌋ duplicate units randomly chosen from the othergroups

end if

if k > 1 then Assuming estimates from the k = 1 stage are correct, estimate $Se(k)=\frac{\text{\#groups}\text{with}\text{at}\text{least}\text{one}\text{positive}\text{member}\text{and}\text{testing}\text{positive}}{\text{\#groups}\text{with}\text{at}\text{least}\text{one}\text{positive}\text{member}}$ and $Sp(k)=\frac{\text{\#groups}\text{with}\text{no}\text{positive}\text{members}\text{and}\text{testing}\text{negative}}{\text{\#groups}\text{with}\text{no}\text{positive}\text{members}}$

end if

end for

Algorithm 2.

Pseudo-code for validation study simulations

Let N = 10,000

Let Nmax = 0

Let Nmin = 0

while true do

for i = 1, 2, …, 50,000 do

Calculate ${\widehat{Se(k)}}_i$ and ${\widehat{Sp(k)}}_i$ using Algorithm 1 for each k = 1, 2, …, 10 Find ${\widehat{k}}_{opt}$ solving (2) with δ = 0.95 based on these estimates

Set ${\psi }_i=\{\begin{array}{ll}1,\hfill & {\widehat{Se({\widehat{k}}_{opt})}}_i>0.95\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$

end for

Calculate $\widehat{\varphi }(0.95)={\sum }_{i=1}^{50,000}\frac{{\psi }_i}{50000}$

if $\widehat{\varphi }(0.95)-0.95>0.01$ then Let Nmax = N Let $N=\lfloor \frac{N+N_{min}}{2}\rfloor$

else if $\widehat{\varphi }(0.95)-0.95<-0.01$ then Let Nmin = N

if Nmax = 0 then Let N = 2N

else Let $N=\lfloor \frac{N+N_{max}}{2}\rfloor$

end if

else exit while loop

end if

end while

To determine the necessary validation size, N, we conducted a simulation study with 50 000 simulations and found the smallest N such that the empirical probability ϕ(0.95) > 0.95. The full simulation algorithm is described in Algorithm 2. As above, we assumed Sp(k)=1 for all k. For the sensitivity functions, we considered several possibilities:

$$S{e}_1(k)=1-0.02(k-1),$$

$$S{e}_2(k)=\{\begin{array}{ll}1-0.02\times 2^{k/2},\hfill & k=1,2,\dots ,11\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array},$$

$$S{e}_3(k)=f_H(p,k,d=0.1),$$

$$S{e}_4(k)=f_H(p,k,d=0.3),$$

Simulations were carried out for p =0.01, 0.02, …, 0.10 and with k_max=10.

Once the smallest N was determined, we found the smallest total population size, N*, required to see a benefit from group testing following such a validation procedure. This value was determined by comparing the expected number of tests required to complete screening the population plus the total number of tests used in the validation study to the total population size, which represents the number of tests required under individual testing. Letting T_V be the total number of tests required in the validation study, N* can be found by solving the inequality

$$\left(N*-N\right)E(T\mid p,k,Se(k))+T_V\le N*,$$

or equivalently

$$\frac{T_V-N\times E(T\mid p,k,Se(k))}{1-E(T\mid p,k,Se(k))}\le N*.$$

The expected value in this expression was taken as the average expected value across all simulations for the given validation sample size. Results are shown in Figure 2.

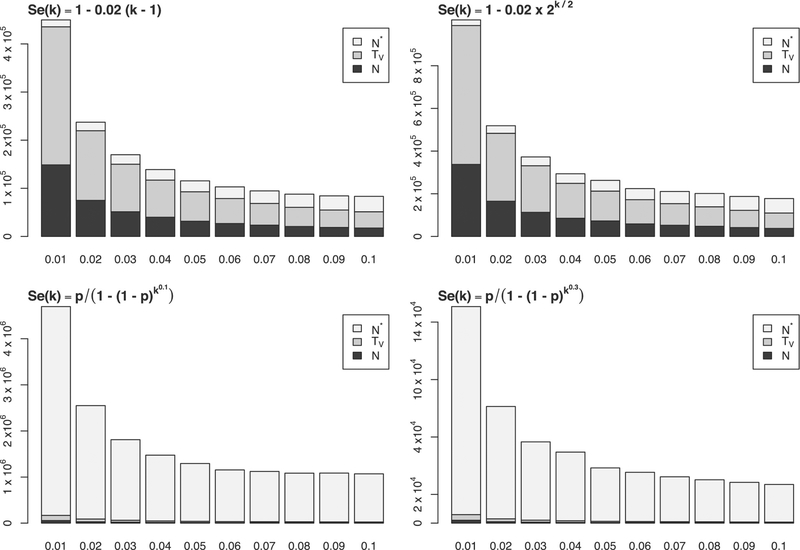
FIGURE 2.

Barplots showing required validation study size, N, total number of assay tests in validation study, T_V, and minimum population size to see a benefit from group testing, N* for various underlying true sensitivity functions. The bottom axes are values of p

Unsurprisingly, for all sensitivity functions we see the required validation sample sizes decrease with increasing prevalence. This is expected as smaller numbers of individuals are required to ensure an adequate number of groups with at least one positive member. For the sensitivity functions on the top row, the decrease in sensitivity is more gradual so that a larger group size can be chosen. For these cases, larger validation sample sizes are required to accurately estimate the sensitivity function. However, since the larger group sizes will allow for a smaller expected number of tests, the additional sample size required to see a benefit from group testing is small.

8 |. REVISITING THE CASE STUDIES

8.1 |. Population-based screening for SARS-CoV-2 infection

Large-scale screening for SARS-CoV-2 is an important and pressing public health issue. Implementation of group testing to facilitate such screening currently faces several obstacles which must be considered before beginning such a program. First, prevalence values in a given region are unknown and constantly changing. This forces any design choices to be made somewhat ad hoc. This is particularly an issue as testing protocols and indications are currently in flux across state and national health departments, so that the underlying screening population characteristics can change at any time. For example, if the positive rate of individual tests in an area is approximately 5%, a procedure testing groups of size 5 could offer significant advantages. If, however, at a later time the prevalence of the screening population increases to 29%, or greater, due to testing only individuals at higher risk such a procedure would require more tests than individual screening. The inability of testing facilities to anticipate such swings could lead to very expensive mistakes.

A second issue is that it is not known a priori how assay sensitivity changes with group sizes. This is particularly true as such values may vary across populations and labs given the wide range of testing techniques currently being implemented. While a validation study would be feasible for such a use case, it is unlikely that public health officials would be willing to reallocate sparse testing materials for large speculative studies at this time. In a public health crisis like COVID-19, we recommend that samples be stored so that, at a minimum, the feasibility of group testing can be evaluated at a later time.

If despite these concerns a group testing program were to be implemented, a basic prevalence estimate could be obtained using recent individual testing data. To carry out a validation procedure as described above we show the estimated validation sample sizes, total number of tests, and population size required to see a benefit from group testing for prevalence values 0.05, 0.1, and 0.25 in Table 2. Values are reported based on two assumed underlying sensitivity functions: 1) a linear function, Se(k)=1−0.02(k −1) and 2) the Hwang function with d=0.1, f_H(d=0.1).

TABLE 2.

Estimated validation sample size, N, number of validation tests, T_V, and necessary population size to see a benefit from group testing, N*, for a COVID – 19 screening program based on prevalence values of 0.05, 0.1, and 0.25

	Se(k) = 1 − 0.02(k − 1)			fH(d = 0.1)
Prevalence	N	TV	N*	N	TV	N*
0.05	31 679	92 789	147 238	13 710	40 158	1 307 444
0.1	17 500	51 259	100 771	8 906	26 090	1 077 732
0.25	1640	4806	31 494	10 781	31 582	4 754 298

Note: Values are calculated separately for two underlying sensitivity functions: Se(k) = 1 − 0.02(k − 1) and f_H(d = 0.1).

8.2 |. Large-scale screening for HIV viral load

The specifics of designing a screening program for monitoring HIV viral load will vary as different regions employ differing testing protocols and thresholds. As an example, we consider a case with suspected ART failure prevalence around 9%, a value reported among those using ART for at least 18 months for a Malawian cohort in Nicholas et al (2019).³⁷ While studies evaluating the pooled sensitivity for fixed group sizes have been done,^14,15 such values are likely cohort specific and would need to be re-estimated before application to a specific population. Furthermore, in order to make informed decisions about an optimal group size it would be necessary to first understand how the sensitivity changes with the group size. Using the procedure outlined above, we can look at the sample sizes required under different assumed sensitivity functions to evaluate how feasible group testing would be in this case. For example, if we assumed the linear sensitivity function Se(k)=1−0.02(k −1) for a prevalence of 0.09 we would require 18 750 individuals to enroll in a validation study requiring 54 920 total tests and a population size to 103 097 to see a benefit from group testing. If, however, the sensitivity function was the Hwang function with d =0.1, we would require 9375 individuals to enroll in a validation study requiring 27 462 tests and a population size of 1 094 884. In either case, for a population of 600 000 screened semiannually there is a clear potential for savings from group testing, even after carrying out a validation procedure. Without any prior knowledge of the sensitivity function, it would be difficult to choose an initial validation sample size as it is impossible to give conservative bounds. Still, if the resources are available for an initial large investment for a validation study, and health officials are able to deal with the possibility that the pooled sensitivity will be too low for practical use, the long term and ongoing nature of HIV viral load screening can potentially benefit largely from group testing.

8.3 |. Stratified cancer screening

For HPV methylation screening, we consider a program aimed at screening the entire US population for HPV related cervical cancer risk. This could be achieved by collecting samples from all women, identifying those with high risk HPV subtypes (ie, those that act as cancer precursors), and finally administering methylation testing for the high risk HPV group. Those with positive methylation tests would then be followed more intensely to ascertain cervical cancer risk. Using 2010 population estimates and estimated prevalences from 2014,³⁸ we could approximate that around 20 million women in the US would test positive for a high risk HPV subtype and we would like to design a group testing procedure to screen each of these women using methylation testing. To date, there are no population based estimates of methylation positive testing rates so we will assume a value of 5% for this example. Using these values and the validation procedure outlined above, if the underlying sensitivity function were the linear function Se(k)=1−0.02(k −1) then we would require a validation sample size of 31 679 and a total of 92 789 tests with a required population size to see a benefit from group testing of 147 238. If, however, the true sensitivity function were the Hwang function with d=0.1, we would require 13 710 women for a validation procedure requiring 40 158 tests and a total population size of 1 307 444 to see a benefit from group testing. In either case, given the large population required for screening, group testing would likely provide large savings in this setting, even with a necessarily large validation study. This would be true even if the actual rate of positive methylation tests in the high risk HPV infected population were much higher. Here, the only real impediment to using group testing would be if health officials were unwilling to accept any additional loss of sensitivity due to pooling.

8.4 |. Biomarker presence in cohort study

For MGUS screening, we assume a prevalence of 3% and that we would like to determine the status of approximately 200 000 individuals. If the true sensitivity function were the linear function Se(k)=1−0.02(k −1) then we would require a sample size of 51 250 individuals for a validation procedure requiring 150 113 tests and a population size of 221 091 to see a benefit from group testing. If, however, the true sensitivity function were the Hwang function with d=0.1, we would require 21 093 individuals for a validation procedure requiring 61 785 tests and a population size of 1 832 663 to see a benefit of group testing. Given these numbers, and lacking any a priori information on the sensitivity function, it is unlikely that researchers would attempt to implement such a validation procedure in this case. While the large sample sizes are offset somewhat by the need for repeat testing, the nontrivial possibility of finding that pooling of any size reduces the sensitivity to an unacceptable level make this an unlikely gamble for resource allocation.

9 |. DISCUSSION

In this article we have reviewed several of the issues faced by practitioners when deciding if group testing can provide a feasible solution for their screening program. In this context we have explored several issues numerically based a simple algorithm (the Dorfman two-stage procedure) and several simplifying assumptions. In practice, there exist many additional considerations which may alter the final decision concerning whether to implement group testing.

For all numerical comparisons, we have assumed grouping does not impact specificity (ie, Sp(k)=1 for all k). While this may be reasonable in some settings, the failure of this assumption can result in large increases in the number of individuals required for a validation sample. In particular, by using a minimum threshold to determine estimation accuracy we have had to assume that ϕ(δ) is monotone as a function of the validation sample size. While this holds for Sp(k)=1, this may not be true otherwise, requiring more complicated evaluation criteria and larger sample sizes. Furthermore, poor assumptions about Sp(k) can contribute to poor estimation of the expected number of tests and, hence, exacerbate the issues of selecting an appropriate group testing design.

When designing our validation procedure, we made the assumption that the sensitivity does not depend on the number of positives in a given group (ie, we have assumed that the sensitivity is only a function of whether or not any group member has the disease, not the full distributional makeup of the group). In practice, this assumption may fail resulting in significantly more complicated sensitivity functions (which must now be a function of both the group size and the number of positives in the group). This could especially be an issue when the test classification is a function of underlying continuous test output. If such issues could reasonably be suspected, it would be necessary to design the validation study which accounts for this issue.

One assumption we have made is that there is a complete lack of a priori information on the underlying sensitivity function, necessitating the validation design to be nonparametric. However, in cases where researchers are able/willing to make certain simplifying assumptions (eg, that sensitivity is linear in k) more efficient validation designs may be possible. In such cases, smaller validation studies could potentially make group testing feasible in a wider range of settings. However, given that the properties of the final design are sensitive to the correct specification of the sensitivity function, we generally make the recommendation of a nonparametric approach when designing important screening programs using group testing. Furthermore, if assumptions such as monotonicity of the sensitivity as a function of group size are made, more efficient adaptive algorithms could possibly be developed. This is an important area for future work.

We have emphasized the importance of estimating the sensitivity and specificity for different size groups in the same population that we intend to screen. The validation study design assumes that sample is collected from a random sample of individuals from the population at hand and groups of varying size be randomly formed from these samples. There are different alternative designs for the validation sample that may lead to efficiency gains in some situations. For example, if a researcher assumes that the specificity is 1 for all group sizes (here, we assumed it was necessary to estimate these specificities in order to confirm this in our calculations), we may save resources by never grouping all negative samples together. Alternatively, rather than attempt to find the optimal design, we could simply evaluate the properties of a group testing design for a single fixed group size. If the false negative rate is too high, we could sequentially evaluate the properties for a smaller group size. This approach may be advantageous for the COVID-19 example, where it is more important to obtain a good design quickly than to spend more time to find the optimal design (ie, the perfect is the enemy of the good). In many cases, obtaining a random sample from a population to do a full validation procedure may be impossible but researchers may still be interested in studying the properties of a group testing procedure. An approach that could be taken in such cases is to use a spiked procedure in which known concentrations of the agent being tested are included in samples of different sizes to simulate the conditions observable in the full population. Such a procedure could greatly reduce the number of validation tests required and could utilize pre-selected samples, resulting in savings of both time and cost. The primary concern with such a procedure is that the validity of the results relies heavily on the correctness of the assumptions made concerning the underlying population characteristics and their relationship to the trait being screened for. For a given application, researchers would have to balance their comfort level with such assumptions with the need for empirically verified estimates.

An additional assumption we have made is that the underlying population is homogeneous with respect to the primary trait of interest. In many cases, this is reasonable as long as the validation sample is chosen representatively across the entire population and the subsequent samples are not grouped based on underlying heterogeneous clusters. The impact of heterogeneity will include additional challenges to determine the size of the validation sample and to ensure a feasible solution to the optimization problem (2). The issue is that even under the perfect assay setting, we need to determine not only group sizes but also the members of the groups, and number of such possibilities (number of the partition of the population) is astronomical even for the small population size. In fact, under error-free testing, the optimal partition is known only for the Dorfman procedure.^27,28 From a the practical perspective, Hwang’s method can be used for Dorfman’s procedure, and the methods developed in References 39,40 can be used for other group testing procedures. Another possibility, which also may be logistically easier to implement, is a stratification of the population, such that in each stratum, there is a homogeneous population. In such a case, the methodology developed in the present work can be used with respect to each stratum separately.

In this article, we have focused exclusively on the Dorfman design. In the case of a homogeneous population, there are more efficient designs than Dorfman’s two-stage procedure.^41–43 In many of these designs, the expected number of tests E(T|p, k, Se(k)) is not given in closed form, but rather calculated using recursion or dynamic programming.³⁹ In the presence of differential misclassification or dilution effects, expressions for the expected number of tests (an important component in the objective function to evaluate) are difficult to obtain in these cases.

Our work focused on the screening of a single disease. However, occasionally screening for multiple diseases from a single assay may be of interest. Group testing for disease screening for multiple diseases with test misclassification is an area for future research. With respect to feasibility, the subject of the current paper, we want to emphasize that any design would need a validation sample sized to be sufficient to estimate the more complex misclassification structure that would be required for such designs.