Hunting for Beneficial Mutations: Conditioning on SIFT Scores When Estimating the Distribution of Fitness Effect of New Mutations

Abstract

The distribution of fitness effects (DFE) of new mutations is a key parameter of molecular evolution. The DFE can in principle be estimated by comparing the site frequency spectra (SFS) of putatively neutral and functional polymorphisms. Unfortunately, the DFE is intrinsically hard to estimate, especially for beneficial mutations because these tend to be exceedingly rare. There is therefore a strong incentive to find out whether conditioning on properties of mutations that are independent of the SFS could provide additional information. In the present study, we developed a new measure based on SIFT scores. SIFT scores are assigned to nucleotide sites based on their level of conservation across a multispecies alignment: the more conserved a site, the more likely mutations occurring at this site are deleterious, and the lower the SIFT score. If one knows the ancestral state at a given site, one can assign a value to new mutations occurring at the site based on the change of SIFT score associated with the mutation. We called this new measure δ. We show that properties of the DFE as well as the flux of beneficial mutations across classes covary with δ and, hence, that SIFT scores are informative when estimating the fitness effect of new mutations. In particular, conditioning on SIFT scores can help to characterize beneficial mutations.

Introduction

Significance

The distribution of fitness effects (DFE) of new mutations plays a key role in evolution but is difficult to estimate. This is particularly true for beneficial mutations that are exceedingly rare. Classically, the DFE is estimated by comparing the distribution of allele frequencies at sites putatively under selection and at neutral sites. In the present study we show, using genomic data from an array of plant species, that adding information on site conservation improves the estimation of the DFE and, more specifically, beneficial part of the distribution.

Surprisingly, given their pivotal role in evolution, many aspects of mutations and of the mutation process remain poorly known. Uncertainty prevails, even regarding mutation rates, a property that is often taken for granted (Moorjani et al. 2016). Another crucial aspect of mutations where knowledge remains insufficient is their effect on fitness.

Depending on their effect on fitness, mutations can be classified as deleterious, neutral, or beneficial. Although it is widely accepted that most new mutations are neutral, the exact proportions of deleterious, neutral, or beneficial mutations remain highly contentious (Galtier 2016). This is far from anecdotal as the distribution of fitness effect (DFE) of new mutations is at the heart of all theories of molecular evolution and comparative genomics. The fitness effect of a new mutation will influence the frequency at which it segregates in a population and therefore the amount and nature of genetic variation present in a given species. This in turn will condition the evolutionary trajectory of the species. It is therefore crucial to be able to estimate the DFE accurately and to understand the factors that influence it. For instance, to what extent does the DFE reflect the biology of the organism and to what extent is it influenced by its recent demographic history?

Unfortunately, the DFE is far from trivial to estimate even though there have been major improvements in available methods (Keightley and Eyre-Walker 2007; Tataru et al. 2017; Huang and Siepel 2019) since the seminal work of Eyre-Walker et al. (2006). These advances, combined with the surge in available genomic data and the widespread availability of multispecies genome alignments, as well as full genome resequencing data sets across many species, offer a unique opportunity to learn more about mutation effects.

There are various approaches to characterize the fitness effect of mutations from sequence data. Two groups of methods that have been particularly popular over the last two decades are based on site conservation across species and on analysis of the site frequency spectrum (SFS), respectively.

The key idea behind the first group of methods is that mutations at sites that are highly conserved across species are likely to be deleterious (Ng and Henikoff 2003; Davydov et al. 2010). Many methods were developed to classify sites based on this principle and they use different data and have different merits (Ng and Henikoff 2003; Adzhubei et al. 2010; Davydov et al. 2010; Huang et al. 2017; Rentzsch et al. 2019). This approach has recently been used to characterize the impact on fitness of amino acid changing mutations in humans (Henn et al. 2016), sorghum (Valluru et al. 2019), or mammals, in particular endangered species (Grossen et al. 2020; van der Valk et al. 2020). In this article, we will use the program SIFT4G (Sorting Intolerant From Tolerant For Genomes) (Ng and Henikoff 2003; Vaser et al. 2016) and also relate our work to a recent simulation study carried out by Huber et al. (2020) that was based on another conservation measure, GERP (Genomic Evolutionary Rate Profiling) (Davydov et al. 2010). Both methods assign a score to the site that measures how much the site departs from the variation that would be observed in an alignment if the sites were evolving neutrally. Hence the resulting score indirectly measures how deleterious mutations at the site are. The pros of this general approach are that it makes single sites predictions, is readily available for an increasing number of species, can easily incorporate additional covariates from in-depth functional genomic studies and does not depend on elusive population genetics parameters (e.g., effective population size, N_e). However, it can be misleading for predictions on extant variation and does not directly estimate fitness effects.

Methods from the second group are based on polymorphism within species and estimate the DFE of new mutations from comparisons of the SFS of putatively neutral and selected sites, for instance synonymous and nonsynonymous sites. Because the SFS can also be affected by demography one needs to correct for it and different ways of doing so have been devised (Eyre-Walker et al. 2006; Keightley and Eyre-Walker 2007; Galtier 2016; Tataru et al. 2017; Tataru and Bataillon 2019). The latest implementations of this approach are not confined to deleterious mutations and allow the consideration of both deleterious and beneficial mutations, although it should be noted that estimating the fraction of beneficial mutations is intrinsically more difficult than estimating deleterious ones, simply because beneficial mutations are exceedingly rare. Estimation of the DFE has often been carried out, for instance to test predictions of the nearly neutral theory of molecular evolution (Castellano et al. 2019; Chen et al. 2020; Galtier and Rousselle 2020; Rousselle et al. 2020). In contrast to the methods of the first group, methods based on the DFE make inference about current patterns of variation and are based on minimal assumptions on the conservation of effects across species. Recent implementations also allow testing for invariance or change of the DFE across species (Tataru and Bataillon 2019). However, all DFE estimation methods require a neutral baseline that accounts for biasing effects of demography and population structure and do not provide inference at single sites because the SFS is built upon (many) exchangeable nucleotide sites.

Three major differences between the two approaches have a direct impact on the way they can be combined. First, SFS-based methods rely on population genetics assumptions and directly provide estimation of (population-scaled) fitness distribution, whereas methods like SIFT4G only provide a conservation score that cannot directly be related to fitness, even if qualitative inference are proposed (typically the tolerated/deleterious classification). Second, SFS-based approaches, only provide a statistical characterization of the DFE of a set of mutations in a given population. The set can be the whole genome or only a class of genes (e.g., with a specific genomic location, a specific expression level, a specific gene ontology, etc.). So nothing can be said about a specific variant (in theory, the posterior probability of having a given selection coefficient could be obtained, however, there is almost no information for a single mutation). In contrast, SIFT4G (and related methods) does not provide a statistical description of the DFE but attributes a score to every single position and nucleotide state in a gene, including nonvariable positions and allelic states that are not observed. In addition, it is not population dependent as scores are given for a focal species and are supposed to be valid for all individuals of the species. The third and last difference relates to the second one but has more subtle and technical implications. As already explained, SIFT4G gives a score to every possible state (nucleotide) at every site. It is thus an absolute property of a site and we could replace A, C, G, and T letters by SIFT scores, or more practically by discrete categories, such as tolerated (TOL) and deleterious (DEL). SFS-based methods, on the other hand, do not consider states but mutations, so changes between two states. Accordingly, the information used for inference is synonymous and nonsynonymous changes, not states. A change can be synonymous or nonsynonymous but a state at a given position cannot. This leads to the problem of counting the number of sites in such methods, where what can be counted (or more properly, estimated) is not the number of synonymous and nonsynonymous sites but the number of opportunities of synonymous and nonsynonymous mutations (see extensive discussion of this problem in Bierne and Eyre-Walker [2003]). A way to avoid this issue is to use mutations at nucleotide sites that can be classified without ambiguity, such as 0-fold and 4-fold degenerated codon positions, for which there is only a single possibility of mutation so the state can be characterized by the opportunity of mutation without ambiguity.

Given these notable differences, making informed comparisons between these two groups of methods and predicting when they will make converging predictions is challenging. Recently, Huber et al. (2020) used computer simulations of population genetics models of purifying selection to compare the two approaches. More specifically, they related GERP scores to the strength of purifying selection (measured as the product of effective population size and selection coefficient, N_es). The GERP score is defined as the reduction in the number of substitutions observed on the multispecies sequence alignment compared with the neutral expectation. A high GERP score means that the observed number of substitutions is much less than expected and therefore that the site is highly conserved. Mutations appearing at highly conserved sites are accordingly given a high GERP score and this agrees with the assumption that these mutations are strongly deleterious. We would therefore expect high GERP scores to be associated to highly negative values of N_es and low GERP scores to be associated to values of N_es closer to zero. What was observed, however, is that very highly negative values of N_es are indeed associated to high GERP scores but values closer to zero can basically take all possible GERP score values. So, the GERP score may not be useful to detect selection acting on individual mutations but it may be useful to separate sites with moderately to strongly deleterious mutations from mildly deleterious and nearly neutral ones. The study by Huber et al. (2020) is important as it emphasizes the limits of using methods based on evolutionary conservation to identify deleterious mutations in extant populations.

Here, we argue that although attempting to establish equivalence of both approaches is not sensible, combining estimates of the deleterious load obtained through both SIFT4G and a DFE from SFS data is informative. We show that previous approaches for inferring DFE conditional on certain type of mutations (e.g., AT to GC) can be leveraged to build valid SFS for DFE estimation using SIFT score as covariates. To test the robustness and range of applicability of our approach, we apply it to an array of plant species varying in effective population size and life history traits. In particular, DFE estimation can be done for distinct classes of nonsynonymous mutations defined from SIFT scores to quantify heterogeneity in DFE within genomes. Conditioning the DFE on a measure, δ, that captures the change in SIFT scores associated with a mutation characterizes well the expected effect of the mutation. We illustrate that changes in SIFT scores is a powerful covariate to capture the expected effect of mutations and we show that conditioning DFE on δ leads to an improved characterization of the properties of beneficial mutations and may even allow us to identify mutations that are likely to be beneficial.

Results

Combining DFE and SIFT Scores: Principle

How to properly combine the two kinds of information given the differences between SIFT and DFE noted in the introduction? An overview of the different steps of our approach is given in figure 1. SFS-based methods require the comparison of at least two SFS, one serving as a neutral reference (typically the synonymous SFS) and the other corresponding to the mutations for which we want to infer fitness (typically the nonsynonymous SFS). We may want to extend the approach to other categories of mutations, for example, to take into account the nature of nucleotides (A, T vs. G, C) to control for the possible impact of GC-biased gene conversion (Rousselle et al. 2019). If we want to infer the DFE for different SIFT categories, the approach will be very similar. The example below is given for two SIFT categories (TOL/DEL) as it is simpler but this can be extended to any number of categories, as shown in the next section. Variation at 0-fold and 4-fold sites, respectively, is also used to avoid additional complications of counting synonymous and nonsynonymous “positions.”

Fig. 1.

Conceptual overview of the approach developed in the present study and of the steps (1–5) we take for conditioning SFS data on genomic features. Here our genomic feature is the change in SIFT scores, δ.

As a toy example, we consider a sequence with only three codons and four individuals and a sequence representing the ancestral states, so that mutations in the SFS can be polarized as needed in PolyDFE (Tataru et al. 2017) (table 1).

Table 1.

Sequences for the “Toy Example” Three-Codon Sequence

Ancestral Seq.	C	C	A	G	G	T	C	A	G
Ind 1	—	—	G	—	—	—	—	—	—
Ind 2	A	—	—	—	—	—	—	C	—
Ind 3	—	—	G	—	—	—	—	C	—
Ind 4	A	—	—	—	T	—	—	—	—

The SIFT scores corresponding to this alignment and to all possible alternative alleles are given in table 2. From this table and the alignment, we can deduce the SFS (minimalist here) for the different categories of SNPs. There are only four SNPs in this example in positions 1, 3, 5, and 8, which can be classified as follows:

Table 2.

Sequences and SIFT Scores for the “Toy Example” Three-Codon Sequence

	Codon 1			Codon 2			Codon 3
Nucleotides	C	C	A	G	G	T	C	A	G
Degeneracy	0	0	4	0	0	4	0	0	4
SIFT for A	TOL	DEL	TOL	TOL	DEL	TOL	TOL	DEL	TOL
SIFT for C	TOL	TOL	TOL	TOL	DEL	DEL	TOL	TOL	TOL
SIFT for G	DEL	DEL	TOL	TOL	TOL	TOL	TOL	DEL	TOL
SIFT for T	DEL	TOL	TOL	TOL	DEL	TOL	DEL	DEL	TOL

											Total
0	TOL → TOL	1/3	1/3	0	1	0	0	2/3	0	0	2.33
0	TOL → DEL	2/3	2/3	0	0	1	0	1/3	0	0	2.66
0	DEL → TOL	0	0	0	0	0	0	0	1/3	0	0.33
0	DEL → DEL	0	0	0	0	0	0	0	2/3	0	0.66
4	TOL → TOL	0	0	1	0	0	2/3	0	0	1	2.66
4	TOL → DEL	0	0	0	0	0	0	0	0	0	0
4	DEL → TOL	0	0	0	0	0	1/3	0	0	0	0.33
4	DEL → DEL	0	0	0	0	0	0	0	0	0	0

Note.—For each position, the SIFT score of the four possible nucleotides is given. The nucleotides present in the alignment are in bold, with the score in italics corresponding to the derived alleles. From this, each polymorphism can be assigned to a degeneracy category (0 or 4) and a delta SIFT score category (TOL →TOL, TOL →DEL, DEL →TOL, DEL →DEL). In the example, SNPs are thus classified as follows: 0-TOL →TOL (pos. 1), 4-TOL →TOL (pos. 3), 0-TOL →DEL (pos. 5), and 0-DEL →TOL (pos. 8). Each position also contributes to the length of the eight possible categories depending on the opportunity of mutations at this site. For example, at position 1, starting from the ancestral nucleotide C (TOL), one possible mutation is TOL →TOL and the two others are TOL →DEL, so this position contributes 1/3 the length of 0-TOL →TOL category and 2/3 to the 0-TOL →DEL category. The contribution of all positions is then summed across the ancestral sequence to obtain the total length of each category.

• Position 1: C → A: nonsynonymous TOL → TOL mutation

• Position 3: A → G: synonymous TOL → TOL mutation

• Position 5: G → T: nonsynonymous TOL → DEL mutation

• Position 8: A → C: nonsynonymous DEL → TOL mutation

Then we need to compute the total length for each category of mutations, which is required for SFS-based methods. To make the parallel with classical methods, this total length corresponds to the total number of nonsynonymous and synonymous “positions.” However, as already noted above, these lengths do not correspond to physical positions but to mutational opportunities. For example, in classical methods a site at third codon position can typically be counted as 1/3 synonymous and 2/3 nonsynonymous (for a 2-fold degenerate amino acid). The same philosophy applies here but for SIFT categories. To fully exemplify our counting procedure, calculations of the total length for the data in table 1 are given in the lower part of table 2.

It is important to note that in this example, the three mutations are equally likely, but transition/transversion ratio or other bias can be incorporated if needed (as it is the case for synonymous/nonsynonymous counts). In the above example, eight SFSs can be defined. The natural choice is to use the synonymous TOL → TOL SFS as the neutral reference and the seven others SFS as potentially nonneutral categories for which we want to infer separately a different DFE category. Some SFS are likely to be empty or to contain very few counts: typically, most synonymous mutations will be TOL → TOL, and categories DEL → TOL or TOL → DEL will be empty for synonymous mutations. However, to be more accurate it is worth properly counting the length for each category.

Genome-Wide Characterization of Polymorphism, DFE, and SIFT Scores

For all species, the distributions of SIFT scores are highly bimodal: sites are enriched at SIFT scores equal to 0 and 1 and there is a dearth of intermediate values (supplementary fig. S1, Supplementary Material online). Counts of polymorphisms, nucleotide diversity at 0-fold and 4-fold sites, π₀ and π₄, respectively, their ratio, ${\pi }_0/{\pi }_4$, and $P_0/P_4$, the ratio of the counts P₀ and P₄ per class of change in SIFT score (see Material and Methods), as well as DFE parameters estimated with PolyDFEv2 are given for the 24 species in supplementary file S1, Supplementary Material online. Because of the diversity of life history traits and mating systems represented by the 24 species, there is a large range of synonymous nucleotide diversity values and ${\pi }_0/{\pi }_4$ ratios. Classically ${\pi }_N/{\pi }_S$ gives the proportion of effectively neutral mutations and, as predicted by the nearly neutral theory, ${\pi }_N/{\pi }_S$ is negatively related to the effective population size (Welch et al. 2008; Castellano et al. 2018; Chen et al. 2020). It is therefore a very informative quantity which tends to covary strongly with the proportion of mutations that fall in the class [−-1, 0] of N_es values in the DFE. Throughout, we shall use $P_0/P_4$, measured from counts and scaled according to their “lengths” as a proxy for ${\pi }_N/{\pi }_S$ (see Materials and Methods for details). Except for a few species, the shape parameter of the gamma distribution of deleterious mutations is lower than 1, as already observed in many other studies (Galtier 2016; Chen et al. 2020).

Conditioning on SIFT Score Change, δ

To combine SIFT score and polymorphism data, we introduced a new statistics. First, instead of considering the two SIFT scores categories (TOL and DEL), we further divided the scores into four discrete categories: fully conserved (FC, score = 0), partly conserved (PC, score $\in$ (0, 0.05]), partly diverse (PD, score $\in$ (0.05, 1)), and fully diverse (FD, score = 1). Note that the same principle can be applied to any number of categories. Then, we attributed the values, 0, −1, −2, and −3 for categories FD to FC. From this, we can define the change in SIFT categories by simply taking the difference between these values. For example, $\delta =-2$ for change from FD to PC, $\delta =+1$ from PC to FD, and δ = 0 if the two alleles belong to the same category. We then analyzed the $P_0/P_4$ ratio and DFE characteristics for the different categories of mutations defined by the change in SIFT categories (δ).

To avoid having too much noise in the data, we filtered out subsets with less than 100 0-fold SNPs and for which the estimated polarization error rate was higher than 10%. We also checked visually that the estimated polarization error rate did not covary with the number of nonsynonymous SNPs in the SFS or δ (supplementary figs. S2 and S3, Supplementary Material online). This left us with 23 species spanning n = 322 SFS distributed in the different δ categories. $P_0/P_4$ ratio was significantly correlated with δ (P value $=9.44e-9$). For mutations in category 0-fold and $\delta =-3$$P_0/P_4$ ranges from 0.043 to 0.1 at the 25–75% quantiles (0.078 at the 50% quantile) and increases with δ. Especially for beneficial mutations $P_0/P_4$ increases much faster, from 0.92 ((0.59, 1.50) for 25–75% quantiles) for slightly beneficial mutations (0-fold and δ = 1) to 53.74 ((31.44, 131.7) for 25–75% quantiles) for the most beneficial ones (0-fold and δ = 3) (table 3). The relationship between $P_0/P_4$ and δ is given in figure 2. We used a series of linear mixed models to quantify how much of the variation in $P_0/P_4$ can be accounted for by variation in δ. A linear model with δ as predictor accounts for ca. 72% of the variation in $P_0/P_4$ and a linear mixed model with a random slope provides the best fit to the data (as compared by AIC) although the gain in terms of R² remains very modest. We tested for the impact of the polarization error, $ϵ$, which was minimal (see supplementary file S3, Supplementary Material online). Note that these analyses remain naive in the sense that they assume no phylogenetic inertia among species included in our data set.

Table 3.

$P_0/P_4$ as a Function of the Change in SIFT Score, δ.

	$P_0/P_4$
Fold	δ	25%	50%	75%
0	−3	0.043	0.078	0.10
0	−2	0.062	0.10	0.14
0	−1	0.14	0.18	0.29
0	0	0.20	0.34	0.51
0	1	0.59	0.92	1.50
0	2	1.55	3.75	8.25
0	3	31.44	53.74	131.70

Fig. 2.

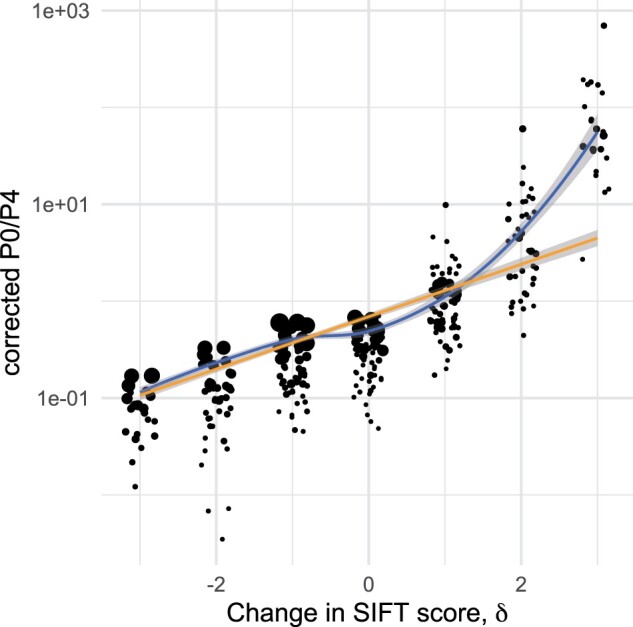
Log(P₀/P₄) as a function of the change in SIFT scores, δ: the orange line denotes a least square regression, the blue curve a local regression (loess). Data points are jittered horizontally for graphical convenience. Shaded gray areas around the curves denote confidence bands around each regression lines. Point size is proportional to the sample size of each SFS (number of nonsynonymous SNPs).

DFE Classes and δ

We divided the deleterious portion of the DFE in four N_es classes ([0, −1], (−1, −10], (−10, −100], and (−100, $-\infty$) (table 4). Figure 3 provides an overview of the relationship between the proportion of mutations in the different DFE classes and δ. The proportion of mutations belonging to the strongly deleterious category falls regularly as δ increases whereas the proportion from the beneficial class follows the opposite pattern. Mutations in the effectively neutral class [0, −1] are mostly confined to negative δ values as mutations belonging to the (−1, −10] DFE class. In all three classes of negative N_es, a nonnegligible proportion is still able to become more beneficial, that is, be associated with a positive δ, especially for the most deleterious class (−100, $-\infty$).

Table 4.

Distribution of the DFE Categories, N_es, as a Function of Site (0-fold vs. 4-fold) and Changes in SIFT Score, δ

			Nes
Fold	δ	pb	$[0,-1]$	$(-1,-10]$	$(-10,-100]$	$(-100,-\infty )$
0	−3	2.3e-6	3e-2	6.4e-2	0.18	0.70
0	−2	3.2e-5	4.8e-2	8.5e-2	0.18	0.66
0	−1	1.5e-4	0.12	0.13	0.21	0.42
0	0	0.11	2.3e-3	1.8e-2	9.2e-2	0.52
0	1	0.60	1.5e-12	5.8e-9	9.9e-6	0.30
0	2	0.99	9.3e-3	2.8e-6	3.3e-5	2.3e-4
0	3	0.99	9.8e-3	8.6e-5	5.4e-6	1.3e-8

Note.—p_b is the proportion of beneficial mutations.

Fig. 3.

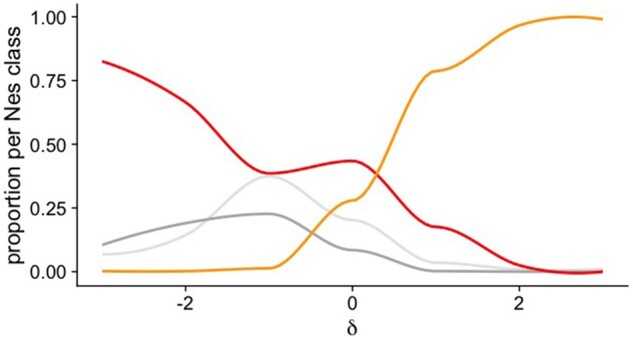
Overview of the proportion of DFE classes versus δ. Shown are the local regression (loess) curves depicting the trend in the observed proportion of mutations falling in each N_es class in the inferred DFE versus δ. In orange, the class of beneficial mutations ($N_{e}s>0$), in red, strongly and very strongly deleterious (N_es within (−10, to $-\infty$), in light gray, slightly deleterious (N_es within (-1, 0)), and in darker gray, mildly deleterious mutations (N_es within (−1, −10)). Note that the data points underlying the fitted curves are not pictured in the figure.

The Flux of Beneficial Mutations

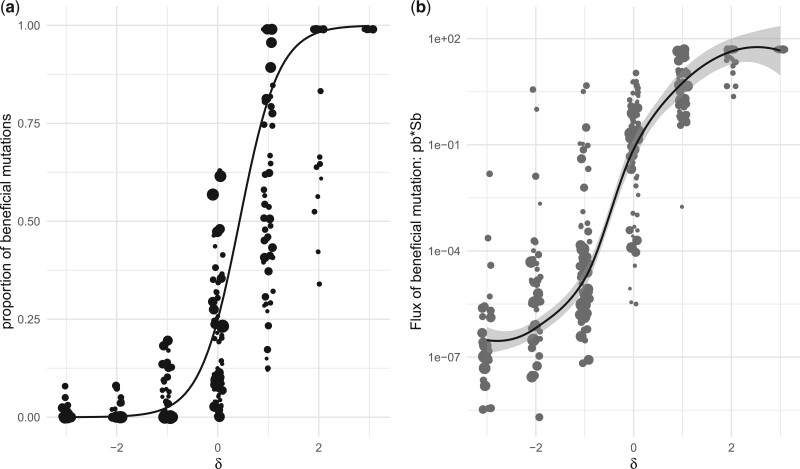
Detecting beneficial mutations is notoriously difficult as they are expected to be generally quite rare and therefore make a modest contribution to SFS counts. δ as a covariate is helpful. The proportion of beneficial mutations (p_b) increases with δ with a linear relationship for δ ranging from −1 to 1 (p_b, fig. 4A). Among the classes of mutations categorized as likely deleterious (negative δ), we have virtually zero flux of beneficial mutations; however, as δ increases, so does the flux of beneficial mutations ($p_b*S_b$, fig. 4B). For intermediate values of δ, the flux of beneficial mutations increases almost linearly with δ.

Fig. 4.

The proportion (p_b) (A) and flux ($p_b{S}_b$) (B) of beneficial mutations covary with δ. The curve in (B) is a loess regression line indicating the local trend in the data. The gray-shaded area represents the 95% confidence interval around the regression lines. Point size is proportional to the sample size of each SFS (number of nonsynonymous SNPs) used for estimating DFE parameters.

We used a series of generalized linear mixed models to quantify how much of the variation in the proportion of beneficial mutations can be accounted for by variation in δ (see supplementary text/report, Supplementary Material online). To do so, we recorded whether each estimated DFE had a proportion of beneficial mutation estimated to be above 10%, and used this as binary response variable (yes/no). A logistic regression model with δ as predictor provided the best fit to the data (as compared by AIC) and it accounted for ca. 65% of the variation (as measured with the ratios of model deviance). Here too, we tested for the impact of the polarization error, $ϵ$, which was minimal (see supplementary file S3, Supplementary Material online). We note again that the gain in fit provided by the random slope or random intercept in terms of (pseudo) R² remains modest. Note that this analysis—as for the $P_0/P_4$ ratio variation—also assumes no phylogenetic inertia among species comprising our data.

Discussion

In the present study, we have explored the extent to which conditioning SFS data on a measure of SIFT score change, δ, helps to parse further the variation in DFEs. Below we discuss the salient features we uncovered, relate our findings to earlier work and sketch a few directions where our new measure, δ, might be a useful covariate to further explore what drives differences in DFE both among species and across genes or types of mutations within species.

We have shown that our new measure based on SIFT scores difference, δ, explained up to 72% of the variation in $P_0/P_4$ and up to 65% of the variation in properties of the DFE such as the probability that the DFE will include more than 10% of beneficial mutations. The fact that a sizeable amount of variation is explained by δ is well illustrated by the substantial covariation between δ and the DFE classes. Because SIFT scores reflect conservation across species and therefore long-term evolution whereas the DFE is built on SFSs and reflects the selective effect of mutations in extant populations, it was not obvious that the two would be closely related. It suggests that the DFE may well be altogether rather stable and somewhat immune to the stochasticities of population demography and environment, but instead constrained by intrinsic properties of a species such as genome characteristics or life-history traits. This is in line with the results recently obtained by Huang et al. (2021) showing that DFEs are highly correlated between populations of the same species or of closely related ones, or by Chen et al. (2017) showing that ${\pi }_N/{\pi }_S$ is almost constant across populations of the same species or between domesticated species and their wild relatives.

Nevertheless, a large amount of variation remains unexplained and the δ = 0 category still contains, depending on the species considered, a large variation in the DFE. Our results are, in this respect, reminiscent of those obtained by Huber et al. (2020) when they investigated via simulations the expected relationship between GERP scores and DFE categories. Huber et al. (2020) observed that very highly negative values of N_es are associated with high GERP scores (corresponding to low SIFT scores) but values of N_es closer to zero can basically take all possible GERP score values. They concluded that GERP scores may not be useful to detect selection acting on individual mutations although they may be useful to separate sites with moderately to strongly deleterious mutations from mildly deleterious and nearly neutral ones. Our analysis relies on examining the DFE of subsets of mutations characterized by the same δ scores, whereas Huber simulated the range of scores obtained given a range of N_es values (essentially the converse of what we did), so a direct comparison is difficult. Nonetheless, our results are consistent and confirm the simulation based intuition of Huber et al. (2020): very highly negative values of N_es are associated with negative δ, and positive values of N_es are associated with positive δ, whereas intermediate values of N_es dominated δ values around zero and below zero. Methods based on conservation such as SIFT or GERP implicitly assume that evolutionary forces have been constant through deep evolution, something that can be questioned and this puts a limit the utility of these methods for inferring sites that are currently under selection. In particular, Huber et al. (2020) show that a model with functional turnover under which sites oscillate between functional and nonfunctional states fits the distribution of GERP scores across the genome better than a model without turnover. Hence, many factors may limit the power of conservation scores to predict current selection. Yet, as shown here, measures derived from these scores have a nonnegligible predictive power. In particular, mutations with delta $\ge$ 2 have 93% chance of being beneficial, which makes the delta statistics an efficient way to individually identify beneficial mutation candidates.

Our study is not the first attempt to combine DFE and predictive genome features such as SIFT scores. For instance, the method implemented in the program LASSIE (Huang and Siepel 2019) relies on two components, an estimation of the DFE via a Poisson random field framework, which is very similar in essence to the polyDFE method used here, and a neural network to exploit numerous predictive genomic features, including SIFT scores. Our approach differs from that of Huang and Siepel (2019) in three major ways. First, our aim was to use SIFT scores to aid in the estimation of the DFE rather than in the prediction of mutations associated with diseases. Second, as it stands LASSIE was developed for species like humans and other model organisms for which there is a large amount of local genomic features data. Our aim was to develop a flexible method that could be applied to a large array of species. Hence our choice of SIFT scores, which can easily be obtained for new species as a covariate of interest to condition SFS counts. Third, by focusing on SIFT scores and their relation to the selective values of mutations instead of using a large number of genomic features and machine learning, an approach primarily geared toward prediction, we may gain in intuition what we loose in predictive power.

Perhaps more similar in spirit to our approach are the studies by Bergman and Eyre-Walker (2019) that conditioned the SFS on amino acids properties or by Moutinho et al. (2019), which conditioned on protein structure covariates. Bergman and Eyre-Walker (2019) showed that the rate of adaptive evolution, as well as the rate of neutral evolution, is highest among the pool of nonsynonymous mutations that entail changes toward amino acids that are more similar. In our case, the flux of beneficial mutations was highest for $\delta \ge -1$ values but the variation was rather large within each category. As for conservation scores, the predictive power of any of these genomic features, taken on their own, remains limited.

Examining the DFE properties conditional on δ reveals that ancestral mutations that were fixed in the past (and deemed deleterious via their SIFT score) create a genomic context where new mutations that can reach a higher SIFT score, are very likely to contain a sizeable number of beneficial mutations. In that respect the sizeable amount of beneficial mutations that we detect with our SFS-based methods reveal that the flux of beneficial mutations in a population might depend on its current load of fixed mutations. A change of status of a population might come from a shift in environmental conditions or a shift of the position of the species with respect to its fitness optimum. This could then lead to an increase in beneficial mutations that can mitigate the effect of the fixed mutation load without requiring the presence of compensatory mutations (Poon and Otto 2000; Bataillon and Bailey 2014; Castellano et al. 2019) that revert deleterious alleles back to their original, fitter versions.

Materials and Methods

Species Used and Inference of Ancestral State

In this study, we selected 24 plant genomes (8 herbaceous and 16 woody species) and polymorphic sites at 4–20 chromosomes within each species were identified (see supplementary file S1, Supplementary Material online). As noted above, we wanted a diverse array of species varying in effective population size and life history traits but the aim of the present study was not to compare them. This will be done in a subsequent study. For 11 species, the ancestral state for each polymorphic site was inferred with two or three outgroup sequences using the program est-sfs (Keightley et al. 2016). For the remaining 13 species, the ancestral state was inferred using the fixed sites of the outgroup.

Classification of Sites Based on Degeneracy and SIFT Score

We used the Uniref database (Suzek et al. 2015), to build a database of SIFT scores for each of the 24 plant genomes. SIFT scores were assigned to each of the four states (A, T, G, and C) at every position in the genome, which can be calculated based on the conservation of clustered amino acid alignments of high similarity. Default settings recommended by the authors were used (Vaser et al. 2016). A score equal to 0 corresponds to the most conserved sites and a score equal to 1 to the least constrained sites. Classically, and as in the toy example above, the sites are classified as deleterious if the score $\in$ (0, 0.05] and tolerated otherwise (Ng and Henikoff 2003; Vaser et al. 2016). Here, we further divided the scores into four discrete categories: fully conserved (FC, score = 0), partly conserved (PC, score $\in$ (0, 0.05]), partly diverse (PD, score $\in$ (0.05, 1)), and fully diverse (FD, score = 1). For every site at which the ancestral state has been inferred, one can then assign 16 “changes in conservation status” to all potential state changes from the ancestral state to the derived state (e.g., FC → FD, PC →PD, and so on). Combining these “changes in conservation status” with the degeneracy (0-fold and 4-fold) and considering those that are possible one obtains a total of 20 possible mutation directions (hereafter called “MD,” see supplementary table S1, Supplementary Material online for details) at each site in the coding regions of the genome. (Sift score is based on amino acid so once one finds that the category changes, e.g., from FD → PD, only nonsynonymous changes are possible.) Like other SFS-based methods, PolyDFE requires a “length” for each category of mutation, so we thus defined the MD weights of each site as their counts across all three possible changes from ancestral state (e.g., a site can be assigned with 1/3 to 0-fold FC →FD and 2/3 to FC →FC). Then to obtain the total “length” of each MD category i, L_i, we summed weights up over all k positions in the genome $L_i=\sum _k{W}_{i,k}$.

Estimation of DFE and $P_0/P_4$

For each genome, we counted the number of polymorphic sites of each frequency class to generate SFS for all MDs. We estimated the distribution of fitness effects for new mutations in the genome using polyDFEv2 (Tataru et al. 2017; Tataru and Bataillon 2019, 2020). Estimation of the DFE in polyDFEv2 assumes a mixture model for the underlying DFE. A proportion, p_b, of beneficial mutations is drawn from an exponential distribution of mean S_b and a proportion $1-p_b$ of mutations have a negative selection coefficient drawn from a gamma distribution with shape parameter β and mean S_d. The SFS of 4-fold FD → FD was used as the neutral category and the SFS of the other 19 MD was used to estimate 19, potentially different, DFEs separately. We used the total “length” of each MD category (the L_i defined above) to scale the SFS of the neutral category (4-fold FD → FD) and that of the other 19 categories. To insure that sites with different delta scores are comparable in terms of possible confounding factors we took SNPs with a given delta SIFT score, say +1, and then calculated their DFE with the SFS of synonymous SNPs located in the same genes, rather than SNPs elsewhere in the genome. Hence the two types of SNPs have the same background and this should minimize the possibility that the relationship between SIFT score and the DFE, or statistics derived from it, is caused by other factors. The effect of using only synonymous SNPs from the same genes or from all genes on the main results was minor as shown, for instance, by the comparison of the results obtained with the two approaches in tables 3 and 4 where synonymous sites from the same genes were used and in supplementary tables S2 and S3, Supplementary Material online, where synonymous sites from all genes were used.

Finally, we also defined the ratio $P_0/P_4$ by calculating P₀ and P₄ and scaling them by L_i for each MD class, respectively. More specifically we have $P_0=(n_0+1)/L_0$, where n₀ is the number of 0-fold polymorphic sites counted along a sequence of length L₀, and $P_4=(n_4+1)/L_4$, where n₄ is the number of 4-fold polymorphic sites counted along a sequence of length L₄. We added 1 to the count of polymorphic site to avoid possible dividing by 0 (see, e.g., Welch [2006]).

SIFT δ Scores

In order to study the dynamics of changes in SIFT scores and relate it to the DFE, we further assigned four values (−3 to 0) to the four SIFT categories defined previously: FC (−3), PC (−2), PD (−1), and FD (0). All 20 MD can then be ranked with a SIFT “δ” score, that is obtained by calculating the difference between the values assigned to two mutation states (e.g., FC → FD will have a “δ” score of +3). Mutations with higher δ values are more likely to be beneficial (i.e., less deleterious) and mutations entailing low δ score values are more likely to be deleterious. The effectively neutral part of the DFE is expected to harbor mutations characterized by δ scores of mixed sign and close to 0, so typically between −1 and +1. In theory, we could also study selection on synonymous mutations by leveraging δ scores but we decided to focus our analyses on nonsynonymous mutations.

The Flux of Beneficial Mutations

When it comes to estimating the effect of beneficial mutations, focus has often been on α, the proportion of amino acid changing mutations that are beneficial (Smith and Eyre-Walker 2002; Galtier 2016). Most published estimates of α are obtained by contrasting observed patterns of nonsynonymous divergence with the ones expected given the deleterious DFE and the observed synonymous divergence. Doing so implies that one assumes that the intensity of purifying selection remains constant during divergence. Violation of the assumption of constant intensity of purifying selection during divergence with the outgroup will automatically inflate or bias downward the estimate of the contribution of beneficial mutations (see Eyre-Walker 2002; Rousselle et al. 2018; Tataru and Bataillon 2019). Testing for the presence of beneficial mutations without relying on divergence counts is theoretically feasible (see, e.g., Schneider et al. 2011; Tataru and Bataillon 2019; Moutinho et al. 2020) but has seldom been done.

Likelihood ratio tests for the occurrence of beneficial mutations relying solely on counts in the SFS and not divergence counts are available but have limited power, unless large amounts of SNPs are available in SFS data. How to increase the power of these tests? One possibility is to focus on sets of genes or genomic regions that are known to harbor more beneficial mutations. These include, among others, genes involved in immunity, sex-linked genes or genes encoding proteins that contain proportionally more exposed residues (Moutinho et al. 2020 and references therein). However, by doing so there is a risk of circularity because we search for beneficial mutations where we think we should find beneficial mutations. Here, instead of first focusing on specific gene sets, we propose to use SFS conditioned on δ. In particular, we test whether the DFEs estimated for each δ covary with p_b, the proportion of beneficial mutations (irrespective of mutation effect S_b), and with the product $p_b*S_b$ that corresponds to the flux of (usable) beneficial mutations. The rationale for using this composite product is 2-fold: under strong selection-weak mutation (SSWM) limit it scales with the amount of new mutations that are not lost early on through drift and therefore are available for adaptation. Second the product $p_b*S_b$ is statistically better behaved than p_b and S_b taken separately as p_b and S_b tend to strongly covary (Schneider et al. 2011; Tataru and Bataillon 2019).

All statistical analyses were carried out using the statistical language R (R Core Team 2013). To examine the covariation between DFE properties and δ, we used linear or generalized (mixed) models where we used $P_0/P_4$ ratios or properties of the DFE as response variables. We used R² and pseudo R² of models to quantify the amount of variation in DFE properties explained by δ. We also checked that the amount of variation explained by δ was not confounded by $ϵ$, the rate of SNPs misorientation when building derived SFS, and by GC3 content. To do so, both variables were used as predictors in the models and variance inflation factors were computed using the vif() function of the R car package (Fox and Weisberg 2011) to check for co-linearity between δ and $ϵ$ or GC3 content. Overall, models selection was insensitive to including/excluding $ϵ$ or GC3 content in predictors along with δ. Moreover, the (pseudo) R² of the best models were barely affected by including $ϵ$ or GC3 content and variance inflation factors where low (<1.2), so for simplicity we only report the effect of δ in the main text. A supplementary text, Supplementary Material online describing the full statistical analysis of the data is available as commented R markdown documents (supplementary file S4, Supplementary Material online).

Supplementary Material

Supplementary data are available at Genome Biology and Evolution online.