Improved contrast and noise of megavoltage computed tomography (MVCT) through cycle-consistent generative machine learning

Abstract

Purpose:

Megavoltage computed tomography (MVCT) has been implemented on many radiation therapy treatment machines as a tomographic imaging modality that allows for three-dimensional visualization and localization of patient anatomy. Yet MVCT images exhibit lower contrast and greater noise than its kilovoltage CT (kVCT) counterpart. In this work, we sought to improve these disadvantages of MVCT images through an image-to-image based machine learning transformation of MVCT and kVCT images. We demonstrated that by learning the style of kVCT images, MVCT images can be converted into high quality synthetic kVCT (skVCT) images with higher contrast and lower noise, when compared to the original MVCT.

Methods:

kVCT and MVCT images of 120 head and neck (H&N) cancer patients treated on an Accuray TomoHD system were retrospectively analyzed in this study. A cycle-consistent generative adversarial network (CycleGAN) machine learning, a variant of the generative adversarial network (GAN), was used to learn Hounsfield Unit (HU) transformations from MVCT to kVCT images, creating skVCT images. A formal mathematical proof is given describing the interplay between function sensitivity and input noise and how it applies to the error variance of a high-capacity function trained with noisy input data. Finally, we show how skVCT shares distributional similarity to kVCT for various macro-structures found in the body.

Results:

Signal to noise ratio (SNR) and contrast to noise ratio (CNR) were improved in skVCT images relative to the original MVCT images and were consistent with kVCT images. Specifically, skVCT CNR for muscle - fat, bone - fat and bone - muscle improved to 14.8 ± 0.4, 122.7 ± 22.6, and 107.9 ± 22.4 compared with 1.6 ± 0.3, 7.6 ± 1.9, and 6.0 ± 1.7, respectively, in the original MVCT images and was more consistent with kVCT CNR values of 15.2 ± 0.8, 124.9 ± 27.0, and 109.7 ± 26.5, respectively. Noise was significantly reduced in skVCT images with SNR values improving by roughly an order of magnitude and consistent with kVCT SNR values. Axial slice mean (S-ME) and mean absolute error (S-MAE) agreement between kVCT and MVCT/skVCT improved, on average, from -16.0 and 109.1 HU to 8.4 and 76.9 HU, respectively.

Conclusions:

A kVCT-like qualitative aid was generated from input MVCT data through a CycleGAN instance. This qualitative aid, skVCT, was robust towards embedded metallic material, dramatically improves HU alignment from MVCT, and appears perceptually similar to kVCT with SNR and CNR values equivalent to that of kVCT images.

1. INTRODUCTION

Kilovoltage computed tomography (kVCT) is the medical standard for radiation therapy treatment planning for most patients. The development of kV on-board imaging on radiation therapy treatment machines has allowed for more accurate localization of patients prior to radiation delivery, and the capability to monitor anatomical changes and adapt the treatment to a patient’s daily anatomy. For on-board imaging, kV cone-beam CT (CBCT) has become the most prominent modality with it being widely used in many medical linear accelerator and proton therapy systems. While kV on-board imaging systems offer strong soft and bony tissue contrast², these systems may also complicate machines by necessitating additional hardware and a separate imaging isocenter (due to an imaging system separate from the treatment beam) and tend to be more susceptible to certain artifacts. In the case of a patient with metal prosthetics, dental fillings, or other embedded metallic material, kVCT can be susceptible to streaking artifacts and increased beam hardening effects³. Previously, megavoltage (MV) imaging was developed as an alternative on-board imaging modality that may not be as susceptible to some of the disadvantages of kV imaging³. MV imaging often relies on the already present high-energy x-ray treatment beams potentially increasing the spatial accuracy if the imaging isocenter is the same as the treatment isocenter. In addition, megavoltage computed tomography (MVCT) circumvents problems related to beam hardening and streaking artifacts through a higher energy spectrum but at the cost of noisy image quality with lower signal-to-noise and lower contrast-to-noise ratios⁴ relative to kVCT. With these advantages of MVCT, groups have worked to mitigate these shortcomings in contrast and noise. There have been recent attempts to minimize the MVCT noise signature through statistical methods^5,6, however even with low noise implementations MVCT has lower tissue contrast values when compared to kVCT tissue contrast. Ideally, we would acquire MVCT’s robustness to implanted metal devices while maintaining kVCT’s high signal-to-noise and contrast-to-noise ratios. Such advantages would potentially allow MVCT to hold an advantage to kVCT for on-board imaging.

In order to transform MVCT images into kVCT-like images without introducing any deformation, the relationship between the appearance of MVCT and kVCT images needs to be learned. Historically, kernel methods and iterative, tolerance methods were the common implementations for learnable or modular transformations in medical imaging^7,8. Kernel methods are attractive due to their easy implementation and theoretical guarantees with iterative, tolerance methods being favored when a common-sense or physics-driven approach is preferred. When compared to modern neural networks, the former applications are described as being more interpretable and driven by first principles. However, both kernel methods and iterative methods fall behind modern machine learning implementations in the field of image recognition and segmentation⁹. Another criticism to modern neural networks is that they are prone to overfitting and behave unexpectedly to unseen inputs. Recent research into neural networks has shown a double descent phenomenon in training where, in the large data regime, the neural network can achieve zero training error without losing the ability to generalize to unseen inputs¹⁰. Accuracy aside, there are compelling runtime reasons to choose neural networks over kernel or iterative methods. For kernel methods, the runtime complexity of evaluating a new point grows naively on the order of N³, where N is the number of total training data points. Approximate kernel methods using M inducing points can improve this complexity to N + M log M¹¹. For iterative, tolerance-based methods, runtime is dependent on the data distribution and the selected error tolerance ϵ. Iterative problems that are convex but not necessarily differentiable can be solved via proximal gradient descent algorithms with an accelerated runtime growing on the order $1/\sqrt{\mathrm{ϵ}}$¹². Neural network implementations sidestep these issues by offering a vectorized solution that runs in constant time at evaluation, regardless of the specific input and size of the training data.

Convolutional neural networks (CNN) have achieved success in many radiation oncology applications such as anatomical segmentation, dose calculation, and deformable image registration^13–18. However, conventional CNNs rely on static loss functions that promote overly smooth predictions. Generative adversarial networks (GAN) solve this problem by training a CNN discriminator to enforce prediction realism^19,20. However, GANs utilize L1 loss which requires paired images between target and source domains. Patients often have different postures between target and source imaging domains so L1 loss is sub-optimal even if deformable image registration is used. Cycle-consistent generative adversarial networks (CycleGAN) overcome this limitation by using pure adversarial loss which enables them to learn from unpaired images²¹. Unsupervised CycleGANs have been used in CT predictive imagery^22,23 showing promising results in transforming cone-beam CT images to kVCT images. In this study, CycleGAN used to generate anatomically accurate kVCT images from MVCT input images. Zhu et al’s CycleGAN²⁴ architecture was used as it is robust towards deformations²⁵ and works well for unaligned anatomy, which is the case for our inter-modality imaging data. To recapitulate, the work describes a CycleGAN architecture that improves the contrast and signal of MVCT by learning a transformation that maps local MVCT information to a local kVCT-like counterpart.

2. MATERIALS AND METHODS

2.A. Data

The kVCT and MVCT images of 120 head and neck (H&N) cancer patients treated on an Accuray TomoHD system were retrospectively analyzed in this IRB-approved study. One hundred patient scans were used for training and validation while 20 patient scans were used for testing. Each patient received a kVCT simulation scan approximately two weeks prior to treatment. Following treatment planning, each patient was imaged daily by MVCT on a TomoHD machine immediately prior to treatment. For each patient, the kVCT was co-registered to the space of their respective MVCT scan in MIM (MIM Software Inc, v 6.8.3 Cleveland, OH) using the automated rigid registration algorithm to produce a match across the entire scan volume then resampled and saved while maintaining the 512×512 16-bit matrix. In this process, the kVCT field of view (FOV) was, in general, reduced to match the MVCT scan FOV. During the training process, both kVCT and MVCT datasets image intensities were renormalized to [−1, 1] for better training stability. Both datasets were later unnormalized for the final comparisons and calculations of error metrics.

2.B. MVCT and kVCT Cyclic Learning

CycleGAN²⁴, a GAN variant, was used to learn the Hounsfield Unit (HU) transformation from MVCT to kVCT images. CycleGAN implements a pair of parallel opposed GANs to simultaneously learn forward (MVCT to kVCT) and backward (kVCT to MVCT) image transformations. Each GAN focuses on optimizing its specified transformation through an adversarial game of generating and identifying fake images. The learning of both GANs are coupled with a cyclic loss which penalizes the degree to which the composed forward and backward transformation varied from the identity function. Figure 1 provides a view of the CycleGAN loss architecture for one of the GAN pairs.

Figure 1.

Loss architecture for an X data-type generator and discriminator. Type X cyclic loss minimization is accounted for when calculating the error backpropagation for Generator Y. Loss architecture for the Y type generator and discriminator is the mirror image with all mentions of types X and Y switched in the mirror image.

Adopting the notation from Zhu et al²⁴, if G:X → Y is the generator producing kVCT images from MVCT images and F:Y → X is the generator producing MVCT images from kVCT images then the cyclic loss can be written as

$$L_{cyc}=\frac{1}{N}{\sum }_{i=1}^N{‖F\left(G\left(x_i\right)\right)-x_i‖}_1+{‖G\left(F\left(y_i\right)\right)-y_i‖}_1$$ (1)

where ‖⋅‖₁ is the L1 norm of a vector, x_i is an MVCT training example, and x_i is a kVCT training example. Early in the training cycle, the cyclic loss is most active in penalizing deformations brought upon by each image transformation. Later in the training, however, the cyclic loss may become less effective in minimizing deformations as the generators learn to “game” the discriminators by encoding missing information across the image²⁶. In the case of MVCT to kVCT training this behavior can prove to our benefit as the high noise ratio in MCVT scans becomes perceived as a structural difference that can be optimized away in the forward MVCT to kVCT transformation. This denoising claim is supported by previous literature²² where CycleGAN was shown to be adept in minimizing the noise and imaging artifacts found in CBCT scans. The benefits to using CycleGAN then become twofold, first a backward transformation (kVCT to MVCT) is gained in conjunction to the desired forward transformation and second the forward transformation becomes equipped with a machine learned denoising measure for MVCT images.

2.C. Validation and Model Specifications

Prior to final training, network and hyperparameter validation was performed on an 85–15 split of the total training data. All image data during the validation phase was downsampled by a factor of 2 to lessen computational burden and accelerate the search for good hyperparameters. Hyperparameters that contributed to the stability and longevity of the training were considered good or strong hyperparameters. During validation, emphasis was placed on running the adversarial learning process long enough for the generator to be expressive enough to realistically simulate kVCT patient scans. Output realism was determined both qualitatively by eye and quantitatively through a degree deviation calculation between real and synthetic kVCT. Examples of this degree deviation calculation are shown on Figure 3, where they are applied to MV vs kV and skV vs kV heatmaps.

Figure 3.

A two-dimensional heatmap comparison of HU values at each voxel of the CT scan data. MVCT HU vs kVCT HU is plotted on (a) and skVCT vs kVCT is plotted on (b). Plots feature log-scale coloring and a gray dotted line representing a 45° reference line. The solid red line is the result of a total least squares fit on the aligned two-dimensional bony tissue data

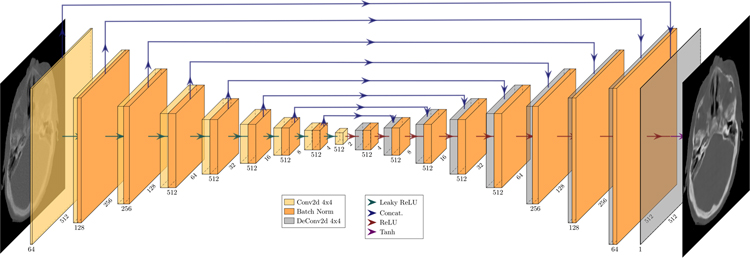
Final network architecture used for the generators was a U-Net architecture with a 2×2 bottleneck for 512×512 sized images and for the discriminators the final architecture was a four-layer PatchGAN²⁷ with an effective receptive field of 142×142. Both networks are readily available in the source code provided by Zhu et al²⁴ and can be modified via command line arguments at the start of training^c). The CycleGAN loss was optimized for 210 epochs with the Adam optimizer and a learning rate of 2.5 × 10⁻⁴, a β₁ of 0.5, a β₂ of 0.999, and an ϵ of 1.0 × 10⁻⁸. During validation, we found that going past 210 epochs negligibly improved generator expressivity at the cost of added adversarial noise. The hyperparameters listed above align closely with another CycleGAN implementation used for CT to on-board treatment machine CT translation²². A visualization of the final U-Net architecture used has been provided in Figure 2.

Figure 2.

U-Net 256 generator architecture. This figure shows the image transformation pipeline from MVCT to skVCT image. Visualization made with PlotNeuralNet²⁸ Github source code.

2.D. Calculations

Tissue segmentation was utilized to compare skVCT HU accuracy at different core areas of interest: bony tissue, soft tissue, fat, and muscle. Tissue segmentation was preformed using standard HU thresholds²⁹ together with the Python library Scikit-Image³⁰ to clean and partition the tissue regions of the 20 test case axial CT slices. A total of five tissue masks were created from kVCT/skVCT data: a body mask, a bony tissue mask, a soft tissue mask, a fat mask, and a muscle mask. The body mask was created by truncating all HU values less than -400 and then segmenting the different connected regions using Scikit-Image. The largest of these connected regions was defined to be the body region. The body region was refined to a mask through a binary fill operation which preserves the nasal and oral cavities as well as the lungs of the body. All voxels inside the body mask with HU value greater than 150 HU are considered to be part of the bony tissue mask. The set subtraction between body mask and bony tissue mask produced the soft tissue mask. Likewise, the fat and muscle masks are subsets of the soft tissue mask respecting the HU bounds found in Lev and Gonazalez²⁹, which are [−70, −30] and [20, 40], respectively. Masks for MVCT and skVCT images were made using skVCT HU data. In order to minimize mask alignment issues between MVCT and kVCT or skVCT and kVCT, the mask intersection between the skVCT mask and kVCT mask was used when calculating error metrics between different image domains. Specific regions of interest (ROI) contours for the head and neck normal organ structures were manually contoured using MIM Software (MIM Software Inc, v 6.8.3 Cleveland, OH). These contours were then filled and used as masks to calculate metrics on the specific ROIs.

In this manuscript we considered primary metrics calculated directly on the source data and results and secondary metrics derived from the regression and interpolation of the target outputs. Primary metrics can be subdivided into two categories, those calculated at the voxel level and those calculated at the slice level. All primary metrics below are shown in mean value form. Let N denote the total number of voxels shared in common between source X and target Y and X_i, Y_i denote the intensity values of the i^th voxel of the respective source and target then voxel mean error (V-ME) and voxel mean absolute error (V-MAE) can be expressed as

$$\text{V-ME}=\frac{1}{N}{\sum }_{i=1}^N{Y}_i-X_i$$ (2)

$$\text{V-MAE}=\frac{1}{N}{\sum }_{i=1}^N\left|Y_i-X_i\right|$$ (3)

All twenty test patients are included in the sums of (2) and (3) and only voxels within the body were included. Mean error and mean absolute error were also considered at the slice level, analogously named S-ME and S-MAE. Suppose a total of K slices were used and N_k is the number of voxels in common shared between source and target at the K^th slice then the slice error metrics become

$$\text{S-ME}=\frac{1}{K}{\sum }_{k=1}^K\left(\frac{1}{N_k}{\sum }_{i=1}^{N_k}{Y}_i^{\left(k\right)}-X_i^{\left(k\right)}\right),$$ (4)

$$\text{S-MAE}=\frac{1}{K}{\sum }_{k=1}^K\left(\frac{1}{N_k}{\sum }_{i=1}^{N_k}\left|Y_i^{\left(k\right)}-X_i^{\left(k\right)}\right|\right),$$ (5)

Three additional slice-level metrics considered were peak signal-to-noise-ratio (PSNR), signal-to-noise ratio (SNR), contrast-to-noise ratio (CNR). Let ${\mathrm{\mu }}_X^{\left(k\right)}$ be the mean of source X at slice k and ${\mathrm{\mu }}_Y^{\left(k\right)}$ be the mirror case for another source Y. We denote the noise present on slice k by the variable σ^(k). We approximate the noise at slice k through calculating the standard deviation of the muscle mask values at that slice. With this notation, the equations for the additional slice-level metrics can be expressed as

$$\text{SNR}=\frac{1}{K}{\sum }_{k=1}^K\frac{{\mu }_X^{\left(k\right)}}{{\sigma }^{\left(k\right)}},$$ (6)

$$\text{CNR}=\frac{1}{K}{\sum }_{k=1}^K\frac{\left|{\mathrm{\mu }}_Y^{\left(k\right)}-{\mathrm{\mu }}_X^{\left(k\right)}\right|}{{\mathrm{\sigma }}^{\left(k\right)}},$$ (7)

$$\begin{gathered} \text{PSNR}=\frac{1}{K}{\sum }_{k=1}^{K}20{\log }_{10}\left(\frac{I_{max}}{MS{E}^{\left(k\right)}}\right),\text{where} \\ MS{E}^{\left(k\right)}=\frac{1}{N_k}{\sum }_{i=1}^{N_k}{\left(Y_i^{\left(k\right)}-X_i^{\left(k\right)}\right)}^2\text{and}{I}_{\mathit{max}}=2^{12}-1. \end{gathered}$$ (8)

In addition, two secondary metrics were considered. The first secondary metric was an absolute difference metric calculated between the estimated probability distributions of X and Y while the other secondary metric was an angle deviation calculation between an optimal reference and a fitted slope. For the first secondary metric, suppose f_X, f_Y are linear interpolants of the bin heights of the normalized histograms of X and Y. If Λ is the union of the supports of f_X and f_fX then the integral absolute difference (IAD) can be expressed as

$$\text{IAD}={\int }_{\Lambda }\left|f_Y\left(x\right)-f_X\left(x\right)\right|\mathrm{ }dx.$$ (9)

Bin and range values were hand-selected for the histogram of each contour. For the second secondary metric, a straightforward dot product, arccosine calculation was done between the optimal reference and fitted slope, ω. The slope, ω, was calculated from a total least squares (orthogonal regression) fit between the source and target data. Simplifying, the result becomes

$$\omega =\frac{a}{b+\sqrt{b^2+a^2}},\text{where}a={\sum }_{i=1}^N{X}_i{Y}_i\text{and}b=\frac{1}{2}\left({\sum }_{i=1}^N{X}_i^2-Y_i^2\right).$$ (10)

Alternatively, one could calculate the angular deviation between the reference line and the best linear predictor of the data (OLS). However, for a geometric calculation like angular deviation it is better to compare the reference line to the best linear geometric (orthogonal) fit to the two-dimensional data.

2.E. Model Error Analysis

The following analysis is provided as an aid to later discussion of the results reported in Sections 3.A. and 3.B. The analysis presented focuses on the relation of a function’s Jacobian J and input variance ${\mathrm{\sigma }}_X^2$, to the model’s total error variance. Let $f:\mathrm{\Omega }\to {\mathbb{R}}^d$ be our machine learned function mapping d dimensional MVCT axial slice images $\overrightarrow{X}$ to d dimensional kVCT axial slice images $\overrightarrow{Y}$. We work with the assumption that the value of $\overrightarrow{X}$ has been truncated sometime during the instrumentation process and as such claim, without loss of generality, that Ω can be described as a compact domain. To see this note, Ω can be defined tightly about $\overrightarrow{X}$ such that all values of Ω that are not realizations of $\overrightarrow{X}$ must be boundary points of Ω and as such have probability zero of occurring. This gives an almost everywhere equivalence between compact Ω and the domain of truncated $\overrightarrow{X}$.

For a proof of concept, we assume that f has learned the MVCT to kVCT HU transition such that ${\mathbb{E}}_Y[\overrightarrow{Y}]=f({\mathbb{E}}_X[\overrightarrow{X}])$. Further we assume that the noise in $\overrightarrow{X}$ is independent to the noise in $\overrightarrow{Y}$ and that the noise between components of $\overrightarrow{X}$ are uncorrelated and have equal variance. Lastly we define a tight bound δ > 0 on the mean error such that for all $i\in \{1,\dots ,d\},|{\mathbb{E}}_{Y,X}[Y_i-f_i(\overrightarrow{X})]|\le \mathrm{\delta }$. Under these assumptions and definition, a lower bound on the total variance of the error can be established (proof can be found in the Appendix, Section A.2.) such that:

$$\begin{gathered} tr\left(Co{v}_{XY}\left(\overrightarrow{Y}-f(\overrightarrow{X}),\overrightarrow{Y}-f(\overrightarrow{X})\right)\right)\ge \rho {\sigma }_X^2{\left({\sum }_{i=1}^{d}Va{r}_X\left({\kappa }_i^2\right)\right)}^{1/2}{\left({\sum }_{i=1}^d\left(Kurt\left[X_i\right]-1\right)\right)}^{1/2} \\ +{\sigma }_X^2{\mathbb{E}}_X\left[{\Vert \overline{J_X}\Vert }_F^2\right]-d{\delta }^2. \end{gathered}$$ (11)

Defining the notation above, $\overline{J_X}$ is the average almost-everywhere equivalent to J between instance $\overrightarrow{X}$ and mean ${\mathbb{E}}_X[\overrightarrow{X}]$, kurt[X_i] is the kurtosis of component X_i, ${\mathrm{\kappa }}_i^2$ is the squared singular value of $\overline{J_X}$, and ρ is a value between -1 and 1. The only lower bound estimate used in (11) was ${\Vert {\mathbb{E}}_{Y,X}[Y_i-f_i(\overrightarrow{X})]\Vert }_2^2\le d{\mathrm{\delta }}^2$, so for tight or small δ lower bound (11) becomes an accurate estimate of the total variance of the error.

The value ${\mathbb{E}}_X[{\Vert \overline{J_X}\Vert }_F^2]$ shares similarities to the function sensitivity, ${\mathbb{E}}_X[{\Vert J\Vert }_F]$, and can be viewed as an average, squared function sensitivity between the instance $\overrightarrow{X}$ and mean $\mathbb{E}[\overrightarrow{X}]$ since,

$$\underset{z\in L_X}{\mathit{min}}J{|}_z\le \overline{J_X}\le \underset{z\in L_X}{\mathit{max}}J{|}_z,$$ (12)

$$\underset{z\in L_X}{\mathit{min}}{\Vert J{|}_z\Vert }_F\le {\Vert \overline{J_X}\Vert }_F\le \underset{z\in L_X}{\mathit{max}}{\Vert J{|}_z\Vert }_F,$$ (13)

where $L_X=\{s\overrightarrow{X}+(1-s)\mathbb{E}[\overrightarrow{X}]|s\in [\mathrm{0,1}]\}$ and the inequality in (12) is respected elementwise. Additionally, the squared Frobenius norm of a matrix A is equivalent to the sum of the square singular values of A, so the term $Va{r}_X({\mathrm{\kappa }}_i^2]$ can be viewed as the variation of the squared, average function sensitivity ${\mathbb{E}}_X[{\Vert \overline{J_X}\Vert }_F^2]$. On a final note the kurtosis is lower bounded by one plus the squared skewness of a random variable³¹ so (11) is always a real-valued estimate.

3. Results

3.A. Alignment Results and In-Voxel Variation

Two-dimensional HU heatmaps for MVCT vs kVCT values and skVCT vs kVCT values were plotted in Figure 3. The heatmaps are colored with a log-scale coloring and include a gray dotted reference line across the diagonal. The diagonal reference denotes a perfect HU alignment result when both the source and target distribution are equal in value everywhere. Equation (10) was applied to voxels in the intersection of the bony tissue masks of the source and target slices. The fitted slope, shown as a solid red line in Figure 3, was used to calculate the angular deviation between bony tissue values and the 45° reference line. The MV, kV heatmap (Figure 3 (a)) had a bony tissue slope of 0.488 and an angular deviation 19.01°. The skV, kV heatmap (Figure 3 (b)) had a bony tissue slope of 1.002 and an angular deviation of 0.05°.

We highlight two key areas of interest in plots (a) and (b) of Figure 3. The first is a soft tissue region plotted as a yellow color around the kV HU interval [−100, 100] and the second is a bony tissue “tail” extending from 150 kV HU to 1500 kV HU. Qualitatively an improvement in alignment, with respect to the reference line, can be seen in both regions when comparing Figure 3 (a) to Figure 3 (b). Due to log scaling, the yellow colored region in Figures 3 (a) and 3 (b) play a dominant role in the soft tissue kVCT HU alignment. A suitable proxy to HU alignment in this case would be to compare the soft tissue mean error differences between MVCT and skVCT. Tables I and II display both average V-ME and S-ME for MVCT and skVCT showing an improvement from 26.7 to 9.0 HU for V-ME and 26.6 to 8.8 HU for S-ME. An important caveat to the previously mentioned results is that, for a fixed kVCT HU value, the spread of skVCT HU values will not be visibly nor numerically more concentrated than the spread of MVCT HU values. This can be verified visibly in Figure 3 by the similar spread of values around both red fitted slopes and numerically in Table I by the large standard deviations for the voxel-wise results V-ME and V-MAE. Contrasting the standard deviations in the error measurements of Table I from Table II, exposes that the root of the problem is the large variation between HU predictions at the voxel level. Table III offers additional information to the voxel prediction problem showing that skVCT does not have generalization issues for common tissues such as muscle and fat. Two-tailed paired t-tests between MV and skV errors were performed to confirm this observed error phenomenon was not an artifact of the underlying MVCT and kVCT data. Tables I to III record computed t-statistics and p-values for tissue-specific errors, while Table VII records equivalent statistical parameters for structure-specific errors. All p-values less than floating point machine precision have been listed as “p < 10⁻¹⁶”.

Table I.

Mean error and mean absolute error at voxel level for skVCT, kVCT, and MVCT on soft tissue and bone. Two-tailed paired t-test between MV errors and skV errors at the voxel level.

Tissue	skV V-ME [HU]	MV V-ME [HU]	skV V-MAE [HU]	MV V-MAE [HU]	Voxel Err. t-stat.	Voxel Err. p-value	Voxel Abs. Err. t-stat.	Voxel Abs. Err. p-value
Soft and Bony Tissue	8.6 ± 147.7	−17.3 ± 189.5	76.3 ± 126.7	109.5 ± 155.6	−8.42e+02	p < 10−16	1.38e+03	p < 10−16
Soft Tissue	9.0 ± 120.6	26.7 ± 126.6	58.9 ± 105.6	77.3 ± 103.7	9.77e+02	p < 10−16	1.17e+03	p < 10−16
Bony Tissue	5.9 ± 257.6	−288.0 ± 270.3	183.1 ± 181.6	307.6 ± 247.7	−2.56e+03	p < 10−16	9.39e+02	p < 10−16

Table II.

Slice-level mean error, mean absolute error, peak signal-to-noise ratio for skVCT, kVCT, and MVCT on soft tissue and bone. Two-tailed paired t-test between MV errors and skV errors at the slice level.

Tissue	skV S-ME [HU]	MV S-ME [HU]	skV S-MAE [HU]	MV S-MAE [HU]	PSNR [dB]	Slice Err. t-stat.	Slice Err. p-value	Slice Abs. Err. t-stat.	Slice Abs. Err. p-value
Soft and Bony Tissue	8.4 ± 13.9	−16.0 ± 31.7	76.9 ± 26.1	109.1 ± 26.2	29.7 ± 2.7	−2.18e+01	p < 10−16	7.03e+01	p < 10−16
Soft Tissue	8.8 ± 12.3	26.6 ± 15.5	60.2 ± 22.2	77.9 ± 17.1	31.6 ± 3.1	3.78e+01	p < 10−16	5.49e+01	p < 10−16
Bony Tissue	10.2 ± 50.7	−272.7 ± 66.4	180.5 ± 44.2	292.2 ± 69.4	24.8 ± 2.3	−1.22e+02	p < 10−16	5.14e+01	p < 10−16

Table III.

Mean error and mean absolute error at voxel level for skVCT, kVCT, and MVCT on common fat and muscle. Two-tailed paired t-test between MV errors and skV errors at the voxel level.

Tissue	skV V-ME [HU]	MV V-ME [HU]	skV V-MAE [HU]	MV V-MAE [HU]	Voxel Err. t-stat.	Voxel Err. p-value	Voxel Abs. Err. t-stat.	Voxel Abs. Err. p-value
Fat	1.8 ± 15.3	42.7 ± 57.8	12.5 ± 9.0	58.1 ± 42.3	5.85e+02	p < 10−16	8.64e+02	p < 10−16
Muscle	0.3 ± 7.3	25.8 ± 42.4	5.9 ± 4.3	39.9 ± 29.6	7.02e+02	p < 10−16	1.32e+03	p < 10−16

Table VII.

Statistical t-test and p values for MV vs kV structure-specific slice errors.

Statistical Values	Brain	Eye	Skull	Spinal Cord	Vertebral Body	Larynx	Mandible	Oral Cavity	Parotid Gland	Pharynx
Slice Err. t-stat.	3.53e+00	3.13e+00	−1.76e+01	−3.72e+00	−1.51e+01	1.82e+00	−1.64e+01	−2.90e+00	1.61e+01	3.74e+00
Slice Err. p-value	2.22e−03	6.48e−03	2.29e−12	7.02e−04	4.49e−10	1.18e−01	2.96e−12	9.58e−03	p < 10−16	6.48e−02
Slice Abs. Err. t-stat.	9.53e+00	5.77e+00	1.10e+01	1.17e+01	1.05e+01	4.87e−05	7.98e+00	1.79e+00	1.80e+01	−1.20e−01
Slice Abs. Err. p-value	1.13e−08	2.89e−05	4.03e−09	1.93e−13	5.06e−08	9.99e−01	2.52e−07	9.06e−02	p < 10−16	9.16e−01

Analyzing the results from Tables I to III one can arrive at the tentative explanation that for organs/tissue types that were less commonly observed in our training datasets, skVCT is not prepared to interpret and extrapolate the noisy MVCT region without introducing an unavoidable uncertainty. To substantiate this point, we refer to Section 2.E. which relates the total error variance to the average, squared function sensitivity ${\mathbb{E}}_X[{\Vert \overline{J_X}\Vert }_F^2]$ and the input variance ${\mathrm{\sigma }}_X^2$. Previous literature has shown that a function’s sensitivity at a point is correlated with how well the function’s behavior generalizes at that point^32,33. Restricting the analysis in (11) to masked images, we expect masked images with predominantly uncommon tissues to have worse test generalization and higher function sensitivities. For large input variances ${\mathrm{\sigma }}_X^2$, even small changes to the function sensitivity can have dramatic changes to the total test error variance. That being said, one should be careful in minimizing the total error variance solely through the function sensitivity as it can risk introducing too much bias to the predicted result (no longer the case that ${\mathbb{E}}_{Y,X}[\overrightarrow{Y}-f(\overrightarrow{X})]\approx 0$). Another approach could be to minimize the input variance through better instrumentation or denoising measures. The first option is costly and the second, depending on methodology, may contaminate or smooth the data, which again would induce a bias in our function. A worthwhile follow-up study could explore the quantitative tradeoff between predictive power and error variance for different smoothing techniques on CycleGAN-style CT prediction.

3.B. Denoising and Structure Specific Results

In Section 3.A., it was discussed that skVCT prediction varied across the whole patient for all HU ranges. To further analyze where skVCT images perform well we restricted our analysis in Section 3.B. to tissues/organs that more commonly appeared in our training datasets. This would be the soft tissues that fall under the yellow colored region of the log-scaled plot in Figure 3. Structures such as fat and muscle, overall, both show great improvements in both mean value and standard deviation, even at the voxel level as shown in Table III. Further emphasizing this improvement, the calculated SNR and CNR values in Tables IV and V highlight the similarity between the macro-behaviors of kVCT and skVCT. SNR and CNR are calculated slice-wise and use the standard deviation of the muscle mask values as an estimate of the noise. Muscle, fat, and bone SNR values for skVCT show a large improvement going from low 20 SNR to 190 SNR for muscle and fat and about 300 SNR for bone. Likewise, muscle-fat CNR improve from ~1 CNR to ~15 CNR and the bone CNR improve from ~6 CNR to ~100 CNR. All of these values are within uncertainty of the SNR and CNR values for regular kVCT, showing a perceptual similarity between skVCT and kVCT images. Figure 4 provides a visual example to accompany these results for example axial images of the head and neck.

Table IV.

Average signal-to-noise ratios for skVCT, kVCT, and MVCT on muscle, fat, and bone.

Tissue	SNR skV	SNR kV	SNR MV
Muscle	195.8 ± 3.7	199.2 ± 9.4	21.9 ± 3.1
Fat	181.0 ± 3.4	184.0 ± 8.6	20.3 ± 2.8
Bone	303.7 ± 24.4	308.9 ± 33.4	27.9 ± 4.0

Table V.

Average contrast-to-noise ratios for skVCT, kVCT, and MVCT muscle, fat, and bone.

Tissue Comparison	CNR skV	CNR kV	CNR MV
Muscle - Fat	14.8 ± 0.4	15.2 ± 0.8	1.6 ± 0.3
Bone - Fat	122.7 ± 22.6	124.9 ± 27.0	7.6 ± 1.9
Bone - Muscle	107.9 ± 22.4	109.7 ± 26.5	6.0 ± 1.7

Figure 4.

Four example axial slices of MVCT, skVCT, and kVCT scans. Absolute HU error plots for MV, kV and skV, kV are shown in the fourth and fifth columns. The fifth column features a deeper blue color and smooths out noise in the soft tissue region.

Four slices from the test set are shown in Figure 4. Row 3 is an example where a kVCT slice has significant anatomical differences from MVCT/skVCT. The oral cavity alignment error shown in Row 3 contributes to the general soft tissue error as both oral cavities would be included in the soft tissue mask intersection. In general, however, Figure 4 shows improvements in contrast with bony tissue regions being brighter and fatty regions being darker when comparing between skVCT and MVCT. The images in the MVCT column of Figure 4 also feature a visible noise signature which is not reproduced in the skVCT column. The last two columns show the general improvements in mean error for soft tissue and bone. Muscle and fat had the most noticeable decrease in variation with both regions adopting a deeper, more homogenous color blue in the fifth column. Numerically, we see an improvement in muscle V-ME from 42.7 ± 57.8 to 1.8 ± 15.3 HU and V-MAE from 58.1 ± 42.3 to 12.5 ± 9.0 HU. Likewise, for fat, the V-ME improved from 25.8 ± 42.4 to 0.3 ± 7.3 HU and V-MAE error improved from 39.9 ± 29.6 to 5.9 ± 4.3 HU. High HU bony tissue and air cavities are two areas where skVCT has problems generalizing. Columns 4 and 5 of Figure 4 show that while the absolute error is smaller in magnitude and more sparse in column 5 as it is in column 4, there is still room for improvement to reach errors similar in magnitude to that in muscle and fat.

Figure 5 highlights potential non-anatomic artifacts and deformations found in the first and fourth row between the MVCT and skVCT images in Figure 4. All deformations and inconsistencies are highlighted in Figure 5 through a red bordered ellipse. In Figure 5 (b), the first skVCT slice shows the shrinkage of small air pockets and contrast inconsistencies while the second skVCT slice Figure 5 (d) shows the addition of what appears to be fiducial markers from the original MVCT slice. As MVCT scans lacked fiducial markers, it appears that the training learned this aspect of kVCT images and attempted to place them at likely positions in the skVCT images. Quantifying the degree of deformation, we run SSIM with parameters equal to Wang et al³⁴ on the skVCT and kVCT images and find an average SSIM of 0.927 ± 0.028 on the test set. SSIM was calculated on the tight bounding rectangle containing each head or neck slice. This SSIM does not take in consideration the alignment issues already present between the MVCT and kVCT data as the data were only rigidly registered to each other. It is possible to minimize the deformations shown in Figure 5 by training skVCT for fewer epochs or by increasing the weighting of the cyclic loss equation (1). Discriminator losses are shown in Figure 6. Both losses followed a rough negative exponential trend until they reached a Nash equilibrium, where the discriminators are no longer able to differentiate between real and fake images²⁰. An early stopping criterion was used which suspended training at 210 epochs but it is important to note that it might be possible to train skVCT for 20 to 40 fewer epochs and still maintain a good degree of perceptual similarity between this skVCT and the fully trained epoch 210 skVCT. Although both the kV and MV discriminator are not shown to have fully converged in the log loss plot displayed in Figure 6, there was only a slight change in CNR and SNR between epoch 170 and epoch 210 for skVCT. Longer training times could benefit from a converged loss but this could come at the cost of added adversarial noise to the generated images.

Figure 5.

Two examples where non-anatomic artifacts or inconsistencies have arisen translating from MVCT to skVCT. Red bordered ellipses highlight areas with inconsistent contrast or small deformations.

Figure 6.

MV and kV discriminator loss plot with number of epochs on the x-axis and loss log-scaled on the y-axis. Losses are plotted according to a 30-term running average. Both discriminator losses are semi-linear with a negative slope, making each loss roughly a negative exponential in the untransformed domain.

Another interesting quality of the CycleGAN training that is not captured by the metrics calculated in Tables I to V is the structure-specific distributional learning done when converting from MVCT to kVCT. Figure 7 provides examples of pre- and post-training distributions for selected normal organ contours. These plots show the nonlinear nature of the learned function and how skVCT is more than a conditional mean shift of values. Specifically, Figure 7 shows how skVCT attempts to match the various peaks and troughs in distribution of various macro-structures in the target distribution. A metric that highlights this improved distributional overlap is the integral absolute difference (IAD). Table VI provides the results for IAD and other metrics for the selected structures in Figure 7. To allow for fair comparison, each titled column of histograms shown in Figure 7 are calculated with the same number of bins and range of values. Similar to Tables I to III, two-tailed paired t-tests were computed between the different structure-specific MV and skV slice errors. Associated t-statistics and p-values were recorded in Table VII.

Figure 7.

HU distributions of five contour regions. The first and third rows of images show kVCT (black) and MVCT (red) HU distributions. The second and fourth rows of images show trained skVCT distribution (red) plotted against the same kVCT (black) distribution.

Table VI.

Mean error, mean absolute error, peak and average signal-to-noise ratio, and integral absolute differences for skVCT, kVCT, and MVCT at different ROIs.

ROIs	skV S-ME [HU]	MV S-ME [HU]	skV S-MAE [HU]	MV S-MAE [HU]	PSNR [dB]	SNR skV	SNR kV	SNR MV	IAD skV	IAD MV
Brain	12.1 ± 14.0	22.2 ± 13.7	31.4 ± 14.6	49.1 ± 11.8	37.8 ± 4.4	202.5 ± 4.0	204.9 ± 7.5	21.8 ± 1.3	0.40	1.03
Eye	4.23 ± 25.9	18.8 ± 25.4	44.9 ± 34.2	57.5 ± 30.5	38.1 ± 6.3	195.8 ± 9.2	204.7 ± 11.0	20.6 ± 1.7	0.40	0.87
Skull	−14.3 ± 30.3	−227.7 ± 55.0	179.2 ± 36.3	265.6 ± 51.7	24.2 ± 1.8	289.5 ± 21.0	299.6 ± 22.6	26.6 ± 1.9	0.12	0.54
Spinal Cord	15.8 ± 16.2	−7.03 ± 36.5	55.5 ± 28.1	72.9 ± 29.8	34.1 ± 5.1	210.7 ± 13.2	211.4 ± 13.5	22.1 ± 1.4	0.20	0.74
Vertebral Body	3.7 ± 17.0	−148.1 ± 35.6	137.9 ± 22.7	178.2 ± 29.5	26.9 ± 1.4	260.4 ± 13.8	263.7 ± 11.2	24.9 ± 1.7	0.18	1.01
Larynx	−8.54 ± 68.5	8.45 ± 63.0	157.4 ± 43.9	157.4 ± 43.6	24.6 ± 2.1	155.1 ± 10.5	153.3 ± 14.2	16.0 ± 1.8	0.34	0.62
Mandible	−15.8 ± 47.0	−267.7 ± 69.9	233.6 ± 61.6	314.7 ± 64.0	22.5 ± 2.2	308.1 ± 26.9	318.1 ± 30.0	28.1 ± 2.4	0.09	0.65
Oral Cavity	26.0 ± 55.5	5.5 ± 65.7	144.0 ± 70.6	150.7 ± 59.7	25.1 ± 5.0	183.5 ± 10.2	183.6 ± 14.4	19.4 ± 1.8	0.18	0.51
Parotid Gland	8.6 ± 11.4	50.4 ± 14.4	34.4 ± 10.7	62.9 ± 8.6	38.0 ± 3.2	189.0 ± 5.3	191.2 ± 10.0	21.2 ± 1.3	0.24	0.99
Pharynx	−58.7 ± 55.2	−38.5 ± 48.8	136.7 ± 55.1	136.0 ± 50.0	26.1 ± 4.7	165.8 ± 23.5	176.2 ± 15.1	17.7 ± 3.7	0.30	0.54

Most structures with large changes in IAD saw significant improvements in average S-ME and S-MAE, the exception of the case being the oral cavity, a non-anatomically based contour. The predicted voxels in the oral cavity are distributionally correct, as shown by Figure 7, but are not correct at the voxel level when skVCT oral cavity voxels are compared to kVCT oral cavity voxels. This result may be reasonable as the exact position of the jaw, teeth, and tongue may deviate between the two scans such that the overall distribution of HU values will be conserved but individual voxels may not perfectly match between the scans, as shown in row 3 of Figure 4. The two structures with the smallest change in IAD, larynx and pharynx, did not display any improvements in S-ME and S-MAE outside of uncertainty. One metric that seemed to improve regardless of change in IAD was SNR. The SNR of all ten skVCT structures matched the SNR of the corresponding kVCT structures within uncertainty. The PSNR of bony tissue dominated contours closely matched the bony tissue mean PSNR value found in the last column of Table II. Soft tissue contours with large air pockets (oral cavity, larynx, and pharynx) all had a lower PSNR than soft tissue mean PSNR in Table II. Other soft tissue contours that did not have large air pockets displayed a significant improvement in PSNR, ranging from 34 to 38 dB compared to the 31 dB PSNR recorded for soft tissues in Table II.

4. Discussion

In this manuscript, we have shown how CycleGAN’s style transfer can be applied to different energy CT scans with minimal loss to structural integrity. When applied to kVCT and MVCT scans, CycleGAN has shown it is capable of learning nonlinear, nonlocal transformations to maximize the distributional overlap between the two different domains. The trained skVCT images have an accurate average behavior and generalize well for common tissues such as fat and muscle. At the same time, we have highlighted where skVCT falls short, suffering from errors of large variation in organs/tissues less commonly observed during training. In Section 3.A., we address this issue by noting that the variation in error observed in less common tissues may be an interplay of poor generalization and high input noise. It is suggested that smoothing to the input distribution may temper large variations in HU prediction. Further, it was noted that this approach could come at the cost of expressibility, but it could be worthwhile to explore this exact tradeoff by optimizing for some specified smoothness hyperparameter. In Section 3.B., we showcased the strengths of skVCT by focusing on metrics that relied on predicted mean behavior and predicted variability on common tissues.

Lastly in Figure 8, we provide 13 examples from the test patient set where skVCT mitigates metal dental streaking artifacts that would otherwise be present in regular kVCT.

Figure 8.

Of the 20 test set patients, 13 where shown to have metal dental artifacts. One slice from each of the affected test set patients are included. MVCT slices are included as an input reference.

Our skVCT results display competitive HU alignment, PSNR, and SSIM values when compared to other medically applied CycleGAN work^22,23. Liang et al²² reported S-MAE value of 29.85 ± 4.94 HU for CycleGAN predicted CBCT to kVCT values which were significantly lower than our skVCT S-MAE value of 76.9 ± 26.1 HU. This discrepancy could be explained by the input noise and function sensitivity interplay as described in Section 3.A., but it is difficult to accurately compare results as slice metrics for specific tissues were not reported by their group. For specific tissues like fat and muscle, our skVCT results again exhibit high degrees of agreement to kVCT with both low V-ME 1.8 ± 15.3 HU and 0.3 ± 7.3 HU and low V-MAE 12.5 ± 9.0 HU and 5.9 ± 4.3 HU for fat and muscle, respectively. Similar to our Figure 3, Liang et al²² reported a regression slope of 0.99 between the CycleGAN predicted kVCT values and true kVCT values. Comparably, the fit found in Figure 3b had a regression slope of 1.002 but this value is not directly comparable to the value reported by Liang et al²² due to three differences in methodology. First, the regression completed in their work was a best predictive linear fit (OLS) while the regression determined in this manuscript was the best geometric linear fit for two-dimensional data (TLS). A small aside motivating this decision can be found in the last paragraph of Section 2.D. Secondly,²² their fit was to the entire kVCT distribution going from -1000 HU to 4000 HU, while our manuscript focused on the HU interval [150, 2¹² – 1] containing all the bony tissue data. As our soft tissue alignment was dominated by the mean behavior of tissues in the [−100, 100] kVCT HU interval of Figure 3, our fit was done to specifically examine and emphasize bony tissue differences. Third,²² they allow both the intercept and slope to vary in their regression fit while this manuscript fixes the regression intercept at 150 HU. Additionally, their reported PSNR and SSIM values are comparable to those found in our skVCT, which were 29.7 ± 2.7 and 0.927 ± 0.028 for PSNR and SSIM, respectively, compared with 30.65 ± 1.36 and 0.85 ± 0.03 for PSNR and SSIM, respectively, as found by Liang et al²². SNR and CNR values are not reported in the other works but this is also a category that our skVCT results appear to mimic kVCT data well.

Many groups have worked on methods to reduce noise in MVCT images. A proposed direct solution to the MVCT noise problem has been to increase the signal through increased radiation dose as in the work of Westerly et al³⁵. In their work, they were able to improve CNR in muscle/soft tissue like synthetic phantom tissues from 1.90 ± 0.15 to 3.43 ± 0.16 for standard and high-dose modes, respectively. As expected by theory, their improved SNR came at the expense of an increase of the square of radiation dose to the patient. As we increased the SNR in this study by roughly an order of magnitude, similar SNR improvements by their method would necessitate a 100 fold increase in radiation dose. Block-matching and framelet algorithms^5,6,36,37 are strong choices for denoising MVCT at nominal radiation doses but are limited in improving contrast due to MVCT having limited true contrast differences between different soft tissues. Liu et al⁵ utilized a block-matching algorithm equipped with a discriminatory feature dictionary to improve H&N MVCT contrast from 1.45 ± 1.51 to 2.09 ± 1.68. In comparison since skVCT mimics the contrast of kVCT images, skVCT is able to improve fat to muscle contrast for H&N from 1.6 ± 0.3 to 14.8 ± 0.4. In both prior works, CNR and SNR improvements were within a factor of 2 as opposed to our work which was about to improve CNR nearly an order of magnitude. Another benefit to skVCT is that each image can be calculated with one forward, vectorized pass through while the algorithms mentioned above rely on iterative solvers to find approximate solutions to different convex, non-differentiable optimization problems.

While an error free, numerically precise skVCT may be some time away, having skVCT function as a qualitative aid to enhance contrast and denoise MVCT may be possible through machine learning. Figure 4 displays two current hurdles to skVCT working as a qualitative aid. First are small non-anatomic artifacts and additions that appear in the synthesized kVCT and second is that skVCT sometimes suffers from inconsistent contrasting. The first issue may be minor depending on the manner which the aide is being used, but the second may need to be addressed if skVCT is to be reliably used as a qualitative aid. One possible solution to this problem could be to introduce an attention-gating mechanism³⁸ to maintain consistent contrast throughout the skVCT image. This attention-gating mechanism has already been applied to the CycleGAN model in both medical²¹ and non-medical³⁹ fields with great success.

As MVCT scans are, to date, only acquired on radiation therapy treatment machines, the clinical implementation of this work might be best suited as a way to improve contrast and noise during the patient localization process of radiation therapy. In these situations, MVCT imaging may be limiting in human visualization of soft tissue cancers due to the lowered CNR of soft tissues by MVCT. With the increased contrast and lowered noise of our skVCT images, it may be possible to more accurately visualize soft tissues targets for localization and even possibly on treatment adaptation. In the work of Reitz et al⁴⁰, they found, using Rose’s model⁴¹, that a CNR change from 2 to 5 reduces human detection error of an object from 10% to 0%, respectively. In this work, we were able to increase CNR for soft tissues and bony tissues by roughly an order of magnitude to CNR values well over 5. This increased contrast should allow a human viewer to have near zero error in ability to detect objects, an important goal when localizing soft tissue or bone for radiation therapy treatment.

5. Conclusions

In this work, we explored the efficacy of CycleGAN in producing kVCT-like images from MVCT inputs. We have shown it is possible to learn the high-contrast and low-noise features that are normally associated with kVCT scans. Various metrics were given quantifying the results of the resulting skVCT images and a novel mathematical proof was provided to explain the predictive variability observed in organs/tissues less commonly observed during training. Finally, we have also shown how skVCT is perceptually similar to kVCT via mean value voxel and slice-wise metrics implying that skVCT images may be useful in clinical settings as a qualitative aid to the current clinically obtained lower-contrast, higher-noise MVCT scans.

Appendix

A.1. Mean Value Theorem Analog for Vector-Valued Functions

Theorem 4.2 of Lang’s Real and Functional Analysis⁴² shows for a C¹ vector-valued function $f:{\mathbb{R}}^d\to {\mathbb{R}}^d,f(x+h)$ can be expressed as

$$f(x+h)=f(x)+{\int }_0^{1}J{|}_{x+th}hdt.$$ (14)

A function trained through stochastic gradient descent is not guaranteed to be C¹. Modern machine learning architectures are implemented such that each nonlinearity and compositional block has a gradient defined everywhere. With this in mind, we prove result (14) for a relaxation where $f:\mathrm{\Omega }\to {\mathbb{R}}^d$ has compact domain $\mathrm{\Omega }\subset {\mathbb{R}}^d$ and first-order partial derivative defined everywhere. In order to prove this, we first show that each component f_i, when restricted to a line segment, is absolutely continuous.

Lemma 1:

Let L_x,h = x + th then $f_i\circ L_{x,h}:[\mathrm{0,1}]\to \mathbb{R}$ is absolutely continuous for i ∈ {1,…,d}.

Given an interval I, function $g(t):I\to \mathbb{R}$ is absolutely continuous if for every positive ϵ >0 there exists some γ > 0 such that for pairwise disjoint ${\{(s_k,t_k)\}}_k$ with (s_k, t_k)⊂I we have

$${\sum }_k(t_k-s_k)<\mathrm{\gamma }\Rightarrow {\sum }_k|g(t_k)-g(s_k)|<\mathrm{ϵ}.$$ (15)

For now we fix δ arbitrarily and solve for the right hand side,

$$\begin{gathered} {\sum }_k|(f_i\circ L_{x,h})(t_k)-(f_i\circ L_{x,h})(s_k)|={\sum }_k\frac{|(f_i\circ L_{x,h})(t_k)-(f_i\circ L_{x,h})(s_k)|}{|t_k-s_k|}|t_k-s_k| \\ \le {\sum }_k|t_k-s_k|\underset{x\in [s_k,t_k]}{\mathit{sup}}\frac{d}{dt}(f_i\circ L_{x,h})(x)\le {\sum }_k|t_k-s_k|\underset{x\in [s_k,t_k]}{\mathit{sup}}{\sum }_{j=1}^d\frac{d{f}_i}{d{x}_j}(x+th)h_j. \end{gathered}$$ (16)

Since Ω is compact and the partial derivatives of f are defined everywhere, we have $\left|\frac{d{f}_i}{d{x}_j}(x)\right|\le M_{ij}<M$ for some $M_{ij},M\in \mathbb{R}$ for all i, j. This allows the following upper bound on the total variation of $f_i\circ L_{x,h}$,

$${\sum }_k|(f_i\circ L_{x,h})(t_k)-(f_i\circ L_{x,h})(s_k)|\le {\sum }_k|t_k-s_k|Mddiam(\mathrm{\Omega })\le \mathrm{\gamma }Mddiam(\mathrm{\Omega }).$$ (17)

So, for every ϵ > 0 we can satisfy absolute continuity for $f_i\circ L_{x,h}$ with a $\mathrm{\gamma }=\frac{\mathrm{ϵ}}{Mddiam(\mathrm{\Omega })}$. □

By Lemma 1 we can use the fundamental theorem of Lebesgue integral calculus⁴³ on $f_i\circ L_{x,h}$ to produce

$$(f_i\circ L_{x,h})(1)=(f_i\circ L_{x,h})(0)+{\int }_0^{1}r(t)dt,$$ (18)

where r(t) is equal to $\frac{d}{dt}(f_i\circ L_{x,h})$ almost everywhere on [0, 1]. Simplifying (17) gives

$$f_i(x+h)=f_i(x)+{\int }_0^1{\sum }_{j=1}^d\frac{d{f}_i}{d{x}_j}{(x+th)h}_{j}dt.$$ (19)

Packaging each i component of (19) yields expression (14).

A.2. A Lower Bound on Total Variance of the Error

Refer to Section 3.A. right above equation (11) for the full list of assumptions. By Section A.1. we re-express the evaluation $f(\overrightarrow{X})$ as the sum

$$f(\overrightarrow{X})=f(\overrightarrow{\mathrm{\mu }})+\left({\int }_0^{1}J{|}_{s\overrightarrow{X}+(1-s)\overrightarrow{\mathrm{\mu }}}\right)(\overrightarrow{X}-\overrightarrow{\mathrm{\mu }})=f(\overrightarrow{\mathrm{\mu }})+\overline{J_X}(\overrightarrow{X}-\overrightarrow{\mathrm{\mu }}),$$ (20)

where $\overrightarrow{\mathrm{\mu }}=\mathbb{E}[\overrightarrow{X}]$, J is equivalent almost everywhere to the Jacobian of f, and $\overline{J_X}$ is the integral of J evaluated at vector $s\overrightarrow{X}+(1-s)\overrightarrow{\mathrm{\mu }}$ for s ∈[0,1]. Through the mean value theorem for integrals it is possible to interpret $\overline{J_X}$ as the average jacobian over the line segment $\{s\overrightarrow{X}+(1-s)\overrightarrow{\mathrm{\mu }}|s\in [\mathrm{0,1}])$. Using ${\mathbb{E}}_Y[\overrightarrow{Y}]=f(\overrightarrow{\mathrm{\mu }})$ and the independence between $\overrightarrow{Y}$ and $\overrightarrow{X}$,

$${\mathbb{E}}_{Y,X}[\overrightarrow{Y}-f(\overrightarrow{X})]={\mathbb{E}}_{Y,X}[\overrightarrow{Y}-f(\overrightarrow{\mathrm{\mu }})]+{\mathbb{E}}_{Y,X}[\overline{J_X}(\overrightarrow{X}-\overrightarrow{\mathrm{\mu }})]=0+{\mathbb{E}}_X[\overline{J_X}(\overrightarrow{X}-\overrightarrow{\mathrm{\mu }})],$$ (21)

Applying (21) and the δ bound to the total variance of the error,

$$\begin{gathered} tr\left(Co{v}_{XY}\left(\overrightarrow{Y}-f(\overrightarrow{X}),\overrightarrow{Y}-f(\overrightarrow{X})\right)\right)={\mathbb{E}}_{Y,X}\left[tr\left(\left(\overrightarrow{Y}-f(\overrightarrow{X})\right){\left(\overrightarrow{Y}-f(\overrightarrow{X})\right)}^T\right)\right]-{\Vert {\mathbb{E}}_{Y,X}\left[\overrightarrow{Y}-f(\overrightarrow{X})]\right)\Vert }_2^2 \\ \le \left[tr\left(\left(\overline{J_X}\left(\overrightarrow{X}-\overrightarrow{\mu }\right)\right){\left(\overline{J_X}\left(\overrightarrow{X}-\overrightarrow{\mu }\right)\right)}^T\right)\right]-d{\delta }^2=\mathbb{E}\left[tr\left({\overline{J_X}}^T\overline{J_X}\left(\overrightarrow{X}-\overrightarrow{\mu }\right){\left(\overrightarrow{X}-\overrightarrow{\mu }\right)}^T\right)\right]-d{\delta }^2. \end{gathered}$$ (22)

De-meaning the expectation in (22)

$$\begin{gathered} \mathbb{E}\left[tr\left({\overline{J_X}}^T\overline{J_X}\left(\overrightarrow{X}-\overrightarrow{\mu }\right){\left(\overrightarrow{X}-\overrightarrow{\mu }\right)}^T\right)\right]=\mathbb{E}\left[tr\left(\left({\overline{J_X}}^T\overline{J_X}-\mathbb{E}\left[{\overline{J_X}}^T\overline{J_X}\right]\right)\left(\left(\overrightarrow{X}-\overrightarrow{\mu }\right){\left(\overrightarrow{X}-\overrightarrow{\mu }\right)}^T-{\mathrm{\Sigma }}_X\right)\right)\right) \\ +tr\left(\mathbb{E}\left[{\overline{J_X}}^T\overline{J_X}\right]{\mathrm{\Sigma }}_X\right). \end{gathered}$$ (23)

where Σ_X is the covariance matrix of $\overrightarrow{X}$. For matrices $A,B\in {\mathbb{R}}^{d\times d}$ with zero mean with respect to X, we define the inner product ${\langle A,B\rangle }_M={\mathbb{E}}_X[tr(A{B}^T)]$ with norm ${\Vert A\Vert }_M=\sqrt{{\langle A,A\rangle }_M}$ such that the expectation in (23) becomes,

$$\mathbb{E}\left[tr\left(\left({\overline{J_X}}^T\overline{J_X}-\mathbb{E}\left[{\overline{J_X}}^T\overline{J_X}\right]\right)\left((\overrightarrow{X}-\overrightarrow{\mu }){(\overrightarrow{X}-\overrightarrow{\mu })}^T-{\mathrm{\Sigma }}_X\right)\right)\right]=\mathrm{\rho }{\Vert {\overline{J_X}}^T\overline{J_X}-\mathbb{E}\left[{\overline{J_X}}^T\overline{J_X}\right]\Vert }_M{\Vert (\overrightarrow{X}-\overrightarrow{\mu }){(\overrightarrow{X}-\overrightarrow{\mu })}^T-{\mathrm{\Sigma }}_X\Vert }_M.$$ (24)

For a given evaluated inner product ${\langle A,B\rangle }_M$, we set $\mathrm{\rho }={\langle A,B\rangle }_M/({\Vert A\Vert }_M{\Vert B\Vert }_M)$. By the Cauchy-Schwarz inequality, ρ is restricted to the interval [−1, 1] for all A,B. Next by the uncorrelated and equal variance assumption ${\mathrm{\Sigma }}_X={\mathrm{\sigma }}_X^2{I}_{d\times d}$,

$$\begin{gathered} {‖\left(\overrightarrow{X}-\overrightarrow{\mu }\right){\left(\overrightarrow{X}-\overrightarrow{\mu }\right)}^T-{\mathrm{\Sigma }}_X‖}_M={\left({\sum }_{i=1}^d{\mathbb{E}}_X\left[{\left(X_i-{\mathbb{E}}_X\left[X_i\right]\right)}^4\right]-d{\mathrm{\sigma }}_X^4\right)}^{1/2}={\mathrm{\sigma }}_X^2{\left({\sum }_{i=1}^d{\mathbb{E}}_X\left[{\left.\left(X_i-{\mathbb{E}}_X\left[X_i\right]\right)/{\mathrm{\sigma }}_X\right)}^4\right]-d\right)}^{1/2} \\ ={\sigma }_X^2{({\sum }_{i=1}^d(Kurt[X_i]-1))}^{1/2}, \end{gathered}$$ (25)

where Kurt [X_i] is the kurtosis of distribution X_i. Likewise for the second norm in (24),

$$\begin{gathered} {‖{\overline{J_X}}^T\overline{J_X}-\mathbb{E}\left[{\overline{J_X}}^T\overline{J_X}\right]‖}_M={\left(\mathbb{E}\left[tr\left({\left({\overline{J_X}}^T\overline{J_X}\right)}^2\right)\right]-\mathbb{E}{\left[tr\left({\overline{J_X}}^T\overline{J_X}\right)\right]}^2\right)}^{1/2}={\left({\sum }_{i=1}^d{\mathbb{E}}_X\left[{\mathrm{\kappa }}_i^4\right]-\mathbb{E}{\left[{\mathrm{\kappa }}_i^2\right]}^2\right)}^{1/2} \\ ={\left({\sum }_{i=1}^{d}Va{r}_X\left({\mathrm{\kappa }}_i^2\right)\right)}^{1/2}. \end{gathered}$$ (26)

Here $Va{r}_X({\mathrm{\kappa }}_i^2)$ is the variance of the i^th squared singular value of average Jacobian $\overline{J_X}$. Altogether we obtain

$$\mathrm{\rho }{\mathrm{\sigma }}_X^2{\left({\sum }_{i=1}^{d}Va{r}_X\left({\mathrm{\kappa }}_i^2\right)\right)}^{1/2}{\left({\sum }_{i=1}^d\left(Kurt\left[X_i\right]-1\right)\right)}^{1/2}+{\mathrm{\sigma }}_{X\mathbb{E}}^2\left[{‖\overline{J_X}‖}_F^2\right]-d{\mathrm{\delta }}^2\le tr\left(Cov\left(\overrightarrow{Y}-f\left(\overrightarrow{X}\right),\overrightarrow{Y}-f\left(\overrightarrow{X}\right)\right)\right),$$ (27)

with ${\Vert A\Vert }_F^2=tr(A{A}^T)$ representing the squared Frobenius norm of a matrix A.