Survival analysis: A primer for the clinician scientists

Abstract

Survival analysis is a collection of statistical procedures employed on time-to-event data. The outcome variable of interest is time until an event occurs. Conventionally, it dealt with death as the event, but it can handle any event occurring in an individual like disease, relapse from remission, and recovery. Survival data describe the length of time from a time of origin to an endpoint of interest. By time, we mean years, months, weeks, or days from the beginning of being enrolled in the study. The major limitation of time-to-event data is the possibility of an event not occurring in all the subjects during a specific study period. In addition, some of the study subjects may leave the study prematurely. Such situations lead to what is called censored observations as complete information is not available for these subjects. Life table and Kaplan–Meier techniques are employed to obtain the descriptive measures of survival times. The main objectives of survival analysis include analysis of patterns of time-to-event data, evaluating reasons why data may be censored, comparing the survival curves, and assessing the relationship of explanatory variables to survival time. Survival analysis also offers different regression models that accommodate any number of covariates (categorical or continuous) and produces adjusted hazard ratios for individual factor.

Introduction

Survival analysis is one of the most common statistical techniques employed to assess the time to an event of interest such as death, relapse of disease, development of an adverse reaction, and of a new disease entity. It is a method for analyzing data which are in the form of “time,” that is, from a well-defined time of origin until the occurrence of some particular event or endpoint. These types of data are called as lifetime, failure time, or survival data [1]. When the endpoint is considered death of a patient (differs according to research objective), the resulting data are referred to as survival data. Survival data include an outcome variable that measures time until occurrence of a specific event (event time, failure time, or survival time) and some independent variables either of qualitative (religion or gender) or continuous type (age, height, or hemoglobin) thought to be associated with the event.

Some of the examples of survival data may include (i) a study of long-term follow-up of patients with ulcerative colitis (UC) in remission to see how long they stay in remission; (ii) a study that aims to follow-up a cohort of patients with acute gastroenteritis over several years to see how often irritable bowel syndrome (IBS) develops among them; (iii) a 5-year follow-up study of severe UC patients to see how long they remain alive; (iv) a study that follows up liver transplant patients to find how long these patients survive? In the first example, the event of interest is “going out of remission” (in other word, occurrence of relapse) and  the time variable is “time until UC relapses”. Table 1 describes the event of interest and outcome for each of the examples mentioned above.

Table 1.

Description of event of interest and outcome variables of survival analysis problem

Example	Event of interest	Outcome variable
Ulcerative colitis (UC) patients/time in remission (in weeks)	Going out of remission	Time in weeks until UC patients goes out of remission
Gastroenteritis cohort/time until irritable bowel syndrome (IBS) develops (years)	Developing IBS	Time in years until gastroenteritis patients develops IBS
Severe UC/time until death (years)	Death	Time in years until death
Liver transplant patients/time until death (months)	Death	Time in  months until death

The aim of this paper is to introduce the concepts of survival analysis and the different modeling approaches used for time-to-event analysis. The non-parametric model is the most commonly used approach that involves the Kaplan–Meier method for estimating the survival function and the Cox proportional hazards model to identify the risk factors and obtain adjusted risk ratios.

Methods

The current review introduces the concept of longitudinal data analysis including Kaplan–Meier analysis using the data created hypothetically. The figures presented in this paper are original graphs generated using R software (R Development Core Team, Vienna, Austria) based on the hypothetical data presented.

Characteristics of survival data

The characteristics of survival data include [1] (i) appropriate definition of the time of origin for each study subject, i.e. time since entry into study; (ii) appropriate definition of the end event (failure), e.g. death, relapse, recovery from a surgery or heart attack, and development of disease; (iii) the study subjects should be comparable at their time of origin, i.e. every enrolled individual will be followed from a baseline date (e.g. in case of cancer; date of diagnosis or date of surgery) until the date of death or termination of study; (iv) survival data can never be negative as these are the response time data. Time is a positive value that may be in hours, days, weeks, months, or years from beginning until an event occurs.

The basic goals of survival analysis are to (i) estimate and interpret survival and/or hazard functions from survival data such as time until relapse for a group of acute severe UC patients; (ii) compare survival and/or hazard functions such as data on acute severe UC patients  treated with two drugs in a randomized controlled trial; and (iii) assess the relationship of explanatory variables to survival time, for example, does weight, insulin resistance, or cholesterol influence survival time of heart disease patients [1].

Censoring

Time-to-event variables are considered one of the unique features of survival data, which might be the time from diagnosis or start of treatment to death, recurrence of a disease, and the time to readmission to hospital after discharge of the patients such as those with IBD, time to and type of pancreatic cancer recurrence [2, 3], and the time to metastasis of a tumor. It consists of pairs of observations for each study subject like time duration during which no event was observed and identification of indicators of whether the end of that period corresponds to an event or the end of the study. The event could be adverse or beneficial and is often termed survival or failure time data. Some of the study subjects may not experience an event of interest; they are said to be “censored.” In censoring, the exact time of the event is not known but if we consider the event occurred after a known time or the true survival time cutoff (censored) at the right side of the observed survival time interval, then that refers to right-censored data [4]. In right-censoring, the true survival time is equal to or greater than the observed survival time (recorded during study period). Data can also be left-censored but that happens less often. In left-censoring, the true survival time is less than or equal to the observed survival time. For example, let us consider that we are following individuals until they test positive for severe acute respiratory syndrome corona virus-2 (SARS-CoV-2) (event of interest). At first, we do not know the exact time of initial exposure of an individual. The survival time is censored on the left side because event of interest (testing positive for SARS-CoV-2) occurred before the observation period starts. Here, the true survival time ends at exposure, which is shorter than the follow-up time (study observation period), which ends when the individual tests positive for SARS-CoV-2. Survival data may also be interval-censored, which can occur in cases where an individual may have had two SARS-CoV-2 tests. At first, the individual tested negative at any time t₁ but tested positive at time t₂. In such a case, the individual’s true survival time occurred after time t₁ and before time t₂. It incorporates the information of both right-censoring and left-censoring [5].

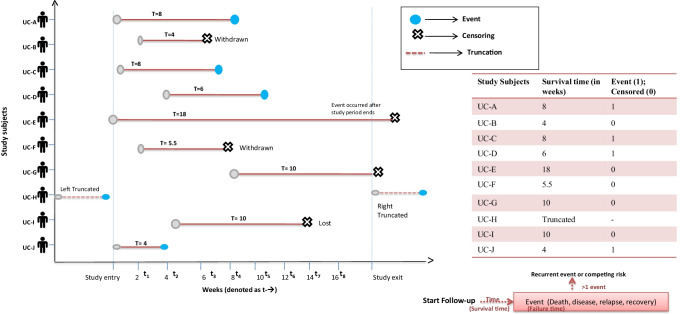
The censoring situations are graphically illustrated in Fig. 1. Patient UC-A, for example, is followed from the start of the study and got the event at 8 weeks (survival time [T = 8]). Patient UC-B enters the study at 2nd week and is followed until he/she withdraws from the study at 6 weeks. The patient’s survival time is clearly censored after 4 weeks. Patient UC-E is observed from the start of the study and is followed up until the end of the study period. Patient UC-E does not get the event during the study period and censor time is 18 weeks. Patient UC-G enters at 8th week and is followed up for the rest of the study period without getting the event; this patient’s censor time is 10 weeks. Patient UC-I enters the study at 4th week and is followed up until week 14 when he/she is lost to follow-up; censor time is 10 weeks.

Fig. 1.

The timeline plot shows the entry, exit and the observations on severe ulcerative colitis (UC) patients at varying period of time. It describes the experience of 10 UC patients (who are in remission) followed over several weeks. A blue dot denotes a patient who got the event (end of remission period)

Table 2 presents hypothetical data from a cohort of UC patients followed up from remission to relapse; these data are used to illustrate survival analysis techniques in this review. The time scale has origin at the time of remission of UC, and the endpoint is at the time of relapse. As an example of the data layout, consider the following set of data for two groups of UC patients: one group of 10 patients who received a specific treatment, the other group of 10 patients who received placebo. The concepts of survival analysis are discussed based on the above data in this review.

Table 2.

A hypothetical data of 10 ulcerative colitis cases and 10 controls with their survival time and survival status

Patient ID	Survival time (t in weeks)	Event	Group	Age (in years)	ESR (mm/h)	C-Reactive protein (mg/L)
UC-A	8	Failed	Treatment	30	44.09	11
UC-B	4	Censored	Treatment	26	32.04	13
UC-C	8	Failed	Treatment	23	29.03	12
UC-D	6	Failed	Treatment	47	23.09	8
UC-E	18	Censored	Treatment	56	15.09	4
UC-F	5.5	Censored	Treatment	36	14.80	5
UC-G	10	Censored	Treatment	19	33.12	2
UC-H	14	Failed	Treatment	29	10	1
UC-I	10	Censored	Treatment	44	11.23	0.02
UC-J	4	Failed	Treatment	60	38.03	2.3
CC-A	2	Failed	Placebo	24	23.09	11
CC-B	3	Failed	Placebo	29	21.45	14
CC-C	4	Failed	Placebo	34	8.08	10
CC-D	4	Failed	Placebo	45	6.03	09
CC-E	8	Failed	Placebo	43	32.01	4
CC-F	11	Failed	Placebo	21	10.09	20
CC-G	12	Failed	Placebo	58	11.34	34
CC-H	17	Failed	Placebo	33	18.33	1
CC-I	15	Failed	Placebo	27	13.7	4
CC-J	8	Failed	Placebo	18	11	5

CC control case, CRP C-reactive protein, ESR erythrocyte sedimentation rate, UC ulcerative colitis

Estimation of survival time

Life tables

The primitive method of estimating survival for the population is with a life-table analysis technique, also called actuarial analysis, because it assumes that censored observations contribute only halfway to the number of patients currently at risk (during given time interval). [6]. It shows the probability of a person dying at a certain age, or living up to a definite age. It is considered one of the oldest methods for analyzing survival data. It is constructed by organizing the data into tables and grouping within intervals of fixed length; for each interval, a number of subjects entered “alive,” several subjects had the event  in the respective interval, or are lost (censored). Several statistics like the number of patients at risk, survival proportion, hazard proportion, median survival time, and the survival rate can also be computed. Two specific types of life tables used widely in the statistical analysis are the cohort life table or follow-up life table [7]. It summarizes the experiences of individuals over a pre-defined follow-up period (cohort or clinical trial) until the event occurred or the study period ends.

To construct a life table, we first organize the follow-up times into equally spaced intervals. In Table 3, we have used the actuarial method to construct the follow-up life table, in which the time is divided into equally spaced intervals. We have depicted the maximum follow-up of 19 weeks (remission period). For the first interval, 0–4 weeks, there are 20 individuals at risk of coming out of remission (event: relapse). Five individuals die in the interval and one is censored. The probability that a participant survives beyond 4 weeks, or passes the first interval (using the upper limit of the interval to define the time), is S₄ = p₄ = 0.744. The probability of surviving successive intervals is dependent on the survivorship of preceding intervals. This analysis table can also be presented graphically as a survival curve, which plots time vs. cumulative survival. This method is not suitable for large intervals. The main limitation of the life table is that the survival probabilities can change depending on how intervals are organized [8]. The Kaplan–Meier approach (product limit approach) overcomes the issues by re-estimating the survival probability each time an event occurs.

Table 3.

Description of a follow-up life table approach

Time intervals (in weeks)	Number at risk during interval, (Nt)	Average number at risk during interval (Nt = Nt − Ct/2)	Number of deaths, during interval (Dt)	Lost to follow-up (Ct)	Proportion dying (qt = Dt/Nt)	Proportion surviving (those at risk) (pt = 1-qt)	Survival probability (St = pt * St-1); (S0 = 1)
0–4	20	20–(1/2) = 19.5	5	1	5/19.5 = 0.256	1–0.256 = 0.744	1 * 0.744 = 0.744
5–9	14	14–(1/2) = 13.5	4	1	4/13.5 = 0.296	1–0.296 = 0.704	0.744 * 0.704 = 0.523
10–14	9	9–(2/2) = 8.0	4	2	4/8.0 = 0.50	1–0.50 = 0.50	0.523 * 0.50 = 0.261
15–19	3	3–(1/2) = 2.5	2	1	2/2.5 = 0.80	1–0.80 = 0.20	0.261 * 0.20 = 0.052

^*Multiplication sign

Kaplan–Meier approach

Kaplan–Meier curves are widely used in clinical research and for the visual representation of survival function (estimated by Kaplan–Meier estimator). Kaplan–Meier measures the survival probability of the study population and is also used to compare two groups of subjects. It is a descriptive method of estimating survivorship as it measures the frequency or the number of patients who survive, and thus considered a better way of analyzing data in a cohort study [6, 9, 10]. The intervention data obtained from randomized controlled studies like clinical trials or community trials can also be assessed. The Kaplan–Meier curves indicate the outcome of interest, censoring, and number of subjects at risk or survival probability. The use of Kaplan–Meier approach depends on the assumption that censoring is independent of the likelihood of developing the event of interest and survival probabilities are comparable in participants who are recruited early and later into the study [11, 12]. In case of comparison of several groups, these assumptions are also needed to be satisfied for each group. The Kaplan–Meier approach is presented using the data used to describe the concepts of the life table. At time = 0 (baseline), all participants are at risk and hence, the survival probability is 1 (or 100%). In this approach, the calculations are done using observed event times and censoring times, whereas equally spaced intervals are used in the life table approach. The calculations of the survival probabilities are detailed in Table 4. The software calculates the survival probabilities in a single click, and Table 4 is just a brief description of how it is calculated.

Table 4.

Description of Kaplan–Meier approach

Time, weeks	Number at risk (Nt)	Number of deaths (Dt)	Number censored (Ct)	Survival probability St + 1 = St * [(Nt + 1 − Dt + 1)/Nt + 1]
0	20	0	0	1
1	20	0	0	1 * ((20 − 0)/20) = 1
2	20	1	0	1 * ((20 − 1)/20) = 0.950
3	19	1	0	0.950 * ((19 − 1)/19) = 0.900
4	18	3	1	0.9 * ((18 − 3)/18) = 0.750
6	14	1	1	0.75 * ((14 − 1)/14) = 0.696
8	12	3	0	0.696 * ((12 − 3)/12) = 0.522
10	09	0	2	0.522 * ((9 − 0)/9) = 0.522
11	07	1	0	0.522 * ((7 − 1)/7) = 0.447
12	06	1	0	0.447 * ((6 − 1)/6) = 0.372
14	05	1	0	0.372 * ((5 − 1)/5) = 0.297
15	04	1	0	0.297 * ((4 − 1)/4) = 0.223
17	03	1	0	0.223 * ((3 − 1)/3) = 0.149
18	02	0	1	0.149 * ((2 − 0)/2) = 0.149
19	01	0	0	0.149 * ((1 − 0)/1) = 0.149

^*Multiplication sign

The main limitation of Kaplan–Meier estimate is that it cannot be used for multivariate analysis as it only studies the effect of one factor at a time. It analyzes the survival time of patients who experienced the event of interest and of them who are censored at a specific period. The clinical survival data use the Kaplan–Meier plots to display prognosis over time. It is also applicable in situations where the comparisons have been made between groups such as for analysis in development of functional gastrointestinal disease (FGID) after 6 months of contacting corona virus disease 2019 (COVID-19) between those having and not having gastrointestinal (GI) symptoms during the initial illness. In evaluating the safety and efficacy of mirikizumab in participants with moderate to severe UC who have had an inadequate response to conventional and biologic therapy. The survival plots, survival table, Kaplan–Meier estimate curve, cumulative incidence plot, and many relevant tables like comparison tables can be generated using statistical software like R (R development core team, Vienna, Austria), Statistical Package for Social Sciences (SPSS, Chicago IL, USA);, and MedCalc (Warandeberg 3, 1000 Brussels, Belgium).

In the survival curve shown in Fig. 2, the symbols represent event time, either an event or a censored time. From the survival curve depicted in Fig. 2, we can also estimate the probability that an individual survives past 10 weeks by locating 10 weeks in the X-axis and reading up and over to the Y-axis. The proportion of participants surviving past 10 years is 84%, and the proportion of participants surviving past 20 years is 68%. The median survival time is estimated by locating 0.5 on the Y-axis and reading over and down to the X-axis. The median survival is approximately 23 years.

Fig. 2.

The Kaplan–Meier survival curve for the hypothetical ulcerative colitis data

Survival and hazard functions

The most important quantitative terms in any survival analysis are the survivor function denoted by S(t) and hazard function, denoted by h(t). The survivor function S(t) gives the probability that a person survives longer than some specified time t: that is, S(t) gives the probability that the random variable T exceeds the specified time t. The “T” denotes the individual’s survival time, and it includes all non-negative numbers (equal to or greater than zero). The “t” denotes the value of interest, e.g. if a patient with UC survives for more than 10 years after surgery, then t = 10 and we will evaluate whether T > (t = 10).

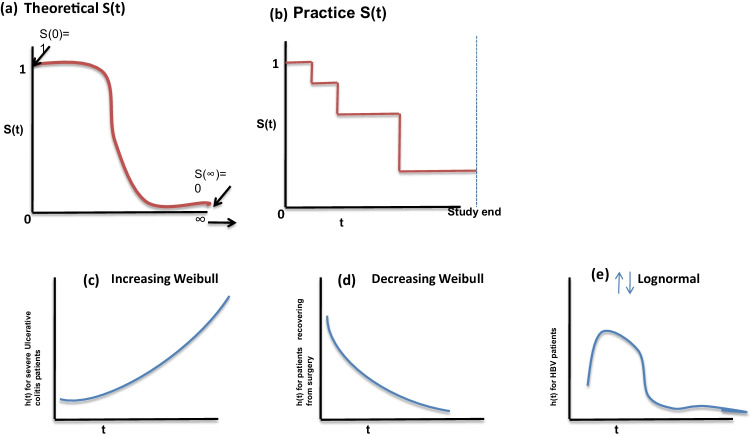
Survivor functions have some theoretical properties; these are non-increasing, that is, these head downward as t increases; at time t = 0, S(t) = S(0) = 1; that is, at the start of the study, since no one has had the event yet, the probability of surviving at time 0 is one (Fig. 3a).

Fig.3.

Illustration of increasing, decreasing Weibull model and lognormal model

In a practical scenario, we obtain the graph (Fig. 3b) of step functions, rather than smooth curves. Moreover, because the study period can't ever be never-ending in length and the possible chances of competing risks for failure, it is possible that not everyone studied gets the event [1]. The hazard function h(t) gives the instantaneous potential per unit time for the event to occur, given that the individual has survived up to time t. The survivor function focuses on surviving whereas the hazard function focuses on failing, given survival up to a certain time point [4, 13]. As with a survivor function, the hazard function h(t) can be graphed as t ranges over various values. The graphs (Fig. 3c–e) illustrate three different hazards. In contrast to a survivor function, the graph of h(t) does not have to start at 1 and go down to zero but rather can start anywhere and go up and down in any direction over time. In particular, for a specified value of t, the hazard function h(t) has the following characteristics: it is always non-negative, that is, equal to or greater than zero; and it has no upper bound. Figure 3c–e show the increasing Weibull model, decreasing Weibull model, and lognormal survival model. The increasing Weibull model can be expected for severe UC patients not responding to treatment and the outcome of interest is death. This can be interpreted as the survival time increases, the potential for dying also increases. An example for decreasing the Weibull model can be expected when the event is death in patients who are recovering from cancer surgery. The lognormal survival model can be expected for Helicobacter pylori infection in relation to age of the population as it increases with increasing age initially and then decreases in older age group. The cumulative hazard statistic is also used as a diagnostic tool in assessing the model validity. The mathematical formula that exists between these two functions helps in calculating the value of unknown if the other is known.

Comparing the survival times of two or more groups and describing the effect of categorical or quantitative variables on survival

We are often interested in assessing whether there are differences in survival among different groups of participants. For example, in a clinical trial with a survival outcome, we might be interested in comparing survival between participants receiving a new drug as compared to a placebo (or standard therapy). In an observational study, we might be interested in comparing survival between men and women, or between participants with and without a particular risk factor (e.g. hypertension or diabetes) or any other categorical variable. There are several tests available to compare survival among independent groups.

If a clinician or a researcher is interested to know whether the groups have statistically meaningful comparisons in survival probability beyond a certain time point or not, then, what statistic should be used? What happens if we use the Chi-squared test? The Chi-squared test focuses on the proportions and does not estimate probabilities adequately in the presence of censoring and also ignores the follow-up time in two different groups. The Chi-squared test would be appropriate to compare event rates in the two groups at a fixed time point if the status (alive or dead) of each patient can be assessed with certainty at that particular time point. But if we need to compare the entire survival experience of the two groups, then a log-rank test should  be used. Log-rank test accommodates censored observations and compares the risk of death over time in the two groups. Through the log-rank test technique, one can test the hypothesis that whether the survival probability beyond a specific time differs between the patient and control group. Figure 4 shows that for any given time t, survival rate of patients who are given treatment is greater than those who received a placebo.

Fig.4.

Comparing survival probabilities of treatment and placebo group

The log-rank test

The researchers may be interested to know how much does the survival S(t) at time t increase or reduce between the two study groups of patients or how to measure the effect of other independent variables like age, erythrocyte sedimentation rate (ESR), and C-reactive protein (CRP) or any other covariates?. It tests the null hypothesis of no difference in survival between two or more independent groups. The test compares the entire survival experience between groups and can be thought of as a test of whether the survival curves are identical (overlapping) or not [14]. Survival curves are also estimated for each group; considered separately, using the Kaplan–Meier method; and compared statistically using the log-rank test. The wholesome measurable solution lies in the class of regression models known as the proportional hazards model. Figure 4 shows the survival probabilities for the treatment group are higher than the survival probabilities for the placebo group, suggesting a survival benefit. However, these survival curves are estimated from small samples. To compare survival between groups, we can use the log-rank test. The null hypothesis is that there is no difference between the populations in the probability of death at any point. The log-rank test is a non-parametric test and makes no assumptions about the survival distributions. In essence, the log-rank test compares the observed number of events in each group to what would be expected if the null hypothesis were true (i.e. if the survival curves were identical).

Cox proportional hazards regression analysis

Survival analysis methods can also be extended to assess several risk factors simultaneously, similar to multiple linear and multiple logistic regression analysis. One of the most popular regression techniques for survival analysis is Cox proportional hazards regression, which is used to identify crucial factor for handling disease. In medical research, prime focus is to determine the cause or the other characteristic of a disease; for example, a patient suffering from lung cancer may have a habit of smoking daily, or may be exposed to cancer-causing agents in the workplace. In general, regression analysis is used for this purpose, but due to the presence of censored data, ordinary regression techniques cannot be used. Therefore, Cox proportional hazards model is more appropriate in such situations [15, 16]. It not only determines a cumulative probability of an event but also accounts for impact of covariates on that probability. If values of covariates change with time, then these are called time-dependent covariates; otherwise the covariates may be time-independent. For example, acute severe UC patient’s performance during the treatment period is time-dependent and sex is time-independent covariate. If time-dependent covariates are involved, Cox proportional hazards model cannot be used. More examples of time-dependent covariates are ESR or total leukocyte values, which change with time in patients with acute severe UC. In case of time-dependent covariates, analysis is performed using Cox-non-proportional hazard model.

Hazard ratio (survival analysis) is analogous to an odds ratio (logistic regression) and can be estimated from the data used to conduct the log-rank test. In most situations, we are interested in comparing groups with respect to their hazards, and we use a hazard ratio, which is analogous to an odds ratio in the setting of multiple logistic regression analysis. Specifically, the hazard ratio is the ratio of the total number of observed to expected events in two independent comparison groups.

In an example of severe UC patients data, consider the regression variables or covariates like age, groups (treatment = 1; placebo = 2), gender (1 = male; 2 = female), ESR, and CRP. The variable “survival time” is a response variable. This model will estimate the expected survival duration (Y) with the help of regression variables or covariates (X).

In conclusion, survival analysis provides a statistical technique that allows us to estimate the survival rates based on survival tables, survival curves, and several statistical tests to compare the survival curves and also deals with the unique features of survival data (censoring). In survival analysis, researchers or clinicians usually fail to use the conventional non-parametric tests to compare the survival functions among different groups because of censoring and truncation; however, Kaplan–Meier statistics eases out the complicated process. In this paper, we have summarized several statistical tests used in the survival analysis.

Author contribution

SR wrote the first draft of the paper. UCG conceptualized, edited the paper, provided the clinical examples and supervised the writing of the draft. PM edited the paper. All the authors approved the final manuscript.

Declarations

Conflict of interest

SR, PM, and UCG declare no competing interests.                                                           

Disclaimer

The authors are solely responsible for the data and the contents of the paper. In no way, the Honorary Editor-in-Chief, Editorial Board Members, the Indian Society of Gastroenterology or the printer/publishers are responsible for the results/findings and content of this article.