Effects of bracket design on critical contact angle

Abstract

Objective:

To explore how the position of the bracket slots relative to the archwire influences the friction between them, and how bracket design affects the critical contact angle (θc).

Materials and Methods:

Two kinds of stainless steel archwires (0.016 and 0.019 × 0.025-inch) were tested against four kinds of brackets (Transmission Straight Archwire bracket, Domestic MBT bracket, Tip-Edge Plus bracket, and BioQuick self-ligation bracket) in the dry state. Resistance to sliding (RS) was measured as an increase in contact angle (θ). The value of θc was calculated by two linear regression lines.

Results:

Friction remained stable when θ < θc, then increased linearly when θ > θc. The θc values of the Tip-Edge Plus bracket and Transmission Straight Archwire bracket were significantly larger than those for the Domestic MBT bracket and BioQuick self-ligation bracket.

Conclusions:

The relationship between the archwire and bracket slot significantly affects the resistance to sliding. The “edge-off” structure of the Tip-Edge Plus bracket and Transmission Straight Archwire bracket could help to increase the θc value, and to expand the passive configuration range.

INTRODUCTION

In clinical orthodontics, friction (or resistance to sliding [RS]) between the brackets and archwire is important. Decreasing friction can reduce patient pain and lower the potential risks of root/alveolar bone resorption and anchorage loss.1–3 Excluding biologic factors, there are three aspects affecting friction in orthodontic sliding mechanics: the bracket, the archwire, and the ligation. Many research experiments have been conducted over the last few years to demonstrate the effects of ligation methods in reducing RS between brackets and archwire.4–6

Clinical trials have shown that teeth can experience a “tip-upright-tip-upright” sequence of movement during orthodontic treatment.1 The relative position of the bracket and archwire changes continuously, with the contact angle (θ) between the archwire and bracket slot changing depending on whether teeth are tipping or uprighting. Kusy and Whitley7–11 demonstrated that when θ was in a certain range, the archwire and bracket were in a passive configuration, and the RS was imparted by classical friction (FR). However, if θ increased to a boundary value with teeth tipping, the archwire and bracket were in an active configuration, and RS was in both classical friction (FR) and elastic binding (BI).4,7–11 The boundary value at which the passive configuration of the archwire and bracket becomes the active configuration is termed the critical contact angle (θc), which is the angle at which the archwire touches the bracket slot when the tooth tips (Figure 1).

Figure 1.

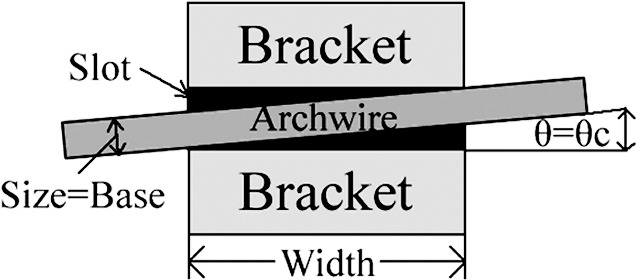
The bracket and archwire structure.

The relative position of the bracket slot and archwire can influence the friction. In the case of a fixed bracket-archwire combination, when the critical contact angle (θc) increases, the passive configuration range is expanded resulting in an increase of the classical friction range.8,9

Previous studies have focused on the ligation method effects on orthodontic friction. This research was to measure θ to explore how the relative position of the bracket slot and archwire influence the friction, and how bracket design affects θc.

MATERIALS AND METHODS

Brackets, Archwires, and Ligatures

Four kinds of brackets in the upper-left arch were selected (Figure 2): the Transmission Straight Archwire bracket (Shinye, Hangzhou, China), Domestic MBT bracket (Shinye, Hangzhou, China), Tip-Edge Plus bracket (TP Orthodontics, La Porte, Ind), and BioQuick self-ligation bracket (Forestadent, Pforzheim, Germany), all of which have a 0.022 × 0.028-inch slot size. All brackets were engaged by elastomeric rings (TP Orthodontics, LaPorte, Ind) except for the self-ligation bracket. Two types of stainless steel (SS) archwires were selected: 0.016 and 0.019 × 0.025-inch (Plasdent, Pomona, Calif).

Figure 2.

Four kinds of canine brackets. Figure (A). Transmission Straight Archwire bracket. Figure (B). Domestic MBT bracket. Figure (C). Tip-Edge Plus bracket. Figure (D). BioQuick self-ligation bracket.

The canine brackets of the Transmission Straight Archwire appliance have a unique “step” structure,12 which provides two ligation mechanisms: full and oblique (Figure 3). The effect of oblique ligation, similar to self-ligation brackets, is to reduce ligation force.

Figure 3.

Two ligation mechanisms for Transmission Straight Archwire canine brackets.

Resistance to Sliding

The RS was tested by the self-designed friction-testing apparatus (Figure 4), which included three parts: bracket control apparatus, archwire control apparatus, and a data acquisition and processing system. Part I is the archwire control apparatus where the tensile force transducer is located Figure 4A. The measure range for the force transducer was 0 to 2 kg, and the precision was 0.05. It is attached to the archwire by the wire jig Figure 4B. The wire jig can adjust the angle and the position of the archwire to match the position of the brackets. The motion device Figure 4C is connected below the force transducer that can pull the archwire moving. Part II is the bracket control apparatus. Each bracket has a fixed jig Figure 4D, which can adjust the bracket's angle, and position through the rotation table Figure 4E and the displacement table Figure 4F. Part III is the data acquisition and processing system. There are five bracket control apparatuses in Part II, and each is independently fixed on the base plate. Therefore, this apparatus can test multiple brackets simultaneously. In addition, a CCD camera Figure 4G can help to observe the relative position of the bracket and the archwire.

Figure 4.

The friction-testing apparatus.

In this study, the canine bracket was selected as the test object, and an incisor bracket was added to simulate the clinical role of adjacent teeth. It tried to simulate the first premolar extraction case during the space-closing stage. The incisor bracket is on one side of the canine bracket, and the first premolar on the other side was extracted. During the space-closing stage, the canine bracket experiences a “tip-upright-tip-upright” sequence of movements.1 Similarly, the canine bracket was tested at different tip angles with the archwire in this study. The interbracket distance was 12 mm.

Before the experiment, the center of the bracket and the archwire were aligned to ensure no separation occurred by touching alone, and to ensure that the archwire and bracket had a 0° torque and tip angle between them (with the help of a CCD camera and 0.022 × 0.028-inch SS). A fresh elastomeric ligature was used for each test, and it was placed 5 minutes before testing. The brackets and archwires were cleaned in 95% alcohol and air-dried.

During the experiment, the archwire was in a straight-line uniform motion (at a velocity of 83 µm/s) that lasted 60 seconds, maintaining 0° torque with the bracket. The drawing force was measured at each tip angle (θ). The Domestic MBT and the BioQuick self-ligation brackets were measured at angles of 0°, 0.5°, 1°, 1.5°, 2°, 2.5°, 3°, 4°, 5°, 6°, 7°, and 8°. Tip-Edge Plus and Transmission Straight Archwire brackets were measured at angles of 0°, 1°, 2°, 3°, 4°, 5°, 6°, 7°, 8°, 9°, 10°, 11°, 12°, 13°, 14°, 15°, 16°, 17°, 18°, 19°, 20°, 21°, 22°, and 23°. A new bracket and a new archwire were changed for each bracket/archwire combination at one particular angle, and all the brackets and archwires were selected randomly from the material depot. The experiments were run in a dry environment at a temperature of 23°C.

Data Analyses

The actual dimensions of the brackets were measured by stereomicroscope (Olympus SZX12, Olympus, Tokyo, Japan). All tested specimens were selected randomly (n  =  10). The theoretical θc value of the Domestic MBT bracket and the BioQuick bracket was calculated using the equation of Kusy and Whitley8: θc  =  57.32 [1−(size)/(slot)]/(width)/(slot). Because the Transmission Straight Archwire bracket and the Tip-Edge Plus bracket have the “edge-off” structure, whose theoretical θc value cannot be simply calculated by the above equation, their θc calculation formulas were derived respectively on the basis of Kusy's equation with the specific attention on the “edge-off” structure.

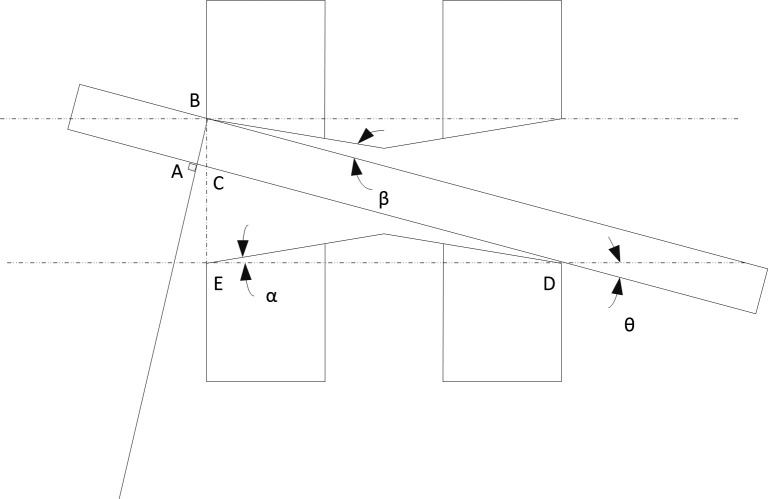
For the Transmission Straight Archwire bracket, based on the actual measurements of the size of the bracket and geometrical relations, its theoretical θc value can be calculated by the equation shown below. For the detailed definitions of segments in the equation, please refer to Figure 5.

Figure 5.

The diagram of Transmission Straight Archwire bracket.

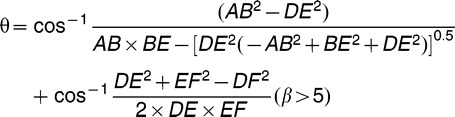For the Tip-Edge Plus bracket, its theoretical θc value can be calculated by the equation shown below. For the detailed definitions of segments in the equation, please refer to Figure 6.

Figure 6.

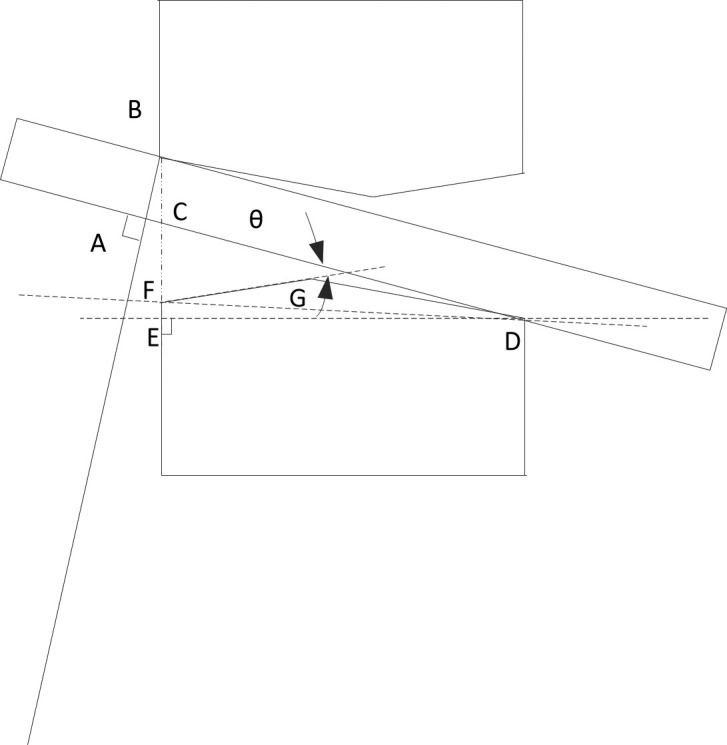
The diagram of Tip-Edge Plus bracket.

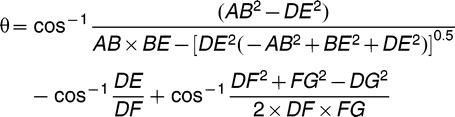Each bracket/archwire combination at one particular angle was tested three times, and the measurement was recorded as a voltage per spent time (seconds) by a computer. The data acquisition rate was 500 times per minute. Only the data between the 10th and 60th seconds, which were considered as the kinetic friction, were selected, and the voltage values were converted to the corresponding RS force values. The RS values were plotted against θ. Two linear regression lines of the passive and active configuration ranges were calculated; the intersection of the lines represented the experimental θc of each combination. The experimental θc values were plotted against the corresponding theoretical θc, and the regression line was determined. The line was compared with another line, which presumed theoretical θc is equivalent to experimental θc.

RESULTS

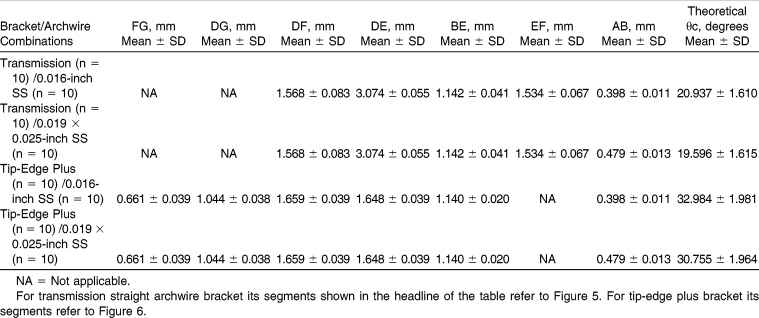
The theoretical θc values, which were calculated by the actual dimensions of the tested brackets, are shown in Tables 1 and 2.

Table 1.

Tested Dimensions of Domestic MBT and BioQuick Brackets and the Calculated Theoretical θc

Table 2.

Tested Dimensions of Transmission Straight Archwire and Tip-Edge Plus Brackets and the Calculated Theoretical θc

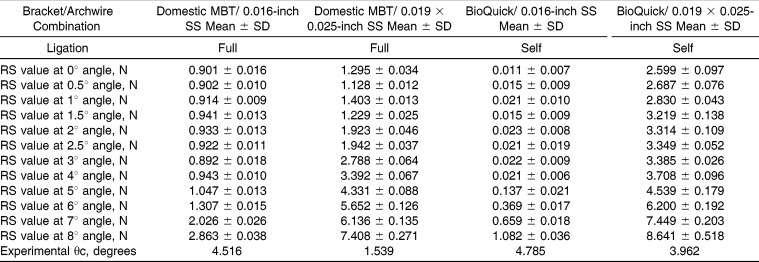
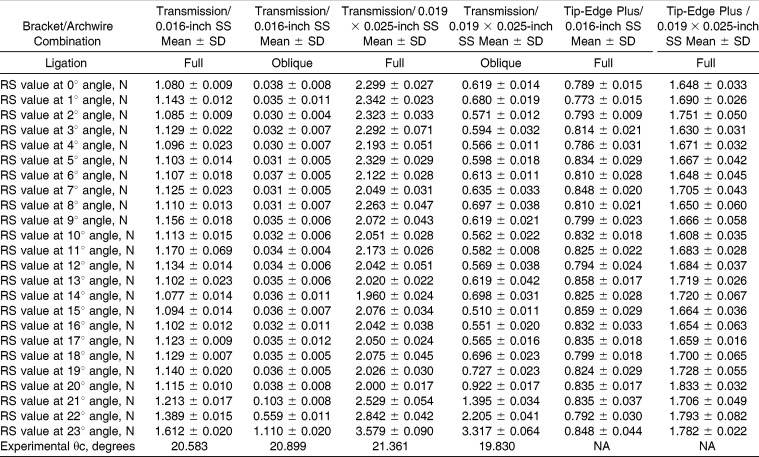
The RS values of different bracket/archwire combinations at each angle and the calculated experimental θc are shown in Tables 3 and 4. The friction generated between the BioQuick self-ligation bracket and the 0.016-inch SS archwire was the least of all the combinations. By contrast, the friction between the BioQuick self-ligation bracket and the 0.019 × 0.025-inch SS combination was the greatest. The regression lines of θ against RS showed a highly significant association (P < .001, Figure 7). The value of RS remained stable up to θc and rose linearly after θc. The θc values of the Tip-Edge Plus bracket and the Transmission Straight Archwire bracket were significantly larger than the other two brackets. In addition, in the same brackets, combinations including the 0.016-inch SS archwire had larger θc values than those using the 0.019 × 0.025-inch SS archwire.

Table 3.

RS Values of Domestic MBT and BioQuick Brackets and the Corresponding Experimental θc

Table 4.

S Values of Transmission Straight Archwire and Tip-Edge Plus Brackets and the Corresponding Experimental θc

Figure 7.

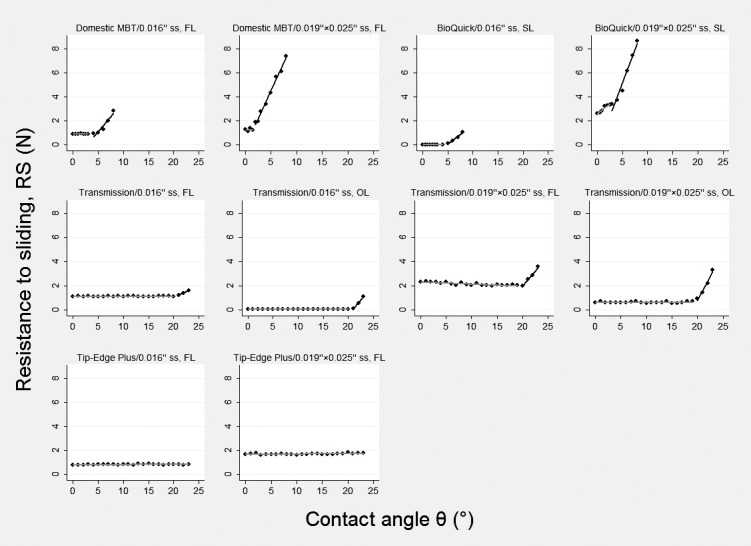
Regression lines of θ against RS.

As shown in Figure 8, the linear regression of the experimental θc vs theoretical θc is significant (r  =  0.996, n  =  8, P < .0001).

Figure 8.

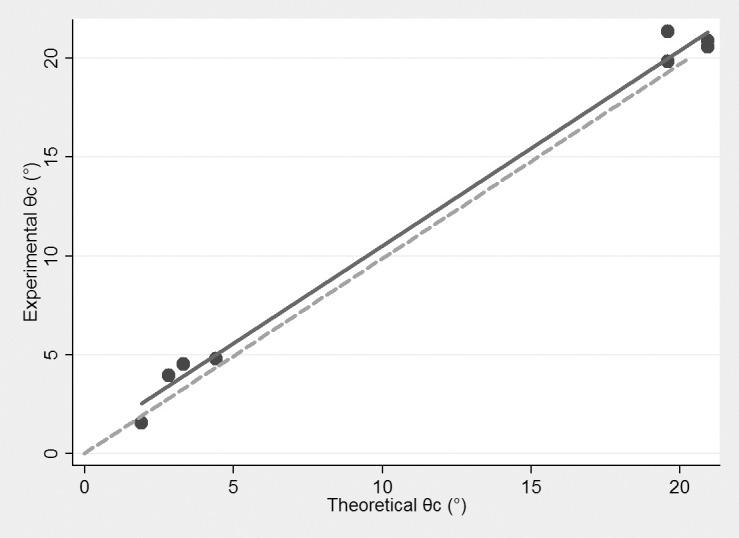
The linear regression line of theoretical and experimental θc values within each bracket-archwire combination and the 45° ideal line.

DISCUSSION

Friction (resistance to sliding) between brackets and archwires is of great importance to the success of orthodontic treatment. It is known that three mechanical factors influence RS: the bracket, the archwire, and the ligation.13,14 However, the relative position of the bracket and archwire change continuously during orthodontic tooth movement. The contact angle (θ) between the archwire and bracket slot increases or decreases, depending on whether the teeth are tipping or uprighting. A specific value of θ, termed the critical contact angle (θc), was first proposed by Kusy and Whitley7 in 1997. This represents the boundary between the passive and active configurations of the archwire and bracket, the relationship that affects the components of RS. This theoretical deduction has been tested experimentally,4 and the results of this study were consistent with these previous investigations (Figure 7). RS remained stable with little change in the passive configuration when θ < θc, but rose linearly into the active configuration when θ > θc.

The theoretical value of θc can be calculated by analyzing the relative relationship between the bracket and archwire. Kusy and Whitley8 deduced by geometry in 1999 that the equation describing the theoretical θc was 57.32 [1−(size)/(slot)]/(width)/(slot) (Figure 1). This equation states that, when the archwire (size) is kept constant, an increase in bracket width (width) and/or a decrease in the dimensions of the bracket slot (slot) leads to a reduced value of θc. Laboratory experiments generated almost identical values of θc to those predicted by the theoretical deduction.9 Therefore, with the archwire being fixed, the slot design is the primary factor influencing θc. The brackets investigated in previous studies had conventional edgewise slots. For nominal archwire sizes and nominal bracket slot sizes, the limits of θc were calculated and ranged from 0°–4.5°.9

This study found that the θc values of the Tip-Edge Plus and Transmission Straight Archwire brackets were significantly larger than the Domestic MBT and BioQuick self-ligation brackets. The difference in these values was more than 15°. As seen in Figure 2, the Tip-Edge Plus and Transmission Straight Archwire brackets have a common “edge-off” structure, which helps to expand significantly the passive configuration range of the bracket-archwire system. The calculated θc equations of this kind of bracket were derived in this study on the deduction of Kusy and Whitley.8 This characteristic is closely linked to teeth tipping in clinical treatment, which occurs until the bracket and archwire achieve an active state. When the bracket and archwire achieve an active configuration, teeth gradually stop tipping and begin to upright instead. Therefore, the range of the Tip-Edge Plus and Transmission Straight Archwire brackets increased the likelihood that clinical treatments using these will achieve tooth tipping rather than uprighting. Within this range, the resistance to sliding included only classical friction with no elastic binding,8,9 and the bracket and archwire remained in a low-friction state. In clinical practice, orthodontists intend to use the Tip-Edge technique to close the extraction space when Tip-Edge Plus and Transmission Straight Archwire brackets are used; accordingly, they intend to use sliding mechanics when the Domestic MBT and BioQuick self-ligation brackets are used.

Because the width of the Tip-Edge Plus bracket was smaller than that of the Transmission Straight Archwire bracket, the θc of the former was larger with the same size archwire, in agreement with Kusy's experiments,10 which state that a large bracket width produces a small θc, and vice versa. The Transmission Straight Archwire bracket had a special “step” structure (Figure 3) which enables two ligation methods. With oblique ligation, the perpendicular force imparted to the bracket by the ligature wire or elastomeric ring is reduced, causing the RS between the bracket and archwire to decrease. This ligation design is similar to the self-ligation bracket, but is not available in Tip-Edge Plus brackets.

As shown in Figure 7, we can see that during the passive configuration, only the RS value of the 0.019 × 0.025-inch SS archwire and BioQuick bracket was not stable. It is because the BioQuick bracket is a kind of active self-ligation bracket. When θ < θc, the 0.016-inch SS archwire is in passive configuration with it, but the 0.019 × 0.025-inch SS archwire is in active configuration. The rectangular wire pushed the spring clip deformed, and the force may change with the changing of the relationship between the bracket and the wire.

In addition, although some differences exist between the theoretical and experimental values of θc, they have an approximately equivalent (1∶1) relationship (Figure 8), consistent with previous experimental studies.4,9,11,15 Allowing for errors introduced by the stability of the laboratory apparatus and experimenter operating error, there were two reasons why these differences occur. First, the assumptions of the theoretical value derivation and the environment used for determining the experimental value were different. Kusy8 applied geometric theory to deduce the equation for calculating theoretical θc in a two-dimensional plane (Figure 1). The bracket slot and archwire were assumed to be straight and with no deformation. However, when the archwire contacts the bracket slot with increasing θ, the archwire deforms due to its flexibility, which may lead to a slight estimation error of the theoretical value, as was observed in our experiments. Second, errors in the precision of the manufacturing processes of the bracket slots and archwires could affect the experimental values of θc. Indeed, Kusy and Whitley9 found that 15% of bracket slots and 30% of archwires were different from their factory standards. The tested results in this study (Tables 1 and 2) also prove this point.

CONCLUSIONS

• The relationship between the archwire and the bracket slot significantly affects the resistance to sliding.

• The design of the bracket slots also significantly affects the θc. The “edge-off” structure of the Tip-Edge Plus bracket and Transmission Straight Archwire bracket helps to expand the passive configuration range.

• The Transmission Straight Archwire bracket produces lower friction when obliquely ligated, similar to a self-ligation bracket.