Spatial organization of chromosomes leads to heterogeneous chromatin motion and drives the liquid- or gel-like dynamical behavior of chromatin

Abstract

Chromosome organization and dynamics are involved in regulating many fundamental processes such as gene transcription and DNA repair. Experiments unveiled that chromatin motion is highly heterogeneous inside cell nuclei, ranging from a liquid-like, mobile state to a gel-like, rigid regime. Using polymer modeling, we investigate how these different physical states and dynamical heterogeneities may emerge from the same structural mechanisms. We found that the formation of topologically associating domains (TADs) is a key driver of chromatin motion heterogeneity. In particular, we showed that the local degree of compaction of the TAD regulates the transition from a weakly compact, fluid state of chromatin to a more compact, gel state exhibiting anomalous diffusion and coherent motion. Our work provides a comprehensive study of chromosome dynamics and a unified view of chromatin motion enabling interpretation of the wide variety of dynamical behaviors observed experimentally across different biological conditions, suggesting that the “liquid” or “solid” state of chromatin are in fact two sides of the same coin.

The structural and dynamical properties of the eukaryotic genome inside the cell nucleus play crucial roles in many cell functions, such as gene regulation (van Steensel and Furlong 2019). Over the last decade, high-throughput chromosome conformation capture (Hi-C) experiments have provided valuable information about how genomes organize by measuring the contact frequencies between all pairs of chromatin loci (Lieberman-Aiden et al. 2009). Analyses of Hi-C contact maps in various species and cell types revealed that interphase chromosomes are partitioned at different scales (Rowley and Corces 2018): from topologically associating domains (TADs) (Dixon et al. 2012) at a few hundreds of kilobase pairs, to the euchromatic “A” and heterochromatic “B” compartments at megabase pair scales, and to chromosome territories at the nuclear scale. Complementary to Hi-C, advances in microscopy on fixed cells confirmed the existence of these architectural motifs at the single-cell level (Bolzer et al. 2005; Boettiger et al. 2016; Wang et al. 2016; Szabo et al. 2018) and showed that at the sub-TAD scale, chromatin organizes into clutches of nucleosomes (Ricci et al. 2015; Ou et al. 2017) clustered into nanodomains (Szabo et al. 2020).

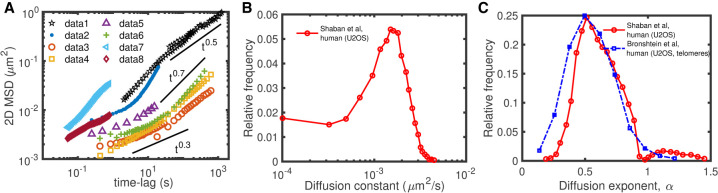
Beyond the “static” picture of a layered spatial organization that contributes to genome regulation, more and more experiments on living cells highlighted the “dynamic” nature of chromatin folding and its importance on key biological functions (Bystricky 2015; Tortora et al. 2020; Shaban et al. 2020a). Chromatin mobility has been proposed to impact the dynamics of promoter–enhancer interactions and thus regulates transcriptional bursting (Bartman et al. 2016; Chen et al. 2018), facilitates homology search after DNA damage (Hauer et al. 2017), or participates in the long-range spreading of epigenomic marks (Jost and Vaillant 2018). Chromatin motion is standardly investigated by monitoring the mean-squared displacement (MSD) after a time lag Δt, that measures the typical space explored by a locus during Δt. Many live-tracking experiments (Cabal et al. 2006; Hajjoul et al. 2013; Zidovska et al. 2013; Bronshtein et al. 2015; Germier et al. 2017; Nozaki et al. 2017; Gu et al. 2018; Shaban et al. 2018, 2020b; Ashwin et al. 2019; Khanna et al. 2019; Nagashima et al. 2019; Socol et al. 2019; Barth et al. 2020) have shown that the MSD of an individual locus can be interpreted by a power-law diffusive model $MSD=D\mathrm{\Delta }{t}^{\alpha }$, where D is the diffusion constant and α is the diffusion exponent. A wide variety of diffusion constants and exponents have been observed experimentally (Fig. 1A) depending on the cell type (Bronshtein et al. 2015), the transcriptional or physiological state of the cell (Germier et al. 2017; Gu et al. 2018; Nagashima et al. 2019), or the presence of DNA damage (Amitai et al. 2017; Hauer et al. 2017; Herbert et al. 2017; Eaton and Zidovska 2020). In many situations, the MSD may show different diffusion regimes (i.e., different α values) at different time lag scales. In addition to such heterogeneity across conditions, chromatin motion is also highly heterogeneous inside individual nuclei (Fig. 1B,C) as observed by genome-wide experiments of chromatin dynamics (Bronshtein et al. 2015; Ashwin et al. 2019; Shaban et al. 2020b), which detected, at a same time, populations of loci with high or low mobility (Ashwin et al. 2019; Lerner et al. 2020; Shaban et al. 2020b). These studies also revealed the presence of spatial chromatin domains of correlated motions (Zidovska et al. 2013; Shaban and Seeber 2020). However, the determinants driving the mobility of individual loci or the formation of such domains are still unclear because some studies associate them with the hetero/euchromatin compartmentalization (Nozaki et al. 2017; Lerner et al. 2020) or cohesin-mediated TAD organization (Ashwin et al. 2019), whereas others did not observe significant correlation between such heterogeneity and chromatin compaction (Shaban et al. 2020b).

Figure 1.

Heterogeneity of chromatin motion. (A) Examples of ensemble-averaged mean-squared displacement (MSD) profiles measured experimentally at individual loci for different organisms and cell lines. The different data sets are from the following: (data1) Mouse pro-B (Khanna et al. 2019); (data2) human MCF-7 (not transcribed gene) (Germier et al. 2017); (data3) human U2OS (centromeres) (Bronshtein et al. 2015); (data4) human U2OS (telomeres) (Bronshtein et al. 2015); (data5) human HeLa cells (Zidovska et al. 2013); (data6) mouse MF (Bronshtein et al. 2015); (data7 and data8) human HeLaS3 (fast loci and slow loci, respectively) (Ashwin et al. 2019). (B,C) Distributions of diffusion constants (B) and diffusion exponents (C) inferred from the time-averaged MSDs of different loci measured in human U2OS cells; data extracted from Bronshtein et al. (2015) and Shaban et al. (2020b).

Biophysical modeling has been instrumental in interpreting and predicting the outcomes of live imaging experiments on chromatin motion (Tortora et al. 2020; Di Stefano et al. 2021). Indeed, in classical kinetic theory, the value of the diffusion exponent α may be a good indicator of the main underlying physical processes driving the motion of the object under study. For small particles, although standard diffusion is characterized by α = 1, subdiffusion (α < 1) and superdiffusion (α > 1) may indicate constrained or facilitated movement, respectively. For polymers that are large molecules with many internal degrees of freedom, the fixed connectivity along the chain constrains the motion of individual monomers. The Rouse model, a standard polymer theory assuming that mobility is only driven by thermal fluctuations (Doi et al. 1988), thus predicts that the loci of the polymer chromatin should experience a subdiffusive motion with α ∼ 0.5, which is the average typical exponent measured experimentally (Fig. 1). One can then define a sub-Rousean (α < 0.5) and a super-Rousean (α > 0.5) diffusion regime for polymers that may translate additional constraints or forces acting on the monomer motion. Therefore, several decorated Rouse-like models have been developed over the years to suggest that the observed sub-Rousean dynamics may be associated with condensation of chromatin (Di Pierro et al. 2018; Shi et al. 2018) and the super-Rousean regimes with active processes (Chaki and Chakrabarti 2019; Foglino et al. 2019; for review, see Tortora et al. 2020). Dynamical simulations of copolymer models capturing quantitatively the different layers of chromosome organization (Shukron and Holcman 2017; Di Pierro et al. 2018; Ghosh and Jost 2018; Liu et al. 2018; Shi et al. 2018; Shukron et al. 2019) are consistent with an average sub-Rousean regime, with different mobilities between euchromatic and heterochromatic regions and with correlated motions associated with compartmentalization. In particular, Shi et al. (2018) associated the experimentally observed heterogeneity in chromatin motion to the intrinsic glassy dynamics of chromosomes, whereas Shukron and Holcman (2017) and Shukron et al. (2019) suggested that it emerges from cell-to-cell variability in cross-linking sites.

All these experimental and theoretical works draw a composite—and relatively controversial—picture of how chromatin moves inside cell nuclei during interphase and of how this heterogeneity in motion emerges from fundamental processes and from chromatin architecture. In particular, this has led to two main descriptions of chromatin motion, based on an analogy with materials science (Strickfaden 2021): chromatin behaves like a “liquid” or a “fluid” (Maeshima et al. 2016; Ashwin et al. 2020) pointing to a dynamic and mobile view of chromatin motion; or it behaves like a “gel” or a “solid” (Khanna et al. 2019; Strickfaden et al. 2020; Eshghi et al. 2021) highlighting a more constrained dynamics and rigid state.

Here, we investigated how the heterogeneous and anomalous behaviors of chromatin mobility may emerge from first principles using polymer modeling. In particular, we addressed the interplay between the three-dimensional chromosome organization and the different diffusion regimes of chromatin observed experimentally by investigating the dynamics of heteropolymer models that quantitatively describe the chromosome architecture.

Results

Quantitative data-driven modeling of 3D chromosome organization

To investigate chromatin motion in situations compatible with experiments, we first developed a data-driven polymer model to quantitatively describe the 3D chromatin organization. We modeled chromatin as a coarse-grained heteropolymer (Fig. 2A). Each monomer, containing 2 kbp of DNA and being of size 50 nm, is characterized by three structural features inferred from Hi-C maps (Methods): its TAD; its compartment (A or B); and, optionally, its anchoring role in CTCF-mediated loops as often observed at TAD boundaries in mammals (Dowen et al. 2014; Rao et al. 2014). The spatiotemporal dynamics of the system is governed by generic properties of a homopolymer (excluded volume and bending rigidity) (Ghosh and Jost 2018) decorated by three types of short-ranged attractive interactions accounting for the heterogeneity of monomer states (Fig. 2A; Methods): intra- and inter-compartment (E_AA, E_BB, E_AB), intra-TAD with a strength that depends on the local compartmentalization (E_TAD,A, E_TAD,B), and looping between CTCF anchors (E_loop). Our approach does not aim to investigate how loops, TADs, or compartments emerge from first-principle mechanisms but rather to fold an effective polymer model that captures the main organizational features of chromosomes from Hi-C and serves to study their consequences on chromatin dynamics. Therefore, our model may account for actual attractive forces mediated by chromatin-binding proteins like PRC1 or HP1 (Isono et al. 2013; Larson et al. 2017; Strom et al. 2017; Plys et al. 2019) but also effectively for other mechanisms acting on genome folding like cohesin-mediated loop extrusion (Sanborn et al. 2015; Fudenberg et al. 2016).

Figure 2.

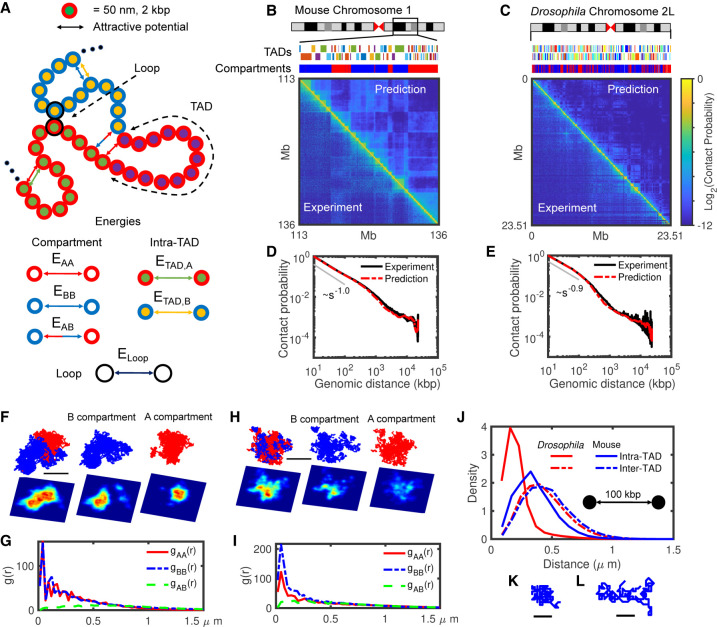
The heteropolymer model and comparison with Hi-C maps. (A) Schematic representation of the heteropolymer model with different structural components and their associated interactions. Each monomer hosts 2 kbp of DNA, and its diameter is 50 nm. The surrounding red (blue) color indicates A (B) compartment, inner different colors correspond to different TADs, and loop anchors are shown by black outer circles. All six possible attractive interactions are shown by arrows in this cartoon. (B,C) Visual comparison of predicted Hi-C maps and the experimental ones for 23 Mbp of mouse Chromosome 1 (113–136 Mbp) and Drosophila Chromosome 2L. The upper tracks show the corresponding TADs and compartments for each chromosome. (D,E) Contact probabilities extracted from predicted (red) and experimental (black) Hi-C maps shown in B and C, respectively. (F,H) Typical snapshots for mouse Chr 1 (F) and Drosophila Chr 2L (H) in mixed and separate A (red) and B (blue) compartments, with corresponding 2D density plots (the lower panels) with axial resolution of 1200 nm, lateral resolution of 100 nm, and pixel size of 50 nm. Bars represent 1 μm of real space. (G,I) Radial distribution functions (g) between A-A (red), B-B (blue), and A-B (green) monomers for mouse (G) and Drosophila (I). (J) Comparison between intra- (full curves) and inter-TAD (dashed curves) distance distributions of pair monomers separated by 100 kbp along the genome for Drosophila (red) and mouse (blue). (K,L) Typical snapshots of ∼300-kbp-long TADs for Drosophila (K) and mouse (L). Bars represent 0.25 μm of real space.

Next, we optimized the parameters (Methods) of the model for two regions of interest (Table 1): a 23-Mbp-long portion of Chromosome 1 (113–136 Mbp) in mouse embryonic stem cells (mESC) (Fig. 2B) and the Chromosome arm 2L in Drosophila melanogaster Kc167 female embryonic cells (Fig. 2C). Our choice for these two cell types aimed to investigate two distinct situations with different TAD and compartment sizes (Fig. 2B,C, upper tracks) and compaction levels but under the same modeling framework. Briefly, we used Hi-C maps as an input to detect TADs, compartments, and loop anchors, and thus to define the state of each monomer. Then, by varying the energy interactions, we inferred for each species the parameter set that best predicts the experimental Hi-C (Methods; Table 2). As expected, TAD and compartment patterns are qualitatively well described in our predictions (Fig. 2B,C) because we used that information directly extracted from experiments to build the model. However, in addition, the heteropolymer model was also able in both cases to quantitatively reproduce the absolute magnitude of the contact frequencies observed in experimental Hi-C data with an overall high accuracy (correlation of 0.95 for mouse data and 0.87 for Drosophila) (Fig. 2B,C). This goodness of fit not only captures the average generic decay of contact frequency as a function of their genomic distance (Fig. 2D,E) but also the structural features of Hi-C maps at different scales, including the intra-TAD and intra-compartment compaction levels (Supplemental Fig. S1).

Table 1.

Hi-C data sets used in this study

Table 2.

Optimized parameter sets and corresponding Pearson's correlation and χ² values for mouse Chromosome 1:113–136 Mbp and Drosophila Chromosome 2L

At large scales, the checkerboard-like patterns observed in Hi-C maps suggest that chromatin compartments are spatially segregated. Typical configuration snapshots from our simulations in Drosophila (Fig. 2H) and mouse (Fig. 2F) indeed illustrate the relative organization of A and B compartments. We quantified this by computing the radial distribution functions (Fig. 2G,I) g_AA (r), g_BB(r), and g_AB(r) that capture the probabilities to find a monomer of a given compartment at a given distance r from a monomer of the same (g_AA(r), g_BB(r)) or of a different (g_AB(r)) compartment. In Drosophila, we observed that the B compartment is locally more compact than A [g_BB(r) > g_AA(r) for small r] (Fig. 2I), whereas compaction is similar in both compartments in mouse (Fig. 2G). We also noticed that the A and B compartments are more segregated in mouse, with g_AB(r) equating g_AA/BB(r) around r* ≃ 700 nm, than in Drosophila (r* ≃ 300 nm), resulting in part from the larger genomic size of compartments in the mouse case (Fig. 2B,C, upper tracks).

At the TAD scale, structural properties are also strongly cell type– and compartment-dependent. On average, TADs in mice (median size ∼120 kbp) are longer than in fly (median size∼40 kbp) (Fig. 2B,C upper tracks). Globally, TADs in Drosophila are more compact than in mice (two typical snapshots of TADs with the same size are drawn in Fig. 2K,L) with a relatively smaller ratio of intra- versus inter-TAD distances of Drosophila compared to mice (Fig. 2J). Similar to the condensation of compartments (Fig. 2F–I), we also observed that TADs in the A compartment are less compacted than those in B for Drosophila (Cattoni et al. 2017; Szabo et al. 2018; Lesage et al. 2019) while being more open and having similar compaction level in mouse (Supplemental Fig. S1G,H; Finn et al. 2019).

Chromatin dynamics are strongly heterogeneous and locus-dependent

Having in hand quantitative polymer models capturing the main structural features of chromosome organization, we investigated the dynamical properties of chromatin predicted by such models. As a reference null model, we also simulated the dynamics of a simple homopolymer where all compartment-, TADs-, or loop-based interactions were switched off (Methods). One standard observable to probe the local chromatin mobility is the mean-squared displacement (MSD) of individual loci as a function of time. Experimentally, this is typically performed either by tracking single fluorescently labeled loci (Cabal et al. 2006) or by monitoring the dynamics of the nuclear local densities of stained histones (Zidovska et al. 2013) during ∼10–30 sec. From these experiments, trajectories of individual loci in single cells can be extracted and analyzed to compute two types of MSD: time-averaged and ensemble-averaged MSDs.

From each single trajectory, time-averaged MSDs can be estimated with

$$MS{D}_{i,c}(\mathrm{\Delta }t)\equiv {⟨{({\overrightarrow{r}}_{i,c}(t+\mathrm{\Delta }t)-{\overrightarrow{r}}_{i,c}(t))}^2⟩}_t,$$

where ${\overrightarrow{r}}_{i,c}(t)$ is the position vector of a given locus i at time t for a trajectory c, and 〈···〉_t is the time-averaging along the trajectory c (i.e., averaged over t). These MSDs can be analyzed by fitting them with a single power-law $MS{D}_{i,c}(\mathrm{\Delta }t)=D_{i,c}\mathrm{\Delta }{t}^{{\alpha }_{i,c}}$ (Methods). Analysis of live experiments have shown high variability in the diffusion constant D_i,c and exponent α_i,c at the single-cell level in many species and for many loci (see examples in Fig. 1B,C;) (Zidovska et al. 2013; Nozaki et al. 2017; Ashwin et al. 2019; Shaban et al. 2020b).

By averaging over all the trajectories c for the same locus i, ensemble-averaged MSDs can be computed with $MS{D}_i(\mathrm{\Delta }t)\equiv {⟨{({\overrightarrow{r}}_{i,c}(t+\mathrm{\Delta }t)-{\overrightarrow{r}}_{i,c}(t))}^2⟩}_{t,c}$. Examples extracted from various single-locus tracking experiments are given in Fig. 1A (Hajjoul et al. 2013; Bronshtein et al. 2015; Germier et al. 2017; Gu et al. 2018; Socol et al. 2019). MSD_i (Δt) can then be fitted by power-law-like functions $MS{D}_i\left(\mathrm{\Delta }t\right)=D_i\mathrm{\Delta }{t}^{{\alpha }_i\left(\mathrm{\Delta }t\right)}$ where the diffusion exponent α_i may now depend on the time lag Δt (Methods). Experiments show a wide variety of subdiffusive α_i-values depending on the locus, species, or transcriptional state, with sometimes crossovers between different regimes (see examples in Fig. 1A).

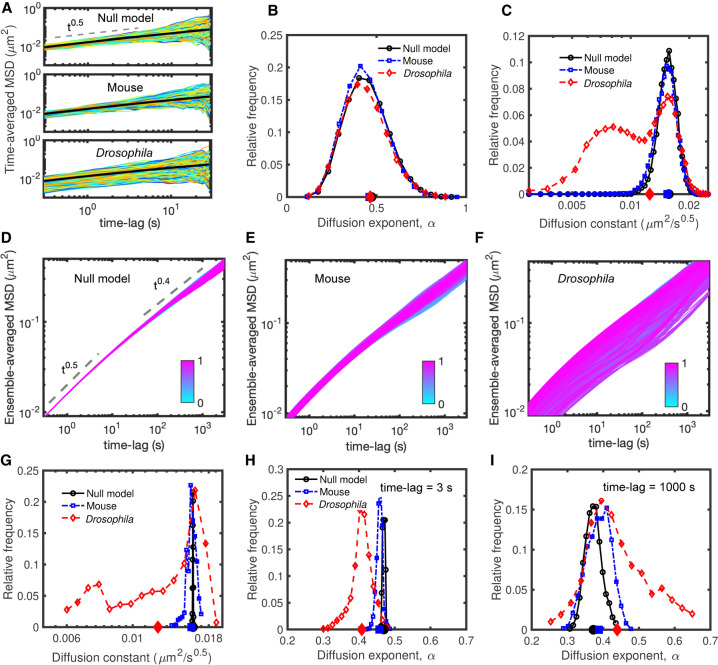
To try to understand the origin of this heterogeneity, we first estimated with our simulations the time-averaged MSD for all the monomers in the Drosophila and mouse cases over 30-sec-long trajectories (Fig. 3A; Supplemental Figs. S2, S3). Distributions of α_i,c are broad (Fig. 3B) and similar in both cases. The diffusion constants D_i,c are also dispersed (Fig. 3C; Supplemental Fig. S3) with a bimodal distribution for Drosophila, exhibiting a population of slowly diffusing trajectories. Our models thus well predict qualitatively the shapes and large variabilities of the distributions of diffusion exponents and constants observed experimentally (Fig. 1B,C). However, this strong variability is also present in the null (homopolymer) model (Fig. 3A–C) at the same degree as in the mouse case. This result suggests that part of the heterogeneity observed in time-averaged MSD does not stem from the multiscale organization of chromosomes in TADs or compartments but rather from a finite-size effect because of the limited duration of the monitored trajectories to measure the MSD (Supplemental Fig. S2).

Figure 3.

Dynamic properties of simulated chromosomes. (A) Time-averaged MSD_i,c of single trajectories of length 30 sec sampled every 0.3 sec for null (upper), mouse (middle), and Drosophila (bottom) models. (B) Distribution of the diffusion exponents α_i,c extracted from the time-averaged MSD curves given in A. (C) Distribution of the diffusion constants D_i,c for the time-averaged MSDs in A having an exponent α_i,c ≈ 0.5. Distributions for other α_i,c values are given in Supplemental Figure S3. In B and C, average values of the distributions are shown on the horizontal x-axis. (D–F) Ensemble-averaged (over all trajectories) MSD_i of all genomic loci for null (D), mouse (E), and Drosophila (F) models. To discard trivial positional effects, we exclude the last 50 monomers at the two ends of the polymers. Individual ensemble-averaged MSDs were colored from cyan (first monomer) to magenta (last monomer). (G–I) The distributions of the diffusion constant D_i (G) and of the diffusion exponent α_i (Δt) for short (Δt = 3 sec) (H), and large (Δt = 1000 sec) (I) time scales, extracted from ensemble-averaged MSD curves in panels D through F. The average values of the distributions are shown on the horizontal axes.

To mitigate this confounding factor and focus on the role of structural heterogeneities on dynamical variabilities, we next computed the ensemble-averaged MSD of all monomers over approximately 2000 roughly 1-h-long trajectories (Fig. 3D–F). In the homopolymer model (Fig. 3D), we observed as expected a uniform (Rousean) behavior for all monomers with α_i (Δt) ≈ 0.5 at short time scales (Δt < 10 sec) and α_i (Δt) ≈ 0.4 at longer time scales (Δt > 100 sec), typical of crumpled polymers (Tamm et al. 2015; Ghosh and Jost 2018; Liu et al. 2018). For mouse and Drosophila chromosomes, simulations predicted heterogeneous locus-dependent MSDs (Fig. 3E,F). The distributions of diffusion constants are broad, implying a large spectrum of loci mobilities (Fig. 3G). This is particularly visible in the Drosophila case (Fig. 3G) in which mobility may vary by up to threefold between two monomers. In Drosophila, we also predicted the distribution to be multimodal with two main peaks at low and high mobility, which is fully consistent with experiments (Gu et al. 2018; Lerner et al. 2020; Shaban et al. 2020b). The distributions of diffusion exponents per locus α_i (Δt) at different time scales (Fig. 3H,I) also support the strong heterogeneities observed in diffusion behaviors. Although at short time scales (Δt < 3 sec) exponents are rather homogeneous (α_i ≈ 0.5), at larger time scales (Δt > 10 sec) α_i becomes highly locus-specific and may strongly vary as a function of time. For example, at Δt = 1000 sec, α_i varies between 0.25 and 0.65 in Drosophila and between 0.3 and 0.5 in mice (Fig. 3I). This broad range of values, including both sub-Rousean (α_i < 0.5) and super-Rousean (α_i > 0.5) exponents, is consistent with the large discrepancy observed experimentally in α_i across loci and conditions (Fig. 1A).

Dissecting the role of compartments and TADs on chromatin motion

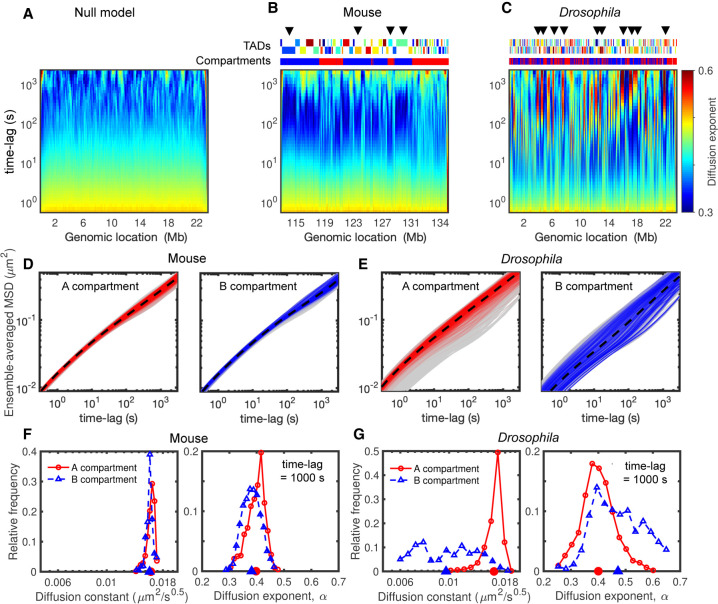
The degree of dynamical heterogeneity predicted by the model can only arise from the different interactions driving the TAD and compartment formation. Figure 4, A through C, illustrates the evolution of the exponent α_i as a function of the time lag Δt along the genome. As expected, we observed for the null model an overall homogeneity in dynamical parameters over time (Fig. 4A). For the mouse and Drosophila models, we measured instead a strong heterogeneity and locus dependency along the genome (Fig. 4B,C). Loci of the same TAD or compartment may have similar time evolutions of α_i (see also Supplemental Fig. S4), suggesting a coupling between dynamics and the different layers of genome folding. Many regions (Fig. 4B,C) show an anomalous and nonmonotonic behavior: α_i is ∼0.5 at short time scales, decreases to ∼0.3 (sub-Rousean regime) at intermediate time scales, increases to ∼0.6 (super-Rousean regime), and then retrieves a standard crumpled polymer-like behavior (α_i ∼ 0.4) at very large time scales. Such crossovers between sub- and super-Rousean regimes or between super-Rousean and normal regimes have also been observed experimentally (Fig. 1A).

Figure 4.

Heterogeneity in dynamics and its relationship with compartments. (A–C) Time evolutions of diffusion exponents along the genome for null model (A), mouse (B), and Drosophila (C), calculated by the derivatives of logarithmic MSD curves (Fig. 3G–I; Methods). The upper tracks in B and C show the corresponding TADs and compartments, and arrows highlight some regions with anomalous behaviors (nonmonotonic evolutions). (D) MSD curves of the monomers in A (left) and B (right) compartments in the mouse case. The dashed black curves show the average MSDs over all loci in the same compartment, and gray shaded areas are MSDs of all monomers. (E) As in D but for the Drosophila model. (F) The distributions of diffusion constant (left) and exponent (right) at 1000-sec time lag for the monomers in A (red) and B (blue) compartments in the mouse case. Their average values are indicated on the horizontal axes. (G) As in F but for Drosophila simulations.

Chromatin mobility is reduced in compact compartments

To quantitatively associate such anomalous behaviors with structural features, we first separately plotted the MSD for loci in active (A) and repressive (B) compartments (Fig. 4D,E). In mice (Fig. 4D), both compartments have a similar (weak) degree of heterogeneity with comparable diffusion constants and exponents (Fig. 4F). This confirms that the dynamical heterogeneity and difference between euchromatic and heterochromatic loci are usually weak in highly plastic cells as experimentally observed in mESCs (Nozaki et al. 2017) and in human cancerous U2OS cells (Shaban et al. 2020b). In Drosophila (Fig. 4E), loci in the A compartment are on average more mobile than those in the B compartment with a mean increase in mobility of ∼60% for A monomers (Fig. 4G, left panel). In fact, the A monomers correspond to the high mobility peak observed in Figure 3G. This is consistent with the observation that differentiated cells (like Kc167) show significant differences in mobility between active and repressive regions (Nozaki et al. 2017; Lerner et al. 2020). We also observed that the distribution of exponents is much broader for B than for A monomers (Fig. 4G, right panel), suggesting globally more heterogeneity and more loci with anomalous behaviors in the B compartment. However, not all the loci in B have anomalous dynamics (Fig. 4E, right panel), and all types of behaviors present in the general population of monomers (Fig. 3F) are observed in the B compartment. This suggests that compartmentalization per se is not the main driving force of heterogeneity in our model.

Anomalous behavior is associated with TAD compaction

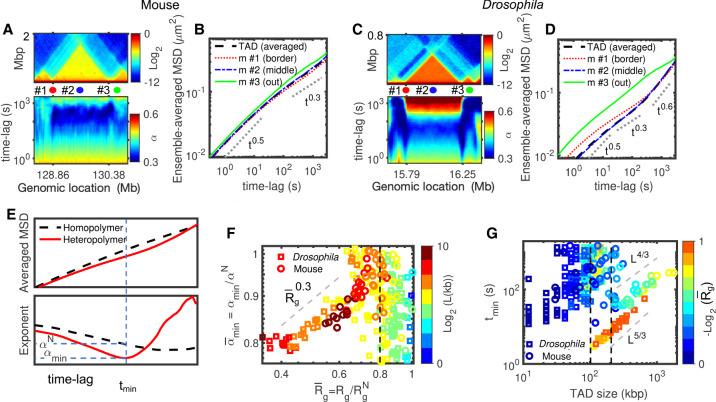
We thus reasoned that TADs may be a good suspect for driving the anomalous, nonmonotonic diffusion observed in our heteropolymer models. To address this, we first selected two TADs, one from Drosophila (size ∼480 kbp, 50% reduction in volume compared to a region of similar size in the null model) and one from mouse (size ∼1.52 Mbp, 30% volume reduction) with different degrees of compaction and different sizes (Fig. 5A,C). For the mouse TAD (Fig. 5A,B), which is bigger but less compact, anomalous behavior is weaker and most of the monomers follow a null model-like behavior. For the Drosophila TAD (Fig. 5C), which is smaller but more compact, we observed that all loci inside the TAD move with anomalous dynamics (Fig. 5D). Because one main difference between mouse and Drosophila heteropolymer models is the intra-TAD strength of interaction (Table 2; Fig. 2J), these observations point toward an important role played by the intra-TAD compaction level on driving anomalous behaviors. Moreover, by visually comparing the local Hi-C maps and the time evolutions of the diffusion exponent (Fig. 5A,C), we also remarked that the small neighboring TADs (quoted #3 in Fig. 5A,C) show null-like dynamics (Fig. 5B,D) while being well formed, suggesting that TAD length might also be an important parameter for anomalousness.

Figure 5.

Compaction leads to anomalous behavior. (A) Comparison of the predicted Hi-C map (top) and the corresponding time-evolution of the diffusion exponent (bottom) for the mouse Chr 1:128.36–130.88 Mbp region, which includes a 1.52-Mbp-long TAD. (B) MSD for three monomers annotated in A (red: m #1 at the border of TAD, blue: m #2 at the middle of the TAD, green: m #3 outside the TAD) and average MSD for all the monomers inside the TAD. (C,D) As in A and B but for the Drosophila Chr 2L:15.64–16.4 Mbp region, which includes a 460-kb-long TAD. (E) Typical average MSDs for a TAD predicted by the homopolymer and heteropolymer models (top) and the time-evolution of the diffusion exponent (bottom). For the heteropolymer curve, we computed the minimum exponent α_min, the corresponding time t_min, and the expected diffusion exponent α^N in the homopolymer model at t_min. (F) $\overline{{\alpha }_{min}}\left(={\alpha }_{min}/{\alpha }^N\right)$ against $\overline{R_g}$ for Drosophila and mice. The symbols are colored by the TAD length, L. (G) t_min as a function of TAD length for Drosophila and mice. Symbols are colored by the compaction level of TADs $\left(-lo{g}_2\left(\overline{R_g}\right)\right)$.

To quantify this, we considered, for each TAD, three “structural” quantities: L, the TAD length; R_g, its radius of gyration that captures its typical 3D size; and $R_g^N$, the radius of gyration for a domain of length L in the null model. Strongly compacted TADs are characterized by low values for $\overline{R_g}\equiv R_g/R_g^N$. And we introduced three “dynamical” observables (Fig. 5E): α_min, the minimum diffusion exponent value over time computed from the average MSD of monomers inside the same TAD; t_min, the time when α_min is reached; and α^N the exponent of the null model at t_min. The strength of the anomalous behavior is thus captured by the ratio $\overline{{\alpha }_{min}}\equiv {\alpha }_{min}/{\alpha }^N$ (low ratios <1 corresponding to strong anomalousness) and its duration by t_min.

We found that $\overline{{\alpha }_{min}}$ is an increasing function of $\overline{R_g}$ for $\overline{R_g}\le 0.8$, whereas we do not observe a clear-cut dependence of $\overline{{\alpha }_{min}}$ on L (Fig. 5F). Drosophila and mouse TADs follow the same scaling law $(\overline{{\alpha }_{min}}\sim {\overline{R_g}}^{0.3})$, suggesting that compaction level is the main driver of the strength of the anomalous behavior. For weakly compacted domains $(\overline{R_g}>0.8)$ or small TADs, the value of $\overline{{\alpha }_{min}}$ is less well defined. We also observed that, beyond a critical size (∼100 kbp for Drosophila and ∼200 kbp for mouse), t_min evolves as ∼L^5/3 for the Drosophila case and ∼L^4/3 for the mouse case, the role of $\overline{R_g}$ being less clear (Fig. 5G). These results show that the duration of the anomalous, nonmonotonic diffusion in heteropolymer models depends on the TAD length and compaction, longer domains being impacted for longer times. As observed for $\overline{{\alpha }_{min}}$, we found that t_min values for small TADs are very dispersed without significant correlation with the TAD length.

Anomalous behavior emerges from a crossover toward collective motion

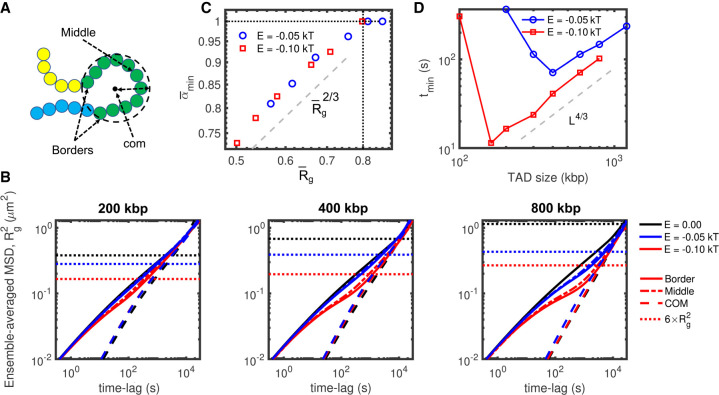
The existence of anomalous behaviors with MSDs exhibiting transitions between different, a priori opposite (sub- vs. super-Rousean), regimes is thus strongly associated with TAD compaction. To go deeper in the analysis of this association and to better understand how these transitions emerge from compaction, we introduced toy heteropolymer models (Methods) where we can independently play with the TAD length and intra-TAD strength of interaction. We considered simplified “uniform” models in which genomes are partitioned into adjacent TADs of the same size (Methods; Supplemental Fig. S5). For given TAD length and intra-TAD strength of interaction, all monomers of the chain have very similar MSDs (Fig. 6A,B), with only a weak positional effect translating the bead positioning inside the TAD, consistent with our observations made on more “complex” models (Fig. 5B,D). As expected, emergence of anomalous behavior occurs for larger TADs and stronger interactions (Fig. 6B; Supplemental Fig. S6) in which compaction starts to be substantial (Supplemental Fig. S7). Merging all the investigated TAD lengths and strengths of interaction together, we confirmed that t_min increases with L (Fig. 6D) and that below a given critical compaction level $(\overline{R_g}\le 0.8)$, $\overline{{\alpha }_{min}}$ is an increasing function of $\overline{R_g}$ (Fig. 6C). The dependency is steeper $(\overline{{\alpha }_{min}}\sim {\overline{R_g}}^{2/3})$ in the uniform models than for the more heterogeneous mouse and Drosophila cases. In the uniform models, for small and weakly compacted TADs, we observe $\overline{{\alpha }_{min}}\sim 1$. This suggests that the variability of $\overline{{\alpha }_{min}}$ values observed at this compaction regime $(\overline{R_g}>0.8)$ in the heterogeneous Drosophila or mouse models (Fig. 5F) reflects in fact the influence of neighbor (more compacted) TADs on these (normally weakly impacted) domains (Supplemental Figs. S8A–C, S9). By introducing A/B compartmentalization in these uniform models (Supplemental Figs. S8D–F, S10), we confirmed that more compact compartments show indeed reduced mobility but that the anomalous behavior mostly emerges from the formation of local interaction domains like TADs.

Figure 6.

Anomalous behavior in uniform models. (A) Cartoon to depict “middle” and “border” monomers, along with the center of mass and the radius of gyration of a TAD. (B) Comparison between MSDs of the monomers in the middle (mid) and borders (bor) of TAD and of the center of mass of the TAD (com) (A) from uniform heteropolymer models with TAD length of 200 kbp (left), 400 kbp (middle), and 800 kbp (right) for two different intra-TAD strength of interaction (black: 0 kT/null model, blue: −0.05 kT, red: −0.1 kT). The spatial sizes $\left(6R_g^2\right)$ for the different strengths of interaction are shown as dotted lines. (C,D) $\overline{{\alpha }_{min}}$ as a function of $\overline{R_g}$ and t_min as a function of the TAD length L for the uniform models and for different strengths of interaction.

By plotting the MSD of the center of mass of TADs in the uniform models (MSD_com), we observed that in the cases of strong anomalous dynamics the MSD of individual monomers MSD_i follows the dynamics of the center of mass in the super-Rousean regime (Fig. 6B). Because MSD_com does not depend strongly on the intra-TAD strength of interaction, the transition between the small time scale (homopolymer-like) diffusion and the large time scale (center-of-mass-like) regime is driven by the degree of compaction of the TAD. The crossover time between these two regimes corresponds typically to the Rouse time of the TAD (Grest and Kremer 1986), that is, the typical time for the center of mass of the TAD to diffuse over the typical 3D physical size of the TAD (given by the average end-to-end distance $\sim \sqrt{6}{R}_g$) (Fig. 6B). Overall, these results suggest that the non-monotonic (anomalous) evolution of α_i represents a crossover between the “fast” diffusion of single monomers at short times and a “slow,” collective regime in which loci of the same TAD move coherently at longer time scales, as recently observed experimentally for heterochromatin compartments (Eshghi et al. 2021).

Coherent motion of intra-TAD monomers

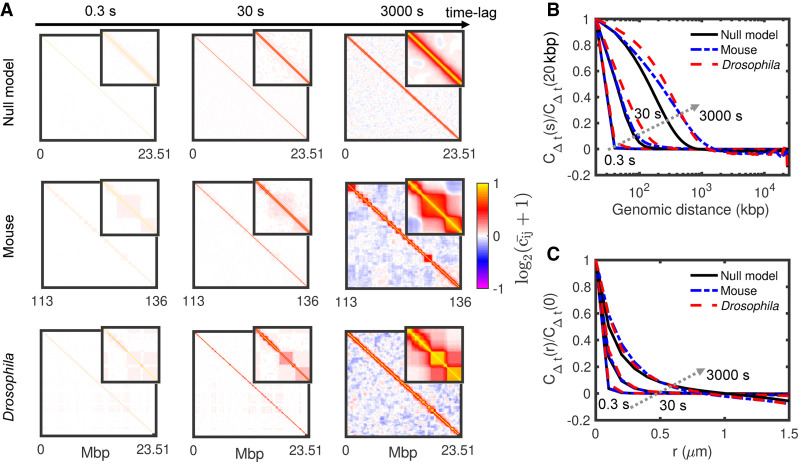
We then reasoned that such coherent moves might lead to correlations in the motion of monomers. We thus computed from our simulations the matrix C_ij (Δt) that describes how the displacements of monomer i after a time lag Δt are correlated with the displacements of another monomer j during the same time period (Methods). Figure 7A shows the normalized pair-correlation matrix $(\overline{C_{ij}}\equiv C_{ij}/\sqrt{C_{ii}{C}_{jj}})$ for different time lags. $\overline{C_{ij}}\sim 1$ (or ∼−1) means that, after Δt, i and j have moved on average along the same (or opposite) direction. For the null, homopolymer model (Fig. 7A), correlations decay uniformly toward zero as the genomic separation increases between the two loci (Fig. 7B). If we note s_corr the typical genomic distance between two monomers beyond that their motions become uncorrelated $(\overline{C_{ij}}\sim 0)$, we remarked that s_corr augments with the time lag from a few dozen kilobase pairs for second-scale displacements to megabase pairs after hours. This is a direct consequence of the polymeric nature of chromosomes and of the conserved connectivity along the chain. For the mouse and the Drosophila cases, we observed patterns in the correlation matrices that are strongly related to the TAD organization as already seen by Di Pierro et al. (2018), more compact TADs (Drosophila) being more impacted (Fig. 7A) as the dynamics of intra-TAD contacts is reduced (Supplemental Fig. S11). This observation confirms the coherent motion of monomers inside TADs and its relationship to intra-TAD compaction (Figs. 5, 6). For longer time lags, correlations between monomers of the same compartment become also significant, in particular, in the mouse case where compartments are more segregated (Fig. 2F–I). Overall, this leads to larger s_corr values (Fig. 7B; Supplemental Fig. S12), the difference with the null model increasing with the time lag.

Figure 7.

Spatiotemporal correlations of loci displacements. (A) Normalized matrices of pair correlation of motions $\overline{C_{ij}}$ for the null model (top), mouse (middle), and Drosophila (bottom) at different time lags. Insets represent zooms of the 2 Mbp × 2 Mbp central parts of the matrices. (B,C) Normalized average correlations as a function of the genomic distance (B) and spatial distance (C) for the time lags displayed in A. Arrows indicate increasing time lag.

Additionally, we looked at the spatiotemporal correlation function C_Δt (r) (Methods) that represents the average correlation between the displacement after a given time lag Δt of two monomers initially separated by a 3D distance r (Fig. 7C; Liu et al. 2018), a quantity more easily accessible experimentally (Zidovska et al. 2013). We found that the typical size of the spatial regions with correlated motions increases with the time lag from ∼100 nm for second-scale displacement to ∼1 μm after hours. These predictions remain however largely underestimated compared to experiments (few microns already after a few seconds) (Zidovska et al. 2013). We also did not find strong differences between the null model and the mouse and Drosophila cases, demonstrating that C_Δt (r), which is an average over all the loci, does not capture the effect of compaction on correlated motion. All this suggests that the larger spatiotemporal correlations observed experimentally are not the signature of TAD formation or A/B compartmentalization.

TAD formation by loop extrusion may also lead to anomalous behaviors

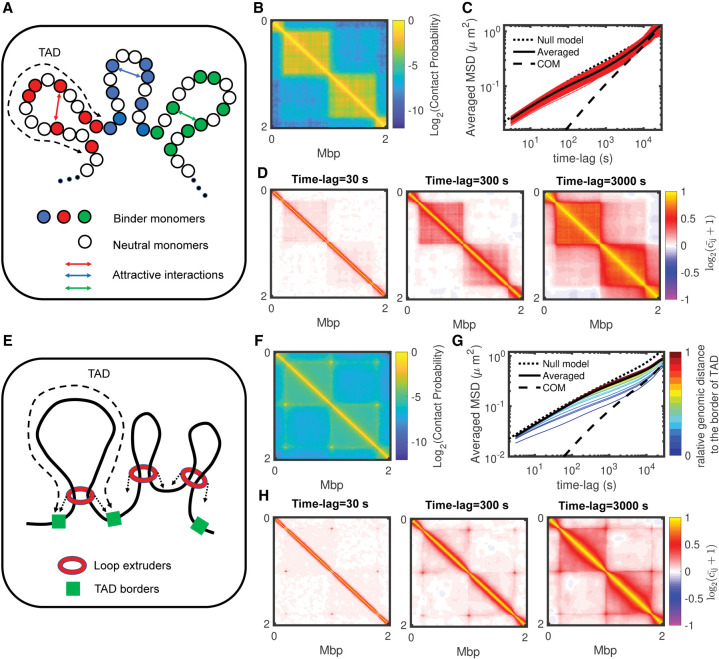
In our data-driven heteropolymer framework, we considered effective, passive interactions to model the patterns observed in experimental Hi-C maps. Although such type of interactions, putatively driven by chromatin-binding proteins associated with specific epigenomic marks, may actually drive the formation of spatial domains like TADs in Drosophila (Jost et al. 2014; Szabo et al. 2019) or constitutive heterochromatin domains in higher eukaryotes (Larson et al. 2017; Strom et al. 2017), other key mechanisms like cohesin-mediated loop extrusion (Fudenberg et al. 2017) may also be involved in TAD formation. To investigate if anomalous dynamics can be observed in different mechanistic contexts, we simulated chromatin mobility for two other mechanisms on toy examples (Methods).

As in our main model, the first simulation set also applies attractive interactions between loci, but only on a fraction (not all) of the monomers inside a TAD (Fig. 8A,B). These monomers may represent the actual binding sites of chromatin-binding proteins like PRC1 or HP1. For similar TAD compaction levels, we observed much more heterogeneous dynamics than in the previously discussed uniform models (Fig. 8C; Supplemental Fig. S13). Monomers of the same TAD may have different MSDs: some react like in the null model but others follow anomalous behaviors, a property that seems independent of their binding site status (Supplemental Fig. S13). However, monomers of the same TAD still move coherently (Fig. 8D).

Figure 8.

Effects of alternative mechanisms for TAD formation on anomalous behaviors. (A) Schematic representation of a binder model for TAD formation. (B) A 2-Mb zoom of the predicted Hi-C map for a toy model with 800-kbp-long TADs, a density of binder monomers of 0.5 and an attractive interaction of −0.2 kT (for other examples, see Supplemental Fig. S13). (C) Ensemble-averaged MSDs of the binder monomers with their average and the MSD of the TAD center of mass for the same parameters as in B. (D) For the example shown in B, 2-Mb zooms in the matrix of pair correlations $\overline{C_{ij}}$ for different time lags. (E) Schematic representation of the loop extrusion model. (F) A 2-Mb zoom of the predicted Hi-C map for a toy model with 800-kbp-long TADs and about 80 bound extruding factors (for other examples, see Supplemental Fig. S14). (G) Ensemble-averaged MSDs colored by the relative position of the monomer to the nearest TAD border for the same parameters as in F. (H) For the example shown in F, 2-Mb zooms in the matrix of pair correlations $\overline{C_{ij}}$ for different time lags.

The second mechanism accounts for the chromatin-loop extrusion by cohesin rings (Sanborn et al. 2015; Fudenberg et al. 2016): loop-extruding factors are loaded onto chromatin, actively extrude loops until they unbind, meet another extruder or reach TAD border (Fig. 8E). For standard parameter values of the loop extrusion process (Methods), the translocation activity of cohesin generates dynamic loops that are stabilized at TAD boundaries, leading to intra-TAD compaction (Fig. 8F). As observed experimentally (Kakui et al. 2020), we found that the loop extrusion mechanism leads to decreased mobility compared to the null model (Fig. 8G). We also detected more dynamical variability between monomers within a domain (Fig. 8G; Supplemental Fig. S14). Strongly anomalous behaviors are found close to TAD borders where contacts mediated by the extruders are more stable, leading to collective motion of the TAD boundaries. Instead, intra-TAD coherent motion is weaker (Fig. 8H).

Discussion

Experiments probing chromatin motion have highlighted the large heterogeneity existing inside cell nuclei and across biological conditions and have suggested that chromatin may behave sometimes like a liquid, sometimes like a gel. In this paper, we investigated chromosome dynamics using biophysical modeling to interpret in a unified framework how these different physical states and dynamical heterogeneities may emerge from the same first principles driving genome folding.

Based on a dynamical data-driven polymer model that captures the main structural properties of chromosome organization, we were able to quantify the motion of chromatin at the sub-chromosome territory level. Previous similar approaches on human chromosomes (Di Pierro et al. 2018; Liu et al. 2018; Shi et al. 2018) have shown that such types of heteropolymer models are consistent with a heterogeneous, sub-Rousean, (A/B) compartment-dependent, and spatially correlated chromatin dynamics. To go beyond these works (Di Pierro et al. 2018; Liu et al. 2018; Shi et al. 2018) and get a broader view of chromatin motion on contrasted situations, we studied in parallel three cases: a reference homopolymer model, and two heteropolymer models of a less-compact stem-cell-like chromatin (mESC), and a more compact differentiated-cell-like organization (Drosophila Kc167).

Our results showed indeed the heterogeneous locus dependency of chromatin motion. The analysis of time-averaged MSDs computed from single-cell trajectories suggests however that great caution should be taken when interpreting the distribution of diffusion exponents from such experiments, because part of the observed heterogeneities may arise from intrinsic variabilities inherent to short trajectories. For the better defined ensemble-averaged MSDs, we found that the observed dynamical heterogeneity reflects the various degree of compaction that may exist along the genome: whereas loci inside small or weakly compacted TADs (or compartments) show a rather homogeneous, fast, Rouse-like diffusion, loci inside compact TADs have a lower mobility and experience crossovers between different diffusion regimes (from Rousean to sub-Rousean to super-Rousean to Rousean modes). Using uniform models and testing several key mechanisms for TAD formation, we showed that such anomalous behavior is the signature of collective coherent motion at the level of strongly compacted regions.

We observed that the existence of 3D chromatin domains of correlated displacements, the so-called dynamically associated domains (DADs) (Zidovska et al. 2013; Shaban et al. 2018), emerges intrinsically from the polymeric nature of chromatin. However, the persistence of these domains is strongly related to the 3D chromosome organization: loci in the same TAD and, to a lesser extent, in the same compartment are more likely to be in the same DAD, as also observed by Di Pierro et al. (2018) for human chromosomes.

In our heteropolymer models, we integrated the multiple layers of chromatin organization using effective passive interactions, that is, ATP-independent processes that satisfy detailed balance (Chandler 1987). Using such interactions we can capture super-Rousean regimes, not as a consequence of directed forces or active processes but as a crossover regime between a slow coherent mode of motion at slow or intermediate time scales to a normal Rouse-like dynamics at longer time scales. However, our analysis reveals that this type of interaction cannot quantitatively capture the fast and large-scale average increase of correlated motion across the nucleus (Zidovska et al. 2013; Zidovska 2020), suggesting that other processes mediate this large-scale growth in spatial correlations (Liu et al. 2018), putatively via the actions of extensile motors on chromatin mediated by hydrodynamics interactions (Saintillan et al. 2018) or crosslinks and interactions with the nuclear membrane (Liu et al. 2021).

Such passive interactions might account for actual mechanisms, like polymer (micro)-phase separations (Jost et al. 2014; Erdel and Rippe 2018; Falk et al. 2019) mediated by homotypic or heterotypic interactions between chromatin-binding proteins, that drive euchromatin/heterochromatin compartmentalization in many species and TAD formation in Drosophila. However, recently an active process, the chromatin-loop extrusion by cohesins or condensins (Fudenberg et al. 2017; Ghosh and Jost 2020), was shown to play a central role in TAD formation in mammals (Sanborn et al. 2015; Fudenberg et al. 2016). This mechanism was suggested to act on chromatin dynamics either by slowing down chromatin motion (Kakui et al. 2020) or by boosting locally the mobility on a short time scale corresponding to the loop extruder residence time at a locus (Nuebler et al. 2018). In our hands, the loop extrusion mechanism leads to an overall reduced and heterogeneous mobility. Coherent motions and anomalous behaviors are also visible for such a process but mainly for genomic regions close to TAD boundaries, where compaction is stronger and cohesin-mediated loops less dynamic.

Our work provides a unified framework to rationalize the wide variety of behaviors observed experimentally. Heterogeneity in the diffusion and exponent constants are driven by heterogeneity in TAD organization and chromatin condensation. The observed fluid-like behavior (Maeshima et al. 2016; Ashwin et al. 2020) of chromatin is likely to be associated with weakly compacted dynamic chromatin. This would typically correspond to stem-cell-like conditions in which A and B compartments are still not entirely formed and architectural proteins driving their organization like HP1 (Strom et al. 2017) are not fully loaded (Poonperm and Hiratani 2021). This may explain why no clear differences are globally observed between euchromatin and heterochromatin in U2OS (Shaban et al. 2020b), a highly plastic and transformed human cell line. The gel-like state of chromatin (Khanna et al. 2019; Eshghi et al. 2021) is associated with strongly compacted regions which, in our examples, mainly correspond to TADs but would also be observed for any chromatin structure with similar degrees of compaction. Within our framework, this corresponds to the weak gelation of a polymeric system (de Gennes 1979; Douglas 2018) for which changes in the effective internal friction or viscosity (Poirier and Marko 2002; Soranno et al. 2012; Socol et al. 2019) emerge from reversible crosslinks (Supplemental Fig. S15). The dynamic signature of such a gel-like state relies on its low mobility, the presence of local coherent motion, and anomalous behaviors with slow internal dynamics and crossovers between different diffusion regimes for individual loci (see above). By combining live imaging and modeling, Khanna et al. (2019) have described such a gel state at the immunoglobulin heavy chain locus in pro-B cells, a highly compacted region. They observed very slow sub-Rousean internal motion between V and DJ segments and a crossover between super-Rousean and Rousean regime for individual MSD of the DJ segment, which is consistent with our analysis of strongly self-interacting regions (Supplemental Fig. S16). At the nuclear scale, this gel state could be only localized on a few compacted regions like on centromeres or telomeres, even in plastic cells (Bronshtein et al. 2015; Eshghi et al. 2021). For example, recent experiments by Eshghi et al. (2021) showed that in mESCs loci within dense heterochromatin compartments show anomalous gel-like MSDs with a crossover toward collective motion for the entire compartment. We expect the gel-like dynamics to become more and more predominant as cell differentiation progresses and compartments like heterochromatin achieve their final compaction state (Lerner et al. 2020). This may lead in extreme cases to a solid state with an almost arrested dynamic of chromatin as recently suggested by FRAP analysis on euchromatin and heterochromatin regions of mouse embryonic fibroblast cells (Strickfaden et al. 2020).

Are the different dynamical regimes of chromatin only readouts of the mechanisms driving chromosome organization or do they carry, in addition, specific biological functions? Regulating chromatin mobility may directly impact gene transcription (Maeshima et al. 2020) by controlling the timing of contact between promoters and distant enhancers and thus the gene bursting frequency (Bartman et al. 2016; Chen et al. 2018). Similarly, the regulation of the epigenomic landscape may be affected by the local dynamical regimes because the kinetics of spreading and maintenance of an epigenomic signal would depend on the capacity of the genomic loci to which histone-modifying enzymes are bound, to explore more or less rapidly their 3D neighborhood and thus to allow the propagation of the corresponding histone modification (Jost and Vaillant 2018; Oksuz et al. 2018). For example, active marks usually found in less-compact, more-fluid compartments have faster dynamics of maintenance than inactive marks (Alabert et al. 2015). More generally, we expect the regulation of a genomic region to be more sensitive and to adapt more efficiently to variations in a fluid-like environment than in a gel-like environment that, conversely, may protect it from spurious nonpersistent perturbations.

A better characterization of the regulation of the fluid-, gel-, or solid-like states of chromatin motion would require the development of upgraded polymer models integrating the main passive and active processes driving genome folding but also the development of new experimental approaches allowing to quantify simultaneously the dynamics of many loci (whose genomic positions are known) at high spatial and temporal resolution. Recent progresses in multiple loci (Zhou et al. 2017) and in super-resolution (Chen et al. 2018; Alexander et al. 2019; Barth et al. 2020; Brandão et al. 2021) live imaging would make it possible to test quantitatively the relationships between mobility, coherent motion, and compaction predicted by our polymer models and the role of basic mechanisms such as phase separation or loop extrusion in regulating chromosome dynamics. For example, live imaging the coupled structural and dynamical responses of chromatin after rapid in vivo perturbations of the amount of key chromatin-binding complexes using the auxin-inducible-degron system (Schwarzer et al. 2017; Dobrinić et al. 2021) or after modifications of their self-interacting capacities using optogenetics (Shin et al. 2019; Shimobayashi et al. 2021) would allow direct investigation of how chromatin dynamics respond to changes in chromatin compaction.

Methods

Analysis of Hi-C data

The experimental Hi-C data sets were downloaded from the NCBI Sequence Read Archive (SRA; https://www.ncbi.nlm.nih.gov/sra) (Table 1) using “fastq-dump” (https://github.com/ncbi/sra-tools/wiki). Each experiment has been processed (i.e., FASTQ quality checks, Mapping to reference genomes, Filtering to remove noninformatic reads, and Merging data together) through the TADbit pipeline (https://github.com/3DGenomes/TADbit) (Serra et al. 2017). Then, we normalized data using the “Vanilla” method at 10 kbp resolution (Lieberman-Aiden et al. 2009). After generating the Hi-C map, we used the “IC-Finder” tool to find TAD boundaries (Haddad et al. 2017). The A/B compartments have been identified by the “hic_data.find_compartments” tool from the TADbit suite, using Principal Component Analysis (PCA) of the observed/expected matrices. Finally, we inferred chromatin loops by using “hicDetectLoops” tool from the “HiCExplorer” package (https://github.com/deeptools/HiCExplorer) (Wolff et al. 2020).

Polymer models and simulations

Each genomic segment under investigation is modeled as a semiflexible self-avoiding polymer in which one monomer consists of 2 kbp of genome and has a diameter of 50 nm (Fig. 2A). The chain is moving on a FCC lattice under periodic boundary conditions to account for confinement by other genomic regions, as previously described (Ghosh and Jost 2018).

The Hamiltonian of a given configuration is given by

$$H=\kappa \sum _{i=2}^{N-1}(1-cos{\theta }_i)+\sum _{i,j}(E_{c\left(i\right),c\left(j\right)}+E_{TAD,c\left(i\right)}{\delta }_{t\left(i\right),t\left(j\right)}{\delta }_{c\left(i\right),c\left(j\right)}+E_{Loop}{\delta }_{l\left(i\right),l\left(j\right)})f_{ij},$$

with f_ij = 1 if monomers i and j occupy nearest neighbor sites on the lattice (=0 otherwise). The first term in H accounts for the bending rigidity of the chain with κ the bending stiffness and θ_i the bending angle between monomers i − 1, i, and i + 1. The second term refers to contact interactions driven by the compartment (c(i)), TAD (t(i)), or loop (l(i)) state of each monomer. E_c(i),c(j) (either E_AA, E_BB, or E_AB) stands for compartment–compartment interactions, E_TAD,c(i) (either E_TAD,A or E_TAD,B) for intra-TAD interactions, E_Loop for loop interactions, and δ_m,n = 1 if m = n (=0 otherwise). In the homopolymer model, all interaction parameters except κ were set to zero.

The lattice volumic fraction (∼0.5) and bending energy (1.2 kT) were chosen to simulate the coarse-grained dynamics of a chromatin fiber of Kuhn length ∼100 nm (Arbona et al. 2017; Socol et al. 2019) and of base pair density ∼0.01 bp/nm³, typical of mammalian and fly nuclei (Milo et al. 2010). The dynamics of the chain were simulated using kinetic Monte Carlo, starting from unknotted initial configurations, as detailed in Ghosh and Jost (2018). Each Monte Carlo step (MCS) consists of N (total number of monomers) local moves including reptation moves. Such implementation has been shown to well reproduce the structural and dynamical properties of long confined polymers (Olarte-Plata et al. 2016; Ghosh and Jost 2018). For each simulation, we discarded the first 10⁶ MCS to reach steady state and then stored snapshots every 10² MCS during 10⁷ MCS. For each situation (homopolymer, mouse and fly heteropolymer models), 20 different independent trajectories were simulated starting from different initial configurations.

Parameter inference of the heteropolymer models

To infer parameters in both (mouse and Drosophila) cases, we first mapped TADs, compartments, and loops extracted from the experimental Hi-C map into the heteropolymer model and then iteratively adjusted the interaction parameters to optimize the correspondence between the predicted and experimental Hi-C maps. For simulations, we estimated the contact frequency P_ij (sim) between any pair (i,j) of monomers as the probability to observe i and j at a distance less than a cutoff value r_c in all our snapshots. To quantitatively compare simulated contact probabilities to experimental Hi-C map, we transformed the experimental contact frequencies (H_ij) to contact probabilities (P_ij(exp)) using the following relation:

$$P_{ij}(\exp )=\min \left(1,{\displaystyle \frac{H_{ij}}{{\underset{\_}{H}}_{\pm 1}}}\right)$$

where H_±1 is the median value of {H_i,i+1} (Szabo et al. 2018). Our criteria for finding the optimal parameter values (energies E_AA, E_BB, E_AB, E_TAD,A, E_TAD,B, E_loop, and cutoff distance r_c) were the maximization of the Pearson's correlation between simulated and experimental matrices and the minimization of the χ² score,

$${\chi }^2={\displaystyle \frac{2}{N(N-1)}\sum _{i,j}{\displaystyle \frac{{\left[P_{ij}(sim)-P_{ij}(exp)\right]}^2}{{\sigma }_{ij}^2(exp)}}}$$

where ${\sigma }_{ij}^2(exp)$ is the experimental standard deviation on P_ij (exp) estimated over experimental replicates. The optimization was performed using a grid-search algorithm over the parameter values in the range [−0.3:0] kT for energy parameters and in the range of [70:200] nm for r_c. In Table 2 we summarized the optimal values for each case with their corresponding χ² and Pearson's correlation. For comparison, we also computed the correlation between P_ij (exp) and random permutations of the P_ij (sim) matrix in which bins corresponding to the same inter-loci genomic distance |j − i| were randomly shuffled to preserve the average contact frequency decay as a function of the genomic distance. For these random matrices, we found a correlation of 0.8414 ± 0.0001 for the mouse case and 0.7852 ± 0.0008 for the Drosophila case (compare to the optimal values in Table 2), showing that our models predict much more than just the average behavior.

Time mapping of simulations

In kinetic Monte Carlo (KMC) frameworks, the dynamics of particles depend on the acceptance ratio of local trial moves. For very small step size in trial moves and very weak potentials, KMC results are equivalent with Brownian dynamics, whereas for longer step sizes and stronger interactions, the KMC time steps need to be rescaled (Sanz and Marenduzzo 2010; Bal and Neyts 2014). Because we are simulating a unique chain in the box in absence of external forces, we expect the MSD (g₃) of the center of mass of the whole polymer to be independent of the investigated model (homopolymer or heteropolymer). However, we found (Supplemental Fig. S17A) g₃ ≅ 5.70 × 10⁻⁸ (μm²/MCS)Δt for the homopolymer model, g₃ ≅ 5.50 × 10⁻⁸ (μm²/MCS)Δt for the mouse case, and g₃ ≅ 2.85 × 10⁻⁸ (μm²/MCS)Δt for the Drosophila case, where g₃ is measured in μm² and Δt in MCS. Therefore, we rescaled time MCS → MCS* for each model to have similar g₃ for all cases (Supplemental Fig. S17B). The rescaled time for mouse is MCS* = 0.96 MCS and for Drosophila MCS* = 0.50 MCS. As expected, the rescaled time is dependent on the strength of interaction, in a way that MCS* decreases for stronger interactions. Then, to translate MCS* to real time (sec), we compare the average simulated 2D-MSD of single loci (in μm²), to the typical value of 0.01(μm²/sec^0.5) × Δt^0.5 (with Δt in sec) that has been measured in yeast (Hajjoul et al. 2013) and that corresponds to an average MSD also observed in other species (Fig. 1A). From this time mapping, we found that each MCS* corresponds to ∼3 msec of real time.

Uniform heteropolymer and loop extrusion models

To separately investigate the effects of TAD compaction, TAD arrangements, and compartments, we introduced toy polymer models. In the first step, to explore the effects of TADs (i.e., TAD length and intra-TAD interaction), we considered “uniform” models in which 20-Mbp-long chromosomal segments are partitioned into consecutive TADs of uniform lengths (Supplemental Figs. S5–S7). Then, to investigate the role of TADs arrangement, we partitioned the polymer into TADs alternating between two different lengths (Supplemental Fig. S8, upper panels; Supplemental Fig. S9). Finally, to investigate the effect of compartments, we alternatively assigned A and B compartments to the uniform TAD models with E_BB < 0 and E_AA = E_AB = 0 (Supplemental Fig. S8, bottom panels; Supplemental Fig. S10).

In another scenario, we introduced toy models to investigate the effect of discrete binding sites on chromosome dynamics. Similar to the uniform models described above, we partitioned the chromosome into TADs of uniform length. In each TAD, we assigned randomly, to a fixed proportion ρ of monomers, the so-called “binder” monomers, the capacity to interact with an attractive energy E_b with other “binders” of the same TAD (Fig. 8A). Other monomers are considered as neutral monomers. To have a similar effective intra-TAD interaction and consequently similar compaction levels, we adjusted E_b and ρ to satisfy ρ² E_b = E. In Figure 8 and Supplemental Figure S13, we chose E = −0.05 kT.

We also investigated the effect of loop extrusion activity on chromosome dynamics (Fig. 8E). We considered N_tot loop extruders that may bind (with rate k_b) or unbind (with rate k_u) from the polymer. Bound extruders are composed of two legs that walk on opposite directions along the polymer at a rate k_m; these legs are linked together by a spring of energy E_aΔr², with E_a = 10 kT and Δr the 3D distance on the lattice between the two legs. If one leg is on a monomer corresponding to a TAD border, its moving rate is set to zero, assuming that this border is enriched in CTCF binding sites (Dowen et al. 2014; Rao et al. 2014) that are known to stop or limit the loop extrusion of cohesins (Nora et al. 2017, 2020). We assumed that two extruding legs walking in opposite directions cannot cross.

In our kinetic Monte Carlo framework, in addition to the standard trial moves of the monomers based on the Hamiltonian of the system (see above) complemented with the spring-like interactions, at every MCS, N_tot trial attempts to bind or unbind extruders, and 2N_tot trial attempts to move a leg of a bound extruder are also performed. k_u was fixed to fit the experimentally observed life time of bound cohesin on chromatin (∼20 min) (Hansen et al. 2017), k_b such that the proportion of bound extruders k_b/(k_b + k_u) is about 40% (Cattoglio et al. 2019), and k_m such that the extruding speed rate matched in vitro experimental values $\left(\sim 50\mathrm{kbp}/\min \right)$ (Golfier et al. 2020). In Figure 8 and Supplemental Figure S14, we explored the effect of TAD length and N_tot on structure and dynamics. For example, N_tot = 200 implies approximately 80 bound extruders on average acting on the chain, corresponding to a density of about one extruder every 250 kbp.

Fitting of the diffusion exponent and constant

To extract the diffusion constant D_i,c and exponent α_i,c for each trajectory c and each monomer i, we fitted the time-averaged mean-squared displacement MSD_i,c by a power-law $D_{i,c}\mathrm{\Delta }{t}^{{\alpha }_{i,c}}$ using the MATLAB function polyfit(LogMSD_i,c,LogΔt,1) over more than three decades. The unit of D_i,c depends on α_i,c and is ${\mu \mathrm{m}}^2/{\sec }^{{\alpha }_{i,c}}$ (Supplemental Figs. S2, S3). For the ensemble-averaged mean-squared displacement MSD_i, we assumed that the diffusion exponent is a function of the time lag Δt: $MS{D}_i\left(\mathrm{\Delta }t\right)=D_i\mathrm{\Delta }{t}^{{\alpha }_i\left(\mathrm{\Delta }t\right)}$ or, in logarithmic scale log MSD_i = log D_i + α_ilogΔt. α_i (Δt) is then given by the local slope of the log-log MSD curves:

$${\alpha }_i(\mathrm{\Delta }t)={\displaystyle \frac{\mathrm{\Delta }\log MS{D}_i\left(\mathrm{\Delta }t\right)}{\mathrm{\Delta }\log \mathrm{\Delta }t}=\underset{\delta t\to 0}{lim}{\displaystyle \frac{\log MS{D}_i\left(\mathrm{\Delta }t+\delta t\right)-\log MS{D}_i\left(\mathrm{\Delta }t\right)}{\log \left(\mathrm{\Delta }t+\delta t\right)-\log \mathrm{\Delta }t},}}$$

and D_i by

$$D_i=\underset{\mathrm{\Delta }t\to 0}{lim}MS{D}_i(\mathrm{\Delta }t)/\mathrm{\Delta }{t}^{{\alpha }_i\left(\mathrm{\Delta }t\right)}.$$

Because ${\alpha }_i\left(\mathrm{\Delta }t\to 0\right)\sim 0.5$, the unit of D_i is μm²/sec^0.5.

Two-dimensional density plot

To construct the 2D density plot of chromosomes shown in Figure 2, F and H, the intensity at a position (x, y) is given by the sum over all monomers of a 2D Gaussian function mimicking the point spread function (PSF) of a microscope as follows:

$$I=\sum _i{e}^{-{\displaystyle \frac{{\left(x-x_i\right)}^2+{\left(y-y_i\right)}^2}{2{\sigma }^2}}}$$

with (x_i, y_i) the position of monomer i and σ = 300 nm chosen to get a spatial resolution of 100 nm in the (x, y)-plane.

Spatiotemporal correlation function

We defined C_ij (Δt), the pair correlation of the displacement vectors after a time lag Δt of the monomers ith and jth as (Di Pierro et al. 2018)

$$C_{ij}(\mathrm{\Delta }t)={⟨{\overrightarrow{\mathrm{\Delta }r}}_i(t;\mathrm{\Delta }t)\cdot {\overrightarrow{\mathrm{\Delta }r}}_j(t;\mathrm{\Delta }t)⟩}_t,$$

with

$${\overrightarrow{\mathrm{\Delta }r}}_m(t;\mathrm{\Delta }t)={\overrightarrow{r}}_m(t+\mathrm{\Delta }t)-{\overrightarrow{r}}_m(t),m\in i,j,$$

where ${\overrightarrow{r}}_m$ is the position of monomer m with respect to the center of mass of the chain. Then we calculated the averaged correlation C_Δt (s) as a function of the genomic distance s between monomers by averaging over all C_ij with same genomic distance

$$C_{\mathrm{\Delta }t}(s)={\displaystyle \frac{{\sum }_{i>j}{C}_{ij}(\mathrm{\Delta }t)\delta (s_{ij}-s)}{{\sum }_{i>j}\delta (s_{ij}-s)},}$$

where s_ij is the genomic distance between monomers ith and jth, and δ(x) is the Kronecker delta function. Additionally, we defined the spatiotemporal correlation function (i.e., averaged correlation as a function of spatial distance) C_Δt (r) as (Liu et al. 2018)

$$C_{\mathrm{\Delta }t}(r)={⟨{\displaystyle \frac{{\sum }_{i>j}[{\overrightarrow{\mathrm{\Delta }r}}_i(t;\mathrm{\Delta }t)\cdot {\overrightarrow{\mathrm{\Delta }r}}_j(t;\mathrm{\Delta }t)]\delta (r_{ij}(t)-r)}{{\sum }_{i>j}\delta \left(r_{ij}\left(t\right)-r\right)}}⟩}_t,$$

where r_ij (t) is the spatial distance between monomers ith and jth.

If we did not correct for the movement of the center of mass (Supplemental Fig. S18) we observed very long-range correlations between loci as the time lag increases, which reflects the global motion of the center of mass.

Software availability

Codes used to simulate the heteropolymer and the loop extrusion models are available on GitHub (https://github.com/physical-biology-ofchromatin/LiquidGel_ChromSimu) and as Supplemental Code.

Competing interest statement

The authors declare no competing interests.