Abstract
This review discusses the properties of candidate compounds for semi-hard and hard magnetic applications. Their general formula is with R = rare earth, T = transition metal and and among them, the focus will be on the ThMn- and ThZn-type structures. Not only will the influence of the structure on the magnetic properties be shown, but also the influence of various R and T elements on the intrinsic magnetic properties will be discussed (R = Y, Pr, Nd, Sm, Gd, … and T = Fe, Co, Si, Al, Ga, Mo, Zr, Cr, Ti, V, …). The influence of the microstructure on the extrinsic magnetic properties of these R–T based intermetallic nanomaterials, prepared by high energy ball milling followed by short annealing, will be also be shown. In addition, the electronic structure studied by DFT will be presented and compared to the results of experimental magnetic measurements as well as the hyperfine parameter determined by Mössbauer spectrometry.
Keywords: rare-earth-transition-metal intermetallics, mechanical alloying, hard magnetic materials, DFT, Mössbauer spectrometry
1. Introduction
Rare-earth (R) and transition-metal ( Co, Fe, Ni) based magnetic intermetallic compounds (IMC) have several key properties. These properties are divided into two categories: the intrinsic properties and the extrinsic properties. The intrinsic properties are the saturation magnetization (), the Curie temperature (), and the magnetocrystalline anisotropy (). For the herein studied IMCs, these properties are determined by the crystallographic structure and the chemical composition, whereas the extrinsic properties are the coercivity and the remanent magnetization , which are mainly a function of the microstructure.
The IMCs’ magnetic properties determine their potential application. Intermetallic compounds of the R–T type are formed with all rare-earths (R), except lanthanum for Fe. These compounds are characterized by a rather low Curie temperature (), which limits their field of application [1,2]. As generally observed for T-rich compounds, the low value of this temperature is attributed to T–T distances that are too short, particularly for T atoms that occupy the positions of the T–T dumbbells. For short distances between the T atoms, antiferromagnetic interactions occur instead of ferromagnetic interactions. As a result, considerable magnetic energy is stored, which leads to the lowering of the values.
In addition, the magnetocaloric effect, around the Curie temperature, in some R–T intermetallic compounds is promising and has been actively studied in recent years [3,4,5].
The magnetocrystalline anisotropy of these compounds is governed by the combined effects of the anisotropy of the rare earth and transition metal atoms. In binary compounds, the rare earth anisotropy is very small at room temperature even though the rare earth sub-lattice has a uniaxial contribution to the anisotropy [6]. It is not sufficient to counteract the anisotropy of the transition metal sub-lattice at room temperature, which favors planar anisotropy.
In order to improve the magnetic properties, partial substitutions of the transition metal must be made and light elements, such as hydrogen, nitrogen or carbon, can be inserted in interstitial positions of the unit cell. The increase in and the change in anisotropy from planar to uniaxial opens the way for the use of these compounds in the field of permanent magnets or high-density magnetic recording. However, in addition to high-performance intrinsic properties, it is necessary to optimize the extrinsic properties (coercivity , remanent magnetization ) by building a suitable microstructure corresponding to the envisaged applications. The microstructure must allow reaching the highest possible coercivity and remanent induction and a magnetization loop close to a rectangular one. The achievement of each of these objectives is facilitated by the existence of a granular microstructure [2,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36].
The IMC can be magnetically hard, semi-hard, or soft. Hard intermetallics are characterized by their large hysteresis. They are used as permanent magnets. Semi-hard ones are used for high-density magnetic recording, while soft ones with a very small hysteresis are utilized in electromagnetic machines [37,38].
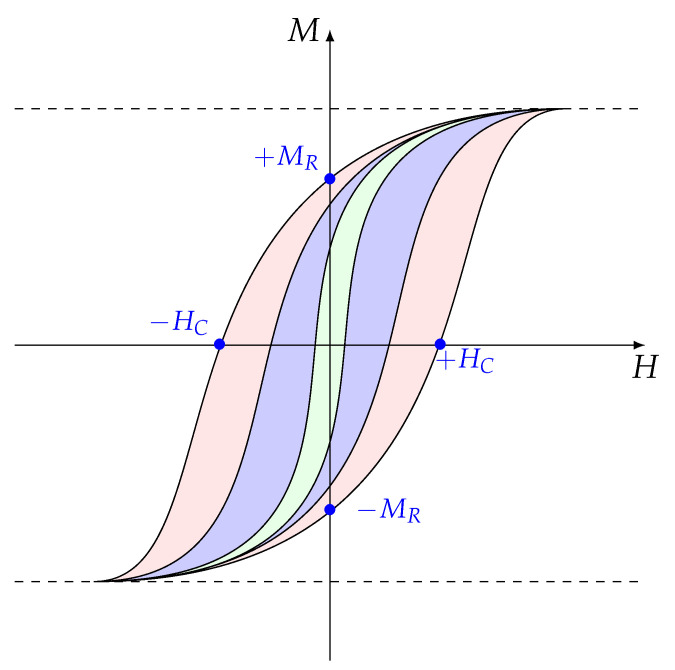
Figure 1 shows a simple approach to distinguish a hysteresis loop from a soft, semihard, or hard magnets, based on the coercivity alone. A very wide loop has a high coercivity, while a narrow loop has a very low coercivity, and a semi-hard cycle has an intermediate coercivity. However, Coey has recently shown that we can define a coefficient, called hardness parameter , that determines more precisely the difference between these three categories of magnetic materials [38]. , where is the anisotropy constant, is the saturation magnetization, and the vacuum permeability. For the magnet is soft, for the magnet is hard, and semihard magnets exhibit .
Figure 1.
Hysteresis loops for hard (light red), semihard (light blue), and soft (light green) magnets. M the magnetization, H the applied magnetic field, remanent magnetization, and the coercivity.
Recently, Kovacs et al. [39] have clearly shown that one cannot expect a coercive field greater than 1 T in most rare-earth-free magnets. For this reason, the IMCs presented in this review are exclusively based on rare-earths and, more specifically, based on CaCu-type structure.
To enhance our understanding of R-T intermetallics for magnetic applications, we gather and discuss, in this review paper, the main achievements made in this field up to now. In particular, the influence of the structure and composition on the intrinsic magnetic properties will be discussed, as well as the effect of the synthesis methods on the extrinsic magnetic properties. A comparison between electronic properties determined by DFT and hyperfine parameters measured by Mössbauer spectrometry will also be shown.
2. Overview of Synthesis Methods for Improved Magnetic Properties
2.1. Methods for Synthesis of Intermetallic Compounds
Conventional techniques for the synthesis of intermetallic compounds consist of the arc or induction melting of pure elements with subsequent annealing. However, in material science, it is often observed that the synthesis method has a significant influence on the compound’s properties. For the herein discussed compounds, it especially affects the microstructure but also the crystal structure, both of which influence the magnetic properties, as explained in the Introduction. Therefore, the choice of the synthesis method is a non-negligible key parameter.
In the example of R–T intermetallic compounds, it is often observed that conventional melting methods lead to polycrystalline alloys [40], whereas other techniques such as melt-spinning result in nanocrystalline alloys [41,42]. High-energy ball milling (HEBM) followed by annealing is another possible technique for the production of nanocrystalline alloys and it is well suited to the case of alloys based on rare-earth atoms, extremely volatile elements, because the reaction takes place below their melting temperature [43,44,45,46,47,48]. The annealing times of the powders can be very short, due to the their high reactivity of the nanometric crystallites obtained after HEBM. Moreover, this technique has the advantage of leading to large and homogeneous quantities of materials with reproducible characteristics. For these reasons, our group have chosen to produce R–T–M (T = Fe, Co, and M = Si, Al, Ga, Mo, Zr, Cr, Ti, V, …) alloys by HEBM followed by annealing.
The powders of R, T, and M, are co-milled in a FRITSCH P7 planetary mill in hermetically sealed jars under a high purity argon atmosphere. The milling is performed in two steps: low energy grinding for half an hour followed by a HEBM for 5 h [44]. The obtained nanocrystalline powders are annealed for 30 min in sealed silica ampoules under a secondary vacuum. The annealing was performed at temperatures between 700 and 1100 C depending on the desired phase, the out-of-equilibrium phase or the equilibrium one. As an example, for the equilibrium SmFe phase the chosen temperature is 1050 C, and to obtain the out-of-equilibrium SmFe phase, the annealing temperature is 700 C.
2.2. Methods for Insertion of Light Elements in the Intermetallics
As mentioned in the Introduction, the insertion of light elements (i.e., H, N, C) in the crystal lattice is crucial for the optimization of the intrinsic magnetic properties.
Coey and Sun [8] introduced nitrogen into SmFe by heating ground powder in 1 bar of N gas. After HEBM, S. V. Veselova et al. performed nitrogenation heat-treating the milled powder with a pressure equal to 40 atm at 450 C for 24 h in the pure nitrogen atmosphere. Samples were nitrogenated with 2.4 nitrogen atoms per formula unit [49].
Phejar et al. have successfully prepared La(Fe,Si)H hydrides by solid/gas reaction with a Sievert apparatus. The powder was introduced into a container, and then plugged to the hydrogenation apparatus. The sample was then submitted to a hydrogen pressure [44].
Unlike hydrides and nitrides, which were obtained exclusively by solid-gas reaction, carbides were elaborated by different methods:
-
(i)
conventional fusion of appropriate quantities of samarium, iron, and gallium with a Fe-C pre-alloy under argon atmosphere with an excess of samarium [50,51];
-
(ii)
a solid-gas reaction of the Sm(Fe,M) alloy (obtained by conventional fusion) with a gaseous hydrocarbon [52,53];
-
(iii)
high-energy ball milling from metallic elements, and reaction with a gaseous hydrocarbon [54].
Compared to nitrides and hydrides, carbides exhibit a greater thermal stability [55,56]. The insertion of the carbon in the elementary unit cell is achieved by a carbonation technique which involves a solid-solid type reaction [57,58,59]. The starting powders, Sm(Fe,M), are finely ground, sieved (grain size less than 32 m) and carefully mixed with the anthracene powder (CH) under high purity argon atmosphere. This technique consists in reacting the powder of SmFe compounds with anthracene, also in powder form, in stoichiometric proportion. Each mixture is annealed, in a sealed silica ampoule under a secondary vacuum, for 24 h. The anthracene decomposes releasing hydrogen gas which is fixed by small pieces of magnesium previously placed in the ampoule and separated from the powder by silica wool. At the same time, the temperature was chosen so as not to modify the microstructure of the initial non-carbide alloys [44]. The carbon atoms, thus liberated, then diffuse in the compound according to the reaction:
3. Structure Analysis
A large number of rare earth-transition metal-based intermetallic alloys, whether equilibrium or non-equilibrium alloys are derived from the CaCu-type structure of space group , for example, SmCo compound (Table 1). This structure is characterized by a crystallographic site () for the rare earth atom at position (0,0,0) and two distinct sites for the transition metal atoms () at position () and () at position (). The structure is shown in Figure 2. Over-stoichiometric cobalt equilibrium compounds of the RCo phase have been studied previously. This results in a slight modification of the lattice due to the presence of cobalt atoms substituted for rare-earth atoms [60]. The general formula of these compounds becomes Co[29,61,62], where a fraction s of the rare earth atoms is randomly replaced by pairs of Co atoms (dumbbell) parallel to the c axis. The deviation from the 1/5 stoichiometry strongly influences the magnetic properties of these compounds. For a higher stoichiometry deviation, (), the structure has been described as TbCu [63,64,65,66].
Table 1.
Atom Wyckoff positions, number of atoms in hexagonal structure. , , and correspond to CaCu, ThZn, and ThMn structure, respectively.
| Atomic | Occup. | |||||
|---|---|---|---|---|---|---|
| Position | CaCu | 2/17 | 1/12 | |||
| R() 0,0,0 | 1 | 0.97 | 0.66 | 0.5 | ||
| T() | 2 | 2 | 1.92 | 0 | 0 | 0 |
| T() | 6s | 0 | 0.18 | 2 | 2 | 2 |
| T() | 3 | 3 | 3 | 3 | 3 | 3 |
| T() | 2s | 0 | 0.06 | 0.66 | 2s | 1 |
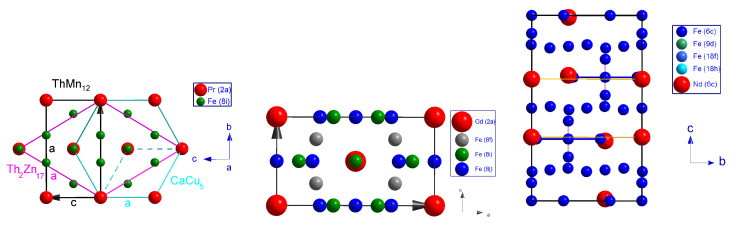
Figure 2.
(Left) Schematic representation of the relationship between CaCu (along [001] axis) ThZn (along [001] axis) and ThMn (along [010] axis) structures, (Center) illustration of atomic arrangements in GdFeCr crystal structure along [010] axis, and (Right) the rhombohedral crystal structure of NdFe along [100] axis.
For specific values of s, the substitution becomes ordered and gives rise to derived crystal structures, among which the well-known equilibrium structures ThMn (), ThNi, and ThZn (). For the latter, one R atom out of three is substituted in an ordered manner by an Fe–Fe pair. Figure 2 shows the relationship between CaCu, ThMn and ThZn structures. In this case, the precursor phase belongs to the space group. For the Sm–Fe binary system, the SmFe phase does not exist and the stoichiometry of the SmFe phase precursor has been described as SmFe[23,29] and, very recently, using synchrotron resonant diffraction (SOLEIL), the stoichiometry of this phase has been definitely found as SmFe[62] whereas it was considered in previous publications as TbCu [63,64,65,66,67,68,69,70,71,72].
Moreover, D. B. de Mooij and K. H. J. Buschow have demonstrated [73] that the RFe binary compound cannot exist. Therefore, a third element M (M = Cr, Al, Ti, Mo, Si, W, or V) was required to stabilize this phase by forming a ternary RFe.
The TbCu designation (phase that can exist) attributed to the SmFe [65,67,72] (phase that cannot exist [73]) adds an additional difficulty to understand the structure of these non-equilibrium phases.
A recent study [62] had the objective to find the structural relation between 2/17 and the non-equilibrium phase 1/9. On the other hand, this study removes the ambiguity that has often existed for the relationship between the hexagonal TbCu phase and the hexagonal phase precursor of the rhombohedral phase.
3.1. ThZn-Type Structure
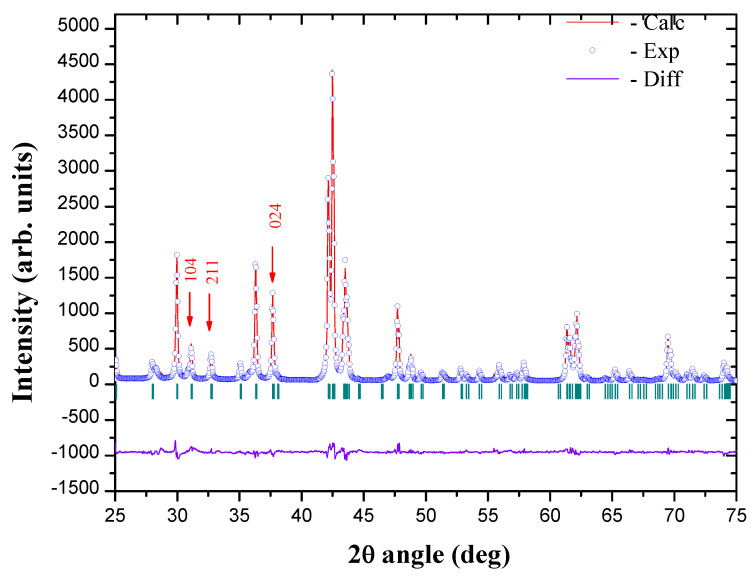
The angular positions of the main diffraction peaks, SmFe, show a crystallographic structure characteristic of the 2/17 phase of space group (Figure 3). The refinement of the X-ray diffraction patterns (XRD) of SmFe, is performed by the Rietveld method with the FULLPROF calculation code. This method also allows to determine the size of self-consistent diffraction domains. In the case of Sm(Fe,M) compounds, the Rietveld refinement has been performed with the iron distributed on the four sites: 6c, 9d, 18f, 18h and the rare earth in site 6c (Table 2). These different crystallographic sites of the 2/17 rhombohedral phase are illustrated in Figure 2.
Figure 3.
Rietveld refinement of XRD for nanocrystalline SmFeGa intermetallic.
Table 2.
Atom and Wyckoff positions for the Fe rhombohedral structure.
| Atom | Wyckoff Position |
|---|---|
| Sm | (0,0,z) |
| Fe1 | (0,0,z) |
| Fe2 | (,0,) |
| Fe3 | (x,0,0) |
| Fe4 | (x,x,z) |
As for the site occupied by M atoms, from the Mössbauer spectra explained later, we clearly exclude the occupation of the 6c sites (external shoulder on the positive velocity side, characteristic of the total occupation of the c site by iron). Site being the smallest among the four sites , , and , was also excluded considering the high radius of M = Ga compared to Fe ( = 1.26 Å, = 1.41 Å) [74]. In these conditions there remain two options: occupation of the site or . We clearly see a deterioration of this factor when gallium gradually occupies the 18f site. We therefore conclude that gallium is localized at 18h, which is in good agreement with the crystallographic results obtained by Teresiak et al. [24]. The structural results of XRD Rietveld refinement are presented for all compositions in Table 3.
Table 3.
XRD analysis results obtained by Rietveld method on the SmFeM (M = Si, Ga, Co, Zr, Cr, Mo) and (x = 0, 0.5, 1, 1.5, 2) alloys [25,26,27,28,29,30,62,75,76].
| Alloy | a(Å) | c(Å) | Sm | Fe | V(Å) | R | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| SmFe | 8.558 | 12.441 | 0.291 | 0.501 | 0.342 | 0.094 | 0.156 | 789 | 5.05 | 1.30 |
| SmFeSi | 8.547 | 12.437 | 0.291 | 0.501 | 0.341 | 0.095 | 0.156 | 787 | 4.62 | 2.10 |
| SmFeSi | 8.542 | 12.436 | 0.291 | 0.501 | 0.342 | 0.096 | 0.157 | 786 | 6.01 | 1.80 |
| SmFeSi | 8.527 | 12.428 | 0.291 | 0.501 | 0.342 | 0.095 | 0.157 | 782 | 4.40 | 2.40 |
| SmFeSi | 8.520 | 12.428 | 0.292 | 0.501 | 0.342 | 0.096 | 0.157 | 781 | 5.69 | 2.20 |
| SmFeGa | 8.567 | 12.457 | 0.289 | 0.502 | 0.343 | 0.096 | 0.156 | 791 | 4.25 | 1.40 |
| SmFeGa | 8.582 | 12.483 | 0.290 | 0.502 | 0.342 | 0.094 | 0.156 | 796 | 6.11 | 2.50 |
| SmFeGa | 8.598 | 12.510 | 0.290 | 0.502 | 0.342 | 0.097 | 0.156 | 801 | 5.63 | 2.70 |
| SmFeGa | 8.619 | 12.540 | 0.291 | 0.502 | 0.342 | 0.097 | 0.156 | 807 | 5.55 | 2.50 |
| SmFeCo | 8.550 | 12.450 | 0.289 | 0.501 | 0.343 | 0.096 | 0.156 | 788 | 4.56 | 1.61 |
| SmFeCo | 8.548 | 12.456 | 0.290 | 0.502 | 0.343 | 0.096 | 0.157 | 788 | 4.73 | 1.58 |
| SmFeCo | 8.545 | 12.463 | 0.291 | 0.501 | 0.343 | 0.096 | 0.156 | 788 | 4.05 | 1.40 |
| SmFeCo | 8.544 | 12.467 | 0.291 | 0.502 | 0.343 | 0.095 | 0.156 | 788 | 3.58 | 1.76 |
| SmFeZr | 8.541 | 12.449 | 0.289 | 0.502 | 0.343 | 0.096 | 0.157 | 786 | 4.53 | 1.34 |
| SmFeZr | 8.532 | 12.465 | 0.290 | 0.502 | 0.343 | 0.096 | 0.157 | 786 | 5.10 | 1.42 |
| SmFeZr | 8.527 | 12.457 | 0.289 | 0.501 | 0.344 | 0.096 | 0.157 | 784 | 4.33 | 1.52 |
| SmFeCr | 8.549 | 12.445 | 0.289 | 0.502 | 0.343 | 0.096 | 0.157 | 787 | 6.91 | 1.26 |
| SmFeCr | 8.542 | 12.450 | 0.290 | 0.502 | 0.343 | 0.096 | 0.157 | 787 | 5.75 | 1.26 |
| SmFeCr | 8.535 | 12.442 | 0.289 | 0.501 | 0.344 | 0.096 | 0.157 | 785 | 4.06 | 1.57 |
| SmFeCr | 8.533 | 12.442 | 0.291 | 0.501 | 0.343 | 0.092 | 0.156 | 784 | 4.49 | 1.16 |
| SmFeMo | 8.558 | 12.472 | 0.289 | 0.502 | 0.342 | 0.096 | 0.157 | 791 | 4.61 | 1.10 |
The unit cell parameters, a and c, as well as the volume increase with x in a linear way. This increase is due to the substitution of iron atoms by M, an element of greater atomic radius than iron. The size of the self-consistent diffraction domains is 60 nm for x = 0.5. Moreover, the Rietveld analysis allowed us to quantify the mass percentages of the phases present in the processed samples.
3.2. ThMn-Type Structure
RFe binary systems do not exist for any rare earth. Indeed, the atomic radius of iron is smaller than that of manganese in ThMn, in addition, according to the Pauling classification of elements, iron has eight valence electrons against seven for manganese with a difference of electronegativity higher for iron compared to that with manganese. This induces a high electron density for the site making the alloy unstable.
The reasons why this structure is unstable are therefore: interatomic distances that are too small and a very high electron density provided by iron. However, it is possible to stabilize the 1/12 structure by partially substituting iron with a third element of larger atomic radius; thus a metal element or with a p-block element, this leads us to consider the chemical elements that are located to the left of iron in the periodic table.
Some authors report the obtaining of the SmFe phase in thin films by non-equilibrium methods such as sputtering [77,78]. However, the obtained XRD pattern shows a simplified line system compared to that corresponding to the 1/12 phase. The explanation given by these authors is the strong texturing of the film along direction (002) obtained along the c axis. A refinement by the least square method was carried out, but adopting three different structures which all derive from the structure CaCu structure; the ThMn, the ThZn (2/17) and also the disordered hexagonal structure TbCu. The obtained lattice parameters are far from those related to the 2/17 phase. The observation of diffraction patterns does not clarify the nature of the phase, which remains ambiguous, since no indexation is provided but only a suggestion that the phase 1/12 is the closest.
The 1/12 phase could be stabilized by several elements such as Ti [25,79,80,81,82,83,84], Si [80], Mo [79,80,85], W [73,79,80], Cr [79,80,86], V [79,83,87], Al [80]. The solubility and the range of existence of the RFeM phase vary from one substituent to another. The interest of these phases lies in their Curie temperature which is relatively high compared to that of the 2/17 alloys. It has been shown [88], by ab-initio calculation, that the solubility of Mo is higher than that of Ti, which is in agreement with experiment [89]. When the M (M = Cr, V, Ti, Mo) atoms substitute the Fe atoms in the site, the cohesive energy decreases in a more significant way than when the M atoms go into the Fe or sites. Therefore, the substituents M preferentially occupy the site. The rare earth occupies the (0,0,0) site. As for the elements Fe and M, they are distributed on three crystallographic sites: (0.36,0,0), (0.27,,0) and () see Figure 2. The atomic positions and the symmetry of the different sites are presented in the Table 4.
Table 4.
Atom and Wyckoff positions for the RFeTi tetragonal structure.
| Atom | Symmetry | Wyckoff Position |
|---|---|---|
| R | (0,0,0) | |
| Fe1 | (,,) | |
| Fe2 | (x,0,0) | |
| Fe3 | (x,,0) |
The works relating to 1:12 phases based on praseodymium and transition metals (Fe, Ti, Mo, V) [90,91] report on the difficulties related to their elaboration. Indeed, the nature of the phases obtained and their relative abundances in the sample are closely linked to the annealing temperature. Thus the PrFeTi phase () is obtained mainly in a very small range of annealing temperatures (80 K) between 1303 K and 1383 K. Below 1173 K the majority phase is the 2:17 phase. On the other hand, above 1383 K a peritectic decomposition leads to the precipitation of (Fe,Ti) which considerably reduces the abundance of the 1:12 phase.
The ThMn structure derives from the CaCu structure and can be schematized by the relation:
Half of the rare earth atoms of the 1/5 structure are replaced by a T–T pair at position in the 1/12 structure. The unit cell parameters of the two related structures are described by the following expressions (Figure 2):
The refinement of the XRD patterns allowed us to derive the size of the self-consistent diffraction domains and to quantify the mass fractions of the minority phases present. Structural study of the unit cell parameters were systematically measured with an Si standard. The refinement of the diffraction patterns was performed by considering the iron atoms statistically distributed on the different sites , and and considering the substituent M atoms on the site . The unit cell parameters are given in Table 5. Note also that the ratio is not far from the theoretical value of the tetragonal structure.
Table 5.
XRD analysis results obtained by Rietveld method on the RFeM (M = Si, Ti, Cr, V, Cr, Mo) and (x = 0, 0.5, 1, 1.5, 2) alloys [25,26,27,28,29,30,62,75,76,82,84].
| Alloy | a(Å) | c(Å) | Ref. |
|---|---|---|---|
| YFeTi | 8.503(3) | 4.789(4) | [84] |
| SmFeTi | 8.555(3) | 4.794(3) | [25] |
| YFeMo | 8.527(2) | 4.784(2) | [92] |
| CeFeMo | 8.535(1) | 4.769(2) | [92] |
| PrFeMo | 8.600(2) | 4.785(3) | [92] |
| NdFeMo | 8.584(1) | 4.780(2) | [92] |
| SmFeMo | 8.565(2) | 4.786(2) | [29] |
| GdFeMo | 8.553(2) | 4.795(1) | [92] |
| TbFeMo | 8.562(2) | 4.782(1) | [92] |
| DyFeMo | 8.523(1) | 4.782(1) | [92] |
| HoFeMo | 8.518(3) | 4.786(3) | [92] |
| ErFeMo | 8.515(2) | 4.783(1) | [92] |
| LuFeMo | 8.483(3) | 4.770(2) | [92] |
| SmFeV | 8.528(6) | 4.770(3) | [83] |
| PrFeTi | 8.594(2) | 4.789(2) | [84] |
| NdFeTi | 8.579(3) | 4.795(2) | [83] |
| GdFeTi | 8.533(3) | 4.789(3) | [93] |
| GdFeCr | 8.480(6) | 4.755(3) | [86] |
E. Tomey et al. [92] found that, for the RFeMo series of compounds, where R goes from Pr to Lu, the lattice parameter a decreases as a function of R while the c parameter remains quasi-constant. The parameter a is governed by the atomic radius of the rare-earth.
4. Intrinsic Magnetic Properties
In this section, we do not present exclusively the IMCs prepared by HEBM, since the intrinsic properties are independent of the microstructure, and therefore of the synthesis method.
4.1. Curie Temperature
For nanocrystalline intermetallics, the Curie temperature, which represents the ferro-paramagnetic transition, must be relatively high for a permanent magnet or for high density magnetic recording applications. Generally, there are two strategies to increase , either substituting the iron by another metal, or inserting a light element (C, H, N …) in the unit cell of the intermetallic compound.
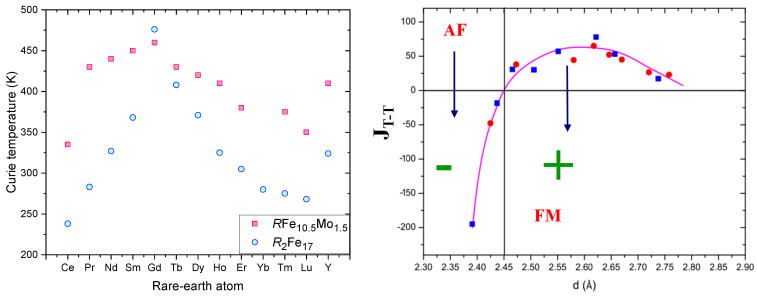
Figure 4 (Left) shows the dependence of Curie temperature on the rare-earth atom for the RFe structure. This behavior is due mainly to the variation of the de Gennes factors of the different rare-earth atoms. The Curie temperature variation for the different rare-earth atom resembles that of the magnetic hyperfine field as we will see later.
Figure 4.
(Left) Curie temperatures for different rare-earth atoms, for Fe and RFeMo[28,30,75,96,97,98]. (Right) Exchange interaction vs. distances between transition metal atoms (T–T) for Sm. For interatomic T–T distances less than 2.45 Å the exchange interaction () is negative, while is positive in the opposite case [94].
The Curie temperatures of SmFe compounds were measured on sealed ampoule samples under the secondary vacuum with an applied field of 1000 Oe. was determined by the minima in curves, derived from the magnetization measurements.
In RFe intermetallic compounds, the Curie temperature () is low, around room temperature (418 K for SmFe) [23]. This is mainly due to the short Fe–Fe inter-atomic distances of the dumbbells ( for the SmFe structure [94] and for SmFe [62]), where the Fe atoms are anti-ferromagnetically coupled. This distance attached to the dumbbell sites, less than 2.45 Å, leads to negative Fe–Fe interactions [7,95] (Figure 4 (Right)).
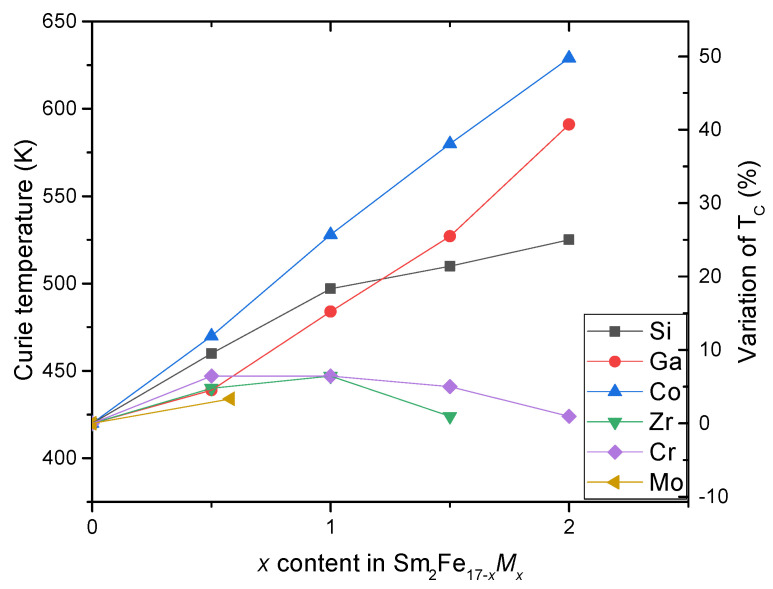
With the substitution of M atoms in the compounds SmFe, the Curie temperature increases monotonically with x, then decreases (Figure 5, Table 6).
Figure 5.
Curie temperature and variation of SmFe for M = Si, Ga, Co, Zr, Cr, Mo [28,30,75,96,97,98].
Table 6.
Curie temperature of SmFeM (M = Si, Ga, Co, Zr, Cr, Mo) and (x = 0, 0.5, 1, 1.5, 2) alloys.
The Curie temperature, for rare-earth-transition-metal compounds, is governed, in general, by three types of interactions:
– () exchange interaction between the magnetic moments of the transition-metal atom sublattice;
–() exchange between – magnetic moments of Sm lattice atoms;
– () exchange between the two – sublattices.
The – exchange interaction can be neglected since it is the weakest of the three interactions. We can consider that the only contribution to the Curie temperature is due to the interaction between the magnetic moments of the iron sublattice (–), if in addition we can also neglect the interactions between the two sublattices (–) by considering an R-Fe system with non-magnetic R atom.
In compounds with a rhombohedral structure, the Fe()–Fe() interactions are negative. This is also the case for Fe()–Fe() (weakly negative), while the other Fe–Fe interactions are positive. It was found, for the SmFe compounds, that the interaction augments up to x = 3. It has also been reported that the coupling constant of the sublattices is very small compared to that of and it is nearly unrelated to the M content. This shows that the Curie temperature is mostly monitored by . The combination of the two effects, magnetovolume and electronic, can explain the evolution of the Curie temperature. The substitution of non-magnetic elements, such as silicon and aluminum on iron sites in RFe compounds, gives a variation of similar to M substitution (Figure 5).
4.2. Hyperfine Parameters
Mössbauer spectrometry is a particularly recommended technique for samarium-based alloys with an absorption coefficient such that neutron diffraction studies remain very difficult to perform. It allows to confirm the structural results and to determine the hyperfine parameters.
The Mössbauer spectra analysis is based on an adapted and precise simulation method which takes into account the isomer shift (). This quantity, which accounts for the density of s electrons at the nucleus, is an essential data to understand the effect of the insertion of the light element.
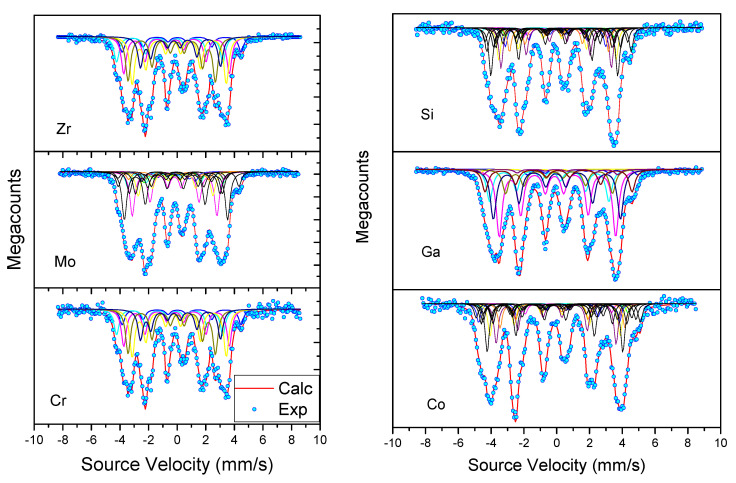
One may be tempted to use a large number of parameters to get a satisfactory simulation. However, the selected solution for the refinement of the Mössbauer spectra must match a physical model supported by several experimental techniques or it could be based on relevant theoretical approaches. The credibility of the suggested model for the fitting of the spectra must be proved by the uniform evolution of the set of hyperfine parameters with a line width slightly higher than the value of 0.25 mm/s, corresponding to the experimental width of the reference –Fe (Figure 6, Figure 7 and Figure 8).
Figure 6.
The room temperature Mössbauer spectra of SmFeM (M = Zr, Mo, Cr, Si, Ga, Co) [28,30,75,96,97,98].
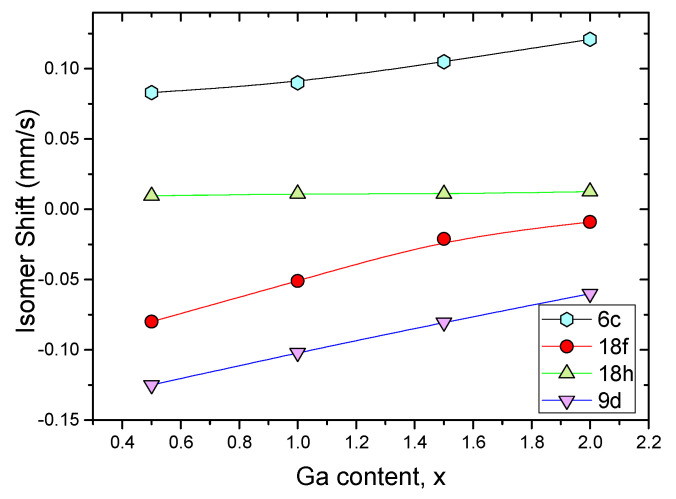
Figure 7.
Isomer shift evolution vs substituted Ga atom composition for SmFeGa.
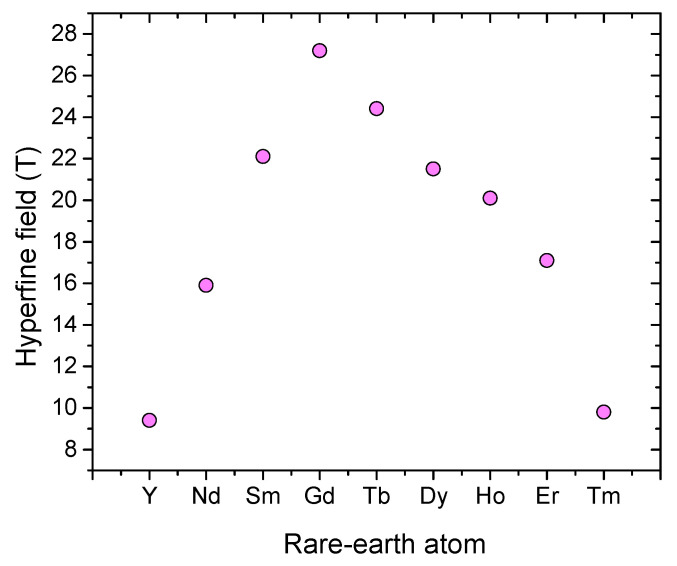
Figure 8.
Hyperfine field for different RFe [38,42,99,100,101,102,103,104].
In addition, the line intensities of the sextuplets were considered in the ratio 3:2:1:1:2:3, assuming a randomly oriented powder, in good agreement with the absence of texture observed on the XRD patterns. A line-width equal to 0.27 mm/s was generally used for each individual sextuplet of the rhombohedral ThZn- and the tetragonal ThMn-type structure. Furthermore, we supposed that the Lamb–Mössbauer absorption factor is the same for all non-equivalent crystallographic sites.
The good resolution of the spectra combined with the crystallographic studies allows a detailed analysis. The refinement of the spectra is then based, on the one hand, on a counting approach of the various magnetic subsites, and on the other hand, on the attribution to these sites of the hyperfine parameters resulting from a good simulation of the spectra for a defined and fixed number of observable sites. Moreover, the evolution of the hyperfine parameters must be coherent and monotonous as a function of the substituted atom rate (Table 7).
Table 7.
Hyperfine parameters of Fe.
The most rigorous method to assign the different sextuplets to the non-equivalent crystallographic sites (, , and for ThZn phase, and , , and for ThMn phase) takes into account the hyperfine fields, and the Wigner–Seitz cell volumes (WSC). The correlation between the Wigner-Seitz cell volumes and the isomer shift has been established [21,25,82,84,86]. The larger the isomer shift, the larger WSC volume. In addition, the larger the number of iron neighbors of a resonant iron atom, the larger the hyperfine field.
The general approach used for the refinement of the spectra of the different structures will take into account, on the one hand, the correlation between the WSC volumes and , and on the other hand, the exact calculation of the abundances of the different sub-sites by means of a binomial distribution law of the substituted atoms.
Mössbauer spectra of the Sm(Fe,M) samples (M = Ga, Zr, Si, Mo, Cr and Co) recorded at room temperature are shown in Figure 6. These spectra are very complex and magnetically ordered. They result from the convolution of many subspectra; this is due to the existence of the four inequivalent Fe sites, disturbed by the substitution of Fe by the M atom at position. The isomer shift of sites slightly increases with the rate of M atoms, while that of the site remains constant within the limits of the experimental precision. This particular behavior of the confirms the position of the M atom in this specific site.
It should be noted that resulting from the sequence of Wigner-Seitz cell calculated volumes: reflect well the perturbations brought by the substitution of iron by the M atom, in perfect agreement with the nature of the different environments. Moreover, the evolution of the hyperfine magnetic fields brings an additional argument to the approach we have led.
Figure 8 shows the dependence of hyperfine field () on the rare-earth atom for RFe structure (Table 7). The change of the with different rare earth atoms resembles that of the Curie temperature (Figure 4).
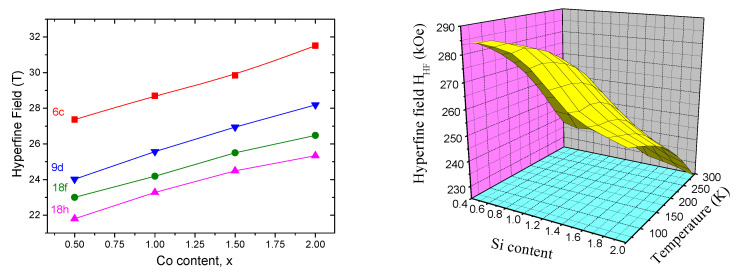
The refinement of the hyperfine fields is derived from the analysis of since the inequivalent iron site is defined by a set of hyperfine parameters and . It follows that . Moreover, strength of a given atom depends on the number of Fe neighbors: the larger the number of Fe neighbors, the higher . The hyperfine field analysis is in perfect agreement with this relationship, site with 13 iron neighbors is by far the largest. Sites and with 10 iron neighbors show average field values, while site with 9 neighbors is the smallest (Figure 9).
Figure 9.
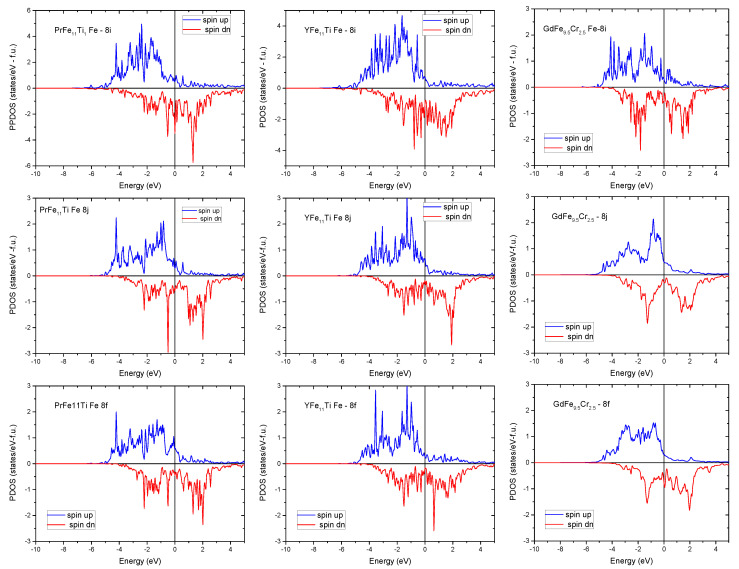
(Left) Hyperfine field evolution vs substituted Co atom composition for SmFeCo. (Right) The dependence of hyperfine field on Si content and temperature for SmFeSi.
Concerning the tetragonal ThMn-type structure several studies were devoted to RFeTi (R = Y, Pr, Nd, Sm, Gd) intermetallics [25,84,86,105,106,107]. The refined hyperfine field (), isomer shift (), and quadrupole interaction () for the studied intermetallics are presented in Table 8. For these compounds the following sequence for the hyperfine field was found , which is coherent with the number of nearest iron neighbors for each inequivalent crystallographic site.
Table 8.
Room temperature Mössbauer hyperfine parameters for RFeM: Hyperfine field (), isomer shift () and quadrupole interaction (). denotes the average of the hyperfine parameters.
| Fe | Fe | Fe | Ref. | ||
|---|---|---|---|---|---|
| YFeTi | [84] | ||||
| (T) | 26.8 | 22.7 | 20.1 | 23.2 | |
| (mm/s) | −0.09 | −0.12 | −0.17 | −0.13 | |
| (mm/s) | 0.08 | 0.07 | 0.04 | 0.06 | |
| PrFeTi | [84] | ||||
| (T) | 27.1 | 23.8 | 21.8 | 24.2 | |
| (mm/s) | −0.08 | −0.10 | −0.12 | −0.09 | |
| (mm/s) | 0.09 | 0.09 | 0.04 | 0.08 | |
| NdFeTi | [105] | ||||
| (T) | 32.6 | 29.6 | 25.2 | 28.1 | |
| (mm/s) | 0.01 | −0.02 | −0.15 | −0.09 | |
| (mm/s) | 0.03 | 0.10 | 0.02 | 0.08 | |
| SmFeTi | [25] | ||||
| (T) | 27.2 | 23.5 | 25.8 | 28.1 | |
| (mm/s) | 0.01 | −0.02 | −0.15 | −0.09 | |
| (mm/s) | 0.03 | 0.10 | 0.02 | 0.08 | |
| GdFeTi | [86] | ||||
| (T) | 26.9 | 25.1 | 23.9 | 25.1 | |
| (mm/s) | −0.06 | −0.11 | −0.13 | 0.14 | |
| (mm/s) | 0.05 | 0.04 | 0.04 | 0.04 |
4.3. DFT Calculation
The DFT calculation is very useful, not only to calculate the formation energy of intermetallic compounds, but also to determine the theoretical hyperfine field and finally to calculate the total and individual partial magnetic moment per crystallographic site. The objective of the theoretical calculations is to compare the formation energies of the compounds in order to be able to evaluate their stability, and to compare the theoretical and experimental magnetic moments deduced from the Mössbauer spectrometry.
Harashima et al. utilizing first-principal calculations have demonstrated that for any rare-earth R atom [108,109] the binary rhombohedral Fe with ThZn-type structure is more stable than the tetragonal RFe with ThMn-type structure. However, if the rare-earth R atom ( Nd or Sm) is partially replaced by Zr, Y or Dy, the difference between the formation energies of 2/17 and 1/12 is lowered.
The magnetic moments for the rhombohedral SmFe compound was calculated by Yamashita et al. [110] using ab initio approach. The results of these calculations give the following values of magnetic moments for the four inequivalent crystallographic sites: 2.67 , 2.49 , 2.39 , and 2.21 . These values are consistent with those found by Ogura et al. using first-principles electronic structure calculations [111] (Figure 10).
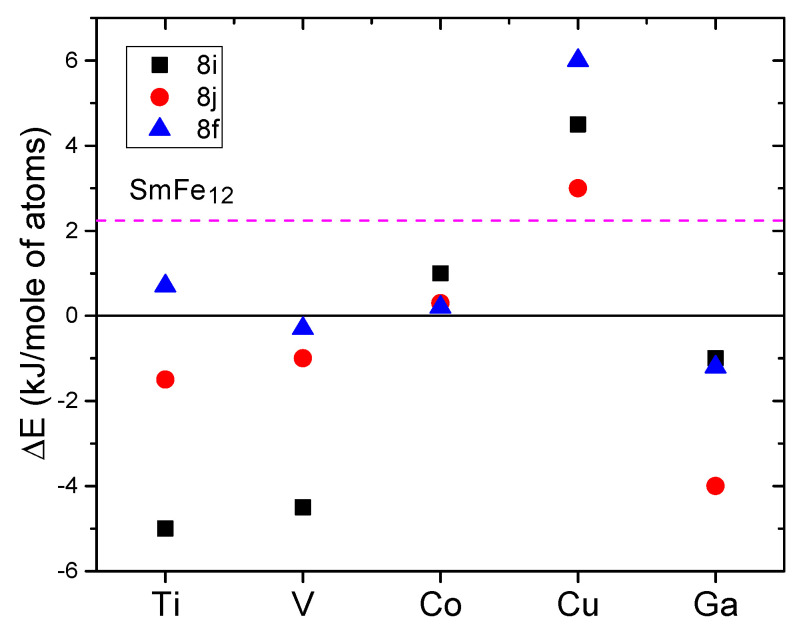
Figure 10.
Partial density of states for Fe-, Fe and Fe- calculated for (left) PrFeTi, (middle) YFeTi and (right) GdFeCr. The origin of the energy is located at Fermi energy (black vertical line).
For the tetragonal GdFeCr compound, the DFT calculation allows, among other things, to determine the site of Cr occupation in the space group. The total energy of GdFeCr has been calculated for the three possible substitution Cr sites. This calculation showed that the lowest total energy is consistent with the substitution of iron with chromium in the site (Table 9), indicating that Cr preferentially occupies this site [86]. This result is in agreement with Moze and Buschow’s study of the YFeCr system [112]. It id also in perfect agreement with the Rietveld refinement of the XRD patterns and with the fitting of the Mössbauer spectra of GdFeCr compounds.
Table 9.
Calculated energy E (Ry) of GdFeCr, YFeCr, YFeTi, and YFeV with Cr, Ti, and V atoms occupying different sites.
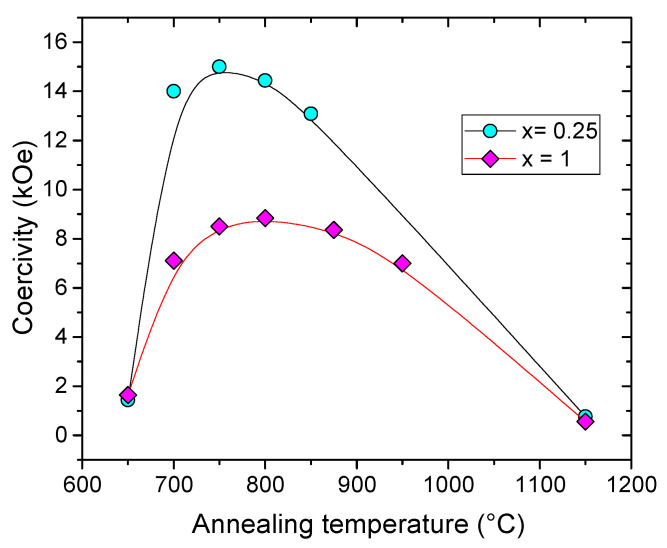
Using first-principle calculations, Dirba et al. [113] determined the formation energy and magnetic moments for the three inequivalent sites , and in the SmFe, for various M elements. The formation energy was calculated as follow:
They found that the substitution of Fe atoms by Ti, V, or Ga enhances the stability of the SmFeM compound (Figure 11), since the calculated formation energies for these elements was found lower than for Co, Cu atoms.
Figure 11.
Calculated formation energy for SmFe (M = Ti, V, Co, Cu, Ga) [113]. The magenta dashed line corresponds to formation energy of the hypothetical SmFe energy.
Using ab-initio calculations, Sikora et al. have determined the electronic structure for GdTbCo intermetallic compound. They have found that cobalt’s magnetic moments, estimated from X-ray photo-electron spectroscopy, are comparable with magnetic moment derived from DFT ab initio calculations [114]. In addition, they showed an anti-parallel alignment between R (R = Gd, Tb) and Co magnetic moments.
Moreover, we have compared the results of magnetic moments between those obtained by experimental measurements (Mössbauer Spectrometry) and those derived using theoretical ab initio DFT calculations for YFeTi, PrFeTi, and GdFeCr compounds. A good agreement have been obtained. These results are summarized in Table 10.
Table 10.
Comparison between magnetic moments, in /at., obtained by experimental measurements (Mössbauer Spectrometry) and by DFT calculations for YFeTi, PrFeTi, and GdFeCr [84,86].
| YFeTi | ||||
| Mössbauer | 1.98 | 1.77 | 1.56 | 1.77 |
| Calculated | 2.49 | 2.07 | 1.88 | 1.90 |
| PrFeTi | ||||
| Mössbauer | 2.00 | 1.84 | 1.69 | 1.82 |
| Calculated | 2.53 | 2.16 | 1.91 | 2.12 |
| GdFeCr | ||||
| Mössbauer | 2.10 | 2.04 | 1.98 | 2.03 |
| Calculated | 2.46 | 2.36 | 2.12 | 2.28 |
5. Extrinsic Magnetic Properties
In this section, we will show the link between microstructure and extrinsic magnetic properties. Before presenting an example of our work on the study of Sm(Fe,Si) carbides, we will summarize the most recent works that concern hard magnetic intermetallics prepared by HEBM.
Pal et al. [117] have found that NdFeB alloy, obtained by HEBM, exhibits high coercivity at room temperature, more than 12 kOe. They concluded that HEBM synthesis method produces effective and less costly as compared to other methods reported earlier. Using HEBM Zhong et al. showed that for the optimized microstructure of Nd(Fe,Co)B alloy the coercivity is about 10 kOe with a equal to 75 emu/g [118]. Nanoflakes of SmCo obtained by HEBM were mixed with Co nanowires in order to obtain SmCo/Co composites, the highest coercivity obtained is equal to 15 kOe [119]. These 3 examples demonstrate an important aspect: without modifying the structure and/or composition, the values for coercivity can be changed and optimized by adapting the synthesis method.
Through the example of SmFeSiC carbides, we will see some synthesis parameters that influence the coercivity and explain the reason. The coercive fields measured at room temperature for the nanocrystalline carbide SmFeSiC compounds () as a function of the annealing temperature of the HEBM samples before carbonation, shown in Figure 12. For C the hexagonal structure turns into rhombohedral one. At C, a maximum of coercive force of 15 kOe was obtained for SmFeSiC compound, while for SmFeSiC, which is described by the space group , the maximum of seems to move towards 800 C. The value of remains high, close to 13 kOe, for but decreases towards 8.5 kOe for . This evolution can be linked to the variation of the crystallographic unit cell volume. Indeed the volume augmentation under the effect of carbonation decreases with the silicon content. The relative increase in volume varies from 3.70% for to 5.05% for . This effect is, on the one hand, in agreement with the increase of the magnetic moment per iron atom, and on the other hand, it might correspond to a reduction of the magnetic anisotropy field with the increase of the silicon content.
Figure 12.
Room temperature coercivity vs annealing temperature for SmFeSiC.
The analysis of the coercivity suggests two different regimes depending on . A too low annealing temperature slows down the reaction in the solid state leading to the metastable Sm(Fe,Si)C phase responsible for the magnetic hardening. A higher annealing temperature reduces the number of defects in the phase. This results in an increase of , but on the other hand, the size of the diffraction domains increases which decreases .
High-resolution transmission electron microscopy (HRTEM) was used to study the morphology of these specific samples (Figure 13). Measurements of inter-reticular distances from fringe system processing offer the possibility to identify grains from their crystallographic parameters. For the SmFeSiC compound, annealed at C, the grain size is small around 10 nm and is equal to 1.5 kOe. For the same sample annealed at a higher temperature (1150 C), the grain size is around 40 nm and the corresponding coercive field is equal to 0.8 kOe.
Figure 13.
High-resolution Transmission Electron Microscopy (HRTEM) image for the best microstructure corresponding to domain size of 22 nm.
For the sample with the best coercive field, 15 kOe, the grain size is on the order of 22 nm in agreement with the Rietveld analysis. It appears that the grain boundaries connect neighboring grains without an inter-granular layer of measurable size, which favors the magnetic exchange coupling between grains. Moreover, a slight increase of the ratio equal to 0.6 is observed ( represents the remanent magnetization and the saturation magnetization). This could be explained by the exchange coupling between the grains of the main phase, rather than by the intermediary of the iron grains found in small quantities by crystallographic analysis and Mössbauer spectroscopy. Indeed the same tendency is observed for the ratio, for the other compositions which do not contain free iron. The high coercivity of these compounds obtained by HEBM followed by annealing results from the non-equilibrium precursor phase Sm(Fe,Si)C rather than from the equilibrium compounds Sm(Fe,Si)C.
In addition, nanocrystalline compounds PrCo, PrCo and PrCo, constituted of intergrowths of AB-AB stacking blocks, were studied [120,121,122]. Thanks to the optimization of their microstructures we obtained the following coercivities 12 kOe, 18 kOe, 15 kOe for PrCo, PrCo, PrCo, respectively. More recently, Bajorek et al. have shown a very significant potential for low-cost synthesis method of nanocrystalline hard magnetic SmCo compound [48]. They used an innovative wet milling method that allowed them to optimize the microstructure for better extrinsic magnetic properties [43,45,46,47,48].
6. Conclusions
In this review, we have presented the structural and magnetic properties of some R-Fe-M-X intermetallics obtained by high energy milling. The combined effect of chemical substitution and light element insertion has been highlighted to optimize the intrinsic magnetic properties. The evolution of the Curie temperature is interpreted in terms of electronic effect and/or magnetovolume effect. The results of the magnetic measurements have been compared to the theoretical ab initio calculations and to the magnetic moments deduced from the hyperfine field measured by Mössbauer spectrometry. Finally, for the nanocrystalline hard magnetic materials, we showed the relationship between the extrinsic magnetic properties and the optimized microstructure of the nanocrystalline intermetallics.
Acknowledgments
The author thanks V. Charbonnier for her help.
Abbreviations
The following abbreviations are used in this manuscript:
| DFT | Density Functional Theory |
| Isomer shift | |
| HEBM | High-energy ball milling |
| HRTEM | High-resolution transmission electron microscopy |
| Hyperfine field | |
| Coercivity | |
| Remanent magnetization | |
| Saturation magnetization | |
| R | Rare-earth |
| Annealing temperature | |
| Curie temperature | |
| WSC | Wigner-Seitz cell |
| XRD | X-ray Diffraction |
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data available on request due to restrictions e.g., privacy or ethical.
Conflicts of Interest
The author declares no conflict of interest.
Footnotes
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Buschow K.H.J. New developments in hard magnetic materials. Rep. Prog. Phys. 1991;54:1123. doi: 10.1088/0034-4885/54/9/001. [DOI] [Google Scholar]
- 2.Burzo E. Exchange Interactions and Transition Metal Moments in Rare-Earth Compounds. J. Synchrotron Investig. 2018;12:431–435. doi: 10.1134/S1027451018030072. [DOI] [Google Scholar]
- 3.Zhang Y. Review of the structural, magnetic and magnetocaloric properties in ternary rare earth RE2T2X type intermetallic compounds. J. Alloys Compd. 2019;787:1173–1186. doi: 10.1016/j.jallcom.2019.02.175. [DOI] [Google Scholar]
- 4.Wang Y., Guo D., Wu B., Geng S., Zhang Y. Magnetocaloric effect and refrigeration performance in RE60Co20Ni20 (RE = Ho and Er) amorphous ribbons. J. Magn. Magn. Mater. 2020;498:166179. doi: 10.1016/j.jmmm.2019.166179. [DOI] [Google Scholar]
- 5.Li L., Yan M. Recent progresses in exploring the rare earth based intermetallic compounds for cryogenic magnetic refrigeration. J. Alloys Compd. 2020;823:153810. doi: 10.1016/j.jallcom.2020.153810. [DOI] [Google Scholar]
- 6.Yin L., Parker D.S. Effect of atom substitutions on the magnetic properties in Ce2Fe17: Toward permanent magnet applications. J. Appl. Phys. 2021;129:103902. doi: 10.1063/5.0042475. [DOI] [Google Scholar]
- 7.Givord D., Lemaire R. Magnetic Tranition and Anomalous Thermal-Expansion in R2Fe17 Compounds. IEEE Trans. Magn. 1974;MAG-10:109. doi: 10.1109/TMAG.1974.1058311. [DOI] [Google Scholar]
- 8.Coey J.M.D., Sun H. Improved Magnetic Properties by Treatment of Iron-Based Rare-Earth Intermetallic Compounds in Ammonia. J. Magn. Magn. Mater. 1990;87:L251–L254. doi: 10.1016/0304-8853(90)90756-G. [DOI] [Google Scholar]
- 9.Rodríguez-Carvajal J., Fernandez-Diaz M.T., Martinez J.L. Neutron-Diffraction Study on Structural and Magnetic Properties of La2NiO4. J. Phys. Condens. Matter. 1991;3:3215. doi: 10.1088/0953-8984/3/19/002. [DOI] [Google Scholar]
- 10.Wang Z., Dunlap R.A. Effects of Al Substitutions on the Magnetic Anisotropy of Sm2Fe17 Compounds. J. Phys. Condens. Matter. 1993;5:2407. doi: 10.1088/0953-8984/5/15/011. [DOI] [Google Scholar]
- 11.Valeanu M., Plugaru N., Burzo E. Effect of Nitrgenation on the Magnetic Properties of Y2Fe17−xMx Compounds, with M = Al, Ga or Si. Solid State Commun. 1994;89:519–522. doi: 10.1016/0038-1098(94)90748-X. [DOI] [Google Scholar]
- 12.Shen B.G., Liang B., Wang F.W., Cheng Z.H., Gong H.Y., Zhang S.Y., Zhang J.X. Magnetic Properties of Sm2Fe17−xSix and Sm2Fe17−xSixC Compounds. J. Appl. Phys. 1995;77:2637. doi: 10.1063/1.358729. [DOI] [Google Scholar]
- 13.Shen B.G., Cheng Z.H., Liang B., Guo H.Q., Zhang J.X., Gong H.Y., Wang F.W., Yan Q.W., Zhan W.S. Structure and Magnetocrystalline Anisotropy of R2Fe17−xGax Compounds with Higher Ga Concentration. Appl. Phys. Lett. 1995;67:1621. doi: 10.1063/1.114959. [DOI] [Google Scholar]
- 14.Middleton D.P., Mishra S.R., Long G.J., Pringle O.A., Hu Z., Yelon W.B., Grandjean F., Buschow K.H.J. Magnetic, Neutron Diffraction, and Mossbauer Spectral Study of the Ce2Fe17−xSix Solid Solutions. J. Appl. Phys. 1995;78:5568–5576. doi: 10.1063/1.359678. [DOI] [Google Scholar]
- 15.Sabirianov R.F., Jaswal S.S. Electronic structure and magnetism in Sm2Fe17−xAx (A=Al,Ga,Si) J. Appl. Phys. 1996;79:5942. doi: 10.1063/1.362114. [DOI] [Google Scholar]
- 16.Yelon W.B., Hu Z., James W.J., Marasinghe G.K. Site affinity of substituents in Nd2Fe17?xTx (T=Cu,Zr,Nb,Ti,V) alloys. J. Appl. Phys. 1996;79:5939. doi: 10.1063/1.362113. [DOI] [Google Scholar]
- 17.Koch E., Fischer W. DIDO95 and VOID95-Programs for the calculation of Dirichlet domains and coordination polyhedra. Z. Kristallogr. 1996;211:251. doi: 10.1524/zkri.1996.211.4.251. [DOI] [Google Scholar]
- 18.Dunlap R.A., MacKay G.R., Wang Z. A Mossbauer effect investigation of site preferences and Fe environments in Ga-substituted Sm2Fe17 compounds. J. Alloys Compd. 1997;260:28–31. doi: 10.1016/S0925-8388(97)00136-9. [DOI] [Google Scholar]
- 19.Girt E., Altounian Z., Yang J. Structural and magnetic properties of Nd2Fe17−δCrδ (δ = 0, 0.5, 1, 1.9) J. Appl. Phys. 1997;8:5118. doi: 10.1063/1.365141. [DOI] [Google Scholar]
- 20.Burzo E. Permanent magnets based on R-Fe-B and R-Fe-C alloys. Rep. Prog. Phys. 1998;61:1099. doi: 10.1088/0034-4885/61/9/001. [DOI] [Google Scholar]
- 21.Forker M., Julius A., Shulte M., Best D. Mossbauer study of the hyperfine interaction of Fe-57 in Y1−sCo5+2s and related compounds. Phys. Rev. B. 1998;57:11565. doi: 10.1103/PhysRevB.57.11565. [DOI] [Google Scholar]
- 22.Givord D., Courtois D. Exchange interactions in R-M intermetallics. J. Magn. Magn. Mater. 1999;196:684. doi: 10.1016/S0304-8853(98)00892-0. [DOI] [Google Scholar]
- 23.Djega-Mariadassou C., Bessais L. Emergence of order in nanocrystalline SmFe9. J. Magn. Magn. Mater. 2000;210:81. doi: 10.1016/S0304-8853(99)00631-9. [DOI] [Google Scholar]
- 24.Teresiak A., Kubis M., Mattern N., Müller K.H., Wolf B. Crystal structure of Sm2Fe17−yMy compounds with M = Al, Si, Ga. J. Alloys Compd. 2001;319:168. doi: 10.1016/S0925-8388(01)00899-4. [DOI] [Google Scholar]
- 25.Bessais L., Djega-Mariadassou C. Structure and magnetic properties of nanocrystalline Sm(Fe1−xCox)11Ti (x≤2) Phys. Rev. B. 2001;63:54412. doi: 10.1103/PhysRevB.63.054412. [DOI] [Google Scholar]
- 26.Bessais L., Djega-Mariadassou C., Koch E. Structural and Mossbauer spectral study of the metastable phase Sm(Fe, Co, Ti)10. J. Phys. Condens. Matter. 2002;14:8111. doi: 10.1088/0953-8984/14/34/329. [DOI] [Google Scholar]
- 27.Bessais L., Djega-Mariadassou C., Nandra A., Appay M.D., Burzo E. Hard magnetic Sm(Fe,Si)9 carbides: Structured and magnetic properties. Phys. Rev. B. 2004;69:64402. doi: 10.1103/PhysRevB.69.064402. [DOI] [Google Scholar]
- 28.Bessais L., Djega-Mariadassou C., Tung D.K., Hong V.V., Phuc N.X. A 57Fe Mossbauer study of nanostructured Sm2Fe17−xCoxC3. J. Alloys Compd. 2008;455:35. doi: 10.1016/j.jallcom.2007.01.068. [DOI] [Google Scholar]
- 29.Khazzan S., Mliki N., Bessais L. Structure and magnetic properties of nanocrystalline Sm1−s(Fe,Mo)5+2s. J. Appl. Phys. 2009;105:103904. doi: 10.1063/1.3129566. [DOI] [Google Scholar]
- 30.Khazzan S., Mliki N., Bessais L., Djega-Mariadassou C. Rare-earth iron-based intermetallic compounds and their carbides: Structure and magnetic behaviors. J. Magn. Magn. Mater. 2010;322:224–229. doi: 10.1016/j.jmmm.2009.08.047. [DOI] [Google Scholar]
- 31.Galler A., Ener S., Maccari F., Dirba I., Skokov K.P., Gutfleisch O., Biermann S., Pourovskii L.V. Intrinsically weak magnetic anisotropy of cerium in potential hard-magnetic intermetallics. NPJ Quantum Mater. 2021;2:6. doi: 10.1038/s41535-020-00301-6. [DOI] [Google Scholar]
- 32.Opelt K., Ahmad T., Diehl O., Schonfeldt M., Brouwer E., Vogel I., Rossa J.D., Gassmann J., Ener S., Gutfleisch O. Upscaling the 2-Powder Method for the Manufacturing of Heavy Rare-Earth-Lean Sintered didymium-Based Magnets. Adv. Eng. Mater. 2021;23:2100459. doi: 10.1002/adem.202100459. [DOI] [Google Scholar]
- 33.Dirba I., Sepehri-Amin H., Skokov K., Skourski Y., Hono K., Gutfleisch O. Magnetic properties and microstructure of Sm5Fe17-based composite magnets. Acta Mater. 2021;212:116912. doi: 10.1016/j.actamat.2021.116912. [DOI] [Google Scholar]
- 34.Hosokawa A., Suzuki K., Yamaguchi W., Takagi K. Mechanism of anomalous α-Fe formation from stoichiometric Sm2Fe17 jet-milled powder during post-pulverization annealing. Acta Mater. 2021;213:116981. doi: 10.1016/j.actamat.2021.116981. [DOI] [Google Scholar]
- 35.Ener S., Skokov K.P., Palanisamy D., Devillers T., Fischbacher J., Eslava G.G., Maccari F., Schafer L., Diop L.V.B., Radulov I., et al. Twins—A weak link in the magnetic hardening of ThMn12-type permanent magnets. Acta Mater. 2021;214:116968. doi: 10.1016/j.actamat.2021.116968. [DOI] [Google Scholar]
- 36.Schafer L., Skokov K., Liu J., Maccari F., Braun T., Riegg S., Radulov I., Gassmann J., Merschroth H., Harbig J., et al. Design and Qualification of Pr-Fe-Cu-B Alloys for the Additive Manufacturing of Permanent Magnets. Adv. Funct. Mater. 2021;31:2102148. doi: 10.1002/adfm.202102148. [DOI] [Google Scholar]
- 37.Coey J.M.D. Novel Permanent Magnetic Materials. Phys. Scr. 1991;T39:21–28. doi: 10.1088/0031-8949/1991/T39/002. [DOI] [Google Scholar]
- 38.Coey J.M.D. Perspective and Prospects for Rare Earth Permanent Magnets. Engineering. 2020;6:119–131. doi: 10.1016/j.eng.2018.11.034. [DOI] [Google Scholar]
- 39.Kovacs A., Fischbacher J., Gusenbauer M., Oezelt H., Herper H.C., Vekilova O.Y., Nieves P., Arapan S., Schrefl T. Computational Design of Rare-Earth Reduced Permanent Magnets. Engineering. 2020;6:148–153. doi: 10.1016/j.eng.2019.11.006. [DOI] [Google Scholar]
- 40.Onoue M., Kobayashi R., Mitsui Y., Umetsu R.Y., Uwatoko Y., Koyama K. Magnetic field-induced nitridation of Sm2Fe17. J. Alloys Compd. 2020;835:155193. doi: 10.1016/j.jallcom.2020.155193. [DOI] [Google Scholar]
- 41.Liu K., Wang S.H., Feng Y.L., Zhang Y.K. Research on Phases and Morphology of Sm2Fe17 Melt-Spun Ribbon. Rare Met. Mat. Eng. 2020;49:3796–3802. [Google Scholar]
- 42.Dahal J.N., Ali K.S.S., Mishra S.R., Neupane D. Effect of Ga and Zr Substitution on the Properties of Dy2Fe17−xZrx and Dy2Fe16Ga1−xZrx (0 ≤ x ≤ 1) Intermetallic Compounds Prepared via Arc Melting Process. Magnetochemistry. 2020;6:9. doi: 10.3390/magnetochemistry6010009. [DOI] [Google Scholar]
- 43.Chrobak A., Bajorek A., Chełkowska G., Haneczok G., Kwiencien M. Magnetic properties and magnetocaloric effect of the Gd(Ni1−xFex)3 crystalline compound and powder. Phys. Stat. Sol. 2009;206:731–737. [Google Scholar]
- 44.Phejar M., Paul-Boncour V., Bessais L. Investigation on structural and magnetocaloric properties of LaFe13−xSix(H,C)y compounds. J. Solid State Chem. 2016;233:95–102. doi: 10.1016/j.jssc.2015.10.016. [DOI] [Google Scholar]
- 45.Bajorek A., Berger C., Pruzik K., Zubko M.K., Wojtyniak M., Chełkowska G. Novel Ho(Ni0.8Co0.2)3 nanoflakes produced by high energy ball-milling. Mater. Charcterisation. 2017;128:45–53. [Google Scholar]
- 46.Łopadczak P., Bajorek A., Prusik K., Zubko M., Chełkowska G. Magnetic hardening induced in RCo5 (R = Y, Gd, Sm) by short HEBM. Acta Phyica Pol. A. 2018;55:2100904. [Google Scholar]
- 47.Bajorek A., Łopadczak P., Prusik K., Zubko M., Chełkowska G. The comparison of magnetic properties at room temperature in RCo5 (R = Y, Sm, Gd) nanoflakes synthesized via time-staged HEBM. IEEE Trans. Magn. 2019;55:2100904. [Google Scholar]
- 48.Bajorek A., Łopadczak P., Prusik K., Zubko M. Correlation between Microstructure and Magnetism in Ball-Milled SmCo5/α-Fe (5%wt. α-Fe) Nanocomposite Magnets. Materials. 2021;14:502. doi: 10.3390/ma14040805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Veselova S., Tereshina I., Verbetsky V., Neznakhin D., Tereshina-Chitrova E., Kaminskaya T., Karpenkov A., Akimova O., Gorbunov D., Savchenko A. Structure and magnetic properties of (Sm,Ho)2Fe17Nx (x = 0; 2.4) J. Magn. Magn. Mater. 2020;502:166549. doi: 10.1016/j.jmmm.2020.166549. [DOI] [Google Scholar]
- 50.Shen B.G., Wang F.W., Gong H.Y., Cheng Z.H., Liang B., Zhang J.X., Zhang S.Y. Magnetic properties of Sm2Fe17−xGaxC2 compounds. J. Phys. Condens. Matter. 1995;7:883. doi: 10.1088/0953-8984/7/5/010. [DOI] [Google Scholar]
- 51.van Lier J., Kubis M., Grünberger W., Shultz L., Kronmüller H. High performance Sm2+δFe15Ga2C2 permanent magnets made by melt spinning and hot pressing. J. Appl. Phys. 1998;83:5549. doi: 10.1063/1.367387. [DOI] [Google Scholar]
- 52.Kubis M., Eckert D., Gebel B., Müller K.H., Schultz L. Intrinsic magnetic properties of Sm2Fe17−xMxNy/Cy (M = Al, Ga or Si) J. Magn. Magn. Mater. 2000;217:14. doi: 10.1016/S0304-8853(00)00084-6. [DOI] [Google Scholar]
- 53.Cao L., Handstein A., Gebel B., Schäfer R., Müller K.H. Thermostability of Sm2(FeGa)17Cy prepared by gas-solid reaction (GSR) J. Appl. Phys. 1997;81:4539. doi: 10.1063/1.365542. [DOI] [Google Scholar]
- 54.Schultz L., Schnitzke K., Wecker J., Katter M., Kuhrt C. Permanent magnets by mechanical alloying. J. Appl. Phys. 1991;70:6339. doi: 10.1063/1.349962. [DOI] [Google Scholar]
- 55.Christodoulou C.N., Takeshita T. Preparation, structural and magnetic properties and stability of interstitial Sm2Fe17-carbonitrohydrides. J. Alloys Compd. 1993;198:1–24. doi: 10.1016/0925-8388(93)90137-C. [DOI] [Google Scholar]
- 56.Mao O., Altounian Z., Yang J., Strom-Olsen O. Thermal stability of nanostructured Sm2Fe17Cx compounds prepared by ball milling. J. Appl. Phys. 1996;79:5536. doi: 10.1063/1.362301. [DOI] [Google Scholar]
- 57.Fersi R., Cabie M., Mliki N., Bessais L. Impact of carbon insertion on the microstructure and magnetic properties of nanocrystalline Pr2Co7 alloys. J. Alloys Compd. 2013;576:415–423. doi: 10.1016/j.jallcom.2013.05.067. [DOI] [Google Scholar]
- 58.Bouzidi W., Mliki N., Bessais L. Effect of carbonation on the structural, magnetic and magnetocaloric properties of uniaxial nanocrystalline Pr5Co19Cx compound. J. Magn. Magn. Mater. 2018;466:411–419. doi: 10.1016/j.jmmm.2018.07.022. [DOI] [Google Scholar]
- 59.Yamkane Z., Fersi R., Rachid F.Z., Moubah R., Lassri H., Mliki N., Alleg S., Sajieddine M., Bessais L. Law of approach to magnetic saturation in nanocrystalline Pr2Co7Cx (x ≤ 1): Effects of carbonation. SPIN. 2020;10:2050016. doi: 10.1142/S2010324720500162. [DOI] [Google Scholar]
- 60.Buschow K.H.J., Goot A.S.V.D. Intermetallic compounds in the system samarium-cobalt. J. Less-Common. Met. 1968;14:323. doi: 10.1016/0022-5088(68)90037-4. [DOI] [Google Scholar]
- 61.Givord D., Laforest J., Scweizer J., Tasset F. Temperature dependence of the samarium magnetic form factor in SmCo5. J. Appl. Phys. 1979;50:2008. doi: 10.1063/1.327141. [DOI] [Google Scholar]
- 62.Bartoli T., Joubert J.M., Provost K., Elkaim E., Paul-Boncour V., Monnier J., Moscovici J., Bessais L. Site Occupancy Determination in Th2Zn17- and TbCu7-types Sm2Fe17−xCox Compounds using Synchrotron Resonant Diffraction. Inorg. Chem. 2021;60:1533–1541. doi: 10.1021/acs.inorgchem.0c02884. [DOI] [PubMed] [Google Scholar]
- 63.Shield J., Meacham B.E. Phase formation in hypostoichiometric Sm2Fe17 alloys modified with Ti and C. J. Appl. Phys. 2000;87:2055. doi: 10.1063/1.372136. [DOI] [Google Scholar]
- 64.Meacham B.E., Shieldm J., Branagan D. Order-disorder effects in nitrided Sm-Fe permanent magnets. J. Appl. Phys. 2000;87:6707. doi: 10.1063/1.372815. [DOI] [Google Scholar]
- 65.Zheng C., Yu D., Li K., Luo Y., Jin J., Lu S., Li H., Mao Y., Quan N. Effect of boron additions on phase formation and magnetic properties of TbCu7-type melt spun SmFe ribbons. J. Magn. Magn. Mater. 2016;412:89–94. doi: 10.1016/j.jmmm.2016.03.082. [DOI] [Google Scholar]
- 66.Yang W., Zha L., Lai Y., Qiao G., Du H., Liu S., Wang C., Han J., Yang Y., Hou Y., et al. Structural and magnetic properties of the R10Fe90−xSix alloys with R=Y, Ce,Pr, Nd, Sm, Gd, Tb, Dy, Ho, and Er. Intermetallics. 2018;90:8–17. doi: 10.1016/j.intermet.2018.05.005. [DOI] [Google Scholar]
- 67.Saito T., Miyoshi H., Nishio-Hamane D. Magnetic properties of Sm-Fe-Ti nanocomposite magnets with a ThMn12 structure. J. Alloys Compd. 2012;519:144–148. doi: 10.1016/j.jallcom.2011.12.156. [DOI] [Google Scholar]
- 68.Luo Y., Zhang K., Li K.S., Yu D.B., Ling J.J., Men K., Dou Q.Y., Yan W.L., Xie J.J., Yang Y.F. Structure and magnetic behaviors of melt-spun SmFeSiB ribbons and their nitrides. J. Magn. Magn. Mater. 2018;405:214–218. doi: 10.1016/j.jmmm.2015.12.080. [DOI] [Google Scholar]
- 69.Takagi K., Jinno M., Ozaki K. Preparation of TbCu7-type Sm-Fe powders by low-temperature HDDR treatment. J. Magn. Magn. Mater. 2018;454:170–175. doi: 10.1016/j.jmmm.2018.01.092. [DOI] [Google Scholar]
- 70.Wu G., Li H., Yu D., Li K., Yan W., Yuan C., Sun L., Luo Y., Zhang K. Effect of niobium substitution on microstructures and thermalstability of TbCu7-type Sm-Fe-N magnets. J. Rare Earths. 2018;36:281–286. doi: 10.1016/j.jre.2017.05.008. [DOI] [Google Scholar]
- 71.Yan W., Quan N., Luo Y., Yu D., Wang Z., Wu G., Zhang K. Structure and hard magnetic properties of TbCu7-type SmFe8.95−xGa0.26Nbx nitrides. J. Rare Earths. 2018;36:165–169. doi: 10.1016/j.jre.2017.11.001. [DOI] [Google Scholar]
- 72.Saito T., Watanabe F., Nishio-Hamane D. Magnetic properties of SmFe12-based magnets produced by sparkplasma sintering method. J. Alloys Compd. 2019;773:1018–1022. doi: 10.1016/j.jallcom.2018.09.297. [DOI] [Google Scholar]
- 73.de Mooij D.B., Buschow K.H.J. Some novel ternary ThMn12-type compounds. J. Less-Common. Met. 1988;136:207. doi: 10.1016/0022-5088(88)90424-9. [DOI] [Google Scholar]
- 74.Teatum E.T., Gschneidner K.A., Waber J.T. Rep. LA-4003. Los Alamos Scientific Lab; Los Alamos, NM, USA: 1968. [Google Scholar]
- 75.Nehdi I., Bessais L., Djega-Mariadassou C., Abdellaoui M., Zarrouk H. X-ray and Mössbauer studies of Sm2Fe17−xCrx materials synthesized by 2 172x xmechanical alloying followed by an appropriate short annealing. J. Alloys Compd. 2003;351:24–30. doi: 10.1016/S0925-8388(02)01033-2. [DOI] [Google Scholar]
- 76.Schramm L., Acker J., Wetzig K. Structural effects of Zr substitution in the 1:7- and 2:17-type structure. J. Alloys Compd. 2006;414:158–168. doi: 10.1016/j.jallcom.2005.03.122. [DOI] [Google Scholar]
- 77.Cadieu F.J., Hegde H., Navarathna A., Rani R., Chen K. High-energy product ThMn12 Sm-Fe-T and Sm-Fe permanent magnets synthesized as oriented sputtered films. Appl. Phys. Lett. 1991;59:875. doi: 10.1063/1.105265. [DOI] [Google Scholar]
- 78.Wang D., Liou S., He P., Sellmyer D., Hadjipanayis G., Zhang Y. SmFe12 and SmFe12Nx films fabricated by sputtering. J. Magn. Magn. Mater. 1993;124:62. doi: 10.1016/0304-8853(93)90070-I. [DOI] [Google Scholar]
- 79.Verhoef R., de Boer F., Zhi-dong Z., Buschow K.H.J. Moment reduction in RFe12−xTx compounds (R=Gd, Y and T=Ti, Cr, V, Mo, W) J. Magn. Magn. Mater. 1988;75:319. doi: 10.1016/0304-8853(88)90037-6. [DOI] [Google Scholar]
- 80.Buschow K.H.J. Permanent magnet materials based on tetragonal rare earth compounds of the type RFe12−xMx. J. Magn. Magn. Mater. 1991;100:79. doi: 10.1016/0304-8853(91)90813-P. [DOI] [Google Scholar]
- 81.Cizmas C.B., Djega-Mariadassou C., Bessais L. Effect of Si content on magnetic properties and intersublattice exchange interactions in GdFe11−xSixTi compounds. J. Magn. Magn. Mater. 2001;226–230:1171–1173. doi: 10.1016/S0304-8853(00)00724-1. [DOI] [Google Scholar]
- 82.Bessais L., Sab S., Djega-Mariadassou C., Greneche J.M. Crystallographic and hyperfine parameters of PrTi(Fe,Co)11 and their carbides. Phys. Rev. B. 2002;66:054430. doi: 10.1103/PhysRevB.66.054430. [DOI] [Google Scholar]
- 83.Bouzidi W., Bartoli T., Sedek R., Bouzidi A., Moscovici J., Bessais L. Low Field Magnetocaloric Effect of NdFe11Ti and SmFe10V2 Compounds. J. Mater. Sci. Mater. Electron. 2021;32:10579–10586. doi: 10.1007/s10854-021-05713-z. [DOI] [Google Scholar]
- 84.Bouhbou M., Moubah R., Hlil E., Lassri H., Bessais L. Electronic structure, hyperfine parameters and magnetic properties of RFe11Ti intermetallic compounds (R = Y, Pr): Ab initio calculations, SQUIDmagnetometry and Mössbauer studies. J. Magn. Magn. Mater. 2021;518:167362. doi: 10.1016/j.jmmm.2020.167362. [DOI] [Google Scholar]
- 85.Khazzan S., Bessais L., Tendeloo G.V., Mliki N. Correlation of nanocrystalline Sm(Fe,Mo)12 and its out of equilibrium phase Sm(Fe,Mo)10. J. Magn. Magn. Mater. 2014;363:125–132. doi: 10.1016/j.jmmm.2014.03.030. [DOI] [Google Scholar]
- 86.Saidi M., Walha S., Hlil E., Bessais L., Jemmali M. Effect of chromium substitution on structural, magnetic and magnetocaloric properties of GdFe12−xCrx intermetallic compounds, Mössbauerspectrometry and ab initio calculations. J. Solid State Chem. 2021;297:122019. doi: 10.1016/j.jssc.2021.122019. [DOI] [Google Scholar]
- 87.de Boer F.R., Huang Y.K., de Mooij D.B., Buschow K.H.J. Magnetic properties of a series of novel ternary intermetallics (RFe10V2) J. Less-Common. Met. 1987;135:139. doi: 10.1016/0022-5088(87)90481-4. [DOI] [Google Scholar]
- 88.Nan-xian C., Shi-qiang H., Yu W., Jiang S. Phase stability and site preference of Sm(Fe,T)12. J. Magn. Magn. Mater. 2001;233:169–180. doi: 10.1016/S0304-8853(01)00251-7. [DOI] [Google Scholar]
- 89.Buschow K.H.J. Structure and properties of some novel ternary Fe-rich rare-earth intermetallics. J. Appl. Phys. 1988;63:3130–3135. doi: 10.1063/1.340865. [DOI] [Google Scholar]
- 90.Tang S.L., Yang C.P., Wang B.W., Jin X.M., Zhang S.Y., Du Y.W. Structure and magnetic properties of PrFe11.5−xVxTi0.5 compounds and their nitrides. J. Magn. Magn. Mater. 1998;189:341–345. doi: 10.1016/S0304-8853(98)00255-8. [DOI] [Google Scholar]
- 91.Tang S.L., Yin J.H., Jin Z.Q., Zhang J.R., Zhang S.Y., Du Y.W. Structure and magnetic properties of PrFe10VxMo2−x compounds and their nitrides. J. Appl. Phys. 1999;85:4687–4689. doi: 10.1063/1.370448. [DOI] [Google Scholar]
- 92.Tomey E., Bacmann M., Fruchart D., Soubeyroux J.L., Gignoux D. Influence of hydrogen on the structural and magnetic properties of the RFe10.5Mo1.5 compounds (R=rare earth) J. Alloys Compd. 1995;231:195–200. doi: 10.1016/0925-8388(95)01814-X. [DOI] [Google Scholar]
- 93.Cizmas C.B., Djega-Mariadassou C., Bessais L. Magnetic properties of GdFe11−xSixTi. J. Alloys Compd. 2002;345:27–35. doi: 10.1016/S0925-8388(02)00330-4. [DOI] [Google Scholar]
- 94.Li Z.W., Morrish A.H. Negative exchange interactions and Curie temperatures for Sm2Fe17−x and Sm2Fe17−xNy. Phys. Rev. B. 1997;55:3670. doi: 10.1103/PhysRevB.55.3670. [DOI] [Google Scholar]
- 95.Burzo E., Laforest J., Plugaru N., Valeanu M., Stanciu L. Magnetic properties of Gd2Fe14−xMx compounds with M= Ni, Si, Cu or V. IEEE Trans. Magn. 1994;30:625. doi: 10.1109/20.312356. [DOI] [Google Scholar]
- 96.Djega-Mariadassou C., Bessais L., Nandra A., Grenèche J.M., Burzo E. Structure and hyperfine properties of Sm2(Fe,Si)17. Phys. Rev. B. 2001;65:14419. doi: 10.1103/PhysRevB.65.014419. [DOI] [Google Scholar]
- 97.Bessais L., Dorolti E., Djega-Mariadassou C. Correlation between Sm2(Fe,Ga)17 and its precursor Sm(Fe,Ga)9. J. Appl. Phys. 2005;87:013902. doi: 10.1063/1.1825626. [DOI] [Google Scholar]
- 98.Bessais L., Younsi K., Khazzan S., Mliki N. X-ray and intrinsic magnetic properties of nanocrystalline Sm2(Fe,M)17 (M = Si,Ga, Co, Cr, Zr or Mo) Intermetallics. 2011;19:997–1004. doi: 10.1016/j.intermet.2011.03.001. [DOI] [Google Scholar]
- 99.Hu B.P., Li H.S., Sun H., Coey J.M.D. A 57Fe Mossbauer study of a new series of rare-earth iron nitrides: R2Fe17N3-δ. J. Phys. Condens. Matter. 1991;3:3983–3995. doi: 10.1088/0953-8984/3/22/010. [DOI] [Google Scholar]
- 100.Bouchaala N., Jemmali M., Bartoli T., Nouri K., Hentech I., Walha S., Bessais L., Salah A.B. Influence of Fe-substitution on structural, magnetic and magnetocaloric properties of Nd2Fe17−xCox solid solutions. J. Solid State Chem. 2018;258:501–509. doi: 10.1016/j.jssc.2017.11.011. [DOI] [Google Scholar]
- 101.Saidi M., Nouri K., Walha S., Dhahri E., Kabadou A., Jemmali M., Bessais L. Structural, Magnetic, Magnetocaloric and Mossbauer Spectrometry Study of Gd2Fe17−xCux (x = 0, 0.5, 1 and 1.5) Compounds. J. Electron. Mater. 2019;48:2242–2253. doi: 10.1007/s11664-019-07027-7. [DOI] [Google Scholar]
- 102.Charfeddine S., Zehani K., Bessais L., Korchef A. Structural, magnetic, magneto-caloric and Mössbauer spectral study of Tb2Fe17 compound synthesized by arc melting. J. Solid State Chem. 2016;238:15–20. doi: 10.1016/j.jssc.2016.03.001. [DOI] [Google Scholar]
- 103.Grandjean F., Isnard O., Long G.J. Magnetic and Mossbauer spectral evidence for the suppression of the magnetic spin reorientationin Tm2Fe17 by deuterium. Phys. Rev. B. 2002;65:064429. doi: 10.1103/PhysRevB.65.064429. [DOI] [Google Scholar]
- 104.Grandjean F., Isnard O., Hautot D., Long G.J. Structural, magnetic, and Mossbauer spectral study of Er2Fe17 and its hydrides. Phys. Rev. B. 2000;63:014406. doi: 10.1103/PhysRevB.63.014406. [DOI] [Google Scholar]
- 105.Sanchez H.M., Salazar D., Zamora L.E., Hernandez J.S.T., Tabares J.A., Alcazar G.A.P. Mössbauer spectroscopy in the system (Nd1−xCex)1.1Fe10CoTi with ThMn12 structure. Hyperfine Interact. 2020;241:44. doi: 10.1007/s10751-020-01716-0. [DOI] [Google Scholar]
- 106.Gjoka M., Psycharis V., Devlin E., Niarchos D., Hadjipanayis G. Effect of Zr substitution on the structural and magnetic properties of the series Nd1−xZrxFe10Si2 with the ThMn12 type structure. J. Alloys Compd. 2016;687:240–245. doi: 10.1016/j.jallcom.2016.06.098. [DOI] [Google Scholar]
- 107.Aubert A., Madugundo R., Schönhöbel A.M., Salazar D., Garitaonandia J.S., Barandiaran J.M., Hadjipanayis G. Structural and magnetic properties of Nd-Fe-Mo-(N) melt-spun ribbons with ThMn12 structure. Acta Mater. 2020;195:519–526. doi: 10.1016/j.actamat.2020.05.045. [DOI] [Google Scholar]
- 108.Harashima Y., Terakura K., Kino H., Ishibashi S., Miyake T. First-principles study on stability and magnetism of NdFe11M and NdFe11MN for M = Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn. J. Appl. Phys. 2016;120:203904. doi: 10.1063/1.4968798. [DOI] [Google Scholar]
- 109.Harashima Y., Fukazawa T., Kino H., Miyake T. Effect of R-site substitution and the pressure on stability of RFe12: A first-principles study. J. Appl. Phys. 2018;124:163902. doi: 10.1063/1.5050057. [DOI] [Google Scholar]
- 110.Yamashita S., Suzuki D., Yoshioka T., Tsuchiura H., Novak P. Finite-temperature magnetic properties of Sm2Fe17Nx using an ab initio effective spin model. Phys. Rev. B. 2020;102:214439. doi: 10.1103/PhysRevB.102.214439. [DOI] [Google Scholar]
- 111.Ogura M., Mashiyama A., Akai H. Role of N in the Permanent Magnet Material Sm2Fe17Nx. J. Phys. Soc. Jpn. 2015;84:084702. doi: 10.7566/JPSJ.84.084702. [DOI] [Google Scholar]
- 112.Moze O., Buschow K.H.J. Magnetic structure and preferred site occupation of Cr in the compound YFe10Cr2. J. Alloys Compd. 1996;233:165. doi: 10.1016/0925-8388(95)01992-8. [DOI] [Google Scholar]
- 113.Dirba I., Harashima Y., Sepehri-Amin H., Ohkubo T., Miyake T., Hirosawa S., Hono K. Thermal decomposition of ThMn12-type phase and its optimum stabilizing elements in SmFe12-based alloys. J. Alloys Compd. 2020;813:152224. doi: 10.1016/j.jallcom.2019.152224. [DOI] [Google Scholar]
- 114.Sikora M., Bajorek A., Chrobak A., Deniszczyk J., Ziółkowski G., Chełkowska G. Magnetic Properties and the Electronic Structure of the Gd0.4Tb0.6Co2 Compound. Materials. 2020;13:5481. doi: 10.3390/ma13235481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Ma H.F., Huang Z., Chen B., Qiang W.R., Pan M. The stabilization effect of substituted atoms and magnetism for intermetallic compounds YFe12−xCrx. Chin. Phys. B. 2009;18:1991–2005. [Google Scholar]
- 116.Ma H.F., Huang Z., Chen B., Qiang W.R., Sun G.A. The stabilization effect of the substituted atoms and the magnetism for intermetallic compounds YFe12−xVx. Sci. China. 2010;53:1239–1243. [Google Scholar]
- 117.Pal A., Gabay A., Hadjipanayis G.C. Mechanochemical synthesis of Nd2Fe14B alloy with high coercivity. J. Alloys Compd. 2012;543:31–33. doi: 10.1016/j.jallcom.2012.07.114. [DOI] [Google Scholar]
- 118.Zhong Y., Chaudhary V., Tan X., Parmar H., Ramanujan R. Kinetic study of the mechanochemical synthesis of Nd2(Fe,Co)14B hardmagnetic nanoparticles. J. Alloys Compd. 2018;747:755–763. doi: 10.1016/j.jallcom.2018.03.077. [DOI] [Google Scholar]
- 119.Zhu K., Xu J., Wang X., Li W., Tian K., Hou Y. Chemical synthesis and coercivity enhancement of Nd2Fe14B nanostructures mediated by non-magnetic layer. Nano Res. 2020;13:1141–1148. doi: 10.1007/s12274-020-2761-5. [DOI] [Google Scholar]
- 120.Younsi K., Russier V., Bessais L. Structure and magnetic properties of nanocrystalline PrCo3. J. Appl. Phys. 2010;107:083916. doi: 10.1063/1.3388364. [DOI] [Google Scholar]
- 121.Fersi R., Mliki N., Bessais L., Guetari R., Russier V., Cabié M. Effect of annealing on structural and magnetic properties of Pr2Co7 compounds. J. Alloys Compd. 2012;522:14–18. doi: 10.1016/j.jallcom.2011.12.069. [DOI] [Google Scholar]
- 122.Bouzidi W., Mliki N., Bessais L. Structural and magnetic properties of new uniaxial nanocrystallinePr5Co19 compound. J. Magn. Magn. Mater. 2017;441:566–571. doi: 10.1016/j.jmmm.2017.06.041. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data available on request due to restrictions e.g., privacy or ethical.