The dynamics of early-stage transmission of COVID-19: A novel quantification of the role of global temperature

Graphical abstract

Abstract

The global outbreak of COVID-19 has emerged as one of the most devastating and challenging threats to humanity. As many frontline workers are fighting against this disease, researchers are struggling to obtain a better understanding of the pathways and challenges of this pandemic. This paper evaluates the concept that the transmission of COVID-19 is intrinsically linked to temperature. Some complex nonlinear functional forms, such as the cubic function, are introduced to the empirical models to understand the interaction between temperature and the “growth” in the number of infected cases. An accurate quantitative interaction between temperature and the confirmed COVID-19 cases is obtained as log(Y) = -0.000146(temp_H)³ + 0.007410(temp_H)² –0.063332 temp_H + 7.793842, where Y is the periodic growth in confirmed COVID-19 cases, and temp_H is the maximum daily temperature. This equation alone may be the first confirmed way to measure the quantitative interaction between temperature and human transmission of COVID-19. In addition, four important regions are identified in terms of maximum daily temperature (in Celsius) to understand the dynamics in the transmission of COVID-19 related to temperature. First, the transmission decreases within the range of −50 °C to 5.02 °C. Second, the transmission accelerates in the range of 5.02 °C to 16.92 °C. Essentially, this is the temperature range for an outbreak. Third, the transmission increases more slowly in the range of 16.92 °C to 28.82 °C. Within this range, the number of infections continues to grow, but at a slower pace. Finally, the transmission decreases in the range of 28.82 °C to 50 °C. Thus, according to this hypothesis, the threshold of 16.92 °C is the most critical, as the point at which the infection rate is the greatest. This result sheds light on the mechanism in the cyclicity of the ongoing COVID-19 pandemic worldwide. The implications of these results on policy issues are also discussed concerning a possible cyclical fluctuation pattern between the Northern and Southern Hemispheres.

1. Introduction

1.1. Emerging facts

Global climate change and urban development are hotly debated topics. The unexpected outbreak and spread of COVID-19 around the world have added fuel to this debate. From the time of the outbreak of the SARS-CoV-2 virus, later formally named for the disease of COVID-19, the globally confirmed cases by December 16, 2021, exceeded 272 million and are still growing rapidly. As medical experts and other frontline workers fight this global threat, researchers have struggled to understand and the pathways and challenges of COVID-19 (Keener, 2020). As the pandemic continues, some strange patterns in the transmission of COVID-19 have emerged.

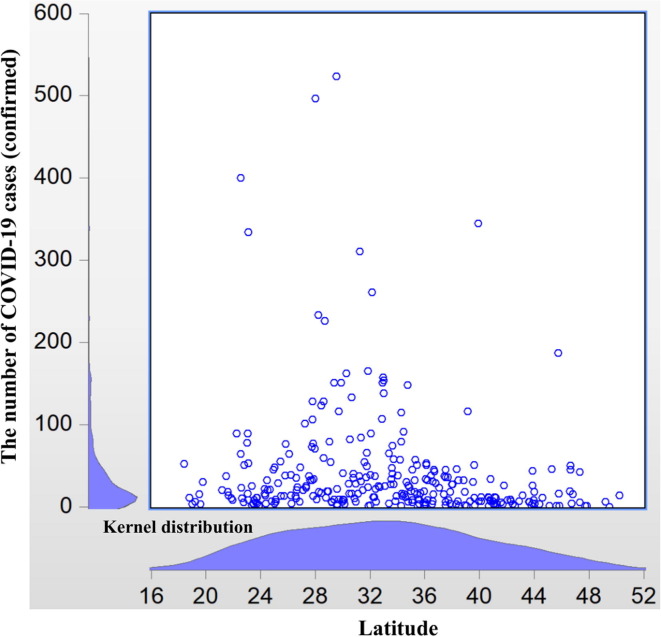
Theoretically, the spread of COVID-19 can be described as a circle, or nearly a circle, with the center as the outbreak epicenter. For the case of China in its early-stage transmission of COVID-19 in early 2020, the epicenter is Wuhan. However, the geographic illustration of transmission indicates that the situation might be more complex. As Fig. 1 shows, transmission outside Hubei Province is centered at 30° north latitude (as of February 16, 2020). This fact suggests that the spread of the epidemic is geographically shaped like a belt, rather than a circle. Economically, this finding is counterintuitive. Wuhan is in the center of China, and the high-speed railway as well as other types of mass transportation from the north to the south that cross Wuhan are more advanced than from east to west across the country. Thus, the transmission of the virus should be distributed more equally from both the social and economic perspectives. As a result, we would expect a rectangular region as shown in Fig. 1.

Fig. 1.

COVID-19 Transmission versus Latitude (without Hubei province).

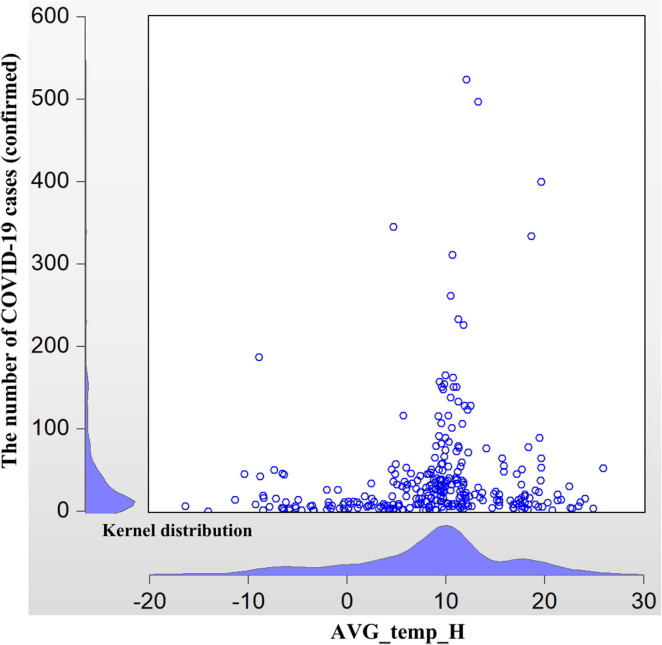
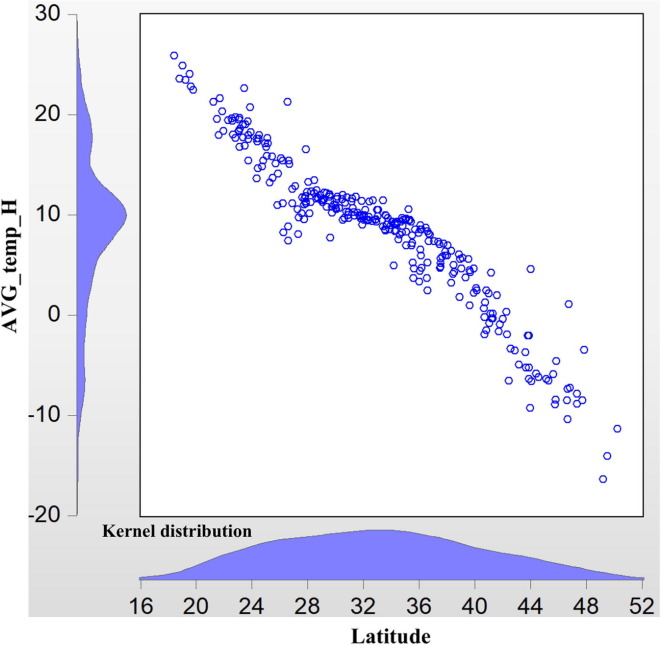
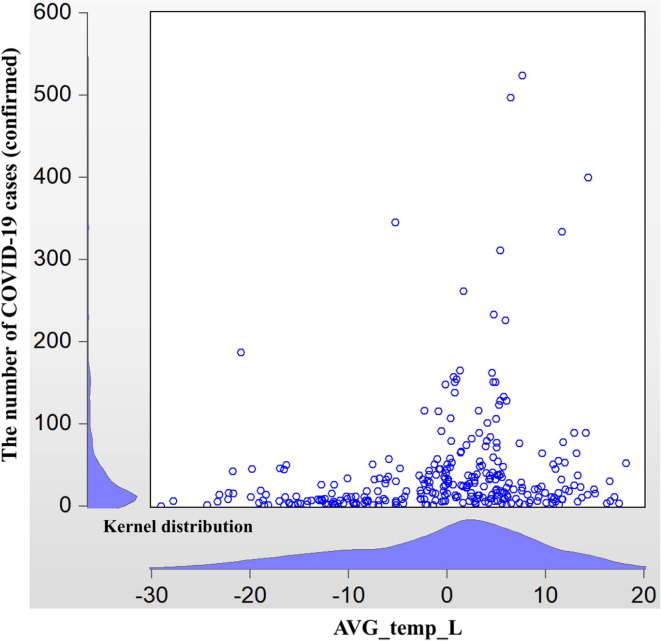
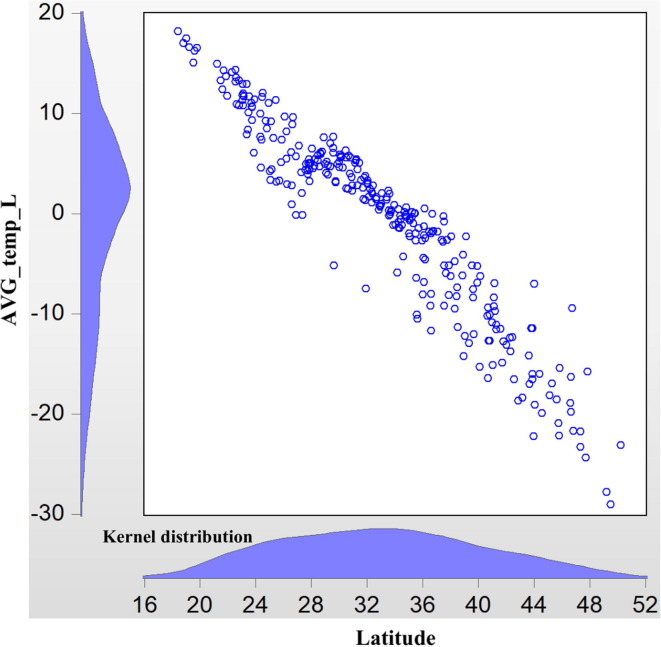
As is well known, the area at 30° north latitude is a mysterious geological belt, and this latitude is closely linked with temperature. As Fig. 2a, Fig. 2b illustrate, the transmission of COVID-19 outside Hubei is almost centered at a maximum daily temperature of around 12 °C. In addition, in Fig. 3a, Fig. 3b , the transmission at the lowest daily temperature is centered at roughly 2 °C. Moreover, the latitude of Wuhan is around 30.52° north, which leads to a similar temperature. These facts suggest that the transmission of COVID-19 may be related to temperature, a hypothesis that is further tested in the latter part of this study.

Fig. 2a.

COVID-19 Transmission versus AVG_temp_H (without Hubei province) for the period T_31.

Fig. 2b.

AVG_temp_H versus Latitude (without Hubei province) for the period T_31.

Fig. 3a.

COVID-19 Transmission versus AVG_temp_L (without Hubei province) for the period T_31.

Fig. 3b.

AVG_temp_L versus Latitude (without Hubei province) for the period T_31.

The situation in China became relatively stable around February 20, 2020, but in other parts of the world, the outbreaks got worse. Here we give a five-day daily temperature comparison of four cities (regions) outside China, in Japan, South Korea, Iran, and Italy, respectively, which had the most confirmed cases of COVID-19 outside China during that period. In fact, this is the other counterintuitive issue identified in this study.

As Table 1 shows, the maximum daily temperature in the four cities (regions) is around 12 °C on February 26, 2020, when the media all over the world began to raise concern, and even the US stock market was affected. This temperature is similar to the maximum daily temperature in the Chinese cities where COVID-19 initially broke out and spread very rapidly.

Table 1.

Daily temperature in some cities with the emerging pandemic outside China.

	Yokohama (Japan)		Daegu (South Korea)		Tehran (Iran)		Lombardia (Italy)
Date	Highest temperature (°C)	Lowest temperature (°C)	Highest temperature (°C)	Lowest temperature (°C)	Highest temperature (°C)	Lowest temperature (°C)	Highest temperature (°C)	Lowest temperature (°C)
22-Feb	16	10	10	2	16	8	13	3
23-Feb	15	10	9	0	17	9	16	3
24-Feb	13	7	14	1	18	10	16	3
25-Feb	15	9	8	6	13	11	14	8
26-Feb	10	8	12	5	11	4	13	4

Source: https://www.timeanddate.com/weather/.

This might be seen as a mere coincidence. Therefore, we need to conduct a thorough investigation of the role of temperature on the dynamics of transmission of COVID-19 in its early stage.

1.2. Related studies

The interaction between climate change and human activity has a long history. The surface temperature on Earth is so important that it determines many critical issues in our daily life (Mills et al., 2019). Earlier classical discussion is seen on the fall of Rome as a consequence of climate change (Huntington 1917). Discussion of the relationship between climate change and migration as well as the local population is also a common topic in this strand of research in modern times (Haurin, 1980, Oliveira and Pereda, 2020). In addition, climate change is linked to the consumption of energy, such as fossil fuels (Newell et al., 1999). Climate change is also studied concerning deforestation as well as biodiversity in tropical regions (Burgess et al., 2012). Furthermore, climate change has also caused great concern in management, in which supply chain management (Jira and Toffel, 2013) as well as catastrophic climate risk (Berger et al., 2017) are studied. The influence of climate change on both agricultural and manufactured commodities has also been studied (Lewis and Witham, 2012a, Lewis and Witham, 2012b).

The correlation between climate change and infectious disease is also a popular topic (Shope, 1991, Semenza et al., 2012), and studies on the health impact of climate change (McMichael et al., 2012, Polivka et al., 2012, José et al., 2018) are emerging. However, although since its outbreak studies on the transmission of COVID-19 are in focus (Li et al., 2020, Wang et al., 2020, Wu et al., 2020), insights into the possible connection between temperature and the spread of the virus are rare at the initial stage of the disease.

Before the outbreak of COVID-19, at least one study discusses the relationship between disease (in this case, schizophrenia in particular) and temperature (Watson, 1984). In some early studies, the effect of temperature on infection is explored—for example, infection and mortality in pectinophora gossypiella larvae within the range of 15.6 °C–38.0 °C (Henneberry et al., 1996). Research that is closer to the present study discusses the local temperature and infection with West Nile disease (Ruiz et al., 2010, Defelice et al., 2018). However, West Nile is spread by mosquitoes, rather than directly from person to person. In fact, before the current pandemic, the interaction between climate change and infectious diseases was already attracting scholarly attention (Wu et al., 2016). Currently, although laboratory-level evidence on isolated virus samples of temperature and mortality has been presented (China National Health Commission, 2020), to our knowledge, studies on the possible connection between temperature and transmission of COVID-19 at a citywide level are not well understood.

Although the relationship between climate and COVID-19 can be very complex (Kassem, 2020, Rosenbloom and Markard, 2020), this relationship has been a hot topic in the environmental science community since April 2020. As noted, sensitivity analyses of the role of ambient temperature on the transmission of COVID-19 have been conducted worldwide, but the direction of the effects is not definitive. Even within the same study area, such as China, some provinces have a positive interaction while others have a negative relationship (Shahzad et al., 2020), and still, others have a neutral relationship between the daily average temperature and daily increase in confirmed cases (Iqbal et al., 2020).

In particular, some studies focus on the decrease in COVID-19 along with the increase in temperature, covering a wide range of countries. Other than China (Shi et al., 2020), this negative correlation is also identified in Iran (Ahmadi et al., 2020). The northern provinces in Iran with less exposure to solar radiation (and hence low temperature) have a higher rate of transmission. However, a positive relationship has been identified in some other regions. For example, research using data on New York City shows a positive correlation (Bashir et al., 2020). In addition, the data from Jakarta also suggest a positive correlation (Tosepu et al., 2020).

In addition, some scholars assert that it is unclear whether temperature affects the infection rate, using the data on Japan (Ujiie et al., 2020). Others draw the same conclusion using data on Spain (Briz-Redón and Serrano-Aroca, 2020). A study using data on Iran shows low sensitivity between temperature and transmission as well (Jahangiri et al., 2020). In fact, similar inconclusive results are seen in studies on many different regions.

1.3. Research gap

In this study, we focus on the related studies at the early stage of the outbreak, many of which become highly cited articles later, to better demonstrate how the pandemic has evolved. However, there are also many recent studies, some typical examples of which are Abraham et al., 2021, Chew et al., 2021, among others.

Now, if we consider the role of temperature on the transmission of COVID-19 as a puzzle, currently an increasing number of scattered pieces of this jigsaw puzzle are emerging as new findings increase, but the overall general theory that can assemble these pieces and thus solve the puzzle remains unclear. In fact, even if we could simulate the interaction between the COVID-19 outbreak and local temperature at the citywide level, it is extremely difficult or even impossible to do so in the lab. It is essential to resort to computer-based simulation and other means.

Researchers are asked to examine the uncharted field of the ongoing pandemic (Fauci et al., 2020), so this study is a timely attempt to examine the neglected but crucial topic of temperature to contribute to knowledge about the pandemic. The purpose of this study is not only to provide an accurate quantitative representation of the specific functional form of COVID-19 propagation for certain ambient factors, such as temperature, but also to gain insight into the mechanism of the role of temperature in the dynamics of transmission of COVID-19 theoretically.

2. Methods

2.1. Data sources and assumptions

Although it is possible to include COVID-19 data from cities outside China, to obtain the maximum systematic homogeneity, this study employs only data on cities in mainland China. In addition, to better study the transmission pattern, we exclude data on cities in Hubei where COVID-19 was the most severe in the early-stage transmission in China. On February 25, 2020, mainland China had 406 newly confirmed COVID-19 cases, of which only 5 were in cities outside Hubei. Therefore, as the spread of the disease outside Hubei stabilized in late February, the data from cities outside Hubei are more useful for this study.

The spread of the COVID-19 epidemic in China can be divided into three critical phases.

The first critical date is January 24, 2020. On January 23, Wuhan was officially sealed off. Therefore, the increase in confirmed infections in regions outside Hubei can be treated as cases of local transmission thereafter.

The second critical date is January 30, 2020. This is the last day of the planned national holiday, and many people were expected to return to their work location on this day. However, because of the pandemic, the return to work after the holiday was postponed to February 3, and in many provinces, to February 10; some companies even extended it further, to February 17.

The third critical date is February 16, 2020. As noted earlier, in most places except Hubei, people went back to work on February 17. The overall rate of return to work in mainland China is estimated at more than 60%, and in some places at more than 80%.

Based on these three critical dates, we designate three corresponding periods. T₃₁ is defined as the period between the first critical date and the third critical date. This is the full period. In addition, we designate two subperiods: the period from the first critical date to the second critical date and the period from the second critical date to the third critical date. In fact, the reported number of confirmed infections in mainland China became stable after February 20, 2020. Thus, the division of such time periods sounds reasonable.

These periodic divisions are essential for this study. Many related studies use new confirmed cases as the dependent variable in the regression. However, because it is common to see a lag in reporting on the daily confirmation of COVID-19 cases worldwide, the use of the number of daily confirmed cases is not the most accurate choice (Liu, 2020). Therefore, we use the periodic growth in confirmed cases, a number that is much more stable and hence reliable for this work. Because the purpose of this paper is to study the role of temperature on the transmission of COVID-19, we are more interested in the “growth” of the number of infections. Hence, we need to match the corresponding periodic data on temperature as well, raising a technical issue as to how the data can be matched.

As original data on the highest and lowest daily temperature recorded from January 24 to February 16, 2020, are available, it is straightforward to calculate the periodic mean average value and the standard deviation of the highest and lowest temperature. In addition, it is possible to calculate the average daily temperature as well as the daily difference between the highest and the lowest temperature. These two results can yield the other two periodic mean average values and the standard deviation of the daily average and difference in temperature. Thus, we obtain eight representations of the temperature for each period.

In this paper, temperature data on all the Chinese cities comes from the website called Weather China (Weather China, 2020). In addition, we obtain original data on confirmed COVID-19 cases from the medical website named Dingxiang Yuan (DingXiang Yuan, 2020), and we calculate the “growth” in the number of infections in each period ourselves. Finally, we match some data of urban characteristics from the China City Statistical Yearbook 2018 (China National Bureau of Statistics, 2019). The summary statistics on the temperature variables as well as some other control variables are presented in Table 2 .

Table 2.

The summary statistics of the variables (without Hubei province, n = 295).

Variables	Explanation	Unit	Mean	Std. Dev.	Min	Max
AVG_temp_H	The periodical average of maximum temperature of the day	°C	8.508	7.595	−16.348	25.870
AVG_temp_L	The periodical average of daily lowest temperature	°C	−0.584	9.522	−29.044	18.174
Lat	Latitude	Degrees north	33.031	7.1530	18.392	50.250
Dist	Distance to Wuhan	kilometer	1,047.034	610.310	119.200	3,263.100
Subway	Length of built urban metro lines	kilometer	14.592	69.429	0.000	668.640
Population_density	Population density	person/square kilometer	3,658.153	2,384.588	77.000	11,602.000
Wastewater	Annual quantity of wastewater discharged	10,000 m3	13,846.550	26,699.770	284.000	229,526.000
Garbage	Residential garbage collected and transported	10,000 ton	57.778	103.396	1.560	924.770
Greenspace	Per capita public recreational green space	Square meter	14.303	4.996	2.450	51.660
N_COVID-19	Number of confirmed COVID-19 cases	person	41.464	70.039	1.000	551.000

Note: The data of N_COVID-19 is for the critical time on February 16, 2020. AVG_temp_H and AVG_temp_L are for the time period T₃₁.

2.2. The model

The basic model specification used in this paper is simple, as follows:

$$Y_i={\beta }_0+{\beta }_{1}f(temp\_x_i)+{\beta }_{\text{2}}{X}_i+{\epsilon }_i$$ (1)

In this equation, Y is the dependent variable, which is the periodic difference in the confirmed COVID-19 cases, where the subscript “i” denotes city “i”. As noted previously, this periodic difference is used to show the “growth” in the number of confirmed infections. Because some of these numbers are zeros, we cannot take the log form of the dependent variable. f(temp_x) stands for the potentially complex expression for temperature, where x is various representations of temperature, as previously discussed. As many values of the temperature variables are either negative or zero, we cannot use the log form of the temperature variables either. In addition, we do not know what the most appropriate representation and functional form are, so they are empirically tested later. Finally, X stands for the control variables, including the distance to Wuhan as well as variables for several urban characteristics. Although the focus throughout this paper is temperature, we also need to control for the heterogeneity of cities. These control variables are essential for isolating the marginal effect of temperature. Notably, the importance of including urban characteristics in the analysis of the spread of COVID-19 is well discussed (Liu, 2020).

Moreover, ordinary least squares regression (OLS) commonly has endogeneity problems, which lead to inconsistent estimation parameters. As a result, it is necessary to find appropriate instrumental variables (IVs) to address this issue. To our knowledge, most related studies mentioned earlier ignore this endogeneity issue. Therefore, their results could be inconsistent from a statistical perspective. As a result, the use of simple multivariate regression is troublesome and even problematic.

In the present study, the local transmission of COVID-19 can be affected by several factors, some of which remain unknown. Thus, using a limited number of independent variables, we may be overlooking many important influential factors. For example, in addition to many unknown biological features, our model might need to account for policy measures and economic and social behavior that could affect viral transmission. Thus, the omission of these factors from the model creates a substantial risk that our estimates suffer from omitted variable bias.

The next question concerns which IVs to choose. Because the target endogenous variable is temperature, the ideal candidate for an IV must be correlated with temperature and uncorrelated with the unobservable error term. After numerous tests, we choose latitude, which is closely related to temperature, and no clear evidence suggests that the undiscovered influential factors of COVID-19 transmission at the citywide level are correlated with this geographical term, i.e., latitude. In addition, because we use the quadratic or cubic form of temperature in the regression, we need to have two or more IVs. After testing for a long time, we found that the best option is to use the IVs Lat, Lat ², and Lat ³ at the same time. The weak instrument diagnostics shown in Table 3 justify this choice because the corresponding Cragg-Donald F-stat values in Models (2), (4), and (6) are all higher than the required value of 10. Notably, we use the generalized method of moments (GMM) in the estimation of Models (2), (4), and (6), where the estimation weight matrix is “White”. This combination of statistical methods gives us the best performance in the empirical models.

Table 3.

Estimation results with dependent variable ΔN_COVID-19 (without Hubei province, n = 295).

	Model (1)	Model (2)	Model (3)	Model (4)	Model (5)	Model (6)
	OLS	GMM	OLS	GMM	OLS	GMM
	(T31)	(T31)	(T21)	(T21)	(T32)	(T32)
AVG_temp_H	−1.461** (−1.968)	−2.508*** (3.680)	0.020 (0.087)	−0.300** (2.353)	−1.436*** (2.637)	−2.150*** (3.641)
(AVG_temp_H)2	0.089** (2.258)	0.136*** (3.5450)	0.010 (0.753)	0.024*** (2.802)	0.076*** (2.710)	0.108*** (3.476)
log(Dist)	–32.998*** (−5.174)	−41.385*** (−5.373)	−5.458*** (−2.932)	−7.574*** (−5.095)	−27.555*** (−5.761)	–33.650*** (−5.207)
Subway	0.424*** (8.822)	0.433*** (4.520)	0.117*** (8.198)	0.117*** (4.113)	0.306*** (8.519)	0.314*** (4.491)
log(Population_density)	3.273 (0.425)	5.409* (1.676)	−0.055 (−0.045)	0.955 (1.312)	3.362 (1.096)	4.365 (1.637)
log(Wastewater)	1.735 (0.267)	5.360 (1.196)	−0.713 (−0.369)	1.115 (1.165)	2.435 (0.500)	4.135 (1.102)
log(Garbage)	19.439** (2.557)	9.961 (1.478)	6.302*** (2.791)	1.758 (1.100)	13.130** (2.305)	8.399 (1.567)
log(Greenspace)	−5.400 (−0.604)	−6.160 (−0.873)	−1.050 (−0.397)	−1.277 (−0.747)	−4.320 (−0.644)	−4.833 (−0.847)
Adjusted R2	0.502	0.489	0.442	0.411	0.496	0.488
Weak Instrument Diagnostics (Cragg-Donald F-stat)		295.844		261.571		287.022

Note: The values of the constant terms are not reported. t statistics in parentheses. Instrumental variables are Lat, Lat², and Lat³.

*** p ≤ 0.01, ** 0.01 < p < 0.05, *0.05 < p < 0.1.

Later in the study, we also use several more advanced statistical and mathematical models. But for better a logical structure, these are discussed in the latter part of this paper.

3. Results

3.1. The insignificant linear form

The eight proxies for temperature mentioned earlier are all found to be insignificant in our examination of the influence of temperature on the spread of COVID-19 using the linear functional form. Although it is not necessary to report the corresponding results in this study, to build a complete theory, the linear functional form is still discussed here. Similar results can be seen in Iqbal et al., 2020, McConnon, 2021, among others.

This finding explains why some other studies mentioned earlier conclude that the interaction between temperature and COVID-19 infection is neutral. Now we understand that it is simply due to the choice of model specification, in which the simple linear model is not capable of producing valid results. Therefore, more complex nonlinear functional forms must be introduced to explore the hidden rules on the infectiousness of COVID-19 related to temperature.

3.2. Preliminary results with the quadratic functional form

Here we show the empirical estimation results of the temperature-related models using the quadratic functional form. As shown in Table 3, in all three models with OLS estimation corresponding to the three periods, i.e., Models (1), (3), and (5), the quadratic form of the periodic average of the maximum daily temperature shows promise as a direction for future study.

A comparison of Models (2), (4), and (6) shows that the control variable Dist is always statistically significant, regardless of the settings. This suggests that places closer to the epicenter of the outbreak in China, i.e., Wuhan, are more vulnerable to the disease. In addition, the subway variable is a strong indicator of viral transmission. Population density is found to be significant, but only in the full period T₃₁. Most importantly, the quadratic form of the periodic average of the maximum daily temperature is significant in both the linear term and the second-order term.

To obtain models with a better fit, the data set is “refined” by deleting the sample of cities with extreme values, most of which are distant and have few confirmed cases. It would be too casual for these cities that no systematic importance is included. The new results are in Table 4 , showing that the variable for garbage has become a significant influential factor in transmission. The significance and the absolute value of the parameters for the temperature variable both tend to be stronger. Indeed, the adjusted R² values are now much larger, which is a good signal of a better fit of the model.

Table 4.

Estimation results with dependent variable ΔN_COVID-19 (without Hubei province, n = 155).

	Model (7)	Model (8)	Model (9)	Model (10)	Model (11)	Model (12)
	OLS	GMM	OLS	GMM	OLS	GMM
	(T31)	(T31)	(T21)	(T21)	(T32)	(T32)
AVG_temp_H	−4.967*** (−5.005)	−4.985*** (−6.205)	−0.483 (−1.455)	−0.551*** (−3.580)	−4.333*** (−5.777)	−4.377*** (−6.028)
(AVG_temp_H)2	0.284*** (5.175)	0.291*** (6.344)	0.044** (2.211)	0.047*** (4.515)	0.230*** (5.696)	0.237*** (6.072)
log(Dist)	−71.519*** (−8.667)	−71.793*** (−8.187)	−12.202*** (−4.769)	−12.509*** (−7.597)	−58.765*** (−9.180)	−59.030*** (−7.630)
Subway	0.469*** (9.779)	0.452*** (4.718)	0.137*** (9.135)	0.122*** (4.434)	0.331*** (8.860)	0.329*** (4.533)
log(Population_density)	5.148 (0.887)	5.975 (1.286)	0.243 (0.132)	0.955 (0.782)	5.152 (1.143)	5.218 (1.275)
log(Wastewater)	3.571 (0.428)	4.232 (0.644)	−0.090 (−0.034)	0.916 (0.623)	3.747 (0.577)	3.833 (0.673)
log(Garbage)	22.418** (2.344)	20.590** (2.437)	6.120** (2.042)	3.882* (1.937)	16.253** (2.183)	16.014** (2.287)
log(Greenspace)	−1.491 (−0.117)	−2.969 (−0.306)	−2.110 (−0.528)	−3.813 (−1.384)	0.964 (0.097)	0.834 (0.106)
Adjusted R2	0.722	0.721	0.644	0.628	0.703	0.703
Weak Instrument Diagnostics (Cragg-Donald F-stat)		213.724		174.205		201.084

Note: The values of the constant terms are not reported. t statistics in parentheses. Instrumental variables are Lat, Lat², and Lat³.

*** p ≤ 0.01, ** 0.01 < p < 0.05, *0.05 < p < 0.1.

Because we use two periods divided by three critical dates, one might wonder whether a structural change occurs between them. In fact, in Table 3, Table 4 we find that the results of periods T₃₁ and T₃₂ do not differ much, but the results of period T₂₁ differ substantially. Thus, we perform a Chow’s breakpoint test, in which the calculated F value is 0.2793. This test result fails to reject the H₀ of “no structural change.” As a result, we consider our estimation coefficients stable across these periods. Perhaps, the seven-day period of T₂₁ is too short to have more significant results, but the “growth” pattern in the local transmission is essentially the same as in the other period.

Because we can empirically identify a quadratic-form relationship of the average of the maximum daily temperature with the “growth” in local transmission of COVID-19, we can take the next step to see whether more information can be obtained.

In Table 4, although the parameters of Models (8) and (12) are very similar, we choose Model (8) for period T₃₁, because of its slightly larger R² as well as the t values for the key explanatory variables. Logically, more valuable information is obtained if we include the first period. The second-order term is positive and significant, and the linear term is negative and significant. Then, if we focus on the temperature variable terms in Model (8), we can construct the following:

$$Y=0.291\ast {(temp\_H)}^2-4.985\ast temp\_H+C$$ (2)

where C is a constant that we do not care about here. Recall that we do have a constant in our regression.

The perfect square trinomial of Eq. (2) can be derived as follows:

$$Y=0.291\ast {(temp\_H-8.565)}^2+C^{\prime }$$ (3)

Eq. (3) suggests a U-shaped relationship, where 8.57 °C is supposed to be the minimum point for growth in local COVID-19 transmission. However, this quadratic form is not easy to understand, at least not well enough. In fact, in another study, a binary relationship is identified around 10 °C as its maximum in China, which indicates both the usefulness and limitations of the quadratic form (Shi et al., 2020). Although the quadratic form is simple, the cubic function appears to be more attractive, which has more desirable attributes in math.

3.3. Introducing the cubic functional form

To the best of our knowledge, only one academic study employs a cubic function to examine the interaction between the temperature and COVID-19 (Prata et al., 2020) in the early stage, for a model with a better fit. However, the cubic function is much more important than “a better fit.” In fact, it is the most essential element for understanding the hidden mechanism in the dynamics of transmission concerning temperature.

Table 5 shows the cubic function of the temperature variable terms. As demonstrated in Model (14), although the cubic term is not statistically significant, it does not affect us to write down the cubic function of temperature as follows.

$$Y=-0.0032\ast {(temp\_H)}^3+0.3449\ast {(temp\_H)}^2-4.6366\ast temp\_H+363.0619$$ (4)

Table 5.

Estimation results with dependent variable ΔN_COVID-19 with cubic function (without Hubei province, n = 155).

	Model (13)	Model (14)	Model (15)	Model (16)	Model (17)	Model (18)
	OLS	GMM	OLS	GMM	OLS	GMM
	(T31)	(T31)	(T21)	(T21)	(T32)	(T32)
AVG_temp_H	−4.882*** (−4.583)	−4.637*** (−4.335)	−0.319 (−0.895)	−0.172 (−0.488)	−4.365*** (−5.427)	−4.332*** (−5.088)
(AVG_temp_H)2	0.307*** (2.635)	0.345*** (2.826)	0.087** (2.189)	0.098** (2.120)	0.221** (2.563)	0.244*** (2.887)
(AVG_temp_H)3	−0.001 (−0.225)	−0.003 (−0.500)	−0.003 (−1.253)	−0.004 (−1.190)	0.0004 (0.111)	−0.0004 (−0.104)
log(Dist)	−70.864*** (−8.074)	−69.137*** (−6.698)	−11.622*** (−4.479)	−10.911*** (−4.969)	−59.051*** (−8.536)	−58.600*** (−6.665)
Subway	0.468*** (9.730)	0.468*** (4.645)	0.136*** (9.020)	0.135*** (4.681)	0.331*** (8.830)	0.331*** (4.418)
log(Population_density)	5.069 (0.869)	5.124 (1.029)	0.169 (0.092)	0.258 (0.1893)	5.183 (1.144)	5.125 (1.219)
log(Wastewater)	3.580 (0.428)	3.633 (0.536)	−0.139 (−0.053)	−0.169 (−0.095)	3.740 (0.574)	3.813 (0.665)
log(Garbage)	22.403** (2.335)	22.185** (2.443)	6.264** (2.092)	6.289** (2.233)	16.270** (2.177)	16.130** (2.267)
log(Greenspace)	−0.957 (−0.074)	−0.100 (−0.009)	−1.179 (−0.291)	−0.775 (−0.202)	0.771 (0.077)	1.178 (0.137)
Adjusted R2	0.720	0.720	0.646	0.645	0.701	0.701
Weak Instrument Diagnostics (Cragg-Donald F-stat)		107.805		84.347		98.046

Note: The values of the constant terms are not reported. t statistics in parentheses. Instrumental variables are Lat, Lat², and Lat³.

*** p ≤ 0.01, ** 0.01 < p < 0.05, *0.05 < p < 0.1.

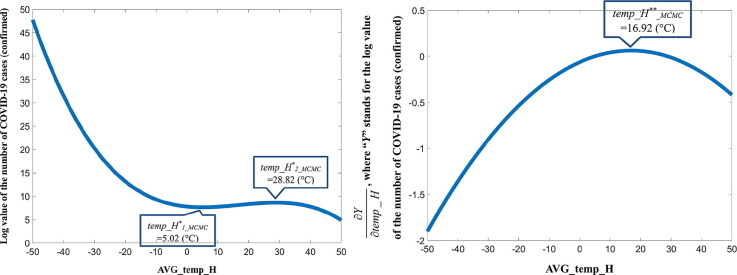
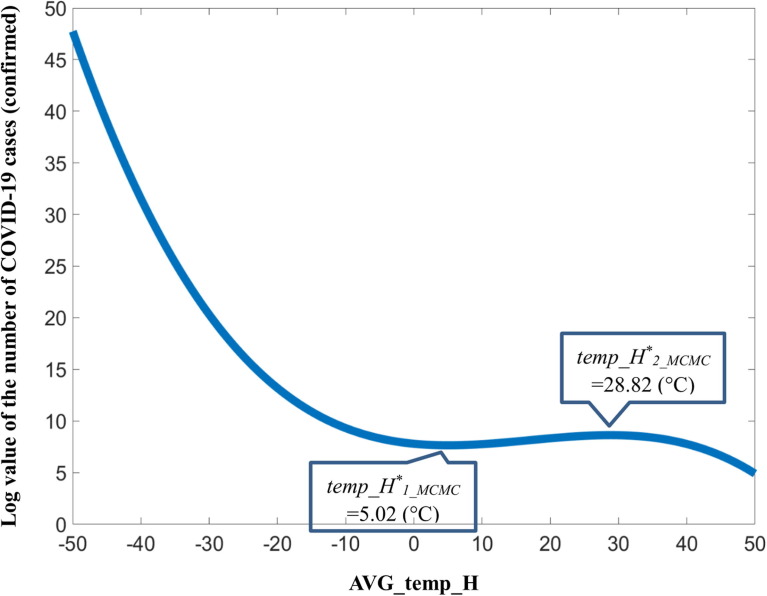
The computer-based simulation of equation (4) is shown in Fig. 4 , which shows that, when the temperature is low, the growth in COVID-19 transmission is very high, and this suggests that the virus might favor low temperatures. It could equally suggest that when temperatures are low, people tend to go indoors, and we already know that transmission is higher in confined spaces than outdoors. So, the model can also account for this explanation. In addition, two inflection points are clear in the figure. The most important implication is that we do not pay attention to this cubic function itself; rather, we are more interested in its first-order derivative, which leads to the following equation:

$$\frac{\partial Y}{\partial temp\_H}=-0.0097\ast {(temp\_H)}^2+0.6898\ast temp\_H-4.6366=0$$ (5)

Fig. 4.

Computer-based simulation of the cubic function of AVG_temp_H.

When we solve Eq. (5), we have two results: temp_H*₁ = 7.52, and temp_H*₂ = 63.40, measured in Celsius.

In Fig. 4, these two critical values for the maximum daily temperature show a range within which COVID-19 transmission increases. But this temperature belt [7.52 to 63.40 °C] covers a wide range of countries and regions on our planet. This finding may be disappointing because almost every country is vulnerable to the virus from this geographic perspective, especially those in the temperate zone of the Northern Hemisphere around January.

3.4. The best result with the refined data set, log form, and Markov chain Monte Carlo (MCMC) simulation

Is it possible to increase the accuracy of the model further to obtain a more useful result? By refining the data set as mentioned above, we can now take the log form of ΔN_COVID-19 for the period T₃₁, but still not for T₂₁ and T₃₂. Table 6 shows the empirical results with the dependent variable log(ΔN_COVID-19) with a cubic function. In Models (19) and (20), the parameters are more significant, and the overall fitness of the model is even better. However, after the refinement process, we only have 155 cities as observations, it might be doubtful that the result will be adequately representative. Therefore, to obtain the maximum accuracy for the functional form regarding the temperature, we employ a linear Gaussian model (LGM) to simulate our results. The sampling method used is Gibbs sampling, followed by a Markov chain Monte Carlo (MCMC) estimation. As shown in Models (21) to (24), we try the MCMC draws for 10,000, 1 million, 10 million, and 20 million respectively. These simulation-based estimation models have very robust results. Hence the limited number of sample cities, i.e., n = 155, is not too small for drawing a representative conclusion. Finally, Model (24) is our best shot for the empirical model specification. As seen, increasing the number of MCMC draws would be meaningless. The results of Model (24) are robust enough to yield a valid conclusion. Notably, the cubic term of the temperature variable is now significant at around the 5% level, with a p-value of 0.0511, which makes us more confident about using the cubic functional form. Now, the counterpart of Eq. (4) is as follows:

$$\mathit{log}(Y)=-0.000146\ast {(temp\_H)}^3+0.00741\text{0}\ast {(temp\_H)}^2-0.063332\ast temp\_H+7.793842$$ (6)

Table 6.

Estimation results with dependent variable log(ΔN_COVID-19) with cubic function (without Hubei province, n = 155).

	Model (19)	Model (20)	Model (21)	Model (22)	Model (23)	Model (24)
	OLS	GMM	LGM	LGM	LGM	LGM
	(T31)	(T31)	MCMC draws: 10,000 (T31)	MCMC draws: 1,000,000 (T31)	MCMC draws: 10,000,000 (T31)	MCMC draws: 20,000,000 (T31)
AVG_temp_H	−0.064*** (−4.852)	−0.076*** (−5.469)	−0.064*** (−4.782)	−0.063*** (−4.819)	−0.063*** (−4.822)	−0.063*** (−4.822)
(AVG_temp_H)2	0.007*** (5.121)	0.007*** (4.112)	0.007*** (5.150)	0.007*** (5.149)	0.007*** (5.142)	0.007*** (5.146)
(AVG_temp_H)3	−0.000144** (−2.145)	−0.000103 (−1.356)	−0.000145* (−2.174)	−0.000146* (−2.189)	−0.000146* (−2.186)	−0.000146* (−2.189)
log(Dist)	−1.296*** (−11.912)	−1.372*** (−12.951)	−1.289*** (−11.750)	−1.288*** (−11.922)	−1.288*** (−11.929)	−1.288*** (−11.929)
Subway	0.001** (1.990)	0.001** (2.238)	0.001* (1.944)	0.001* (1.983)	0.001* (1.982)	0.001* (1.983)
log(Population_density)	0.123* (1.701)	0.112 (1.365)	0.127 (1.767)	0.128 (1.783)	0.128 (1.781)	0.128 (1.781)
log(Wastewater)	0.136 (1.315)	0.136 (1.108)	0.141 (1.378)	0.141 (1.372)	0.141 (1.369)	0.141 (1.369)
log(Garbage)	0.518*** (4.352)	0.527*** (3.891)	0.513*** (4.365)	0.513*** (4.334)	0.513*** (4.329)	0.513*** (4.330)
log(Greenspace)	0.025 (0.155)	0.008 (0.039)	0.031 (0.192)	0.033 (0.207)	0.033 (0.206)	0.033 (0.206)
Adjusted R2	0.782	0.781
Weak Instrument Diagnostics (Cragg-Donald F-stat)		107.805

Note: The values of the constant terms are not reported. t statistics in parentheses of OLS and GMM models. Posterior t values in parentheses of the Linear Gaussian Models (LGM). Instrumental variables are Lat, Lat², and Lat³.

*** p ≤ 0.01, ** 0.01 < p < 0.05, *0.05 < p < 0.1

As noted in the introduction, the understanding of the effect of temperature on the spread of COVID-19 could be very sensitive to data. Because in reality variation in the range of temperatures in regions with confirmed COVID-19 data is limited compared to the possible need for a wider range to reveal the hidden mechanism in the dynamics of COVID-19 transmission, extrapolating the temperature range from the sample data is a necessity.

The ability to extrapolate data using a linear model is very limited, so we need to use a more complex nonlinear model specification. However, the outcome of using nonlinear models, unlike the simple linear models, depends heavily on precise knowledge about the functional form of the nonlinear model. Thus, accurate information about the functional form is an essential prerequisite to its successful application. Therefore, everything we needed to boost our effort to the extreme could be sued.

Following the same approach as in Eq. (5), we can solve for two new critical values: temp_H*_{1_MCMC} = 5.02, and temp_H*_{2_MCMC} = 28.82, all in °C. This is a much more promising result than we mentioned earlier, because the threshold value of the upper level of the inflection point is much lower and can be achieved more easily.

Furthermore, our next finding may be more exciting. Technically speaking, the transmission of a virus is not the same as the initial outbreak. If the number of infections increases slowly, then the situation can be kept under control. But, if the rate of infection grows too quickly, then an outbreak occurs; therefore, speed is essential. The method we use to quantify the concept of speed in COVID-19 transmission is similar to the approach to velocity in Physics, i.e., we take the derivative. In the dynamics of Physics, the first-order derivative of a motion is the speed, and the second-order derivative is its acceleration.

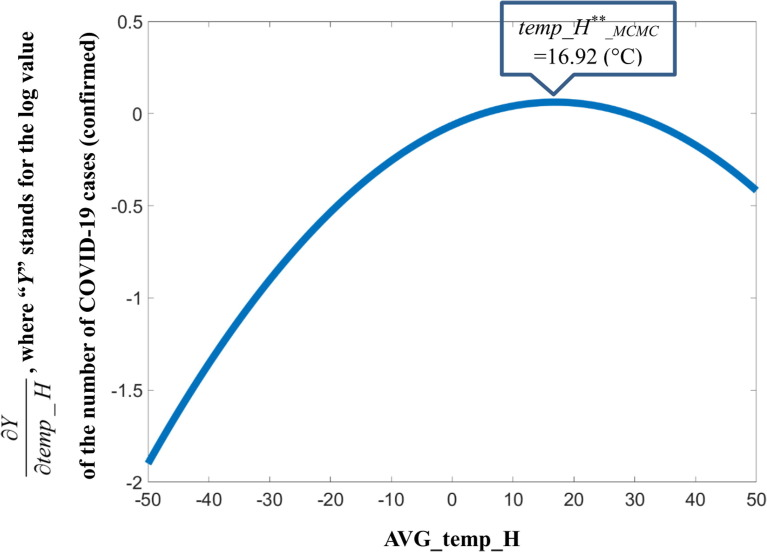
In addition, Eq. (5) is again a quadratic form. As simulated in Fig. 5 , the inverted U-shaped curve suggests an inflection point, beyond which the transmission speed decreases. Thus, differentiating Eq. (6) twice, we have the following equation:

$$\begin{array}{c}\frac{d^{2}log(Y)}{dtemp\_H^2}=-0.000876\ast temp\_H+0.014820=0\\ \end{array}$$ (7)

Fig. 5.

Computer-based simulation of the first-order derivative of the cubic function of AVG_temp_H.

When we solve Eq. (7), we come to a core understanding of the COVID-19 pandemic in this study: temp_H^**_{_MCMC} = 16.92 (°C). This result confirms our initial hypothesis that the temperature matters not only in COVID-19 transmission but also in its outbreak. The optimistic perspective indicated by both Fig. 5 and the solution of temp_H^**_{_MCMC} shows that when the temperature is higher than the calculated critical value, the speed of urban COVID-19 transmission tends to slow down, and hence the risk of outbreak diminishes.

Table 7 compares the dynamics of COVID-19 transmission related to the temperature using different models. As discussed previously, the best result is in the last column of Table 7. This study identifies four important temperature zones (in Celsius) to enable us to understand the dynamics of COVID-19 transmission and its relationship to temperature. First, in the temperature range of −50 to 5.02, transmission decreases. Second, in the range of 5.02 to 16.92, transmission accelerates. Essentially, this is the temperature range for an outbreak. Third, in the range of 16.92 to 28.82, the transmission still increases but more slowly. Finally, in the range of 28.82 to 50, transmission decreases, and the pandemic gradually dies out. In addition, it is important to understand the critical value of 16.92 °C. Based on our analysis of the speed and acceleration, this temperature can be considered the most dangerous, i.e., the temperature with the highest rate of infection.

Table 7.

Comparison of the dynamics of transmission of COVID-19 related to the temperature using different models.

Corresponding model	Model (14) GMM (T31)	Model (20) GMM (T31)	Model (24) LGM (T31)
Description	GMM without the log form of ΔN_COVID-19	GMM with the log form of ΔN_COVID-19	MCMC draws: 20,000,000
Transmission decreases	(−50, 7.52)	(−50, 6.31)	(−50, 5.02)
Transmission increases in the acceleration manner	[7.52, 35.46]	[6.31, 22.60]	[5.02, 16.92]
Transmission increases in the deceleration manner	(35.46, 63.40]	(22.60, 38.88]	(16.92, 28.82]
Transmission decreases	(63.40, 100)	(38.88, 50)	(28.82, 50)
Unit	°C	°C	°C

Note: All the temperature values mentioned above are the maximum temperature of the day.

Recall that this is the maximum daily temperature, so the corresponding average daily temperature is lower. For example, in a typical Chinese city where the maximum daily temperature is around 35 °C in the summer, the recorded average daily temperature is usually from 25 °C to 30 °C.

Although the calculation results presented here appear to be novel, other studies are also available that support these results. Using data on China, some scholars find that, with an average temperature range of < 3 °C, when the temperature increases, the confirmed daily cases increase (Xie and Zhu, 2020). In our calculation, the infection starts to increase when the maximum daily temperature is above 5.02 °C. Moreover, a descriptive study using global data shows that the temperature range of 5 °C to 15 °C covers about 60.0% of infections, which is considered the “optimal temperature zone” for the spread of the virus. The most confirmed cases are in the maximum temperature range of 5 °C to 30 °C (Huang et al., 2020). This is again an interesting coincidence. As we can see, the results of computer-based simulation in this study, which are also solutions to an estimated function, match the reality.

In addition, a study using data on Barcelona, Spain, shows that 60% of the cases occur when the maximum daily temperature is in the range of 12.2 °C to 22.8 °C, in which the negative connection is identified (Tobías and Molina, 2020). Notably, an interesting study using data on Brazil shows a critical temperature range between 16.8 °C and 25.8 °C, in which a negative linear relationship exists between the temperature and new cases. Moreover, going beyond the threshold of 25.8 °C, the correlation curve becomes flat, hence even higher temperature does not decrease transmission (Prata et al., 2020). Is this 16.8 °C another coincidence? Based on the novel theory proposed in this study, we calculate a critical value of 16.92 °C, beyond which the transmission increases with the maximum daily temperature up to 28.82 °C but more slowly. Therefore, in a more general sense, the temperature range between 16.8 °C and 25.8 °C proposed in the other study does not really proxy for the negative linear relationship. Instead, it should correspond to the negative relationship in the dimension of the second-order derivative.

In addition to the temperature range issue, the speed or velocity of COVID-19 spread is also noted in some emerging studies. For example, in France, the speed of infection decreases with the temperature at the initial stage of the pandemic, but seasonal fluctuation with temperature is unknown (Demongeot et al., 2020). Another study indicates that countries with a higher average temperature in February have a slower spread at the early stage of the pandemic (Holtmann et al., 2020). In fact, all these findings can be unified by a more general theory proposed in this study.

4. Discussion

4.1. Supporting evidence from Wuhan, China

On February 13, 2020, the maximum daytime temperature in Wuhan reached 17 °C. From February 20 to February 25, the local temperature began to rise, and at the same time, the rate of growth in new COVID-19 infections began to slow compared to the rate before this period.

4.2. The coincidence of the shifting outbreak line in latitude

Growing evidence from around the world supports our hypothesis. For example, in Italy, the outbreak of infection started in the north, rather than the south, where the temperature is higher. In India in early March 2020, the new infections were mostly in the north. In addition, the outbreaks in Germany and the UK in early March 2020 might be linked to the temperature.

Moreover, geographic evidence shows that all these cities outside China with outbreaks of infection from late February to early March 2020 are at approximately 35 to 45° latitude north. For example, Yokohama (Japan), Daegu (South Korea), and Tehran (Iran) are all at around 35° latitude north. Some European countries with the COVID-19 outbreak are at around 40 to 45° latitude north. In fact, because of the effect of ocean currents, in wintertime, western European countries are typically warmer than countries in eastern Asia at a similar latitude.

As mentioned above, the cities in China with earlier outbreaks are centered at 30° latitude north. Over time, between January and March, the temperature in the Northern Hemisphere rises, and the line of the outbreak in eastern Asia shifts from 30° north to 35° north, which is roughly comparable to the temperature at 40° to 45° in western Europe. This can help clarify the outbreak outside China in early March 2020.

4.3. More emerging evidence worldwide in March 2020

The temperature records on March 9, 2020, in some European cities were Paris (6–12 °C), London (5–11 °C), Milan (4–9 °C), Rome (0–14 °C), and Berlin (5–11 °C)—all in the temperature range consistent with the viral outbreak as calculated in this study. Thus, the rapidly increasing rate of infection in the western European countries in early March 2020 corresponds with the temperature range [5.02 °C to 16.92 °C], at which transmission accelerates, as hypothesized. Similarly, in the US, the temperature on March 11, 2020, was 4–10 °C in Seattle and 2–12 °C in New Rochelle, NY—two cities that experienced a rapid increase in the infection on that day. Three days later, when the confirmed COVID-19 cases in Italy approached 20,000, the temperature in Milan was 7–11 °C, which is very similar to the temperature in Wuhan in early February 2020, at the time of its outbreak.

Still more evidence to support our theory is given by the temperature in some Asian cities. On March 9, 2020, the temperature in Yokohama was 9–18 °C, in Daegu 3–17 °C, and in Tehran 6–14 °C; this shows that the rate of infection began to slow in South Korea and Japan that day but accelerated in Italy, France, and Germany, offering strong evidence of the threshold value of 16.92 °C. In particular, a comparison of South Korea and Iran shows that on March 9 the temperature was lower in Iran than in South Korea, and the rate of infection correspondingly accelerated more quickly in Iran.

Over time, some counties in western Europe at higher latitudes faced a greater risk of infection, but at the same time, South America as a whole had only 98 reported COVID-19 cases, and all of Oceania has only 122 as of March 11, 2020. This supports the theory implied by this study: in March 2020, when the Northern Hemisphere largely remained cold, the Southern Hemisphere was much less vulnerable to infection with COVID-19 because it had moderate and high temperatures. This is a pattern that reversed with the seasons, as seen later.

The week from March 16 to March 22, 2020, provides still more evidence. The pandemic suddenly worsened in many places, with a daily increase in infection that reached its maximum to that point in many countries. Table 8 compares the maximum daily temperature and the evolution in the pandemic that week in many cities worldwide. In most of these examples, the temperature range for an outbreak as well as the critical value of 16.92 °C, which corresponds to the maximum acceleration in the growth of the infection, can help explain the patterns in the pandemic. Table 8 has too many coincidences that we cannot ignore. In the following week (i.e., the week ending March 30, 2020), conditions in both Europe and the US were out of control. The temperature records in those regions correlate well with the temperature range for an outbreak outlined above.

Table 8.

The “crazy” week of March 16 to March 22, 2020: some evidence about the temperature and the COVID-19 outbreak.

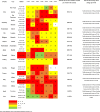4.4. Later lines of evidence in 2020

Still more persuasive events emerged in April, May, and June 2020 that emphasize the role of temperature.

The first was in Canada and Mexico, which are both next to the US. The temperature is much lower in Canada than in Mexico, and the rate of infection accelerated more in Canada, especially in April.

Second, in Italy and Spain, in the week of April 15, 2020, the temperature is higher in Italy than in Spain (above 17 °C), and the growth rate in infection is lower in Italy than in Spain. The situation is similar in Turkey.

The third is Russia, which presents robust evidence for our theory. In March 2020, infections in western Europe accelerated rapidly, yet in Russia, the spread seemed rather low. At that time, the highest daily temperature in Moscow is slightly below 5 °C, just below the temperature range for an outbreak hypothesized in our model. Later, when the temperature rose, Russia experienced a massive outbreak. Russia had taken precautionary activities beginning in late January, so imported infections were not widespread. But, beginning in late March, infection rates accelerated. From May 13 to 25, the maximum daily temperature in Moscow was below 15 °C, and the daily increases in infection in Russia remained high.

The fourth is the UK. Around the week of May 7, the daily increase in the confirmed caseloads gradually slowed in many European countries, yet it rose in the UK. The temperature records for London show that the maximum daily temperature for several days was around 17 °C, which is consistent with the value calculated in this paper as the height for acceleration in viral transmission. In terms of the daily increase, this result suggests that the daily increase in infection was at its height during this temperature range, precisely the situation in the UK.

The fifth is China. Although the COVID-19 outbreak was largely contained in China, the risk of a second round was still high in its northeastern regions in April and May. Most of the new infections were imported, so why were they centered in the northeastern regions, not the southern regions, which had much more international interaction? One reason is that the temperature is lower in northeastern China than in the southern regions. Shulan, in Jilin Province, experienced a small-scale outbreak, which resulted in a long chain of local transmission (Chinanews, 2020). On May 23, 2020, the maximum daily temperature there was 17 °C, the critical level, as calculated in this study.

The sixth is a few Latin American countries. From May 18 to 28, 2020, Santiago, Chile, has colder weather, with a maximum daily temperature from 29 °C to 12 °C, and infections with COVID-19 there increased very rapidly. The other emerging epicenter in South America during that period was Peru, which had a sharply increasing number of infections in May. In Lima, the capital, in the week from May 17 to 28, the maximum daily temperature was around 19 °C. In Ambato, in the middle of Ecuador, another emerging epicenter in South America, the maximum daily temperature in the week of May 27 was around 17 °C. Moreover, in Buenos Aires, Argentina, the maximum daily temperature from May 21 to 28 was around 17 °C, just when it had a substantial increase in the rate of infection.

The seventh relates to frozen food. In June 2020, new evidence emerged. Our analytical model employs a temperature range (-50 °C to 5.02 °C) that we have difficulty explaining. According to the model and its results, the SARS-CoV-2 virus is supposed to be very active at this low-temperature range, but it was difficult to find global evidence. Then, more new reports began to appear. In June 2020, during a resurgence in infection in Beijing, frozen salmon was suspected to be a potential carrier (China Daily, 2020a). Experts believe that the virus might be able to survive for 20 years at a temperature of −20 °C (Xinhua News, 2020a). In addition, in Germany, meat processing plants (i.e., slaughterhouses) experienced 770 infections (China Daily, 2020b), and Australia had a high jump in cases during that period as well (Xinhua News, 2020b), when some experts said that the virus could even survive at a temperature of −80 °C (National Business Daily, 2020). These new cases support our findings and results, which explain why infection outbreaks are easily linked with scenarios such as wholesale markets with frozen food and slaughterhouses in which the temperature spans from freezing to normal. The threshold temperature in the model is 5.02 °C. The temperature for cold storage in the freezers is normally set at 4 °C. When meat is taken out and attains a normal indoor temperature, if it contains the frozen virus, the infection can occur.

Returning to Argentina, the daily number of new infections in September grew to around 10,000. From September 8 to 16, 2020, the maximum daily temperature in Buenos Aires was around 17 °C. In addition, the second wave of infection in Europe shows strong evidence to support our proposed theory. For example, during the week of September 29, 2020, the highest daily temperature in Moscow was around 17 °C when the daily increase in infection dramatically accelerated again. The same thing also happened in London after September 28 (around 17 °C), Paris after September 29 (around 17 °C), and Madrid after October 2.

4.5. The “exception” of tropical regions

In March 2020, the number of infections in South American countries also increased but much more slowly, because of the temperature there. In addition, Australia experienced more infections, but more than 80% were imported.

Although this theory does not precisely explain the evolution of the pandemic in every country due to several influential factors, it works well in most situations. The most obvious “exception” is Brazil, which is in a tropical region. Brazil had a high rate of infection as well as high temperatures, so it does not appear to be a good case for the application of this theory. However, the COVID-19 outbreak in Brazil can be explained by three facts.

First, some studies hold that the infections in countries in the Southern Hemisphere comprise more imported cases (Rio and Camacho-Ortiz, 2020). Second, studies in Brazil show that relative humidity might be another influential factor in the transmission rate, but it is not discussed in this paper. Third, Brazil covers a large territory, with a wide range of latitudes. Although many parts of Brazil are in a tropical zone, the southern part of the country is in a subtropical zone, which is farther from the equator and hence has lower temperatures, even much lower.

São Paulo, which had the most infections in Brazil, is in the far south corner of the country. The temperature is much lower in São Paulo than in Brazilian regions close to the equator. As a result, the maximum daily temperature there is <30 °C, which is in the transmission range proposed in this study. Notably, on May 23, 2020, when the daily infections in Brazil reached a high of 16,508, the maximum daily temperature in São Paulo was around 21 °C. Then, on May 24, the maximum daily temperature fell to only 15 °C and on May 25–26 it was 19 °C. Another example is Rio de Janeiro, which had the second-largest outbreak in Brazil and is also in the southern corner of the country (Auler et al., 2020).

4.6. The cyclicity of the ongoing COVID-19 pandemic

This study also reveals the cyclicity of the ongoing COVID-19 pandemic worldwide. The pandemic may alternate between the Northern and Southern Hemispheres. In addition, the official website of the World Health Organization (WHO) says there is a lack of evidence to show that people will not be infected in environments in which the temperature is above 25 °C. This study indicates that when the temperature is high, the urban transmission is slower, so it is not a matter of whether infections will spread, only of the speed of transmission.

In May 2020, as the Northern Hemisphere began to warm in the runup to summer, the situation in the Southern Hemisphere, especially in Latin American countries, began to deteriorate. On May 23, WHO officially declared Latin America a new epicenter (China China Daily, 2020c, National Business Daily, 2020). Africa, which has fewer medical resources, is also in the Southern Hemisphere. Over time, conditions there might become more difficult. On May 25–26, when COVID-19 infections increased very rapidly in Johannesburg, South Africa, the maximum daily temperature there was 17 °C.

4.7. The latest evidence in 2021

In early 2021, when the Delta variant and other variants of SARS-CoV-2 developed, the story changed. This is why we focus on the early-stage transmission of COVID-19 throughout this paper. Nonetheless, the analytical framework proposed in this study is still useful. The wave of transmission in China since October 2021 offers another clear evolutionary pattern. First, the outbreak began in northern China and then spread to the southern part of the country when the temperature dropped there. Second, in many cities, the outbreak started right after a period with the highest daily temperature of around 17 °C, which fully demonstrates the fitness of our model. A similar situation has occurred in Europe and elsewhere since October 2021 as well.

5. Conclusions and recommendations

On March 6, 2020, the WHO official in Geneva said that “currently we are unclear about the activity and performance of COVID-19 under different climate conditions” (Xinhua News, 2020c). The present study offers a theoretical framework to understand this issue supported by several lines of evidence.

This study estimates a cross-sectional model that links the growth rate of confirmed COVID-19 infections with linear, quadratic, and cubic terms for temperature with a sample of 295 cities in China, for the period of the initial outbreak of COVID-19 in early 2020. To identify the causal effect, it uses latitude as the instrumental variable for temperature. We find that 16.92 °C is a critical point for the spread of infection, which is a novel finding. In this study, we add complex nonlinear functions, such as quadratic and cubic functions, to the empirical model. OLS, GMM, and LGM models are used to obtain an accurate quantitative interaction between the temperature and confirmed infections through continuous optimization. The results of this study are consistent with actual conditions in the COVID-19 pandemic in many regions of the world, even those in northern China since October 2021.

The sample data used in this study come from cities in mainland China, which is geographically large enough to cover a wide range of climatic conditions as well as urban patterns and a very large urban population. The results and findings in this paper are adequate for drawing a general conclusion. In terms of population, the sample cities in China are comparable to small counties in Europe, and some provinces in China with significant COVID-19 outbreaks are comparable to large countries in Europe. This comparison helps study the evolving pattern in the pandemic in Europe and elsewhere. In addition, although the number of cities used in this paper is not large enough to call it a “big data analysis,” we use MCMC simulation for 20 million draws, and the results confirm the robustness of the analysis.

In view of the ongoing nature of the pandemic worldwide, this research also has important policy implications. If people are not fully immunized against COVID-19 in a timely fashion, mankind will be living with COVID-19 for a long time, in the cyclical pattern of fluctuation shown to date. The failure to pay attention to the evidence revealed so far presents a great and continuing risk, especially at this critical moment in the global COVID-19 pandemic.

In the scientific community, an increasing number of researchers believe that transmission of this disease is associated with temperature. The Centers for Disease Control and Prevention (CDC) in the US also issued official alerts that viral transmission might increase in the winter of 2020, which is precisely what happened. However, a coherent theoretical base to link the temperature with the pandemic is still absent. This paper is therefore of general interest regarding the current COVID-19 crisis and has important implications on the future evolution of the pandemic and how we need to prepare for it (Walenta, 2018, Meynard et al., 2020).

The world is at a crossroads right now, and we must do every possible before it is too late (Aleta et al., 2020, Nuñez et al., 2020, Soong et al., 2021). The relationship between climate and man (Billington, 1986) is being reshaped by the ongoing COVID-19 pandemic along with climate change, which is the other type of “weather shock” (Corno et al., 2020). The issues related to this study are important and timely, as an increasing number of emerging infections are being reported in association with frozen food. In addition, the role of wastewater in viral transmission (Bivins et al., 2020, Liu, 2020, Mao et al., 2020, Randazzo et al., 2020, Wang and Liu, 2021) needs to be investigated more thoroughly.

Future studies could follow this paper by conducting further investigations on the relationship between temperature and the pandemic, which is an urgent response called for in recent studies (Ma et al., 2021). The construction of an appropriate analytical framework is badly needed, and that is what we have done in this study.

Although this study discusses the mathematical and statistical relationship between temperature and viral transmission, the internal mechanism in the influence of air temperature on transmission is still a mystery. In addition, although this study has discussed the relationship between temperature and virus transmission, the other parameters such as aerosol transmission, also have impacts on the COVID-19 pandemic. Several papers have argued the importance of the aerosol transmission of SARS-CoV-2 (Kassem, 2020, Cao et al., 2021, Shao et al., 2021, Wang and Liu, 2021). This cannot be ignored when discussing virus transmission. However, due to data limitations, we have to leave such an issue for future researches. But this study can still inspire the possible interaction between temperature and aerosol transmission. More interdisciplinary investigations from the perspective of biology, medicine, chemistry, physics, and so on are needed to unravel that mystery.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Handling Editor: M. Santosh