Abstract
Social distance will remain the key measure to contain COVID-19 before the global widespread vaccination coverage expected in 2024. Containing the virus outbreak in the office is prioritised to relieve socio-economic burdens caused by COVID-19 and potential pandemics in the future. However, “what is the transmissible distance of SARS-CoV-2” and “what are the appropriate ventilation rates in the office” have been under debate. Without quantitative evaluation of the infection risk, some studies challenged the current social distance policies of 1–2 m adopted by most countries and suggested that longer social distance rule is required as the maximum transmission distance of cough ejected droplets could reach 3–10 m. With the emergence of virus variants such as the Delta variant, the applicability of previous social distance rules are also in doubt. To address the above problem, this study conducted transient Computational Fluid Dynamics (CFD) simulations to evaluate the infection risks under calm and wind scenarios. The calculated Social Distance Index (SDI) indicates that lower humidity leads to a higher infection risk due to weaker evaporation. The infection risk in office was found more sensitive to social distance than ventilation rate. In standard ventilation conditions, social distance of 1.7 m–1.8 m is sufficient distances to reach low probability of infection (PI) target in a calm scenario when coughing is the dominant transmission route. However in the wind scenario (0.25 m/s indoor wind), distance of 2.8 m is required to contain the wild virus type and 3 m is insufficient to contain the spread of the Delta variant. The numerical methods developed in this study provide a framework to evaluate the COVID-19 infection risk in indoor environment. The predicted PI will be beneficial for governments and regulators to make appropriate social-distance and ventilation rules in the office.
Keywords: COVID-19, CFD, Social distance
1. Introduction
Latest statistics show the COVID-19 pandemic has infected more than 256 million people and claimed over 5.14 million deaths (WHO, 2021). Novel factors such as high contagiousness, multiple transmission routes and long incubation period have contributed to wide range transmission of COVID-19 around the world. Although the rapid design of new vaccines and therapeutics bring the hope to end the pandemic, due to the emerging virus variants, bottlenecks in vaccine mass production and distribution logistics especially in low-income countries, the epidemiological end of the pandemic might not be reached until 2024 (Mullard, 2020). In fact, the Delta variant has been dominating the global pandemic since the middle of 2021 and has posed challenges to the efficacy of current vaccines. It is expected that social distance rules are necessary for years even though widespread vaccination is reached (Elliott et al., 2021). In addition, the highly interconnected globalised economy, the biodiversity loss and climate change may increase pandemics in frequency. Considering the emergence of SARS-CoV-1, MERS, H1N1(Swine Flu) and SARS-CoV-2, it is expected to encontour new pandemics caused by respiratory epidemics in the near future (Daszak et al., 2020, Health, 2021, Lytras et al., 2021). The social distance rules, mask-wearing mandate, work-from-home orders and large scales of temporary furlough/unemployed workers are applied to reduce virus spread at office, which also impose significant socio-economic burdens on individuals and businesses.
As droplets and aerosols have been widely recognised as the major transmission routes of respiratory epidemics (Prather et al., 2020, Wiersinga et al., 2020), social distancing by avoiding close contact with other people have been adopted as the major measure to effectively reduce the spread of the virus. Various levels of social distancing measures have been implemented in each country according to their different conditions regarding economic scale and medical system capacity as well as the period and scale of COVID-19 spread. For example, the World Health Organisation (WHO) recommends that a distance of 1 m (3.3 ft) or more is safe. Australia, Belgium, Germany, Greece, Italy, Netherlands, Portugal and Spain have adopted 1.5 m. The United States has adopted 1.8 m (6 ft) distancing, and Canada has adopted a policy of 2 m (6.6 ft) (Centers for Disease Control and Prevention, 2020, Giordano et al., 2020, of Health Australian Government, 2020, WHO, 2020). However, recent studies suggested that virus-laden aerosol transmission distance could reach as far as 3–10 m (Bourouiba, 2020, Feng et al., 2020, Gammaitoni and Nucci, 1997, Morawska and Cao, 2020, Setti et al., 2020, Sun and Zhai, 2020). The increased transmissibility of Delta variant also made the previously proposed rules in debate. According to these experimental and numerical results, current social distance policies by most countries over the World will need to be updated and this is expected to bring significant challenges for offices to re-open. In addition, social distancing measures were found to be only moderately effective and a one-size-fits-all social distancing rule is often inconsistent with the underlying science of indoor airborne transmission of virus (Miller et al., 2017). To mitigate the impact of preventive measures on workplace productivity, there is a pressing need for governments and relevant regulatory authorities to quantitatively evaluate the virus infection risk at a certain distance and tailor these rules to the local context, which relies greatly on an in-depth knowledge of the mechanisms underlying the indoor airborne transmission of virus-laden droplets.
Coughing droplets and aerosol characteristics have been experimentally measured (Bourouiba, 2020, Bourouiba et al., 2014, Chao et al., 2009, Zayas et al., 2012). In general, during the droplet transmission process, large droplets rapidly fall to the ground and only small droplets can remain suspend in the air and be transmitted over metres. Real-world situations are often associated with coughing and sneezing, where expelled droplets are composed of different sizes. However, most of these previous experiments focused only on the maximum travel distance of the small size expelled coughing droplets. Despite of their large travel distances (3–10 m), the amount of virus carried by the small droplets is small, and therefore the associated infection risk is expected to be low. Without quantitatively linking the infection probability with the social distance, it is difficult to determine the optimal social distance.
Numerical studies have also been performed to investigate coughing travel distance in both outdoor and indoor environments (Feng et al., 2020, Li et al., 2018, Yang et al., 2017). Compared to experiments, numerical studies can gain insights of the detailed airflow patterns and aerosol movement, and therefore can be used to quantitatively relate the social distance to the probability of infection (PI). Recently, many studies have identified the key environmental parameters such as the wind speed/direction, whether or not wearing a mask and the exposure durations (Dbouk and Drikakis, 2020, Feng et al., 2020, Ho, 2021). However, offices are characterised as confined spaces with high personnel densities, long contact hours and frequent communications. Therefore the investigation focus needs to be shifted from the outdoor wind scheme and face covering to temperature, humidity, indoor wind scheme and the selection of the infection risk modelling. To investigate the virus transmission in indoor environment, Sun and Zhai (2020) proposed a novel infection risk model, which was developed by modifying the classical perfect-mixing-based Wells–Riley model (Riley, Murphy, & Riley, 1978). A target probability of infection value, 2%, was set to evaluate the appropriate social distances in different scenarios. The authors also proposed a critical parameter named social distance index (abbreviated as in their study). However, in this work, the travel distance of the expelled droplet was calculated under over-simplified assumptions. The inclusion of more office related parameters, such as horizontal drag force, air humidity, thermal plume and droplet–airflow interactions, are expected to improve the infection risk model and hence derive a more accurate estimation of reliable social distances for an office environment.
In this study, we developed a new CFD based numerical model to predict realistic transmission of COVID-19 droplets in an office environment. This model includes the office relevant parameters such as horizontal drag force, air humidity, thermal plume and droplet–airflow interactions, and using this model we were able to deduce the relationship between the infection risk and the social distance. The coughing flow profile and droplets movement after expelled from a sitting person with natural thermal plumes were simulated under different humidity levels. The droplets’ evaporation process was validated and included in the analysis of droplet sedimentation and travelling distance to reflect a comprehensive evaluation of the typical office social distancing requirements. The improved Wells–Riley model was calibrated by real cases to predict the PI under a certain condition. The concept of social distance index (SDI) proposed by Sun and Zhai (2020) was re-defined by calculating the fraction of expelled virus entering into a respiratory zone, where droplets are considered respirable only when entering it. Our results quantified the virus infection risk in the office by estimating PI over different social distance, humidity and ventilation rate. The calm and wind scenarios are simulated to investigate the effect of typical indoor wind on the transport of cough expelled droplets. The infection risk of the Delta variant is also taken into consideration and compared with the SARS-CoV-2 wild type. This study is expected to provide supporting information for policy makers to determine the required distancing policies and required ventilation rate for densely populated offices before reaching widespread vaccination coverage for COVID-19. It will also provide a numerical framework to evaluate infection risks for future epidemic outbreaks.
2. Material and methods
2.1. Geometry, mesh and computational setups
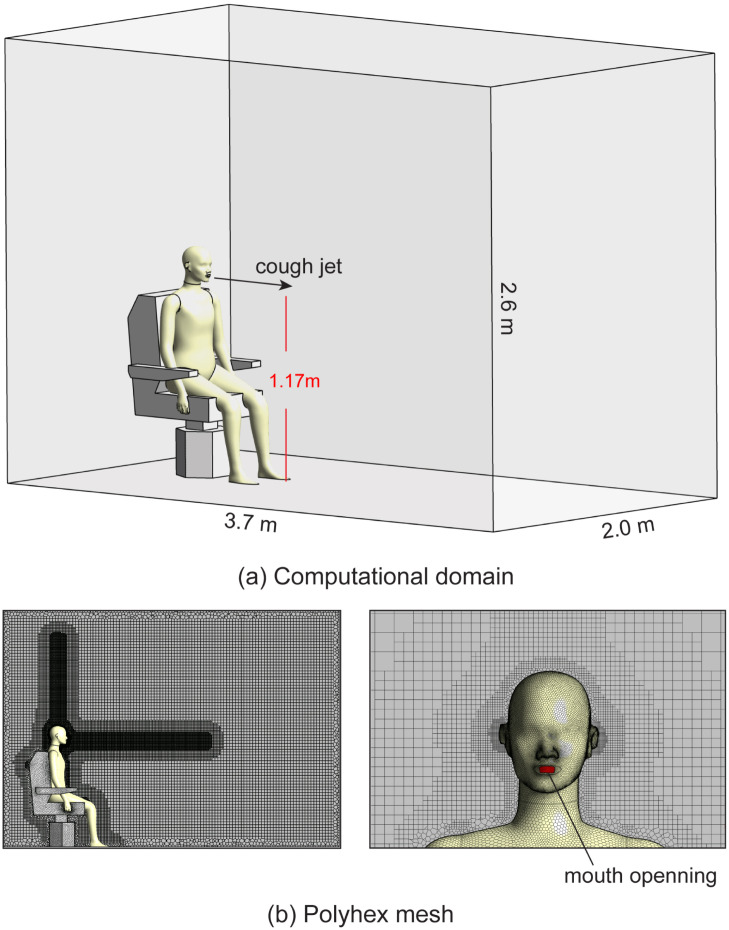
The computational domain is a representative domain for a typical office scenario which consists of a confined space with dimensions of and a sitting manikin on a chair, as shown in Fig. 1. The manikin and the chair models were reproduced from Yan, Li, Yang, Yan, and Tu (2020). The manikin’s mouth is at a height of 1.2 m, with a distance of 3 m to the domain boundary in front and 1.4 m to the ceiling. A coughing jet is expelled from the mouth opening with an area of .
Fig. 1.
Computational geometries and mesh grid generations. (a) The geometries of the room and the sitting manikin used to mimic a calm office environment. The mouth opening is at a height of 1.17 m; (b) Polyhex mesh around the manikin. The volume mesh is further refined in front of the face and above the head to capture detailed cough jet and thermal plume airflow characteristics.
Surrounding the manikin is polyhedral mesh with size 0.5 mm at the mouth opening, 1 mm on the face and 4 mm on the body surface. Five fine prism layers were created around the body to accurately capture the thermal plume and near-wall flow characteristics. The first layer thickness was set 0.2 mm and the growth rate was set 1.2 to make sure , as suggested by the requirements of the Transition SST turbulence model (Feng et al., 2020, Menter et al., 2003). The surface of the manikin is covered with polyhedral mesh and it is transitioned to hexahedral(cut-cell) mesh to fill the volume of the computational domain. As shown in Fig. 1b, the volume mesh is refined in front of the face and above the head to capture detailed cough jet and thermal plume airflow characteristics. Three volume meshes with cell numbers of 1.23 million, 1.67 million and 2.01 million were created to perform mesh independency test. The velocity data along a 40 cm vertical line 0.5 m in front of the mouth at time 0.5 s were extracted and found the increase of cell number from 1.67 million to 2.01 million only produced a negligible change () on the velocity profile. The final mesh for the simulation consists of 1.67 million polyhedral–hexahedral mixed cells, 6.55 million faces and 3.38 million nodes, with the maximum skewness of 0.87.
2.2. Boundary conditions
The floor, the ceiling and the chair were set no-slip walls at room temperature of 25 °C. The surface temperature of the manikin body was set to 32 °C. With the constant temperature between the manikin body and the room temperature, natural convection occurs and thermal plume rises along the body surface. The humidity was modelled by activating species transport model. For saturated humidity conditions, the mass fraction of water in the air are 1.9% and 3.3% for temperature 25 °C and 32 °C, respectively. The initial cough airflow was set to 32 °C at saturated humidity.
Calm and wind scenarios were investigated in this study. For the calm scenario, the indoor airflow is dominated by the thermal plume generated by the manikin. Four side walls (left, right, front and back) of the confined box were set pressure outlet with static pressure of 0 Pa. For the wind scenario, typical indoor wind is applied with the direction from the back to the front of the manikin to address the maximum effect of the air current on droplet transmission. The back and front walls were set velocity inlet and outlet, respectively, with a constant wind speed. Wind speed in indoor office environment is 0.05–0.25 m/s (Baldwin and Maynard, 1998, Ge et al., 2013, Schmees et al., 2008). The maximum wind speed 0.25 m/s was used as the worst case scenario to illustrate the cough expelled droplets transmission in a typical indoor environment with wind.
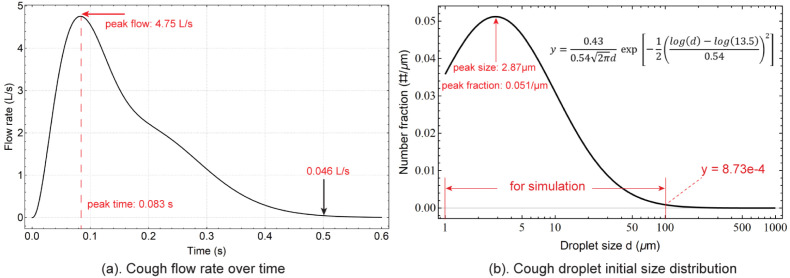
The cough jet direction was set horizontal and the coughing flow rate at the manikin’s mouth opening was extracted from the measured data of Gupta, Lin, and Chen (2009), in which the fitted equation was described in detail. According to the flow rate, a transient mass flow rate boundary condition was converted and defined at the mouth opening, with Cough Peak Flow Rate (CPFR) of 4.81 L/s, Peak Velocity Time (PVT) of 0.083 s and Cough Expired Volume (CEV) of 875 ml, as shown in Fig. 2a. It represents averaged coughing pattern for normal adults in the room environment, in which the peak flow rate occurs at 4.81 L/s at 0.083 s and gradually decreases to 0.046 L/s in about 0.5 s.
Fig. 2.
Boundary conditions of a transient mass flow rate and a droplet initial size distribution are applied at the mouth opening. (a) Coughing flow rate profile reproduced from Gupta et al. (2009) and (b) expelled coughing droplet size distribution reproduced from Chao et al. (2009). The range of the droplet initial size adopted in this study is 1–100 .
Prior to the cough process, the steady simulation was conducted to form the air velocity/temperature distribution and to establish the thermal plume. Transition SST model was used to simulate the turbulent effect as it is more consistent with the natural convection scenario (Feng et al., 2020). The SIMPLE scheme was selected for the pressure–velocity coupling and Second Order Upwind scheme was selected for momentum spatial discretisation. A transient simulation was conducted starting from the converged steady results. Adaptive time steps were used to maintain the Courant number below 1. The minimum time step was 0.002 s when the cough flow rate reached its peak at 0.083 s. 10,000 droplets were released 2 mm in front of the mouth opening and they were released at the time of 0.05 s to mimic the travelling time of cough droplets from throat to the mouth. The initial velocity of droplets released is consistent with the cough jet flow velocity at 0.05 s.
2.3. Determination of droplet sizes
The size of cough expelled droplets ranges from submicron to hundreds of microns. Zayas et al. (2012) measured droplet size distribution from 0.12 to 858 and found 97% of droplets are smaller than 1 . Specifically, most droplets are concentrated at size around 0.3 . However, as viral load is proportional to the droplet volume and considering the volume of a 0.3 droplet is merely of a 10 droplet, this study focuses on droplets larger than 1 . Asadi et al. (2019) measured droplet size distribution under different speech voice loudness, a scenario that is slightly different with this study. Morawska et al. (2009) measured droplet size distributions generated by cough. However, the size range was truncated at . For detailed size distributions covering a wide range of micron particles, Chao et al. (2009) experimentally measured the sizes of droplets expelled from coughs and derived a size distribution by curve fitting ranging from to . The original unit of the number fraction was “number of particles per unit ln()”. In this study, the droplet number fraction is converted to a more convenient unit “num of particles per unit ” as shown in Fig. 2b. Accordingly, the fitting equation is converted to,
| (1) |
Where is the droplet size in and fitted parameters are , and , as calculated in Shang, Tao, Dong, He, and Tu (2021).
WHO previously suggested that the droplets larger than 5–10 would quickly drop to the ground within 1 m (WHO, 2014). However, recent studies updated this criteria and suggested a cut-off size of 100 (Prather et al., 2020). On the other hand, the number fraction distribution peaks at 2.87 and then sharply decreases. When the droplet size reaches 100 , the number fraction drops to , merely 1.7% of its peak value. Therefore in this study, 100 is considered as a cut-off size and only droplets were taken into consideration. Unsteady Lagrangian method is used to track droplets’ trajectories. The tracking scheme is set trapezoidal with a step length factor of 5. The evaporation and temperature dependent latent heat model were activated during the simulation. The number of droplets was analysed by checking the vapour concentration field. When the number reached 10,000, the predicted vapour concentration field was found to be free from the droplet number. 20 representative initial droplet sizes: 1 , 2 , 3 , 4 , 5 , 10 , 13 , 16 , 20 , 25 , 30 , 35 , 40 , 45 , 50 , 60 , 70 , 85 and 100 were selected to mimic the 1–100 size range and 500 droplets were released for each size to statistically calculate their movements and size changing due to evaporation.
2.4. Governing equations
The airflow is solved by the Navier–Stokes governing equations in Eulerian method. The mass and momentum conservation equations are,
| (2) |
| (3) |
Where the is the air velocity vector, is the static air pressure, is the gravity, is the air density and is the air viscosity. The shear stress transport (SST) transition model is used to predict the laminar-to-turbulent cough jet airflow. This turbulence model has been extensively validated with a good balance of computational cost and accuracy compared to LES simulations (Feng et al., 2020, Menter et al., 2003).
The droplet evaporation process requires the air and water species to be calculated separately. The species transport model is used to simulate the air water-vapour mixture airflow. The evaporation process is simulated by a multi-component Eulerian–Lagrangian model. The humid air is depicted as a mixture of dry air and water vapour and is treated in the Eulerian framework,
| (4) |
Where is a physical material property such as density and thermal capacity, is the mass fraction of a species.
The continuity equation is solved separately for air and water species, with shared density and shared velocity ,
| (5) |
| (6) |
Where and are the kinematic diffusivity of water vapour and mass source of water vapour caused by evaporation process. Momentum and energy equations were solved under shared velocity, temperature and pressure for air and water species,
| (7) |
| (8) |
Where is the interfacial forces acting on the droplet surfaces and is the momentum source caused by buoyancy. , and are enthalpy, temperature and interphase heat transfer rate, respectively. The evaporation process is controlled by the equilibrium vapour pressure relative to the ambient pressure at the surface of droplets. The mass transfer rate and the droplet temperature were calculated by,
| (9) |
| (10) |
Where is the dynamic diffusivity of water vapour and is the Sherwood number. and are molecular weights of vapour and the mixture. and are partial vapour pressures on the droplet surface and in the humid air. and are heat capacity of the droplet and latent heat of water.
The droplets were treated as a discrete phase and the their aerodynamic motion is modelled in a Lagrangian framework. The drag force and the gravity (buoyancy) force are the dominant factors for aerodynamics of micron sized droplets,
| (11) |
Where , and are droplet’s mass, density and velocity, respectively, and the drag coefficient is estimated as,
| (12) |
Where , and are empirical constants defined by Morsi and Alexander (1972). In order to accurately model the droplet dispersion with the turbulent airflow, the Discrete Random Walk Model was activated with the time scale constant 0.15.
2.5. Evaporation validation
The expelled droplets are composed of water and non-volatile solid components, known as nuclei. The detailed properties of non-volatile solutes can be referred to mucus composition, which are dominated by Na+, K+, Cl-, lactate and glycoprotein. Nicas, Nazaroff, and Hubbard (2005) suggested the mass fraction of the non-volatile components could be as low as 0.88% and Li et al. (2018) estimated a 1.8% mass fraction. In this study, when expelled from mouth, the evaporation of water and the shrinkage of particles are expected. In this study we adopt the nuclei density as estimated by Nicas et al. (2005) and assume the evaporable water takes 98.2% of the total mass. Assume the droplet nuclei has the same density with water, the nucleus size is estimated by,
| (13) |
This leads to the fully evaporated size . In moderately humid and dry environments, the size of a free-falling droplet could decrease 73.8% and thus shrink into a airborne droplet through evaporation process, especially when the thermal plume generated by the human body heat is present (Prather et al., 2020). The parameters of temperature (T), relative humidity (RH) and droplet sizes were considered to affect evaporation of droplet particles.
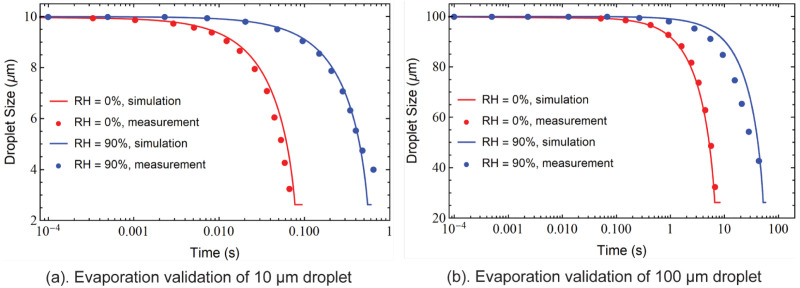
The droplet evaporation modelling is validated with measured evaporation data from Wei and Li (2015) for 10 droplets and 100 droplets at RH 0% and RH 90% (Fig. 3). Droplets evaporate faster for larger-sized droplets and in low-humidity environments. For a 10 droplet, the evaporation process terminates within 1 s whereas a 100 droplet takes much longer time (60 s) to fully evaporate when the environment is humid (RH 90%). The simulation-predicted droplet size variation due to evaporation over time showed good agreement with the experimentally measured data.
Fig. 3.
Evaporation validation. The numerical results are compared with measured data from Wei and Li (2015) for droplet evaporation process validations. Two humidity levels (RH 0% and RH 90%) are considered for two droplet initial sizes (a) 10 and (b) 100 cases.
2.6. Modified Wells–Riley model
The Wells–Riley model has been widely used to estimate the epidemic infection risk. The Probability of Infection (PI), which is defined as the ratio of infected people and susceptible people in a confined space, can be estimated by a classic equation (Riley et al., 1978),
| (14) |
Where is the number of infectors, is the quantum generation rate from one infector that is determined by reverse calculations from actual events, is the pulmonary ventilation rate, is the exposure time and is the room ventilation rate. For a sitting person, the pulmonary ventilation rate is estimated as (Sun & Zhai, 2020).
The classical equation does not involve room ventilation modes and social distance among people. To address this problem, Sun and Zhai (2020) improved the evaluation equation by introducing a social distance index SDI, air distribution effectiveness and initial infection rate ,
| (15) |
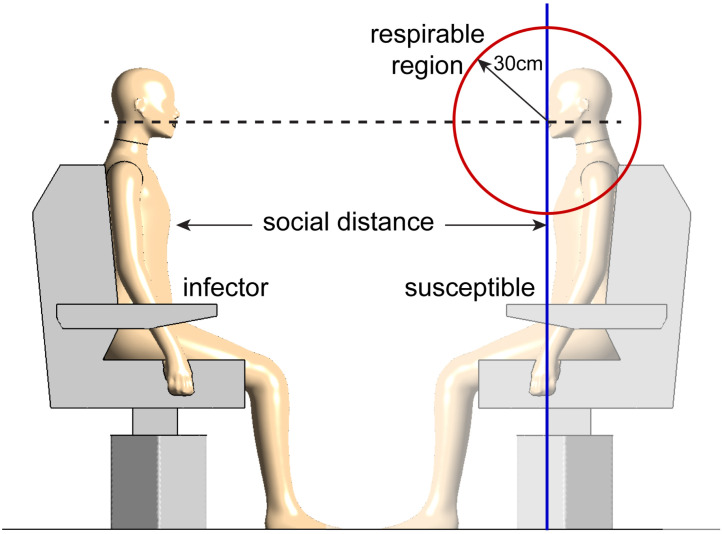
The SDI determines the cumulative fraction of cough-expelled droplets that reaches the respirable region at distance that are potentially inhaled by the susceptible people.
However, Sun and Zhai (2020) calculated the distribution of SDI using a over-simplified “distance reaching method”, in which the travelling time was calculated by assuming droplets constantly reached their terminal velocity to satisfy the balancing of drag force, gravity and buoyancy. In addition, the height of a droplet when reaching a certain travel distance was not considered in the previous calculation as shown in blue plane in Fig. 4. However, this assumption was not reasonable for realistic case as the probability of inhaling micron-sized particles away from the breathing zone is extremely low. Shang, Inthavong, and Tu (2015) investigated the influence of airflow on the micron particles inhalation close to the nostrils and found that only the breathing zone with a radius significantly affected the particle respirability. WHO (2002) and Safe Work Australia (Working with silica and silica containing products - Assessing the risk, 2019) both suggested that 30 cm is a proper range for the breathing zone. In this study, transient CFD simulations were conducted to calculate the SDI with improved accuracy. The “spherical zone method”, in which virus-laden droplets reaching 30 cm from the centre of the susceptible person’s mouth were considered as respirable droplets, as shown in the red circle in Fig. 4. Therefore, the equation to calculate the social distance index is modified to,
| (16) |
Fig. 4.
A comparison of the respirable region defined in this study and the others. Different from the classic definition (distance reaching method) where the respiration region is a vertical plane (blue), in this study we define this region as a sphere with a radius of 30 cm (spherical zone method), shown as the red circle.
Where is the cumulative number of virus reached the respirable region at the distance d, is the total number of virus expelled. is the virus concentration in the droplet when expelled (before evaporation) and is the original diameter of the th expelled droplet.
3. Results and discussions
3.1. Airflow fields and droplets transport characteristics
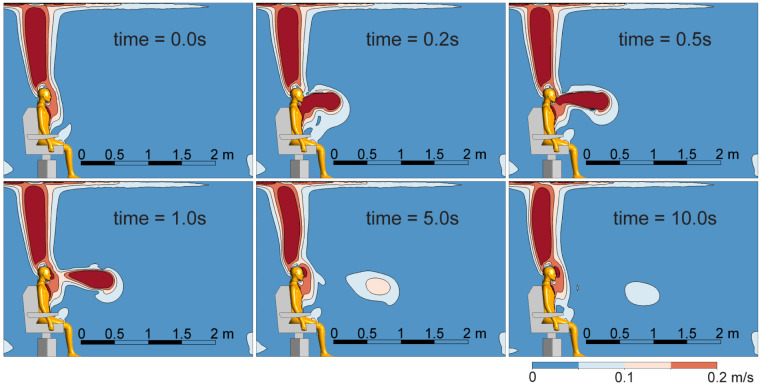
The airflow field characteristics, such as the cough jet flow and the thermal plume, have a strong impact on the travel distance of expelled virus-laden droplets. Velocity contours on the middle plane at different time points are presented in Fig. 5 to provide insights of the cough jet flow travelling in the air. In general, the cough jet exhibits a fast decay after being expelled into the air, and a maximum travel distance of 1.7 m is observed at t = 10.0 s. Prior to the start of a cough (t = 0 s), due to the natural convection effect driven by the temperature difference between the manikin body and the room environment, a relatively stable rising plume with upward thermal buoyancy flow is established near the body, especially for the upper part of the body (head, arms, chest, and the thighs). During coughing, an elongated flow jet with high velocity magnitudes is formed, which quickly reaches to a length of 1 m by the end of the coughing (t = 0.5 s). At t = 1.0 s when the cough ends, a wake region detached from the thermal plume is created and the horizontal travelling distance of this wake remains relatively unchanged. At a later time t = 5.0 s, the wake region travels further downstream and reaches to a horizontal distance of nearly 1.7 m without significant vertical drop. By the end of the simulation at t = 10.0 s, a slight drop of 0.3 m is observed for the wake region. Despite this vertical change, the wake region remains suspended in the air with no apparent horizontal motion. Therefore, it is expected that virus-laden droplets can travel at least 1.7 m after being released from an infected person due to the entrainment effect of coughing.
Fig. 5.
The overall airflow velocity distributions over 0–10 s. The thermal plume is formed before the start of the cough (0 s).
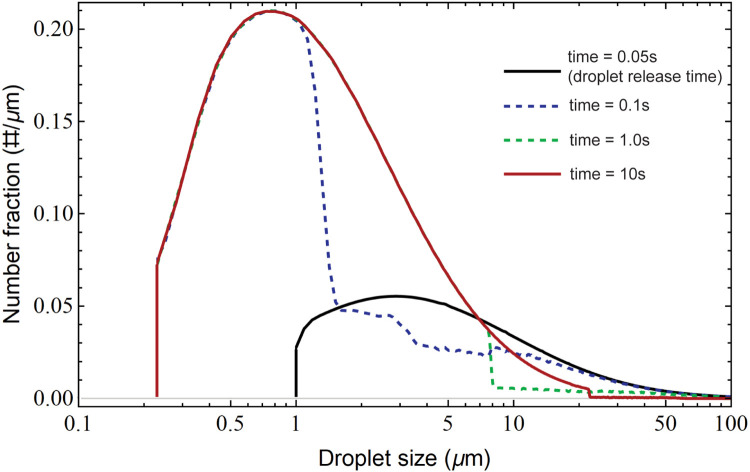
To manifest how cough expelled droplets evaporate as travelling in the air, the variation of droplet size distributions at different time events (t = 0.05 s, 0.1 s, 1.0 s and 10.0 s) under the relative humidity (RH) of 50% are presented in Fig. 6 to reflect the droplets shrinkage due to the evaporation. At the beginning of the cough (t = 0.05 s), the droplet size distribution remains almost identical to its initial condition (Fig. 2b), which generally has larger but fewer droplets. Over the course of time, expelled droplets experienced dramatic number and size changes as travelling in the air. The evaporation process of small droplets occurs at a faster rate than that of large droplets. Our results indicate that the evaporation can be divided into two stages: Firstly, fast evaporation occurs among small droplets ranging from , which forms the ub-micron part of the droplets at t = 0.1 s. Secondly, the evaporation of larger droplets is concluded, which forms additional droplets with medium size (ranging between 1 to 8 ) at t = 1.0 s. Consequently, the terminal size distribution (the red curve at t = 10.0 s) exhibits a wider diameter range extending from sub-micron to 100 . Meanwhile, the droplet size with peaking number fraction is reduced from 2.9 at the beginning of the cough to 0.8 at 10.0 s. These findings are consistent with the literature study conducted by Yan, Li, and Tu (2019), which indicates the evaporation time for 3.5 droplets is nearly 0.1 s.
Fig. 6.
Droplet size distribution changes over time. The droplets are released at 0.05 s and the initial size distribution (black curve) is identical with that in Fig. 2b and it gradually evolves to the red curve at 10 s, where the large droplets evaporate to smaller droplets.
Predicted trajectories of cough droplets at different sizes are presented in Fig. 7. For small respiratory droplets with an initial size of 10 , before evaporation occurs, a cone-shaped bundle of trajectories is observed in front of the mouth. However, the 30 cm travel distance (red lines) remains relatively short, indicating a quick onset of evaporation. Beyond this distance range, expelled droplets rapidly evaporate into to terminal nuclei with a size of 2.6 (blue lines). As a result, those droplet nuclei with significantly reduced diameter sizes can travel a relatively long distance along with the coughed airflow. Besides the dominant bundle of trajectories, few droplet nuclei are captured by the body thermal plume, which turns their motion from longitudinal to vertical. Therefore, for smaller sized respiratory droplets, they are expected to remain airborne in the room for a prolonged period over at least 10 s.
Fig. 7.
Trajectories of droplets with selected initial sizes are plotted to show how the coughing droplets transmit through air. Initial sizes of 10 , 60 and 100 representing small, medium and large droplets present different trajectory features.
For medium respiratory droplets with a diameter of 60 , predicted trajectories corresponding to the original droplet size (red lines) are much longer than that of the small-sized droplets (approximately 1 m). As evaporation occurs, expelled droplets undergo significant size reduction. Because of the relatively large initial droplet size, the evaporation (with size changing from 60 to 15.7 ) takes longer period (in seconds). Different from small sized droplets, most terminal nuclei of medium sized droplets are found at the bottom of the descending cloud. Consequently, despite the reduced extent of dispersion process, more terminal nuclei are found in front of the body, which are effectively pulled back and raised upwards by the body thermal plume.
For large sized droplets (diameter size of 100 ), a completely different dispersion pattern is observed. At the beginning, the trajectory angle for expelled droplets remains relatively unchanged with no distinct vertical displacement. After all droplets have travelled a projectile length around 1 m, they start to descend to the ground due to the combination effect of aerodynamic drag and gravitational force. As the size of droplets is very large, the evaporation is delayed, where the final droplet size (before reaching the ground) is estimated as 50 , being nearly twice of the corresponding nuclei size (26.2 ).
Fig. 8 examines the spatial distribution of expelled cough droplets at five vertical planes with different longitudinal distances (d) in front of the sitting manikin, and the releasing point (0, 0) at d = 0 represents the location of the mouth opening. To better distinguish droplets covering a large size range (with the upper and lower limits of 100 and 0.32 , respectively), the colour bar representing droplet size is shown in log scale.
Fig. 8.
Droplet distributions on planes with distances 0.1 m, 0.2 m, 0.4 m, 1.0 m and 1.7 m to the manikin mouth opening. Locations of planes are plotted from side view. The droplets’ instant sizes are shown in different colours.
For planes d = 0.1 m and 0.2 m, most droplets concentrate around the original releasing point, with droplets on the periphery showing reduced size. This indicates that the majority of the expelled droplets are carried forward by the cone-shaped cough jet. In the meantime, evaporation tends to start from the outer side of the droplet cloud due to a better contact between droplets and environment. Besides the dominant droplets cloud, some small-sized droplets are found in a strip-shaped region, which extends from = −0.7 m to upwards, which corresponds to droplet trajectories that are diverted by the body thermal plume as shown in Fig. 7.
For plane d = 0.4 m, the dominant space of the droplets further expands radially, and large-sized droplets start to descend from the dominant core region due to the gravitational effect. For vertical plane d = 1.0 m, the droplets cloud continues to drift downwards. Because most suspending droplets are in the size range of , a strong extent of droplet dispersion is observed. For plane d = 1.7 m, only few droplets (with the size smaller than 5 ) remain suspended in the air.
3.2. Evaluation of the social distance index
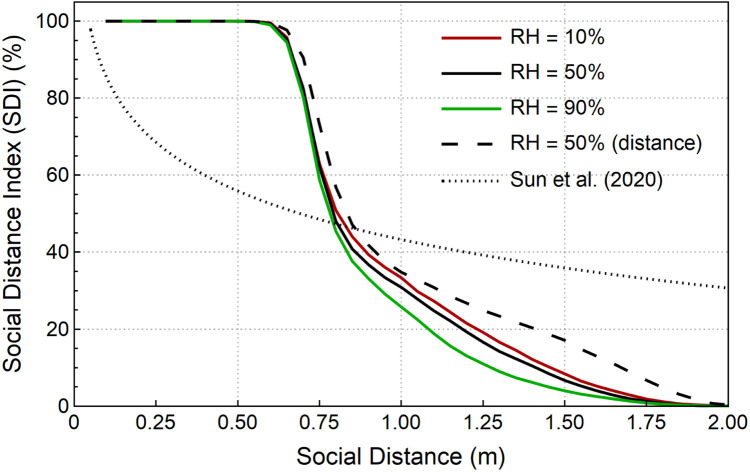
The study revised the social distance index (SDI) by adding a respirable region for respirable virus-laden aerosols, in which the definition is changed to a spherical shape centred at the mouth opening with a radius of 30 cm. The revised SDI stands for the fraction of respirable virus over total expelled virus. The correlation between this SDI and social distance is plotted in Fig. 9, where effects of different relative humidity (RH) are also considered.
Fig. 9.
Social Distance Index (SDI) calculated as the number fraction of virus entering respirable areas. Results are compared with the “distance reaching method” and the simplified analytical solution from Sun and Zhai (2020).
In general, for the RH 50% case, predicted SDI remains nearly 100% for indoor office with social distance less than 0.6 m, which presents strong safety alerts for potential virus spread. As the social distance increases to 0.75 m, the SDI rapidly reduces to 50%. It gradually decreases to 10% when the social distance reaches 1.5 m and finally, a 2 m social distance can ideally prevent the airborne transmission. Results also show that the relative humidity can affect the virus-laden droplet transmission in a certain social distance range, extending from 0.75 to 1.75 m. Specifically, dryer environment (RH = 10%) slightly increases the SDI, while wetter environment (RH = 90%) tends to lower the SDI. This is because dryer environment enables a higher evaporation rate for expelled droplets, which contributes to a much faster droplets sizes reduction and a longer airborne transmission distance. Consistent findings can be found in Ward, Xiao, and Zhang (2020), which reports an increase of 6.11% in COVID-19 cases due to a 1% reduction in RH.
The “distance reaching method” considerably overestimates the SDI, with the major difference between the “spherical zone method” and the “distance reaching method” being found among the distance 0.7 m–1.8 m. Noticeably, Compared to the SDI curve in the study of Sun and Zhai (2020), the current study predicts a much sharper decrease of SDI for the distances between 0.6 m and 1.5 m, which makes the probability of infection rate more sensitive to the social distance around this range. This is mainly due to significantly different social distance index profiles caused by the different calculation methods adopted in two studies. First, Sun and Zhai (2020) used a simplified approximate model to calculate droplets trajectories rather than conducting CFD simulations. The model only calculated the time for a droplet to fall to ground and ignored the horizontal drag force, which significantly overestimated the droplets’ travel distance. Second, Sun and Zhai (2020) adopted the assumption that all droplets that reach a certain distance are respirable, whereas in this study, as shown in Fig. 4, the respirable zone is changed to a sphere with radius 30 cm.
3.3. Effects of social distance and ventilation on the infection risk
In the modified Wells–Riley model, the parameter of quantum generation rate q has not been determined. It needs to be reversely calculated through actual cases. We collected actual data from 4 published COVID-19 superspreading events including 3 events in confined bus spaces in China and 1 event in a call centre in Korea. The calculated corresponding q values are listed in Table 1. The calculated q is between 0.142–0.168 quantum/s and the average value 0.158 quantum/s is used for the infection risk evaluation.
Table 1.
Calculation of the quantum generation rate . Some parameters were estimated in Sun and Zhai (2020).
| Case | Duration (hour) |
No. infected |
No. infectors |
Total people |
Distance (m) |
Ventilation rate [m/(h.p)] |
q (quantum/s) |
|---|---|---|---|---|---|---|---|
| Hunan bus 1 (Luo et al., 2020) | 2 | 8 | 1 | 46 | 0.76 | 20 | 0.142 |
| Hunan bus 2 (Luo et al., 2020) | 1 | 2 | 1 | 12 | 1.07 | 20 | 0.168 |
| Ningbo bus (Shen et al., 2020) | 4 | 23 | 1 | 68 | 0.70 | 20 (GB9673-1996, 1996) | 0.16 |
| Korean call centre (Park et al., 2020) | 32 | 79 | 1 | 137 | 1.00 | 29 (G. & S.S., 2007) | 0.162 |
| Average q | 0.158 | ||||||
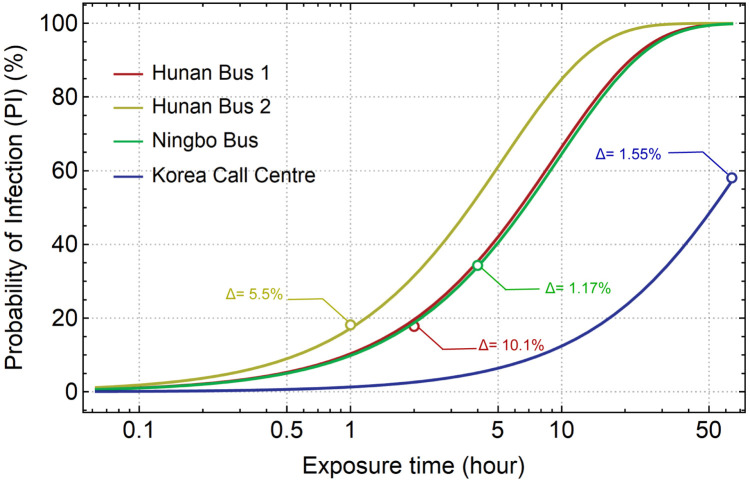
The estimation of q is considerably stable as the variation among 4 cases is less than 10%. To validate the reliability of the estimated q value, four probability of infection (PI) curves over exposure time curves are plotted along with the reported PI values in the actual cases, as indicated by circles in Fig. 10. In general, the comparison shows that the predictions from the modelling match the actual data very well, with the largest difference of 10.1% found in the Hunan Bus 1 case. However, Sun and Zhai (2020) used the similar method and estimated the infective quantum q to be 0.238 quantum/s, 51% higher than that in the current study. As comparisons, Buonanno, Stabile, and Morawska (2020) estimated the q under different scenarios and found the high quanta emission rate could reach up to 1000 quanta/h (0.278 quantum/s). Miller et al. (2021) calculated q 970 quanta/h (0.269 quantum/s) based on a superspreading event.
Fig. 10.
The Probability of Infection over exposure time curves reproduced by the current model and their comparisons with numbers in real cases.
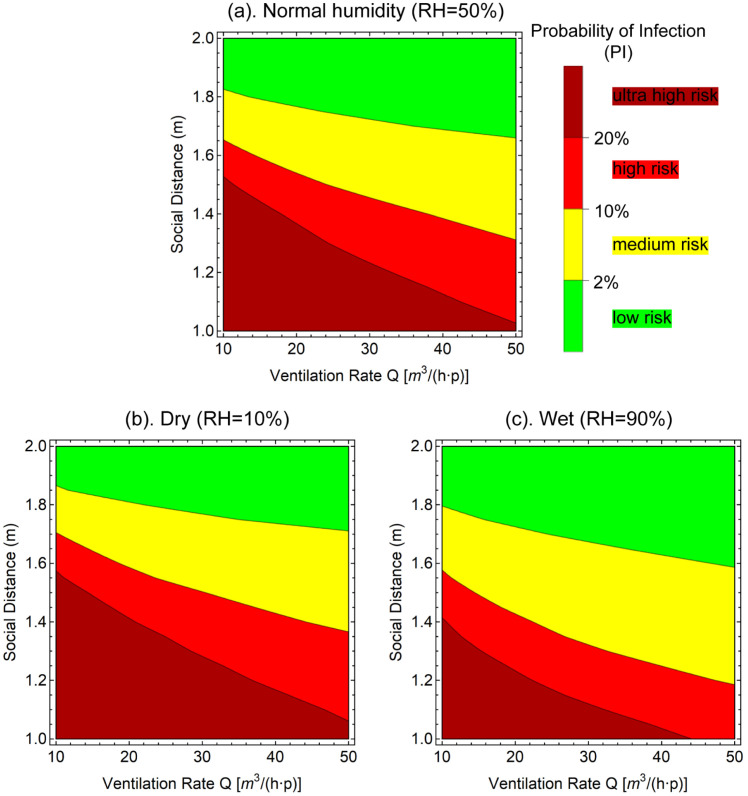
Based on the reversed calculated quantum generation rate, the infection risk in a typical workplace is predicted in the contour plots to present the effects of social distance and ventilation rate (Fig. 11). A 8-h working exposure scenario and a ceiling supply, floor return ventilation form (Ez 1) were selected to represent the typical working environment and low, medium and high (RH 10%, 50% and 90%) humidity conditions were considered. The initial infection rate is assumed 2.8% based on the estimation from existing antibody tests (Mallapaty, 2020, Sun and Zhai, 2020). Three contour lines indicating infections rates of 2%, 10% and 20% were plotted to classify the contour plots into low, medium, high and ultra high risk categories.
Fig. 11.
Contour of Probability of Infection (PI) after typical 8 h-working time in a ventilated office environment. RH 50%, 10% and 90% conditions are plotted to represent normal, dry and wet environments, respectively. The contour plots are split into low, medium, high and ultrahigh risks zones by three PI lines.
In general, the downward inclined contour lines demonstrated that longer social distance and higher ventilation rate effectively lead to lower infection risk. In the medium humidity (RH 50%) case, considering most standards for the workplace ventilation rates are higher than 15 , 1.8 m could be considered as a safe social distance that effectively controls the PI below 2%. The 2% separation contour line is found more sensitive to the social distance than the ventilation rate. At a extreme ventilation rate as high as , nearly 1.7 m is still required maintain the low PI of 2%. To maintain the risk level at the 10% separation contour line, a social distance of is required for a typical ventilation rate. The 20% separation contour line is more dependent on the ventilation rate. To maintain this risk level, a ventilation rate of merely 10 is required to a 1.5 m social distance arrangement. When the social distance decreased to 1.05 m, this risk level could still be achieved if the ventilation rate is adjusted to 50 . The low and high humidity cases exhibited the similar trend with the medium humidity case. The major difference is that the lower humidity drives the separation lines upwards (longer social distance required) and the higher humidity drives them downwards (shorter social distance required).
3.4. Effects of wind and virus variants on the infection risk
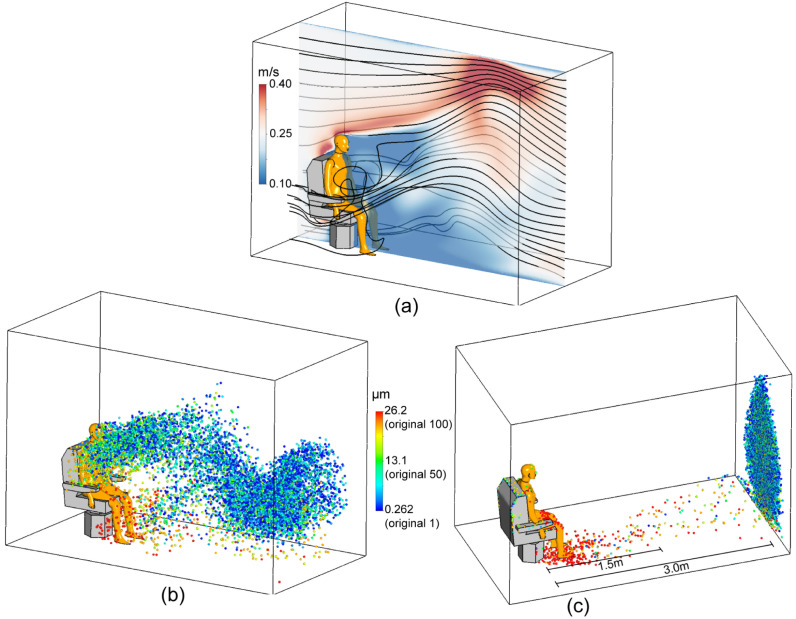
When there is indoor ventilation, the air flow is expected to have a significant impact on the transport of the cough expelled droplets. We, therefore, simulated the worst case scenario when there is wind blowing from the manikin’s back to the front and compared to the results under the calm scenario. According to the literatures, indoor air flow rate is in the range of . Here, the air flow rate was chosen to be 0.25 m/s in order to simulate the worst scenario. To illustrate the effect of indoor wind on the virus-laden droplet transmission, the airflow field and the droplet transmission with wind under relative humidity of 50% are shown in Fig. 12. Fig. 12(a,b) show the airflow and the distribution of the droplets at a representative time t = 10 s. The distribution of the droplets that deposit or escape the computational domain is visualised in Fig. 12c.
Fig. 12.
Airflow and cough expelled transmission in a representative wind scenario. Wind speed is 0.25 m/s. (a). Airflow velocity distribution in the middle plane and streamline around the manikin. (b). The droplet dispersion at time 10 s. (c). Droplet deposition and exiting locations.
The velocity contour and airflow streamlines in Fig. 12a show that a wake region is formed in front of the manikin with relatively low velocity and strong vortices. The wind accelerates upwards above the chair and manikin’s head, reaches 0.4 m/s near the ceiling and then decelerates downwards to the outlet. The dispersion of droplets in Fig. 12b shows that large droplets ( post-evaporation, shown in red) quickly deposit on the floor. However the transports of droplets smaller than (post-evaporation, shown in blue) are mostly dominated by the airflow field. Interestingly, large amount of droplets are trapped in the airflow wake region and are gradually released forward by the wind, thus forming a continuous droplets band from the breathing zone to the outlet of the computational domain. Consequently, as shown in Fig. 12c, large particles ( post-evaporation, shown in red) tend to deposit on the manikin and on the floor within 1.5 m from the manikin. Deposition of droplets with size (shown in yellow) scatter 1.5 m–3 m in distance and almost all droplets (shown in blue) suspend in the air, being carried away by the wind and escape the computational domain. This is consistent with literatures that it takes at least 30 min for 1–5 particles to deposit on the ground (Wang et al., 2021).
Since the middle of 2021, the Delta variant has been dominating the global pandemic. According to reports about transmissibilities of major SARS-CoV-2 variants, the Delta variant is roughly 200% transmissible compared with the original virus strain (wild type) (Blanquart et al., 2021). Therefore, the q of the Delta variant in this study is estimated as 0.316 quantum/s.
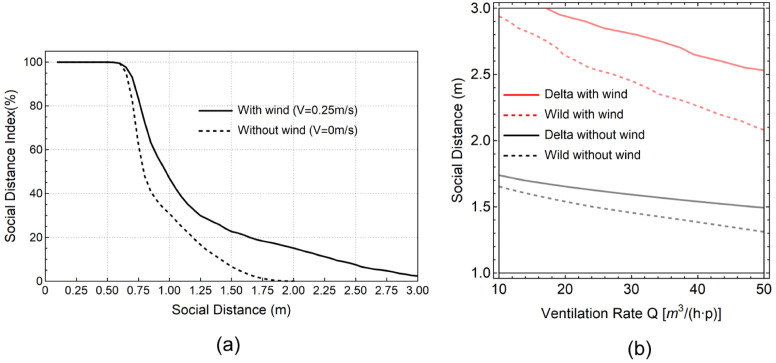
The SDI and the PI are estimated in the wind scenario for the wild SARS-CoV-2 strain and the Delta variant (Fig. 13), and compared with the wild virus type case in the calm scenario (without wind). Similar with the calm scenario, the SDI remains 100% when the distance is within 0.6 m from the manikin. When the distance is larger than 0.6 m, the SDI for the wind scenario decreases at a slower rate than that for the calm scenario. When the distance reaches 1.8 m, the SDI for the wind scenario remains at 18%, while the SDI for the calm scenario reaches 0. The SDI for the wind scenario drops to 2% at a distance of 3 m.
Fig. 13.
Comparisons of SDI and infection risks between calm and wind scenarios. (a). Comparisons of SDI between two scenarios at different social distances. (b). Comparisons of PI 10% lines between calm and wind scenarios and between wild virus type and Delta variant.
In order to keep the infection under control, social distance rule needs to be designed to control the reproduction number R not higher than 1. Considering a typical office with 10 people, adopting an PI value of 10% would result in . We further considered the impact of two virus types (the wild type vs the Delta variant) and plotted the constant PI 10% lines after typical 8 h-working time for both calm and wind scenarios (Fig. 13b). According to our results, longer social distance and higher ventilation rate are required for the Delta variant under the representative wind scenario to maintain such a low infection risk. Considering the ventilation rate of 15 for typical workplace standards, the required social distance for the Delta variant increases from 1.6 m to 1.7 m in a calm indoor environment. This is consistent with the estimation from Bazant and Bush (2021) that social distance of 1.66 m is required for an 8-h working time office scenario when containing the spread of the Delta variant. The presence of wind further increases the required social distance to 2.8 m. As shown in the Fig. 13b, the largest social distance is required for the Delta variant under the wind scenario, in which even 3 m is insufficient to maintain a 10% infection risk.
4. Conclusions
To safely reopen the office before reaching the comprehensive COVID-19 vaccination, the social distance rule applied in the indoor environment needs to be carefully evaluated. This study used Computational Fluid Dynamics(CFD) techniques and investigated how probability of infection (PI) of COVID-19 changes with different social distance. The study was carried out by simulating a typical office environment under variant humidity levels, wind scenarios and virus types. Several conclusions can be addressed from the CFD results:
-
(1)
Most of the cough expelled droplets evaporate to nuclei within 1 s at the room temperature and a relative humidity (RH) of 50%. It is essential to include the evaporation process into the virus-laden droplets transmission simulations;
-
(2)
In the calm environment, 2-metre social distance is a sufficient measure to maintain a low risk of infection in present office environment. PI is slightly higher in a dryer environment due to the stronger evaporation effect, which leads to longer suspension time for cough expelled droplets. On the contrary, a wet environment reduces the droplet evaporation and decreases PI. In general, a social distance of 1.8 m is recommended to maintain a low infection risk target when the ventilation rate meets the standards 15. At a higher ventilation rate, the required social distance can be slighted decreased;
-
(3)
The presence of indoor wind and the Delta variant of SARS-CoV-2 significantly affects the existing social distance rule. With a wind speed of 0.25 m/s, social distance of 2.8 m is recommended for the wild virus type and 3 m is insufficient to contain the transmission of the Delta variant.
The results from this study can offer practical references to adjust social distance rules and ventilation rates under different PI risk targets and actual humidity levels. Future works will focus on conducting CFD simulations to fine-tune the parameters in the modified Wells–Riley model by considering effects of different ventilation schemes and multiple human manikins on airflow patterns.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This study was funded by the National Natural Science Foundation of China (Grant No. 81800096) and Australian Research Council (Project ID: DE210101549, DE180101138). Research was also supported by the Program for Professor of Special Appointment (Eastern Scholar) at Shanghai Institutions of Higher Learning (Project ID: 0920000016).
Editor: Dr. Chris Hogan
References
- Asadi S., Wexler A.S., Cappa C.D., Barreda S., Bouvier N.M., Ristenpart W.D. Aerosol emission and superemission during human speech increase with voice loudness. Scientific Reports. 2019;9(1):1–10. doi: 10.1038/s41598-019-38808-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baldwin P.E., Maynard A.D. A survey of wind speeds in indoor workplaces. The Annals of Occupational Hygiene. 1998;42(5):303–313. doi: 10.1016/s0003-4878(98)00031-3. [DOI] [PubMed] [Google Scholar]
- Bazant M.Z., Bush J.W. A guideline to limit indoor airborne transmission of COVID-19. Proceedings of the National Academy of Sciences. 2021;118(17) doi: 10.1073/pnas.2018995118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blanquart F., Abad C., Ambroise J., Bernard M., Cosentino G., Giannoli J.-M., et al. 2021. Spread of the delta variant, vaccine effectiveness against PCR-detected infections and within-host viral load dynamics in the community in France. 40%-60%. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bourouiba L. Turbulent gas clouds and respiratory pathogen emissions: potential implications for reducing transmission of COVID-19. Jama. 2020;323(18):1837–1838. doi: 10.1001/jama.2020.4756. [DOI] [PubMed] [Google Scholar]
- Bourouiba L., Dehandschoewercker E., Bush J.W. Violent expiratory events: on coughing and sneezing. Journal of Fluid Mechanics. 2014;745:537–563. [Google Scholar]
- Buonanno G., Stabile L., Morawska L. Estimation of airborne viral emission: Quanta emission rate of SARS-CoV-2 for infection risk assessment. Environment International. 2020;141 doi: 10.1016/j.envint.2020.105794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Centers for Disease Control and Prevention G. 2020. Social distancing - keep a safe distance to slow the spread. [Google Scholar]
- Chao C.Y.H., Wan M.P., Morawska L., Johnson G.R., Ristovski Z., Hargreaves M., et al. Characterization of expiration air jets and droplet size distributions immediately at the mouth opening. Journal of Aerosol Science. 2009;40(2):122–133. doi: 10.1016/j.jaerosci.2008.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daszak P., das Neves C., Amuasi J., Haymen D., Kuiken T., Roche B., et al. 2020. Workshop report on biodiversity and pandemics of the intergovernmental platform on biodiversity and ecosystem services. [Google Scholar]
- Dbouk T., Drikakis D. Weather impact on airborne coronavirus survival. Physics of Fluids. 2020;32(9) doi: 10.1063/5.0024272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elliott P., Haw D., Wang H., Eales O., Walters C., Ainslie K., et al. 2021. React-1 round 13 final report: exponential growth, high prevalence of SARS-CoV-2 and vaccine effectiveness associated with delta variant in England during May to July 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng Y., Marchal T., Sperry T., Yi H. Influence of wind and relative humidity on the social distancing effectiveness to prevent COVID-19 airborne transmission: A numerical study. Journal of Aerosol Science. 2020 doi: 10.1016/j.jaerosci.2020.105585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- G. L.Y., S.S. K. Ventilation in Korea. AIVC Technical Note 64. 2007;18(pp) [Google Scholar]
- Gammaitoni L., Nucci M.C. Using a mathematical model to evaluate the efficacy of TB control measures. Emerging Infectious Diseases. 1997;3(3):335. doi: 10.3201/eid0303.970310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- GB9673-1996 L. 1996. Hygienic standard for public means of transportation. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China. [Google Scholar]
- Ge Q., Li X., Inthavong K., Tu J. Numerical study of the effects of human body heat on particle transport and inhalation in indoor environment. Building and Environment. 2013;59:1–9. [Google Scholar]
- Giordano G., Blanchini F., Bruno R., Colaneri P., Di Filippo A., Di Matteo A., et al. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nature Medicine. 2020:1–6. doi: 10.1038/s41591-020-0883-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta J.K., Lin C., Chen Q. Flow dynamics and characterization of a cough. Indoor Air. 2009;19(6):517–525. doi: 10.1111/j.1600-0668.2009.00619.x. [DOI] [PubMed] [Google Scholar]
- Health T.L.P. A pandemic era. The Lancet. Planetary Health. 2021;5(1) doi: 10.1016/S2542-5196(20)30305-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- of Health Australian Government D. 2020. Physical distancing for coronavirus (COVID-19) [Google Scholar]
- Ho C.K. Modeling airborne pathogen transport and transmission risks of SARS-CoV-2. Applied Mathematical Modelling. 2021 doi: 10.1016/j.apm.2021.02.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X., Shang Y., Yan Y., Yang L., Tu J. Modelling of evaporation of cough droplets in inhomogeneous humidity fields using the multi-component Eulerian-Lagrangian approach. Building and Environment. 2018;128(Supplement C):68–76. doi: 10.1016/j.buildenv.2017.11.025. URL http://www.sciencedirect.com/science/article/pii/S0360132317305322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo K., Lei Z., Hai Z., Xiao S., Rui J., Yang H., et al. Transmission of SARS-CoV-2 in public transportation vehicles: A case study in hunan province, China. Open Forum Infectious Diseases. 2020;7(10):ofaa430. doi: 10.1093/ofid/ofaa430. Hunan Bus. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lytras S., Xia W., Hughes J., Jiang X., Robertson D.L. The animal origin of SARS-CoV-2. Science. 2021:e. doi: 10.1126/science.abh0117. URL http://science.sciencemag.org/content/early/2021/08/16/science.abh0117.abstract. [DOI] [PubMed] [Google Scholar]
- Mallapaty S. Antibody tests suggest that coronavirus infections vastly exceed official counts. Nature. 2020 doi: 10.1038/d41586-020-01095-0. [DOI] [PubMed] [Google Scholar]
- Menter F.R., Kuntz M., Langtry R. Ten years of industrial experience with the SST turbulence model. Turbulence, Heat and Mass Transfer. 2003;4(1):625–632. [Google Scholar]
- Miller S.L., Clements N., Elliott S.A., Subhash S.S., Eagan A., Radonovich L.J. Implementing a negative-pressure isolation ward for a surge in airborne infectious patients. American Journal of Infection Control. 2017;45(6):652–659. doi: 10.1016/j.ajic.2017.01.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller S.L., Nazaroff W.W., Jimenez J.L., Boerstra A., Buonanno G., Dancer S.J., et al. Transmission of SARS-CoV-2 by inhalation of respiratory aerosol in the skagit valley chorale superspreading event. Indoor Air. 2021;31(2):314–323. doi: 10.1111/ina.12751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morawska L., Cao J. Airborne transmission of SARS-CoV-2: The world should face the reality. Environment International. 2020;139 doi: 10.1016/j.envint.2020.105730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morawska L., Johnson G., Ristovski Z., Hargreaves M., Mengersen K., Corbett S., et al. Size distribution and sites of origin of droplets expelled from the human respiratory tract during expiratory activities. Journal of Aerosol Science. 2009;40(3):256–269. doi: 10.1016/j.jaerosci.2008.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morsi S., Alexander A. An investigation of particle trajectories in two-phase flow systems. Journal of Fluid Mechanics. 1972;55(2):193–208. [Google Scholar]
- Mullard A. How COVID vaccines are being divvied up around the world. Nature. 2020 doi: 10.1038/d41586-020-03370-6. [DOI] [PubMed] [Google Scholar]
- Nicas M., Nazaroff W.W., Hubbard A. Toward understanding the risk of secondary airborne infection: emission of respirable pathogens. Journal of Occupational and Environmental Hygiene. 2005;2(3):143–154. doi: 10.1080/15459620590918466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park S.Y., Kim Y.-M., Yi S., Lee S., Na B.-J., Kim C.B., et al. Coronavirus disease outbreak in call center, South Korea. Emerging Infectious Diseases. 2020;26(8):1666. doi: 10.3201/eid2608.201274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prather K.A., Marr L.C., Schooley R.T., McDiarmid M.A., Wilson M.E., Milton D.K. Airborne transmission of SARS-CoV-2. Science. 2020;370(6514):303–304. doi: 10.1126/science.abf0521. [DOI] [PubMed] [Google Scholar]
- Riley E., Murphy G., Riley R. Airborne spread of measles in a suburban elementary school. American Journal of Epidemiology. 1978;107(5):421–432. doi: 10.1093/oxfordjournals.aje.a112560. [DOI] [PubMed] [Google Scholar]
- Schmees D.K., Wu Y.-H., Vincent J.H. Visualization of the airflow around a life-sized, heated, breathing mannequin at ultralow windspeeds. Annals of Occupational Hygiene. 2008;52(5):351–360. doi: 10.1093/annhyg/men022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Setti L., Passarini F., De Gennaro G., Barbieri P., Perrone M.G., Borelli M., et al. 2020. Airborne transmission route of COVID-19: why 2 meters/6 feet of inter-personal distance could not be enough. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shang Y., Inthavong K., Tu J. Detailed micro-particle deposition patterns in the human nasal cavity influenced by the breathing zone. Computers & Fluids. 2015;114:141–150. Q1. [Google Scholar]
- Shang Y., Tao Y., Dong J., He F., Tu J. Deposition features of inhaled viral droplets may lead to rapid secondary transmission of COVID-19. Journal of Aerosol Science. 2021;154 doi: 10.1016/j.jaerosci.2021.105745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen Y., Li C., Dong H., Wang Z., Martinez L., Sun Z., et al. Community outbreak investigation of SARS-CoV-2 transmission among bus riders in eastern China. JAMA Internal Medicine. 2020;180(12):1665–1671. doi: 10.1001/jamainternmed.2020.5225. Ningbo Bus. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun C., Zhai Z. The efficacy of social distance and ventilation effectiveness in preventing COVID-19 transmission. Sustainable Cities and Society. 2020;62 doi: 10.1016/j.scs.2020.102390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang C.C., Prather K.A., Sznitman J., Jimenez J.L., Lakdawala S.S., Tufekci Z., et al. Airborne transmission of respiratory viruses. Science. 2021;373(6558):eabd9149. doi: 10.1126/science.abd9149. URL http://science.sciencemag.org/content/373/6558/eabd9149.abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ward M.P., Xiao S., Zhang Z. The role of climate during the COVID-19 epidemic in New South Wales, Australia. Transboundary and Emerging Diseases. 2020;67(6):2313–2317. doi: 10.1111/tbed.13631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei J., Li Y. Enhanced spread of expiratory droplets by turbulence in a cough jet. Building and Environment. 2015;93:86–96. [Google Scholar]
- WHO J. 2002. Hazard prevention and control in the work environment: Airborne dust. [Google Scholar]
- WHO J. 2014. Infection prevention and control of epidemic-and pandemic-prone acute respiratory infections in health care. [PubMed] [Google Scholar]
- WHO J. 2020. Information for the public: Covid-19 physical distancing. [Google Scholar]
- WHO J. 2021. Weekly operational update on COVID-19. [Google Scholar]
- Wiersinga W.J., Rhodes A., Cheng A.C., Peacock S.J., Prescott H.C. Pathophysiology, transmission, diagnosis, and treatment of coronavirus disease 2019 (COVID-19): A review. Jama. 2020;324(8):782–793. doi: 10.1001/jama.2020.12839. [DOI] [PubMed] [Google Scholar]
- Working with silica and silica containing products - Assessing the risk. (2019) Safe Work Australia.
- Yan Y., Li X., Tu J. Thermal effect of human body on cough droplets evaporation and dispersion in an enclosed space. Building and Environment. 2019;148:96–106. doi: 10.1016/j.buildenv.2018.10.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan Y., Li X., Yang L., Yan P., Tu J. Evaluation of cough-jet effects on the transport characteristics of respiratory-induced contaminants in airline passengers’ local environments. Building and Environment. 2020;183 doi: 10.1016/j.buildenv.2020.107206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Y.K., Kang I.S., Hwang J.H., Park J.C. CFD simulation for air-borne infection analysis in AII-room. International Journal of Mechanical and Mechatronics Engineering. 2017;11(5):1047–1052. [Google Scholar]
- Zayas G., Chiang M.C., Wong E., MacDonald F., Lange C.F., Senthilselvan A., et al. Cough aerosol in healthy participants: fundamental knowledge to optimize droplet-spread infectious respiratory disease management. BMC Pulmonary Medicine. 2012;12(1):11. doi: 10.1186/1471-2466-12-11. [DOI] [PMC free article] [PubMed] [Google Scholar]