Feasibility of MR fingerprinting using a high-performance 0.55 T MRI system

Abstract

Background:

MR fingerprinting (MRF) is a versatile method for rapid multi-parametric quantification. The application of MRF for lower MRI field could enable multi-contrast imaging and improve exam efficiency on these systems. The purpose of this work is to demonstrate the feasibility of 3D whole-brain T1 and T2 mapping using MR fingerprinting on a contemporary 0.55 T MRI system.

Materials and methods:

A 3D whole brain stack-of-spirals FISP MRF sequence was implemented for 0.55 T. Quantification was validated using the NIST/ISMRM Quantitative MRI phantom, and T1 and T2 values of white matter, gray matter, and cerebrospinal fluid were measured in 19 healthy subjects. To assess MRF performance in the lower SNR regime of 0.55 T, measurement precision was calculated from 100 simulated pseudo-replicas of in vivo data and within-session measurement repeatability was evaluated.

Results:

T1 and T2 values calculated by MRF were strongly correlated to standard measurements in the ISMRM/NIST MRI system phantom (R² > 0.99), with a small constant bias of approximately 5 ms in T2 values. 3D stack-of-spirals MRF was successfully applied for whole brain quantitative T1 and T2 at 0.55 T, with spatial resolution of 1.2 mm × 1.2 mm × 5 mm, and acquisition time of 8.5 min. Moreover, the T1 and T2 quantifications had precision <5%, despite the lower SNR of 0.55 T.

Conclusion:

A 3D whole-brain stack-of-spirals FISP MRF sequence is feasible for T1 and T2 mapping at 0.55 T.

1. Introduction

Magnetic resonance fingerprinting (MRF) is a versatile method for rapid multiparametric quantitative imaging [1,2], which has been implemented across multiple field strengths and MRI platforms. MRF uses a variable acquisition scheme which is designed to sensitize MRI signal to predefined quantitative parameters, such as T1 and T2. Multiple MR parameters are simultaneously estimated using pattern recognition to match the signal evolution to a dictionary simulated from the Bloch equations. Quantitative MRI offers standardization compared with contrast-weighted imaging, and MRF has been deployed for the evaluation of multiple pathologies [3–5]. Alternatively, MRF can be used to generate synthetic image contrast [6–8]. Importantly, MRF has been demonstrated to be reproducible between sessions and across MRI systems [9].

We recently described a 0.55 T MRI system that integrates contemporary clinical MRI technology at a lower magnetic field strength [10]. This system configuration may offer high quality imaging at lower cost, and therefore is attractive for both high-volume and low-resource imaging environments. Moreover, modern lower field MRI scanners may enable new clinical opportunities in point-of-care imaging, MRI-guided invasive procedures, improved implant safety, and imaging near high-susceptibility anatomy such as the lungs [10–14]. The short T1 and longer T2* offer advantages for SNR-efficiency, and the B0 uniformity enables spiral, radial, and EPI acquisitions with limited imaging artifacts.

Rapid quantitative imaging, using MRF and other multi-contrast methods, is attractive at lower fields [14–16]. Low-field MRI acquisitions are often longer than contemporary clinical MRI protocols to maintain SNR [13], and therefore, the ability to generate multiple quantitative maps in a single acquisition may reduce imaging time. Quantitative parametric mapping also reduces reliance on carefully optimized contrast-weighted imaging that may vary between field strengths. The application of pattern recognition using MRF increases its robustness to lower SNR [17]. Moreover, this prototype 0.55 T system offers improved B0 and B1 field uniformity compared to 1.5 T and 3 T, which can be exploited to reduce the dictionary size or eliminate the need for B0 and B1 mapping in conjunction with MRF.

Here, we used a stack-of-spirals 3D MRF acquisition to assess the feasibility of MRF at 0.55 T for whole-brain T1 and T2 mapping. We demonstrate mapping in the ISMRM/NIST quantitative MRI phantom and in healthy subjects.

2. Materials and methods

2.1. Imaging methods

We used an MRI system modified to operate at 0.55 T (prototype MAGNETOM Aera, Siemens Healthcare, Erlangen, Germany). This system has contemporary magnet design, receiver architecture, and gradient performance (maximum amplitude = 45mT/m, maximum slew rate = 200 T/m/s). The modern magnet design is important for B0 uniformity, multi-channel receiver arrays are required for imaging speed, and high-fidelity shielded gradients are beneficial for spiral acquisitions. Neuroimaging was performed using a 16 channel head coil modified to operate at 23.6 MHz.

A prototype 3D slab-selective stack-of-spirals MRF sequence [18] was applied at 0.55 T. A 48-arm spiral design with 4.6 ms FISP readout was used (TE/TR = 1.36/8.88 ms, FOV = 300 mm × 300 mm, in-plane resolution = 1.2 mm × 1.2 mm, variable flip angle range = 0–74°, slice thickness = 5 mm, TI = 21 ms, 36 slices). The 4.6 ms spiral readout length exploits the favorable long T2* properties of lower fields, with limited blurring. The pulse sequence is the same as described in Ma et al. [18] with a total of 1500 time points acquired, and k_z fully sampled with a linear ordering. One adiabatic inversion pulse was played at the beginning of the sequence to improve sensitivity to T1 [8]. Total acquisition time for a 3D volume was 8:30 min. The same acquisition was used for phantom and in vivo imaging.

Single-shot (48× undersampled) images were reconstructed using a gpuNUFFT [19]. Spiral trajectories were measured using a spherical phantom [20]. Pixel-wise signal evolution curves were fit to a simulated signal evolution dictionary to quantify T1, T2 and proton density. The dictionary was generated using 263 possible T1 values (10 to 2000 ms in 10 ms steps, 2020 to 3000 in 20 ms steps, 3050 to 3500 ms in 50 ms steps, and 4000 to 5000 ms in 500 ms steps), and 133 possible T2 values (2 to 100 ms in 2 ms steps, 105 to 300 ms in 5 ms steps, 310 to 500 ms in 10 ms steps, 520 to 800 ms in 20 ms steps, and 850 to 1200 ms in 50 ms steps). We calibrated a system-specific constant B1 scaling factor to relate the pulse shape used in the transmit adjustment to the pulse used during the acquisition [18]. B1 scaling factors of 0.8 to 1 were evaluated in the ISMRM/NIST phantom for accuracy, and we selected a scaling factor of 0.9, similar to previous implementations on Siemens MRI systems. We did not use a spatial B1+ homogeneity correction. Pattern recognition selected the dictionary entry that generated the maximum inner product between the measured signal time course and the simulated dictionary signal time course. The dictionary was compressed using singular value decomposition to accelerate the pattern recognition step [21].

Image reconstruction and dictionary fitting was performed in MATLAB (2018b, Mathworks Inc., Natick MA) on a machine using two GPUs (Tesla P100, Nvidia, Santa Clara, CA) and running Ubuntu 18.04.

2.2. Phantom validation

Quantitative T1 and T2 mapping was validated using the ISMRM/NIST MRI system phantom. 3D MRF was compared to conventional measurements with inversion recovery T1 mapping (spoiled gradient echo acquisition, TE/TR = 5.82/15000 ms, in-plane resolution = 1.2 mm × 1.2 mm, slice thickness = 5 mm, TI = 10, 20, 30, 40, 80, 160, 320, 640, 1300, 2600, 5000, 8000 ms) and multiple TEs for T2 mapping (spin echo acquisition, TE = 10, 20, 40, 80, 160, 320, 640, 1000 ms, TR = 15,000 ms, slice thickness = 5 mm, in-plane resolution = 1.2 mm × 1.2 mm).

2.3. Healthy volunteer imaging

Healthy volunteer imaging was approved by the local Institutional Review Board. 3D MRF was evaluated in the brain of 19 healthy volunteers (12 females, age 31 ± 13 years). White matter, gray matter and cerebrospinal fluid T1 and T2 values were calculated using large 3D regions-of-interest (ROIs) generated semi-automatically by a k-means clustering algorithm applied to 10 slices in the brain (Supplementary Fig. 1).

T1 and T2 measurement precision was calculated from 100 pseudo replicas with white noise added to raw data in one healthy volunteer. The measurement noise covariance matrix was calculated from a noise-only calibration scan, with no RF pulse applied, in the healthy volunteer. Simulated noise was used during pre-whitening of k-space data [22], and repeated for 100 pseudo-replicas. Image reconstruction and dictionary fitting was repeated for each replica. Coefficients of variation (CVs) and voxel-wise maps of the measurement range, normalized to the mean value, were calculated from the distribution of fitted T1 and T2 values by:

$$\mathit{\text{Normalized range}}=\frac{\mathit{\text{max}}\left(T_{1,2}\right)-\mathit{\text{min}}\left(T_{1,2}\right)}{\mathit{\text{mean}}\left(T_{1,2}\right)}\cdot 100\%$$ (n.1)

$$\mathit{\text{Coefficient of variation}}=\frac{\mathit{\text{standard deviation}}\left(T_{1,2}\right)}{\mathit{\text{mean}}\left(T_{1,2}\right)}$$ (n.2)

In 4 healthy subjects, MRF measurements were repeated twice within the same session to estimate physiological variability. CVs of T1 and T2 measurement from repeated measures were calculated for each subject and the Bland-Altman bias was calculated from the 4 subjects.

3. Results

3.1. Phantom validation

T1 and T2 values calculated by MRF were strongly correlated to standard measurements in the ISMRM/NIST MRI system phantom (R² > 0.99, Fig. 1). We measured a small bias of approximately 5 ms in T2 values compared with spin echo T2 measurements. By comparison, at 3 T, a 2D FISP sequence generated 4 ms T2 bias in the NIST phantom across all vials [23], with higher bias in the physiological range of T2 values.

Fig. 1.

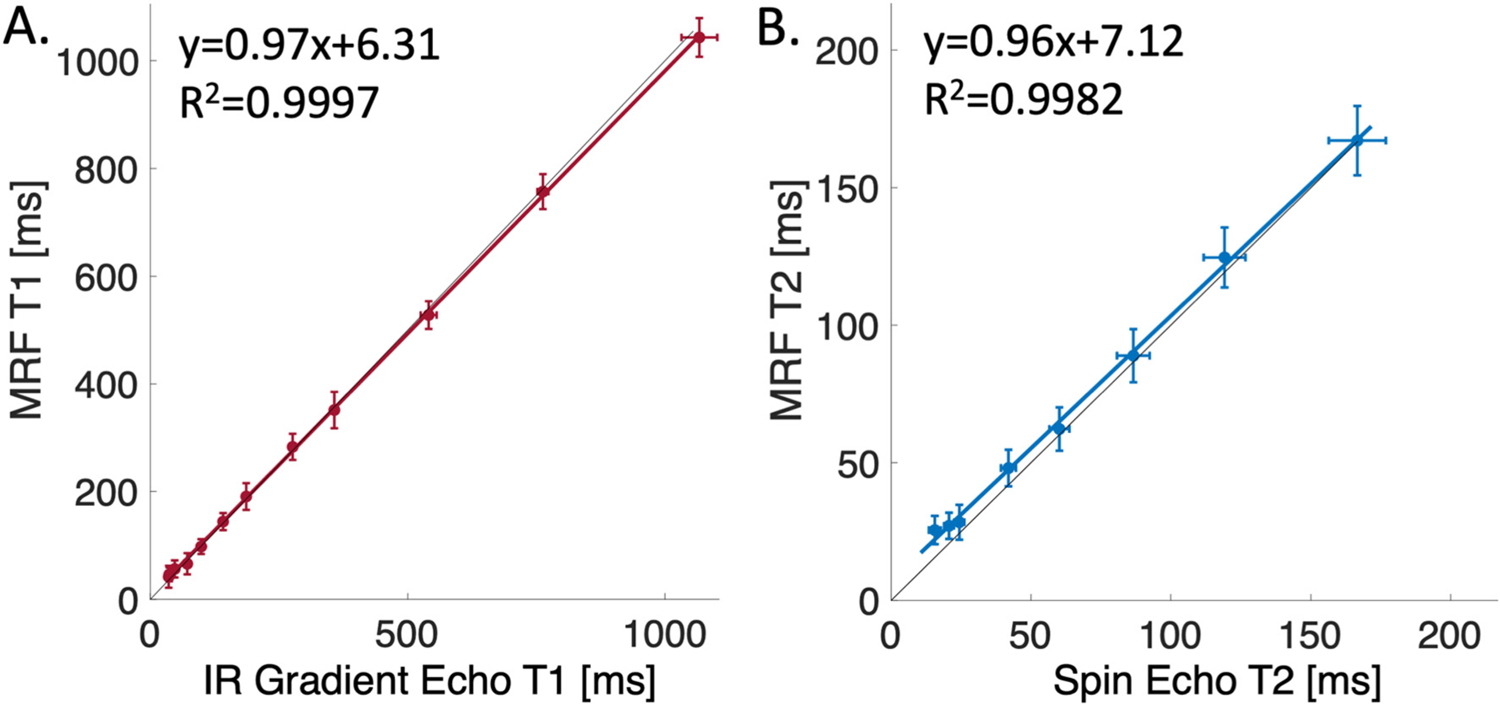
ISMRM/NIST MRI system phantom measurements. Correlation of MRF T1 values (A) and T2 values (B) to standard T1 and T2 measurements. The black line is the line of identity and error bars represent standard deviations within each vial.

3.2. Healthy volunteer imaging

T1 maps, T2 maps, and proton density maps for 24 slices in a healthy volunteer are provided in Fig. 2 to demonstrate image quality. Fig. 3 provides a single axial slice through the ventricles from all 19 healthy volunteers. Image quality was good for these quantitative T1 and T2 maps with in-plane spatial resolution of 1.2 mm at 0.55 T. No correction for off-resonance blurring was required for spiral readout length of 4.6 ms. Low signal intensity was observed in the center of the proton density maps due to limited coil penetration from prototype receiver arrays. Mean T1 and T2 values for white matter and gray matter and standard deviation across 19 healthy volunteers are provided in Table 1.

Fig. 2.

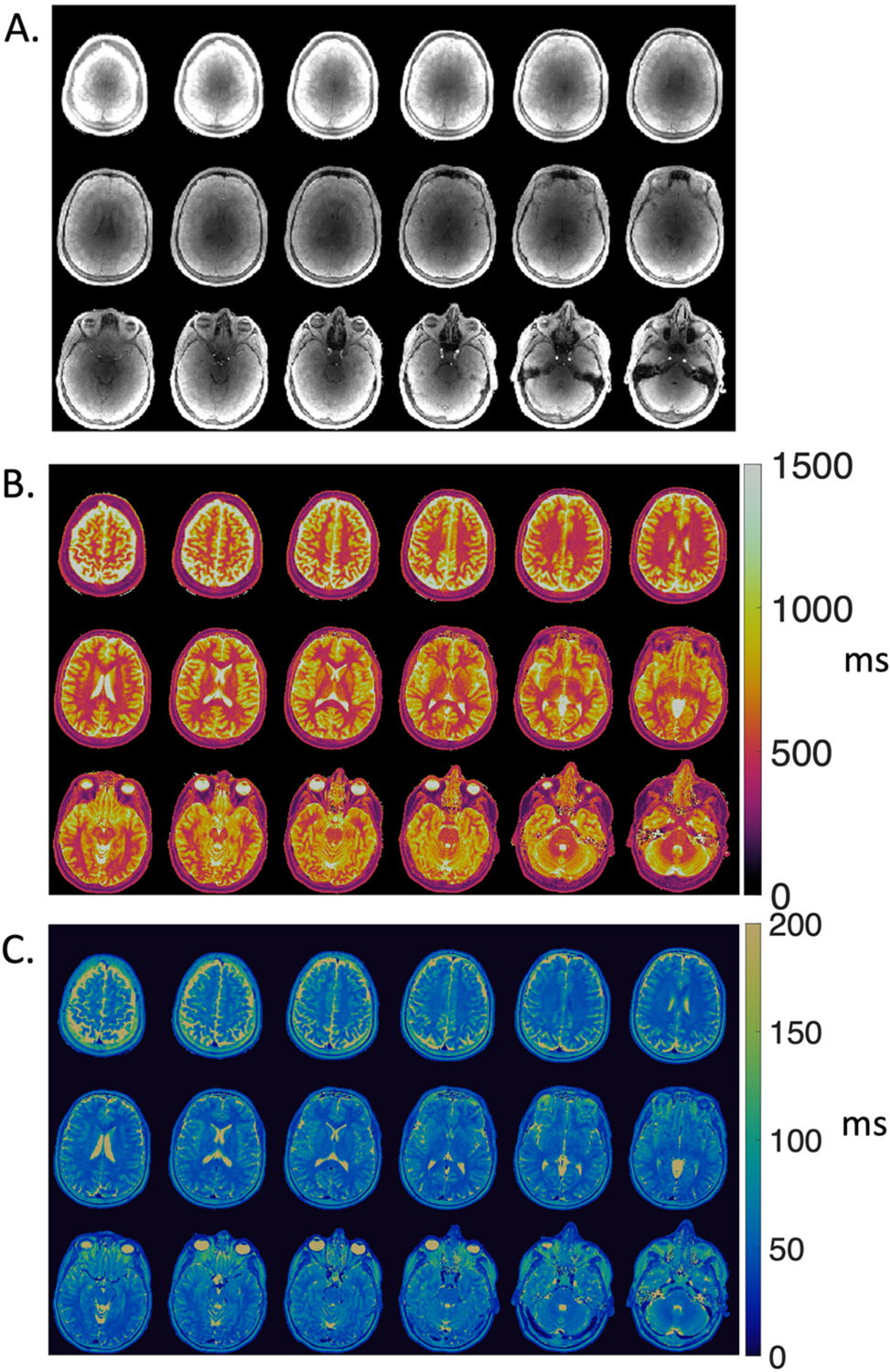
Multi-slice (A) proton density maps, (B) T1 maps, and (C) T2 maps from MRF in a single volunteer demonstrating volumetric MRF coverage at 0.55 T.

Fig. 3.

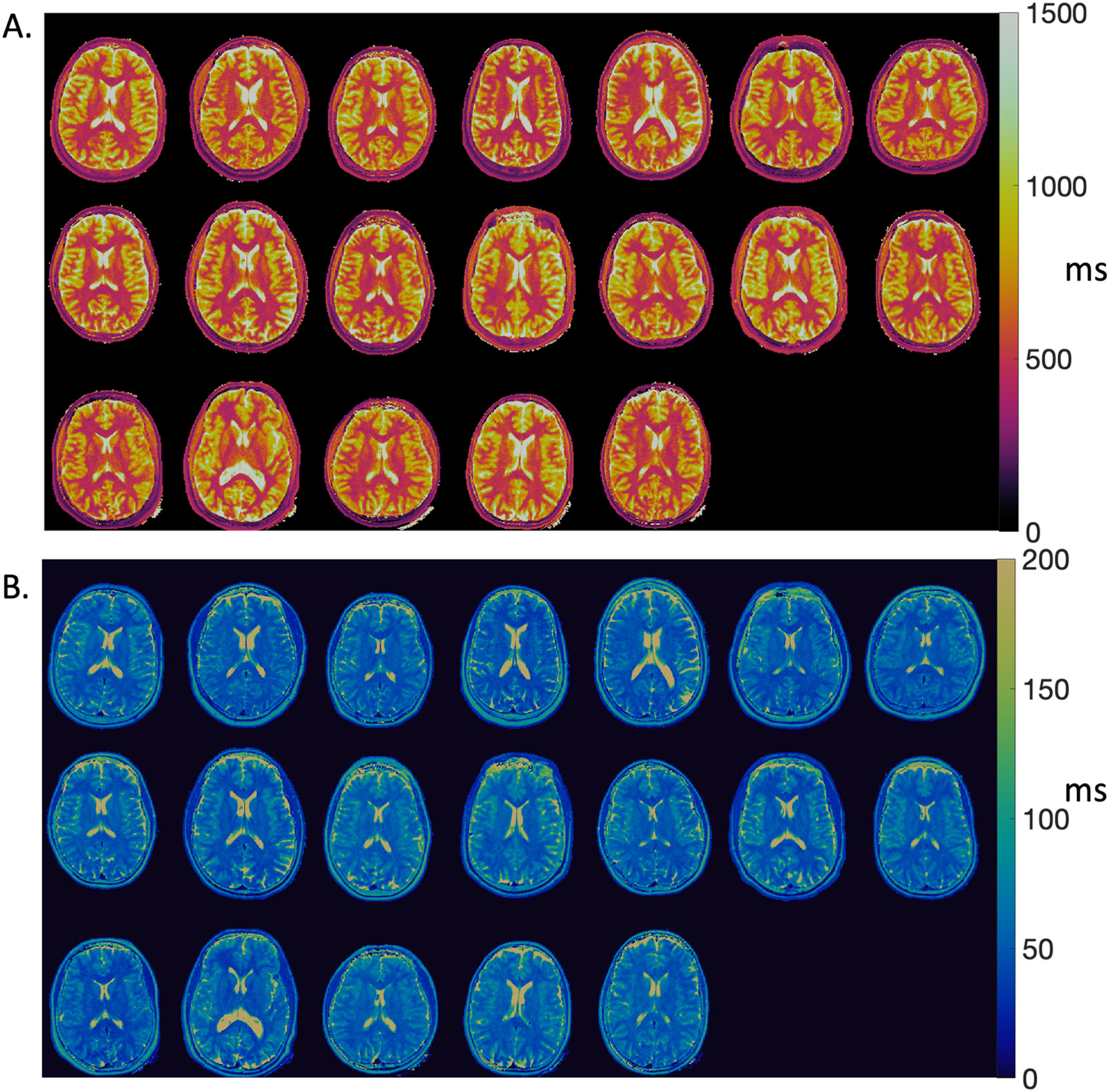
(A) T1 maps and (B) T2 maps from 19 healthy subjects in a single axial slice.

Table 1.

Quantitative T1 and T2 values from white matter, gray matter, and cerebrospinal fluid measured using 3D whole brain MRF at 0.55 T (n = 19 healthy volunteers). Mean and standard deviations across 19 subjects are provided for 3D regions-of-interest (ROIs).

	T1 (ms)	T2 (ms)	3D ROI size (voxels)
White Matter	492 ± 14	48 ± 2	31,957 ± 4718
Gray Matter	881 ± 41	77 ± 8	37,443 ± 4456
Cerebrospinal fluid	2625 ± 131	485 ± 73	4701 ± 2000

3.3. Measurement precision

The values of the inner-product used for pattern recognition in a single volunteer ranged between 0.9857 and 0.9998 (mean = 0.9972 ± 0.0017) for the whole head. This indicates confidence in pattern recognition.

Precision was calculated for in vivo measurements at 0.55 T using 100 pseudo-replicas. CVs calculated using the distribution of T1 and T2 measurements across all replicas from the same 3D ROIs are provided in Table 2. CVs were < 0.03% for all measurements from 3D ROIs. Fig. 4 provides voxel-wise maps of the normalized range of T1 and T2 values generated from the pseudo replicas. For example, for a voxel with T1 value of 500 ms, MRF fit values of 500–520 ms across replicas (normalized range = 3.9%, CV = 1.0%); and, for a voxel with T2 value of 50 ms, MRF fit values of 48–50 ms across pseudo replicas (normalized range = 4.1%, CV = 2.0%). Pseudo-replica calculations capture the variability introduced by thermal noise, whereas repeated measures capture physiological variability, which was higher as expected. Table 2 summarizes the within-session repeatability of T1 and T2 measurements by MRI at 0.55 T. CVs calculated from within-session repeated measures using 3D ROIs were ≤ 11% across all T1 and T2 measurements in all subjects.

Table 2.

Pseudo replica coefficients of variation (CVs) and within-session repeatability of MRF T1 and T2 measurements in 4 healthy volunteers. For each tissue type, T1 and T2 was calculated from 3D regions-of-interest. The mean ± standard deviation (SD) across subjects is reported for the repeated measures CV and the Bland-Altman bias is calculated from the group.

		Pseudo-replica CV	Repeated measures CV (mean ± SD)	Bland Altman Bias ± 1.96 SD
White Matter	T1	0.008%	0.76 ± 0.35%	1.5 ± 12 ms
	T2	0.014%	3.8 ± 5.0%	−1.9 ± 6.1 ms
Gray Matter	Tl	0.007%	0.7 ± 0.5%	5.0 ± 19.1 ms
	T2	0.009%	3.8 ± 5.2%	−2.8 ± 10.9 ms
Cerebrospinal fluid	T1	0.011%	2.5 ± 1.7%	6.0 ± 236.1 ms
	T2	0.028%	3.5 ± 0.6%	1.4 ± 57.9 ms

Fig. 4.

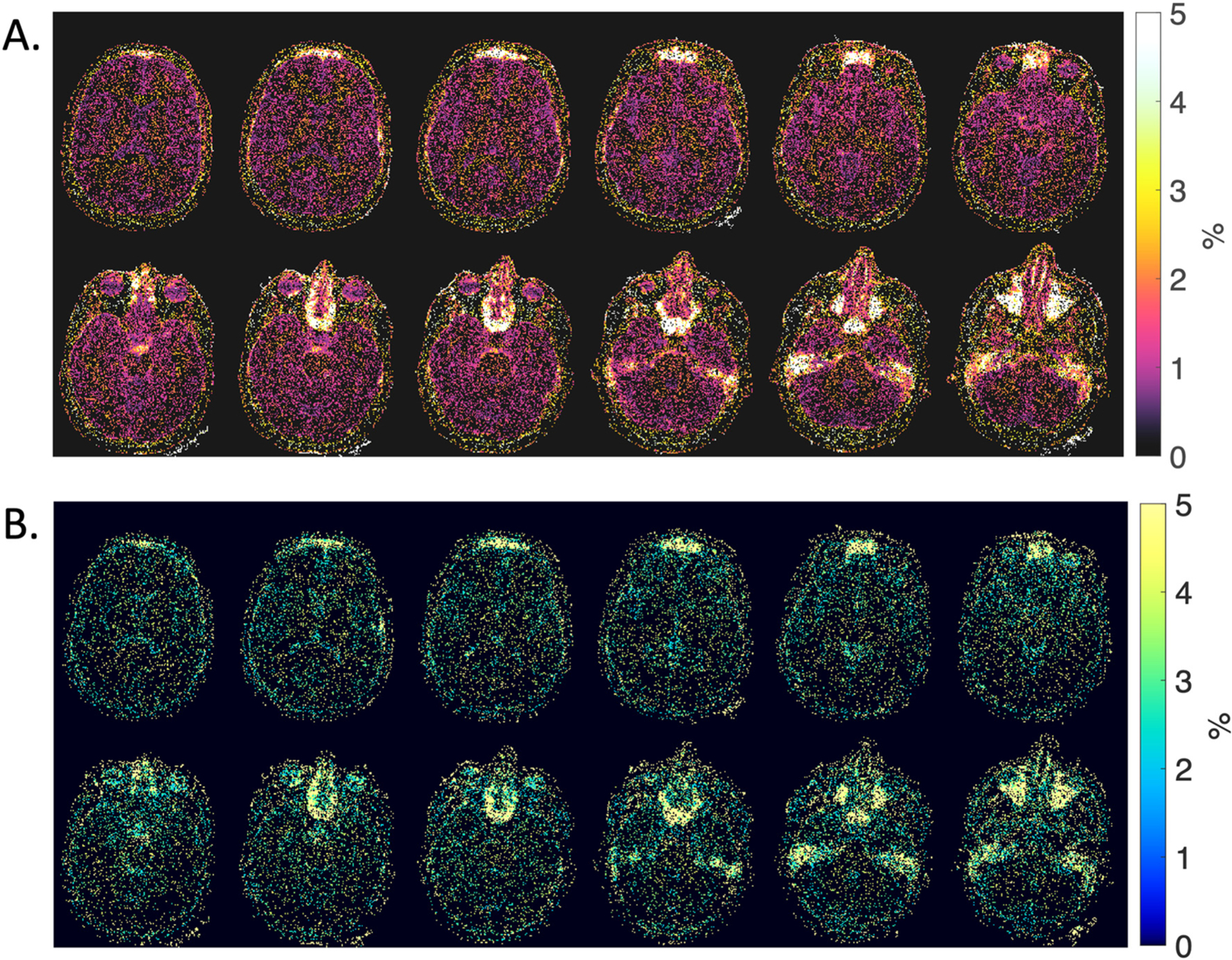
Precision maps showing the normalized range of A) T1 and B) T2 values calculated using MRF. The range of fitted T1 and T2 values, normalized to the mean, was generated from 100 pseudo-replicas with white noise in a single healthy volunteer. Pixels with 0% value indicate no deviations in quantitative value across 100 pseudo-replicas.

4. Discussion

We have demonstrated the feasibility of whole-brain MR fingerprinting using a prototype 0.55 T MRI system for quantitative T1 and T2 mapping in healthy volunteers. The method was validated using the ISMRM/NIST quantitative MRI phantom, and in vivo image quality was reasonable. As expected, the in vivo T1 values at 0.55 T were shorter than at 1.5 T. Modern acquisition strategies, such as MRF, may offer advantages for this lower-field MRI system configuration.

Although MRI field strengths <1.5 T have been available for decades, commercial low field systems are designed for niche clinical applications, and therefore have compromised system performance, or permanent magnet design that limits B0 homogeneity [13]. Previous work has demonstrated that MRF can be deployed on older 1.5 T systems to good effect [24]. Here, we used a commercial 1.5 T system modified to operate at 0.55 T, in order to exploit modern state-of-the-art system performance and imaging methods at a lower field strength. Lower-field MRI equipped with high performance hardware offers unique opportunities for lower cost imaging, point-of-care imaging, and new clinical applications. MRF is especially attractive for high-volume settings that depend on efficient multi-contrast imaging. Clinical imaging workflow at 1.5 T and 3 T relies heavily on a large number of contrast-weighted imaging protocols that have been refined over many years at an individual institution. Embracing quantitative imaging can overcome the need for optimization of multiple contrast weighted sequences for new system configurations. Previous studies at ultra-low field (6.5mT) have used a 3D balanced steady-state free precession EPI acquisition for multi-contrast imaging [15]. Whereas, here we were able to use a 3D stack-of-spirals FISP acquisition similar to previous 3 T implementations.

The original implementation of 3D FISP MRF generated 1.2 mm × 1.2 mm × 3 mm spatial resolution and used undersampling in the k_z direction for a total acquisition time of <5 min at 3 T. At 0.55 T, we maintained in-plane resolution of 1.2 mm × 1.2 mm, but used thicker slices of 5 mm. In addition, we fully sampled in k_z for the purposes of this feasibility study, resulting in an acquisition time of 8 min 30 s. Some sequence parameters were modified from the predecessor 3D FISP MRF at 3 T, namely TR (8.88 ms at 0.55 T vs. 10 ms at 3 T) and maximum flip angle (75° at 0.55 T vs. 60° at 3 T). Precision measured using 50 pseudo-replicas for a similar 2D FISP MRF sequence at 3 T demonstrated coefficients of variation of 0.4% for T1 = 400 ms and 0.5% for T2 = 59 ms from 5 × 5 pixel regions in phantoms [8]. By comparison at 0.55 T, we measured coefficients of variation for a single pixel in vivo of 1.0% for T1 = 500 ms and 2.0% for T2 = 50 ms. Using MRF at 0.55 T, white matter and gray matter T1 values were 32% shorter than MRF measurements at 1.5 T [1].

We used spiral data sampling for MRF, which is well-suited to lower field due to the SNR-efficiency and reduced off-resonance blurring 0.55 T [10]. The precision of MRF has previously been demonstrated be non-linearly related to SNR since it uses pattern recognition rather than direct imaging [17]. We did not perform B0 and B1+ mapping measurements at this field strength since the B0 and B1+ fields are homogenous using this system configuration. Future studies could investigate the impact of this. We did apply a constant B1 scaling factor of 0.9. A small bias in MRF T2 values, compared to gold standard spin echo T2 mapping, was measured in the ISMRM/NIST phantom. This is not unexpected as previous studies have indicated increased T2 bias in lower SNR regimes with conventional MRF, which can be corrected using sophisticated optimization schemes [17]. In vivo, T1 values were comparable to previous in vivo measurements at 0.55 T using standard methods, whereas T2 measured by MRF was shorter (eg. gray matter T2 = 77 ms using MRF vs T2 = 112 ms using standard measurement reported previously [10]). Hilbert et al. demonstrated similar discrepancies using MRF at 3 T, which they compensated by incorporating magnetization transfer into MRF [25].

This feasibility study has several limitations. The reduced resolution and increased scan time, compared with similar acquisitions at 3 T, will be addressed in future studies. At 1.5 T and 3 T, additional studies have further optimized 3D multicontrast protocols [26,27], and these optimization steps have not yet been applied to 0.55 T. We used a 1.5 T head/neck receiver array that is retuned to operate at 0.55 T. The proton density maps suffered from the poor coil performance, which resulted in limited penetration depth and lower signal intensity in the center of the brain. Image quality would benefit from the development and optimization of coils for this specific field strength, as was done for 1.5 T and 3 T after the introduction of receiver arrays. An additional limitation of this study was the enrollment of only healthy volunteers for the assessment of feasibility. The performance of this MRF protocol will be assessed in patients with pathology in the future. In addition, future work will explore k_z undersampling for shorter acquisition and longer spiral readouts for improved SNR efficiency, exploiting the B0 homogeneity and long T2* at 0.55 T.

5. Conclusions

A 3D FISP MRF sequence was implemented for a 0.55 T system equipped with contemporary hardware and software, and we demonstrated the feasibility of whole-brain T1 and T2 mapping using MRF in healthy volunteers.

Abbreviations:

3D

Three dimensional

CV

Coefficient of variation

FISP

Fast imaging with steady state precession

GPU

Graphical processing unit

MRF

Magnetic resonance fingerprinting

NUFFT

Nonuniform fast Fourier transform

ROI

Region of interest

SNR

Signal-to-noise ratio