Multi-Phase Boltzmann Weighting

Abstract

Accurately computing partition coefficients is a pivotal part of drug discovery. Specifically, octanol-water partition coefficients can provide information into hydrophobicity of drug-like molecules, as well as a de facto representation of membrane permeability. However, one challenge facing the computation of partition coefficients is the need to encapsulate various microscopic environments. These include areas of largely bulk solvent (i.e., either water or octanol) or regions where octanol is saturated with water or areas of higher salt concentration. Also, tautomeric effects require consideration. Thus, we present a Boltzmann weighting approach that incorporates transfer free energies across varying microscopic media, as well as varying tautomeric state, to compute partition coefficients in the SAMPL6 challenge.

1. Introduction

The ability to correctly identify thermochemical properties of drug-like molecules is an essential step in the drug design process [1]. Some examples include the resolution of major tautomeric and protonation states, as well as solvent affinity (e.g., solvation free energies and partition coefficients). Various methods exist for these computations ranging a gamut of theoretical rigor (e.g., empirical and physicsbased) [2]. However, comparing accuracy and precision across methods is difficult. Thus, the statistical assessment of the modelling of proteins and ligands (SAMPL) challenge has become a pivotal benchmark to the computational chemistry community [3–8].

This work is a molecular simulation study. We describe an attempt to determine water-octanol partition coefficients from alchemical free energy simulations in the context of the SAMPL6 log P prediction challenge [9]. Logarithmic partition coefficients, log P, are an often-used indicator for drug efficacy, mainly because they reveal a substance’s ability to permeate through cell membranes and access binding targets. The correlation between partitioning into an organic phase and permeability is famously stated by Overton’s rule [10]. While permeability measurements are tedious in both simulation and experiment, partition coefficients are generally easier to obtain with both methodologies [11]. Although Overton’s rule does not explicitly state a solvent of choice for the organic phase, hexadecane and octanol are the most popular phases in practice [12]. Hexadecane resembles the hydrophobic interior of lipid bilayers, which is often most informative of the permeability [13]. Octanol, in contrast, better models the amphiphilic molecular structure of lipids which contain apolar tails as well as polar head groups. This leads to a richer microsopic structure; octanol forms inverse micelles in bulk since the polar hydroxyl groups cluster. The non-negligible amount of water that gets solvated in bulk octanol further amplifies the structural heterogeneity; differentsized water clusters and chains form, around which octanol organizes in micelle- and column-like structures [14, 15].

The microscopic heterogeneity in the octanol phase presents a challenge for classical approaches that calculate partition coefficients based on atomistic simulations [16]. Compared to hexadecane, the presence of substructure increases the effective dimension of the configurational space and sampling this space exhaustively becomes computationally expensive. Free energy simulations in different alchemical states cause a reorganization of solvent in the presence or absence of solute and converging those simulations in each state becomes tedious. In addition, various microscopic environments coexist throughout both the organic (i.e. octanol) and aqueous phases. This includes environmental heterogeneity in the octanol phase from water saturation, as well as the salt accumulation in the aqueous phase (as salt ions do not cross into the octanol [17] and phases are never perfectly mixed on the nano-scale). Other effects to consider in the classical scheme are the possibility of major tautomeric changes between phases, and thus the need to accommodate possible tautomeric states [18–21].

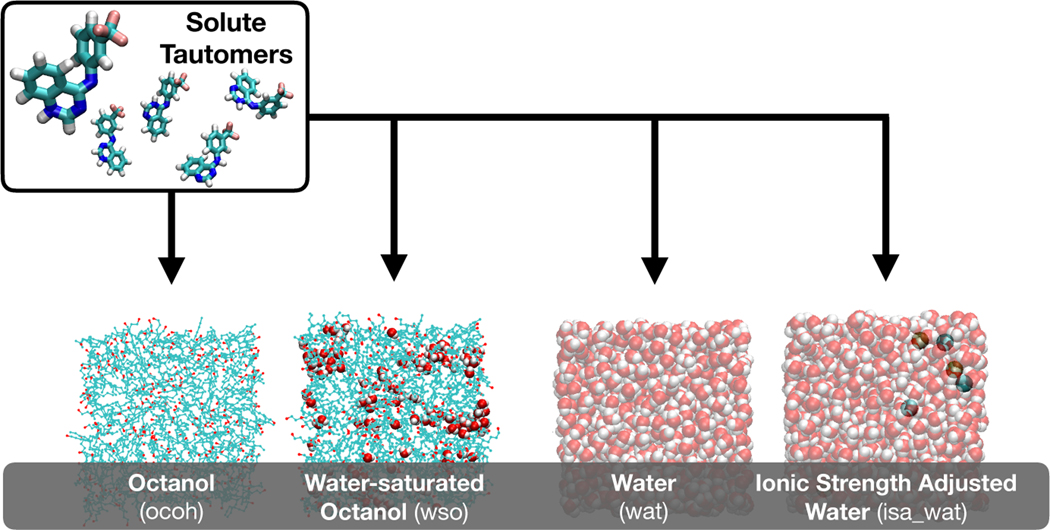
To account for local (and spontaneous) inhomogeneity, the present work follows a multi-phase approach, where both solvents are represented by multiple systems that contain different mixtures of octanol, water, and ions, see Fig. 1. Free energies of solvation for all considered tautomers in all solvent phases are calculated using the CHARMM generalized force field (CGenFF) [22] and a standard free energy simulation protocol. To combine the solvation free energies for these systems into a single partition coefficient, each mixture is assumed to be equally accessible to the solutes. Boltzmann weighting is performed with respect to a mutual reference state, namely the lowest-energy tautomer in gas phase. This approach captures the local inhomogeneity of the system, while allowing a small system size for each simulation.

Fig. 1.

Illustration of the various environments considered in this work.

This manuscript presents the methods and results for SAMPL6 submissions ujsvj, 3wvyh, 2mi5w, 5855v, and tzzb5. As detailed later, the results submitted as a blind prediction were affected by a numerical inconsistency in an analysis script. This error was fixed in post-submission analysis and we mostly discuss the updated results. The manuscript is structured as follows: Section 2 presents the methods that were used to identify and parameterize tautomers, set up and run the simulations, and compute partition coefficients. Section 3 describes the results. Section 4 discusses the results and some of the challenges faced on the way. Section 5 provides concluding remarks.

2. Methodology

2.1. Generation of tautomers

Tautomer identification was performed through the OpenBabel, MolVS, and RD-Kit interfaces for converting SMILES strings into XYZ files [23, 24]. Following this, the resulting preliminary tautomers were examined for possible E/Z isomerization through which IQMol was used to generate initial configurations [25]. All the identified tautomers (labeled with letters a, b, c, etc.) are provided as PDB files in supplemental data. Once all tautomers were identified, geometry optimizations were performed at the PM7 level of theory using MOPAC [26].

Relative energy differences between tautomers, $\text{Δ}{A}_{\text{gas}}^{\text{ref}\to \text{tautomer}}$, were computed via geometry optimizations of all possible tautomers using MP2 [27] with 6–31G* [28–31] via Gaussian09 [32] or Gaussian16 [33]. Following this, frequency calculations were used to determine thermal corrections to the free energy with a tight SCF convergence threshold.

2.2. Parameterization

Initial CHARMM tautomer parameters (i.e., CSET) were obtained via the Paramchem server [34]. Reparameterization for each respective set of tautomers was attempted via the FFTK program available in VMD [35, 36]. This process was performed in a two-fold approach: once where only parameters with penalties based on the Paramchem output were adjusted (i.e. PSET), and fitting based on reparameterizing each molecule from scratch (i.e., ASET). However, a handful of problems occured in the parameterization process with the FFTK interface. First, through successive rounds of simulated annealing to obtain partial atomic charges, it was found that the resulting charges had fallen outside of the constraint bounds for select cases (e.g., hydrogens with a negatively assigned charge and halogens with a positive charge). This was the case for molecules SM04, SM07, SM12, and SM13 of the PSET as well as SM07 and SM11 of the ASET. A second problem occurred based a hard coded bug in the FFTK interface, where the standard TIP3 water-solute QM interaction energy required for CHARMM charge parameterization had an erroneous water OH bond length (0.9527 Å as opposed to 0.9572 Å) in the generated Gaussian input files. This bug seems to be specific to halogenated species SM02, SM04, SM12, and SM16, and had a non-negligible effect on interaction energies (e.g., ~0.5 kcal/mol difference). Also, based on an update to the treatment of halogen complexes in the CHARMM general force field [37], lone pairs are needed to encapsulate “sigma hole” effects. At present, FFTK does not support lone pairs, as the background functionality implements NAMD, which does not have lone pair functionality [38]. Furthermore, fitting of Urey-Bradley terms and improper dihedrals is not currently supported by FFTK. Due to the lack of support, lone pairs were ommitted in all calculations (e.g., the +0.05e charge on the lone pairs were added onto their respective parent atom for the CSET parameters).

2.3. System Preparation

Four solvent environments were considered in the log P calculations (see Table 1). For bulk water (wat), a box of 1000 TIP3 waters [39] was constructed, and equilibrated for 500 ps at 1 atm and 300 K under the isobaric-isothermal ensemble to obtain a consensus box size of ~31 Å. The equilibration was run in CHARMM c41b2 [40] using a Nosé-Hoover themostat [41, 42], Particle-mesh Ewald (PME) for electrostatics, and a polynomial potential switching function between 10 and 12 Å for Lennard-Jones interactions. A water-saturated octanol (wso) box was constructed by randomly placing and orienting 356 octanol molecules and 132 TIP3 waters to approximate the experimentally observed mole fraction of water found in octanol (≈0.2705) [43]. The box was equilibrated at 1 atm and 300 K for 2.5 ns in the isobaric-isothermal ensemble in CHARMM, followed by 10 ns equilibration in the same ensemble in OpenMM 7.3.1 [44]. The equilibration yielded a consensus box size of ~45 Å. The pure octanol phase box was constructed from the equilibrated water saturated octanol box via removal of waters (i.e, a box composed of 356 octanols). The ionic strength adjusted (isa wat) water was setup by adding 3 K⁺/Cl⁻ to the bulk water box.

Table 1.

Designation of solvent systems.

Abbreviation	Name	Number of Molecules/Ions in Solvent
		Water	Octanol	K+	Cl−
wat	pure water	1000	0	0	0
isa_wat	ionic strength adjusted water 0.15 M KCl	1000	0	3	3
ocoh	pure octanol	0	356	0	0
wso	water-saturated octanol	132	356	0	0
gas	gas phase	0	0	0	0

The solvated systems were initialized by dragging each tautomer into the center of the solvent box by imposing a center of mass restraint. The initial restraint force constant was set to 0.00001 kcal/mol·Å² and increased by an order of magnitude every 1 ps over 5 iterations. Some systems ended up with octanol sticking through rings of the solute molecules. These systems were manually postprocessed by shifting the coordinates of the penetrating octanols and running a short equilibration at 200 K.

2.4. Molecular Dynamics Simulations

Simulations were run in OpenMM 7.3.1 using Langevin Dynamics with a 1 fs time step and a 5/ps friction coefficient [44]. Nonbonded interactions were calculated as described in the previous subsection. Preceded by an energy minimization, each solute/solvent system was first equilibrated in the isothermal-isobaric ensemble. A Monte-Carlo barostat [45] was used for pressure control. For the first 20 ps, the reference pressure and temperature were set to 1000 atm and 200 K, respectively, ensuring stable simulations for all systems and preventing blow-ups. The box size was then equilibrated at atmospheric pressure, where the temperature was gradually increased from 200 K to 298.15 K for 250 ps, and left constant at 298.15 K for another 250 ps.

Starting from the equilibrated configurations, independent alchemical simulations were run in parallel in 13 λ-states. Each of these 13 equilibrium simulations redefines the electrostatic and van-der-Waals interactions between solute and solvent atoms, and among solute atoms: At lambda index Λ = 0, the solvent and solute are fully interacting. At Λ = 12, the intermolecular interactions of the solute are fully annihilated. In order to enable simulations of all tautomers in all phases within a reasonable amout of time, larger errors (i.e., ~1 kcal/mol) were tolerated and the lambda spacing was intentionally chosen somewhat wider than usual.

Each λ-state in Table 2 defines the solute’s intermolecular interactions as follows: The electrostatic scaling parameter, λ_elec, is multiplied onto the solute’s partial charges. The van-der-Waals scaling parameter, λ_vdw, designates a soft-core Lennard-Jones (LJ) potential between atoms i and j, where either i or j, or both, represent the index of a solute atom,

$$U_{{\lambda }_{\text{vdw}}\text{LJ}}^{\text{LJ}}\left(r_{ij}\right)=4{\epsilon }_{ij}^{\text{eff}}\left({\left(\frac{\sigma }{r_{ij}^{\text{eff}}}\right)}^{12}-{\left(\frac{\sigma }{r_{ij}^{\text{eff}}}\right)}^6\right).$$ (1)

Table 2.

Parameters for alchemical states. Lambda index Λ and decoupling parameters for van-der-Waals and electrostatic interactions in each λ-state, λ_vdw and λ_elec.

Λ	0	1	2	3	4	5	6	7	8	9	10	11	12
λ vdw	1.0	1.0	1.0	1.0	1.0	1.0	0.9	0.8	0.7	0.6	0.4	0.2	0.0
λ elec	1.0	0.8	0.6	0.4	0.2	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0

The effective well-depth and radius are defined as

$${\epsilon }_{ij}^{\text{eff}}={\lambda }_{\text{vdw}}{\epsilon }_{ij}$$

and

$$r_{ij}^{\text{eff}}=r_{ij}+{\sigma }_{ij}\left(1-{\lambda }_{\text{vdw}}\right),$$

respectively, where ${\sigma }_{ij}=\left({\sigma }_i+{\sigma }_j\right)/2$ and ${\epsilon }_{ij}=\sqrt{{\epsilon }_i{\epsilon }_j}$ are the Lennard-Jones parameters. The use of soft-core potentials prevents the van-der-Waals endpoint problem [46] as well as van-der-Waals clashes, i.e. too short interatomic distances r_ij that would lead to large potential energies and thereby cause instabilities. For ${\lambda }_{\text{vdw}}=1,U_{{\lambda }_{\text{vdw}}}^{\text{LJ}}$ represents the customary Lennard-Jones potential, while for ${\lambda }_{\text{vdw}}\to 0$, steric interactions are gradually switched off. The potentials were used as implemented in openmmtools [47], version 0.18.0. Note that openmmtools did not support soft-core potentials for systems that contain any NBFIXes (pair-specific Lennard-Jones parameters), a restriction that initially prevented alchemical simulations for the tautomers m16a, m16c and m16e, and for all systems containing ions.

The energy minimization and equilibration were repeated in each λ-state (now with the box size fixed) allowing 500 ps for the system to adapt to the alchemically modified potential energy function. Production simulations, 10 ns in each state, were run in the canonical ensemble. Regarding the potentially slow relaxation times of octanol configurations, this simulation time presents a compromise between accuracy and computational cost that values efficiency over accuracy. Trajectory frames and energies were saved once per picosecond. Gas phase calculations were carried out in a cubic box spanning 30 Å in each direction. The annihilation of electrostatic and steric interactions was done in the same way as for the solvated systems.

2.5. Free Energy Calculations

The Hamiltonian from each λ-state was cross-evaluated in each trajectory frame from all other λ-states. Free energies of annihilation, $\text{Δ}{A}_{\text{solvent}\to \text{off}}^{\text{tautomer}}$, were calculated using the Multistate Bennett Acceptance Ratio method (MBAR) for each tautomer and solvent (including gas phase), following a subsampling of statistically uncorrelated data [48].

Using the free energies of annihilation, the free energy of solvation for each tautomer and solvent is given as

$$\Delta A_{\text{gas}\to \text{solvent}}^{\text{tautom}}=\Delta A_{\text{gas}\to \text{off}}^{\text{tautomer}}-\Delta A_{\text{solvent}\to \text{off}}^{\text{tautomer}},$$

see Fig. 2. Statistical errors were calculated by averaging $\Delta A_{\text{gas}\to \text{solvent}}^{\text{tautomer}}$ over five 2 ns blocks. In contrast to the error estimate provided by MBAR, the error of the block-averaging recognizes configurational changes of the solvent that take place within a few nanoseconds.

Fig. 2.

Schematic diagram of the individual terms used in the free energy calculations. Tautomers are represented by orange circles, solvent phases are represented by blue, green, and yellow rectangles. The tautomers’ intermolecular interactions were alchemically switched off from both solvent and gas phase to compute annihilation free energies, $\Delta A_{\text{solvent}\to \text{off}}^{\text{tautomer}}$ and $\Delta A_{\text{gas}\to \text{off}}^{\text{tautomer}}$. These were related to a mutual reference state through their relative free energies in gas phase $\Delta A_{\text{gas}}^{\text{ref}\to \text{tautomer}}$.

2.6. Multi-Phase Boltzmann Weighting

Finally, the solvation free energies for all tautomers of a given solute molecule were combined into a single partition coefficient log P. To determine the partitioning into different solvent systems and to identify the prevalent tautomers, the free energy differences between tautomers in solution were evaluated with respect to the reference tautomer, i.e. the one with the lowest QM energy in gas phase

$$\Delta A_{\text{gas}\to \text{solvent}}^{\text{ref}\to \text{tautomer}}=\Delta A_{\text{gas}}^{\text{ref}\to \text{tautomer}}+\Delta A_{\text{gas}\to \text{solvent}.}^{\text{tautomer}}$$

These free energies with respect to a mutual reference point determine the partitioning through Boltzmann weighting. If different solvent systems are equally accessible to the solute, the probability of finding a given tautomer in a given solvent is

$$P(\text{tautomer},\text{solvent})=\frac{\exp \left(-\beta \Delta A_{\text{gas}\to \text{solvent}}^{\text{ref}\to \text{tautomer}}\right)}{{\text{Σ}}_0},$$

where the normalization factor Σ₀ is the sum over all tautomers and solvent systems

$${\Sigma }_0=\sum _{\text{tautomers}}\sum _{\text{solvents}}\exp \left(-\beta \text{Δ}{A}_{\text{gas}\to \text{solvent}}^{\text{ref}\to \text{tautomer}}\right).$$

Consequently, to determine the octanol/water partitioning, these probabilities are summed over, and normalized with the number of different water and octanol systems, n_w and n_o, as follows:

$$\log P={\log }_{10}\left(\frac{n_{\text{w}}}{n_{\text{o}}}\cdot \frac{{\sum }_{\text{tautomers}}{\sum }_{\text{octanol}\text{systems}}P(\text{tautomer},\text{solvent})}{{\sum }_{\text{tautomers}}{\sum }_{\text{water}\text{systems}}P(\text{tautomer},\text{solvent})}\right).$$

3. Results

3.1. Predictions Submitted to the SAMPL6 Challenge

Three sets of partition coefficients were submitted to the SAMPL6 challenge based on the above-described protocol and the CSET (CGenFF) parameters, see Table S2. The simulations differed by the solvents that were considered in the log P calculation: pure water/pure octanol; pure water/wet octanol; pure water/pure octanol/wet octanol. (At the time of submission, the results for the ion-saturated water box were not available due to lacking support for NBFIXes in openmmtools’s alchemy module.) Also, a reweighting to CHARMM energies was included to account for the different van-der-Waals switching functions as described in the Supplementary Information, Section S3. The submissions all achieved mean absolute errors (MAE) and root mean squared errors (RMSE) below 1 kcal/mol and positive correlation with experiment, see supplementary information, Figures S1–S3. The partition coefficients were also evaluated for the reoptimized parameters PSET and ASET, see Figs S4 and S5, respectively. The optimized parameters worsened match with experiment due to the aforementioned problems with FFTK.

In a follow-up analysis we found a numerical inconsistency in an analysis script that changed the result drastically and for the worse with the CSET parameters. Moreover, in one of the simulations for SM09 an octanol molecule stuck through a ring of the solute during the entire simulation, causing large potential energies and effectively removing this tautomer (m9e) from the Boltzmann weighting. In fact, this situation occurred for multiple solutes after the initial generation of the solvation box but all other systems were detected and fixed earlier. Lastly, three tautomers of SM16 (m16a, m16c, and m16e) could not be considered in the submissions due to NBFIXes in their CGenFF parameters. Due to these major flaws in the original results, the remainder of this paper will only discuss the post-submission results where these problems were resolved. The original submissions are briefly described in the supplementary information (see Section S1).

3.2. Consistency between CHARMM and OpenMM

OpenMM was chosen as the molecular dynamics engine for efficiency reasons (CHARMM does not yet have a fast implementation of its alchemical functionality). One concern in using OpenMM instead of CHARMM for sampling was the consistency of CHARMM parameters with the OpenMM simulation program [49, 50]. Some measures had to be taken to improve consistency. First, the analytic long-range correction that was customary in OpenMM systems generated from CHARMM PSF files had to be manually removed. Second, trajectory files generated by the OpenMM DCD reporter were not flawlessly readable by CHARMM due to inconsistent indexing of the trajectory frames (zero-based versus one-based). Therefore, the reporter had to be customized to match the format expected by CHARMM. Third, the selection of the alchemical region had to be handled carefully, since OpenMM’s PSF parser merged residues from different segments together. These three problems were fixed and the fixes were included into OpenMM Version 7.4.0. (Note that OpenMM version 7.4.0 also supports lone pairs more comprehensively which further extends compatibility with the CHARMM force field.)

Another difference between the two programs is the van-der-Waals switching function. While CHARMM implements the potential switching and force switching schemes introduced by Steinbach and Brooks [51], OpenMM’s polynomial switching function has a different functional form. This is an important detail, for example, in simulations of lipid bilayers. Therefore, the influence of the switching function on potential and free energies was studied. In OpenMM, the average potential energy of a 5 ns long simulation in the fully solvated state of m11b (a tautomer of SM11) in water was −16852.3 kcal/mol with a standard deviation of 72.191 kcal/mol. Reevaluating the energies for this trajectory in CHARMM with the VSWITCH potential switching function yielded good agreement with OpenMM, an average of −16851.4 kcal/mol and standard deviation 72.196 kcal/mol. The free energy difference between the two programs was evaluated from Zwanzig’s rule [52] as $\Delta A_{\text{Λ}=0}^{\text{openmm}\to \text{charmm}}=0.66\pm 0.01$ kcal/mol, 2.4 ± 0.2 kcal/mol, and 2.6 ± 0.2 kcal/mol for pure water, pure octanol, and water-saturated octanol, respectively. See Supplementary Information, Section S3, for details. Note that all interactions (solvent-solvent, solvent-solute, and solute-solute) contribute to this difference so that the influence on the solvation free energy, approximately 0.02 kcal/mol, is negligible. Nevertheless, the CHARMM switching functions were implemented for openmmtools, mostly with respect to lipid bilayer applications but also to further improve consistency in the present work. Since this implementation achieved consistent energies between CHARMM and OpenMM, the reweighting to CHARMM was not performed for the post-submission results presented in this manuscript.

Lastly, the soft-core functionality of openmmtools was expanded to these new switching functions as well as to NBFIXes. The soft-core implementations were tested by comparing the potential energies of SM14 solvated in ionic strength adjusted water. Both end states (fully solvated and fully annihilated) were in excellent agreement with the corresponding CHARMM energies for the initial coordinates. ¹

3.3. Free Energies of Solvation

The free energies of solvation for all tautomers and all solvents are given in the supplementary information, Table S3. The wide lambda spacing and relatively short simulations resulted in large uncertainties. On average the errors were 0.43 kcal/mol in water and 0.78 kcal/mol in octanol, which in combination amounts to approximately 1 log P unit.

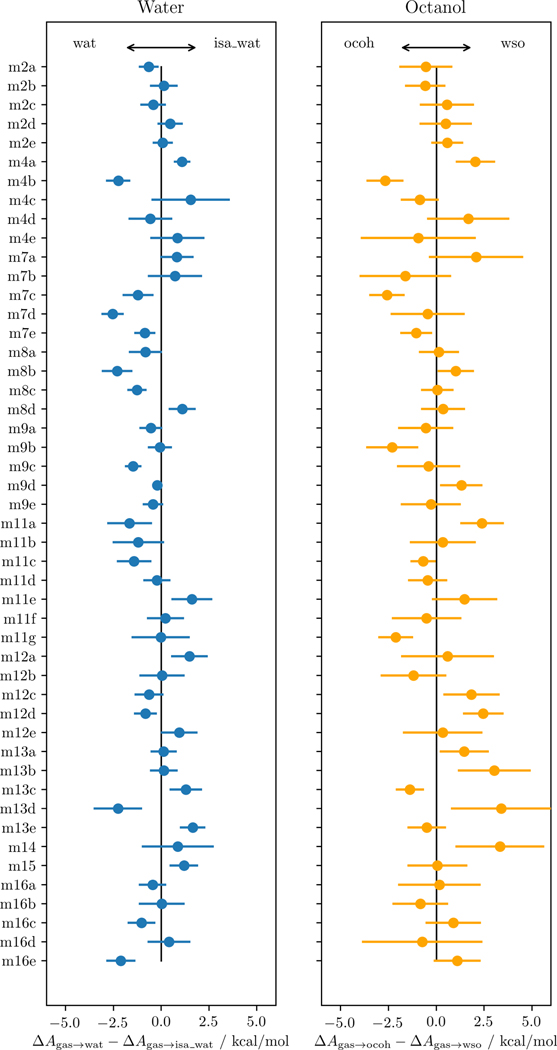
The solvation free energies were remarkably sensitive to the solvent composition (e.g., isa wat vs wat). Fig. 3 shows the differences in solvation free energies between the pure solvents and the experimental compositions. Some of the tautomers were more soluble in one than the other systems by up to 2.5 kcal/mol. For example, SM04’s tautomer (m4a) was a factor of ~30 more soluble in water-saturated octanol than pure octanol, whereas, in contrast, m4b was a factor of ~100 more soluble in pure octanol, see probabilities in Table S4. Despite large error bars, these differences were statistically significant. Similar findings were observed for the same tautomers regarding the two water systems.

Fig. 3.

Differences in solvation free energies between the pure solvents (wat and ocoh) and the experimental compositions (isa wat and wso).

The compilation of all different tautomers (Fig. 3) did not reveal a general preference for either the pure or mixed phases; the results were highly tautomer-dependent and in many cases statistically significant.

3.4. Partition Coefficients

Table 3 lists log P for four different solvent combinations, the three combinations that were submitted to the prediction challenge as well as one that included all four phases. Fig. 4 shows the correlation with experiment for three of them. As expected from the discrepancies and uncertainties in the solvation free energies, the partition coefficients varied depending on the choice of solvents for many of the molecules. The greatest difference, 2.4 log P units, was observed for SM14, which lost its preference for the organic solvents when water-saturated octanol was excluded from the Boltzmann weighting. The best consistency between the different solvent systems was observed for SM08 (0.2 log P).

Table 3.

Logarithmic water-octanol partition coefficients, log P, for simulations including four different combinations of solvent and from experiment.

	ocoh/wat	wso/wat	ocoh/wso/wat	ocoh/wso/wat/isa_wat	Experiment [9]
SM02	0.4 ± 1.1	0.0 ± 1.0	0.2 ± 1.0	0.2 ± 1.0	4.1
SM04	5.4 ± 1.2	6.8 ± 1.0	6.5 ± 1.1	6.1 ± 1.0	4.0
SM07	1.0 ± 0.8	2.5 ± 0.9	2.3 ± 0.8	1.9 ± 0.8	3.2
SM08	5.0 ± 1.1	5.1 ± 1.0	5.0 ± 1.1	5.2 ± 1.1	3.1
SM09	0.6 ± 0.9	1.3 ± 0.8	1.1 ± 0.9	1.2 ± 0.8	3.0
SMll	2.6 ± 0.6	2.3 ± 0.7	2.5 ± 0.7	2.6 ± 0.7	2.1
SM12	3.8 ± 0.7	5.2 ± 0.7	4.9 ± 0.7	4.2 ± 0.7	3.8
SM13	1.7 ± 1.4	1.3 ± 1.2	1.5 ± 1.3	0.6 ± 1.3	2.9
SM14	-0.1 ± 0.7	2.3 ± 0.5	2.0 ± 0.6	1.6 ± 0.6	2.0
SM15	1.2 ± 0.5	1.3 ± 0.6	1.2 ± 0.6	0.6 ± 0.5	3.1
SM16	0.8 ± 0.6	1.6 ± 0.6	1.4 ± 0.6	1.6 ± 0.7	2.6

Fig. 4.

Simulated versus experimental water-octanol partition coefficients [9], log P, for three different combinations of solvent.

The overall performance with respect to experiment was ~1.7 in terms of the mean absolute error (MAE) and ~2 in terms of the root mean squared error (RMSE). In most cases, the partition coefficients obtained from only two solvent phases bracketed the multiple-solvent results, as expected from a Boltzmann weighted average. The inclusion of all four solvents led to an overall stronger solubility in the organic phase in comparison to the ocoh/wat and wso/wat systems. The molecule that was most soluble in octanol experimentally, SM02, was a major outlier in the simulations. While all other solutes matched experiment within at least 2 log P units, SM02 consistently underestimated the experimental value by at least 3.7 log P units for all solvent combinations. For most solvent combinations, SM02 was even the least soluble in octanol.

The result for SM02 had a strongly negative effect on the overall correlation with experiment. Table 4 shows that R² was in the range of 0.05–0.15. In all cases, the inclusion of water-saturated octanol led to better match with experiment over pure octanol, whereas the inclusion of isa wat deteriorated accuracy. The best result was obtained using a combination of pure water and the two different octanol phases, where the MAE and RMSE were 1.57 log P units and 1.86 log P units, respectively.

Table 4.

Statistics for all considered solvent combinations. Mean absolute error (MAE), root mean squared error (RMSE) and squared correlation coefficient R². All data is in log P units

	MAE	RMSE	R 2
ocoh/wat	1.74	1.98	0.15
ocoh/isa_wat	1.99	2.26	0.07
ocoh/wat/isa_wat	1.98	2.17	0.12
wso/wat	1.60	1.93	0.10
wso/isa_wat	1.70	2.10	0.04
wso/wat/isa_wat	1.64	2.01	0.07
ocoh/wso/wat	1.57	1.86	0.10
ocoh/wso/isa_wat	1.68	2.04	0.05
ocoh/wso/wat/isa_wat	1.66	1.96	0.08

4. Discussion

The calculated solvation free energies and log P show unequivocally that solvent composition matters in molecular dynamics studies of solvation. The presence of salt in the water phase and water in the octanol phase had a non-trivial, strongly tautomer-dependent effect. While some differences in solubility due to solvent composition are expected [53, 54], the ~2 kcal/mol disparity observed in the simulations for many tautomers, to the knowledge of the authors, has no experimental precedent. These discrepancies are explained by flaws in both the entropic and enthalpic contributions to the free energy, as detailed in the succeeding subsections 4.1 and 4.2, respectively.

4.1. Sampling Issues

Part of the problem may be the imprecision of the free energy estimates in this work. While a certain degree of uncertainty was intentionally tolerated for computational efficiency, the overall error margins were rather large for alchemical free energy simulations. The average statistical uncertainty over all annihilation free energies was 0.83 kcal/mol from the block-averaging. (In comparison, the MBAR error estimates were 0.32 kcal/mol on average even after subsampling the data according to statistical inefficiency.) The large errors are a result of wide lambda spacings specifically in the annihilation of van-der-Waals interactions and of relatively short simulations (10 ns) in each λ-state.

Specifically the octanol phases could require longer simulations due to slow solvent reorganization in the presence or absence of solute. Unfortunately, the slow relaxation does not only affect the initial system setup but extends to every λ-state: In principle, the annihilation of a solute’s electrostatic interactions turns it maximally hydrophobic, which would likely cause a reorientation of all its surrounding octanol molecules and ultimately affect the whole system [55]. Such drastic configurational changes are easily missed on the 10 ns timescale used by the presented free energy protocol [16, 56].

To get an idea of the timescales involved in octanol equilibration, we ran a microsecond long simulation of a larger water/octanol system that started out with ionic strength adjusted water in one slab and pure octanol in the other (see Section S2 in the SI for details). Even after 300 ns, the slab had yet to reach equilibrium, with the concentration of water in the octanol slab steadily increasing. Water transport into the organic phase was mediated by potassium ions approaching the octanol/water interface, which fits in with the overestimated coordination of TIP3 water with potassium [57]. The slab simulation served as proof of concept of two things. First, over the course of the entire simulation, no ions permeated into octanol. Second, the time scales required to properly relax the octanol layer are computationally infeasible. This observation shows that equilibration and sampling of water-saturated octanol are major concerns, even in the absence of solute.

To demonstrate and quantify the convergence problems in the present simulations, we studied radial distribution functions and interaction energies of the tautomer m2a in water-saturated octanol, see Supplementary Figures S8 and S9. The observed discrepancies between four blocks of the simulations are sobering and suggest that simulations much longer than 10 ns are required to sample the configurational space. A detailed discussion of these results is provided in Supplementary Section S4.

Since the equilibration and sampling problems scale with system size, the multi-phase approach provides some alleviation. Various other methods could be considered to further improve sampling, such as a more favorable alchemical transformation, Hamiltonian replica exchange, or nonequilibrium approaches [58–60].

4.2. Force Field Deficiencies

Despite large statistical uncertainty, the widely different solubilities observed for the different water and octanol phases were statistically significant. This points out severe flaws in the employed force field parameters. In part, these issues can be blamed on deficiencies in the TIP3P water model (e.g., overestimation of K⁺ interaction and under-structuring in the second and third shells). More importantly though, the CGenFF parameters for the different tautomers are assigned by analogy. They have not been validated for the molecules under consideration. Aggregate statistics of intramolecular and charge parameter penalties for tautomer sets are provided in the supporting information. On average, the penalties are high, particularly for the partial atomic charges.

The largest outlier from experiment, SM02, proved particularly problematic due to the trifluoromethyl substituent attached. The abberative behavior of fluorinated complexes in the context of partition coefficients is well documented, and highlights the need for more sophisticated treatment of non-covalent interactions for fluorinated species [61]. This is emphasized by the fact that efforts to reparameterize this (as well as other complexes) resulted in a net increase in hydrophilicity. Charge penalties (i.e., measures of how reliable initial guess charges are) of SM02 give an average penalty of 156.34, indicating initial charges to be highly suspect.

Large deviations from experimental partition coefficients are therefore not surprising. Even for simple, well-optimized compounds such as amino-acid side chains, Ahmed and Sandler found that CGenFF yields deviations from experiment as large as of 0.45 in terms of the RMSD [62]. This result demonstrates the need for force fields that better describe the intermolecular interactions. In particular, recent calculations of hexadecane/water partition coefficients show that transfer free energies can be drastically improved by including explicit polarizability [63]. Alternatives to assignment via Paramchem, such as MATCH (particularly the machine learning variants of MATCH) are also attractive as a way to better assign initial parameters [64].

4.3. Gas-Phase Calculations

The weighting scheme employed for calculating the free energies between tautomers in gas phase was heavily dependent on the level of theory implemented. In principle, using QM calculations to weight MM solvation free energies can be precarious, as there is a level of “error cancellation” granted by using a consistent level of theory for all calculations. However, the MM free energy differences between gas phase tautomers are physically unreasonable, requiring corrections to QM. Hence, using a QM/MM Hamiltonian for all free energy calculations is desirable. In fact, use of indirect approaches to free energy calculations is strongly advised for these scenarios [65–74].

4.4. High-throughput Parameterization in CHARMM

The parameterization process of CHARMM is somewhat controversial in nature, particularly the ad-hoc nature of potentials added (e.g., Urey Bradley terms, improper dihedrals, CMAP terms, etc). However, for most intramolecular terms, the LSFITPAR [75] tool has been released to accommodate quick and efficient term fitting. However, the fitting of intramolecular parameters requires consistency with intermolecular terms (i.e., charge and vdw parameters). Unfortunately, the charge fitting in CHARMM is somewhat ill-defined, and ill-advised for large scale parameterization. In particular, the nature of charge parameterization in CHARMM (e.g., matching to idealized interaction of molecules with TIP3 waters) requires a fair amount of user intervention. This is largely due to the requirement of user defined “building blocks” as parameterization components to the larger system of interest. Although the FFTK toolkit can be used for de novo parameterization of molecules, there is still a fair amount of user input required via a GUI interface, making it a poor choice for high-throughput parameterization. However, with FFTK amongst the only automated interfaces for CHARMM parameterization, the need for a more streamlined approach to parameter optimization in the CHARMM force field is more apparent than ever.

4.5. CHARMM Force Fields in the OpenMM Ecosystem

The CHARMM force fields remain among the most-used force fields in the MD community. While OpenMM generally supported CHARMM input files, the present work has improved the integration between the programs. All bugfixes and newly implemented features were made available in OpenMM 7.4.0 and through openmmtools (pull request under review). These include: fixes in the PSF parser and DCD reporter, an implementation of CHARMM’s van-der-Waals switching functions, and support for softcore potentials. With these amendments, OpenMM can be utilized as a highly efficient MD engine for alchemical simulations using CHARMM force fields.

5. Conclusion

This work presents a physics-based approach for predicting water-octanol partition coefficients in the SAMPL6 log P prediction challenge. This task is well-suited to empirical approaches due to the wealth of experimental data. In contrast, methods based on molecular mechanics are troubled by long octanol relaxation times that require extensive simulations to equilibrate the systems and sample all relevant molecular configurations. Additionally, assigning force field parameters in a consistent and program-independent manner remains challenging, which reflects the general immaturity of the tools available to the community for these tasks. The emergence of more suitable descriptions of the molecular interactions [76–78] as well as better algorithms and software for automated force field development promises alleviation [79–83]. With these improvements underway, the presented multi-phase reweighting presents a propitious path to mitigate the sampling problem by breaking a complex molecular system into smaller, more tangible subsystems.