Theoretical principles for illuminating sensorimotor processing with brain-wide neuronal recordings

Abstract

Modern recording techniques now permit brain-wide sensorimotor circuits to be observed at single-neuron resolution in small animals. Extracting theoretical understanding from these recordings requires principles that organize findings and guide future experiments. Here we review theoretical principles that shed light onto brain-wide sensorimotor processing. We begin with an analogy that conceptualizes principles as streetlamps that illuminate the empirical terrain, and we illustrate the analogy by showing how two familiar principles apply in new ways to brain-wide phenomena. We then focus the bulk of the review on describing three more principles that have wide utility for mapping brain-wide neural activity, making testable predictions from highly parameterized mechanistic models, and investigating the computational determinants of neuronal response patterns across the brain.

Multiple principles will be needed to understand sensorimotor processing

Understanding brain-wide circuit mechanisms of behavior is a central goal of neuroscience. Sensorimotor circuits require multiple processing stages to extract relevant sensory information, select a course of action, and generate appropriate motor commands. Considerable effort has already gone into deciphering individual stations within such circuits, but understanding integrated sensorimotor processing remains challenging. In particular, sensorimotor information flow is flexible, state-dependent, and multidirectional. How does the brain integrate multiple sensory streams with the outcomes of past behavior to holistically guide action selection? How do memory and motivation shape sensorimotor processing, and how are they shaped by it? Inputs and outputs both shape representation in neural networks, so an integrated view is also needed to decipher the logic of sensorimotor coding. For example, to what extent does the animal’s behavioral repertoire shape the priorities of sensory computation? These questions are becoming increasingly experimentally accessible [1, 2], yet they are formidable, and their answers will be complicated. We argue here that quantitative testable theories will be needed to organize empirical findings and prioritize future experiments [3].

One can conceptualize a successful theoretical science as a well-lit terrain (Figure 1a). Like someone metaphorically looking for lost keys only under a streetlamp, scientists are limited by the conceptual frameworks they use to understand the world. Scientists need streetlamps to ensure that they not only see but also comprehend whatever is in front of them. We believe that theoretical principles provide the best streetlamps, as once found they can illuminate many phenomena quantitatively. We consider their light as concrete models and derivable results, and the illuminated terrain as the principle’s domain of applicability. A famous example from the history of physics is the principle that mass can be neither created nor destroyed. Physicists extracted light from this principle by deriving and using the continuity equation, which quantifies how the amount of matter in a given region changes via inward and outward flow. The continuity equation in turn implied the diffusion equation, revealing this principle’s wide domain of applicability to phenomena spanning statistical physics, chemistry, and biology.

Figure 1:

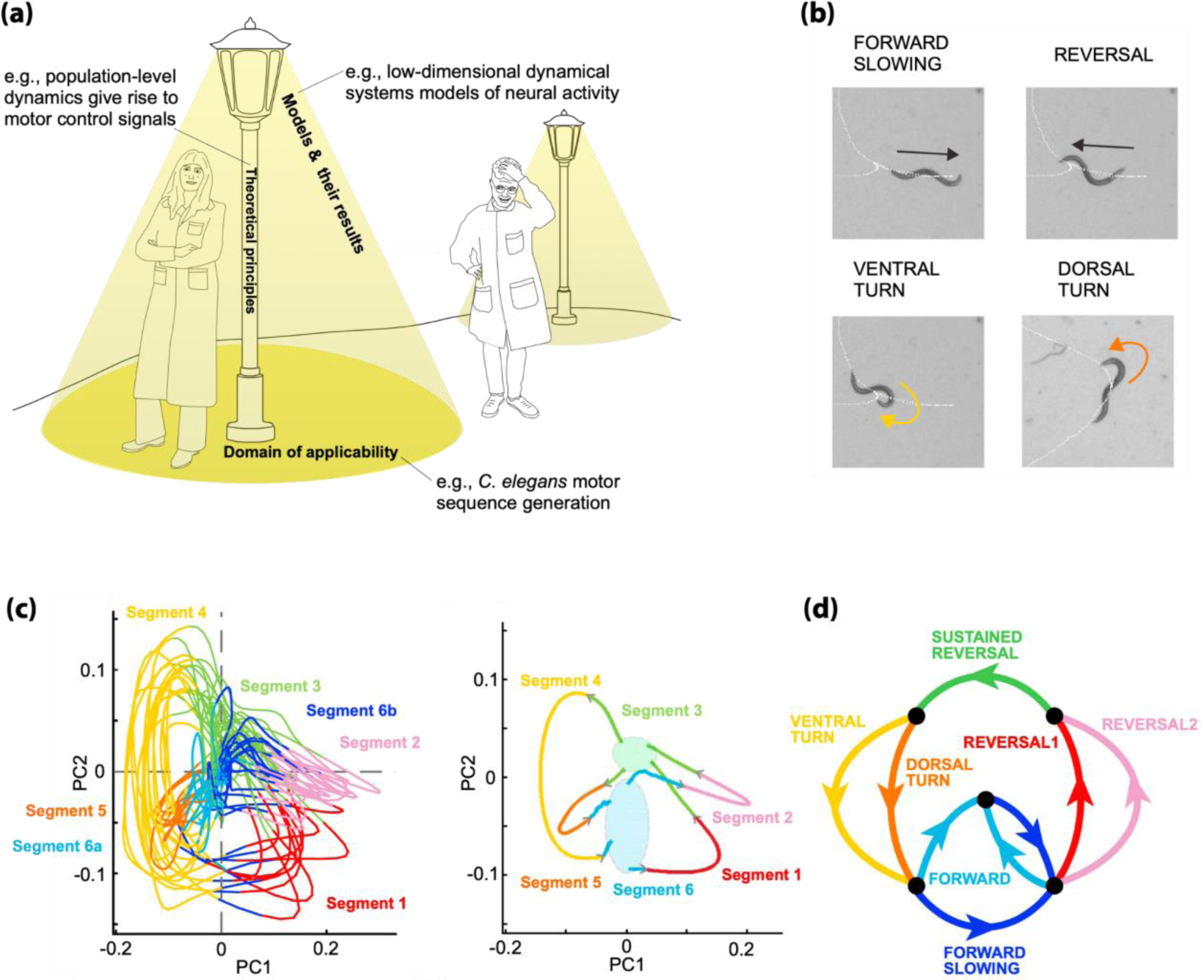
(a) We conceptualize theoretical principles as streetlamps, related models and their derivable results as emitted light, and the empirical domain of applicability as the illuminated terrain. For example, the principle that neurons involved in movement production serve primarily to support the ongoing dynamics of a large dynamical system has led to low-dimensional dynamical systems models that provide means of interpreting the activity of large populations of neurons. This principle was articulated in the domain of primate motor cortex and recently applied by Kato et al. [8] to study the control of motor-sequences in C. elegans. Multiple streetlamps are required to illuminate the full landscape of neuroscience phenomena. The job of the neuroscientist is hardest when they find themselves outside the guiding light of all available streetlamps. (b) Kato et al. recorded brain-wide neuronal activity from immobilized C. elegans fictively performing stereotyped movement sequences known as pirouettes. A pirouette consists of a reversal from forward to backward crawling, followed by a turn along either the dorsal or ventral body axis, and finally by the resumption of forward crawling. (c, left) Principal component analysis (PCA) on the brain-wide recordings revealed trajectories in neural population activity space that cyclically followed stereotyped paths. By analyzing single neuron and population activity, the authors were able to decompose neural state space trajectories into several segment types (colors). See Kato et al. for details. (c, right) Average segment trajectories illustrate the brain’s cyclical dynamics. Ovals indicate regions where different bundles of the trajectories mix. They serve to graphically connect segment averages to each other. (d) The individual segment types of the identified brain cycle could be reliably mapped to the major components of the worm’s movement sequence (colors coded to match (c)). This correspondence was made by comparing brain-wide neuronal recordings during fictive behavior to single neuron recordings in freely moving worms.

Useful principles can have limited domains of applicability for two reasons. First, useful principles can fundamentally fail, as when Einstein realized that mass could be converted to energy. This particular failure led to generalization, as the principle of conservation of energy gracefully absorbed the conservation of mass. The generalized continuity equation could then be applied to new domains like cosmology. Second, a principle’s domain of applicability is limited by its relevance to specific questions of interest. For example, the continuity equation contributes centrally to the theory of fluid flow but not rigid-body motion, even though it’s valid in both settings. Moreover, P. W. Anderson argued in “More is Different” that understanding a complex system requires fundamentally different concepts and laws at each scale [4]. The multiscale nature of the brain is well appreciated [5], and we will probably need many streetlamps to illuminate sensorimotor processing. For instance, the conservation of mass can help a neuroscientist calculate the time required for neurotransmitter diffusion, but it predicts little about neuronal population coding. We must develop a good understanding of when each principle works, when it breaks down, and when it becomes irrelevant. Only then can we choose the right principles to analyze the question at hand.

In this review we highlight five theoretical principles that are shedding light onto brain-wide sensorimotor processing. In the next section we briefly illustrate the streetlamp analogy with two example principles that show the utility of familiar principles for brain-wide neuroscience. In the remaining three sections we discuss three more principles that we consider especially applicable to brain-wide recordings of sensorimotor processes.

Models of brain-wide phenomena can further reveal a principle’s domain of applicability

We begin by illustrating the analogy with two familiar principles that have successfully driven experimental and theoretical progress in brain-wide neuroscience. First, much recent work has emphasized the principle that neurons in motor regions serve primarily as participants in a large dynamical system that collectively generates bodily movements through ongoing neuronal dynamics [6, 7] (Figure 1a). Single neuron tuning properties may or may not be interpretable, so it can be critical to characterize the dynamical system holistically. Kato et al. revealed new domains of applicability for this principle by using it to explain how the C. elegans brain generates stereotyped movement sequences [8] (Figure 1b). In particular, they attributed the activity of most neurons to shared low-dimensional dynamics that followed highly stereotyped periodic trajectories (Figure 1c). Different parts of these trajectories reliably mapped to different movements in the behavioral sequence (Figure 1d), and subtle differences between nearby trajectories corresponded to behavioral variations. Spontaneous and stimulus-evoked population dynamics were robust to single neuron silencing, highlighting globally distributed sensorimotor processing. This example principle thus allowed Kato et al. to illuminate brain-wide mechanisms of sequential behavior that were not localized to single neurons or brain areas.

A second familiar principle is that cortical circuits operate in a state of balanced excitation and inhibition [9]. The theoretical appeal of balanced excitation and inhibition is multifaceted and deep [10, 11], but the basic principle makes intuitive sense. Too much excitation destabilizes network dynamics, and too much inhibition prevents information transmission. Many computational properties of local cortical processing emerge in inhibition-stabilized networks [12, 13], a model variant of balance where strong excitation would lead to instability without inhibition. Joglekar et al. [14] cast light from the balance principle onto multi-regional cortical networks by generalizing the balanced amplification model of Murphy et al. [12] to a global form that balanced strong long-range excitation with local inhibition. Joglekar et al. found that their global balanced amplification model enhanced signal propagation throughout the cortical hierarchy [14], so balance might facilitate hierarchical sensorimotor processing in cortex.

Certain principles may be particularly useful for understanding brain-wide recordings of sensorimotor processing. We therefore devote each of the next three sections to highlighting a principle that has repeatedly proven its worth. Measurements of cellular-resolution brain-wide activity excite us because they can act as the keystone of a bridge spanning local circuits and systems. The next two sections explain this bridge through its top-down arc from larger-scale task variables to cellular activity and its bottom-up arc from smaller-scale biological mechanisms to the same activity. The final section discusses comparisons of brains to performance-optimized artificial neural networks.

Parsing brain-wide activity through quantitative algorithms of behavior

The empirical basis of the top-down arc from task variables to cellular activity is brain activity mapping. Single neuron activity is heterogeneously shaped by many environmental, behavioral, and cognitive task variables [8, 15–18], but a global organization coexists with this heterogeneity. A systems-scale understanding of the brain requires us to resolve how brain activity is simultaneously distributed across the brain and specialized within its subdivisions. The principle that cellular activity, somewhere in the brain, represents task-variables linearly underlies most brain activity mapping studies [9, 19]. In order to maximize the utility of this principle, researchers must build quantitative algorithmic models that explain how a multitude of behavioral, environmental, and cognitive variables unfold throughout the task. An important caveat is that correlative maps are not causal, and this principle does not imply that the task variables capture what matters most to the neural circuit dynamics and behavior.

Multiple recent papers focused on different aspects of the behavioral algorithm for the zebrafish optomotor response and thereby discovered a diversity of cellular participants in the sensorimotor transformation [20–25]. Here we illustrate the principle through Dragomir et al. [23] and Bahl et al. [24], who found congruent results by independently performing similar experiments and analyses. These authors recorded behavioral and neuronal responses to random dot stimuli with variable right-left motion coherence (Figure 2a). Momentary turning rates followed a continuous evidence accumulation model (Figure 2b), which temporally integrated stimuli over the previous few trials to explain long timescale behavior correlations (Figures 2c). The behavioral model thereby identified evidence accumulation as a covert computation that must occur in the brain (Figure 2b), leading the authors to map brain activity by the timescales on which neurons integrate directional motion signals (Figure 2d). This revealed significant neuronal diversity within and across brain regions, with some neurons responding rapidly to stimuli and others integrating signals within and across trials. Bahl et al. additionally found that the behavior was better explained if the behavior model included a dynamic decision threshold, and both sets of authors ultimately mapped their behavioral models onto neuronal signals by combining these and other results (Figure 2e).

Figure 2:

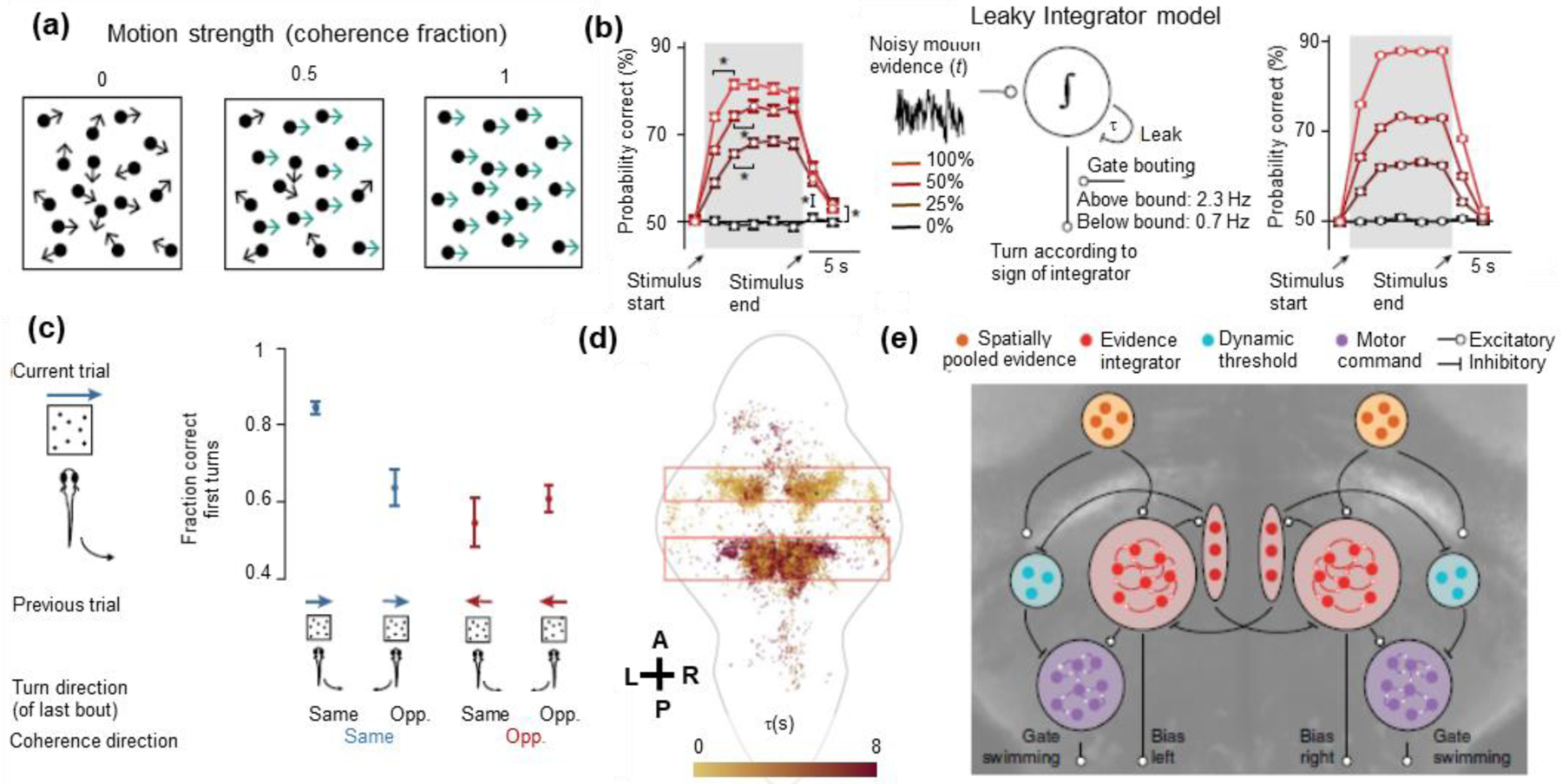
Mapping distributed sensorimotor processing in larval zebrafish using an evidence accumulation model. (a) Dragomir et al. [23] and Bahl et al. [24] used visual motion stimuli to drive turning behavior. Stimuli with three different strengths of rightward motion are shown (coherence fraction = 0, 0.5, 1). Panel from [23]. (b, left) The probability of correct turns (i.e. turns in the direction of motion) increased over time within the trial and also increased with higher coherence fractions. (b, middle) These results suggest an evidence accumulation model, whereby zebrafish leakily integrate noisy motion evidence to determine the direction of visual motion and set the rates of leftward and rightward turning. (b, right) The model successfully reproduces the observed behavioral patterns. Panel from [24]. (c) Motor actions do not reset the evidence accumulator, and its integration time scale is long enough to span several bouts and trials. The fraction of correct first turns accordingly depended on the direction of visual motion in the preceding trial and on the direction of the last turn. Panel from [23]. (d) Implementing the leaky integrator model would require the brain to first detect fast changes in sensory signals and then integrate them temporally. The authors therefore mapped brain activity by the integration time constant that best modeled each neuron’s stimulus responses. The map of model time constants showed a diversity of neuronal responses that were organized anatomically and could realize the computational steps of the behavioral models. Each colored dot is a segmented neuron, A-P denotes the anterior-posterior axis, and L-R denotes the left-right axis. Also shown are an outline of the zebrafish brain and boxes that highlight regions with many task-relevant neurons. Panel from [23]. (e) The authors ultimately superimposed their behavioral models onto cellular-resolution brain-wide maps, revealing neurons that detected motion signals in each direction, neurons that competitively pooled leftward and rightward motion signals, neurons that dynamically set the threshold separating low and high values of accumulated evidence, and neurons that represented stochastically generated leftward and rightward motor turning commands. Panel from [24].

Evidence accumulation is a canonical computation for decision making, and these zebrafish studies illustrate the synergy between behavioral modeling and cellular-resolution brain-wide recordings. Similar approaches will also be useful for dissecting sensorimotor decision-making processes in higher vertebrates. For example, several recent studies used sophisticated behavioral models to provide a nuanced view of rodent evidence accumulation [26, 27]. The authors’ inferred behavioral algorithms permitted them to correlate neuronal activity in specific cortical regions with subtle cognitive variables [28], and brain activity mapping showed that decision-making variables are widely distributed [29]. As large-scale recording techniques continue their rapid rise [16, 17, 29, 30], behavior-model driven brain mapping will surely produce countless discoveries. Nevertheless, the domain of applicability of this principle is likely limited, as the brain may not linearly represent all relevant task variables [31, 32]. Conceptual and technical progress is needed to derive principled methodology for nonlinear brain activity mapping.

Making predictions with mechanistic models: finding constraints amongst uncertainty

Mapping sensory, cognitive, and behavioral variables does not explain how the brain actually builds these representations from related sensory inputs and motor outputs. This is the purview of the bottom-up arc from biological mechanism to cellular-resolution brain-wide activity. One generally hopes to construct a mechanistically detailed dynamical system model that can elucidate the causal flow of information throughout the sensorimotor network, and several recent studies followed brain-wide activity mapping with multi-regional neural network modeling [20, 24, 33, 34]. Complete system specification is challenging [35, 36], but the principle that relatively few combined parameters control emergent properties in high-dimensional physical systems [3, 37] provides a guide for nevertheless designing, constraining, and testing large-scale neural network models [38].

This principle has two facets relevant for mechanistically understanding distributed neural networks. First, many cellular and circuit mechanisms may be irrelevant for explaining the neuronal responses underlying specific sensorimotor transformations [20, 36, 39]. For instance, brain-wide sensorimotor circuits overlap with each other and operate concurrently with unrelated behavioral and cognitive processes [8, 15, 16, 40–42]. Some low-level mechanisms will only be needed to generate responses in these unrelated contexts. Models can therefore be simplified by ignoring these irrelevant details. Second, other mechanistic details may be critical for explaining the functional responses in focus [43]. This means that incompletely constrained models may still be able to make accurate experimental predictions.

Many neural network models are parametrized by their synaptic weights. Critical synaptic connections could provide compelling experimental predictions, but discerning critical model parameters is generally hard computationally [43–45]. This further increases the appeal of simple models [3], especially when analytical methods can relate synaptic weights and neuronal responses comprehensively [46]. Biswas and Fitzgerald [47] recently developed a theoretical formalism to find synaptic connections required for stimulus responses in threshold-linear recurrent neural networks (Figure 3a), a rich nonlinear model class with promising analytical tractability [48]. The authors first analytically found all synaptic weight matrices with specified steady state neural responses (Figure 3b). They then sought critical synaptic connections that must be present (Figures 3c). When compared to linear neural networks, threshold nonlinearities increased the size of the solution space by permitting variability in “semi-constrained” dimensions that appear when a neuron does not respond to a stimulus (Figure 3d). Nevertheless, the authors derived a geometric formula that could analytically pinpoint many critical synaptic connections, even in large networks. This theoretical approach could thus be used to make rigorous anatomical predictions from brain-wide neuronal responses [1].

Figure 3:

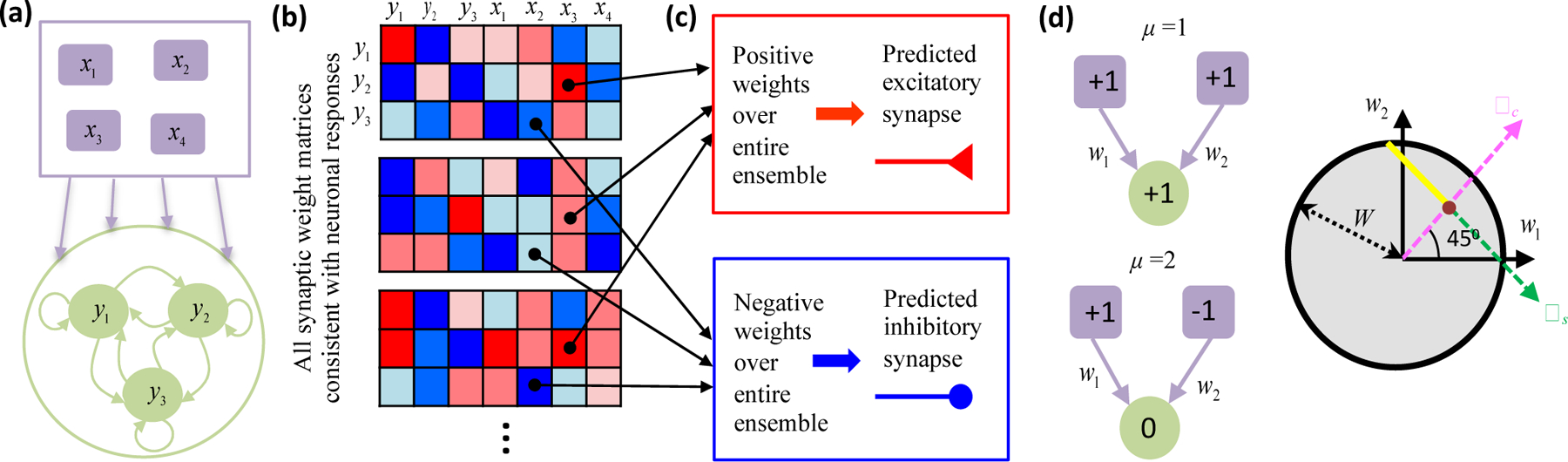
(a) Biswas and Fitzgerald [47] first specified steady-state responses of a recurrent threshold-linear neural network (green neurons) receiving feedforward input (purple neurons). (b) Assuming that the number of specified responses does not exceed the number of synapses onto each neuron, they then found all synaptic weight matrices having fixed points at the specified responses. Red (blue) matrix elements denote positive (negative) synaptic weights. (c) When a weight was consistently positive (or consistently negative) across all possibilities, then the model needed a nonzero synaptic connection to generate the responses. The model thus predicts that this synapse should exist experimentally. (d) The threshold nonlinearity provides flexibility, but some features of connectivity can nevertheless be definite. (d, left) Cartoon depicting steady state response patterns of a simple feedforward network under two stimulus conditions. The driven neuron responds in one stimulus condition (top) but is silent in the other (bottom). Numbers inside the neurons indicate activity levels. (d, right) The circle represents the two-dimensional space of allowed synaptic weights, assuming that the total weight norm is bounded by W. The two response conditions would uniquely determine the weight magnitudes in a linear neural network (brown dot, w₁ = w₂ = 1/2). However, the driven neuron’s silent response in the threshold-linear neural network only implies that the synaptic weight component along the ω_s direction is negative, because any sub-threshold input would suffice. All points on the semi-infinite yellow line thus reproduce the observed responses. Biswas and Fitzgerald refer to the ω_s direction as a “semi-constrained” dimension in the solution space. Despite this flexibility, all model solutions require w₂ > 0.

Performance-optimized artificial neural networks as models of brain-wide computation

We now turn to the fifth and final principle. Analyzing brain-wide computation is complicated by our limited knowledge of the brain’s high-level functions and constituent mechanisms, with mechanistic access most limited for large animals. However, the principle that evolutionary convergence of neural computations highlights computational mechanisms suited to solve general problems under common constraints allows neuroscientists to understand complex brains via comparisons to simpler ones. An interesting twist of this principle treats artificial neural networks (ANNs) as uniquely tractable model systems, whose functions and mechanisms are fully known [49, 50]. ANNs currently achieve remarkable performance in multiple artificial intelligence tasks. Such tasks require ANNs to transform low-level sensory information into task-relevant representations that support goal-directed outputs. Biological neural networks (BNNs) perform analogous tasks using neurons that span much of the brain, so comparing network-wide sensorimotor processing in ANNs and BNNs may provide insights into many brain areas [51, 52]. Not all aspects of ANNs will translate to BNNs, but the same is true when comparing two BNNs from different animal species [25, 53, 54].

Recent work by Haesemeyer et al. shows the utility of this comparative approach [51]. The authors trained an ANN to predict temperature changes enabling a virtual agent to navigate heat gradients. The authors then compared activity in the ANN to activity previously recorded in larval zebrafish [33, 51]. Neuron types emerged in the ANN with response properties matched to the BNN [51]. This permitted experiments in the ANN that made predictions for the BNN. For example, targeted ablation of some ANN neuron types substantially reduced the agent’s navigational abilities, and the authors predicted that these neuron types are critical in the BNN. Most impressively, the ANN predicted a critical neuron type that was not previously seen in the zebrafish brain. This prediction prompted the authors to reanalyze their brain-wide imaging data and discover a neuron type in the cerebellum that matched the ANN. This illustrates why brain-wide neuronal recordings are valuable for facilitating comparisons to large-scale ANNs. The authors did not know a priori where to look.

The notion that representations converge in ANNs and BNNs is increasingly familiar, as neuroscientists have repeatedly found this outcome in sensory and cognitive neuroscience [55–57]. If neuroscientists can understand how ANN representation emerges from its optimization function, network architecture, and learning dynamics [50], then ANN modeling will become an immensely useful tool for examining the principles of comparative computational neuroscience. It is therefore crucial to train ANNs using many learning paradigms, optimization criteria, and regularization schemes. For example, studies have ascribed importance to regularization that promotes “simple” activity patterns in ANNs [58]. Convergences could be enhanced by the development of ANNs that explicitly respect biological findings [59]. The field is probably only beginning to glimpse the full potential of this comparative approach.

Outlook

In this review, we’ve likened the importance of theoretical principles to that of streetlamps. Scientists can get lost in the dark without them, and beautiful things may go unnoticed if hidden in shadow. We’ve provided examples of five principles that have utility in brain-wide neuroscience, and each principle had a broad but limited domain of applicability. Neuroscientists will thus have to bring these and other principles together to understand brain-wide sensorimotor circuits. We would refer to the resulting theoretical system as a framework. Frameworks can be far more illuminating than any of their constituent principles. For example, Galileo’s law of inertia was an insightful principle that changed how his contemporaries saw motion, but it became inestimably more powerful once absorbed into the framework of Newtonian mechanics as its first law. In neuroscience, the Hodgkin-Huxley framework is exceptionally powerful because it coherently integrated many principles of neuronal excitability whose concepts fundamentally changed how experimenters interpreted their data. We are optimistic that the principles highlighted here are synergistic and complementary. They may therefore contribute productively to whatever theoretical framework eventually systematizes the fundamentals of brain-wide sensorimotor computation.

HIGHLIGHTS:

• Multiple theoretical principles are needed to understand brain-wide neural activity

• Brain-wide recordings provide new opportunities for testing familiar principles

• Quantitative behavioral models reveal target variables for brain activity mapping

• Sensitivity analyses aid mechanistic predictions from highly parameterized models

• Artificial neural networks can serve as tractable model systems for neuroscience