Development of a method for generating SNP interaction-aware polygenic risk scores for radiotherapy toxicity

Abstract

Aim:

To identify the effect of single nucleotide polymorphism (SNP) interactions on the risk of toxicity following radiotherapy (RT) for prostate cancer (PCa) and propose a new method for polygenic risk score incorporating SNP-SNP interactions (PRSi).

Materials and methods:

Analysis included the REQUITE PCa cohort that received external beam RT and was followed for 2 years. Late toxicity endpoints were: rectal bleeding, urinary frequency, haematuria, nocturia, decreased urinary stream. Among 43 literature-identified SNPs, the 30% most strongly associated with each toxicity were tested. SNP-SNP combinations (named SNP-allele sets) seen in ≥ 10% of the cohort were condensed into risk (RS) and protection (PS) scores, respectively indicating increased or decreased toxicity risk. Performance of RS and PS was evaluated by logistic regression. RS and PS were then combined into a single PRSi evaluated by area under the receiver operating characteristic curve (AUC).

Results:

Among 1,387 analysed patients, toxicity rates were 11.7% (rectal bleeding), 4.0% (urinary frequency), 5.5% (haematuria), 7.8% (nocturia) and 17.1% (decreased urinary stream). RS and PS combined 8 to 15 different SNP-allele sets, depending on the toxicity endpoint. Distributions of PRSi differed significantly in patients with/without toxicity with AUCs ranging from 0.61 to 0.78. PRSi was better than the classical summed PRS, particularly for the urinary frequency, haematuria and decreased urinary stream endpoints.

Conclusions:

Our method incorporates SNP-SNP interactions when calculating PRS for radiotherapy toxicity. Our approach is better than classical summation in discriminating patients with toxicity and should enable incorporating genetic information to improve normal tissue complication probability models.

Recent efforts attempted to include individual patient genetic data in Normal Tissue Complication Probability (NTCP) models [1,2]. As with any predictive model, a clinically useful genetic-based NTCP model requires a sufficient number of common variants, given that each likely has a small effect on risk of complications. Radiogenomic studies are finding an increasing number of common (i.e. seen in > 1% of the population) single nucleotide polymorphisms (SNPs) that can be combined to derive a polygenic risk score (PRS). A PRS is calculated as a sum of phenotype-associated risk alleles, usually weighted by the effect sizes estimated from a genome-wide association study [3,4,5]. There is also increasing awareness that epistasis, or SNP-SNP interactions, affect polygenic susceptibility to common human diseases [6,7]. These interactions occur when a combination of two or more SNPs affect a phenotype more/differently than the effect seen with an individual gene. Epistasis is considered an ubiquitous component of the genetic architecture of common human diseases with complex interactions being more important than the effects of any single common genetic variant [7]. Epistasis is also likely to affect risk of radiation toxicity, but to date genetically-based NTCP models have not accounted for SNP interaction effects.

Here we aim to identify the combined effect of several SNPs on late radiotherapy toxicity and propose a novel scoring method to summarise genetic information that incorporates epistatic effects. Our work builds on the results of a previous study where SNPs identified as affecting risk of late radio-induced toxicity were confirmed by external independent validation [8]. There, the authors considered a pool of 43 SNPs associated with late radiotherapy toxicity from the literature. The SNPs were then filtered through a Deep Sparse AutoEncoder (DSAE), and those that were most relevant in separating patients with toxicity were selected for each toxicity endpoint. Within the present work, we start from these selected SNPs and propose a new method for deriving PRSs for late toxicity that account for SNP-SNP interactions (termed PRSi) while preserving interpretability, i.e. allowing users to understand why certain predictions are made. Indeed, our proposed PRSi shows which SNPs and alleles are included, whether they increase or decrease the risk of toxicity and their combined effect sizes.

Materials and methods

Population

We included REQUITE prostate cancer patients recruited before radiotherapy between April 2014 and October 2016 in eight countries (Belgium, France, Germany, Italy, the Netherlands, Spain, UK, US) and treated with external beam radiotherapy (with/without hormonal therapy, with/without a previous prostatectomy, no brachytherapy) who had complete 2-year follow-up. Details on the REQUITE population are published [9]. REQUITE was approved by local Ethical Committees and registered at www.controlled-trials.com (ID ISRCTN98496463).

Outcome endpoints

Toxicity endpoints were scored using CTCAE v4.0 by health professionals and using patient reported outcome (PRO) questionnaires. The following endpoints were considered: late rectal bleeding grade ≥ 1 (CTCAE), late urinary frequency grade ≥ 2 (CTCAE), late haematuria grade ≥ 1 (CTCAE), late nocturia grade ≥ 2 (PROs) and late decreased stream grade ≥ 1 (PROs). Detailed information on toxicity endpoint definitions can be found in the Supplementary Material (Section A).

SNP selection

For each toxicity endpoint, we considered the top 30% most relevant SNPs according to [8], among the 43 initially included in that study. Specifically, these are the SNPs found the most effective in separating patients with/without toxicity [8].

Statistical methods

To identify the combined effect of several SNPs on each outcome separately, we exploited the methodology proposed in [10]. Thanks to that, we were able to summarize a patient’s genetic information into a risk (RS) and a protection (PS) score that respectively indicate an increase or decrease in the risk of late toxicity. To build RS and PS we first identified a relevant set of high-order SNP-SNP interactions, termed SNP-allele sets.

Fig. 1 illustrates our methodology. At the patient level, each SNP is considered a trichotomic categorical variable with values of 0, 1 or 2 indicating absence, heterozygosity or homozygosity of the considered minor allele (Fig. 1a). In the case of imputed values, we round to the closest integer. Starting from there, we derive SNP-allele sets, which indicate the simultaneous presence of multiple SNP-allele combinations. Of note, SNP-allele sets can include a variable number of SNPs, from 2 to the maximum number of SNPs considered.

Fig. 1.

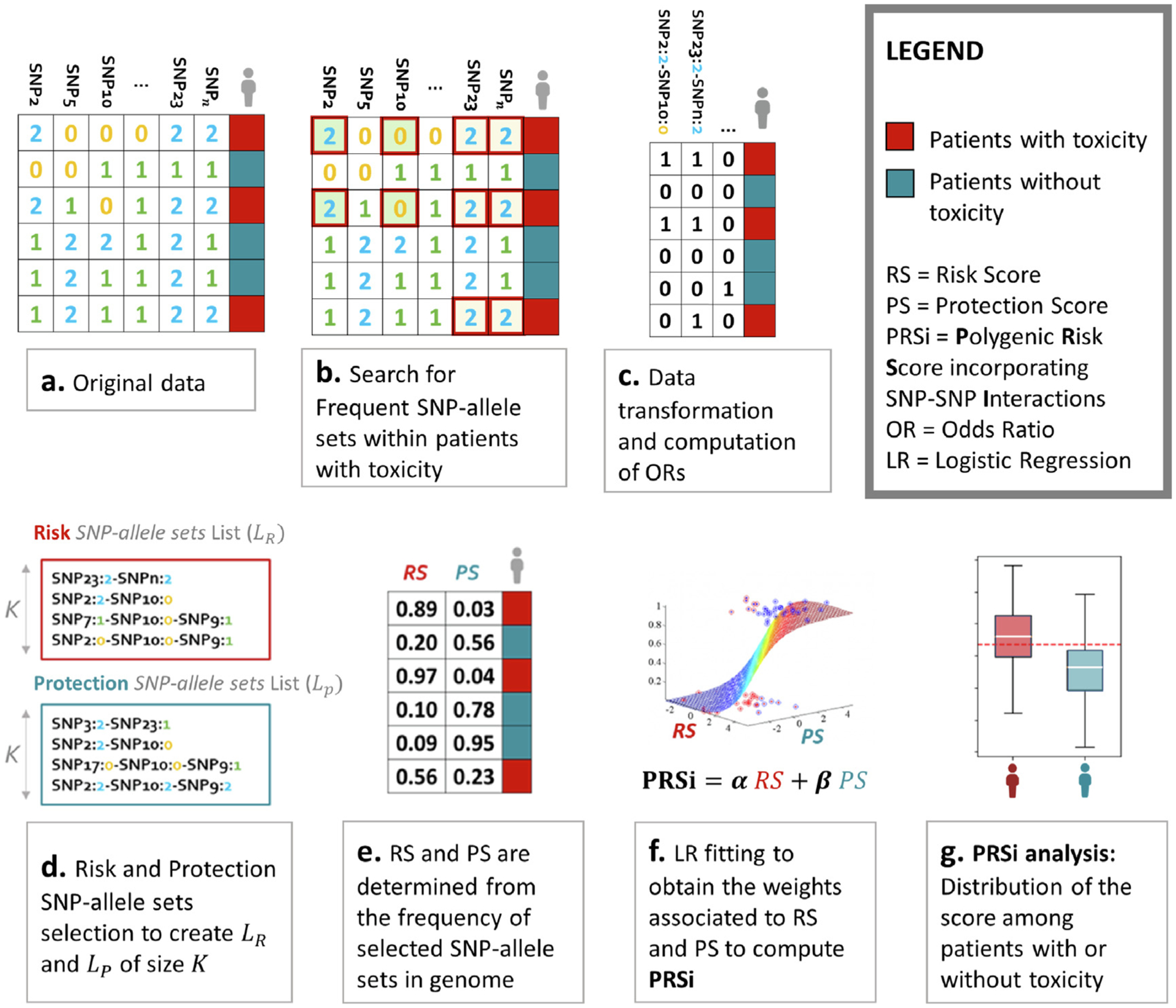
An illustration of the methodology used to generated polygenic risk scores incorporating SNP-SNP interactions (PRSi). (a) Data are available for multiple SNPs for patients identified as with (red) or without (blue) radiotherapy toxicity. (b) Our algorithm computes frequent (arbitrarily defined as seen in ≥ 10% of patients) SNP-SNP combinations, termed SNP-allele sets, associated with radiotherapy toxicity (i.e. the minority class). For example both the first and the third patient have a SNP2 value of 2 (i.e. homozygosity of the minor allele) and SNP10 value of 0 (i.e. homozygosity of the major allele). We call this SNP2 = 2, SNP10 = 0 combination a SNP-allele set. As a further example both the fifth and the sixth patient have SNP2 = 1, SNP5 = 2, SNP10 = 1 and SNP23 = 2: this is another SNP-allele set. (c) SNP-allele sets are transformed into patient-specific features, with a “1/yes” value if the patient harbours the considered SNP-allele set and a “0/no” value if the patient does not. Odds ratios are calculated for each SNP-allele set on the risk of toxicity. (d) Lists of risk SNP-allele sets associated with increased (risk) and decreased (protection) toxicity probability are generated. (e) Risk Score (RS) and Protection Score (PS) are calculated for each patient as the frequency in an individual’s genome of SNP-allele sets in the “Risk List” and in the “Protection List”, thus generating a table as in the Figure. Patients with toxicity should have RS near 1 and PS near 0, the converse for patients without toxicity. RS and PS data are fit to a logistic regression model to estimate weights for RS and PS for calculating the final PRSi. The distribution of PRSi should be different for patients with and without toxicity. The more separated the two distributions are, the better the PRSi is discriminating patients with toxicity.

SNP-allele sets were identified using a methodology developed previously [10], which was specifically designed to find high-order interaction terms in imbalanced binary classification settings with categorical covariates. Indeed in our context, for each toxicity endpoint, the dataset consists of N (genome, outcome) pairs D = {(x₁, y₁), …, (x_N, y_N)} where, for each patient i ∈ {1, …, N}, ${\mathit{x}}_i\in {ℝ}^J$ is the vector containing the values {0, 1, 2} of the J SNPs considered for that specific endpoint, while y_i ∈ {0, 1} indicates the absence (y_i = 0, red in Fig. 1a) or presence (y_i = 1, blue in Fig. 1a) of the endpoint. We search for SNP-allele sets s that occur in patients with toxicity with a frequency of at least 10%, and store them in a list S (Fig. 1b). Note that from now on we use bold letters for SNP-allele sets, as they involve multiple SNPs, while capital letters denote lists of SNP-allele sets. The cutoff frequency of 10% was arbitrarily chosen to select SNP-allele sets that would be common in a real-world patient population. For each s ∈ S we compute its frequency in both the majority (patients without toxicity, y_i = 0) and the minority (patients with toxicity, y_i = 1) classes. This allows us to compute an odds ratio (OR, defined as the ratio of the two frequencies) for each SNP-allele set (Fig. 1c.)

Then,

1. We subdivide S into two lists, S_R = {s ∈ S with OR_s > 1} and S_P = {s ∈ S with 0 < OR_s < 1}, of risk and protection SNP-allele sets, which we respectively rank by descending and ascending OR.

2. From each list (S_R and S_P) we extract the top K most relevant SNP-allele sets, starting from the one with highest (respectively, lowest) OR and including the next most diverse ones. The driving idea is to avoid redundancy and keep SNP-allele sets that carry different information. For details on how this diversity is defined see the Supplementary Material B or refer to [10]. This selection process leaves us with two filtered lists, L_R and L_P, each of length K (Fig. 1d).

3. For each patient i we define the scores RS_i (respectively PS_i), as the percentage of risk (protection) SNP-allele sets in L_R (L_P) that appear in his genome (Fig. 1e).

4. To evaluate the predictive capability of RS and PS we fit a logistic model (Fig. 1f) of the form:

   $$P\left(y_i=1\right)=\frac{1}{1+\text{exp}\left(-\left(\gamma +\alpha R{S}_i+\beta P{S}_i\right)\right)},$$ (1)

   where α, β and γ are the model parameters. We would expect the a coefficient associated with RS to be positive (as it represents an increased risk of belonging to the minority class of patients with toxicity), and β to take negative values (as PS should be protective with respect to the toxicity outcome).
5. Once obtained the two scores’ coefficients of the fitted model (α and β), we consider them as weights to define a combined polygenic risk score (Fig. 1g) incorporating SNP-SNP interactions (PRSi):

   $$\text{PRSi=}\alpha RS+\beta PS$$ (2)

We analyse the PRSi performance in separating the two classes through the area under the Receiver Operating Characteristics (ROC) curve (AUC).

For each endpoint we must choose a value for the parameter K and the number of SNP-allele sets considered per score. As we have no prior knowledge on the optimal K, we repeat the procedure from point (ii) to point (v) through a range of values (K = 1, …, 15) that ensure both interpretability and readability of the SNP-allele sets lists; then for each endpoint independently, we pick the one K guaranteeing the highest classification performance.

Results

Cohort

REQUITE enrolled 1,681 prostate cancer patients who were treated with external beam radiotherapy without brachytherapy. There were 1,436 patients with complete 2-year follow-up available for analysis. Forty-nine patients were excluded because of an intrinsic higher risk of exhibiting radiation toxicity, due to their co-morbidities (patients with a diagnosis of systemic lupus erythematosus, rheumatoid arthritis and other collagen vascular diseases). Cohort details are described in the Supplementary Material, Table E1.

Polygenic risk score incorporating SNP-SNP interactions

The analysis presented below was carried out through an algorithm developed by the authors in Python 3.7. More details can be found in [10] and the code is available upon request.

Filtering of the top 30% most relevant SNPs among the 43 initially included in [8] resulted in groups of 13 SNPs for each of the five toxicity endpoint as listed in Table 1.

Table 1.

Considered SNPs for each toxicity endpoint. SNPs selected for SNP-allele sets learning for each toxicity endpoint. The SNPs in the table are those identified as relevant in [8] to separate between patients with/without late toxicity symptoms. ▼.

Late Urinary Frequency grade ≥ 2	Late Haematuria grade ≥ 1	Late Nocturia grade ≥ 2	Late Decreased Urinary Stream grade ≥ 1	Late Rectal Bleeding grade ≥ 1
rs141799618	rs10101158	rs10969913	rs10209697	rs62091368
rs8075565	rs708498	rs77530448	rs1799983	rs4775602
rs12591436	rs77530448	rs62091368	rs17362923	rs264631
rs76273496	rs17055178	rs11219068	rs673783	rs17599026
rs10969913	rs147596965	rs264651	rs8098701	rs11122573
rs1799983	rs7366282	rs1799983	rs77530448	rs76273496
rs8098701	rs10969913	rs8098701	rs6535028	rs17362923
rs17599026	rs12591436	rs7366282	rs7366282	rs10969913
rs7366282	rs79604958	rs11122573	rs845552	rs6535028
rs708498	rs8098701	rs17055178	rs1045485	rs10209697
rs17055178	rs845552	rs17599026	rs76273496	rs141799618
rs11122573	rs7829759	rs10497203	rs17055178	rs8098701
rs10209697	rs10209697	rs6432512	rs11122573	rs1045485

Tables 2 and 3 summarise the quantitative results describing the logistic regression models’ parameters and performances and the PRSi distributions for the five endpoints. Fig. 2 shows the identified SNP-allele sets and the PRSi performance for one of the four urinary endpoints. Fig. 3 shows the results for the bleeding endpoint. Figures for the other endpoints are in the Supplementary Material (Figs. C1, C2 and C3). To benchmark and highlight the performance and the value of our method for generating PRSi, Supplementary Material (Section D) show the AUC results for PRS estimates obtained using a classical summation approach without SNP-SNP interactions. The benchmark PRS was computed for each endpoint using the same 13 SNPs used to build the PRSi.

Table 2.

Performance of Logistic Models fitted with RS and PS. Results of logistic models for the 5 considered toxicity endpoints. The values chosen for the hyperparameter K are reported in the third row. The fitted values for α and β are reported together with their 95% confidence intervals. (*) The rows Sensitivity, Specificity and OR, refer to the metrics obtained by thresholding the predicted probabilities in the logistic model using the cutoff that maximizes the Youden index. The value of such cutoff is also reported in the table (last row). ▼.

	Late Urinary Frequency grade ≥ 2	Late Haematuria grade ≥ 1	Late Nocturia grade ≥ 2	Late Decreased Urinary Stream grade ≥ 1	Late Rectal Bleeding grade ≥ 1
Patients	1,334	1,343	1,250	1,234	1,366
With toxicity N (%)	56 (4.2%)	74 (5.5%)	223 (17.8%)	211 (17.1%)	160 (11.7%)
K	15	13	8	15	12
α	13.25 ± 3.86	9.63 ± 3.43	3.22 ± 1.57	7.04 ± 1.94	3.73 ± 1.84
β	−5.37 ± 2.62	−4.60 ± 2.53	−3.82 ± 1.57	−4.51 ± 1.66	−2.48 ± 1.66
γ	−3.27	−3.13	−1.32	−1.63	−2.16
AUC	0.78	0.71	0.61	0.68	0.63
Sensitivity*	67.9%	71.6%	77.6%	64.9%	75.6%
Specificity*	77.9%	60.2%	38.6%	65.6%	45.5%
OR*	7.456	3.818	2.171	3.529	2.593
Probability cutoff	5.1%	4.5%	17.6%	18.8%	10.3%

Table 3.

Comparison of PRSi distribution between patients with and without toxicity. Comparison of the polygenic risk score incorporating SNP-SNP interactions (PRSi) distribution for patients with and without toxicity (separately for each of the 5 considered toxicity endpoints). The PRSi medians in the two classes are reported and compared with the Wilcoxon test for independent samples; the p-value of such test is reported (third row). The distribution of the score as a whole is also compared in the two classes using the Kolmogorov-Smirnov two-samples test; p-values of the latter are reported in the table (last row). ▼.

	Late Urinary Frequency grade ≥ 2	Late Haematuria grade ≥ 1	Late Nocturia grade ≥ 2	Late Decreased Urinary Stream grade ≥ 1	Late Rectal Bleeding grade ≥ 1
Median (patients with toxicity)	0.611	0.740	−0.149	0.168	0.208
Median (patients without toxicity)	−0.357	0.033	−0.224	−0.133	0.001
Wilcoxon	p = 5.76e-13	p = 9.73e-10	p = 3.48e-07	p = 2.35e-16	p = 8.73e-08
Kolmogorov-Smirnov	p = 3.39e-10	p = 1.41e-06	p = 1.44e-04	p = 1.41e-14	p = 6.52e-06

Fig. 2.

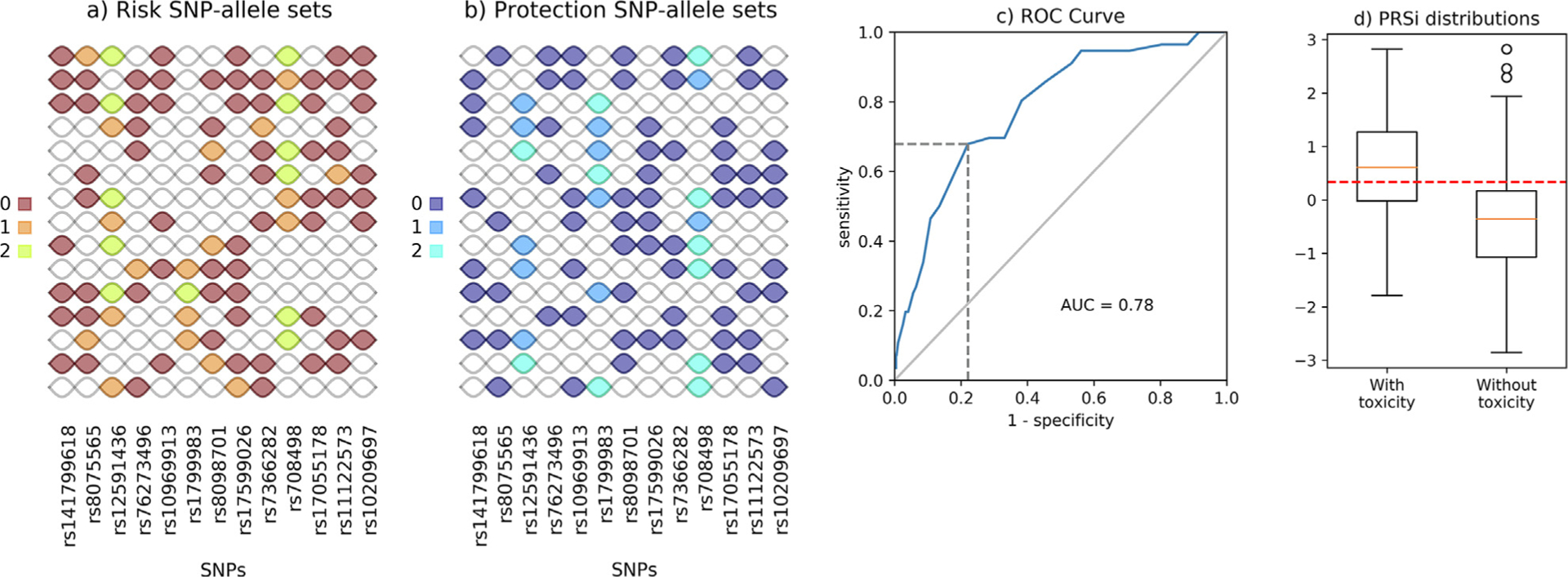
Results for grade 2 late urinary frequency. Panel (a): SNP-allele sets participating in the definition of Risk Score (RS); panel (b) SNP-allele sets participating in the definition of the Protection Score (PS). In both cases, each row identifies a SNP-allele set, with SNPs running along columns. Different colours correspond to different alleles of each single SNP in the SNP-allele set. Note that SNP-allele sets are, in general, defined by different numbers of alleles. For example, the first Risk SNP-allele set (starting from top) is defined through 8 alleles (rs141799618 = 0, rs8075565 = 1, rs12591436 = 2, rs1096913 = 0, rs17599026 = 0, rs808498 = 2, rs11122573 = 0 and rs10209697 = 0) while the last one involves 4 alleles only (rs12591436 = 1, rs76273496 = 0, rs17599026 = 1 and rs7366282 = 0). Each SNP can participate in the definition of multiple SNP-allele sets (e.g. rs10209697 is included in 7 SNP-allele sets for RS and in 7 SNP-allele sets for PS). Panel (c) ROC curve for the logistic model described in Equation 1 and calculated with best-fit parameters α and β reported in Table 1. AUC and the point in the ROC curve identifying the best probability cutoff value (according to the Youden index) are also reported; panel (d) Box-plot representation for the distribution of the polygenic risk score incorporating SNP-SNP interactions (PRSi) for patients with and without toxicity calculated using equation (2). The red-dashed line represents the thresholding value for the PRSi related to the probability cutoff in Table 2: patients with a score above this threshold will have a predicted probability, according to equation 1, that is above the cutoff, and viceversa.

Fig. 3.

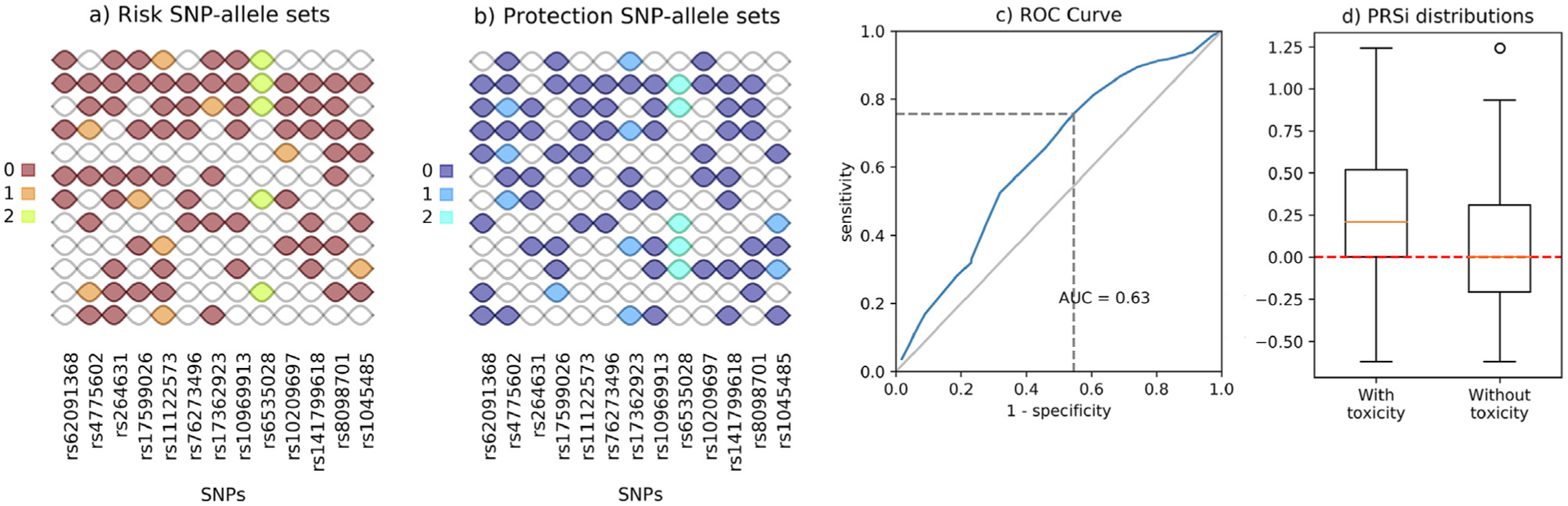
Results for grade ≥ 1 late rectal bleeding. Panels read as in Fig. 2.

Toxicity model results

Fifty-six of 1,334 available patients (4.2%) experienced late urinary frequency grade ≥ 2. Risk and protection SNP-allele sets identified as described previously are reported in Fig. 2a and b (here K = 15). The logistic model fitted using the corresponding RS and PS has parameters behaving as expected: the α coefficient associated with RS is positive (13.25, p = 1.36×10⁻¹¹) while the β coefficient associated with PS is negative (−5.37, p = 5.61 × 10⁻⁵). The model has good discrimination power with an AUC of 0.78 (Fig. 2c), further details on the model performance can be found in Table 2. Finally, as shown in Fig. 2d and reported in Table 3, the PRSi computed with the fitted α and β results in significantly different distributions in the two classes of patients with and without toxicity (median PRSi 0.611 vs −0.357, Wilcoxon test for independent samples p-value = 5.76×10⁻¹³; two-sample Kolmogorov-Smirnov test p-value = 3.39×10⁻¹⁰).

Late haematuria grade ≥ 1 was seen in 74 of 1,343 available patients (5.5%). Identified risk and protection SNP-allele sets are reported in Supplementary Fig. C1, here using K = 13. Supplementary Figs. C1c and C1d report details on the fit of the logistic model and PRSi distributions.

Late nocturia grade ≥ 2 was seen in 223 of 1,250 available patients (17.8%). Risk and protection SNP-allele sets (K = 8) together with details on the ROC curve for the logistic model and PRSi distributions are presented in Supplementary Fig. C2.

There were 211 of 1,234 (17.1%) patients who experienced late decreased stream grade ≥ 1. Identified risk and protection SNP-allele sets are presented in Supplementary Figs. C3a and C3b, K = 15. Supplementary Figs. C3c and C3d describe the ROC curve for the logistic model and the PRSi distributions.

One hundred and sixty of 1,366 available patients (11.7%) had late rectal bleeding grade ≥ 1. Identified risk and protection SNP-allele sets are presented in Fig. 3a and b, K = 12, while Fig. 3c and d show the ROC curve for the logistic model and the PRSi distributions.

Discussion and conclusions

Risk of radiotherapy toxicity is influenced by both environmental and genetic factors. In terms of genetics, the radiosensitivity of most individuals can be considered a complex trait with a continuous range of variation that is not explained by the segregation of a single gene. The application of PRSs could help in estimating before treatment an individual patient’s susceptibility, thus allowing personalised treatments that improve health outcomes [11]. PRSs are being tested for clinical utility for individualised preventative management with particular promise for identifying increased risks of cardiovascular diseases and breast cancer [12,13], and might similarly be used for radiotherapy outcomes.

GWAS-identified loci tend to have small individual effects, and PRS are needed for prediction. Some researchers highlight a need to move beyond simple weighted sums of risk alleles [14]. While there is currently little evidence for including SNP-SNP interactions in PRS, there is a recognised need to explore alternative modeling strategies [15]. A comprehensive search for SNP-SNP interactions among ~ 300,000 SNPs with minor allele frequencies ≥ 0.15 found no evidence for a role across 10 human diseases [16], highlighting the challenge of achieving adequate statistical power.

In this paper we present a methodology to tackle this complex scenario. Based on [10], our approach can identify high-order interaction terms while maintaining the model dimensionality under control. While machine learning has already been proposed as a promising alternative for estimating the overall genetic risk in the presence of high-order interactions [17,18], the additional value of our PRSi is the readability and interpretability of the results. The algorithm returns two lists of SNP-allele sets whose length is specified by the user and that can be easily inspected. These lists are used to define the RS and PS. The two scores are then weighted with coefficients that have a clear and straightforward meaning in building the PRSi for new patients.

While methods are being developed to improve the detection of interaction in genome-wide scans [19], another approach is to start with a smaller candidate gene list [20]. Here, to develop our methodology we chose to consider only 13 SNPs for each endpoint and only used SNPs previously identified with different radiotherapy toxicity endpoints [10]. The method can in principle be scaled to any number of SNPs nonetheless. The computational workload will obviously increase more than linearly with the number of SNPs, but the high computational burden is restricted to the development phase (i.e. the identification of SNP-allele sets, steps (i) and (ii) in the workflow presented in the Section “Statistical methods”). All the other steps do not require high power computation, and calculation of the PRSi for new patients can be readily done with a pocket calculator or a spreadsheet.

One interesting aspect of our methodology is that the genotype at one locus can be a risk factor when coupled to a genotypes at other loci or a protective factor when coupled with a genotype at another loci. For example, Fig. 2a shows that the SNP rs141799618 appears with the same allele in 7 risk SNP-allele sets and in 7 protective SNP-allele sets - but in each of them it is accompanied by different alleles from other SNPs.

Another relevant characteristic of the algorithm is the enforcement of a lower bound on the frequency of SNP-allele sets considered to build the Scores (at least 10% of patients with toxicity). This, together with the diversity-based SNP-allele sets selection (see Supplementary Material B), avoids overfitting and fosters generalizability of the derived PRSi and its performance on new cohorts.

The performance of the PRSi was evaluated through its discriminative power and the obtained results are encouraging. Additionally, the PRSi demonstrated its superiority in terms of AUC with respect to a traditional PRS where only additive contributions of the single SNPs are considered (late urinary frequency: 0.78 vs 0.65, late haematuria: 0.71 vs 0.63; Results shown in Table D.1 in Supplementary Material). Moreover, the parameters associated to Risk and Protection Scores in the PRSi preserve their statistical significance thanks to the limited number of covariates introduced in the logistic regression model, fact that is instead unlikely in PRSs with an extremely high number of interactions (Supplementary Material D).

Within the present work, we only considered genetic markers, without explicitly accounting for other clinical/treatment factors, such as radiation dose, treated volumes, and comorbidities. However, we do not see this as a significant limitation, but rather a choice grounded on the underlying hypothesis of this study. In the modern radiotherapy scenario, doses to healthy tissues after radiotherapy for prostate cancer are reduced to the minimum and patients suffering from late toxicity are a significantly small portion of the population. In this perspective, we hypothesized that genetic variants are the main factors that determine late toxicity. Therefore, the results proposed in the paper aim at demonstrating the predictive and descriptive capability of SNP-allele sets only. Additional insights on the matter can be found in Section E of the Supplementary Material. There, we partially investigated the interplay between the PRSi and other clinical factors, by evaluating the model performance over several subpopulations. The corresponding results are promising, and the proposed score seems to behave robustly, coherently with our preliminary hypothesis.

An important further step will be to include the PRSi into integrated normal tissue complication probability models, together with validated dosimetric and clinical risk factors, to prove its added value as a radiosensitivity biomarker. In fact, the approach presented here is extremely flexible and the PRSi can be easily included in larger models to potentially aid prediction. A further possibility is the adaptation for radiotherapy treatment for patients with high PRSi, which could for example entail either a decreased prescription dose or the use of specific aid devices like rectum spacers [21,22].

A limitation of the method here exploited is that it heavily builds upon data and not on prior biological knowledge. Therefore, evaluation of different cohorts would be highly desirable to enhance reliability. Of note, the data-driven discovery of epistasis/statistical interaction does not necessarily imply interaction at the biological/mechanistic level. Nonetheless, results from this kind of analyses can be considered hypothesis-generating, thus inspiring new experiments to evaluate epistasis at the biological level [23].

In summary, our method incorporates SNP-SNP interaction effects in the definition of a PRS for radiotherapy toxicity. Our approach is better than using classical summation in discriminating patients with toxicity, particularly for 3 out of 5 endpoints. It should improve the ability of incorporating genetic information into normal tissue complication probability models.