Skip to main content
PMC home page
eLife logoLink to eLife
. 2022 Jan 12;11:e72884. doi: 10.7554/eLife.72884

Systematic investigation of the link between enzyme catalysis and cold adaptation

Catherine Stark 1,2, Teanna Bautista-Leung 2, Joanna Siegfried 2, Daniel Herschlag 1,2,3,✉
Editors: Frank Raushel4, Philip A Cole5
PMCID: PMC8754429  PMID: 35019838

Abstract

Cold temperature is prevalent across the biosphere and slows the rates of chemical reactions. Increased catalysis has been predicted to be a dominant adaptive trait of enzymes to reduced temperature, and this expectation has informed physical models for enzyme catalysis and influenced bioprospecting strategies. To systematically test rate enhancement as an adaptive trait to cold, we paired kinetic constants of 2223 enzyme reactions with their organism’s optimal growth temperature (TGrowth) and analyzed trends of rate constants as a function of TGrowth. These data do not support a general increase in rate enhancement in cold adaptation. In the model enzyme ketosteroid isomerase (KSI), there is prior evidence for temperature adaptation from a change in an active site residue that results in a tradeoff between activity and stability. Nevertheless, we found that little of the rate constant variation for 20 KSI variants was accounted for by TGrowth. In contrast, and consistent with prior expectations, we observed a correlation between stability and TGrowth across 433 proteins. These results suggest that temperature exerts a weaker selection pressure on enzyme rate constants than stability and that evolutionary forces other than temperature are responsible for the majority of enzymatic rate constant variation.

Research organism: None

Introduction

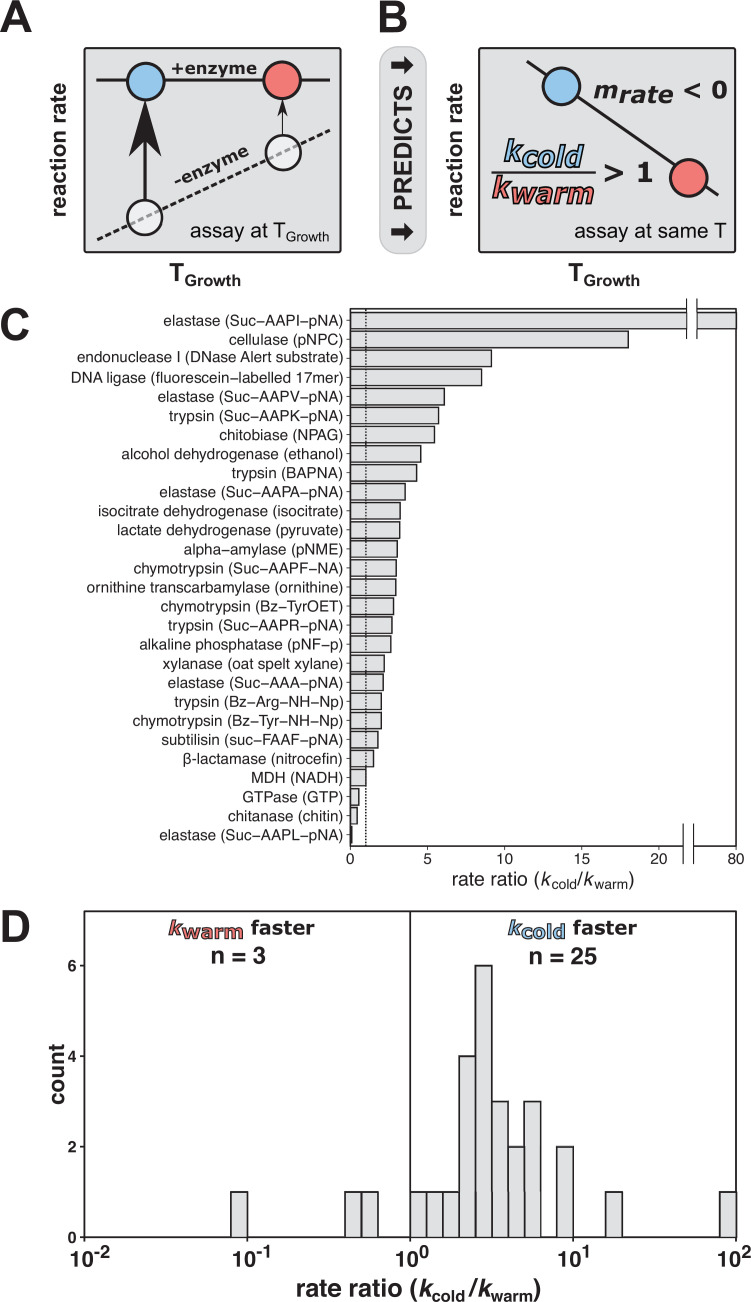
Temperature is a ubiquitous environmental property and physical factor that affects the evolution of organisms and the properties and function of the molecules within them. As reaction rates are reduced at lower temperatures (Arrhenius, 1889; Wolfenden et al., 1999), the maintenance of enzyme rates has been suggested to be a universal challenge for organisms at colder temperatures that do not regulate their internal temperature (D’Amico et al., 2003; Fields et al., 2015; Siddiqui and Cavicchioli, 2006; Zecchinon et al., 2001). According to what we term the rate compensation model of temperature adaptation, this challenge has been suggested to be met by cold-adapted enzyme variants providing more rate enhancement than the corresponding warm-adapted variants (Figure 1A). This model predicts that cold-adapted variants are generally faster than warm-adapted variants when assayed at a common temperature (Figure 1B). Indeed, this behavior has been reported for diverse enzymes, and these observations have been taken as support for this model (Figure 1C and D; Collins and Gerday, 2017; Feller and Gerday, 1997; Siddiqui and Cavicchioli, 2006; Smalås et al., 2000).

Figure 1. The rate compensation model of cold adaptation predicts that cold-adapted enzymes exhibit greater catalysis and are faster at a common temperature than their warm-adapted counterparts.

Figure 1.

Open in a new tab

(A) According to the rate compensation model of cold adaptation, a cold-adapted variant (blue circle) has larger rate enhancement than a warm-adapted variant (red circle). The dashed line represents the uncatalyzed reaction, the solid line represents the catalyzed reaction, and the arrows represent the rate enhancement at the respective organism TGrowth. (B) When variants are assayed at a common temperature, rate compensation predicts a faster reaction for the enzyme from the cold-adapted organism, corresponding to a rate ratio (kcold/kwarm) of greater than one and a negative slope of rate vs. TGrowth (mrate). (C, D) Rate comparisons of warm-adapted and cold-adapted enzyme variants made at identical temperatures from cold adaptation literature spanning indicated reactions with substrate specified in parentheses (Collins and Gerday, 2017; Feller and Gerday, 1997; Siddiqui and Cavicchioli, 2006; Smalås et al., 2000). The black vertical lines represent no rate enhancement change with temperature (i.e., rate ratio = 1).

Figure 1—source data 1. Rate comparisons of warm-adapted and cold-adapted enzyme variants made at identical temperatures from cold adaptation literature.

The observed effects on enzymatic rate constants (Figure 1C and D) have also led to proposals of general physical models for cold adaptation linked to flexibility, as outlined in Feller and Gerday, 2003; Fields et al., 2015; Åqvist et al., 2017; Arcus et al., 2016; Nguyen et al., 2017; Saavedra et al., 2018. Further, features identified in comparative structural analyses of cold- and warm-adapted enzymes, such as fewer surface hydrogen bonds and salt bridges (Cai et al., 2018), have been suggested to increase flexibility and thereby increase catalysis (Mandelman et al., 2019; Park et al., 2018a; Park et al., 2018b). Correspondingly, the study of cold adaptation may have the potential to provide generalizable insights into physical properties of enzymes that make them better catalysts, a longstanding challenge in the field (Blow, 2000; Hammes et al., 2011; Kraut et al., 2003; Ringe and Petsko, 2008). From a practical perspective, the prediction of enhanced catalysis by cold-adapted enzymes has motivated low-temperature bioprospecting for biocatalysts to use in industrial processes (Bhatia et al., 2021; Bruno et al., 2019; Kuddus, 2018; Santiago et al., 2016).

Given the theoretical and practical implications of the proposed relationship between enzyme rate enhancement and organism growth temperature, we sought to test the generality of the rate compensation model of temperature adaptation. We collated enzyme rate constant data (Chang et al., 2021) and organism optimal growth temperature (TGrowth) (Engqvist, 2018) for 2223 reactions using public databases. The results revealed no enrichment of faster reactions with colder growth temperatures, and thus did not support increased rate enhancement with decreasing environmental temperature as a prevalent adaptation in nature. Further, we found that most rate constant variation for the enzyme ketosteroid isomerase (KSI) is not accounted for by TGrowth despite strong evidence for temperature adaptation within its active site (Pinney et al., 2021). In contrast, a similar broad analysis revealed that stability correlates with TGrowth, as expected. Our results suggest that temperature exerts a weaker selection pressure on enzyme rate enhancement than stability and that other evolutionary forces are responsible for most variation in enzymatic rate enhancements.

Results

Systematically testing the rate compensation model

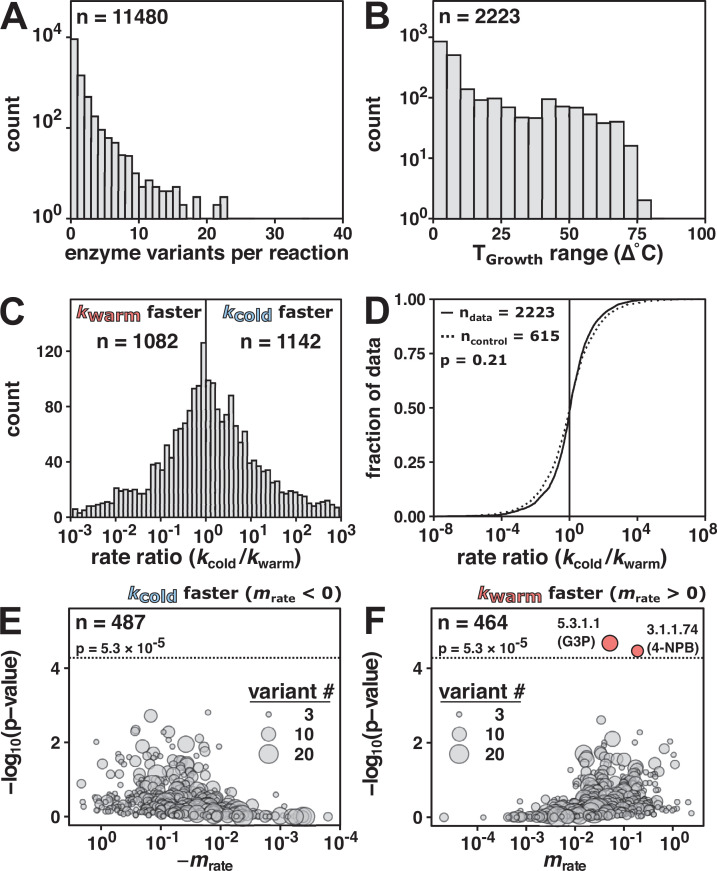
To investigate temperature adaptation of enzyme rate enhancement, we paired rate constant data from the BRENDA database (Chang et al., 2021) to organism growth temperatures. We simplified organism temperatures that may span changing conditions (Doblin and van Sebille, 2016) by matching the species name associated with the enzyme variant with the organism optimal growth temperature (TGrowth) (Engqvist, 2018). Of 76,083 kcat values in BRENDA, we found that 49,314 were for wild-type enzymes. Of these data, 16,543 values matched to microorganisms with known TGrowth values. We selected reactions in the database with variants from more than one organism, spanning 7086 kcat values for 2223 reactions across 815 organisms with at least two variants per reaction (Figure 2A). These reactions spanned a temperature range of 1–83°C (Figure 2B).

Figure 2. Enzyme rate constant data (kcat) do not indicate general rate compensation.

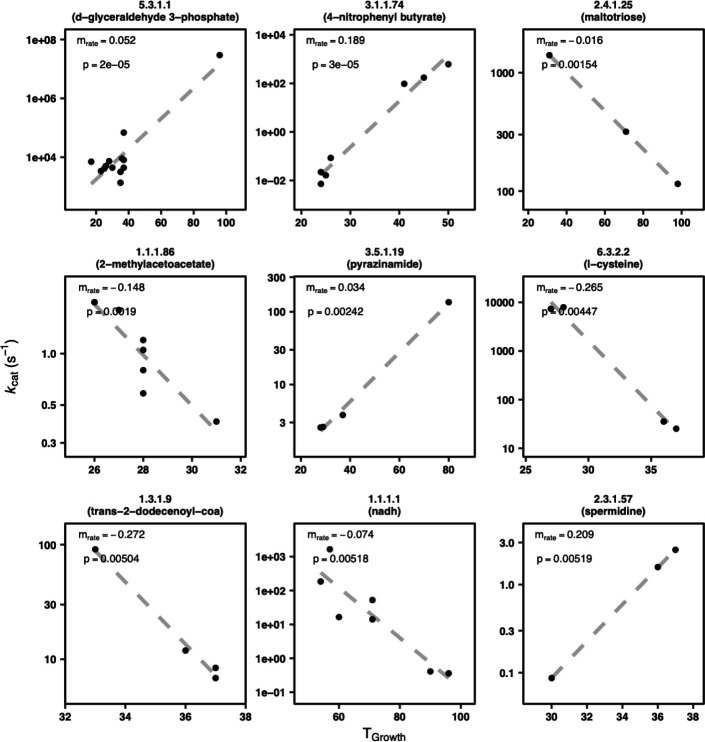
(A) Enzyme variants per reaction of wild-type enzyme kcat values (n = 11,480 reactions) matched to TGrowth. (B) Reactions with more than one enzyme variant (n = 2223 reactions). (C) Rate ratio distribution of the rate at the coldest TGrowth (kcold) divided by the rate of the variant from the warmest TGrowth (kwarm) (median = 1.1-fold, 95% CI [1.00, 1.22], n = 2223 reactions). Vertical line at rate ratio = 1. For clarity, only data with rate ratios between 10–3 and 103 are shown (>95% of the reactions). (D) Rate ratio (kcold/kwarm) data (solid line, n = 2223 from panel C) compared to fold change control distribution (same TGrowth; dashed line, median = 1.0-fold, 95% CI [0.89, 1.13], n = 615 reactions; p = 0.21, Mann–Whitney U test, two-sided). The black vertical line represents no rate enhancement change with temperature (i.e., rate ratio = 1). (E, F) The significance and magnitude of the linear fit of reaction rate as a function of TGrowth for negative slopes (E, n = 487) and positive slopes (F, n = 464) in log space. Enzyme Commission (E.C.) number and (substrate) indicated for reactions significantly associated with temperature (Bonferroni correction; p-value < 5.3 × 10–5, n = 951). Dotted horizontal lines at p = −log10(5.3 × 10–5). 5.3.1.1: triose-phosphate isomerase; G3P: glyceraldehyde 3-phosphate; 3.1.1.74: cutinase; 4-NPB: 4-nitrophenyl butyrate.

Figure 2—source code 1. Retrieval of updated BRENDA enzyme entries.
Figure 2—source code 2. Analysis of BRENDA enzyme rate constant entries.
Figure 2—source code 3. Control analysis of temperature-matched BRENDA enzyme rate constant entries.
Figure 2—source data 1. Downloaded BRENDA enzyme entries (July 2021).
Figure 2—source data 2. Analyzed BRENDA enzyme entries.

Figure 2.

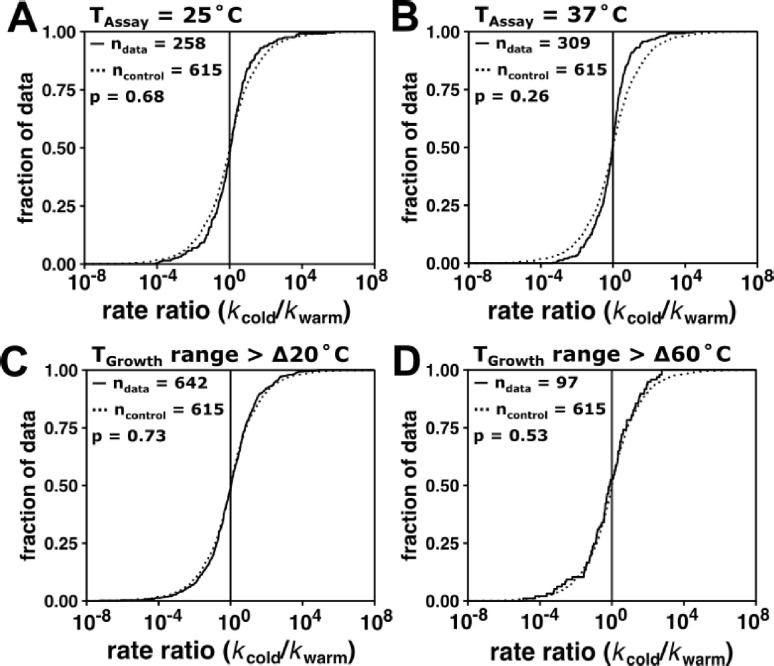
Figure 2—figure supplement 1. Specifying assay temperature and organism optimal growth temperature range per reaction does not alter conclusions.

Figure 2—figure supplement 1.

(A) Distribution of kcat rate ratio values including only measurements made at 25°C and (B) 37°C. (C) Distribution of rate ratios with TGrowth range >∆20°C and (D) TGrowth range >60°C. Reported p-values from two-sided Mann–Whitney U test comparing filtered data (solid line) and the control data (dotted line, see Materials and methods).
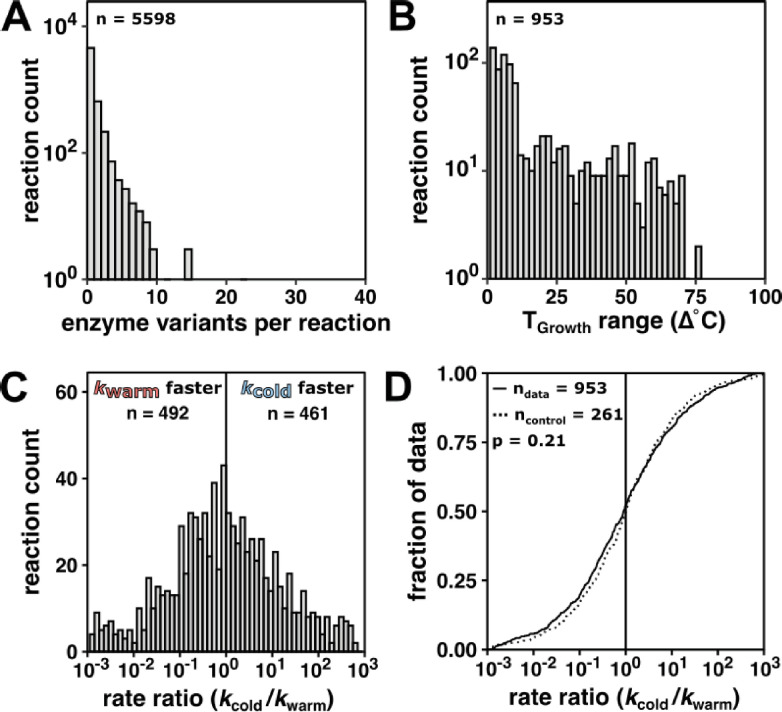
Figure 2—figure supplement 2. Enzyme rate constant data for kcat/KM do not indicate rate compensation, supporting the conclusions from the kcat analysis in the main text.

Figure 2—figure supplement 2.

(A) Variants per reaction of wild-type enzyme kcat values (n = 5598 reactions) matched to TGrowth. (B) Number of reactions spanning the specified TGrowth range (n = 953 reactions with >1 variant). (C) kcat/KM rate ratio (kcold/kwarm) distribution (median = 0.93-fold, 95% CI [0.78, 1.12], n = 953 reactions). Gray vertical line at rate ratio = 1. (D) kcat/KM rate ratio (kcold/kwarm) data (black line, n = 953 reactions) with kcat/KM rate ratio control (gray line, median = 1.00-fold, 95% CI [0.82, 1.21], n = 307 reactions) determined in the same way as the kcat rate ratio control in the main text (see Materials and methods) (p = 0.80, Mann–Whitney U test, two-sided). For clarity, only data with rate ratios between 10–3 and 103 are shown, representing >90% rate ratio data in (C) and >83% of rate ratio control values in (D). Black vertical line represents no rate change with temperature (i.e., rate ratio = 1).
Figure 2—figure supplement 3. Example mrate plots (9 of 951 reactions shown).

Figure 2—figure supplement 3.

Reactions with the rate constants of constituent variants in order of mrate p-value (for all reactions shown, p < 5.2 × 10–3). mrate is the slope of log10(kcat) vs. TGrowth. Note different scales for the axes. 5.3.1.1: triose-phosphate isomerase; 3.1.174: cutinase; 2.4.1.25: 4-alpha-glucanotransferase; 1.1.1.86: ketol-acid reductoisomerase; 3.5.1.19: nicotinamidase; 6.3.2.2: glutamate-cysteine ligase; 1.3.1.9: enoyl-[acyl-carrier-protein] reductase (NADH); 1.1.1.1: alcohol dehydrogenase; 2.3.1.57: diamine N-acetyltransferase.
Open in a new tab

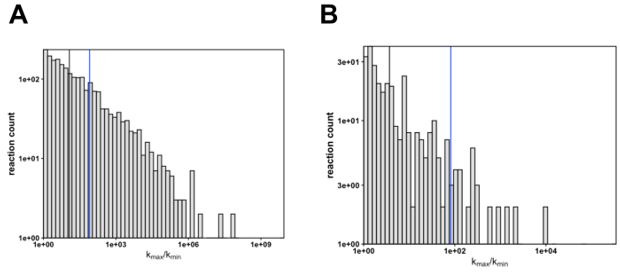
For each enzyme reaction, we first calculated the rate ratio (kcold/kwarm) between the rate constant of the variant from the lowest growth temperature organism and the rate constant of the variant from the highest growth temperature organism. We observed rate ratios greater than one (1142 reactions) as predicted by rate compensation, but nearly the same number of rate ratios of less than one (1082 reactions) (Figure 2C, compare with Figure 1D), providing no support for widespread or predominant rate compensation.

To assess whether rate constant trends were obscured by mixed assay temperatures or narrow TGrowth ranges, we analyzed the distributions of rate ratios separated by assay temperature (25°C or 37°C; Figure 2—figure supplement 1A and B) and the rate ratios for data representing wider TGrowth ranges (>∆20°C or >∆60°C; Figure 2—figure supplement 1C and D). No temperature-dependent trends emerged, supporting the above conclusion of an absence of widespread rate compensation.

To derive a control distribution, we compared enzyme variant rate constants originating from different organisms with identical TGrowth values. We found 615 reactions with more than one variant assigned the same TGrowth, and we calculated the rate ratio and its reciprocal (kmax/kmin and kmin/kmax) for each reaction. This control distribution (dashed line, Figure 2D) was indistinguishable from the data distribution of rate ratios across TGrowth (solid line, Figure 2D; p = 0.21, Mann–Whitney U test, two-sided). Analogous analyses of kcat/KM values lead to the same conclusions (Figure 2—figure supplement 2).

As it is not possible to prove the absence of a relationship (Altman and Bland, 1995), we examined the slope (mrate) of kcat values vs. TGrowth for each of the 951 reactions with >2 variants (Figure 2D and E, Figure 2—figure supplement 3) to address whether there might be a limited set of enzyme reactions exhibiting significant cold adaptation through a mechanism of enhanced rate. We found two reactions (triose-phosphate isomerase with glyceraldehyde 3-phosphate and cutinase with 4-nitrophenyl butyrate) significantly but positively associated with TGrowth (Bonferroni correction; p-value < 5.3 × 10–5, n = 951).

In summary, the data provide no indication of increased rate enhancements as a consequence of decreasing TGrowth. These results suggest that rate compensation is not a universal or prevalent consequence of temperature adaptation. The prior conclusion of widespread temperature adaptation may have arisen from the use of a small set of enzymes (n = 28; Figure 1C and D) or from inadvertent confirmation bias (Nickerson, 1998).

Testing the rate compensation model for the enzyme KSI

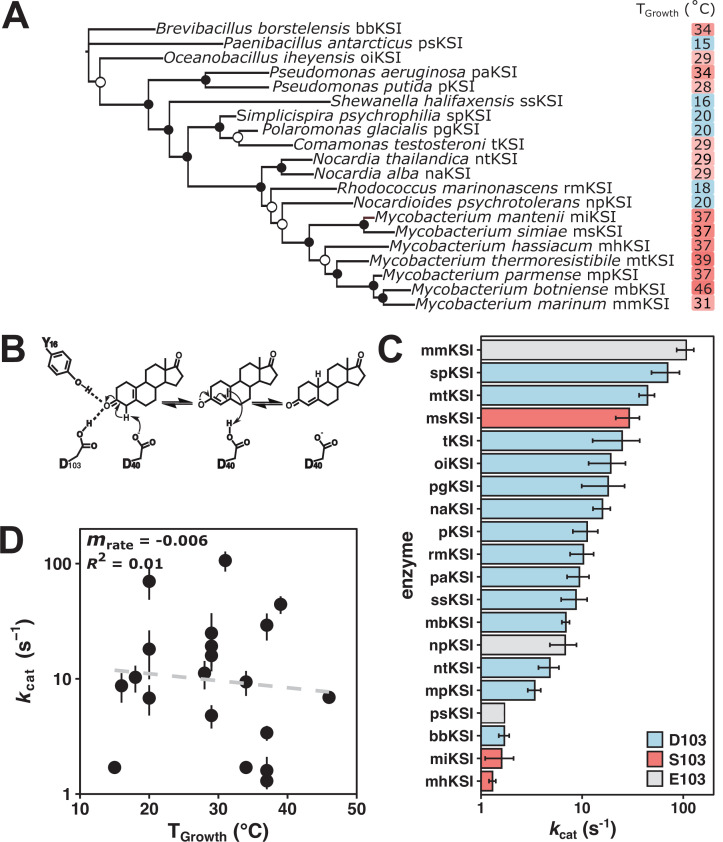
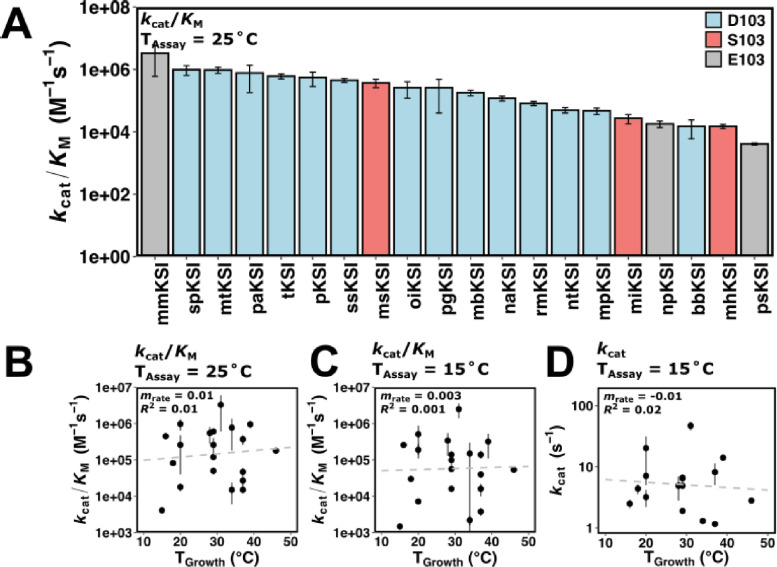
To probe rate compensation in greater depth, we turned to the enzyme KSI for which recent data has demonstrated rate compensation (Pinney et al., 2021). Specifically, the change of a single active site residue at position 103 from serine (S103, prevalently found in warm-adapted KSI variants) to protonated aspartic acid (D103, prevalently found in mesophilic KSI variants) provided improved activity from a stronger hydrogen bond while also sacrificing stability by introducing an unfavorable protonation coupled to folding. We therefore used KSI to more deeply investigate the potential for rate compensation by assaying 20 variants that vary in sequence and TGrowth (Figure 3A).

Figure 3. Ketosteroid isomerase (KSI) rate enhancements do not indicate rate compensation.

(A) Unrooted maximum likelihood phylogenetic tree of KSI variants. Closed circles represent bootstrap values of >70%; open circles represent bootstrap values of 40–70%. (B) The mechanism of isomerization of the steroid 5 (10)-estrene-3,17-dione by KSI. 5 (10)-EST was used to allow direct measurement of the rate-limiting chemical step kcat (Pollack et al., 1986). (C) Activity of KSI variants (kcat) at a common assay temperature of 25°C. Error bars represent standard deviation of at least two different experimental replicates varying [E] at least 5-fold. KSI variants with D103 are represented in blue, S103 in red, and E103 in gray (Pseudomonas putida numbering throughout). (D) Activity (log10(kcat)) of KSI variants at a common assay temperature (25°C) vs. organism growth temperature (TGrowth) (n = 20, mrate = –0.006, R2 = 0.01, p = 0.02).

Figure 3—source data 1. Ketosteroid isomerase (KSI) origins and organism growth temperatures.
a (Engqvist, 2018). b Alternatively reported to grow optimally at 65°C (Schröder et al., 1997). For consistency, curated values from Engqvist, 2018, are used in this work.
Figure 3—source data 2. Kinetic measurement of ketosteroid isomerases (KSIs) at 25°C with substrate 5 (10)-estrene-3,17-dione.
a (Engqvist, 2018). b Reported assay temperatures are the average of at least three measurements per experiment. c aAverage ± standard deviation from two to nine independent experiments with enzyme concentration varied by at least 5-fold. Values measured with substrate concentrations from 9 to 600 µM. Value of kcat/KM are less than 107 M–1 s–1 and thus unlikely to be limited by substrate binding. Reported assay temperatures are the average of at least three measurements per experiment.
Figure 3—source data 3. Kinetic measurement of ketosteroid isomerases (KSIs) at 15°C with substrate 5 (10)-estrene-3,17-dione.
a (Engqvist, 2018). b Reported assay temperatures are the average of at least three measurements per experiment. c Average ± standard deviation from two to four independent experiments with enzyme concentration varied by at least 2-fold. Values measured with substrate concentrations from 9 to 600 µM.

Figure 3.

Figure 3—figure supplement 1. ketosteroid isomerase (KSI) variant similarity.

Figure 3—figure supplement 1.

The primary sequence variation of each KSI variant ranges from 20% to 75% amino acid identity.
Figure 3—figure supplement 2. ketosteroid isomerase (KSI) variant circular dichroism (CD) spectra are indistinguishable at cold and warm temperature.

Figure 3—figure supplement 2.

Far ultraviolet CD spectra at 5°C (blue) and 25°C (red) are indistinguishable. Measurements for each variant were made at an enzyme concentration of 20 µM.
Figure 3—figure supplement 3. Ketosteroid isomerase (KSI) rate enhancements vary with organism growth temperature in kcat and in kcat/KM.

Figure 3—figure supplement 3.

(A) Rate of KSI variants (kcat/KM) at a common assay temperature (TAssay) of 25°C. KSI variants with D103 are represented in blue, S103 in red, and E103 in gray (Pseudomonas putida numbering). (B) Rates (kcat/KM) of KSI variants at 25°C assay temperature (TAssay) vs. organism growth temperature (TGrowth) (n = 20, mrate = 0.01, R2 = 0.01, p = 4 × 10–7). (C) Rates (kcat/KM) of KSI variants at 15°C assay temperature (TAssay) vs. organism growth temperature (TGrowth) (n = 20, mrate = 0.003, R2 = 0.001, p = 3 × 10–7). (D) Rates (kcat) of KSI variants at 15°C assay temperature (TAssay) vs. organism growth temperature (TGrowth) (n = 20, mrate = –0.01, R2 = 0.02, p = –0.11). Error bars represent standard deviation of at least two different experimental measurements varying [E] at least 5-fold (25°C) or 2-fold (15°C).
Open in a new tab

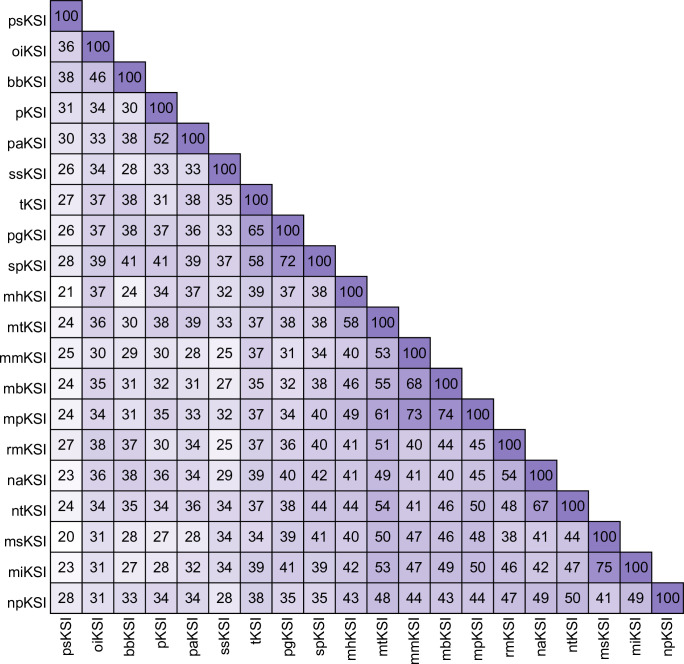
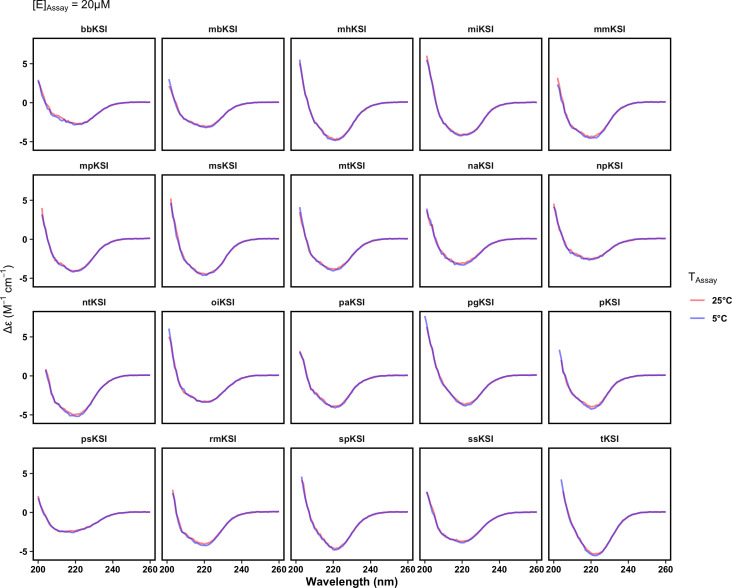
KSI catalyzes the double bond isomerization of steroid substrates (Figure 3B) and is predicted to be part of a pathway that enables degradation of steroids for energy and carbon metabolism in bacteria (Horinouchi et al., 2010). KSI variants were identified by sequence relatedness to known KSIs. The 20 selected KSI variants ranged between 20% and 75% sequence identity to each other (Figure 3—figure supplement 1) and were selected from bacteria originating from environments spanning glaciers, ocean floor, soil, and wastewater with reported TGrowth values from 15°C to 46°C (Figure 3—source data 1). Each purified KSI demonstrated similar circular dichroism (CD) spectra at 5°C and 25°C, suggesting that variants were not unfolding at the 25°C assay temperature (Figure 3—figure supplement 2). All putative KSI variants exhibited isomerase activity on the steroid substrate 5 (10)-estrene-3,17-dione (5 (10)-EST) (Figure 3C).

We observed that the KSIs with the prevalent cold-adapted residue (D103 and the similar residue E103, Pseudomonas putida numbering) were not uniformly faster than other KSIs in kcat (Figure 3C) or kcat/KM (Figure 3—figure supplement 3). The observation that one of the fastest variants contained serine at this position indicates that there are additional factors that influence its rate enhancement (Figure 3C and see Discussion).

For KSI, the value of kcat decreased as a function of TGrowth, but the shallow slope (mrate = –0.006, p = 0.02) (Figure 3D) and the small coefficient of determination (R2 = 0.01) of this relationship indicate that TGrowth accounts for little of the observed 80-fold rate variation. Similar activity trends were observed at an assay temperature of 15°C (Figure 3—figure supplement 3).

Testing stability compensation using literature data

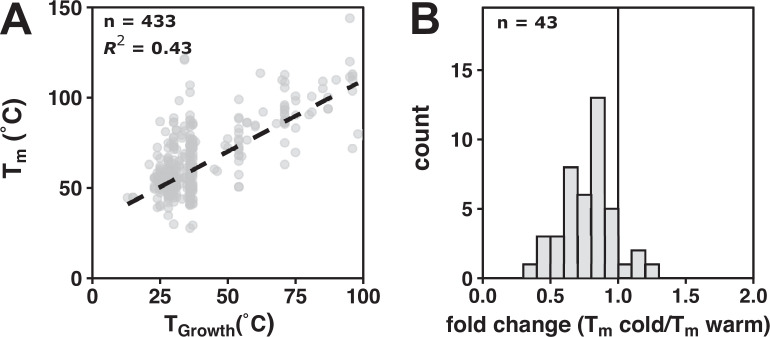
The absence of evidence for rate compensation led us to reinvestigate the widely accepted relationship between stability and growth temperature. Prior work has shown that the mean temperature optimum of enzymes correlates well with organism TGrowth (r = 0.75, Engqvist, 2018), but enzyme temperature optima reflect a combination of rate and stability effects. To isolate stability, we surveyed the relationship between stability and TGrowth using the ProThermDB, a collection of experimental data of protein and mutant stability (Nikam et al., 2021). Across 433 wild-type variants present in this database, we observed a significant relationship between Tm and TGrowth (Figure 4A, R2 = 0.43, p = 2 × 10–54). For the 43 protein families with more than one reported variant, 39 had a higher melting temperature than their cold-adapted counterpart (Figure 4B).

Figure 4. Protein stability data display stability compensation.

Figure 4.

Open in a new tab

(A) Wild-type Tm stability data from ProThermDB as a function of organism TGrowth. Dashed black line represents a linear fit (n = 433, R2 = 0.43). (B) Fold change (Tm cold/Tm warm) of wild-type protein variants (n = 43, median = 0.81, 95% [0.70, 0.85]). The black vertical line represents no change (i.e., fold change = 1).

Figure 4—source data 1. ProThermDB wild-type protein stability entries.
Figure 4—source data 2. ProThermDB wild-type protein stability entries of protein families with more than one reported variant.

Discussion

Enzymes have been widely posited to adapt to reduced temperature by increasing rate enhancement (Figure 1A and B; Collins and Gerday, 2017; D’Amico et al., 2003; Siddiqui and Cavicchioli, 2006; Zecchinon et al., 2001). Our results do not support this intuitive and common model as we found that cold-adapted enzyme variants are not generally faster than their warm-adapted counterparts. Even though there was prior evidence for temperature adaptation of the enzyme KSI that is accompanied by rate effects, we found that little of its overall rate variation was accounted for by organismal TGrowth, suggesting instead that stability is the dominant driving force underlying the previously identified changes. Our observations suggest that enzyme rate enhancement is unlikely to be the primary trait selected for during adaptation to colder environmental temperatures, broadly and in the model system KSI. It has been assumed throughout the literature that cold-adapted enzymes are faster than warm-adapted enzymes, based on the data presented in Figure 1C and D; however, our results do not support this model (Figure 2C and D).

Perhaps implicit in the expectation that catalysis will increase in cold adaption is the perspective that faster enzymes are better enzymes, with enzymes reacting at the diffusional limit denoted as ‘perfect’ (Knowles and Albery, 1977). However, most enzymes operate well below the diffusional limit (Bar-Even et al., 2011), underscoring that an optimal reaction rate constant may be different than the maximal enzyme rate constant. There are multiple reasons why optimal or observed enzyme rate constants may differ from maximal rate constants. Rate optimization in vivo may be accomplished by altering gene expression (Somero, 2004), isoform expression (Somero, 1995), or cellular pH and osmolytes (Hochachka and Lewis, 1971; Yancey and Somero, 1979). Alternatively, the optimal enzyme rate may be lower than the maximal rate to channel metabolites and coordinate metabolism (Prentice et al., 2020; Wortel et al., 2018). Further, models of enzyme-metabolite pathway evolution predict that the subset of enzymes that govern pathway flux through rate-limiting steps are under strong rate selection (Noda-Garcia et al., 2018), and it is also possible that maximal enzyme rates are not evolutionarily accessible (Obolski et al., 2018). We speculate that rate compensation may be more probable for highly related species that live in similar environments, such as marine species that live at different latitudes or depths but otherwise experience little environmental difference (Dong and Somero, 2009).

In contrast to our findings with rate, we observed strong evidence for stability compensation. The temperature dependence of protein unfolding (Becktel and Schellman, 1987) may exert a larger driving force on adaptation than the temperature dependence of rate. There may be an additional strong selection pressure to avoid unfolded states, as misfolded protein has been demonstrated to have deleterious fitness effects (Geiler-Samerotte et al., 2011) and cells expend considerable energy to clear misfolded variants using chaperones and degradation pathways (Clague and Urbé, 2010; Hartl et al., 2011; Lund, 2001). Additionally, adaptive paths toward stability may be more abundant and more accessible than analogous paths toward rate enhancement, given that each protein may be stabilized individually through a wide variety of mechanisms (Hart et al., 2014) and less constrained by biological context than an enzyme evolving synergistically with complex metabolic networks. The recent discovery of 158,184 positions from 1005 enzyme families that vary with growth temperature may further expand our understanding of the molecular strategies that underlie protein stabilization (Pinney et al., 2021).

The observation that KSI variants from high temperature correlate with serine at position 103 may reflect selection for the stabilizing effects of S103 (Pinney et al., 2021). In contrast, the observation that one of the fastest KSI variants contains the stabilizing but slowing active site residue (the serine at position 103 in msKSI, Figure 3C) may illustrate some of the evolutionary complexity alluded to above. As observed with other KSI variants, the msKSI variant with the wild-type serine residue mutated to aspartic acid (S103D) has increased activity and decreased stability. However, in msKSI, the decreased stability from the S103D mutation renders it partially unfolded even in the absence of denaturants (Pinney et al., 2021). This result suggests a model where drift or other factors have led to an overall destabilized scaffold, such that msKSI cannot accommodate the activating S103D change (without unfolding) and has made other as yet unidentified amino acid changes to increase activity.

Flexibility has been posited to mechanistically link rate and stability, with multiple underlying interconnections discussed (see Supplementary file 1; Åqvist et al., 2017; Arcus et al., 2016; D’Amico et al., 2003; Daniel and Danson, 2010; Nguyen et al., 2017; Saavedra et al., 2018). Nevertheless, there are many degrees of freedom in an enzyme and most motions are not expected to be coupled to the enzyme reaction coordinate. Our observation of the absence of widespread rate compensation to temperature in contrast to observed stability compensation is consistent with this perspective, as are prior examples of enzyme stabilization in the absence of detrimental rate effects (Minges et al., 2019; Miyazaki et al., 2000; Siddiqui, 2017; Wintrode and Arnold, 2000; Zhao and Feng, 2018). A more complex relationship between these traits seems likely and underscores the need to relate individual and coupled atomic motions to overall flexibility, catalysis, and stability to unravel their intricate interconnections.

To understand why enzyme properties such as rate and stability measured with purified enzymes vary across organisms, we will need to determine their effects on fitness across biological and environmental contexts, including environments that vary in temperature. Such studies may synergistically deepen our understanding of enzyme function, organismal evolution, and ecosystems.

Materials and methods

Key resources table.

Reagent type (species) or resource Designation Source or reference Identifiers Additional information
Strain, strain background (Escherichia coli) BL21(DE3) Sigma-Aldrich CMC0016 Electrocompetent cells for protein expression
Chemical compound, drug 5 (10)-estrene-3,17-dione Steraloids E4500-000 Ketosteroid isomerase reaction substrate
Open in a new tab

Literature enzyme rate analysis

To capture enzyme rates reported throughout the literature, the BRENDA database was accessed using SOAP July 2021 (Chang et al., 2021) (www.brenda-enzymes.org) and the kcat and kcat/KM database entries retrieved by Enzyme Commission (E.C.) number were parsed for measurement value, substrate, rate, assay temperature, and variant (wild-type or mutant) status (Source Code 1). Microbial optimum growth temperature (Engqvist, 2018) values from median organism optimal growth temperatures for microbes in culture (TGrowth) were matched by organism name to rate entries. (Natural temperatures in the wild may differ. The definition of TGrowth used herein is the same as that used in the studies leading to the rate compensation model.) Rate data were filtered for kcat and kcat/KM values of wild-type enzymes. Reactions are defined by E.C. number–substrate pair. The median value was taken in the case of multiple measurements of the same enzyme variant with the same substrate.

The rate ratio kcold/kwarm per reaction was determined by dividing rate constant of the enzyme from the organism with the minimum TGrowth by the rate constant of the enzyme from organism with the maximum TGrowth. We use the term ‘cold-adapted variant’ to refer to an enzyme from an organism annotated with lower TGrowth values. If a maximum or minimum TGrowth was shared between enzyme variants, then the median rate of the two variants was used in the rate ratio calculation. To account for enzyme rate variation arising independently of temperature, a control distribution from reactions with variants of the same TGrowth was derived. The fold change of the maximum value over the minimum value kmax/kmin and its reciprocal kmin/kmax was calculated for each reaction from the same TGrowth with at least two variants. To compare the rate ratio distribution of the data to the rate ratio control, the nonparametric two-sided Mann–Whitney U test was used with a significance threshold of p < 0.05. As no temperature-dependent trends emerged when data were restricted to measurements made at 25°C or 37°C or when the TGrowth range was limited to >∆20°C and >∆60°C, we used all data in the main analysis. We determined confidence intervals of the median parameters of the rate ratio distributions by bootstrap analysis (boot package in R, 10,000 replications) (Canty and Ripley, 2021; Davison and Hinkley, 1997). The mrate values (slopes) per reaction were calculated by performing a linear regression relating the log10(rate) vs. organism TGrowth. Significance threshold, corrected for multiple tests, was p < 5.33 × 10−5 (Bonferroni correction; p < 0.05/951).

KSI variant identification, cloning, expression, and purification

Putative KSI variants were identified by sequence relatedness to known KSI variants. Selection of variants was guided by associating putative KSI sequences with TGrowth by species (Engqvist, 2018). Seventeen variants were synthesized (GenScript or Twist Biosciences) and cloned (Gibson Assembly Protocol, New England Biolabs or Twist Biosciences) into pET-21(+) vectors. KSI variants were aligned using default parameters of Clustal Omega (Madeira et al., 2019) and the maximum likelihood tree was constructed using IQ-TREE with default parameters (Hoang et al., 2018; Nguyen et al., 2015). The constructs were expressed in Escherichia coli BL21(DE3) cells and purified as previously described (Kraut et al., 2010).

KSI kinetic measurements

The KSI substrate 5 (10)-estrene-3,17-dione (5 (10)EST) was purchased from Steraloids (Newport, RI). Reactions of purified KSIs with 5 (10)EST were monitored continuously at 248 nm using a Perkin Elmer Lambda 25 UV/Vis spectrometer with an attached VWR digital temperature controlled circulating water bath (Pinney et al., 2021). Temperatures within the cuvettes were measured post-reaction using a platinum electrode thermistor (Omega Engineering) and the temperature of the circulating water bath was modified to maintain a constant internal cuvette temperature between reactions. Reactions were conducted in 40 mM potassium phosphate buffer, pH 7.2, 1 mM disodium EDTA, with 2% DMSO as a co-solvent to maintain substrate solubility. The kinetic parameters kcat and KM were determined by fitting the observed initial velocity of each reaction as a function of 5 (10)EST concentration (9–600 µM; six to seven different substrate concentrations per experiment) to the Michaelis–Menten equation. Reported values of kcat and KM are the average of three to nine independent experiments with at least two different enzyme concentrations varied by at least 5-fold. Reported errors are the standard deviations of these values.

KSI CD

CD spectra were collected for each KSI variant in 40 mM potassium phosphate buffer, pH 7.2, 1 mM EDTA, at enzyme concentration 20 µM at 5°C and 25°C. Measurements were made on a J-815 Jasco Spectrophotometer between 190 and 250 nm at 1 nm bandwidth and 50 nm/min scanning speed in a 0.1 cm cuvette (Hellma Analytics).

Literature stability analysis

Wild-type mutation type stability data were downloaded from ProThermDB (Nikam et al., 2021) with the following fields: protein information (entry, source, mutation, E.C. number), experimental conditions (pH, T, measure, method), thermodynamic parameters (Tm, state, reversibility), and literature (PubMed ID, key words, reference, author). Wild-type protein data were matched by species name to microbial optimal growth temperatures TGrowth (Engqvist, 2018).

Acknowledgements

We thank M Pinney, H McShea, D Mokhtari, C Markin, IN Zheludev, J Cofsky, EE Duffy, P Harbury, C Khosla, and members of the Herschlag lab for thought-provoking discussions and review of this manuscript. We also thank F Sunden, A Chu, IN Zheludev, and F Yabukarski for experimental assistance and B Eskildsen and D Mokhtari for computational assistance. This research was supported by NSF Grant MCB-1714723, Stanford ChEM-H Chemistry-Biology Interface Training Program, and an NSF Graduate Research Fellowship to CDS and an NSF RET Supplement to JS.

Funding Statement

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Contributor Information

Daniel Herschlag, Email: herschla@stanford.edu.

Frank Raushel, Texas A&M University, United States.

Philip A Cole, Harvard Medical School, United States.

Funding Information

This paper was supported by the following grants:

  • National Science Foundation Graduate Research Fellowship to Catherine Stark.

  • National Science Foundation MCB-1714723 to Catherine Stark, Teanna Bautista-Leung, Joanna Siegfried, Daniel Herschlag.

  • Chemistry, Engineering and Medicine for Human Health, Stanford University Chemistry-Biology Interface Training Program to Catherine Stark.

Additional information

Competing interests

No competing interests declared.

No competing interests declared.

Author contributions

Conceptualization, Data curation, Formal analysis, Funding acquisition, Software, Supervision, Visualization, Writing – original draft, Writing – review and editing.

Investigation.

Investigation.

Conceptualization, Formal analysis, Funding acquisition, Methodology, Project administration, Supervision, Writing – original draft, Writing – review and editing.

Additional files

Transparent reporting form
Supplementary file 1. Overview of proposed molecular models of cold adaptation.
elife-72884-supp1.docx (16.6KB, docx)
Supplementary file 2. Ketosteroid isomerase (KSI) sequences.
elife-72884-supp2.docx (19.4KB, docx)

Data availability

All data generated or analysed during this study are included in the manuscript and supporting files; Source Data files have been provided for Figures 1, 2, 3, and 4.

The following previously published datasets were used:

Chang A , Jeske L , Ulbrich S , Hofmann J , Koblitz J , Schomburg I , Neumann-Schaal M , Jahn D , Schomburg D . 2021. BRENDA, the ELIXIR core data resource in 2021: new developments and updates. The Comprehensive Enzyme Information System.

References

  1. Altman DG, Bland JM. Absence of evidence is not evidence of absence. BMJ. 1995;311:485. doi: 10.1136/bmj.311.7003.485. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Åqvist J, Isaksen GV, Brandsdal BO. Computation of enzyme cold adaptation. Nature Reviews Chemistry. 2017;1:e0051. doi: 10.1038/s41570-017-0051. [DOI] [Google Scholar]
  3. Arcus VL, Prentice EJ, Hobbs JK, Mulholland AJ, Van der Kamp MW, Pudney CR, Parker EJ, Schipper LA. On the Temperature Dependence of Enzyme-Catalyzed Rates. Biochemistry. 2016;55:1681–1688. doi: 10.1021/acs.biochem.5b01094. [DOI] [PubMed] [Google Scholar]
  4. Arrhenius S. Über die Dissociationswärme und den Einfluss der Temperatur auf den Dissociationsgrad der Elektrolyte. Zeitschrift Für Physikalische Chemie. 1889;4U:96–116. doi: 10.1515/zpch-1889-0408. [DOI] [Google Scholar]
  5. Bar-Even A, Noor E, Savir Y, Liebermeister W, Davidi D, Tawfik DS, Milo R. The moderately efficient enzyme: evolutionary and physicochemical trends shaping enzyme parameters. Biochemistry. 2011;50:4402–4410. doi: 10.1021/bi2002289. [DOI] [PubMed] [Google Scholar]
  6. Becktel WJ, Schellman JA. Protein stability curves. Biopolymers. 1987;26:1859–1877. doi: 10.1002/bip.360261104. [DOI] [PubMed] [Google Scholar]
  7. Bhatia RK, Ullah S, Hoque MZ, Ahmad I, Yang YH, Bhatt AK, Bhatia SK. Psychrophiles: A source of cold-adapted enzymes for energy efficient biotechnological industrial processes. Journal of Environmental Chemical Engineering. 2021;9:104607. doi: 10.1016/j.jece.2020.104607. [DOI] [Google Scholar]
  8. Blow D. So do we understand how enzymes work? Structure. 2000;8:R77–R81. doi: 10.1016/s0969-2126(00)00125-8. [DOI] [PubMed] [Google Scholar]
  9. Bruno S, Coppola D, di Prisco G, Giordano D, Verde C. Enzymes from Marine Polar Regions and Their Biotechnological Applications. Marine Drugs. 2019;17:544. doi: 10.3390/md17100544. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Cai ZW, Ge HH, Yi ZW, Zeng RY, Zhang GY. Characterization of a novel psychrophilic and halophilic β-1, 3-xylanase from deep-sea bacterium, Flammeovirga pacifica strain WPAGA1. International Journal of Biological Macromolecules. 2018;118:2176–2184. doi: 10.1016/j.ijbiomac.2018.07.090. [DOI] [PubMed] [Google Scholar]
  11. Canty A, Ripley BD. boot: Bootstrap R (S-Plus) Functions. R package version 1.3-28Www.R-Project.Org 2021
  12. Chang A, Jeske L, Ulbrich S, Hofmann J, Koblitz J, Schomburg I, Neumann-Schaal M, Jahn D, Schomburg D. BRENDA, the ELIXIR core data resource in 2021: new developments and updates. Nucleic Acids Research. 2021;49:D498–D508. doi: 10.1093/nar/gkaa1025. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Clague MJ, Urbé S. Ubiquitin: Same Molecule, Different Degradation Pathways. Cell. 2010;143:682–685. doi: 10.1016/j.cell.2010.11.012. [DOI] [PubMed] [Google Scholar]
  14. Collins T, Gerday C. Enzyme Catalysis in Psychrophiles. Psychrophiles: From Biodiversity to Biotechnology. 2017;1:209–235. doi: 10.1007/978-3-319-57057-0_10. [DOI] [Google Scholar]
  15. Daniel RM, Danson MJ. A new understanding of how temperature affects the catalytic activity of enzymes. Trends in Biochemical Sciences. 2010;35:584–591. doi: 10.1016/j.tibs.2010.05.001. [DOI] [PubMed] [Google Scholar]
  16. Davison AC, Hinkley DV. Bootstrap Methods and Their Application. Cambridge: Cambridge University Press; 1997. [DOI] [Google Scholar]
  17. Doblin MA, van Sebille E. Drift in ocean currents impacts intergenerational microbial exposure to temperature. PNAS. 2016;113:5700–5705. doi: 10.1073/pnas.1521093113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Dong Y, Somero GN. Temperature adaptation of cytosolic malate dehydrogenases of limpets (genus Lottia): differences in stability and function due to minor changes in sequence correlate with biogeographic and vertical distributions. The Journal of Experimental Biology. 2009;212:169–177. doi: 10.1242/jeb.024505. [DOI] [PubMed] [Google Scholar]
  19. D’Amico S, Marx JC, Gerday C, Feller G. Activity-stability relationships in extremophilic enzymes. The Journal of Biological Chemistry. 2003;278:7891–7896. doi: 10.1074/jbc.M212508200. [DOI] [PubMed] [Google Scholar]
  20. Engqvist MKM. Correlating enzyme annotations with a large set of microbial growth temperatures reveals metabolic adaptations to growth at diverse temperatures. BMC Microbiology. 2018;18:177. doi: 10.1186/s12866-018-1320-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Feller G, Gerday C. Psychrophilic enzymes: molecular basis of cold adaptation. Cellular and Molecular Life Sciences. 1997;53:830–841. doi: 10.1007/s000180050103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Feller G, Gerday C. Psychrophilic enzymes: hot topics in cold adaptation. Nature Reviews. Microbiology. 2003;1:200–208. doi: 10.1038/nrmicro773. [DOI] [PubMed] [Google Scholar]
  23. Fields PA, Dong Y, Meng X, Somero GN. Adaptations of protein structure and function to temperature: there is more than one way to “skin a cat.”. The Journal of Experimental Biology. 2015;218:1801–1811. doi: 10.1242/jeb.114298. [DOI] [PubMed] [Google Scholar]
  24. Geiler-Samerotte KA, Dion MF, Budnik BA, Wang SM, Hartl DL, Drummond DA. Misfolded proteins impose a dosage-dependent fitness cost and trigger a cytosolic unfolded protein response in yeast. PNAS. 2011;108:680–685. doi: 10.1073/pnas.1017570108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Hammes GG, Benkovic SJ, Hammes-Schiffer S. Flexibility, diversity, and cooperativity: pillars of enzyme catalysis. Biochemistry. 2011;50:10422–10430. doi: 10.1021/bi201486f. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Hart KM, Harms MJ, Schmidt BH, Elya C, Thornton JW, Marqusee S. Thermodynamic system drift in protein evolution. PLOS Biology. 2014;12:e1001994. doi: 10.1371/journal.pbio.1001994. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Hartl FU, Bracher A, Hayer-Hartl M. Molecular chaperones in protein folding and proteostasis. Nature. 2011;475:324–332. doi: 10.1038/nature10317. [DOI] [PubMed] [Google Scholar]
  28. Hoang DT, Chernomor O, von Haeseler A, Minh BQ, Vinh LS. UFBoot2: Improving the Ultrafast Bootstrap Approximation. Molecular Biology and Evolution. 2018;35:518–522. doi: 10.1093/molbev/msx281. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Hochachka PW, Lewis JK. Interacting effects of pH and temperature on the K m values for fish tissue lactate dehydrogenases. Comparative Biochemistry and Physiology. B, Comparative Biochemistry. 1971;39:925–933. doi: 10.1016/0305-0491(71)90116-7. [DOI] [PubMed] [Google Scholar]
  30. Horinouchi M, Kurita T, Hayashi T, Kudo T. Steroid degradation genes in Comamonas testosteroni TA441: Isolation of genes encoding a Δ4(5)-isomerase and 3α- and 3β-dehydrogenases and evidence for a 100 kb steroid degradation gene hot spot. The Journal of Steroid Biochemistry and Molecular Biology. 2010;122:253–263. doi: 10.1016/j.jsbmb.2010.06.002. [DOI] [PubMed] [Google Scholar]
  31. Knowles JR, Albery WJ. Perfection in enzyme catalysis: the energetics of triosephosphate isomerase. Accounts of Chemical Research. 1977;10:105–111. doi: 10.1021/ar50112a001. [DOI] [Google Scholar]
  32. Kraut DA, Carroll KS, Herschlag D. Challenges in enzyme mechanism and energetics. Annual Review of Biochemistry. 2003;72:517–571. doi: 10.1146/annurev.biochem.72.121801.161617. [DOI] [PubMed] [Google Scholar]
  33. Kraut DA, Sigala PA, Fenn TD, Herschlag D. Dissecting the paradoxical effects of hydrogen bond mutations in the ketosteroid isomerase oxyanion hole. PNAS. 2010;107:1960–1965. doi: 10.1073/pnas.0911168107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Kuddus M. Cold-active enzymes in food biotechnology: An updated mini review. Journal of Applied Biology & Biotechnology. 2018;1:58–63. doi: 10.7324/JABB.2018.60310. [DOI] [Google Scholar]
  35. Lund PA. Microbial molecular chaperones. Advances in Microbial Physiology. 2001;44:93–140. doi: 10.1016/s0065-2911(01)44012-4. [DOI] [PubMed] [Google Scholar]
  36. Madeira F, Park YM, Lee J, Buso N, Gur T, Madhusoodanan N, Basutkar P, Tivey ARN, Potter SC, Finn RD, Lopez R. The EMBL-EBI search and sequence analysis tools APIs in 2019. Nucleic Acids Research. 2019;47:W636–W641. doi: 10.1093/nar/gkz268. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Mandelman D, Ballut L, Wolff DA, Feller G, Gerday C, Haser R, Aghajari N. Structural determinants increasing flexibility confer cold adaptation in psychrophilic phosphoglycerate kinase. Extremophiles. 2019;23:495–506. doi: 10.1007/s00792-019-01102-x. [DOI] [PubMed] [Google Scholar]
  38. Minges H, Schnepel C, Böttcher D, Weiß MS, Sproß J, Bornscheuer UT, Sewald N. Targeted Enzyme Engineering Unveiled Unexpected Patterns of Halogenase Stabilization. ChemCatChem. 2019;12:818–831. doi: 10.1002/cctc.201901827. [DOI] [Google Scholar]
  39. Miyazaki K, Wintrode PL, Grayling RA, Rubingh DN, Arnold FH. Directed evolution study of temperature adaptation in a psychrophilic enzyme. Journal of Molecular Biology. 2000;297:1015–1026. doi: 10.1006/jmbi.2000.3612. [DOI] [PubMed] [Google Scholar]
  40. Nguyen L-T, Schmidt HA, von Haeseler A, Minh BQ. IQ-TREE: a fast and effective stochastic algorithm for estimating maximum-likelihood phylogenies. Molecular Biology and Evolution. 2015;32:268–274. doi: 10.1093/molbev/msu300. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Nguyen V, Wilson C, Hoemberger M, Stiller JB, Agafonov RV, Kutter S, English J, Theobald DL, Kern D. Evolutionary drivers of thermoadaptation in enzyme catalysis. Science. 2017;355:289–294. doi: 10.1126/science.aah3717. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Nickerson RS. Confirmation Bias: A Ubiquitous Phenomenon in Many Guises. Review of General Psychology. 1998;2:175–220. doi: 10.1037/1089-2680.2.2.175. [DOI] [Google Scholar]
  43. Nikam R, Kulandaisamy A, Harini K, Sharma D, Gromiha MM. ProThermDB: thermodynamic database for proteins and mutants revisited after 15 years. Nucleic Acids Research. 2021;49:D420–D424. doi: 10.1093/nar/gkaa1035. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Noda-Garcia L, Liebermeister W, Tawfik DS. Metabolite-Enzyme Coevolution: From Single Enzymes to Metabolic Pathways and Networks. Annual Review of Biochemistry. 2018;87:187–216. doi: 10.1146/annurev-biochem-062917-012023. [DOI] [PubMed] [Google Scholar]
  45. Obolski U, Ram Y, Hadany L. Key issues review: evolution on rugged adaptive landscapes. Rep Prog Phys Phys Soc G B. 2018;81:012602. doi: 10.1088/1361-6633/aa94d4. [DOI] [PubMed] [Google Scholar]
  46. Park HJ, Lee CW, Kim D, Do H, Han SJ, Kim JE, Koo BH, Lee JH, Yim JH. Crystal structure of a cold-active protease (Pro21717) from the psychrophilic bacterium, Pseudoalteromonas arctica PAMC 21717, at 1.4 Å resolution: Structural adaptations to cold and functional analysis of a laundry detergent enzyme. PLOS ONE. 2018a;13:e0191740. doi: 10.1371/journal.pone.0191740. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Park SH, Yoo W, Lee CW, Jeong CS, Shin SC, Kim HW, Park H, Kim KK, Kim TD, Lee JH. Crystal structure and functional characterization of a cold-active acetyl xylan esterase (PbAcE) from psychrophilic soil microbe Paenibacillus sp. PLOS ONE. 2018b;13:e0206260. doi: 10.1371/journal.pone.0206260. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Pinney MM, Mokhtari DA, Akiva E, Yabukarski F, Sanchez DM, Liang R, Doukov T, Martinez TJ, Babbitt PC, Herschlag D. Parallel molecular mechanisms for enzyme temperature adaptation. Science. 2021;371:eaay2784. doi: 10.1126/science.aay2784. [DOI] [PubMed] [Google Scholar]
  49. Pollack RM, Bantia S, Bounds PL, Koffman BM. pH dependence of the kinetic parameters for 3-oxo-delta 5-steroid isomerase Substrate catalysis and inhibition by (3S)-spiro[5 alpha-androstane-3,2’-oxiran]-17-one. Biochemistry. 1986;25:1905–1911. doi: 10.1021/bi00356a011. [DOI] [PubMed] [Google Scholar]
  50. Prentice EJ, Hicks J, Ballerstedt H, Blank LM, Liáng LNL, Schipper LA, Arcus VL. The Inflection Point Hypothesis: The Relationship between the Temperature Dependence of Enzyme-Catalyzed Reaction Rates and Microbial Growth Rates. Biochemistry. 2020;59:3562–3569. doi: 10.1021/acs.biochem.0c00530. [DOI] [PubMed] [Google Scholar]
  51. Ringe D, Petsko GA. How Enzymes Work. Science. 2008;320:1428–1429. doi: 10.1126/science.1159747. [DOI] [PubMed] [Google Scholar]
  52. Saavedra HG, Wrabl JO, Anderson JA, Li J, Hilser VJ. Dynamic allostery can drive cold adaptation in enzymes. Nature. 2018;558:324–328. doi: 10.1038/s41586-018-0183-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Santiago M, Ramírez-Sarmiento CA, Zamora RA, Parra LP. Discovery, Molecular Mechanisms, and Industrial Applications of Cold-Active Enzymes. Frontiers in Microbiology. 2016;7:1408. doi: 10.3389/fmicb.2016.01408. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Schröder KH, Naumann L, Kroppenstedt RM, Reischl U. Mycobacterium hassiacum sp. nov., a new rapidly growing thermophilic mycobacterium. International Journal of Systematic Bacteriology. 1997;47:86–91. doi: 10.1099/00207713-47-1-86. [DOI] [PubMed] [Google Scholar]
  55. Siddiqui KS, Cavicchioli R. Cold-adapted enzymes. Annual Review of Biochemistry. 2006;75:403–433. doi: 10.1146/annurev.biochem.75.103004.142723. [DOI] [PubMed] [Google Scholar]
  56. Siddiqui KS. Defying the activity-stability trade-off in enzymes: taking advantage of entropy to enhance activity and thermostability. Critical Reviews in Biotechnology. 2017;37:309–322. doi: 10.3109/07388551.2016.1144045. [DOI] [PubMed] [Google Scholar]
  57. Smalås AO, Leiros HK, Os V, Willassen NP. Cold adapted enzymes. Biotechnology Annual Review. 2000;6:1–57. doi: 10.1016/s1387-2656(00)06018-x. [DOI] [PubMed] [Google Scholar]
  58. Somero GN. Proteins and temperature. Annual Review of Physiology. 1995;57:43–68. doi: 10.1146/annurev.ph.57.030195.000355. [DOI] [PubMed] [Google Scholar]
  59. Somero GN. Adaptation of enzymes to temperature: searching for basic “strategies.”. Comparative Biochemistry and Physiology. Part B, Biochemistry & Molecular Biology. 2004;139:321–333. doi: 10.1016/j.cbpc.2004.05.003. [DOI] [PubMed] [Google Scholar]
  60. Wintrode PL, Arnold FH. Temperature adaptation of enzymes: lessons from laboratory evolution. Advances in Protein Chemistry. 2000;55:161–225. doi: 10.1016/s0065-3233(01)55004-4. [DOI] [PubMed] [Google Scholar]
  61. Wolfenden R, Snider M, Ridgway C, Miller B. The Temperature Dependence of Enzyme Rate Enhancements. Journal of the American Chemical Society. 1999;121:7419–7420. doi: 10.1021/ja991280p. [DOI] [Google Scholar]
  62. Wortel MT, Noor E, Ferris M, Bruggeman FJ, Liebermeister W. Metabolic enzyme cost explains variable trade-offs between microbial growth rate and yield. PLOS Computational Biology. 2018;14:e1006010. doi: 10.1371/journal.pcbi.1006010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Yancey PH, Somero GN. Counteraction of urea destabilization of protein structure by methylamine osmoregulatory compounds of elasmobranch fishes. The Biochemical Journal. 1979;183:317–323. doi: 10.1042/bj1830317. [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. Zecchinon L, Claverie P, Collins T, D’Amico S, Delille D, Feller G, Georlette D, Gratia E, Hoyoux A, Meuwis MA, Sonan G, Gerday C. Did psychrophilic enzymes really win the challenge. Extremophiles: Life under Extreme Conditions. 2001;5:313–321. doi: 10.1007/s007920100207. [DOI] [PubMed] [Google Scholar]
  65. Zhao HY, Feng H. Engineering Bacillus pumilus alkaline serine protease to increase its low-temperature proteolytic activity by directed evolution. BMC Biotechnology. 2018;18:34. doi: 10.1186/s12896-018-0451-0. [DOI] [PMC free article] [PubMed] [Google Scholar]

Editor's evaluation

Frank Raushel 1

Are enzymes found in organisms that optimally grow at colder temperature are more active than the same enzymes found in organisms that optimally grow at warmer temperatures? Here, an assessment of the catalytic constants for approximately 2200 enzymes (obtained from the BRENDA database) showed no correlation between the relative catalytic activity and the optimum growth temperature. Further support for this conclusion was obtained from the measurement of the catalytic constants from a selection of ketosteroid isomerases from organisms that optimally grow between 15 and 46 degrees centigrade. Therefore, additional factors must dominate the selection pressure used to evolve enzymes of the appropriate catalytic activity. In contrast, growth temperature exerts a significant selective pressure on protein stability.

Decision letter

Editor: Frank Raushel1

Our editorial process produces two outputs: (i) public reviews designed to be posted alongside the preprint for the benefit of readers; (ii) feedback on the manuscript for the authors, including requests for revisions, shown below. We also include an acceptance summary that explains what the editors found interesting or important about the work.

Decision letter after peer review:

Thank you for submitting your article "Systematic investigation of the link between enzyme catalysis and cold adaptation" for consideration by eLife. Your article has been reviewed by 3 peer reviewers, one of whom is a member of our Board of Reviewing Editors, and the evaluation has been overseen by Philip Cole as the Senior Editor. The reviewers have opted to remain anonymous.

The reviewers have discussed their reviews with one another, and the Reviewing Editor has drafted this to help you prepare a revised submission.

Essential revisions:

1. Additional discussion regarding the apparent effect of optimal growth temperature and the kinetic constants is warranted for Figures 1C/D in contrast to the data presented in Figures 2C/D.

2. For the data presented in Figure 2C the authors should comment on the apparent fact that the rate constants for catalytic activity for the cold and warm adapted enzyme were not conducted at the same temperature. This issue is further complicated by the issue raised by reviewer 3 with regard to the results for amylase conducted at 3 different temperatures.

3. The revision should also address a supplementary issue raised by reviewer 2 with regard to the definition of optimal growth temperature: What does the optimal growth temperature for an organism tell us about an organisms response to evolutionary pressure in the wild? Organisms generally evolve to grow over a fairly wide range of temperatures, not at a single temperature. Optimal growth temperatures are determined for growth in a defined medium, generally one that favors growth; and, not the more rigorous conditions for growth in the wild.

Reviewer #1 (Recommendations for the authors):

1. Figure 1C appears to show that those enzymes from the cold adapted organisms are more catalytically active than those from warm adapted organisms. The authors should be required explain in more detail why the correlations that they observe from the data obtained from BRENDA are more appropriate than the correlations observed by others.

2. The paragraph from lines 188 through 195 is confusing. When the authors write S103D to designate a mutation it is not so clear as to what residue now constitutes the "wild-type" and what is considered the "mutation" when they are discussing msKSI.

3. I was surprised to find that the kcat values for KSI vary by approximately 100. Since the growth temperature apparently not contribute to this difference what other factors would lead to such large differences in these rate constants?

Reviewer #2 (Recommendations for the authors):

The manuscript lacks precision in the use of the term rate. For example:

"Prior work has shown that temperature optima for observed enzyme rates.…. Rate has no meaning in this sentence. Temperature optima are determined for plots of temperature against some kinetic parameter, such as kcat.

"The observed rate effects (Figure 1C, Figure 1D)." These Figures describe effects on the rate constant kcat.

"Testing the rate compensation model….." What is meant by "rate compensation model"? Nothing came up in a Google search for this term.

Reviewer #3 (Recommendations for the authors):

The title of the paper is not appropriate. The data survey here is not a systematic investigation of the whole question of the relationship of enzyme catalysis to cold adaptation. For example, the focus here is on single enzymes only without consideration of pathway kinetics.

The discussion of existing proposals on temperature dependence of activity is limited and somewhat superficial, particularly with regard to proposals lumped together under the general headings of flexibility ('specific' and 'general'). Previous relevant work of Danson et al., showing that different conformational states can account for observed behavior, should be considered. SI: "Flexibility has been posited to mechanistically link rate and stability, with multiple underlying interconnections discussed" – yes, there have been many such proposals, but most of the references cited here do not do so. Rather, they discuss temperature dependence of rates independent of stability.

Altogether, the presentation is not clear and is confusing. The hypothesis that the authors outline is clear, but the approach is too simplistic. If we take the classic amylase example from Feller and Gerday (cited by the authors), then the ratio of rates at a common temperature for the psychrophile and mesophile would give ratios of >1 for T<37, ~1 at T=37 and <1 for T>37. So it really depends on the common temperature that chosen for the comparison and cannot provide a general explanation.

The data presented are useful, but the accompanying discussion is significantly incomplete. As a whole, this work does not provide significant new insight.

eLife. 2022 Jan 12;11:e72884. doi: 10.7554/eLife.72884.sa2

Author response

Essential revisions:

1. Additional discussion regarding the apparent effect of optimal growth temperature and the kinetic constants is warranted for Figures 1C/D in contrast to the data presented in Figures 2C/D.

As this comparison –the main finding of this paper– was not clear to the reviewers, we now use language that underscores this comparison in the Discussion:

“It has been assumed throughout the literature that cold-adapted enzymes are faster than warm-adapted enzymes, based on the data presented in Figure 1C and 1D; however, our results do not support this model (Figure 2C, Figure 2D).”

We theorize that multiple studies seeming to support the prior model (which the more extensive data herein do not support) resulted from confirmation bias; we surmise that this was not intentional, as well-meaning and thorough scientists may prioritize communicating positive results that appear to contribute to the understanding of natural phenomena. However, the penetrance of the idea of rate compensation into multiple fields (e.g., enzyme mechanism and enzyme engineering) underscores the necessity of being explicit about our findings. We have worked hard in our presentation to respect the contributions of these different groups while presenting our results clearly, now stating in the Results:

“In summary, the data provide no indication of increase rate enhancements as a consequence of decreasing TGrowth. […] The prior conclusion of widespread temperature adaptation may have arisen from the use of a small set of enzymes (n = 28; Figure 1C, Figure 1D) or from inadvertent confirmation bias (Nickerson, 1998).”

2. For the data presented in Figure 2C the authors should comment on the apparent fact that the rate constants for catalytic activity for the cold and warm adapted enzyme were not conducted at the same temperature. This issue is further complicated by the issue raised by reviewer 3 with regard to the results for amylase conducted at 3 different temperatures.

Analysis at a common temperature supports the conclusions of this work. We now make it clear that this comparison has been made. More specifically, we begin by analyzing all data and then ask if the trends observed with all data are observed with the subset of data at identical temperatures. We have revised the text in the Results to make this clearer –i.e., that this important analysis (presented in Figure 2—figure supplement 1) was carried out and supports our conclusions:

“To assess whether rate constant trends were obscured by mixed assay temperatures or narrow TGrowth ranges, we analyzed the distributions of rate ratios separated by assay temperature (25°C or 37°C; Figure 2—figure supplement 1A, 1B) and the rate ratios for data representing wider TGrowth ranges (>∆20˚C or >∆60˚C; Figure 2—figure supplement 1C, 1D). No temperature-dependent trends emerged, supporting the above conclusion of an absence of widespread rate compensation.”

For the amylase measurements, this is a case where the enzyme rate dependence on temperature differs between three amylase variants (D’Amico et al., 2003). Rate enhancement measurements spanning the larger family of amylases will test whether the observed pattern generally holds across amylase variants. There may be individual instances of more complex behaviors or more patterns to be uncovered in particular enzyme types or families, and we look forward to future research addressing these questions. We did not observe significantly different trends for the 20 KSI variants we investigated at 15 vs. 25°C. In this manuscript, to be clear, our overall ais to address the question and test the model that rate adaptation to temperature is a phenomenon that is general to enzymes. By looking systematically at the available data, we found that the data did not support this model that was previously proposed based on a limited number of published examples.

3. The revision should also address a supplementary issue raised by reviewer 2 with regard to the definition of optimal growth temperature: What does the optimal growth temperature for an organism tell us about an organisms response to evolutionary pressure in the wild? Organisms generally evolve to grow over a fairly wide range of temperatures, not at a single temperature. Optimal growth temperatures are determined for growth in a defined medium, generally one that favors growth; and, not the more rigorous conditions for growth in the wild.

This is an interesting (and complex) question but is not directly relevant to our analyses and results. In this manuscript, we are using the definition of growth temperature that was used previously in the literature and used to derive the general model that we present and test; given that our goal was to test this prior model –and in particular, whether it was supported by data when all available data were included– it was important to maintain the prior definition of growth temperature (e.g., Engqvist, 2018).

We have clarified this in the Materials and methods:

“Natural temperatures in the wild may differ. The definition of TGrowth used herein is the same as that used in the studies leading to the rate compensation model.”

Further, if the proposed activity-growth temperature trend were general, we would still expect to see it if the temperature values represented an average.

Nevertheless, this reviewer brings up fascinating evolutionary considerations. Models for temperature adaptation through rate or other adaptation should consider and address other environmental differences including the range of temperatures that an organism experiences, as we have noted in the Discussion:

“To understand why enzyme properties such as rate and stability measured with purified enzymes vary across organisms, we will need to determine their effects on fitness across biological and environmental contexts, including environments that vary in temperature.”

Reviewer #1 (Recommendations for the authors):

1. Figure 1C appears to show that those enzymes from the cold adapted organisms are more catalytically active than those from warm adapted organisms. The authors should be required explain in more detail why the correlations that they observe from the data obtained from BRENDA are more appropriate than the correlations observed by others.

We have clarified this in Essential Revision #1 above. Briefly, the prior data were based on a limited number of anecdotal studies (n = 28). In contrast, the BRENDA data we curated represents over 2200 enzymatic reactions, a collation of approximately 100-fold more data than the prior combined studies. Our analysis includes all of the data that are published and catalogued, without regard to whether the system under examination is behaving in the predicted manner. We have emphasized that approach is less biased and is expected to be more representative.

2. The paragraph from lines 188 through 195 is confusing. When the authors write S103D to designate a mutation it is not so clear as to what residue now constitutes the "wild-type" and what is considered the "mutation" when they are discussing msKSI.

We have indicated that serine at position 103 is the wild-type residue in the Discussion:

“The observation that KSI variants from high temperature correlate with serine at position 103 may reflect selection for the stabilizing effects of S103 (Pinney et al., 2021). […] As observed with other KSI variants, the msKSI variant with the wild-type serine residue mutated to aspartic acid (S103D) has increased activity and decreased stability.”

3. I was surprised to find that the kcat values for KSI vary by approximately 100. Since the growth temperature apparently not contribute to this difference what other factors would lead to such large differences in these rate constants?

We were surprised as well. After obtaining this result, we realized that there was little data about how enzyme families vary in reaction parameters. We observe that the median fold change (kmax/kmin) is about 10-fold (black line), as compared to the fold change of approximately 100-fold of KSI (blue line) with a wide range of distribution (Author response image 1) .

Author response image 1. Differences in rate constants between enzyme variants.

Author response image 1.

Open in a new tab

(A) The fold change in kcat (kmax/kmin) of enzyme reactions (n = 2223). The black line indicates the fold change median value (median kmax/kmin = 11.8) and the blue line indicates the fold change value of KSI (kmax/kmin = 82). (B) The fold change in kcat (kmax/kmin) of enzyme reactions measured at 37°C (n = 319). The black line indicates the fold change median value (median kmax/kmin = 3.7) and the blue line indicates the fold change value of KSI (kmax/kmin = 82); while the median is much smaller there remain a number of enzymes with fold change values similar or larger than the KSIs.

We agree that identifying other factors that affect rates is an important area of future study. For example, how much do differential selective pressure of metabolic networks lead to different optimized rates? Addressing the question of how differential selective pressures affect rate constants will require systematic studies of enzyme variances across multiple organisms, as we note in the Discussion (and above):

“To understand why enzyme properties such as rate and stability measured with purified enzymes vary across organisms, we will need to determine their effects on fitness across biological and environmental contexts, including environments that vary in temperature.”

Reviewer #2 (Recommendations for the authors):

The manuscript lacks precision in the use of the term rate. For example:

"Prior work has shown that temperature optima for observed enzyme rates.…. Rate has no meaning in this sentence. Temperature optima are determined for plots of temperature against some kinetic parameter, such as kcat.

"The observed rate effects (Figure 1C, Figure 1D)." These Figures describe effects on the rate constant kcat.

"Testing the rate compensation model….." What is meant by "rate compensation model"? Nothing came up in a Google search for this term.

Thank you for these specific comments. We have clarified the terminology around rate throughout the manuscript. For rate compensation, we have clarified that this is a term that we have introduced in the Introduction.

Reviewer #3 (Recommendations for the authors):

The title of the paper is not appropriate. The data survey here is not a systematic investigation of the whole question of the relationship of enzyme catalysis to cold adaptation. For example, the focus here is on single enzymes only without consideration of pathway kinetics.

Systematic is defined as “methodical in procedure or plan” or “marked by thoroughness and regularity” (Merriam-Webster). Our title references that our data survey in this work is systematic with respect to existing data.

The discussion of existing proposals on temperature dependence of activity is limited and somewhat superficial, particularly with regard to proposals lumped together under the general headings of flexibility ('specific' and 'general'). Previous relevant work of Danson et al., showing that different conformational states can account for observed behavior, should be considered. SI: "Flexibility has been posited to mechanistically link rate and stability, with multiple underlying interconnections discussed" – yes, there have been many such proposals, but most of the references cited here do not do so. Rather, they discuss temperature dependence of rates independent of stability.

Danson et al. address how enzyme rates ‘drop off’ with temperature at temperatures lower than needed to unfold them. Their model –of multiple states with differential activity– provides a very reasonable explanation. This behavior though is distinct from the topic of our work –which is a comparison of rate constants for different enzymes from organisms with different growth temperatures, not the same enzyme vs. temperature. Regardless, we appreciate that Reviewer #3 has brought this work to our attention and we have included it in the revised manuscript.

Altogether, the presentation is not clear and is confusing. The hypothesis that the authors outline is clear, but the approach is too simplistic. If we take the classic amylase example from Feller and Gerday (cited by the authors), then the ratio of rates at a common temperature for the psychrophile and mesophile would give ratios of >1 for T<37, ~1 at T=37 and <1 for T>37. So it really depends on the common temperature that chosen for the comparison and cannot provide a general explanation.

As noted above, the reported data on amylase is a case (with n = 3 variants) where we know the enzyme activity depends on temperature in different ways for the different variants. The benefit of using broad data is that we are able to test the generality of a hypothesis across different enzyme families and more variants (please see Essential Revision #1 above). We also emphasize that we do see the same absence of a trend when carrying out the analysis at 25°C or 37°C (Figure 2—figure supplement 1).

The data presented are useful, but the accompanying discussion is significantly incomplete. As a whole, this work does not provide significant new insight.

The conclusion of our paper is that a general trend predicted by a widely accepted model is not supported by the data. This is significant, as it disproves a widely accepted trend and especially as there has been much discussion and models already in the literature based on the assumption that this trend is correct. We felt it best to mainly present this new result, point out complexities in selection that might lead to the absence of a general trend, but not speculate about topics not directly linked to the current results.

Associated Data

    This section collects any data citations, data availability statements, or supplementary materials included in this article.

    Data Citations

    1. Chang A , Jeske L , Ulbrich S , Hofmann J , Koblitz J , Schomburg I , Neumann-Schaal M , Jahn D , Schomburg D . 2021. BRENDA, the ELIXIR core data resource in 2021: new developments and updates. The Comprehensive Enzyme Information System. [DOI] [PMC free article] [PubMed]

    Supplementary Materials

    Figure 1—source data 1. Rate comparisons of warm-adapted and cold-adapted enzyme variants made at identical temperatures from cold adaptation literature.
    elife-72884-fig1-data1.csv (19.8KB, csv)
    Figure 2—source code 1. Retrieval of updated BRENDA enzyme entries.
    elife-72884-fig2-code1.zip (3KB, zip)
    Figure 2—source code 2. Analysis of BRENDA enzyme rate constant entries.
    elife-72884-fig2-code2.zip (4.9KB, zip)
    Figure 2—source code 3. Control analysis of temperature-matched BRENDA enzyme rate constant entries.
    elife-72884-fig2-code3.zip (2.6KB, zip)
    Figure 2—source data 1. Downloaded BRENDA enzyme entries (July 2021).
    elife-72884-fig2-data1.csv (12.4MB, csv)
    Figure 2—source data 2. Analyzed BRENDA enzyme entries.
    elife-72884-fig2-data2.csv (983.3KB, csv)
    Figure 3—source data 1. Ketosteroid isomerase (KSI) origins and organism growth temperatures.

    a (Engqvist, 2018). b Alternatively reported to grow optimally at 65°C (Schröder et al., 1997). For consistency, curated values from Engqvist, 2018, are used in this work.

    elife-72884-fig3-data1.docx (78.5KB, docx)
    Figure 3—source data 2. Kinetic measurement of ketosteroid isomerases (KSIs) at 25°C with substrate 5 (10)-estrene-3,17-dione.

    a (Engqvist, 2018). b Reported assay temperatures are the average of at least three measurements per experiment. c aAverage ± standard deviation from two to nine independent experiments with enzyme concentration varied by at least 5-fold. Values measured with substrate concentrations from 9 to 600 µM. Value of kcat/KM are less than 107 M–1 s–1 and thus unlikely to be limited by substrate binding. Reported assay temperatures are the average of at least three measurements per experiment.

    elife-72884-fig3-data2.pdf (125.1KB, pdf)
    Figure 3—source data 3. Kinetic measurement of ketosteroid isomerases (KSIs) at 15°C with substrate 5 (10)-estrene-3,17-dione.

    a (Engqvist, 2018). b Reported assay temperatures are the average of at least three measurements per experiment. c Average ± standard deviation from two to four independent experiments with enzyme concentration varied by at least 2-fold. Values measured with substrate concentrations from 9 to 600 µM.

    elife-72884-fig3-data3.pdf (114.1KB, pdf)
    Figure 4—source data 1. ProThermDB wild-type protein stability entries.
    elife-72884-fig4-data1.csv (154.1KB, csv)
    Figure 4—source data 2. ProThermDB wild-type protein stability entries of protein families with more than one reported variant.
    elife-72884-fig4-data2.csv (4.2KB, csv)
    Transparent reporting form
    elife-72884-transrepform1.docx (113.5KB, docx)
    Supplementary file 1. Overview of proposed molecular models of cold adaptation.
    elife-72884-supp1.docx (16.6KB, docx)
    Supplementary file 2. Ketosteroid isomerase (KSI) sequences.
    elife-72884-supp2.docx (19.4KB, docx)

    Data Availability Statement

    All data generated or analysed during this study are included in the manuscript and supporting files; Source Data files have been provided for Figures 1, 2, 3, and 4.

    The following previously published datasets were used:

    Chang A , Jeske L , Ulbrich S , Hofmann J , Koblitz J , Schomburg I , Neumann-Schaal M , Jahn D , Schomburg D . 2021. BRENDA, the ELIXIR core data resource in 2021: new developments and updates. The Comprehensive Enzyme Information System.

    Articles from eLife are provided here courtesy of eLife Sciences Publications, Ltd

    RESOURCES