A two-phase Bayesian methodology for the analysis of binary phenotypes in genome-wide association studies

Abstract

Recent advances in sequencing and genotyping technologies are contributing to a data revolution in genome-wide association studies that is characterized by the challenging large p small n problem in statistics. That is, given these advances, many such studies now consider evaluating an extremely large number of genetic markers (p) genotyped on a small number of subjects (n). Given the dimension of the data, a joint analysis of the markers is often fraught with many challenges, while a marginal analysis is not sufficient. To overcome these obstacles, herein, we propose a Bayesian two-phase methodology that can be used to jointly relate genetic markers to binary traits while controlling for confounding. The first phase of our approach makes use of a marginal scan to identify a reduced set of candidate markers which are then evaluated jointly via a hierarchical model in the second phase. Final marker selection is accomplished through identifying a sparse estimator via a novel and computationally efficient maximum a posteriori estimation technique. We evaluate the performance of the proposed approach through extensive numerical studies, and consider a genome-wide application involving colorectal cancer.

1. Introduction

In genetics, a genome-wide association study (GWAS) is an observational study of a genome-wide set of genetic markers across individuals with the intent of identifying one or more markers that are associated with a trait of interest. For example, recent GWAS have led to the identification of common genetic variants which are predictive of a subject’s predisposition towards colorectal cancer (Peters et al., 2015). Regretfully, the field of complex disease genetics has been plagued by irreproducibility with respect to marker identification and low predictive fidelity; for further discussion see Zeggini and Ioannidis (2009). There remains a gap between the estimated genetic component of most complex diseases and the associated genetic variants discovered so far (Manolio et al., 2009). This “missing heritibility” problem cannot be completely solved by association scans on increasing sample sizes. Methods are needed that acknowledge the inherent complexity of both the genome and these diseases. While new approaches have emerged that attempt to aggregate results based on linkage disequilibrium patterns (Bulik-Sullivan et al., 2015) or that use biological knowledge to focus on relevant regions of the genome (Baurley and Conti, 2013), comprehensive genome-wide analytic approaches are still lacking.

In general, GWAS focuses on measuring and analyzing single-nucleotide polymorphisms (SNPs) across the genome. Historically, researchers have primarily focused on marginal screening methods (i.e., one at a time analyses of the available SNPs) for the purpose of detecting associations, while appropriately adjusting for false discoveries. This approach tends to be conservative and has the propensity to miss important joint behaviour. As a solution, the current research paradigm is shifting to SNP assessment via joint models. This new direction also poses significant challenges; i.e., given the advances in sequencing and genotyping technologies, modern GWAS considers millions of SNPs. From a statistical point of view, this is the classic large p small n problem (i.e., p >> n) encountered in high-dimensional regression. In general, high-dimensional regression techniques leverage the bias-variance trade-off by imposing penalties on the regression coefficients. For a continuous outcome, through specifying an L₁ penalty, Tibshirani (1996) proposed the LASSO which is able to identify a sparse estimator of the regression coefficients, thus completing model fitting and variable selection simultaneously. Following the seminal work of Tibshirani (1996), many other proposals have been developed under other penalization schemes; e.g., see Fan and Li (2001), Zou and Hastie (2005), Zou (2006), and Candes and Tao (2007). Extensions of penalized regression methods have been made to generalized linear models; e.g., Wu et al. (2009) and Friedman et al. (2010) incorporated the LASSO and elastic net penalties, respectively, when fitting the logistic regression model. Interestingly, many of these frequentist based techniques have Bayesian analogs which make use of shrinkage priors; e.g., the Bayesian LASSO (Park and Casella, 2008). In many instances, analytic and computational tractability are aided by the fact that shrinkage priors can be represented as scale mixtures of normals; e.g., see Park and Casella (2008) and Armagan et al. (2013). Though theoretically justified in the case of high-dimensional data, the aforementioned techniques are known to struggle and provide inaccurate results when p is large relative to n, which is unarguably the norm in GWAS. To pointedly address this feature, Yazdani and Dunson (2015) proposed a hybrid Bayesian approach for quantitative traits which combined the marginal scan and joint modeling paradigms.

Motivated by the work of Yazdani and Dunson (2015) and a recent colorectal cancer study, herein we develop a two-phase Bayesian methodology that can be used to identify significant polygenic effects in genome-wide association studies of binary traits. Like Yazdani and Dunson (2015), we advocate for the use of a preliminary scan, via Bayes factors, of the available SNPs in an effort to form a reduced set of promising markers. These markers are then analyzed by a joint model along with other confounding variables. The generalized double Pareto shrinkage prior of Armagan et al. (2013) is specified for the regression coefficients in the joint model and a sparse estimator of these quantities is obtained via a novel maximum a posteriori (MAP) estimation technique. For finding the MAP estimator, an expectation-maximization (EM) algorithm is derived by introducing carefully constructed latent variables. In particular, through the introduction of these latent variables both the data model and shrinkage prior are decomposed into a convenient hierarchical form. The proposed methodology is thoroughly vetted through an extensive numerical study, and is further illustrated through an analysis of a genome-wide association study of colorectal cancer in Indonesia.

The remainder of this article is organized as follows. Section 2 provides the details of the proposed methodology to include the data augmentation steps and EM algorithm development. Section 3 provides the results of an extensive numerical study conducted to assess the performance of the proposed methodology. Section 4 presents the results of the analysis of the motivating colorectal cancer data. Section 5 concludes with a summary discussion.

2. Methodology

In the context of the motivating example, we wish to relate a binary trait (e.g., presence/absence of colorectal cancer) to genetic markers. Let Y_i encode the binary trait for the ith individual, for i = 1, ..., n, with the event Y_i = 1 denoting that the individual is a case and Y_i = 0 otherwise. Similarly, we let E_iq, for $q=1,\dots ,q_1$, denote the qth confounding variable (e.g., age, BMI, smoking status, etc.) measured on the ith individual. For notational ease, we aggregate these variables as ${\mathbf{E}}_i={\left(E_{i1},\dots ,E_{i{q}_1}\right)}^{\prime }$. Finally, let $S_{iq}^{\ast }$, for $q=1,\dots ,q_2^{\ast }$, denote the qth SNP genotype of the ith individual. In order to evaluate both the confounding variables and genetic markers, we propose the following two-phase methodology.

2.1. Phase 1

In Phase 1 of our approach, the genetic markers undergo a preliminary scan to identify a promising set of possible significant genotypes, while controlling for confounding variables. More specifically, in this phase, we seek to rank order each of the SNPs via Bayes factors. Briefly, a Bayes factor is a summary of the evidence provided by the data for a model relative to another model. This evidence is computed as

$$B_{q0}=\underset{{\mathbf{\Theta }}_q}{\int }{p}_q\left(\mathbf{Y}\mid {\mathit{\theta }}_q\right){\pi }_q\left({\mathit{\theta }}_q\right)d{\mathit{\theta }}_q{\left\{\underset{{\mathbf{\Theta }}_0}{\int }{p}_0\left(\mathbf{Y}\mid {\mathit{\theta }}_0\right){\pi }_0\left({\mathit{\theta }}_0\right)d{\mathit{\theta }}_0\right\}}^{-1},\text{for}q=1,\dots ,q_2^{\ast },$$

where p₀ and p_q are binary data models (e.g., logisitic or probit regression models) for the observed data $\mathbf{Y}={\left(Y_1,\dots ,Y_n\right)}^{\prime }$, θ₀ and θ_q denote collections of regression coefficients, and π₀ and π_q are prior distributions. Here, the baseline model (p₀) makes use of a linear predictor consisting of only linear effects in the confounding variables, while p_q considers the same and adds a linear effect associated with $S_{iq}^{\ast }$, for $q=1,\dots ,q_2^{\ast }$. If B_q0 is large then there exists strong evidence in favor of p_q when compared to p₀; e.g., B_q0 > 20 and B_q0 > 150 offer strong and very strong evidence, respectively. In addition to comparing various models to the baseline model, one may rank order models without the need to recompute Bayes factors. For example, the event $B_{q^{\prime }0}>B_{q0}$ suggests that $p_{q^{\prime }}$ is favorable when compared to p_q, given the available data. In order to avoid prior influence, it is standard to specify non-informative or vague priors which are often improper. It is well known that Bayes factors should not be computed using improper priors (Wasserman, 2000), and thus we suggest the use of vague independent normal priors for the regression coefficients; i.e., ${\mathit{\theta }}_0\sim N\left(\mathbf{0},{\sigma }^2{\mathbf{I}}_{q_1+1}\right)$ and ${\mathit{\theta }}_q\sim N\left(\mathbf{0},{\sigma }^2{\mathbf{I}}_{q_1+2}\right)$, where I_q denotes a q × q identity matrix.

The multi-dimensional integrals depicted in the numerator and denominator of (1) are analytically intractable and therefore have to be approximated. Many techniques for approximating such integrals have been proposed; e.g., see Raftery (1996). Herein, we proceed to approximate the necessary integrals through the following Laplacian approximation:

$${\widehat{p}}_q(\mathbf{Y})=p_q\left(\mathbf{Y}\mid {\tilde{\mathit{\theta }}}_q\right){\pi }_q\left({\tilde{\mathit{\theta }}}_q\right)|\mathbf{C}{|}^{1/2}{(2\pi )}^{\dim (\tilde{\mathit{\theta }})/2}\approx \underset{{\mathbf{\Theta }}_q}{\int }{p}_q\left(\mathbf{Y}\mid {\mathit{\theta }}_q\right){\pi }_q\left({\mathit{\theta }}_q\right)d{\mathit{\theta }}_q,\text{for}q=0,\dots ,q_2^{\ast }$$ (2)

where ${\tilde{\mathit{\theta }}}_q$ is the minimizer of $h\left({\mathit{\theta }}_q\right)=-\log \left\{p_q\left(\mathbf{\text{Y}}\mid {\theta }_q\right){\pi }_q\left({\mathit{\theta }}_q\right)\right\}$, C is the inverse of the hessian of h(·) evaluated at ${\tilde{\mathit{\theta }}}_q$, and the function dim(·) provides the dimension of the vector argument. Thus, an approximation to B_q0 can be constructed as ${\widehat{B}}_{q0}={\widehat{p}}_q(\mathbf{Y})/{\widehat{p}}_0(\mathbf{Y})$. After computing this approximate Bayes factor for each of the genetic markers, Phase 1 of our methodology concludes by rank ordering the SNPs based on ${\widehat{B}}_{q0}$ and retaining the top q₂ as promising markers. Let the q₂-dimensional vector ${\mathbf{S}}_i={\left(S_{i1},\dots ,S_{i{q}_2}\right)}^{\prime }$ aggregate the SNP genotypes that were identified as promising markers. In Section 3 we discuss a pragmatic approach that can be used to choose the value of q₂.

2.2. Phase 2

In this phase, we build a joint model which relates the confounding variables and all SNPs selected in Phase 1 to the binary trait. To this end, we proceed under the following generalized linear model (GLM):

$$g^{-1}\left\{P\left(Y_i=1\mid {\beta }_0,{\mathit{\beta }}_1,{\mathit{\beta }}_2\right)\right\}={\beta }_0+{\mathbf{E}}_i^{\prime }{\mathit{\beta }}_1+{\mathbf{S}}_i^{\prime }{\mathit{\beta }}_2,$$ (3)

where g(·) is the link function. For the purposes of this work, we allow g(·) to take on two forms (i.e., logisitic and probit) and provide details of implementation under each. The regression coefficients ${\mathit{\beta }}_1={\left({\beta }_{11},\dots ,{\beta }_{1q_1}\right)}^{\prime }$ and ${\mathit{\beta }}_2={\left({\beta }_{21},\dots ,{\beta }_{2q_2}\right)}^{\prime }$ are covariate and genetic marker effects, respectively, with β₀ denoting the usual intercept. Throughout, it is assumed that the independent variables (i.e., E_i and S_i) have been standardized.

To complete the proposed Bayesian GLM and to induce sparsity into the estimation of the effects (i.e., β_lq), we impose a vague independent normal prior on β₀ and independent shrinkage priors on the other regression coefficients through the following specifications:

$$\begin{gathered} {\beta }_0\mid T_0\sim N\left(0,T_0\right), \\ {\beta }_{lq}\mid \alpha ,\eta \sim \text{GDP}(\psi =\eta /\alpha ,\alpha ),\text{for}q=1,\dots ,q_l\text{and}l=1,2, \end{gathered}$$

where $\text{GDP}(\psi ,\alpha )$ refers to the generalized double Pareto distribution outlined in Armagan et al. (2013). Under these prior choices, setting T₀ to be large provides a vague prior on β₀, while the hyper-parameters α > 0 and η > 0 govern the amount of shrinkage which is imparted on the regression coefficients. In particular, the density of the generalized double Pareto distribution becomes more peaked with lighter tails as α is increased, while larger values of η provide for less shrinkage through a flatter density. Armagan et al. (2013) suggest a default setting of $\alpha =\eta =1$, leading to a prior density similar to that of a Cauchy distribution. However, given the computationally efficient nature of our approach, one may explore multiple settings for these hyper-parameters and make use of model selection criteria (e.g., AIC, BIC, cross-validation, etc.) to choose the “optimal” configuration.

In order to avoid the computational burden of Markov chain Monte Carlo in high dimensions and to identify a sparse estimator of the regression coefficients, we develop a computationally efficient EM algorithm that can be used to compute the MAP estimator. To develop this algorithm, we introduce two different sets of latent variables which allow us to decompose both the proposed data model and shrinkage priors into a convenient hierarchical representation. In particular, a hierarchical representation of the proposed data model is formed by introducing latent random variables ω_i, for i = 1, ..., n. The specific structure of these random variables is inherently tied to the chosen link function, with the distribution of ω_i being normal or Polya gamma if one proceeds under the probit or logistic link, respectively; for further detailś see Albert and Chib (1993) and Polson et al. (2013). Under either specification, the joint density of the observed and latent data is given by

$$\pi (\mathbf{Y},\mathit{\omega }\mid \mathit{\beta })\propto \exp \left\{-\frac{1}{2}(\mathbf{h}-\mathbf{X}\mathit{\beta }{)}^{\prime }\mathbf{\Omega }(\mathbf{h}-\mathbf{X}\mathit{\beta })\right\}\prod _{i=1}^n\xi \left({\omega }_i\right),$$ (4)

where $\mathit{\omega }={\left({\omega }_1,\dots ,{\omega }_n\right)}^{\prime }$, $\mathit{\beta }={\left({\beta }_0,{\mathit{\beta }}_1^{\prime },{\mathit{\beta }}_2^{\prime }\right)}^{\prime }$, $\mathbf{\text{X}}={\left({\mathbf{\text{X}}}_1,\dots ,{\mathbf{\text{X}}}_n\right)}^{\prime }$, and ${\mathbf{X}}_i={\left(1,{\mathbf{E}}_i^{\prime },{\mathbf{S}}_i^{\prime }\right)}^{\prime }$. Under the probit link, $\mathbf{h}={\left({\omega }_1,\dots ,{\omega }_n\right)}^{\prime }$, $\mathbf{\text{Ω}}=\mathbf{\text{I}}$, and $\xi \left({\omega }_i\right)=I\left({\omega }_i\ge 0,Y_i=1\right)+I\left({\omega }_i<0,Y_i=0\right)$, where $I(\cdot )$ denotes the usual indicator function. In contrast, under the logistic link, $\mathbf{h}={\left({\kappa }_1/{\omega }_1,\dots ,{\kappa }_n/{\omega }_n\right)}^{\prime }$, ${\kappa }_i=Y_i-1/2$, $\mathbf{\text{Ω}}=\text{diag}(\mathit{\omega })$, and $\xi \left({\omega }_i\right)=f\left({\omega }_i\mid 1,0\right)\exp \left\{{\kappa }_i^2/\left(2{\omega }_i\right)\right\}$, where $f\left({\omega }_i\mid a,b\right)$ denotes the Pólya-Gamma density with parameters (a, b); see Polson et al. (2013).

Attention is now turned to constructing a hierarchical representation of the joint prior distribution. As noted by Proposition 1 in Armagan et al. (2013), the generalized double Pareto shrinkage prior can be represented as a scale mixture of normal distributions. Thus, for the regression coefficients, the following hierarchical representation provides for the same prior specifications as those given above:

$$\begin{gathered} \beta \mid \mathbf{\text{T}}\sim N(\mathbf{0},\mathbf{\text{T}}), \\ {T}_{lq}\mid {\lambda }_{lq}\sim \text{Exponential}\left({\lambda }_{lq}^2/2\right),\text{for}q=1,\dots ,q_l\text{and}l=1,2, \\ {\lambda }_{lq}\mid \alpha ,\eta \sim \text{Gamma}(\alpha ,\eta ),\text{for}q=1,\dots ,q_l\text{and}l=1,2, \end{gathered}$$

where $\mathbf{\text{T}}=\text{diag}\left(T_0,{\mathbf{\text{T}}}_1^{\prime },{\mathbf{\text{T}}}_2^{\prime }\right)$ and ${\mathbf{\text{T}}}_l={\left(T_{l1},\dots ,T_{l{q}_l}\right)}^{\prime }$. Here the rate parametrization of both the exponential and gamma distributions are utilized.

Given these hierarchical representations, our proposed EM algorithm can be derived viewing ω, T, and ${\lambda }_{lq}$, for $q=1,\dots ,q_l$ and $l=1,2$, as missing data. The E-step of our algorithm identifies the function $Q(\cdot ,\cdot )$ as the conditional expectation of the natural logarithm of the posterior distribution, given the observed data (denoted as $\mathcal{D}$) and the current set of parameter estimates (denoted as β^(d)). This yields

$$\begin{gathered} Q\left(\mathit{\beta },{\mathit{\beta }}^{(d)}\right)=-\frac{1}{2}E\left\{(\mathbf{h}-\mathbf{X}\mathit{\beta }{)}^{\prime }\mathbf{\Omega }(\mathbf{h}-\mathbf{X}\mathit{\beta })\mid \mathcal{D},{\mathit{\beta }}^{(d)}\right\} \\ -\frac{1}{2}{\beta }_0^2{T}_0^{-1}-\frac{1}{2}\sum _{l=1}^2\sum _{q=1}^{q_l}{\beta }_{lq}^{2}E\left(T_{lq}^{-1}\mid \mathcal{D},{\mathit{\beta }}^{(d)}\right)+Q_r\left({\mathit{\beta }}^{(d)}\right), \end{gathered}$$ (5)

where $Q_r\left({\mathit{\beta }}^{(d)}\right)$ is a function which is free of β. The M-step of the algorithm then updates the set of unknown parameters as the maximizer of $Q(\cdot ,\cdot )$. Given the form of (5), the maximizer obtained in the M-step of the algorithm is given by

$${\mathit{\beta }}^{(d+1)}={\left({\mathbf{X}}^{\prime }{\mathbf{\Omega }}^{(d)}\mathbf{X}+{\mathbf{D}}^{(d)}\right)}^{-1}{\mathbf{X}}^{\prime }{\mathbf{\Omega }}^{(d)}{\mathbf{h}}^{(d)}={\text{argmax}}_{\mathit{\beta }}Q\left(\mathit{\beta },{\mathit{\beta }}^{(d)}\right),$$ (6)

where ${\mathbf{\text{D}}}^{(d)}=E\left({\mathbf{\text{T}}}^{-1}\mid \mathcal{D},{\mathit{\beta }}^{(d)}\right)$ and $E\left(T_{lq}^{-1}\mid \mathcal{D},{\mathit{\beta }}^{(d)}\right)=(\alpha +1)/\left\{\left|{\beta }_{lq}^{(d)}\right|\left(\left|{\beta }_{lq}^{(d)}\right|+\eta \right)\right\}$. The form of ${\mathbf{\text{Ω}}}^{(d)}$ and ${\mathbf{h}}^{(d)}$ in (6) are link function dependent. In particular, under the probit link ${\mathbf{\text{Ω}}}^{(d)}=\mathbf{\text{I}}$ and ${\mathbf{h}}^{(d)}=E\left(\mathit{\omega }\mid \mathcal{D},{\mathit{\beta }}^{(d)}\right)$, where

$$\begin{gathered} E\left({\omega }_i\mid \mathcal{D},{\mathit{\beta }}^{(d)}\right)={\mathbf{X}}_i^{\prime }{\mathit{\beta }}^{(d)}+Y_i\varphi \left({\mathbf{X}}_i^{\prime }{\mathit{\beta }}^{(d)}\right){\left\{\text{Φ}\left({\mathbf{X}}_i^{\prime }{\mathit{\beta }}^{(d)}\right)\right\}}^{-1} \\ -\left(1-Y_i\right)\varphi \left({\mathbf{X}}_i^{\prime }{\mathit{\beta }}^{(d)}\right){\left\{1-\text{Φ}\left({\mathbf{X}}_i^{\prime }{\mathit{\beta }}^{(d)}\right)\right\}}^{-1}, \end{gathered}$$

with $\varphi (\cdot )$ and $\text{Φ}(\cdot )$ denoting the density and cumulative distribution functions of the standard normal distribution, respectively. Under the logistic link ${\mathbf{\Omega }}^{(d)}=E\left(\mathbf{\Omega }\mid \mathcal{D},{\beta }^{(d)}\right)$ and ${\mathbf{h}}^{(d)}={\left({\mathbf{\Omega }}^{(d)}\right)}^{-1}\kappa$, where $\mathit{\kappa }={\left({\kappa }_1,\dots ,{\kappa }_n\right)}^{\prime }$ and

$$E\left({\omega }_i\mid \mathcal{D},{\mathit{\beta }}^{(d)}\right)=\left\{P\left(Y_i=1\mid {\mathit{\beta }}^{(d)}\right)-0.5\right\}{\left({\mathbf{X}}_i^{\prime }{\mathit{\beta }}^{(d)}\right)}^{-1}.$$

Thus, the proposed EM algorithm continues to update ${\mathit{\beta }}^{(d)}$ via these two steps until convergence is attained; see Abbi et al. (2008) for a discussion on convergence criterion. At the point of convergence, the final update of ${\mathit{\beta }}^{(d)}$ is our sparse MAP estimator. For computational reasons, it is important to note that due to the carefully constructed hierarchical representations provided above, we are able to identify closed form expressions for all of the necessary expectations in (5) as well as to compute closed form updates of the regression coefficients in the M-step given in (6).

From a computational perspective, the proposed approach has a few key attributes which are worth outlining. First, due to the nature of the penalty arising from the GDP prior, once a regression coefficient is dropped from the model (i.e., is set to zero), it cannot return. This fact can be exploited to reduce the number of computational steps required to compute ${\mathit{\beta }}^{(d)}$, thus alleviating a computational bottle neck. Second, in scenarios where $p>>n$, with $p=1+q_1+q_2$, which are common among GWAS, the computationally expensive aspect of the proposed EM algorithm involves the inversion of a p × p dense matrix in order to compute ${\mathit{\beta }}^{(d)}$. This computational burden can be avoided by exploiting the Sherman-Morrison-Woodbury formula, which allows one to effectively compute the inversion of the p × p matrix at the same computational expense as inverting a n × n matrix. Specifically, we may compute the necessary inversion in (6) as

$${\left({{\mathbf{\text{X}}}^{\prime }\mathbf{\text{Ω}}}^{(d)}\mathbf{\text{X}}+{\mathbf{\text{D}}}^{(d)}\right)}^{-1}={\mathbf{\text{D}}}^{{(d)}^{-1}}-{\mathbf{\text{D}}}^{{(d)}^{-1}}{\mathbf{\text{X}}}^{\prime }{\left({\mathbf{\text{Ω}}}^{{(d)}^{-1}}+{\mathbf{\text{XD}}}^{{(d)}^{-1}}{\mathbf{\text{X}}}^{\prime }\right)}^{-1}{\mathbf{\text{XD}}}^{{(d)}^{-1}},$$

where the inversion of D^(d) and ${\mathbf{\text{Ω}}}^{(d)}$ are trivial since they are diagonal matrices and the other matrix inversion step on the right-hand side involves only an n × n matrix. Lastly, the proposed EM algorithm can easily, through the point of initialization, accommodate warm starts (Koh et al., 2007) when fitting models for multiple specifications of the hyper-parameters α and η.

3. Numerical studies

In order to evaluate the finite sample performance of the proposed approach, the following simulation study was conducted. Given that Bayes factors are a common tool and have been well vetted, this study focuses on assessing the performance of the MAP estimator developed in Section 2.2. The assessed characteristics include the method’s ability to 1) identify significant covariates under various signal strengths, 2) accurately estimate the effect size of significant covariates, 3) classify covariates not related to the response as such, and 4) capably handle the complex data structures that are ubiquitous in GWAS. To accomplish this, datasets were simulated to mimic our motivating application; i.e., we consider simulating data for n individuals, where n ∈ {200, 500}. For each individual, we simulate the collection of confounding variables ${\mathbf{E}}_i=\left(E_{i1},E_{i2}\right)$, where E_i1 and E_i2 are standardized draws that were sampled independently from a N(0, 1) and Bernoulli(0.5) distribution, respectively. For this study, we consider SNP vectors of various lengths for the different sample sizes; specifically, we consider q₂ ∈ {100, 200, 500}. Rather than randomly generating these variables, we make use of the SNP data from our motivating example. Proceeding in this fashion allows us to capture the complex SNP relationships that naturally exist and would be hard to simulate. To have adequate representation with respect to minor allele frequency, SNPs were first classified according to their minor allele frequency into one of two categories: low (0.20–0.35) and high (0.35–0.50). Then, at random, the q₂ SNPs used in this study were selected from the two categories, with equal representation being taken from each. Let S_i denote the vector of selected SNPs for subject i, after standardization. The individuals’ statuses were then simulated according to the following model:

$$g^{-1}\left\{P\left(Y_i=1\mid {\beta }_0,{\beta }_1,{\mathit{\beta }}_2\right)\right\}={\mathit{\beta }}_0+{\mathbf{E}}_i^{\prime }{\mathit{\beta }}_1+{\mathbf{S}}_i^{\prime }{\mathit{\beta }}_2,$$

where ${\beta }_0=-1,{\mathit{\beta }}_1=(1,1{)}^{\prime }$, ${\mathit{\beta }}_2={\left({\mathit{\beta }}^{\ast },{\mathit{\beta }}^{\ast },{\mathbf{0}}_{q_2-12}^{\prime }\right)}^{\prime }$, ${\mathit{\beta }}^{\ast }=(0.25,0.25,0.5,0.5,1.0,1.0)$, ${\mathbf{0}}_q$ is a q-dimensional vector of zeros, and g(·) is the logistic link. This data generating process was used to create 500 independent data sets.

A few comments on the design of this study are warranted. First, the SNPs S_i1 through S_i6 were selected from the low minor allele frequency category and SNPs S_i7 through S_i12 were selected from the high frequency category. This allows us to examine the ability of the proposed approach to identify small (0.25), medium (0.50), and large (1.00) effects across these different allelic frequencies. Second, this study focuses on the logistic link. Complementary studies were performed under the probit link and resulted in a practically identical conclusion and are therefore omitted for purposes of brevity.

The proposed methodology was used to analyze each of the generated data sets. In this implementation, a vague prior was placed on the intercept by specifying T₀ = 1000 and we considered different values of the penalty parameters; i.e., $\alpha \in \{0.1,0.2,\dots ,1.0\}$ and $\eta \in \{0.1,0.2,0.3\}$. These choices were made based on prior experience which showed that η should be set to a small value and that values of α ∈ (0.1, 1) perform well for binary outcomes. It is important to note that a MAP estimator is computed under each of these hyper-parameter configurations. Thus, to choose the “best” from among them we make use of the Bayesian information criterion (Neath and Cavanaugh, 2012). The computational expense associated with identifying all of the MAP estimators under the various configuration of (α, η) was minimal and scalable.

Table 1 summarizes the MAP estimators that were obtained from analyzing the 500 data sets when n = 200. This summary includes the empirical bias and standard deviation of the MAP estimators of the truly nonzero coefficients, as well as the percentage of the time that they were identified to be nonzero; i.e., the percentage of time that they were found to be related to the response. We also summarize the false discovery proportion which we define to be the proportion of coefficients which are truly zero but are identified to be nonzero by the MAP estimator. Table 2 provides an analogous summary when n = 500. From these results, one can see that the proposed approach can be used to reliably identify important explanatory variables as well as estimate their effects. In general, the observed bias is small and is on the same scale as the bias resulting from the oracle model (results not shown); i.e., the model which is provided the correct set of covariates. Moreover, the bias tends to fade as the sample size increases and more importantly does not tend to grow rapidly in the number of considered variables; i.e., in q₂. With respect to selection accuracy, for smaller sample sizes (e.g., n = 200) the proposed approach can aptly and reliably detect moderate and strong signals, across different allelic frequencies and values of q₂. The ability to detect smaller signals improves, as one would imagine, when a larger sample size is available. Further, the small false discovery proportions convey that the proposed approach is capable of identifying unrelated coefficients as being such. Finally, Tables 1 and 2 also report the average time required to compute the MAP estimator that minimizes BIC over the considered (α, η) combinations. From these results, one can see that the proposed approach is both computationally efficient and scalable. In summary, this study has demonstrated the strengths of the proposed MAP estimator with regard to identifying coefficients that are truly related to a binary response. These results also serve to indicate that Phase 1 of our methodology should be used to create a set of candidate SNPs which are on the same order as the available sample size.

Table 1.

Simulation results when n = 200 and q₂ ∈ {100, 200, 500}. The summary includes the empirical bias (Bias) and standard deviation (SD) of the MAP estimates, as well as the percent of times the significant variable remained in the model (Perc). The SNP coefficients are categorized according to their allelic frequencies (AF). The empirical false discovery proportion (FDP) for the truly unrelated variables is also included. The average times required to analyze each data set were 9.1, 12.6, and 46.9 seconds when q₂ = 100, 200, 500, respectively. This time includes the grid search over the various (α, η) settings.

		q2 = 100			q2 = 200			q2 = 500
AF	Parameter	Bias	SD	Perc	Bias	SD	Perc	Bias	SD	Perc
Non-SNP coefficients
	β0 = −1	0.00	0.28	100%	−0.05	0.31	100%	−0.16	0.36	100%
	β1, 1 = 1	−0.09	0.32	99%	0.03	0.36	99%	0.13	0.45	99%
	β1, 2 = 1	−0.06	0.32	99%	0.02	0.34	99%	0.11	0.41	99%
SNP coefficients
Low	β2, 1 = 0.25	−0.22	0.15	6	−0.24	0.09	3%	−0.25	0.02	1%
	β2, 2 = 0.25	−0.21	0.15	7	−0.23	0.11	3%	−0.24	0.14	3%
	β2, 3 = 0.5	−0.21	0.33	51%	−0.22	0.36	45%	−0.29	0.35	31%
	β2, 4 = 0.5	−0.28	0.32	37%	−0.31	0.32	30%	−0.38	0.28	18%
	β2, 5 = 1	−0.08	0.32	99%	−0.01	0.38	98%	0.04	0.43	97%
	β2, 6 = 1	−0.10	0.37	96%	−0.07	0.43	94%	−0.24	0.55	76%
High	β2, 7 = 0.25	−0.16	0.23	16%	−0.19	0.18	11%	−0.20	0.20	8%
	β2, 8 = 0.25	−0.13	0.25	22%	−0.17	0.22	13%	−0.19	0.20	10%
	β2, 9 = 0.5	−0.27	0.32	38%	−0.36	0.28	23%	−0.46	0.17	8%
	β2, 10 = 0.5	−0.17	0.35	54%	−0.15	0.38	54%	−0.19	0.40	43%
	β2, 11 = 1	−0.21	0.39	92%	−0.44	0.53	60%	−0.53	0.54	51%
	β2, 12 = 1	−0.18	0.41	90%	−0.25	0.48	80%	−0.39	0.57	61%
		FDP: 3.6%			FDP: 3.2%			FDP: 1.8%

Table 2.

Simulation results when n = 500 and q₂ ∈ {100, 200, 500}. The summary includes the empirical bias (Bias) and standard deviation (SD) of the MAP estimates, as well as the percent of times the significant variable remained in the model (Perc). The SNP coefficients are categorized according to their allelic frequencies (AF). The empirical false discovery proportion (FDP) for the truly unrelated variables is also included. The average times required to analyze each data set were 30.2, 36.1, and 85.8 seconds when q₂ = 100, 200, 500, respectively. This time includes the grid search over the various (α, η) settings.

		q2 = 100			q2 = 200			q2 = 500
AF	Parameter	Bias	SD	Perc	Bias	SD	Perc	Bias	SD	Perc
Non-SNP coefficients
	β0 = −1	0.05	0.15	100%	0.04	0.16	100%	0.01	0.15	100%
	β1, 1 = 1	−0.07	0.15	100%	−0.07	0.16	100%	−0.04	0.17	100%
	β1, 2 = 1	−0.07	0.15	100%	−0.06	0.15	100%	−0.03	0.17	100%
SNP coefficients
Low	β2, 1 = 0.25	−0.19	0.14	19	−0.22	0.10	9%	−0.24	0.05	2%
	β2, 2 = 0.25	−0.20	0.13	15	−0.21	0.12	11%	−0.23	0.08	4%
	β2, 3 = 0.5	−0.09	0.20	91%	−0.12	0.23	83%	−0.18	0.24	70%
	β2, 4 = 0.5	−0.14	0.22	80%	−0.17	0.24	73%	−0.26	0.25	53%
	β2, 5 = 1	−0.10	0.17	100%	−0.09	0.19	100%	−0.09	0.19	100%
	β2, 6 = 1	−0.08	0.16	100%	−0.07	0.18	100%	−0.10	0.19	99%
High	β2, 7 = 0.25	−0.17	0.15	28%	−0.20	0.13	17%	−0.22	0.10	11%
	β2, 8 = 0.25	−0.10	0.18	45%	−0.13	0.18	32%	−0.17	0.17	22%
	β2, 9 = 0.5	−0.14	0.21	82%	−0.24	0.23	61%	−0.37	0.21	32%
	β2, 10 = 0.5	−0.09	0.20	90%	−0.09	0.20	89%	−0.09	0.23	84%
	β2, 11 = 1	−0.14	0.17	100%	−0.26	0.34	86%	−0.24	0.28	93%
	β2, 12 = 1	−0.12	0.19	100%	−0.16	0.18	99%	−0.17	0.24	98%
		FDP: 2.8%			FDP: 2.4%			FDP: 1.3%

4. Colorectal cancer data

Colorectal cancer is one of the most common forms of cancer and is a leading cause of cancer related deaths (Jemal et al., 2011). Genetic association studies have previously identified markers associated with colorectal cancer risk, but have predominantly focused on subjects from European ancestory. Given the potential differences between South East Asia and European ancestry, a recent study conducted in South Sulawesi, Indonesia was aimed at investigating the genetic and environmental risk factors of colorectal cancer within this South East Asian population. To aid in the discovery of genetic and environmental risk factors, the analysis presented herein focuses on data arising from this seminal study.

The data available for this analysis consists of 173 observations which were taken on 84 cases and 89 controls. These participants were recruited from throughout Makassar, Indonesia between the years of 2014 and 2016. Environmental risk factor information was collected via voluntary questionnaires and medical records. This information includes, but is not limited to, demographics, family history, smoking behavior, alcohol use, and dietary history. To collect genetic information, each participant provided a blood sample for genotyping. DNA was extracted from these samples at Mochtar Riady Institute for Nanotechnology Laboratory in Tangerang, Indonesia. After extraction, the DNA was sent to RUCDR Infinite Biologics for genotyping (Piscataway, NJ, USA). Genotyping was completed using the Smokescreen Genotyping Array (BioRealm LLC). Analysis of the raw data was performed using Affymetrix Power tools (APT) v-1.16 according to the Affymetrix best practices workflow. Additional quality control steps were performed using SNPolisher to identify and select best performing probe sets and high quality SNPs for analysis. After QC filtering, 495, 532 SNPs remained for analysis.

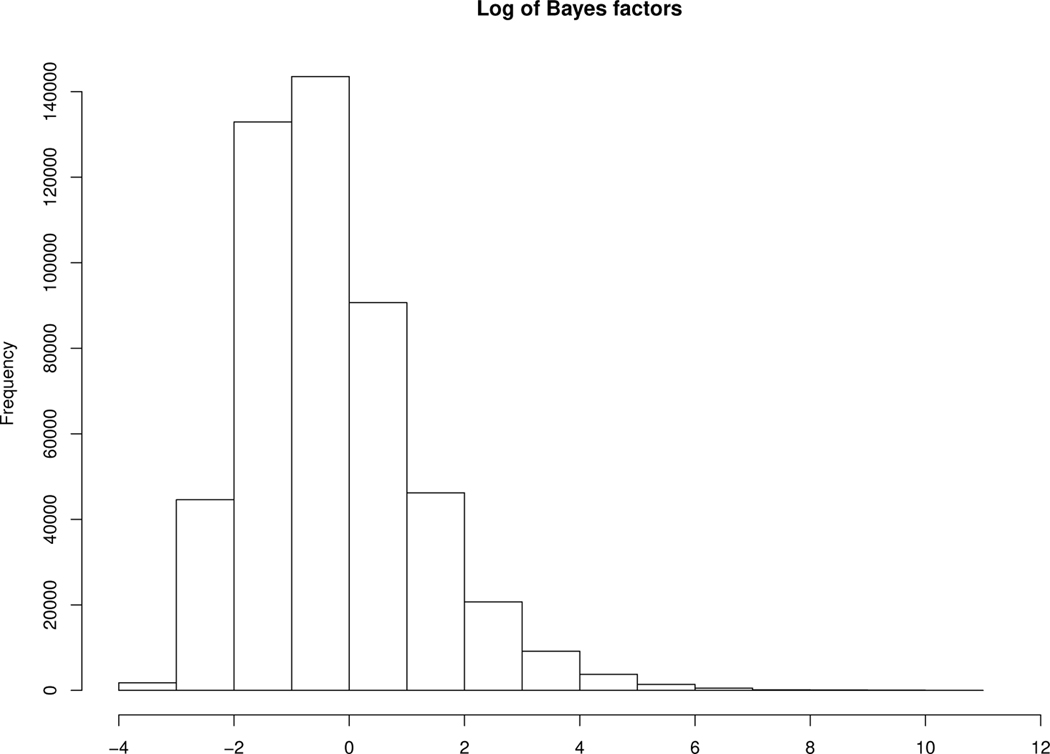
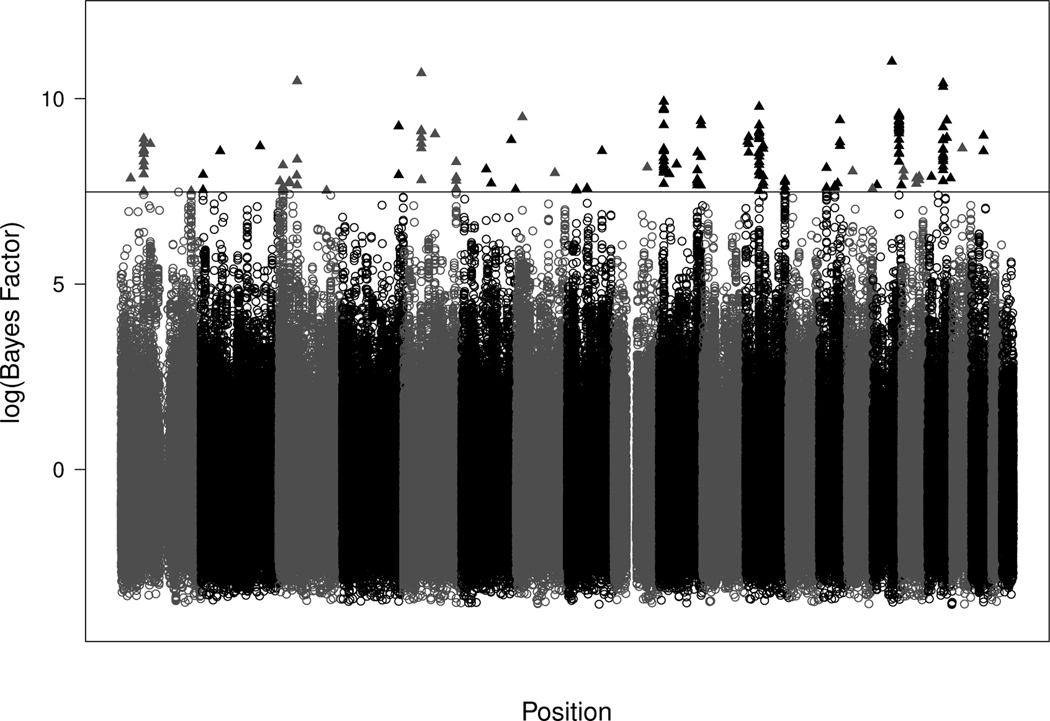
To reduce the number of candidate SNPs, Phase 1 of our methodology was used to conduct a preliminary scan of the SNP data, while accounting for environmental risk factors. In this analysis, we control for gender (1=male, 0=female), age (in years), body mass index (BMI), and smoking status (1=Yes, 0=No). In the specification of the Bayes factors, the prior variance (i.e., σ²) was set to be 100 to provide a vague, yet proper, prior on the regression coefficients. Figure 1 provides a histogram of the Bayes factors associated with the 495, 532 SNPs and Figure 2 provides a plot of the same across chromosomes. From this initial phase, and the results obtained in Section 3, we decided to focus attention on the top 200 SNPs; i.e., the SNPs with largest associated Bayes factors. This set of candidate SNPs are denoted as triangles in Figure 2. In Phase 2, we fit the following first order model to the data:

$$\text{logit}\left\{P\left(Y_i=1\mid {\beta }_0,{\mathit{\beta }}_1,{\mathit{\beta }}_2\right)\right\}={\mathit{\beta }}_0+{\mathbf{\text{E}}}_i^{\prime }{\mathit{\beta }}_1+{\mathbf{S}}_i^{\prime }{\mathit{\beta }}_2,$$

where E_i is the vector of environmental risk factors, and S_i is the vector of top SNPs identified in Phase 1 for the ith participant. Note that all variables in E_i and S_i were standardized. Here, ${\mathbf{E}}_i={\left(E_{i1},\dots ,E_{i4}\right)}^{\prime }$, where E_i1 denotes standardized gender, E_i2 denotes standardized age, E_i3 denotes standardized BMI, and E_i4 denotes standardized smoking status. The proposed EM algorithm was used to fit this model and identify the hyper-parameter dependent MAP estimator for each considered configuration of (α, η), where $\alpha \in \{0.1,0.2,\dots ,1.0\}$ and $\eta \in \{0.1,0.2,0.3\}$ with T₀ = 1000. Final model selection, as in Section 3, was guided by the Bayesian information criterion.

Figure 1.

Histogram depicting the natural logarithm of the Bayes factors which were computed for each of 495, 532 SNPs available in the CRC data.

Figure 2.

Plot of the natural logarithm of the Bayes factors which were computed for each of 495, 532 SNPs verses their position in the genome. Each shade change represents the transition to a new chromosome and the black triangles above the horizontal line depict the 200 SNPs with the largest Bayes factors.

Table 3 presents the results of this analysis. These results include the chromosome number, coordinate, reference allele, minor allele frequency, and estimated effect for all SNPs identified by the proposed MAP estimator to be the related to colorectal cancer. Also included are effect estimates for the considered environmental risk factors. First, the interpretation of the results pertaining to the environmental risk factors should be made cautiously. That is, by design, the study at enrollment frequency matched cases and controls based on age, sex, and ethnicity. Thus, the interpretation of the findings associated with the various environmental risk factors is limited but important to take account of when assessing genetic risk factors. Second, this analysis identified 10 SNPs which appear to have a relatively strong association (i.e., large effect size) with the risk of developing colorectal cancer. Four of these SNPs lie in intergenic regions; four lie in introns of ARHGEF3, PLCG2, RGMB, and CTC-340A15.2; one is a deletion in PIGN; and one is an insertion in SHISA9. ARHGEF3 has been implicated in promoting nasopharyngeal carcinoma in Asians Liu et al. (2016). RGMB has been shown to promote colorectal cancer growth Shi et al. (2015).

Table 3.

Summary of the analysis of the Colorectal cancer data. Presented results include the chromosome number (Chr) and coordinate (Coordinate) of the identified SNPs, the gene they lie on (Gene), reference allele (Ref), minor allele frequency (MAF), and estimated effect (Estimate).

Description	Chr	Coordinate	Gene	Ref	MAF	Estimate
Intercept						0.90
Gender						0.00
Age						−3.75
BMI						0.00
Smoking						1.32
S 3	3	57086348	ARHGEF3	G	0.07	2.40
S 19	16	81947156	PLCG2	C	0.08	0.85
S 27	10	129963848	intergenic	C	0.34	−1.32
S 51	5	98125016	RGMB	G	0.05	1.95
S 58	18	59822981	PIGN	TC	0.19	−1.39
S 118	5	164113078	intergenic	T	0.12	1.65
S 128	6	77328692	intergenic	A	0.04	1.22
S 154	17	45800299	intergenic	T	0.36	1.32
S 172	16	13018917	SHISA9	C	0.11	1.67
S 200	3	12816282	intergenic	A	0.03	2.13

5. Discussion

Motivated by a recent study aimed at assessing environmental and genetic risk factors associated with colorectal cancer, we have proposed a Bayesian two-phase methodology for the analysis of binary phenotypes in GWAS. Phase 1 of our methodology makes use of a preliminary scan, via Bayes factors, of the available SNPs. The primary goal of this phase is to render a reduced set of promising markers. These markers are then analyzed via a joint model along with other confounding variables in Phase 2. Through utilizing the generalized double Pareto shrinkage prior and constructing a novel EM algorithm, we are able to develop a computationally efficient approach to identifying a sparse MAP estimator. The performance of the proposed methodology has been illustrated thorough an extensive numerical study, and was used to analyze the motivating cancer data. Through this application, 10 SNPs were identified to be associated with colorecetal cancer via the proposed approach. To further disseminate this work, scripts written in R which implement all aspects of these techniques have been developed and are available in the supporting information accompanying this work, while the motivating colorectal cancer data is available either from the corresponding author upon request or from the Genetics and Epidemiology of Colorectal Cancer Consortium (GECCO).

Given statistical limitations with respect to the classic large p small n problem and recent advances in sequencing and genotyping technologies, it is natural to believe that two-phase methodologies such as the one proposed here will become standard in GWAS. For this reason, future work could be aimed at examining different marginal analysis techniques that could be used to identify a reduced set of promising SNPs. This could be accomplished by using sparse estimation techniques (e.g., LASSO, elastic net, etc.) or through adopting ideas from the recent advances in polygenic risk scores Dudbridge (2013). Though prescan techniques, such as Phase 1 of the proposed approach, are common (e.g., see Wang et al., 2018), it is important to note that they in fact limit the set of candidate variables that can be considered in the joint model; i.e., once a set of candidate SNPs have been identified additions in Phase 2 are not considered. For this reason, it could be of interest to merge the goals of Phase 1 and 2 into a more flexible formulation that would allow one to consider all available SNPs in the joint model. With that being said, an approach of this nature would likely pose many challenges from both a methodological and a computational perspective.