The relay for human longevity: country-specific contributions to the increase of the best-practice life expectancy

Abstract

This study investigates the long-term dynamics of longevity by taking into account the specific contribution of each country, and how this has changed over time, thus highlighting different timing and speeds of the evolution of life expectancy among the low-lowest mortality countries. Leveraging on quantile regression, we analyze the specific position of countries that have recorded the maximum (BPLE) and second-best life expectancy value at least once in the period 1960-2014, both at ages 0 and 65. Moving in this direction, the purpose of our contribution is to provide new perspectives on the untracked behavior that may be overshadowed by the maximum longevity levels. Our results provide a comprehensive picture of the different phases and transitions experienced by developed countries in the evolution of life expectancy that has led to a continuous increase in the BPLE. This study is a prominent practice in detecting untracked behaviors, providing imminent onsets on the maximum and sub-maximum values, thus contributing to new clues for future longevity.

Introduction

In the last decades, developed countries have seen an important mortality decline at all ages, which has been determined by different factors, such as medical progress, prevention, healthier lifestyles and better living conditions (Crimmins et al. 2010).

The decrease in mortality has continued over time at increasingly higher ages (Rau et al. 2008; Vaupel 1997) leading life expectancy at birth of developed countries to considerably increases, without evidence of a slowdown, giving thus scope to the most optimistic views about the maximum human life expectancy. Indeed, the empirical evidence of mortality improvements (Oeppen and Vaupel 2002; Tuljapurkar et al. 2000; Barbi et al. 2018), Zuo et al. (2018)) disproves pessimistic views by other studies (Fries 1980; Olshansky et al. 1990, 2001, 2002, 2005; Dong et al. 2016) speculating that there may be a ceiling on life expectancy for humans. Oeppen and Vaupel (2002) introduced the term “ best practice life expectancy” (BPLE) that is the annual world record life expectancy. They observed a linear growth of the BPLE at birth since 1840, suggesting that there is no sign of a looming limit. More in detail, the BPLE has remarkably raised at a constant rate of almost two years and a half every ten years (i.e. three months per year) in 2014, reaching a value of 86.8 years, held by Japanese women, which also brings evidence of the mortality regularities.

Oeppen and Vaupel’s findings have received great attention all over the world, opening a broad debate on the adequacy of linear extrapolation in life expectancy forecasting. Vallin and Meslé (2009) showed that the original Oeppen-Vaupel straight line can be divided into several segments, each of them characterized by a specific slope corresponding to a major advance in the health transition. They argue that the main key to predicting future life expectancy lies in anticipating the next major health improvement that will lead to an additional increase in life expectancy, rather than knowing whether the observed straight line can be extrapolated, as asserted by Oeppen and Vaupel (2002).

BPLE has taken on a central role in longevity studies, becoming also a key point in the forecasting of life expectancy at birth (Torri and Vaupel 2012; Raftery et al. 2013; Pascariu et al. 2018; Nigri et al. 2020).

As a result, demographers used to observe the boundary of mortality using mortality rates (Canudas-Romo et al. 2019). More specifically, those who are willing to speculate about the future of longevity, have started to constantly track maximum levels of life expectancy at birth (Vaupel et al. 2021) reached by the best-performing country which has changed 9 times from 1960 to 2014 (Norway in 1960, 1965-1970, 1974; Island in 1961-1964, 1975-1981, 1983; Sweden in 1971-1973; Japan in 1982 and 1984-2014). Despite recent improvements, achieved by gains made at age 65 and older, relevant cross-country heterogeneity persists. Indeed, while some Eastern European countries witnessed gains in life expectancy in the past decade (Aburto and van Raalte 2018), others experienced phases of slowdowns and stagnation with limited gains in the last decade (Mehta et al. 2020; Leon et al. 2019; Nigri et al. 2021).

This paper contributes to the literature by studying the shape of the life expectancy distribution over time by focusing on the countries that have recorded the maximum life expectancy value at least once in the period 1960-2014. We highlight the different timing and speed of the evolution of life expectancy among the low-lowest mortality countries. We also consider those countries, which are in the second position in the ranking of the maximum life expectancy. These countries are, in fact, the best candidates to reach the maximum value of life expectancy in the next years. Indeed, in the last decades, Japan has driven the BPLE distribution becoming the record holder for thirty years. But what if Japan slows down? What candidate will become the best performer? In recent years, France and Spain have shifted from the left to the right tail of the life expectancy distribution, showing that one of them might become the BPLE leader in the future. We aim to track the possible candidates analyzing the gaps between first and second-best, in order to monitor some longevity regularities, which may be overshadowed by the BPLE. Aiming at analyzing best practice and sub-maximum levels as new most likely candidates for the record, we found it proper to consider I and II-BPLE. In fact, selecting also the third-best, about 60% of the HMD would have appeared at least once, putting at risk the interpretability of the analysis.

The analysis is carried out by using the quantile regression and considering both life expectancy at birth and age 65 for the female population. Quantile regression is gaining prominence also in longevity studies (Santolino 2020), allowing monitoring both the location and the spread of the response variable. Specifically, in this paper, we use quantiles to better identify the position of each country belonging to the set of BPLE (and second BPLE), their collocation in the life expectancy distribution in a specific year, and how these countries have changed over time.

To the best of our knowledge, there are few scientific contributions studying the shape of the life expectancy distribution over time in the developed countries contextualizing the temporal dynamic of the BPLE (Liu and Li 2019; Li and Liu 2020).

This work is structured as follows. Section 2 introduces data and methods. Section 3 illustrates the results on life expectancy at birth and age 65. Section 4 provides case studies linking our findings to the demographic literature. Section 5 concludes the work.

Data and methods

Data

Life expectancy over the period 1960-2014 is taken from the Human Mortality Database (HMD 2012). The HMD contains original calculations of death rates and life tables for national populations. The input data consist of death counts from vital statistics, plus census counts, birth counts, and population estimates from various sources. A detailed description of the methodology is contained in the methods protocol section available on the HMD site. We consider the female life expectancy at birth and age 65 for each year of the study period. From the HMD database, we select the most longevous countries based on a ranking that takes life expectancy into account over a fixed time horizon (1960-2014). We define the ranking in a generic year as an integer positive number reporting the position of a country with respect to the maximum life expectancy. According to the set theory, we denote A as the set of countries that have recorded the maximum value of life expectancy, i.e. which have a ranking equal to 1 at least once in the reference period. Therefore, A contains the "BPLE countries". Then, we denote B as the set of countries that have a ranking equal to 2. Therefore, B contains the "II-BPLE countries". We analyze the behavior of the joint set $A\cup B$ over time. We denote the set $A\cup B$ as the "I-II BPLE countries".

Methodology

Suppose Y is the response variable, and X is the p-dimensional predictor. Let $F_Y(y\mid \mathbf{X}=$ $x)=P(Y\le y\mid \mathbf{X}=x)$ be the conditional cumulative distribution function (CDF) of Y given $\mathrm{X}=x.$ Then the $\tau$-th conditional quantile of Y is defined as the inverse of the CDF or mathematically:

$$\begin{array}{c}\hfill Q_{\tau }(Y\mid \mathbf{X}=x)=inf\{y:F(y)\ge \tau \}\end{array}$$

This can be extended to the general linear quantile regression model:

$$\begin{array}{c}\hfill Q_{\tau }(Y\mid \mathbf{X}=x)={\mathbf{X}}^T\mathit{\beta }(\tau ),0<\tau <1\end{array}$$

where $\mathit{\beta }(\tau )={\left({\beta }_1,(\tau ),,,\dots ,,,{\beta }_p,(\tau )\right)}^T$ is the quantile coefficient that may depend on $\tau$ and represents the marginal change in the $\tau$-th quantile due to the marginal change in x. Whereas the linear regression coefficients are solved by minimizing least squares,

$$\begin{array}{c}\hfill \widehat{\beta }=arg\underset{\beta }{min}\sum _{i=1}^n{\left(y_i,-,{\mathbf{x}}_i^T,\beta \right)}^2,\end{array}$$

the $\tau$-th regression quantile of the linear conditional quantile function, $Q_{\tau }(Y\mid \mathbf{X}=x)$, is estimated by minimizing a weighted sum of the absolute deviations for any quantile $\tau \in (0,1)$:

$$\begin{array}{c}\hfill \widehat{\beta }(\tau )=arg\underset{\beta }{min}\sum _{i=1}^n{\rho }_{\tau }\left(y_i,-,{\mathbf{x}}_i^T,\beta \right),\end{array}$$

where ${\rho }_{\tau }(u)=u(\tau -I(u<0))$ is the quantile loss function.

Model application

Overall, the country-specific life expectancy exhibits a linear growth, and it is not stationary over time: this is true for all the countries around the globe (Torri and Vaupel 2012), and the linearity is much more evident for the maximum value (Oeppen and Vaupel 2002). We found more appropriate leveraging on a linear assumption, even more, in order not to compromise the model interpretability incorporating the non-linearity through a non-parametric model. Thus, we use quantile regression to estimate the life expectancy distribution and then collocate the set of I-II BPLE countries over time. This methodology allows to analyses how the I-II BPLE changes into the life expectancy distribution, and therefore the position of each country belonging to the set of maximum and sub maximum values in a specific part of the life expectancy distribution over time.

Koenker and Bassett (1978) introduced the quantile regression that generalizes rank statistics to the regression setting and provides medians, lower and higher quantiles, allowing both the location and the spread of the response variable to be studied. Quantile regression is particularly useful when the rate of change in the conditional quantile, expressed by the regression coefficients, depends on the quantile. For a random variable Y with a probability distribution function

$$\begin{array}{c}\hfill F(y)=P(Y\le y)\end{array}$$

the $\tau$-th quantile of Y is defined as the inverse function,

$$\begin{array}{c}\hfill Q_{\tau }(Y)=inf\{y:F(y)\ge \tau \},\end{array}$$

where $0<\tau <1$ is the quantile level. For example, $Q_{0.5}$ is the median; $Q_{0.75}$ is the third quartile, or 75-th percentile. In our particular case, for a given age $x\in X=\{0,65\}$, we fit the following model for any choice of quantile $\tau$:

$$\begin{array}{c}\hfill Q_{\tau }(e_x\mid \text{Year})={\beta }_0(\tau )+{\beta }_1(\tau )\times \text{Year}\end{array}$$

The model coefficients are estimated using the quantreg package of the R statistical software program (R Core Team 2016).

Results

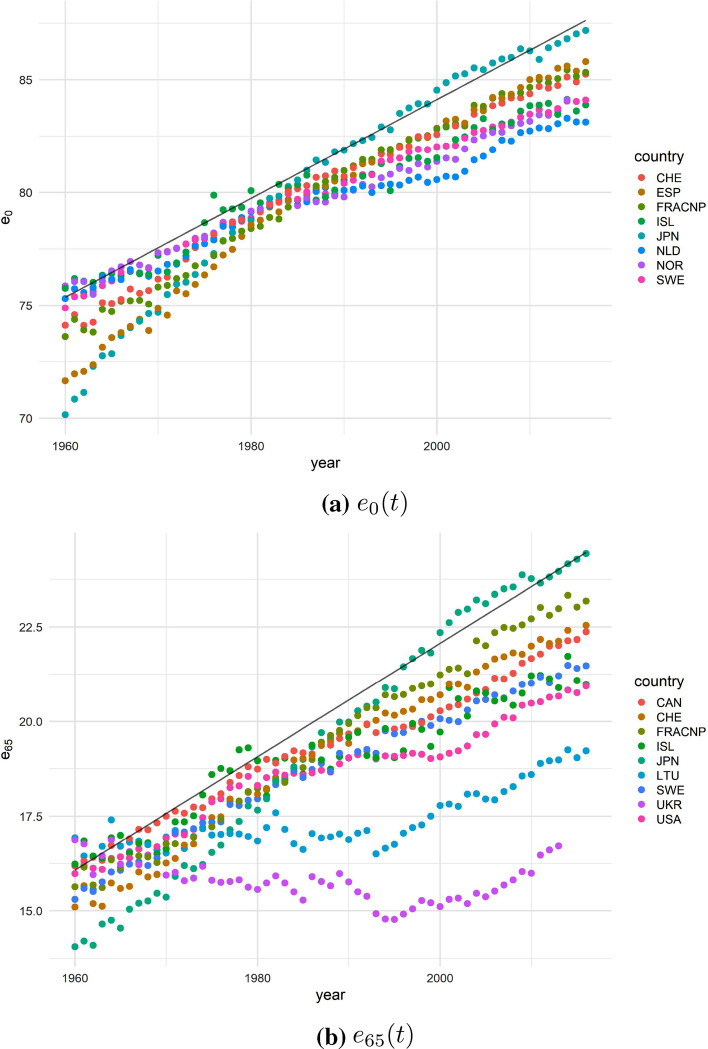
Figure 1 shows the values of $e_0(t)$ (panel a) and $e_{65}(t)$ (panel b) of the BPLE and II-BPLE countries, i.e. the I-II BPLE countries over the selected time horizon. The black line represents the linear regression of the BPLE values.

Fig. 1.

The I-II BPLE countries in 1960-2014. Women

The female record life expectancy at birth belongs to Japan since 1985. This country experienced a $e_0$ significant growth from 1960 to 1980, and in 1982 was the best candidate to become the BPLE country. As early as the late 1980s, Japan had moved away from competing countries, leaving Spain and France, albeit far behind, to compete for second place since 2000. Similar behavior is also observed for the record $e_{65}$, where Japan has been consistently in the first place since 1990. France follows, representing the most probable candidate to reach first place since 1987. However, unlike the record life expectancy at birth, the record life expectancy at age 65 is clearly non-linear, except for the most recent years from 2011.

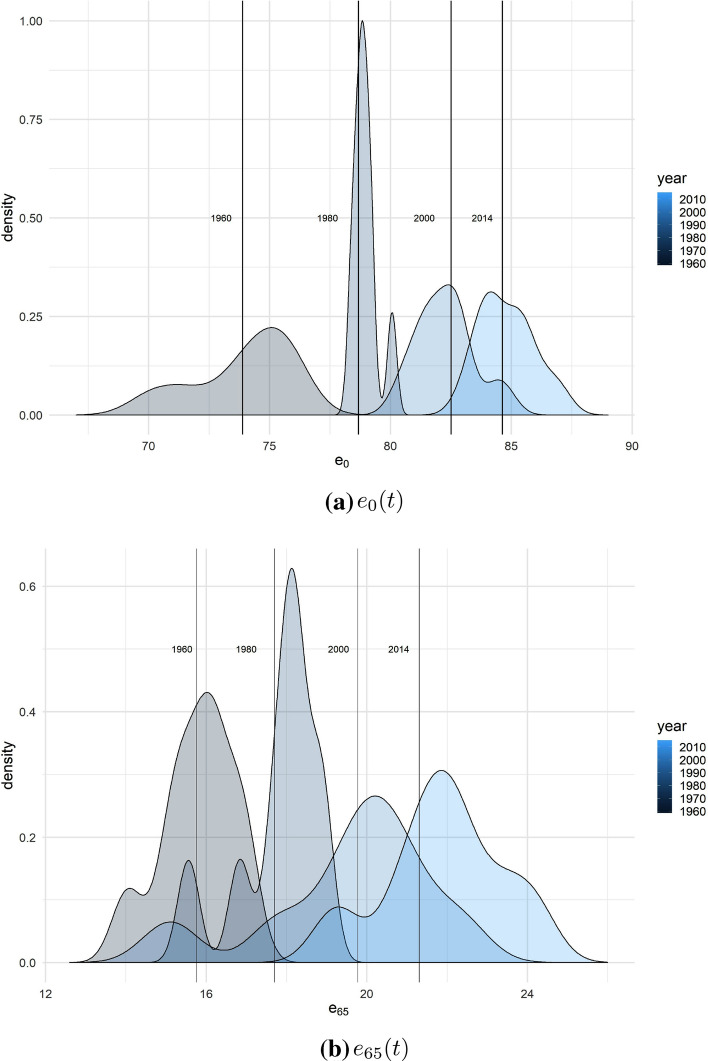
Now we carry out the estimation fitting the quantile regression for $\tau =0.01,0.2,0.5,0.8,0.99$. Thus, to clearly detect the pattern of the life expectancy distribution, we perform smoothing of the empirical histogram by a kernel density estimation.1. The density distribution estimated by the Gaussian kernel density function is shown in Fig. 2, both at birth (panel a) and age 65 (panel b). In 1960 $e_0$ shows a left-skewed distribution, while in 1980 the distribution is compressed indicating a global convergence towards the maximum and a strong variability reduction. In 2000 the distribution of $e_0$ shows a right-skewed distribution, and in 2014 it reaches a good symmetry level.

Fig. 2.

Evolution of the I-II BPLE distribution at birth (panel a) and age 65 (panel b) and central quantiles. Years 1960, 1980, 2000 and 2014. Women

After the convergence in the ’80s, when almost all developed countries share very close levels of life expectancy at birth, countries of northern Europe experience a stagnating trend, leading thus to greater variability. This heterogeneity is much more evident when looking at the life expectancy at age 65 (Fig. 1, panel b). Here, starting already during the ’70s, the divergence trend among the various countries is much more marked due to considerable stagnation in mortality improvement at adult-old ages experienced in some developed countries, especially in the US.

These patterns are fully confirmed when, at a given year, we look at the countries of I-II BPLE on the estimated quantiles, located on the life expectancy density function (Fig. 2). From 1960 the distribution of the life expectancy at birth becomes less variable until 1980, when it reaches the maximum concentration, then it shows a reversed trend towards greater variability. For life expectancy at age 65, the picture is rather similar but the distribution reaches a higher level of variability with respect to that found for life expectancy at birth in the last decades although, for very recent years, it shows a bit higher concentration. Thus, since 1980 BPLE improvements are mainly due to the shift of the central trend rather than a reduction in variability. To visualize the position of a specific country within the I-II BPLE over time, we split the distribution depicted in the previous figure for single years. Figures 3 and 4 show the I-II BPLE set at birth and age 65, respectively, for selected years, focusing thus on the position of a country on life expectancy distribution and its shifts over time.

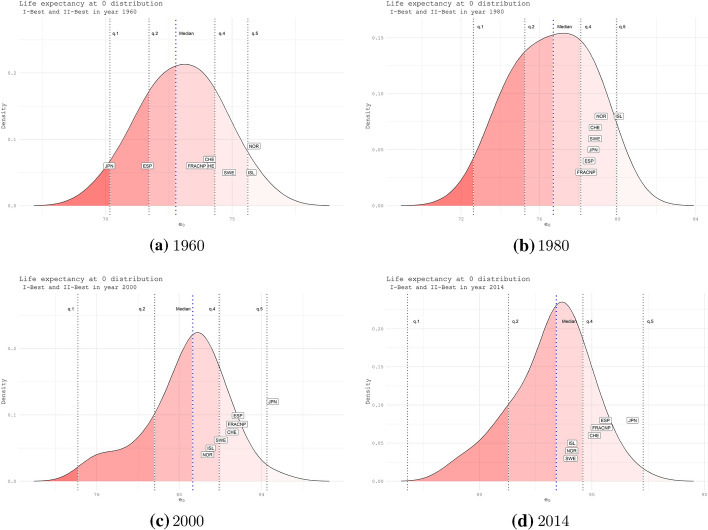
Fig. 3.

Life expectancy distribution at birth with the quantile-specific position of the I-II BPLE countries. Years 1960 (panel a), 1980 (panel b), 2000 (panel c) and 2014 (panel d). Women

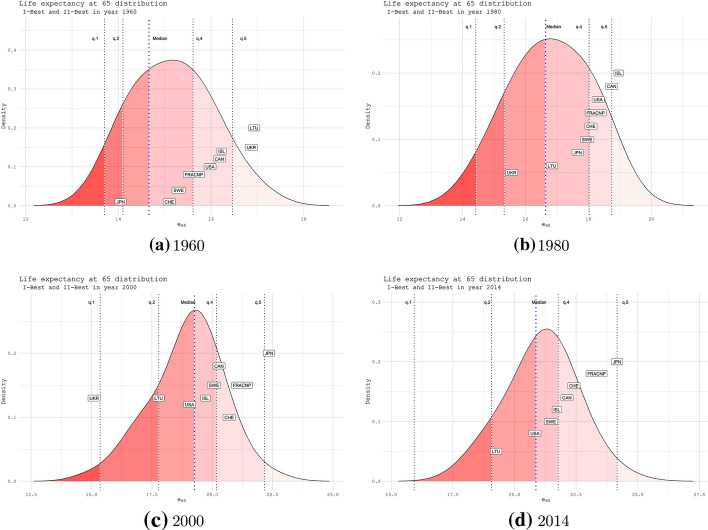
Fig. 4.

Life expectancy distribution at age 65 with the quantile-specific position of the I-II BPLE countries. Years 1960 (panel a), 1980 (panel b), 2000 (panel c) and 2014 (panel d). Women

As shown in Fig. 3, Japan in only 20 years shifts from the first quantile to a position above the median and, in other 20 years, becomes the country leader with the highest life expectancy. The countries of northern Europe positioned on the right side of the distribution of life expectancy at birth until 1980 gradually loose positions and are set today under the median. An opposite behavior is shown by France and Spain, which move over time more and more towards the right tail of the distribution, and today they are just behind Japan. It is worth highlighting the behavior of Switzerland that does not exhibit changes over distribution, remaining stable above the median.

Figure 4 highlights high levels of heterogeneity up to 2000, after that, we notice that the main spread is due to the Eastern countries diverging (UKR and LTU), which shift on the lowest quantile. Similarly to the $e_0$ case, we underline the significant rises of Japan up to the top of the life expectancy at 65 in 2014, starting behind the second quantile in 1960. Countries that experienced high levels of life expectancy ad birth show a stagnating behavior at age 65. This is the case of Sweden that slightly fluctuates above the median. It is worth noting that, although France and Switzerland were the next candidates since 1960, they never reached the leading of BPLE at age 65. In particular, since 1960 France shows regularities concerning its position among quantiles, allowing for a better depiction of sub-maximum longevity records.

Referring to the gaps between best and second-best practice, our findings portray the emerging of France and Spain, which are constantly placed among the recent II-BLE values at age 0. Their gap with respect to Japan has been going on for years, starting from the ’90s up to 2010, where trajectories show the widest gap. Our results provide evidence of a sign of approaching starting from 2014 due to Japan’s deceleration. Nevertheless, the magnitude of this gap seems still relevant. Similar evidence comes from life expectancy at age 65, where the second place is stably owned by France starting from 2000 up to 2014, showing a narrow gap from 2010 when Japan shifted down, and then stable converged again to a growing trend.

Case studies

Portraying heterogeneous longevity scenarios is not straightforward. Our proposal might play a relevant role in understanding different timing and speed of life expectancy evolution that might hinder an accurate evaluation. With this in mind, we link our findings to the commonly observed scenarios among demographic literature, namely: regularities (Japan), improvements (Spain), stagnation (USA).

Albeit longevous populations keep growing at a steady pace, the rise in longevity stalled in many countries, slowing improvements in life expectancy (Nigri et al. 2021). Low longevity populations provide peculiar behaviors showing diverging trends, with some decelerating, and others accelerating at different speeds. Overall, Levantesi et al. (2021) identify the high, medium, low, and medium-low clusters to bring evidence of the different phases and transitions experienced by HMD countries. We improve such literature by analyzing the best records.

In recent years, among longevous populations, Japan, after a long period of low longevity levels, is the one that exhibits the most relevant regularities in leading the BPLE at birth. In 20 years, it shifts very rapidly from the bottom to the higher tail of the distribution, for both life expectancy at birth and age 65. Nevertheless, Japan experienced a noticeable mortality compression process and a consequently rapid decline in lifespan disparity that levels off in recent years. This could explain the recent deceleration in gains until the stagnation at the beginning of the twenty-first century, where life expectancy diverges from the BPLE value without, however, losing its leading position. Our study provides the emerging of Spain, which increasing more rapidly than the EU average, it is constantly placed among the recent II-BPLE at birth values. Spanish life expectancy started at a very low position, collocated at the bottom of the left tail. It provides an interesting example of the results that can be achieved by a mix of relatively healthy lifestyles and an efficient health system, bringing evidence of a sign of approaching the BPLE. The USA evolution represents an additional scenario. The USA life expectancy at age 65 in the 1960s was placed on the right side of the distribution, showing high levels of longevity. Our study clearly supports the stagnation over the first decade of the new millennium, where after decades of remarkable growth, the USA life expectancy at age 65 is placed around the median value. Scholars bring evidence of a stagnating decline in cardiovascular disease mortality (Mehta et al. 2020), settling down in the middle of the world life expectancy distribution levels.

Covid-19 implications

The recent Covid-19 pandemic may well have had an impact on the scenarios described above. Several studies show that, in 2020, life expectancy at birth has increased in almost all developed countries, especially due to increased mortality after age 60 linked to the pandemic. However, in some countries, the worsening of mortality has been limited, while other countries have even recorded a gain in life expectancy (Aburto et al. 2021; Islam et al. 2021). For instance, and just to mention some of the countries considered in this study, in 2020, the life expectancy at birth has remained stable in Iceland and even increased in Norway. On the contrary, Spain, Lithuania, and the US were among those countries experiencing the highest loss in life expectancy at birth, although in the US the worsening was mainly observed in the working-age mortality. These heterogeneous patterns may determine an increase in the variability of life expectancy experienced in the study of low-mortality countries, already observed since 1980, and reverse the trend of higher concentration recently recorded in life expectancy at age 65. Moreover, Spain may have already lost its recently conquered position in the distribution of the second-best life expectancy just as the US may be relegating from its median position. However, other studies (Onozuka et al. 2021; Kawashima et al. 2021) found a much lower overall excess-mortality burden due to COVID-19 in Japan than in Europe and the US. This would confirm that the record holder is not close to being changed.

Conclusion

This study investigates the long-term dynamics of life expectancy in the developed world, taking into account the specific contribution of each country, and how this has changed over time. We have applied a quantile regression whose main advantage is to analyze both the distribution spread and the country-specific location over time. Our results provide a comprehensive picture of the different phases and transitions experienced by developed countries in the evolution of life expectancy that has led to a continuous increase in the BPLE. The evolution of BPLE, and that of every single country, suggest that longevity records might be rapidly disproved. Thereby, despite regularities that have lasted for decades, the incoming records should not be taken for granted. Albeit the constant monitoring of maximal records of human longevity, its sub-maximum levels are still neglected. We contribute to providing new evidence on the untracked behavior that may be overshadowed by the BPLE. After the convergence in the ’80s, when almost all developed countries share very close levels of life expectancy at birth, countries have peculiar behaviors showing quite diverging trends, with some countries stagnating, some decelerating, others accelerating albeit showing different speeds. This heterogeneity is much more evident when looking at the life expectancy at age 65. However, in the last period, it shows a bit higher concentration. In very recent years, BPLE improvements are mainly due to the shift of the central trend rather than a reduction in variability. The fact that, for the catching-up countries, the gap to the maximum value does not narrow, suggests that there are no signs of an imminent change of the record holder.

Our critical view regarding the concept of records can offer an opportunity for new insights to depict the evolution of longevity in the forthcoming years. We highlight that, despite the presence of records that have lasted for decades (e.g. Japan), investigating the hidden behavior of the second-best (e.g France and Spain) should be good practice. We also have expanded our discussion in light of the COVID-19 pandemic, which may increase life expectancy variability experienced in the study of low-mortality countries. Our basic finding supports the clear need for a careful analysis of the maximum and sub-maximum longevity levels that may conceal untracked regularities. In other words, the best and the second-best practice distributions should be deeply investigated for a better understanding of the upcoming and future longevity regularities. We conclude that using quantiles to collocate the entire I-II BPLE countries and their dynamics over time is a prominent practice in detecting untracked behaviors, providing imminent onsets on the maximum and sub-maximum values, thus contributing to new clues for future longevity.

Appendix

Tables 1 and 2 summarize the results of the quantile regression coefficients estimation for life expectancy at birth and age 65, respectively. We also show the values of the pseudo-$R^2$, which is a goodness-of-fit measure suggested by Koenker and Machado (1999) that compares the sum of weighted deviations for the model of interest with the same sum for a model in which only the intercept appears. It is calculated as

$$\begin{array}{c}\hfill R_1(\tau )=1-\frac{{\sum }_{y_i\ge {\widehat{y}}_i}\tau ·\left|y_i,-,{\widehat{y}}_i\right|+{\sum }_{y_i<{\widehat{y}}_i}(1-\tau )·\left|y_i,-,{\widehat{y}}_i\right|}{{\sum }_{y_i\ge \overline{y}}\tau ·\left|y_i,-,\overline{y}\right|+{\sum }_{y_i<{\overline{y}}_i}(1-\tau )·\left|y_i,-,\overline{y}\right|}\end{array}$$

where ${\widehat{y}}_i={\alpha }_{\tau }+{\beta }_{\tau }x$ is the fitted $\tau$-th quantile for observation i, and $\overline{y}={\beta }_{\tau }$ is the fitted value from the intercept-only model. The introduction of the pseudo-$R^2$ (for a given quantile) is motivated by the need for a measure similar to the ordinary $R^2$ used in the least-squares regression.

Table 1.

Quantile regression estimates for life expectancy at birth

$\tau$	Coeff.		s.e.	p.value	$pseudo-R^2$
0.1	${\beta }_0$	−224.31	10.08	<0.01	0.58
	${\beta }_1$	0.15	0.005	<0.01
0.2	${\beta }_0$	−275.90	7.81	<0.01	0.65
	${\beta }_1$	0.18	0.004	<0.01
0.5	${\beta }_0$	−313.38	4.54	<0.01	0.75
	${\beta }_1$	0.20	0.002	<0.01
0.8	${\beta }_0$	−298.86	8.16	<0.01	0.73
	${\beta }_1$	0.19	0.004	<0.01
0.9	${\beta }_0$	−288.68	4.51	<0.01	0.73
	${\beta }_1$	0.18	0.002	<0.01

Table 2.

Quantile regression estimates for life expectancy at 65

$\tau$	Coeff.		s.e.	p.value	$pseudo-R^2$
0.1	${\beta }_0$	−147.35	5.44	<0.01	0.46
	${\beta }_1$	0.08	0.002	<0.01
0.2	${\beta }_0$	−166.32	5.37	<0.01	0.52
	${\beta }_1$	0.09	0.002	<0.01
0.5	${\beta }_0$	−210.74	3.510	<0.01	0.62
	${\beta }_1$	0.12	0.001	<0.01
0.8	${\beta }_0$	−207.97	4.057	<0.01	0.60
	${\beta }_1$	0.11	0.002	<0.01
0.9	${\beta }_0$	−220.35	3.785	<0.01	0.59
	${\beta }_1$	0.12	0.002	<0.01