Abstract
Clustering cells and depicting the lineage relationship among cell subpopulations are fundamental tasks in single-cell omics studies. However, existing analytical methods face challenges in stratifying cells, tracking cellular trajectories, and identifying critical points of cell transitions. To overcome these, we proposed a novel Markov hierarchical clustering algorithm (MarkovHC), a topological clustering method that leverages the metastability of exponentially perturbed Markov chains for systematically reconstructing the cellular landscape. Briefly, MarkovHC starts with local connectivity and density derived from the input and outputs a hierarchical structure for the data. We firstly benchmarked MarkovHC on five simulated datasets and ten public single-cell datasets with known labels. Then, we used MarkovHC to investigate the multi-level architectures and transition processes during human embryo preimplantation development and gastric cancer procession. MarkovHC found heterogeneous cell states and sub-cell types in lineage-specific progenitor cells and revealed the most possible transition paths and critical points in the cellular processes. These results demonstrated MarkovHC’s effectiveness in facilitating the stratification of cells, identification of cell populations, and characterization of cellular trajectories and critical points.
INTRODUCTION
High-throughput single-cell omics technologies, such as single-cell RNA sequencing (scRNA-Seq), single-cell ATAC sequencing (scATAC-Seq), and mass cytometry, provide a tremendous amount of data resource that can be used in studying functional cell subpopulations and their lineage relationships. Currently, cell clustering, cellular trajectory reconstruction, and critical point detection are typically done through separate analyses. Modern clustering algorithms include Seurat (1), SC3 (2), SIMLR (3), etc. (4–8) Classical ones include K-Means (9), hierarchical clustering (10), density-based methods (11–13) spectral method (14), and model-based method (15). After clustering, cellular trajectories analysis is performed to study relationships among cell populations. These trajectories correspond to biological processes such as lineage development and cell differentiation. Among existing trajectory reconstruction tools (16–22), monocle (16–18) is very popular. After this, an important downstream analysis is to detect critical or branching points on the cellular trajectory. Within the tipping-point theory (23,24), the transitions among cellular clusters occur when small perturbations at a cellular critical point result in moving from one stable cluster to another. SGE (25) and scRCMF (26) are two useful tools for this task. These separate tools may perform reasonably well in their respective tasks, but we found it inconvenient to combine these independent tools in a joint analysis.
An ideal approach to performing these three analyses jointly could allow users to explore cell subpopulations and their lineage relationships more efficiently and more effectively with customized resolutions, this motivated us to develop MarkovHC. As shown in Figure 1A, MarkovHC can stratify common cell populations and their sub-populations by a hierarchy, and simultaneously detect trajectories and critical points among the cell populations on each resolution. The resolution of cell stratification unduly influences cell population identification in single-cell data analyses. For example, a resolution separating human ES cells from neuronal progenitor cells may not readily subdivide sub-types in neuronal progenitor cells. In the human cell atlas (27), cell lineage means the developmental relationship of cells; cell type implies a notion of homeostatic persistence; cell state refers to more inducible or transient properties. However, the boundaries among these concepts at the gene transcriptional level can be fuzzy, partly due to the limit of our knowledge and the understanding of cellular dynamics. A bottom-up cellular hierarchy is intrinsic in single-cell omics data (28). Recent works (4–8) have shown that hierarchies of cell populations can be used to effectively interrogate the echelons of cells. The primary aim of our algorithm is a hierarchical and interpretable clustering for systematic and multiscale single-cell omics data analysis. Reconstructing differentiation paths and detecting critical points can also be influenced by the clustering resolution. For instance, to detect the lineage path and critical points from the 8-cell embryo stage to the inner cell mass stage, an appropriate clustering resolution should be chosen to discriminate them. To this end, MarkovHC is designed to build a cellular hierarchy and solve the two related problems on each resolution simultaneously.
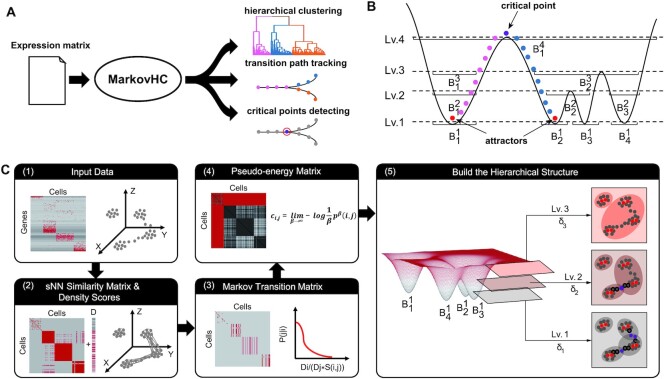
Figure 1.
Overview of MarkovHC. (A) MarkovHC simultaneously performs hierarchical clustering, transition path tracking, and critical points detecting. (B) The intuitive idea behind MarkovHC. (C) The workflow of MarkovHC: (1) The original input data is the matrix of genes by cells. (2) We calculate sNN (shared Nearest Neighbours) among cells to get the cell by cell similarity matrix. Then we construct a cellular network using the similarity matrix and calculate each cell's degree (D scores) in the network. (3) The Markov transition matrix is calculated using the similarity matrix and D scores. (4) The pseudo-energy matrix is calculated based on the Markov transition matrix. (5) The hierarchical structure is constructed based on attractors, basins, and critical points on each level.
We demonstrate the effectiveness of MarkovHC through several benchmark analyses. Five simulated datasets and ten publicly available datasets including scRNA-Seq, scATAC-Seq, and mass cytometry datasets were used for comparative tests. MarkovHC performed equal to or better than the state-of-the-art methods in terms of clustering accuracy when compared to known labels. Additionally, MarkovHC correctly stratified mouse lineage-specific progenitor cells and was able to reconstruct the path in ‘continuum’ data and detect critical points between stages. We further used MarkovHC to explore cell differentiation in human preimplantation embryo development and disease progression in gastric cancer. MarkovHC reconstructed the correct lineage tree from the 8-cell stage to sub-populations in trophectoderm and inner cell mass. MarkovHC also revealed two potential ‘hidden’ trajectories from mesenchymal stem cells to early gastric cancer cells.
MATERIAL AND METHODS
Overview
The basic idea behind MarkovHC is intuitive. Waddington's epigenetic landscape (29,30) is a classical and metaphysical concept. For high-dimensional single-cell omics data that can be embedded in low-dimensional manifolds (31), it is feasible to explore the cellular landscape by utilizing these data. In Figure 1B, four basins correspond to four cell populations on the cellular landscape. Pouring water into this landscape, these basins will merge gradually as the water level increases from level1 (Lv.1) to level4 (Lv.4). The basins on these four levels form a four-level hierarchy which is consistent with the topology of the landscape deriving based on the geodesic distance. On each level (resolution), the bottom of the basin (cell cluster) is the attractor (cluster core), the water-flowing path among basins is the most possible transition path (cellular trajectory), and the tipping (critical) point is the critical point on the cellular trajectory. Moving cells across different basins will cost energy which we call pseudo-energy in this work. Further, an explanation of the basic idea from the perspective of the dynamics and intuitive illustration of concepts including basins, attractors, transition paths, and critical points are available in Supplementary Text S1 and Supplementary Figure S1.
Technically, we employed a Markov chain with an adjustable coarse-graining scale (‘temperature’) parameter to model the hypothetical random walk of a cell over possible gene expression states. The transition probability matrix is defined using similarity and density. Similarity characterizes the degree of flow conductance among cells and density measures the degree of cell concentration. As shown in Figure 1C, MarkovHC algorithm consists of five steps which are elaborated in the following section.
Model
The input data. A gene expression or other molecular quantities data matrix (A = {agc: g = 1,2,…,G; c = 1,2,…,C} is taken as a generic input (Figure 1C). We can view each distinct cell as a unique state in the G-dimensional ‘expression’ space.
-
Shared nearest neighbours and density scores. The similarity between two states can be calculated using the cells shared between nearest neighbour states (sNN and Jaccard index (32)), and the density can be defined as the node degree.
In a high-dimensional space, sNN can explore the natural geodesic distance on the underlying manifolds and has been proved to be robust in recovering cell subpopulations and reconstructing trajectories (33,34). We define sNN similarity si,j between node i and node j as
where KNNi is the K nearest neighbours of node i.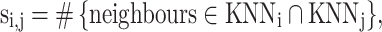
(1) For the robustness of our algorithm, the degree of each node (density score) in the sNN network is used to measure the cell aggregation density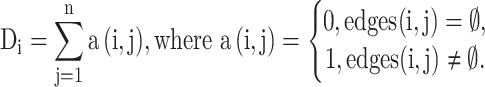
(2) The density scores of the nodes are used together with the similarity matrix to define the basic Markov transition probability.
-
Initial Markov transition matrix. Intuitively, the basic idea of the transition probability is that the larger the similarity among nodes, the larger the probability of transition. Besides, nodes with high-density transit to nodes with low-density with low probabilities, vice versa.
The transition probability from node i to node j is defined as
We denote the Markov transition matrix by P1.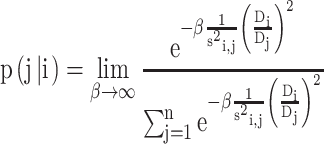
(3) -
Pseudo-energy matrix. Based on the metastability theory developed by one of us (35), the pseudo-energy matrix is all we need to build the hierarchical structure. The pseudo-energy consumed by the direct transition from node i to node j is defined as
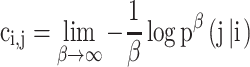
(4) This formula transforms the transition probability matrix P1 to the pseudo-energy matrix C1 representing the pseudo-energy cost. We can calculate the multi-step pseudo-energy cost between nodes by calculating the length of the shortest path, which is equal to geodesics on the surface of this ‘energy landscape’ (36) using the Dijkstra algorithm (37). If node i cannot transit to node j, the corresponding entry in matrix C1 is set to be infinite.
Build the hierarchical structure. We term basins as clusters and attractors as highest-density cores of these clusters. Attractors are steady states in multi-stable systems and basins consist of attractors and their subsidiary points. These two notions have been widely used in previous works (38) modelling the nonlinear dynamics of organisms and biological phenomena as dynamics systems.
The hierarchical structure is built in an iterative manner. As shown in step 5 of Figure 1C, for any given pseudo-energy threshold δ > 0, nodes with ‘distances’ (i.e. the asymmetric amount of pseudo-energy cost ci,j in step 4) smaller than δ are partitioned into one basin. From Lv.1 to Lv.3, the basin merges as δ increases from δ1 to δ3, and thus forms a hierarchical structure. With a given δ, points in the core of each basin are attractors (red); points connecting attractors are transition paths (black border); tipping points on transition paths are critical points (purple). A more detailed description of this step is available in Supplementary Text S1. For easy level selection, we also provided an algorithm reconciling four indexes to automatically choose levels with probable and interpretable clusters from the hierarchy in Supplementary Text S2. In addition, we put the technical details of MarkovHC in Supplementary Text S3 and the mathematical details of the metastability of exponentially perturbed Markov chains in Supplementary Text S4.
RESULTS
MarkovHC stratifies cells in agreement with known identities
To assess the performance of MarkovHC in stratification, we used it to stratify five simulation datasets and two scRNA-Seq datasets with known identities. For the five simulation datasets, four of these are 2 or 3-dimensional datasets (Figure 2A, B and Supplementary Figure S2) and the remaining one is a 1000 cells × 5000 genes dataset generated by splatter (39) (Figure 2C). MarkovHC was able to cluster hetero-density basins (Figure 2A), non-convex (the blue basin in Figure 2A and helixes in Supplementary Figure S2M), and continuum basins (Figure 2C), which correspond to hetero-density cell populations, complex cluster shapes, and differentiation states or lineages in single-cell omics data. Meanwhile, the hierarchy in Figure 2B is consistent with the distance among the basins in Figure 2A. Figure 2C shows the successfully detected trajectory and critical points. Supplementary Figure S2N and O show the differentially expressed genes (DEGs) along this trajectory.
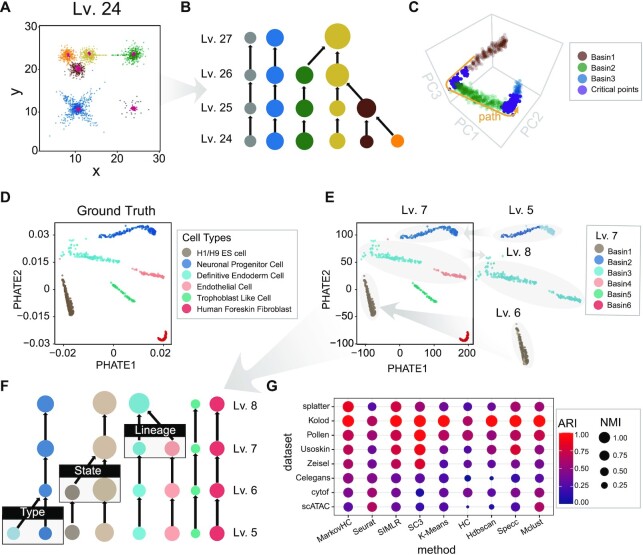
Figure 2.
MarkovHC stratifies and clusters cells in agreement with known identities. (A) These 2-dimensional basins and attractors (red) found by MarkovHC are consistent with the topology. (B) The hierarchy from Lv.24 to Lv.27 of basins in (A). The sizes of basins represent the number of samples and the colors indicate different basins. (C) These 1000 cells × 5000 genes data were projected into 3-dimensional space by principal component analysis. Three basins were clustered (brown, green, and blue; the purple points are critical points; the yellow arrow shows the path from basin1 to basin 3). (D) scRNA-Seq data (40) of 1018 human ES cell-derived lineage-specific progenitors were projected into 2-dimensional space by phateR. (E) Basins from Lv.5 to Lv.8 reveal known cell types and sub-basins in the neuronal progenitor cells and H1/H9 ES cells. (F) From the bottom to the top, levels of the hierarchical structure correspond to cell types, cell states, and cell lineages. (G) ARI (Adjusted Rand Index) and NMI (Normalized Mutual Information) show MarkovHC performed equal to or better than these methods in clustering.
For the two scRNA-Seq datasets, we used MarkovHC to interrogate the echelons of cells. From the bottom to the top, cell types, cell states, and cell lineages were presented on the cellular hierarchy. Chu et.al. (40) sorted and sequenced 1018 cells of six cell types including undifferentiated H1/H9 human ES cells, neuronal progenitor cells, definitive endoderm cells, endothelial cells, trophoblast-like cells, and human foreskin fibroblasts (Figure 2D). This dataset can be considered as a ‘gold-standard’ for stratification. Lv.7 was automatically chosen from the hierarchy (Figure 2F). There are six basins (Figure 2E) that perfectly match the six known cell types in Figure 2D. The H1/H9 ES basin and the neuronal progenitor basin separate into two basins on Lv.6 and Lv.5 respectively (Figure 2E, F). The patterns of top 50 DEGs (Supplementary Figure S3A, left; Supplementary Table S1) and 34 lineage-specific markers from Chu's paper (40) (Supplementary Figure S3A, right) suggested the cells of each Lv.5-basin were homogeneous. In H1/H9 ES cells, the up-regulated genes of the dark brown basin (Figure 2F) were enriched in cell division and cell cycle-related terms (Supplementary Figure S3B), which suggested these cells were in a more active division stage. In neuronal progenitor cells, the up-regulated genes of the light blue basin (Figure 2F) were enriched in cerebral cortex development-related terms (Supplementary Figure S3C), while those of the dark blue basin (Figure 2F) were enriched in forebrain development and synapse organization-related terms (Supplementary Figure S3D), which suggested that two sub-cell types might be found in these neuronal progenitor cells. The definitive endoderm cell and endothelial cell were two lineages that were merged on Lv.8.
The classification and hierarchical structures of human peripheral blood mononuclear cells (PBMCs) have been well studied previously (41–43). The echelon of PBMCs also can be considered as a ‘gold-standard’ for cellular stratification. We used MarkovHC to stratify a scRNA-Seq dataset of 33,000 PBMCs in Supplementary Figure S4A and Supplementary Text S5. To automatically identify cell population transition on the hierarchy with biological meaning, we provided a strategy, BHI selection, based on the biological homogeneity index (the details are available in Supplementary Text S6). Basins correspond to B cells, T cells, NK cells, megakaryocyte, monocyte, pDC, and their sub-cell populations were identified by MarkovHC. Thus, these results demonstrate that MarkovHC is able to automatically stratify common cell populations and their sub-populations simultaneously.
Benchmark MarkovHC against current methods for clustering
To assess the performance of MarkovHC in clustering, we benchmarked it against eight existing methods for clustering (Figure 2G): Seurat (1), SIMLR (3), SC3 (2), K-Means (9), hierarchical clustering with average linkage (HC) (10), Hdbscan (13), spectral clustering (Specc) (14) and model-based clustering (Mclust) (15). We used one simulation dataset (splatter) and seven previously analysed single-cell datasets including five scRNA-Seq datasets (Kolod (44), Pollen (45), Usoskin (46), Zeisel (8), and Celegans (47)), one mass cytometry dataset (cytof (48)) and one scATAC-Seq dataset (scATAC; detailed analyses of this dataset are available in Supplementary FigureS4 and Supplementary Text S7) from a variety of biological systems. For each of these datasets, cell labels have been well identified. In order to measure the agreement between known identities and clustering labels, we used adjusted rand index (ARI) (49) and normalized mutual information (NMI) (50) as test statistics.
Cells were coloured by the cluster labels from the original study and each clustering method in Supplementary FigureS5. Splatter is a ‘continuum’ dataset. Celegans have been considered ‘gold-standard’ to test lineage clustering algorithms as Packer et al. (47) carefully annotated these cells and lineages. In tissue development and cell differentiation, the single-cell data are in a ‘continuum’, which makes it harder to cluster. As MarkovHC depends on topological connectivity (51,52) and local density, it outperformed the other methods in clustering these two datasets (‘splatter’ and ‘Celegans’ in Figure 2G and Supplementary Figure S5). MarkovHC performed equal to or better than those methods in clustering scRNA-Seq datasets (Kolod (44), Pollen (45), Usoskin (46), Zeisel (8), and Celegans (47) in Figure 2G). Since MarkovHC is free of data distribution assumption, it can be applied to other omics data such as mass cytometry data and scATAC-Seq data, too. MarkovHC, Seurat, and Mclust performed better than the rest in clustering the cytof (48) and scATAC datasets. In Supplementary Text S7, we applied MarkovHC on two scATAC-Seq datasets with matching scRNA-Seq datasets. The results showed its good scalability in clustering scATAC-Seq data. We also noticed that using scRNA-Seq and scATAC-Seq datasets together could improve clustering accuracy and identify more and better sub-cell types. We also theoretically compared MarkovHC with eighteen popular clustering methods (1–7,10–14,53–62), topological data analysis (51), and four representative trajectory construction methods (16–18,20–22) in Supplementary Text S8 and Supplementary Table S2.
To sum up, overall, MarkovHC, Seurat, SIMLR, and SC3 exhibited superior performance in clustering against the others. As MarkovHC utilizes connectivity and density derived from data, it outperformed all other algorithms in clustering ‘continuum’ datasets (‘splatter’ and ‘Celegans’ in Figure 2G and Supplementary Figure S5). Besides, as MarkovHC is free of data distribution assumption, it can be used to cluster other omics data as long as the ‘similarity’ between cells can be reliably calculated using the data.
MarkovHC revealed transition paths and critical points in human preimplantation embryo development
To reveal transition paths among lineage-related cell types and detect critical points in human preimplantation embryo development, we applied MarkovHC to analyse the scRNA-Seq dataset (63) of 1529 single-cells collected from 88 human preimplantation embryos at seven stages (Figure 3A). Petropoulos et al. (63) identified eight groups in these cells, including pre-lineages, trophectoderm (TE), inner cell mass (ICM), epiblast (EPI), primitive endoderm (PE), E5mid, mural, and polar in these data.
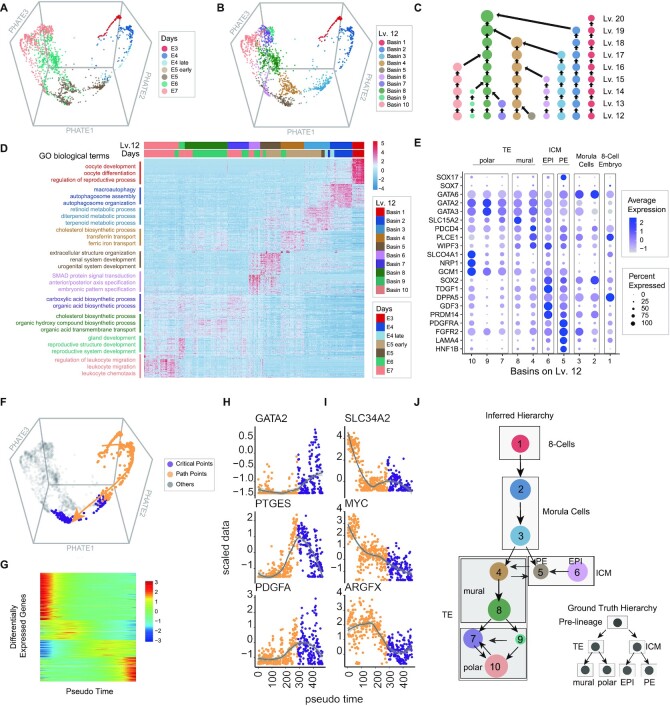
Figure 3.
MarkovHC revealed transition paths and critical points in human preimplantation embryo development. (A) The scRNA-Seq data (63) of 1529 human preimplantation embryos cells from the E3 stage to the E7 stage were projected into 3-dimensional space by phateR. E3–E7 indicates the embryonic day. E4.late and E5.early indicate cells picked 4–6 hours later and earlier than that in the E4 stage and the E5 stage, respectively. (B) Ten basins on Lv.12 correspond to ten asynchronous development stages in human preimplantation embryos cells. (C) The cellular hierarchy from Lv.12 to Lv.20. (D) The heatmap of the top 50 DEGs and enriched GO terms per basin. (E) Four main cell types with sub-populations which are 8-cell embryo, morula cell, ICM (inner cell mass), and TE (trophectoderm) were identified according to marker genes expression. (F) The transition path (yellow arrow) from the 8-cell embryo to ICM was tracked. The yellow points indicate cells along the path and the purple points indicate the critical points from morula cells to ICM. (G) DEGs along the transition path in (F). (H, I) Important marker genes show increasing and decreasing ‘gene-flow’ trends along the path. Gene expression varies dramatically around critical points (purple points). (J) The inferred development hierarchy is consistent with the ground truth of the development hierarchy (in the lower right corner).
The basins on Lv.12 (Figure 3B) were automatically chosen from the cellular hierarchy (Figure 3C) by MarkovHC. To reveal the biological processes in each basin, the top 50 DEGs of each basin (Supplementary Table S3) were enriched in GO terms related to the process of embryonic development (Figure 3D; Supplementary Table S4). We used canonical marker genes from the paper of Petropoulos et al. (63) and LifeMap Discovery (https://discovery.lifemapsc.com/in-vivo-development/) to identify the basins in Figure 3E: four main cell types were 8-cell embryo (GATA6-, SOX7-, SOX17-), morula cell (GATA6+, SOX7-), ICM (inner cell mass; SOX2+, PDGFRA+) and TE (trophectoderm; GATA2+, GATA3+); sub-groups (63) in ICM and TE were polar cells (GCM1+, NRP1+, SLCO4A1+), mural (WIPF3+, PLCE1+, PDCD4+, SLC15A2+), EPI (SOX2, TDGF1, DPPA5, GDF3, PRDM14) and PE (PDGFRA, FGFR2, LAMA4, HNF1B).
We also used MarkovHC to reconstruct the transition path and detect the critical points from the 8-cell embryo to ICM as shown in Figure 3F. In this figure, yellow points indicate cells on the transition path and purple points indicate critical points from morula cells to ICM. There were 2476 DEGs (Supplementary Table S5) along this path (Figure 3G). The expression of significant genes dramatically changed around critical points (purple points in Figure 3H and I) indicating that these points may play pivotal roles in the developmental process. The development hierarchy (Figure 3J) was also inferred according to the transition probability matrix (Supplementary FigureS6A) and the trajectories (Supplementary FigureS6B), which is consistent with the ground truth hierarchy of human embryo development (in the lower right corner of Figure 3J).
MarkovHC detected clinical related pathways from MSCs to gastric cancer cells
The transition process from normal gastric cells to cancer cells is complex and not fully described. Many studies have been carried out to better understand carcinogenesis (64–66). For example, Zhang et al. (67) conducted a single-cell transcriptomic study on gastric antral biopsies and identified gastric cancer-related cell populations. We used MarkovHC to analyse the scRNA-Seq data of 831 mesenchymal stem cells (MSCs) and 695 MSC-origin early gastric cancer cells (EGCs) (Figure 4A) from their study.
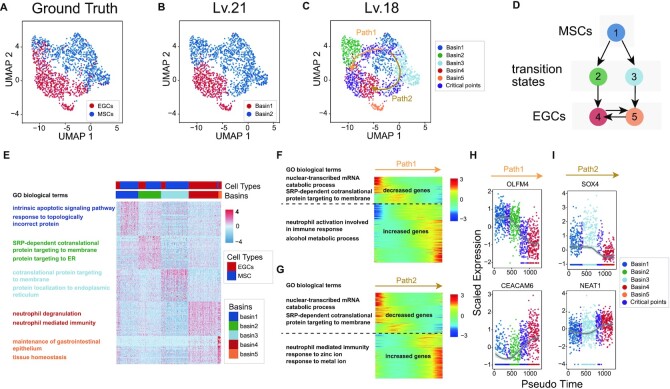
Figure 4.
MarkovHC detected critical points from MSCs to gastric cancer cells. (A) 831 mesenchymal stem cells (MSCs) and 695 MSC-origin early gastric cancer cells (EGCs) (67) were projected into 2-dimensional space by UMAP. (B) MarkovHC found two basins on Lv.21. (C) Five basins were clustered and two transition paths from MSCs to EGCs were inferred by MarkovHC. Purple points indicate critical points on the transition paths. (D) The inferred transitions among basins in (C). (E) The heatmap and enriched GO terms of the top 50 DEGs per basin in (C). (F, G) DEGs along Path1 and Path2 in (C). (H-I) OLFM4 and CEACAM6 showed opposite ‘gene-flow’ trends along Path1 (H). SOX4 and NEAT1 showed opposite ‘gene-flow’ trends along Path2 (I). The expression values of these genes dramatically changed around the critical points.
To identify the cell types, we used MarkovHC to automatically choose two basins on Lv.21 (Figure 4B) and their sub-basins on Lv.18 (Figure 4C, D). GO analysis of the top 50 DEGs of each basin on Lv.18 (Supplementary Table S6) were related to gastric cancer progression (Supplementary Table S7; Figure 4E). To reconstruct the trajectories from MSCs to EGCs, we used MarkovHC to detect two transition paths with critical points from Basin 1 to Basin 4 (Figure 4C). MSC markers (OLFM4, EPHB2, SOX9) gradually decreased from MSCs to EGCs, while EGC markers (KLK10, SLC11A2, SULT2B1, KLK7, ECM1, LMTK3) gradually increased (Supplementary Figure S6C) (67). The inferred transitions among these basins based on the transition probability matrix (Supplementary FigureS6D) were shown in Figure 4D.
In Figure 4F, G, and Supplementary Table S8, the decreased genes of Path1 and Path2 were enriched in protein targeting, protein stabilization, and cell cycle arrest-related terms. The increased genes of Path1 were enriched in neutrophil-mediated immunity and alcohol metabolic process-related terms, suggesting that the potential disease progress might be driven by alcohol stimulus (68). Interestingly, this was partially supported by the fact that this patient (p8 in Zhang et al.’s paper (67)) had a chronic alcohol consumption history. In Path2, the increased genes were enriched in neutrophil-mediated immunity and response to metal ion-related terms suggesting this path could be driven by metal pollution stimulus (69). As shown in Figure 4H, we observed OLFM4, a marker for stem cells in the human intestine, decreased along Path1 (70), while CEACAM6, which plays important role in invasion and metastasis in Gastric Cancer, increased (71). In Figure 4I, SOX4 decreased along Path2, which was consistent with the results that MiR-596 down-regulates SOX4 expression and was a potential novel biomarker for gastric cancer (72), while NEAT1, a long non-coding RNA promoting viability and migration of gastric cancer cells through up-regulation of microRNA-17, increased (73). Furthermore, expression values of these genes dramatically changed around the critical points (purple points in Figure 4H, I), which suggested these were unstable cells in the trajectories. Thus, these two paths might be two potential routes from MSCs to EGCs for this patient, which could be valuable in revealing the underlying mechanisms of the disease progression.
DISCUSSION
In this paper, we developed MarkovHC based on the metastability of exponentially perturbed Markov chain to jointly perform hierarchical clustering, trajectory reconstruction, and critical point detection. We also developed a user-friendly R package, ‘MarkovHC’ (https://github.com/ZhenyiWangTHU/MarkovHC). For ease of use, we provided algorithms to automatically choose the number of PCs (Supplementary Text S3 and Supplementary Figure S7), to recommend levels with the reasonable number of clusters, and to identify levels with biologically meaningful basin transitions. The results showed that MarkovHC could accurately cluster cells into populations at different resolutions, in terms of the established knowledge. Besides, MarkovHC performed equal to or better than the state-of-the-art algorithms in clustering specific tasks. Since MarkovHC is free of data distribution assumption, it can be applied to other omics data such as mass cytometry data and scATAC-Seq data. Furthermore, the transition paths and the critical points among cell populations detected by MarkovHC could reveal certain developmental processes well, such as human embryonic development or cancer progression from MSCs to EGCs.
Besides the analyses described above, there could be some other analyses where MarkovHC is helpful. Firstly, one could calculate pseudo-time (16–19) on a customized resolution (the details are available in Supplementary Text S3 and Supplementary Figure S8). Secondly, one could start out from a given relevant biological level, e.g. based on prior knowledge or other clustering methods, and use MarkovHC to explore the next level up or down in the hierarchy. Thirdly, the hierarchical structure obtained by MarkovHC could be used to jointly analyse multi-omics data, e.g. by using UnionCom (74) recently developed by Cao et al. for the unsupervised topological alignment of single-cell multi-omics data. In addition, we put the detailed time complexity analysis of MarkovHC in Supplementary Text S8 and Supplementary Table S9. Although our method costs more time than Seurat, it can get more information from data including a cluster hierarchy, transition paths, and critical points among clusters. Compared with all the other methods, MarkovHC has a better computational complexity.
Finally, as our method is based on a general mathematics theory (Supplementary Text S4 and Supplementary Figure S9), it is robust as long as the input matrix reliably measures the ‘similarity’ among samples (Supplementary Text S7, Supplementary Text S8, and Supplementary Figure S10). It is possible to further apply the metastability of exponentially perturbed Markov chain to develop algorithms for spatial transcriptomic data analysis.
DATA AVAILABILITY
R package ‘MarkovHC’ is an open source available in the GitHub repository (https://github.com/ZhenyiWangTHU/MarkovHC).
The scRNA-Seq dataset used in Figure 2D was downloaded from GEO under accession number GSE75748. In these data, the labeled cell types include neuronal progenitor cells (NPCs, ectoderm derivatives, n = 173), DE cells (endoderm derivatives, n = 138), endothelial cells (ECs, mesoderm derivatives, n = 105), trophoblast-like cells (TBs, extraembryonic derivatives, n = 69), undifferentiated H1 (n = 212) and H9 (n = 162) human ES cells, and human foreskin fibroblasts (HFFs, n = 159).
The scRNA-Seq datasets and labels in Figure 2G (‘Kolod’, ‘Pollen’, ‘Usoskin’, ‘Zeisel’) were downloaded from ‘SIMLR’ repository (https://github.com/BatzoglouLabSU/SIMLR).
The scRNA-Seq dataset and lineage labels of C. elegans embryogenesis in Figure 2G (‘Celegans’) were downloaded from GEO under accession number GSE126954.
The mass cytometry dataset of PBMC in Figure 2G (‘cytof’) was downloaded from the Supplementary materials of Anchang's paper (48) (https://www.nature.com/articles/nprot.2016.066).
The scRNA-Seq dataset of 33k PBMCs in Supplementary Figure S4A was downloaded from 10X genomics support (https://support.10xgenomics.com/single-cell-gene-expression/datasets/1.1.0/pbmc33k).
The scRNA-Seq and scATAC-seq datasets in Supplementary Figure S4B, C and D were downloaded from GEO under accession numbers GSE115968 and GSE107651.
The single-cell datasets in Supplementary Figure S4E, F, and G measuring both DNA accessibility and gene expression in the same cells were downloaded from 10x genomics support (Count matrix: https://cf.10xgenomics.com/samples/cell-arc/1.0.0/pbmc_granulocyte_sorted_10k/pbmc_granulocyte_sorted_10k_filtered_feature_bc_matrix.h5; ATAC fragment file: https://cf.10xgenomics.com/samples/cell-arc/1.0.0/pbmc_granulocyte_sorted_10k/pbmc_granulocyte_sorted_10k_atac_fragments.tsv.gz; ATAC fragment file index: https://cf.10xgenomics.com/samples/cell-arc/1.0.0/pbmc_granulocyte_sorted_10k/pbmc_granulocyte_sorted_10k_atac_fragments.tsv.gz.tbi)
The scRNA-Seq dataset of 1529 single-cells in Figure 3 was downloaded from EMBL-EBI under accession number E-MTAB-3929 (https://www.ebi.ac.uk/arrayexpress/experiments/E-MTAB-3929/).
The scRNA-Seq dataset of 831 mesenchymal stem cells (MSCs) and 695 MSC-origin early gastric cancer cells (EGCs) was downloaded from GEO under accession number GSE134520.
The scRNA-Seq dataset of 242,533 single-cells from mouse cell atlas (MCA) was downloaded from https://www.dropbox.com/s/8d8t4od38oojs6i/MCA.zip?dl=1
Supplementary Material
ACKNOWLEDGEMENTS
The authors wish to thank Peng Zhang, Yuyao Song and Kui Hua for the discussions.
Authors’ Contributions: M.P.Q., M.Q.Z., Z.Y.W. and Y.J.Z. conceived the project. Z.Y.W. and Y.J.Z. conducted the research. M.P.Q. and M.Q.Z. supervised the research. Z.Y.W. implemented the R package ‘MarkovHC’. Z.Y.W. did the Formal Analysis. Z.Y.W., Z.F.Y., L.Z. and M.L.S. did investigation. Z.Y.W. wrote the original draft; M.Q.Z., Z.F.Y., Z.Y.W., Y.J.Z., L.Z., Y.C., M.L.S., Z.Y.Y., Q.M.Z. and M.P.Q. contributed to the writing of the manuscript. Z.F.Y. and Z.Y.W. did the visualization. All authors read and approved the final manuscript.
Contributor Information
Zhenyi Wang, MOE Key Laboratory of Bioinformatics; Bioinformatics Division and Center for Synthetic & Systems Biology, BNRist; Department of Automation, Tsinghua University, Beijing 100084, China.
Yanjie Zhong, School of Mathematical Sciences, Peking University, Beijing 100871, China; Department of Mathematics and Statistics, Washington University in St. Louis, St. Louis, MO 63130, USA.
Zhaofeng Ye, MOE Key Laboratory of Bioinformatics; Bioinformatics Division and Center for Synthetic & Systems Biology, BNRist; School of Medicine, Tsinghua University, Beijing 100084, China.
Lang Zeng, Department of Biostatistics, University of Michigan, Ann Arbor, MI 48109, USA.
Yang Chen, MOE Key Laboratory of Bioinformatics; Bioinformatics Division and Center for Synthetic & Systems Biology, BNRist; Department of Automation, Tsinghua University, Beijing 100084, China.
Minglei Shi, MOE Key Laboratory of Bioinformatics; Bioinformatics Division and Center for Synthetic & Systems Biology, BNRist; School of Medicine, Tsinghua University, Beijing 100084, China.
Zhiyuan Yuan, MOE Key Laboratory of Bioinformatics; Bioinformatics Division and Center for Synthetic & Systems Biology, BNRist; Department of Automation, Tsinghua University, Beijing 100084, China.
Qiming Zhou, MOE Key Laboratory of Bioinformatics; Bioinformatics Division and Center for Synthetic & Systems Biology, BNRist; School of Life Sciences, Tsinghua University, Beijing 100084, China.
Minping Qian, School of Mathematical Sciences, Peking University, Beijing 100871, China.
Michael Q Zhang, MOE Key Laboratory of Bioinformatics; Bioinformatics Division and Center for Synthetic & Systems Biology, BNRist; Department of Automation, Tsinghua University, Beijing 100084, China; MOE Key Laboratory of Bioinformatics; Bioinformatics Division and Center for Synthetic & Systems Biology, BNRist; School of Medicine, Tsinghua University, Beijing 100084, China; Department of Biological Sciences, Center for Systems Biology, The University of Texas, Richardson, TX 75080-3021, USA.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
This work was supported by Natural Science Foundation of China [81890991, 62050152] to M.L.S; the Natural Science Foundation of China [81890994], National Key Research and Development Program [2018YFA0801402] to Y.C; M.Q.Z acknowledges the support by the Cecil H. and Ida Green Distinguished Chair.
Conflict of interest statement. None declared.
REFERENCES
- 1. Butler A., Hoffman P., Smibert P., Papalexi E., Satija R.. Integrating single-cell transcriptomic data across different conditions, technologies, and species. Nat. Biotechnol. 2018; 36:411–420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Kiselev V.Y., Kirschner K., Schaub M.T., Andrews T., Yiu A., Chandra T., Natarajan K.N., Reik W., Barahona M., Green A.R.et al.. SC3: consensus clustering of single-cell RNA-seq data. Nat. Methods. 2017; 14:483–486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Wang B., Zhu J., Pierson E., Ramazzotti D., Batzoglou S.. Visualization and analysis of single-cell RNA-seq data by kernel-based similarity learning. Nat. Methods. 2017; 14:414–416. [DOI] [PubMed] [Google Scholar]
- 4. Lin P., Troup M., Ho J.W.. CIDR: Ultrafast and accurate clustering through imputation for single-cell RNA-seq data. Genome Biol. 2017; 18:59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Zurauskiene J., Yau C.. pcaReduce: hierarchical clustering of single cell transcriptional profiles. BMC Bioinformatics. 2016; 17:140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Chen J., Schlitzer A., Chakarov S., Ginhoux F., Poidinger M.. Mpath maps multi-branching single-cell trajectories revealing progenitor cell progression during development. Nat. Commun. 2016; 7:11988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Schwartz G.W., Zhou Y., Petrovic J., Fasolino M., Xu L., Shaffer S.M., Pear W.S., Vahedi G., Faryabi R.B.. TooManyCells identifies and visualizes relationships of single-cell clades. Nat. Methods. 2020; 17:405–413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Zeisel A., Munoz-Manchado A.B., Codeluppi S., Lonnerberg P., La Manno G., Jureus A., Marques S., Munguba H., He L., Betsholtz C.et al.. Cell types in the mouse cortex and hippocampus revealed by single-cell RNA-seq. Science. 2015; 347:1138–1142. [DOI] [PubMed] [Google Scholar]
- 9. MacQueen J. Some methods for classification and analysis of multivariate observations. Proceedings of the fifth Berkeley symposium on mathematical statistics and probability. 1967; 1:281–297. [Google Scholar]
- 10. Sokal R.R., Michener C.D.. A statistical method for evaluating systematic relationships. Univ. Kansas, Sci. Bull. 1958; 38:1409–1438. [Google Scholar]
- 11. Ester M., Kriegel H.P., Sander J., Xu X.. A density-based algorithm for discovering clusters in large spatial databases with noise. Kdd. 1996; 96:226–231. [Google Scholar]
- 12. Ankerst M., Breunig M.M., Kriegel H-P, Sander J.. OPTICS: Ordering Points To Identify the Clustering Structure. ACM Sigmod record. 1999; 28:49–60. [Google Scholar]
- 13. Campello R.J.G.B., Moulavi D., Zimek A., Sander J.. Hierarchical Density Estimates for Data Clustering, Visualization, and Outlier Detection. TKDD. 2015; 10:1–51. [Google Scholar]
- 14. Ng. A.Y., Jordan M.I., Weiss Y.. On spectral clustering: Analysis and an algorithm. Adv. Neural Inf. Process. Syst. 2002; 2:849–856. [Google Scholar]
- 15. Fraley C., Raftery A.E.. Model-based clustering, discriminant analysis, and density estimation. J. Am. Stat. Assoc. 2002; 97:611–631. [Google Scholar]
- 16. Trapnell C., Cacchiarelli D., Grimsby J., Pokharel P., Li S., Morse M., Lennon N.J., Livak K.J., Mikkelsen T.S., Rinn J.L.. The dynamics and regulators of cell fate decisions are revealed by pseudotemporal ordering of single cells. Nat. Biotechnol. 2014; 32:381–386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Qiu X., Mao Q., Tang Y., Wang L., Chawla R., Pliner H.A., Trapnell C.. Reversed graph embedding resolves complex single-cell trajectories. Nat. Methods. 2017; 14:979–982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Cao J., Spielmann M., Qiu X., Huang X., Ibrahim D.M., Hill A.J., Zhang F., Mundlos S., Christiansen L., Steemers F.J.et al.. The single-cell transcriptional landscape of mammalian organogenesis. Nature. 2019; 566:496–502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Ji Z., Ji H.. TSCAN: Pseudo-time reconstruction and evaluation in single-cell RNA-seq analysis. Nucleic. Acids. Res. 2016; 44:e117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Farrell J.A., Wang Y., Riesenfeld S.J., Shekhar K., Regev A., Schier A.F.. Single-cell reconstruction of developmental trajectories during zebrafish embryogenesis. Science. 2018; 360:6392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Schiebinger G., Shu J., Tabaka M., Cleary B., Subramanian V., Solomon A., Gould J., Liu S., Lin S., Berube P.et al.. Optimal-Transport Analysis of Single-Cell Gene Expression Identifies Developmental Trajectories in Reprogramming. Cell. 2019; 176:928–943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Qiu P., Simonds E.F., Bendall S.C., Gibbs K.D., Bruggner R.V., Linderman M.D., Sachs K., Nolan G.P., Plevritis S.K. Extracting a cellular hierarchy from high-dimensional cytometry data with SPADE. Nat. Biotechnol. 2011; 29:886–891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Lenton T.M., Livina V.N.. Detecting and anticipating climate tipping points. Geophys. Monogr. 2016; 214:51–62. [Google Scholar]
- 24. Clements C.F., McCarthy M.A., Blanchard J.L.. Early warning signals of recovery in complex systems. Nat. Commun. 2019; 10:1681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Zhong J., Han C., Zhang X., Chen P., Liu R.. Predicting cell fate commitment of embryonic differentiation by single-cell graph entropy. 2020; bioRxiv doi:24 April 2020, preprint: not peer reviewed 10.1101/2020.04.22.055244. [DOI]
- 26. Zheng X., Jin S., Nie Q., Zou X.. scRCMF: Identification of cell subpopulations and transition states from Single-Cell transcriptomes. IEEE. Trans. Biomed. Eng. 2019; 67:1418–1428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Regev A., Teichmann S.A., Lander E.S., Amit I., Benoist C., Birney E., Bodenmiller B., Campbell P., Carninci P., Clatworthy M.et al.. Science forum: the human cell atlas. Elife. 2017; 6:e27041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Miller J.G. Living systems: Basic concepts. Behav. Sci. 1965; 10:193–237. [DOI] [PubMed] [Google Scholar]
- 29. Wright S. The roles of mutation, inbreeding, crossbreeding and selection in evolution. Proc. XI Int. Congr. Genet. 1932; 1:356–366. [Google Scholar]
- 30. Waddington C.H. The Strategy of the Genes. 1957; London: Allen & Unwin. [Google Scholar]
- 31. van Dijk D., Sharma R., Nainys J., Yim K., Kathail P., Carr A.J., Burdziak C., Moon K.R., Chaffer C.L., Pattabiraman D.et al.. Recovering Gene Interactions from Single-Cell Data Using Data Diffusion. Cell. 2018; 174:716–729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Jaccard P. The distribution of the flora in the alpine zone. New Phytol. 1912; 11:37–50. [Google Scholar]
- 33. Haghverdi L., Buttner M., Wolf F.A., Buettner F., Theis F.J.. Diffusion pseudotime robustly reconstructs lineage branching. Nat. Methods. 2016; 13:845–848. [DOI] [PubMed] [Google Scholar]
- 34. Setty M., Tadmor M.D., Reich-Zeliger S., Angel O., Salame T.M., Kathail P., Choi K., Bendall S., Friedman N., Pe’er D.. Wishbone identifies bifurcating developmental trajectories from single-cell data. Nat. Biotechnol. 2016; 34:637–645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Chen D., Feng J., Qian M.. Metastability of exponentially perturbed Markov chains. Science in China Series A: Mathematics. 1996; 39:7. [Google Scholar]
- 36. Chen Z., An S., Bai X., Gong F., Ma L., Wan L.. DensityPath: an algorithm to visualize and reconstruct cell state-transition path on density landscape for single-cell RNA sequencing data. Bioinformatics. 2019; 35:2593–2601. [DOI] [PubMed] [Google Scholar]
- 37. Dijkstra E.W. A note on two problems in connexion with graphs. Numer. Math. 1959; 1:269–271. [Google Scholar]
- 38. Ao P., Galas D., Hood L., Zhu X.. Cancer as robust intrinsic state of endogenous molecular-cellular network shaped by evolution. Med. Hypotheses. 2008; 70:678–684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Zappia L., Phipson B., Oshlack A.. Splatter: simulation of single-cell RNA sequencing data. Genome Biol. 2017; 18:174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Chu L.F., Leng N., Zhang J., Hou Z., Mamott D., Vereide D.T., Choi J., Kendziorski C., Stewart R., Thomson J.A.. Single-cell RNA-seq reveals novel regulators of human embryonic stem cell differentiation to definitive endoderm. Genome Biol. 2016; 17:173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Papalexi E., Satija R.. Single-cell RNA sequencing to explore immune cell heterogeneity. Nat. Rev. Immunol. 2018; 18:35–45. [DOI] [PubMed] [Google Scholar]
- 42. Villani A.C., Satija R., Reynolds G., Sarkizova S., Shekhar K., Fletcher J., Griesbeck M., Butler A., Zheng S., Lazo S.et al.. Single-cell RNA-seq reveals new types of human blood dendritic cells, monocytes, and progenitors. Science. 2017; 356:eaah4573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Bendall S.C., Simonds E.F., Qiu P., Amir el A.D., Krutzik P.O., Finck R., Bruggner R.V., Melamed R., Trejo A., Ornatsky O.I.et al.. Single-cell mass cytometry of differential immune and drug responses across a human hematopoietic continuum. Science. 2011; 332:687–696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Kolodziejczyk A.A., Kim J.K., Tsang J.C., Ilicic T., Henriksson J., Natarajan K.N., Tuck A.C., Gao X., Buhler M., Liu P.et al.. Single Cell RNA-Sequencing of Pluripotent States Unlocks Modular Transcriptional Variation. Cell Stem Cell. 2015; 17:471–485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Pollen A.A., Nowakowski T.J., Shuga J., Wang X., Leyrat A.A., Lui J.H., Li N., Szpankowski L., Fowler B., Chen P.et al.. Low-coverage single-cell mRNA sequencing reveals cellular heterogeneity and activated signaling pathways in developing cerebral cortex. Nat. Biotechnol. 2014; 32:1053–1058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Usoskin D., Furlan A., Islam S., Abdo H., Lonnerberg P., Lou D., Hjerling-Leffler J., Haeggstrom J., Kharchenko O., Kharchenko P.V.et al.. Unbiased classification of sensory neuron types by large-scale single-cell RNA sequencing. Nat. Neurosci. 2015; 18:145–153. [DOI] [PubMed] [Google Scholar]
- 47. Packer J.S., Zhu Q., Huynh C., Sivaramakrishnan P., Preston E., Dueck H., Stefanik D., Tan K., Trapnell C., Kim J.et al.. A lineage-resolved molecular atlas of C. elegans embryogenesis at single-cell resolution. Science. 2019; 365:6459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Anchang B., Hart T.D., Bendall S.C., Qiu P., Bjornson Z., Linderman M., Nolan G.P., Plevritis S.K.. Visualization and cellular hierarchy inference of single-cell data using SPADE. Nat. Protoc. 2016; 11:1264–1279. [DOI] [PubMed] [Google Scholar]
- 49. Hubert L., Arabie P.. Comparing partitions. J. Classification. 1985; 2:193–218. [Google Scholar]
- 50. Vinh N.X., Epps J., Bailey J.. Information theoretic measures for clusterings comparison: Variants, properties, normalization and correction for chance. The Journal of Machine Learning Research. 2010; 11:2837–2854. [Google Scholar]
- 51. Wasserman L. Topological data analysis. Annu. Rev. Stat. Appl. 2018; 5:501–532. [Google Scholar]
- 52. Wolf F.A., Hamey F.K., Plass M., Solana J., Dahlin J.S., Gottgens B., Rajewsky N., Simon L., Theis F.J.. PAGA: graph abstraction reconciles clustering with trajectory inference through a topology preserving map of single cells. Genome Biol. 2019; 20:59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Sibson R. SLINK: an optimally efficient algorithm for the single-link cluster method. The Computer Journal. 1973; 16:30–34. [Google Scholar]
- 54. Defays D. An efficient algorithm for a complete link method. The Computer Journal. 1977; 20:364–366. [Google Scholar]
- 55. Blondel V.D., Guillaume J.L., Lambiotte R., Lefebvre E.. Fast unfolding of communities in large networks. J. Stat. Mech. Theory Exp. 2008; 10:P10008. [Google Scholar]
- 56. Rodriguez M.Z., Comin C.H., Casanova D., Bruno O.M., Amancio D.R., Costa L.D.F., Rodrigues F.A.. Clustering algorithms: A comparative approach. PLoS One. 2019; 14:e0210236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Kiselev V.Y., Andrews T.S., Hemberg M.. Challenges in unsupervised clustering of single-cell RNA-seq data. Nat. Rev. Genet. 2019; 20:273–282. [DOI] [PubMed] [Google Scholar]
- 58. Wolf F.A., Angerer P., Theis F.J.. SCANPY: large-scale single-cell gene expression data analysis. Genome Biol. 2018; 19:15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Guo M., Wang H., Potter S.S., Whitsett J.A., Xu Y.. SINCERA: A Pipeline for Single-Cell RNA-Seq Profiling Analysis. PLoS Comput. Biol. 2015; 11:e1004575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Ertöz L, Steinbach M, Kumar V.. Finding clusters of different sizes, shapes, and densities in noisy, high dimensional data. Third SIAM International Conference on Data Mining(SDM). 2003; San Fransico. CA: 47–58. [Google Scholar]
- 61. Bhargav S., Pawar M.. A review of clustering methods forming non-convex clusters with missing and noisy data. IJCSE. 2016; 4:39–44. [Google Scholar]
- 62. van Dongen S. A Cluster Algorithm for Graphs. 2000; Amsterdam: INS-R0010 National Research Institute for Mathematics and Computer Science in the Netherlands; Technical Report(Stichting Mathematisch Centrum, Amsterdam). [Google Scholar]
- 63. Petropoulos S., Edsgard D., Reinius B., Deng Q., Panula S.P., Codeluppi S., Plaza Reyes A., Linnarsson S., Sandberg R., Lanner F.. Single-Cell RNA-Seq Reveals Lineage and X Chromosome Dynamics in Human Preimplantation Embryos. Cell. 2016; 165:1012–1026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Cheng J., Fan X.M.. Role of cyclooxygenase-2 in gastric cancer development and progression. World J. Gastroenterol. 2013; 19:7361–7368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Boussioutas A., Li H., Liu J., Waring P., Lade S., Holloway A.J., Taupin D., Gorringe K., Haviv I., Desmond P.V.et al.. Distinctive patterns of gene expression in premalignant gastric mucosa and gastric cancer. Cancer Res. 2003; 63:2569–2577. [PubMed] [Google Scholar]
- 66. Alzahrani S., Lina T.T., Gonzalez J., Pinchuk I.V., Beswick E.J., Reyes V.E.. Effect of Helicobacter pylori on gastric epithelial cells. World J. Gastroenterol. 2014; 20:12767–12780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67. Zhang P., Yang M., Zhang Y., Xiao S., Lai X., Tan A., Du S., Li S.. Dissecting the Single-Cell Transcriptome Network Underlying Gastric Premalignant Lesions and Early Gastric Cancer. Cell Rep. 2019; 27:1934–1947. [DOI] [PubMed] [Google Scholar]
- 68. Zali H., Rezaei-Tavirani M., Azodi M.. Gastric cancer: prevention, risk factors and treatment. Gastroenterol. Hepatol. Bed Bench. 2011; 4:175–185. [PMC free article] [PubMed] [Google Scholar]
- 69. Yuan W., Yang N., Li X.. Advances in Understanding How Heavy Metal Pollution Triggers Gastric Cancer. Biomed. Res. Int. 2016; 2016:7825432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70. van der Flier L.G., Haegebarth A., Stange D.E., van de Wetering M., Clevers H.. OLFM4 Is a Robust Marker for Stem Cells in Human Intestine and Marks a Subset of Colorectal Cancer Cells. Gastroenterology. 2009; 137:15–17. [DOI] [PubMed] [Google Scholar]
- 71. Zang M., Zhang B., Zhang Y., Li J., Su L., Zhu Z., Gu Q., Liu B., Yan M.. CEACAM6 Promotes Gastric Cancer Invasion and Metastasis by Inducing Epithelial-Mesenchymal Transition via PI3K/AKT Signaling Pathway. PLoS One. 2014; 9:e112908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72. Chen Y., Gong W., Dai W., Pan Z., Xu X., Jiang H.. MiR-596 down regulates SOX4 expression and is a potential novel biomarker for gastric cancer. Translational Cancer Research. 2020; 9:1294–1302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73. Wang C.L., Wang D., Yan B.Z., Fu J.W., Qin L.. Long non-coding RNA NEAT1 promotes viability and migration of gastric cancer cell lines through up-regulation of microRNA-17. Eur. Rev. Med. Pharmacol. Sci. 2018; 22:4128–4137. [DOI] [PubMed] [Google Scholar]
- 74. Cao K., Bai X.Q., Hong Y.G., Wan L.. Unsupervised topological alignment for single-cell multi-omics integration. Bioinformatics. 2020; 36:i48–i56. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
R package ‘MarkovHC’ is an open source available in the GitHub repository (https://github.com/ZhenyiWangTHU/MarkovHC).
The scRNA-Seq dataset used in Figure 2D was downloaded from GEO under accession number GSE75748. In these data, the labeled cell types include neuronal progenitor cells (NPCs, ectoderm derivatives, n = 173), DE cells (endoderm derivatives, n = 138), endothelial cells (ECs, mesoderm derivatives, n = 105), trophoblast-like cells (TBs, extraembryonic derivatives, n = 69), undifferentiated H1 (n = 212) and H9 (n = 162) human ES cells, and human foreskin fibroblasts (HFFs, n = 159).
The scRNA-Seq datasets and labels in Figure 2G (‘Kolod’, ‘Pollen’, ‘Usoskin’, ‘Zeisel’) were downloaded from ‘SIMLR’ repository (https://github.com/BatzoglouLabSU/SIMLR).
The scRNA-Seq dataset and lineage labels of C. elegans embryogenesis in Figure 2G (‘Celegans’) were downloaded from GEO under accession number GSE126954.
The mass cytometry dataset of PBMC in Figure 2G (‘cytof’) was downloaded from the Supplementary materials of Anchang's paper (48) (https://www.nature.com/articles/nprot.2016.066).
The scRNA-Seq dataset of 33k PBMCs in Supplementary Figure S4A was downloaded from 10X genomics support (https://support.10xgenomics.com/single-cell-gene-expression/datasets/1.1.0/pbmc33k).
The scRNA-Seq and scATAC-seq datasets in Supplementary Figure S4B, C and D were downloaded from GEO under accession numbers GSE115968 and GSE107651.
The single-cell datasets in Supplementary Figure S4E, F, and G measuring both DNA accessibility and gene expression in the same cells were downloaded from 10x genomics support (Count matrix: https://cf.10xgenomics.com/samples/cell-arc/1.0.0/pbmc_granulocyte_sorted_10k/pbmc_granulocyte_sorted_10k_filtered_feature_bc_matrix.h5; ATAC fragment file: https://cf.10xgenomics.com/samples/cell-arc/1.0.0/pbmc_granulocyte_sorted_10k/pbmc_granulocyte_sorted_10k_atac_fragments.tsv.gz; ATAC fragment file index: https://cf.10xgenomics.com/samples/cell-arc/1.0.0/pbmc_granulocyte_sorted_10k/pbmc_granulocyte_sorted_10k_atac_fragments.tsv.gz.tbi)
The scRNA-Seq dataset of 1529 single-cells in Figure 3 was downloaded from EMBL-EBI under accession number E-MTAB-3929 (https://www.ebi.ac.uk/arrayexpress/experiments/E-MTAB-3929/).
The scRNA-Seq dataset of 831 mesenchymal stem cells (MSCs) and 695 MSC-origin early gastric cancer cells (EGCs) was downloaded from GEO under accession number GSE134520.
The scRNA-Seq dataset of 242,533 single-cells from mouse cell atlas (MCA) was downloaded from https://www.dropbox.com/s/8d8t4od38oojs6i/MCA.zip?dl=1