Abstract
Motivation
The acid dissociation constant (pKa) is a critical parameter to reflect the ionization ability of chemical compounds and is widely applied in a variety of industries. However, the experimental determination of pKa is intricate and time-consuming, especially for the exact determination of micro-pKa information at the atomic level. Hence, a fast and accurate prediction of pKa values of chemical compounds is of broad interest.
Results
Here, we compiled a large-scale pKa dataset containing 16 595 compounds with 17 489 pKa values. Based on this dataset, a novel pKa prediction model, named Graph-pKa, was established using graph neural networks. Graph-pKa performed well on the prediction of macro-pKa values, with a mean absolute error around 0.55 and a coefficient of determination around 0.92 on the test dataset. Furthermore, combining multi-instance learning, Graph-pKa was also able to automatically deconvolute the predicted macro-pKa into discrete micro-pKa values.
Availability and implementation
The Graph-pKa model is now freely accessible via a web-based interface (https://pka.simm.ac.cn/).
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
The acid dissociation constant pKa, an equilibrium constant defined as the negative logarithm of the ratio of the protonated and deprotonated form of a compound, is a key parameter to describe the ionization ability of substances. It has been reported that about two-thirds of marketed drugs are ionizable in the aqueous solution (Manallack, 2007). Hence, in the design of new drugs, pKa is a crucial physical property to be considered, which has profound effects on biological activities, ADMET (absorption, distribution, metabolism, excretion and toxicity) properties and other properties of drugs (Charifson and Walters, 2014; Manallack et al., 2013). Apart from the pharmaceutical industry, the pKa is also related to environmental ecotoxicology, agriculture and chemical industries. Hence, the fast and accurate prediction of pKa values of chemical compounds from their structures is of great interest.
Graph neural networks (GNN) are a type of neural network to process graph structure data (Defferrard et al., 2016; Niepert et al., 2016). Since first introduced into the prediction of molecular properties several years ago (Duvenaud et al., 2015), reports of different GNN architectures and their successful applications have been rapidly accumulating in this field (Sun et al., 2020; Zhang et al., 2021). However, so far, graph neural networks have rarely been applied in the prediction of pKa, presumably because the pKa values are not only molecular-level ‘global’ properties but also atomic-level ‘local’ properties (Fig. 1). The molecular-level ‘global’ properties refer to the macro-pKa, the acid dissociation constant related to the observable loss or gain of a proton from a molecule regardless of specific ionization site. The ‘local’ properties refer to micro-pKa, the acid dissociation constant related to the loss or gain of a proton from a single titratable site (Işık et al., 2018). Apart from the macro-pKa, a powerful pKa prediction model should also be capable of providing micro-pKa information at the atomic level. Such information can not only enhance our confidence in the predicted results but also provide useful reference information for the structural modification of compounds, chemical reaction prediction and other related studies. However, for a molecule with multiple ionization sites, usually, we can only measure one or a few macro-pKa values experimentally, but not the micro-pKa values of all individual sites. Thus, it is intricate to predict micro-pKa values, posing a significant challenge to the overall prediction of pKa.
Fig. 1.

The relationship between macro- and micro-pKa of basic compounds. pKa(macro) refers to the macro-pKa; pKa1, pKa2 and pKa3 refer to the micro-pKa
In 2019, Roszak et al. built a graph convolution model for the prediction of the pKa value of the C-H bond in organic solvents and applied this model to predict the products of hydrogen abstraction reaction (Roszak et al., 2019). To the best of our knowledge, this study was the only attempt to predict compound pKa with graph neural networks. However, the training of their model relied on the pKa dataset containing atomic level labels, which were mainly obtained from quantum chemical calculation or molecules with a single ionizable site. Hence, this method is difficult to extend to the pKa prediction of heterogeneous chemical classes with multiple ionizable sites. Another alternative strategy to obtain micro-pKa data is to assign the macro-pKa value of a molecule to its major responsible ionization site and take it as an approximation of the micro-pKa value. Recently, some pKa prediction models have used this strategy (Hunt et al., 2020; Yang et al., 2020), but there are also two significant problems. As illustrated in Figure 1, (i) for molecules such as propane-1,2,3-triamine, there are multiple sites having similar ionization capacity, this approximate treatment may bring large errors; (ii) the selection of major responsible ionization site is a non-trivial process and requires substantial chemical domain knowledge, and in many cases, a macro-pKa value could not be unambiguously assigned to one major ionizable group.
Multi-instance learning (MIL) is a kind of weakly supervised learning algorithm for data with only coarse-grained labels (Zhou, 2018). In classic MIL, the training set is composed of many ‘bags’, each of which contains a series of ‘instances’. A bag is labeled as positive if containing at least one positive instance; otherwise, it is labeled as negative. The goal of MIL is to train a classifier that can correctly label unseen bags. Due to the ability to provide instance-level interpretation, MIL has attracted extensive attention in many classification tasks such as medical image analysis, text classification and video annotation (Carbonneau et al., 2018; Wang et al., 2019; Zhou et al., 2017). However, so far, MIL has rarely been used in regression tasks. This is because a necessary prerequisite for obtaining instance labels through MIL is that there should be a clear mathematical relationship between instance labels and bag labels. This relationship is common in classification tasks (such as ‘or’ relationship) but rare in regression tasks. For pKa, there is a relatively clear relationship between macro-pKa and micro-pKa. For example, Figure 1 shows the formula between macro-pKa and micro-pKa of basic compounds.
Here, combining multi-instance learning and graph neural networks, we designed a novel pKa prediction model named Graph-pKa. In Graph-pKa, a molecule is regarded as a ‘bag’, and those ionizable atoms in this molecule are regarded as ‘instances’. It means that the macro-pKa value of a molecule is designated as the label of a bag, which is available in the training set, and the unavailable information regarding to the micro-pKa values of ionizable sites are considered as the labels of instances. Under this scheme, Graph-pKa can follow the MIL framework to learn the labels of instances through training against the labels of bags (Fig. 2). Furthermore, it should be noted that those molecules containing multiple ionization sites may have multiple macro-pKa values. In this work, we only consider the most acidic and basic pKa values, which are key parameters that can unambiguously and concisely describe the ionization capabilities of compounds. Some chemical information websites, including ChEMBL (Gaulton et al., 2017) and DrugBank (Wishart et al., 2018) also describe the prediction for the pKa of compounds in terms of the most acidic and basic pKa values.
Fig. 2.
The schematic representation of the proposed Graph-pKa model
2 Materials and methods
2.1 S-pka dataset
A large pKa dataset named S-pKa was compiled, mainly from three main sources: (i) datasets used in several previous studies on pKa, (ii) a free software named QSAR Toolbox, (iii) manual extraction from various literature. Those chemical structures from different sources were standardized and then merged. The structure standardization procedure includes removing all salts from molecules, neutralizing charged molecules, and standardizing SMILES strings. In addition, considering that the accuracy of publicly available experimentally determined pKa values was often dubious (Rupp et al., 2011), each data would undergo manual inspection to ensure that it belongs to the most acidic or basic pKa value of its corresponding molecule before adding to the S-pKa dataset. The detailed processes of data collection and cleaning is given in Supplementary Material and Supplementary Figure S1. The S-pKa dataset can be separated into an acidic subset and a basic subset, containing the most acidic pKa values of 9043 chemical structures and the most basic pKa values of 8436 chemical structures, respectively (Supplementary Fig. S2a). The distribution of pKa values in the acidic and basic subset is shown in Figure 3a. The most acidic pKa values varied from -3.3 to 40, while the most basic pKa values varied from -10.1 to 14. Since to learn micro-pKa via MIL is a critical concept utilized in the establishment of the Graph-pKa model, the acidic or basic ionizable sites of compounds in the S-pKa dataset are all enumerated and displayed (Fig. 3b). In this study, the acidic ionizable sites are defined as non-carbon atoms connected with at least one hydrogen atom, and the basic ionizable sites are defined as nitrogen atoms with no positive formal charge. The distribution of the molecular weight of compounds across the S-pKa dataset is also shown in Supplementary Figure S2b.
Fig. 3.

The distributions of simple compound properties in the S-pKa dataset. (a) The experimental pKa values. (b) The number of ionizable sites
2.2 Graph-pKa model
The architecture of Graph-pKa is shown in Figure 2. It begins by describing each molecule as an undirected graph where nodes and edges correspond to atoms and chemical bonds, respectively. The molecular graph is then input into the graph neural layers where atoms receive the message of other atoms in the molecule and use the aggregated messages to update their own features. The graph neural layer in Graph-pKa is the same as our previously developed Attentive FP (Xiong et al., 2020), a molecular representation learning scheme that uses a graph attention mechanism. Here, six graph neural layers are stacked in Graph-pKa for the extraction of atom features.
The major difference between Graph-pKa and other graph neural networks lies in the approach to deal with the features of nodes extracted by graph neural network layers. In molecular graph neural networks such as GCN (Duvenaud et al., 2015), MPNN (Gilmer et al., 2017) and Attentive FP (Xiong et al., 2020), those node features are aggregated with various pooling operations such as average pooling and Set2Set to generate the features of the whole molecule, which are next used to fit and predict the molecular properties. However, in Graph-pKa those learned node features are directly fed into a fully connected (FC) layer to predict the pKa values of atoms. Since some atoms in molecules are not ionizable, their predicted pKa values will be masked. In the acidic and basic pKa prediction model, the mask values are respectively positive infinity and negative infinity. Finally, the macro-pKa values of molecules are calculated according to the approximate mathematical relationships between them and the predicted pKa values of ionizable atoms. More specifically, given an atom Ai with features Xi, the above process can be formulated as follows:
In acidic pKa prediction model:
| (1) |
| (2) |
| (3) |
In basic pKa prediction model:
| (4) |
| (5) |
| (6) |
where is referred to a fully connected neural network layer, P is the acidic ionizable sites, Q is the basic ionizable sites, is the number of heavy atoms in a molecule, is the positive infinity, and are the most acidic/basic pKa values of a molecule.
Obviously, formula 3 and 6 are the key formulas for MIL. Yang et al. also had used formula 6 to calculate the macro-pKa values in their study (Yang et al., 2020). Here, we provided the derivation of formula 3 and 6 in Supplementary Material and Supplementary Figure S3.
2.3 Implement of Graph-pKa and other benchmark methods
In Graph-pKa, the conversion from a SMILES string to an undirected graph and initialization for it was implemented with the DGL-LifeSci package. The representations of the graph were initialized with eight kinds of atom features and four kinds of bond features (Supplementary Table S1). The Graph-pKa model was implemented using the PyTorch and DGL. The loss function used to train Graph-pKa was MSELoss. Attentive FP and four machine learning models, including SVM, RF, XGBoost and ANN were implemented as baseline models. XGBoost was implemented with the XGBoost package, SVM, RF and ANN were implemented with the Scikit-learn package. Attentive FP is a graph neural network with the same GNN layers as Graph-pKa but without MIL, which was also implemented as a control for model performance evaluation. For baseline models except Attentive FP, the molecular fingerprints used to encode the molecular structures were a kind of combined molecular fingerprint that integrated eight types of common molecular fingerprints including CDK, Estate, CDK graph only, MACCS, PubChem, Substructure, Klekota-Roth and 2D atom pairs. Those molecular fingerprints had 9121 bits in total and were calculated using PaDEL(Yap, 2011).
2.4 Model training and evaluation
In the experiment of predicting macro-pKa, the S-pKa dataset was randomly split into training/validation/test set in a 70:15:15 ratio. Graph-pKa and other models were trained on the same training set. The best set of hyperparameters for each model were determined based on the result on the validation set. The search ranges and optimal values of these hyperparameters are provided in Supplementary Table S2. The final model performance was assessed on the test set and two external tests set through three independent runs. The metrics for evaluating model performance were mean absolute error (MAE), root mean squared error (RMSE) and coefficient of determination (R2). The structural similarity between the two molecules was calculated using the 1024-bit Morgan2 fingerprints and the Tanimoto coefficient.
In the experiment of predicting micro-pKa, about 500 molecules that possessed multiple different acidic/basic ionization sites and whose dominant ionization sites had been uniquely assigned by Hunt et al. (2020) were extracted as test data. Those molecules were then removed from the S-pKa Dataset. Graph-pKa was retrained on the remaining dataset with the same set of hyperparameters previously used. The metrics for evaluating the model are consistency rate and difference values. Consistency rate is the probability that the dominant ionization sites of molecules selected by Graph-pKa are the same as that of human experts. Different value is used to quantify the degree of divergence between Graph-pKa and human experts. They are calculated as follows:
| (7) |
| (8) |
| (9) |
where is the most acidic/basic atom of molecule selected by human experts, is the most acidic/basic atoms of molecule predicted by Graph-pKa, is an arbitrary element in , the reason why is a collection is that some molecules have multiple dominant ionization sites with the same ionization ability, is referred to a function of Graph-pKa for atomic pKa prediction.
3 Results and discussion
3.1 Comparison with benchmark methods
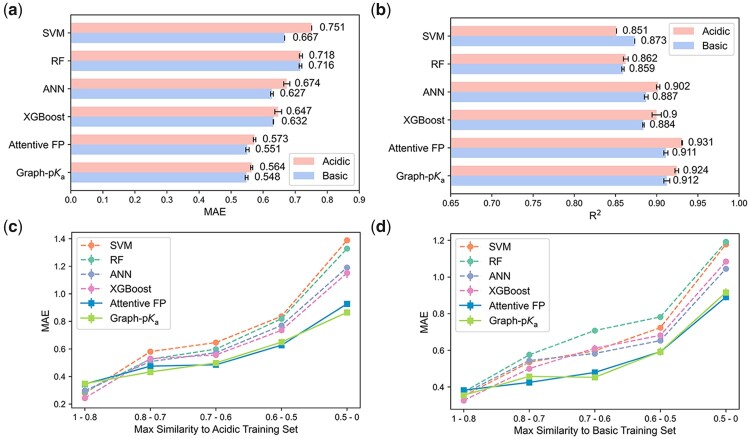
In order to evaluate the performance of Graph-pKa, four conventional machine learning models were implemented and taken as benchmark methods. A kind of combined molecular fingerprints was used as the representation of molecules and the input of these machine learning models, due to its good performance on a previous study for pKa prediction (Mansouri et al., 2019). The comparison between Graph-pKa and other models was carried out on the S-pKa dataset that was randomly divided into training, validation and test set. The performances of those models on the test set are shown in Figure 4. Among the four machine learning models, ANN and XGBoost performed comparatively well, which was consistent with some previous studies (Mansouri et al., 2019; Yang et al., 2020). However, the performances of these two models still obviously fell behind Graph-pKa, which achieved a MAE around 0.55 and a R2 around 0.92 on the test sets (Fig. 4a and b). As known, the performance of QSAR models is closely related to the similarity between predicted molecules and the molecules of the training set. To evaluate the generalization capability of different models, we also calculated the pairwise similarity of test set molecules to the training set molecules, and split the test set molecules into five individual subsets according to their maximum similarity to training set molecules (Supplementary Table S3). Then, the MAE of those models on each subset was compared. As shown in Figure 4c and d, the Graph-pKa outperformed other machine learning models on nearly all similarity subsets, which demonstrated it possesses high robustness and generalization ability. For the molecules with max similarity higher than 0.5 to the training set, the MAE of the model was lower than 0.65. If using it as the threshold for acceptable errors, 81.1% of test molecules were within the applicability domain of the models. Furthermore, the performance of Attentive FP on macro-pKa prediction was not better than that of Graph-pKa, meaning that MIL could endow Graph-pKa with the prediction ability of micro-pKa without significant trade-off on its prediction ability of macro-pKa.
Fig. 4.
The performance of the various model on macro-pKa prediction on the S-pKa dataset. (a,b) The MAE and R2 of those models on the test dataset. (c,d) The MAE of those models for acidic (c) and basic (d) pKa prediction on a series of similarity subsets. Error bars represent standard deviations
3.2 Evaluation on external datasets
The performance of Graph-pKa was further validated by testing against two external datasets that were obtained from two blind pKa prediction challenges named SAMPL6 and SAMPL7. These two challenges were launched by the Drug Design Data Resource Community in 2018 and 2020, respectively. The SAMPL6 dataset comprises 24 kinase inhibitor-like molecules with 31 experimental pKa values, and the SAMPL7 dataset comprises 22 molecules (most are sulfonamides) with 20 experimental pKa values. There are two pKa values not belonging to the most acidic or basic pKa values in the SAMPL6 dataset and two molecules without corresponding experiment pKa values in the SAMPL7 dataset, they were excluded from this testing. The performances of Graph-pKa and some commonly used software and models on these two external datasets are shown in Table 1 and Supplementary Table S4. Graph-pKa achieved a low MAE of 0.594 and 0.758 as well as a high R2 of 0.918 and 0.839 on SAMPL6 and SAMPL7 datasets, respectively, comparable to the performance of those commercial software established based on large collections of proprietary data.
Table 1.
Performance of Graph-pKa and other models on the SAMPL6 and SAMPL7 external test sets
| Dataset | Model name | Model class | MAE | RMSE | R 2 |
|---|---|---|---|---|---|
|
SAMPL6 |
Epik Scana | Commercial | 0.784 | 0.962 | 0.857 |
| Epik Microa | Commercial | 0.783 | 0.972 | 0.854 | |
| ACD/pKaa | Commercial | 0.550 | 0.783 | 0.905 | |
| MoKaa | Commercial | 0.854 | 0.970 | 0.854 | |
| ChemAxona | Commercial | 1.007 | 1.248 | 0.759 | |
| Hunt’s modelb | Academic | 0.687 | 0.864 | 0.885 | |
| Yang’s XGBb | Academic | 0.767 | 1.011 | 0.842 | |
| Yang’s NNb | Academic | 0.832 | 1.141 | 0.799 | |
| OPERAd | Academic | 0.970 | 1.283 | 0.619 | |
|
Graph-pKa |
Academic |
0.594 |
0.726 |
0.918 |
|
| SAMPL7 | Epik Scanc | Commercial | 1.121 | 1.648 | 0.508 |
| ChemAxonc | Commercial | 0.559 | 0.708 | 0.909 | |
| Yang’s XGBc | Academic | 1.476 | 1.622 | 0.523 | |
| Yang’s NNc | Academic | 0.932 | 1.156 | 0.758 | |
| OPERAd | Academic | 2.135 | 2.515 | −3.752 | |
| Graph-pKa | Academic | 0.758 | 0.934 | 0.839 |
The bold entries in the “MAE”, “RMSE”, and “R2” columns represent the best results in corresponding datasets.
The results are cited from a summary of the SAMPL6 challenge results. (https://github.com/samplchallenges/SAMPL6/blob/master/physical_properties/pKa/analysis/).
The results are cited from articles of Hunt et al. (2020) and Yang et al. (2020).
The results of Epik predictions are from Schrödinger Suite 2017; the results of ChemAxon predictions are from ChemAxon Marvin Suite 20.15.0. The results of Yang’s XGB and Yang’s NN are from a webserver (http://pka.luoszgroup.com/prediction).
The results are from OPERA 2.7. Nine pKa values that OPERA2.7 failed to predict were excluded.
Although our Graph-pKa model has achieved satisfactory prediction performance, there are potentially two limitations. Frist, Graph-pKa is only trained to predict the most acidic and basic pKa values and its capability to predict other types of pKa values such as the 2nd strongest acidic and basic pKa values has not been fully evaluated. This is mainly because of the difficulty in the collection, cleaning, and labeling of this kind of training data. Second, the tautomerism of molecules has not been taken into account in Graph-pKa, which means that the model will give different prediction results for different tautomers of the same molecule. We leave this issue to follow-up studies, such as averaging the predicted values of different tautomers.
3.3 Performance on micro-pKa prediction
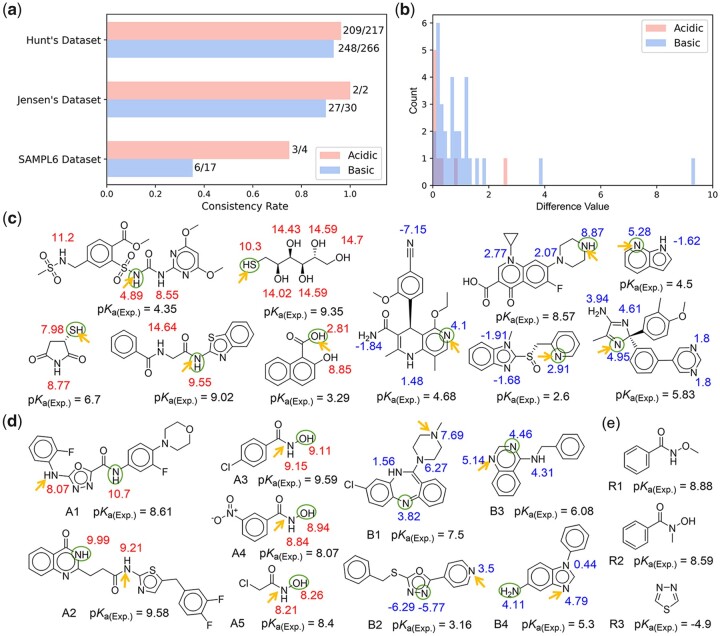
Macro-pKa values can describe the ionization degree of the molecule in the solvent but can't pinpoint the ionization state of each atom in this molecule. To acquire more comprehensive knowledge about the ionization of molecules, the prediction of micro-pKa values is equally important. Thus, the performance of Graph-pKa on predicting micro-pKa was also evaluated here. Unfortunately, the experimental determination of micro-pKa values is highly complicated, and there is currently no available micro-pKa dataset. Given this situation, a Turing-like test was designed to determine if Graph-pKa exhibited the intelligent behavior (i.e. to designate the most acidic/basic atoms in a molecule structure) that was indistinguishable from that of a human expert. The results of expert judgments were obtained from a recent work of Hunt et al. for pKa prediction (Hunt et al., 2020), where each pKa value in their collected dataset (Hunt’s dataset) and two external test sets (Jensen’s dataset and SAMLP6 dataset) was carefully inspected and assigned to a specific site by human experts. As shown in Figure 5a, the overall consistency rates between the most acidic/basic atoms predicted by Graph-pKa and the most acidic/basic atoms selected by the human experts were over 90%. To further quantify the degree of divergence between Graph-pKa and human experts on those controversial molecules, the difference values of the predicted pKa between the most acidic/basic atoms predicted by Graph-pKa and those selected by the human experts are shown in Figure 5b. It could be observed that the difference values of 80% these controversial molecules were within 1.2 pKa units, which indicated that the divergences between Graph-pKa and human expert mainly derived from those molecules whose several atoms had similar ionization capability.
Fig. 5.
Application of Graph-pKa to predict the dominant ionization sites of molecules. (a) The consistency rates between the prediction of Graph-pKa and the judgment of human experts. (b) The distribution of difference values representing the degree of divergence between Graph-pKa and human experts on controversial molecules. (c,d) Some examples of molecules on which the predictions of Graph-pKa and human experts are consistent (c) and different (d), the arrows and circles denote to the dominant ionization sites selected by Graph-pKa and human experts, respectively, red and blue numbers, respectively, denote to the predicted acidic and basic pKa values of atoms by Graph-pKa. (e) Some molecules and their pKa values for reference
Some examples of agreement and disagreement between Graph-pKa and human experts are respectively shown in Figure 5c and d. In the assignment of the most acidic atoms, two controversial molecules of note were A1 and A2, and most of the others were hydroxamic acid derivatives. Hunt et al. attributed the acidities of hydroxamic acid derivatives all to their hydroxyls. In fact, the dissociation ability of hydroxylic hydrogen and amino hydrogen in hydroxamic acids was quite similar (Bartmess, 2010) (also see R1, R2 in Fig. 5e, http://ibond.nankai.edu.cn), and the prediction results of Graph-pKa supported their equivalent protonation potential. In the assignment of the most basic atoms, the two most controversial molecules were B1 and B2. Our prediction for B1 was supported by a record from PubChem that the pKa value of the amine in B1 was 7.75 (https://pubchem.ncbi.nlm.nih.gov/compound/135398737). In addition, the basicity of the 1,3,4-Oxadiazol ring in B2 should be very weak, given that the pKa of 1,3,4-thiadiazole was only -4.9 (R3 in Fig. 5e, https://www.scripps.edu/baran/heterocycles/Essentials1-2009.pdf). According to Graph-pKa prediction, the basicity of B2 was attributed to the pyridine ring, instead of the 1,3,4-Oxadiazol ring. This assignment was further confirmed by quantum chemical calculation. As shown in Supplementary Figure S4, the protonation energies of nitrogen atom in the pyridine ring were -5.25 kcal/mol, significantly lower than that of nitrogen atoms in the 1,3,4-Oxadiazol ring (4.74 and 5.39 kcal/mol). The methods of quantum chemistry calculation are described in Supplementary Material. Besides, two molecules (B3, B4) in SAMPL6 datasets (Işık et al., 2018), whose dominant ionization sites have been determined by nuclear magnetic resonance, are also shown in Figure 5d. The predicted results of Graph-pKa were consistent with the experimental results. The above results demonstrated that Graph-pKa performed outstandingly in the prediction of micro-pKa. It is impressive that in many cases the capability of Graph-pKa to locate the most acidic/basic sites of molecules is equivalent to or better than that of human experts, while all the chemical insight has been learned without explicit supervision in multi-instance learning. It can be expected that when there are more available training data in the future, the capability will be further improved.
3.4 Visualization of the atomic embeddings
In order to visualize the features of the atoms learned by the Graph-pKa model, the embeddings in the last hidden layer of several types of acidic ionization sites in the training data were extracted and submitted to principal component analysis. As shown in Figure 6, after training, the atomic embeddings from phenol hydroxyl, carboxyl, and sulfonamide groups were respectively gathered together. However, the distributions of atomic embeddings from alcoholic hydroxyl and amide groups were still relatively dispersed. These patterns suggest that alcoholic hydroxyl or amide groups in different chemical environments exhibit relatively larger variances, posing challenges for accurate micro-pKa prediction. We speculated that a possible reason was that, although alcoholic hydroxyl and amide groups widely existed in the training set, they have less contribution to the macro-pKa of the whole molecule due to their weak acidity. Therefore, they had lower weights and were less supervised during model training. Three molecules and their atomic embeddings visually display such a situation. After training, the atomic embeddings from carboxyl groups of the three similar molecules are close, whereas the atomic embeddings from amide groups of the three molecules are dispersed. Apparently, adding more samples whose dominant ionization groups are alcoholic hydroxyl groups or amide groups into training data may alleviate this problem.
Fig. 6.

Visualizing the atomic embeddings in last hidden layer using principal component analysis
3.5 Web server for the prediction of pKa
For the convenience of the community, a free web server wrapping the Graph-pKa model has been developed (https://pka.simm.ac.cn/). This web server was built using the python language and could be simultaneously accessed by multiple users. The web server can take multiple types of inputs including drawing a molecule from the molecular editor or uploading a txt/mol/sdf file. There are two main functions in this web server: pKa prediction and similarity search (Supplementary Fig. S5). In the pKa prediction module, the most acidic/basic pKa values and their corresponding micro-pKa values of the input molecule are predicted. The Monte Carlo dropout is used to evaluate the uncertainty of the prediction results and calculate the 95% confidence interval of the predicted value (Gal and Ghahramani, 2016). It is noteworthy that, due to our definition of possible ionization sites and the processing of input molecules, the web server does not support the pKa prediction for C-H bonds and ionized molecules. In the similarity search module, the most acidic/basic atoms of the molecules from the S-pKa dataset and the most acidic/basic atoms of the molecule input by the user are first predicted by Graph-pKa. Then, the embeddings of those predicted most acidic/basic atoms in the last hidden layer are extracted. Finally, the Euclidean distances between the atomic embeddings of the input molecule and that of the molecules in the S-pKa dataset are calculated. If the Euclidean distance is close enough (the threshold is set as less than 0.05), molecules are considered to be similar, and for each input molecule, up to four similar molecules and their experimentally determined pKa values will be output for reference.
4 Conclusions
In this work, we have developed a novel in silico pKa prediction model named Graph-pKa. Combining multi-instance learning into graph neural network, Graph-pKa not only outperforms those conventional machine learning models based on molecular fingerprints in predicting macro-pKa, but more significantly, can learn the micro-pKa values of atoms through training against the macro-pKa values of molecules. A Turing-like test demonstrated that it gained chemical insights to locate the most acidic/basic sites of molecules, which compared favorably with that of human experts. Such micro-pKa inference ability greatly enhances the interpretability and practicability of this model. Furthermore, in Graph-pKa, the fitting and prediction of macro-pKa are all dependent on the reasoning of micro-pKa, which can also avoid shortcut learning to some extent (Geirhos et al., 2020). In the end, a Web application based on Graph-pKa model has been made freely available at https://pka.simm.ac.cn.
Funding
This work was supported by the Project supported by Shanghai Municipal Science and Technology Major Project, National Natural Science Foundation of China [81773634] and Tencent AI Lab Rhino-Bird Focused Research Program [JR202002].
Conflict of Interest: none declared.
Supplementary Material
Contributor Information
Jiacheng Xiong, Drug Discovery and Design Center, State Key Laboratory of Drug Research, Shanghai Institute of Materia Medica, Chinese Academy of Sciences, Shanghai 201203, China; College of Pharmacy, University of Chinese Academy of Sciences, Beijing 100049, China.
Zhaojun Li, Development Department, Suzhou Alphama Biotechnology Co., Ltd, Suzhou City 215000, China.
Guangchao Wang, College of Computer and Information Engineering, Dezhou University, Dezhou City 253023, China.
Zunyun Fu, Drug Discovery and Design Center, State Key Laboratory of Drug Research, Shanghai Institute of Materia Medica, Chinese Academy of Sciences, Shanghai 201203, China.
Feisheng Zhong, Drug Discovery and Design Center, State Key Laboratory of Drug Research, Shanghai Institute of Materia Medica, Chinese Academy of Sciences, Shanghai 201203, China; College of Pharmacy, University of Chinese Academy of Sciences, Beijing 100049, China.
Tingyang Xu, Tencent AI Lab, Tencent, Shenzhen 518057, China.
Xiaomeng Liu, Drug Discovery and Design Center, State Key Laboratory of Drug Research, Shanghai Institute of Materia Medica, Chinese Academy of Sciences, Shanghai 201203, China; College of Pharmacy, University of Chinese Academy of Sciences, Beijing 100049, China.
Ziming Huang, Drug Discovery and Design Center, State Key Laboratory of Drug Research, Shanghai Institute of Materia Medica, Chinese Academy of Sciences, Shanghai 201203, China; College of Pharmacy, University of Chinese Academy of Sciences, Beijing 100049, China.
Xiaohong Liu, Drug Discovery and Design Center, State Key Laboratory of Drug Research, Shanghai Institute of Materia Medica, Chinese Academy of Sciences, Shanghai 201203, China; Development Department, Suzhou Alphama Biotechnology Co., Ltd, Suzhou City 215000, China; Shanghai Institute for Advanced Immunochemical Studies, and School of Life Science and Technology, ShanghaiTech University, Shanghai 200031, China.
Kaixian Chen, Drug Discovery and Design Center, State Key Laboratory of Drug Research, Shanghai Institute of Materia Medica, Chinese Academy of Sciences, Shanghai 201203, China; College of Pharmacy, University of Chinese Academy of Sciences, Beijing 100049, China.
Hualiang Jiang, Drug Discovery and Design Center, State Key Laboratory of Drug Research, Shanghai Institute of Materia Medica, Chinese Academy of Sciences, Shanghai 201203, China; College of Pharmacy, University of Chinese Academy of Sciences, Beijing 100049, China; Shanghai Institute for Advanced Immunochemical Studies, and School of Life Science and Technology, ShanghaiTech University, Shanghai 200031, China.
Mingyue Zheng, Drug Discovery and Design Center, State Key Laboratory of Drug Research, Shanghai Institute of Materia Medica, Chinese Academy of Sciences, Shanghai 201203, China; College of Pharmacy, University of Chinese Academy of Sciences, Beijing 100049, China.
References
- Bartmess J.E. (2010) The Brønsted Acid/Base Character of Hydroxylamines, Oximes and Hydroxamic Acids. Patai's Chemistry of Functional Groups. John Wiley & Sons, Ltd., Chichester, UK.
- Carbonneau M.-A. et al. (2018) Multiple instance learning: a survey of problem characteristics and applications. Pattern Recognit., 77, 329–353. [Google Scholar]
- Charifson P.S., Walters W.P. (2014) Acidic and basic drugs in medicinal chemistry: a perspective. J. Med. Chem., 57, 9701–9717. [DOI] [PubMed] [Google Scholar]
- Defferrard M. et al. (2016) Convolutional neural networks on graphs with fast localized spectral filtering. In: Proceedings of the 30th International Conference on Neural Information Processing Systems. New York, USA, pp. 3844–3852.
- Duvenaud D. et al. (2015) Convolutional networks on graphs for learning molecular fingerprints. In: Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, Canada, pp. 2224–2232.
- Gal Y., Ghahramani Z. (2016) Dropout as a Bayesian approximation: representing model uncertainty in deep learning. In: International Conference on Machine Learning. New York, USA, pp. 1050–1059.
- Gaulton A. et al. (2017) The ChEMBL database in 2017. Nucleic Acids Res., 45, D945–D954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geirhos R. et al. (2020) Shortcut learning in deep neural networks. Nat. Mach. Intell., 2, 665–673. [Google Scholar]
- Gilmer J. et al. (2017) Neural message passing for quantum chemistry. In: International Conference on Machine Learning. Sydney, Australia, pp. 1263–1272.
- Hunt P.A. et al. (2020) Predicting pKa using a combination of semi-empirical quantum mechanics and radial basis function methods. J. Chem Inf. Model., 60, 2989–2997. [DOI] [PubMed] [Google Scholar]
- Işık M. et al. (2018) pka measurements for the sampl6 prediction challenge for a set of kinase inhibitor-like fragments. J. Comput. Aided Mol. Des., 32, 1117–1138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manallack D.T. (2007) The pKa distribution of drugs: application to drug discovery. Perspect. Med. Chem., 1, 25–28. [PMC free article] [PubMed] [Google Scholar]
- Manallack D.T. et al. (2013) The significance of acid/base properties in drug discovery. Chem. Soc. Rev., 42, 485–496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mansouri K. et al. (2019) Open-source QSAR models for pKa prediction using multiple machine learning approaches. J. Cheminf., 11, 1–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niepert M. et al. (2016) Learning convolutional neural networks for graphs. In: International Conference on Machine Learning. New York, USS, pp. 2014–2023.
- Roszak R. et al. (2019) Rapid and accurate prediction of p K a values of C–H acids using graph convolutional neural networks. J. Am. Chem. Soc., 141, 17142–17149. [DOI] [PubMed] [Google Scholar]
- Rupp M. et al. (2011) Predicting the pKa of small molecules. Comb. Chem. High Throughput Screen., 14, 307–327. [DOI] [PubMed] [Google Scholar]
- Sun M. et al. (2020) Graph convolutional networks for computational drug development and discovery. Brief. Bioinform., 21, 919–935. [DOI] [PubMed] [Google Scholar]
- Wang S. et al. (2019) RMDL: recalibrated multi-instance deep learning for whole slide gastric image classification. Med. Image Anal., 58, 101549. [DOI] [PubMed] [Google Scholar]
- Wishart D.S. et al. (2018) DrugBank 5.0: a major update to the DrugBank database for 2018. Nucleic Acids Res., 46, D1074–D1082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiong Z. et al. (2020) Pushing the boundaries of molecular representation for drug discovery with the graph attention mechanism. J. Med. Chem., 63, 8749–8760. [DOI] [PubMed] [Google Scholar]
- Yang Q. et al. (2020) Holistic prediction of pKa in diverse solvents based on machine-learning approach. Angew. Chem. Int. Ed., 59, 19282–19291. [DOI] [PubMed] [Google Scholar]
- Yap C.W. (2011) PaDEL‐descriptor: an open source software to calculate molecular descriptors and fingerprints. J. Comput. Chem., 32, 1466–1474. [DOI] [PubMed] [Google Scholar]
- Zhang Z. et al. (2021) FraGAT: a fragment-oriented multi-scale graph attention model for molecular property prediction. Bioinformatics, 37, 2981–2987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou Y. et al. (2017) Adaptive pooling in multi-instance learning for web video annotation. In: Proceedings of the IEEE International Conference on Computer Vision Workshops. Venice, Italy, pp. 318–327.
- Zhou Z.-H. (2018) A brief introduction to weakly supervised learning. Natl. Sci. Rev., 5, 44–53. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.