Optimized Artificial Neural Network for Evaluation: C4 Alkylation Process Catalyzed by Concentrated Sulfuric Acid

Abstract

In this work, an artificial neural network was first achieved and optimized for evaluating product distribution and studying the octane number of the sulfuric acid-catalyzed C4 alkylation process in the stirred tank and rotating packed bed. The feedstock compositions, operating conditions, and reactor types were considered as input parameters into the artificial neural network model. Algorithm, transfer function, and framework were investigated to select the optimal artificial neural network model. The optimal artificial neural network model was confirmed as a network topology of 10-20-30-5 with Bayesian Regularization backpropagation and tan-sigmoid transfer function. Research octane number and product distribution were specified as output parameters. The artificial neural network model was examined, and 5.8 × 10^–4 training mean square error, 8.66 × 10^–3 testing mean square error, and ±22% deviation were obtained. The correlation coefficient was 0.9997, and the standard deviation of error was 0.5592. Parameter analysis of the artificial neural network model was employed to investigate the influence of operating conditions on the research octane number and product distribution. It displays a bright prospect for evaluating complex systems with an artificial neural network model in different reactors.

1. Introduction

As the number of motor vehicles increases, the gasoline quality of vehicles is of great significance to the environment.¹ Alkylate oil is considered as a typical clean fuel blending component with a low-sulfur content and high research octane number (RON),² which is obtained from the alkylation process of isobutane and butene catalyzed by strong acid. Currently, large-scale industrial plants still adopt concentrated sulfuric acid (H₂SO₄) as the mainstream alkylation catalyst.³ The alkylation process has several rapid reactions with a large number of products, many of them isomers, which make the reaction network and product distribution not easy to deal with,⁴ and the trimethylpentanes (TMPs, RON = 100–109.6) are main products.⁵ Besides, there are various byproduct components with different RONs, including C_5–7 (light ends, LEs, RON = 24.8–93.0), dimethylhexanes (DMHs, RON = 55.5–76.3), methylheptanes (RON = 21.7–26.8), and C₉₊ (heavy ends, HEs, RON = 70–91).⁶ Moreover, RON is regarded as a core index of alkylate oil, and it can be measured by running the fuel in a cooperative fuel research engine with a standard test condition.⁷ This method is time-consuming, expensive, and labor-intensive. In the lab, product components are usually analyzed by gas chromatography, and RON is calculated by eq 1

1

where RON_i is the RON of each component and y_i represents the yield of each component.⁶

Owing to the low reciprocal solubility of hydrocarbons and H₂SO₄, the isobutane/butene alkylation system is heterogeneous,⁸ and reactions occur either in the acid phase or phase interface,⁹ which lead to the complex product component distribution. Therefore, mass transfer among the different phases plays a vital role in the alkylation process.¹⁰ Various reactors have been applied to intensify alkylation processes, such as the stirred tank reactor (STR), STRATCO horizontal stirred reactor,⁸ eductor reactor,¹¹ liquid–liquid cyclone reactor,¹² microstructured reactor,¹³ rotating packed bed (RPB),¹⁴ and so forth. Lots of research studies indicate that the RON and product components are dramatically affected by feedstock compositions, reactor structure, operating conditions, and so on. Thus, some mathematical and correlation models were proposed for the estimation on RON and distribution of products in the specified reactors. Nurmakanova et al. calculated the thermodynamic characteristics and reaction kinetics factors using density functional theory (DFT) to build a mathematical model of isobutane alkylation with olefins catalyzed by H₂SO₄ in a hollow horizontal cylinder, which was used to predict the product distribution of alkylation caused by the changes in the feedstock compositions.¹⁵ Ivashkina et al. also employed the DFT calculation and developed a mathematical model in a STRATCO reactor to define the influence of feedstock compositions on product distribution and RON of alkylate oil.¹⁶ Besides, Liu et al. established a correlation model of the ionic liquid catalyzed alkylation process in STR, and the effects of different operating conditions on the product distribution and RON were associated effectively in this model.⁶ These mathematical models demanded plenty of foundational data based on thermodynamic characteristics, reaction kinetics factors, reaction mechanisms, and reactor characteristics, which were difficult to be acquired entirely for complex alkylation processes. Various reactors have different equipment structures and hydrodynamics parameters. Hence, the existing correlation model relied heavily on each variable used and only worked for the specified reactor, where the RON and product components are simply related to operating conditions. In the view of different alkylated reactors, three features significantly influence the accurate prediction of the alkylation process, which is given as follows: (1) the different feedstock components and operating conditions on alkylation processes;¹⁷ (2) the intricate reaction mechanisms for complex product distribution;¹⁸ and (3) the diverse mass transfer characteristic of each reactor. Therefore, the RON and product distribution in different research systems is a multidimensional nonlinear issue, and a novel model is worthy of construction for effectively solving multidimensional nonlinear problems.

Deep learning has made a significant progress in addressing the issues that have been resisting the artificial intelligence community for many years,¹⁹ and it has been proven to be excellent in discovering a intricate structure of the multidimensional data.^20,21 There were kinds of successful applications in deep learning, such as crystal identification and discovery,²² thermodynamic properties prediction for complex materials,²³ predictions of chemical reactions,²⁴ process performances,²⁵⁻³¹ and so forth. The artificial neural network (ANN), as a typical sort of deep learning, is prevalently and widely employed in the chemistry and chemical industry.³²⁻⁴⁰ The ANN can learn and adapt in response to the given input–output patterns and adjust itself to minimize the fitting error. Furthermore, the ANN can ascertain the essential of relationships.⁴¹ When the ANN was applied, there is no need to consider the inherent mechanism of processes or phenomena. Some highly nonlinear, multidimensional, and complex problems can be solved efficiently by the ANN model. As a part of intelligent engineering, the ANN displays the tremendous potential for different chemical systems via the training of experimental data.

In this work, the ANN model was first adopted and optimized to evaluate the C4 alkylation process catalyzed by H₂SO₄ in the STR and RPB. Ten-independent input parameters, including feedstock compositions, operating conditions, and reactor types, were involved in the ANN model. Three significant elements of the ANN model, which contained algorithm, transfer function, and framework, were investigated to select the most suitable model. The product distribution and RON of the H₂SO₄-catalyzed isobutane/butene alkylation process both in the STR and RPB were predicted, and the parameter analysis was conducted.

2. Model Section

As a basic building block, we used a fundamental ANN model, which had the feedback and feedforward capabilities to fitting the multidimensional and nonlinear issue. The ANN framework and result analysis process were stated in the following text.

2.1. Data Preparation

Limited by the publicly reported data, the feasibility of the ANN model as a general model for multiple reactors was demonstrated by taking the STR and RPB data as examples. 36% data points were obtained in the STR, and 64% data points were obtained in the RPB.^14,42 The detail data sets are given in Tables S1–S3 of the Supporting Information. The structures of STR and RPB are presented in Figure 1. The operating conditions and reactor types were considered as input parameters of the ANN model, and the detailed data have been listed in Table 1. Particularly, as the input parameters, the mixing state in STR was set as Boolean, who only has the value of true or false. The true represented the mixing with feeding in STR, and the false represented the mixing after feeding in STR.

Figure 1.

Schematic diagram of STR and RPB. (a) Structure diagram of stirring paddle and vessel body in STR; (b) structure diagram of RPB and size of packing.

Table 1. Input Parameters of the ANN Model.

no.	input parameters	ranges	data type
1	reaction time(t)	2–15 min in STR 2–10 min in RPB	numeric
2	temperature (T)	0–8 °C	numeric
3	volume ratio of acid to hydrocarbon (A/HC)	0.5–2	numeric
4	stirring speed of STR (NSTR)	0–1400 rpm	numeric
5	rotational speed of RPB (NRPB)	none or 150–1200 rpm	numeric
6	pressure (P)	0.3–1 MPa	numeric
7	mole percentage of isobutane (n1)	86.5–96.8%	numeric
8	mole percentage of 2-butene (n2)	0–13.5%	numeric
9	mole percentage of isobutene (n3)	0–3.2%	numeric
10	mixing with/after feeding in STR (mSTR)	mixing with feeding or mixing after feeding in STRa	Boolean

^aIn the STR, mixing with feeding or mixing after feeding would affect the product distribution.⁴²

RON was determined by the product distribution of alkylate oil. In this work, the yield of C_5–7 (y_C5–7), C₈ (y_C8), C₉₊ (y_C9+), TMPs (y_TMPs), and DMHs (y_DMHs), the yield ratio of TMPs to DMHs (TMPs/DMHs), and RON were considered as the output parameters. The relationship of the product distribution is shown in eq 2. TMPs and DMHs were the two components with the highest and lowest RON in octane, respectively, and their ratio was considered as eq 3.

2

3

Equations 2 and 3 reveal the two simple linear programming problems in this multidimensional issue. Hence, y_C5–7, y_C9+, y_TMPs, y_DMHs, and RON were training in this model. TMPs/DMHs and y_C8 were marked as checking parameters through linear programming. At first, the absolute value of the maximum fitting error was required below 100% for the preliminary selection. When the most maximum error absolute value of some ANN models below 50% frequently, the check standard limited as 50%. In other words, if the absolute value of maximum error over 50%, the ANN results would be given up and retrained again.

In the training step, the data were divided into the training (70%), testing (15%), and validation (15%) groups, randomly. All data were normalized in −1 to 1 at first avoiding a large gap among the original data. The mapping relations of data normalization were retained to reverse the fitting results.

2.2. ANN Framework

The ANN model was trained by the most input data with the corresponding output data (input/output pairs), which obtained from literatures.^14,42 Each set of inputs produced a specific set of target outputs.⁴³

Figure 2 shows the calculation flow chart of the ANN model. It is well known that main elements of the ANN, such as transfer function, algorithm, and framework,⁴³ which needs to be considered carefully during the process of designing and training. The term “framework” refers to the layer number of the ANN and the neuron number of each layer. In general, the layers are consisted of an input layer, one or more hidden layers, and an output layer. The number of neurons in the input layer and the output layer is determined by the numbers of input and output parameters, respectively. In order to explore the optimal framework, the number of neurons in each hidden layer and the number of the hidden layers need to be determined. The nodes are similar to the neurons of the nervous system of humans communicating with the brain. The nodes of the input layer triggered signals to the nodes of the hidden layer, and the hidden layer may be single or multilayered. Afterward, these signals from the hidden nodes propagate to the output layer and generate the output signal.⁴⁴ The training process consists of adjusting the weight associated with each connection between neurons until the predicted outputs for each set of input–output data were as close as possible to the experimental data.

Figure 2.

Calculation flow chart of the ANN model. (k₁ⁱ and b₁ⁱ are the weights and biases of the first hidden layer; k_j^u and b_j^u are the weights and biases of each next hidden layer; k_o^v and b_o^v are the weights and biases of the output layer).

The most widely widespread use of the network type is a multilayered feedforward network trained with the back-propagation learning algorithm. The back-propagation learning algorithm is based on the selection of a suitable error function, whose values are determined by the experimental and predicted outputs of the network.

2.3. Statistical Analysis

The mean square error (MSE) was employed as a standard index to investigate the model accuracy, which can be computed via eq 4.

4

where s_i represents the predicted value, e_i means the experimental value (including y_C5–7, y_C8, y_C9+, y_TMPs, y_DMHs, TMPs/DMHs, and RON), and n is the number of the aggregate data.

The definition of the correlation coefficient (R²) was on behalf of the percentage of the predicted value matching the experimental value. R² is determined as follows

5

where e̅ shows the average value of the experimental results. R² is always between 0 and 1. In general, the higher the R², the better the model fits the data.

The standard deviation of error (STD_error) can be regarded as an essential indicator of the estimation and was mostly used by researchers, which refers to a group of statistics that provide information about the dispersion of the predicted values.²⁹ STD_error was calculated as given below

6

where the error indicates the residual of the predicted and experimental value and 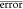means the average of errors.

3. Results and Discussion

We used a workstation (Dawning Information Industry Co., LTD.) with double Intel Xeon Silver 4116 CPUs (2.1 GHz and 12 cores 24 threads), 128 GB DDR4 2666 MHz error correcting code memory, and a NVIDIA Quadro P2000 GPU. The data normalization, ANN model realization, and result check were performed in MATLAB.

3.1. Transfer Function Choosing

The transfer function was the ligament between the upper and lower neural network layers. The tan-sigmoid transfer function, log-sigmoid transfer function, and purelin function were considered in this model, and the functions were as follows

7

8

9

where x_i was input data, f(x_i) stood for on behalf of output data.

From the input layer to the final hidden layer, the data were learned and feedbacked to modify the weights and biases. Nonlinear functions were more suitable in these parts. Because of the input-data normalization in −1 to 1, only the tan-sigmoid can hold the data integrity. Herein, the tan-sigmoid was chosen as the transfer function from the input layer to the hidden layers. The output layer was just a data export without data learning ability, which means that the purelin function was an appropriate choice between the final hidden layer and the output layer.

3.2. Algorithm Selection

As the core of the model, the algorithm should be considered cautiously. There were 13 algorithms listed in Table 2. Besides, the number of neurons in the first hidden layer was dependent on both the number of inputs and inner relationship of inputs. Each neuron covered some characteristic of all the inputs. When several input variables had the apparent linear fitting relationship, the number of neurons can be reduced. In the alkylation process, the effects of each operating condition are nonlinear and irreplaceable. Hence, the inputs constituted a multidimensional and multicharacteristic matrix and needed at least 10 neurons to achieve the ANN model. In order to achieve the quick calculation and comparison,⁴³ an ANN model with 10 nodes in the single hidden layer was applied to test 13 algorithms.

Table 2. Thirteen Tested Algorithms in the ANN Model.

no.	algorithm name	abbreviation
1	BFGS quasi-Newton backpropagation	BFG
2	conjugate gradient backpropagation with Powell–Beale restarts	CGB
3	conjugate gradient backpropagation with Fletcher–Reeves updates	CGF
4	conjugate gradient backpropagation with Polak–Ribiére updates	CGP
5	gradient descent backpropagation	GD
6	gradient descent with adaptive learning rate backpropagation	GDA
7	gradient descent with momentum backpropagation	GDM
8	gradient descent with momentum and adaptive learning rate backpropagation	GDX
9	Levenberg–Marquardt backpropagation	LM
10	one-step secant backpropagation	OSS
11	resilient backpropagation	RP
12	scaled conjugate gradient backpropagation	SCG
13	bayesian regularization backpropagation	BR

Figure 3 displays the MSEs of different algorithms in the ANN model with the tan-sigmoid as transfer function, and the separated figures are listed in Figure S1 in the Supporting Information. From the comparison of algorithms, the MSE curves of BFG, CGF, CGB, SCG, and OSS had some similar features, where the training MSE curves were divergent and the testing MSE curves were prone to fall in local nadir. Local nadir affected the convergence significantly, and it was difficult to seek out the authentic convergence. The GD and its derivative algorithms (GDX, GDM, and GDA) had the problem of slow convergence. Besides, the MSE curves of GDA were oscillating. The CGP and RP were also not recommended because they both had the issue that the testing MSE curves had local valley and the training MSE curves did not converge totally. Based on the LM model, training MSE had a sharp gradient decline, which had the apparent local valley point and influenced the training MSE curve to converge. However, testing the MSE curve was divergent directly. The convergence speed of the BR algorithm was fast, and the BR model was not dropped into the local nadir. Hence, BR was the optimal choice, and it was adopted in the following models. The training MSE was 1.624 × 10^–3 and the testing MSE was 5.245 × 10^–2, and all the MSEs of each algorithm are presented in Table 3.

Figure 3.

MSEs of different algorithms in the ANN model.

Table 3. Comparison of Different Algorithms in ANN Models.

no.	algorithms	hidden nodes	max. error %	training MSE × 102	testing MSE × 102
1	BFG	10	55%	0.164	1.651
2	CGB	10	50%	0.156	3.036
3	CGF	10	67%	0.078	12.848
4	CGP	10	67%	0.207	2.200
5	GD	10	86%	0.891	3.757
6	GDA	10	86%	0.541	2.107
7	GDM	10	95%	1.484	2.355
8	GDX	10	75%	4.641	3.462
9	LM	10	61%	0.082	263.479
10	OSS	10	55%	0.277	2.738
11	RP	10	61%	0.216	3.783
12	SCP	10	68%	0.178	19.883
13	BR	10	46%	0.162	5.245

3.3. Network Optimization

Because the algorithm was determined, the number of layer nodes and number of hidden layers were further optimized. ANN models with different numbers of nodes and different hidden layers were investigated in Table 4. When node numbers in the first hidden layer increased to 20, the max error was decreased from 46 to 40% of 10 nodes. The training MSE of 20 nodes was close to the model of 10 nodes, but the testing MSE decreased to 3.159 × 10^–2. Therefore, 20 nodes in the first hidden layer were the optimal choice. Although the number of nodes in the first hidden layer increased, the model still cannot fit well with the data due to the fitting error and the MSEs were large. Afterward, double hidden layers were explored with 20 nodes in the first layer. As a consequence, the model with 30 nodes in the second layer has the lowest MSE and deviation. The max error declined to 22%. The training MSE was only 5.8 × 10^–4, and the testing MSE dropped to 8.66 × 10^–3. When nodes in the second hidden layer were further added, the overfitting phenomenon would occur in the model. The overfitting would appear excellent fitting of training data, but it would lose the equal fitting effect of the testing data. Therefore, the optimal ANN model consists of 20–30 hidden topological layers, tan-sigmoid transfer function from the input layer to the second hidden layer, and purelin transfer function in the output layer.

Table 4. Comparison of Different Structures in ANN Models.

no.	algorithms	hidden nodes	max. error %	training MSE × 102	testing MSE × 102
1	BR	10	46%	0.162	5.245
2	BR	20	40%	0.170	3.159
3	BR	20, 10a	44%	0.075	1.221
4	BR	20, 20a	25%	0.074	1.200
5	BR	20, 30a	22%	0.058	0.866
6	BR	20, 40a	22%	0.071	0.950
7	BR	20, 50a	31%	0.063	2.070

^aIt is a double-hidden layer network.

Figures 4 and 5 exhibit convergence and deviations of the double hidden layer model with 20 and 30 nodes. As displayed in Figure 4, the MSE converged within 2245 epochs. The training MSE and testing MSE were 5.8 × 10^–3 and 8.66 × 10^–3, respectively. The linear correlation equation between experimental results and ANN predicted values was y = 0.9992x (fairly close to y = x), and R² was 0.9997. STD_error of this model was 0.5592. Consequently, the model output was fitting to the experimental data dramatically. In Figure 5a, the deviation among the whole experimental data and ANN predicted data was within ±22%. Figure 5b–h representsdeviations of y_C5–7, y_C8, y_C9+, RON, y_TMPs, y_DMHs, and TMPs/DMHs. Especially, the deviation of RON was within ±2%, as presented in Figure 5e. Herein, an optimal ANN model was completed as the network topology of 10-20-30-5 with Bayesian Regularization backpropagation and tan-sigmoid transfer function.

Figure 4.

Convergence curves of training MSE and testing MSE with epochs in 20 and 30 nodes in double hidden layers.

Figure 5.

Deviations of 20 and 30 nodes in two hidden layers. (a) Whole deviation between the experimental results and ANN predicted values; (b) deviations of y_C5–7; (c) deviations of y_C8; (d) deviations of y_C9+; (e) deviations of RON; (f) deviations of y_TMPs; (g) deviations of y_DMHs; and (h) deviations of TMPs/DMHs.

Furthermore, the influence of input parameters on output parameters was obtained by parameter analysis from the optimal ANN model. Parameter analysis was obtained by multiplying weights between each layer, as shown in eq 10,²⁸ and it is shown in Figure 6.

10

Figure 6.

Parameter analysis among inputs and outputs.

The numerical value of parameter analysis indicated whether the input parameter has a positive or passive effect on the output parameter including the influence degree. According to weights comparison of parameter analysis in RON, A/HC > t > N_RPB > n₁ ≈ P ≈ N_STR (positive effects), and n₃ > T > n₂ (negative effects). By contrast, A/HC and t has dramatic effects on the RON. In the view of current reports and industrial processes, A/HC was usually around 1.^8,45−47 However, the mass transfer and micromixing of the reactor would affect t; thus, 5–6 min was the optimal choice both in RPB and STR.^14,42 Then, raising the ratio of isobutane to butene (n₁/n₂ or n₁/n₃), increasing N_RPB, and decreasing T were important for producing the better alkylate oil. When the weight of n₃ is larger than that of n₂, 2-butene was beneficial for obtaining higher quality alkylate oil rather than isobutene. In Figure 5, m_STR was beneficial for improving the high-RON components, indicating that the hydrocarbon should be fed along with liquid acid during the process. Last but not the least, P and N_STR, which were able to control the liquid phase of hydrocarbon and the liquid–liquid mixing, respectively, were considered as experimental conditions. N_RPB > N_STR meant that the RPB was more suitable than the STR to intensify the liquid–liquid two-phase mass transfer and micromixing for the H₂SO₄ alkylation process.¹⁴ The ANN model was able to learn the experimental data of various reactors independently and obtain a multidimensional nonlinear model. By the method of parameter analysis, the effects of different conditions on product quality were obtained and assessed. RPB and STR were also compared and evaluated in the ANN model. As a consequence, the ANN model has excellent prospects in the field of multidimensional data simulation.

4. Conclusions

ANN has been adopted successfully to develop an optimal model for the prediction and estimation of the product distribution and RON synchronously in the RPB and STR. Various influential variables (including feedstock compositions, operating conditions, and reactor types) were considered as independent factors. Three significant factors, transfer function, training algorithm, and framework, were investigated to obtain the optimal ANN model: a network topology of 10-20-30-5 with the BR main algorithm and tan-sigmoid transfer function. By the method of the ANN model, the obtained results were more realistic, and it has the ability to tolerate greater noise in the data set, where a similar level of correlation was obtained between the experimental and predicted product qualities for the training set, the testing set, and the validation set. The ANN model was examined to obtain the 0.58 × 10^–3 training MSE, 0.866 × 10^–2 testing MSE, and ±22% deviation for the global data set, occupying R² = 0.9997 and STD_error = 0.5592. Particularly, the ANN model shows a much higher correlation with a deviation of ±2% between the experimental and predicted values for predicting RON. Parameter analysis of the ANN model was applied to obtain the influence of operating conditions on products in STR and RPB, displaying that the rotational speed deeply affected the alkylation process. The unified ANN model has an obvious superiority in quickly predicting the product distribution and RON for the alkylation process, expressing a promising application prospect in solving multidimensional nonlinear complex systems.

Glossary

Nomenclatures2-col

RON

research octane number, dimensionless

MSE

mean square error, dimensionless

R²

correlation coefficient, dimensionless

STD_error

standard deviation of error, dimensionless

RON_i

RON of each component, dimensionless

y_i

yield of each component, %

t

reaction time, min

T

reaction temperature, °C

A/HC

volume ratio of acid to hydrocarbon, dimensionless

N_STR

stirring speed of STR, rpm

N_RPB

rotational speed of RPB, rpm

P

system pressure, MPa

n₁

mole percentage of isobutane in the feed, %

n₂

mole percentage of 2-butene in the feed, %

n₃

mole percentage of isobutene in the feed, %

m_STR

mixing with/after feeding especially in STR, Boolean

y_C5–7

yield of C_5–7, %

y_C8

yield of C₈, %

y_C9+

yield of C₉₊, %

y_TMPs

yield of TMPs, %

y_DMHs

yield of DMHs, %

TMPs/DMHs

ratio of TMPs to DMHs, dimensionless

k₁ⁱ

weights of first hidden layer, dimensionless

k_j^u

weights of each next hidden layer, dimensionless

k_o^v

weights of output layer, dimensionless

b₁ⁱ

biases of first hidden layer, dimensionless

b_j^u

biases of each next hidden layer, dimensionless

b_o^v

biases of output layer, dimensionless

s_i

predicted value (including y_C5–7, y_C8, y_C9+, y_TMPs, y_DMHs, TMPs/DMHs, and RON)

e_i

experimental value (including y_C5–7, y_C8, y_C9+, y_TMPs, y_DMHs, TMPs/DMHs, and RON)

n

number of the aggregate data

e̅

average value of the experimental results

error

residual of predicted and experimental value

average of errors

x_i

input data

f(x_i)

output data

Glossary

Abbreviations

ANN

artificial neural network

H₂SO₄

concentrated sulfuric acid

TMPs

trimethylpentanes

LEs

light ends, including C_5–7

DMHs

dimethylhexanes

HEs

heavy ends, including C₉₊

STR

stirred tank reactor

RPB

rotating packed bed

DFT

density functional theory

BFG

BFGS quasi-Newton backpropagation

CGB

conjugate gradient backpropagation with Powell–Beale restarts

CGF

conjugate gradient backpropagation with Fletcher–Reeves updates

CGP

conjugate gradient backpropagation with Polak–Ribiére updates

GD

gradient descent backpropagation

GDA

gradient descent with adaptive learning rate backpropagation

GDM

gradient descent with momentum backpropagation

GDX

gradient descent with momentum and adaptive learning rate backpropagation

LM

Levenberg–Marquardt backpropagation

OSS

one-step secant backpropagation

RP

resilient backpropagation

SCG

scaled conjugate gradient backpropagation

BR

Bayesian regularization backpropagation

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c04757.

• (PDF)

The authors declare no competing financial interest.