Abstract

This work presents a mechanistic study of the electrochemical synthesis of magnetite nanoparticles (NPs) based on the analysis of the electrochemical impedance spectroscopy (EIS) technique. After a discussion of the mechanisms reported in the literature, three models are devised and a prediction of their EIS spectra is presented. The approach consisted of the simulation of EIS spectra as a tool for assessing model validity, as EIS allows to characterize the relaxation of adsorbed intermediates. The comparison between the simulated impedance spectra and the experimental results shows that the mechanisms proposed to date do not explain all of the experimental results. Thus, a new model is proposed, in which up to three adsorbed intermediate species are involved. This model accounts for the number of loops found in experimental impedance data. The closest approximation of the features found in the experimental spectra by this proposed model suggests a better representation of the reaction mechanism within the evaluated potential range.
1. Introduction
Magnetite nanoparticles (NPs) are materials of growing interest in various scientific and technological disciplines due to their specific properties,1 such as magnetism and biocompatibility.2−4 The diversity of synthesis methods allows to tune the properties of NPs, such as their size and size distribution.5 Among them, electrochemical synthesis methods (based on the application of a current or potential to oxidize an iron electrode) allows to obtain small size distributions6,7 that are ideal for biomedical uses.5 The reaction mechanism of electrochemically synthesized magnetite has been studied by various methods. These methods generally consist of measurements performed to the electrolyte by spectrometric methods, which may lack time-resolved information to accurately quantify the changes occurring at the interface. Several articles have reported and described magnetite formation, starting from metallic iron and iron hydroxides as precursors.8,9 The formation mechanism of magnetite NPs is often regarded as complex and is still under debate. Cabrera et al.10 have reported species that would be identified as precipitates in their stable form and that are generated at the anode and must travel through the solution to be reduced at the cathode and then produce magnetite. Manrique-Julio et al. have proposed that the formation of magnetite occurs in the bulk solution according to mechanisms in which iron hydroxides react with H2, the latter being evolved at the cathode surface.11 Such a mechanism implies that hydrogen diffuses from the cathode to the bulk solution to react. The probability of having enough H2 in the bulk solution is minimal because the coalescence and buoyancy phenomena favor its release from the solution, so that this synthesis pathway cannot be the main one. Lozano et al.12 and Montoya et al.13 have assumed that the reaction occurring on the anodic surface is simply iron oxidation
| 1 |
followed by subsequent homogeneous reactions. However, anodic iron dissolution is a process that has been extensively investigated.14−21 Indeed, studies by electrochemical impedance spectroscopy (EIS) have concluded that iron oxidation involves several steps, which are observed from the Nyquist diagrams as more than one time constant in the spectra, some involving adsorbed intermediate species.17,18 All of these results suggest that additional studies are still required to accurately describe the NP synthesis mechanism.
The use of EIS is common in this kind of study as it has been demonstrated to be a useful tool to describe reaction mechanisms, providing kinetic information and predicting the electrochemical behavior of the system.22,23
EIS has been employed to assess reactions mechanisms including metals corrosion,24−29 mass transport phenomenon,30 and the hydrogen evolution reaction (HER),31 among others.
In this work, EIS was employed to evaluate the consistency of various mechanisms published in the literature where electrochemical synthesis of magnetite NPs is described. The original mechanisms were adapted into models, considering the possibility of having adsorbed species as intermediates. This is a prime condition to apply the methodology to develop the impedance response models. Four different mechanisms were thus analyzed, and the analytical expression of impedance was established for each of them. Simulations were compared to experimental results and their similarities were discussed.
2. Results and Discussion
2.1. Analysis of the Possible Mechanisms
The different mechanisms in the literature range from the simplest, i.e., the direct reaction between Fe2+ and Fe3+ in presence of OH–,9 to the most complex ones, involving iron hydroxides formed in the anode or in the bulk solution travel to the cathode where the hydroxides are reduced to form magnetite (reactions 2 and 3).8,10 Most of the authors agree with a reaction occurring on the cathode surface (reaction 4, water reduction) and that magnetite formation occurs in the bulk solution.
| 2 |
| 3 |
| 4 |
One of the most widely cited mechanisms was devised by Cabrera et al.,10 who proposed the oxidation of metallic iron (Fe0) to Fe3+ on the electrode surface following a two-step mechanism (reactions 5 and 6). Then, Fe3+ reacts with the OH– formed at the cathode, producing Fe(OH)3 near the anode (reaction 7). They suggested that Fe(OH)3 travels to the cathodic surface where it is reduced to form magnetite NPs (reactions 9 and 10).
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
| 10 |
and the reduction of water occurs as eq 4 indicates.
Lozano et al.12 reported a deep analysis of the mechanisms in which they made a series of experimental measurements to validate some of the elementary steps previously proposed. They concluded that the steps involving the reduction of iron oxides and hydroxides on the cathodic surface are unlikely to occur since they demonstrated that magnetite formation takes place in the vicinity of the anode, only.
Franger et al.32 proposed a single anodic reaction: the oxidation of metallic iron to iron oxyhydroxide (FeOOH) (reaction 11). This species then reacts in the bulk solution with dissolved dihydrogen formed in the cathode to obtain the magnetite (reaction 12). However, the anodic reaction involving three electrons and three hydroxide molecules is unlikely to occur in a single step.
| 11 |
At the cathode, water reduction (reaction 4) occurs, and in the bulk solution
| 12 |
Conversely, Lozano et al.12 showed that hydrogen is not a reducing agent of lepidocrocite (γ-FeOOH)32 (reaction 11), which is also in agreement with the work of Montoya et al.13
Indeed, Lozano et al.12 and Montoya et al.13 devised mechanisms in which only Fe2+ is generated at the anode, while the other reactions of the mechanism take place in the homogeneous phase.
Lozano et al.12 stated the following mechanism: At the anode, the simple oxidation of Fe to Fe2+ occurs as reaction 1 indicates. At the cathode, water oxidation (reaction 4) occurs, in agreement with the other authors. Also, in the bulk solution, the next reactions occur
| 13 |
| 14 |
| 15 |
Their mechanism involved only one single reaction at the anode (reaction 1), followed by a reaction between γ-FeOOH and Fe(OH)2 in the bulk solution to form magnetite (reaction 15).
On the other hand, Montoya et al.13 proposed the same reactions as proposed by Lozano at the anode and cathode and only reaction 13 to describe the bulk solution.
Additionally, they reported a number of reactions related to the formation of green rust in the homogeneous phase, which consisted of unstable compounds containing a mixture of ferrous and ferric iron.13
As previously mentioned, the mechanism for the oxidation of Fe to Fe2+ is complex since the experimental results obtained by EIS show inductive and capacitive loops in different media, which can be associated with adsorption phenomena of intermediate species.33 So, we assume that EIS spectral modeling can assess the cited mechanisms and help to unveil fine details of the mechanism. It is worth noting that the described mechanisms do not state whether some of the involved species are adsorbed at the electrode. Thus, to obtain a model to describe impedance spectra, it is necessary to hypothesize that some of the presented species are adsorbed intermediaries.
2.2. Development and Simulation of the Reaction Mechanism-Based Impedance Models
From the analysis of the literature and our experimental results (see Section 2.3), we concluded that four different pathways can be envisioned for describing the formation of magnetite NPs from iron oxidation. To devise the electrochemical impedance analytical expression, only the reactions occurring at the anode were considered. This assumption is used since the electrochemical technique relies on the measurement of the potential between the working electrode and the reference electrode, thus allowing to disregard the reaction kinetics at the counter electrode.
The approach used to model the electrochemical impedance response requires in the first step identifying the elementary reactions and then writing mass and charge balances to calculate the transfer functions associated with the overall mechanism.
Further, adsorbed intermediates are taken into account to obtain the mass balance associated with a fraction of surface coverage θi for the adsorbed species.33 The method has already been used to determine kinetic parameters, assess mechanisms, and predict system behavior.34
In the case of electrochemically produced magnetite, metallic iron (Fe0) is used as a precursor, and thus, all of the devised mechanisms consider iron oxidation as the initial step.
2.2.1. Model I
This first proposed mechanism relies on the work of Cabrera et al.,10 where we assume that both Fe2+ and Fe3+ species are adsorbed intermediates. The mechanism can thus be written as
| 16 |
| 17 |
| 18 |
For simplicity, the concentration of OH– is considered constant (1 × 10–3 mol cm–3, which corresponds to a bulk solution) and the contribution of diffusion to the impedance is disregarded for all of the models. This mechanism is rewritten as a general scheme, which is valid for any participating species (reactions 19–21); thus, at this point, the actual chemical identity of the adsorbates is not needed to build the impedance expression. Therefore, the overall impedance expression will be the same for any mechanisms involving the same number of adsorbates, steps, and exchanged electrons. This general scheme, accounting for reactions 16–18, is expressed as
| 19 |
| 20 |
| 21 |
where the rate constants (Ki) for the electrochemical reactions are potential-dependent and are expressed as Ki = ki ebiE, bi is the Tafel coefficient (positive for anodic reactions and negative for the cathodic ones), E is the polarization potential, and Ki is independent of the potential for a chemical reaction. The concentration of the adsorbed species given by βiθi obeys a Langmuir’s isotherm with a maximum number of sites per surface unit β and a fraction of surface coverage θi.
The impedance expression for this system is obtained from mass and charge balances. For the adsorbate intermediates, it comes
| 22 |
| 23 |
where θ1 is related in this mechanism to Fe(II) species and θ2 is related to Fe(III) species. Equations 22 and 23 describe the changes in the surface coverage as a function of time and are the evolution equations that depend on E and θi. These expressions are thus linearized
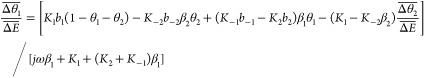 |
24 |
and
| 25 |
whereas the charge balance expresses as
 |
26 |
The time constants τi associated with this model are
| 27 |
| 28 |
Equation 26 is the ratio of the changes in the current to the potential, i.e., the admittance of the electrochemical process. This expression allows the faradaic impedance, Zf, to be expressed as a function of the different parameters of the model
| 29 |
The total impedance (Zt) of the system is obtained by taking into account the interfacial capacitance Cint and the solution resistance Rs, as depicted in Figure 1, as the nonfaradic contributions are always present in experimental EIS spectra and eq 30 expresses the total impedance of system Zt
| 30 |
The simulations for the models presented in this work were obtained at different values of E. The same value for βi (1 × 10–8 mol cm–2) was used for all simulations, which corresponds approximately to a monolayer of adsorbate bonded to a surface metal atom.17 The limiting step for this model is the conversion of Fe0 to Fe2+, where its associated k1 has been evaluated in other works related to corrosion science.35 As for Fe2+, as soon as it is formed, it rapidly oxidizes to Fe3+ and subsequently reacts to yield Fe(OH)3 in neutral or alkaline solutions. Thus, the associated ki values to the aforementioned species are faster as compared to k1, and k3 is assumed to be the highest one; thus, the intermediaries are expected to be short-lived. Both proposed backward rate constants k–i are smaller than the corresponding forward ki. Furthermore, the values of ki were selected taking into account that the time constants associated with the model could be observed within the frequency range commonly explored in the experimental measurements (i.e., k1 is small enough so that 1/τ1 could be in the range of 100 kHz to 1 mHz). The Tafel coefficients can vary from 0 to 38.4, 0 to 76.8, and 0 to 115.2 V–1 for one, two, and three transferred electrons, respectively. Table 1 summarizes the different values used for calculating the impedance expression corresponding to model I, which are presented in Figure 2.
Figure 1.

Equivalent circuit representing the total impedance for the system.
Table 1. Parameters Values Used in the Simulation of Model I.
|
K1 |
K–1 |
K2 |
K–2 |
K3 | ||||
|---|---|---|---|---|---|---|---|---|
| k1 (mol cm–2 s–1) | b1 (V–1) | k–1 (s–1) | b–1 (V–1) | k2 (s–1) | b2 (V–1) | k–2 (s–1) | b–2 (V–1) | k3 (s–1) |
| 1 × 10–8 | 30 | 8 × 10–11 | 9 | 0.1 | 10 | 8 × 10–4 | 19 | 1 × 104 |
| β1 = β2 = 1 × 10–8 mol cm–2; Cint = 1 × 10–4 F cm–2; [D] = 1 × 10–3 mol cm–3 | ||||||||
Figure 2.
Nyquist diagrams of EIS response simulated for model I for different values of E: (a) 0, (b) 50 mV, (c) 100 mV, (d) 150 mV, (e) 200 mV, and (f) variation of θ1 and θ2 with E. Parameters used for these simulations are summarized in Table 1.
Figure 2 shows the different responses of the simulated spectra for this model when E is varied from 0 to 200 mV. This same figure shows the Nyquist diagrams for E = 0, 50, 100, 150, and 200 mV and the variations of θ1 and θ2 as a function of E.
The Nyquist diagrams presented in Figure 2a–c show two time constants (two capacitive loops), whereas Figure 2d,e shows three time constants (two capacitive loops and an additional inductive loop). The high-frequency capacitive loop is ascribed to the interfacial capacitance in parallel to the charge-transfer resistance Rct, with an associated time constant defined as τHF = RctCint. The two time constants at lower frequencies (corresponding to the capacitive and inductive loops) are ascribed to the adsorbed species, and their associated time constants are defined by eqs 27 and 28. It is known that adsorbed species can be observed either as a capacitive or an inductive loop,33 also depending on the polarization potential.
The charge-transfer resistance decreases as the potential increases, evidenced by the variation of the diameter of the high-frequency capacitive loop. Table 2 shows the values of Rct calculated with the analytical expression corresponding to the third term in eq 26, that is, the term that is independent of frequency.
Table 2. Charge-Transfer Resistances Calculated from Equation 26.
| E (mV) | Rct (Ω) |
|---|---|
| 0 | 34.6 |
| 50 | 15.9 |
| 100 | 8.9 |
| 150 | 5.7 |
| 200 | 4.0 |
Figure 2f shows the variation of θ1 and θ2 as a function of the potential, where it is possible to observe that with increasing anodic potential, the value of θ2 increased, whereas θ1 has a maximum in approximately 100 mV and then start decreasing. This behavior is also observed in Figure 2d,e, where the presence of a third time constant as an inductive loop is evidenced.
2.2.2. Model II
The second model was inspired by the mechanism reported by Franger et al.,32 where a rather unusual assumption with a three-electron transfer (reaction 31) was used. Similar to model I, an adsorbed intermediate species is proposed (FeOOHads), and the different steps involved in the mechanism are expressed as
| 31 |
| 32 |
Thus, the general scheme is
| 33 |
| 34 |
This model associates only one electrochemical reaction with a three-electron transfer and only one adsorbed intermediate species for the FeOOH species. The relaxation of the adsorbate can be expressed as
| 35 |
and the admittance as
| 36 |
The time constant associated with this model is
| 37 |
The simulations for this model were performed using the parameters shown in Table 3. This model considers the electrochemical reaction reversible, but the backward kinetic constant k–1 is 5 orders of magnitude smaller than the forward kinetic constant k1, thus assuming that this last is highly favored. The second reaction is a chemical step and thus independent of E. For this model, the limiting step is the formation of adsorbed FeOOH. In this case, complete iron oxidation is considered to take place in a single step; thus, k1 is 3 orders of magnitude higher than model I. The difference between k1 and k2 is about 7 orders of magnitude, implying that the adsorbed FeOOH is short-lived, as expected.
Table 3. Parameter Values Used in the Simulation of Model II.
|
K1 |
K–1 |
K2 | ||
|---|---|---|---|---|
| k1 (cm s–1) | b1 (V–1) | k–1 (s–1) | b–1 (V–1) | k2 (s–1) |
| 2.1 × 10–6 | 25 | 4 × 10–11 | 26 | 24 |
| [D] = 1 × 10–3 mol cm–3; β1 = 1 × 10–8 mol cm–2; Cint = 1 × 10–4 F cm–2 | ||||
Figure 3 shows the evolution of Nyquist diagrams as a function of the electrode potential for model II, where it is possible to observe only one time constant in Figure 3a,b, whereas two time constants are shown in Figure 3c–e. For Figure 3a,b, the contribution of adsorbates is not visible in this frequency range (100 kHz to 1 mHz) and the diameter of the loop corresponds to the Rct values, calculated from the second term of the analytical expression given by eq 36. The variations of Rct are reported in Table 4, and as expected, it decreases when the potential increases. As the potential increases, the surface coverage θ1 increases (Figure 3f), and from 100 mV to more positive potentials, it is possible to observe the time constant related to the adsorbate in the Nyquist diagrams (Figure 3c–e). For this model, the contribution of the adsorbate intermediate on the EIS diagram results in a single capacitive loop.
Figure 3.
Nyquist diagrams of EIS response simulated for model II for different values of E: (a) 0, (b) 50 mV, (c) 100 mV, (d) 150 mV, (e) 200 mV, and (f) variation of θ1 with E. Parameters used for these simulations are summarized in Table 3.
Table 4. Charge-Transfer Resistances Calculated from eq 36.
| E (mV) | Rct (Ω) |
|---|---|
| 0 | 66.4 |
| 50 | 19.4 |
| 100 | 5.9 |
| 150 | 2.1 |
| 200 | 1.0 |
2.2.3. Model III
The third model was developed assuming a single two-electron transfer electrochemical reaction at the anode,12,13 yielding the simplest behavior for the electrochemical system analyzed in this work. If there is no assumption of adsorbed species, then the faradic impedance Zf becomes, in this case, identical to the charge-transfer resistance Rct, and the Nyquist diagram only shows a capacitive loop corresponding to the resistance in parallel to the interfacial capacitance. To explore beyond this rather simple scenario, we can develop the case where the ionic species formed are first adsorbed onto the electrode surface.
The adsorbed intermediate to consider in this model is Feads2+, following the steps
| 38 |
| 39 |
Thus, the general scheme of model III can be expressed as
| 40 |
| 41 |
The linearized expressions of the parameters are thus given by
| 42 |
| 43 |
Also, the associated time constant is
| 44 |
A maximum of two time constants can be obtained from this model, as only one adsorbate is involved in the mechanism and diffusion is disregarded. Similarly, as in model I, we assume that the limiting step is the conversion of Fe0 to Fe2+; thus, the same value of k–1 is used. A significant difference between the ki magnitudes is noted, which implies fast desorption of Fe2+. A summary of the parameters used for the simulation of model III is presented in Table 5. The corresponding simulated Nyquist diagrams are shown in Figure 4.
Table 5. Parameter Values Used in the Simulation of Model III.
|
K1 |
K2 | |
|---|---|---|
| k1 (mol cm–2 s–1) | b1 (V–1) | k2 (s–1) |
| 1 × 10–8 | 13 | 6.1 |
| β1 = 1 × 10–8 mol cm–2; Cint = 1 × 10–4 F cm2 | ||
Figure 4.
Nyquist diagrams of EIS response simulated for model III for different values of E: (a) 0, (b) 50 mV, (c) 100 mV, (d) 150 mV, (e) 200 mV, and (f) variation of θ1 with E. Parameters used for these simulations are summarized in Table 5.
The reactions proposed for this model are irreversible. The EIS responses show two time constants, one time constant in the range of high frequencies, that are ascribed to Rct and Cint in parallel. The values of Rct can be obtained from the analysis of the Nyquist diagrams (Figure 4) and can be calculated from the analytical expression given by eq 43, as shown in Table 6.
Table 6. Charge-Transfer Resistances Calculated from Equation 43.
| E (mV) | Rct (Ω) |
|---|---|
| 0 | 46.4 |
| 50 | 27.3 |
| 100 | 17.4 |
| 150 | 12.0 |
| 200 | 9.5 |
When the potential increases, the surface coverage θ1 increases (Figure 4f); however, the characteristic time constant associated with the relaxation of the adsorbate does not change significantly with the potential. This is due to the fact that β1K2 > K1 and K2 do not change with the potential. The notable increase of the second loop is caused by an increase of K1 with the potential (eq 44).
2.3. Impedance Measurements
To verify the accuracy of the different hypotheses in each of the proposed mechanisms, the magnetite NP formation was also investigated experimentally at different potentials. Six anodic potentials were explored to compare with the models. Kramers–Kroning analysis was carried out for all of the spectra to confirm the congruence of the experimental data, and the frequency range where they are consistent is presented in Table 7.
Table 7. Frequency Limits where the Impedance Experimental Data were Found Consistent, as Obtained by Applying the Kramers-Kronig Analysis.
| E (mV) | fmax (kHz) | fmin (Hz) |
|---|---|---|
| –880 | 10 | 1 |
| –860 | 10 | 2.7 |
| –840 | 10 | 0.1 |
| –820 | 10 | 0.1 |
| –760 | 10 | 0.1 |
| –740 | 10 | 0.1 |
The experimental spectra are presented in Figure 5. Figure 5b,d shows magnifications of the shaded area in Figure 5a,c, respectively, to better illustrate the response.
Figure 5.
(a) Experimental Nyquist diagrams at different potentials of anodic polarization (−880, −860, −840, −820, −760, and −740 vs Hg|Hg2SO4) in 0.1 M K2SO4 using a 98% purity iron bar as the working electrode. (b) Magnification of the shaded area in (a). (c) Single response for −840 mV vs Hg|Hg2SO4. (d) Magnification of the shaded area in (c).
In Figure 5, it is possible to observe that the spectra corresponding to the less anodic potentials (−880 and −860 mV) have significant differences compared to the other spectra at more anodic potentials. These spectra show only one capacitive and one inductive loop. This difference may indicate a different mechanism, which is probably influenced by the phenomena taking place at the open-circuit potential (OCP). Thus, there is no certitude that magnetite formation is the only reaction to consider at these potentials.
A more regular trend is observed for more anodic potentials: The experimental spectra displayed up to four time constants (related to the loops), three of them, in the low-frequency range, associated with adsorbed intermediates. Our experimental measurements show that the mechanism is more complex than those previously analyzed involving several additional steps. It also reveals the possible existence of up to three adsorbed intermediaries in the reaction mechanism, by the fact that three loops are observed. Two of these loops are capacitive and one is inductive, indicating that two of the adsorbed intermediaries hinder somehow the reaction, while one of them enhances it. Diffusion contribution is not observed in the spectra at the explored polarization potentials. Meng et al.36 reported measurements of localized electrochemical impedance spectroscopy (LEIS) for a pipeline in a near-neutral pH condition at the corrosion potential and showed similar behavior to that presented in this work. Given the more complex shape of the spectra at more anodic potentials, in the following section, we focus on the proposal of a new mechanism based on the more consistent steps, plus some added, of the previously described mechanisms to explain the shape of the spectra in this potential range.
2.4. Proposed Model
While none of the three previous models include three adsorbed species in their mechanism, Model I shows the closest resemblance to the experimental results. However, based only on this approach and in the previous simulations, we can conclude that none of these mechanisms could accurately describe the reactions steps for all of the investigated potentials. It is thus required to propose a mechanism that satisfies the different features observed in the experimental spectra, mainly for the more anodic polarization potentials.
Following the same methodology, three adsorbed intermediates, Fe+, Fe2+, and Fe3+, can be involved. The presence of these species as adsorbed intermediates during iron dissolution in acid media has been described previously.17,37
The mechanism can thus be expressed as
| 45 |
| 46 |
| 47 |
| 48 |
| 49 |
Also, the oxidation of Feads2+ to Feads is as described in model I reaction 17.
In solution
| 50 |
| 51 |
Also, the formation of magnetite is given by reaction 15.
This model describes the consecutive formation of Fe2+ and Fe3+, with a dependency of Fe3+ and Fe(OH)2 on Fe2+. It is well known that Fe2+ oxidation is enhanced in alkaline media to give Fe3+.38 Subsequently, there might be junction sites where the Fe2+ species generate Fe(OH)2. While this process is expected to occur at the interface, all of these three species are then desorbed into the electrolyte, where they react in the homogeneous phase and form magnetite NPs (reactions 50, 51, 15). Taking into account the three species that are desorbed into the electrolyte, the presence of both ionic iron species (Fe2+ and Fe3+) leads to magnetite formation (reaction 50). This step contributes to a part of the magnetite nanoparticles; the rest of the magnetite is formed as reaction 15 indicates, where a combination of iron hydroxide and iron oxyhydroxide occurs. Reaction 15 was proposed by Lozano et al.12
The simplified reaction mechanism for the anodic reactions (reactions 17 and 45–49) is thus given by
| 52 |
| 53 |
| 54 |
| 55 |
| 56 |
| 57 |
The transfer functions were obtained in a similar way to the other mechanisms
 |
58 |
 |
59 |
| 60 |
 |
61 |
and the time constants associated with the relaxation of the concentration of adsorbed species are given by
| 62 |
| 63 |
| 64 |
Attempts were made to fit the expression for the overall impedance to the experimental spectra, but they were not successful. This can be due to the high number of parameters involved in the function to fit. In consequence, we instead did simulations, giving to the parameters some values based on the previous models and checking for their congruency to get similar shapes of the experimental EIS spectra. To compare the simulations with the experimental results, the behavior of Cint was adjusted by a constant phase element (CPE) to better describe the experimental results, as shown in eq 65:
| 65 |
where p is a parameter <1 for nonideal capacitances. Y0 is a coefficient related to the apparent capacitance Capp(39)
| 66 |
The EIS spectral simulation was performed as a function of the potential for the different parameters. The values to describe the CPE were estimated using Zview software, fitting the high-frequency time constant. The fitting was made from 1 kHz to 10 mHz. In this model, Fe0 oxidation to Fe+, represented by k1, was proposed 1 order of magnitude smaller than the reactions involving two-electron transfer in previous models, becoming then the limiting step. Since the Fe+ species is considered an intermediate but not a stable ionic species, the value of k2 is expected to be significantly higher, which suggests that oxidation of Fe+ to Fe2+ is fast as it is generated. The similarity in the ki values for the conversion of adsorbed Fe2+ results in a competition for the generation of the proposed species (reactions 17, 47, and 48). The values of the parameters that better represent the experimental results are presented in Table 8.
Table 8. Values of the Parameters Used in the Simulation for the Proposed Model.
|
K1 |
K2 |
K–2 |
K3 |
K–3 |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| k1(mol cm–2 s–1) | b1 (V–1) | k2 (s–1) | b2 (V–1) | k–2 (s–1) | b–2 (V–1) | k3 (s–1) | b3 (V–1) | k–3 (s–1) | b–3(V–1) | K4 (cm s–1) | K5 (s–1) | K6 (s–1) |
| 7.0 × 10–9 | 24 | 1.4 × 103 | 30 | 1.7 × 10–3 | 12 | 18 | 23 | 1 × 10–4 | 15 | 800 | 85 | 8 |
| [D] = 1 × 10–3 mol cm–3; β1= 1 × 10–8 mol cm–2; Y0 = 4.3 × 10–4; p = 0.79 | ||||||||||||
Figure 6 shows the EIS spectra obtained for this new model at different E values. As three intermediate adsorbates were proposed for this model, it is possible to obtain up to four time constants, three of them ascribed to the adsorbed intermediates with their associated time constants presented in eqs 62–64. In Figure 6, two overpotentials were simulated, 60 and 80 mV, corresponding to −840 and −820 mV vs Hg|Hg2SO4 for the experimental measurements since the OCP is −900 mV vs Hg|Hg2SO4.
Figure 6.
Nyquist diagrams showing experimental data compared with the simulated one for the proposed model at different values of E: (a) 60 and (b) 80 mV. Parameters used for these simulations are summarized in Table 8.
It is possible to observe that the simulations follow the shape of the experimental data, but more accurately at 60 mV than at 80 mV. It can be said that the simulation, even if it needs improvements, predicts well the shape of the spectra, indicating that the mechanism on which it is based is more consistent than the previous mechanisms. Thus, we conclude that model IV can describe more accurately the experimental spectra of magnetite NP formation. Despite the lack of additional experimental evidence to support the existence and nature of the adsorbed species to validate this mechanism, the analyzed simulations provide some elements to consider their existence. While the development of a new reaction mechanism to describe the different characteristics of the experimental spectra has been proposed, the calculation of the reaction rates has yet to be carried out more rigorously. This will require further experimental studies as a function of the electrode potential and electrolyte composition.
3. Conclusions
The formation of magnetite was studied from a mechanistic point of view by four different models. Three of these models were based on the literature results, while the fourth was proposed in this work. Simulations of the EIS diagrams for the models were compared with experimental measurements. It was concluded that the mechanism for electrochemical magnetite formation is more complex than the mechanisms proposed until now in the literature. EIS analysis leads to the conclusion that at least three intermediate adsorbed species are involved in the mechanism.
The new model was proposed to better describe the phenomena occurring in the anode, involving three adsorbates, as observed in the features of the experimental spectra. This model was based on previous analyses performed for describing the anodic dissolution of iron. Finally, the model rendered a closer approximation of the features found in the experimental spectra, suggesting a better representation of the reaction mechanism.
4. Experimental Section
The impedance measurements were performed with a potentiostat/galvanostat (Gamry, reference 600+) with an amplitude of 10 mVrms in the potentiostatic mode. The frequencies ranged from 10 kHz to 10 mHz, with seven points per frequency decade. For each frequency, three cycles were integrated into the calculation of the impedance. A DC polarization potential from −880 to −740 mV vs. Hg|Hg2SO4 was applied, and the system was stabilized for 300 s at each potential before the EIS measurement.
All solutions were prepared from deionized water, with 0.1 M K2SO4 as the supporting electrolyte. A Hg|Hg2SO4 electrode in saturated K2SO4 solution, a platinum wire, and an iron rod (+98% purity, Goodfellow), with 0.21 cm2 of the exposed area, insulated with electrophoretic paint were used as reference, auxiliary, and working electrodes, respectively, in a conventional three-electrode array cell.
Acknowledgments
R.R. gratefully acknowledges a scholarship for doctoral studies granted by CONACYT (467055). R.A. thanks to CONACYT for the support of the development of this work through project 256248.
The authors declare no competing financial interest.
References
- Rodríguez-López A.; Cruz-Rivera J. J.; Elías-Alfaro C. G.; Betancourt I.; Ruiz-Silva H.; Antaño-López R. Fine Tuning of Magnetite Nanoparticle Size Distribution Using Dissymmetric Potential Pulses in the Presence of Biocompatible Surfactants and the Electrochemical Characterization of the Nanoparticles. Mater. Sci. Eng., C 2015, 46, 538–547. 10.1016/j.msec.2014.10.052. [DOI] [PubMed] [Google Scholar]
- Noqta O. A.; Aziz A. A.; Usman I. A.; Bououdina M. Recent Advances in Iron Oxide Nanoparticles (IONPs): Synthesis and Surface Modification for Biomedical Applications. J. Supercond. Novel Magn. 2019, 32, 779–795. 10.1007/s10948-018-4939-6. [DOI] [Google Scholar]
- Nikitin A.; Fedorova M.; Naumenko V.; Shchetinin I.; Abakumov M.; Erofeev A.; Gorelkin P.; Meshkov G.; Beloglazkina E.; Ivanenkov Y.; Klyachko N.; Golovin Y.; Savchenko A.; Majouga A. Synthesis, Characterization and MRI Application of Magnetite Water-Soluble Cubic Nanoparticles. J. Magn. Magn. Mater. 2017, 441, 6–13. 10.1016/j.jmmm.2017.05.039. [DOI] [Google Scholar]
- Jordan A.; Scholz R.; Wust P.; Fähling H.; Felix R. Magnetic Fluid Hyperthermia (MFH): Cancer Treatment with AC Magnetic Field Induced Excitation of Biocompatible Superparamagnetic Nanoparticles. J. Magn. Magn. Mater. 1999, 201, 413–419. 10.1016/S0304-8853(99)00088-8. [DOI] [Google Scholar]
- Laurent S.; Forge D.; Port M.; Roch A.; Robic C.; Vander Elst L.; Muller R. N. Magnetic Iron Oxide Nanoparticles: Synthesis, Stabilization, Vectorization, Physicochemical Characterizations, and Biological Applications. Chem. Rev. 2010, 110, 2574 10.1021/cr900197g. [DOI] [PubMed] [Google Scholar]
- Rodríguez-López A.; Paredes-Arroyo A.; Mojica-Gomez J.; Estrada-Arteaga C.; Cruz-Rivera J. J.; Elías Alfaro C. G.; Antaño-López R. Electrochemical Synthesis of Magnetite and Maghemite Nanoparticles Using Dissymmetric Potential Pulses. J. Nanopart. Res. 2012, 14, 993 10.1007/s11051-012-0993-3. [DOI] [Google Scholar]
- Mosivand S.; Kazeminezhad I. Structural and Magnetic Characterization of Electro-Crystallized Magnetite Nanoparticles under Constant Current. Mater. Res. Bull. 2015, 70, 328–335. 10.1016/j.materresbull.2015.04.053. [DOI] [Google Scholar]
- Ibrahim M.; Serrano K. G.; Noe L.; Garcia C.; Verelst M. Electro-Precipitation of Magnetite Nanoparticles: An Electrochemical Study. Electrochim. Acta 2009, 55, 155–158. 10.1016/j.electacta.2009.08.026. [DOI] [Google Scholar]
- Ying T. Y.; Yiacoumi S.; Tsouris C. An Electrochemical Method for the Formation of Magnetite Particles. J. Dispersion Sci. Technol. 2002, 23, 569–576. 10.1081/DIS-120014025. [DOI] [Google Scholar]
- Cabrera L.; Gutierrez S.; Menendez N.; Morales M. P.; Herrasti P. Magnetite Nanoparticles: Electrochemical Synthesis and Characterization. Electrochim. Acta 2008, 53, 3436–3441. 10.1016/J.ELECTACTA.2007.12.006. [DOI] [Google Scholar]
- Manrique-Julio J.; Machuca-Martinez F.; Marriaga-Cabrales N.; Pinzon-Cardenas M. Production of Magnetite by Electrolytic Reduction of Ferric Oxyhydroxide. J. Magn. Magn. Mater. 2016, 401, 81–85. 10.1016/j.jmmm.2015.10.018. [DOI] [Google Scholar]
- Lozano I.; Casillas N.; de León C. P.; Walsh F. C.; Herrasti P. New Insights into the Electrochemical Formation of Magnetite Nanoparticles. J. Electrochem. Soc. 2017, 164, D184–D191. 10.1149/2.1091704jes. [DOI] [Google Scholar]
- Montoya P.; Marín T.; Mejía S.; Arnache O.; Calderón J. A. Elucidation of the Mechanism of Electrochemical Formation of Magnetite Nanoparticles by In Situ Raman Spectroscopy. J. Electrochem. Soc. 2017, 164, D1056–D1065. 10.1149/2.0181802jes. [DOI] [Google Scholar]
- Kabanov B.; Burstein R.; Frumkin A. Kinetics of Electrode Processes on the Iron Electrode. Discuss. Faraday Soc. 1947, 1, 259–269. 10.1039/DF9470100259. [DOI] [Google Scholar]
- Bechet B.; Epelboin I.; Keddam M. New Data from Impedance Measurements Concerning the Anodic Dissolution of Iron in Acidic Sulphuric Media. J. Electroanal. Chem. Interfacial Electrochem. 1977, 76, 129–134. 10.1016/S0022-0728(77)80013-2. [DOI] [Google Scholar]
- Vela M. E.; Vilche J. R.; Arvia A. J. The Dissolution and Passivation of Polycrystalline Iron Electrodes in Boric Acid-Borate Buffer Solutions in the 7.5-9.2 PH Range. J. Appl. Electrochem. 1986, 16, 490–504. 10.1007/BF01006844. [DOI] [Google Scholar]
- Keddam M.; Mattos O. R.; Takenouti H. Reaction Model for Iron Dissolution Studied by Electrode Impedance: I. Experimental Results and Reaction Model. J. Electrochem. Soc. 1981, 128, 257–266. 10.1149/1.2127401. [DOI] [Google Scholar]
- Keddam M.; Mattos O. R.; Takenouti H. Reaction Model for Iron Dissolution Studied by Electrode Impedance II. Determiation of the Reaction Model. J. Electrochem. Soc. 1981, 128, 266–274. 10.1149/1.2127402. [DOI] [Google Scholar]
- Barcia O. E.; Mattos O. R. The Role of Chloride and Sulphate Anions in the Iron Dissolution Mechanism Studied by Impedance Measurements. Electrochim. Acta 1990, 35, 1003–1009. 10.1016/0013-4686(90)90035-X. [DOI] [Google Scholar]
- Barcia O. E.; Mattos O. R. Reaction Model Simulating the Role of Sulphate and Chloride in Anodic Dissolution of Iron. Electrochim. Acta 1990, 35, 1601–1608. 10.1016/0013-4686(90)80016-H. [DOI] [Google Scholar]
- Ma H.; Li G.; Chen S.; Zhao S.; Cheng X. Impedance Investigation of the Anodic Iron Dissolution in Perchloric Acid Solution. Corros. Sci. 2002, 44, 1177–1191. 10.1016/S0010-938X(01)00145-7. [DOI] [Google Scholar]
- Harrington D. A.; van den Driessche P. Mechanism and Equivalent Circuits in Electrochemical Impedance Spectroscopy. Electrochim. Acta 2011, 56, 8005–8013. 10.1016/j.electacta.2011.01.067. [DOI] [Google Scholar]
- Holm T.; Sunde S.; Seland F.; Harrington D. A. Understanding Reaction Mechanisms Using Dynamic Electrochemical Impedance Spectroscopy: Methanol Oxidation on Pt. Electrochim. Acta 2019, 323, 134764 10.1016/j.electacta.2019.134764. [DOI] [Google Scholar]
- Cordeiro G. G. O.; Barcia O. E.; Mattos O. R. Copper Electrodissolution Mechanism in a 1M Sulfhate Medium. Electrochim. Acta 1993, 38, 319–324. 10.1016/0013-4686(93)85146-P. [DOI] [Google Scholar]
- Gabrielli C.; Keddam M.; Minouflet-Laurent F.; Ogle K.; Perrot H. Investigation of Zinc Chromatation - Part II. Electrochemical Impedance Techniques. Electrochim. Acta 2003, 48, 1483–1490. 10.1016/S0013-4686(03)00029-X. [DOI] [Google Scholar]
- Gomes M. P.; Costa I.; Pébère N.; Rossi J. L.; Tribollet B.; Vivier V. On the Corrosion Mechanism of Mg Investigated by Electrochemical Impedance Spectroscopy. Electrochim. Acta 2019, 306, 61–70. 10.1016/j.electacta.2019.03.080. [DOI] [Google Scholar]
- Gregori J.; García-Jareño J. J.; Giménez-Romero D.; Vicente F. Kinetic Calculations of the Ni Anodic Dissolution from EIS. J. Solid State Electrochem. 2005, 9, 83–90. 10.1007/s10008-004-0557-2. [DOI] [Google Scholar]
- Baranwal P. K.; Prasanna Venkatesh R. Investigation of Carbon Steel Anodic Dissolution in Ammonium Chloride Solutions Using Electrochemical Impedance Spectroscopy. J. Solid State Electrochem. 2017, 21, 1373–1384. 10.1007/s10008-016-3497-8. [DOI] [Google Scholar]
- Nagendra Prasad Y.; Vinod Kumar V.; Ramanathan S. Electrochemical Impedance Spectroscopic Studies of Copper Dissolution in Arginine-Hydrogen Peroxide Solutions. J. Solid State Electrochem. 2009, 13, 1351–1359. 10.1007/s10008-008-0682-4. [DOI] [Google Scholar]
- Holm T.; Ingdal M.; Fanavoll E. V.; Sunde S.; Seland F.; Harrington D. A. Mass-Transport Impedance at Channel Electrodes: Accurate and Approximate Solutions. Electrochim. Acta 2016, 202, 84–89. 10.1016/j.electacta.2016.03.096. [DOI] [Google Scholar]
- Lasia A. Mechanism and Kinetics of the Hydrogen Evolution Reaction. Int. J. Hydrogen Energy 2019, 44, 19484–19518. 10.1016/j.ijhydene.2019.05.183. [DOI] [Google Scholar]
- Franger S.; Berthet P.; Berthon J. Electrochemical Synthesis of Fe3O4 Nanoparticles in Alkaline Aqueous Solutions Containing Complexing Agents. J. Solid State Electrochem. 2004, 8, 218–223. 10.1007/s10008-003-0469-6. [DOI] [Google Scholar]
- Epelboin I.; Keddam M.; Lestrade J. C. Faradaic Impedances and Intermediates in Electrochemical Reactions. Faraday Discuss. Chem. Soc. 1973, 56, 264–275. 10.1039/DC9735600264. [DOI] [Google Scholar]
- Harrington D. A.; van den Driessche P. Stability and Electrochemical Impedance of Mechanisms with a Single Adsorbed Species. J. Electroanal. Chem. 2001, 501, 222–234. 10.1016/S0022-0728(00)00532-5. [DOI] [Google Scholar]
- Mehtani H. K.; Khan M. I.; Jaya B. N.; Parida S.; Prasad M. J. N. V.; Samajdar I. The Oxidation Behavior of Iron-Chromium Alloys: The Defining Role of Substrate Chemistry on Kinetics, Microstructure and Mechanical Properties of the Oxide Scale. J. Alloys Compd. 2021, 871, 159583 10.1016/j.jallcom.2021.159583. [DOI] [Google Scholar]
- Meng G. Z.; Zhang C.; Cheng Y. F. Effects of Corrosion Product Deposit on the Subsequent Cathodic and Anodic Reactions of X-70 Steel in near-Neutral PH Solution. Corros. Sci. 2008, 50, 3116–3122. 10.1016/j.corsci.2008.08.026. [DOI] [Google Scholar]
- Plonski I.-H. Effect of Surface Structure and Adsorption Phenomena on the Active Dissolution of Iron in Acid Media. Mod. Aspects Electrochem. 1996, 29, 203–310. 10.1007/978-1-4613-0327-5_3. [DOI] [Google Scholar]
- Parsons R. Atlas of electrochemical equilibria in aqueous solutions. J. Electroanal. Chem. Interfacial Electrochem. 1967, 13, 471 10.1016/0022-0728(67)80059-7. [DOI] [Google Scholar]
- Orazem M. E.; Tribollet B.. Electrochemical Impedance Spectroscopy; Wiley, 2008. [Google Scholar]







