Abstract
The blood–brain barrier remains a major roadblock to the delivery of drugs to the brain. While in vitro and in vivo measurements of permeability are widely used to predict brain penetration, very little is known about the mechanisms of passive transport. Detailed insight into interactions between solutes and cell membranes could provide new insight into drug design and screening. Here, we perform unbiased atomistic MD simulations to visualize translocation of a library of 24 solutes across a lipid bilayer representative of brain microvascular endothelial cells. A temperature bias is used to achieve steady state of all solutes, including those with low permeability. Based on free-energy surface profiles, we show that the solutes can be classified into three groups that describe distinct mechanisms of transport across the bilayer. Simulations down to 310 K for solutes with fast permeability were used to justify the extrapolation of values at 310 K from higher temperatures. Comparison of permeabilities at 310 K to experimental values obtained from in vitro transwell measurements and in situ brain perfusion revealed that permeabilities obtained from simulations vary from close to the experimental values to more than 3 orders of magnitude faster. The magnitude of the difference was dependent on the group defined by free-energy surface profiles. Overall, these results show that MD simulations can provide new insight into the mechanistic details of brain penetration and provide a new approach for drug discovery.
Introduction
The development of drugs for central nervous system (CNS) diseases is more challenging and more costly than for non-CNS diseases,1−4 largely due to the difficulty in crossing the blood–brain barrier (BBB).5−7 The transport of solutes across the BBB is usually described in terms of a generalized rate—the permeability.8 However, the permeability does not carry any mechanistic insight and hence the details of molecular transport remain poorly understood.
Empirical criteria for predicting brain penetration of small molecules include Lipinski’s rule of 59 and modifications based on retrospective analysis of permeability and other physicochemical data10−13 but have had limited success.14 Experimental values of permeability derived from the 2D transwell assay (Papp) are widely used to predict brain penetration of small molecules, and the transwell assay is often considered the gold standard assessing barrier function of other in vitro models.15In vivo estimates of permeability can be obtained from in situ brain perfusion in a rat model (P3D);16,17 however, the correlation between in vitro and in vivo values is also limited.18 While empirical models and in vitro and in vivo measurements can provide useful relative comparisons, there are no standard values of permeability for different solutes and there are limited tools for predicting brain penetration, a key requirement for CNS drugs.
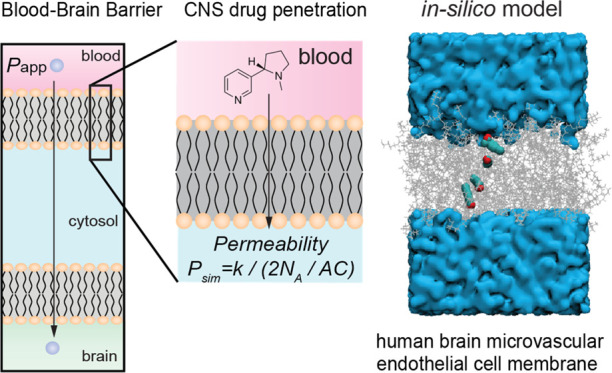
Permeability describes the diffusion of a solute across a thin volume element. For solute penetration into the brain, this volume element is the vascular wall formed by brain microvascular endothelial cells (BMECs). This is a complex barrier to solute transport involving, in the simplest case, diffusion across the luminal membrane, transport within the cell, and diffusion across the abluminal membrane. Transport may also involve interaction with the cell surface. Permeability values provide little insight into the mechanistic details of transport, such as molecular interactions or thermodynamics of entry. In silico simulations have the potential to provide valuable mechanistic insight into the kinetics of solute transport across the BBB and enable new approaches for the design and screening of neuropharmaceuticals. While high-temperature simulations cannot accurately describe transport properties in water, due to the inability of standard water models to describe phase transitions accurately, this methodology is applicable to solute translocation across low dielectric media, such as a lipid bilayer.
Previous computational work has demonstrated the feasibility of capturing spontaneous translocation of solutes through model membranes with timescales above 1 μs.19−21 To resolve timescale issues, biased-sampling approaches have been developed, these include using a single lipid model of the BMEC cell membrane (e.g., POPC),19,20,22−26 or an implicit membrane model in which the membrane is represented by a background dielectric constant.27 The biased-sampling approaches, however, do not directly provide transport rates, but only thermodynamics, without the need for reweighting the resulting ensemble. Unlike any other technique, unbiased in silico models provide unprecedented atomic detail of the molecular mechanisms associated with transport across a cell membrane by not requiring a priori knowledge of the translocation pathway or coordinates. The kinetics can be obtained from biased simulations only through an inhomogenenous-solubility-diffusion (ISD) framework, which requires the unbiasing of the rate, for example, using a Bayesian postprocessing methodology.22,24 For this reason, we sought to employ microsecond unbiased MD simulations to calculate solute permeability using a transition-based counting method. This method does not require a priori knowledge of the translocation pathway and has been shown to converge on similar timescales.20,21 This approach still requires simulation times in the tens to hundreds of microseconds per to achieve converged atomistic estimates of thermodynamics of membrane penetration at 310 K (37 C), which is above the limit of realistic sampling for routine MD simulations at present. For this reason, high-temperature simulations can be used in combination with a transition-based approach.
In this work, we employ unbiased atomistic MD simulations to study the passive transport of a library of 24 solutes across a lipid bilayer representative of BMECs. Our work constitutes the first step toward an atomistic simulation model of the blood–brain barrier. As described above, brain penetration from systemic circulation involves transport across BMECs that form the cerebrovasculature. Our simulations consist of a lipid bilayer placed in a rectangular solvent box, containing a fixed number of solute molecules. We show that solutes can be classified into three groups based on free-energy surface profiles that describe distinct mechanisms of transport across the bilayer. The permeabilities obtained from simulations vary from close to values obtained from the in vitro transwell assay and in situ brain perfusion, to more than 3 orders of magnitude faster. We show that the magnitude of the difference between simulated values and experimental values is dependent on the group defined by the free-energy surface profile. Overall, these results show that MD simulations can provide new insight into the mechanistic details of brain penetration and provide a new approach for drug discovery.
Results
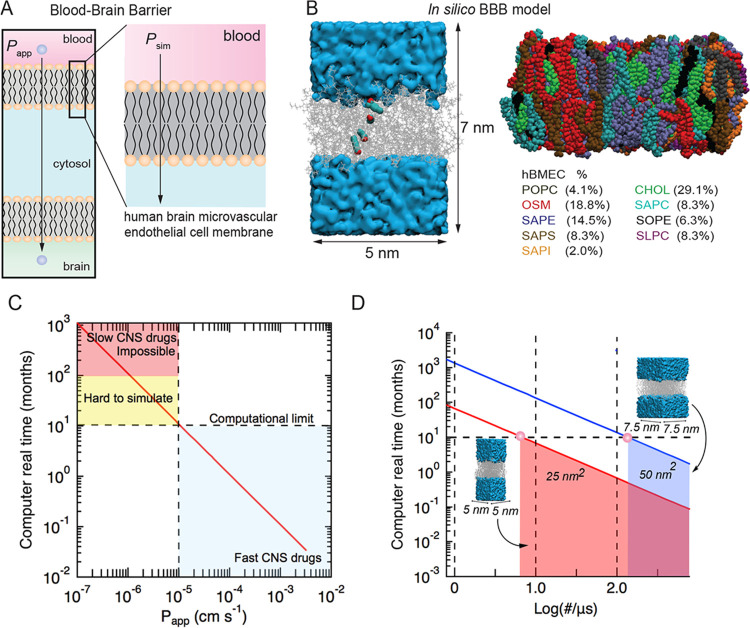
Experimentally, the transport of small molecules across the BBB is characterized by the permeability, P, which typically varies from about 10–7 to 10–3 cm s–1 for neuropharmaceuticals. Passive transport of a solute across the BBB involves diffusion across the luminal cell membrane, transport within the cell in the cytosol, and diffusion across the abluminal membrane. Here, we consider passive transport across a single-cell membrane (Figure 1A,B). Assuming that the translocation frequency k (s–1) across luminal and abluminal membranes is the same, and that diffusion within the cell is fast, then P = k/(2NAAC) where A is the area of the cell membrane, C is the solute concentration, and NA is Avogadro’s constant.8 Therefore, for typical values of permeability, the time between translocation events (1/k) across a small area of the lipid bilayer (e.g., 5 × 5 nm2) would be on the order of microseconds to seconds at a concentration of 10 mM. Therefore, for molecules with low to moderate permeability, it is extremely difficult to accumulate a sufficient number of translocation events in simulations to enable reliable determination of solute permeability within a reasonable computational time (typically 24–72 h on a standard GPU) (Figure 1C,D). Therefore, simulations were performed for a library of 24 solutes at 440 K (see Figure S1 for the molecular structure of all solutes). For solutes with relatively fast permeability, simulations were also performed at 310 K.
Figure 1.
Developing an in silico model of solute transport across a lipid bilayer model of the blood–brain barrier and benchmarking simulations. (A) Schematic illustration of the luminal and abluminal membranes of a brain microvascular endothelial cell. Passive transport into the brain involves diffusion across both membranes. (B) Overlays from a simulation showing the location of a solute during translocation across the lipid bilayer. The lipid bilayer consists of nine lipids: POPC (dark gray), OSM (red), SAPE (purple), SAPS (brown), SAPI (orange), cholesterol (green), SAPC (cyan), SOPE (black), and SLPC (magenta). Atomic detail models were constructed using the CHARMM-GUI membrane builder. (C) Molecular dynamics simulations of BBB permeability showing the real computational time (in months) to simulate solute transport at 310 K using a modern graphics processing unit (GPU) based on a solution volume of 100 nm3 and a bilayer area of 25 nm2. We assume that 100 translocation events are necessary to determine the steady-state permeability, and that simulation of 100 ns takes 1 day. Experimental values of solute permeability range from about 10–6 cm s–1 (slowest) to 10–3 cm s–1 (fastest). (D) Relationship between bilayer dimensions and computational time, with smaller bilayer areas enabling longer simulation times.
To enable assessment of a solute’s free-energy surface (FES) through the bilayer, which provides insight into the mechanism of translocation, we used long timescale equilibrium simulations. In contrast, enhanced sampling techniques, such as umbrella sampling, use biasing potentials to evaluate FES profiles along an empirical reaction coordinate. In addition, our approach also provides transport kinetics, as well as atomic resolution mechanistic details of solute transport without bias, which cannot be obtained by any other method.
Most simulations were performed on a bilayer area of 5 × 5 nm2 located in the middle of a box 7.5 nm high (Figure 1A). The aqueous volume was seeded with 20 solute molecules. In validation experiments, simulations were performed with different bilayer areas, water volumes, and solute concentrations see Supporting Information endothelial cells that contain sphingolipids (SM),29 cholesterol (CH), and phosphatidylcholine (PC),30,31 as well as phosphatidylethanolamine (PE), phosphatidylinositol (PI) lipids (Figure 1B),32 on a bilayer average.
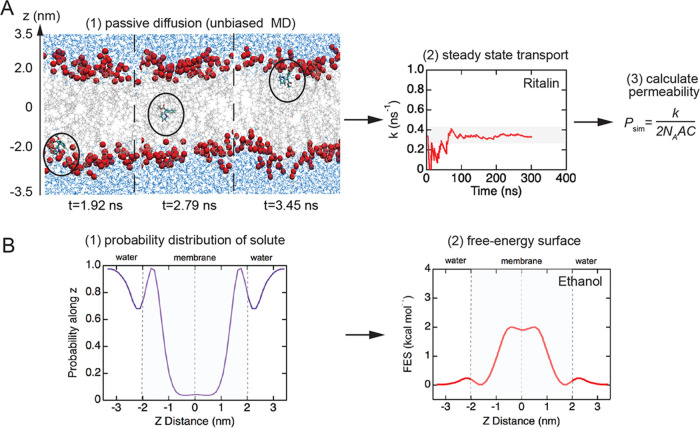
From the simulations, we obtained the steady-state rate of translocation across the bilayer (Figure 2A) and the FES profile (Figure 2B) for each solute. A translocation event is defined when a solute molecule moves from bulk solution on one side of the lipid bilayer, diffuses across the bilayer, and then appears in bulk solution on the opposite side. Examples of the translocation frequency k versus time (Figures S3 and S4) are provided for the complete solute library. The translocation rates and permeabilities for our solute library at 440 and 400 K are summarized in Table 1. The translocation frequencies varied from 0.0066 ns–1 (doxorubicin) to 1.52 ns–1 (propanol). The FES for each solute was determined from the weighted spatial probability distribution normal to the bilayer (z-direction) (see the Materials and Methods section for details) (Figure 2B). The FES curves for the solute library are described in more detail below.
Figure 2.
Simulation workflow for determination of translocation frequency and free-energy surface (FES) profiles. (A) Translocation rate and permeability: (1) perform unbiased MD simulations to obtain the translocation frequency, k (s–1), (2) determine the steady-state translocation frequency, and (3) estimate the permeability P (cm s–1) from P = k/(2NAAC), where A is the area of the cell membrane, C is the solute concentration, and NA is Avogadro’s constant. (B) FES profiles: (1) calculate the spatial probability distribution for the solute along the z-direction and (2) reweigh the probability distribution to obtain the FES profile.
Table 1. Kinetic Parameters Extracted from Simulations of the Library of Solutes at 440 and 400 Ka.
| molecule | k (ns–1) 400 K | k (ns–1) 440 K | Psim,400 K (cm s–1) | Psim,440 K (cm s–1) |
|---|---|---|---|---|
| glycerol | n/a | 0.0137 | n/a | 1.01 × 10–1 |
| temozolomide | n/a | 0.0178 | n/a | 1.32 × 10–1 |
| caffeine | n/a | 0.0069 | n/a | 6.60 × 10–2 |
| ethanol | 0.4100 | 1.3580 | 3.08 ×100 | 9.99 × 100 |
| propanol | 0.4980 | 1.5119 | 3.74 ×100 | 1.12 × 101 |
| doxorubicin | n/a | 0.0066 | n/a | 6.34 × 10–2 |
| ethosuximide | n/a | 0.0869 | n/a | 7.09 × 10–1 |
| atenolol | 0.0103 | 0.0385 | 7.73 × 10–2 | 6.99 × 10–1 |
| diazepam | 0.0361 | 0.0564 | 2.71 × 10–1 | 3.88 × 10–1 |
| nadolol | 0.0160 | 0.0714 | 1.20 × 10–1 | 6.48 × 10–1 |
| lacosamide | 0.0786 | 0.2350 | 5.90 × 10–1 | 2.65 × 100 |
| abilify | 0.0357 | 0.1361 | 2.68 × 10–1 | 1.01 × 100 |
| risperdal | 0.0285 | 0.2010 | 2.14 × 10–1 | 1.49 × 100 |
| rhodamine-123 | 0.0638 | 0.2220 | 4.79 × 10–1 | 1.64 × 100 |
| dilantin | 0.0245 | 0.1665 | 1.84 × 10–1 | 1.23 × 100 |
| ketoprofen | 0.0282 | 0.1610 | 2.12 × 10–1 | 2.72 × 100 |
| naproxen | 0.0220 | 0.2000 | 1.65 × 10–1 | 3.37 × 100 |
| nicotine | 0.3346 | 0.9700 | 2.51 × 100 | 1.21 × 101 |
| ibuprofen | 0.0120 | 0.1441 | 9.01 × 10–2 | 1.60 × 100 |
| effexor | 0.0161 | 0.0878 | 1.21 × 10–1 | 6.49 × 10–1 |
| ritalin | 0.0868 | 0.2396 | 6.51 × 10–1 | 1.77 × 100 |
| sertraline | 0.0021 | 0.0238 | 1.58 × 10–2 | 2.29 × 10–1 |
| duloxetine | 0.0076 | 0.0810 | 5.73 × 10–2 | 7.81 × 10–1 |
| bupropion | 0.0099 | 0.0925 | 7.41 × 10–1 | 8.92 × 10–1 |
For five solutes, the translocation frequency did not reach a steady-state value at 400 K (indicated by n/a).
Free-Energy Surfaces at 440 K
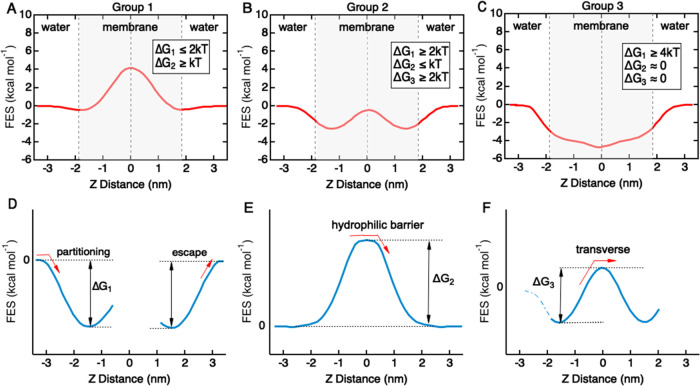
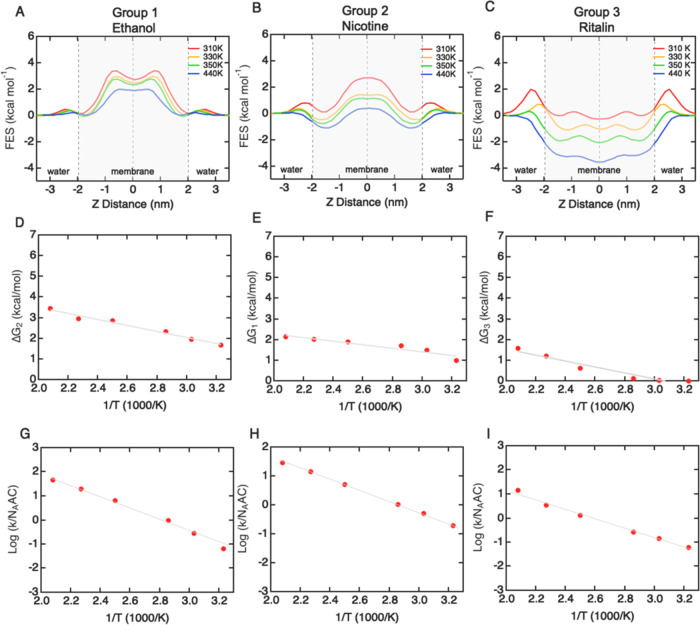
The FES profiles for the solute library can be categorized into three distinct groups with characteristic topological shapes (Figure 3A–C). A similar classification approach has been proposed to describe solute permeability across an implicit membrane model based on the Heterogeneous Dielectric Generalized Born (HDGB) equation.27 Each FES profile is described in terms of three parameters: ΔG1, ΔG2, and ΔG3 (Figure 3D–F). Energy minima in the head group regions result in an energy well for partitioning and an energy barrier to escape from the bilayer (ΔG1). An energy barrier in the center of the bilayer provides an energy barrier for translocation across the hydrophobic core (ΔG2). Energy minima in the head group regions combined with an energy barrier in the center of the bilayer result in an energy barrier for hopping between the energy minima (ΔG3).
Figure 3.
Characterizing free-energy surface profiles for BBB translocation for the solute library. (A) Group 1 solutes have an energy barrier located in the hydrophobic core in the center of the bilayer (ΔG2 ≥ kT). In some cases, there are energy minima located in the head group regions, with a barrier to escape from the bilayer (ΔG1 ≤ 2kT) and an energy barrier between the two minima (ΔG3 ≤ kT). (B) Group 2 solutes have two energy minima located in the head group regions of the bilayer separated by a small energy barrier in the hydrophobic core. This profile results in a barrier to escape from the bilayer ΔG1 ≥ 2kT and an energy barrier associated with hopping between the two minima in the hydrophobic core (ΔG3 ≤ kT). (C) Group 3 solutes have an energy minimum in the center of the bilayer, resulting in a barrier to escape from the bilayer (ΔG1 ≥ 4kT). (D) Energy minima in the head group regions result in an energy barrier to escape from the bilayer (ΔG1). (E) Energy barrier in the center of the bilayer provides an energy barrier to translocation across the hydrophobic core (ΔG2). (F) Energy minima in the head group regions combined with an energy barrier in the center of the bilayer result in an energy barrier for hopping between the energy minima (ΔG3).
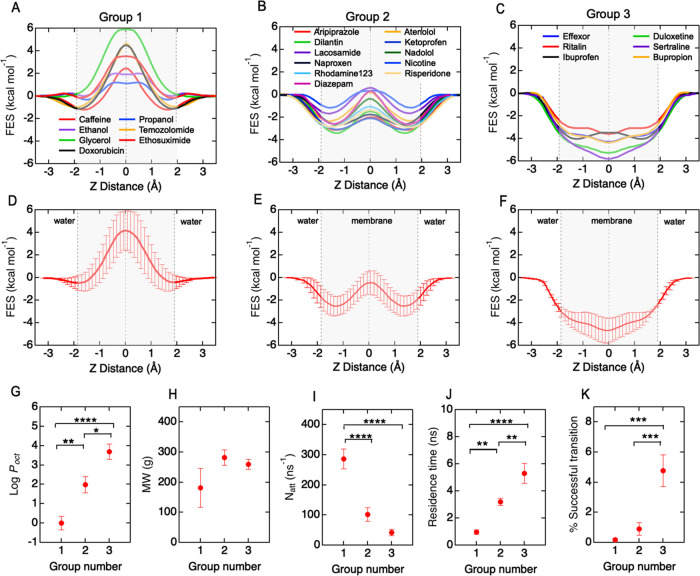
Group 1 molecules (N = 7) include ethanol, propanol, caffeine, glycerol, doxorubicin, ethosuximide, and temozolomide (Figure 4A). The FES profiles are characterized by a large energy barrier at the core of the bilayer with no significant minima (ΔG1 ≤ 2kT; ΔG2 ≥ kT; ΔG3 ≈ 0). These molecules are hydrophilic and have a low concentration within the bilayer. Group 2 molecules (N = 11) include nicotine, atenolol, diazepam, nadolol, lacosamide, abilify, risperdal, rhodamine-123, dilantin, ketoprofen, and naproxen (Figure 4B). The FES profiles have energy wells in the head group regions within the bilayer and an energy barrier at the hydrophobic core (ΔG1 ≥ 2kT; ΔG2 ≤ kT; ΔG3 ≥ 2kT). These molecules partition into the bilayer head group regions but must surmount the energy barrier at the core to occupy the adjacent well prior to escaping the bilayer. Group 3 molecules (N = 6) include solutes ibuprofen, effexor, ritalin, sertraline, duloxetine, and bupropion (Figure 4C). The FES profiles have a broad energy minimum in the hydrophobic core, with a near-zero probability of finding a molecule outside the bilayer core (ΔG1 ≥ 4kT; ΔG2 ≈ 0; ΔG3 ≈ 0). These molecules are typically lipophilic drugs. The molecular structures for the three groups are shown in Figure S7. The average FES profiles for each group show the characteristic shapes (Figure 4D–F).
Figure 4.
Free-energy surface profiles, translocation kinetics, and physicochemical properties of a 24 solute library. Free-energy surface (FES) profiles can be classified into three groups based on energy barriers ΔG1, ΔG2, and ΔG3. (A) Group 1: ethanol, propanol, caffeine, glycerol, doxorubicin, ethosuximide, and temozolomide. (B) Group 2: nicotine, atenolol, diazepam, nadolol, lacosamide, abilify, risperdal, rhodamine-123, dilantin, ketoprofen, and naproxen. (C) Group 3: ibuprofen, effexor, ritalin, sertraline, duloxetine, and bupropion. (D–F) Average free-energy surface profiles for each group. (G–K) Dependence of hydrophobicity (log Poct), molecular weight, attempt frequency for bilayer entry, residence time in the bilayer, and the fraction of successful translocation events for each group. Bars represent mean ± standard error (SE). Statistical significance was tested with an ANOVA test with a posthoc Tukey test. Symbol meaning, *P ≤ 0.05, **P ≤ 0.01, ***P ≤ 0.001, and ****P ≤ 0.0001.
The classification of solutes into three groups is based solely on thermodynamic considerations (barrier heights), and not on chemistry or transport kinetics. To assess differences between the three groups, we considered a number of physicochemical parameters (Table S1) along with metrics associated with the simulations (Tables S6–S9).
Group 1 solutes are highly polar (average log Poct = 0.0 ± 0.4) and have the lowest percentage of successful translocation events (0.1 ± 0.1%). The number of failed translocation attempts (based on molecules entering the bilayer) was 214 ± 56 ns–1. Group 2 solutes have a higher lipophilicity (average log Poct = 2.1 ± 0.4) and have an intermediate percentage of successful translocation events (2.2 ± 0.7%), and a lower number of failed attempts (27 ± 13 ns–1). Group 3 solutes are highly lipophilic (average log Poct = 3.7 ± 0.4) and have the highest percentage of successful translocation events (4.2 ± 0.7%) and the lowest number of failed translocation events (3.3 ± 1 ns–1).
The translocation frequency was not statistically different between groups, despite the differences in an energy barrier, indicating that different FES profiles, and hence different translocation pathways, can have similar rates. The lipophilicity (log Poct), attempt frequency, residence time, and fraction of successful translocation events (Figure 4G,I–K) were different between groups. Solute molecular weight was also not significantly different between groups (Figure 4H), which is consistent with previous observations that molecular weight is a poor descriptor of permeability and entry into the brain.33−35 There are two important implications of the existence of discrete groups. First, it suggests that solutes utilize different mechanisms for passive transport across the BBB. Second, it is possible to classify new solutes into one of the three groups based on their physicochemical properties.
Mechanisms of Passive Diffusion
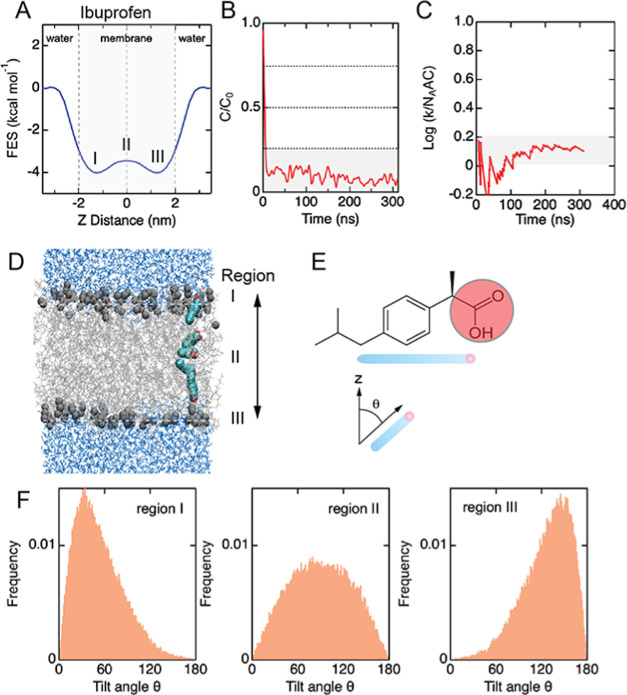
The relationship between the trajectory of molecules and FES profiles provides insight into the mechanism of translocation. As an example, here we considered passive diffusion of the group 3 solute ibuprofen (Figure 5). Ibuprofen is widely used to treat pain and has a free-energy curve characterized by a double well with no significant barrier in the hydrophobic core (Figure 5A). Ibuprofen accumulates in the center of the bilayer (Figure 5B) and is characterized by a translocation rate of 0.144 ± 0.003 ns–1 at 440 K (Figure 5C). On entry into the bilayer, ibuprofen is oriented at an average angle of 30° to the bilayer normal, with the hydrophilic head group facing away from the hydrophobic core (Figure 5D–F). On approaching the hydrophobic core, the molecule rotates to be approximately parallel to the bilayer (on average 90° to the bilayer normal). Then, on moving into the lower leaflet, the molecule rotates to 30° from the bilayer normal with the head group region again facing away from the hydrophobic core. This is an example of an orientation inversion mechanism.
Figure 5.
Mechanism of ibuprofen translocation. (A) Free-energy surface profile for ibuprofen at 440 K with a characteristic double minima. (B) Steady-state concentration (C/C0) relative to initial bulk concentration shows majority of ibuprofen accumulates in a membrane. (C) Translocation rate (k/NAAC) reaches a steady state after about 200 ns. (D) Images from a single ibuprofen translocation event across the bilayer. (E) Schematic illustration showing the reference for orientation of ibuprofen. (F) Distribution of ibuprofen orientations in regions I–III of the bilayer during translocation.
Temperature Dependence of Translocation Rates
To assess the temperature dependence of translocation rates and FES profiles, we performed simulations of selected molecules from each of the three groups: ethanol (group 1), nicotine (group 2), and ritalin (group 3). For all three molecules, the translocation frequency was sufficiently high at 310 K to enable accurate evaluation within accessible computational times. Over the temperature range from 440 K down to 310 K, the main features of the FES profiles were preserved (Figure 6A–C). For ethanol, as the temperature decreased the main barrier at the center of the bilayer broadened and a small well developed (although it was less than kT). In addition, small energy minima developed in the head group regions. For nicotine, the double-well shape was preserved at all temperatures. For ritalin, a peak emerged (>kT) associated with partitioning through the polar head group region of the bilayer. The values of ΔG1, ΔG2, or ΔG3 used to define the three groups increased monotonically as the temperature was lowered from 440 to 310 K (Figure 6A–C). To characterize the temperature dependence of the translocation process, we considered the largest of the energy barriers in the FES profiles for each solute: ΔG2 for ethanol, ΔG1 for nicotine, and ΔG3 for ritalin. In all three cases, the maximum energy barrier followed Arrhenius behavior (Figure 6D–F). At physiological temperature, the barrier properties of group 3 change somewhat compared to that at 440 K. In particular, the hydrophobicity that dominates this group gives rise to a barrier at the head group region (Figure 6C), which corresponds to the penalty from partitioning through the polar head group region of the membrane, but once partitioned, these molecules have an energy minimum in the lipid tail region, which is in agreement with our high-temperature simulations.
Figure 6.
Temperature dependence of free-energy surface (FES) profiles and translocation rates for ethanol (group 1), nicotine (group 2), and ritalin (group 3). (A–C) FES profiles obtained at 310, 330, 350, 400, 440, and 480 K. (D–F) Temperature dependence of FES profiles. (G–I) Temperature dependence of translocation rates (310–480 K).
The translocation rates for ethanol, nicotine, and ritalin also follow Arrhenius behavior (Figure 6G–I). For ethanol, the permeability obtained from the simulations (P = k/(2NAAC)) at 310 K was Psim = 3.00 × 10–2 cm s–1. This is an order of magnitude larger than a reported experimental value, Papp = 1.10 × 10–3 cm s–1.36 However, we note that the experimental permeability is not from a transwell measurement but is inferred from uptake in red blood cells. A recent simulation at 308 K using a mammalian bilayer estimated an ethanol permeability of 1.2 ± 0.1 × 10–2 cm s–1,37 close to the value found here.
For nicotine, the permeability obtained from simulations at 310 K was 1.09 × 10–1 cm s–1, about 3 orders of magnitude faster than the reported experimental value from the transwell assay (Papp = 1.78 × 10–4 cm s–1). Similarly, the permeability obtained from simulations for ritalin at 310 K was 4.61 × 10–2 cm s–1, also about 3 orders of magnitude faster than the experimental value (Papp = 2.47 × 10–5 cm s–1).
Since translocation rates follow Arrhenius behavior, we can consider estimating the translocation rate at 310 K from extrapolation of high-temperature simulations (at 440 and 400 K). For ethanol, the extrapolated permeability was 1.16 × 10–1 cm s–1, 3-fold higher than the value obtained at 310 K (Psim = 3.00 × 10–2 cm s–1). For nicotine, the extrapolated value at 310 K was 1.18 × 10–1 cm s–1, very close to the simulation result of 0.99 ×10–3 cm s–1. For ritalin, the extrapolated value at 310 K was 3.02 × 10–2 cm s–1, close to the simulation result of 4.00 × 10–2 cm s–1. At temperatures above physiological temperatures, the kinetic energy of solutes is higher and the energy barriers for passive diffusion are reduced (Figure 6A–C), resulting in an increase in translocation rates and implying that high-temperature MD simulations can be viewed as physiological with a temperature-dependent bias.21 The results for these molecules suggest that the extrapolation can be used to make a comparison of simulation results to experimental values of Papp at 310 K (Table 2).
Table 2. Translocation Frequency and Permeability at 310 K Obtained from Values at 440 and 400 K, and Experimental Values of In Vitro Permeability (Papp) from Transwell Measurements.
| molecule | group | k (ns–1) 310 K | Psim,310 K (cm s–1) | Papp (cm s–1) | log Psim,310 K – log Papp |
|---|---|---|---|---|---|
| glycerol | 1 | 2.05 × 10–3 | 2.00 × 10–2 | 9.50 × 10–6 | 3.32 |
| temozolomide | 1 | 3.19 × 10–3 | 3.12 × 10–2 | 1.86 × 10–6 | 4.22 |
| caffeine | 1 | 3.34 × 10–3 | 3.27 × 10–2 | 2.10 × 10–5 | 3.19 |
| ethanol | 1 | 1.62 × 10–2 | 1.58 × 10–1 | 1.10 × 10–3 | 2.53 |
| propanol | 1 | 3.13 × 10–2 | 3.06 × 10–1 | 3.30 × 10–3 | 2.23 |
| doxorubicin | 1 | 4.78 × 10–3 | 4.68 × 10–2 | 1.00 × 10–7 | 5.67 |
| ethosuximide | 1 | 2.45 × 10–2 | 2.40 × 10–1 | 9.00 × 10–6 | 4.43 |
| atenolol | 2 | 4.79 × 10–7 | 9.38 × 10–6 | 1.30 × 10–6 | 2.37 |
| diazepam | 2 | 5.21 × 10–5 | 5.10 × 10–4 | 4.60 × 10–5 | 1.56 |
| nadolol | 2 | 1.28 × 10–6 | 1.25 × 10–5 | 3.30 × 10–7 | 3.02 |
| lacosamide | 2 | 1.87 × 10–4 | 2.61 × 10–3 | 1.60 × 10–5 | 3.02 |
| risperdal | 2 | 3.40 × 10–6 | 3.33 × 10–5 | 3.00 × 10–5 | 1.31 |
| rhodamine-123 | 2 | 8.49 × 10–5 | 8.31 × 10–4 | 0.80 × 10–7 | 4.80 |
| dilantin | 2 | 2.36 × 10–6 | 2.31 × 10–5 | 2.70 × 10–5 | 1.12 |
| ketoprofen | 2 | 4.43 × 10–6 | 8.68 × 10–5 | 8.00 × 10–5 | 1.17 |
| naproxen | 2 | 1.17 × 10–6 | 2.30 × 10–5 | 3.90 × 10–5 | 1.15 |
| nicotine | 2 | 1.10 × 10–2 | 2.16 × 10–1 | 1.78 × 10–4 | 3.55 |
| ibuprofen | 3 | 1.48 × 10–7 | 1.45 × 10–6 | 2.70 × 10–5 | 0.54 |
| effexor | 3 | 9.91 × 10–7 | 9.70 × 10–6 | 6.00 × 10–5 | 0.65 |
| ritalin | 3 | 2.75 × 10–4 | 2.69 × 10–3 | 2.47 × 10–5 | 2.77 |
| sertraline | 3 | 1.25 × 10–9 | 1.22 × 10–8 | 2.10 × 10–6 | –1.60 |
| duloxetine | 3 | 4.97 × 10–8 | 4.86 × 10–7 | 1.66 × 10–5 | 0.21 |
| bupropion | 3 | 1.21 × 10–7 | 1.18 × 10–6 | 4.75 × 10–5 | 0.09 |
Discussion
Translocation Pathway
Based on the FES profiles for translocation, we showed that a library of 24 solutes can be classified into three groups based on the quantitative values of energy barriers. The FES profile for each group has a distinct shape that is characteristic of the translocation pathway. Group 1 solutes are characterized by a large energy barrier located in the hydrophobic core. These molecules are generally lipophobic (log Poct ≈ 0) and, due to the energy barrier, have a small residence time in the membrane. For ethanol at lower temperatures, the energy barrier separates into two peaks, resulting in a small energy well at the center of the bilayer, suggesting a metastable state in the region between the two leaflets.
Group 2 solutes have an energy barrier in the hydrophobic core of the membrane separated by two energy wells. These molecules have intermediate lipophilicity (log Poct ≈ 2) and are partition into the energy wells that are located just inside the head group region. The translocation pathway for these molecules is more complicated compared to group 1, which primarily involves surmounting a single energy barrier. Group 2 molecules first partition into the energy well of the leaflet proximal to the solution/membrane interface. From this energy well, the solute can escape back into bulk solution or hop to the second energy well. The energy barrier to re-enter the bulk solution is typically slightly higher (up to 2-fold), and hence there is generally a slightly higher probability of hopping to the second energy well. From the second energy well, the solute can escape across the bilayer (into the cytosol) or hop back to the first energy well. Since the probability for escape is typically higher, the solute can oscillate between the two wells. For these molecules, the attempt frequency is higher and the residence time longer than for group 1 solutes.
The FES profiles for group 3 solutes are characterized by a large energy well within the hydrophobic core of the membrane. These molecules have relatively high lipophilicity (log Poct ≈ 4) and are partition into the membrane core. The translocation pathway involves partitioning into the membrane, across the lipid head group region, and then escaping back into the bulk solution or across the membrane. The attempt frequency is the highest of the three groups, and the residence time is the longest due to the large energy well. For ibuprofen, we found that the trajectory through the bilayer involves changes in orientation in different regions.
Although the solutes in the three groups have statistically significant differences in lipophilicity (log Poct), an important metric in Lipinski’s rule of 5, there was no correlation in translocation frequency between the three groups. The different translocation pathways identified in the three groups have important implications for other processes. For example, solutes with long residence times have more chance to interact with membrane proteins, such as efflux pumps, compared to solutes with low residence time.
Translocation Rate and Permeability
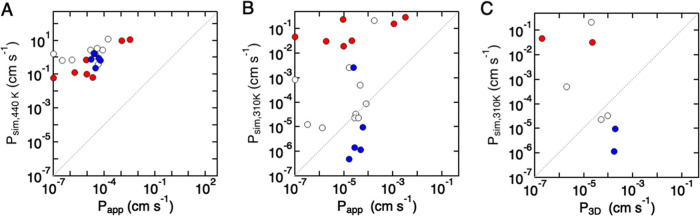
To determine translocation frequencies for all solutes, including those with low permeabilities, simulations were performed at 440 K. Comparison of simulated permeabilities at 440 K and in vitro permeabilities (310 K) (Figure 7A) shows that simulated values are consistently higher than in vitro experimental values by 4–5 orders of magnitude, although there is a general correlation between values (r2 = 0.50). The correlation for group 3 solutes was highest (r2 = 0.78) compared to groups 1 and 2 (r2 = 0.57 and 0.08, respectively), further supporting differences in the translocation mechanism between groups.
Figure 7.
Comparison of permeabilities from simulations (Psim) and values obtained from in vitro experiments (Papp) or in situ brain perfusion (P3D). (A) Permeability obtained from simulations at 440 K (Psim,440 K) versus in vitro permeability (Papp) at 310 K. (B) Permeability obtained from simulations at 310 K (Psim,310 K) versus permeability obtained from in vitro permeability (Papp). (C) Permeability obtained from simulations at 310 K (Psim,310 K) versus permeability (P3D) obtained from in situ brain perfusion (red: group 1; white: group 2; blue: group 3).
To compare permeabilities for all solutes at 301 K, values from simulations were obtained by extrapolation of values at higher temperatures. Comparison of simulations for ethanol, nicotine, and ritalin at temperatures from 310 to 440 K (Figure 6) suggests that this approach is reasonable. The permeability values from simulations at 310 K (Psim,310 K) show no correlation with in vitro (Papp) (Figure 7B) or in vivo (P3D) (Figure 7C) values, with differences of several orders of magnitude (Table 2). However, four molecules show excellent agreement between Psim,310 K and Papp (dilantin, ketoprofen, naproxen, risperdal: all group 1), and four molecules are within 10-fold (effexor and ritalin in group 3, and atenolol and diazepam in group 1). The difference between simulation and in vitro permeabilities may be derived from the simulations or the experimental methods, which we consider in more detail below. These results suggest that experimental permeabilities are in many cases not limited by simple passive diffusion but are dependent on other factors associated with transport.
The brain penetration of solutes can be estimated using a number of in vivo and in vitro methods.15 In the in vitro transwell assay, the permeability is determined from the time-dependent amount of solute crossing a confluent monolayer of endothelial cells supported on a porous membrane and is determined by an appropriate analytical method.8,15,38 Values of solute permeability can also be obtained from in vivo experiments, typically from in situ brain perfusion in a rat model (P3D).16,17 In this model, a solute of interest is introduced into one hemisphere of the brain by interarterial injection, and the amount in that hemisphere is determined by mass spectroscopy following removal of blood and homogenization. These in vivo measurements require estimates for the luminal area of the vasculature and the vascular volume.
Experimental values of permeability derived from the 2D transwell assay (Papp) are widely used to predict brain penetration of small molecules.15 However, there are many implicit simplifying assumptions associated with transwell measurements. A study of 50 solutes found a modest correlation (Pearson correlation coefficient = 0.82) between P3D and Papp for solutes with log Poct ≤ 3 but no correlation for drugs with log Poct ≥ 3.18 Typically, values of P3D were between 1 and 100 times faster than values obtained from the transwell assay. The differences were, in part, correlated with the unbound fraction of the solute in the brain. These results highlight the variability in measurements of permeability and indicate that there is no gold standard for benchmarking permeability. Understanding the origin of these differences will be key to the development of future neuropharmaceuticals.
The average differences between simulated and in vitro permeabilities (log Psim,310 K – log Papp) for the solute library varied from about 5 orders of magnitude faster to about 3 orders of magnitude slower (Table 2 and Figure 8A). However, the difference was dependent on the solute group (Figure 8B–D). The average values of log Psim,310 K – log Papp were 3.57 (3000-fold) for group 1 solutes, 1.2 (15-fold) for group 2, and −1.0 (10-fold) for group 3 (Table 2 and Figure 8A). The differences between simulated and in vivo permeabilities (log Psim,310 K – log P3D) were 4.27 (15 000-fold) for group 1, 2.27 (158-fold) for group 2, and −1.04 (10-fold) for group 3 (Table 3).
Figure 8.
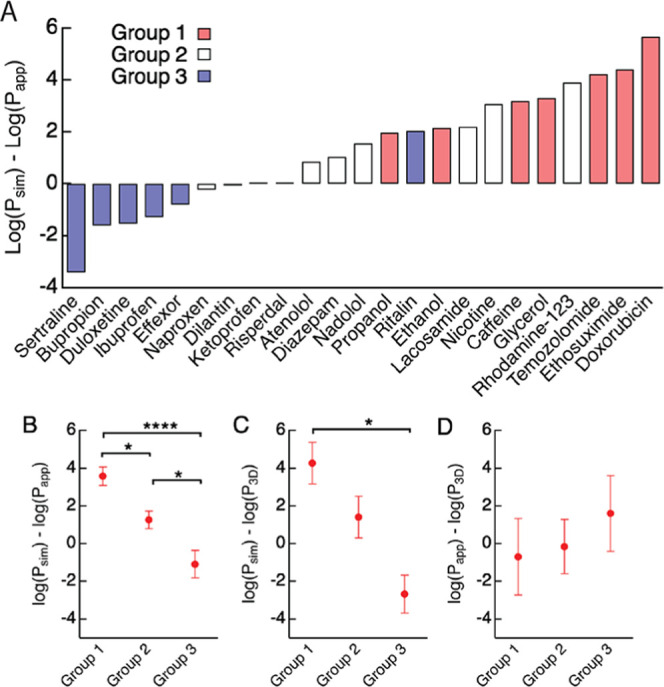
Difference between permeabilities obtained from simulations (Psim,310 K) and in vitro (Papp) and in vivo (P3D) values for the three groups. (A) Difference in permeability (log Psim,310 K – log Papp) for each solute at 310 K, color coded by group (red: group 1; white: group 2; blue: group 3). (B) Difference between simulations and in vitro permeabilities (log Psim,310 K – log Papp). (C) Difference between simulations and in vivo permeabilities (log Psim,310 K – log P3D). (D) Difference between in vitro and in vivo permeabilities (log Papp – log P3D). Bars represent mean ± SE.
Table 3. Translocation Frequency at 310 K Obtained from Values at 440 and 400 K, and Experimental Values of Permeability from In Situ Brain Perfusion (P3D).
| molecule | group | k (ns–1) at 310 K | Psim,310 K (cm s–1) | P3D (cm s–1) | log Psim,310 K – log P3D |
|---|---|---|---|---|---|
| caffeine | 1 | 3.34 × 10–3 | 3.27 × 10–2 | 2.22 × 10–5 | 3.17 |
| doxorubicin | 1 | 4.78 × 10–3 | 4.68 × 10–2 | 2.00 × 10–7 | 5.37 |
| diazepam | 2 | 5.21 × 10–5 | 5.10 × 10–4 | 2.00 × 10–6 | 2.92 |
| risperdal | 2 | 3.40 × 10–6 | 3.33 × 10–5 | 9.44 × 10–5 | 0.81 |
| dilantin | 2 | 2.36 × 10–6 | 2.31 × 10–5 | 5.00 × 10–5 | 0.85 |
| nicotine | 2 | 1.10 × 10–2 | 2.16 × 10–1 | 2.02 × 10–5 | 4.48 |
| effexor | 3 | 9.91 × 10–7 | 9.70 × 10–6 | 1.88 × 10–4 | 0.15 |
| sertraline | 3 | 1.25 × 10–9 | 1.22 × 10–8 | 4.88 × 10–4 | –2.81 |
| bupropion | 3 | 1.21 × 10–7 | 1.18 × 10–6 | 1.69 × 10–4 | –0.46 |
Molecules with simulated permeabilities at 310 K within 100-fold of the experimental in vitro permeabilities are propanol (group 1), diazepam (group 2), nadolol (group 2), risperdal (group 2), dilantin (group 2), ketoprofen (group 2), naproxen (group 2), and effexor (group 3). Comparison of the differences between simulated and in vivo permeabilities (Figure 8A) shows that group 3 solutes are typically faster in simulations, but that group 1 and 3 solutes are typically slower, although, on average, group 2 solutes are closest to experimental values (Figure 8A,B). In addition, group 2 solutes show the smallest difference between in vitro (Papp) and in vivo (P3D) measurements, although the result is not statistically significant.
In relating the translocation frequency from simulations to permeability (Papp), it is assumed that to enter the brain, a solute must cross both luminal and abluminal membranes, and that transport inside the cell is fast in comparison to translocation across the bilayer. In this situation, the permeability is directly related to the translocation frequency (i.e., P = k/(2NAAC)). This simple model also assumes that the solute is not sequestered in the glycocalyx or within the cell, the solute does not dissociate or undergo enzymatic degradation, and there is no efflux.39,40 All of these processes can result in a lower apparent permeability in in vitro experiments compared to the ideal case where the slow step is passive diffusion across cell membranes. Therefore, one reason for the simulations being faster than experiments is that the experimental assumptions are not satisfied, i.e., the permeability cannot be modeled by simple passive transport across two bilayer membranes. The simulated permeabilities for group 1 and 2 solutes are typically the same or faster than experimentally reported in vitro values, suggesting that transport cannot be modeled as simple passive diffusion across a lipid bilayer. This suggests that these solutes are more susceptible to sequestration, dissociation, degradation, and/or efflux. In contrast, the permeabilities in simulations were typically slower than experimental values for group 3 solutes. Group 3 solutes have high lipophilicity, and, as described above, a previous study found no correlation between in vitro and in vivo permeabilities for solutes with lipophilicity >3.18 The reason for this difference remains to be established.
Conclusions
The transport of small molecules across the BBB is complex and poorly understood. Empirical predictions of brain penetration are inconsistent, and there is considerable disagreement between in vitro and in vivo measurements of permeability. Atomistic simulations have the potential to unravel these inconsistencies and enable new mechanistic insight into solute transport into the brain. The work reported here provides the foundations for developing more complex models that incorporate other processes, such as solute interactions with the cell membrane, sequestration within the cell, efflux, dissociation, or enzymatic degradation, all processes that are ignored in the simple passive diffusion model and are difficult to study experimentally.
Materials and Methods
Simulation Details
Unbiased atomic detail molecular dynamics (MD) simulations were performed using GROMACS (www.gromacs.org)41 in combination with the CHARMM general force field for molecular solutes and the TIP3P water model as a solvent.42 Lipid parameters were taken from the CHARMM36 all-atom force field.43 Electrostatic interactions were computed using particle-mesh-Ewald (PME),44 and a cutoff of 10 Å was used for van der Waals interactions. Bonds involving hydrogen atoms were restrained using LINCS45 to allow a 2 fs time step. Neighbor lists were updated every five steps. All simulations were performed in the NPT ensemble, with water, lipids, and drug molecules coupled separately to a heat bath with temperatures in the range of 310–440 K using a time constant τT = 0.1 ps in combination with the velocity rescaling algorithm.46 An atmospheric pressure of 1 bar was maintained using the Berendsen semi-isotropic pressure coupling with compressibility κz = κxy = 4.6 × 10–5 bar–1. Production runs were performed with the Parrinello–Rahman semi-isotropic pressure coupling with compressibility κz = κxy = 4.6 × 10–5 bar–1 and time constant τP = 20 ps.47 To capture diffusion events at sufficiently high resolution, trajectories were recorded every 1 ps, such that each 1 ms of trajectory comprises a data set of 1 × 107 observations.
Lipid Bilayer Model of Human Brain Microvascular Endothelial Cells (BMECs)
An atomic detail molecular model of the apical BMEC lipid bilayer was constructed by replicating physiological lipid compositions.21 The BMEC bilayer model with 96 lipids (48 per leaflet) in an area of about 25 nm2 was set up using the composition for polarized endothelial cell membranes,14,30,31 which contain a high content of sphingolipids (SM),29 cholesterol (CH), and phosphatidylcholine (PC),30,31 as well as phosphatidylethanolamine (PE), phosphatidylinositol (PI) lipids (see the Supporting Information for details).32 Information about the lipid distribution in the individual leaflets was not available and was not incorporated in the model. Physical bilayer parameters were determined to assess bilayer stability with temperature and were compared to experimental measurements. In particular, the average lipid diffusion coefficient in the plane of the membrane (DL(T)) and the area-per-lipid (APL) were validated to reference parameters. DL(T) was calculated by averaging the diffusion of heavy atoms for all lipid species in the bilayer for the lipids POPC, SAPE, SOPE, and cholesterol.
Compound Library of the CNS Drug Space
A library of molecular solutes (N = 24; Table S1 and molecular structures in Figure S1) was chosen to be sufficiently broad and representative of CNS drugs, spanning a range of permeabilities (from 10–7 to 10–3 cm s–1), charge (neutral, cationic, anionic, and zwitterionic), and lipophilicity (log Poct values from −1.8 (polar) to 5.10 (nonpolar)). Solute transport is dependent, in part, on the choice of solute force field.19,23,27 Force-field parameters were obtained in a standardized fashion using the CGenFF program48,49 (version 2.0) to obtain bonded and nonbonded parameters via the automated parameter assignment tool (Paramchem)50 of CGenFF. The quality of similarity assignment for bonded and nonbonded parameters was monitored by penalty scores (Table S2).
Simulations of Solute Translocation
The standard simulation system contains 2913 water molecules, 96 lipids, and 20 solute molecules distributed randomly with PACKMOL.51 The standard box areas were approximately 25 nm2 (310 K) to 33 nm2 (440 K), with total volumes of approximately 175 nm3 (310 K) to 220 nm3 (440 K). The water volumes were approximately 83 nm3 (310 K) to 100 nm3 (440 K). Solute translocation across the BMEC lipid bilayer model was validated by computing the permeability at different solute concentrations (N = 1–20) for ethanol, when varying the lipid bilayer area (96 lipids, 192 lipids, 384 lipids; Figure S2), and when varying the water volume (2913 water molecules and 7372 water molecules). Simulations of solute translocation were performed at temperatures from 310 to 440 K. Simulations at elevated temperatures were necessary to enable accurate determination of the translocation frequency for solutes with low permeability. This high-T MD methodology is applicable to lipid membranes in conjunction with small-molecule solutes that do not denature at 440 K ≥ T > 310 K.21 The use of nonpolarizable water models, such as TIP3P, at high temperatures carries limitations. While high-temperature simulations are well established in the field of MD simulation, the water models do not accurately describe the phase transitions associated with heating (or cooling). However, since we are not aiming to describe transport properties in water, we hold that the methodology is applicable to solute translocation across low dielectric media, such as a lipid bilayer.
Quantifying Solute Translocation across the Lipid Bilayer
There are two general approaches for calculating permeability in simulations: Fick’s law counting-based methods (used in this work) and methods based on the inhomogeneous solubility-diffusion (ISD) equation.52 The ISD model is more complex since it requires accurate determination of the diffusion coefficient and free-energy surface at each location (i.e., position in the bilayer), both of which are challenging.53−56 Here, we use direct observation from simulations to identify individual translocation events.
The solute translocation frequency (k) across the bilayer is the number of translocation events per unit time. A translocation event is defined when a solute molecule moves from bulk solution on one side of the lipid bilayer, across the bilayer, and crosses a plane 1.0 nm beyond the bilayer on the opposite side. In the simulations, we define the steady-state translocation k frequency as the average value when the derivative is less than a threshold value: i.e., dk/dt = [(k(i + 1) – k(i))/Δt] < 0.004.
Free-Energy Surfaces (FES) and Grouping of Solutes
FES profiles were calculated by first binning the z-positions of a solute to generate a one-dimensional probability distribution P(z). The free energy, F(z), was calculated by Boltzmann reweighting of the probability distribution (see the Supporting Information for details).
Statistics
The statistical significance of parameters between groups of solutes was determined using analysis of variance (ANOVA) with a posthoc Tukey HSD (Honestly Significant Difference) test.57
Experimental Values of Permeability
Experimental values of permeability from in vitro transwell experiments and from in vivo in situ brain perfusion experiments used for comparison to simulation results are provided in the Supporting Information (Table S2), along with the source references. The in vitro data comes from various cell lines, Madin–Darby Canine Kidney (MDCK), human colorectal adenocarcinoma cells (Caco-2), and stem cell-derived brain microvascular endothelial cells, as well as inferences from red blood cell (RBC) or the parallel artificial membrane permeability assay (PAMPA). In vivo data were obtained from rat brain perfusion, involving the cannulation of the carotid artery and infusing whole blood, physiological buffer, or saline to determine solute uptake.
Acknowledgments
The authors gratefully acknowledge support from DTRA (HDTRA1-15-1-0046). This research project was conducted using computational resources at the Maryland Advanced Research Computing Center (MARCC). The authors acknowledge insightful discussions with Erin Gallagher and Raleigh Linville.
Glossary
Glossary
- Papp
experimental permeability from the transwell assay (cm s–1)
- P3D
permeability from in situ brain perfusion (cm s–1)
- Psim,T
permeability from simulations at temperature T (cm s–1)
- k
translocation frequency (s–1)
- A
area (of lipid bilayer) (cm–2)
- C
concentration of solute in bulk water (mol cm–3)
- Natt
attempt frequency for solute translocation (ns–1)
- Poct
octanol–water partition coefficient
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c05679.
Chemical structures of the library (N = 24) of molecules (Figure S1); membrane area (Figure S2); translocation frequency (k) convergence (Figure S3); convergence threshold for the numerical evaluation of the rate constant k based on forward-difference gradient (Figure S4); temperature dependence of the diffusion coefficients (Figure S5); consistency of Psim values (Figure S6); chemical structures of the library (N = 24) arranged by energy-clustered groups 1–3 (Figure S7); temperature dependence of the transbilayer free-energy surfaces (FES) (Figure S8); solute steady-state concentration (C/C0) (Figure S9); spontaneous transbilayer transition rate (k) convergence (Figure S10); convergence threshold for the numerical evaluation of the rate constant k based on forward-difference gradient (Figure S11); comparison of permeability values (Figure S12); force-field penalty scores for solute library (Figure S13); reference physicochemical parameters (Table S1); experimental values of permeability (Table S2); position of phosphorous (P) atom (Table S3); comparison of lipid lateral diffusivity and lipid area-per-lipid (APL) (Table S4); ethanol permeability (440 K) (Table S5); kinetic and thermodynamic parameters (Table S6); kinetic parameters extracted from simulations of the library of solutes (Table S7); group-based average (Table S8); and references (PDF)
Author Present Address
∥ Department of Physics, Georgetown University, Washington, District of Columbia, United States
The authors declare no competing financial interest.
Supplementary Material
References
- Pankevich D. E.; Altevogt B. M.; Dunlop J.; Gage F. H.; Hyman S. E. Improving and accelerating drug development for nervous system disorders. Neuron 2014, 84, 546–553. 10.1016/j.neuron.2014.10.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kesselheim A. S.; Hwang T. J.; Franklin J. M. Two decades of new drug development for central nervous system disorders. Nat. Rev. Drug Discov. 2015, 14, 815–816. 10.1038/nrd4793. [DOI] [PubMed] [Google Scholar]
- Butlen-Ducuing F.; Petavy F.; Guizzaro L.; Zienowicz M.; Haas M.; Alteri E.; Salmonson T.; Corruble E. Regulatory watch: Challenges in drug development for central nervous system disorders: a European Medicines Agency perspective. Nat. Rev. Drug Discov. 2016, 15, 813–814. 10.1038/nrd.2016.237. [DOI] [PubMed] [Google Scholar]
- Kola I.; Landis J. Can the pharmaceutical industry reduce attrition rates?. Nat. Rev. Drug Discov. 2004, 3, 711. 10.1038/nrd1470. [DOI] [PubMed] [Google Scholar]
- Pardridge W. M. Blood–brain barrier delivery. Drug Discov. Today 2007, 12, 54–61. 10.1016/j.drudis.2006.10.013. [DOI] [PubMed] [Google Scholar]
- Pardridge W. M. Drug and gene targeting to the brain with molecular Trojan horses. Nat. Rev. Drug Discov. 2002, 1, 131. 10.1038/nrd725. [DOI] [PubMed] [Google Scholar]
- Di L.; Rong H.; Feng B. Demystifying brain penetration in central nervous system drug discovery. Miniperspective. J. Med. Chem. 2013, 56, 2–12. 10.1021/jm301297f. [DOI] [PubMed] [Google Scholar]
- Wong A.; Ye M.; Levy A.; Rothstein J.; Bergles D.; Searson P. C. The blood-brain barrier: an engineering perspective. Front. Neuroeng. 2013, 6, 7. 10.3389/fneng.2013.00007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lipinski C. A. Rule of five in 2015 and beyond: Target and ligand structural limitations, ligand chemistry structure and drug discovery project decisions. Adv. Drug Delivery Rev. 2016, 101, 34–41. 10.1016/j.addr.2016.04.029. [DOI] [PubMed] [Google Scholar]
- Wager T. T.; Hou X.; Verhoest P. R.; Villalobos A. Moving beyond rules: the development of a central nervous system multiparameter optimization (CNS MPO) approach to enable alignment of druglike properties. ACS Chem. Neurosci. 2010, 1, 435–449. 10.1021/cn100008c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bickerton G. R.; Paolini G. V.; Besnard J.; Muresan S.; Hopkins A. L. Quantifying the chemical beauty of drugs. Nat. Chem. 2012, 4, 90–98. 10.1038/nchem.1243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martins I. F.; Teixeira A. L.; Pinheiro L.; Falcao A. O. A Bayesian approach to in silico blood-brain barrier penetration modeling. J. Chem. Inf. Model. 2012, 52, 1686–1697. 10.1021/ci300124c. [DOI] [PubMed] [Google Scholar]
- Liu X.; Tu M.; Kelly R. S.; Chen C.; Smith B. J. Development of a computational approach to predict blood-brain barrier permeability. Drug Metab. Dispos. 2004, 32, 132–9. 10.1124/dmd.32.1.132. [DOI] [PubMed] [Google Scholar]
- Leeson P. D.; St-Gallay S. A. The influence of the ’organizational factor’ on compound quality in drug discovery. Nat. Rev. Drug Discov. 2011, 10, 749–765. 10.1038/nrd3552. [DOI] [PubMed] [Google Scholar]
- Cecchelli R.; Berezowski V.; Lundquist S.; Culot M.; Renftel M.; Dehouck M.-P.; Fenart L. Modelling of the blood–brain barrier in drug discovery and development. Nat. Rev. Drug Discov. 2007, 6, 650. 10.1038/nrd2368. [DOI] [PubMed] [Google Scholar]
- Smith Q. R.Brain Perfusion Systems for Studies of Drug Uptake and Metabolism in the Central Nervous System. In Models for Assessing Drug Absorption and Metabolism; Springer, 1996; pp 285–307. [DOI] [PubMed] [Google Scholar]
- Hammarlund-Udenaes M.; Friden M.; Syvanen S.; Gupta A. On the rate and extent of drug delivery to the brain. Pharm. Res. 2008, 25, 1737–50. 10.1007/s11095-007-9502-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Summerfield S. G.; Read K.; Begley D. J.; Obradovic T.; Hidalgo I. J.; Coggon S.; Lewis A. V.; Porter R. A.; Jeffrey P. Central nervous system drug disposition: the relationship between in situ brain permeability and brain free fraction. J. Pharmacol. Exp. Ther. 2007, 322, 205–213. 10.1124/jpet.107.121525. [DOI] [PubMed] [Google Scholar]
- Menichetti R.; Kanekal K. H.; Bereau T. Drug-Membrane Permeability across Chemical Space. ACS Cent. Sci. 2019, 5, 290–298. 10.1021/acscentsci.8b00718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gumbart J. C.; Ulmschneider M. B.; Hazel A.; White S. H.; Ulmschneider J. P. Computed free energies of peptide insertion into bilayers are independent of computational method. J. Membr. Biol. 2018, 251, 345–356. 10.1007/s00232-018-0026-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y.; Gallagher E.; Jorgensen C.; Troendle E. P.; Hu D.; Searson P. C.; Ulmschneider M. B. An experimentally validated approach to calculate the blood-brain barrier permeability of small molecules. Sci. Rep. 2019, 9, 6117 10.1038/s41598-019-42272-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Badaoui M.; Kells A.; Molteni C.; Dickson C. J.; Hornak V.; Rosta E. Calculating Kinetic Rates and Membrane Permeability from Biased Simulations. J. Phys. Chem. B 2018, 122, 11571–11578. 10.1021/acs.jpcb.8b07442. [DOI] [PubMed] [Google Scholar]
- Dickson C. J.; Hornak V.; Bednarczyk D.; Duca J. S. Using membrane partitioning simulations to predict permeability of forty-nine drug-like molecules. J. Chem. Inf. Model. 2019, 59, 236–244. 10.1021/acs.jcim.8b00744. [DOI] [PubMed] [Google Scholar]
- Lee C. T.; Comer J.; Herndon C.; Leung N.; Pavlova A.; Swift R. V.; Tung C.; Rowley C. N.; Amaro R. E.; Chipot C.; et al. Simulation-based approaches for determining membrane permeability of small compounds. J. Chem. Inf. Model. 2016, 56, 721–733. 10.1021/acs.jcim.6b00022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bennion B. J.; Be N. A.; McNerney M. W.; Lao V.; Carlson E. M.; Valdez C. A.; Malfatti M. A.; Enright H. A.; Nguyen T. H.; Lightstone F. C.; et al. Predicting a drug’s membrane permeability: a computational model validated with in vitro permeability assay data. J. Phys. Chem. B 2017, 121, 5228–5237. 10.1021/acs.jpcb.7b02914. [DOI] [PubMed] [Google Scholar]
- Lindqvist A.; Fridén M.; Hammarlund-Udenaes M. Pharmacokinetic considerations of nanodelivery to the brain: Using modeling and simulations to predict the outcome of liposomal formulations. Eur. J. Pharm. Sci. 2016, 92, 173–182. 10.1016/j.ejps.2016.07.003. [DOI] [PubMed] [Google Scholar]
- Brocke S. A.; Degen A.; MacKerell A. D. Jr; Dutagaci B.; Feig M. Prediction of Membrane Permeation of Drug Molecules by Combining an Implicit Membrane Model with Machine Learning. J. Chem. Inf. Model. 2019, 59, 1147–1162. 10.1021/acs.jcim.8b00648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marsh D., CRC Handbook of Lipid Bilayers, 1990.
- Spector A. A.; Hoak J. C.; Fry G. L.; Denning G. M.; Stoll L.; Smith J. Effect of fatty acid modification on prostacyclin production by cultured human endothelial cells. J. Clinic. Invest. 1980, 65, 1003–1012. 10.1172/JCI109752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spector A. A.; Yorek M. A. Membrane lipid composition and cellular function. J. Lipid Res. 1985, 26, 1015–1035. 10.1016/S0022-2275(20)34276-0. [DOI] [PubMed] [Google Scholar]
- Tewes B.; Galla H.-J. Lipid polarity in brain capillary endothelial cells. Endothelium 2001, 8, 207–220. 10.1080/10623320109051566. [DOI] [PubMed] [Google Scholar]
- Pan W.; Kastin A. J. Changing the chemokine gradient: CINC1 crosses the blood–brain barrier. J. Neuroimmunol. 2001, 115, 64–70. 10.1016/S0165-5728(01)00256-9. [DOI] [PubMed] [Google Scholar]
- Banks W. A.; Kastin A. J.; Coy D. H. Delta sleep-inducing peptide crosses the blood-brain-barrier in dogs: Some correlations with protein binding. Pharmacol., Biochem. Behav. 1982, 17, 1009–1014. 10.1016/0091-3057(82)90486-5. [DOI] [PubMed] [Google Scholar]
- Egleton R. D.; Mitchell S. A.; Huber J. D.; Janders J.; Stropova D.; Polt R.; Yamamura H. I.; Hruby V. J.; Davis T. P. Improved bioavailability to the brain of glycosylated Met-enkephalin analogs. Brain Res. 2000, 881, 37–46. 10.1016/S0006-8993(00)02794-3. [DOI] [PubMed] [Google Scholar]
- Brahm J. Diffusional water permeability of human erythrocytes and their ghosts. J. Gen. Physiol. 1982, 79, 791–819. 10.1085/jgp.79.5.791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tse C.-H.; Comer J.; Sang Chu S. K.; Wang Y.; Chipot C. Affordable membrane permeability calculations: Permeation of short-chain alcohols through pure-lipid bilayers and a mammalian cell membrane. J. Chem. Theory Comput. 2019, 15, 2913–2924. 10.1021/acs.jctc.9b00022. [DOI] [PubMed] [Google Scholar]
- Avdeef A. The rise of PAMPA. Expert Opin. Drug Metab. Toxicol. 2005, 1, 325–342. 10.1517/17425255.1.2.325. [DOI] [PubMed] [Google Scholar]
- Kutuzov N.; Flyvbjerg H.; Lauritzen M. Contributions of the glycocalyx, endothelium, and extravascular compartment to the blood–brain barrier. Proc. Natl. Acad. Sci. U.S.A. 2018, 115, E9429–E9438. 10.1073/pnas.1802155115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avdeef A.Absorption and Drug Development: Solubility, Permeability, and Charge State.; John Wiley & Sons, 2012. [Google Scholar]
- Van Der Spoel D.; Lindahl E.; Hess B.; Groenhof G.; Mark A. E.; Berendsen H. J. GROMACS: fast, flexible, and free. J. Comput. Chem. 2005, 26, 1701–18. 10.1002/jcc.20291. [DOI] [PubMed] [Google Scholar]
- Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
- Brooks B. R.; Brooks C. L. 3rd; Mackerell A. D. Jr.; Nilsson L.; Petrella R. J.; Roux B.; Won Y.; Archontis G.; Bartels C.; Boresch S.; Caflisch A.; Caves L.; Cui Q.; Dinner A. R.; Feig M.; Fischer S.; Gao J.; Hodoscek M.; Im W.; Kuczera K.; Lazaridis T.; Ma J.; Ovchinnikov V.; Paci E.; Pastor R. W.; Post C. B.; Pu J. Z.; Schaefer M.; Tidor B.; Venable R. M.; Woodcock H. L.; Wu X.; Yang W.; York D. M.; Karplus M. CHARMM: the biomolecular simulation program. J. Comput. Chem. 2009, 30, 1545–1614. 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darden T.; York D.; Pedersen L. Particle Mesh Ewald - an N.Log(N) Method for Ewald Sums in Large Systems. J. Chem. Phys. 1993, 98, 10089–10092. 10.1063/1.464397. [DOI] [Google Scholar]
- Hess B. P-LINCS: A Parallel Linear Constraint Solver for Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 116–122. 10.1021/ct700200b. [DOI] [PubMed] [Google Scholar]
- Bussi G.; Donadio D.; Parrinello M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
- Parrinello M.; Rahman A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. App. Phys. 1981, 52, 7182–7190. 10.1063/1.328693. [DOI] [Google Scholar]
- Vanommeslaeghe K.; MacKerell A. D. Jr. Automation of the CHARMM General Force Field (CGenFF) I: bond perception and atom typing. J. Chem. Inf. Model. 2012, 52, 3144–3154. 10.1021/ci300363c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vanommeslaeghe K.; Raman E. P.; MacKerell A. D. Jr. Automation of the CHARMM General Force Field (CGenFF) II: assignment of bonded parameters and partial atomic charges. J. Chem. Inf. Model. 2012, 52, 3155–3168. 10.1021/ci3003649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghosh J.; Marru S.; Singh N.; Vanomesslaeghe K.; Fan Y.; Pamidighantam S.. Molecular Parameter Optimization Gateway (ParamChem): Workflow Management through TeraGrid ASTA, Proceedings of the 2011 TeraGrid Conference: Extreme Digital Discovery, 2011.
- Martínez L.; Andrade R.; Birgin E. G.; Martínez J. M. PACKMOL: a package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. 10.1002/jcc.21224. [DOI] [PubMed] [Google Scholar]
- Venable R. M.; Krämer A.; Pastor R. W. Molecular dynamics simulations of membrane permeability. Chem. Rev. 2019, 119, 5954–5997. 10.1021/acs.chemrev.8b00486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen M. P.; Tildesley D. J.. Computer Simulations of Liquids; Clarendon Press, 1987. [Google Scholar]
- Hummer G. Position-dependent diffusion coefficients and free energies from Bayesian analysis of equilibrium and replica molecular dynamics simulations. New J. Phys. 2005, 7, 34 10.1088/1367-2630/7/1/034. [DOI] [Google Scholar]
- Comer J.; Chipot C.; Gonzalez-Nilo F. D. Calculating Position-Dependent Diffusivity in Biased Molecular Dynamics Simulations. J. Chem. Theory Comput. 2013, 9, 876–882. 10.1021/ct300867e. [DOI] [PubMed] [Google Scholar]
- Ghaemi Z.; Minozzi M.; Carloni P.; Laio A. A novel approach to the investigation of passive molecular permeation through lipid bilayers from atomistic simulations. J. Phys. Chem. B 2012, 116, 8714–8721. 10.1021/jp301083h. [DOI] [PubMed] [Google Scholar]
- Abdi H.; Williams L. J. Tukey’s honestly significant difference (HSD) test. Encycl. Res. Des. 2010, 3, 583–585. 10.4135/9781412961288.n478. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.